Numerical Investigation on Backward-Injection Film Cooling with Upstream Ramps
Abstract
:1. Introduction
2. Description of Research Procedures
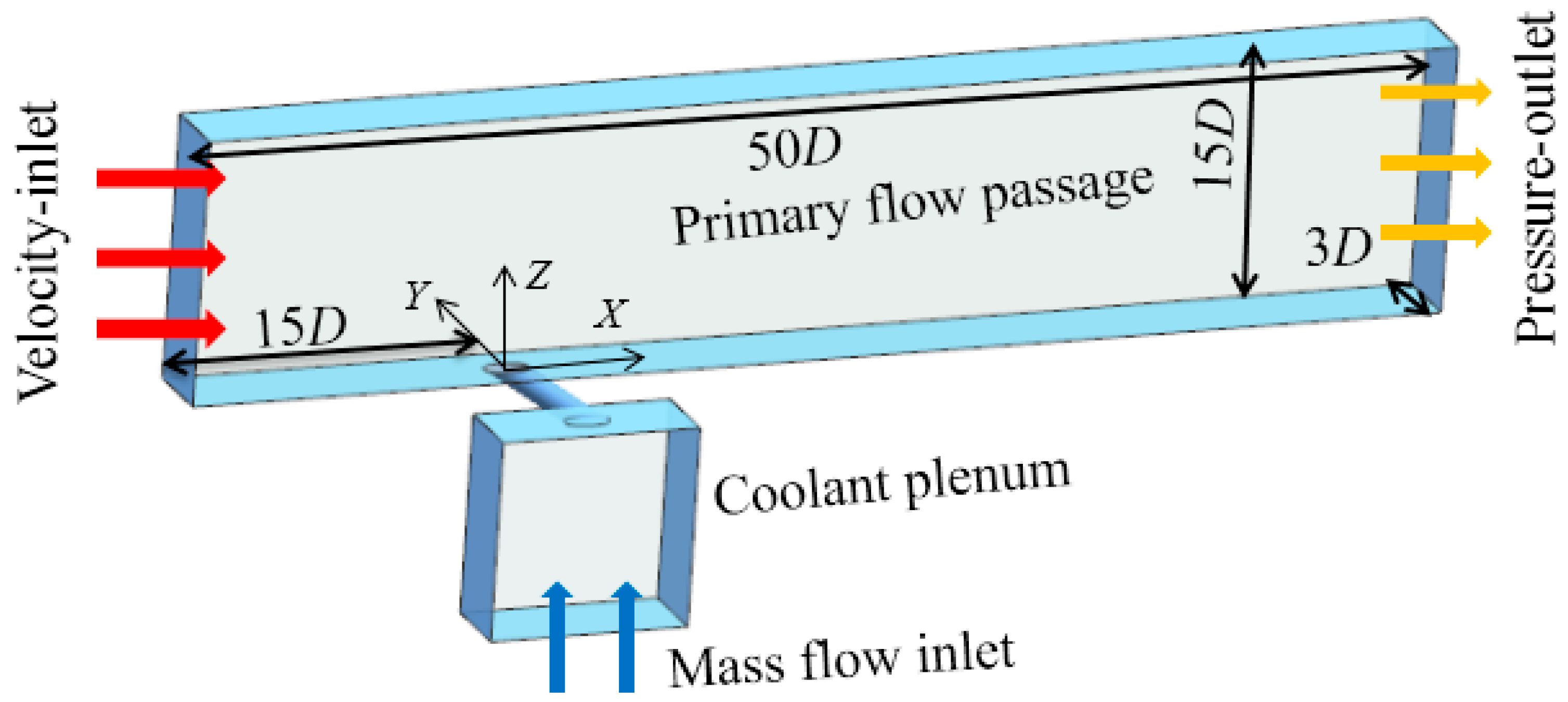
2.1. Computational Model
2.2. Boundary Conditions
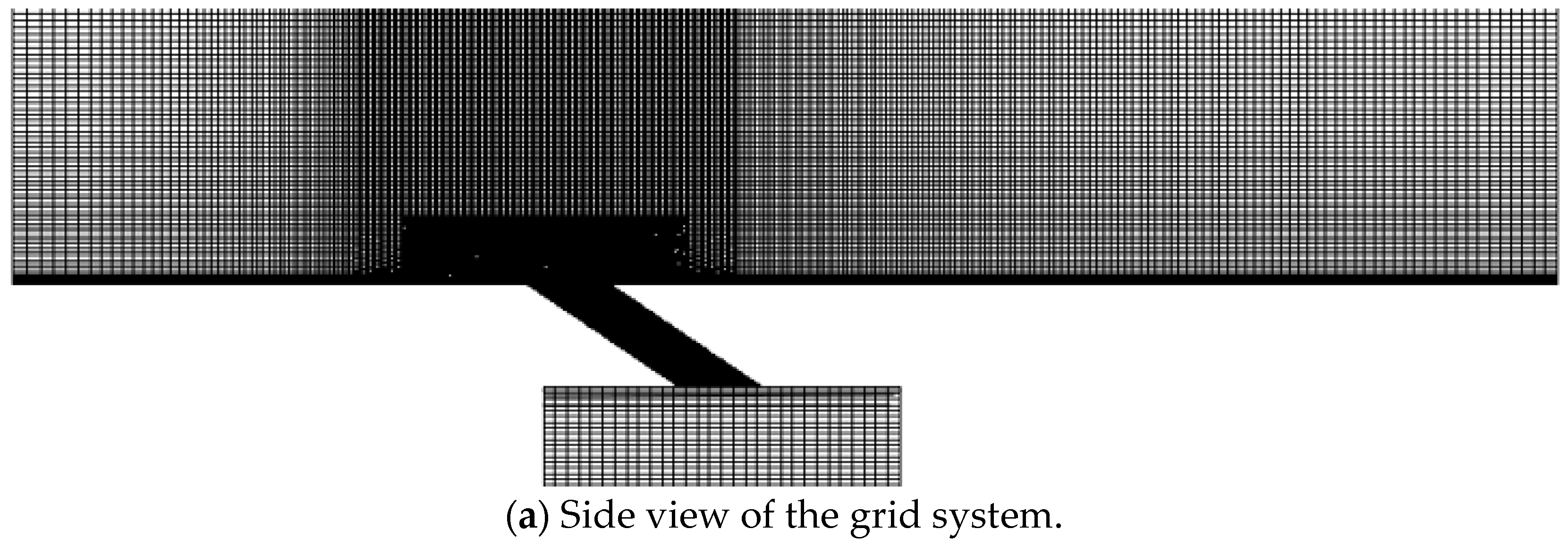
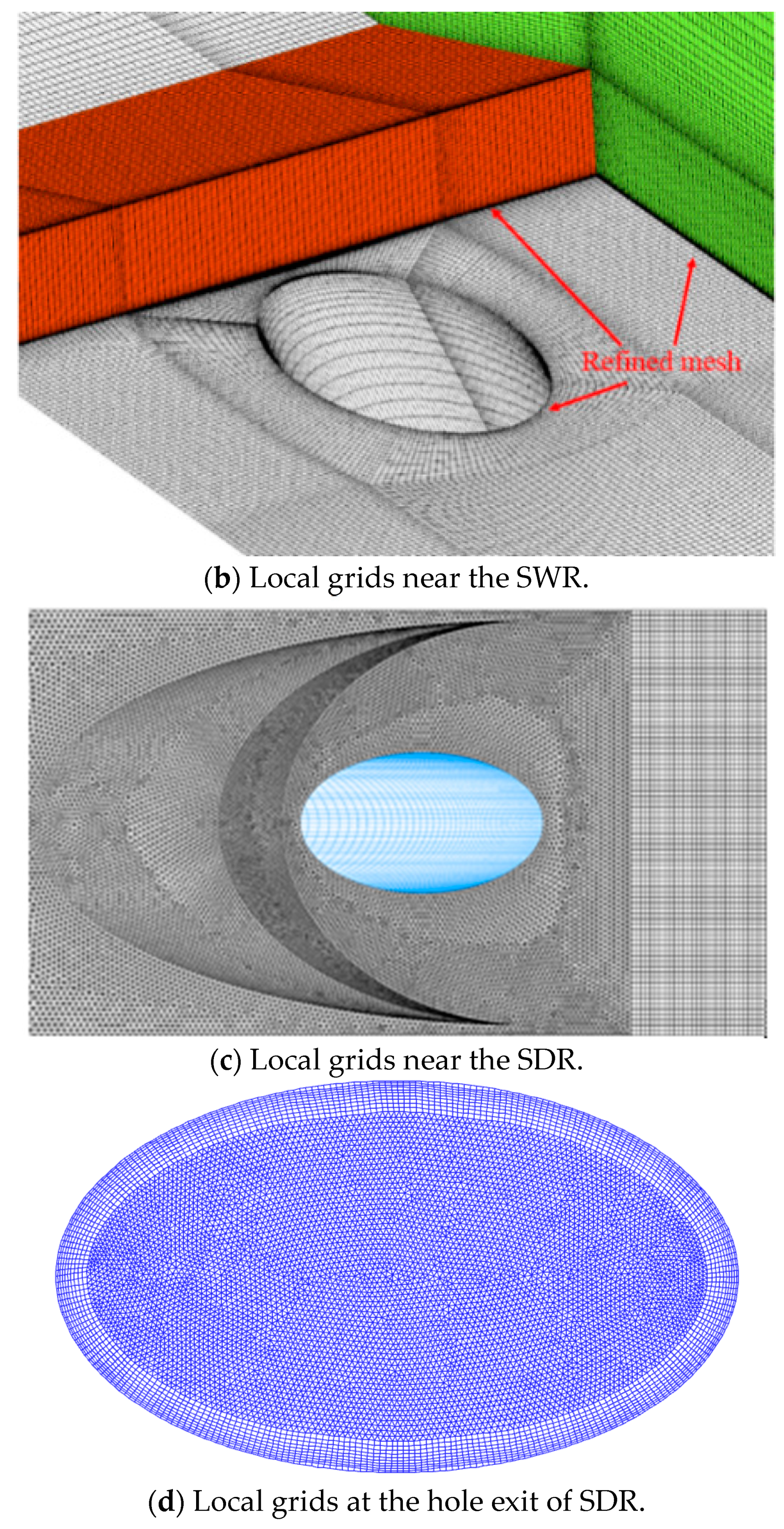
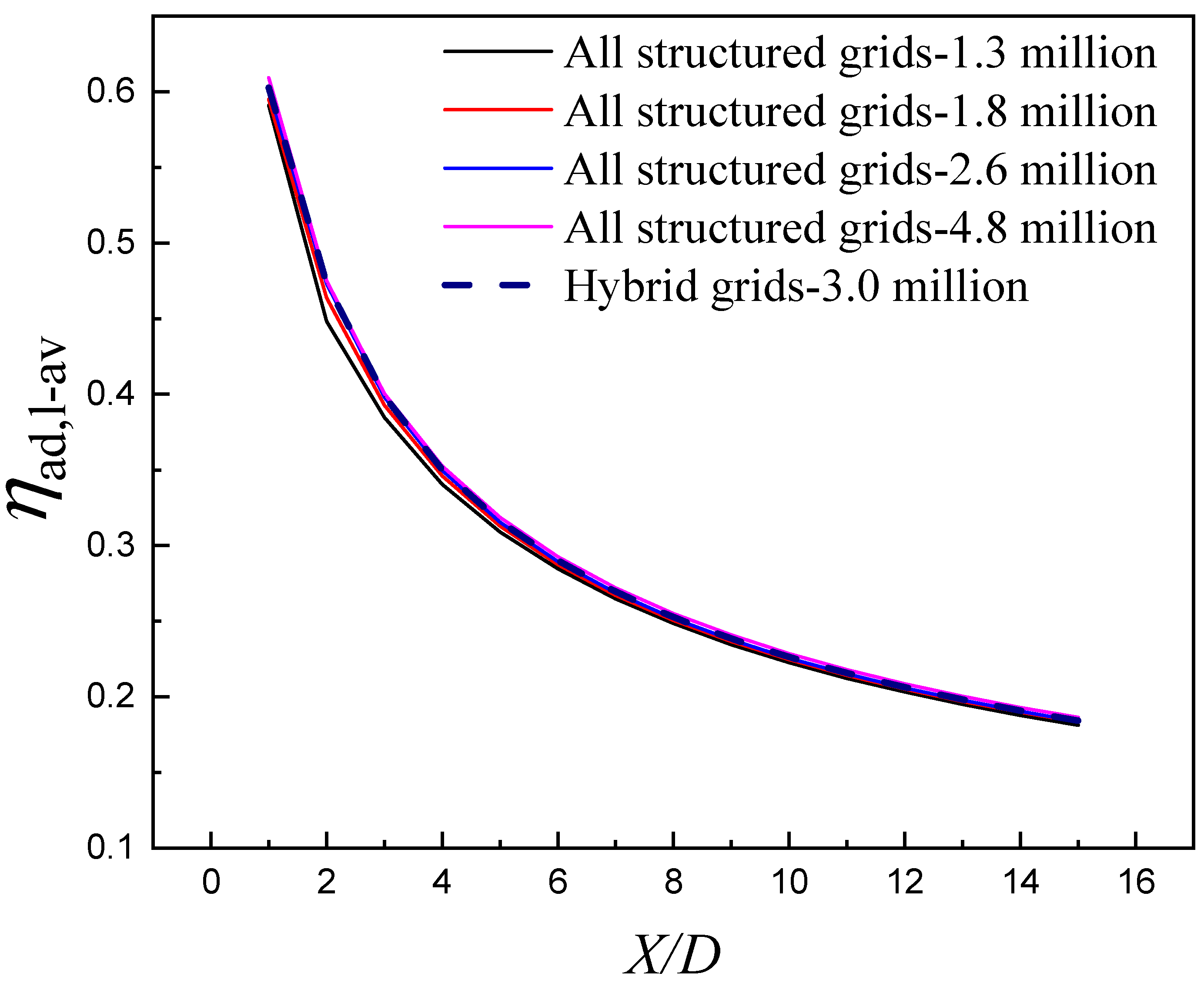
2.3. Computational Scheme
3. Results and Discussions
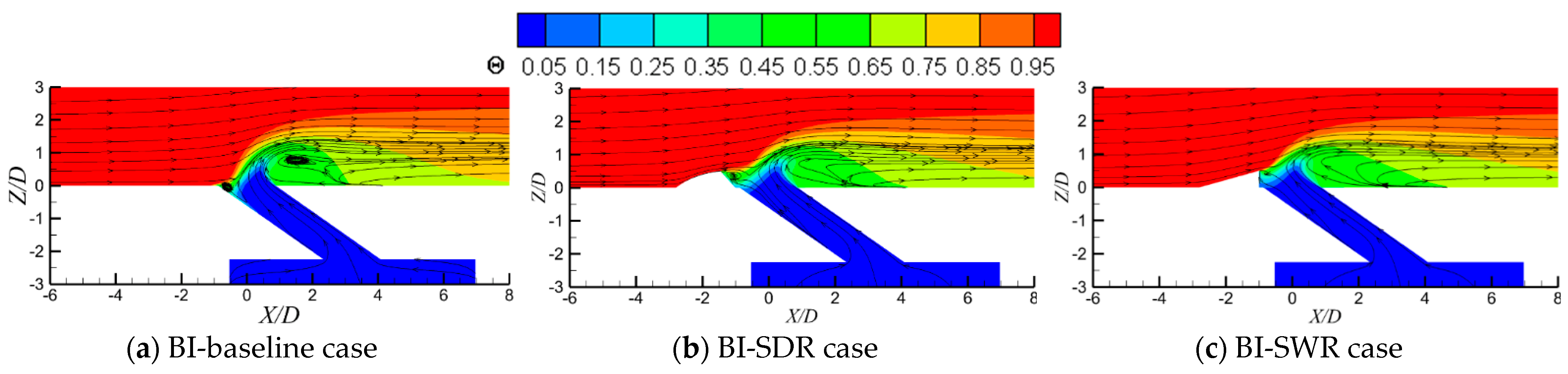
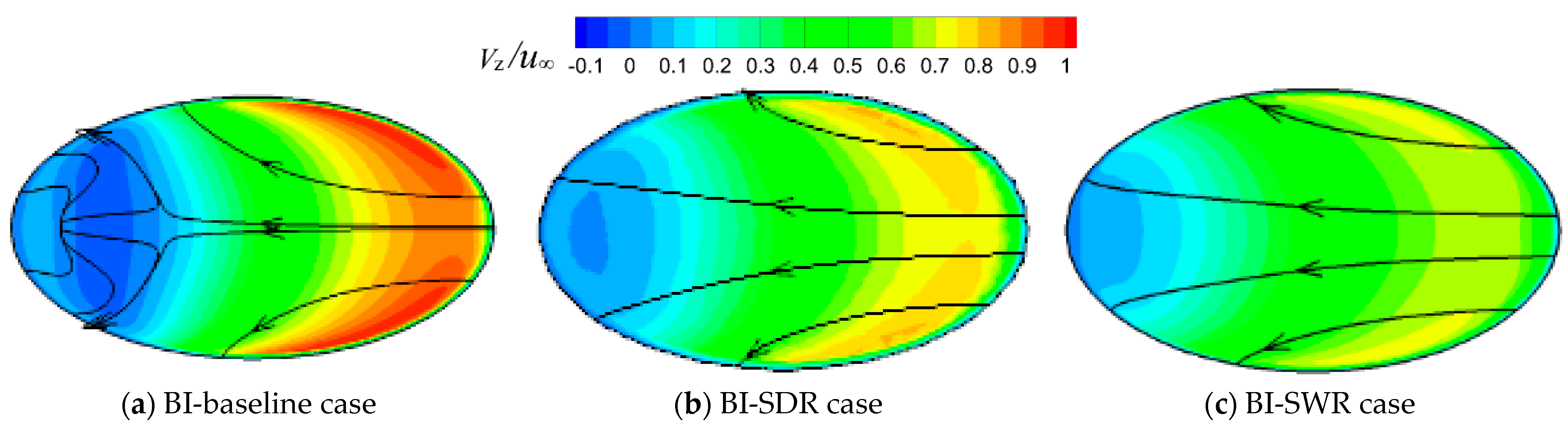
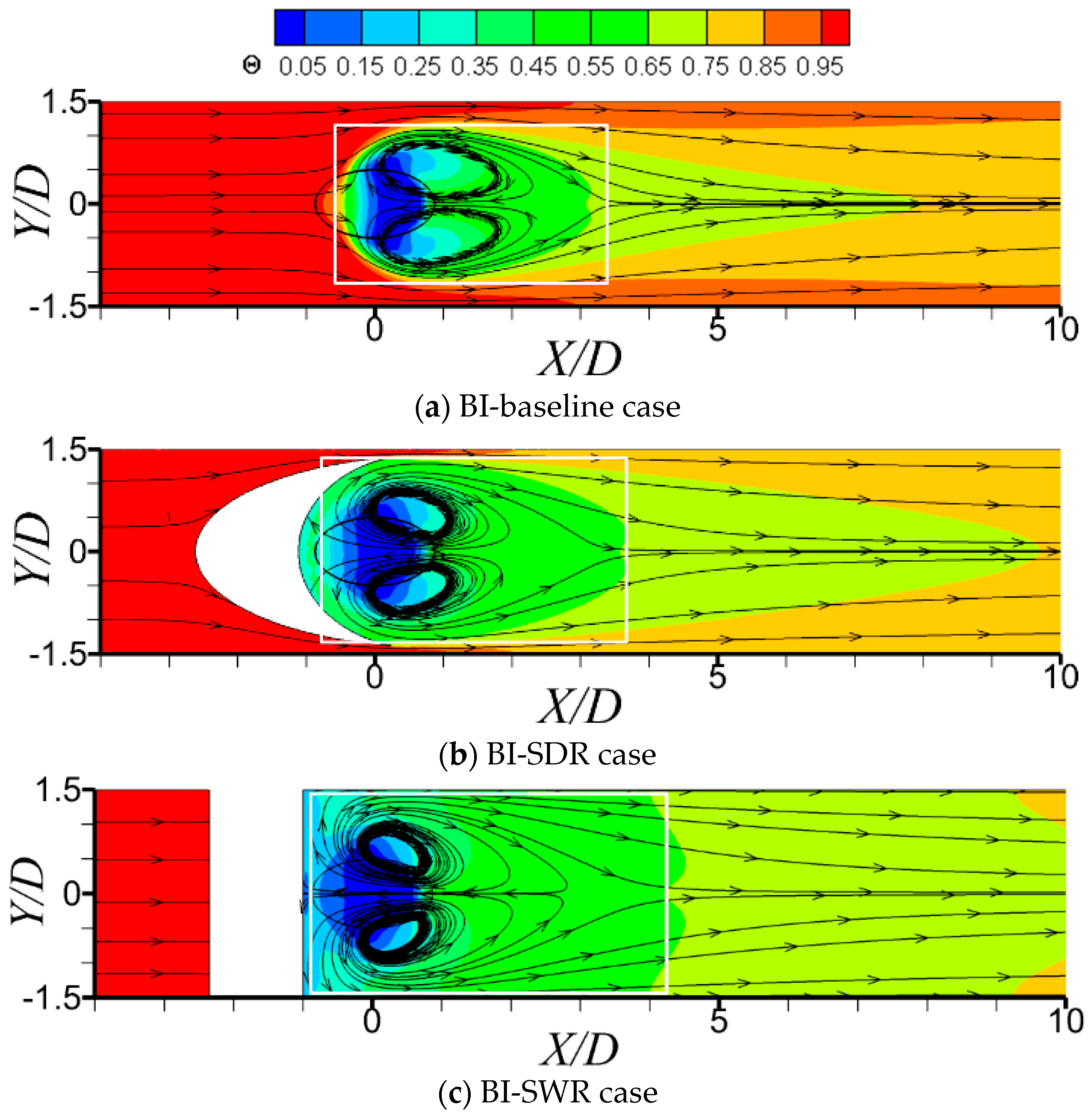
3.1. Fundamental Dynamics of Jet-in-Crossflow
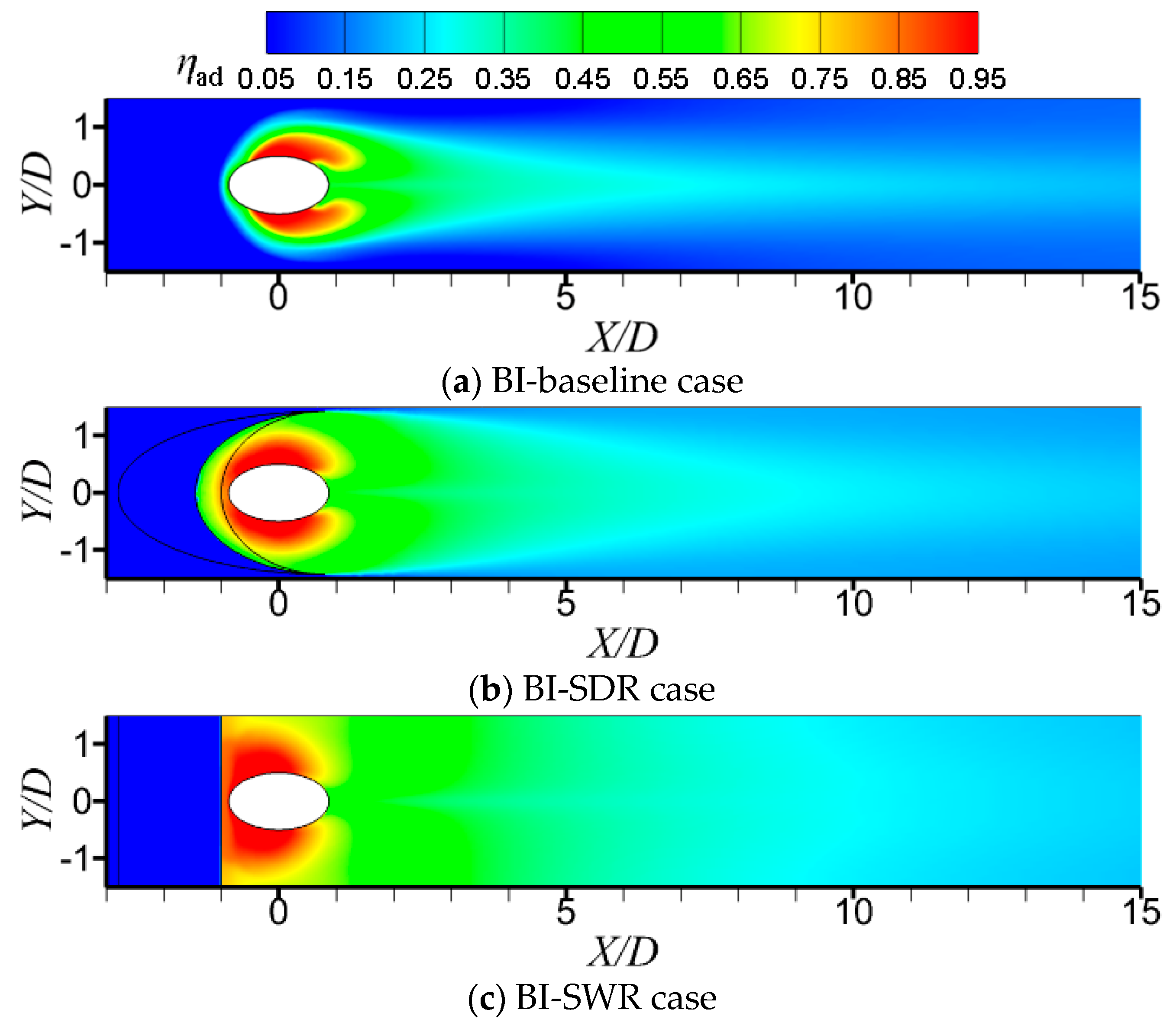
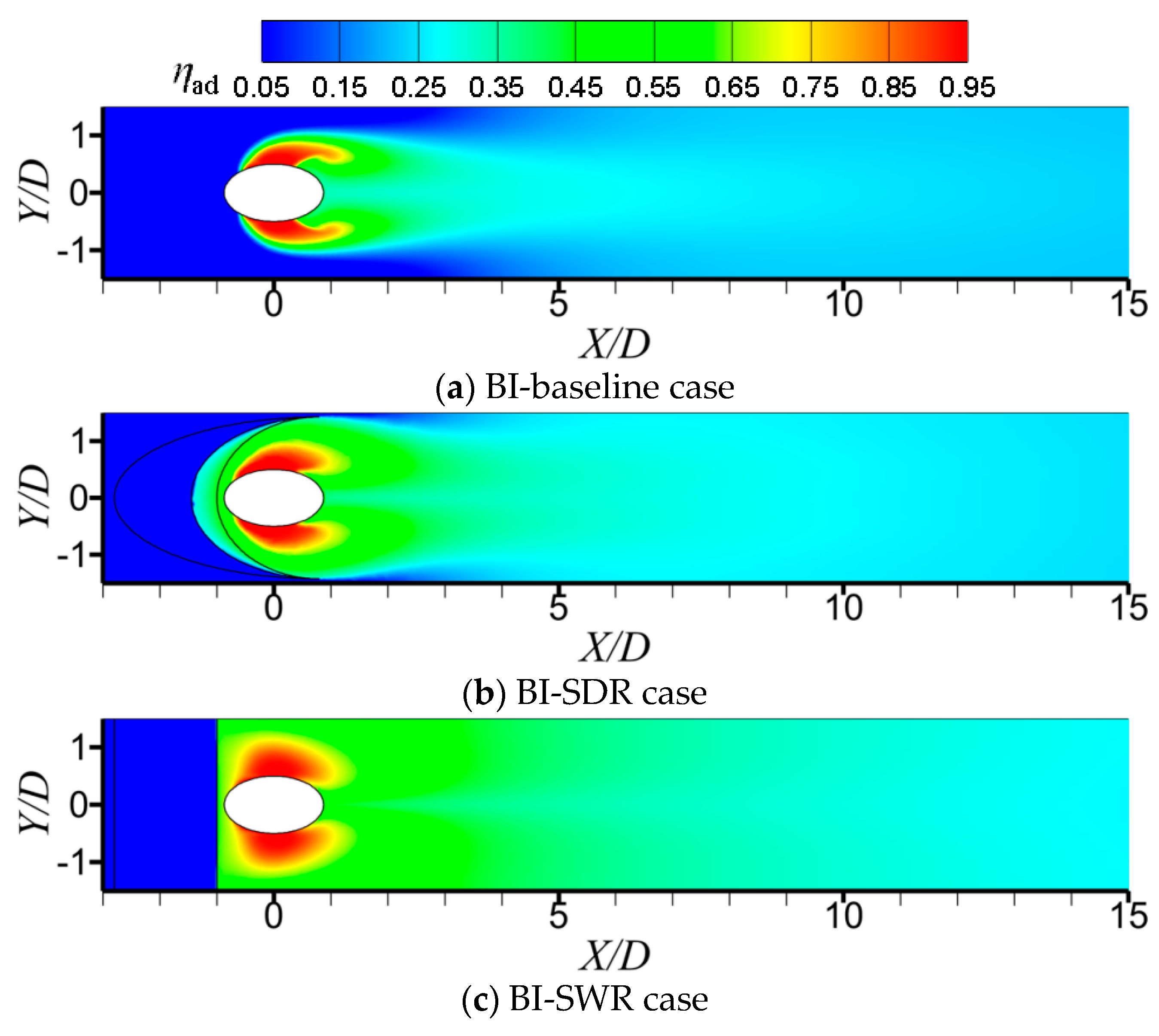
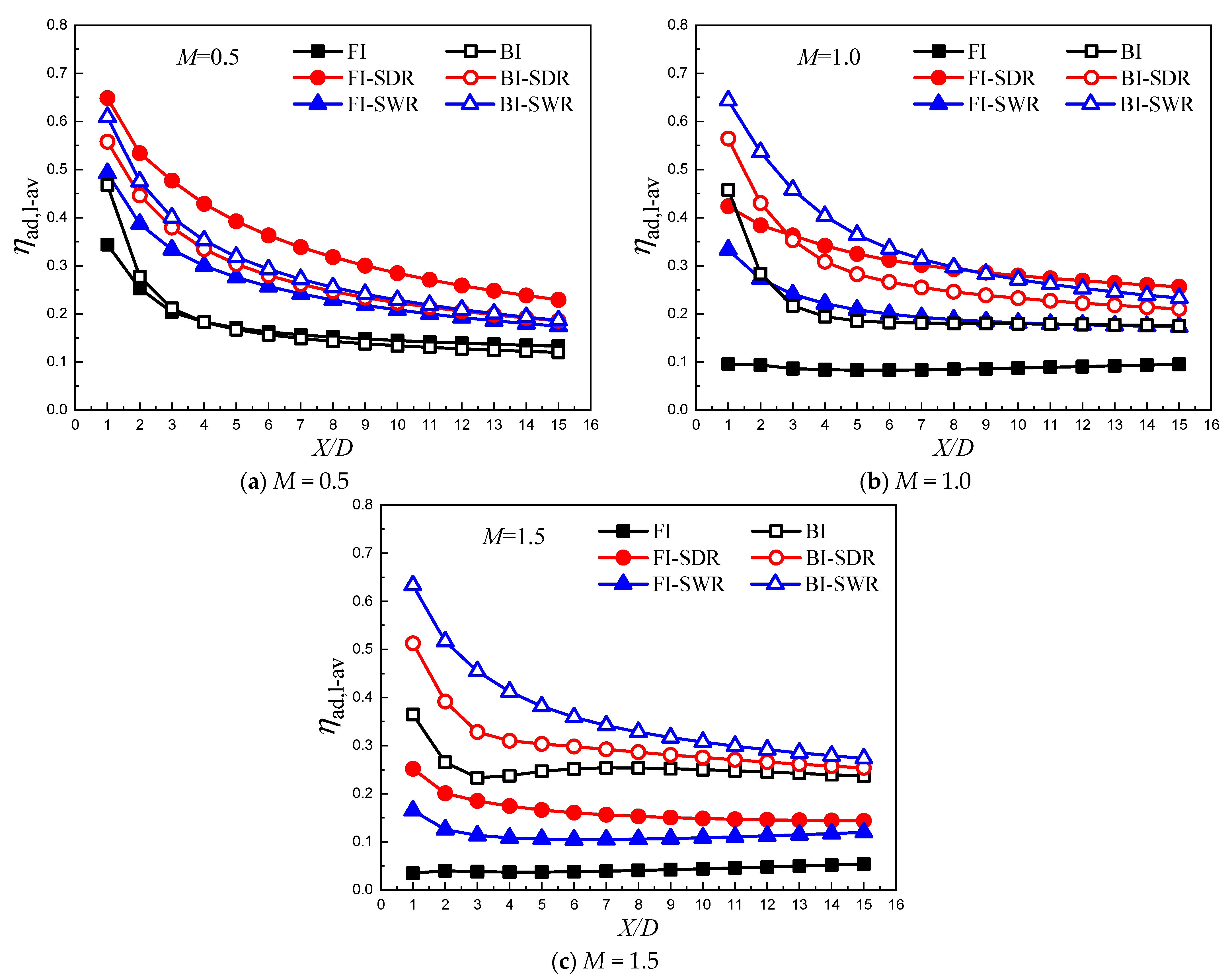
3.2. Adiabatic Film Cooling Effectiveness Distributions
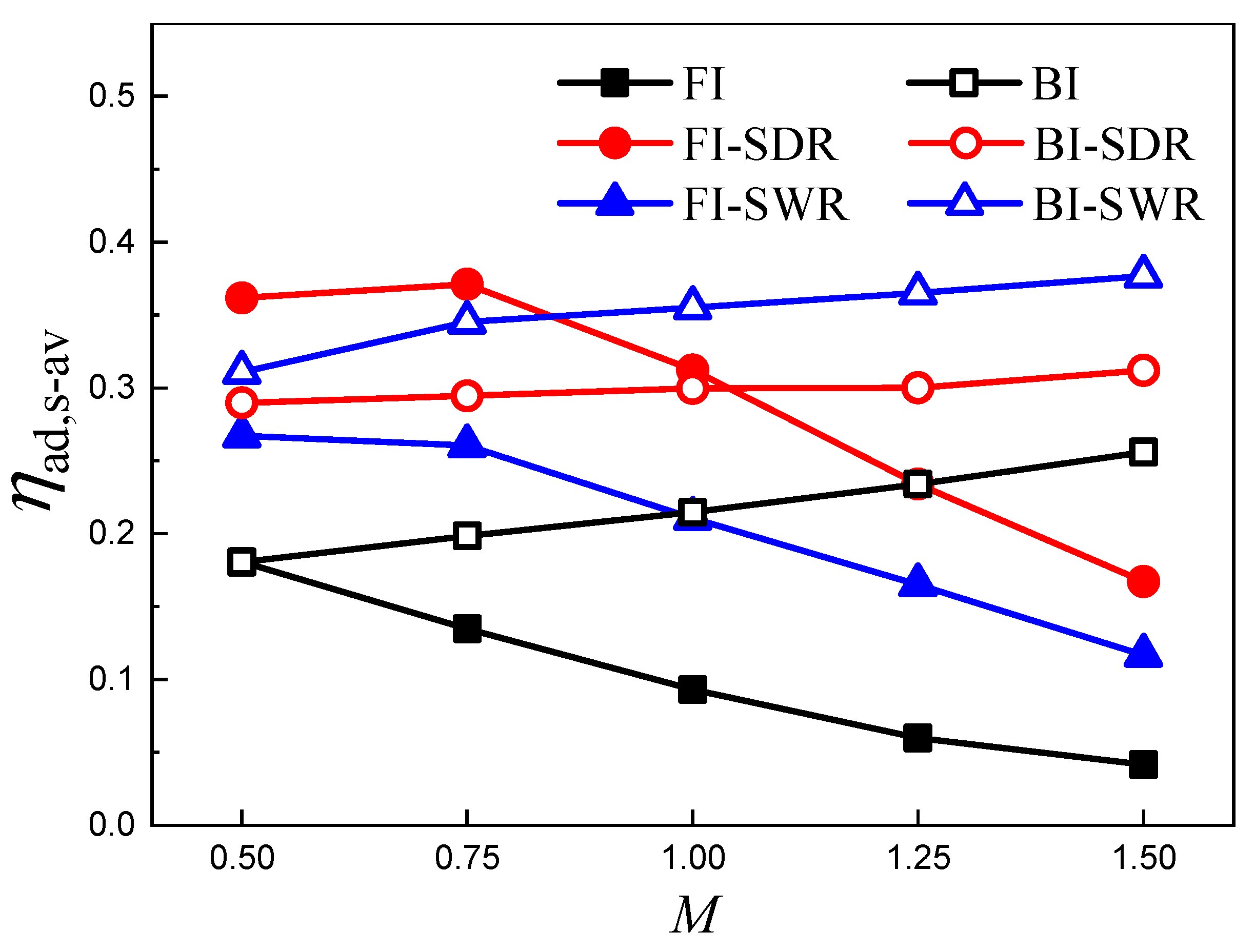
3.3. Different Roles of Upstream Ramps on Film Cooling Enhancement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Cp | dimensionless pressure coefficient |
| D | film hole diameter (mm) |
| DR | density ratio |
| H | film hole height (mm) |
| Hr | ramp height (mm) |
| L1 | distance between central slope edge of SDR and film-hole center (mm) |
| L2 | distance between rear step of SWR and film-hole center (mm) |
| Lf | front-body length of SDR (mm) |
| Lm | middle-body length of SDR (mm) |
| Lr | ramp length (mm) |
| M | blowing ratio |
| P | hole-to-hole pitch (mm) |
| p | pressure (Pa) |
| Re | Reynolds number |
| T | temperature (K) |
| Tu | turbulence intensity level |
| u | velocity (m/s) |
| W | horn-spacing of SDR (mm) |
| X | x-direction, streamwise distance (mm) |
| Y | y-direction, normal distance (mm) |
| Z | z-direction, spanwise distance (mm) |
| Greek Letters | |
| α | inclination angle of film hole (°) |
| ηad | adiabatic film cooling effectiveness |
| ρ | density (kg/m3) |
| Θ | dimensionless temperature |
| Subscripts | |
| aw | relative to adiabatic wall |
| c | relative to coolant |
| l-av | laterally averaged |
| s-av | spatially averaged |
| w | relative to wall |
| ∞ | relative to primary flow |
References
- Acharya, S.; Kanani, Y. Advances in film cooling heat transfer. Adv. Heat Transfer 2017, 49, 91–156. [Google Scholar]
- Zhang, J.Z.; Zhang, S.C.; Wang, C.H.; Tan, X.M. Recent Advances in Film Cooling Enhancement: A Review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Aga, V.; Rose, M.; Abhari, R.S. Experimental Flow Structure Investigation of Compound Angled Film Cooling. ASME J. Turbomach. 2008, 130, 031005. [Google Scholar] [CrossRef]
- Kannan, E.; Sivamani, S.; Roychowdhury, D.G.; Prekumar, T.M.; Hariam, V. Improvement in Film Cooling Effectiveness Using Single and Double Rows of Holes with Adverse Compound Angle Orientations. ASME J. Therm. Sci. Eng. Appl. 2019, 11, 021014. [Google Scholar] [CrossRef]
- Baek, S.I.; Ahn, J. Large Eddy Simulation of Film Cooling Involving Compound Angle Hole with Bulk Flow Pulsation. Energies 2021, 14, 7659. [Google Scholar] [CrossRef]
- Bunker, R.S. A Review of Turbine Shaped Film Cooling Technology. ASME J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Kim, S.M.; Lee, K.D.; Kim, K.Y. A comparative analysis of various shaped film-cooling holes. Heat Mass Transf. 2012, 48, 1929–1939. [Google Scholar] [CrossRef]
- Lee, S.I.; Jung, J.Y.; Song, Y.J.; Kwak, J.S. Effect of Mainstream Velocity on the Optimization of a Fan-Shaped Film-Cooling Hole on a Flat Plate. Energies 2021, 14, 3573. [Google Scholar] [CrossRef]
- Baek, S.I.; Ryu, J.; Ahn, J. Large Eddy Simulation of Film Cooling with Forward Expansion Hole: Comparative Study with LES and RANS Simulations. Energies 2021, 14, 2063. [Google Scholar] [CrossRef]
- Bunker, R.S. Film Cooling: Breaking the Limits of Diffusion Shaped Holes. Heat Transf. Res. 2010, 41, 627–650. [Google Scholar] [CrossRef]
- Lee, K.D.; Kim, W.Y. Film Cooling Performance of Cylindrical Holes Embedded in a Transverse Trench. Num. Heat Transf. A 2014, 65, 127–143. [Google Scholar] [CrossRef]
- Song, Y.J.; Park, S.H.; Kang, Y.J.; Kwak, J.S. Effects of Configuration on Film Cooling Effectiveness of a Fan-Shaped Hole. Int. J. Heat Mass Transf. 2021, 178, 121655. [Google Scholar] [CrossRef]
- Na, S.; Shih, T.I.-P. Increasing Adiabatic Film-cooling Effectiveness by Using an Upstream Ramp. ASME J. Heat Transf. 2007, 129, 464–471. [Google Scholar] [CrossRef]
- Barigozzi, G.; Franchini, G.; Perdichizzi, A. The Effect of an Upstream Ramp on Cylindrical and Fan-Shaped Hole Film Cooling: Part I-Aerodynamic Results. In Proceedings of the ASME Turbo Expo 2007, GT2007-27077, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Barigozzi, G.; Franchini, G.; Perdichizzi, A. The Effect of an Upstream Ramp on Cylindrical and Fan-Shaped Hole Film Cooling: Part II-Adiabatic Effectiveness Results. In Proceedings of the ASME Turbo Expo 2007, GT2007-27079, Montreal, QC, Canada, 14–17 May 2007. [Google Scholar]
- Chen, S.P.; Chyu, M.K.; Shih, T.I.-P. Effects of Upstream Ramp on the Performance of Film Cooling. Int. J. Therm. Sci. 2011, 50, 1085–1094. [Google Scholar] [CrossRef]
- Rallabandi, A.P.; Grizzle, J.; Han, J.C. Effect of Upstream Step on Flat Plate Film Cooling Effectiveness Using PSP. ASME J. Turbomach. 2011, 133, 041024. [Google Scholar] [CrossRef]
- Abdala, A.M.; Elwekeel, F.N. An Influence of Novel Upstream Steps on Film Cooling Performance. Int. J. Heat Mass Transf. 2016, 93, 86–96. [Google Scholar] [CrossRef]
- Abdala, A.M.; Elwekeel, F.N.; Huang, D. Film Cooling Effectiveness and Flow Structures for Novel Upstream Steps. Appl. Therm. Eng. 2016, 105, 397–410. [Google Scholar] [CrossRef]
- Hammami, Z.; Dellil, Z.A.; Nemdili, F.; Azzi, A. Improving Adiabatic Film-Cooling Effectiveness by Using an Upstream Pyramid. Comput. Therm. Sci. 2016, 8, 135–146. [Google Scholar]
- Zhang, F.; Wang, X.; Li, J. The Effects of Upstream Steps with Unevenly Spanwise Distributed Height on Rectangular Hole Film Cooling Performance. Int. J. Heat Mass Transf. 2016, 102, 1209–1221. [Google Scholar] [CrossRef]
- Zhou, W.; Hu, H. Improvements of Film Cooling Effectiveness by Using Barchan Dune Shaped Ramps. Int. J. Heat Mass Transf. 2016, 103, 443–456. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Hu, H. A Novel Sand-Dune-Inspired Design for Improved Film Cooling Performance. Int. J. Heat Mass Transf. 2017, 110, 908–920. [Google Scholar] [CrossRef] [Green Version]
- Zhou, W.; Peng, D.; Wen, X.; Liu, Y.Z.; Hu, H. Unsteady Analysis of Adiabatic Film Cooling Effectiveness behind Circular, Shaped, and Sand-Dune-Inspired Film Cooling Holes: Measurement Using Fast-Response Pressure-Sensitive Paint. Int. J. Heat Mass Transf. 2018, 125, 1003–1016. [Google Scholar] [CrossRef]
- Zhang, S.C.; Zhang, J.Z.; Tan, X.M. Numerical Investigation of Film Cooling Enhancement Using an Upstream Sand-Dune-Shaped Ramp. Computation 2018, 6, 49. [Google Scholar] [CrossRef] [Green Version]
- Zhang, S.C.; Zhang, J.Z.; Tan, X.M. Film Cooling Enhancement by Using Upstream Sand-Dune-Shaped Ramp. J. Aerosp. Power 2020, 35, 973–982. [Google Scholar]
- Zhang, S.C.; Zhang, J.Z.; Wang, C.H.; Tan, X.M. Improvement on Shaped-Hole Film Cooling Effectiveness by Integrating Upstream Sand-Dune-Shaped Ramps. J. Aeronaut. 2021, 34, 42–55. [Google Scholar] [CrossRef]
- Li, X.C.; Subbuswamy, G.; Zhou, J. Performance of Gas Turbine Film Cooling with Backward Injection. Energy Power Eng. 2013, 5, 132–137. [Google Scholar] [CrossRef]
- Subbuswamy, G.; Li, X.C.; Gharat, K. Numerical Simulation of Backward Film Cooling with Fan-Shaped Holes. In Proceedings of the ASME 2013 Heat Transfer Summer Conference, HT2013-17801, Minneapolis, MN, USA, 14–19 July 2013. [Google Scholar]
- Subbuswamy, G.; Li, X.C.; Gharat, K. Numerical Study of Aerodynamic Performance of Film Cooling with Backward Injection Holes. In Proceedings of the ASME 2013 Heat Transfer Summer Conference, HT2013-17803, Minneapolis, MN, USA, 14–19 July 2013. [Google Scholar]
- Park, S.; Jung, E.Y.; Kim, S.H.; Sohn, H.S.; Cho, H.H. Enhancement of Film Cooling Effectiveness Using Backward Injection Holes. Int. J. Therm. Sci. 2016, 110, 314–324. [Google Scholar] [CrossRef]
- Singh, K.; Premachandran, B.; Ravi, M.R. Experimental and Numerical Studies on Film Cooling with Reverse/Backward Coolant Injection. Int. J. Therm. Sci. 2017, 111, 390–408. [Google Scholar] [CrossRef]
- Prenter, R.; Hossain, M.A.; Agricola, L.; Ameri, A.; Bons, J.P. Experimental Characterization of Reverse-Oriented Film Cooling. In Proceedings of the ASME Turbo Expo 2017, GT2017-64731, Charlotte, NC, USA, 26–30 June 2017. [Google Scholar]
- Wang, J.; Liu, C.; Zhao, Z.M.; Baleta, J.; Sunden, B. Effect and Optimization of Backward Hole Parameters on Film Cooling Performance by Taguchi Method. Energy Convers. Manag. 2020, 214, 112809. [Google Scholar] [CrossRef]
- Chen, A.F.; Li, S.J.; Han, J.C. Film Cooling with Forward and Backward Injection for Cylindrical and Fan-Shaped Holes Using PSP Measurement Technique. In Proceedings of the ASME Turbo Expo 2014, GT2014-26232, Dusseldorf, Germany, 16–20 June 2014. [Google Scholar]
- Li, S.J.; Chen, A.F.; Wang, W.; Han, J.C. Experimental and Computational Film Cooling with Backward Injection for Cylindrical and Fan-Shaped Holes. Proceedings of 15th International Heat Transfer Conference 2014, IHTC-15, Kyoto, Japan, 15 August 2014. [Google Scholar]
- Zhao, Z.C.; He, L.M.; Dai, S.J.; Shao, S. Computational Research on Film Cooling Performance of Different Shaped Holes with Backward and Forward Injection. AIP Adv. 2019, 9, 055009. [Google Scholar] [CrossRef] [Green Version]
- Jeong, Y.S.; Park, J.S. Effect of Inlet Compound Angle of Backward Injection Film Cooling Hole. Energies 2020, 13, 808. [Google Scholar] [CrossRef] [Green Version]
- Singh, A.K.; Singh, K.; Singh, D.; Sahoo, M. Large Eddy Simulations for Film Cooling Assessment of Cylindrical and Laidback Fan-Shaped Holes with Reverse Injection. ASME J. Therm. Sci. Eng. Appl. 2021, 13, 031027. [Google Scholar] [CrossRef]
- Zheng, D.R.; Wang, X.J.; Yuan, Q. Numerical Investigation on the Effect of Upstream Ramps on Film Cooling Performance with Backward Injection. Microsyst. Technol. 2019, 25, 3559–3570. [Google Scholar] [CrossRef]
- Ali Kouchih, F.B.; Boualem, K.; Grine, M.; Abbes Azzi, A. The Effect of an Upstream Dune-Shaped Shells on Forward and Backward Injection Hole Film Cooling. ASME J. Heat Transf. 2020, 142, 122302. [Google Scholar] [CrossRef]
- Choi, Y.K.; Hwang, H.G.; Lee, Y.M.; Lee, J.H. Effects of the Roughness Height in Turbulent Boundary Layers over Rod- and Cuboid-Roughened Walls. Int. J. Heat Fluid Flow 2020, 85, 108644. [Google Scholar] [CrossRef]
- Mori, E.; Quadrio, M.; Fukagata, K. Turbulent Drag Reduction by Uniform Blowing over a Two-Dimensional Roughness. Flow turbul. Combust. 2017, 99, 765–785. [Google Scholar] [CrossRef]
- Hamed, A.M.; Nye, C.E.; Hall, A.J. Effects of Localized Blowing on the Turbulent Boundary Layer over 2D Roughness. Exp. Fluids 2021, 62, 1–13. [Google Scholar] [CrossRef]
- Djenidi, L. Kamruzzaman, M.; Dostal, L. Effects of Wall Suction on a 2D Rough Wall Turbulent Boundary Layer. Exp. Fluids 2019, 60, 43. [Google Scholar] [CrossRef]
- Ghanadi, F.; Djenidi, L. Reynolds Number Effect on the Response of a Rough Wall Turbulent Boundary Layer to Local Wall Suction. J. Fluid. Mech. 2021, 916, A25. [Google Scholar] [CrossRef]
- ANSYS Fluent 14.0 User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2012.
- Ely, M.J.; Jubran, B.A. A Numerical Evaluation on the Effect of Sister Holes on Film Cooling Effectiveness and the Surrounding Flow Filed. Heat Mass Transf. 2009, 45, 1435–1446. [Google Scholar] [CrossRef]
- Foroutan, H.; Yavuzkurt, S. Numerical Simulations of the Near-Field Region of Film Cooling Jets under High Free Stream Turbulence: Application of RANS and Hybrid URANS/Large Eddy Simulation Models. ASME J. Heat Transf. 2015, 137, 011701. [Google Scholar] [CrossRef]
- Zhu, R.; Simon, T.W.; Xie, G.N. Influence of secondary hole injection angle on enhancement of film cooling effectiveness with horn-shaped or cylindrical primary holes. Num. Heat Transf. Part A 2018, 74, 1207–1227. [Google Scholar] [CrossRef]
- Hang, J.; Zhang, J.; Wang, C.; Shan, Y. Numerical Investigation of Single-Row Double-Jet Film Cooling of a Turbine Guide Vane under High-Temperature and High-Pressure Conditions. Energies 2022, 15, 287. [Google Scholar] [CrossRef]






| Parameters | Symbol | Value |
|---|---|---|
| ramp height | Hr | 2.0 mm (0.5 D) |
| length of SDR | Lr | 14.4 mm (3.6 D) |
| front-wedge length of SDR | Lf | 5.4 mm (1.35 D) |
| middle-slope length of SDR | Lm | 1.8 mm (0.45 D) |
| horn-spacing of SDR | W | 11.4 mm (2.85 D) |
| hole-to-ramp distance | L1 | 4.0 mm (1.0 D) |
| Length of SWR | L2 | 7.2 mm (1.8 D) |
| Items | Boundary Conditions | |
|---|---|---|
| Primary flow at the inlet | Velocity, | u∞ = 25 m/s |
| Temperature, | T∞ = 360 K | |
| Turbulence intensity, | Tu = 2% | |
| Cooling air at plenum inlet | Blowing ratio, | M = 0.5~1.5 |
| Temperature, | Tc = 300 K | |
| Density ratio, | DR = 1.2 | |
| Mixing flow at the outlet | Static pressure, | pout = 101,325 Pa |
| Channel-top plane | Symmetry | |
| Channel-side planes | Periodic boundary condition | |
| Film-cooled surface | No-slip and adiabatic-thermal condition | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wang, C.; Tan, X.; Zhang, J.; Guo, J. Numerical Investigation on Backward-Injection Film Cooling with Upstream Ramps. Energies 2022, 15, 4415. https://doi.org/10.3390/en15124415
Zhang S, Wang C, Tan X, Zhang J, Guo J. Numerical Investigation on Backward-Injection Film Cooling with Upstream Ramps. Energies. 2022; 15(12):4415. https://doi.org/10.3390/en15124415
Chicago/Turabian StyleZhang, Shengchang, Chunhua Wang, Xiaoming Tan, Jingzhou Zhang, and Jiachen Guo. 2022. "Numerical Investigation on Backward-Injection Film Cooling with Upstream Ramps" Energies 15, no. 12: 4415. https://doi.org/10.3390/en15124415
APA StyleZhang, S., Wang, C., Tan, X., Zhang, J., & Guo, J. (2022). Numerical Investigation on Backward-Injection Film Cooling with Upstream Ramps. Energies, 15(12), 4415. https://doi.org/10.3390/en15124415







