A Novel Single-Phase Shunt Active Power Filter with a Cost Function Based Model Predictive Current Control Technique
Abstract
:1. Introduction
2. A Modeling and Control Algorithm
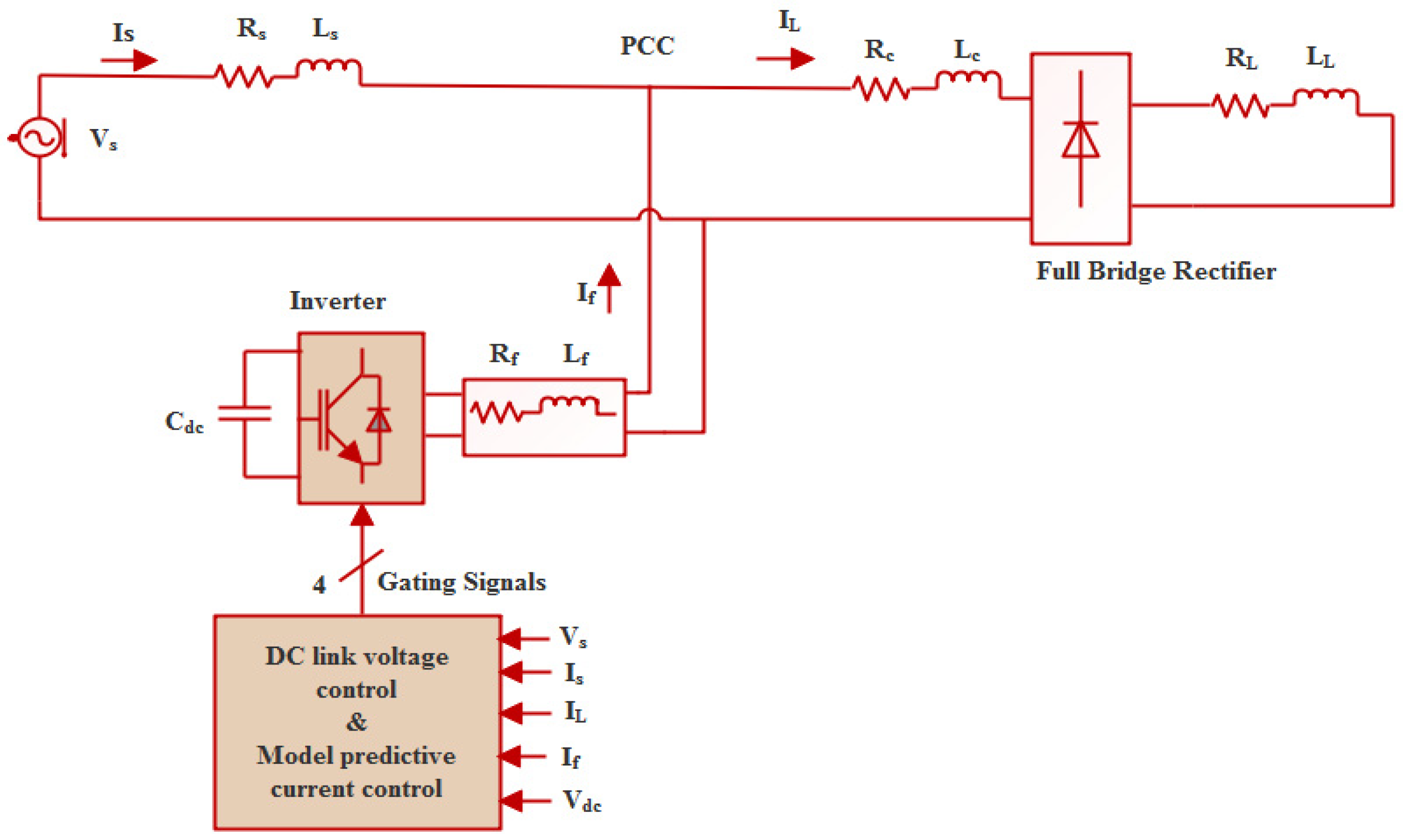
2.1. Single-Phase SAPF Description and Modeling
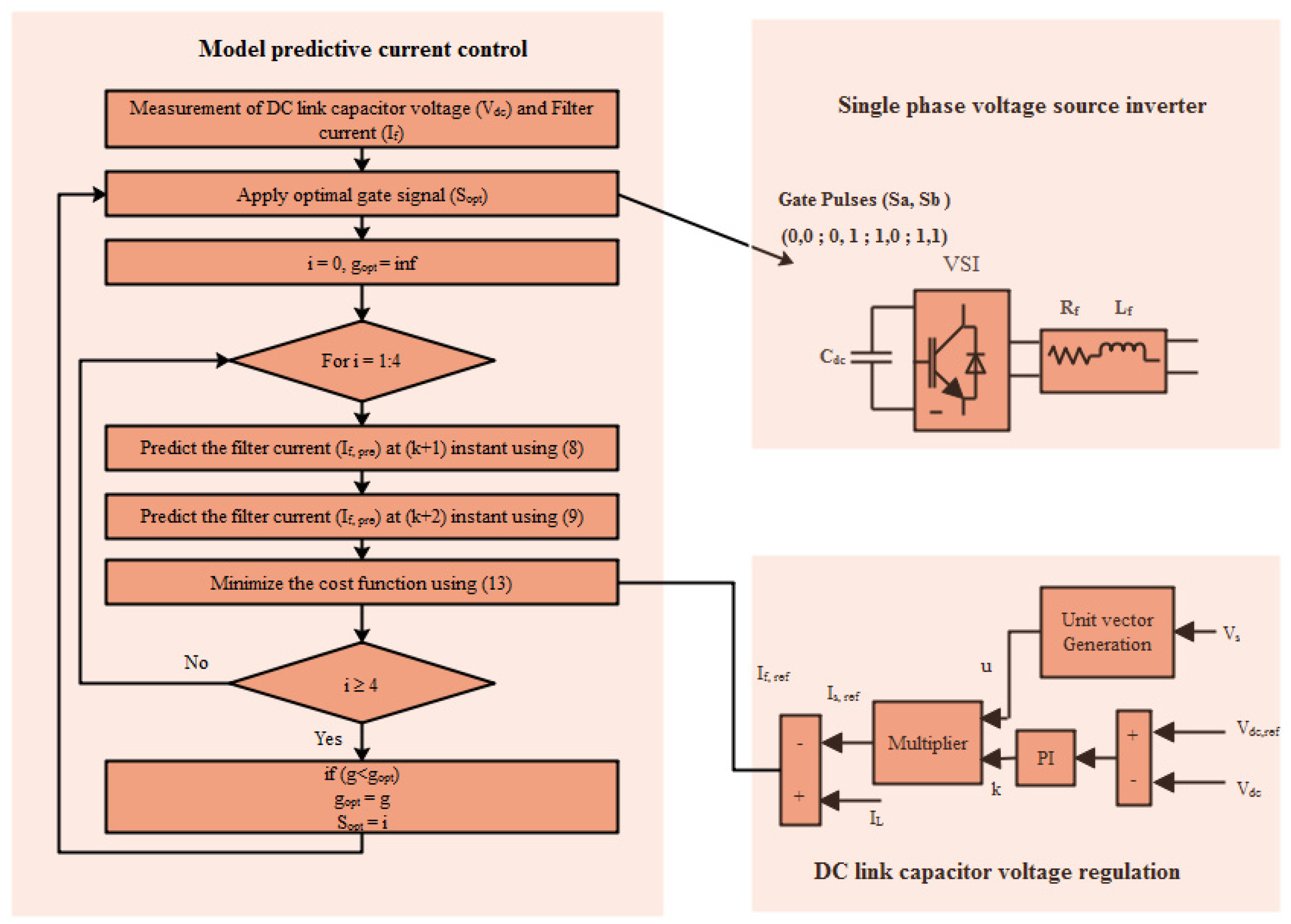
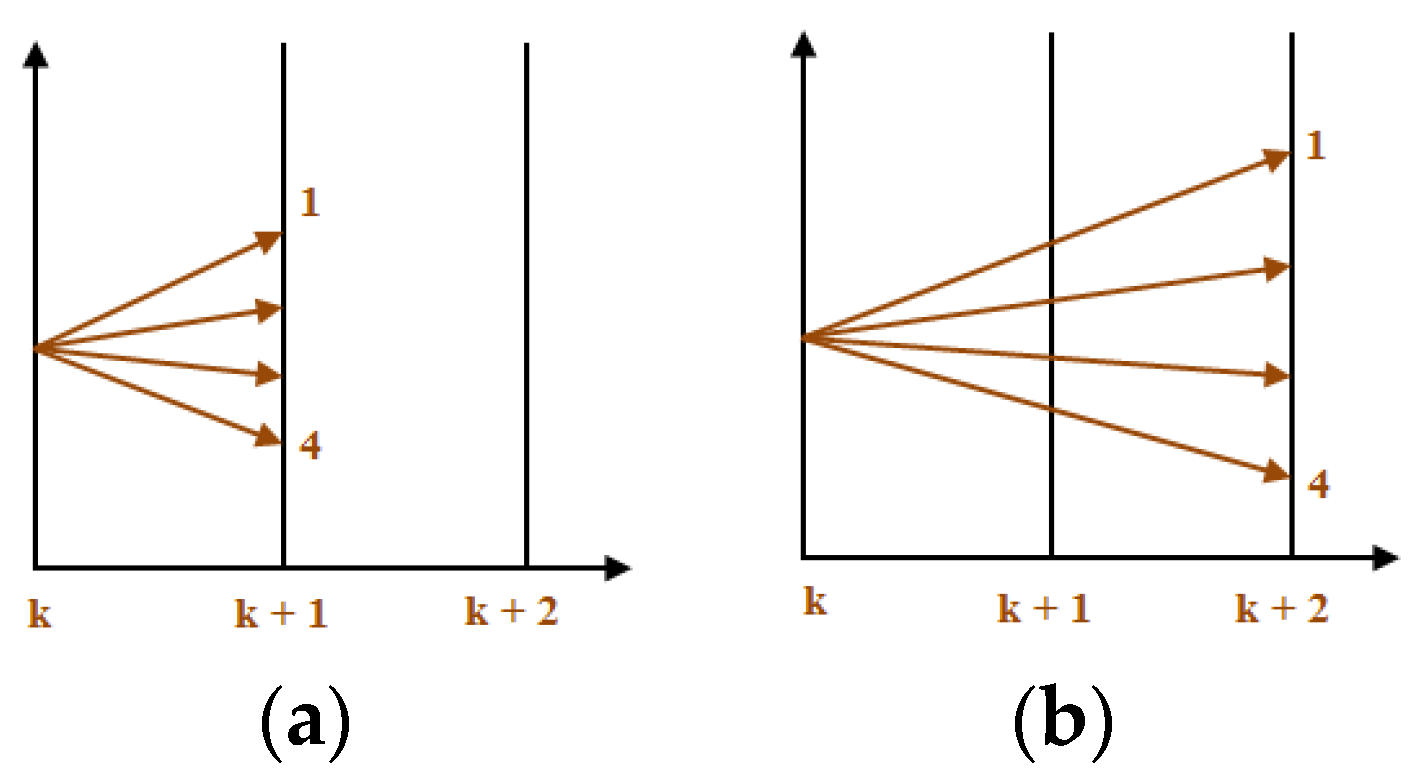
2.2. Model Predictive Current Control Algorithm
| Algorithm 1. Cost Function-Based Model Predictive Current Control Algorithm |
| ) Step 1: At the instant (k + 1) based on (8), predict the filter current Step 2: At the instant (k + 2) based on (9), predict the filter current Step 3: Calculate for all switching states based on (12) Step 4: Evaluate the cost function (g) based on (13) Step 5: Choose the ideal switching state and apply to the SAPF. Return to Step 1 |
2.3. DC-Link Capacitor Voltage Control PI Control Scheme
3. Simulation Results
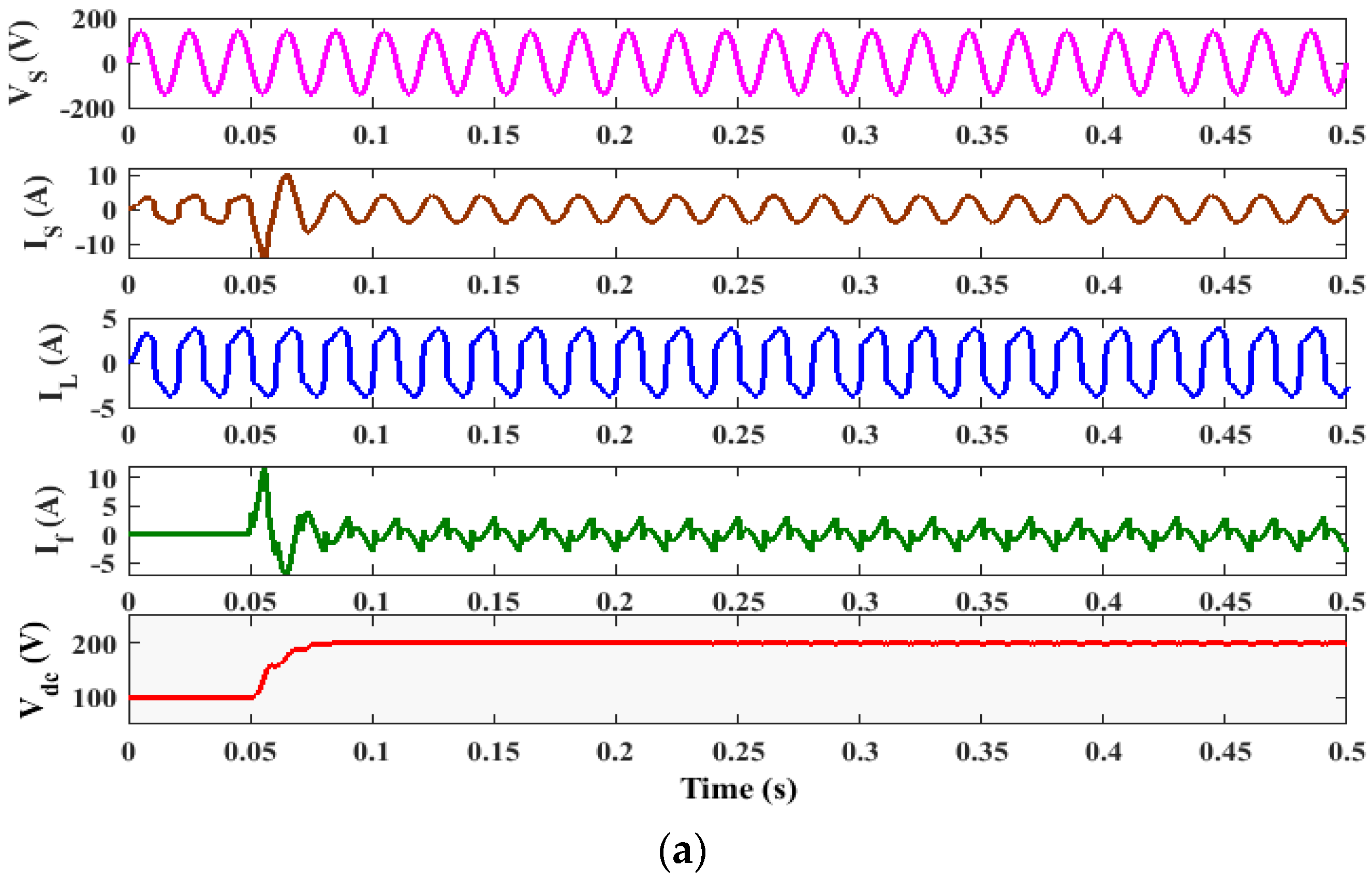
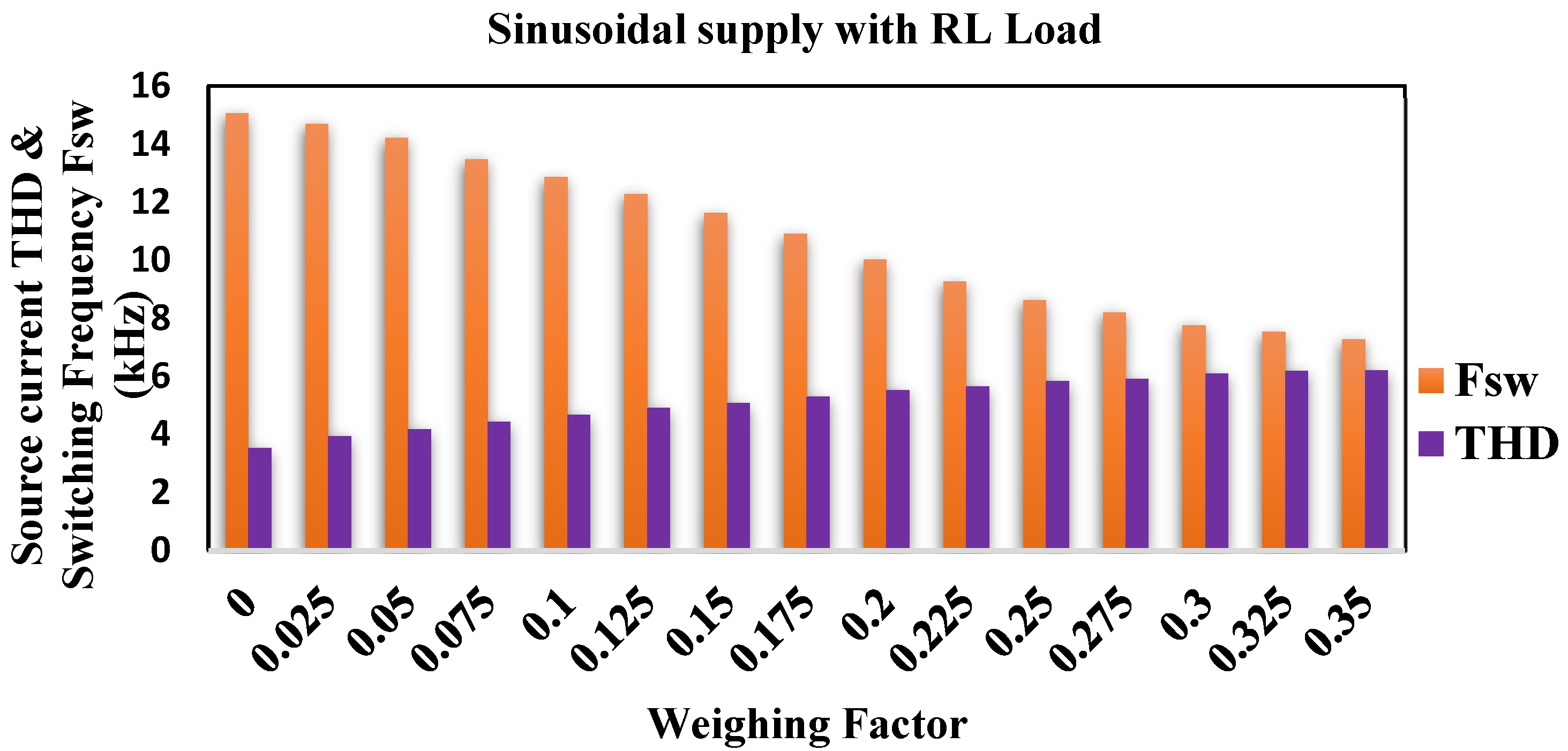
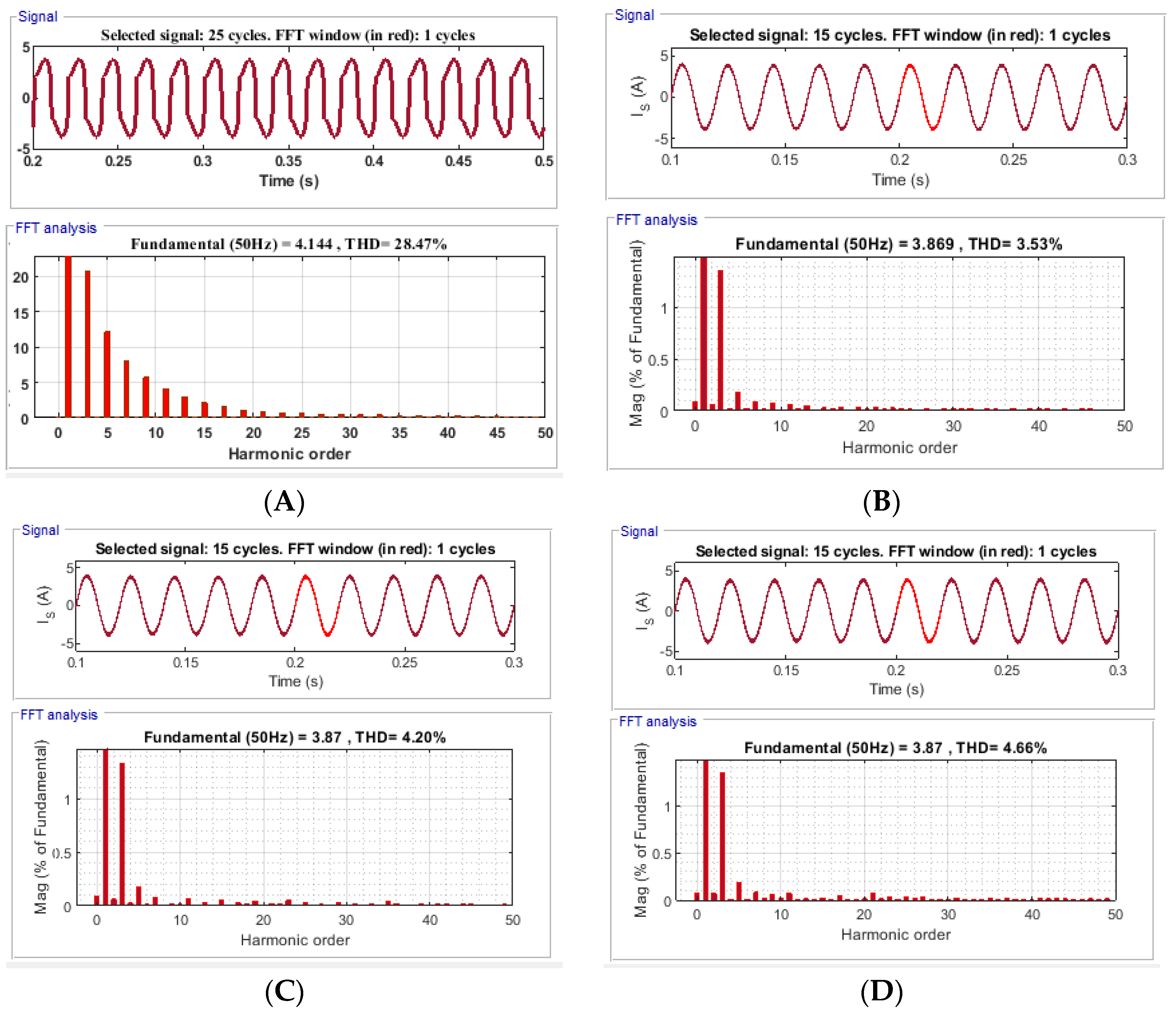
3.1. Performance Analysis with Resistive and Inductive (RL) Load Condition
3.2. Performance Analysis with Resistive and Capacitive (RC) Load
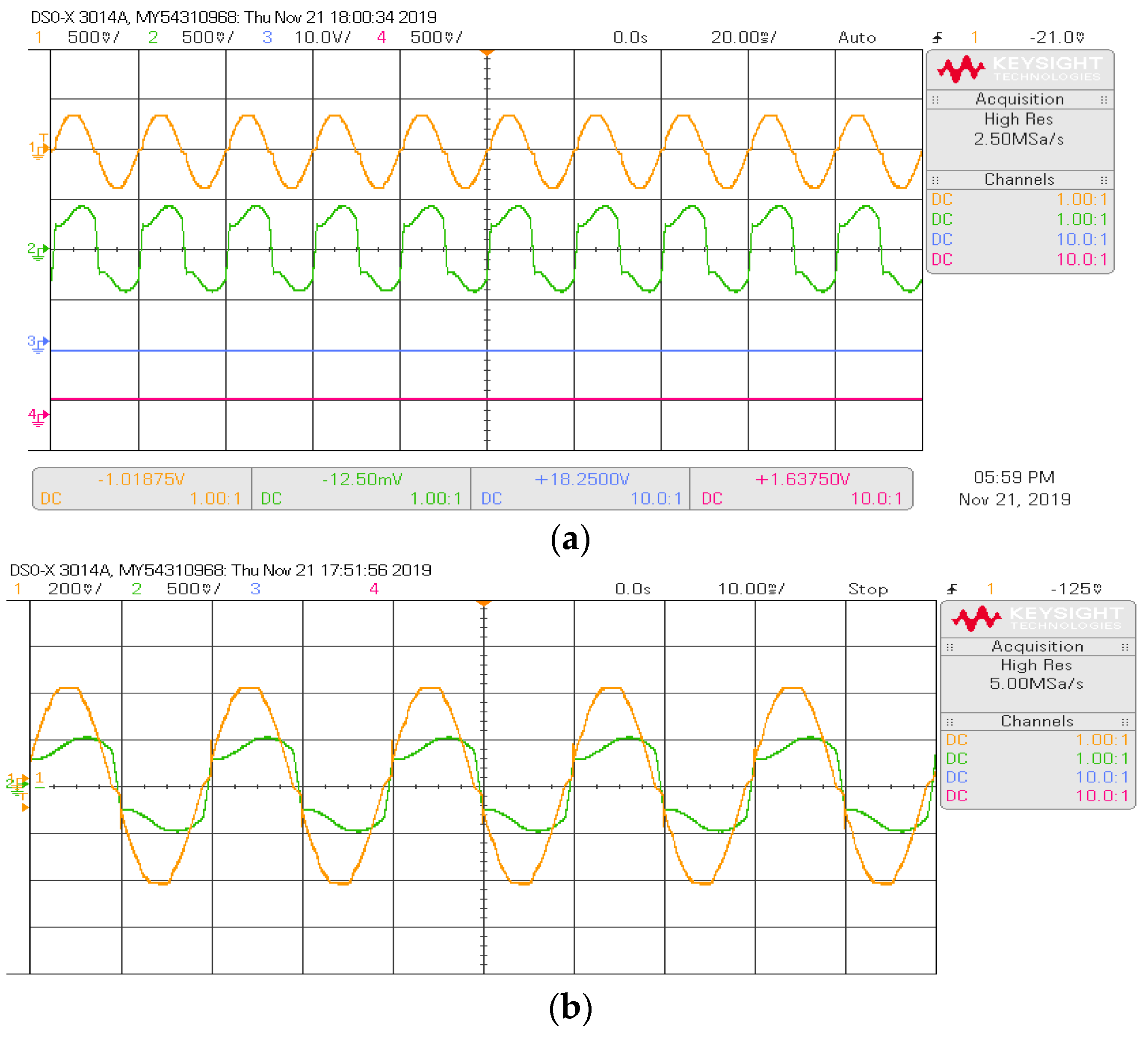
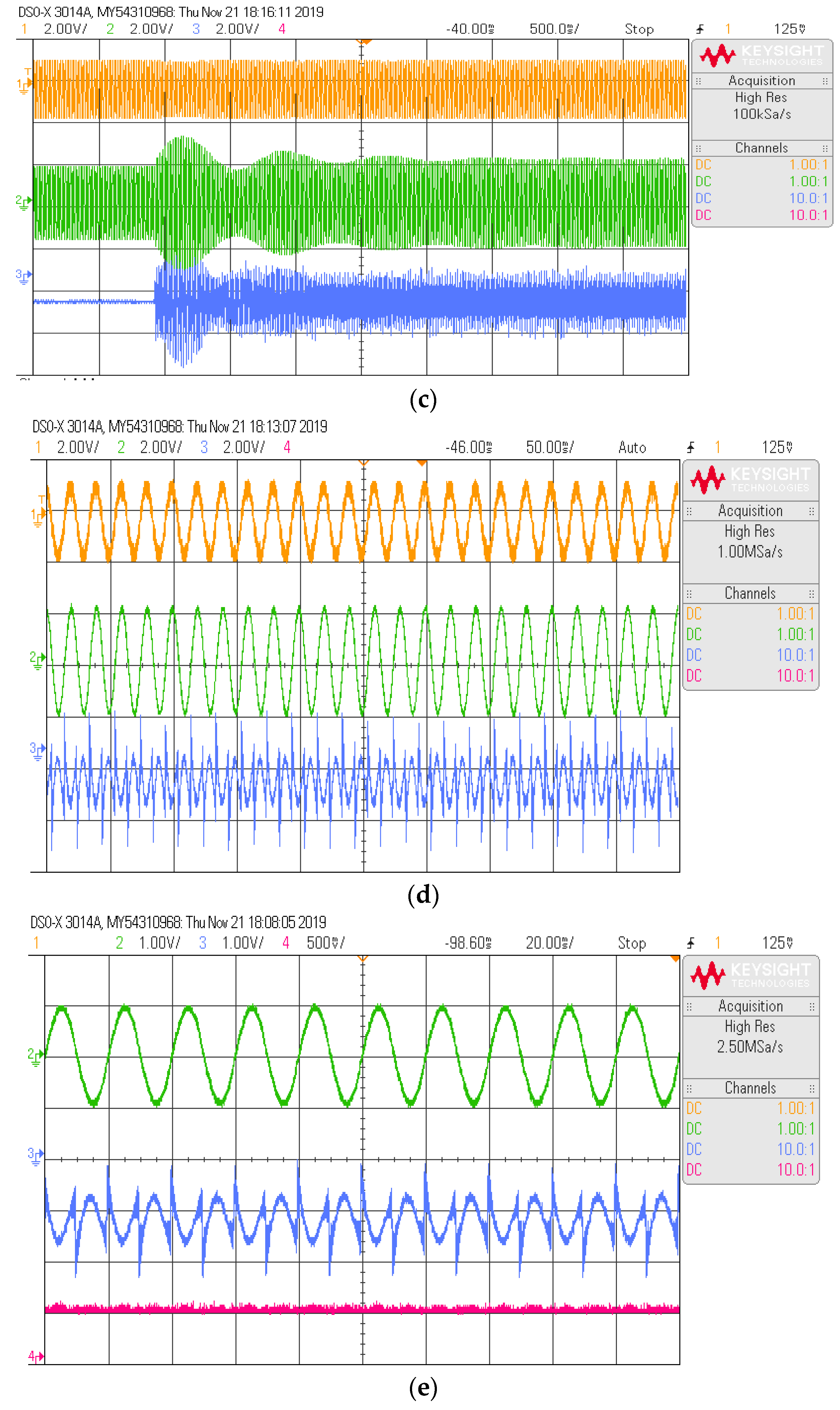
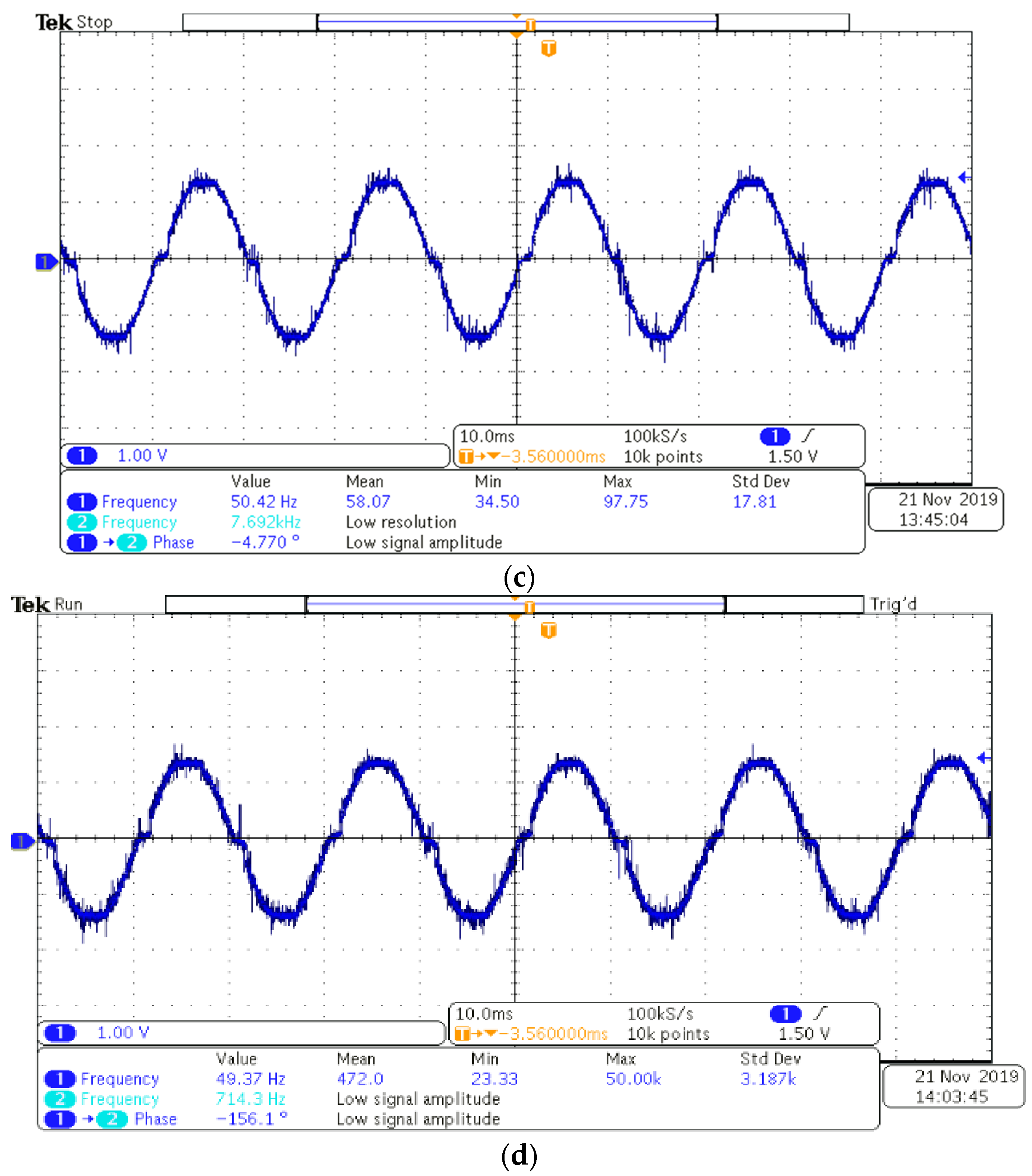
4. Experimental Results
- The NLL’s current harmonics and reactive power were efficiently adjusted.
- The supply current took on a sine wave and aligned with the supply voltage.
- Under all working conditions, the DC-link capacitor voltage returned to its reference value. The suggested control approach also reduced supply current THD to far below 5% within the IEEE 519-2014 standard.
- When compared to traditional current control approaches, the MPCC algorithm based on a cost function provided a great trade-off between VSI switching frequency and harmonic performance. The results show that this technology is suited for both commercial and industrial applications.
- The proposed SAPF system was realized with the Cyclone-IV EP4CE30F484 FPGA controller. From the hardware outcomes, it can be seen that, during the load changing condition, the source current is sinusoidal in nature and in phase with the source voltage.
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Mahela, O.P.; Shaik, A.G. Topological aspects of power quality improvement techniques: A comprehensive overview. Renew. Sustain. Energy Rev. 2016, 1, 1129–1142. [Google Scholar] [CrossRef]
- Singh, B.; Chandra, A.; Al-Haddad, K. Power Quality: Problems and Mitigation Techniques; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]
- Kumar, P.; Mahajan, A. Soft computing techniques for the control of an active power filter. IEEE Trans Power Deliv. 2009, 24, 452–461. [Google Scholar] [CrossRef]
- Singh, B.; Al-Haddad, K.; Chandra, A. A universal active power filter for single-phase reactive power and harmonic compensation. In Proceedings of the Power Quality, Hyderabad, India, 18 June 1998; IEEE: Manhattan, NY, USA, 1998; pp. 81–87. [Google Scholar]
- Khadkikar, V.; Chandra, A.; Singh, B.N. Generalised single-phase pq theory for active power filtering: Simulation and DSP-based experimental investigation. IET Power Electron. 2009, 2, 67–78. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.S.; Kim, Y.S. A new control method for a single-phase hybrid active power filter based on a rotating reference frame. J. Power Electron. 2009, 9, 718–725. [Google Scholar]
- Gupta, R. Generalized frequency domain formulation of the switching frequency for hysteresis current controlled VSI used for load compensation. IEEE Trans Power Electron. 2012, 27, 2526–2535. [Google Scholar] [CrossRef]
- Mahanty, R. Indirect current controlled shunt active power filter for power quality improvement. Electr. Power Energy Syst. 2014, 62, 441–449. [Google Scholar] [CrossRef]
- Komurcugil, H. Double-band hysteresis current-controlled single-phase shunt active filter for switching frequency mitigation. Int. J. Electr. Power Energy Syst. 2015, 69, 131–140. [Google Scholar] [CrossRef]
- Hamad, M.S.; Fahmy, A.M.; Abdel-Geliel, M. Power quality improvement of a single-phase grid-connected PV system with fuzzy MPPT controller. In Proceedings of the Industrial Electronics Society, IECON 2013—39th Annual Conference of the IEEE, Vienna, Austria, 10–13 November 2013; Volume 213, pp. 1839–1844. [Google Scholar]
- Rodriguez, J.; Kazmierkowski, M.P.; Espinoza, J.R. State of the art of finite control set model predictive control in power electronics. IEEE Trans. Ind. Inf. 2013, 9, 1003–1016. [Google Scholar] [CrossRef]
- Kouro, S.; Cortés, P.; Vargas, R.; Ammann, U.; Rodríguez, J. Model predictive control—A simple and powerful method to control power converters. IEEE Trans. Ind. Electron. 2008, 56, 1826–1838. [Google Scholar] [CrossRef]
- Yaramas, V.; Rivera, M.; Narimani, M.; Wu, B.; Rodriguez, J. High performance operation for a four-leg NPC inverter with two-sample-ahead predictive control strategy. Electr. Power Syst. Res. 2015, 123, 31–39. [Google Scholar] [CrossRef]
- Yaramasu, V.; Wu, B.; Rivera, M.; Rodriguez, J. A new power conversion system for megawatt PMSG wind turbines using four-level converters and a simple control scheme based on two-step model predictive strategy—Part I: Modeling and theoretical analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2013, 2, 3–13. [Google Scholar] [CrossRef]
- Vyncke, T.; Thielemans, S.; Melkebeek, J. Finite-set model-based predictive control for flying-capacitor converters: Cost function design and efficient fpga implementation. IEEE Trans. Ind. Inform. 2013, 9, 1113–1121. [Google Scholar] [CrossRef]
- Kanagavel, R.; Vairavasundaram, I.; Padmanaban, S. Design and prototyping of single-phase shunt active power filter for harmonics elimination using model predictive current control. Int. Trans. Electr. Energy Syst. 2020, 30, 2. [Google Scholar] [CrossRef]
- Acuna, P.; Moran, L.; Rivera, M.; Dixon, J.; Rodriguez, J. Improved active power filter performance for renewable power generation systems. IEEE Trans. Power Electron. 2014, 29, 687–694. [Google Scholar] [CrossRef]
- Acuna, P.; Morán, L.; Rivera, M.; Aguilera, R.; Burgos, R.; Agelidis, V.G. A single-objective predictive control method for a multivariable single-phase three-level NPC converter-based active power filter. IEEE Trans. Ind. Electron. 2015, 62, 4598–4607. [Google Scholar] [CrossRef]
- Sahli, A.; Krim, F.; Laib, A.; Talbi, B. Model predictive control for single phase active power filter using modified packed U-cell (MPUC5) converter. Electr. Power Syst. Res. 2020, 180, 106139. [Google Scholar] [CrossRef]
- Boukezata, B.; Gaubert, J.P.; Chaoui, A.; Hachemi, M. Predictive current control in multifunctional grid connected inverter interfaced by PV system. Sol. Energy 2016, 139, 130–141. [Google Scholar] [CrossRef]






| 1 | 0 | |
| 0 | 1 | |
| 1 | 1 | 0 |
| 0 | 0 | 0 |
| S. No | Description | Components | Value |
|---|---|---|---|
| 1 | Supply voltage | Vs | 100 V (rms) |
| 2 | DC-link capacitor voltage | Vdc | 200 V |
| 3 | Supply frequency | F | 50 Hz |
| 4 | Switching Frequency | Fsw | 15 kHz |
| 5 | DC-link capacitance | Cdc | 800 µF |
| 6 | Filter resistance and inductance | Rf and Lf | 0.01 Ω and 5 mH |
| 7 | Source resistance and inductance | Rs and Ls | 0.1 Ω and 1 mH |
| 8 | AC side resistance and inductance | Rc and Lc | |
| 9 | DC side resistance, inductance, and capacitance | RLCdc | 28 Ω, 160 mH, and 100 µF |
| 10 | Voltage sensor | LEM-V | LV 25-p |
| 11 | Processor | Cyclone-IV EP4CE30F484 FPGA | - |
| 12 | Power-quality analyzer | Fluke 435 | - |
| 13 | Mixed-signal oscilloscope | Agilent DSO-X 3014A | - |
| RC Load | Before Compensation | After Compensation | |
|---|---|---|---|
| MPCC | Proposed MPCC | ||
| Source Current THD (%) | 35.36 | 3.58 | 3.97 |
| FSW (kHz) | - | 14.307 | 12.620 |
| Source Current THD (%) (RL Load) | Before Compensation | After Compensation | ||||
|---|---|---|---|---|---|---|
| Hysteresis Controller | Predictive PWM Controller | (Weighting Factor-based MPCC) | ||||
| 0 | 0.05 | 0.1 | ||||
| Simulation Results | 28.47 | 3.82 | 4.5 | 3.53 | 4.20 | 4.66 |
| Hardware Results | 24.9 | 3.76 | 4.21 | 3.7 | 4.6 | 4.8 |
| Switching Frequency (Fsw) in kHz | Before Compensation | Hysteresis Controller | Predictive PWM Controller | After Compensation (Weighting Factor-based MPCC) | ||
| 0 | 0.05 | 0.1 | ||||
| Simulation Results | 0 | 15.27 | 15 | 15.071 | 14.208 | 12.866 |
| Hardware Results | 0 | 15.13 | 15 | 15.200 | 14.600 | 13.400 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aljafari, B.; Rameshkumar, K.; Indragandhi, V.; Ramachandran, S. A Novel Single-Phase Shunt Active Power Filter with a Cost Function Based Model Predictive Current Control Technique. Energies 2022, 15, 4531. https://doi.org/10.3390/en15134531
Aljafari B, Rameshkumar K, Indragandhi V, Ramachandran S. A Novel Single-Phase Shunt Active Power Filter with a Cost Function Based Model Predictive Current Control Technique. Energies. 2022; 15(13):4531. https://doi.org/10.3390/en15134531
Chicago/Turabian StyleAljafari, Belqasem, Kanagavel Rameshkumar, Vairavasundaram Indragandhi, and Selvamathi Ramachandran. 2022. "A Novel Single-Phase Shunt Active Power Filter with a Cost Function Based Model Predictive Current Control Technique" Energies 15, no. 13: 4531. https://doi.org/10.3390/en15134531
APA StyleAljafari, B., Rameshkumar, K., Indragandhi, V., & Ramachandran, S. (2022). A Novel Single-Phase Shunt Active Power Filter with a Cost Function Based Model Predictive Current Control Technique. Energies, 15(13), 4531. https://doi.org/10.3390/en15134531









