Dynamic Response of Lining Structure in a Long Tunnel with Different Adverse Geological Structure Zone Subjected to Non-Uniform Seismic Load
Abstract
:1. Introduction
2. Numerical Model and Non-Uniform Ground Motion
2.1. Numerical Model
2.2. Non-Uniform Acceleration–Time History Curves
2.3. Analysis Plan
3. Internal Force of Lining Structure
3.1. Internal Force Calculation of Lining Structure
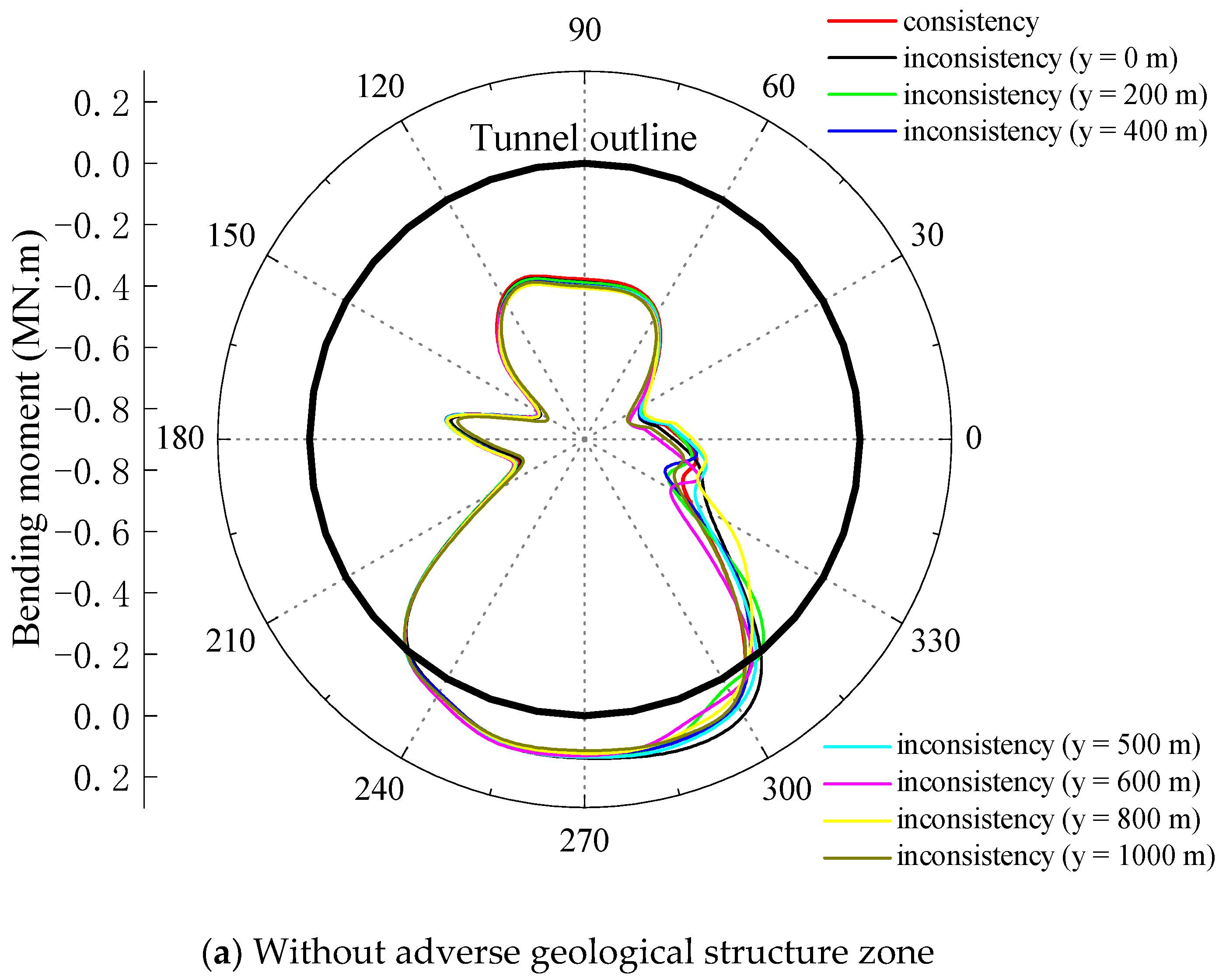
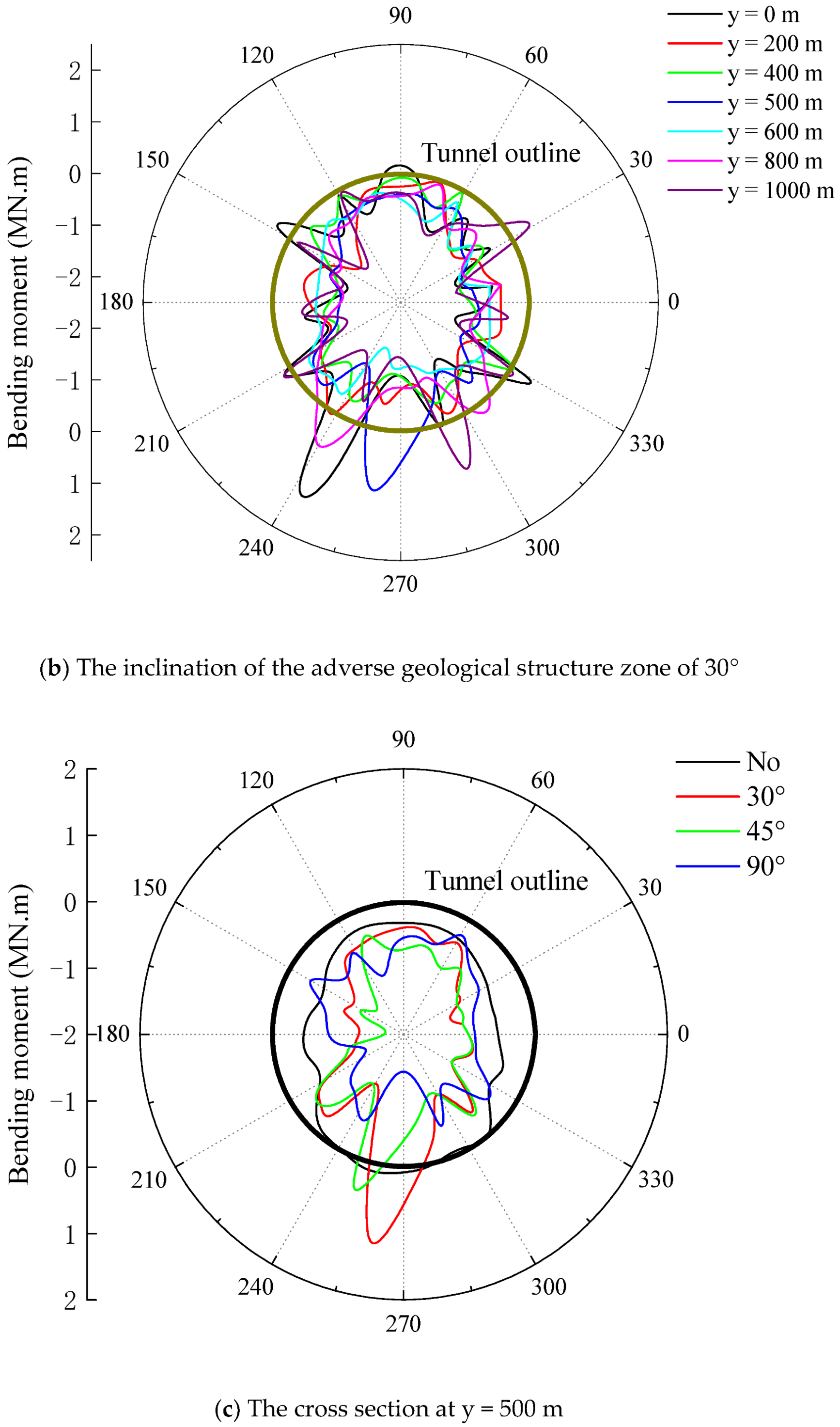
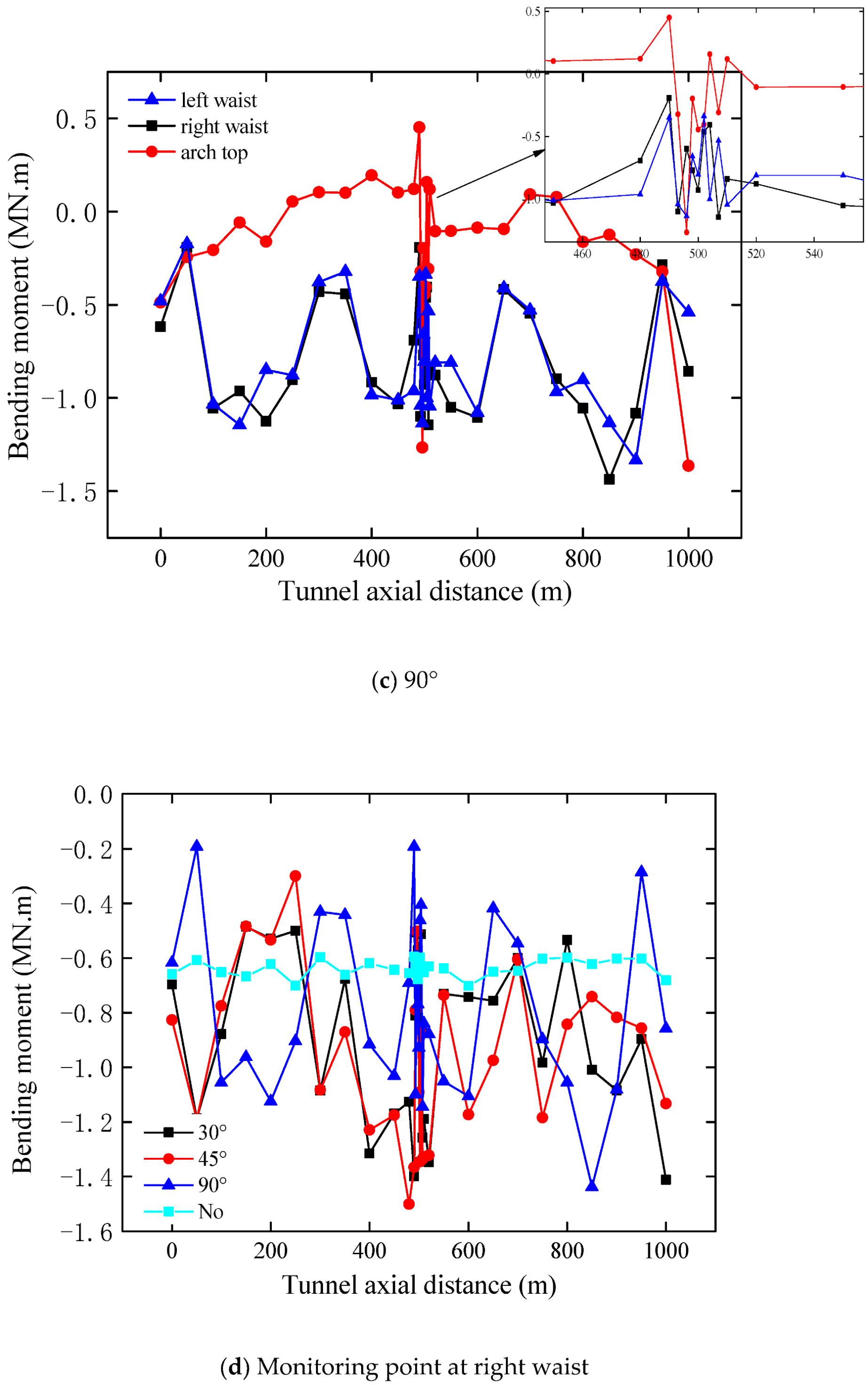
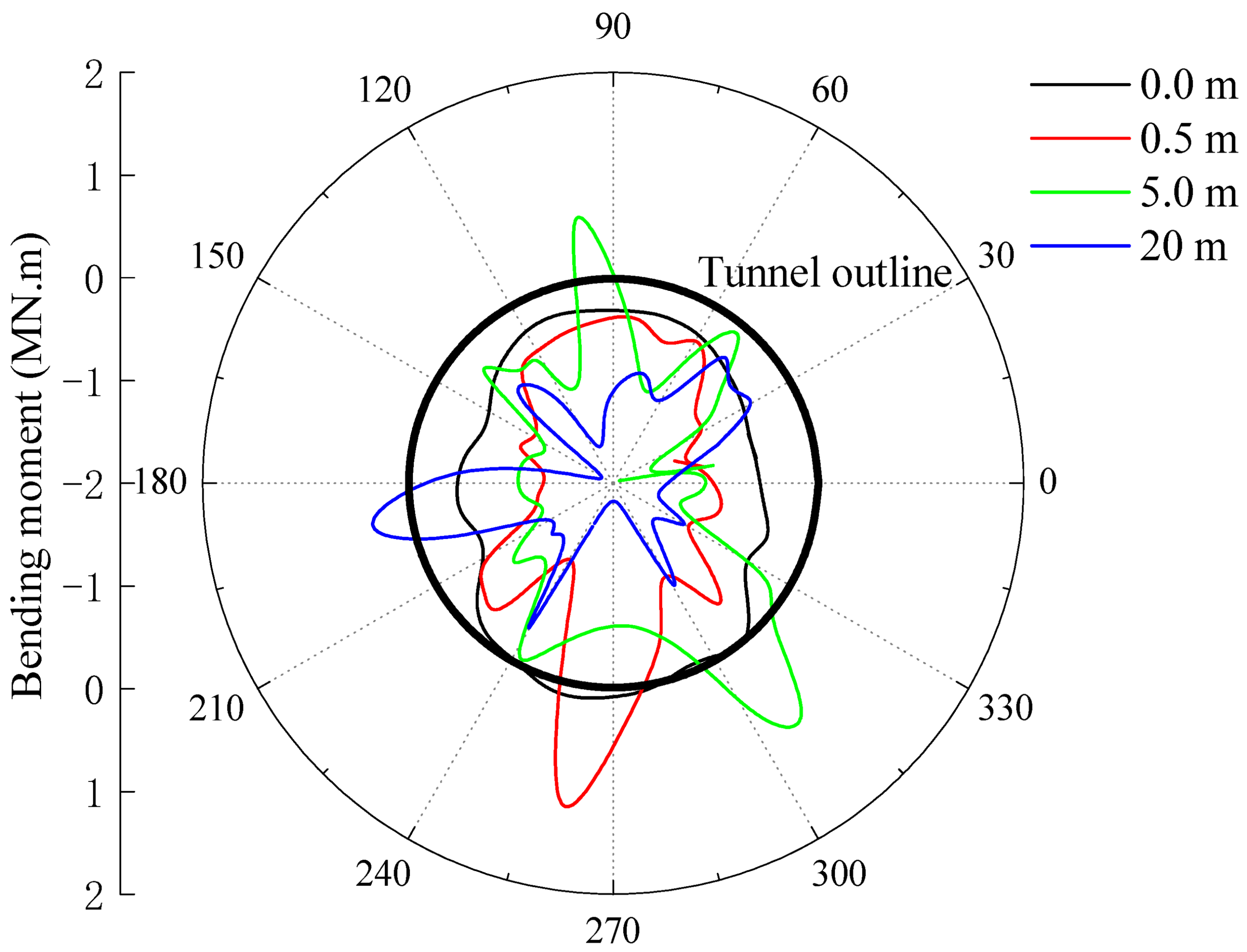
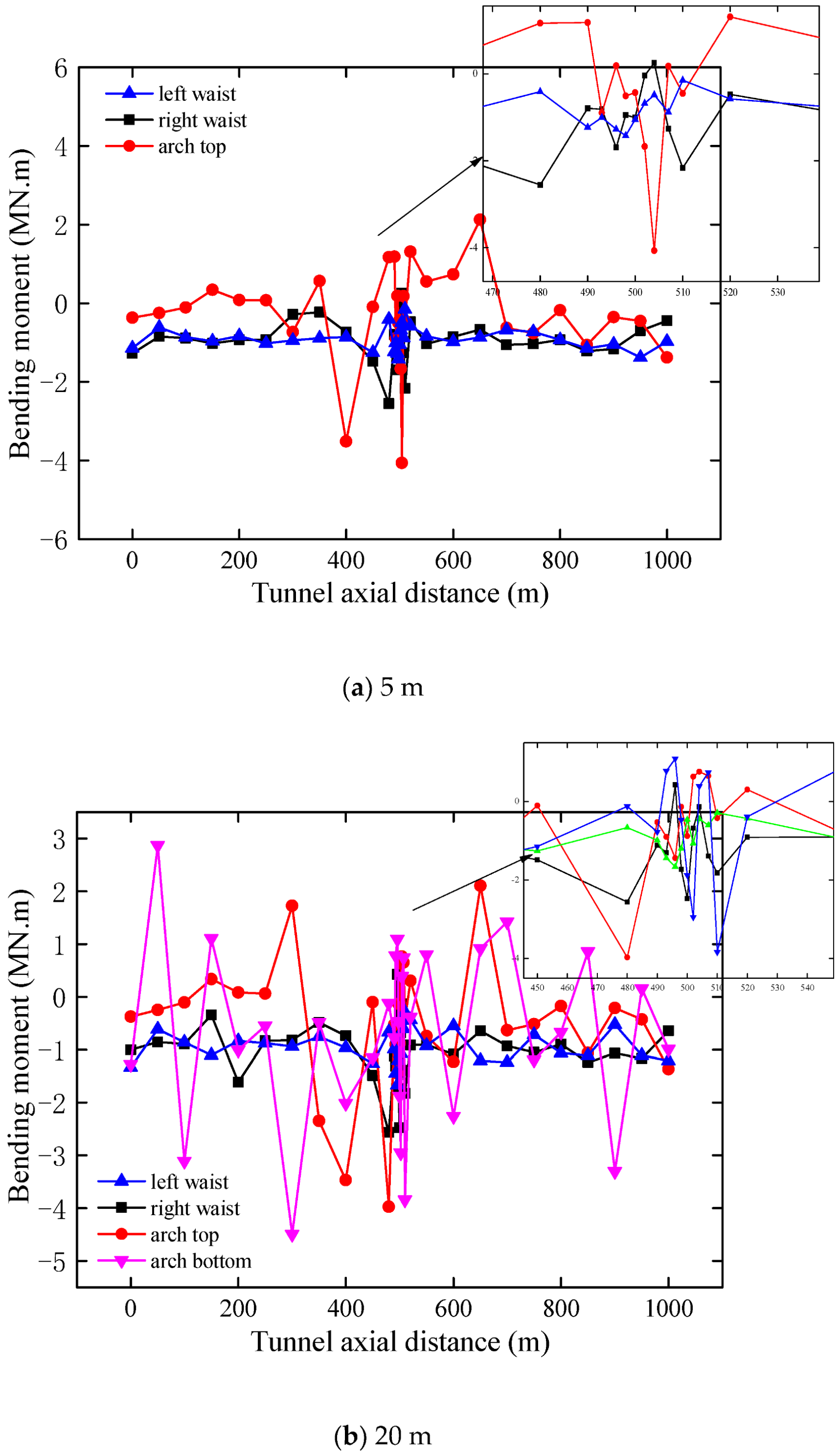
3.2. Distribution of Bending Moment of Lining
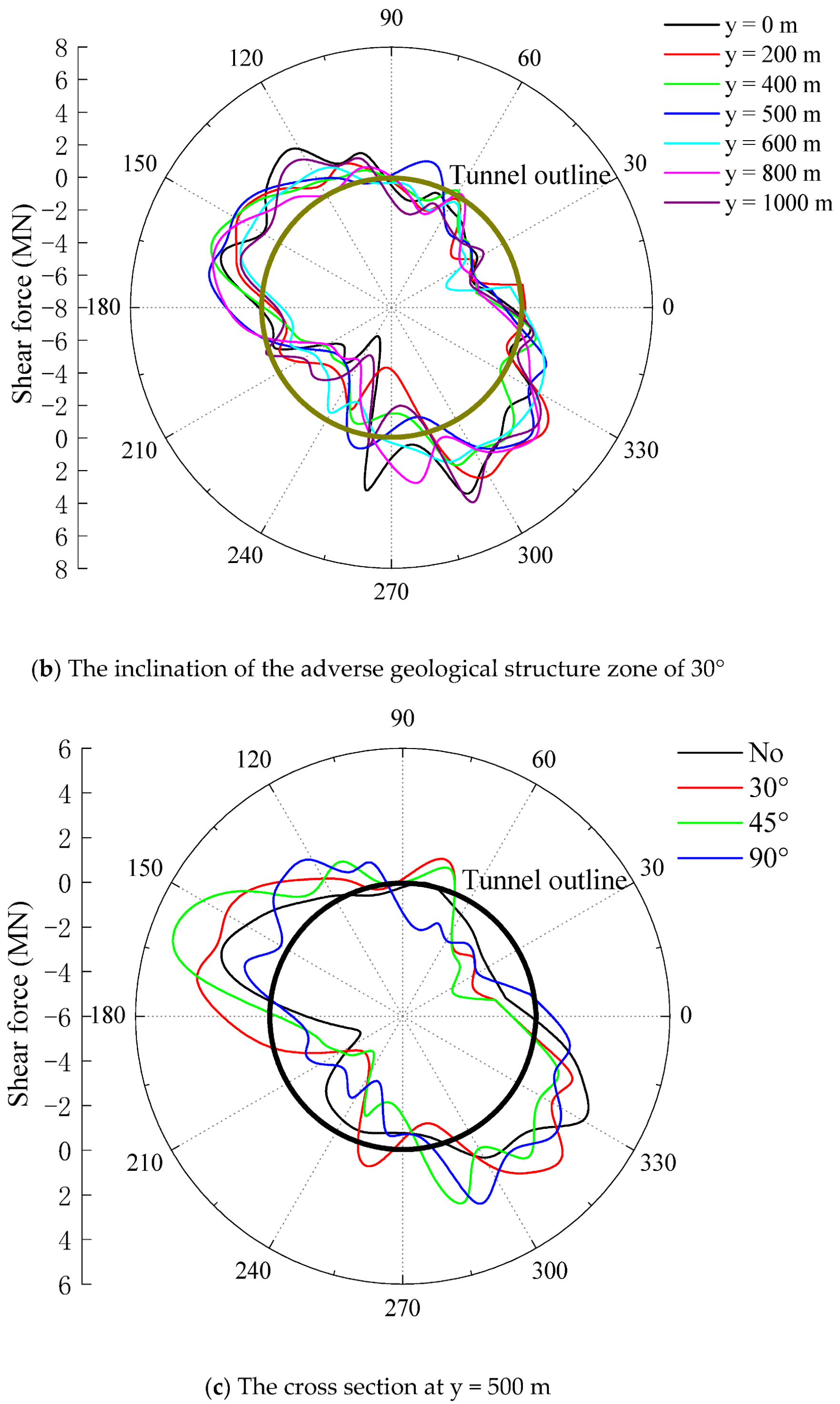
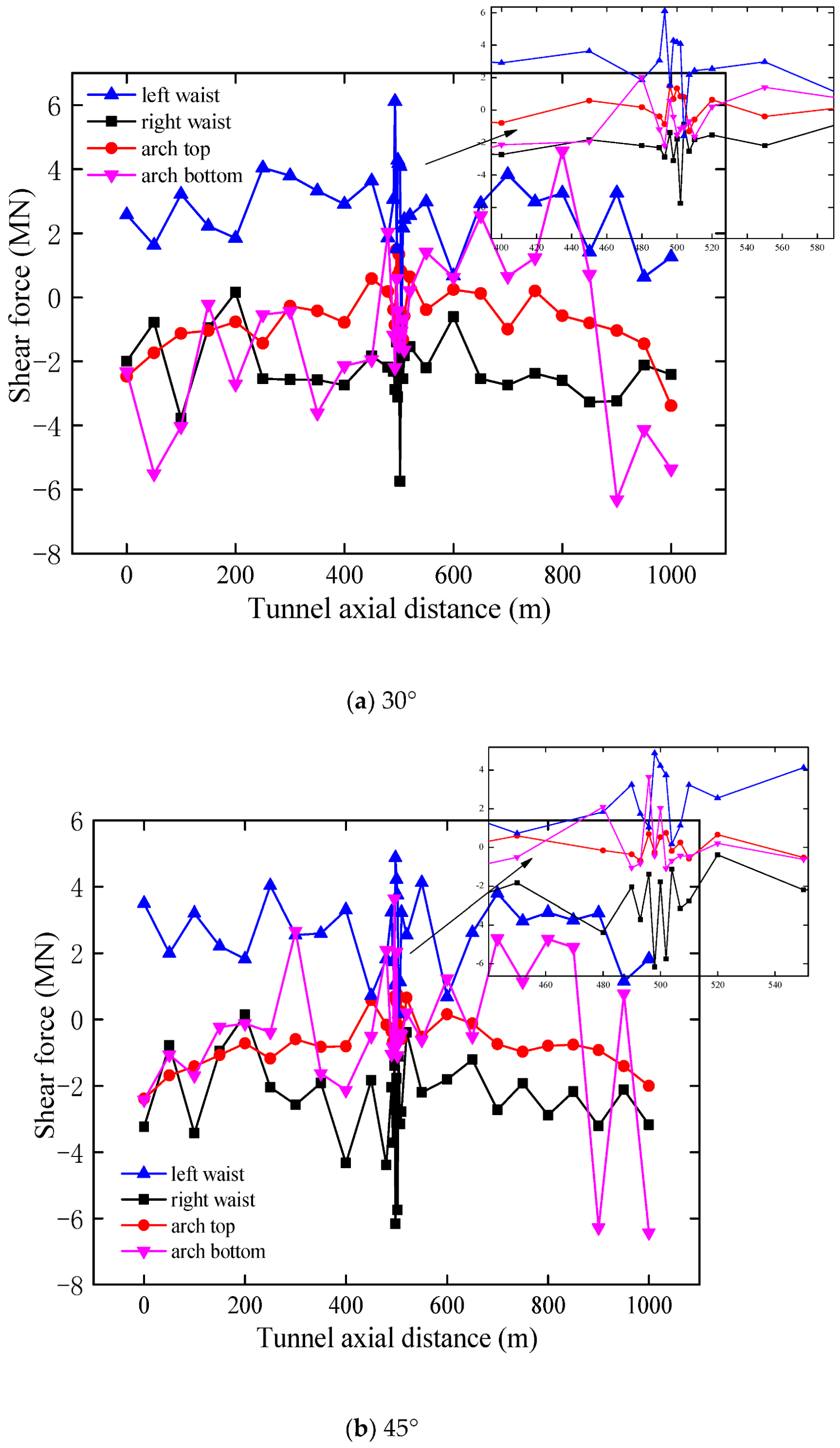
3.2.1. Influence of Inclination
3.2.2. Influence of Thickness
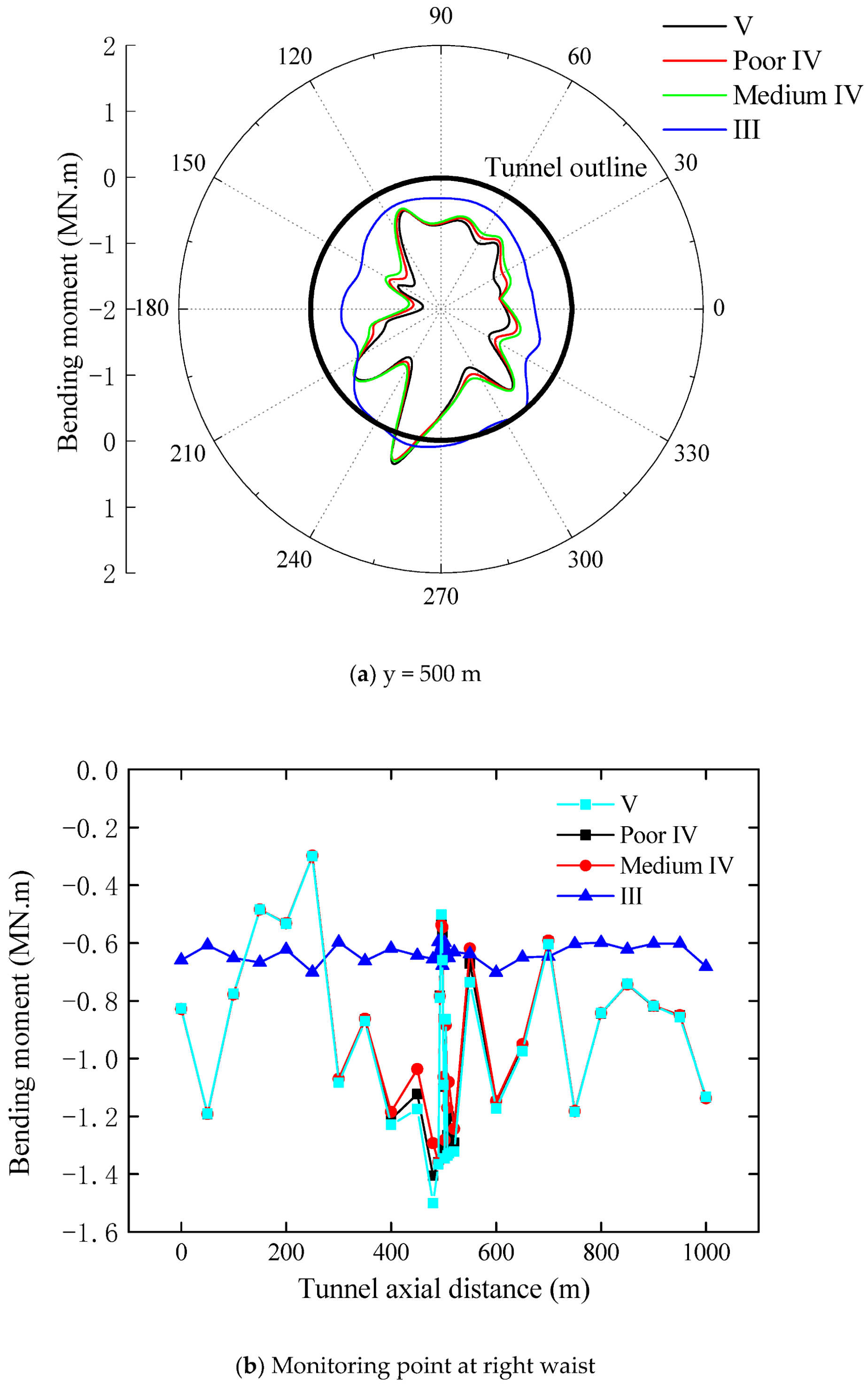
3.2.3. Influence of Lithology
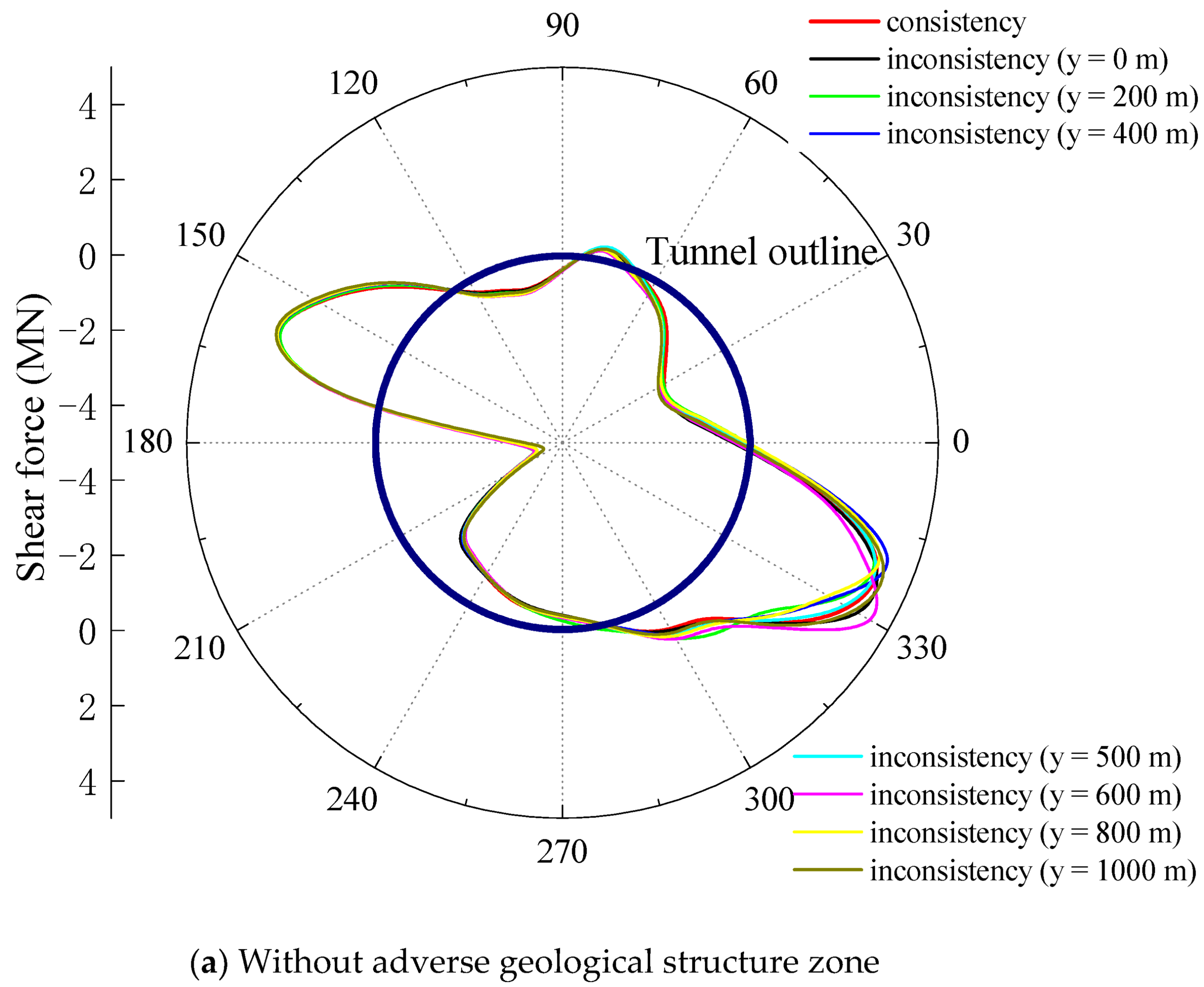
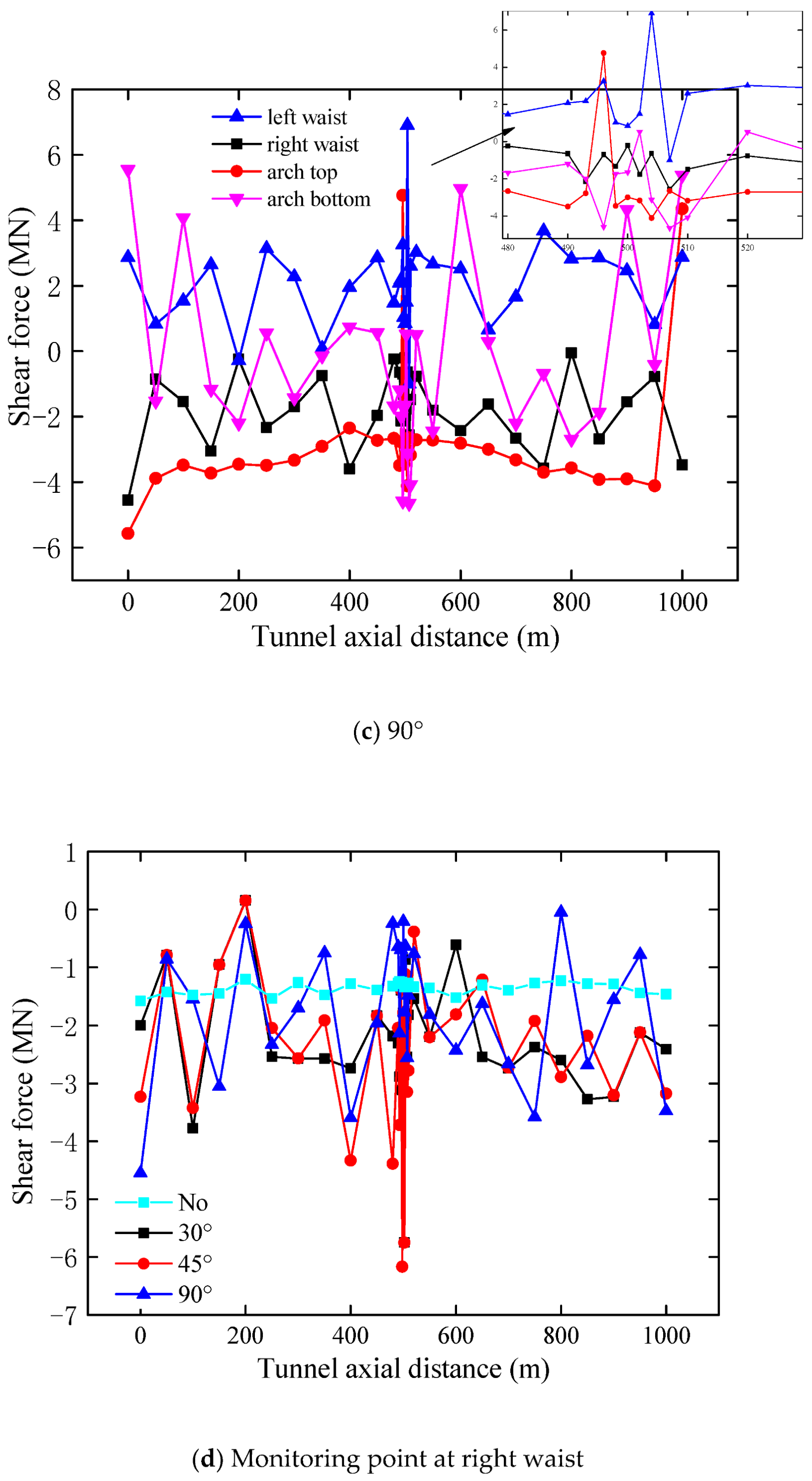
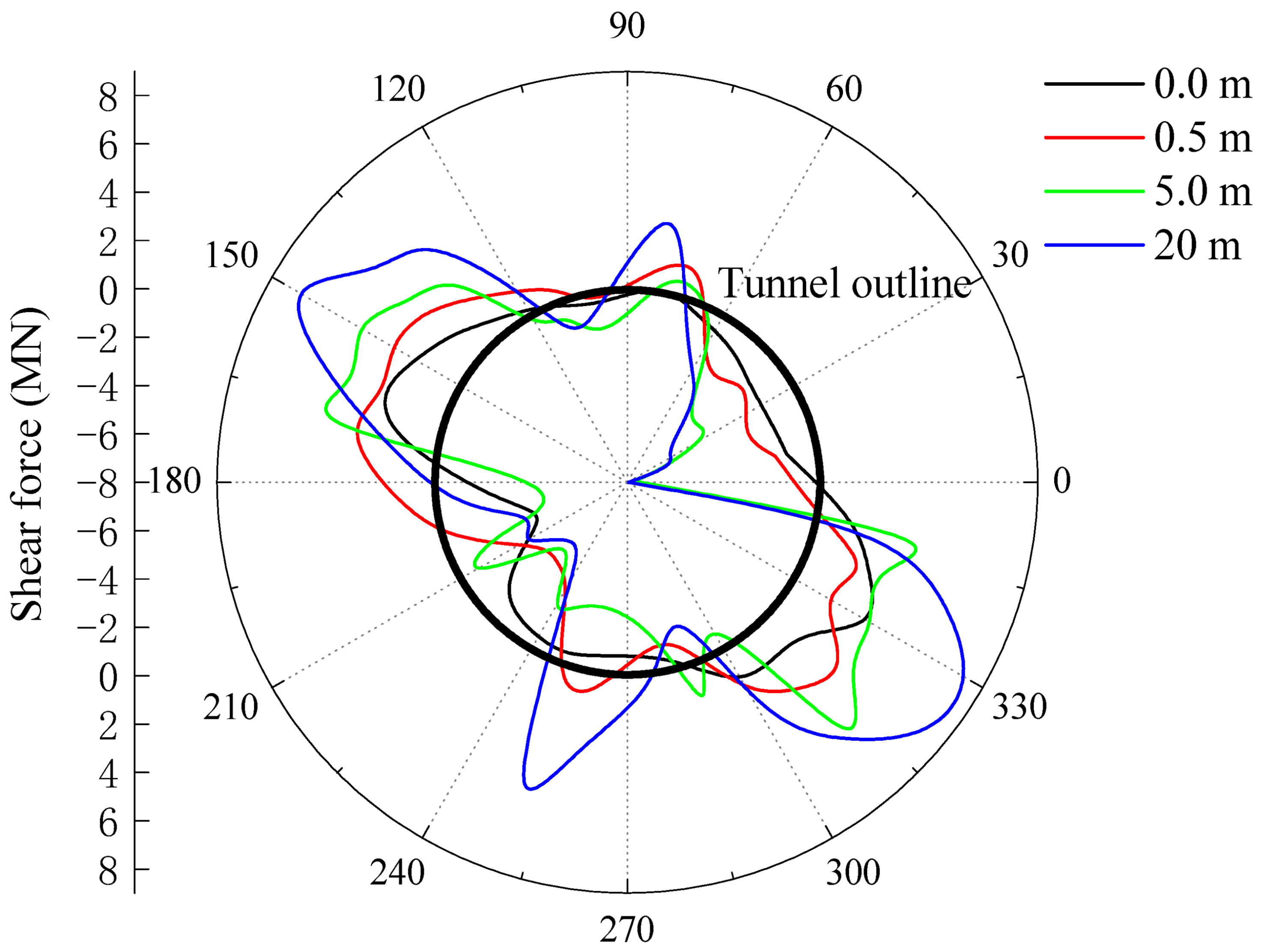
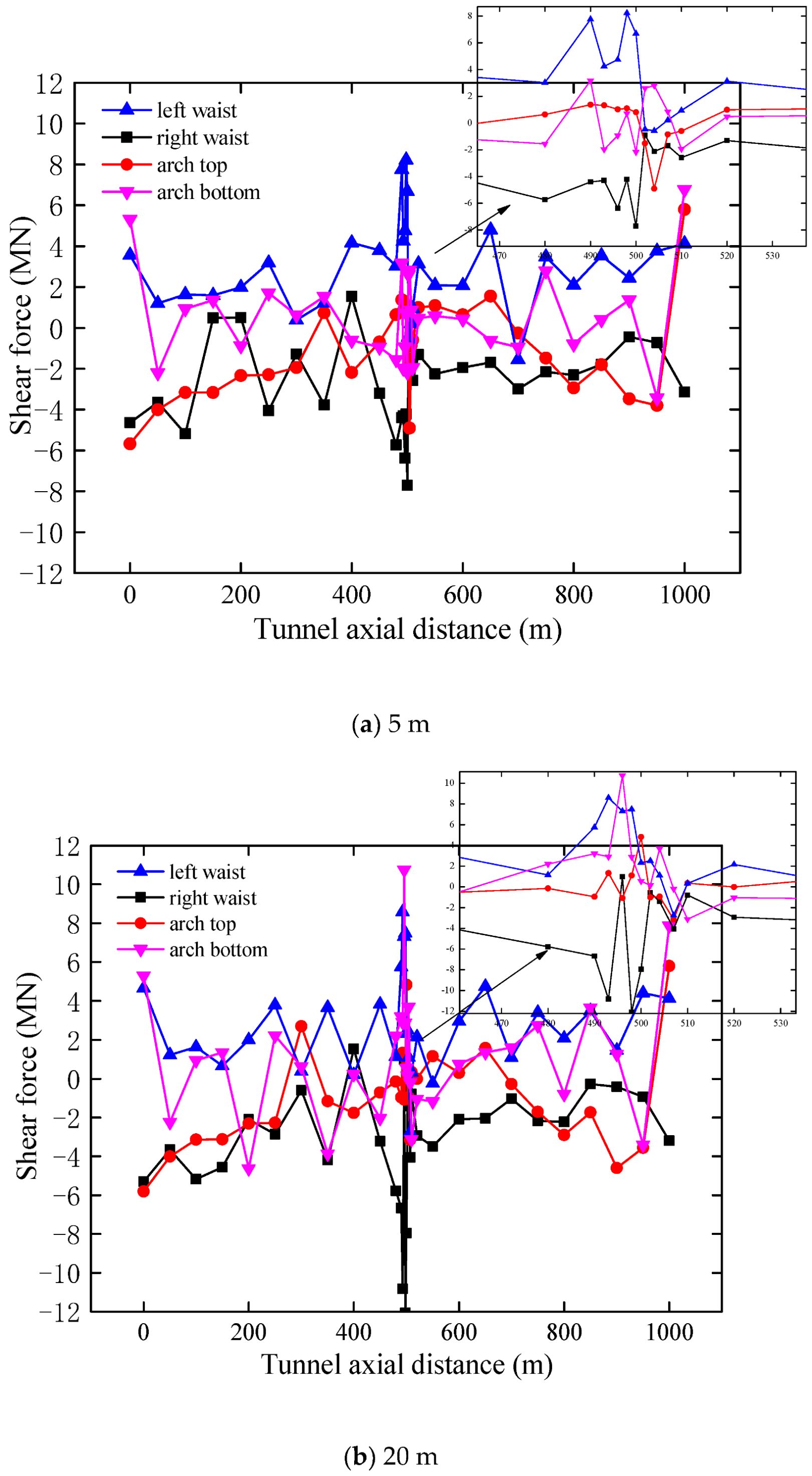
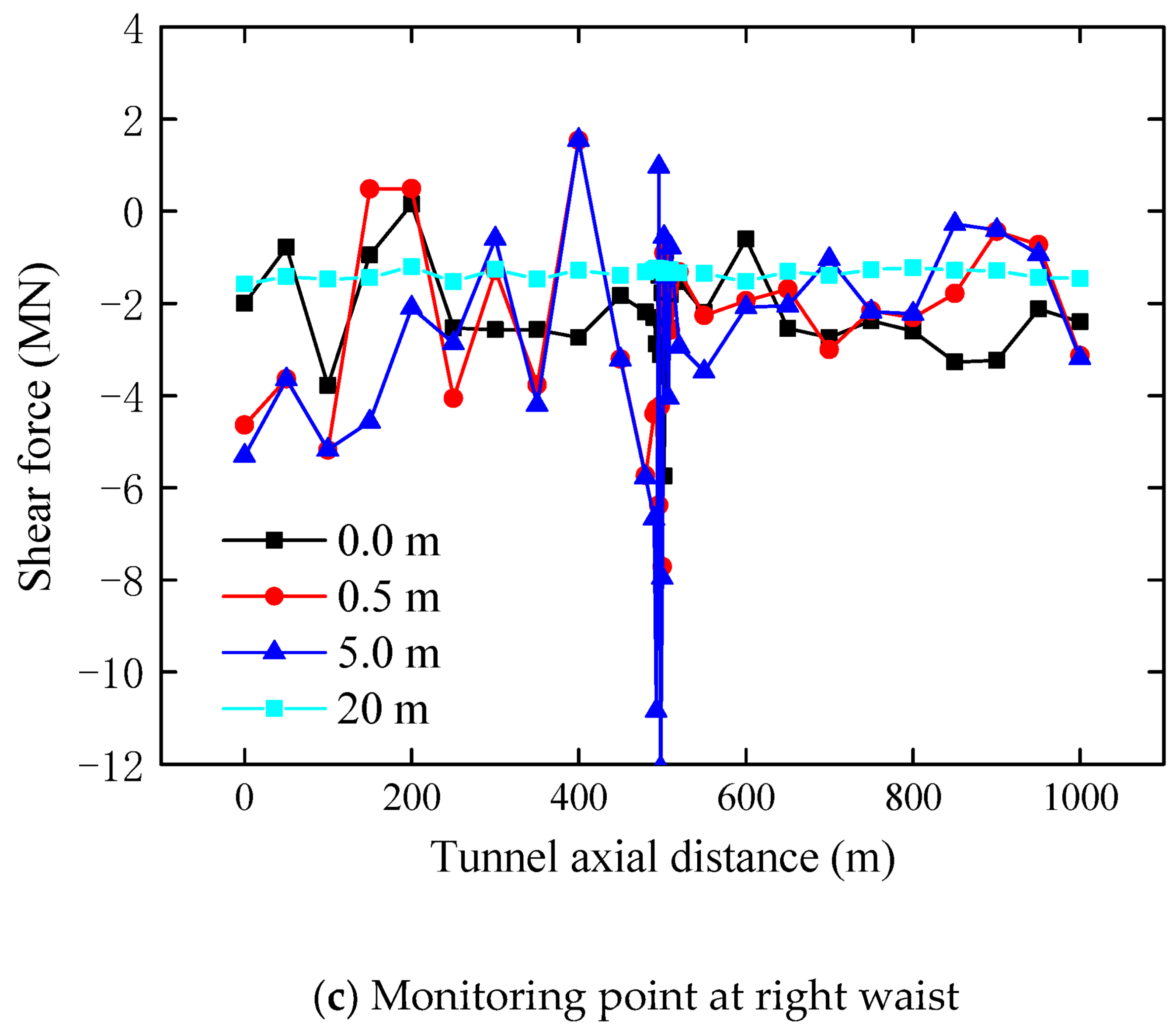
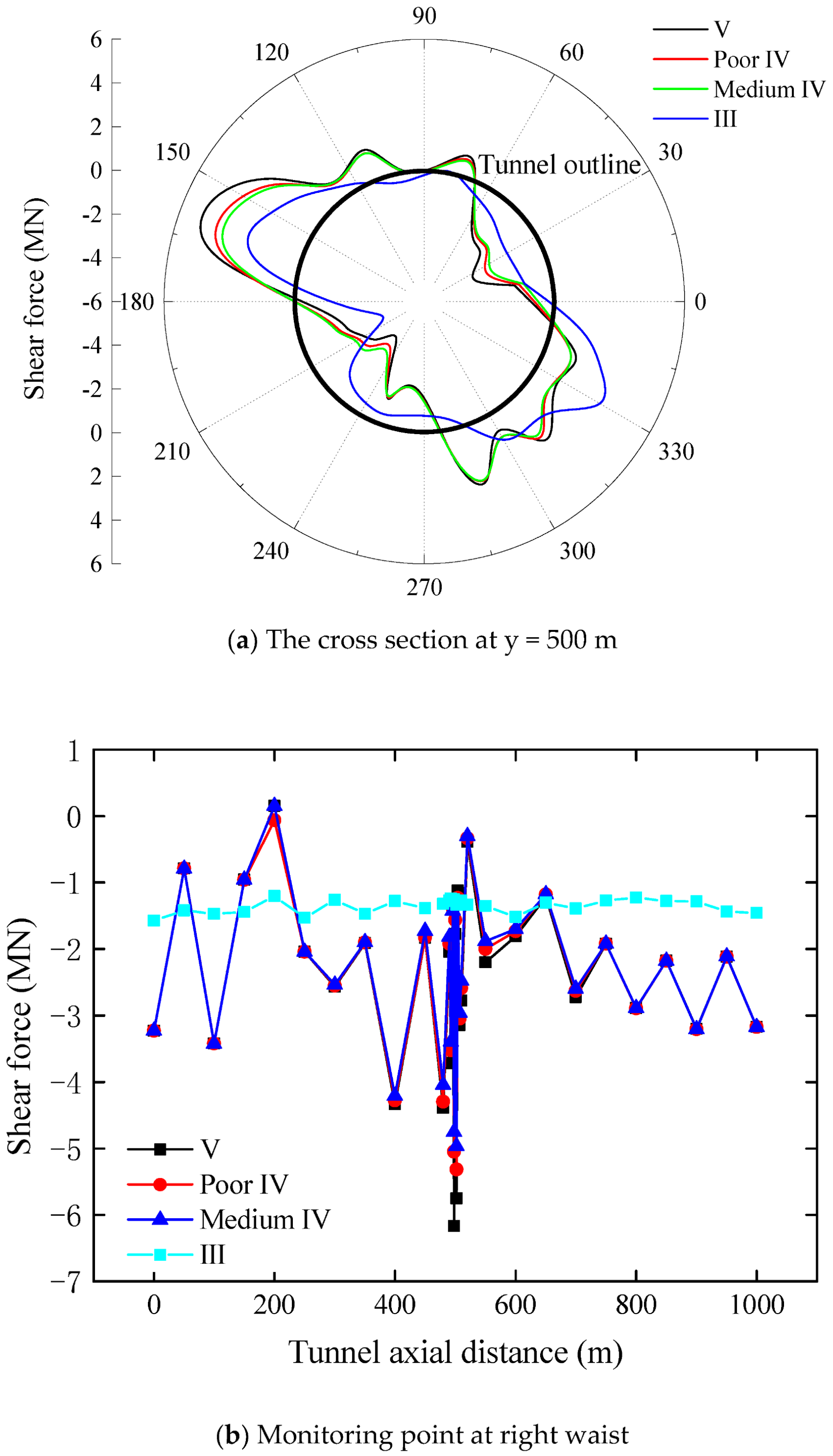
3.3. Distribution of Shear Force of Lining
3.3.1. Influence of Inclination
3.3.2. Influence of Thickness
3.3.3. Influence of Lithology
4. Safety Factor of Lining Structure
4.1. Calculation of Safety Factor
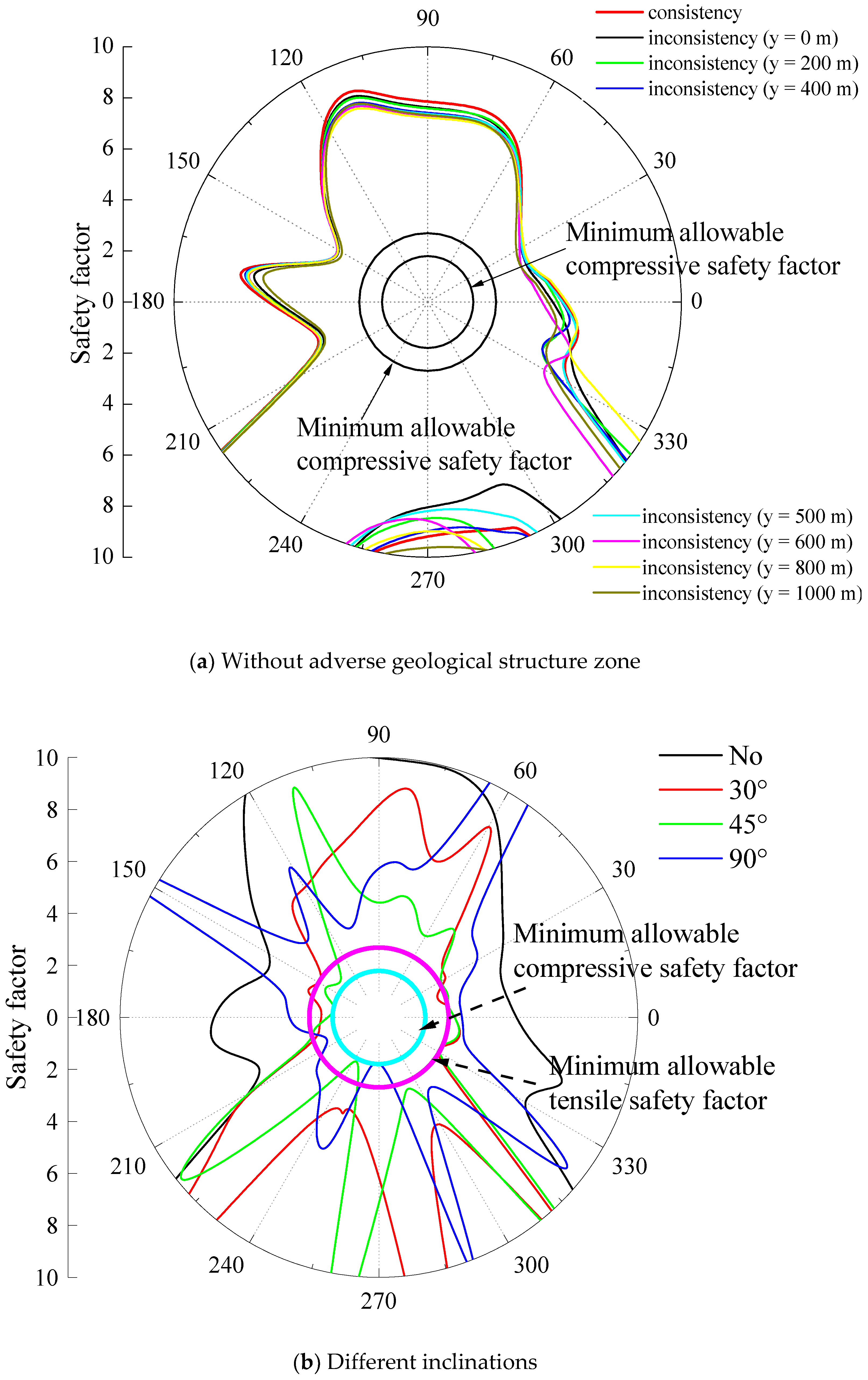
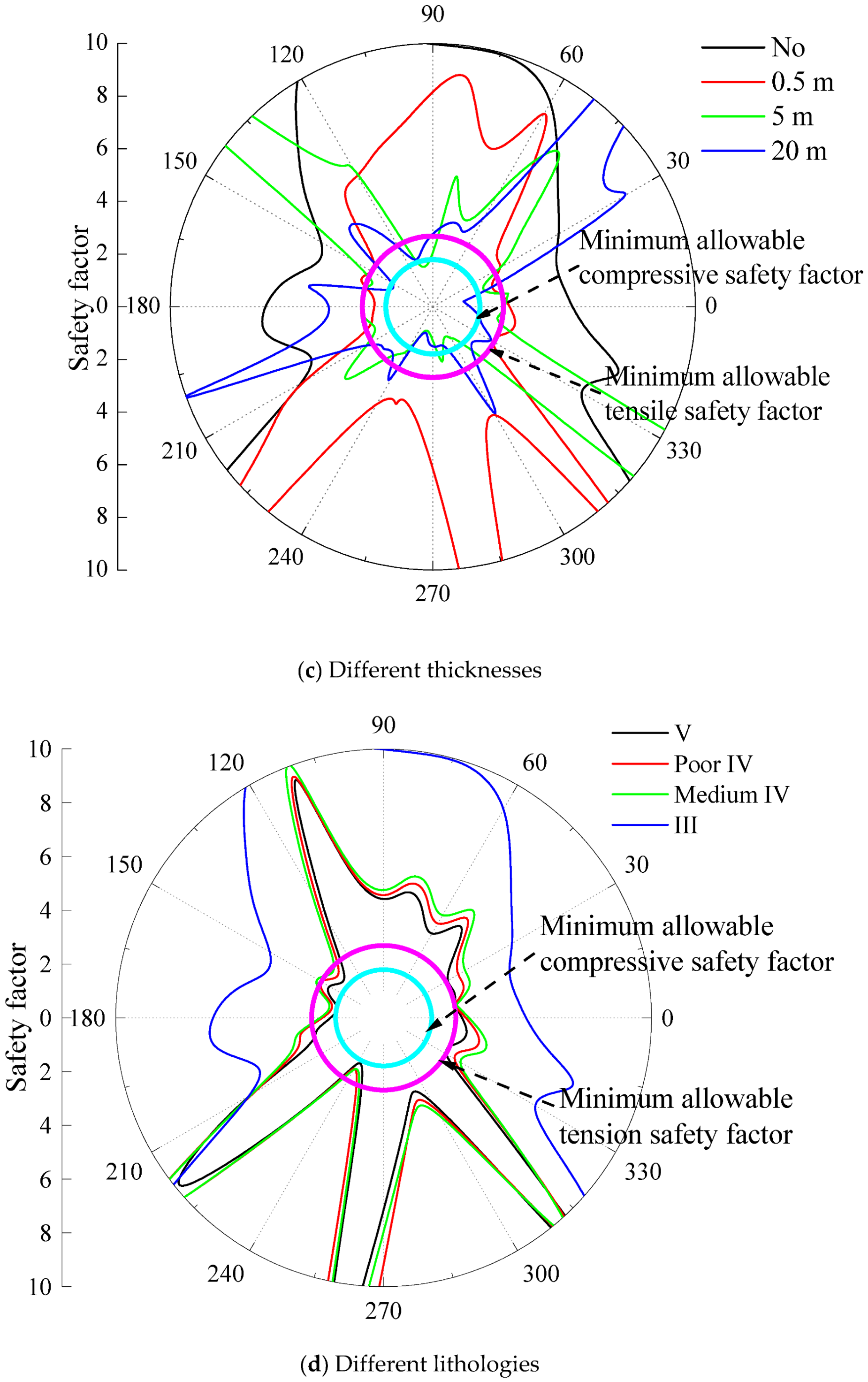
4.2. Distribution of Lining Safety Factor
4.3. Distribution of Lining Safety Factor
5. Conclusions
- (1)
- The variation degree of the tunnel-lining internal force along the tunnel axial direction in the adverse geological structure zone is significantly greater and shows a stronger inconsistency than those in other parts of the tunnel.
- (2)
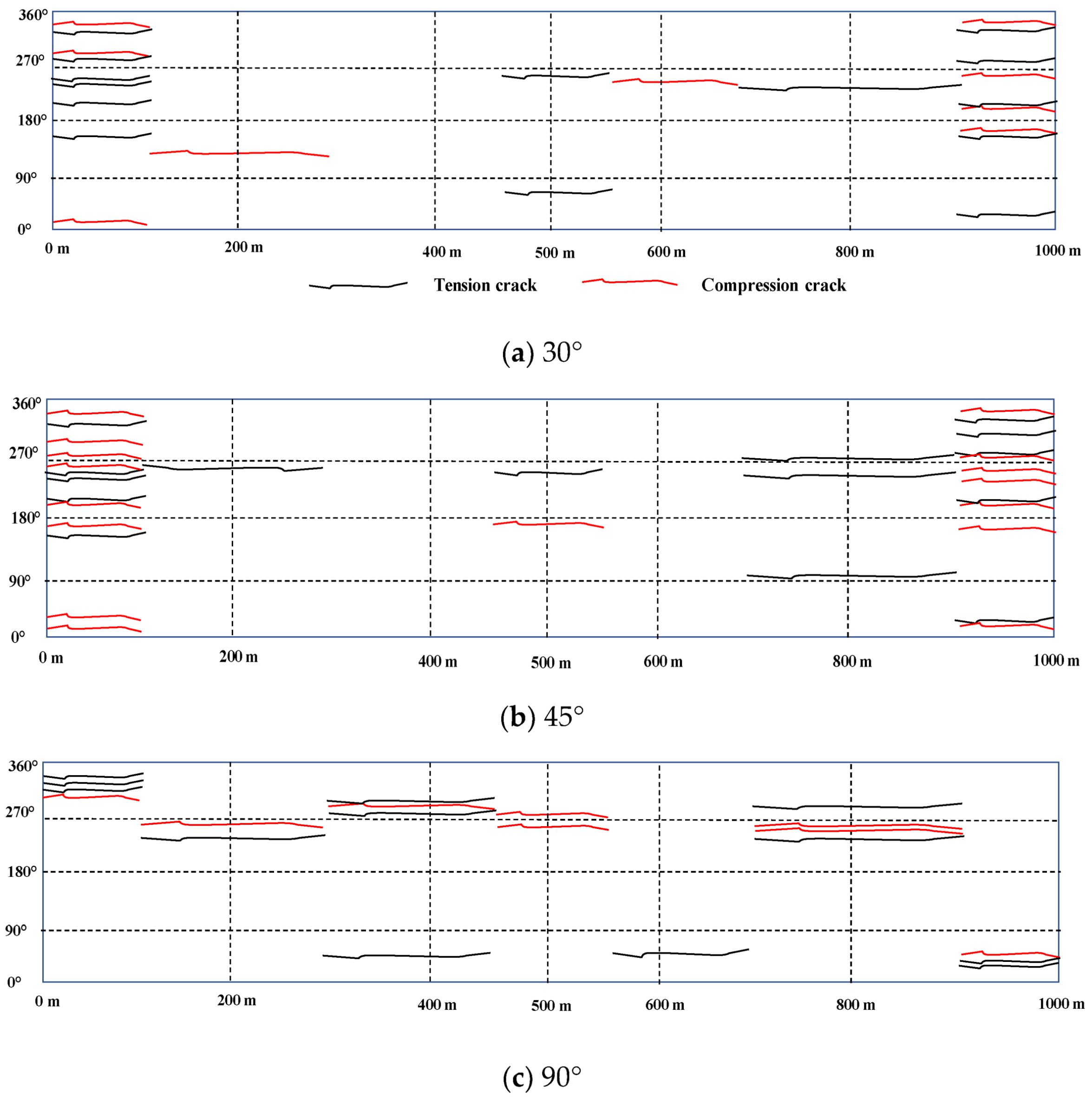
- The inclinations of the adverse geological structure zone play an important role in the dynamic response of the lining. When the inclination angle is 45°, the bending moment and shear force of the lining structure are the largest. Meanwhile, the tunnel lining has the most cracks with large areas of compression-bending cracks at the entrance and exit parts of the tunnel.
- (3)
- The internal force of the lining crossing through different thicknesses of the adverse geological structure zone shows a regional effect. The lining internal force shows strong inconsistency from the tunnel entrance to the section of the adverse geological structure zone, while the lining internal force is relatively stable from the adverse geological structure to the exit section.
- (4)
- The influence of the lithology of the adverse geological structural zone on the dynamic response of the tunnel lining is smaller than that of the inclination and thickness.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aygar, E.B.; Gokceoglu, C. A special support design for a large-span tunnel crossing an active fault (T9 Tunnel, Ankara–Sivas high-speed railway project, Turkey). Environ. Earth Sci. 2021, 80, 37–53. [Google Scholar] [CrossRef]
- Iwatate, T.; Kobayashi, Y.; Kusu, H.; Rin, K. Investigation and shaking table tests of subway structures of the hyogoken-nanbu earthquake. In Proceedings of the 12th World Conference on Earthquake Engineering, Auckland, New Zealand, 30 January–4 February 2000; pp. 1043–1051. [Google Scholar]
- Tsai, J.S.; Chung, L.L.; Liu, K.G.Y. Damage and recovery from the 1999 Chichi earthquake in Taiwan. In Progress of Geo-Disaster Mitigation Technology in Asia; Springer: Berlin/Heidelberg, Germany, 2013; pp. 171–186. [Google Scholar]
- Wang, W.L.; Wang, T.T.; Su, J.J.; Lin, C.H.; Seng, C.R.; Huang, T.H. Assessment of damage in mountain tunnels due to the Taiwan Chi-Chi earthquake. Tunn. Undergr. Space Technol. 2001, 16, 133–150. [Google Scholar] [CrossRef]
- Cui, G.Y.; Wang, M.N.; Yu, L.; Lin, G.J. Study on the characteristics and mechanism of seismic damage for tunnel structures on fault rupture zone in wenchuan seismic disastrous area. China Civ. Eng. J. 2013, 46, 122–127. [Google Scholar]
- Li, H.B.; Zhu, L.; Lv, T.; Yang, J.H.; Xia, X.; Liu, Y.Q. Seismic response analysis of an underground cavern groups in rock subjected to spatially non-uniform seisnic ground motion. Chin. J. Rock Mech. Eng. 2008, 27, 1757–1766. [Google Scholar]
- Yu, H.T.; Chen, J.T.; Bobet, A.; Yuan, Y. Damage observation and assessment of the longxi tunnel during the Wenchuan earthquake. Tunn. Undergr. Space Technol. 2016, 54, 102–116. [Google Scholar] [CrossRef]
- Ardeshiri Lajimi, S.; Yazdani, M.; Assadi Langroudi, A. Control of fault lay-out on seismic design of large underground caverns. Tunn. Undergr. Space Technol. 2015, 50, 305–316. [Google Scholar] [CrossRef]
- Zhu, J.P. Study on dynamic response of different surrounding rock levels on both sides of tunnel fault unfavorable geological structure zone. Int. J. Civ. Mach. Manuf. 2019, 4, 39–42. [Google Scholar]
- Wang, X.W.; Xiong, Q.R.; Zhou, H.; Chen, J.T.; Xiao, M. Three-dimensional (3D) dynamic finite element modeling of the effects of a geological fault on the seismic response of underground caverns. Tunn. Undergr. Space Technol. 2020, 96, 103210. [Google Scholar] [CrossRef]
- Wang, T.T.; Kwok, O.L.A.; Jeng, F.S. Seismic response of tunnels revealed in two decades following the 1999 Chi-Chi earthquake (mw 7.6) in Taiwan: A review. Eng. Geol. 2021, 287, 106090. [Google Scholar] [CrossRef]
- Li, P.; Song, E.X. Three-dimensional numerical analysis for the longitudinal seismic response of tunnels under an asynchronous wave input. Comput. Geotech. 2015, 63, 229–243. [Google Scholar] [CrossRef]
- Qiu, D.P.; Chen, J.Y.; Xu, Q. Dynamic responses and damage forms analysis of underground large scale frame structures under oblique sv seismic waves. Soil Dyn. Earthq. Eng. 2019, 117, 216–220. [Google Scholar] [CrossRef]
- Sun, B.B.; Deng, M.J.; Zhang, S.R.; Cui, W.; Wang, C.; Yu, L.C.; Cao, K.L. Inelastic dynamic analysis and damage assessment of a hydraulic arched tunnel under near-fault sv waves with arbitrary incoming angles. Tunn. Undergr. Space Technol. 2020, 104, 103523. [Google Scholar] [CrossRef]
- Huang, J.Q.; Du, X.L.; Zhao, M.; Zhao, X. Impact of incident angles of earthquake shear (S) waves on 3-D non-linear seismic responses of long lined tunnels. Eng. Geol. 2017, 222, 168–185. [Google Scholar] [CrossRef]
- Sun, W.Y.; Ma, Q.G.; Yan, S.H.; Luo, X.X.; Wang, J.H.; Liang, Q.G. Seismic response and damage characteristics of the shallow tunnel with asymmetric loess cover under the oblique incidence of seismic SV wave. Arab. J. Sci. Eng. 2022, 1–19. [Google Scholar] [CrossRef]
- Yu, H.T.; Yan, X.; Bobet, A.; Yuan, Y.; Xu, G.P.; Su, Q.K. Multi-point shaking table test of a long tunnel subjected to non-uniform seismic loadings. Bull. Earthq. Eng. 2017, 16, 1041–1059. [Google Scholar] [CrossRef]
- Yu, H.T.; Yuan, Y.; Xu, G.P.; Su, Q.K.; Yan, X.; Li, C. Multi-point shaking table test for long tunnels subjected to non-uniform seismic loadings—Part II: Application to the hzm immersed tunnel. Soil Dyn. Earthq. Eng. 2018, 108, 187–195. [Google Scholar] [CrossRef]
- Yuan, Y.; Yu, H.T.; Li, C.; Yan, X.; Yuan, J.Y. Multi-point shaking table test for long tunnels subjected to non-uniform seismic loadings—Part I: Theory and validation. Soil Dyn. Earthq. Eng. 2018, 108, 177–186. [Google Scholar] [CrossRef]
- Han, J.Y.; El Naggar, M.H.; Zhao, M.; Zhong, Z.L.; Hou, B.W.; Du, X.L. Longitudinal response of buried pipeline under non-uniform seismic excitation from multi-point shaking table tests. Soil Dyn. Earthq. Eng. 2021, 140, 106440. [Google Scholar] [CrossRef]
- Chen, J.; Shi, X.J.; Li, J. Shaking table test of utility tunnel under non-uniform earthquake wave excitation. Soil Dyn. Earthq. Eng. 2010, 30, 1400–1416. [Google Scholar] [CrossRef]
- Chen, J.; Jiang, L.Z.; Li, J.; Shi, X.J. Numerical simulation of shaking table test on utility tunnel under non-uniform earthquake excitation. Tunn. Undergr. Space Technol. 2012, 30, 205–216. [Google Scholar] [CrossRef]
- Yu, H.T.; Yuan, Y.; Qiao, Z.Z.; Gu, Y.; Yang, Z.H.; Li, X.D. Seismic analysis of a long tunnel based on multi-scale method. Eng. Struct. 2013, 49, 572–587. [Google Scholar] [CrossRef]
- Li, C.; Yuan, J.Y.; Yu, H.T.; Su, Q.K.; Yuan, Y. Seismic response analysis of long immersed tunnel to longitudinal non-uniform excitation. In Proceedings of the 11th World Congress on Computational Mechanics, Barcelona, Spain, 20–25 July 2014; pp. 1416–1424. [Google Scholar]
- Fabozzi, S.; Bilotta, E.; Yu, H.; Yuan, Y. Effects of the asynchronism of ground motion on the longitudinal behaviour of a circular tunnel. Tunn. Undergr. Space Technol. 2018, 82, 529–541. [Google Scholar] [CrossRef]
- Tarinejad, R.; Fatehi, R.; Harichandran, R.S. Response of an arch dam to non-uniform excitation generated by a seismic wave scattering model. Soil Dyn. Earthq. Eng. 2013, 52, 40–54. [Google Scholar] [CrossRef] [Green Version]
- Isari, M.; Tarinejad, R.; Taghavi Ghalesari, A.; Sohrabi Bidar, A. A new approach to generating non-uniform support excitation at topographic sites. Soils Found. 2019, 59, 1933–1945. [Google Scholar] [CrossRef]
- Zhou, Y.Q.; Sheng, Q.; Li, N.N.; Fu, X.D. Preliminary study on time-space effect of the dynamic response of long tunnel under non-uniform ground motion. Rock Soil Mech. 2021, 42, 2287–2297. [Google Scholar]
- Xue, B.; Du, X.; Wang, J.; Yu, X. A Scaled Boundary Finite-Element Method with B-Differentiable Equations for 3D Frictional Contact Problems. Fractal Fract. 2022, 6, 133. [Google Scholar] [CrossRef]
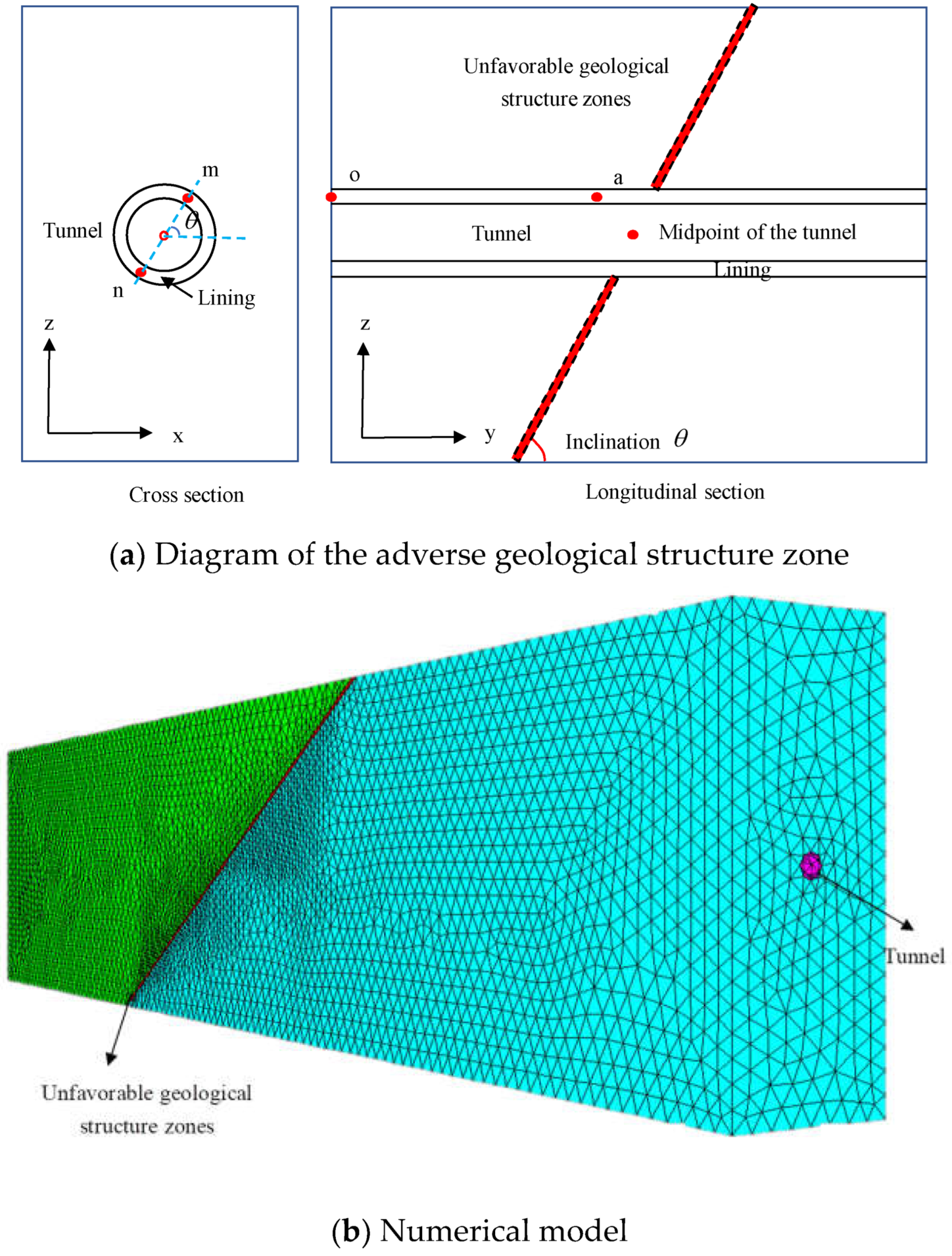
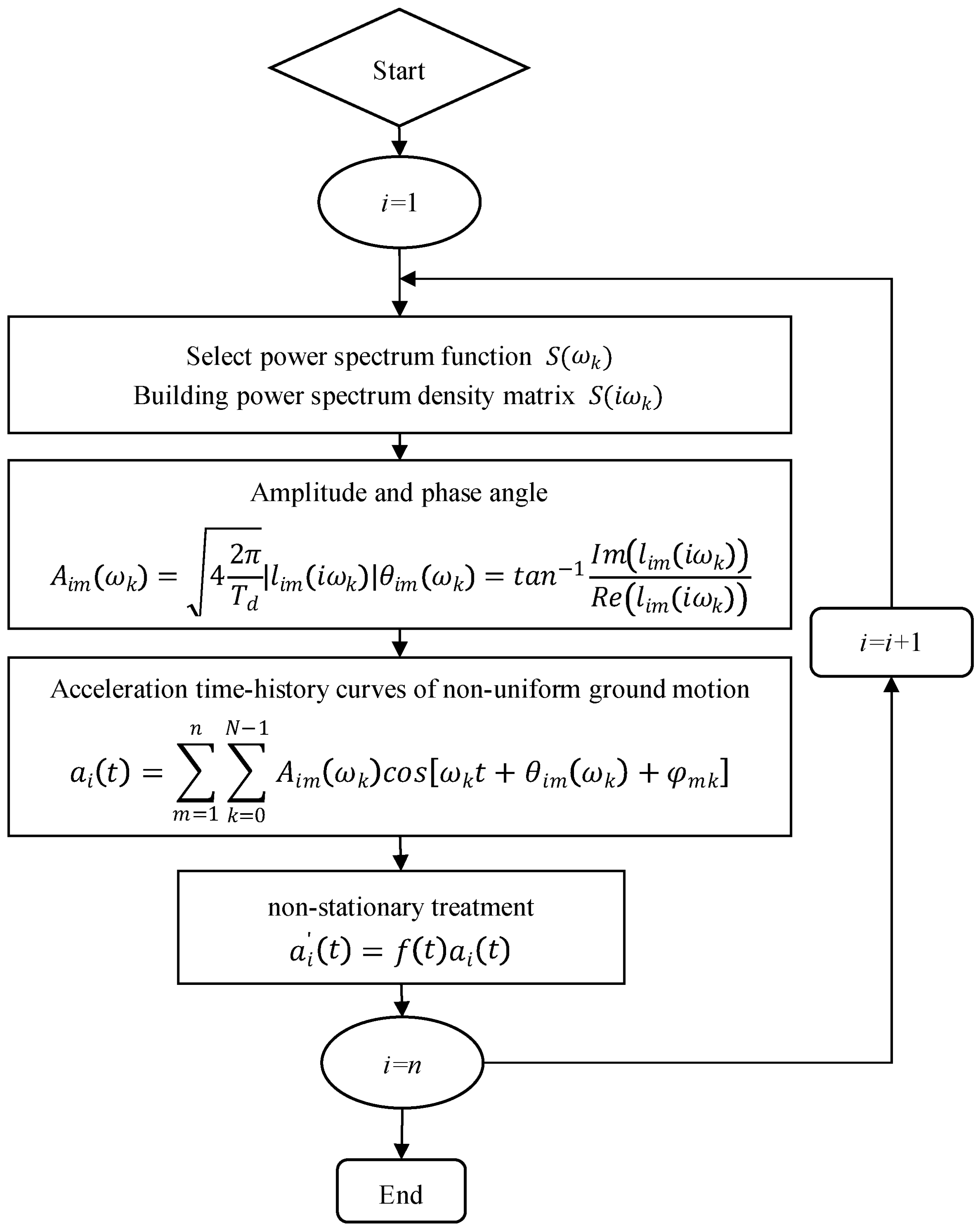

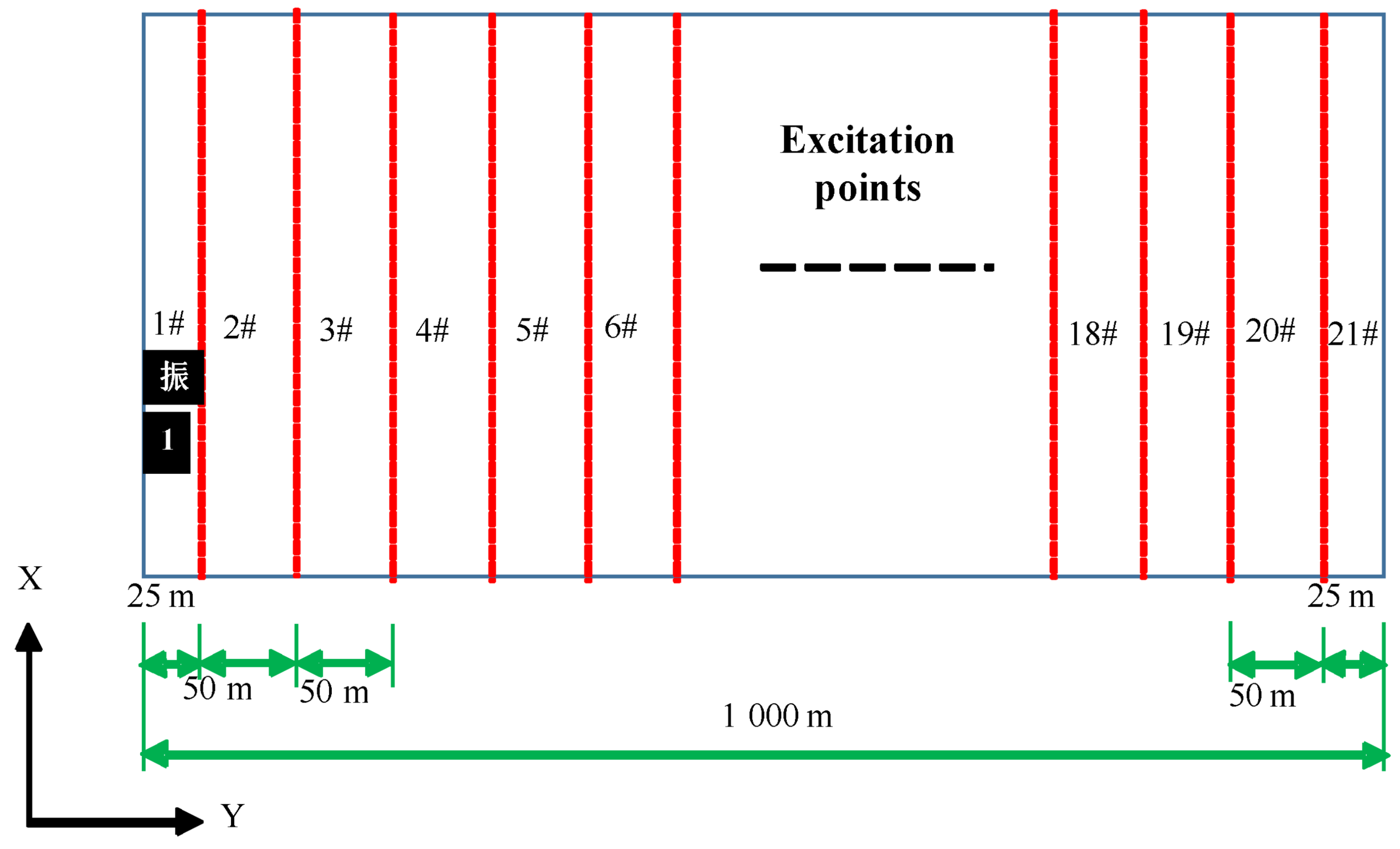



| Material | Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Internal Friction Angle (°) | Cohesion (MPa) | Tension (MPa) |
|---|---|---|---|---|---|---|
| rock | 2720 | 3.62 | 1.97 | 38.6 | 1.4 | 3.0 |
| lining | 2500 | 16.67 | 12.50 | —— | —— | —— |
| contact | —— | 6 (Normal stiffness) | 6 (Shear stiffness) | 30.0 | 1.2 | 1.6 |
| Number | Thickness (m) | Inclination (°) | Lithology |
|---|---|---|---|
| A1 | 0 | 30 | V |
| A2 | 0.5 | ||
| A3 | 5 | ||
| A4 | 20 | ||
| B1 | 0.5 | 45 | |
| B2 | 90 | ||
| C1 | 45 | Medium IV | |
| C2 | Poor IV | ||
| C3 | III |
| Lithology | Density (kg/m3) | Bulk Modulus (GPa) | Shear Modulus (GPa) | Internal Friction Angle (°) | Cohesion (MPa) | Tension (MPa) |
|---|---|---|---|---|---|---|
| III | 2720 | 3.62 | 1.97 | 38.6 | 1.4 | 3.0 |
| Medium IV | 2500 | 3.47 | 1.38 | 33 | 0.45 | 0.6 |
| Poor IV | 2500 | 2.15 | 0.84 | 29.79 | 0.42 | 0.37 |
| V | 2500 | 0.83 | 0.30 | 26.57 | 0.4 | 0.15 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Wang, H.; Song, D.; Sheng, Q.; Fu, X.; Ding, H.; Chai, S.; Yuan, W. Dynamic Response of Lining Structure in a Long Tunnel with Different Adverse Geological Structure Zone Subjected to Non-Uniform Seismic Load. Energies 2022, 15, 4599. https://doi.org/10.3390/en15134599
Zhou Y, Wang H, Song D, Sheng Q, Fu X, Ding H, Chai S, Yuan W. Dynamic Response of Lining Structure in a Long Tunnel with Different Adverse Geological Structure Zone Subjected to Non-Uniform Seismic Load. Energies. 2022; 15(13):4599. https://doi.org/10.3390/en15134599
Chicago/Turabian StyleZhou, Yongqiang, Hongchao Wang, Dingfeng Song, Qian Sheng, Xiaodong Fu, Haifeng Ding, Shaobo Chai, and Wei Yuan. 2022. "Dynamic Response of Lining Structure in a Long Tunnel with Different Adverse Geological Structure Zone Subjected to Non-Uniform Seismic Load" Energies 15, no. 13: 4599. https://doi.org/10.3390/en15134599
APA StyleZhou, Y., Wang, H., Song, D., Sheng, Q., Fu, X., Ding, H., Chai, S., & Yuan, W. (2022). Dynamic Response of Lining Structure in a Long Tunnel with Different Adverse Geological Structure Zone Subjected to Non-Uniform Seismic Load. Energies, 15(13), 4599. https://doi.org/10.3390/en15134599








