Rotor Investigation of High-Speed Permanent Magnet Motor with Roundness Error and CFD-Thermal Distribution Analysis

Abstract

The rotor overtemperature caused by losses is one of the important issues for the high-speed electrical machine. This paper focuses on the rotor loss analysis and CFD-thermal coupling evaluation for 105 kW, 36,000 r/min HSPMSM. Three types of sleeve materials as carbon-fiber, Titanium alloy, and stainless steel are introduced in this paper, researching the effects of sleeve conductivity, thickness and rotational speed on rotor eddy current loss, balancing rotor mechanical strength. The sleeve made of titanium alloy material with a thickness of 3.5 mm is chosen to effectively suppress the rotor eddy current loss in high-speed motors in the paper. The air friction loss becomes significant based on the PM motor at high rotational speed. The roundness error of the rotor sleeve has the important impact on the air friction loss of the rotor and the rotor temperature of the motor, which leads to the over temperature of the rotor. Therefore, based on the CFD fluid model, the influence of roundness error, cooling parameters, rotational speed and temperature boundary on the air friction loss is studied in detail, and the expression is summarized to provide reference for estimating the air friction loss. According to the rotor structure in this paper, the optimal cooling air inlet velocity is 10 m/s. Finally, the loss separation method is used to obtain the air friction loss measurement results. The accuracy of the finite element calculation results of air friction loss is verified through the experimental data. The temperature rise of the HSPMSM was also measured with 5.5% error. In this paper, the conclusion and analysis method could provide some reference for the research of the rotor structure and the improvement of the efficiency of HSPMMs.

1. Introduction

High-speed permanent magnet motors (HSPMM) have been widely used in various new energy industries due to their high efficiency and high-power density. However, HSPMM requires consideration of various factors including power losses, thermal distribution, rotor stress, rotor dynamics and permanent magnet demagnetization [1,2].

In the literature [3,4], the loss types of amorphous metal stator cores were analyzed and experimentally verified by numerical analysis methods for motors at no-load and rated load, while motors made of silicon steel have high losses and relatively poor performance under no-load conditions. The results are useful for the design and optimization of high-speed motors with amorphous metal stator cores and titanium alloy housings. Fluid 2D finite element analysis is used to optimize the torque quality and reluctance losses of high-speed PMSMs with concentrated windings operating in a wide range of speed regulation [5]. AC copper losses in the stator coil and iron losses at high frequencies were also investigated in the literature [6]. In addition, AC copper losses and iron losses at high frequencies in the stator coils were also studied. In the literature [7], the electromagnetic and temperature fields of SMPMSM were analyzed using the coupled method of electromagnetic and temperature fields and the data of losses and temperature rise were obtained. Based on these calculation results. The effect of voltage harmonics on the SMPMSM was quantified.

In order to reduce the motor over-temperature problem due to the high speed of the HSPMM, the literature [8] analyzed the three-dimensional model of the FEPM with a water jacket constructed a three-dimensional model of the FEPM equipped with a water jacket and analyzed the temperature distribution by thermal fluid numerical analysis. The literature [9,10] investigated the relationship between ambient pressure, cooling medium temperature and temperature distribution and observed the effect of helium on the heat transfer of the drive motor. The literature [11] compared and analyzed the effect of the existing water jacket and the circular spiral channel on the temperature rise and found that the latter was more favorable for heat dissipation. In addition, the width of the circular spiral water channel is the most reasonable at 40 mm. In the literature [12,13], in order to solve the serious heating problem of high-efficiency high-voltage motors due to high power density and high electromagnetic load, the study carried out fluid network research to predict the temperature and analyze the motor energy efficiency by global fluid-solid coupling. In the literature [14], a water-cooled structure with a water-cooling plate between the primary double-layer windings of a permanent magnet synchronous linear motor was designed and investigated.

Due to the high power and ultra-high speed of this permanent magnet synchronous motor, the influence of the mechanical form of the rotor at high speed is a non-negligible aspect. In the literature [15], in order to analyze the mechanism of TRUM efficiency improvement, the contact interface and rotor vibration information were extracted. The literature [16] proposed a hybrid sleeve topology, which contains a titanium inner cylinder and an outer cylinder made of carbon fiber composite (CFC), to suppress the rotor vortex losses. Theoretical approximate solutions for the mean coefficients of hydrostatic journal bearings with different recesses were obtained in the literature [17,18,19]. Theoretical approximate solutions of the mean coefficients of hydrostatic bearings with different recesses were obtained, pointing out the harmonic components of the roundness errors that have a major influence on the rotational accuracy.

The above literature provides some analysis of high-speed permanent magnet (PM) motors, but some factors are not considered. For example, the outer surface of the rotor is usually not machined in order to avoid the mechanical structure strength of the high-speed motor rotor to be affected. However, this practice leads to a certain roundness error of the rotor, which in turn affects the air friction loss on the rotor surface and the temperature distribution of the motor. This problem cannot be neglected in the research in order to ensure the safety and reliability of the motor operation. The problem has not been well solved yet, and this paper will analyze and study it in detail.

In this paper, a 105 kW 36,000 r/min HSPMSM is studied to provide some technical references for rotor sleeve selection by coupling analysis of eddy current loss and stress field of the rotor sleeve. Since the study of rotor sleeve roundness error and rotor air friction loss, cooling air path and thermal field variation has not been covered, and it is difficult to consider the effect of roundness error by empirical formula method. Therefore, we innovatively investigate the effect of roundness error on air friction loss and analyze the forced air-cooled air inlet speed suitable for high-speed permanent magnet motors by bi-directional FEM-CFD-thermal coupling. In this way, the effect of roundness error on the air friction loss of the motor can be reduced. In this process, the air friction loss of HSPMSM is analyzed in detail. The above research has significant implications for the design of high-speed permanent magnet motors. Finally, the feasibility of the theoretical analysis is verified by experiments.

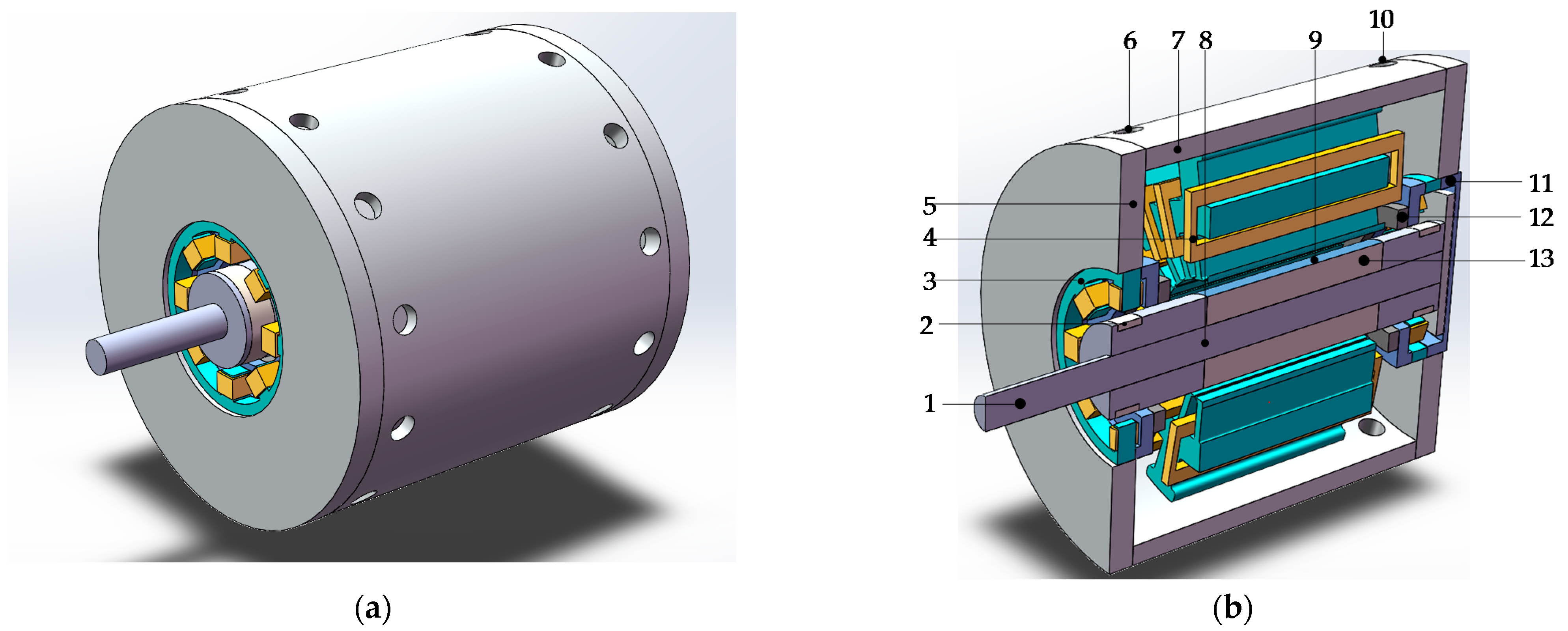
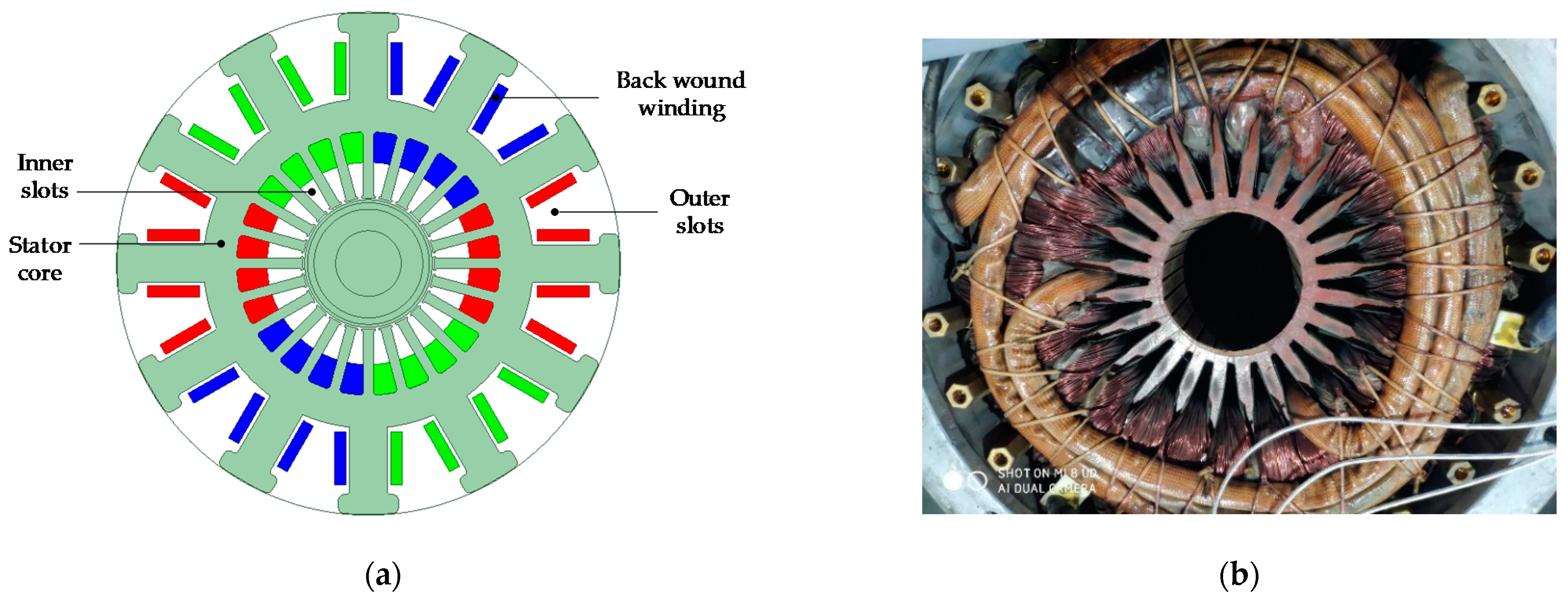
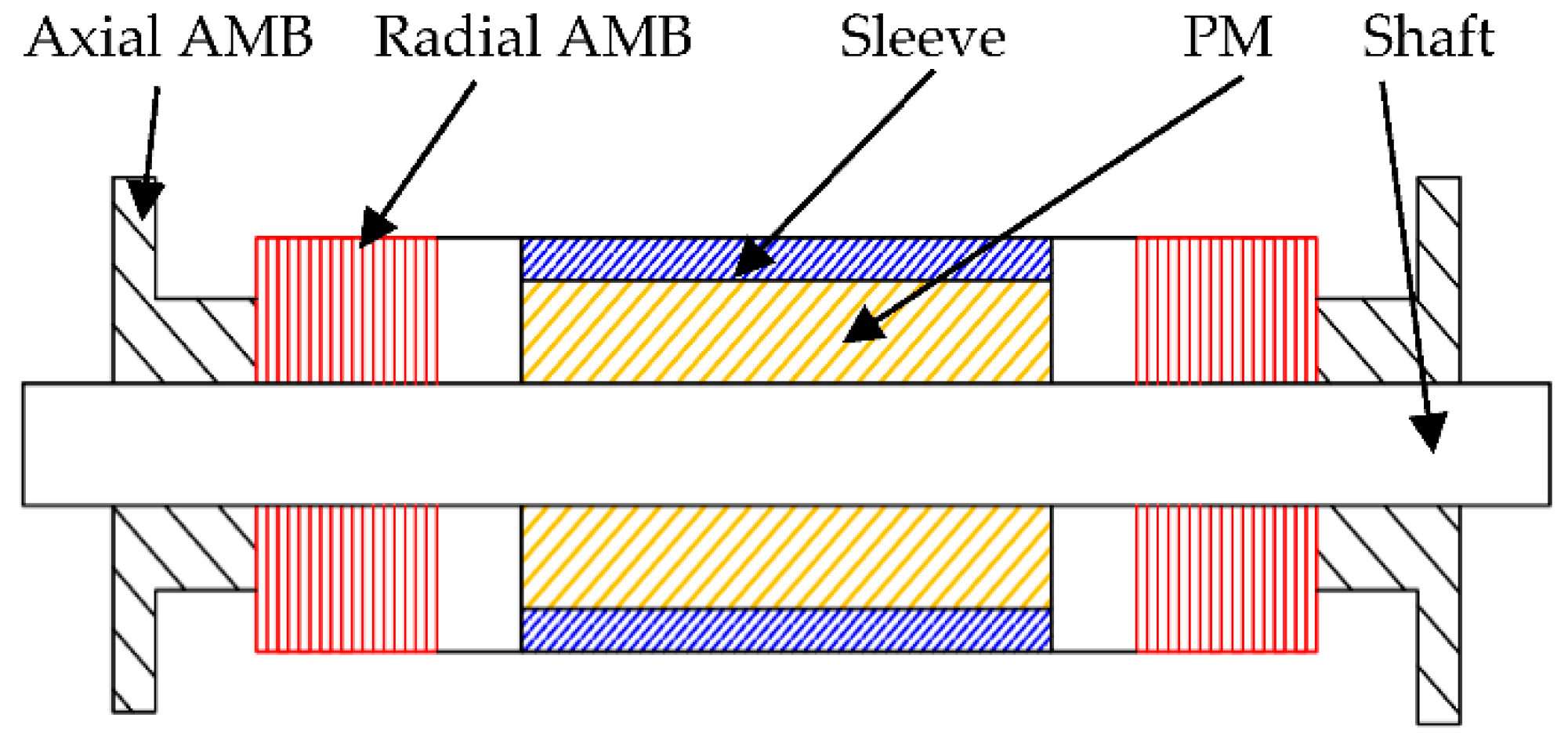
2. Motor Structure

In the section, a 105 kW 36,000 r/min HSPMSM with a surface-mounted PM is designed. The structure contains of the motor stator, composite rotor, two radial active magnet bearings (AMBs), an axial active magnet bearing, shell and so on. In addition, the transverse section of the machine is shown in Figure 1. The motor is designed with 2-poles 24 slots structure. The stator core consists of 0.2 mm silicon steel sheet. The main parameters of the electrical machine are listed in

Table 1. Parameters of HSPMSM.

Parameter	Value	Unit
Rated Power	105	kW
Rated speed	36,000	r/min
Number of poles	2
Frequency	600	Hz
Efficiency	95	%
Power factor	0.94
Inner and outer slot area ratio	2/5
Outer diameter of stator core	180	mm
Stator Core length	140	mm
Phases resistance	1785	Ω
Slot fill factor	60	%
Air gap length	2.5	mm
Rotor outer diameter	65	mm
PM grade	N33EH
Remanent flux density of PM/Br	1.15	T
Intrinsic coercivity of PM/Hcj	30	kOe

.

In the paper, because of the large pitch of 2 pole motor, the use of the traditional winding form will result in high leakage resistance at the end of the high-speed motor winding, which will increase the amount of copper and the overall axial length of the motor. Therefore, the back wound winding is adopted to avoid too large pitch, as shown in Figure 2. It can improve the efficiency a little. More importantly, one merit of the back wound winding is no space occupied by the ends of the winding, avoiding too long rotor to reduce stiffness. In order to solve the problem of overheating at the end of motor winding, the motor adopts back winding, which is beneficial to air cooling duct, enhancing heat dissipation capacity.

Due to the PM with large compression strength but small tensile strength, it needs heat shrink to fit metallic sleeve, bearing the strong mechanical stress produced by high-speed centrifugal force. A thin sleeve will be recommended to increase the air-gap width on the premise of meeting the strength. In addition, the PM demagnetization is related with the overtemperature of the rotor, which is the main issue in the HSPMSM. In the paper, N33EH is adopted as PM, withstanding the maximum of 200 °C.

Based on the theoretical analysis and experience, a major improvement has been made to acquire a better cooling and motor reliability. In addition, the force cooling air inlet is arranged on the end of the motor. The rotor is cooled by the axial forced cooling air through gap and part slot. After the cooling airflow is pressurized by the blower on the right side of the housing, it enters the housing from the air duct inlet on the distribution housing to cool the winding end and rotor, respectively. At the same time, in order to achieve better rotor cooling effect, the area of the left and right air inlets and air outlets of the housing are designed differently so that a certain pressure difference is formed between the left and right ends of the air gap, thus allowing the cooling airflow to pass through the motor air gap.

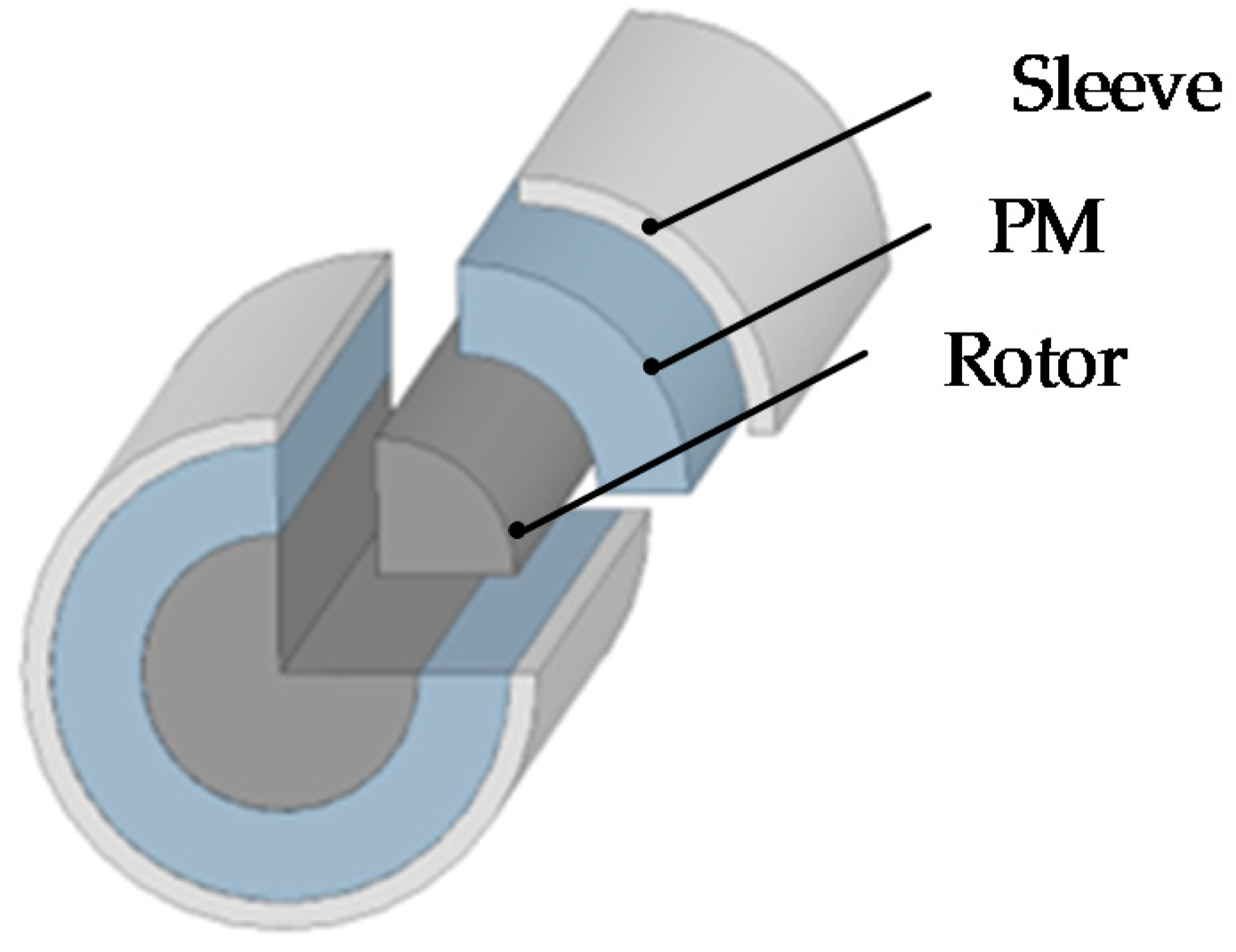
3. Rotor Sleeve Analysis

The rotor is the part of the motor that outputs energy to the outside, and it is essential to study it. The radial structural surface of the rotor of the high-speed motor studied in this paper is shown in the Figure 3. As can be seen from the figure, the rotor adopts a surface-mounted 2-pole PM circuit structure. The PM poles are symmetrically arranged on the outer surface of the rotor core. The permanent magnets are fixed to the outer surface of the rotor core using a sleeve. The shaft and rotor are integrated solid structure.

The target motor in this paper has a rated operating condition of 600 Hz and 36,000 r/min. Compared with other types of motors, its speed is relatively high, so the losses in its rotor area are also higher. In order to reduce the eddy current losses at the rotor sleeve location, this section uses the FEM to perform a comprehensive analysis of eddy current losses and mechanical stresses for sleeve of different conductivity, different materials and thicknesses.

3.1. Theoretical Analysis of Eddy Current Loss with Sleeve

When the rotor sleeve is made of titanium, the eddy current loss of the rotor is calculated as shown in Figure 4.

The influence of eddy current loss on rotor was analyzed by studying the relationship between eddy current loss and the rotor diameter, the PM size, magnetic field generated by PM, the rotational speed, the conductivity of rotor sleeve, the material properties of sleeve and sleeve thickness, etc.

The mathematical expression of eddy current loss on sleeve surface is as follows [20]:

$$P_{eddy}=K_{\mathrm{e}}(\frac{b}{4{\psi }_1})\alpha L\sigma B_{\delta }^2{n}^2(a+H)e^{(-2\beta H)(1-e^{-2{\psi }_{{}_1}m})}$$

(1)

$$\alpha =\pi (a+H)\frac{\theta }{180}+\frac{1}{k}(\frac{d_1+d_2}{2})$$

(2)

$$\beta =\frac{\pi }{2b+\frac{d_1+d_2}{2}}$$

(3)

$$\gamma =0.5\arctan [-\frac{2\pi n}{60}\mu (a+H)\frac{\sigma }{\beta }]$$

(4)

$${\psi }_1={[{\beta }^4+(n\mu {\sigma }^2)]}^{0.25}\cos \gamma$$

(5)

From Formula (1) above, it can be seen that the difference of rotor sleeve materials has an impact on eddy current loss. From Formula (1) above, it can be seen that the difference of rotor sleeve materials has an impact on eddy current loss. The electrical conductivity of sleeve is one of the key factors affecting the eddy current loss of rotor, and the eddy current loss will increase with the increase of electrical conductivity. In addition, because of the metal properties of titanium alloy, its electrical conductivity is lower than stainless steel. To maintain the same air magnetic flux density, eddy current losses are analyzed with different conductivity, different speed by FEM.

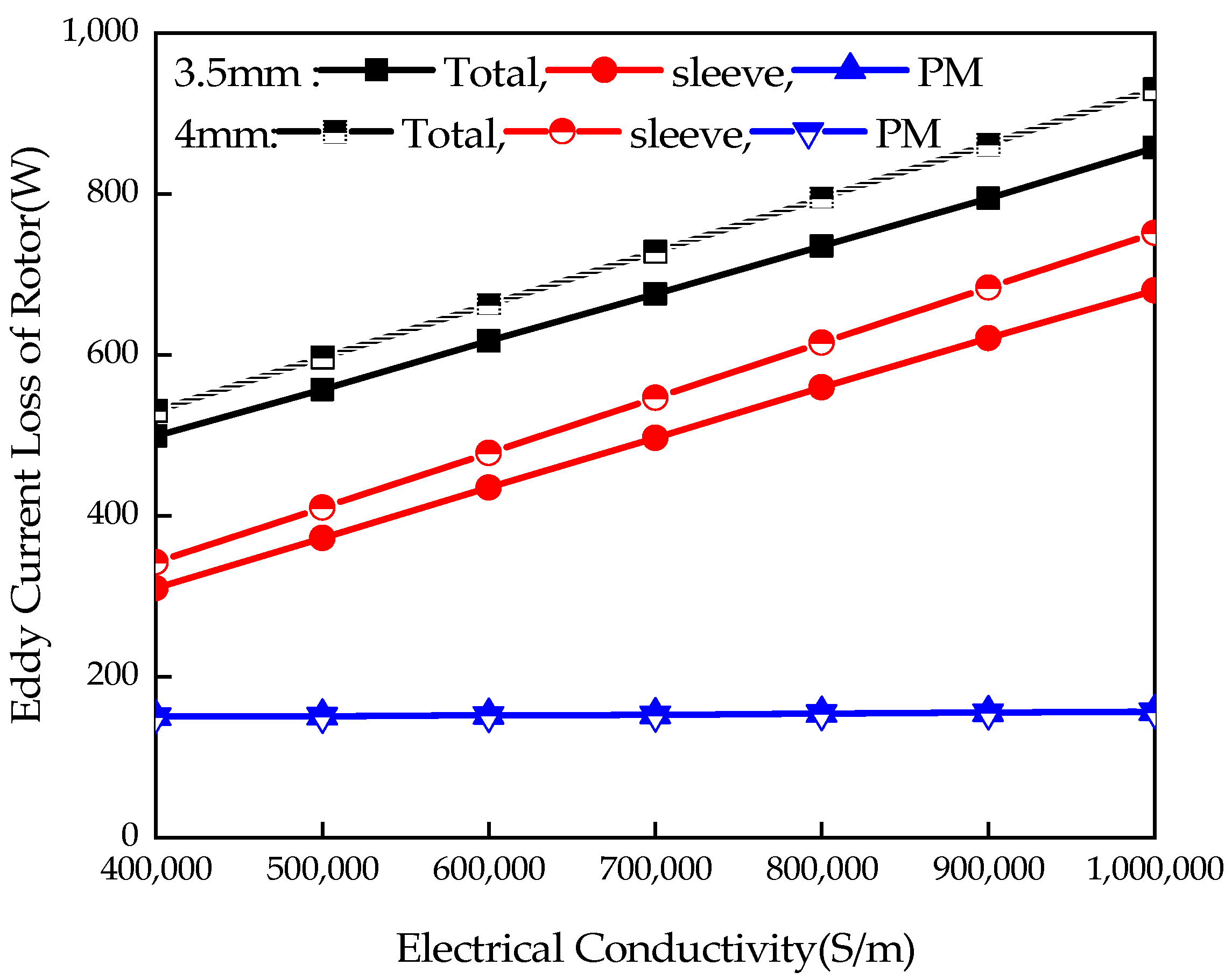
3.2. Eddy Current Loss Calculation with Different Sleeve Conductivity

As known, eddy current loss is affected by the material characteristics of rotor sleeve. The difference is helpful to choose the appropriate sleeve material. According to the above Formula (1), the different conductivity of the sleeve material has a great impact on the eddy current loss. With the increase of conductivity, the eddy current loss increases.

In order to investigate the law of conductivity and eddy current loss, it was calculated with the sleeve conductivity of 0, 500,000 S/m, 600,000 S/m, 700,000 S/m, 800,000 S/m, 900,000 S/m, …, 1,400,000, respectively. The sleeve thickness is varied with 3.5 mm and 4 mm, the PM size is from Appendix A, and it is at the rated frequency of 36,000 r/min. The calculation results are shown in Figure 5.

And because of the conductor properties of sleeve, where the electrical conductivity of the carbon fiber, titanium alloy, and stainless steel are 2 × 10⁴, 4.375 × 10⁵, and 1.0 × 10⁶ S/m, respectively. Figure 5 shows the eddy current losses with different conductivity and different thickness. Therefore, at the same speed, the eddy current loss of stainless-steel rotor sleeve will increase correspondingly, compared with titanium alloy sleeve. It is the lowest with carbon fiber.

Based on calculation results of Figure 5, the relationship between the eddy current loss of the sleeve conductivity and thickness can be fitted, and Formulas (6) and (7) can be summarized.

$$P_{\mathrm{sleeve}}=6.19\times {10}^{-4}\sigma +63.311 (\mathrm{thickness} \mathrm{is} 3.5\mathrm{mm})$$

(6)

$$P_{\mathrm{sleeve}}=6.823\times {10}^{-4}\sigma +69.319 (\mathrm{thickness} \mathrm{is} 4\mathrm{mm})$$

(7)

3.3. Eddy Current Loss Calculation at Different Rotational Speed

In the paper, three types of sleeve materials as carbon-fiber, titanium alloy, and stainless steel are introduced in this paper. Eddy current loss is studied with the conductivity of sleeve, as Figure 5. Furthermore, it is analyzed that the eddy current loss of sleeve is calculated with different speeds, different thickness for three types of sleeve materials.

By analyzing the calculated eddy current loss results in Figure 6, it can be seen that the carbon fiber sleeve has the lowest eddy current loss of 110 W at the same sleeve thickness, which basically does not change with the speed, but its thermal conductivity is poor according to the thermal conductivity parameters in

Table 2. Thermal conductivity of different sleeve materials.

Material	Heat Conduction Coefficient (W/m·K)	Density (g/cm3)	Specific Heat Capacity (J/g·°C)
Titanium alloy	7.955	4.51	0.612
Stainless steel	16.3	7.9	0.46
Carbon fiber	0.7	1.8	0.170

. Under the same sleeve thickness, the rotor sleeves made of stainless steel and titanium alloy have eddy current losses of 680 W and 310 W, respectively, at the rated speed of the motor of 36,000 r/min, but the thermal conductivity of these two materials is better. Therefore, considering the eddy current loss, heat dissipation, processing and manufacturing difficulty of the motor rotor sleeve, titanium alloy is chosen as the production material of the high-speed motor rotor sleeve in this paper. It is worth noting that as the sleeve thickness increases, the eddy current loss produced by any material tends to increase.

Based on the above calculation results, the relationship between the eddy current loss of the titanium alloy rotor sleeve and the motor speed frequency can be fitted, and formula (8) can be summarized. This relationship provides a reference for calculating the eddy current loss on the surface of the rotor sleeve at different frequencies of the high-speed motor.

$$P_{\mathrm{sleeve}}=1.51{{\displaystyle f}}^{1.68}$$

(8)

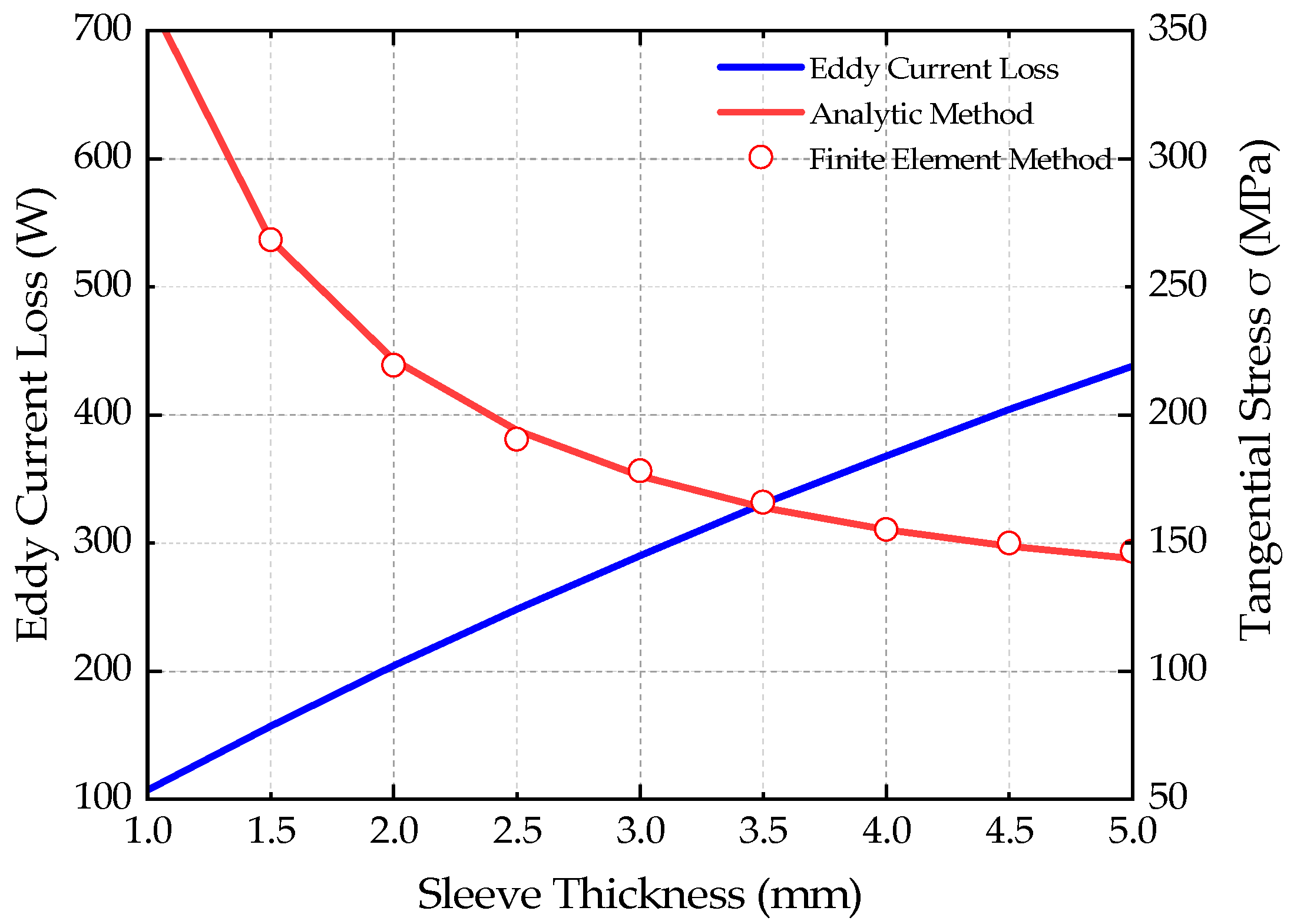
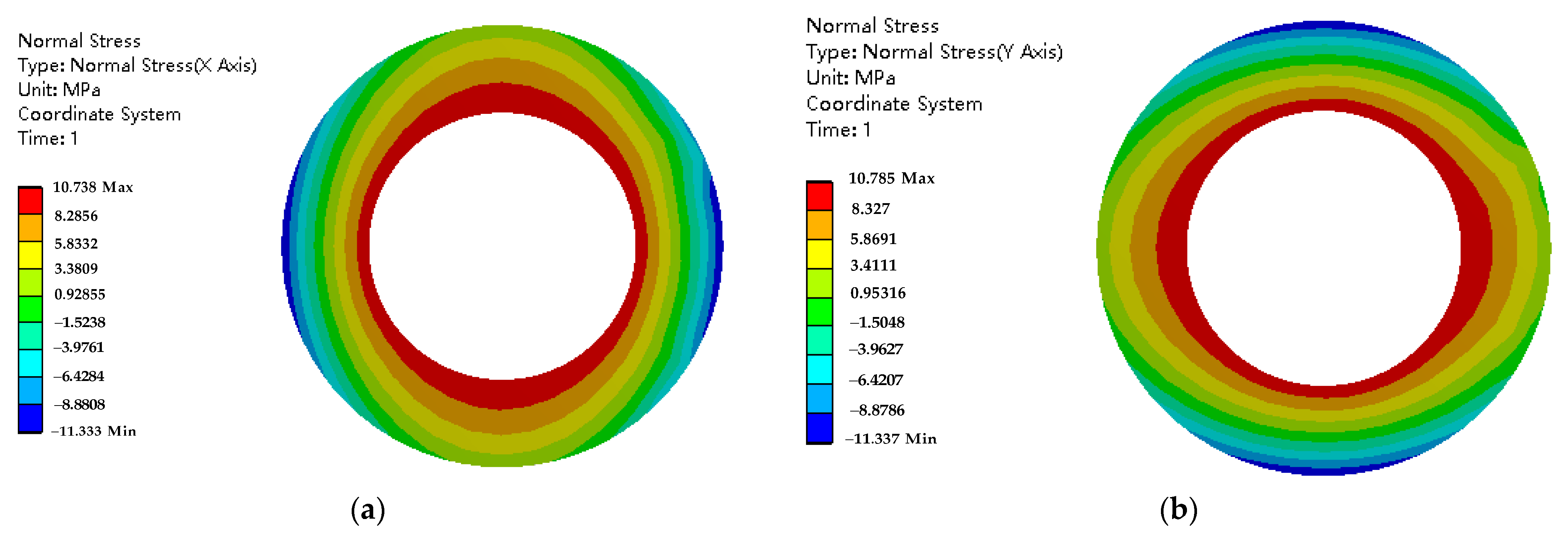
3.4. Calculation of Mechanical Stress at Different Sleeve Thicknesses

Based on the analytical theory of the rotor strength, the analytical Lame equation [21,22,23,24] of the static and rotation condition are all studied.

$$\{\begin{array}{l}{\sigma }_{\mathrm{re}}={\sigma }_{\mathrm{re}}\prime +{\sigma }_{\mathrm{re}}″\\ {\sigma }_{\mathsf{\theta }\mathrm{e}}={\sigma }_{\mathsf{\theta }\mathrm{e}}\prime +{\sigma }_{\mathsf{\theta }\mathrm{e}}″\end{array} \{\begin{array}{l}{\sigma }_{\mathrm{rm}}={\sigma }_{\mathrm{rm}}\prime +{\sigma }_{\mathrm{rm}}″\\ {\sigma }_{\mathsf{\theta }\mathrm{m}}={\sigma }_{\mathsf{\theta }\mathrm{m}}\prime +{\sigma }_{\mathsf{\theta }\mathrm{m}}″\end{array}$$

(9)

$$\{\begin{array}{l}{\sigma }_{\mathrm{re}}\prime =\frac{b^2{p}_s}{c^2-b^2}(1-\frac{c^2}{r^2})\\ {\sigma }_{\mathrm{rm}}\prime =-\frac{b^2{p}_s}{b^2-a^2}(1-\frac{a^2}{r^2})\end{array}$$

(10)

$$\{\begin{array}{l}{\sigma }_{\mathsf{\theta }\mathrm{e}}\prime =\frac{b^2{p}_s}{c^2-b^2}(1+\frac{c^2}{r^2})\\ {\sigma }_{\mathsf{\theta }\mathrm{m}}\prime =-\frac{b^2{p}_s}{b^2-a^2}(1+\frac{a^2}{r^2})\end{array}$$

(11)

$$\{\begin{array}{l}{\sigma }_{\mathrm{re}}″=\frac{3-2{\gamma }_e}{8(1-{\gamma }_e)}{\rho }_e{\omega }^2(b^2+c^2+\frac{c^2{b}^2}{r^2}-r^2)\\ {\sigma }_{\mathrm{rm}}″=\frac{3-2{\gamma }_{\mathrm{m}}}{8(1-{\gamma }_{\mathrm{m}})}{\rho }_{\mathrm{m}}{\omega }^2(b^2+a^2+\frac{a^2{b}^2}{r^2}-r^2)\end{array}$$

(12)

$$\{\begin{array}{l}{\sigma }_{\mathsf{\theta }\mathrm{e}}″=\frac{3-2{\gamma }_e}{8(1-{\gamma }_e)}{\rho }_e{\omega }^2(b^2+c^2+\frac{c^2{b}^2}{r^2}-\frac{1+2{\gamma }_e}{(3-2{\gamma }_e)r^2})\\ {\sigma }_{\mathsf{\theta }\mathrm{m}}″=\frac{3-2{\gamma }_{\mathrm{m}}}{8(1-{\gamma }_{\mathrm{m}})}{\rho }_m{\omega }^2(b^2+a^2+\frac{a^2{b}^2}{r^2}-\frac{1+2{\gamma }_{\mathrm{m}}}{(3-2{\gamma }_{\mathrm{m}})r^2})\end{array}$$

(13)

According to Formula (1), when the thickness of the rotor sleeve increases, the rotor eddy current loss of the HSPMSM also increases. Therefore, the thickness of the rotor sleeve should be thinner as much as possible, while it should meet the requirement of the rotor strength. In this paper, the effect of rotor sleeve thickness variation on rotor eddy current loss and rotor strength is investigated. According to the rotor dimensions and parameters in the Appendix A, the results of rotor sleeve eddy current loss and sleeve stress under different thickness of titanium sleeve are shown in Figure 7.

In order to prevent the PM from falling off and the sleeve from breaking, the contact pressures between the shaft and the PM, between the PM and the sleeve shall be greater than 10 MPa; The allowable stress of the sleeve should be greater than the tangential stress of the sleeve. k is safety factor. Based on these two requirements, the relationship between the rotor stress and sleeve thickness is investigated, and the appropriate sleeve thickness is selected.

$$\left|{\sigma }_{\mathrm{r}}\right|>10\mathrm{MPa}$$

(14)

$${\sigma }_{\mathsf{\theta }\mathrm{e}}<[{\sigma }_{\mathrm{e}}]/k_{}^{}{=}_{}420/2.5=168 \mathrm{MPa}$$

(15)

According to the calculation results in Figure 7 and the simulation analysis above, it can be concluded that the thinner the rotor sleeve is, the smaller the eddy current loss generated by the rotor will be. However, as the thickness of the sleeve decreases, the tangential stress will increase accordingly. The rotor sleeve of the high-speed motor should avoid additional deformation caused by the rotor running at high speed, and the tangential stress should be less than 168 MPa. In summary, a titanium-zinc alloy rotor sleeve with a thickness of 3.5 mm is selected from the Figure 7.

In addition, according to the curve of rotor sleeve thickness and eddy current loss made of titanium alloy, the relationship between rotor sleeve thickness and eddy current loss can be analyzed and fitted. Its expression is (16). Where, m is the thickness of titanium alloy.

$${\mathit{P}}_{\mathrm{sleeve}}=120\times e^{(0.2688m_{})}$$

(16)

And furthermore, it is used in FEM to simulate the sleeve stress with 3.5 mm thickness, shown in Figure 8a,b, and PM stress as Figure 9a,b. The simulation results in FEM are consistent with the analytical method. It can be seen from Figure 8b, the sleeve stress in the tangential direction is 170 MPa as maximal value, which is very close to the limit of 168 MPa. In addition, it can be also seen from Figure 9a,b, the PM stress in the radial and tangential direction is 10.7 MPa with shaft, and 11.3 MPa with sleeve, which is bigger than the limit of 10 MPa.

4. Analysis of Air Friction Loss of HSPMSM

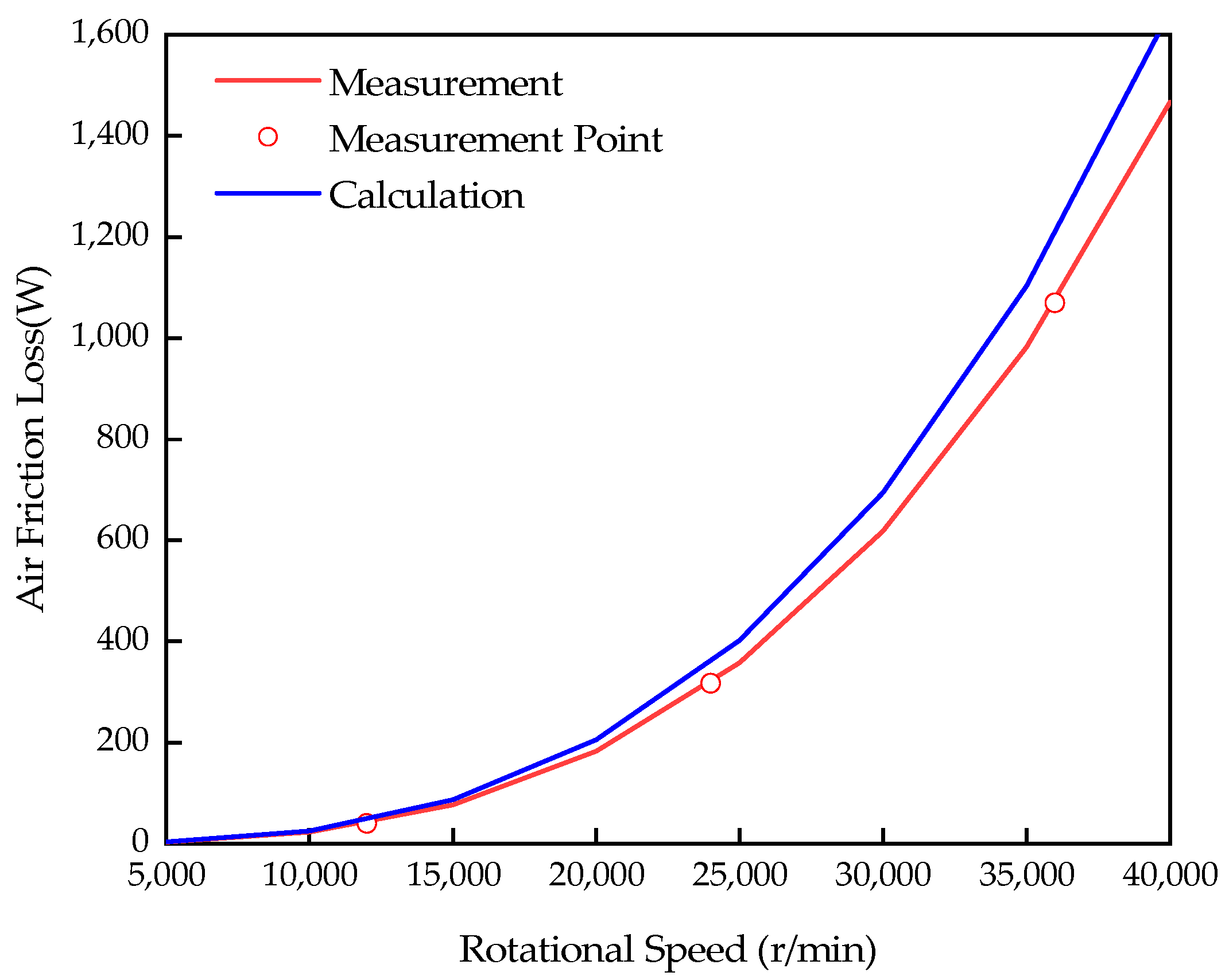
4.1. The Effect of Rotational Speed on the Air Friction Loss

When the motor from the start to work at the rated point of this period of time, the speed of rotor is increasing, and the relative speed of the surrounding air increases, and the loss caused by mutual friction increases [2]. Therefore, air friction loss is particularly important for the loss analysis of HSPMSM. In this paper, the rotor structure of the HSPMSM with magnetic levitation bearing is shown in Figure 10.

The motor air friction loss caused by rotor rotation can be divided into two parts. The first part is the loss caused by friction between the axial and end surfaces of the rotor and the air gap of the motor. The other part is the loss caused by the acceleration of external air into the motor air gap due to rotor rotation.

This section mainly studies and analyzes the air friction loss of the motor, and the calculation formula of the air friction loss on the rotor surface is as (17). The axial and radial Reynolds coefficients can be expressed as [25]:

$$P_{\mathrm{fric}1}=k{C}_f\pi \rho {\omega }^3{r}^{4}l$$

(17)

$$C_{\mathrm{f}}=\frac{0.0152}{{\mathrm{Re}}_{\delta }^{0.24}}{\left[1+{\left(\frac{8}{7}\right)}^2{\left(\frac{4{\mathrm{Re}}_{\partial }}{{\mathrm{Re}}_{\delta }}\right)}^2\right]}^{0.38}$$

(18)

$$\{\begin{array}{l}{\mathrm{Re}}_{\delta }=\frac{{\rho }_{\partial }{\omega }_{m}r\delta }{{\mu }_{\partial }}\\ {\mathrm{Re}}_{\partial }=\frac{{\rho }_{\partial }{v}_{\partial }2\delta }{{\mu }_{\partial }}\end{array}$$

(19)

The calculation formula of air friction loss after rotor end face generation is as follows. The expressions of Reynolds coefficients on the end face of the rotor are shown in equations:

$$P_{\mathrm{f}\_\mathrm{end}}=\frac{1}{2}{C}_{\mathrm{M}}\rho {\omega }^3\left(r_2^5-r_1^5\right)$$

(20)

$$C_{\mathrm{M}}=\frac{3.87}{{\mathrm{Re}}_{\mathrm{M}}^{0.5}} {\mathrm{Re}}_{\mathrm{M}}<3\times {10}^5$$

(21)

$${\mathrm{Re}}_{\mathrm{M}}=\frac{\rho {\omega }^{}{r}_2^2}{4\mu }$$

(22)

According to Formula (17), air friction loss caused by external air entering the air gap due to rotor acceleration can be calculated.

$$P_{\mathrm{acc}}=\frac{2}{3}\pi {\rho }_{\mathrm{air}}{v}_{\mathrm{a}}{v}_{\mathrm{t}}\left(r_{\mathrm{s}1}^3-r_r^3\right)\mathsf{\Omega }$$

(23)

Based on the above theoretical analysis, this paper uses FE simulation method to calculate the air friction loss. The FE calculation model used for solving is shown in Figure 11. In order to further analyze the influence of air friction on the high-speed motor, the variation trend of air friction at different speeds was calculated, as shown in Figure 12.

According to the above graph, it is seen when the motor speed is low, the air friction loss is small and almost negligible. However, when the speed exceeds 15,000 r/min, the rotor air friction increases rapidly at the corresponding speed, as shown in Figure 12. It is obvious the rotor air friction loss of high-speed motors accounts for a considerable relative percentage, compared with normal motors.

As can be seen from Figure 12, when the motor does not provide strong cooling air, the air friction loss is only caused by the speed. The loss in the FE calculation results is proportional to the cubic power of the velocity, and the simulation results are consistent with the calculation Formulas (18) and (19). At rated speed of 36,000 r/min, the FE calculation result of air friction loss is 1050 W. However, when the axial cooling wind speed v is greater than 0 m/s, the air friction loss of the motor becomes the loss caused by the combined action of speed and strong air cooling through the air gap. The FE calculation results show that the larger v is, the greater the air friction loss of the motor is. Therefore, in order to reduce the air friction loss of high-speed motor and ensure that the motor will not overheat, the appropriate axial cooling wind speed should be selected.

4.2. The Effect of Roundness Error on Air Friction Loss

The Figure 13 shows the structure of the rotor when the sleeve produces roundness error, which is a problem caused by the outer surface of the sleeve without mechanical processing, and there are two cases that often occur in actual engineering, which are elliptical and trilobal. Figure 13a,b show, respectively, where $R_s$ and $R_r$ are the inner diameter of the sleeve and PM of the rotor without roundness error, and $A_{Err}$ is the error between the inner diameter of the rotor sleeve $R_s$ and the error generated after the roundness error. In the above analysis, it is assumed that the circularity error generated by the sleeve is a uniform deformation.

The geometric parameters of the finite element model of the motor rotor based on the circularity errors generated above are shown in

Table 3. Geometric parameters of the FEM of the rotor.

Geometric Parameters	Value (mm)
Rotor outer diameter	65
Stator inner diameter	70
Core length	140
Roundness error amplitude	0; 0.1; 0.2 0.3; 0.4; 0.5

. For the roundness error magnitudes listed in the table, the rotor finite element model needs to be reconstructed once its magnitude is changed.

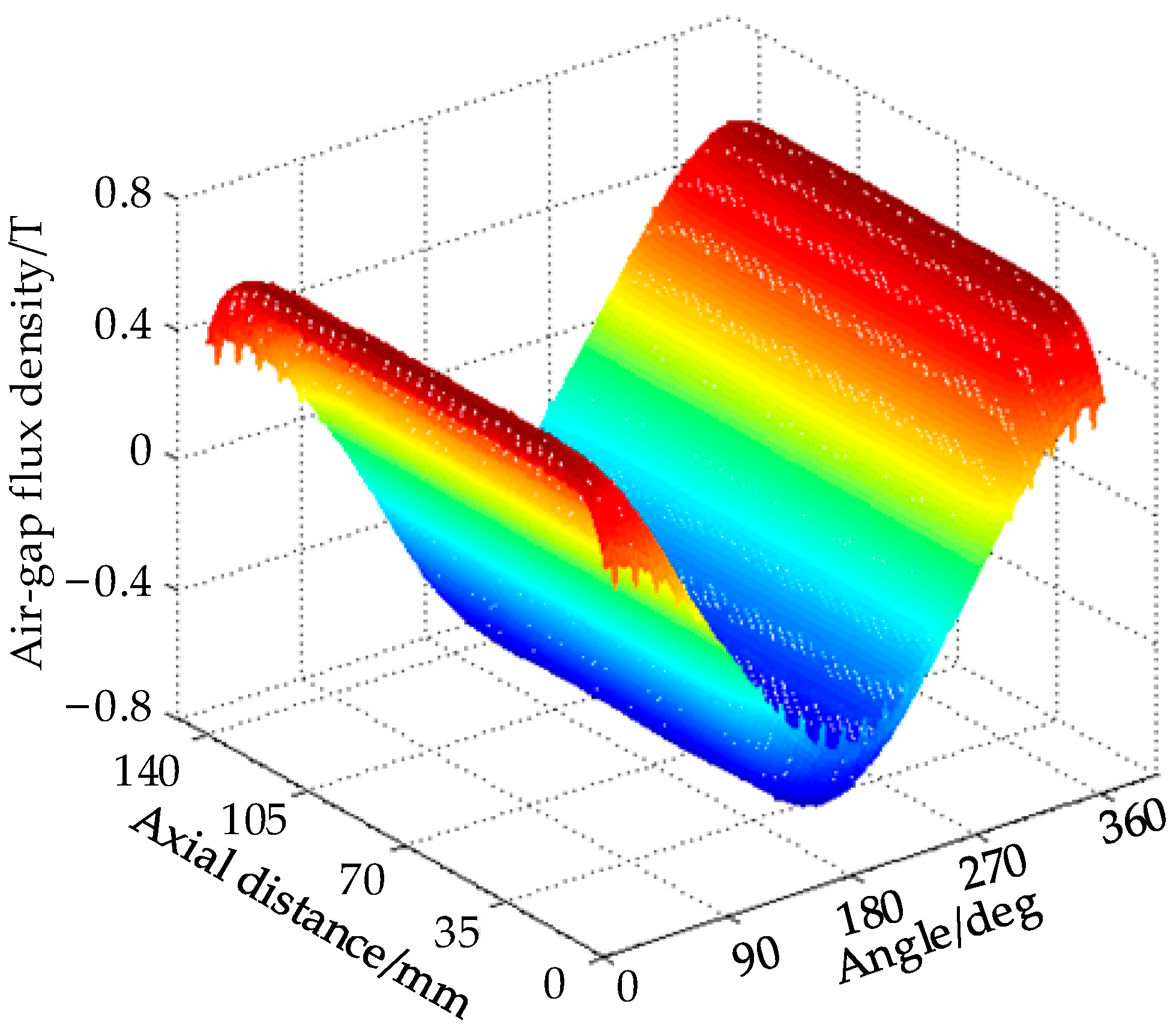
4.2.1. Mathematical Model of Motor Air Gap Considering Sleeve Roundness Error

The motor rotor is forced air-cooled, and the following basic assumptions can be made when mathematically modeling the three-dimensional flow in the motor air gap [26].

(1)

The airflow in the air gap of the motor is an incompressible fluid;

(2)

The effect of air gravity is not considered;

(3)

The airflow in the air gap is turbulent;

According to the above assumptions, the control equation for the airflow in the air gap of the motor can be expressed as (24):

$$\{\begin{array}{c}\frac{\partial \rho u}{\partial x}+\frac{\partial \rho v}{\partial y}+\frac{\partial \rho w}{\partial z}=0\\ \rho \frac{\mathrm{d}\mathrm{v}}{\mathrm{d}\mathrm{t}}=-\nabla p+\mathit{pF}+\mu \mathsf{\Delta }V\\ \frac{\partial \left(\rho T_t\right)}{\partial t}+\mathit{div}\left(\rho \mathit{uT}\right)=\mathit{div}\left(\frac{k_t}{c_p}\mathit{gradT}\right)+S_T\end{array}$$

(24)

Since the turbulent shear stress contains the viscous shear stress term and the additional shear stress term, and the velocity field distribution is obtained by the control equation, the rotor outer wall surface shear stress can be expressed as (25):

$$\tau =\mu \frac{{\mathit{du}}_x}{\mathit{dy}}-\rho u_x^{\prime }{u}_y^{\prime }$$

(25)

The air friction loss on the outer surface of the sleeve can be expressed as the area division of the inner product of the two vectors of sleeve surface linear velocity and outer surface tangential stress along the outer surface of the sleeve:

$$P_f={\displaystyle \int \left(\stackrel{\rightharpoonup }{\omega }\times \stackrel{\rightharpoonup }{r}\right)}·\stackrel{\rightharpoonup }{\tau }\mathit{dA}$$

(26)

After determining the mathematical model of motor FE solution, Fluent is used to mesh the motor FEM, as shown in Figure 14. The mesh of the model is divided into tetrahedral units, and the minimum size of the mesh is controlled at 0.50 mm, the thickness of the first layer is 0.00025 mm, the thickness of the expansion layer is 20 layers, and the thickness of the other layers increases at a growth rate of 2.4 per layer.

The velocity boundary condition is used for the inlet of the motor air gap and the pressure boundary condition is used for the outlet. The inlet velocity is set to 0.13 m/s, except for the effect of the inlet velocity condition, and the outlet pressure is set to standard atmospheric pressure. The inner surface of the stator is set as the static boundary, the outer surface of the rotor is set as the rotational boundary, and the axis of rotation is the Z-axis. The stator inner surface temperature was set to 90 °C and the rotor outer surface temperature was set to 25 °C, except for the effect of wall temperature conditions.

The energy equation is opened, the standard k-e model is used, the enhanced wall function is selected, and the SIMPLE semi-implicit algorithm coupled with the pressure-velocity numerical iteration is used to solve the pressure and velocity field distribution of the airflow in the air gap of the motor. In order to ensure the computational efficiency without losing the computational accuracy, the convergence residual value of the flow field calculation is set to 1 × 10⁻³, and the convergence residual value of the temperature field calculation is set to 1 × 10^−6.

4.2.2. The Variation Law of Air Friction Loss on the Outer Surface of the Rotor

In this section, the effect of titanium alloy sleeve with roundness error on the air friction loss on the outer surface of the sleeve is first studied by changing the amplitude and type of roundness error, keeping the other main parameters of the motor unchanged, and the wind speed of the forced air-cooling inlet of the motor is 0 m/s. The Figure 15 shows the air friction loss on the outer surface of the sleeve at a speed of 36,000 r/min with two common types of roundness error, calculated by using the FEM.

According to the analysis of the calculation results, the roundness error amplitude increases from 0 to 0.50 mm, and when the rotor sleeve roundness error is elliptical, the air friction loss is greater than that of the trilobal roundness error, and the difference between the two is the largest when the roundness error amplitude is 0.50 mm, which is 3.48%. This is because the average air gap thickness of the motor is smaller for the same amplitude of elliptical circularity error than that of trilobal circularity error, which leads to the increase of air friction loss on the outer surface of the sleeve. According to the finite element calculation results, the results of fitting the curve of air friction loss with error amplitude under elliptical roundness error are shown in the following formula:

$$P_{\mathrm{fric}}=1839.927-\frac{699.715}{1+e^{\frac{A_{\mathrm{Err}}-0.5773}{0.1428}}}$$

(27)

Based on the above simulation results, we can determine that, among the two forms of rotor sleeve roundness errors that often occur in high-speed motors, the elliptical roundness error has a greater impact on the motor, so the paper will analyze the elliptical roundness error. The

Table 4. The air friction loss on the outer surface of the rotor corresponding to the elliptical roundness error at different magnitudes.

Roundness Error Type	Magnitude (mm)	Tangential Stress (N)	Rotor Surface Air Friction Loss (W)
ellipsoidal	0	5.18	1152.7
	0.1	5.38	1162.8
	0.2	5.51	1187.9
	0.3	5.67	1227.3
	0.4	5.89	1297.1
	0.5	6.01	1397.5

shows the results of the FE calculation of the air friction loss on the outer surface of the rotor for different magnitudes of the elliptical roundness error.

The analysis of the Table 4 shows that when the roundness error of the titanium alloy sleeve increases, the air friction loss on the outer surface of the sleeve will also increase accordingly. The air friction loss on the outer surface of the rotor increases by 21.23% when the roundness error is 0.50 mm compared with 0 mm error. Furthermore, the FEA result of the tangential stress of the rotor sleeve is simulated with the roundness error, as shown in Figure 16.

According to the calculation results in the previous Table 4, Figure 16 shows the relationship between the roundness error $A_{\mathrm{Err}}$ and the tangential stress ${\sigma }_{\theta e}^{″}$ on the outer surface of the rotor, and fit the expression of the function between the amplitude of roundness error $A_{\mathrm{Err}}$ and the tangential stress ${\sigma }_{\theta e}^{″}$ on the outer surface of the rotor according to the calculation results:

$${\sigma }_{\theta e}″=25.24-20.053e^{-\frac{A_{\mathrm{Err}}}{11.77}}$$

(28)

where $A_{\mathrm{Err}}$ is the ellipsoidal roundness error on the outer surface of the rotor of the high-speed motor, and ${\sigma }_{\theta e}^{″}$ is the tangential stress on the outer surface of the rotor at this amplitude of roundness error. This is of central importance for the design of high-speed motor rotor.

The reason for the increase in air friction loss can be explained by the calculated results of the cloud diagram of airflow pressure distribution inside the motor air gap. As can be seen from Figure 17, with the increase in the amplitude of the roundness error, the pressure distribution of the flow field inside the motor air gap is uneven, which leads to an increase in the tangential stress on the inner wall surface of the air gap.

4.2.3. Analysis of the Effect of Forced Air-Cooling Inlet Velocity on the Air Friction Loss

In this section, the effect of forced air-cooling inlet velocity on the rotor surface air friction loss is investigated, only the forced air-cooling inlet velocity is changed and other motor parameters are kept constant. The rotor speed is 36,000 r/min and the roundness error of the titanium alloy sleeve is 0–0.5 mm. The variation curve of the rotor surface air friction loss with the forced air-cooling inlet velocity is obtained by the FE calculation of the flow field inside the motor, as shown in Figure 18.

The analysis of the Figure 18 shows that the fixed roundness error, the rotor surface air friction loss increases continuously with the motor forced air cooling inlet velocity. The reason is that in the case of constant air inlet and outlet area, the motor forced air inlet velocity mainly affects the size of the viscous tangential stress. When the forced air inlet velocity increases, the air friction loss generated on the outer surface of the high-speed motor rotor also increases accordingly. That is, the forced cold air inlet velocity has a greater effect on the turbulent tangential stress and air friction loss on the rotor surface. At the same time, when the forced air-cooling inlet velocity is fixed, the air friction loss on the outer surface of the rotor also increases with the increase of the sleeve roundness error. The reason is that when the roundness error increases, keeping the forced air-cooling inlet velocity unchanged will lead to uneven pressure distribution in the flow field inside the motor air gap, resulting in an increase in tangential stress and thus an increase in the motor air friction loss.

Since roundness error cannot be avoided in the manufacture of motor rotor. Therefore, researchers can reduce the air friction loss of high-speed motors by selecting a suitable motor forced air-cooling inlet velocity, which is an additional loss due to the roundness error that occurs during the assembly of the rotor sleeve.

Since the analysis of the forced air-cooling inlet velocity involves the turbulent tangential stress of the motor, i.e., the pressure in the air gap of the motor, the thermal distribution of the motor during rated operation is required as a condition for selecting the appropriate forced air-cooling inlet velocity. In summary, in order to reduce the tangential stress on the outer surface of the rotor during normal operation of the high-speed motor, and thus reduce the additional air friction loss of the motor due to the roundness error. Therefore, the FE calculation method in this section is used to calculate the fluid and thermal distribution of the motor, and the overall flow chart of the FE calculation is shown in Figure 19.

The range of roundness error $A_{\mathrm{Err}}$ is 0 mm, 0.1 mm, 0.2 mm, 0.3 mm, 0.4 mm, and 0.5 mm. Under this range, the overall thermal distribution and pressure change of the motor is observed by changing the forced air-cooling inlet velocity, which ranges from 0 m/s, 5 m/s, 10 m/s, 15 m/s, and 20 m/s. In order to see the motor temperature variation more intuitively, the calculation results are summarized, and area stacked graphs are produced in this paper, as Figure 20.

Through the analysis of the above calculation results, it can be seen that the fixed roundness error, with the increase of the motor forced air cooling inlet velocity, the overall maximum temperature of the motor is decreasing trend, and the air gap pressure shows a rising trend. This is because the forced air-cooling inlet velocity increases, the cold air flow into the cavity becomes larger when the motor is running, and the heat exchange airflow increases, so the temperature decreasing trend is obvious. When fixed forced air-cooling inlet velocity, with the increase of roundness error, the motor air gap pressure and temperature show a rising trend, but it can be seen in the forced air-cooling inlet velocity of 10 m/s, the pressure increases rapidly, and the change is more obvious than below 10 m/s, and the forced air-cooling inlet velocity of 10 m/s, the motor cooling effect is also better. Therefore, in this paper, 10 m/s is selected as the forced air-cooling inlet velocity of the target motor. The following Figure 21 shows the calculated rotor thermal distribution when the target motor is operated at rated operating conditions and the forced cold air inlet velocity is 10 m/s.

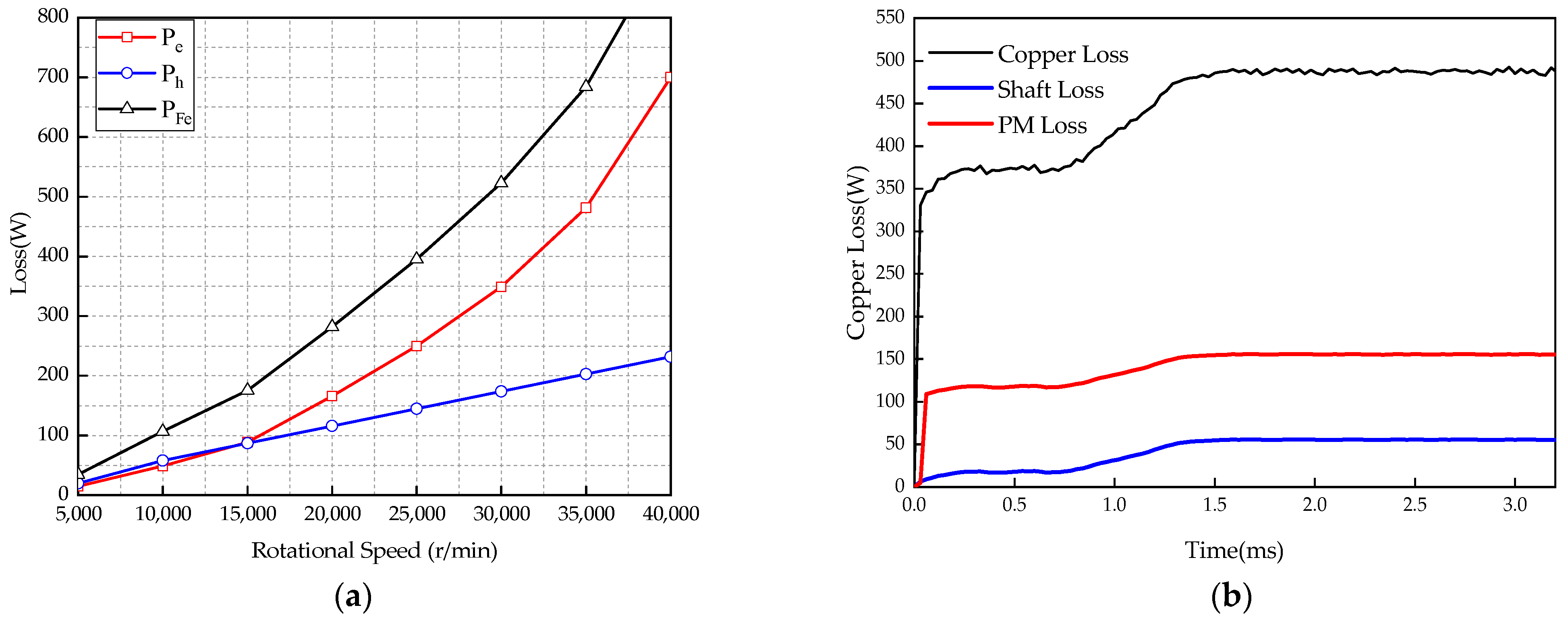
5. Analysis of Overall Motor Loss

In this section, the total loss of high-speed motor includes stator copper loss, stator iron loss, rotor sleeve eddy current loss, rotor permanent magnet loss, air friction loss and other stray loss of mechanical loss, and etc. The specific loss values are shown in

Table 5. Various loss values of high-speed motor by FE.

Loss	Value/W
Stator copper loss	500
Stator iron loss–Eddy current loss	503
Stator iron loss–Hysteresis loss	211
Rotor eddy current loss of sleeve	310
Rotor PM loss	151
Shaft loss	56
Air friction loss	2150
Mechanical additional loss	1120
Total loss	5001

. From the Table 5, it can be obtained the total loss is 5 kW. The rated output power of this HSPMSM is 105 kW, and the efficiency is 95%.

Among them, rotor eddy current loss and air friction loss have been described, with greatly calculated and analyzed in detail in this paper, and their influencing factors and their relations are investigated. In addition, the values of the loss are in Table 5.

Among them, stator iron loss of eddy current and hysteresis section, the stator copper loss and permanent magnet, shaft loss are simulated through the finite element model. The simulated magnetic field cloud diagram is shown in Figure 22, the air gap magnetic density is shown in Figure 23, the simulation curve of stator iron loss, the copper loss, PM loss and shaft loss is shown in Figure 24b or Figure 24a. In addition, from the figure, the values of the stator iron are 503 W of eddy current loss, and 211 W of hysteresis loss. The copper loss, PM loss and shaft loss are 500 W, 151 W and 56 W.

6. HSPMSM Thermal Analysis

In this section, the forced axial cooling method is used in the HSPMSM. This motor is mainly used in blowers, but the special feature is that part of the airflow generated by the motor’s rotating shaft can be used as an external air source to circulate into the motor chamber for circulation purposes, as in Figure 25. The air duct is set at the air gap and the bottom of the slot, which can directly cool the surface of the stator core, some windings in the slot, the rotor sleeve and its rotating shaft. The temperature rise of the rotor is effectively inhibited under its influence. As the forced air-cooling air mainly comes from the impeller, the cold air entering the motor gradually increases with the increase of the rotor speed, and the corresponding air flow of forced-air cooling also increases accordingly, and finally reaches the thermal stability state. Due to the different boundary conditions of the temperature field under this above cooling mode, there is some certain influence of the stator temperature on the rotor.

Since the cooling method of the high-speed motor is convective heat transfer between the air in the stator-rotor air gap and the outer surface of the rotor sleeve. In addition, the heat transfer coefficient can be calculated by the following formula [25]:

$${\alpha }_{}=1+\frac{0.25v_a}{0.045}$$

(29)

And $\alpha$ is the heat transfer coefficient when acting on the outer surface of the air gap and rotor sleeve of the high-speed motor can be expressed as:

$${\alpha }_g=\frac{\mathrm{N}\mathrm{u}\lambda }{\delta }$$

(30)

Nussle number $\mathrm{N}\mathrm{u}$ can be calculated by the following formula:

$$\mathrm{N}\mathrm{u}=\frac{0.3887 {\mathrm{Re}}^{0.5}{\mathrm{Pr}}^{0.3}}{{\left[1+{\left(\frac{0.0486}{\mathrm{Pr}}\right)}^{0.67}\right]}^{0.25}}$$

(31)

Reynolds number and Nussle number in the stator slot of the motor can be calculated using the following formulas:

$${\mathrm{Re}}_{\mathrm{t}}=\frac{2\pi {\mathit{nR}}_{\mathrm{t}}{}^2}{60{\upsilon }_{\mathrm{t}}}$$

(32)

$${\alpha }_{\mathrm{t}}=\frac{\mathrm{N}{\mathrm{u}}_{\mathrm{t}}^{}\lambda }{R_{\mathrm{t}}}$$

(33)

$$\mathrm{N}{\mathrm{u}}_{\mathrm{t}}=0.021{\mathrm{Re}}_{\mathrm{t}}{}^{0.8}{\left({\mathrm{Pr}}_{\mathrm{t}}\right)}^{0.3}$$

(34)

$${\mathrm{Pr}}_{\mathrm{t}}=\frac{{\upsilon }_{\mathrm{t}}}{\mathrm{a}}$$

(35)

Meanwhile, the heat transfer coefficient of the rotor end face can be found by the following empirical formula [26]:

$${\alpha }_{\mathrm{r}}=28\left(1+\sqrt{0.45{\omega }_{\mathrm{R}}}\right)$$

(36)

When the motor is working normally, the temperature of the stator will have a direct influence on the temperature rise of the rotor because the air friction loss formed in the air gap and the eddy current loss in the stator will act on the inner and outer surfaces of the stator and rotor simultaneously. The influence of stator on rotor temperature rise can also be reduced by strong cold air structure. In this section, the FEM is used to calculate the magneto-fluid-thermal field of HSPMSM with multiple physical field coupling. The axial section of the calculated results is shown in Figure 26.

According to the results of the analysis in Section 3, Section 4 and Section 5, the analysis of the results of the multi-physics field calculation for the whole motor shows that the temperature at the center surface of the sleeve is still the highest, reaching 140.38 °C, which is 8.5% higher than the result of the multi-physics field calculation for the rotor thermal rise only. This is because the stator temperature has some influence on the rotor. However, when the forced air speed is 10 m/s, the additional air friction loss due to the roundness error generated on the outer surface of the sleeve is greatly reduced, so the effect of the stator core inner surface thermal on the rotor surface thermal is small.

7. Experimental Verification

The experiments focus on the loss analysis and study of the thermal field of the motor. During the experiments, the no-load losses and overall temperature rise of the prototype were measured, and the accuracy of the finite element calculation results was verified by analyzing the experimental data. The test rig of the high-speed motor was conducted in no-load and load experiments, as shown in Figure 27. The load is a blower box. The instruments included in the experiment are included of TongHui LCR digital bridge TH2811D; PF5000 electric power analyzer; AS862A non-contact infrared thermometer; pipeline ultrasonic flow meter and DC power supply, etc.

In the no-load test, the total no-load loss of the motor is calculated by measuring the power of the motor at different speeds. When analyzing the test results, the air friction loss is separated from the total loss by using the relationship between the air friction loss and the motor speed. At the same time, the relation between stator iron loss and rotational speed is fitted according to experimental data. Since the additional loss is constant and has nothing to do with the speed, there is no need to analyze and calculate it. The relevant loss calculation formula is as follows [27,28]:

$$P_0=P_{\mathrm{Fe}}+P_{\mathrm{fric}}+P_{\mathrm{add}0}$$

(37)

$$P_{\mathrm{Fe}}=k_{\mathrm{Fe}}{f}^{{\alpha }_{\mathrm{f}}}$$

(38)

$$P_{\mathrm{fric}}=k_{\mathrm{fric}}{f}^{{\beta }_{\mathrm{f}}}$$

(39)

For stator iron loss, it is determined by the rotational speed. According to the measured data of stator iron loss of 0.2 mm silicon steel sheet and based on the Leven-berg-Marquardt method, the fitting curve of stator iron loss versus frequency is shown in Figure 28.

$$P_{\mathrm{Fe}}=k_{\mathrm{Fe}}{f}^{1.536}$$

(40)

When the forced cold air inlet velocity is 10 m/s, the FE calculation results of the air friction loss of the motor are shown in Figure 28. In addition, based on the Leven-berg-Marquardt method [20], the fitted curve of air friction loss versus frequency is shown in Figure 28.

$$P_{\mathrm{fric}}=k_{\mathrm{fric}}{f}^3$$

(41)

Based on the Levenberg-Marquardt method, the experimental results can be transformed into the relationship between the measured loss and frequency of the motor when it is not loaded, which is expressed as:

$$P_0=k_{\mathrm{Fe}}{f}^{1.536}+k_{\mathrm{fric}}{f}^3+P_{\mathrm{add}0}$$

(42)

According to Formula (42) and Table 5, three sets of equations are listed to solve through the given three frequencies and the measured no-load loss P₀.

$$\{\begin{array}{c}255=k_{\mathrm{Fe}}(200{)}^{1.536}+k_{\mathrm{fric}}(200{)}^3+P_{\mathrm{add}0}\\ 836=k_{\mathrm{Fe}}(400{)}^{1.536}+k_{\mathrm{fric}}(400{)}^3+P_{\mathrm{add}0}\\ 2071=k_{\mathrm{Fe}}(600{)}^{1.536}+k_{\mathrm{fric}}(600{)}^3+P_{\mathrm{add}0}\end{array}$$

(43)

According to Formula (43) and Table 5, three sets of equations are listed to solve through the given three frequencies and the measured no-load loss P₀.

By solving the above equations, the coefficients of $k_{\mathrm{F}\mathrm{e}}$, $k_{\mathrm{F}\mathrm{r}\mathrm{i}\mathrm{c}}$ and $P_{\mathrm{a}\mathrm{d}\mathrm{d}\mathrm{0}}$ can be calculated as 3.77 × 10⁻² and 4.25 × 10⁻⁶, 78 W respectively from the test data. The measured results of losses and separated losses are listed in

Table 6. Losses separation based on total losses of measurement at different speeds.

n (r/min)	f (Hz)	PFe (W)	Pfric (W)	Padd0 (W)	Measured P0 (W)
12,000	200	129	40	78	247
24,000	400	374	317	78	769
36,000	600	697	1107	78	1844

.

Comparing the FEA calculation of the air-friction loss in Figure 28. with the measurement from losses separation in Table 6, the change curve is shown in Figure 29. It can be seen that the calculated results are slightly larger than the experimental results, but the change trend is consistent. At the rated speed of 36,000 rpm, the calculated air friction loss is 1200 W, the measured value from Table 6 is 1107 W at the forced air inlet velocity is 0 m/s. In addition, the difference is 7.75%, less than 10% between measurement and calculation.

The temperature rise measurement experiment of HSPMSM under rated working condition is carried out on the motor load experimental platform. In the paper, the average winding temperature is indirectly obtained on the basis of resistance change method. First, $R_{s20}$ was measured at 20 °C. Then, the $R_{s\theta }$ was measured after the motor running at rated load for 120 min. At this time, θ is the temperature rise of the winding after the motor runs stably and heat balance. Finally, the winding temperature can be calculated through the resistance conversion formula. The conversion formula is as follows:

$$R_{s\theta }=\left[\frac{\left(234.5+\theta \right)}{\left(234.5+20\right)}\right]\times R_{s20}$$

(44)

$$\theta =\left(234.5+20\right)\times \left(\frac{R_{s\theta }}{R_{s20}}\right)-234.5$$

(45)

Further, the shell and shaft temperatures at the steady-state operation are recorded by the infrared thermometer, seen in Figure 30. The measured experimental data of HSPMSM are shown in

Table 7. Temperature results of HSPMSM between experiment and FEA calculation.

Part	FEA Result	Experiment Result	Unit	Tolerance
Winding	123	117.5	°C	4.7%
Shell	52	49.3	°C	5.5%
Inlet right Shaft	64.5	61.2	°C	5.4%

.

Since the temperature of PM and rotor sleeve of high-speed motor cannot be measured directly, the indirect converting method is adopted to assess the rotor temperature in the paper. As seen in Table 7, the FEA result of the winding temperature is 123 °C, and the experiment one is 117.5 °C. By comparing the experimental results of winding temperature with the FE calculation results, it can be drawn that the difference is about 5%, which is in good agreement. Therefore, it can be determined that the rotor sleeve and PM temperature of HSPMSM is 137.9 °C and 124.2 °C, respectively.

In the paper, the temperature maximal error between FEA and the measurement is 5.5%, which is acceptable. It is analyzed of the calculation errors. The FEA result is calculated in multi-fields coupling simulation, and the accuracy of simulation results is affected by the factors such as meshing, convergence value, loss distribution, ambient temperature. In the simulation, the ambient temperature is as 20 °C. Another calculation error of air friction loss between measurement and calculation is 7.75%. The possible factor is that when the rotor rotates, the ventilation hole will disturb the air flow of the rotor, and the poor sealing of the casing will also affect the air flow of the rotor, thus affecting the measurement accuracy of air friction loss. As uncontrolled factors, it maybe the test accuracy of equipment. In this experiment, the loss measurement and analysis of the prototype were carried out using TongHui LCR digital bridge TH2811D, PF5000 electric power analyzer, pipe flow meter and non-contact infrared thermometer and other related equipment. However, some uncontrollable factors in the experimental process led to errors. These factors affect the experiments, including: the ambient temperature change, the error in the prototype fabrication, and the variation of the output current of the power supply.

8. Conclusions

In the paper, the various loss and thermal field distribution are studied in FEA, and the effect of some factors on loss are investigated for the 105 kW HSPMSM. By comprehensively analyzing the simulation and experimental results, the following conclusions can be drawn:

(1)

The influence of sleeve material conductivity, rotating speed and sleeve thickness on the eddy current loss can be summarized, providing some reference of the research for the rotor sleeve of high-speed motor, especially for titanium alloy sleeve. The eddy current loss of the sleeve is expressed as followings.

$$\{\begin{array}{l}{P}_{\mathrm{sleeve}}=6.19\times {10}^{-4}\sigma +63.311 (\mathrm{thickness} \mathrm{is} 3.5\mathrm{mm})\\ P_{\mathrm{sleeve}}=6.823\times {10}^{-4}\sigma +69.319 (\mathrm{thickness} \mathrm{is} 4.0\mathrm{mm})\\ P_{\mathrm{sleeve}}=1.51{{\displaystyle f}}^{1.68} (\mathrm{Sleeve} \mathrm{is} \mathrm{titanium} \mathrm{alloy})\\ P_{\mathrm{sleeve}}=120\times e^{(0.2688m)} (\mathrm{Sleeve} \mathrm{is} \mathrm{titanium} \mathrm{alloy})\end{array}$$

(46)

(2)

By analyzing the relationship between rotor sleeve material, thickness and rotor eddy current loss and mechanical stress, it is concluded that in this thesis, the sleeve made of titanium alloy material with a thickness of 3.5 mm is chosen to effectively suppress the rotor eddy current loss in high-speed motors.

(3)

The air friction loss becomes significant at the high-speed motor. It will rapidly increase to high-speed rotational rotors. The influences of the roundness error, the rational speed and the axial forced-air velocity on air-friction loss are analyzed in detail, which provide a reference of calculate the air friction loss of HSPMM.

(4)

By analyzing the roundness error, it can be concluded that the overall maximum motor temperature tends to decrease, and the air gap pressure tends to increase with the increase of the motor forced air cooling inlet velocity for a fixed roundness error. Through comprehensive analysis of the relationship between the flow rate of forced air cooling and rotor temperature, air friction loss and air pressure, the optimal air inlet velocity is 10 m/s. Furthermore, the air friction loss is concluded with roundness error (A_Err) as following, providing some reference for the rotor design of HSPMM.

$$P_{\mathrm{fric}}=1839.927-\frac{699.715}{1+e^{\frac{A_{\mathrm{Err}}-0.5773}{0.1428}}}$$

(47)

(5)

The influence of stator temperature on the rotor was analyzed by coupled magnetic-thermal multi-physical field calculations. The forced-air inlet velocity of 10 m/s is adopted by studying the air friction loss due to the roundness error, avoiding rotor overheating, in the paper.

(6)

The loss separation method is used to obtain the air friction loss measurement results. The accuracy of the finite element calculation results of air friction loss is verified through the experimental data. Under load testing, the stator winding temperature in FEA calculation is verified by experiment on the basis of resistance change method. The temperature maximal difference is 5.5%, which is acceptable.