Aerodynamic Interactions of Wind Lenses at Close Proximities
Abstract
:1. Introduction
1.1. Examination of Multirotor Work
1.2. Prior Work
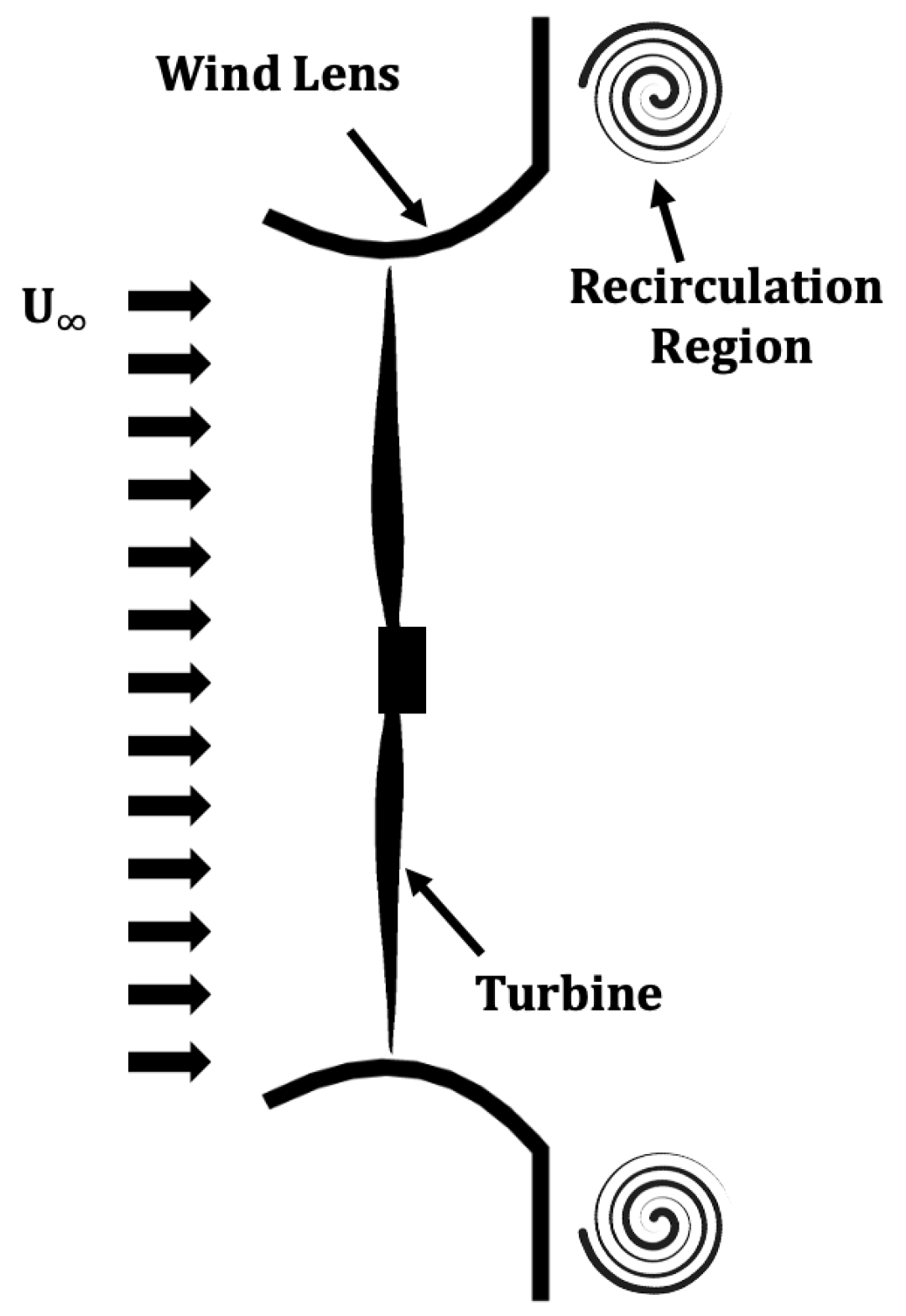
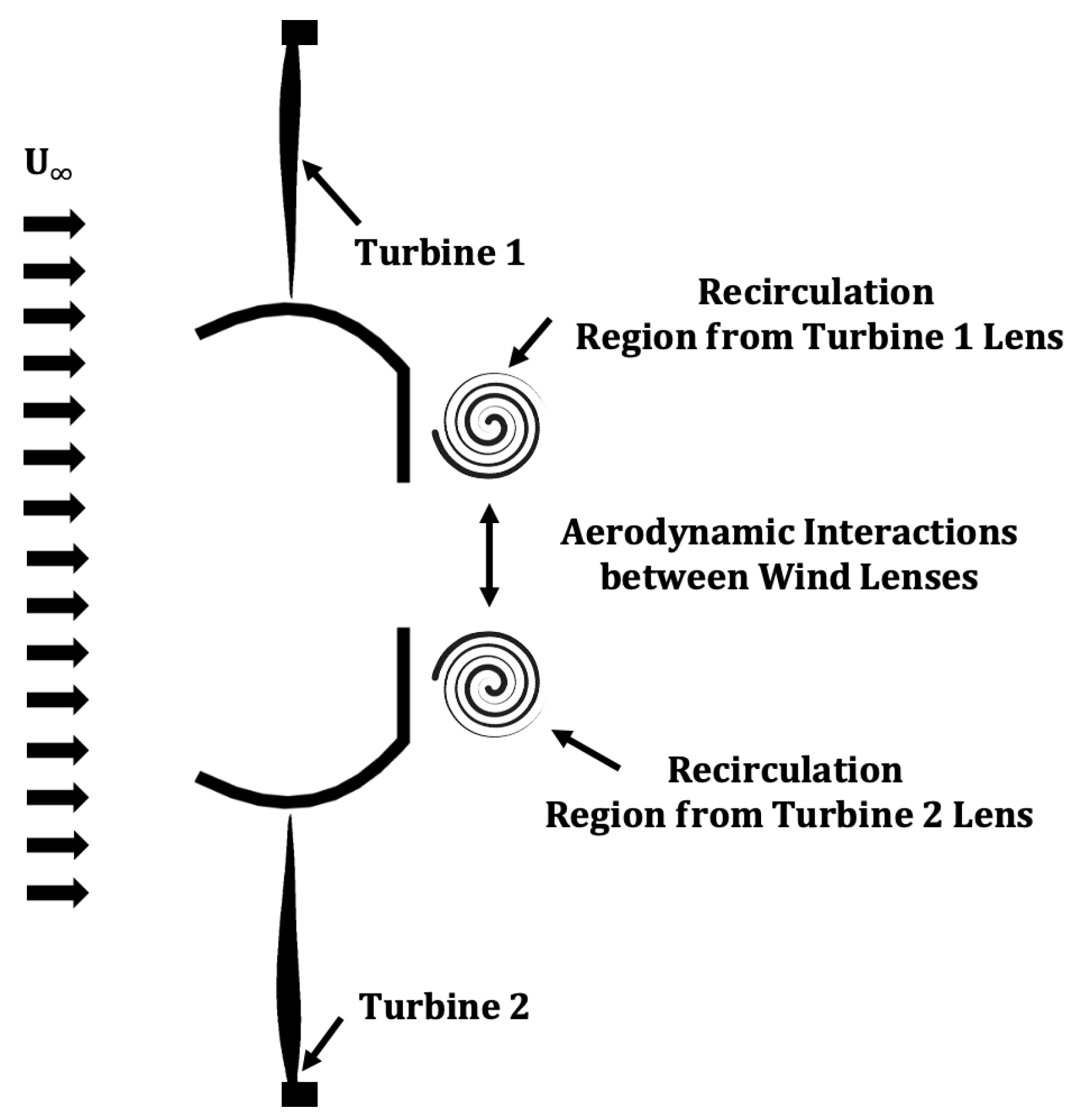
1.3. Aerodynamic Interactions between Bluff Bodies
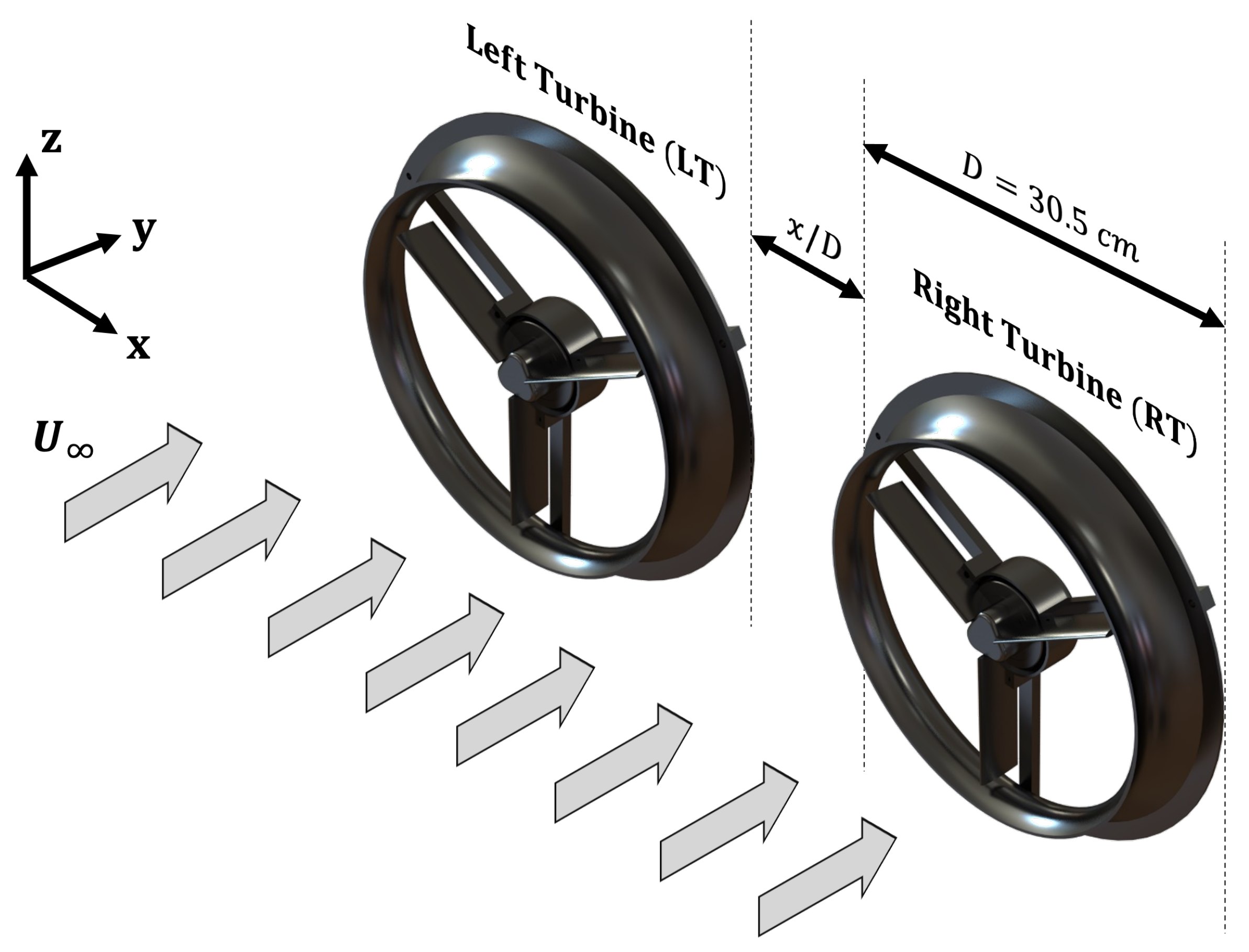
2. Experimental Setup
2.1. Wind Tunnel
2.2. Wind Lens Models
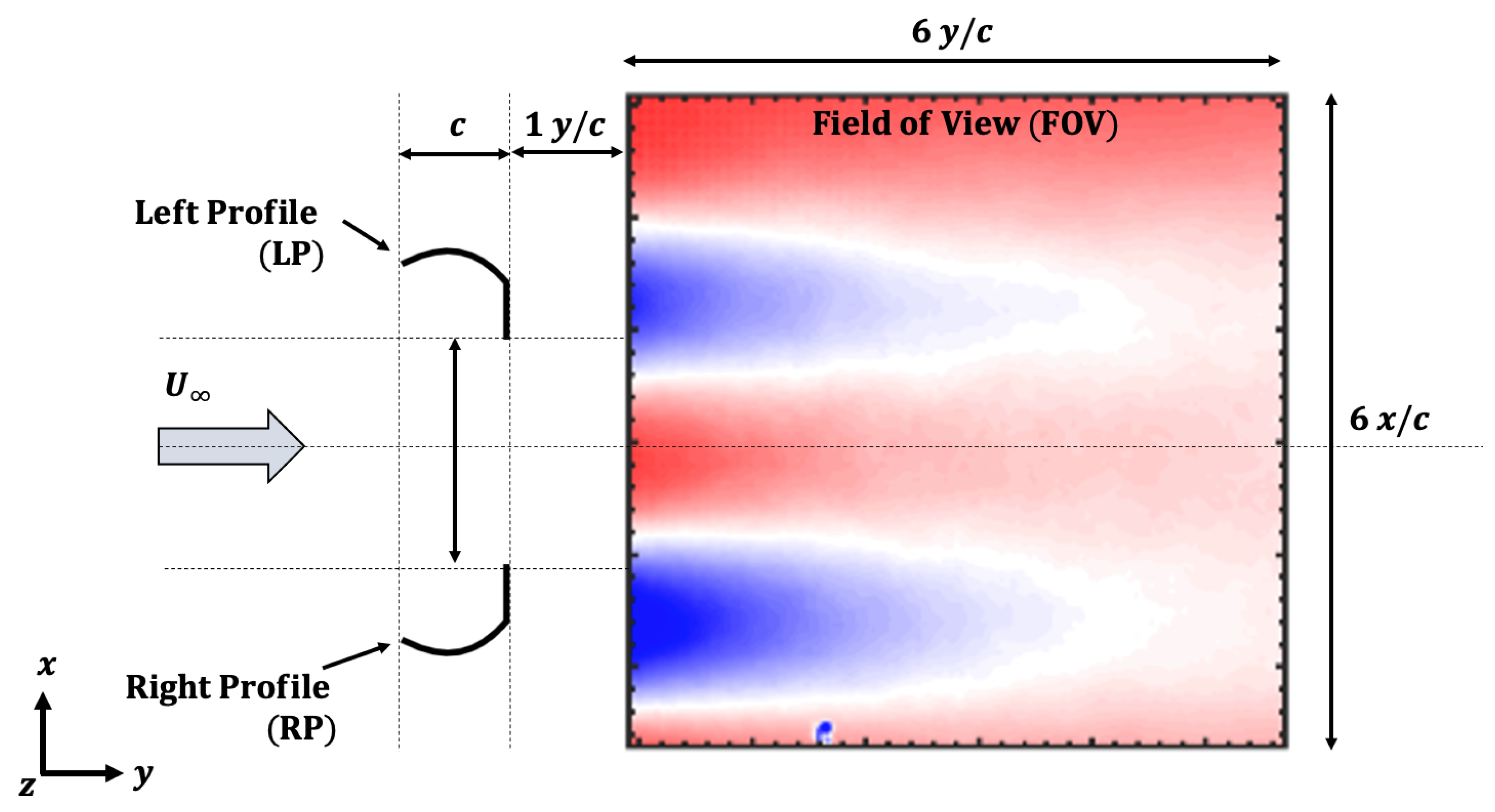
2.3. PIV Setup
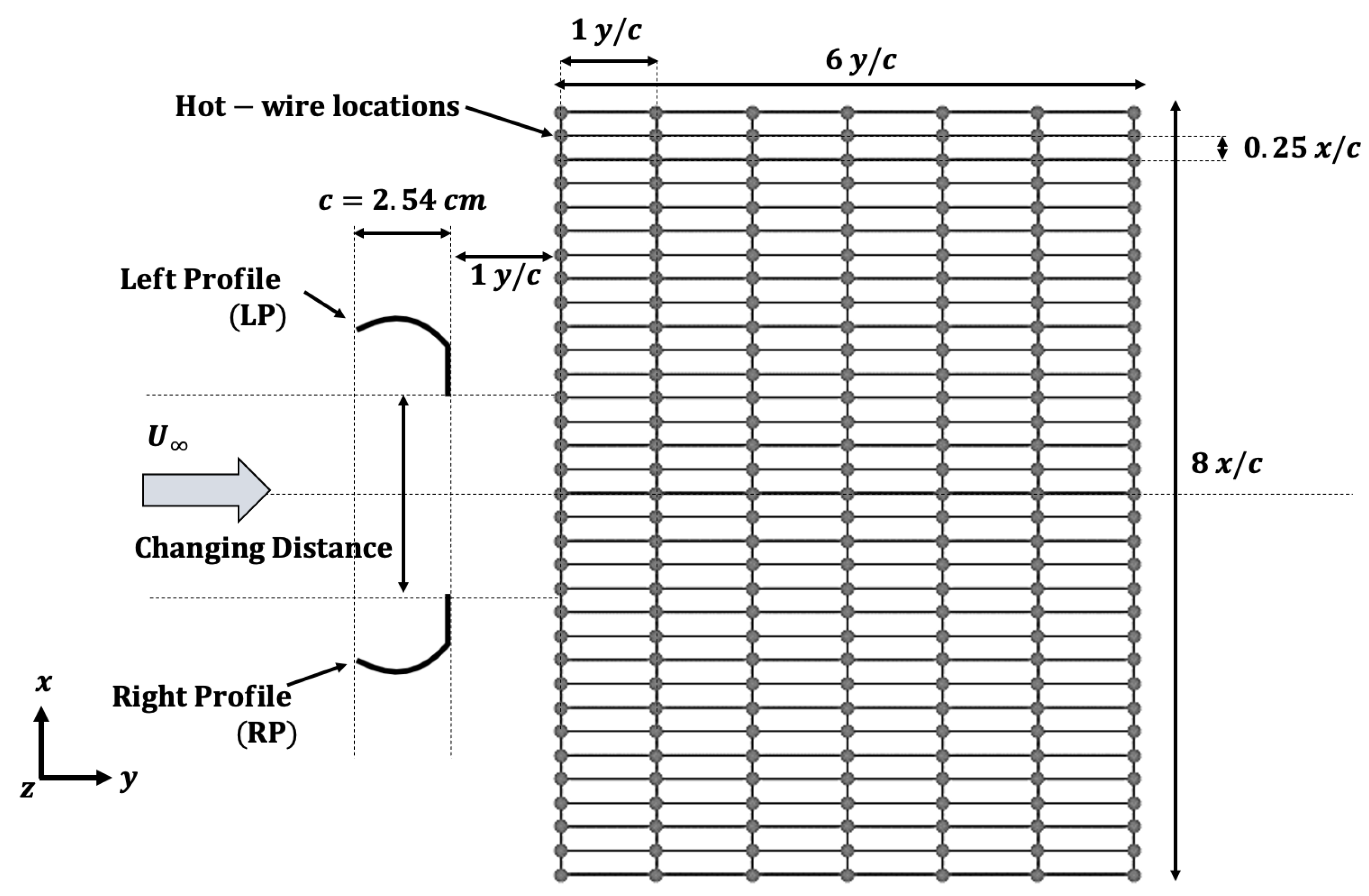
2.4. Hotwire Anemometry Testing
3. Results
3.1. PIV Results
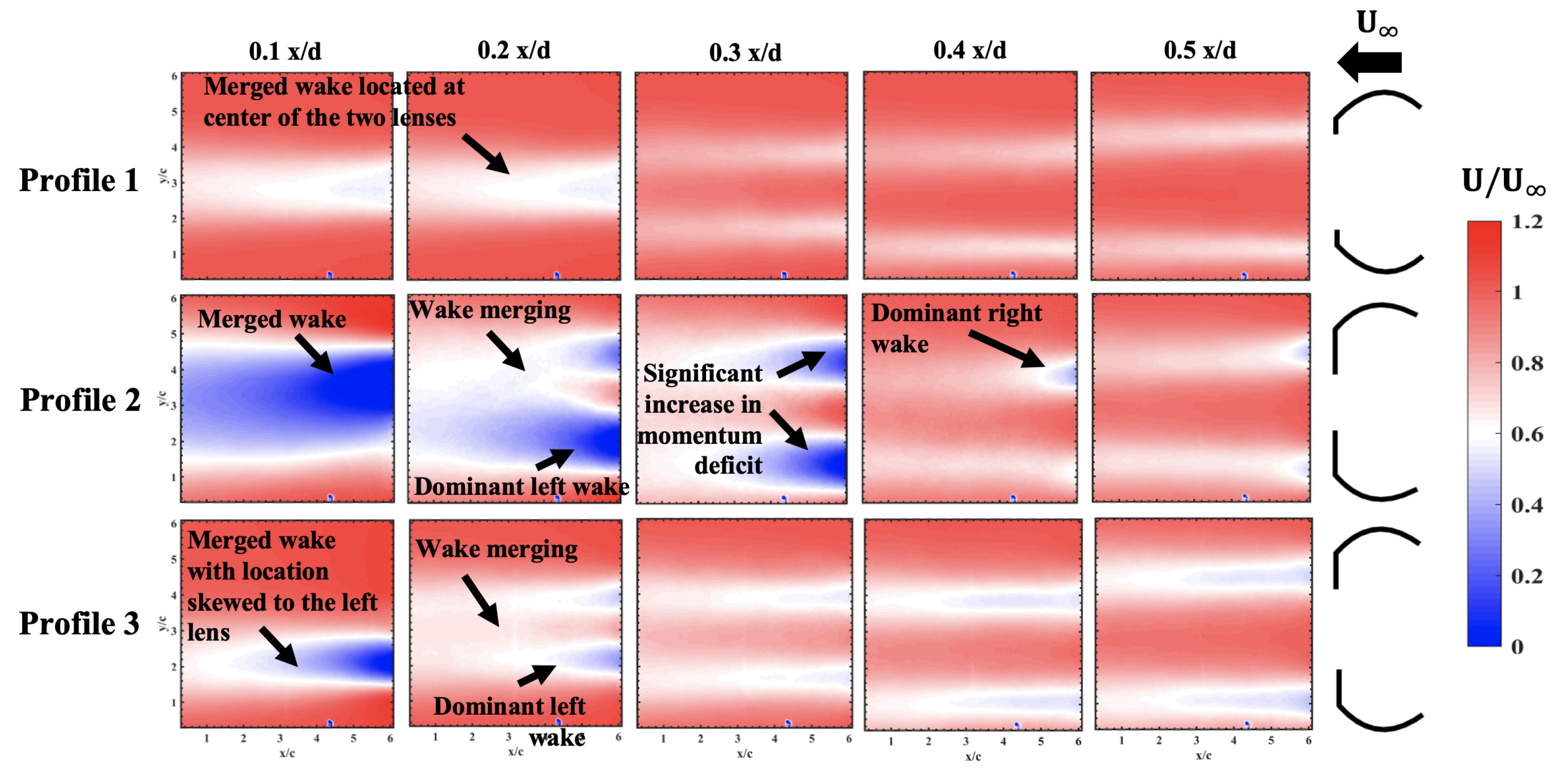
3.1.1. U Velocity Results
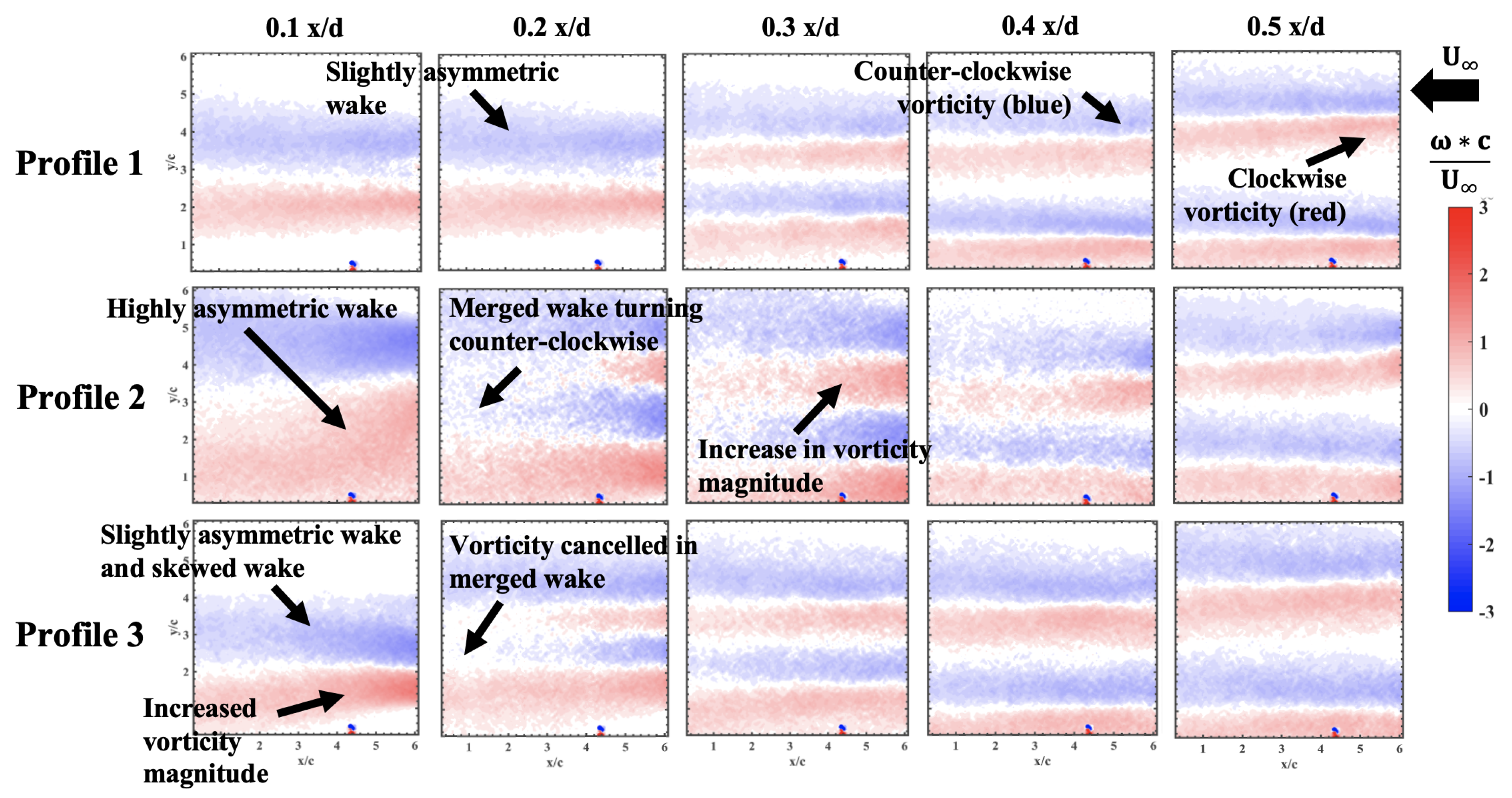
3.1.2. Mean Vorticity Results
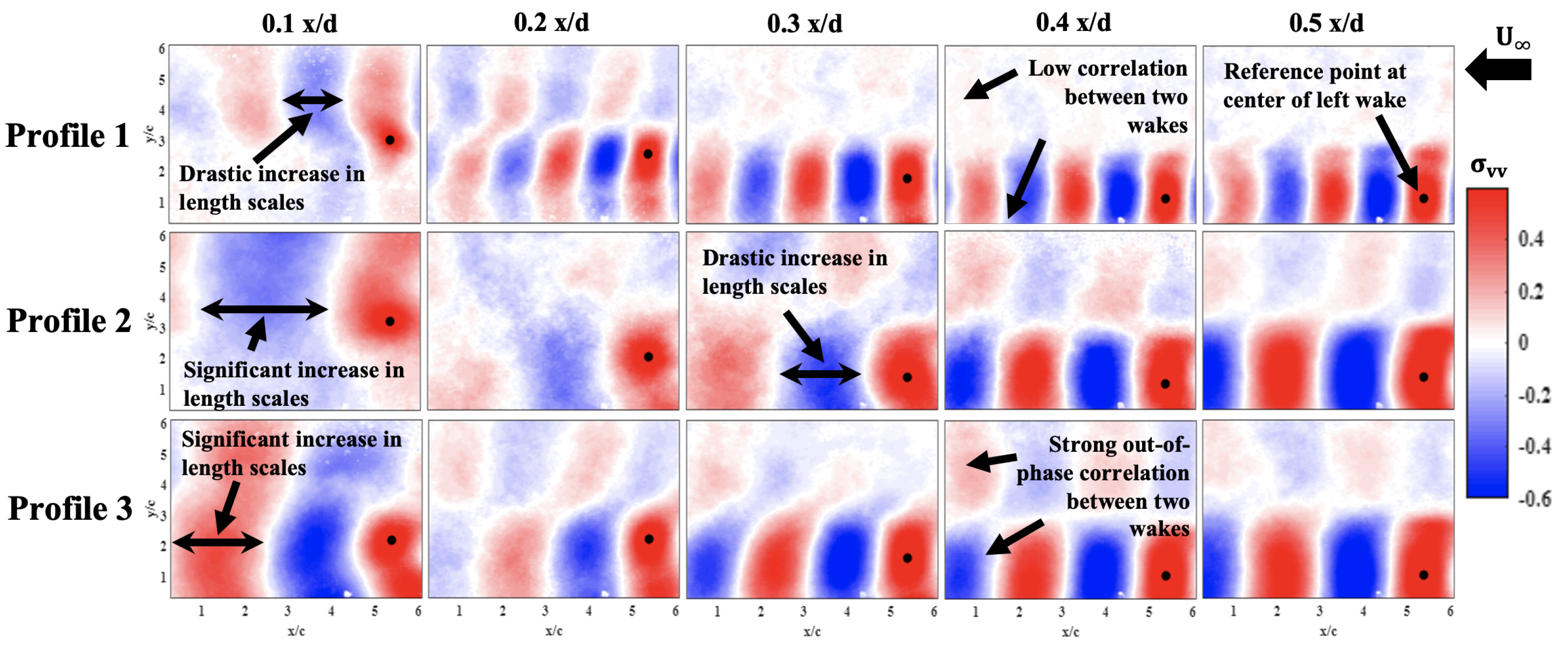
3.1.3. Two-Point Correlations
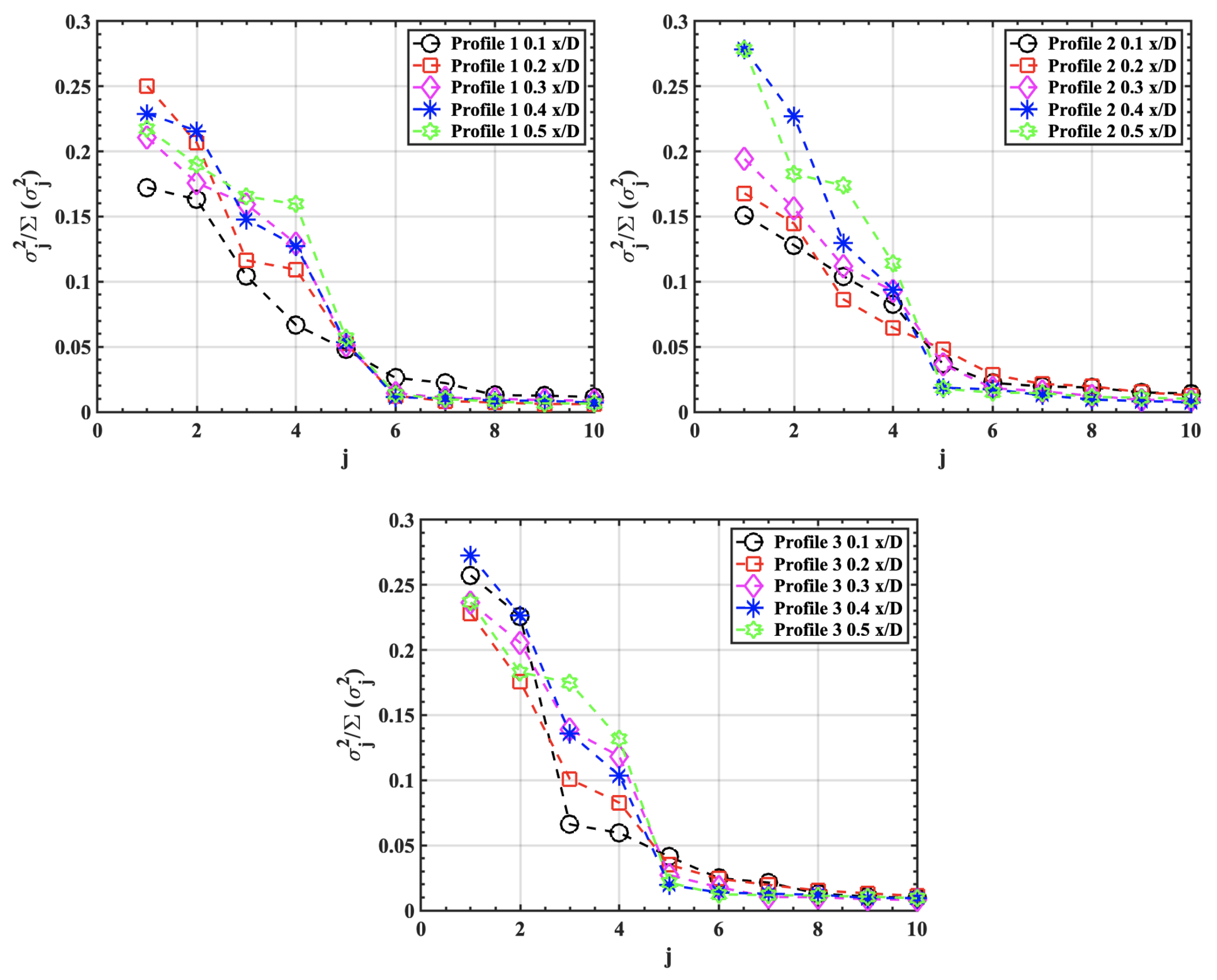
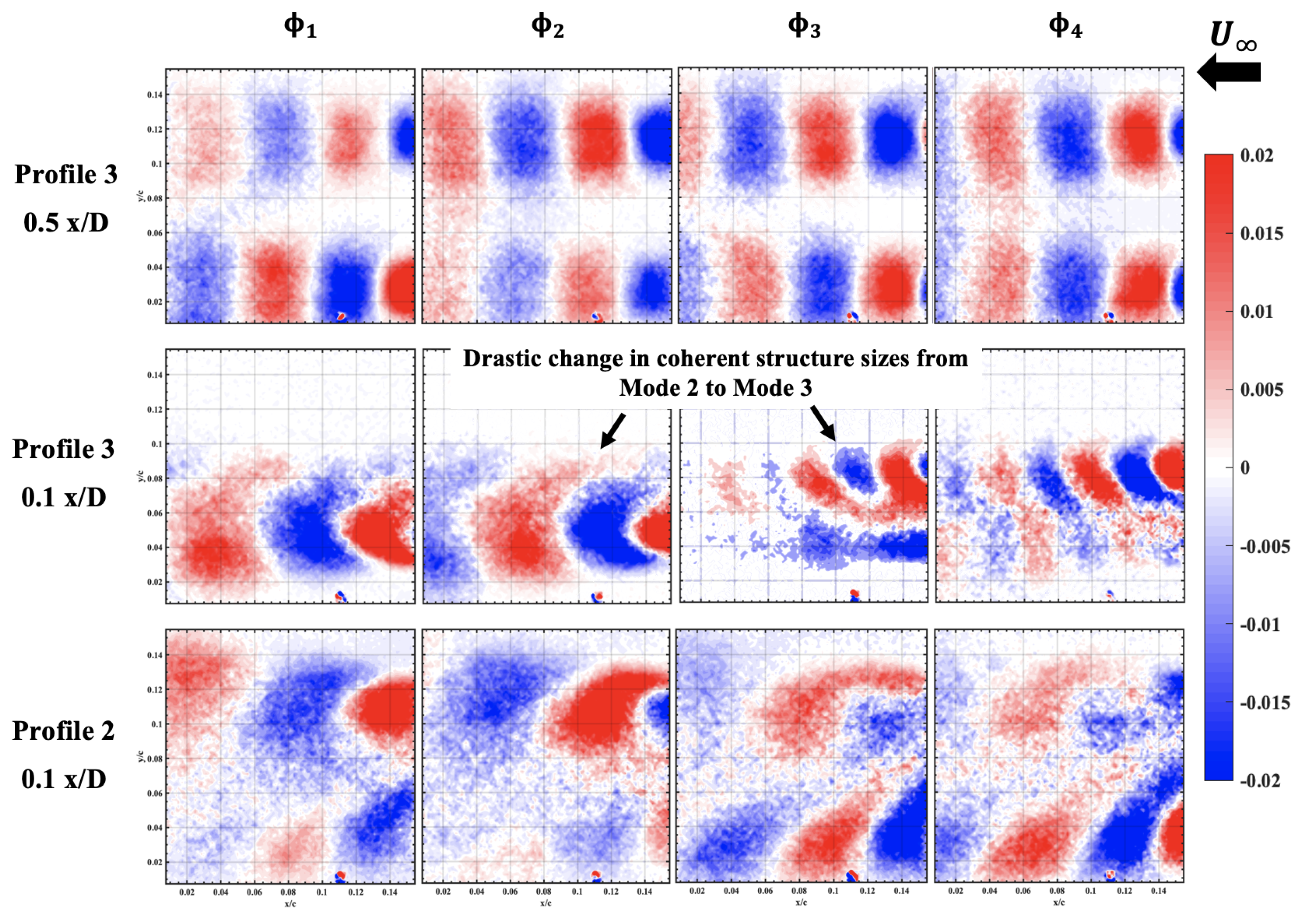
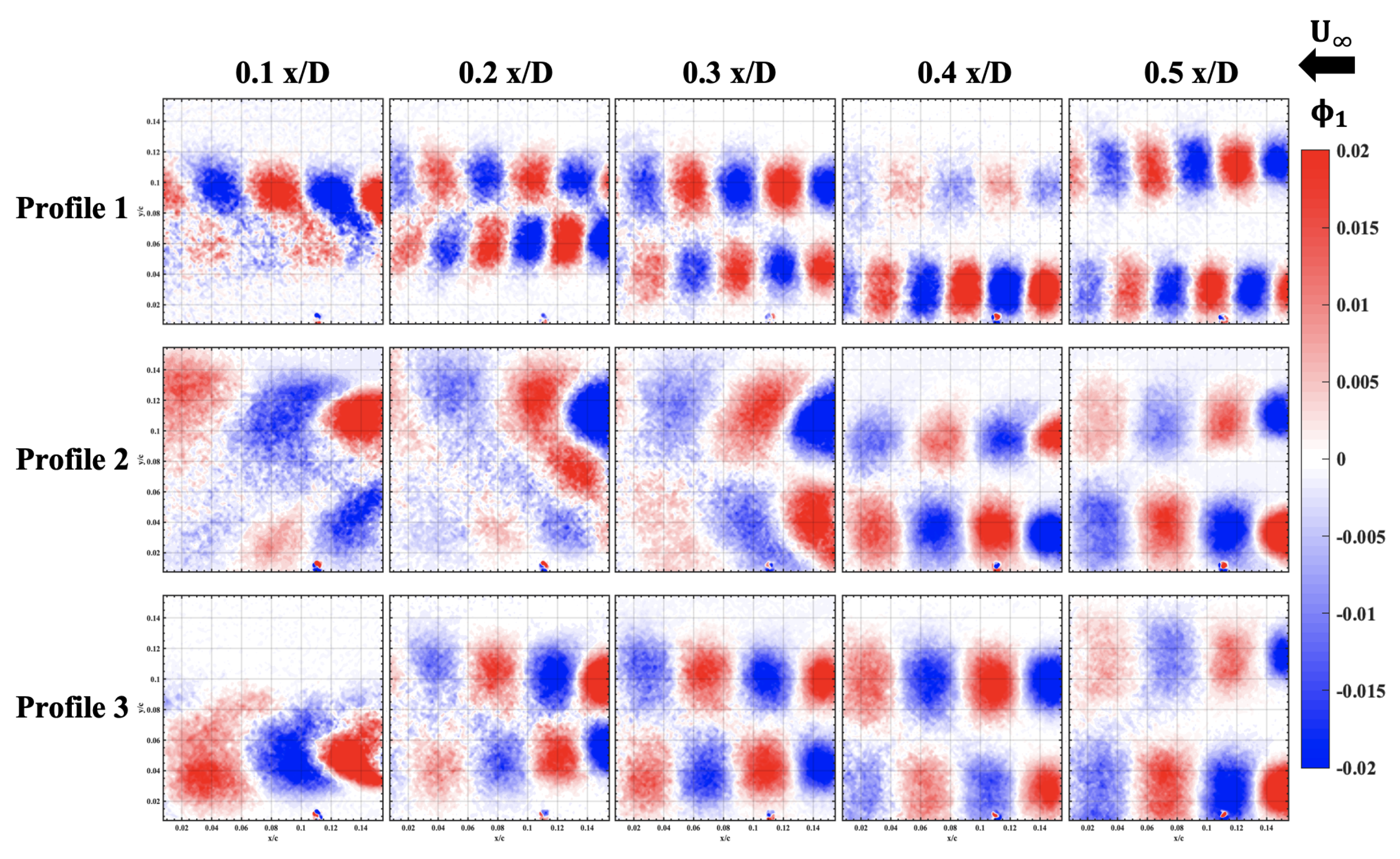
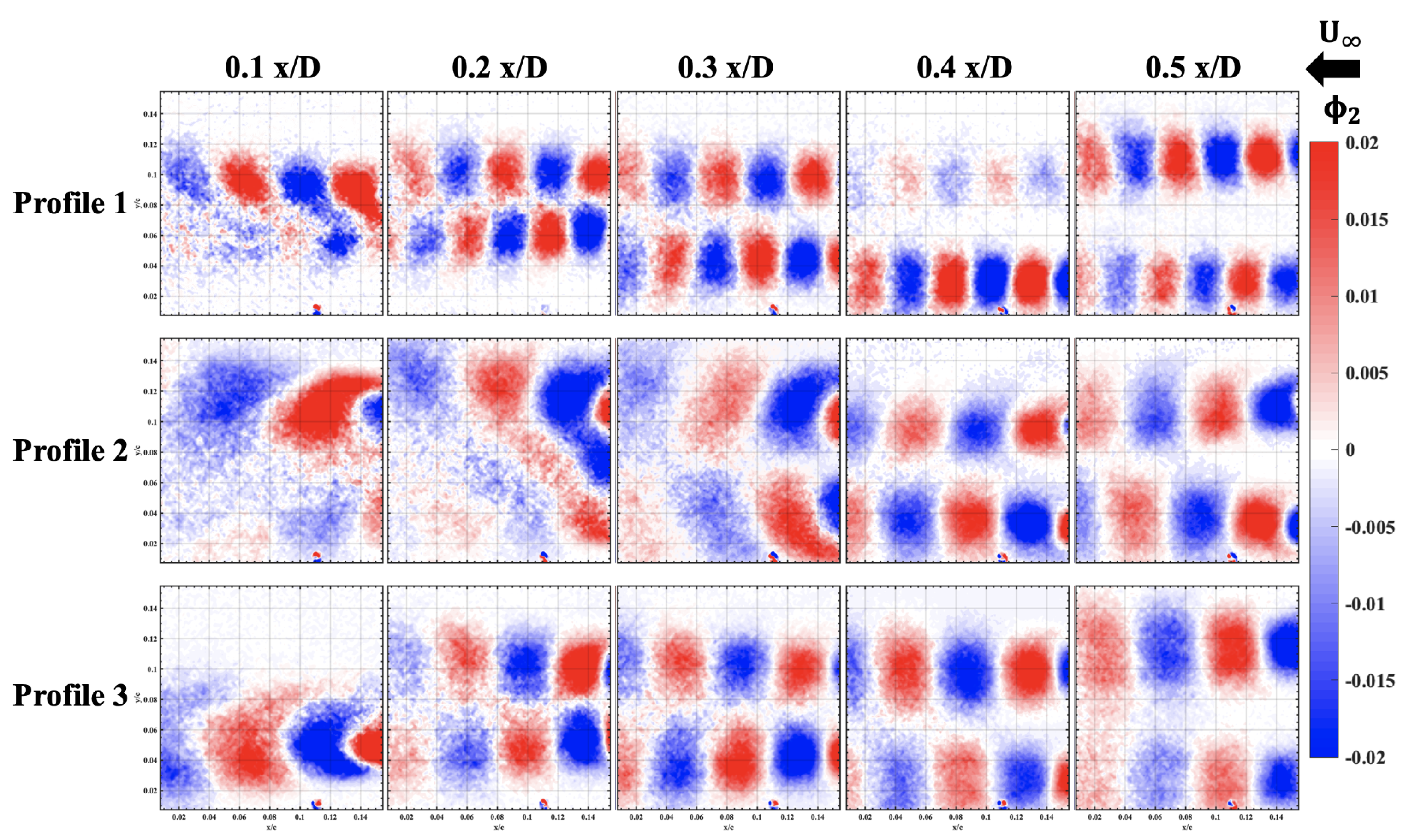
3.1.4. Modal Analysis
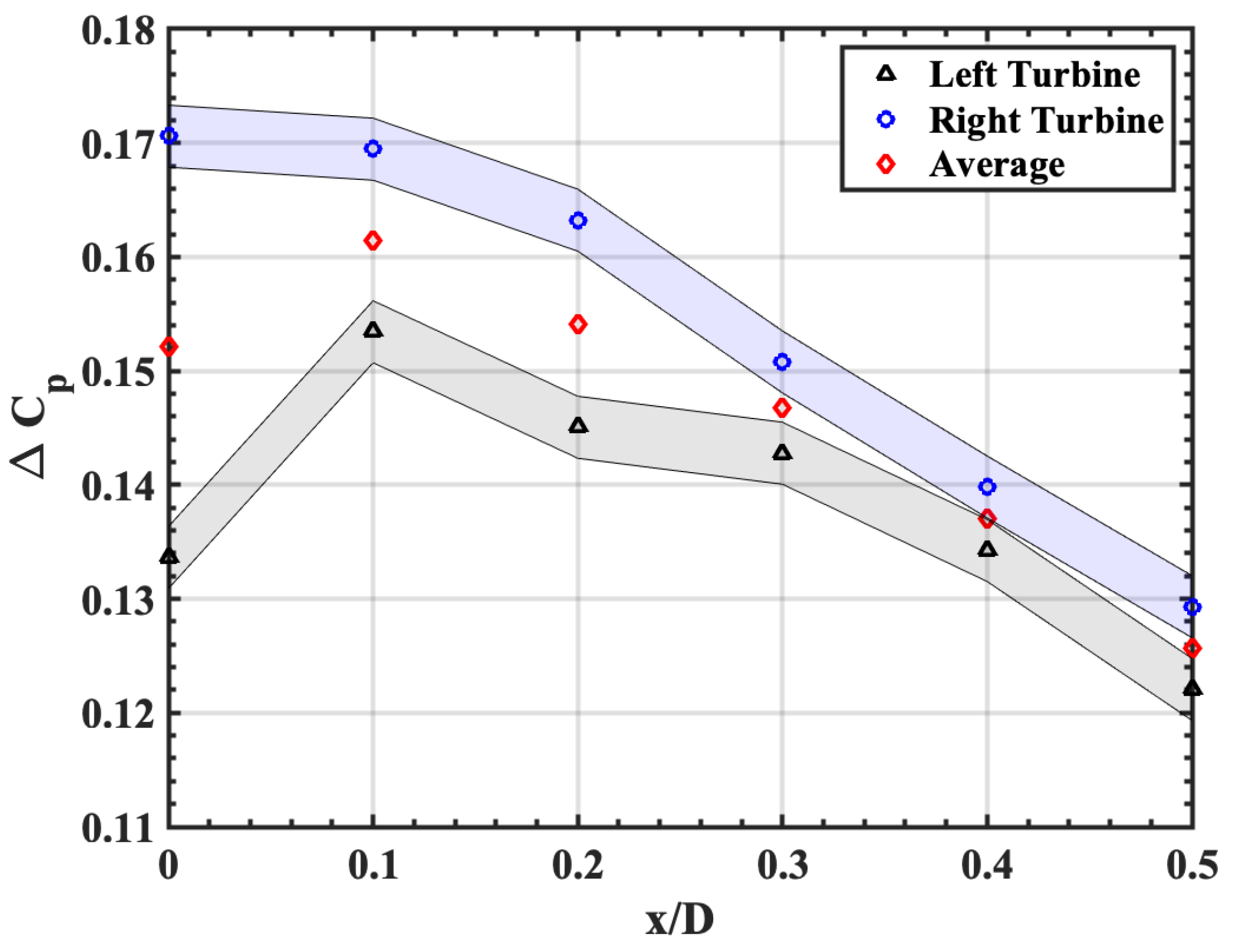
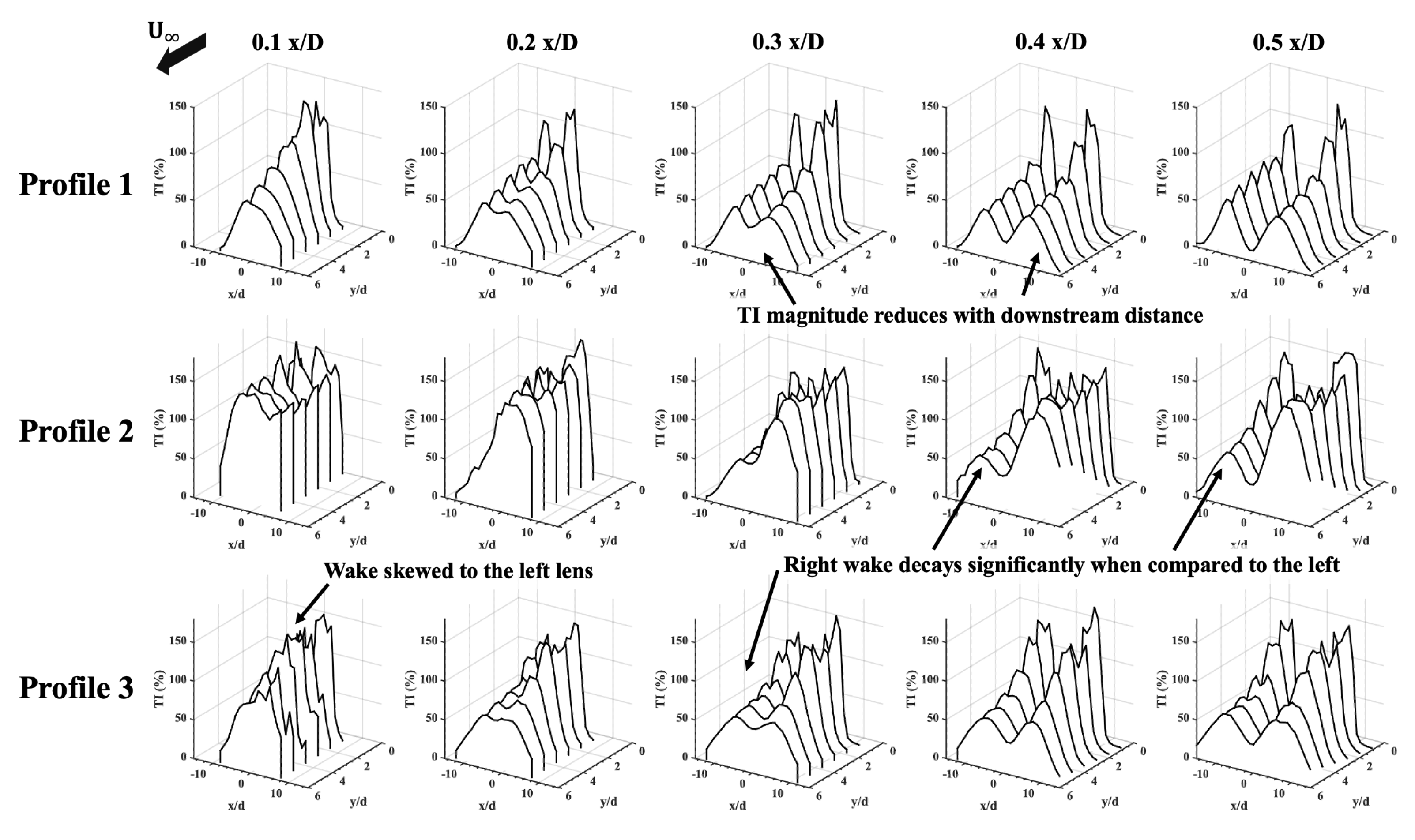
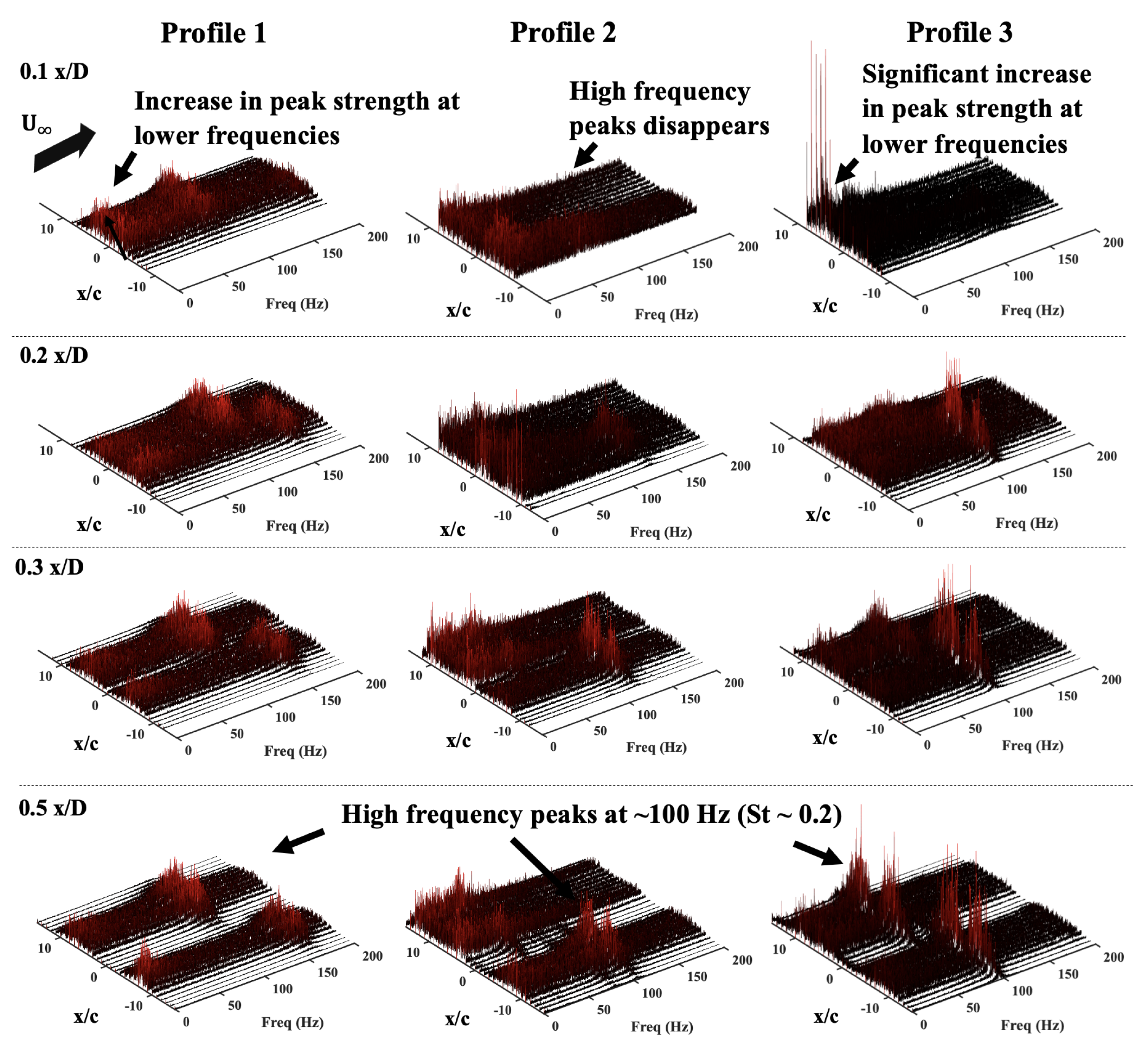
3.2. Hotwire Anemometry Results
4. Conclusions
- The two wakes sense the presence of each other such that the peak shedding frequency for one of the wakes is lowered when compared to the other. This causes changes in the mean flow parameters such as the mean velocity and vorticity. The relative energy in the POD modes starts to decrease.
- Reducing the spacing between the lenses further results in the onset of wake merging that causes significant changes in the vortex shedding frequency, and the size of the coherent structures in the wake starts to increase. This results in that wake having a higher momentum deficit and a higher turbulence intensity.
- The choice of the direction of the skewness in the wake is hypothesized to be due to the extent of cancellation on the inboard vorticity magnitude from the two wakes. If the vorticity is perfectly canceled between the wakes, little to no wake skewness is observed. The direction of skewness of the merged wake causes one of the turbines in the lens turbine pair to outperform the other, as seen in the wind tunnel results.
- When the lenses are brought even closer, the high-frequency shedding disappears, and the lower frequency shedding starts to dominate. This results in a longer resting time of the vortex behind the lenses that results in a more stable low-pressure zone, as seen in two-point correlation and modal analysis, which draws in air more consistently at higher speeds than when the lenses are spaced at greater distances, resulting in higher power production.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| PIV | Particle image velocimetry |
| POD | Proper orthogonal decomposition |
| SVD | Singular value decomposition |
References
- Department of Energy, Unlocking Our Nation’s Wind Potential. Available online: www.energy.gov/eere/articles/unlocking-our-nation-s-wind-potential (accessed on 25 May 2022).
- Schubel, P.; Crossley, R. Wind turbine blade design. Energies 2015, 5, 3425–3449. [Google Scholar] [CrossRef] [Green Version]
- Ohya, Y.; Karasudani, T. A shrouded wind turbine generating high output power with wind-lens technology. Energies 2010, 3, 634–649. [Google Scholar] [CrossRef] [Green Version]
- Ohya, Y.; Miyazaki, J.; Göltenbott, U.; Watanabe, K. Power augmentation of shrouded wind turbines in a multirotor system. J. Energy Resour. Technol. 2017, 139, 051202. [Google Scholar] [CrossRef]
- Ohya, Y. Multi-rotor systems using five ducted wind turbines for power output increase (multi lens turbine). In Proceedings of the AIAA Scitech 2019 Forum, San Diego, CA, USA, 7–11 January 2019. [Google Scholar]
- Ohya, Y. Bluff body flow and vortex—Its application to wind turbines. Fluid Dyn. Res. 2014, 46, 061423. [Google Scholar] [CrossRef]
- Khamlaj, T.; Rumpfkeil, M. Optimization study of shrouded horizontal axis wind turbine. In Proceedings of the 2018 Wind Energy Symposium, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Jamieson, P. Innovation in Wind Turbine Design; John Wiley & Sons: Hoboken, NJ, USA, 2018. [Google Scholar]
- Sandhu, N.; Chanana, S. Performance and Economic Analysis of Multi-Rotor Wind Turbine. EMIT. Int. J. Eng. Technol. 2018, 6, 289–316. [Google Scholar] [CrossRef]
- Ransom, D.; Moore, J.; Heronemus-Pate, M. Performance of wind turbines in a closely spaced array. Renew. Energy World 2010, 2, 32–36. [Google Scholar]
- Göltenbott, U.; Ohya, Y.; Yoshida, S.; Jamieson, P. Flow interaction of diffuser augmented wind turbines. J. Phys. Conf. Ser. 2016, 753, 022038. [Google Scholar] [CrossRef]
- Watanabe, K.; Ohya, Y. Multirotor systems using three shrouded wind turbines for power output increase. J. Energy Resour. Technol. 2019, 141, 051211. [Google Scholar] [CrossRef] [Green Version]
- Novotny, N.; Gunasekaran, S. Performance and Proximity Investigations on Small Scale Lensed Turbines. In Proceedings of the AIAA Scitech 2020 Forum, Orlando, FL, USA, 6–10 January 2020; p. 1242. [Google Scholar]
- Bearman, P.; Wadcock, A. The interaction between a pair of circular cylinders normal to a stream. J. Fluid Mech. 1973, 61, 499–511. [Google Scholar] [CrossRef]
- Zdravkovich, M. REVIEW—Review of flow interference between two circular cylinders in various arrangements. J. Fluids Eng. 1977, 99, 618–633. [Google Scholar] [CrossRef]
- Williamson, C. Evolution of a single wake behind a pair of bluff bodies. J. Fluid Mech. 1985, 159, 1. [Google Scholar] [CrossRef]
- Behr, M.; Tezduyar, T.; Higuchi, H. Wake interference behind two flat plates normal to the flow: A finite-element study. Theor. Comput. Fluid Dyn. 1991, 2, 223–250. [Google Scholar] [CrossRef]
- Kim, H.; Durbin, P. Investigation of the flow between a pair of circular cylinders in the flopping regime. J. Fluid Mech. 1988, 196, 431–448. [Google Scholar] [CrossRef]
- Zdravkovich, M. The effects of interference between circular cylinders in cross flow. J. Fluids Struct. 1987, 1, 239–261. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhang, H.; Yiu, M. The turbulent wake of two side-by-side circular cylinders. J. Fluid Mech. 2002, 458, 303–332. [Google Scholar] [CrossRef] [Green Version]
- Ng, C.; Cheng, V.; Ko, N. Numerical study of vortex interactions behind two circular cylinders in bistable flow regime. Fluid Dyn. Res. 1997, 19, 379–409. [Google Scholar] [CrossRef]
- Higuchi, H.; Lewalle, J.; Crane, P. On the structure of a two-dimensional wake behind a pair of flat plates. Phys. Fluids 1994, 6, 297–305. [Google Scholar] [CrossRef]
- Burattini, P.; Agrawal, A. Wake interaction between two side-by-side square cylinders in channel flow. Comput. Fluids 2013, 77, 134–142. [Google Scholar] [CrossRef]
- Roshko, A.; Steinolfson, A.; Chattoorgoon, V. Flow Forces on a Cylinder near a Wall or near Another Cylinder; California Institute of Technology: Pasadena, CA, USA, 1975. [Google Scholar]
- Wang, X.; So, R.; Xie, W. Wavelet analysis of flow-induced forces on two side-by-side stationary cylinders: Reynolds number effect. In Proceedings of the 6th FSI, AE And FIV And N Symposium, Vancouver, BC, Canada, 23–27 July 2006; Volume 9. [Google Scholar]
- Miau, J.; Wang, G.; Chou, J. Intermittent switching of gap flow downstream of two flat plates arranged side by side. J. Fluids Struct. 1992, 6, 563–582. [Google Scholar] [CrossRef]
- Lazar, E.; DeBlauw, B.; Glumac, N.; Dutton, C.; Elliott, G. A practical approach to PIV uncertainty analysis. In Proceedings of the 27th AIAA Aerodynamic Measurement Technology And Ground Testing Conference, Chicago, IL, USA, 28 June–1 July 2010. [Google Scholar]
- Guan, Y.; Morris, S. Experimental investigation of flow field around an asymmetric beveled trailing edge and aerodynamic sound. In Proceedings of the 23rd AIAA/CEAS Aeroacoustics Conference, Denver, CO, USA, 5–9 June 2017. [Google Scholar]
- Bendat, J.; Piersol, A. Random Data; Wiley-Blackwell: Hoboken, NJ, USA, 2010. [Google Scholar]
- Shlizerman, E.; Ding, E.; Williams, M.; Kutz, J. The proper orthogonal decomposition for dimensionality reduction in mode-locked lasers and optical systems. Int. J. Opt. 2012, 2012, 1–18. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, A. An introduction to the proper orthogonal decomposition. Curr. Sci. 2000, 78, 808–817. [Google Scholar]
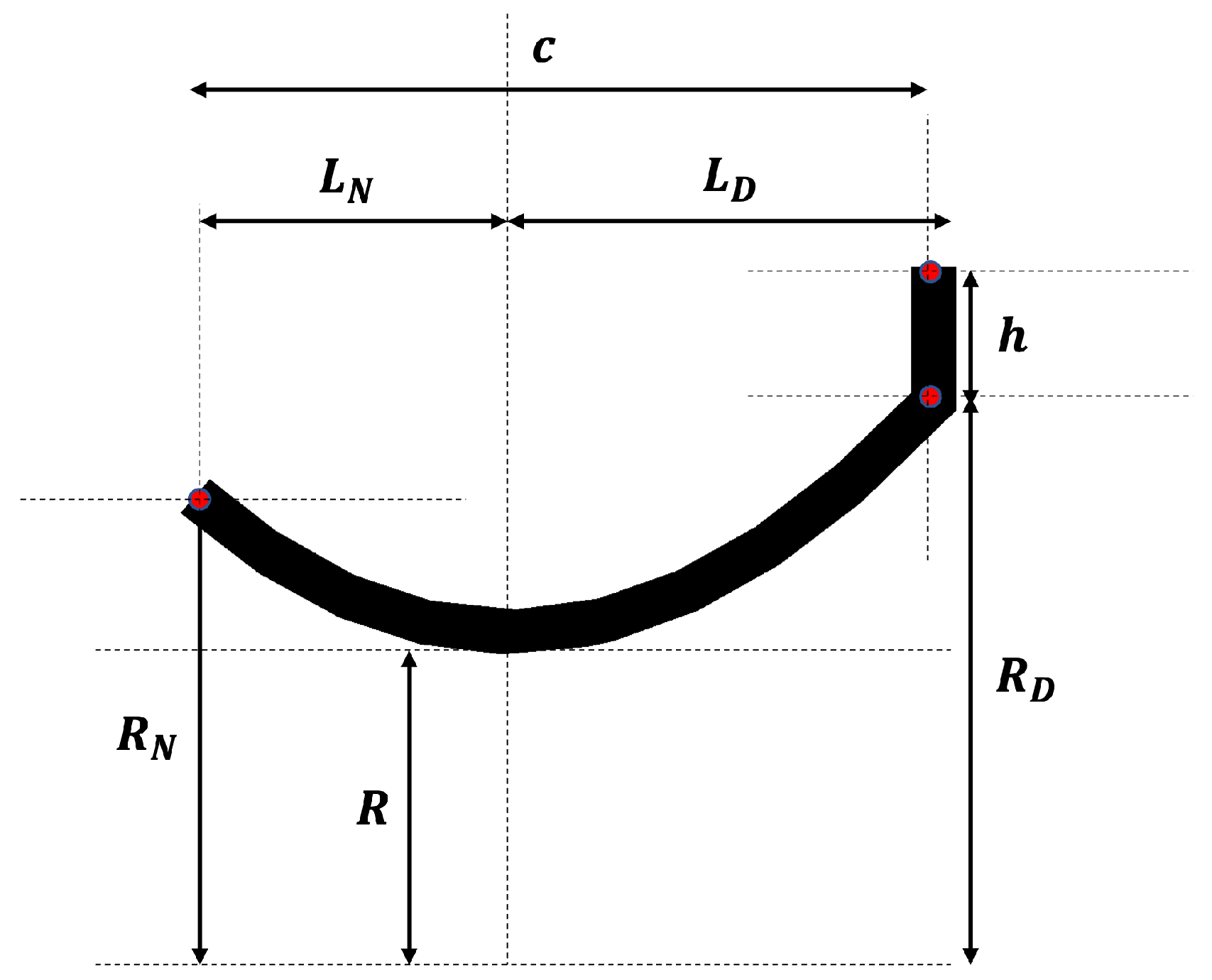
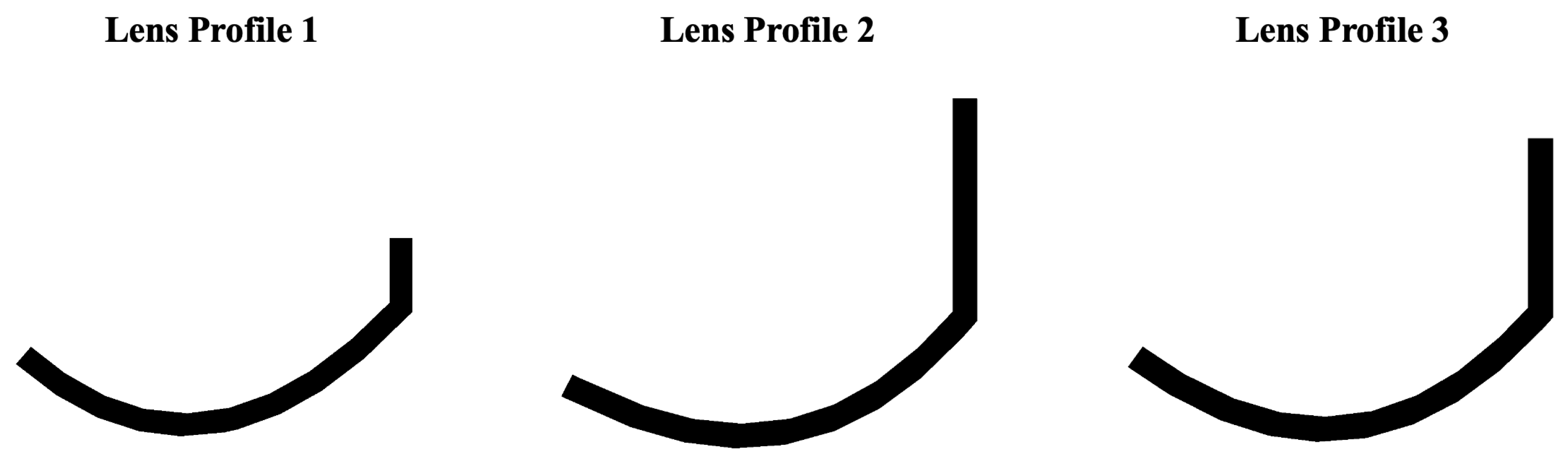
| Lens Profile | /c | h/c | /c | /c | /c | ||
|---|---|---|---|---|---|---|---|
| Profile 1 | 0.574 | 0.250 | 1.705 | 0.426 | 1.824 | 0.896 | 0.664 |
| Profile 2 | 0.533 | 0.547 | 1.539 | 0.467 | 1.702 | 1.056 | 1.055 |
| Profile 3 | 0.523 | 0.436 | 1.509 | 0.477 | 1.669 | 1.003 | 0.876 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gunasekaran, S.; Peyton, M.; Novotny, N. Aerodynamic Interactions of Wind Lenses at Close Proximities. Energies 2022, 15, 4622. https://doi.org/10.3390/en15134622
Gunasekaran S, Peyton M, Novotny N. Aerodynamic Interactions of Wind Lenses at Close Proximities. Energies. 2022; 15(13):4622. https://doi.org/10.3390/en15134622
Chicago/Turabian StyleGunasekaran, Sidaard, Madison Peyton, and Neal Novotny. 2022. "Aerodynamic Interactions of Wind Lenses at Close Proximities" Energies 15, no. 13: 4622. https://doi.org/10.3390/en15134622
APA StyleGunasekaran, S., Peyton, M., & Novotny, N. (2022). Aerodynamic Interactions of Wind Lenses at Close Proximities. Energies, 15(13), 4622. https://doi.org/10.3390/en15134622





