Finite Element Method for Non-Newtonian Radiative Maxwell Nanofluid Flow under the Influence of Heat and Mass Transfer
Abstract
:1. Introduction
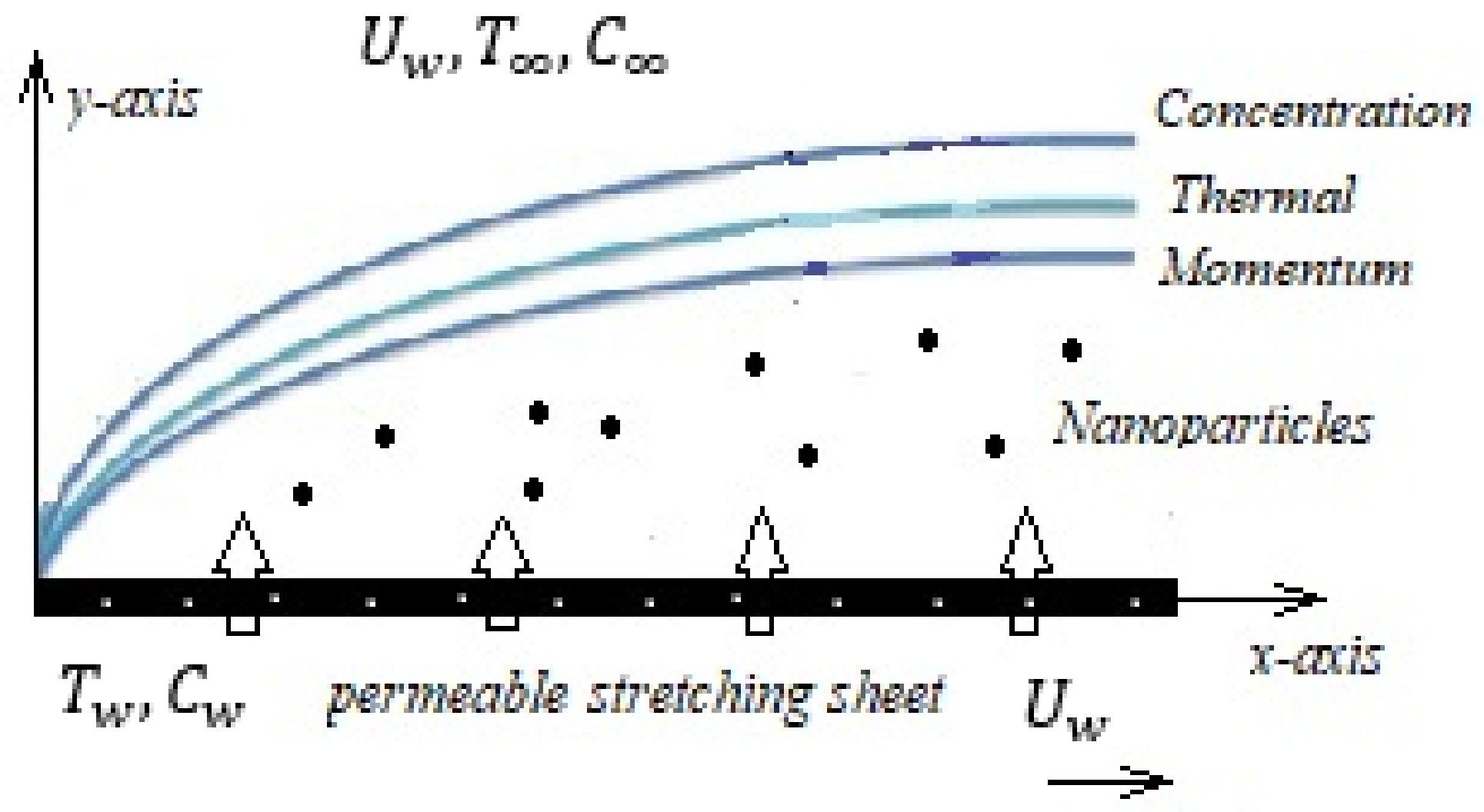
2. Problem Formulation
3. Finite Element Method
4. Validations
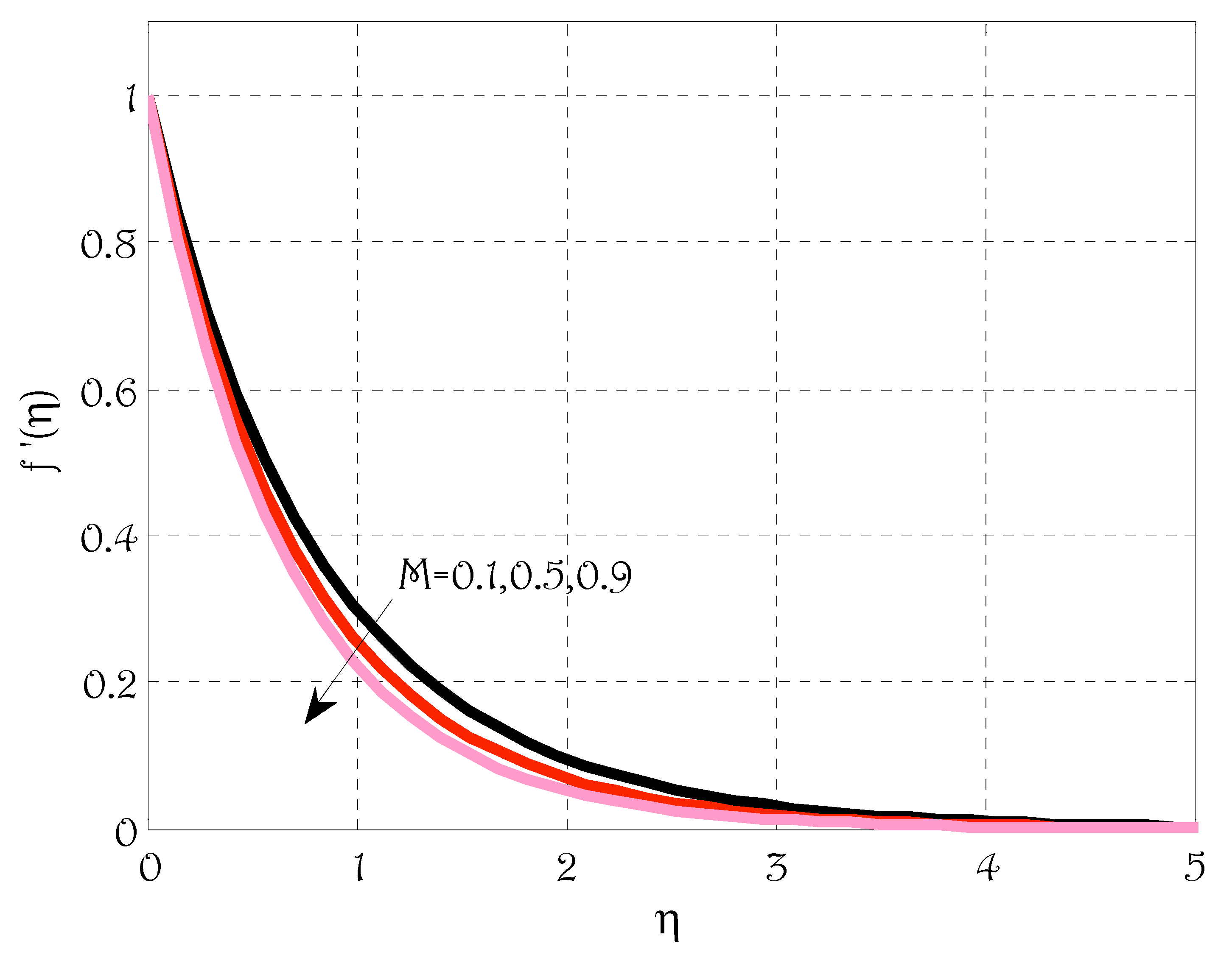
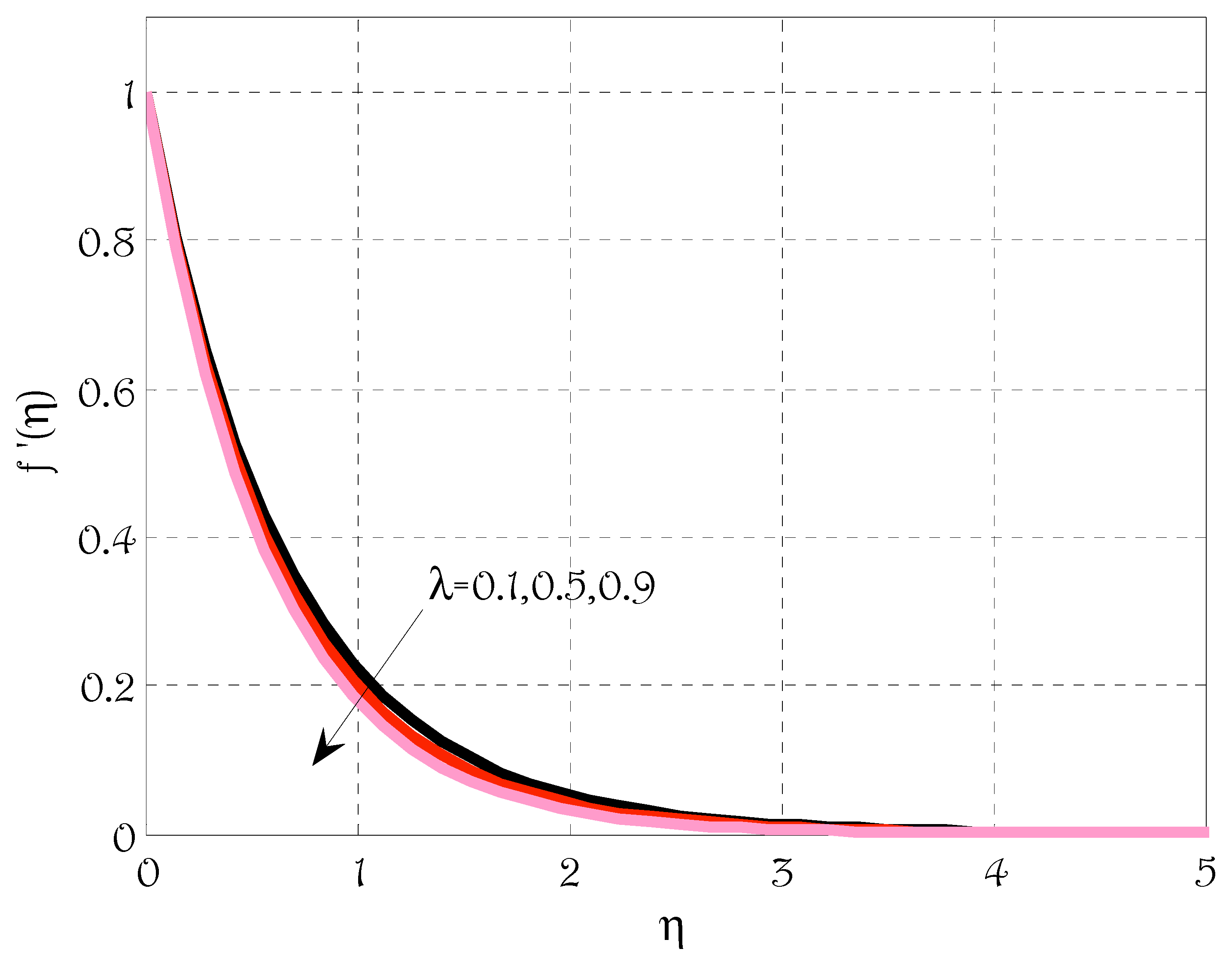
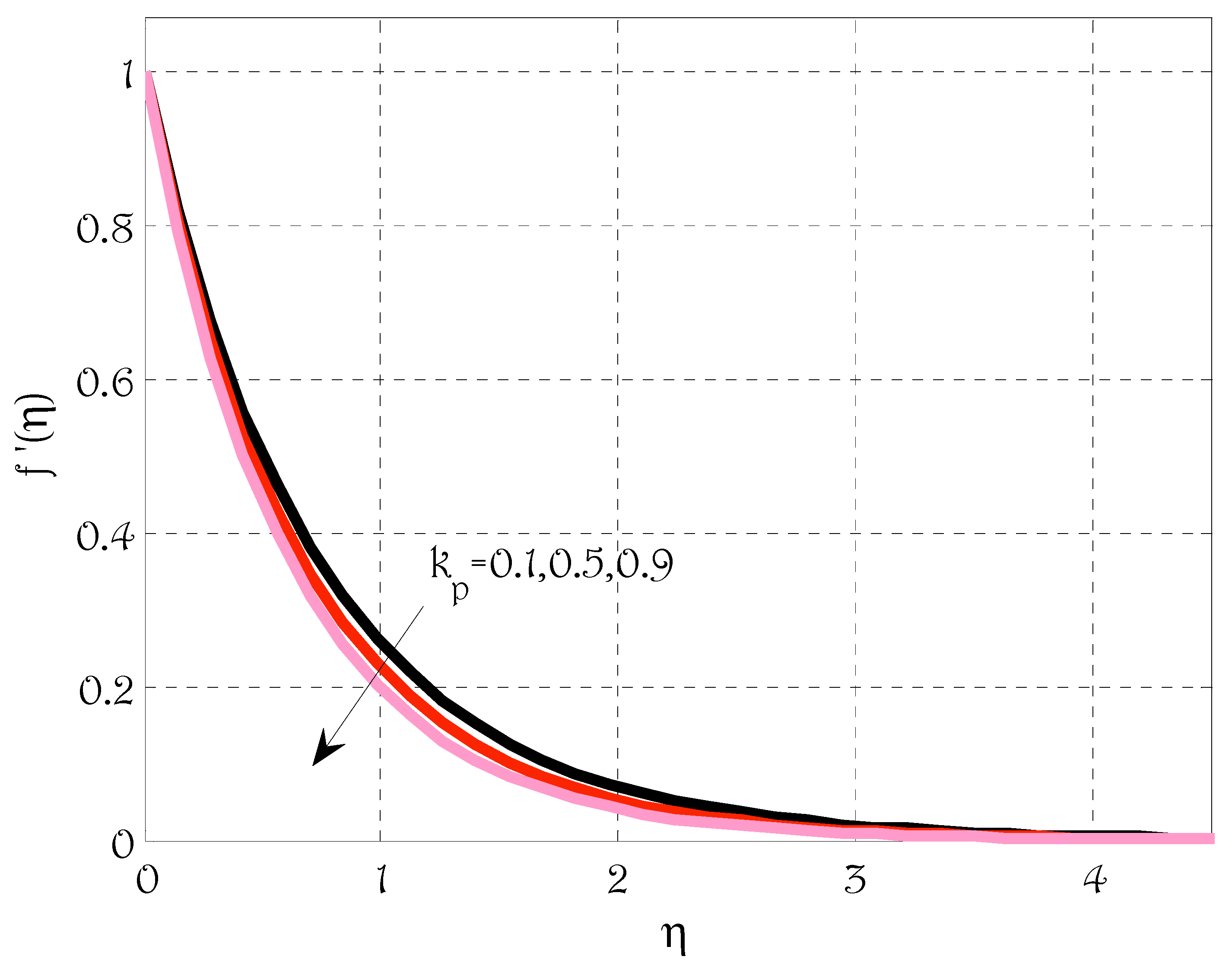
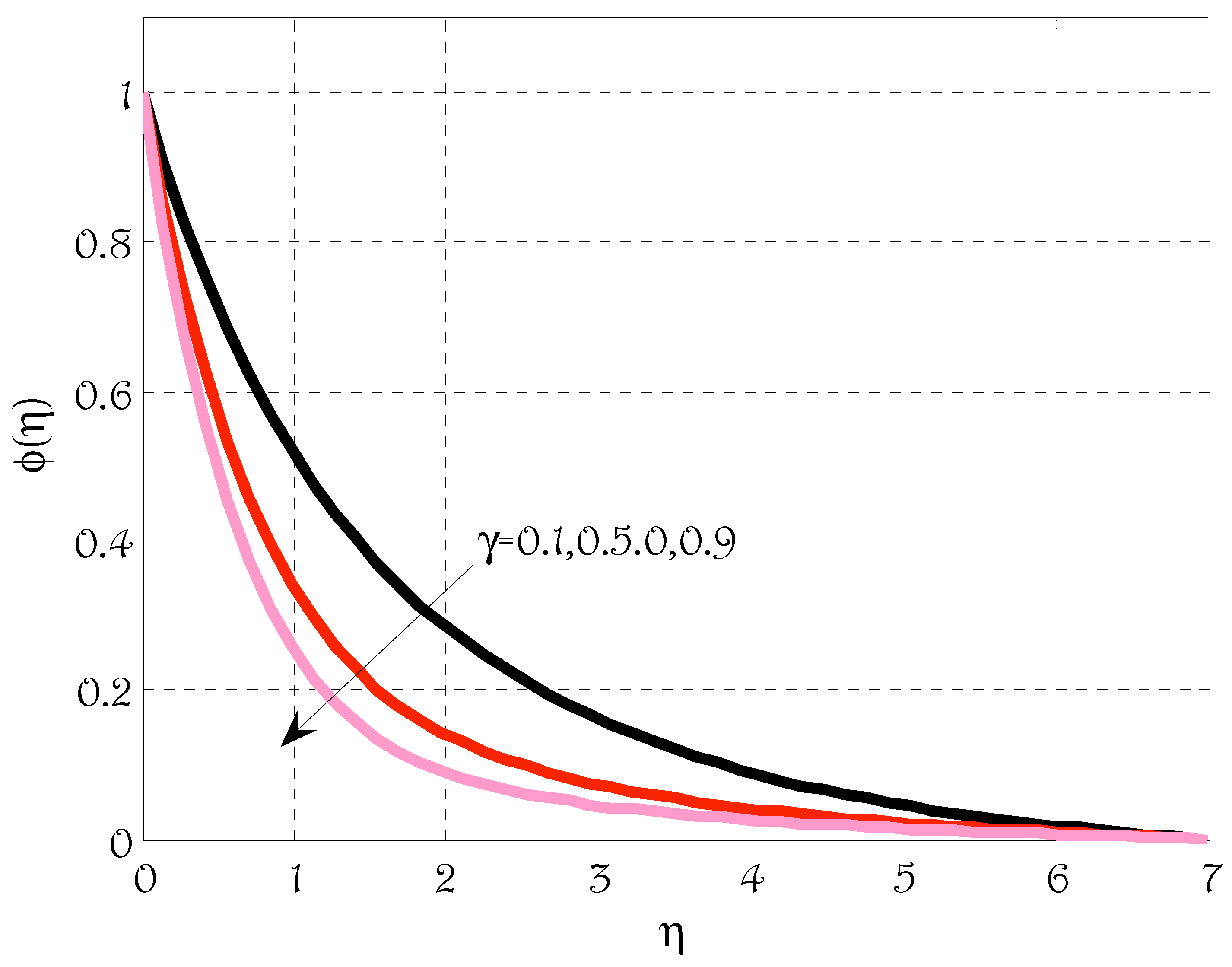
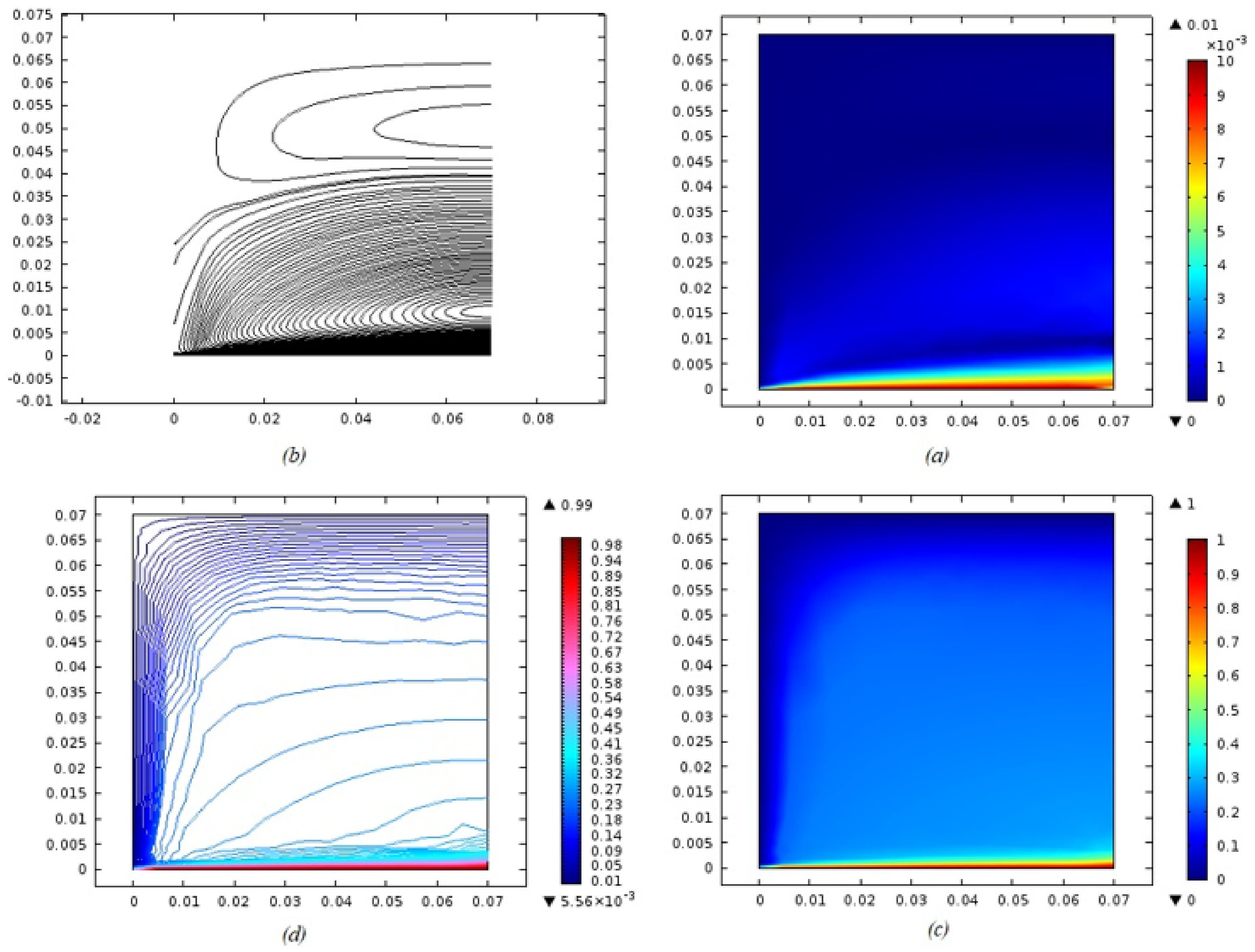
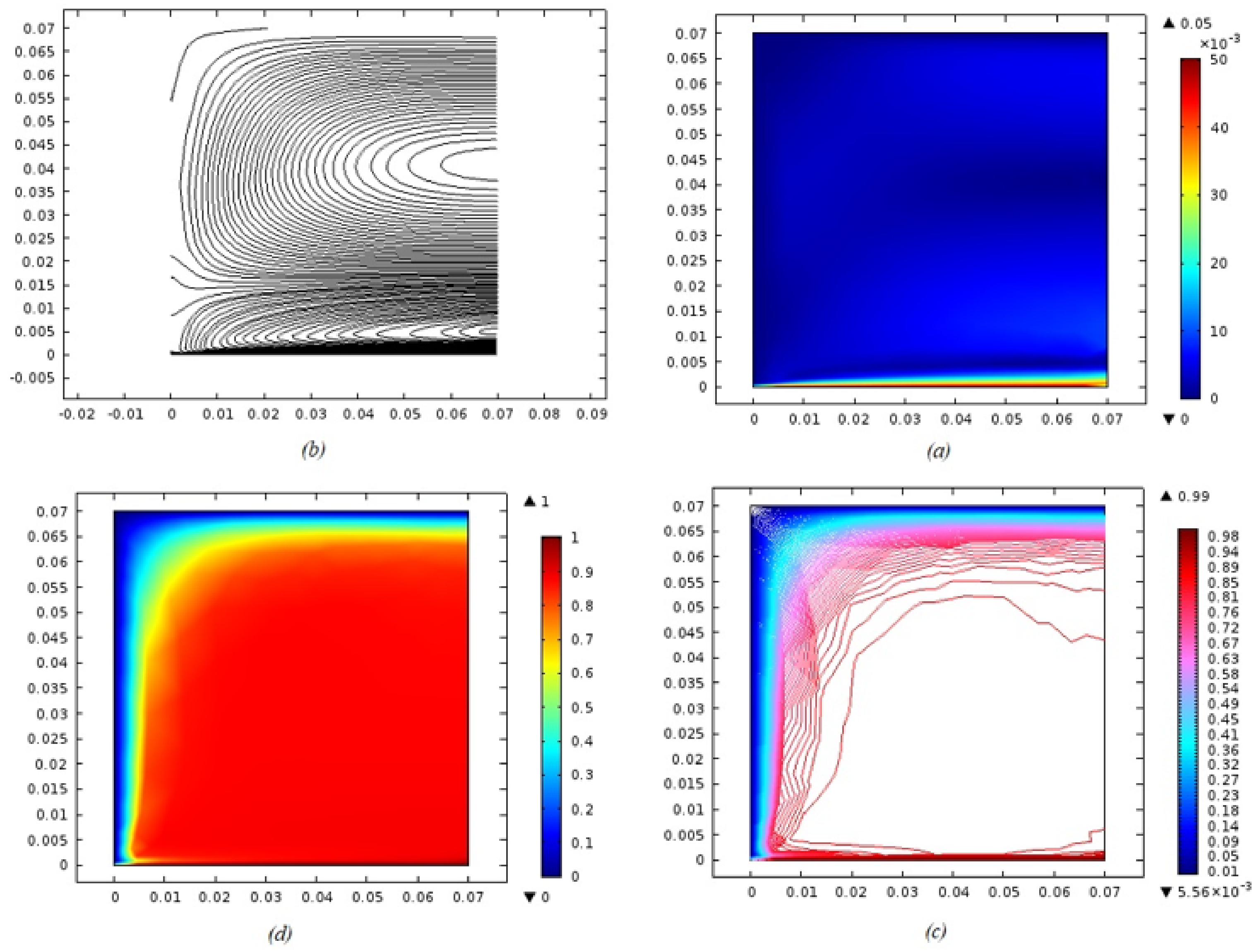
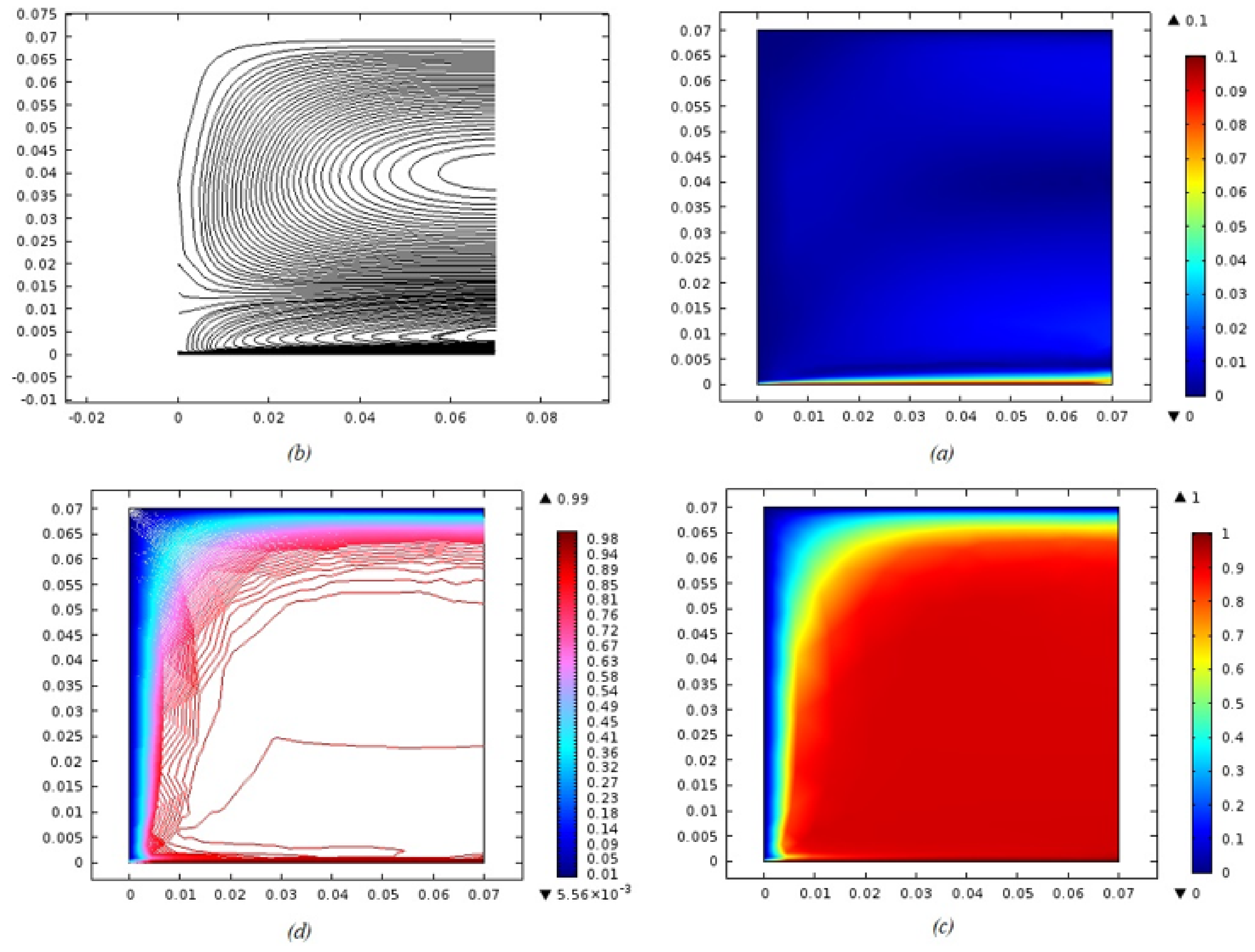
5. Results and Discussions
6. Conclusions
- Velocity profile was de-escalated by escalating magnetic parameter, Deborah number and porosity parameter;
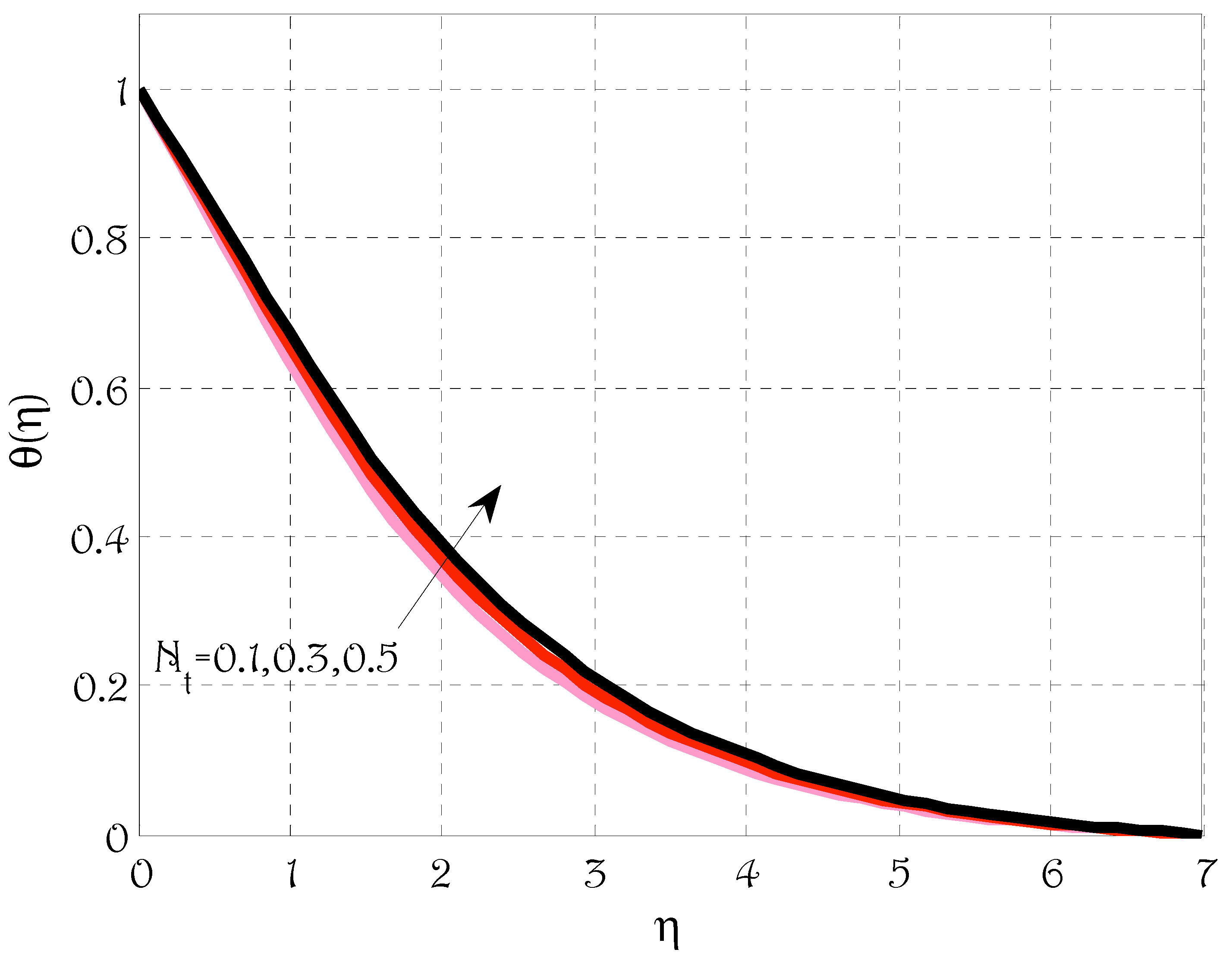
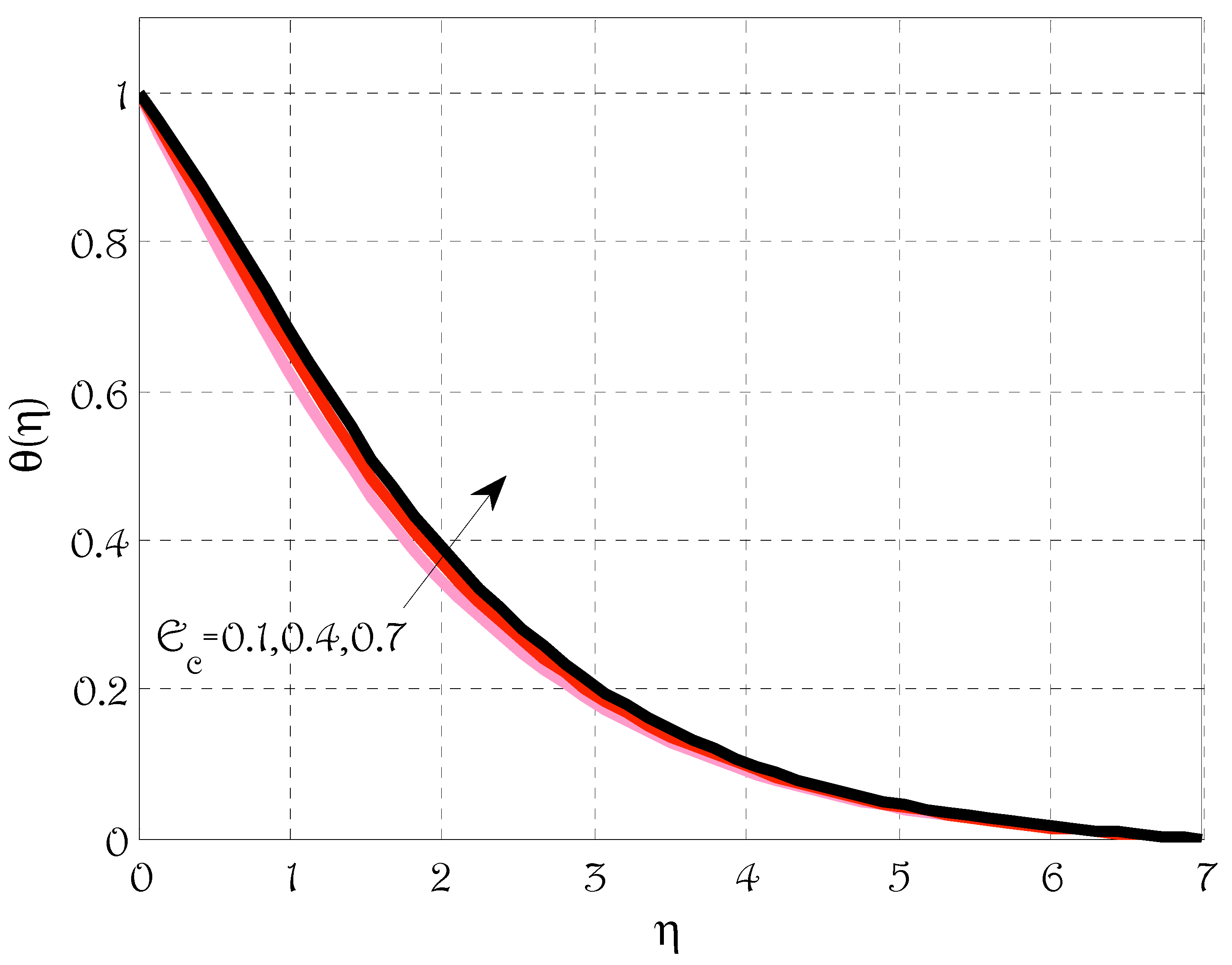
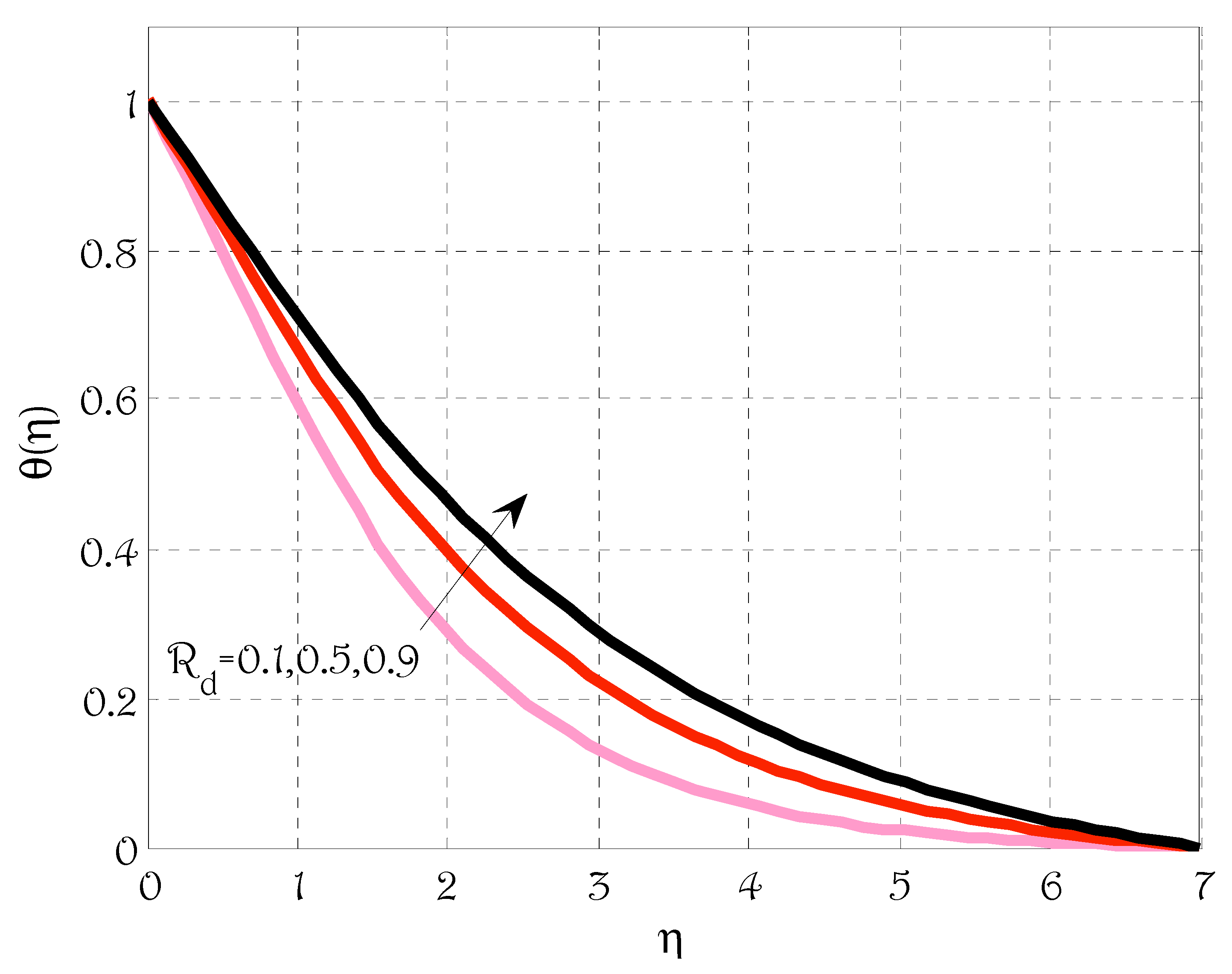
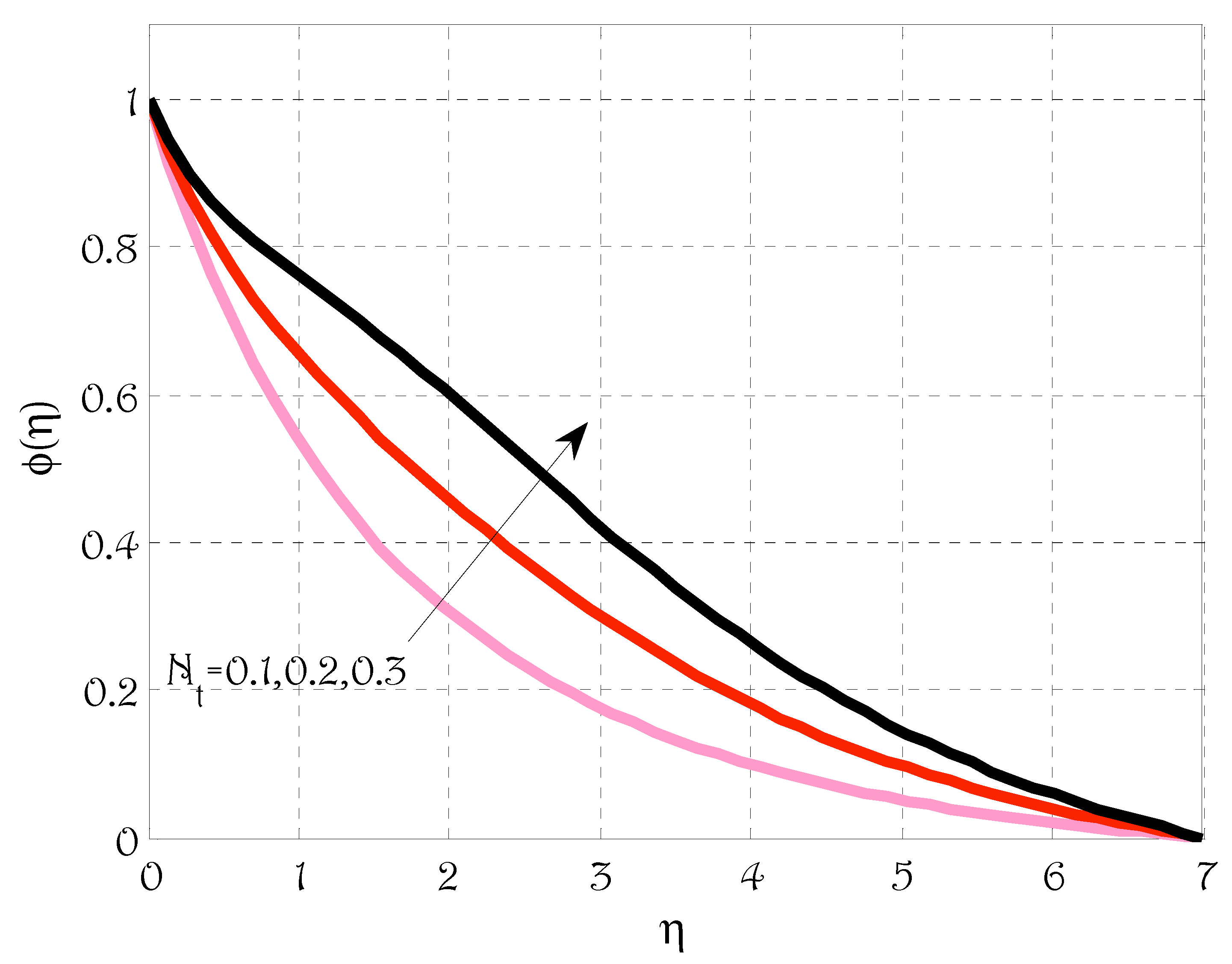
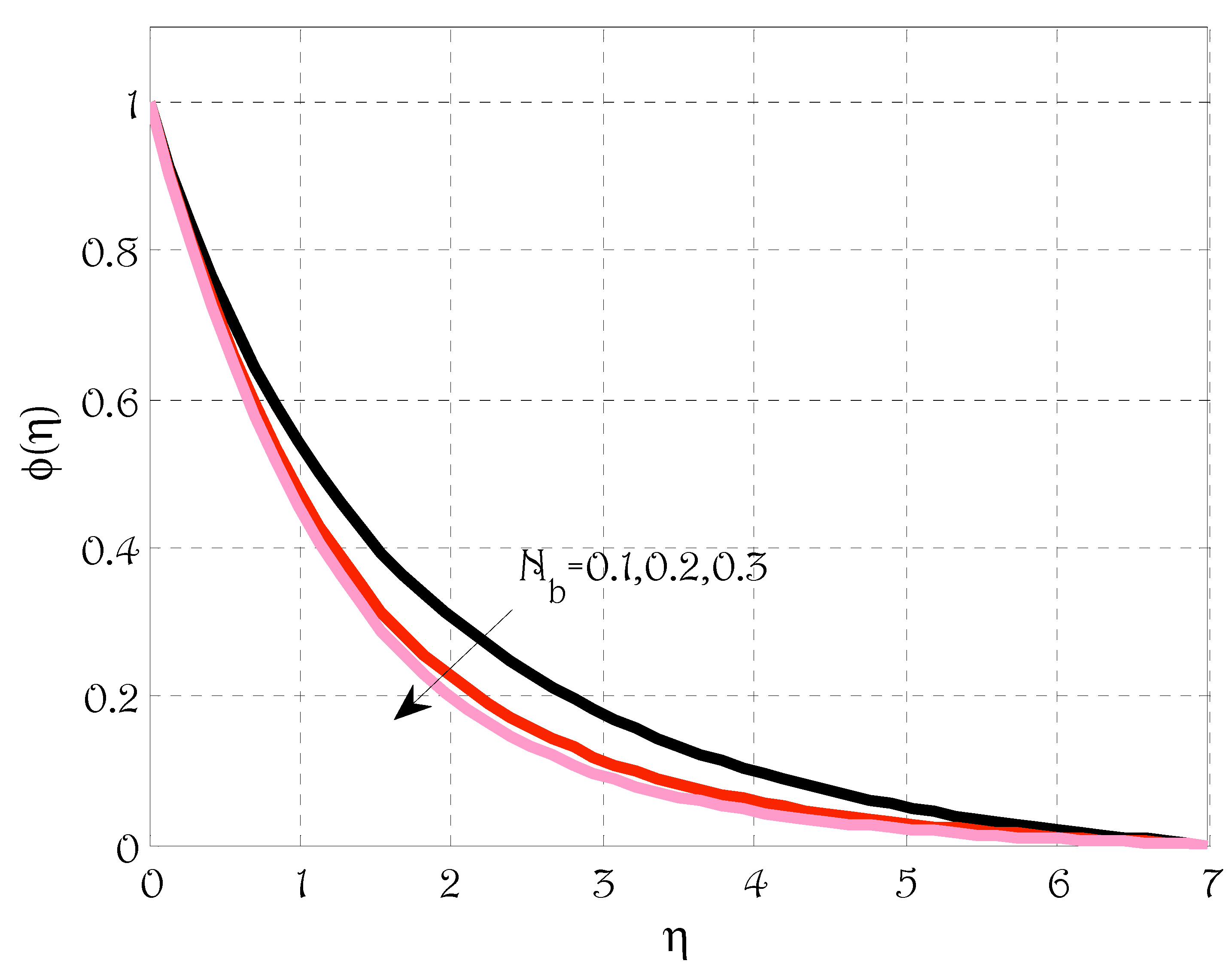
- The temperature profile was grown by rising values of radiation parameters, Brownian motion and thermophoretic parameters;
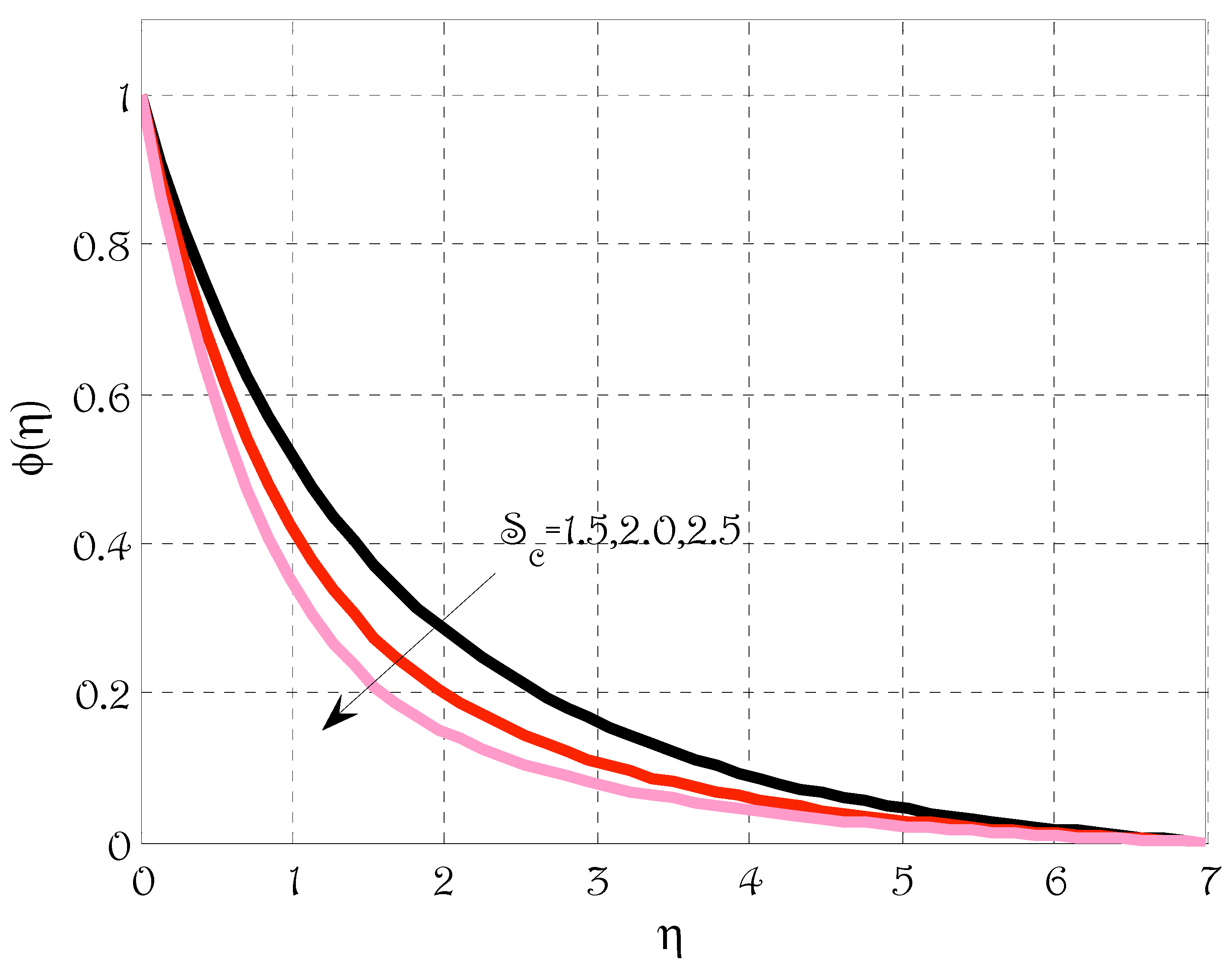
- The concentration profile was escalated by enhancing the Brownian motion and thermophoretic parameters and de-escalating by rising Schmidt number and reaction rate parameters.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rivlin, R.S.; Ericksen, J.L. Stress deformation relation for isotropic materials. J. Rat. Mech. Anal. 1955, 4, 323–425. [Google Scholar] [CrossRef]
- Hayat, T.; Awais, M. Three-dimensional flow of upperconvected Maxwell (UCM) fluid. Int. J. Numer. Methods Fluids 2011, 66, 875–884. [Google Scholar]
- Hayat, T.; Mustafa, M.; Shehzadand, S.A.; Obaidat, S. Melting heat transfer in the stagnation-point flow of an upper-convected Maxwell (UCM) fluid past a stretching sheet. Int. J. Numer. Methods Fluids 2012, 68, 233–243. [Google Scholar] [CrossRef]
- Mukhopadhyay, S. Upper-Convected Maxwell Fluid Flow over an Unsteady Stretching Surface Embedded in Porous Medium Subjected to Suction/Blowing. Z. Nat. A 2012, 67, 641–646. [Google Scholar] [CrossRef] [Green Version]
- Adegbie, K.S.; Omowaye, A.J.; Disu, A.B.; Animasaun, I.L. Heat and Mass Transfer of Upper Convected Maxwell Fluid Flow with Variable Thermo-Physical Properties over a Horizontal Melting Surface. Appl. Math. 2015, 6, 1362–1379. [Google Scholar] [CrossRef] [Green Version]
- Maxwell, J.C. On the dynamical theory of gases. In The Kinetic Theory of Gases: An Anthology of Classic Papers with Historical Commentary, Philosophical Transactions of the Royal Society of London; Cambridge University Press: Cambridge, UK, 2003; pp. 197–261. [Google Scholar]
- Mukhopadhyay, S.; Bhattacharyya, K. Unsteady flow of a Maxwell fluid over a stretching surface in presence of chemical reaction. J. Egypt. Math. Soc. 2012, 20, 229–234. [Google Scholar] [CrossRef] [Green Version]
- Nadeem, S.; Ahmad, S.; Muhammad, N. Cattaneo-Christov flux in the flow of a viscoelastic fluid in the presence of Newtonian heating. J. Mol. Liquids 2017, 237, 180–184. [Google Scholar] [CrossRef]
- Nadeem, S.; Ahmad, S.; Muhammad, N.; Mustafa, M. Chemically reactive species in the flow of a Maxwell fluid. Results Phys. 2017, 7, 2607–2613. [Google Scholar] [CrossRef]
- Khan, M.; Malik, M.Y.; Salahuddin, T.; Khan, F. Generalized diffusion effects on Maxwell nanofluid stagnation point flow over a stretchable sheet with slip conditions and chemical reaction. J. Braz. Soc. Mech. Sci. Eng. 2019, 41, 138. [Google Scholar] [CrossRef] [Green Version]
- Yang, W.; Chen, X.; Zhang, X.; Zheng, L.; Liu, F. Flow and heat transfer of double fractional Maxwell fluids over a stretching sheet with variable thickness. Appl. Math. Model. 2020, 80, 204–216. [Google Scholar]
- Wang, F.; Liu, J. The first solution for the helical flow of a generalized Maxwell fluid within annulus of cylinders by new definition of transcendental function. Math. Probl. Eng. 2020, 2020, 8919817. [Google Scholar] [CrossRef]
- Recebli, Z.; Selimli, S.; Gedik, E. Three dimensional numerical analysis of magnetic field effect on Convective heat transfer during the MHD steady state laminar flow of liquid lithium in a cylindrical pipe. Comput. Fluids 2013, 15, 410–417. [Google Scholar] [CrossRef]
- Recebli, Z.; Selimli, S.; Ozkaymak, M. Theoretical analyses of immiscible MHD pipe flow. Int. J. Hydrogen Energy 2015, 40, 15365–15373. [Google Scholar] [CrossRef]
- Selimli, S.; Recebli, Z.; Arcaklioglu, E. Combined effects of magnetic and electrical field on the hydrodynamic and thermophysical parameters of magnetoviscous fluid flow. Int. J. Heat Mass Transf. 2015, 86, 426–432. [Google Scholar] [CrossRef]
- Hayat, T.; Waqas, M.; Ijaz Khan, M.; Alsaedi, A. Impacts of constructive and destructive chemical reactions in magnetohydrodynamic (MHD) flow of Jeffrey liquid due to nonlinear radially stretched surface. J. Mol. Liq. 2017, 225, 302–310. [Google Scholar] [CrossRef]
- Hayat, T.; Abbas, Z.; Sajid, M. Series solution for the upperconvected Maxwell fluid over a porous stretching plate. Phys. Lett. A 2006, 358, 396–403. [Google Scholar] [CrossRef]
- Raftari, B.; Yildirim, A. The application of homotopy perturbation method for MHD flows of UCM fluids above porous stretching sheets. Comput. Math. Appl. 2010, 59, 3328–3337. [Google Scholar] [CrossRef] [Green Version]
- Sajid, M.; Iqbal, Z.; Hayat, T.; Obaidat, S. Series Solution for Rotating Flow of an Upper Convected Maxwell Fluid over a Stretching Sheet. Commun. Theor. Phys. 2011, 56, 740–744. [Google Scholar] [CrossRef]
- Abel, M.S.; Tawade, J.V.; Nandeppanavar, M.M. MHD flow and heat transfer for the upper-convected Maxwell fluid over a stretching sheet. Meccanica 2012, 47, 385–393. [Google Scholar]
- Abbasi, M.; Rahimipetroudi, I. Analytical solution of an upperconvective Maxwell fluid in porous channel with slip at the boundaries by using the Homotopy Perturbation Method. IJNDES 2013, 5, 7–17. [Google Scholar]
- Nadeem, S.; Ul Haq, R.; Khan, Z.H. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. J. Taiwan Inst. Chem. E. 2014, 45, 121–126. [Google Scholar] [CrossRef]
- Afify, A.A.; Elgazery, N.S. Effect of a chemical reaction on magnetohydrodynamic boundary layer flow of a Maxwell fluid over a stretching sheet with nanoparticles. Particuology 2016, 29, 154–161. [Google Scholar] [CrossRef]
- Sarpkaya, T. Flow of non-Newtonian fluids in a magnetic field. AIChE J. 1961, 7, 324–328. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Thermal radiation effects on the time-dependent MHD permeable flow having a variable viscosity. Int. J. Therm. Sci. 2011, 50, 88–96. [Google Scholar] [CrossRef]
- Turkyilmazoglu, M. Multiple analytic solutions of heat and mass transfer of magnetohydrodynamic slip flow for two types of viscoelastic fluids over a stretching surface. J. Heat Transfer. 2012, 134, 071701. [Google Scholar] [CrossRef]
- Dhanai, R.; Rana, P.; Kumar, L. Multiple solutions in MHD flow and heat transfer of Sisko fluid containing nanoparticles migration with a convective boundary condition: Critical points. Eur. Phys. J. Plus 2016, 131, 142. [Google Scholar] [CrossRef]
- Ellahi, R.; Bhatti, M.M.; Pop, I. Effects of hall and ion slip on MHD peristaltic flow of Jeffrey fluid in a nonuniform rectangular duct. Int. J. Numer. Methods Heat Fluid Flow 2016, 26, 1802–1820. [Google Scholar] [CrossRef]
- Ahmad, S.; Nadeem, S. Flow analysis by Cattaneo–Christov heat flux in the presence of Thomson and Troian slip condition. Appl. Nanosci. 2020, 10, 4673–4687. [Google Scholar] [CrossRef]
- Farooq, U.; Lu, D.; Munir, S.; Ramzan, M.; Suleman, M.; Hussain, S. MHD flow of Maxwell fluid with nanomaterials due to an exponentially stretching surface. Sci. Rep. 2019, 9, 7312. [Google Scholar] [CrossRef] [Green Version]
- Ramadevi, B.; Sugunamma, V.; Kumar, A.; Ramana, R.J.V. MHD flow of Carreau fluid over a variable thickness melting surface subject to Cattaneo-Christov heat flux. Multidiscip. Modeling Mater. Struct. 2019, 15, 2–25. [Google Scholar]
- Kumar, K.A.; Reddy, J.V.R.; Sugunamma, V.; Sandeep, N. MHD Carreau fluid flow past a melting surface with Cattaneo-Christov heat flux. In Applied Mathematics and Scientific Computing; Rushi Kumar, B., Sivaraj, R., Prasad, B., Nalliah, M., Reddy, A., Eds.; Birkhäuser: Cham, Switzerland, 2019; pp. 325–336. [Google Scholar]
- Fourier, J.B.J. Theorie analytique de la chaleur, paris. Acad. Sci. 1822, 3, 1–636. [Google Scholar]
- Fick, A. Poggendorff’s flannel. Ann. Phys. Chem. 1855, 170, 59–86. [Google Scholar] [CrossRef]
- Javed, F.; Nadeem, S. Numerical solution of a Casson nanofluid flow and heat transfer analysis between concentric cylinders. J. Power Technol. 2019, 99, 25–30. [Google Scholar]
- Mallawi, F.; Bhuvaneswari, M.; Sivasankaran, S.; Eswaramoorthi, S. Impact of double-stratification on convective flow of a non-Newtonian liquid in a Riga plate with CattaneoChristov double-flux and thermal radiation. Ain Shams Eng. J. 2020, 12, 969–981. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Farshad, S.A.; Shafee, A.; Babazadeh, H. Performance of solar collector with turbulator involving nanomaterial turbulent regime. Renew. Energy 2021, 163, 1222–1237. [Google Scholar] [CrossRef]
- Sheikholeslami, M.; Farshad, S.A. Nanoparticle transportation inside a tube with quad-channel tapes involving solar radiation. Powder Technol. 2021, 378, 145–159. [Google Scholar] [CrossRef]
- Waqas, H.; Farooq, U.; Alshehri, H.M.; Goodarzi, M. Marangoni-bioconvectional flow of Reiner–Philippoff nanofluid with melting phenomenon and nonuniform heat source/sink in the presence of a swimming microorganisms. Math. Methods Appl. Sci. 2021, 1–19. [Google Scholar] [CrossRef]
- Alazwari, M.A.; Abu-Hamdeh, N.H.; Goodarzi, M. Entropy Optimization of First-Grade Viscoelastic Nanofluid Flow over a Stretching Sheet by Using Classical Keller-Box Scheme. Mathematics 2021, 9, 2563. [Google Scholar] [CrossRef]
- Alazwari, M.; Safaei, M. Non-isothermal hydrodynamic characteristics of a nanofluid in a fin-attached rotating tube bundle. Mathematics 2021, 9, 1153. [Google Scholar] [CrossRef]
- Fetecau, C.; Ellahi, R.; Sait, S.M. Mathematical Analysis of Maxwell Fluid Flow through a Porous Plate Channel Induced by a Constantly Accelerating or Oscillating Wall. Mathematics 2021, 9, 90. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S. An effective modification of finite element method for heat and mass transfer of chemically reactive unsteady flow. Comput. Geosci. 2020, 24, 275–291. [Google Scholar] [CrossRef]
- Sadiq, M.A.; Hayat, T. Darcy–Forchheimer flow of magneto Maxwell liquid bounded by convectively heated sheet. Results Phys. 2016, 6, 884–890. [Google Scholar] [CrossRef] [Green Version]
- Turkyilmazoglu, M. The analytical solution of mixedconvection heat transfer and fluid flow of a MHD viscoelastic fluid over a permeable stretching surface. Int. J. Mech. Sci. 2013, 77, 263–268. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Shatanawi, W.; Nazeer, A. An explicit fourth-order compact numerical scheme for heat transfer of boundary layer flow. Energies 2021, 14, 3396. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Shatanawi, W.; Ashraf, M.U. A Fourth Order Numerical Scheme for Unsteady Mixed Convection Boundary Layer Flow: A Comparative Computational Study. Energies 2022, 15, 910. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Shatanawi, W. A New Fourth-Order Predictor–Corrector Numerical Scheme for Heat Transfer by Darcy–Forchheimer Flow of Micropolar Fluid with Homogeneous–Heterogeneous Reactions. Appl. Sci. 2022, 12, 6072. [Google Scholar] [CrossRef]
- Nawaz, Y.; Arif, M.S.; Abodayeh, K. A Compact Numerical Scheme for the Heat Transfer of Mixed Convection Flow in Quantum Calculus. Appl. Sci. 2022, 12, 4959. [Google Scholar] [CrossRef]


| F.E.M | bvp4c | F.E.M | bvp4c | F.E.M | bvp4c | |
|---|---|---|---|---|---|---|
| Ref. [45] | Ref. [44] | Present | |||
|---|---|---|---|---|---|
| F.E.M | M.F.E.M | F.D.M | |||
| F.E.M | M.F.E.M | F.D.M | F.E.M | M.F.E.M | F.D.M | ||||
|---|---|---|---|---|---|---|---|---|---|
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nawaz, Y.; Arif, M.S.; Abodayeh, K.; Bibi, M. Finite Element Method for Non-Newtonian Radiative Maxwell Nanofluid Flow under the Influence of Heat and Mass Transfer. Energies 2022, 15, 4713. https://doi.org/10.3390/en15134713
Nawaz Y, Arif MS, Abodayeh K, Bibi M. Finite Element Method for Non-Newtonian Radiative Maxwell Nanofluid Flow under the Influence of Heat and Mass Transfer. Energies. 2022; 15(13):4713. https://doi.org/10.3390/en15134713
Chicago/Turabian StyleNawaz, Yasir, Muhammad Shoaib Arif, Kamaleldin Abodayeh, and Mairaj Bibi. 2022. "Finite Element Method for Non-Newtonian Radiative Maxwell Nanofluid Flow under the Influence of Heat and Mass Transfer" Energies 15, no. 13: 4713. https://doi.org/10.3390/en15134713
APA StyleNawaz, Y., Arif, M. S., Abodayeh, K., & Bibi, M. (2022). Finite Element Method for Non-Newtonian Radiative Maxwell Nanofluid Flow under the Influence of Heat and Mass Transfer. Energies, 15(13), 4713. https://doi.org/10.3390/en15134713








