Abstract
On the basis of theoretical considerations (mechanistic model), an equation was determined that allowed to calculate the free energy (Helmholtz) of a spherical droplet deposited on a flat surface in a system without external forces. Assuming isochoric and isothermal transformation of the system and a very fast conversion of mechanical energy into heat, the obtained equation allows to determine the trajectory of thermodynamic transformation consisting of the spreading of the droplet on the surface of the substrate. The similarities and differences in the behaviour of spherical droplets described by the mechanistic model and Young’s model, together with its improvements, were discussed. The trajectories of free energy changes during the spreading of droplets in a system in which the adhesive force acting perpendicular to the wetted surface was considered as well.
1. Introduction
The phenomenon of wetting has accompanied mankind for thousands of years. Probably, at first, it was important mainly during washing, then indirectly during drying clothes. However, just over two hundred years ago, the first papers that attempted a mathematical description of this phenomenon appeared. At present, this phenomenon is important not only at home, but also during manufacturing processes (e.g., painting and varnishing), transport (e.g., lubrication), chemical and medical analysis (microfluidics), and many others.
The most cited paper is that written as an essay by Young in 1805 [1]. It contains a description (in words) of the balance of forces, or rather stresses, acting on a spherical droplet at the point where all phases meet—the droplet, its fluid surroundings, and the flat surface of the solid substrate. It is worth noting that this relationship was written in the form of an equation only over 100 years later [2]. This equation correlates the surface tension at the interface of liquid phases with the tangential stresses to the surface to be wetted. These stresses reflect the intermolecular interactions characterizing the interfacial surfaces and therefore have the properties of physicochemical parameters. The equation shows that for a given three—hase system, the contact angle should be independent of the droplet volume. However, based on the results of the experiments, it is known that the contact angle changes with the volume of the droplets [3]. This effect is especially visible with small, but still macroscopic, droplets.
Due to these observations, an additional term was introduced into Young’s equation corresponding to the stresses acting along the three—phase contact line [4]. This hypothesis was verified based on the experimentally measured contact angle of gas bubbles deposited on a solid substrate. It is worth adding that these stresses may cause shrinking or stretching of this line, depending on the direction of action of this force described by its sign (positive or negative). It should be noted that the introduction of an additional term improved the accuracy of matching the experimental results to the modified Young’s equation. Apart from the fact that the modified Young’s equation is not the best representation of the experimental results, the determined values of the forces acting along the three—phase contact lines are greater by 5–6 orders of magnitude than their values calculated on the basis of molecular simulation [5].
Also in 1805, Laplace published his multi—volume work on mechanics [6]. In one of the chapters, he proved that the curvature of a flexible surface requires that a certain force acts perpendicular to it. If this flexible surface is an interphase surface, its curvature is due to the pressure difference on both sides of it. One can find out about it by observing the column of liquid in the thin capillaries immersed in it. However, even in 1883, when mathematically modeling the shape of the droplets was performed, a constant parameter was adopted instead of this pressure difference [7]. The current form of Laplace–Young’s equation (taking into account pressures) is due to Neuman [8]. It is worth emphasizing here that a perfectly spherical shape of a drop is possible only when the pressure inside it is identical throughout its volume.
In the first half of the twentieth century, the phenomenon of spreading liquid droplets on porous or rough surfaces was mainly studied. Wenzel [9] noticed that the actual wetted surface on the surface of such materials is larger than the geometrically determined one. As a result of this observation, he introduced the roughness coefficient to the Young’s equation, which is the ratio of the two surfaces mentioned. It is worth emphasizing that this factor only affects the tangential stress to the wetted surface of the solid substrate. Cassie and Baxter [10] took into account that as the liquid spreads over the porous surface, it closes a certain amount of gas contained in the pores. As a result of this approach to Young’s equation, another factor was introduced, which modified the value of the contact angle on the flat substrate to the contact angle at the inlet to the pores. This coefficient did not take into account the dependence on the pore diameter, and the determined contact angle for the pores was not compared to the contact angle observed on a flat substrate. Also in this case, the introduced factor only influenced the tangential stress between the spreading liquid and the substrate.
The first relationship based on thermodynamic considerations was derived by Reiss [11] who determined the work of creating a spherical drop in a system not subjected to external forces. The derivation was made on the basis of the free energy (Helmholtz) definition for a two—phase liquid droplet—fluid environment. It is worth noting that during the derivation, no potential mechanism ensuring the isochoric nature of the system was indicated (despite the liquid evaporation), assuming only its isothermal nature.
In 1977, Boruvka and Neuman published a paper in which they derived equations for the internal energy of a macroscopic three—phase system based on the equations used to describe molecular systems [11]. In the obtained equation, apart from typical thermodynamic parameters, the internal energy depended on the interfacial areas, the length of the lines separating the three phases, and the force acting along them, as well as on point energy sources corresponding to local point forces acting in the system. In the case of a spherical droplet deposited on a solid substrate, determining its minimum internal energy requires maintaining the same entropy of all phases present in the system. On the other hand, further determination of the sufficient condition for this minimum is very complicated from the mathematical point of view and is not presented in this paper.
The need for entropy balancing in all phases has been eliminated by using free energy (Helmholtz) for thermodynamic analysis of a liquid droplet deposited on a solid substrate and assuming the isothermal nature of the system [12,13]. This approach made it possible to precisely define the necessary condition for the occurrence of the minimum free energy [14], but still it was not possible to determine the sufficient condition determined on the basis of equilibrium thermodynamics. Only the analysis based on non—equilibrium thermodynamics made it possible to determine the equation which was the condition of a sufficient minimum of free energy (Helmholtz) [15], and also allowed to determine the trajectories of free energy changes during droplet deposition on a solid substrate. On this basis, it was possible to determine whether the droplet spreading over the surface is spontaneous or forced. It is worth noting that the thermodynamic trick described in Appendix [15] ensured the isochoric nature of each of the fluid phases present in the isothermal system under consideration.
It should be emphasized that the equations describing thermodynamic functions (internal energy, thermodynamic potential, free energy) in multi—phase systems were formulated on the basis of ad hoc summation of the energy of interfacial surfaces, energy of phase contact lines, etc. However, the definitions of these state functions (among others in [16]) link their change during thermodynamic transformations with the work performed by the system or performed on the system. It is only as a result of these works that the interfacial surfaces, phase contact lines, etc. change. Each of the performed works results from the forces acting in the system and the change of interfacial surfaces, the position of the phase dividing lines, etc. Therefore, it is surprising that the equations obtained from the models [11,12,13,14,15] do not indicate the existence of adhesion forces perpendicular to the interface at the liquid–solid substrate boundary. After all, the change of molecules from the continuous phase to the droplet molecules should be associated with a change in the energy of the system due to the differentiation of forces acting between the molecules and the surface of the solid substrate. The Lenard–Jones model [17] shows such an impact.
In the available literature, one can find a mathematical model which takes into account all known forces acting on a droplet depositing on a solid substrate [18]. The balance of forces causing the droplet spreading was determined as the minimum of its mechanical energy. Apart from the necessary condition, a sufficient condition for the occurrence of such a minimum has also been established. So far, this model has not been associated with any of the thermodynamic state functions.
From the beginning of the second half of the 20th century until now, a number of mathematical models less related to thermodynamics, or rather to thermodynamic functions, were also formulated. In each of them, hypotheses of phenomena were formulated, which would allow for the balancing of force or stress components perpendicular to the substrate, acting along the three—phase contact line. The first hypothesis was put forward by Deriagin, assuming the existence of a jointing–disjoining pressure characteristic for a given system [19,20]. The result of the occurrence of such a phenomenon would have to be a deformation of the curvature of the interfacial surface between the liquid phases in the immediate vicinity of the three—phase contact line, i.e., the pressure occurring there that differs from the pressure in the remaining droplet volume. Unfortunately, this contradicts the Laplace condition [6] imposing a constant pressure in its entire volume, because in the event of a pressure difference, forces forcing the liquid to move would appear. The second hypothesis formulates the phenomenon of pinning occurring in the substrate along the three—phase contact line [21]. This phenomenon would be associated with a change in the structure of the substrate and the appearance of forces attracting or repelling the liquid forming the droplet in this place. Considering the large variety of wetted substrates, such a phenomenon would have to occur from the molecular to the macroscopic scale. So far, it has not been possible to illustrate it experimentally.
It is worth noting that in both models [19,20,21], there is no adhesion phenomenon consisting in the interaction with the substrate of all the liquid molecules located next to it, see the Lenard—Jones interaction [17]. On the other hand, the interactions between the droplet liquid and the substrate occur only along the three—phase contact line.
The droplet size that can be simulated in molecular modeling ( molecules at most) is not yet in the range that can be studied experimentally. However, the numerical contact angles determined can be compared to those calculated from the Laplace—Young equation with the experimentally determined constants for macroscopic droplets. Unfortunately, the first attempts were unsuccessful [22] and it was necessary to apply appropriate computational schemes to obtain the compliance of both results [23,24]. It should be noted, however, that the simulations are performed for two—dimensional droplets and partially end when Rayleigh instabilities occur, which means that the simulated droplets are far from thermodynamic equilibrium.
A negative or positive sign of a change in free energy during a thermodynamic transformation indicates whether the transformation is spontaneous or forced (inter alia [16]). However, in order to be able to make such an assessment, it is necessary to know the equation describing this thermodynamic function, or rather the trajectory of its changes while spreading over a solid substrate. In the case of Laplace—Young’s equation, such a relationship has been derived [15].
The aim of this work is to formulate an equation defining the free energy (Helmholtz) of a drop resting on a solid substrate based on a mechanistic model taking into account the forces of adhesion between a liquid and a solid [18]. With some simplifications, this relationship would allow the determination of the areas of spontaneous or forced spreading of the droplets on the substrate. It should be emphasized that formulating conclusions regarding the nature of the transformation (spontaneous or forced) is possible based on the sign of the free energy difference between the final and the initial state of the system, but it is not possible based on the magnitude of the forces acting in the system in each of these states.
2. Theory
The analysis of the behavior of a droplet spreading on the surface of the substrate should be started with writing the equation defining its free energy (Helmholtz):
and description of the geometry of the system under consideration.
The system consists of a droplet whose volume corresponds to the volume of a fully spherical drop of radius . The droplet spreading on the flat surface of the substrate forms a segment of a sphere with a radius and a height . Both these values characterize the contact angle . The relationships between the mentioned parameters are determined by the following equations:
Figure 1 schematically shows the adopted coordinate system and geometric parameters used in Equation (2a–d). It should be emphasized that the wetted surface is circular due to the spherical shape of the droplet segment.
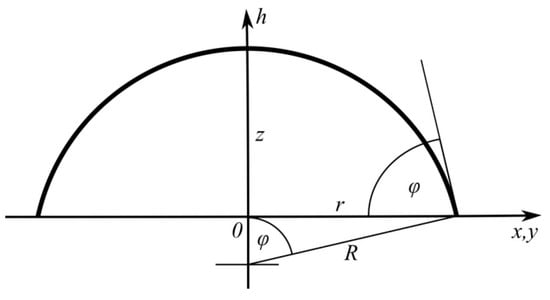
Figure 1.
The geometric meaning of the parameters indicated in the figure and applied in the formulae.
In our previous paper [18], the equation describing the differential mechanical work performed by the droplet spreading on the substrate in a system not affected by external forces was derived:
in which the constant parameters , , are defined analogously to those given in our previous paper [18] as:
Before proceeding to further discussion, it is necessary to quote the conditions and limitations that were applied during the derivation of the above equation [18]:
- In the vicinity of the state of equilibrium of forces acting on the droplet, it takes the shape of a sphere segment, and the fluid velocity and its changes become so small that the inertial forces of the moving fluid and its impact on the surface between fluids due to the so—called dynamic pressure become negligible.
- During droplet deposition on the substrate, the temperature of any of the system components does not change.
- The liquid forming the droplet does not change its volume—the entire system under nature of the system, it is possible to avoid the need to consider the issue of droplet evaporation [15]. On the other hand, the assumption of complete insolubility of the components of both fluid phases allows to ignore the influence of the Marangoni effect.
Due to the isothermal and isochoric nature of the system under consideration, Equation (1) is simplified to the following form:
Free energy is a function of state, therefore its change does not depend on the transformation trajectory, but only on the parameters characterizing the initial and final state of the system. This means that the droplet transformation from the moment it touches the substrate at one point until reaching the equilibrium state is described by the following integral:
and as a result, we get the equation:
in which the expression denotes the hypergeometric function described by Gauss back in the 19th century [25].
Before the drop spreads and reaches the state of equilibrium of forces, the liquid fragments inside it will obtain a certain kinetic energy not included in Equation (7). As a result of the viscosity of the fluid, this kinetic energy will be converted into heat, causing an increase in the entropy of the system, which, due to its isothermal nature, will not change the expression in Equation (1). Moreover, in our considerations, we do not analyze the kinetics (hydrodynamics) of the liquid flow and, as a result, the appearance and disappearance of its kinetic energy. Therefore, we can assume that the kinetic energy that appears is transformed infinitely fast into heat, and according to the isothermal condition of the system, this heat is infinitely removed outside the system. This assumption corresponds exactly to the infinitely high viscosity of the liquid or the infinitely slow spreading of the droplet. It is also worth noting that such an assumption does not affect the form of Equations (6) and (7) because the viscosity of the liquid and time are not parameters of the model, but only affect the shape of the thermodynamic transformation trajectory, determining its asymptotic course. This, in turn, allows one for the determination of areas for which the droplet spreading is spontaneous or forced.
Based on the above observations, it is possible to interpret the relationship of the following terms in Equations (6) and (7) with specific sources (forces) in the system under consideration. The first term is related to the pressure changes inside the droplet caused by the change in the curvature of the interfacial surface between the fluid phases, and actually with the technical work () performed in the system. The second term describes the change in free energy caused by the adhesive force acting between the liquid and the substrate—perpendicular to the substrate. The third one corresponds to the free energy changes due to the force acting on the three—phase contact line—tangent to the substrate. On the other hand, the fourth one corresponds to the free energy changes caused by the force acting along the three—phase contact line causing it to shrink or stretch.
The hypergeometric function is expressed as a series with an infinitely large number of terms. Therefore, instead of calculating it, it is much more convenient to perform a numerical calculation of the dimensionless free energy using Equation (6).
3. Results and Discussion
Due to the large variety of behaviors of the analyzed system, a detailed analysis was carried out for only three cases identical to those described in [18].
3.1. Young’s Solution
The classical Young’s equation takes into account only surface tension stresses (forces) acting at the interface of liquid phases and tangential stresses to the substrate surface, stresses shrinking or stretching the wetted circumference [1,2]. In the case of the derived model [18], the balance of forces is described by the following equation:
a stable solution is obtained only for [18], i.e., when the sufficient condition for the occurrence of the minimum free energy is fulfilled. It is also worth noting that real solutions can only be obtained for .
It should be emphasized that the contact angle tends to the right angle () while the value of the parameter tends to unity (), which means that the surface tension stress is balanced by the force stretching the wetted circuit. On the other hand, in Young’s equation, the contact angle reaches this value when , which means that the droplet is not affected by any forces, and yet it rests on the substrate.
In the case under consideration, the dimensionless free energy is described by the equation:
Changes in the free energy of a spherical droplet during its spreading on a solid substrate (Young’s case) are shown in Figure 2. After a droplet comes into contact with the substrate, it is necessary to supply it with some mechanical energy in order to initiate its spreading. Only after reaching a certain maximum value of free energy, corresponding to the unstable balance of forces, the drop will start to spread spontaneously. This maximum is higher the higher the parameter value is. After this maximum is exceeded, the droplet spreads spontaneously on the substrate until it reaches the minimum free energy value. The droplet can spread further only as a result of supplying it with additional mechanical energy. It is worth noting that for the level of this minimum corresponds to the free energy of the drop characterizing its state before contact with the substrate. For higher values of this parameter, the free energy at its minimum point is higher than the initial one. For the value of , the minimum of free energy disappears, and there is only the inflection point. It is also worth noting that for , there is no local free energy maximum and the droplet spreads spontaneously over the entire surface of the flat substrate. Moreover, the free energy of a fully spherical droplet is higher than that of a flat liquid surface. This means that this spherical droplet is characterized by a thermodynamically unstable being.
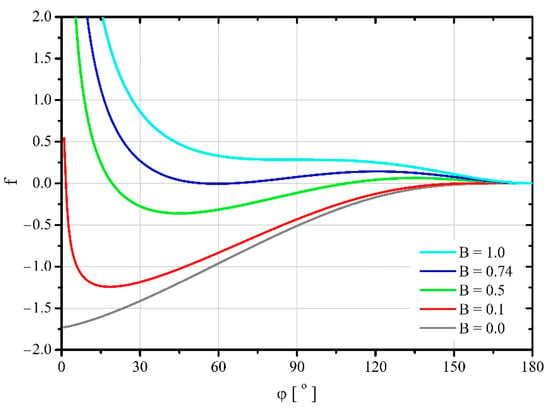
Figure 2.
Changes in the dimensionless free energy of a spherical droplet during its spreading on a solid surface—the Young case.
In the traditional Young’s model [1,2], for the value of the parameter , the contact angle is equal to . For such a system, there is a minimum area of the spherical cup, which justifies the existence of the minimum free energy determined on the basis of the so—called surface energy of the drop. However, in such a system, the balance of forces acting in the direction perpendicular to the surface of the substrate is evidently not satisfied. There is simply no stress along the three—phase contact line to balance the surface tension of the contacting interface between the fluid phases at this point.
3.2. Improved Young’s Solution
When the droplet is subjected to a force tangential to the surface of the substrate and a force that stretches or shrinks the three—phase contact line, the balance of forces (minimum free energy) is described by the following equation [18]:
On the other hand, the equation describing the dimensionless free energy (6) simplifies to the form:
Due to the richness of the behavior of the considered system and the limited volume of the article, only three graphs shown in Figure 3, Figure 4 and Figure 5 were prepared for illustration. A single, stable minimum of free energy (Helmholtz) occurs whenever one of the following conditions is met [18]: or . In such cases, the droplets spread spontaneously on the substrate. However, due to the very significant values of parameter , the analysis of this issue would not assess the impact of parameter on the solutions of Young’s Equation (8), but would only contribute to the discussion of an unrelated case.
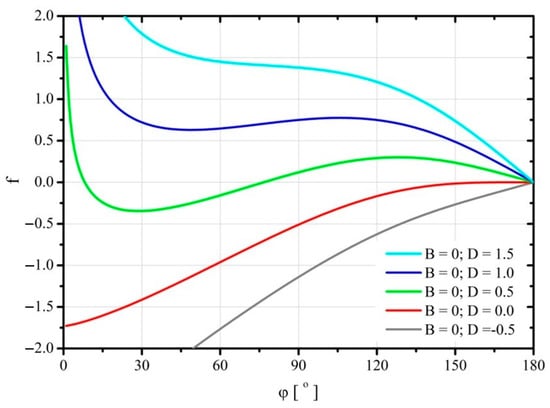
Figure 3.
Change of the dimensionless free energy of the system during spreading of the droplet for the parameter .
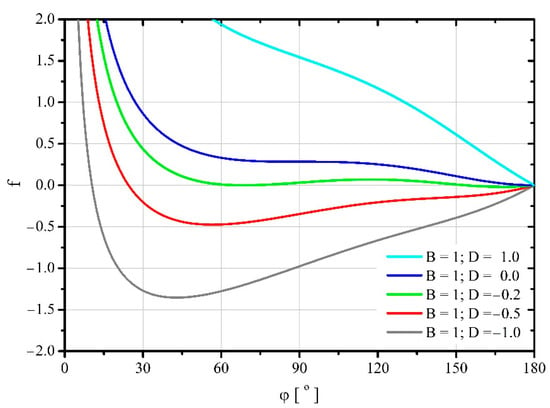
Figure 4.
Change of the dimensionless free energy of the system during spreading of the droplet for the parameter .
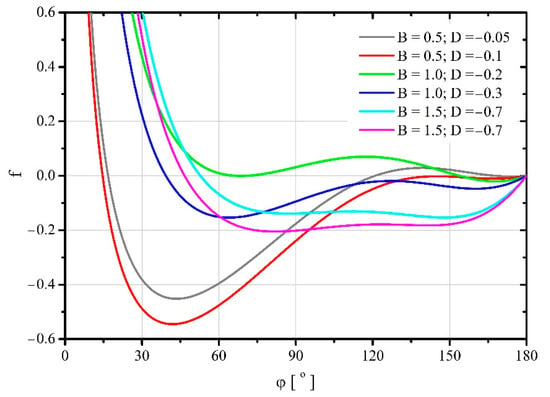
Figure 5.
Changes of dimensionless free energy during droplet spreading for the values of parameters and for which there are two stable minima of this function.
In the considered case, a single and stable minimum of free energy also occurs when one of the following conditions is met: and or and [18]. Thus, the analysis covered two extreme cases for which Young’s solution should be met, i.e., for the parameters and . The results are shown in Figure 3 and Figure 4. However, in order to initiate the spontaneous spread of the droplet on the substrate, initially it is necessary to provide the droplet with a certain amount of mechanical energy so as to exceed a certain threshold value of free energy. The graphs also show example curves for which the conditions for the occurrence of a single stable minimum of free energy were not met. Thus, in Figure 3 it is the curve for and , and in Figure 4 the curve for and . In both cases, the spreading of the liquid on the substrate requires additional energy to be supplied to the system. Moreover, the curve for and was also plotted in Figure 3. For such parameter values, the droplet will spontaneously spread over the entire surface of the substrate. Figure 4 also shows the curve corresponding to the values of parameters and . In this case, the spreading droplet can reach two free energy minima corresponding to two contact angle values.
The formulated model [18] predicts the occurrence of two minima of the free energy of a droplet deposited on a flat surface. These stable minima occur when one of the following conditions is met: and or and [18]. For such parameter values, the droplets spread spontaneously after contact with the substrate reaching the first minimum of free energy. Moving to the next minimum requires a certain amount of mechanical energy to be supplied. Therefore, it is important to determine this energy, or rather its minimum value, which is a measure of the system durability. For this purpose, Figure 5 was prepared, showing exemplary free energy trajectories of spreading droplets on the substrate.
With the increase in the value of the parameter, the trajectories of free energy changes during the spreading of the droplet, shown in Figure 5, become increasingly flat. This means that a smaller and smaller portion of mechanical energy has to be delivered to the droplet so that it passes from one state to another one that meet the conditions of a stable balance of forces.
It is worth noting that the thermodynamic description of the phenomenon related to the improved Young’s equation [15] does not indicate the existence of two stable minima of free energy. These minima represent the balance of forces acting on the droplet and can potentially correspond to the advancing and receding contact angles observed during the experiments [5].
3.3. Influence of Adhesion Force on Free Energy Variation
The cases described so far were related to the Young’s equation [1,2] because they took into account only the same forces; more specifically, forces tangential to the surface of the substrate stretching or shrinking the wetted surface, stretching or shrinking the three—phase contact line, and the surface tension acting at the interface of fluid phases. On the other hand, the Young’s equation does not take into account the adhesive force acting between the molecules of the liquid forming the drop and the substrate material and directed perpendicularly to it. This in turn means that the zero value of the parameter appearing in Equations (3), (6) and (7).
Let us consider a typical case of Young, in which, apart from the forces tangential to the substrate, stretching or shrinking the wetted surface [1,2], we also take into account the adhesion force acting perpendicular to the surface of the substrate. Then, the equation describing the balance of forces is described by the following equation [18]:
In such a case, the Equation (6) describing the dimensionless free energy is simplified to the form:
The characteristic point of Young’s equation, mentioned in Section 3.1, is determined by the contact angle , for which there is evidently no equilibrium of forces acting perpendicular to the substrate to be wetted. On the other hand, transforming the Equation (12) in the absence of forces acting tangentially to the wetted substrate (), the following equation can be obtained:
which proves that the adhesion forces balance the surface tension forces acting on the wetted perimeter, and more precisely, the adhesion forces balance the overpressure inside the droplet caused by the curvature of the interfacial surface between the fluid phases. It is also worth noting that this balance of forces will be stable, which can be determined based on the sufficient condition of presence of the minimum free energy [18], and .
The results shown in [18] imply that for a surface adhesion force greater than or equal to zero ( or ), the equilibrium of forces in the analyzed system can only occur when . In addition, as shown in the previous paper [18], the solutions to the equilibrium equation of forces acting on the droplet for the value of the parameter divide the entire area of solutions to the equilibrium equation of forces into two parts. In the first region where the parameters can vary within the range and , a stable equilibrium of forces cannot exist for large values of the contact angle . On the other hand, in the second, for and , this stable equilibrium of forces cannot occur for small values of this angle. Since the relationship between the free energy and the forces acting on the droplet (3) and (5) is the same for both areas, the shapes of the free energy changes as a function of the contact angle should have a topologically similar course. To explore this, Figure 6 was created, on which several trajectories for each of the areas were plotted.
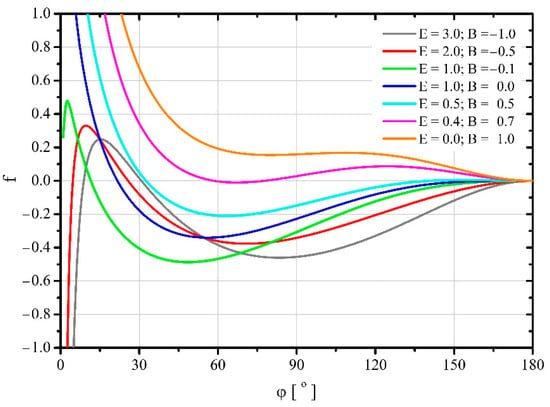
Figure 6.
Changes in dimensionless free energy in a system in which there is no force acting along the three—phase contact line causing its stretching or shrinking ().
For negative values of parameter , for which the forces tangential to the surface of the substrate cause shrinkage of the wetted area, after contact with the substrate, the droplets spread out spontaneously reaching the minimum free energy. However, further spreading of the droplets requires the application of mechanical energy to them until free energy reaches a certain maximum value. After this maximum is exceeded, further spreading of the droplets occurs spontaneously again until the surface of the substrate is completely covered with the liquid. On the other hand, for non—negative values of this parameter (), after the droplet comes into contact with the substrate, it is initially necessary to supply the droplet with a certain amount of mechanical energy to drive it to spread. Only after exceeding a certain maximum free energy of the system, the spontaneous spread of the droplets begins until the minimum of this energy is reached. Further spreading of the droplet requires the supply of mechanical energy to it. A certain exception is the course of the trajectory for , for which the initial maximum of energy does not occur and the droplet spreads spontaneously from the moment it touches the substrate.
It is worth noting that for positive values of parameter pairs and , the free energy characterizing its minimum may be greater than the initial free energy of the droplet. This means that achieving a stable balance of forces requires the supply of a certain amount of mechanical energy to a droplet.
Although the derivation of the equations shown in the paper concern the spherical shape of the droplet, the results of the experiments show that droplets of other shapes can also form on solid substrates [5]. Looking from the point of view of thermodynamics, such cases are very rarely analyzed mainly due to obvious mathematical difficulties. Currently published papers [26] concern the description of surface energy rather than the description of the total or free energy of such systems. The basic problem seems to be the combination of all types of energy (e.g., surface and adhesion) as a function of the state.
4. Conclusions
This work is an extension of the mechanistic model of liquid distribution on the surface of a solid substrate [18]. It presents the analytical derivation of the equation of the dependence of free energy (Helmholtz) on the contact angle, which allows to determine the nature of the spherical droplet spreading (spontaneous or forced) on a solid substrate. Appropriate calculations can be performed based on the knowledge of the unit forces (physicochemical parameters) acting parallel and perpendicular to the surface to be wetted and on the interface between the fluids.
In the case of solutions corresponding to the Young model [1,2], the minimum free energy (stable force equilibrium) may occur only when the stretching force of the wetted perimeter acts parallel to the substrate and perpendicular to the three—phase contact line. However, the free energy of a droplet sessile on the substrate will be lower than the energy of the spherical droplet floating above the substrate when the ratio of the stretching force of the wetted perimeter to the surface tension at the interface of fluid phases will be less than . This means that for higher values of this ratio, the droplet spreading will be forced.
The solutions corresponding to the improved Young’s equation indicate that only in certain ranges of variability of physicochemical parameters (surface tension between fluid phases, tension stretching or shrinking the wetted area, unit force acting along the three—phase contact line), there is at least one stable minimum of free energy. The most important, however, is that in the case of tangential stress to the wetted surface stretching the wetted perimeter and the unitary force shrinking the wetted perimeter acting along the line of contact of three phases, there are two stable minima of the free energy of the system. This behavior confirms the results of experiments in which two contact angles advancing and receding are observed [5]. It is also important that the energy barrier (free energy change) necessary to overcome when passing from one minimum to another may be relatively small. It should be emphasized that such a theoretical explanation is provided only by a formulated mechanistic model.
In the case of very high adhesion forces, the free energy reaches a stable minimum, practically regardless of whether there is a stretching or shrinking tension of the wetted perimeter. Only after the droplet comes into contact with the substrate and the stretching tension on the wetted perimeter occurs is it necessary to provide a certain amount of work to the droplet so that it starts to spread spontaneously. For the shrinking tension acting on this perimeter, such spreading occurs spontaneously from the moment the droplet contacts the substrate.
If, during the spreading of the droplet, the mechanical energy is infinitely fast converted into heat, the derived dependence of the free energy on the contact angle can be treated as a trajectory of such isochoric and isothermal thermodynamic transformation.
Author Contributions
Conceptualization, J.A.M. and S.J.; methodology, J.A.M. and S.J.; validation, J.A.M. and S.J.; formal analysis, J.A.M. and S.J.; investigation, J.A.M. and S.J.; writing—original draft preparation, J.A.M. and S.J.; writing—review and editing, J.A.M. and S.J.; visualization, S.J. and J.A.M.; supervision, J.A.M. and S.J.; project administration, J.A.M. and S.J. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding. The APC was funded by Warsaw University of Technology.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| Nomenclature | |
| constant parameter | |
| constant parameter | |
| dimensionless free energy | |
| constant parameter | |
| free energy (Helmholtz) | |
| force acting along three-phase contact line | |
| pressure | |
| radius of the wetted surface | |
| radius of the droplet bowl | |
| radius of the sphere with a volume equal to the volume of the droplet | |
| entropy | |
| temperature | |
| droplet volume | |
| work | |
| droplet height | |
| Greek Letters | |
| unitary adhesion force perpendicular to solid surface (droplet–substrate interface) | |
| perimeter of the wetted surface | |
| contact angle | |
| tension parallel to the substrate surface, perpendicular to the three-phase contact line, stretching or shrinking wetted area | |
| surface tension (droplet—fluid surrounding interface) |
References
- Young, T. An Essay on the Cohesion of the Fluids. Philos. Trans. R. Soc. Lond. 1805, 95, 65–87. [Google Scholar]
- Maxwell, J.C.; Strut, J.W. Capillary Action. In Encyclopædia Britannica, 11th ed.; Encyclopædia Britannica Inc.: London, UK; New York, NY, USA, 1911; pp. 256–277. [Google Scholar]
- Good, R.J.; Koo, M.N. The Effect of Drop Size on Contact Angle. J. Colloid Interface Sci. 1979, 71, 283–292. [Google Scholar] [CrossRef]
- Vesselovsky, V.C.; Pertzov, V.N. Adhesion of Air Bubbles to the Solid Surface. Zhurnal Fiz. Khimii 1936, 8, 245–259. [Google Scholar]
- Erbil, H.Y. The debate on the dependence of apparent contact angles on drop contact area or three-phase contact line: A review. Surf. Sci. Rep. 2014, 69, 325–365. [Google Scholar] [CrossRef]
- Laplace, P.S. Traite de Mecanique Celeste. In Chez Courcier; Imprimeur-Libraire pour les Mathematiques: Paris, France, 1805; Volume 4. [Google Scholar]
- Bashforth, F.; Adams, J.C. An Attempt to Test. In The Theories of Capillary Action; University Press Warehouse: Cambridge, UK, 1883. [Google Scholar]
- Neuman, F. Theorie der Capillarität: Leipzig, Verlag von B. G. Teubner; University of California Libraries: Los Angeles, CA, USA, 1894. [Google Scholar]
- Wenzel, R.N. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Cassie, A.B.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Boruvka, L.; Neuman, A.W. Generalization of the classical theory of capillarity. J. Chem. Phys. 1977, 66, 5464–5476. [Google Scholar] [CrossRef]
- Drelich, J.; Miller, J.D. The Line/Pseudo-Line Tension in Three Phase System. Part. Sci. Technol. 1992, 10, 1–20. [Google Scholar] [CrossRef]
- Drelich, J. The Significance and Magnitude of the Line Tension in Three-Phase (Solid-Liquid-Fluid) Systems. Colloid Surf. A 1996, 116, 43–54. [Google Scholar] [CrossRef]
- Widom, B. Line Tension and the Shape of a Sessile Drop. J. Phys. Chem. 1995, 99, 2803–2806. [Google Scholar] [CrossRef]
- Torbus, S.; Dolata, M.; Jakiela, S.; Michalski, J.A. Analysis of Existing Thermodynamic Models of the Liquid Drop Deposited on the Substrate—A Sufficient Condition of the Minimum Free Energy of the System. Coatings 2019, 9, 791. [Google Scholar] [CrossRef] [Green Version]
- Pohorecki, R.; Wronski, S. Kinetyka I Termodynamika Procesów Inżynierii Chemicznej; Wydawnictwo Naukowo-Techniczne: Warsaw, Poland, 1979. [Google Scholar]
- Lennard-Jones, J.E. On the Determination of Molecular Fields. Proc. R. Soc. Lond. A 1924, 106, 463–477. [Google Scholar]
- Michalski, J.A.; Jakiela, S. Spherical Droplet Deposition—Mechanistic Model. Coatings 2021, 11, 248. [Google Scholar] [CrossRef]
- De Gennes, P.-G.; Brochard-Wyart, F.; Quéré, D. Capillarity and Wetting Phenomena; Springer: New York, NY, USA, 2004. [Google Scholar]
- Kuchin, I.; Starov, V. Hysteresis of Contact Angle of Sessile Droplets on Smooth homogeneous Solid Substrates via Disjoining/Conjoining Pressure. Langmuir 2015, 31, 5345–5352. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tadmor, R. Open Problems in Wetting Phenomena: Pinning Retention Forces. Langmuir 2021, 37, 6357–6372. [Google Scholar] [CrossRef] [PubMed]
- Nijmeijer, M.J.P.; Bruin, C.; Bakker, F.A. Wetting and drying of an inert wall by a fluid in a molecular-dynamic simulation. Phys. Rev. A 1990, 42, 6052–6059. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Schmelzer, J. The curvature dependence of surface tension of small droplets. J. Chem. Soc. Faraday Trans. 1986, 82, 1421–1428. [Google Scholar] [CrossRef]
- Kanduc, M. Going beyond the standard line tension: Size-dependent contact angles of water nanodroplets. J. Chem. Phys. 2017, 147, 174701-1–174701-8. [Google Scholar] [CrossRef] [PubMed]
- Gauss, C.F. Disquisitiones Generales Circa Seriem Infinitam; Typis Dieterichianis: Gottingae, Germany, 1878. [Google Scholar]
- Siqveland, L.M.; Skjaeveland, S.M. Derivations of the Young-Laplace equation. Capillarity 2021, 4, 23–30. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).