Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model
Abstract
:1. Introduction
2. Gas–Solid Flow and Reaction
2.1. Gas–Solid Flow Model
2.2. Chemical Reaction Model
2.3. Main Reactions in the Simulation
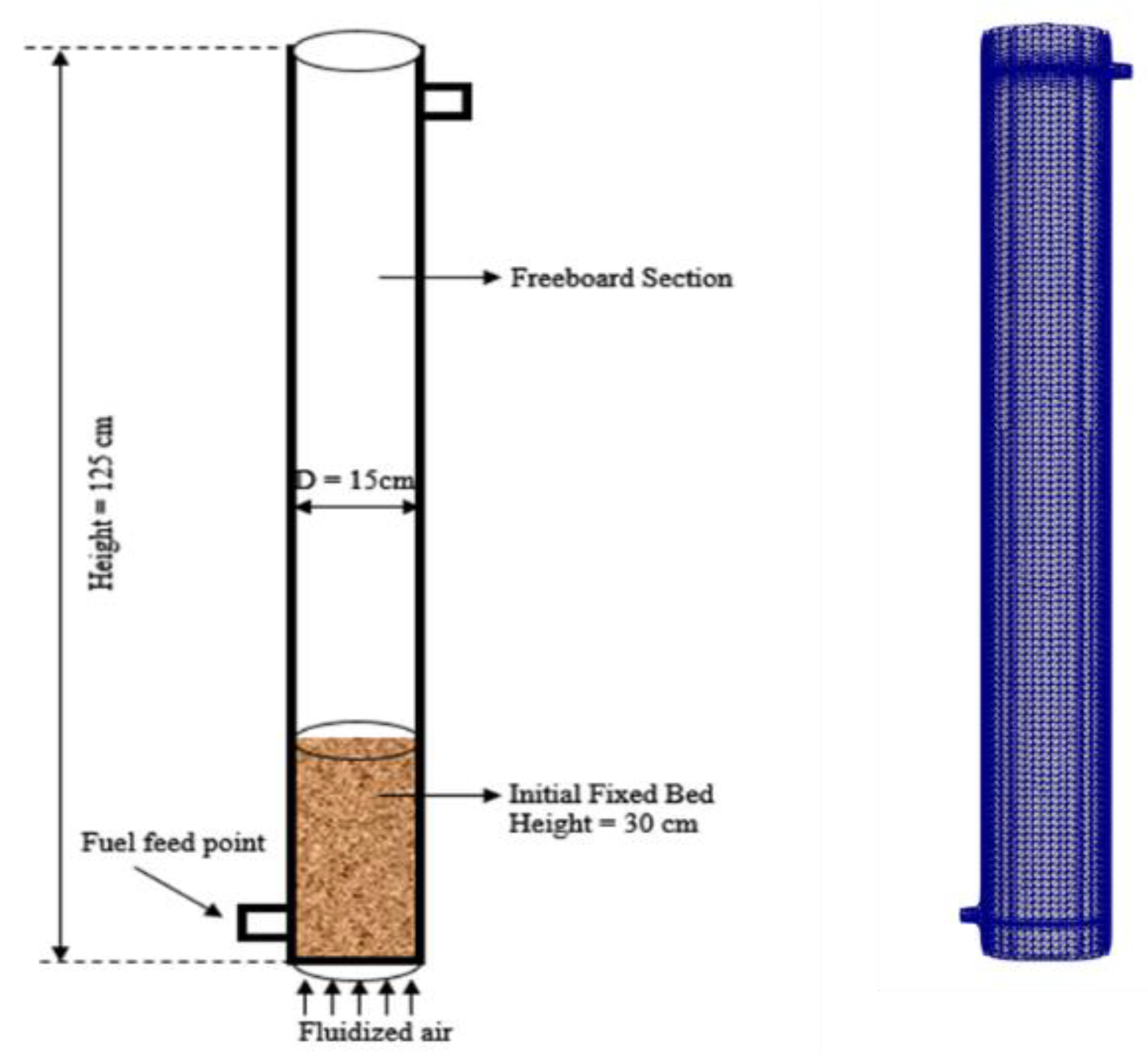
3. The Research Object
4. Simulation Conditions
5. Results and Discussion
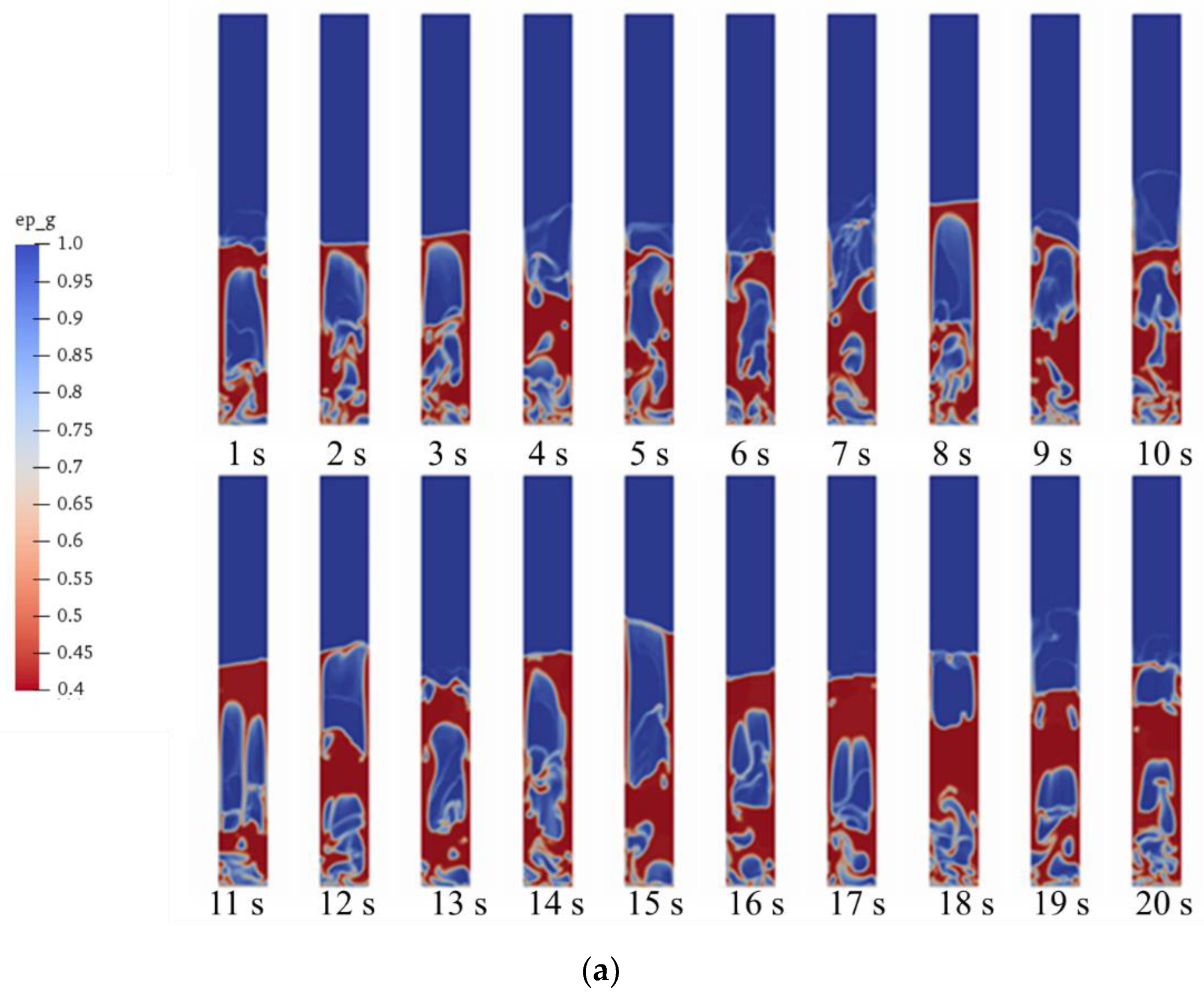
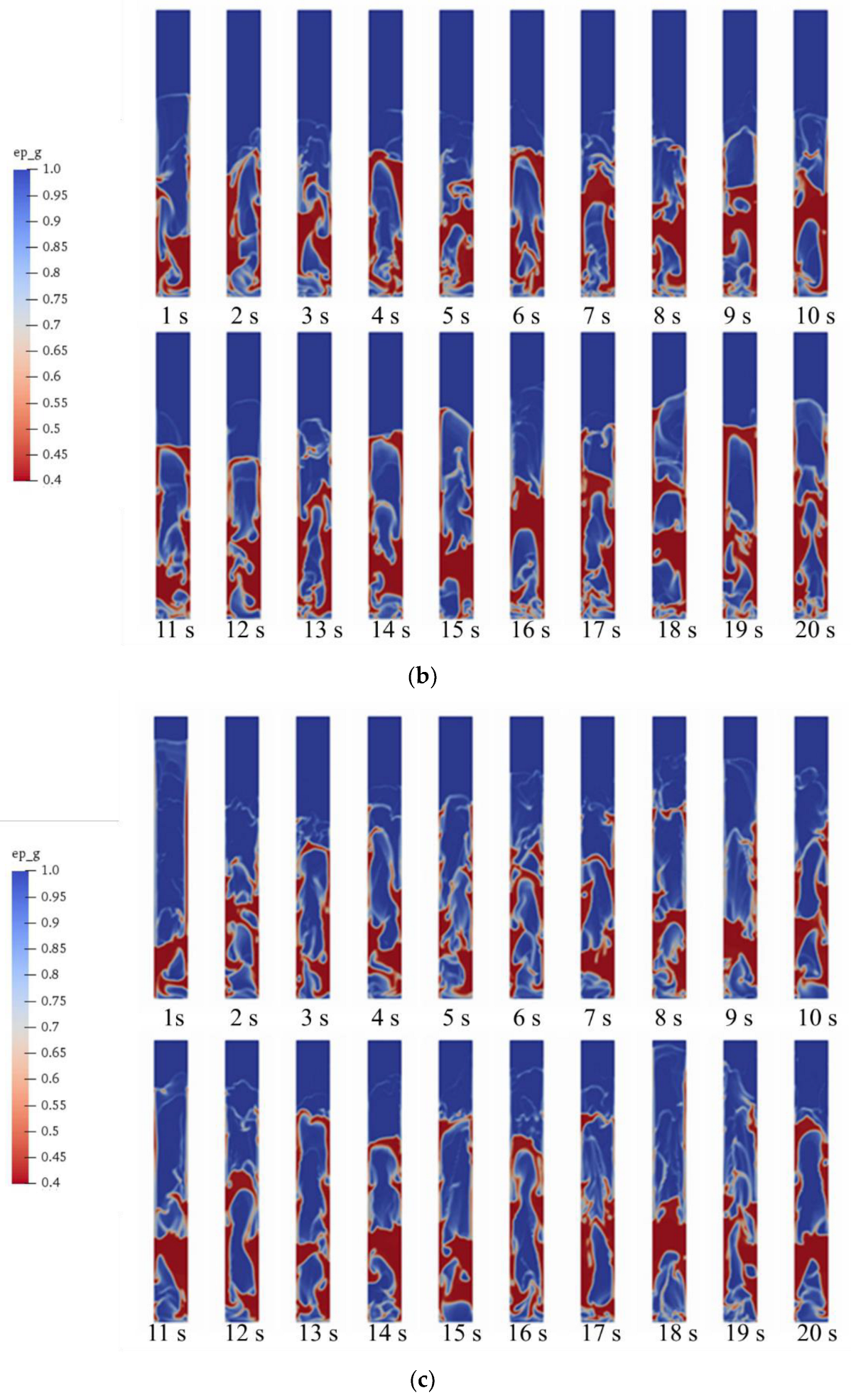
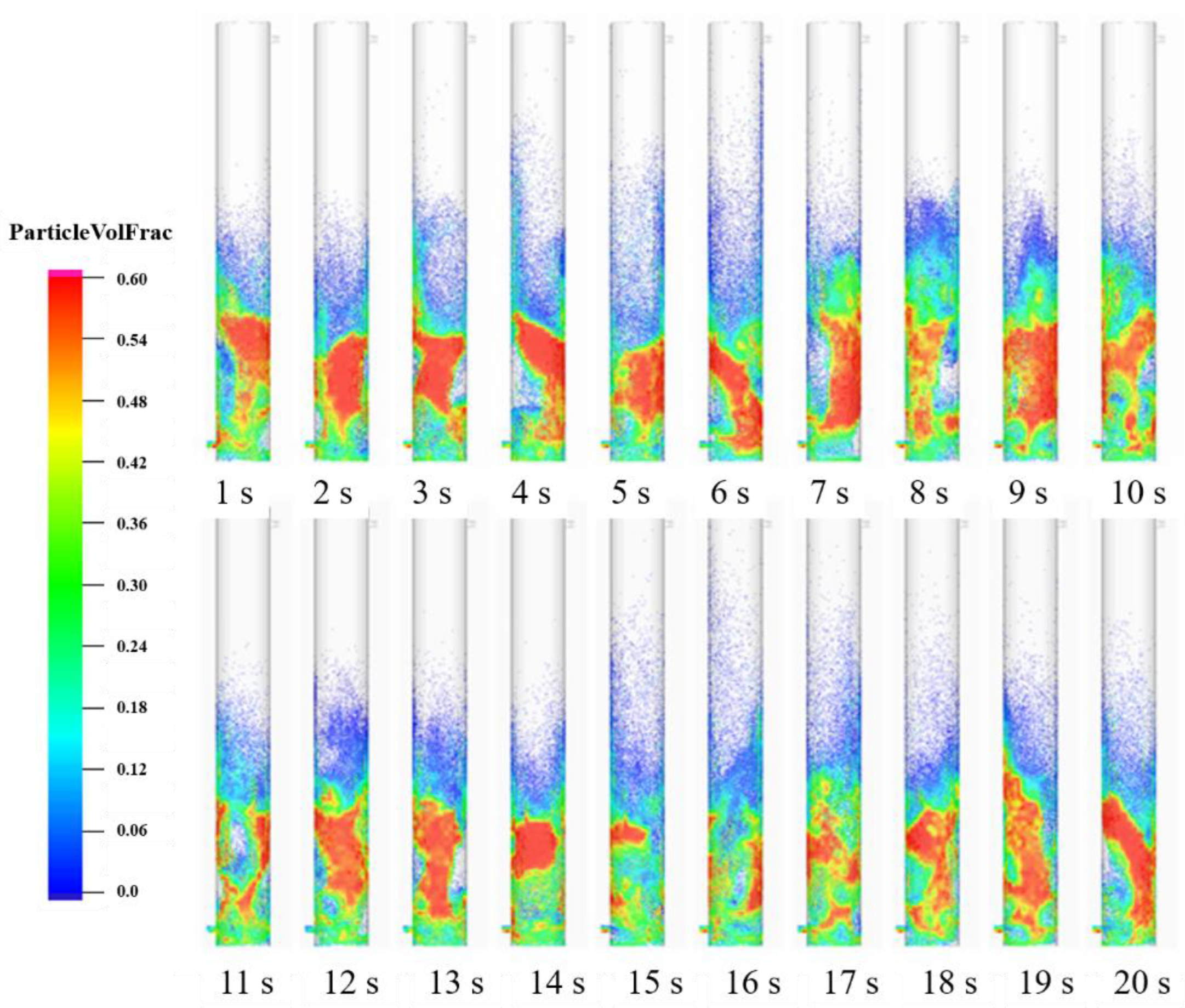
5.1. Gas–Solid Flow in Fluidized Bed Gasifier
5.2. Chemical Reaction Model Validation
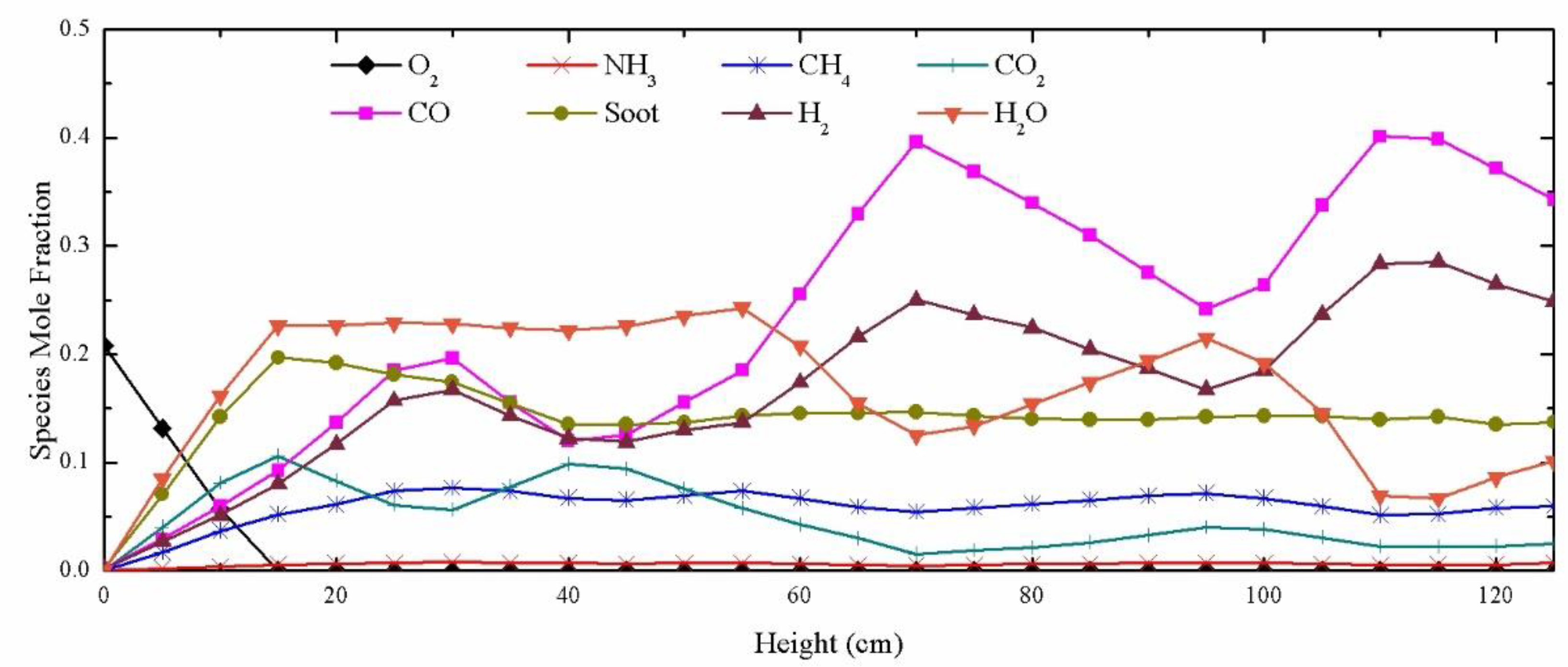
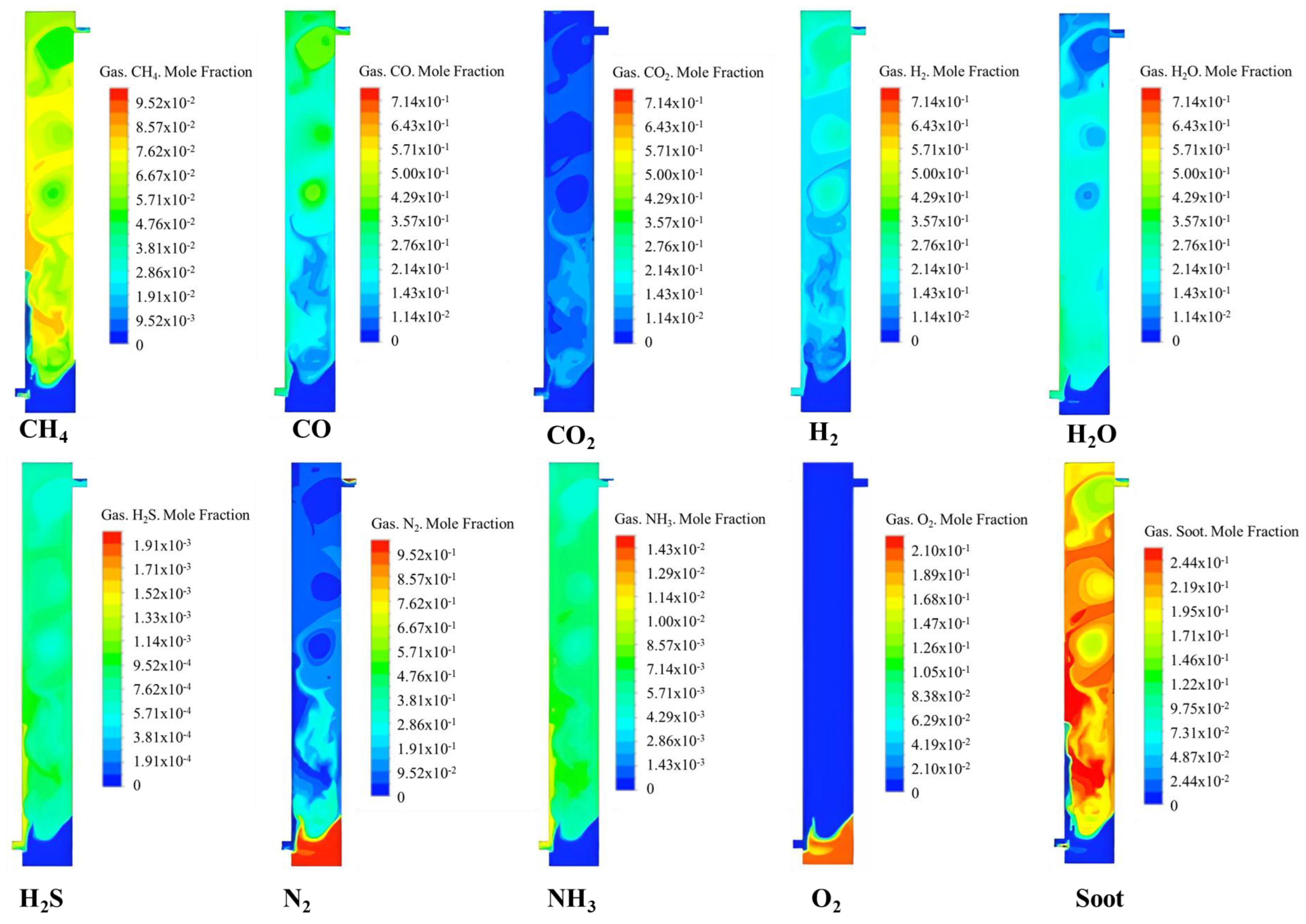
5.3. Distribution of Syngas Components in the Gasifier
5.4. Analysis of Factors Influencing Syngas Generation
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Odgaard, O.; Delman, J. China’s energy security and its challenges towards 2035. Energy Policy 2014, 71, 107–117. [Google Scholar] [CrossRef]
- Guo, X.; Xiao, B.; Zhang, X.; Luo, S.; He, M. Experimental study on air-stream gasification of biomass micron fuel (BMF) in a cyclone gasifier. Bioresour. Technol. 2009, 100, 1003–1006. [Google Scholar] [CrossRef] [PubMed]
- Ngusale, G.K.; Luo, Y.; Zhang, R.-z.; Yin, R.-h.; Zhao, W.-l. Gasification of wood pellets in a bench-scale updraft gasifier. Energy Sources Part A Recovery Util. Environ. Eff. 2016, 38, 1875–1881. [Google Scholar] [CrossRef]
- Wu, K.; Ren, T.; Chen, H.; Zhu, Y. Experimental investigation of whole tires and biomass mixed firing in reverse burning fixed-bed gasifier. Energy Procedia 2017, 105, 583–589. [Google Scholar] [CrossRef]
- You, Z.; You, S.; Ma, X. Studies on Biomass Char Gasification and Dynamics; IOP Conference Series: Earth and Environmental Science; IOP Publishing: Bristol, UK, 2018; p. 052032. [Google Scholar]
- Zhang, Z.; Pang, S. Experimental investigation of biomass devolatilization in steam gasification in a dual fluidised bed gasifier. Fuel 2017, 188, 628–635. [Google Scholar] [CrossRef]
- Ding, J.; Gidaspow, D. A bubbling fluidization model using kinetic theory of granular flow. AIChE J. 1990, 36, 523–538. [Google Scholar] [CrossRef]
- Lathouwers, D.; Bellan, J. Modeling of dense gas–solid reactive mixtures applied to biomass pyrolysis in a fluidized bed. Int. J. Multiph. Flow 2001, 27, 2155–2187. [Google Scholar] [CrossRef]
- Lathouwers, D.; Bellan, J. Yield optimization and scaling of fluidized beds for tar production from biomass. Energy Fuels 2001, 15, 1247–1262. [Google Scholar] [CrossRef]
- Zhang, H.; Yu, C.; Luo, Z.; Li, Y.A. Investigation of Ash Deposition Dynamic Process in an Industrial Biomass CFB Boiler Burning High-Alkali and Low-Chlorine Fuel. Energies 2020, 13, 1092. [Google Scholar] [CrossRef] [Green Version]
- Yu, X.; Blanco, P.H.; Makkawi, Y.; Bridgwater, A.V. CFD and experimental studies on a circulating fluidised bed reactor for biomass gasification. Chem. Eng. Process.-Process Intensif. 2018, 130, 284–295. [Google Scholar] [CrossRef] [Green Version]
- Xu, Y.; Liu, X.; Qi, J.; Zhang, T.; Xu, M.; Fei, F.; Li, D. Compositional and structural study of ash deposits spatially distributed in superheaters of a large biomass-fired CFB boiler. Front. Energy 2021, 15, 449–459. [Google Scholar] [CrossRef]
- Unchaisri, T.; Fukuda, S.; Phongphipat, A.; Saetia, S.; Sajjakulnukit, B. Experimental study on combustion characteristics in a CFB during Co-firing of coal with biomass pellets in Thailand. Int. Energy J. 2019, 19, 101–114. [Google Scholar]
- Ahmad, A.A.; Zawawi, N.A.; Kasim, F.H.; Inayat, A.; Khasri, A. Assessing the gasification performance of biomass: A review on biomass gasification process conditions, optimization and economic evaluation. Renew. Sustain. Energy Rev. 2016, 53, 1333–1347. [Google Scholar] [CrossRef]
- Tang, Y.-l.; Liu, D.-j.; Liu, Y.-h.; Luo, Q. 3D computational fluid dynamics simulation of natural coke steam gasification in general and improved fluidized beds. Energy Fuels 2010, 24, 5602–5610. [Google Scholar] [CrossRef]
- Loha, C.; Gu, S.; De Wilde, J.; Mahanta, P.; Chatterjee, P.K. Advances in mathematical modeling of fluidized bed gasification. Renew. Sustain. Energy Rev. 2014, 40, 688–715. [Google Scholar] [CrossRef]
- Wu, H.; Yang, C.; He, H.; Huang, S.; Chen, H. A hybrid simulation of a 600 MW supercritical circulating fluidized bed boiler system. Appl. Therm. Eng. 2018, 143, 977–987. [Google Scholar] [CrossRef]
- Yang, C.; Wu, H.; Deng, K.; He, H.; Sun, L. Study on Powder Coke Combustion and Pollution Emission Characteristics of Fluidized Bed Boilers. Energies 2019, 12, 1424. [Google Scholar] [CrossRef] [Green Version]
- Ismail, T.M.; Ramos, A.; Monteiro, E.; Abd El-Salam, M.; Rouboa, A. Parametric studies in the gasification agent and fluidization velocity during oxygen-enriched gasification of biomass in a pilot-scale fluidized bed: Experimental and numerical assessment. Renew. Energy 2020, 147, 2429–2439. [Google Scholar] [CrossRef]
- Chapman, S.; Cowling, T.G. The Mathematical Theory of Non-Uniform Gases: An Account of the Kinetic Theory of Viscosity, Thermal Conduction and Diffusion in Gases; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Jenkins, J.T.; Savage, S.B. A theory for the rapid flow of identical, smooth, nearly elastic, spherical particles. J. Fluid Mech. 1983, 130, 187–202. [Google Scholar] [CrossRef]
- Syamlal, M.; O’Brien, T.J. Computer simulation of bubbles in a fluidized bed. AIChE Symp. Ser. 1989, 85, 22–31. [Google Scholar]
- Snider, D.M.; Clark, S.M.; O’Rourke, P.J. Eulerian–Lagrangian method for three-dimensional thermal reacting flow with application to coal gasifiers. Chem. Eng. Sci. 2011, 66, 1285–1295. [Google Scholar] [CrossRef]
- Srinivas, S.; Field, R.P.; Herzog, H.J. Modeling tar handling options in biomass gasification. Energy Fuel 2013, 27, 2859–2873. [Google Scholar] [CrossRef]
- Li, C.; Suzuki, K. Tar property, analysis, reforming mechanism and model for biomass gasification—An overview. Renew. Sustain. Energy Rev. 2009, 13, 594–604. [Google Scholar] [CrossRef]
- Syamlal, M.; Bissett, L.A. METC Gasifier Advanced Simulation (MGAS) Model; USDOE Morgantown Energy Technology Center: Morgantown, WV, USA, 1992.
- Hobbs, M.L.; Radulovic, P.T.; Smoot, L.D. Modeling fixed-bed coal gasifiers. Aiche J. 1992, 38, 681–702. [Google Scholar] [CrossRef]
- Armstrong, L.-M.; Gu, S.; Luo, K.H. Effects of limestone calcination on the gasification processes in a BFB coal gasifier. Chem. Eng. J. 2011, 168, 848–860. [Google Scholar] [CrossRef] [Green Version]
- Armstrong, L.; Gu, S.; Luo, K. Parametric study of gasification processes in a BFB coal gasifier. Ind. Eng. Chem. Res. 2011, 50, 5959–5974. [Google Scholar] [CrossRef]
- He, P.-w.; Luo, S.-y.; Cheng, G.; Xiao, B.; Cai, L.; Wang, J.-b. Gasification of biomass char with air-steam in a cyclone furnace. Renewable Energy 2012, 37, 398–402. [Google Scholar] [CrossRef]
- Gerber, S.; Behrendt, F.; Oevermann, M. An Eulerian modeling approach of wood gasification in a bubbling fluidized bed reactor using char as bed material. Fuel 2010, 89, 2903–2917. [Google Scholar] [CrossRef]
- Xiao, R.; Zhang, M.; Jin, B.; Huang, Y.; Zhou, H. High-temperature air/steam-blown gasification of coal in a pressurized spout-fluid bed. Energy Fuels 2006, 20, 715–720. [Google Scholar] [CrossRef]
- Liu, H.; Elkamel, A.; Lohi, A.; Biglari, M. Computational fluid dynamics modeling of biomass gasification in circulating fluidized-bed reactor using the Eulerian–Eulerian approach. Ind. Eng. Chem. Res. 2013, 52, 18162–18174. [Google Scholar] [CrossRef]
- Radmanesh, R.; Chaouki, J.; Guy, C. Biomass gasification in a bubbling fluidized bed reactor: Experiments and modeling. AIChE J. 2006, 52, 4258–4272. [Google Scholar] [CrossRef]



| 0.09 | 1.44 | 1.92 | 1.3 | 0.5 | 1.0 | 1.3 | 0.75 |
| Fuel → Char + Ash + Moisture (H2O) +Volatile Matter | Srinivas [24], Li [25] |
| H2O (l) → H2O (g) | [26] |
| olatile → α1CO + α2CO2 + α3CH4 + α4H2 + α5H2S + α6NH3 + α7H2O + α8Tar | [26] |
| C + O2 → CO2 | [27,28,29] [30] |
| C + CO2 →2 CO | [30] |
| C + H2O → CO + H2 | [31] |
| C +2 H2 → CH4 | |
| Tar → β1CO + β2C + β3CH4 | [31,32] |
| Tar + γ1O2 → γ2CO2 + γ3H2O | |
| CO + 0.5O2 → CO2 | [31,32] |
| H2 + 0.5O2 → H2O | [31,32] |
| CH4 + 2O2 → CO2 + 2H2O | [31,32] |
| CO + H2O ↔ CO2+ H2 | [31,32] |
| Components | Unit | Value |
|---|---|---|
| Moisture | % | 10.1 |
| Ash | % | 6.4 |
| Volatile | % | 67.2 |
| Fixed carbon | % | 16.3 |
| C | % | 49.4 |
| H | % | 43.6 |
| O | % | 6.1 |
| N | % | 0.7 |
| S | % | 0.17 |
| ER | Initial Bed Temperature (K) | Flowrate of Air (Nm3/h) |
|---|---|---|
| 0.2 | 1000 | 81 |
| 0.2 | 1050 | 81 |
| 0.2 | 1100 | 81 |
| 0.3 | 1000 | 121.68 |
| 0.3 | 1050 | 121.68 |
| 0.3 | 1100 | 121.68 |
| 0.4 | 1000 | 162 |
| 0.4 | 1050 | 162 |
| 0.4 | 1100 | 162 |
| Gas Phase | Solid Phase | |
|---|---|---|
| Inlet | ||
| Wall | ||
| Outlet | ||
| Experiment | Simulation | |
|---|---|---|
| Biomass feed rate (kg/h) | 74.8 | 75 |
| Air (Nm3/h) | 84.5 | 81 |
| ER | 0.22 | 0.2 |
| Gasification Temperature (°C) | 815 | 800 |
| Gas Composition (dry vol. %) | ||
| H2 | 14.7 | 17.71 |
| CO2 | 11.8 | 5.94 |
| O2 | 0.00 | 0.00 |
| CO | 20.2 | 20.1 |
| CH4 | 4.4 | 3.77 |
| N2 | 49.0 | 52.48 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, H.; Yang, C.; Zhang, Z.; Zhang, Q. Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model. Energies 2022, 15, 4800. https://doi.org/10.3390/en15134800
Wu H, Yang C, Zhang Z, Zhang Q. Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model. Energies. 2022; 15(13):4800. https://doi.org/10.3390/en15134800
Chicago/Turabian StyleWu, Haochuang, Chen Yang, Zonglong Zhang, and Qiang Zhang. 2022. "Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model" Energies 15, no. 13: 4800. https://doi.org/10.3390/en15134800
APA StyleWu, H., Yang, C., Zhang, Z., & Zhang, Q. (2022). Simulation of Two-Phase Flow and Syngas Generation in Biomass Gasifier Based on Two-Fluid Model. Energies, 15(13), 4800. https://doi.org/10.3390/en15134800







