Dynamic Modeling of a PEM Fuel Cell Power Plant for Flexibility Optimization and Grid Support

Abstract

The transition toward high shares of non-programmable renewable energy sources in the power grid requires an increase in the grid flexibility to guarantee grid reliability and stability. This work, developed within the EU project Grasshopper, identifies hydrogen Fuel Cell (FC) power plants, based on low temperature PEM cells, as a source of flexibility for the power grid. A dynamic numerical model of the flexible FC system is developed and tested against experimental data from a 100-kW pilot plant, built within the Grasshopper project. The model is then applied to assess the flexible performance of a 1 MW system in order to optimize the scale-up of the pilot plant to the MW-size. Simulations of load-following operation show the flexibility of the plant, which can ramp up and down with a ramp rate depending only on an externally imposed limit. Warm-up simulations allow proposing solutions to limit the warm-up time. Of main importance are the minimization of the water inventory in the system and the construction of a compact system, which minimizes the distance between the components.

1. Introduction and Background

To achieve greenhouse gas emission targets that many countries have set in the last years [1], a significant increase in the penetration of Renewable Energy Sources (RES) in the power grid is required. However, the growth in non-programmable resources such as solar photovoltaics and wind [2,3] hinders the reliability and stability of the electric grid [4] because (i) their discontinuous and uncertain generation causes unforeseeable oscillations in the net load and (ii) their modularity favors the diffusion of distributed generators, connected to the distribution grid and close to the demand. Thus, energy flows become unpredictable both in quantity and direction.

To allow the deployment of RES to grow without affecting the grid reliability, it is necessary to rethink the design, operation, and planning of the power system, both on a technical and on an economic level. On the technical side, it is necessary to increase the system flexibility with fast-ramping dispatchable plants, energy storage systems, demand-side management, and interconnections to the adjacent power grids for trading [5,6,7,8]. On the economic side, the regulatory framework must be adjusted to allow new services and business models. New rules for the electricity market have been set in the European Union with the Clean Energy for All European package [9], which aims at helping the energy markets to better manage the energy flows across Europe, to empower the consumers, and to include more renewables. With these rules, the prosumers (both producers and consumers) can vary their consumption and production based on price changes, thus participating in the energy market and contributing to grid efficiency and integration of RES.

At the same time, in this scenario characterized by stringent greenhouse gas reduction targets, the development of a hydrogen economy has gained renewed interest. Indeed, the key role that hydrogen can play in fostering the clean energy transition has been recognized at an international level by the Hydrogen Council, gathering a number of industrial entities [10], as well as by the International Energy Agency [11]. On the one hand, the deployment of hydrogen technologies has the potential to increase the penetration of renewables in the power system, allowing demand–supply balancing and avoiding renewable energy curtailment. On the other hand, hydrogen technologies have sector coupling capability, and clean hydrogen can be used to decarbonize either the industrial sector, the transport sector, or the heating and cooling sector. For instance, hydrogen is used in refinery and for the production of clean fuels (e.g., ammonia and methanol).

At the European level, the European Green Deal [12] includes the European hydrogen strategy, aiming at making clean hydrogen a viable solution to decarbonize the different energy sectors over time across Europe, enabling the European Union to play a global pioneering role in this field. The priority is the development of renewable hydrogen, although in the short-term, other forms of low-carbon hydrogen are necessary to support the creation of a profitable market. Another important aspect is that the targets set by the European hydrogen strategy (e.g., 24% of hydrogen in its energy mix by 2050) also require the import of renewable electricity or of green hydrogen from overseas. Thus, the European hydrogen strategy promotes the deployment of renewable energy sources in developing countries, and especially in the countries of the African Union, bridging the energy transition between advanced and developing countries [13].

In this framework, this work identifies MW-scale Fuel Cell (FC) power plants based on low temperature Proton Exchange Membrane (PEM) cells as a source of flexibility for the future high-RES penetration electric grid, providing grid ancillary services thanks to their fast ramp rate and the load-following capability. The potential of this technology is being investigated within the EU H2020 project GRASSHOPPER, whose main features are described in Section 2. This work focuses on the development of a dynamic numerical model of a flexible PEM FC power plant, based on the layout of the 100-kW pilot unit built within the GRASSHOPPER project. The purpose is to develop an instrument to simulate the system operation, aimed at maximizing the system efficiency and flexibility while limiting the degradation rate.

The topic of dynamic modeling of fuel cell systems has been already addressed in the literature, where the case of stationary fuel cell power plants has been discussed, mostly focusing on the case of high temperature fuel cells, in particular solid oxide fuel cells for stand-alone and hybrid configurations, including combined heat and power applications [14,15,16]. Their off-design and transient behavior is investigated by the point of view of their safe and reliable operation as well as performance improvement, degradation minimization, and control improvement [17,18,19,20]. On the other hand, PEM-based systems have been mostly addressed for mobile applications [21,22,23,24], and in few cases for stationary use [25].

This work instead focuses on low temperature systems for stationary use, with the particular target of discussing fast-ramping applications for grid support. A detailed description of the model is presented in Section 3, while in Section 4, the model is tested against experimental data and subsequently applied to simulate plant load-following operation and cold start up.

2. GRASSHOPPER Project

The demonstration of the feasibility of stationary large-scale FC power plants, using PEM cells, has been accomplished in many projects. For example, ref. [26] describes a 70-kW_el PEM FC power plant that uses by-product hydrogen from the electrolysis of brine. The pilot plant performance is analyzed over 30,000 h of operation, showing cell irreversible and reversible decay. Ref. [27] shows that the operation of a 50-kW_el PEM FC plant over 4400 h, with relatively low-quality hydrogen from a sodium chlorate production process with standard industry purification, does not lead to extensive cell degradation. The feasibility of MW-scale PEM FC power plant has been demonstrated in [28,29], which tested a 2-MW_e plant with by-product hydrogen from a chlor-alkali process. The flexibility of PEM FC stacks is also well demonstrated since PEM FCs are used in the automotive sector. However, the flexibility of stationary FC power plant has never been tested.

The GRASSHOPPER project studies how to use FC power plants, adopting low temperature PEM cells to provide balancing services to the power grid. The aim is to demonstrate MW-scale plant capability to operate dynamically, to realize the next-generation cost-effective FC power plant for stationary application and grid stabilization. The target CAPEX for a production of 25 MW_el per year is below 1500 €/kW_el, reached through joint design of MEA (membrane electrode assembly), stack, and system.

The project has designed a 100 kW_el pilot unit, whose construction was finalized in September 2021. The plant successfully completed factory acceptance tests and is to be demonstrated in the field in Delfzij (NL), with 8 months of continuous operation.

Experience from the 100-kW_el pilot plant is the basis for the design of a MW-scale unit. To support the scale-up, important outcomes are also derived from numerical simulations. The work presented in this paper falls within this scope.

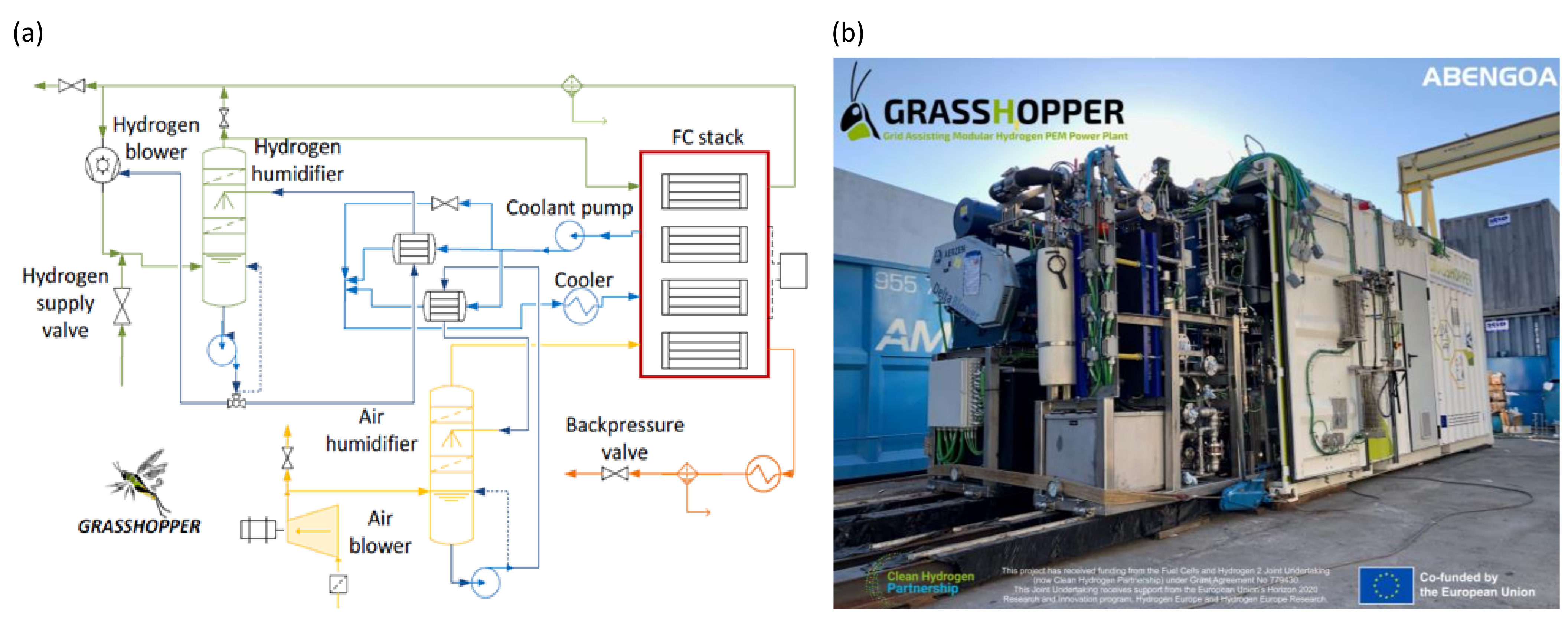
100 kW Pilot Plant Layout

The layout of the GRASSHOPPER 100 kW_el plant is shown in Figure 1a, while Figure 1b shows the real plant configuration.

Filtered air and pure hydrogen are humidified and supplied to the stack. The operating temperature of the stack is maintained at the desired value by the coolant, flowing in a dedicated loop. Heat exchangers allow the recovery of the stack dissipated thermal power for air and hydrogen humidification. The excess heat is dissipated in a dedicated cooler. The cathode backpressure is controlled with a valve, while the regulation of the rotational speed of the air blower and a purge valve allow the control of the ‘air stoichiometry’ (i.e., the ratio of air flowrate with respect to the stoichiometric flow). Fresh hydrogen is injected into the system through a controlled valve (hydrogen it is available above 4 bar). A liquid ring compressor recirculates the excess hydrogen and the ‘hydrogen stoichiometry’ (i.e., the ratio of hydrogen flowrate with respect to the stoichiometric flowrate) is controlled with a stack bypass.

The system has been designed to work flexibly between 20% (200 mA/cm²) and 100% (1000 mA/cm²) of the nominal current density value. Its performance is optimized and stack degradation is limited thanks to a precise control system.

3. Methods for Dynamic Modeling

This work implements, with the software Simulink, a dynamic model of a PEM FC plant, referring to the Grasshopper 100 kW_el plant configuration. Models that solve energy and mass balances during operation with a variable load are built for each plant component, as described in the following paragraphs, reporting also the assumptions for model scale-up. The models of the components are combined to build the model of the entire system. To allow control of the system operation, PI-type and on-off controllers are then implemented.

3.1. Thermodynamic Properties

The model is based on the hypothesis of ideal gas, ideal gas mixture, and ideal liquid. For water and coolant, enthalpy is computed, assuming constant specific heat capacity (Equation (1)), equal to 4.186 kJ/kg/K for water and to 3.52 kJ/kg/K for the water–glycol mixture.

$${\mathrm{h}}_{\mathrm{liquid}}={\mathrm{c}}_{\mathrm{L}} \left(\mathrm{T}-{\mathrm{T}}_{\mathrm{ref}}\right)$$

(1)

For the gas, enthalpy is computed with NASA polynomial equations [30] (Equation (2)), where ${\mathrm{a}}_1$–${\mathrm{a}}_7$ are numerical coefficients available on NASA thermodynamic libraries for 1130 solid, liquid, and gaseous pure chemical species.

$$\mathrm{h} \left[\frac{\mathrm{J}}{\mathrm{mol}}\right]=\mathrm{R} \mathrm{T}· \left({\mathrm{a}}_1+\frac{{\mathrm{a}}_2\mathrm{T}}{2}+\frac{{\mathrm{a}}_3{\mathrm{T}}^2}{3}+\frac{{\mathrm{a}}_4{\mathrm{T}}^3}{4}+\frac{{\mathrm{a}}_5{\mathrm{T}}^4}{5}+\frac{{\mathrm{a}}_6}{\mathrm{T}}\right)$$

(2)

When a gaseous mixture of different species is present (e.g., moist air/hydrogen), its enthalpy is computed from the enthalpy (${\mathrm{h}}_{\mathrm{J}}$) and the molar fraction (${\mathrm{x}}_{\mathrm{J}}$) of each species in the mixture, assuming the ideal gas mixture behavior (Equation (3)). For liquid water, the density is assumed to be constant and enthalpy variation with pressure is taken into account.

$${\mathrm{h}}_{\mathrm{mix}}={\displaystyle \sum }_{\mathrm{J}}\left({\mathrm{h}}_{\mathrm{J}}·{\mathrm{x}}_{\mathrm{J}}\right)+\frac{{\mathrm{x}}_{\mathrm{H}2\mathrm{O},\mathrm{liq}}}{{\mathsf{\rho }}_{\mathrm{H}2\mathrm{O},\mathrm{liq}}} \left(\mathrm{p}-{\mathrm{p}}_{\mathrm{atm}}\right)$$

(3)

Water in the liquid phase and in the vapor phase is treaded as two different species. When the partial pressure of the water in the mixture is below its saturation pressure, the water is in the vapor phase. Otherwise, it is partially in the condensate liquid phase. The maximum molar fraction of water in the vapor phase coincides with the water molar fraction at saturation. Saturation pressure of water is computed as a function of the temperature, according to a polynomial equation (Equations (4) and (5)) derived in [31] and valid for temperature values ranging from water triple point (${\mathrm{T}}_{\mathrm{tr}}$ = 273.16 K) to the critical point (${\mathrm{T}}_{\mathrm{cr}}=$647.096 K, ${\mathrm{p}}_{\mathrm{cr}}$ = 220.64 bar).

$${\mathrm{p}}_{\mathrm{H}2\mathrm{Osat},\mathrm{T}}\left[\mathrm{bar}\right]={\mathrm{p}}_{\mathrm{cr}}\left[\mathrm{bar}\right] ·{ \mathrm{e}}^{\frac{{\mathrm{b}}_1 · \mathsf{\theta }+{\mathrm{b}}_2 ·{ \mathsf{\theta }}^{1.5}+{\mathrm{b}}_3 ·{ \mathsf{\theta }}^3+{\mathrm{b}}_4 ·{ \mathsf{\theta }}^{3.5}+{\mathrm{b}}_5 ·{ \mathsf{\theta }}^4+{\mathrm{b}}_6 ·{ \mathsf{\theta }}^{7.5}}{1-\mathsf{\theta }}}$$

(4)

$$\mathsf{\theta }=1-\frac{\mathrm{T}\left[\mathrm{K}\right]}{{\mathrm{T}}_{\mathrm{cr}}\left[\mathrm{K}\right]}$$

(5)

3.2. PEM FC Stack

A single cell is modeled with a lumped-volume approach, considering performance data acquired from detailed cell simulations, thus allowing to simulate large scale effects. Given the stack modularity, the FC stack model is then built, assuming that many identical cells are electrically connected in series.

The model is divided into three subsystems: electrochemical model, fluid dynamic model, and thermodynamic model.

Regarding the electrochemical model, FC voltage and gross electrical power are calculated with semi-empirical current-voltage curves, combining cell theoretical polarization curve equations and experimental datasets, as detailed in [32]. The resulting formulation is shown in Equation (6), where the first term represents an apparent open circuit voltage, the second term the ohmic losses, and the third and the last terms the activation and the concentration overvoltage, respectively. The equation takes into account voltage dependence on backpressure, air stoichiometry, and air relative humidity. It catches the real cells performance with a good approximation, mainly for the range of current density where the cell will generally operate (relative errors <1% for relevant currents values: 200–1000 mA/cm²). A detailed description of the terms appearing in Equation (6) is presented in [32], together with the coefficients calibration procedure.

$$\begin{array}{c}{\mathrm{V}}_{\mathrm{cell}}={ \mathrm{V}}_{\mathrm{OC}}+\frac{{\mathrm{R}}_{\mathrm{ohm},1}}{{\left(\frac{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O}}}{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O},\mathrm{ref}}}\right)}^{{\mathrm{G}}_{\mathrm{ohm}}}}· \mathrm{i} +\left({\mathrm{K}}_{\mathrm{act},1}+{ \mathrm{K}}_{\mathrm{act},2 }{\left(\frac{\mathrm{p}}{{\mathrm{p}}_{\mathrm{ref}}}\right)}^{\frac{{\mathrm{x}}_{{\mathrm{O}}_2}}{{\mathrm{x}}_{{\mathrm{O}}_2,\mathrm{ref}}} }\right)· \ln \left(1+\frac{\mathrm{i}}{{\mathrm{i}}_0}\right)\\ +\left({\mathrm{K}}_{\mathrm{conc}}· {\left(\frac{\mathrm{p}}{{\mathrm{p}}_{\mathrm{ref}}}·\frac{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O}}}{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O},\mathrm{ref}}}\right)}^{{\mathrm{G}}_{\mathrm{conc}}} \right) · \ln \left(1-\frac{\mathrm{i}}{{\mathrm{i}}_{\mathrm{L}}·\frac{\mathrm{p}}{{\mathrm{p}}_{\mathrm{ref}}}}\right)\end{array}$$

(6)

In order to simulate cold start-up, semi-empirical corrections have been considered to model the effects of the cell temperature on ohmic losses and activation losses. Temperature effects on the concentration losses are not modeled since they impact on the cell performance only with high current density, outside the range of operability of the cells. The ohmic resistance $({\mathrm{R}}_{\mathrm{ohm}})$ varies exponentially with the temperature [33], according to Equation (7), while the activation losses vary because of the exponential variation with the temperature of the exchange current density (${\mathrm{i}}_0$) [33], according to Equation (8).

$${\mathrm{R}}_{\mathrm{ohm},\mathrm{T}}=\left( \frac{{\mathrm{R}}_{\mathrm{ohm},1}}{{\left(\frac{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O}}}{{\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O},\mathrm{ref}}}\right)}^{{\mathrm{G}}_{\mathrm{ohm}}}}\right)·{\mathrm{e}}^{{\mathrm{C}}_{\mathrm{ohm}}\left(\frac{1}{\mathrm{T}}-\frac{1}{{\mathrm{T}}_{\mathrm{ref}}}\right)}$$

(7)

$${\mathrm{i}}_{0 , \mathrm{T}}={\mathrm{i}}_{0 } ·{ \mathrm{e}}^{\frac{\mathrm{Cact}}{ \mathrm{T}}\left(1-\frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{ref}}}\right)}$$

(8)

The values of the coefficients ${\mathrm{C}}_{\mathrm{ohm}}$and ${\mathrm{C}}_{\mathrm{act}}$ are determined by comparing the regressed polarization curves with an experimental dataset obtained from a similar FC stack, characterized by temperatures ranging between 15 °C and 62 °C, constant stoichiometry, relative humidity, and backpressure. The coefficients are chosen such that the gradient with the temperature for the ohmic resistance and the open circuit overvoltage are equal to the ones measured in the reference database. The value of temperature adopted in the equations is the average temperature of the coolant flowing over the stack, assumed as representative of the stack temperature. The reference temperature is equal to 65 °C. Polarization curves obtained with this model for different values of temperature and air ratio to stoichiometry are shown in Figure 2, where backpressure is 1.35 bar and the average air relative humidity is 100% (i.e., ${\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O}}$/${\mathrm{x}}_{{\mathrm{H}}_2\mathrm{O},\mathrm{ref}}$ = 1). The numerical values of the regressed coefficients are summarized in

Table 1. Polarization curve coefficients regressed on experimental data.

Coefficient	Regressed Value
${\mathrm{V}}_{\mathrm{O}\mathrm{C}}$	928.24	mV
${\mathrm{R}}_{\mathrm{ohm}}$	−0.045	Ω·cm2
${\mathrm{G}}_{\mathrm{ohm}}$	0.837	-
${\mathrm{C}}_{\mathrm{ohm}}$	1700	-
${\mathrm{K}}_{\mathrm{act},1}$	−41.06	mV
${\mathrm{K}}_{\mathrm{act},2}$	5.62	mV
${\mathrm{i}}_0$	4.86	mA/cm2
${\mathrm{C}}_{\mathrm{act}}$	−1047	-
${\mathrm{K}}_{\mathrm{conc}}$	126.50	mV
${\mathrm{i}}_{\mathrm{L}}$	2600	mA/cm2
${\mathrm{G}}_{\mathrm{conc}}$	1.183	-

.

The electrochemical model computes the stack voltage and the gross DC electric power respectively with Equations (9) and (10), where${ \mathrm{N}}_{\mathrm{cells}}$ is the number of cells composing the stack and ${\mathrm{A}}_{\mathrm{cell}}$ is the active area of each cell.

$${\mathrm{V}}_{\mathrm{STACK}}={\mathrm{V}}_{\mathrm{CELL} }·{ \mathrm{N}}_{\mathrm{CELLS}}$$

(9)

$${\mathrm{P}}_{\mathrm{gross},\mathrm{stack}}=\mathrm{i} ·{\mathrm{A}}_{\mathrm{cell}}·{\mathrm{V}}_{\mathrm{stack}}$$

(10)

In regard to the cell dynamic behavior, the charge and discharge of the cell double layer is the main phenomenon affecting the cell voltage when the load is varied [34,35,36,37]. It can be modeled though a capacitance, whose value varies between 0.01 and 0.05 F/cm² according to literature [35]. Since these phenomena are much faster than other dynamic effects, such as the ones associated with the thermal inertia, the double layer capacitance is not included in this model.

Regarding the fluid dynamic model, it solves mass conservation equations over the FC stack for each chemical species (H₂, O₂, N₂, and H₂O) flowing through the anodic and the cathodic channels, to determine flowrate and composition of the anodic and cathodic streams leaving the stacks. Hydrogen and oxygen consumptions and water production are computed as a function of the stack current density, knowing the reaction in the stacks, according to Equations (11)–(13).

$${ \dot{\mathrm{m}}}_{{\mathrm{H}}_2, \mathrm{cons}}=\frac{\mathrm{i}}{2\mathrm{F}}·{\mathrm{A}}_{\mathrm{cell}}·{ \mathrm{N}}_{\mathrm{cells}}·3.6 ·{\mathrm{MM}}_{{\mathrm{H}}_2} \left[\frac{\mathrm{kg}}{\mathrm{h}}\right]$$

(11)

$${ \dot{\mathrm{m}}}_{{\mathrm{O}}_2, \mathrm{cons}}=\frac{\frac{{ \dot{\mathrm{m}}}_{{\mathrm{H}}_2,\mathrm{cons}}}{{\mathrm{MM}}_{{\mathrm{H}}_2}}}{2} ·{\mathrm{MM}}_{{\mathrm{O}}_2}\left[\frac{\mathrm{kg}}{\mathrm{h}}\right]$$

(12)

$${ \dot{\mathrm{m}}}_{{\mathrm{H}}_2\mathrm{O}, \mathrm{prod}}=\frac{{ \dot{\mathrm{m}}}_{{\mathrm{H}}_2,\mathrm{cons}}}{{\mathrm{MM}}_{{\mathrm{H}}_2}}·{\mathrm{MM}}_{{\mathrm{H}}_2\mathrm{O}}\left[\frac{\mathrm{kg}}{\mathrm{h}}\right]$$

(13)

Additionally, according to experimental evidence, the model considers a net transport of H₂O from cathode to anode equal to 0.1 mol/h, a net diffusion of H₂ from anode to cathode corresponding to an internal current density equal to 0.002 A/cm², a net transport of N₂ form cathode to anode such that the mass fraction of N₂ in the outlet anodic stream is 10%, and a null net transport of O₂ from cathode to anode or vice versa.

The accumulation of gasses in the cell channels is not included in the model because the channel volume is negligible with respect to the other component volumes.

Pressure drops in the channels are linearly dependent on the volumetric flowrate of coolant and of reactants at the stack inlet, according to prior experimental stack tests and justified by the low velocities in the flow field, which leads to a laminar regime.

Regarding the thermodynamic model, it solves energy balances on the stack (Equation (14)) to determine the average temperature of the cell and the temperature of the flows leaving the FC stack. Temperature dynamic (Equation (15)) is taken into account through the heat capacity of the stack, which is lumped in the Bipolar Plates (BP). The gross DC electric power (${\mathrm{P}}_{\mathrm{gross},\mathrm{stack}}$) is an output of the electrochemical subsystem. Heat transfer from the reactants to the bipolar plants (${\mathrm{Q}}_{\mathrm{acc} \mathrm{stack}}$) and to the coolant fluid (${\dot{\mathrm{Q}}}_{\mathrm{to} \mathrm{coolant}}$) is computed, assuming constant heat transfer coefficients. No heat losses to the environment are assumed.

$${ \dot{\mathrm{H}}}_{\mathrm{fuel},\mathrm{out}}+{ \dot{\mathrm{H}}}_{\mathrm{air},\mathrm{out}}={ \dot{\mathrm{H}}}_{\mathrm{fuel},\mathrm{in}}+{ \dot{\mathrm{H}}}_{\mathrm{air},\mathrm{in}}-{\mathrm{P}}_{\mathrm{gross},\mathrm{stackC}}-{ \dot{\mathrm{Q}}}_{\mathrm{to} \mathrm{coolant}}-{\mathrm{Q}}_{\mathrm{acc} \mathrm{stack}}$$

(14)

$${\mathrm{Q}}_{\mathrm{acc},\mathrm{stack}}={ \mathrm{C}}_{\mathrm{BP},\mathrm{anode}}\frac{{\mathrm{dT}}_{\mathrm{BPanode}}}{\mathrm{dt}}+{\mathrm{C}}_{\mathrm{BP},\mathrm{cathode}}\frac{{\mathrm{dT}}_{\mathrm{BPcathode}}}{\mathrm{dt}}$$

(15)

The system can be scaled up by increasing the number of cells in each stack or by installing more stacks of the same size. In the first case, more cells are connected in series, resulting in higher voltage and requiring and increase in the flowrate of hydrogen and air supplied to each stack. The resulting wider voltage range is not compatible with commercially available Power Control Systems. In the second case, which is applied in this work, a greater number of stacks is electrically connected in parallel, requiring more converters or a converter able to work with a higher current, although each stack remains identical in geometry and operation.

3.3. Air Blower

The air blower model follows a lumped-parameter approach. It includes dynamic effects related to the mechanical inertia and thermal inertia, while it neglects mass accumulation.

The unit stationary performances are based on the machine performance maps, available on the commercial datasheet and implemented through polynomial functions. The maps give the volumetric flowrate of air processed by the machine, its temperature gain at thermal equilibrium, and the blower mechanical power, as a function of air inlet temperature and pressure (ambient conditions), air outlet pressure (determined by the pressure drops in the downstream components), and the blower rotational speed. Isentropic efficiency and mechanical efficiency are computed.

The blower rotational speed (ω_c [rad/s]) is computed according to Equation (16), representing a balance between the torque generated by the electric motor (${\mathsf{\tau }}_{\mathrm{m}}$, defined in Equation (17)) and the torque required by the blower (${\mathsf{\tau }}_{\mathrm{c}}$, defined in Equation (18)), where ${\mathrm{J}}_{\mathrm{cm}}$ is compressor-motor block inertia [38], ${\mathrm{P}}_{\mathrm{el},\mathrm{m}}$ is the electrical power supplied to the motor (external input), ${\mathsf{\eta }}_{\mathrm{el},\mathrm{m}}$is the motor electrical efficiency, and ${\mathrm{P}}_{\mathrm{c}}$ is the blower mechanical power.

$${\mathrm{J}}_{\mathrm{cm}}\frac{{\mathrm{d}\mathsf{\omega }}_{\mathrm{c}}}{\mathrm{dt}}=\left({\mathsf{\tau }}_{\mathrm{m}}-{\mathsf{\tau }}_{\mathrm{c}}\right)$$

(16)

$${\mathsf{\tau }}_{\mathrm{m}}=\frac{{\mathrm{P}}_{\mathrm{el},\mathrm{m}}·{ \mathsf{\eta }}_{\mathrm{el},\mathrm{m}}}{{\mathsf{\omega }}_{\mathrm{c}}}$$

(17)

$${\mathsf{\tau }}_{\mathrm{c}}=\frac{{\mathrm{P}}_{\mathrm{c}}}{{\mathsf{\omega }}_{\mathrm{c}}}$$

(18)

The blower thermal inertia was initially not included in the model, but experimental data showed the importance of the temperature dynamics: the temperature gain of the air flowing through the blower matches the performance maps value in stationary conditions, but a smaller gain is shown during warm-up.

In general, the thermal power generated in the compression phase (${\dot{\mathrm{Q}}}_{\mathrm{gen}})$ is in part responsible for the air temperature increase (${\dot{\mathrm{Q}}}_{\mathrm{air}})$ and in part transferred to the machine (${\dot{\mathrm{Q}}}_{\mathrm{trasf}}$). This second part is in turn partially absorbed by the machine steel mass (${\dot{\mathrm{Q}}}_{\mathrm{steel}}$), and partially dissipated towards the environment (${\dot{\mathrm{Q}}}_{\mathrm{diss}}$) (Equation (19)).

$${ \dot{\mathrm{Q}}}_{\mathrm{gen}}={ \dot{\mathrm{Q}}}_{\mathrm{air}}+{ \dot{\mathrm{Q}}}_{\mathrm{trasf}}={ \dot{\mathrm{Q}}}_{\mathrm{air}}+{ \dot{\mathrm{Q}}}_{\mathrm{steel}}+{ \dot{\mathrm{Q}}}_{\mathrm{diss}}$$

(19)

At thermal equilibrium (${\dot{\mathrm{Q}}}_{\mathrm{steel}}=0)$, the air temperature gain is known from the performance maps. This allows to compute the heat absorbed by the air (Equation (20)), the heat dissipated (Equation (21)), and therefore the generated heat. According to the lumped volume approach, the steel temperature is homogeneous and equal, at thermal equilibrium, to the average air temperature between inlet and outlet (Equation (22)).

$${ \dot{\mathrm{Q}}}_{\mathrm{air},\mathrm{stationary}}={ \dot{\mathrm{m}}}_{\mathrm{air} }{\mathrm{c}}_{\mathrm{p},\mathrm{air} }\Delta {\mathrm{T}}_{\mathrm{air}, \mathrm{map}}={ \dot{\mathrm{m}}}_{\mathrm{air}}{ \mathrm{c}}_{\mathrm{p},\mathrm{air}} \left({\mathrm{T}}_{\mathrm{air},\mathrm{out},\mathrm{stationary}}-{ \mathrm{T}}_{\mathrm{air},\mathrm{in}}\right)$$

(20)

$${ \dot{\mathrm{Q}}}_{\mathrm{diss},\mathrm{stationary}}={\mathrm{hA}}_{\mathrm{ext}}\left({\mathrm{T}}_{\mathrm{blower},\mathrm{stationary}}-{\mathrm{T}}_{\mathrm{amb}}\right)$$

(21)

$${\mathrm{T}}_{\mathrm{blower},\mathrm{stationary}}=\frac{{\mathrm{T}}_{\mathrm{air},\mathrm{in}}+{\mathrm{T}}_{\mathrm{air},\mathrm{out},\mathrm{stationary}}}{2}$$

(22)

During thermal transients, the generated heat (${\dot{\mathrm{Q}}}_{\mathrm{gen}})$ is the same computed for steady state, and Equations (23)–(26) allow computing the air temperature at blower outlet (${\mathrm{T}}_{\mathrm{air},\mathrm{out}}$).

$${ \dot{\mathrm{Q}}}_{\mathrm{air}}={ \dot{\mathrm{Q}}}_{\mathrm{gen}}-{ \dot{\mathrm{Q}}}_{\mathrm{trasf}}={ \dot{\mathrm{m}}}_{\mathrm{air}}·{\mathrm{c}}_{\mathrm{p},\mathrm{air}}\Delta {\mathrm{T}}_{\mathrm{air}}$$

(23)

$${ \dot{\mathrm{Q}}}_{\mathrm{trasf}}-{ \dot{\mathrm{Q}}}_{\mathrm{diss}}={ \dot{\mathrm{Q}}}_{\mathrm{steel}}={\mathrm{hA}}_{\mathrm{int}}\left({\mathrm{T}}_{\mathrm{air},\mathrm{avg}}-{\mathrm{T}}_{\mathrm{blower}}\right)={\mathrm{C}}_{\mathrm{blower}}·\frac{{\mathrm{dT}}_{\mathrm{blower}}}{\mathrm{dt}}$$

(24)

$${ \dot{\mathrm{Q}}}_{\mathrm{diss}}={\mathrm{hA}}_{\mathrm{ext}}\left({\mathrm{T}}_{\mathrm{blower}}-{\mathrm{T}}_{\mathrm{amb}}\right)$$

(25)

$${\mathrm{T}}_{\mathrm{air},\mathrm{avg}}=\frac{{\mathrm{T}}_{\mathrm{air},\mathrm{in}}+{\mathrm{T}}_{\mathrm{air},\mathrm{out}}}{2}$$

(26)

The values of the heat transfer coefficients (${\mathrm{hA}}_{\mathrm{int}}$ and ${\mathrm{hA}}_{\mathrm{ext}}),$ the blower heat capacity (${\mathrm{C}}_{\mathrm{blower}}$), and the mechanical inertia (${\mathrm{J}}_{\mathrm{cm}})$ have been calibrated on experimental data.

The model scale-up procedure assumes:

• Flowrate (${\mathrm{V}}_{\mathrm{air}})$ , isentropic efficiency (${\mathsf{\eta }}_{\mathrm{is}}$), and mechanical efficiency (${\mathsf{\eta }}_{\mathrm{m}}$) curves derived from the regressed performance curves, assuming different sizes but the same efficiency profile for the blowers.
• Blower heat capacity proportional to the blower mass (representing the case assembly and excluding the motor, whose mass is expected to increase less than linearly).
• The blower surface in contact with the compressed air (named ‘Internal area’) and the blower surface in contact with the environment (named ‘external area’) are functions of the machine diameter. Indeed, by approximating the rotary lobe compressors as two identical cylinders (the lobes, with diameter D_L and height L) contained in a larger cylinder (the case, with diameter D_C and height L), and assuming that the diameter of the single lobe is equal to half the diameter of the case (D_L = D_C/2), the relations in Equations (27) and (28) are obtained. Additionally, neglecting the thickness of the case, the volume of the machine can be expressed as the sum of the volume of the lobes and the void volume, which is occupied by air (Equation (29)). Assuming that the void volume is proportional to the nominal volumetric air flowrate and that the ratio between the cylinders diameters remains the same for blowers of different sizes, the ratio between the diameters of the two machines of size A and B is expressed as a function of the ratio between the nominal volumetric air flowrates by Equation (30).

$${\mathrm{A}}_{\mathrm{ExternalArea}}={ \mathsf{\pi } \mathrm{D}}_{\mathrm{C}} \mathrm{L}$$

(27)

$${\mathrm{A}}_{\mathrm{InternalArea} }=\left({\mathsf{\pi } \mathrm{N}}_{\mathrm{lobes}}{ \mathrm{D}}_{\mathrm{L}}+{ \mathsf{\pi } \mathrm{D}}_{\mathrm{C}}\right) \mathrm{L}$$

(28)

$$\mathsf{\pi }\frac{{\mathrm{D}}_{\mathrm{C}}^2}{4}\mathrm{L}=\mathsf{\pi }\frac{{\mathrm{D}}_{\mathrm{L}}^2}{4}\mathrm{L}+{\mathrm{V}}_{\mathrm{void}}$$

(29)

$${\mathrm{D}}_{\mathrm{C},\mathrm{B}}={ \mathrm{D}}_{\mathrm{C},\mathrm{A}} ·\sqrt[3]{\frac{{ \dot{\mathrm{V}}}_{\mathrm{air},\mathrm{nom},\mathrm{B}}}{{ \dot{\mathrm{V}}}_{\mathrm{air},\mathrm{nom},\mathrm{A}}}}$$

(30)

3.4. Humidifier

The humidifier is composed by two sections, the packed-bed column and the water tank. These two sections are modeled separately with a lumped-volume approach.

Regarding the packed-bed column, the gas (hydrogen or air) enters at the bottom and flows upwards, while the water is sprayed at the top and flows downwards. Thus, the humidity of the gas increases while flowing thorough the column because of water evaporation. The column model computes flowrate, composition, pressure, and temperature of the outlet flows by knowing the same properties at inlet. It is assumed, according to industrial experience, that the humidifier effectiveness is 100%: the outlet gas is fully saturated and in thermal equilibrium with the water spray. Additionally, a demister at the top of the column removes the water drops that may be present in the outlet gas. Temperature dynamic in the column is negligible with respect to the water tank and is therefore neglected by the model. For the air humidifier, although the void fraction of the column is the 90% of its total volume, the column model neglects air build-up (the volume of all the air supply line components is lumped in the air manifold). Conversely, for the hydrogen humidifier, the column model includes hydrogen build-up. Pressure drops of the gasses flowing through the humidifier are then taken as constant and set equal to the nominal values reported on the datasheet.

The water tank collects the water that is sprayed in the column. The water tank model includes water build-up and temperature dynamic (the thermal inertia is associated to the heat capacity of the stored water). Perfect mixing in the water tank is assumed. The inputs to the model are the flowrate of the outlet water stream, set by the recirculation pump, and the flowrate and temperature of the water coming from the packed bed column. In addition, a purge or a refill of water can be introduced to regulate the water level in the tank. With the given assumptions, the model computes the amount of water that is accumulated in the tank, its temperature and the temperature of the water that is pumped out.

The model of the humidifier is scaled up, assuming that the size of the water tank is proportional to the system nominal power. The pressure drops in the humidifier column are assumed constant.

3.5. Air Supply Manifold

The air supply manifold model allows to simulate the build-up of the air in the supply line. Indeed, the volume of all components in the supply line is lumped in the manifold, which is located between the air blower and the air humidifier.

The manifold model assumes uniform temperature in the manifold itself (equal to the temperature of the inlet air) and ideal gas behavior. It computes the time variation of the pressure in the air supply line as in Equation (31). The air blower sets the flowrate at manifold inlet (${\dot{\mathrm{m}}}_{\mathrm{in}, \mathrm{manifold}}$), while the pressure drops in the components downstream set the air flowrate at the manifold outlet (${\dot{\mathrm{m}}}_{\mathrm{out}, \mathrm{manifold}}$).

$$\frac{{\mathrm{dm}}_{\mathrm{acc}}}{\mathrm{dt}}=\frac{{\mathrm{V}}_{\mathrm{manifold}}}{{\mathrm{R}}^{*}·{\mathrm{T}}_{\mathrm{manifold}}}·\frac{{\mathrm{dp}}_{\mathrm{manifold}}}{\mathrm{dt}}={ \dot{\mathrm{m}}}_{\mathrm{in}, \mathrm{manifold}}-{ \dot{\mathrm{m}}}_{\mathrm{out}, \mathrm{manifold}}$$

(31)

To scale up the model, the manifold volume is varied proportionally to the void volume in the air humidifier column, which most contributes to the volume of the air supply line.

3.6. Backpressure Valve

The backpressure valve is modeled as an orifice, through which a one-dimensional isentropic flow of a compressible fluid flows [39,40]. The orifice model reported for subcritical flow is adopted, since the ratio between valve inlet pressure (max 1.6 bar) and outlet pressure (ambient pressure) is always above the critical pressure ratio. According to Equation (32), the flowrate of air through the valve is computed knowing the upstream pressure and temperature, the pressure ratio across the valve, and the valve effective area (${\mathrm{A}}_{\mathrm{e}})$.

$${ \dot{\mathrm{m}}}_{\mathrm{out},\mathrm{valve}}=\frac{{\mathrm{A}}_{\mathrm{e}}·{\mathrm{p}}_{\mathrm{valve},\mathrm{in}}}{\sqrt{{\mathrm{R}}_{\mathrm{air}}·{\mathrm{T}}_{\mathrm{valve},\mathrm{in}}}}{\left(\frac{{\mathrm{p}}_{\mathrm{valve},\mathrm{out}}}{{\mathrm{p}}_{\mathrm{valve},\mathrm{in}}}\right)}^{\frac{1}{{\mathsf{\gamma }}_{\mathrm{air}}}}\sqrt{\frac{2{\mathsf{\gamma }}_{\mathrm{air}}}{{\mathsf{\gamma }}_{\mathrm{air}}-1} \left(1-{\left(\frac{{\mathrm{p}}_{\mathrm{valve},\mathrm{out}}}{{\mathrm{p}}_{\mathrm{valve},\mathrm{in}}}\right)}^{\frac{{\mathsf{\gamma }}_{\mathrm{air}}-1}{{\mathsf{\gamma }}_{\mathrm{air}}}}\right)}$$

(32)

To scale-up the model, the valve effective area is varied proportionally to the nominal air flowrate.

3.7. Liquid Ring Compressor

The liquid ring compressor is modeled through a stationary model because its rotational speed can vary only in a narrow range, making dynamic effects negligible. Two sequential steps are considered: hydrogen compression and hydrogen-water mixing.

In the first step, the hydrogen stream coming from the FC anode and from the hydrogen humidifier (if hydrogen recirculation over the humidifier is required to guarantee the minimum hydrogen flow to the liquid ring compressor) is compressed. Knowing flowrate, composition, temperature, and pressure of the inlet moist hydrogen, as well as the outlet pressure that the stream has to reach (determined by the hydrogen humidifier located downstream), the model computes the temperature of the hydrogen flow after compression and the electrical power required for hydrogen compression, assuming constant isentropic efficiency (${\mathsf{\eta }}_{\mathrm{is}}$) and mechanical efficiency (${\mathsf{\eta }}_{\mathrm{m}})$. The water contained in the inlet hydrogen streams is assumed to be in vapor phase.

In the second step, the compressed hydrogen flow is mixed with the water stream from the hydrogen compressor tank. The mixing process is modeled as an adiabatic process. The flowrate of the water is assumed to be constant since the pump is not controlled and works with a constant rotational speed. The inlet water stream is assumed to be in the liquid phase.

The liquid ring compressor model is scaled up, assuming constant isentropic and mechanical efficiencies and that the water flowrate required by the compressor is proportional to the nominal hydrogen flowrate.

3.8. Heat Exchanger

The heat exchangers are plate-type counter-current heat exchangers, working with liquid on both sides. Given the modular structure of the plates and assuming that the fluids equally distribute among the channels, the model considers a number of identical sub-units. Each of them includes a plate and half of the adjacent hot and cold channels. In each sub-unit, control volumes are then identified through a discretization along the channel direction (1D-model). The model solves mass and energy balances for each control volume, to compute the heat transferred, the plates temperature, and the outlet streams temperature. The model assumes that, in the control volume, the temperature of each plate is uniform, and it considers constant values for the heat transfer coefficients and the heat capacities. The temperature dynamic is associated to the heat capacity of the heat exchanger materials. Conduction along the direction of the flows, thermal resistance of the plate, heat losses toward the environment, and mass accumulation in the channels are neglected. Pressure drops are modeled, assuming the pressure will vary linearly with the volumetric flowrates.

The model is scaled up by increasing the number of plates, so that the total area of heat transfer varies proportionally to the system nominal power. The heat transfer coefficients and the pressure drops are assumed unchanged. The model is representative of a counter-current plate-type heat exchanger or of a more compact plate-and-shell heat exchanger.

3.9. Pumps

A stationary model of the pump is realized, since they are expected to work at constant rotational speed (such as in the air and hydrogen humidifier water circuit) or the dynamic effects are assumed negligible (as for the coolant circuit pump, whose rotational speed is varied to control the coolant temperature gain over the stack). The model computes the pump electrical consumption and the outlet flow pressure and temperature, assuming constant mechanical and isentropic efficiency and knowing flowrate, temperature, and pressure of the inlet flow, as well as the pressure gain that the pump has to provide.

When the model is scaled up, mechanical and isentropic efficiencies are assumed unchanged.

3.10. Pipelines

Pipelines are used to connect the plant components and are responsible of transport delays and pressure drops. These phenomena are included in the pipeline model. The transport delay depends on pipe diameter and length and on the volumetric flowrate, as in Equation (33). Pressure drops depend on the volumetric flowrate, as in Equation (34), where λ is assumed to be constant. The fluid is assumed to be incompressible (as already mentioned, hydrogen build-up is lumped in the hydrogen humidifier volume and air build-up in the air supply manifold volume).

$${\mathrm{t}}_{\mathrm{delay}}=\mathrm{L} \frac{{\mathsf{\pi } \mathrm{D}}^2}{4} ·\frac{1}{ \dot{\mathrm{V}}}$$

(33)

$$\mathsf{\Delta }\mathrm{p}= \mathsf{\lambda } \mathsf{\rho }\frac{\mathrm{L}}{\mathrm{D}}\frac{{\mathrm{v}}^2}{2}= \mathsf{\lambda } \mathsf{\rho } \frac{8 \mathrm{L}}{{\mathsf{\pi }}^2{\mathrm{D}}^5}{ \dot{\mathrm{V}}}^2$$

(34)

The pipeline model scale-up is based on the assumption that bigger components need to be more distant from each other, therefore the length of the pipes connecting the components increases with the plant nominal power. Additionally, the scale-up assumes that the nominal pressure drops are the same for systems of different sizes. Thus, being the pressure drops calculated with the assumption of turbulent flowrate (Equation (34)), the relationship between the pipes diameters for the two systems of size A and B is given by Equation (35).

$${\mathrm{D}}_{\mathrm{B}}=\sqrt[5]{{\mathrm{D}}_{\mathrm{A}}^5{\left(\frac{{ \dot{\mathrm{V}}}_{\mathrm{B}}}{{ \dot{\mathrm{V}}}_{\mathrm{A}}}\right)}^2\frac{{\mathrm{L}}_{\mathrm{B}}}{{\mathrm{L}}_{\mathrm{A}}} }$$

(35)

3.11. Power Conversion System (PCS)

The PCS includes the components required to connect the plant to the electric grid, namely a DC/DC converter and an inverter. The PCS is simulated through a constant conversion efficiency, which is set equal to 80%, as experimentally measured on the 100 kW_el unit at low current density operation. The choice of these value is conservative since higher values are expected at higher currents, but an experimental performance curve is not available. Additionally, the DC/DC converter is not required for the MW size plant, where a higher stack voltage is expected.

3.12. Control Method

The control strategy is implemented in the model with PID controllers, when a precise control of the variable is required, and with on-off controllers, when it is sufficient to guarantee that the variable remains within a given range of values.

A PID controller is generally characterized by three different control actions: a proportional action, an integral action, a derivative action. In this system, the derivative part in not implemented and a PI configuration is used, characterized by the proportional gain ${\mathrm{K}}_{\mathrm{P}}$ and the integral gain ${\mathrm{K}}_{\mathrm{I}}$ (Equation (36)).

$${\mathrm{K}}_{\mathrm{P}}+{\mathrm{K}}_{\mathrm{I}}\frac{1}{\mathrm{s}}$$

(36)

Each controller takes into account the physical characteristic of the system components, allowing the manipulated variable to vary only within a given range of values. To avoid wind-up, clamping of the integral is adopted: the integral in each PI controller is switched off (${\mathrm{K}}_{\mathrm{I}}$ = 0) when the manipulated variable reaches its minimum or maximum limit, allowing a faster response when the error changes its sign.

Table 2. Control system: controlled variables, manipulated variables, and controller type.

Controlled Variable	Manipulated Variable	Controller Type
Cathode backpressure	Backpressure valve opening area	PI
Air stoichiometry;	Blower rotational speed + air purge	PI
Air temperature at stack inlet	Coolant flowrate to the air heat exchanger	PI
Hydrogen temperature at stack inlet	Coolant flowrate to the hydrogen heat exchanger	PI
Hydrogen pressure at stack inlet	Fresh hydrogen flowrate	PI
Hydrogen stoichiometry	Hydrogen recirculation	PI
Coolant temperature gain over the stack	Rotational speed of the coolant pump	PI
Coolant temperature at stack inlet	Water flowrate to the cooler heat exchanger	PI
water level in the air humidifier tank	water flow to refill the air humidifier tanks	ON/OFF
water level in the hydrogen humidifier tank	water flow to refill the hydrogen humidifier tanks	ON/OFF

details the controller implemented in the model.

3.13. System Performance Evaluation

The performances of the fuel cell system are evaluated through the stack gross power (defined by Equation (10)), the system net power (Equation (37)), the stack gross efficiency (Equation (38)), and the system net efficiency (Equation (39)). Stack gross efficiency and net efficiency are referred to the Low Heating Value (LHV) of the consumed hydrogen.

$${\mathrm{P}}_{\mathrm{NET},\mathrm{SYSTEM}}={\mathrm{P}}_{\mathrm{GROSS},\mathrm{STACK}}{·}_{\mathrm{PCS}}-{\mathrm{P}}_{\mathrm{AUXILIARIES}}$$

(37)

$${\mathsf{\eta }}_{\mathrm{GROSS}, \mathrm{STACK}}=\frac{{\mathrm{P}}_{\mathrm{GROSS}, \mathrm{STACK}}}{{ \dot{\mathrm{M}}}_{{\mathrm{H}}_{2,\mathrm{CONS}}}·{\mathrm{LHV}}_{\mathrm{H}2}}$$

(38)

$${\mathsf{\eta }}_{\mathrm{NET},\mathrm{SYSTEM}}=\frac{{\mathrm{P}}_{\mathrm{NET}, \mathrm{SYSTEM}}}{{ \dot{\mathrm{M}}}_{{\mathrm{H}}_{2,\mathrm{CONS}}}·{\mathrm{LHV}}_{\mathrm{H}2}}$$

(39)

4. Results and Discussion

4.1. Comparison of Simulation Results and Experimental Data

The model is tested against experimental data collected during preliminary testing of the 100 kW_el Grasshopper pilot plant. Six datasets are identified, including variable load operation (spanning through the entire range of current density) and plant cold start-up. The data include temperatures, pressures, and flowrates in different points of the system, stack current and voltage, and the power consumptions of the main plant auxiliaries.

To validate and calibrate the model, the following simulation inputs are set equal to the experimental values:

• stack current density,
• coolant flowrate,
• setpoint for the air flowrate entering the humidifier,
• setpoint for the hydrogen flowrate entering the stack.

Additionally, the following parameters are initialized equal to the values measured at test start:

• plant container temperature,
• liquid ring compressor temperature,
• air temperature at the blower outlet,
• water temperature in the humidifier tanks,
• air and hydrogen temperature at the stack inlet,
• coolant temperature at the stack inlet,
• cathode backpressure.

A preliminary calibration of the parameters affecting the warm-up time (e.g., pipes lengths and heat capacities) was performed by minimizing the difference between the simulated and the measured temperature, in different points of the plant, for one of the available datasets. Comparison of experimental data and simulation results for the other five datasets shows the ability of the model to reproduce the real plant behavior, obtaining negligible errors on the prediction of the gross and net power, flowrate, temperature, and pressure in different point of the plant. As an example, for all the six datasets, the RMSE for the gross power is always below 3 kW_el and the RMSE for the net power (Figure 3) has a maximum of 4.6 kW_el (dataset 6). The plant gross power generation is slightly underestimated by the model, while the net power generation is sometimes slightly underestimated and sometimes slightly overestimated, independent of the power itself. This is related to the impact on the net power of the consumption of the auxiliaries that are not simulated (e.g., fans, coolant circuits auxiliaries).

4.2. MW-Size Plant Flexibility Improvementthrough Simulation

The developed model was applied to analyze the performance of a 1-MW PEMFC power plant under a wide range of operating conditions, to point out the main criticalities and to propose solutions to improve the plant design and operation strategy. Simulations include both load-following operation, as required to provide grid ancillary services, and system warm-up.

4.2.1. Load-Following Operation

Load-following operation simulations impose a current setpoint characterized by step changes every 5 min and spanning through the entire operation range. The most extreme case is studied by applying the maximum current step (0.2–1 A/cm²) in both directions. The actual current variation of the system is limited to 2.5%/s, as decided by the Grasshopper consortium to limit stack degradation.

Figure 4a compares the current density setpoint and the actual value resulting from the simulation. When the setpoint is changed, the current starts changing immediately and reaches the new setpoint in a few seconds (~79 s with the maximum step change). The current density growth results are always limited by the imposed 2.5%/s constraint only, thus reaching the project flexibility targets.

No issues emerge from the control of the cathode and anode backpressures (Figure 4c). However, the temperature of the coolant at the stack inlet and the average temperature of the coolant over the stack show a fluctuating behavior (Figure 4b), leading to deviations from the setpoint up to 3 °C. This shows that the PI-type controller is inefficient and suggests the use of more advanced control strategies. Following this conclusion, the Grasshopper pilot plant implements a smith predictor controller, based on the model itself.

A precise control of the air dew-point temperature at the stack inlet is possible (Figure 5a) by regulating the flowrate of the coolant sent to the air humidifier heat exchanger, thus providing the required heat. However, the air average relative humidity over the stack deviates from the setpoint due to delays in the control of the air utilization factor (Figure 5b). Indeed, while the current (and the reactant consumption) changes almost instantaneously, the air flowrate sent to the stack varies more slowly, altering the air utilization factor.

Good control of the hydrogen dewpoint temperature is possible (Figure 5c). Unlike the air side, the water sprayed in the hydrogen humidifier is not heated up (the dew-point temperature is equal to the temperature of the water in the humidifier tank), and it is necessary to cool the water sent to the Liquid Ring Compressor (LRC) in order to avoid the water in the hydrogen humidifier tank to overcome the desired hydrogen dew-point temperature. As for the air, a deviation from the RH setpoint is observed when the current is changed, because of the non-instantaneous control of the hydrogen stoichiometry (Figure 5d). Additionally, an unexpected fluctuation of the fuel utilization factor up to 100% happens before the current is increased from 0.2 to 0.4 A/cm² and from 0.2 to 1 A/cm², because of the too fast control. Otherwise, a slower control was shown to lead to too slow changes in the fuel utilization factor at higher load. This points out the need to use more advanced controllers.

Figure 6 shows the stack gross power, the power consumption of the system auxiliaries, the resulting system net power, and the gross and net efficiency.

Regarding the plant auxiliaries, the consumption of the pumps is negligible, the hydrogen compressor consumption is almost constant at any load (10–20 kW_el), while the air blower consumption increases proportionally to the load (from 10 kW_el to 50 kW_el). The Power Conversion System (PCS), whose efficiency was assumed equal to 80%, accounts for 2/3 of the total power losses. Indeed, this component represents the major source of losses when its efficiency is lower than 90%.

Regarding the efficiencies, the stack gross efficiency shows a minimum of 52% at the maximum current (1 A/cm²) and a maximum of 63% at the minimum current (0.2 A/cm²). The net efficiency reflects the gross efficiency profile: it is 38% at 1 A/cm² and 44% at 0.2 A/cm². The net efficiency values would increase to 50% at 0.2 A/cm² and 43% at 1 A/cm² with a PCS efficiency of 90%. As a reference, the maximum net efficiency, excluding the PCS losses, would be equal to 56% at 0.2 A/cm² and 48% at 1 A/cm².

4.2.2. Warm-Up

Cold start-up simulations are performed to understand the time span that the plant requires to reach nominal operating conditions, when it is started from ambient temperature, such as after a long shut-down. This information is important to plan when to start-up the system, according to the services it has to provide.

Warm-up simulations assume a constant ambient temperature equal to 20 °C. In the simulations, the warm-up initial state sets:

• air compressor at nominal speed (giving nominal air stoichiometry at nominal current);
• cathode backpressure 1.35 bar (activated controller);
• LRC at nominal point;
• no hydrogen bypass;
• nominal coolant temperature gain over the stack (activated controller);
• minimum amount of coolant (10%) to heat exchangers to heat up the humidifiers;
• FC stack at its minimum load (0.2 A/cm²).

Then, the current density is increased up to the nominal value (1 A/cm²) according to a warm-up procedure proposed by the Grasshopper consortium to limit stack degradation. The rate of increase of the current density is limited to ensure a correct humidification of the membrane: a maximum current density is permitted for each value of the air temperature at the stack inlet and for each value of the average coolant temperature along the stack. Only when current density and stack temperature setpoints are reached, all controllers are activated, thus the choice of the control does not affect the warm-up results.

Simulation results show that the current density is limited by the average coolant temperature over the entire warm-up procedure (Figure 7a). The current remains at its minimum for 71 min, then it starts rising and it reaches the nominal value after 2 h and 28 min. The coolant temperature at stack inlet reaches the setpoint after 5 additional minutes (Figure 7b). Conversely, the pressure reaches the nominal value in about 2 s.

Figure 7c,d show the average air and hydrogen relative humidity (RH) over the stack, computed with respect to the coolant average temperature. The air average RH decreases over time because the average coolant temperature increases faster than the temperature of the air at the humidifier outlet, which determines the air absolute humidity at the stack inlet, but the air average RH is above 100% during the entire warm-up process. The hydrogen average RH is close to 100% during the warm-up process.

The air utilization factor increases with the current (Figure 7e), starting from ~10% and reaching the nominal point (50%) at 1 A/cm², as expected. A very low fuel utilization factor (between 6% and 30%, respectively, at 0.2 and 1 A/cm²) is obtained with the LRC at nominal speed and no hydrogen bypass (Figure 7f). However, when the bypass is activated, the desired setpoint (67%) is reached.

Finally, Figure 8 shows a small increase of both the gross and net efficiency over time at the beginning of the simulation, before the current starts to increase, which is explained by the stack temperature increase. Then, as expected, the gross efficiency decreases when the current increases. Conversely, the net efficiency increases, reflecting the lower impact of the constant internal power consumptions.

The parameters that mostly affect the warm-up time are identified through a sensitivity analysis, performed with the final goal of identifying strategies to accelerate the system warm-up. The analysis considers:

A.

A different warm-up strategy, which does not limit the current rise at low temperature. The maximum current rate of increase is set equal to 2.5%/s (same limit set at the nominal point).

B.

A reduced amount of water in the humidifiers, assuming a 50% reduction of the water inventory in the humidifier tank when the simulation starts, reducing the humidifier thermal inertia.

C.

A more compact system, assuming to connect the system components with pipes three times shorter and with diameters computed to have the same pressure drops as in the base case.

Table 3. Water content (inventory) in the main plant component for the base case and cases A, B, and C of the sensitivity analysis.

	Base—A	B	C
Coolant in pipes	2416.5 (49.0%tot)	2416.5 L (64.0%tot)	711.9 L (23.2%tot)
Water in air humidifiers pipes	102.1 (2.1%tot)	102.1 L (2.7%tot)	23.6 L (0.8%tot)
Water in H2 humidifiers pipes	102.3 L (2.1%tot)	102.3 L (2.7%tot)	16.3 L (0.5%tot)
Water in air humidifiers tanks	1650 L (33.4%tot)	825 L (21.9%tot)	1650 L (53.9%tot)
Water in H2 humidifiers tanks	660 L (13.4%tot)	330 L (8.7%tot)	660 L (21.6%tot)
Total	4930.9 L	3775.9 L	3061.8 L

characterizes, for each case, the system in terms of water inventory (i.e., water content in the main plant components at the beginning of the simulation). The total amount of liquid in the system is −5% in case B and −38% in case C, with respect to the base case. Additionally, in case C, the amount of coolant in the pipes is −70%. This information is important in order to understand the simulation results since the heat capacity of the water influences the overall thermal inertia of the system.

Results of the simulations are summarized in

Table 4. Warm-up simulations: warm-up time, amount of hydrogen consumed, delivered electric energy generated and average specific hydrogen consumption during warm-up, for the base case and for cases A, B, and C of the sensitivity analysis.

	Base	A	B	C
Warm-up time	2 h 38 min	34 min	2 h 27 min	46 min
Consumed hydrogen during warm-up [kgH2]	51.2	32.0	49.4	16.1
Delivered energy during warm-up [kWhel]	608.7	372.5	588.3	192.4
Specific consumption during warm-up [kgH2/kWhel]	0.08	0.08	0.08	0.08

, which characterizes the warm-up, indicating the time required for the system to reach full load and nominal operating conditions (‘Warm-up time’), the amount of hydrogen consumed during the warm-up time, the net electric energy that is delivered during the warm-up time (assuming no external limits on the net power output), and the specific hydrogen consumption during the warm-up time.

The warm-up time is shorter in case A with respect to the base case, because of the higher stack thermal losses (higher power and lower efficiency) at higher currents. Indeed, while in the base case, the current rise is proportional to the temperature and the nominal current is reached only at the end of the warm-up process (2 h 38 min), in case A the nominal current is reached in less than 2 min. It can be concluded that the choice of the warm-up strategy strongly affects the warm-up time. The reduction of the amount of water in the humidifier tanks slightly reduces the warm-up time. In case B, the 5% reduction in the total water inventory leads to a 9% reduction of the warm-up time. Conversely, the design of a compact system is very effective. In case C, a 38% reduction in the water inventory leads to a 71% reduction in the warm-up time. In this case, the shorter pipes allow having smaller diameters and higher velocity, keeping constant the total pressure drops. Thus, the reduction of the pipe lengths positively affects the results because of the lower total thermal inertia and because the time needed for the coolant to go from the FC stack to the heat exchangers and vice-versa decreases.

5. Conclusions

Future evolution of the electric grid in a low-CO₂ emission and high renewable-based scenario will increasingly require the availability of clean and dispatchable energy resources. In this framework, hydrogen-based fuel cell systems could provide a modular, reliable, and zero-emission solution to the necessity of distributed grid support, providing grid ancillary services thanks to their fast ramp rate and the load-following capability. This work contributes to the analysis of the dynamic behavior of fuel cell power plants based on low temperature Proton Exchange Membrane cells, focusing on the development of a dynamic numerical model of a flexible PEM FC power plant based on the layout of the 100-kW pilot unit built within the EU Horizon 2020 GRASSHOPPER project. The purpose is to develop an instrument to simulate the system operation, aiming at maximizing the system efficiency and flexibility while limiting the degradation rate.

The dynamic model includes FC stack, all main plant components, and controllers. The comparison of simulation results with experimental data from a 100 kW_el plant has shown that the model reproduces, with good accuracy, both the components stationary behavior at different load (e.g., stationary values of pressure, temperature, power consumptions, etc.) and the system dynamics (e.g., thermal transients, effects related to delays in mass transfer, etc.)

The validated model has been applied to assess the flexible performance of a 1-MW_el unit, providing a suggestion to improve the plant scale-up.

Load-following operation simulations showed that the system is able to follow a load setpoint. When the current setpoint is changed stepwise, a precise backpressure control and a good temperature control are possible. Conversely, deviations of the air and fuel utilization factors from their setpoints affect air and fuel average relative humidity over the stack and suggest the adoption of more advanced controllers (e.g., smith predictors). Both stack gross efficiency and system net efficiency increase while the load decreases. The power conversion system, having an 80% efficiency, results in the main component limiting the system net efficiency, and an improvement of the plant net efficiency up to 10 percentage points is possible by acting on the PCS efficiency only. Indeed, a PCS efficiency higher than 80% is expected for the MW-scale system where, thanks to the higher number of cells and the consequently higher stack voltage, the DC/DC converter is not needed and only the inverter (with efficiency higher than 90%) can be installed.

Simulations of cold start-up show that, starting from 20 °C and limiting the current density at low temperature, the plant takes 2 h 38 min to reach the nominal point. The warm-up time decreases substantially if the stack is operated at maximum current (34 min), thanks to the higher thermal losses of the stack. However, operating at high current and low temperature may reduce the lifetime of the cells. Other solutions to reduce the warm-up time, without affecting the stack, consider a reduction of the water inventory. Halving the water content in the humidifier slightly reduces the warm-up time (−9%), while using pipes three times shorter to connect the plant components appears as the best solution (−70%). The design of a compact system should therefore be a priority in the perspective of building a flexible unit, able to rapidly start-up.

These suggestions have been taken into account in the design of the flexible 1-MW FC power plant, which is the target of the Grasshopper project. Thus, the commercial FC system design will combine the technical improvements deriving from the simulation results with improvements deriving from an economic analysis.