Multi-Model-Based Predictive Control for Divisional Regulation in the Direct Air-Cooling Condenser
Abstract
:1. Introduction
2. Description of the System
3. Model Development
3.1. Process Model Development
- Conservation of steam mass and energy
- 2.
- Conservation of finned tube wall energy
- 3.
- Conservation of air energy
- 4.
- Air plume recirculation
- 5.
- Heat transfer coefficient
- 6.
- Axial fan
- 7.
- Exhaust steam mass flow and enthalpy
- 8.
- Governing equations
3.2. Optimum Condenser Pressure
3.3. Model Validation
3.4. Model Performance Analysis
- Step test response
- 2.
- Steady-state performance
- 3.
- Optimum backpressure
4. Control Methodology
4.1. Global Structure
4.2. Bank of Local Model
4.3. Model Predictive Control
4.4. Model Switching Rules
4.5. Simulation Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
References
- Huang, C.; Hou, H.; Hu, E.; Yu, G.; Peng, H.; Yang, Y.; Wang, L.; Zhao, J. Performance Maximization of a Solar Aided Power Generation (SAPG) Plant with a Direct Air-Cooled Condenser in Power-Boosting Mode. Energy 2019, 175, 891–899. [Google Scholar] [CrossRef]
- Liu, J.; Hu, Y.; Zeng, D.; Wang, W. Optimization of an Air-Cooling System and Its Application to Grid Stability. Appl. Therm. Eng. 2013, 61, 206–212. [Google Scholar] [CrossRef]
- Du, X.; Liu, L.; Xi, X.; Yang, L.; Yang, Y.; Liu, Z.; Zhang, X.; Yu, C.; Du, J. Back Pressure Prediction of the Direct Air Cooled Power Generating Unit Using the Artificial Neural Network Model. Appl. Therm. Eng. 2011, 31, 3009–3014. [Google Scholar] [CrossRef]
- Marincowitz, F.S.; Owen, M.; Muiyser, J. Experimental Investigation of the Effect of Perimeter Windscreens on Air-Cooled Condenser Fan Performance. Appl. Therm. Eng. 2019, 163, 114395. [Google Scholar] [CrossRef]
- Li, X.; Wang, N.; Wang, L.; Kantor, I.; Robineau, J.-L.; Yang, Y.; Maréchal, F. A Data-Driven Model for the Air-Cooling Condenser of Thermal Power Plants Based on Data Reconciliation and Support Vector Regression. Appl. Therm. Eng. 2018, 129, 1496–1507. [Google Scholar] [CrossRef]
- Li, X.; Wang, N.; Wang, L.; Yang, Y.; Maréchal, F. Identification of Optimal Operating Strategy of Direct Air-Cooling Condenser for Rankine Cycle Based Power Plants. Appl. Energy 2018, 209, 153–166. [Google Scholar] [CrossRef]
- He, W.F.; Chen, J.J.; Han, D.; Wen, T.; Luo, L.T.; Li, R.Y.; Zhong, W.C. Numerical Analysis from the Rotational Speed Regulation within the Fan Array on the Performance of an Air-Cooled Steam Condenser. Appl. Therm. Eng. 2019, 153, 352–360. [Google Scholar] [CrossRef]
- Duvenhage, K.; Kröger, D.G. The Influence of Wind on the Performance of Forced Draught Air-Cooled Heat Exchangers. J. Wind. Eng. Ind. Aerodyn. 1996, 62, 259–277. [Google Scholar] [CrossRef]
- Salta, C.A.; Kröger, D.G. Effect of Inlet Flow Distortions on Fan Performance in Forced Draught Air-Cooled Heat Exchangers. Heat Recovery Syst. CHP 1995, 15, 555–561. [Google Scholar] [CrossRef]
- Fourie, N.; van der Spuy, S.J.; von Backström, T.W. Simulating the Effect of Wind on the Performance of Axial Flow Fans in Air-Cooled Steam Condenser Systems. J. Therm. Sci. Eng. Appl. 2015, 7, 21011. [Google Scholar] [CrossRef] [Green Version]
- Yang, L.J.; Du, X.Z.; Zhang, H.; Yang, Y.P. Numerical Investigation on the Cluster Effect of an Array of Axial Flow Fans for Air-Cooled Condensers in a Power Plant. Sci. Bull. 2011, 56, 2272–2280. [Google Scholar] [CrossRef] [Green Version]
- Louw, F.G. Performance Trends of a Large Air-Cooled Steam Condenser during Windy Conditions; Stellenbosch University: Stellenbosch, South Africa, 2011. [Google Scholar]
- Guo, Y.; Zhang, D.; Wan, J.; Yu, D. Influence of Direct Air-Cooled Units on Primary Frequency Regulation in Power Systems. IET Gener. Transm. Distrib. 2017, 11, 4365–4372. [Google Scholar] [CrossRef]
- Yang, T.; Wang, W.; Zeng, D.; Liu, J.; Cui, C. Closed-Loop Optimization Control on Fan Speed of Air-Cooled Steam Condenser Units for Energy Saving and Rapid Load Regulation. Energy 2017, 135, 394–404. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhang, F.; Shen, J. On the Dynamic Modeling and Control of the Cold-End System in a Direct Air-Cooling Generating Unit. Appl. Therm. Eng. 2019, 151, 373–384. [Google Scholar] [CrossRef]
- Liu, L.; Du, X.; Xi, X.; Yang, L.; Yang, Y. Experimental Analysis of Parameter Influences on the Performances Ofdirect Air Cooled Power Generating Unit. Energy 2013, 56, 117–123. [Google Scholar] [CrossRef]
- Li, J.; Bai, Y.; Li, B. Operation of Air Cooled Condensers for Optimised Back Pressure at Ambient Wind. Appl. Therm. Eng. 2018, 128, 1340–1350. [Google Scholar] [CrossRef]
- Huang, W.; Chen, L.; Wang, W.; Yang, L.; Du, X. Cooling Performance Optimization of Direct Dry Cooling System Based on Partition Adjustment of Axial Flow Fans. Energies 2020, 13, 3179. [Google Scholar] [CrossRef]
- Huang, W.; Chen, L.; Yang, L.; Du, X. Energy-Saving Strategies of Axial Flow Fans for Direct Dry Cooling System. Energies 2021, 14, 3176. [Google Scholar] [CrossRef]
- Luo, Z.; Liu, J.; Huusom, J.K. Energy-Efficient Operation of a Direct Air-Cooled Condenser Based on Divisional Regulation. Int. J. Refrig. 2021, 132, 233–242. [Google Scholar] [CrossRef]
- Qiao, H.; Laughman, C.R.; Aute, V.; Radermacher, R. An Advanced Switching Moving Boundary Heat Exchanger Model with Pressure Drop. Int. J. Refrig. 2016, 65, 154–171. [Google Scholar] [CrossRef]
- Zhu, H.; Shen, J.; Lee, K.Y.; Sun, L. Multi-Model Based Predictive Sliding Mode Control for Bed Temperature Regulation in Circulating Fluidized Bed Boiler. Control Eng. Pract. 2020, 101, 104484. [Google Scholar] [CrossRef]
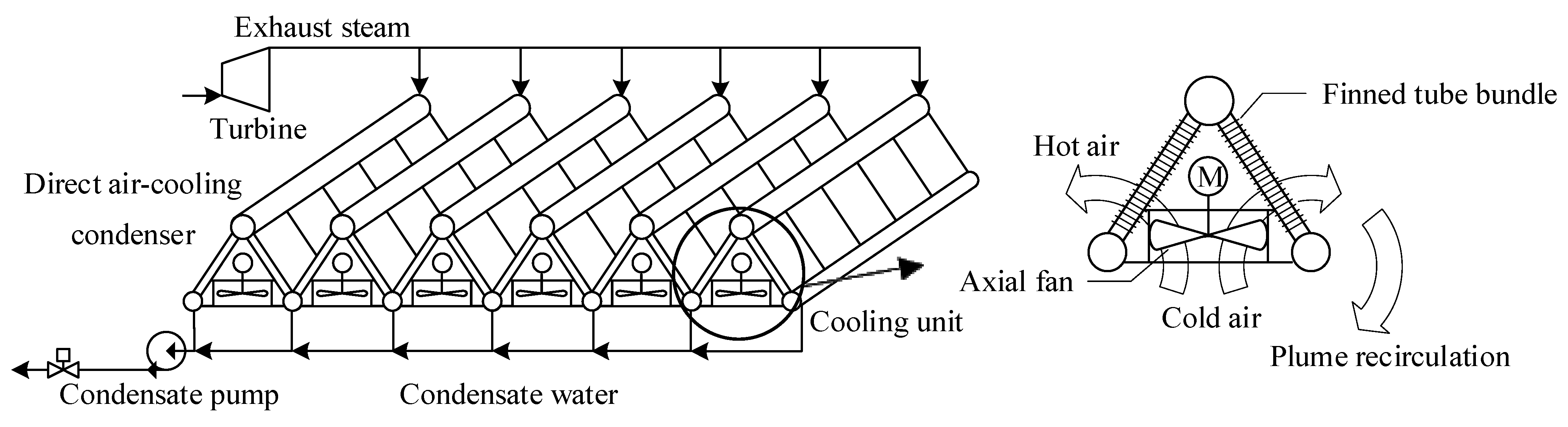
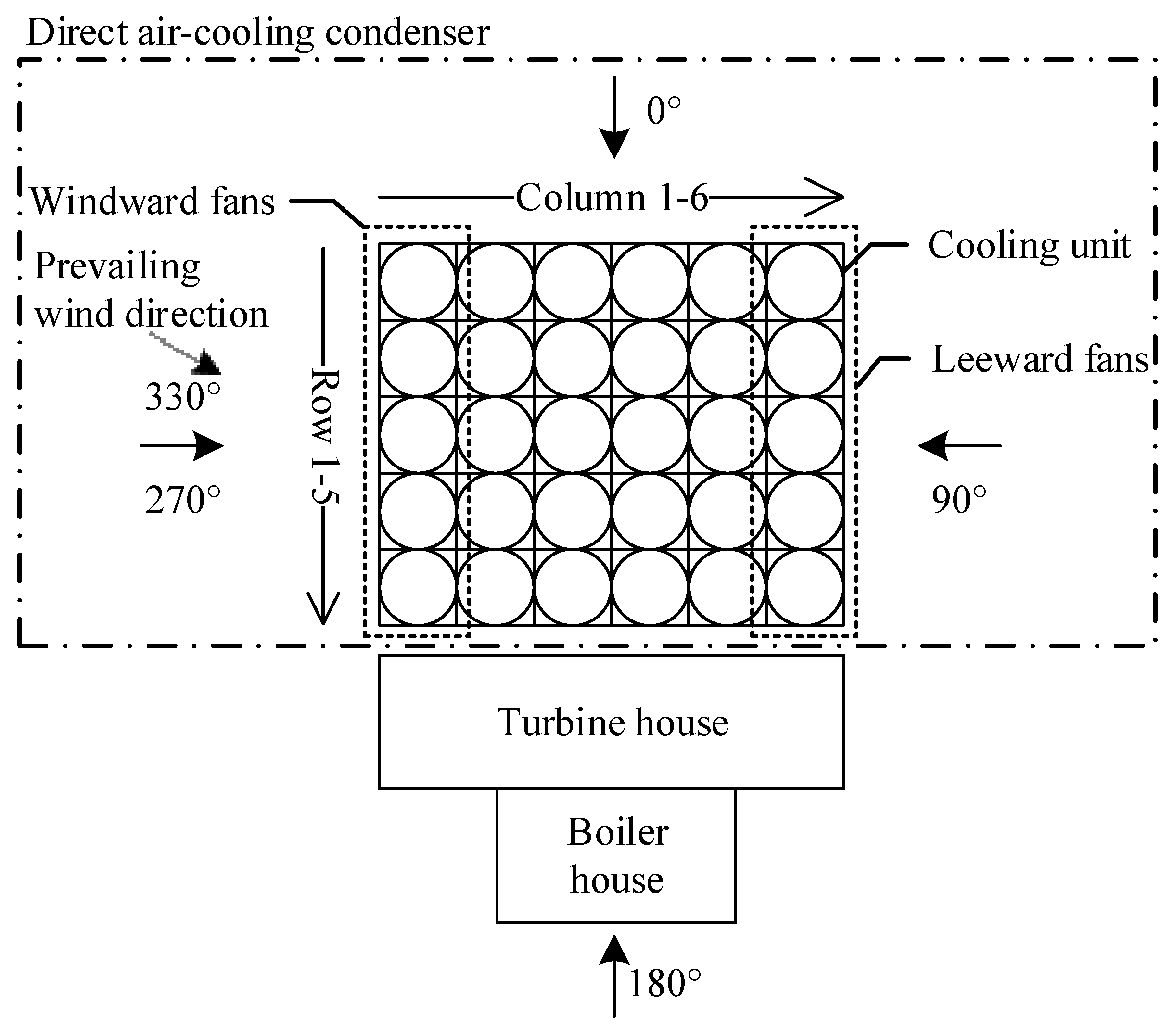








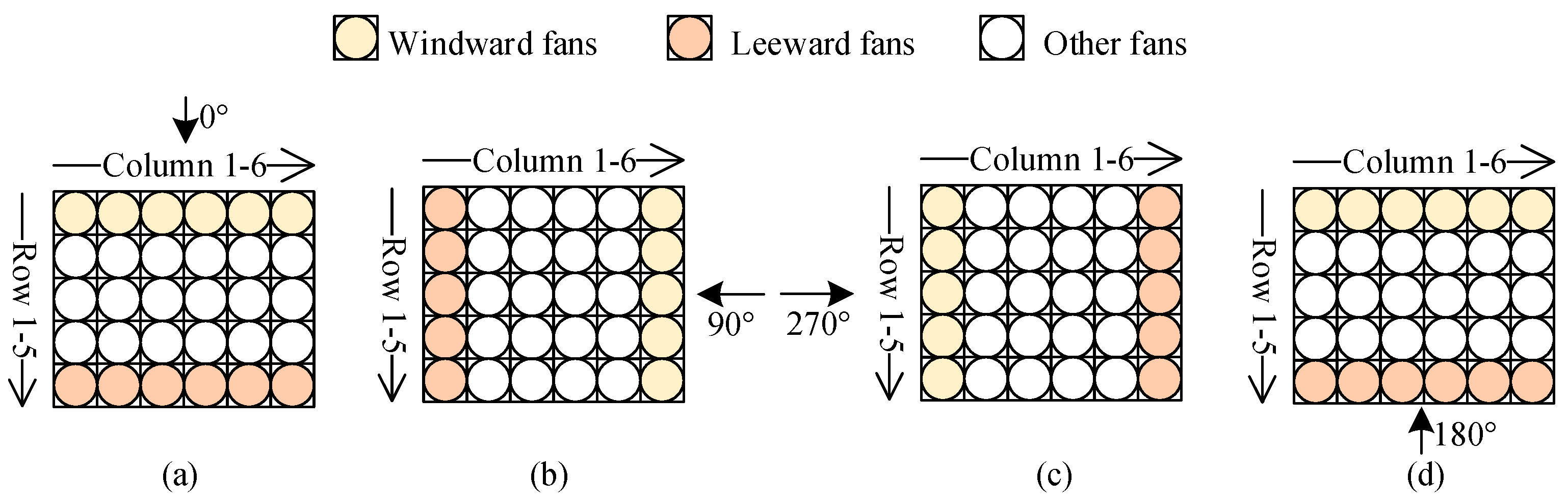

| Parameter (Unit) | Value |
|---|---|
| Power plant nominal power (MW) | 330 |
| Exhaust steam mass flow rate (t/h) | 741 |
| Exhaust steam enthalpy (kJ/kg) | 2531 |
| Backpressure (kPa) | 15 |
| Ambient temperature (°C) | 15 |
| Fan rotational speed (r/min) | 100 |
| Fan nominal power (kW) | 110 |
| Fan front face area (m2) | 211 |
| Fan face velocity (m/s) | 2.46 |
| Finned tube number of each cooling unit (-) | 370 |
| Finned tube length (m) | 10.4 |
| Finned tube mass (kg) | 15.2 |
| Finned tube combined specific heat capacity (kJ/(kg·K)) | 2.72 |
| Finned tube wall density (kg/m3) | 7850 |
| Finned tube cross-section area (m2) | 0.0033 |
| Finned tube inner surface area (m2) | 2.06 |
| Finned tube outer surface area (m2) | 61.9 |
| Finned tube inner surface heat transfer coefficient (W/(m2·K)) | 7200 |
| Finned tube outer surface heat transfer coefficient (W/(m2·K)) | 35 |
| Wind Direction (°) | Average Plume Recirculation Rate (-) | Volumetric Effectiveness (-) | ||
|---|---|---|---|---|
| Windward Fans | Leeward Fans | Other Fans | ||
| 0 | 0.036 | 0.55 | 0.85 | 0.78 |
| 270 | 0.06 | 0.5 | 0.97 | 0.79 |
| 180 | 0.15 | 0.55 | 0.85 | 0.78 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, Z.; Yao, Q. Multi-Model-Based Predictive Control for Divisional Regulation in the Direct Air-Cooling Condenser. Energies 2022, 15, 4803. https://doi.org/10.3390/en15134803
Luo Z, Yao Q. Multi-Model-Based Predictive Control for Divisional Regulation in the Direct Air-Cooling Condenser. Energies. 2022; 15(13):4803. https://doi.org/10.3390/en15134803
Chicago/Turabian StyleLuo, Zhiling, and Qi Yao. 2022. "Multi-Model-Based Predictive Control for Divisional Regulation in the Direct Air-Cooling Condenser" Energies 15, no. 13: 4803. https://doi.org/10.3390/en15134803
APA StyleLuo, Z., & Yao, Q. (2022). Multi-Model-Based Predictive Control for Divisional Regulation in the Direct Air-Cooling Condenser. Energies, 15(13), 4803. https://doi.org/10.3390/en15134803





