Modal Analysis of a Lithium-Ion Battery for Electric Vehicles
Abstract
1. Introduction
2. Formulations
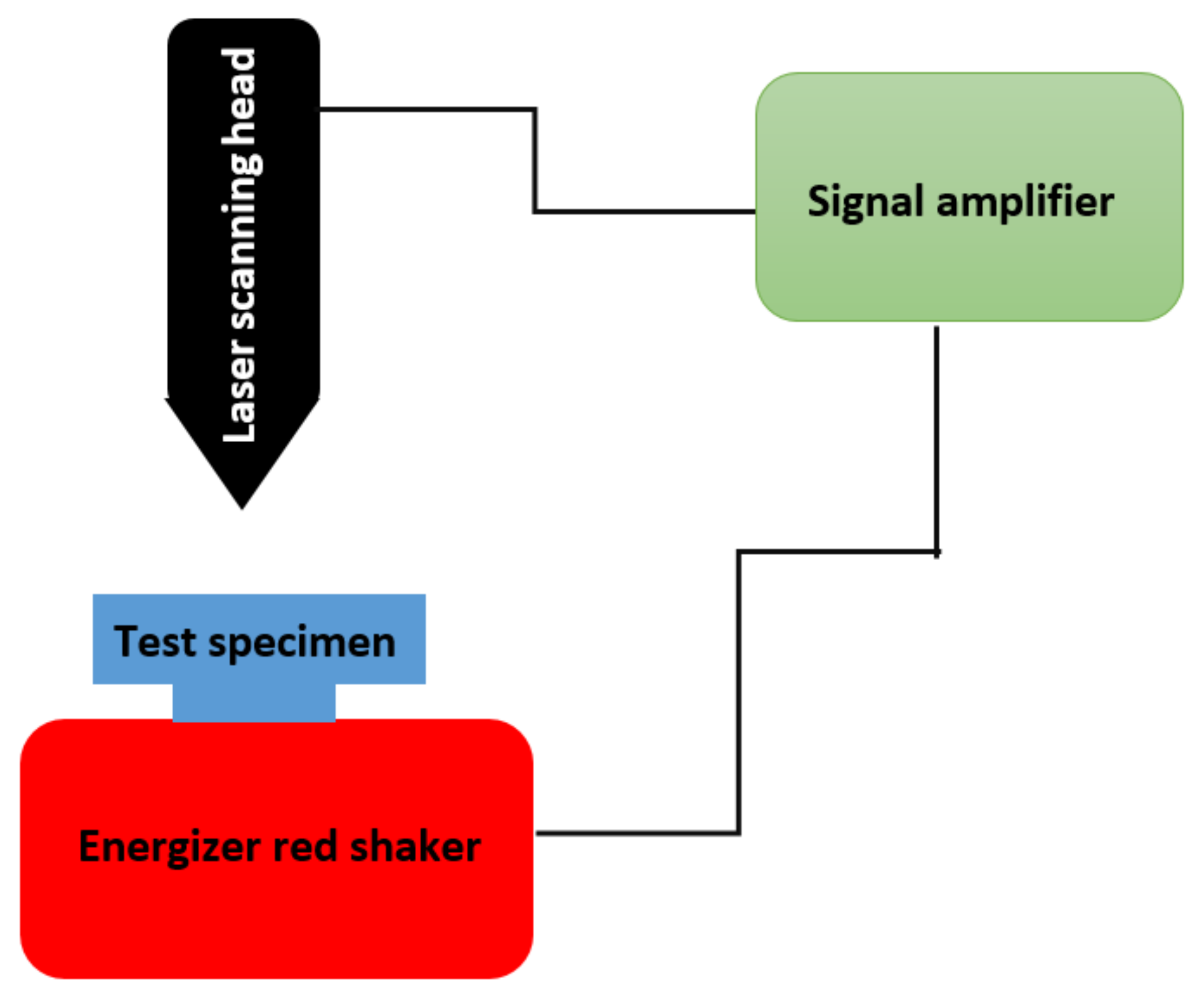
3. Experimental
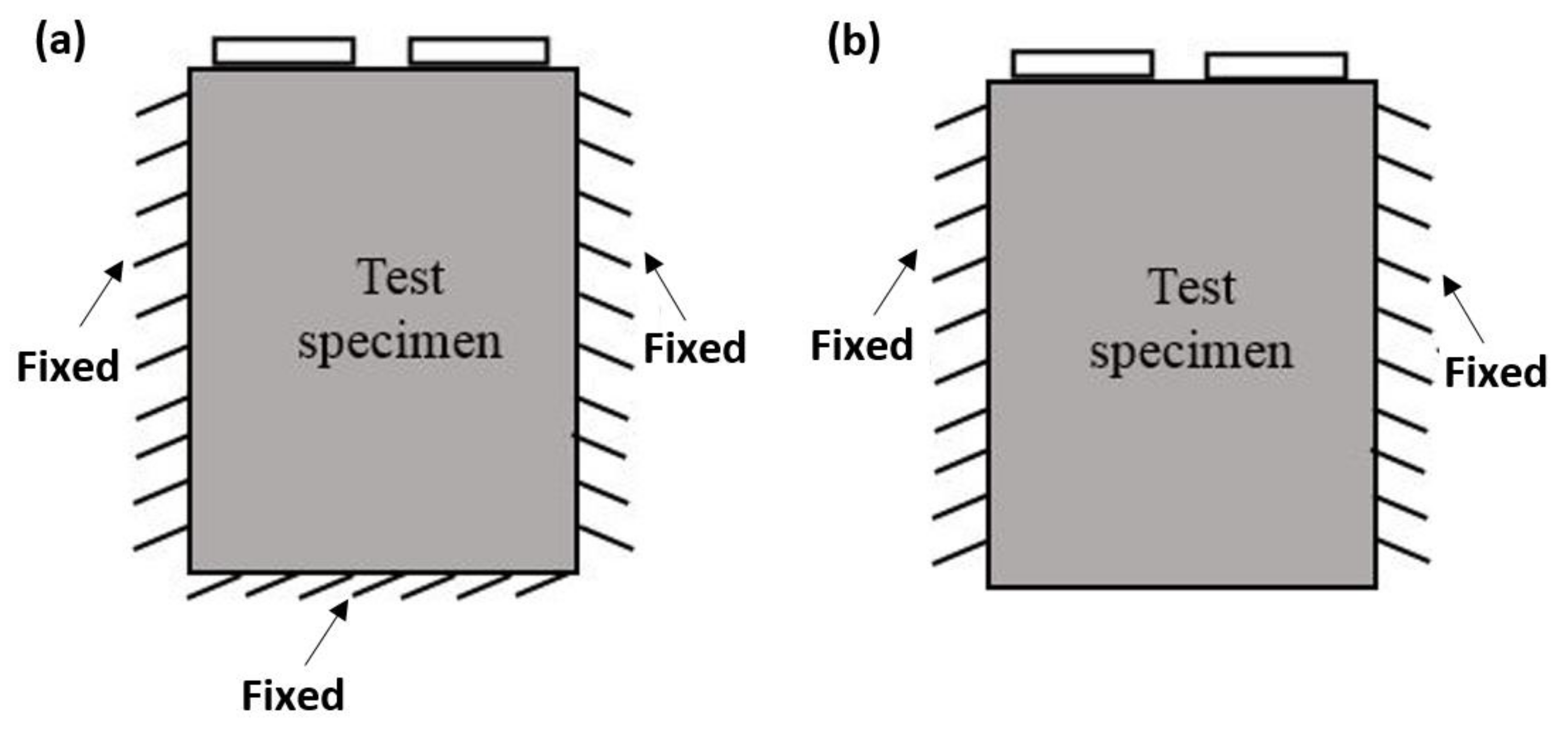
3.1. Boundary Conditions
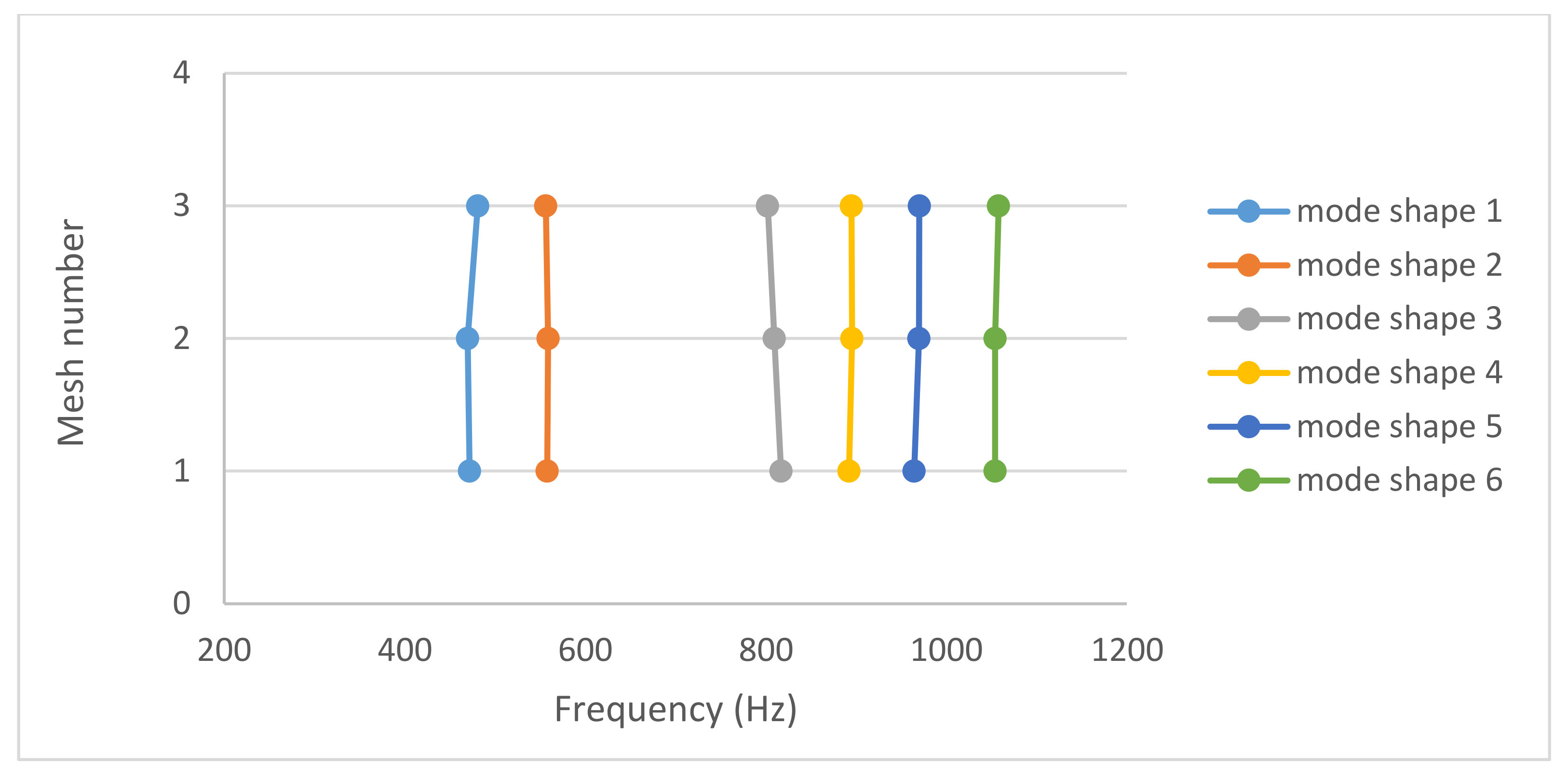
3.2. Grid Convergence
4. Results and Discussion
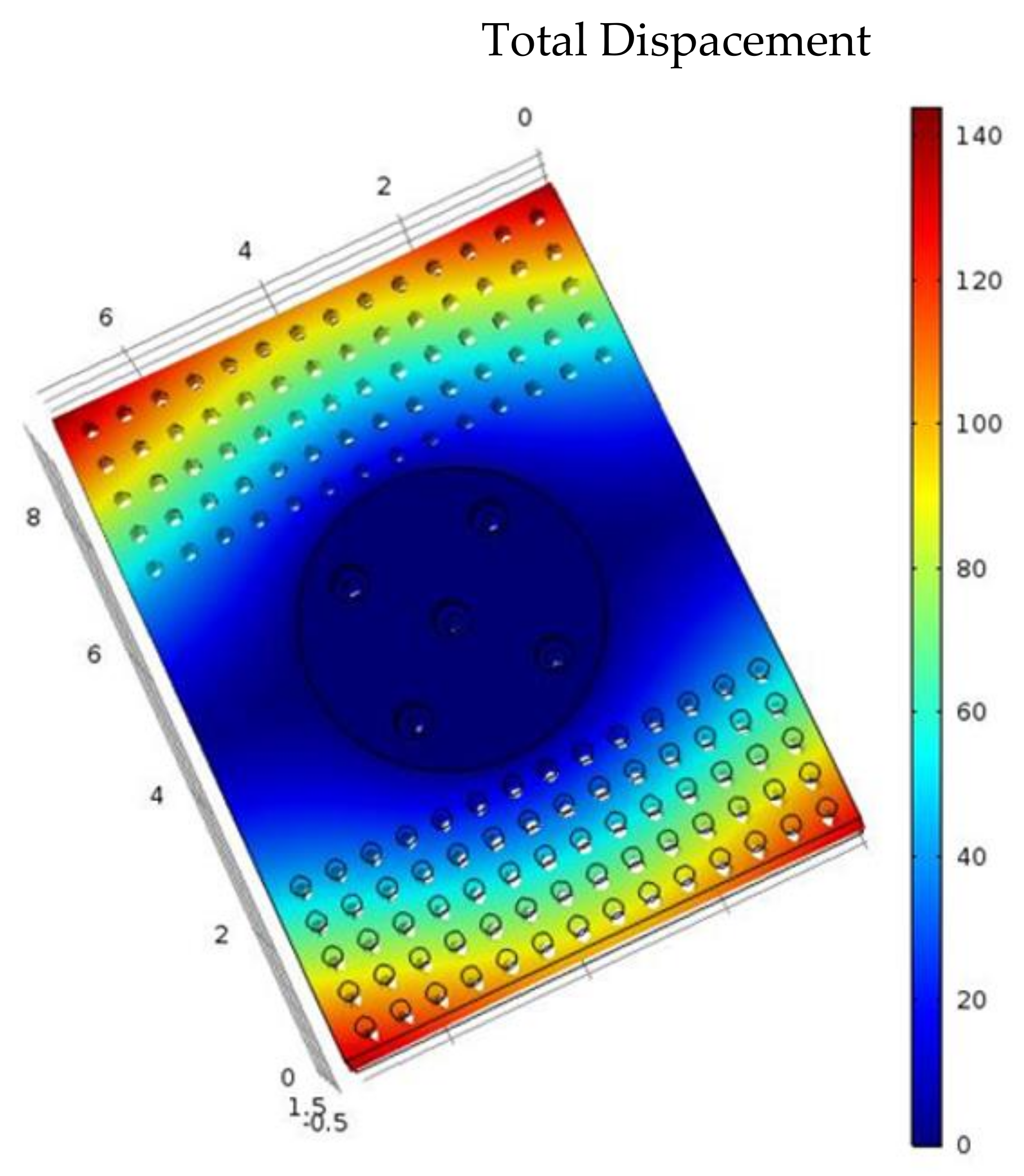
4.1. Baseplate
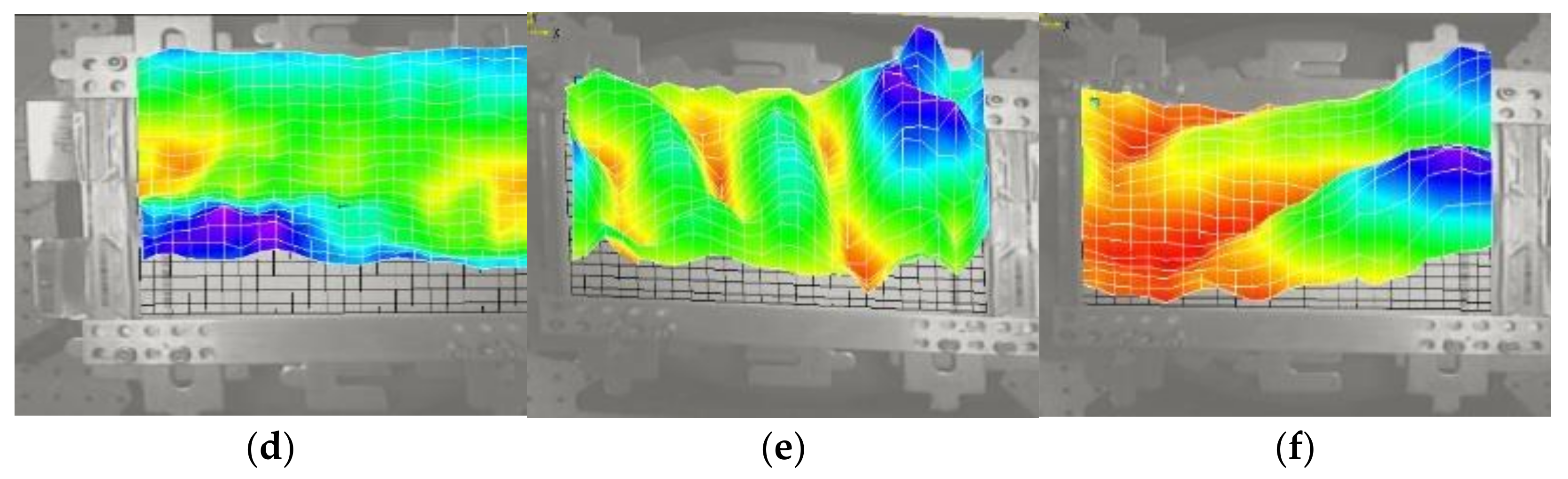
4.2. Battery Mode Shapes
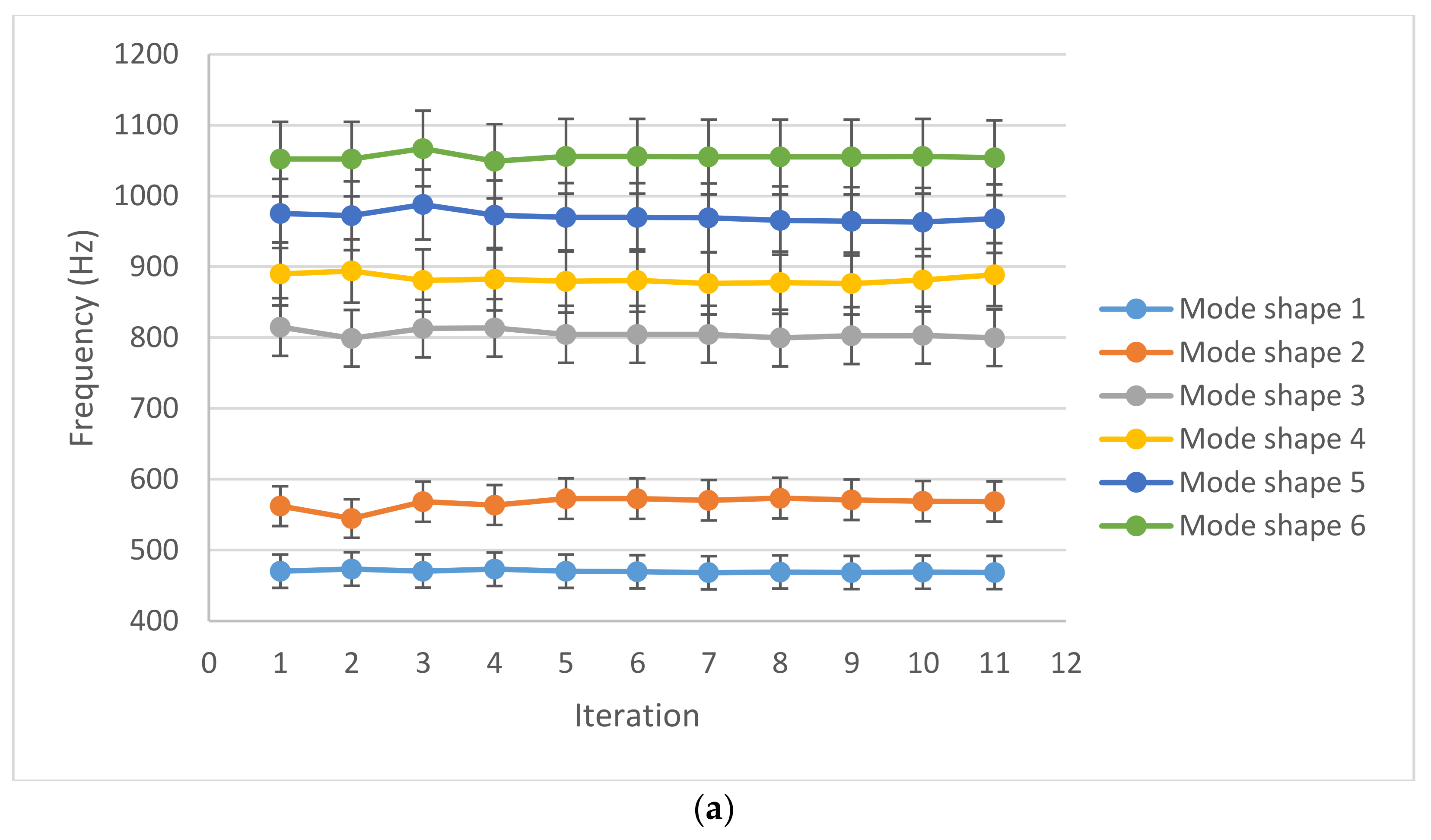
4.3. Repeatability Analysis
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Foreman, E.; Zakri, W.; Sanatimoghaddam, M.H.; Modjtahedi, A.; Pathak, S.; Kashkooli, A.G.; Garafolo, N.G.; Farhad, S. A review of inactive materials and components of flexible lithium-ion batteries. Adv. Sustain. Syst. 2017, 1, 1700061. [Google Scholar] [CrossRef]
- Iordache, A.; Bresser, D.; Solan, S.; Retegan, M.; Bardet, M.; Skrzypski, J.; Picard, L.; Dubois, L.; Gutel, T. From an enhanced understanding to commercially viable electrodes: The case of PTCLi4 as sustainable organic lithium-ion anode material. Adv. Sustain. Syst. 2017, 1, 1600032. [Google Scholar] [CrossRef]
- Sasi, R.; Chandrasekhar, B.; Kalaiselvi, N.; Devaki, S.J. Green solid ionic liquid crystalline electrolyte membranes with anisotropic channels for efficient li-ion batteries. Adv. Sustain. Syst. 2017, 1, 1600031. [Google Scholar] [CrossRef]
- Feng, X.; Sun, J.; Ouyang, M.; Wang, F.; He, X.; Lu, L.; Peng, H. Characterization of penetration induced thermal runaway propagation process within a large format lithium ion battery module. J. Power Sources 2014, 275, 261–273. [Google Scholar] [CrossRef]
- Avdeev, I.; Gilaki, M. Structural analysis and experimental characterization of cylindrical lithium-ion battery cells subject to lateral impact. J. Power Sources 2014, 271, 382–391. [Google Scholar] [CrossRef]
- Greve, L.; Fehrenbach, C. Mechanical testing and macro-mechanical finite element simulation of the deformation, fracture, and short circuit initiation of cylindrical Lithium-ion battery cells. J. Power Sources 2012, 214, 377–385. [Google Scholar] [CrossRef]
- Sahraei, E.; Meier, J.; Wierzbicki, T. Characterizing and modeling mechanical properties and onset of short circuit for three types of lithium-ion pouch cells. J. Power Sources 2014, 247, 503–516. [Google Scholar] [CrossRef]
- Shi, F.; Yu, H.; Chen, X.; Cui, T.; Zhao, H.; Shi, X. Mechanical performance study of lithium-ion battery module under dynamic impact test. In Proceedings of the 19th Asia Pacific Automotive Engineering Conference & SAE-China Congress 2017: Selected Papers; Springer: Singapore, 2019; pp. 1–11. [Google Scholar]
- Spinner, N.S.; Field, C.R.; Hammond, M.H.; Williams, B.A.; Myers, K.M.; Lubrano, A.L.; Rose-Pehrsson, S.L.; Tuttle, S.G. Physical and chemical analysis of lithium-ion battery cell-to-cell failure events inside custom fire chamber. J. Power Sources 2015, 279, 713–721. [Google Scholar] [CrossRef]
- Liu, X.; Stoliarov, S.I.; Denlinger, M.; Masias, A.; Snyder, K. Comprehensive calorimetry of the thermally-induced failure of a lithium ion battery. J. Power Sources 2015, 280, 516–525. [Google Scholar] [CrossRef]
- Huo, H.; Xing, Y.; Pecht, M.; Züger, B.J.; Khare, N.; Vezzini, A. Safety requirements for transportation of lithium batteries. Energies 2017, 10, 793. [Google Scholar] [CrossRef]
- Farrington, M.D. Safety of lithium batteries in transportation. J. Power Sources 2001, 96, 260–265. [Google Scholar] [CrossRef]
- Ruiz, V.; Pfrang, A.; Kriston, A.; Omar, N.; van den Bossche, P.; Boon-Brett, L. A review of international abuse testing standards and regulations for lithium ion batteries in electric and hybrid electric vehicles. Renew. Sustain. Energy Rev. 2018, 81, 1427–1452. [Google Scholar] [CrossRef]
- Zhang, X.; Wierzbicki, T. Characterization of plasticity and fracture of shell casing of lithium-ion cylindrical battery. J. Power Sources 2015, 280, 47–56. [Google Scholar] [CrossRef]
- Choi, Y.; Jung, D.; Ham, K.; Bae, S. A study on the accelerated vibration endurance tests for battery fixing bracket in electrically driven vehicles. Procedia Eng. 2011, 10, 851–856. [Google Scholar] [CrossRef]
- Moon, S.-I.; Cho, I.-J.; Yoon, D. Fatigue life evaluation of mechanical components using vibration fatigue analysis technique. J. Mech. Sci. Technol. 2011, 25, 631–637. [Google Scholar] [CrossRef]
- Hooper, J.M.; Marco, J. Experimental modal analysis of lithium-ion pouch cells. J. Power Sources 2015, 285, 247–259. [Google Scholar] [CrossRef]
- Hooper, J.M.; Marco, J. Characterising the in-vehicle vibration inputs to the high voltage battery of an electric vehicle. J. Power Sources 2014, 245, 510–519. [Google Scholar] [CrossRef]
- Hooper, J.M.; Marco, J.; Chouchelamane, G.H.; Chevalier, J.S.; Williams, D. Multi-axis vibration durability testing of lithium-ion 18650 NCA cylindrical cells. J. Energy Storage 2018, 15, 103–123. [Google Scholar] [CrossRef]
- Choi, H.Y.; Lee, I.; Lee, J.S.; Kim, Y.M.; Kim, H. A study on mechanical characteristics of lithium-polymer pouch cell battery for electric vehicle. In Proceedings of the 23rd International Technical Conference on the Enhanced Safety of Vehicles (ESV) National Highway Traffic Safety Administration, Seoul, Korea, 27–30 May 2013. [Google Scholar]
- Ewins, D.J. Basics and state-of-the-art of modal testing. Sadhana 2000, 25, 207–220. [Google Scholar] [CrossRef][Green Version]
- Available online: www.mtixtl.com/UN38.3/UN_Test_Manual_Lithium_Battery_Requirements.PDF (accessed on 23 June 2022).
- Available online: https://unece.org/fileadmin/DAM/trans/main/wp29/wp29regs/2013/R100r2e.pdf (accessed on 23 June 2022).
- Available online: www.sae.org/standards/content/j2380_201312/ (accessed on 23 June 2022).
- User Manual of Red Energizer, MB Dynamics. Available online: https://www.mbdynamics.com/wp-content/uploads/2018/10/MB-BSR-ENRGZR-RED-1018-FINAL.pdf (accessed on 23 June 2022).
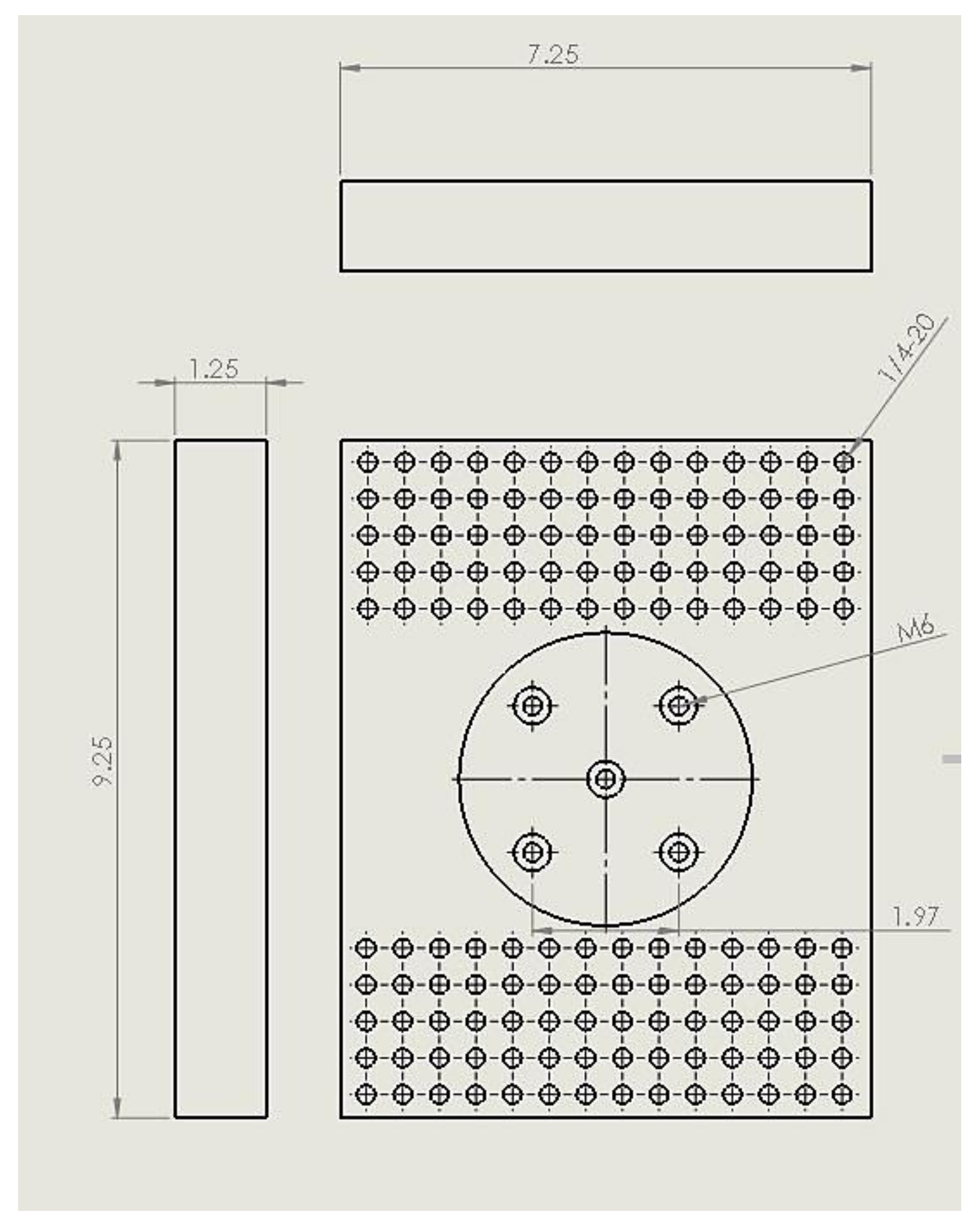




| Specifications | Value |
|---|---|
| Force output-cooling (convection) | 55 pounds (peak) |
| Stroke | 1.5 inch (peak-peak) |
| Distance between stops | 1.5 inch |
| Armature axial stiffness | 65 pounds/inch |
| Armature weight | 2.6 pounds |
| The frequency range of shaker | DC to 5000 Hz |
| Driver coil current | 22 Amperes Maximum |
| Driver coil DC resistance | 41 Ohms (@ amplifier connector on shaker) |
| Shaker attachments | Floor mount trunnion base |
| Dimensions | 13.1 in high (to top of mounting table) 14 in × 10.75 in footprint |
| Weight | 85 lbs. |
| Item | Value |
|---|---|
| The thickness of copper current collector | 10 μm |
| The thickness of aluminum current collector | 20 μm |
| Thickness of anode | 57 μm |
| Thickness of cathode | 65 μm |
| Thickness of separator | 48 μm |
| Anode material | Graphite |
| Cathode material | Lithium iron phosphate, LiFePO4 (LFP) |
| Mesh Number | Mesh Points | Mesh Representation | Scan Duration |
|---|---|---|---|
| Mesh 1 | 117 |  | 35 min |
| Mesh 2 | 425 |  | 1 h 25 min |
| Mesh 3 | 1247 |  | 6 h 20 min |
| Frequency No. | Natural Frequency |
|---|---|
| 1 | 2716.3 Hz |
| 2 | 2999.0 Hz |
| 3 | 3013.8 Hz |
| 4 | 3118.5 Hz |
| 5 | 4247.1 Hz |
| 6 | 5398.7 Hz |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Garafolo, N.G.; Farhad, S.; Koricherla, M.V.; Wen, S.; Esmaeeli, R. Modal Analysis of a Lithium-Ion Battery for Electric Vehicles. Energies 2022, 15, 4841. https://doi.org/10.3390/en15134841
Garafolo NG, Farhad S, Koricherla MV, Wen S, Esmaeeli R. Modal Analysis of a Lithium-Ion Battery for Electric Vehicles. Energies. 2022; 15(13):4841. https://doi.org/10.3390/en15134841
Chicago/Turabian StyleGarafolo, Nicholas Gordon, Siamak Farhad, Manindra Varma Koricherla, Shihao Wen, and Roja Esmaeeli. 2022. "Modal Analysis of a Lithium-Ion Battery for Electric Vehicles" Energies 15, no. 13: 4841. https://doi.org/10.3390/en15134841
APA StyleGarafolo, N. G., Farhad, S., Koricherla, M. V., Wen, S., & Esmaeeli, R. (2022). Modal Analysis of a Lithium-Ion Battery for Electric Vehicles. Energies, 15(13), 4841. https://doi.org/10.3390/en15134841







