An DPWM for Active DC-Link Type Quasi-Z-Source Inverter to Reduce Component Voltage Rating

Abstract

The conventional DC-link type quasi-Z-source inverter has been known as a buck–boost inverter with a low component voltage rating. This paper proposes an active DC-link type quasi-Z-source inverter by adding one active switch and one diode to the impedance-source network to enhance the voltage gain of the inverter. As a result, the component voltage rating of the inverter is significantly reduced, which is demonstrated through some comparisons between the proposed topology and others. A discontinuous pulse width modulation (DPWM) scheme is proposed to control the inverter, which reduces the number of commutations compared to the traditional strategy. Under this approach, the insertion of a shoot-through state does not cause any extra commutations compared to the conventional voltage-source inverter. Details about control implementation, steady-state analysis, and design guidelines are also presented in this paper. Simulation and a laboratory prototype have been built to test the proposed inverter. Both buck and boost operations of the proposed inverter are implemented to validate the performance of the inverter.

1. Introduction

Presently, inverters that convert energy from a DC input source to AC output voltage play an important role in the renewable energy system. Because of their simple structure, low component utilization, and high power density, conventional two-level inverters are used in a wide range of industrial applications [1,2,3,4]. Two forms of traditional two-level inverters are voltage source inverters (VSI) and current source inverters (CSI). The VSI works as a voltage buck converter, where the peak-to-peak value of the AC output phase voltage is smaller than the DC link voltage. In comparison with VSI, the CSI is known as a boost converter, which uses many extra elements such as diodes [3]. Nowadays, inverters adopting a wide range of input voltage have attracted many researchers. However, conventional VSI and CSI do not adopt a wide range of input sources. In fact, the traditional solution installs a DC–DC boost converter in front of the conventional VSI to provide buck–boost characteristics in two-stage power conversion. In this way, the input voltage is enhanced before feeding to the inverter circuit. In this solution, a short-circuit current generated by activating all switches in one or more phase legs can destroy the system. This state is known as the shoot-through (ST) state and is forbidden in VSI. To avoid this dangerous situation, dead-time control is adopted to generate control signals for inverter switches [5,6]. In this case, the rising edge of the control signal is delayed to avoid the ST state. It causes distortion at output voltage and an increment in total harmonic distortion (THD) of output current. Many pulse-width modulation (PWM) methods based on the direction of output current have been explored to compensate for the negative effects of dead time [5,6]. However, these studies introduced more control complexity and required many additional current sensors.

In the last two decades, impedance source inverters (ISIs) (known as single-stage inverters) have been considered to solve the problems of buck–boost operation and the ST immunity of conventional VSI. The Z-source inverter (ZSI) is the first generation of ISIs, which was explored by Professor Peng in 2003 [7]. In ZSI, two capacitor voltages of the ZS network are subtracted by input voltage to produce the DC link voltage of the inverter side. Thus, it can be concluded that the capacitors are badly utilized. The quasi-Z-source inverter (qZSI) introduced a new connection type of impedance source network to overcome the limit of ZSI [8,9]. Two main types of qZSI are continuous qZSIs (CqZSI) and DC-link type/discontinuous qZSI (DqZSI). These two topologies have the same boost factor. However, the DqZSI topology has a smaller voltage rating of a capacitor than CqZSI, as presented in [8]. The main advantage of the CqZSI compared to DqZSI is that this topology has a continuous input current [8]. Many comparisons between ISIs and traditional two-stage inverters have demonstrated that single-stage inverters have better system reliability and output quality [10,11,12]. Moreover, when the voltage gain of the inverter is less than two, the ZSI and qZSI have higher efficiency than the conventional two-stage inverter [10,12]. The work in [13] introduced a combination of a qZS network and a single-phase neutral point clamped inverter for photovoltaic (PV) applications. With generic semiconductor devices, this work can obtain 97% conversion efficiency, just like any two-stage inverter. It demonstrated that the single-stage inverter is one of the promising topologies.

Two main issues of the impedance source inverter can be listed as (1) improving boost factor and voltage gain, and (2) reducing the number of switching commutations. When the boost factor/voltage gain is improved, the required ST duty ratio is also reduced. It results in reducing conduction loss and increasing system efficiency [14]. Moreover, the ST duty ratio also affects the inductor’s current profile. Thus, a lower ST duty ratio causes a smaller inductor current ripple, which reduces the size of the inductor and increases the power density of the inverter. The switching commutation increment is mainly due to ST insertion. At least two extra commutations are generated for ST insertion in conventional methods for ISIs. It leads to increased switching losses of the semiconductor devices. Many studies have discussed switching commutation and ST duty ratio reductions, as follows.

The switching commutations can be minimized by correspondingly placing ST state, which is reported in [15,16,17]. Accordingly, the number of switching commutations is reduced to equal that of conventional VSI in [15,16,17]. Many studies have reported on voltage gain improvement methods for qZSI [18,19,20,21,22]. The first solution to increasing voltage gain is to add more extra passive components like inductors and diodes into the impedance-source network [18,19]. The other one is using active switches in the intermediate network [20,21,22]. In [18,19], one or more switched inductor (SL) units, which consist of two inductors and three diodes, are used to replace single inductors in the conventional topology of ZSI/qZSI to increase voltage gain. This solution increases the cost and size of the inverter because it utilizes many inductors. In comparison to the first solution in [18,19], the second one in [20,21,22] can save many inductors and diodes by using one extra active switch. It is worth noting that the boost factor and voltage gain of the topologies in [20,21,22] are very flexible to be controlled and higher than that in [18,19]. The work in [21] presented a combination of both solutions, which adopts both SL unit and active switch in the intermediate network. Although the voltage gain of these works has increased significantly, it remains low. Moreover, the boost factor is controlled by only the ST duty ratio, which makes the inverter inflexible.

This paper presents a new topology of active DC link type qZSI (ADC-qZSI) by adding one active switch and one diode into the conventional DqZSI. With the help of these extra devices, the proposed topology introduces one extra mode besides two conventional operating modes for ISIs (ST mode and non-ST mode). In this mode, the current of the inductor is kept constant and the voltage gain is increased. It results in component voltage rating reduction. A discontinuous PWM (DPWM) control method is proposed to control this topology. In this control technique, the ST state is inserted into the phase operating with the highest reference signals. It leads to reducing the number of switching commutations down to equal to conventional two-level VSI. The next parts of this paper include seven sections. The inverter structure and steady-state analysis and design guidelines of the proposed inverter are presented in Section 2 and Section 3, respectively. Section 4 presents the semiconductor loss calculation. The comparison study, simulation and experimental results are attached in Section 5, Section 6 and Section 7.

2. Proposed Active DC-Link Type Quasi-Z-Source Inverter (ADC-qZSI) Topology

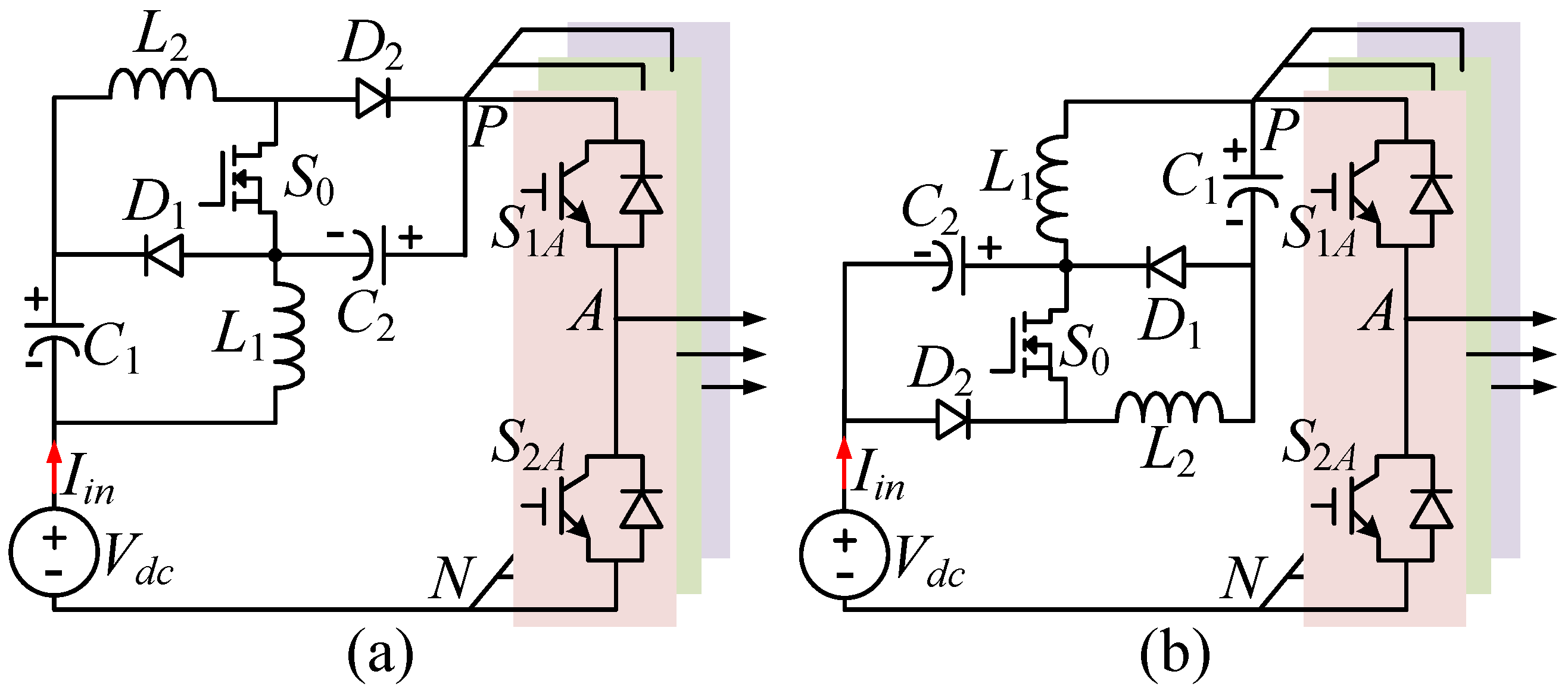
Two types of proposed ADC-qZSIs have been drawn in Figure 1. Both types are constructed by an ADC-qZS network followed by a conventional two-level inverter. The impedance source network is known as the boost unit and is formed by two inductors (L₁ and L₂), two capacitors (C₁ and C₂), one active switch (S₀), and two diodes (D₁ and D₂). Compared to traditional DC-link qZSI in [8], the proposed inverter has one extra active switch, S₀, and one extra diode, D₂. This insertion makes this topology flexible to control and increases the boost factor and voltage gain of the inverter. The conventional two-level inverter is responsible for buck operation. With the corresponding control method, the proposed inverter can buck and boost the output voltage from a single DC source, V_dc. Each leg of the inverter side consists of two active switches, S_1X and S_2X, which ensures a two-level voltage at the output terminals, +V_PN and zero. In general, two types of ADC-qZSIs have similar operations, thus, type 1 shown in Figure 1a is selected for analysis.

2.1. Operating States

Like any single-stage inverter, the ADC-qZSI is also proposed to operate under ST mode and non-ST mode, as shown in Figure 2. The on/off states of inverter switches and diodes are listed in

Table 1. On/Off states of ADC-qZSI (X = A, B, C).

Mode	ON Switch	ON Diode	VXN
ST	S1X, S2X	D2	0
non-ST 1	S0, S1X/S2X	D1	+VPN, 0
non-ST 2	S1X/S2X	D1, D2	+VPN, 0

.

In the ST state, as shown in Figure 2a, the inverter side is able to produce value of 0 V at three-phase output voltages by turning on two switches in one phase leg, while switch S₀ is gated off. As a result, the DC-link voltage, V_PN, is shorted and has a value of zero. This ST state reverses diode D₁ and forward diode D₂ of impedance source circuit. In this mode, inductor L₁ is stored energy from DC input voltage and capacitor C₂, while inductor L₂ is stored energy from DC input voltage and capacitor C₁. The inductor voltages and capacitor currents are expressed as follows:

$$\{\begin{array}{ll}{L}_1\frac{d{i}_{L1}}{dt}=V_{dc}+V_{C2};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& L_2\frac{d{i}_{L2}}{dt}=V_{dc}+V_{C1}\\ C_1\frac{d{v}_{C1}}{dt}=-i_{L2};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& C_2\frac{d{v}_{C2}}{dt}=-i_{L1}\end{array}$$

(1)

where V_dc is DC input source; V_C1 and V_C2 are capacitor C₁ and C₂ voltages; i_L1, i_L2, and i_PN are instantaneous values of inductor currents and equivalent inverter side current.

In non-ST mode, the DC-link voltage obtains maximum value, which is determined by the summing DC input source and two capacitor voltages. With one extra switch, S₀, the non-ST mode consists of two sub-modes depending on the state of S₀. When S₀ is gated on, non-ST mode 1 shown in Figure 2b is achieved. Diode D₂ is reversed bias, whereas diode D₁ is forward bias. It results in shorting inductor L₂ and discharging capacitor C₂. While capacitor C₁ is charged from inductor L₁. The following equations are obtained:

$$\{\begin{array}{l}{L}_1\frac{d{i}_{L1}}{dt}=-V_{C1};L_2\frac{d{i}_{L2}}{dt}=0\\ C_1\frac{d{v}_{C1}}{dt}=i_{L1}-i_{PN};C_2\frac{d{v}_{C2}}{dt}=-i_{PN}\end{array}$$

(2)

It can be seen that this non-ST mode maintains the energy of inductor L₂ instead of discharging like conventional ISI, which increases the boost factor of the inverter.

Non-ST mode 2 of the proposed inverter, as shown in Figure 2c, is like any single-stage inverter. Switch S₀ is gated off, whereas the inverter side switches operate like conventional inverters. Two inductors transfer energy to capacitors. The following equations are achieved:

$$\{\begin{array}{ll}{L}_1\frac{d{i}_{L1}}{dt}=-V_{C1};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& L_2\frac{d{i}_{L2}}{dt}=-V_{C2}\\ C_1\frac{d{v}_{C1}}{dt}=i_{L1}-i_{PN};\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}& C_2\frac{d{v}_{C2}}{dt}=i_{L2}-i_{PN}\end{array}$$

(3)

2.2. Proposed DPWM Control Strategy

To reduce the switching commutation, the proposed method uses a DPWM strategy to generate the control signals to inverter switches. To detail this modulation method, let us first define three signals v_X (X = A, B, and C) as follows:

$$\{\begin{array}{l}{v}_A=1/\sqrt{3}\times M\times \sin (2\pi f_{o}t)\\ v_B=1/\sqrt{3}\times M\times \sin (2\pi f_{o}t-2\pi /3)\\ v_B=1/\sqrt{3}\times M\times \sin (2\pi f_{o}t-2\pi /3)\\ M\le 1\end{array}$$

(4)

where M is modulation index; f_o is fundamental frequency.

Three reference signals $v_X^{*}$ (X = A, B, C), as shown in Figure 3, can be obtained by subtracting v_X from minimum value of v_A, v_B, v_C as follow:

$$v_X^{*}=v_X-\min (v_A,v_B,v_C)$$

(5)

These three reference signals are compared to high-frequency carrier V_tri like a conventional two-level inverter, to produce on/off switching signals for inverter side switches. In this scheme, one-third of the output period has no switching commutation in any phase leg, as shown in Figure 3. Thus, the switching loss can be reduced when compared to the conventional sinusoidal PWM method.

In the conventional PWM control method for single-stage inverters, the constant signal is used to generate the ST signal of the inverter leg. When this ST signal is inserted into the switching sequence, it produces at least two extra commutations in any phase leg. To overcome this, the proposed method uses discontinuous modulation signal v_ST and the maximum value of $v_X^{*}$ to produce ST signal, as presented in Figure 3. In more detail, the ST signal is activated when $\max (v_A^{*},v_B^{*},v_C^{*})$ ≤ V_tri ≤ v_ST. Then, this ST signal is inserted into the phase which has the maximum value of reference signal $v_X^{*}$ by triggering on both switches S_1X and S_2X of that phase leg. In this way, the ST insertion does not generate any extra switching commutation compared to conventional two-level VSI. For example, as shown in zoom-in waveforms of switches S_1A and S_2A control signals, there are only two switching commutations for each switch, which equals the conventional two-level inverter.

Like any impedance source two-level inverter, the ST state must be inserted within zero vectors. Therefore, ST duty ratio D_ST is not larger than (1 − M) and can be controlled independently by M. The v_ST signal and ST duty ratio are expressed as follows:

$$\{\begin{array}{l}{v}_{ST}=\max (v_A^{*},v_B^{*},v_C^{*})+D_{ST}\\ D_{ST}\le 1-M\end{array}$$

(6)

where D_ST is ST duty ratio.

The control signal of S₀ is generated by comparing control signal v_con to carrier signal V_tri, as shown in Figure 3. The v_con is identified as:

$$v_{con}=D_0$$

(7)

where D₀ is duty ratio of switch S₀.

In order not to affect the operating modes of the inverter, v_con must be satisfied with the following term:

$$v_{con}\le \sqrt{3}M/2\iff D_0\le \sqrt{3}M/2$$

(8)

2.3. Steady-State Analysis

Figure 4 shows the profiles of inductor currents and capacitor voltages under one switching period, T_s. It is clear that the total time of ST mode is D_ST∙T_s for any period T_s. The time interval of non-ST mode 1 is equal to the on-time of switch S₀ which is determined as D₀∙T_s. The rest time of T_s is (1 − D_ST − D₀)∙T_s, which is the time interval of non-ST mode 2. By applying the volt-second balanced principle to two inductors, L₁ and L₂, the capacitor and DC link voltages can be identified as:

$$\{\begin{array}{l}{V}_{C1}=V_{dc}(1-D_0)D_{ST}/(1-D_0-2D_{ST}+D_0{D}_{ST})\\ V_{C2}=V_{dc}{D}_{ST}/(1-D_0-2D_{ST}+D_0{D}_{ST})\\ V_{PN}=V_{dc}(1-D_0)/(1-D_0-2D_{ST}+D_0{D}_{ST})\end{array}$$

(9)

Assuming that the equivalent inverter current, i_PN, is constant, the average values of inductor currents can be approximately calculated by applying capacitor charge-balanced principle to capacitor C₁ and C₂ currents, as follows:

$$\{\begin{array}{l}{I}_{L1}=i_{PN}(1-D_0)(1-D_{ST})/(1-D_0-2D_{ST}+D_0{D}_{ST})\\ I_{L2}=i_{PN}(1-D_{ST})/(1-D_0-2D_{ST}+D_0{D}_{ST})\end{array}$$

(10)

The boost factor, B, of the inverter is identified as:

$$B=\frac{V_{PN}}{V_{dc}}=\frac{1-D_0}{1-D_0-2D_{ST}+D_0{D}_{ST}}$$

(11)

The peak value of fundamental component of output phase voltage is calculated as:

$${\widehat{v}}_X=1/\sqrt{3}\times M\times V_{PN}$$

(12)

where ${\widehat{v}}_X$ is the peak value of output phase voltage.

The voltage gain, G, of proposed inverter is expressed as:

$$G=\frac{{\widehat{v}}_X}{V_{dc}/2}=\frac{2}{\sqrt{3}}\times \frac{M\times (1-D_0)}{1-D_0-2D_{ST}+D_0{D}_{ST}}$$

(13)

By setting D₀ to max value which is expressed in (8), the max voltage gain can be obtained.

3. Parameter Selection

3.1. Inductor and Capacitor Selection

As shown in Figure 4, the inductor current ripples are depended on the time interval of non-ST mode 2, (1 − v_ST)T_s. When v_ST is maximum, the inductor current ripple is maximum. Based on (4)–(6), the maximum value of v_ST can be calculated as:

$$v_{ST,\max }=M+D_{ST}$$

(14)

Based on (1)–(3) and (14), the maximum value of inductor current ripples can be expressed as:

$$\{\begin{array}{l}\Delta I_{L1}=V_{dc}M(1-D_0)/(K{L}_1{f}_s)\\ \Delta I_{L2}=V_{dc}{D}_{ST}(M-D_0)/(K{L}_2{f}_s)\\ K=1-D_0-2D_{ST}+D_0{D}_{ST}\end{array}$$

(15)

where ΔI_Lj (j = 1, 2) is inductor L_j current ripple; f_s = 1/T_s is switching frequency.

The capacitor voltage ripples are calculated as:

$$\{\begin{array}{l}\Delta V_{C1}=i_{PN}M{D}_{ST}/(K{C}_1{f}_s)\\ \Delta V_{C2}=i_{PN}[M{D}_{ST}-(K-D_{ST})D_0]/(K{C}_2{f}_s)\end{array}$$

(16)

Based on (9), (10), (15) and (16), the inductors and capacitors are selected in terms of ΔI_Lj/I_Lj ≤ k₁%, and ΔV_Cj/V_Cj ≤ k₂%, where k₁% and k₂% are max acceptable ratios of inductor current and capacitor voltage ripples, respectively.

3.2. Semiconductor Device Selection

The maximum reversed voltage of diode D₁ is DC-link voltage, which is obtained in ST mode. The max reversed voltage of diode D₂ equals the capacitor C₂ voltage, which is achieved in non-ST mode 1.

The maximum value of diode D₂ current is equal to the maximum value of inductor L₂ current, which is obtained in non-ST mode 2, while the current through diode D₁ achieves its maximum value in non-ST modes, which is calculated as:

$$\{\begin{array}{l}{i}_{D1,\max }=i_{L1,\max }+i_{L2,\max }-i_{PN}\\ i_{Lj,\max }=I_{Lj}+\Delta I_{Lj}/2 \mathrm{where} j=1,2\end{array}$$

(17)

where i_Lj,max is the maximum value of inductor L_j current, which can be calculated by applying (10) and (15).

Switch S₀ is only installed to transfer the energy of inductor L₂, and its current is constant when it is turned on, as shown in Figure 4. Thus, its current is the average value of the inductor L₂ current, which is expressed in (10). As shown in (9), the voltage across S₀ equals the voltage across capacitor C₂.

The voltage across the inverter side switches is equal to the DC link voltage. The maximum current through switch S_1X is ST current, which is determined by summing two max values of two-inductor currents.

4. Semiconductor Loss Contribution

The power loss of semiconductor devices is classified into two groups: (1) loss of semiconductor devices of an impedance source circuit, and (2) power loss of inverter side switches. MOSFET devices are adopted for switching devices in this analysis.

4.1. Loss of Switching Devices of Impedance-Source Network

As shown in Figure 3, the S₀ switch of the intermediate circuit has one switching action per switching period, T_S. The switching voltage and current of switch S₀ are capacitor C₂ voltage and inductor L₂ current, respectively. When S₀ is gated on, the current across S₀ is I_L2 and the time interval of this state is D₀T_s. Therefore, the power loss of switch S₀ is calculated as:

$$\{\begin{array}{l}{P}_{S0,cond}=r_{ds,on}\times D_0\times I_{L2}\\ P_{S0,sw}=\frac{1}{2}{V}_{C2}\times I_{L2}\times \left(t_{ri}+t_{fu}+t_{ru}+t_{fu}\right)\times f_s\end{array}$$

(18)

where P_S0,cond and P_S0,sw are conduction and switching losses of S₀; t_ri, t_fu, t_ru and t_fu are respectively current rise time, current fall time, voltage rise time, and voltage fall time of MOSFET.

In any switching cycle, diode D₁ has two switching events when the ST state is activated. When diode D₁ is reverse biased, it blocks DC link voltage. When D₁ is forward biased, it transfers inductor L₁ current in non-ST mode two and two inductor currents in non-ST mode one. The conduction loss and reverse recovery loss of diode D₁ are expressed as:

$$\{\begin{array}{l}{P}_{D1,cond}=V_F\times (1-D_{ST})\times I_{L1}+V_F\times D_0\times I_{L2}\\ P_{D1,rr}=2\times V_{PN}\times Q_{rr}\times f_s\end{array}$$

(19)

where P_D1,cond and P_D1,rr are conduction and reverse recovery losses of D₁; V_F and Q_rr are forward voltage and reverse recovery charge of diode, respectively.

Diode D₂ has one switching action per switching cycle when the S₀ switch is turned on. The reverse voltage of diode D₂ is the capacitor C₂ voltage. When diode D₂ is forward biased in ST mode and non-ST mode two, it transfers inductor L₂ current. The power loss of this diode is calculated as follows:

$$\{\begin{array}{l}{P}_{D2,cond}=V_F\times (1-D_0)\times I_{L1}\\ P_{D2,rr}=V_{C2}\times Q_{rr}\times f_s\end{array}$$

(20)

4.2. Loss of Switching Devices of Inverter Side Circuit

Three phase legs of the inverter side circuit have the same operating principle. Therefore, only the S_1A and S_2A switches of the phase A leg are considered in this analysis.

From π/6 to 5π/6 of output voltage, the reference signal $v_A^{*}$ of phase A is the maximum. Thus, the ST state is inserted into this phase. This insertion makes S_2A switch at two-inductor currents. Similar to switch S_2A, the switching current of switch S_1A is the sum of two-inductor currents and phase A load current. From 0 to π/6 and 5π/6 to π, switch S_1A is switched at phase A load current. When switch S_1A is gated on, there is one reverse recovery action generated at the anti-parallel diode of switch S_2A. From π to 7π/6 and 11π/6 to 2π, switch S_2A is switched at phase A load current while there is one switching event of the body-diode of switch S_1A. Switches S_1A and S_2A have no switching action in the time interval from 7π/6 to 11π/6. Both switches S_1A and S_2A block DC link voltage like any conventional two-level VSI. The switching losses of both S_1A and S_2A are expressed as follows:

$$\{\begin{array}{ll}{P}_{S1A,sw}& =\frac{2}{2\pi }{\displaystyle \underset{0}{\overset{\pi /6}{\int }}\frac{1}{2}{V}_{PN}{i}_A(\theta )\left(t_{ri}+t_{fu}+t_{ru}+t_{fu}\right)f_{s}d\theta }\\ & +\frac{1}{2\pi }{\displaystyle \underset{\pi /6}{\overset{5\pi /6}{\int }}\frac{1}{2}{V}_{PN}\left[I_{L1}+I_{L2}+i_A(\theta )\right]\left(t_{ri}+t_{fu}+t_{ru}+t_{fu}\right)f_{s}d\theta }+\frac{2}{2\pi }{\displaystyle \underset{\pi }{\overset{7\pi /6}{\int }}{V}_{PN}{Q}_{rr}{f}_{s}d\theta }\\ P_{S2A,sw}& =\frac{2}{2\pi }{\displaystyle \underset{0}{\overset{\pi /6}{\int }}{V}_{PN}{Q}_{rr}{f}_{s}d\theta }+\frac{1}{2\pi }{\displaystyle \underset{\pi /6}{\overset{5\pi /6}{\int }}\frac{1}{2}{V}_{PN}\left(I_{L1}+I_{L2}\right)\left(t_{ri}+t_{fu}+t_{ru}+t_{fu}\right)f_{s}d\theta }\\ & +\frac{2}{2\pi }{\displaystyle \underset{\pi }{\overset{7\pi /6}{\int }}\frac{1}{2}{V}_{PN}\left|i_A(\theta )\right|\left(t_{ri}+t_{fu}+t_{ru}+t_{fu}\right)f_{s}d\theta }\end{array}$$

(21)

where P_S1A,sw and P_S2A,sw are switching losses of switches S_1A and S_2A, respectively.

The conduction losses of switches S_1A and S_2A are expressed as:

$$\{\begin{array}{ll}{P}_{S1A,cond}& =\frac{1}{2\pi }{\displaystyle \underset{5\pi /6}{\overset{13\pi /6}{\int }}{r}_{ds,on}{i}_A^2(\theta )v_a^{*}(\theta )(d\theta }\\ & +\frac{1}{2\pi }{\displaystyle \underset{\pi /6}{\overset{5\pi /6}{\int }}{r}_{ds,on}\left\{i_A^2(\theta )v_a^{*}(\theta )+{\left[i_A(\theta )+I_{L1}+I_{L2}\right]}^2{D}_{ST}\right\}d\theta }\\ P_{S2A,cond}& =\frac{1}{2\pi }{\displaystyle \underset{5\pi /6}{\overset{13\pi /6}{\int }}{r}_{ds,on}{i}_A^2(\theta )\left[1-v_a^{*}(\theta )\right](d\theta }\\ & +\frac{1}{2\pi }{\displaystyle \underset{\pi /6}{\overset{5\pi /6}{\int }}{r}_{ds,on}\left\{i_A^2(\theta )\left[1-v_a^{*}(\theta )\right]+{\left[I_{L1}+I_{L2}\right]}^2{D}_{ST}\right\}d\theta }\end{array}$$

(22)

where P_S1A,cond and P_S2A,cond are conduction losses of switches S_1A and S_2A, respectively.

4.3. Power Loss Comparison between Proposed Topology and Conventional DqZSI

The proposed ADC-qZSI is compared to conventional DqZSI in [8] for semiconductor loss. In this comparison, two inverters are designed to operate under 200 V DC input source, 220 V_RMS/380 V_RMS AC output voltage, and 1.5 kW. The semiconductor components and operating parameters are listed in

Table 2. Semiconductor and operating parameters.

Component	Proposed ADC-qZSI	Conventional DqZSI [8]
Switch S0	IMZA65R030M1H (650 V, rds,on = 30 mΩ)	NA
Switches S1X and S2X	IMZ120R030M1H (1200 V, rds,on = 30 mΩ)	C2M0080170P (1700 V, rds,on = 80 mΩ)
Diode D1	GD2X30MPS12D (1200 V, VF = 1.5 V)	GB50MPS17 (1700 V, VF = 1.5 V)
Diode D2	AIDW40S65C5 (650 V, VF = 1.5 V)	NA
Modulation index, M	0.86	0.61
ST duty ratio, DST	0.14	0.39
Extra duty ratio, D0	0.74	NA
Switching frequency, fs	50 kHz	50 kHz

. With these parameters, the proposed topology needs 620-V DC-link voltage to generate 220 V_RMS AC output voltage. While it is 910 V DC-link voltage for conventional DqZSI. As a result, the proposed topology used 1200 V switching devices instead of 1700 V devices such as the conventional topology in [8]. In the proposed configuration, the voltage stresses of switch S₀ and diode D₂ are capacitor C₂ voltage, which is 340 V. Thus, switch S₀ and diode D₂ are 650 V switching devices. The result of the power loss comparison is shown in Figure 5. The proposed ADC-qZSI introduces two more power losses at S₀ and diode D₂ compared to the traditional DqZSI. However, the other semiconductor losses of the proposed topology are smaller than DqZSI because of having a smaller DC link voltage. As a result, the total semiconductor loss of introduced ADC-qZSI is smaller than the conventional DqZSI.

5. Comparison Study

The main contributions of the proposed configuration can be listed as (1) using a small number of passive components, (2) high voltage gain, and (3) low component voltage rating, which are verified by comparing to some previous single-stage inverters such as conventional DqZSI in [8], SL-qZSI in [18], rSL-qZSI in [19], ASC-EqZSI in [20], ASC/SL-qZSI in [21], and HG-qSBI in [22]. The comparison study concludes three sub-sections, which are (1) the number of components comparison; (2) boost factor and voltage gain comparison, and (3) component voltage stress comparison. Note that the proposed ADC-qZSI has two coefficients (D₀ and D_ST) to control the boost factor. Their relationship is shown in (6) and (8). Thus, in this comparison study, both maximum boost and minimum boost control are considered. In detail, the maximum boost control can be obtained by setting the value $\sqrt{3}(1-D_{ST})/2$ for D₀, and the minimum boost control can be achieved by setting the zero value for D₀. It is worth noting that the ST duty ratios, D_ST, of these works are set as (1 − M).

5.1. Number of Components

The overall comparison between these configurations has been summarized in

Table 3. Overall Comparison Between Proposed Inverter and Other Single-Stage Inverters.

	DqZSI [8]	SL-qZSI [18]	rSL-qZSI [19]	ASC-EqZSI [20]	ASC/SL-qZSI [21]	HG-qSBI [22]	Proposed ADC-qZSI
Boost factor, B	$\frac{1}{1-2D_{ST}}$	$\frac{1+D_{ST}}{1-2D_{ST}-D_{ST}^2}$	$\frac{1+D_{ST}}{1-3D_{ST}}$	$\frac{1}{1-3D_{ST}+D_{ST}^2}$	$\frac{1+D_{ST}}{1-3D_{ST}}$	$\frac{1}{1-4D_{ST}+D_{ST}^2}$	$\frac{1-D_0}{1-D_0-2D_{ST}+D_0{D}_{ST}}$
Voltage gain, G	1.15·MB	1.15·MB	1.15·MB	1.15·MB	1.15·MB	1.15·MB	1.15·MB
Capacitor voltage stress, Vc/Vdc	$D_{ST}B,C_1\&C_2$	$\begin{array}{l}\frac{2D_{ST}}{1+D_{ST}}B,C_1\\ \frac{1-D_{ST}}{1+D_{ST}}B,C_2\end{array}$	$\begin{array}{l}\frac{2D_{ST}}{1+D_{ST}}B,C_1\\ \frac{1-D_{ST}}{1+D_{ST}}B,C_2\end{array}$	$\begin{array}{l}(1-D_{ST})B,C_1\\ B,C_2\end{array}$	$B$	$\begin{array}{l}{D}_{ST}B,C_1\\ (1-D_{ST})B,C_2\end{array}$	$\begin{array}{l}{D}_{ST}B,C_1\\ \frac{D_{ST}}{1-D_0}B,C_2\end{array}$
Diode voltage stress, VD/Vdc	$B$	$\begin{array}{l}B,D_{in}\\ \frac{1-D_{ST}}{1+D_{ST}}B,D_1\\ \frac{D_{ST}}{1+D_{ST}}B,D_{2÷3}\end{array}$	$\begin{array}{l}B,D_{in}\\ \frac{D_{ST}}{1+D_{ST}}B,D_{1÷4}\\ \frac{1-D_{ST}}{1+D_{ST}}B,D_{5÷6}\end{array}$	$\begin{array}{l}B,D_0\\ (2-D_{ST})B,D_1\end{array}$	$\begin{array}{l}B,D_{in}\\ \frac{D_{ST}}{1+D_{ST}}B,D_{1÷2}\\ \frac{2-2D_{ST}}{1+D_{ST}}B,D_3\end{array}$	$\begin{array}{l}B,D_1\\ (1-D_{ST})B,D_2\end{array}$	$\begin{array}{l}B,D_1\\ \frac{D_{ST}}{1-D_0}B,D_2\end{array}$
Switch voltage stress, VS/Vdc	NA	NA	NA	$(1-D_{ST})B$	$B$	$(1-D_{ST})B$	$D_{ST}/(1-D_0)B$
Inductors	2	3	4	2	2	2	2
Capacitors	2	2	2	2	1	2	2
Diodes	1	4	7	2	5	2	2
Impedance Switches	0	NA	NA	1	1	1	1
Common ground	Yes	Yes	Yes	Yes	No	No	Yes

. Among these topologies, the conventional DqZSI topology in [8] uses the smallest number of elements compared to others. However, it makes conventional topology have lower voltage gain and higher voltage stress compared to others, which is detailed in the next section. The SL-qZSI in [18] and rSL-qZSI in [19] do not use active switching devices in impedance source networks. Instead, they use more inductors and diodes to enhance voltage gain. In detail, the SL-qZSI in [18] uses one more inductor and two more diodes, while the rSL-qZSI in [19] uses two-more inductors and five more diodes compared to the proposed ADC-qZSI. The use of active switches in intermediate network topologies like [20,21,22] and the proposed topology helps save a large number of passive components like inductors and capacitors. The work in [21] uses two fewer inductors, one fewer capacitor, and two fewer diodes than in [19]. However, it still utilizes three more diodes than the proposed ADC-qZSI. Moreover, the use of only one capacitor [21] causes high capacitor voltage stress, which is detailed in the next part of this section. The proposed topology has the same number of components as ASC-EqZSI in [20] and HG-qSBI in [22], which are two inductors, two capacitors, two diodes, and only one active semiconductor device in the impedance-source network. Note that the inverter sides of these configurations use a conventional two-level inverter, thus, the number of elements for the inverter side circuit is the same for all these topologies.

5.2. Boost Factor and Voltage Gain

The boost factor and voltage gain of these topologies are shown in Figure 6. According to some studies [18,19,20,21,22], the HG-qSBI in [22] has the largest boost factor, as presented in Figure 6a, thus it also has the largest voltage gain. When the minimum boost control is applied, the boost factor of the proposed inverter is 1/(1 − 2D_ST), which is equal to conventional qZSI in [8]. As a result, the proposed topology produces the smallest boost factor and voltage gain compared to the works in [18,19,20,21,22]. However, the boost factor of the proposed ADC-qZSI can be extended by increasing the duty ratio D₀ of switch S₀. When the duty ratio D₀ obtains a value of 0.5, the boost factor and voltage gain of the proposed method are equal to HG-qSBI in [22] and also higher than the works in [18,19,20,21]. When the maximum value of D₀, $\sqrt{3}(1-D_{ST})/2$, is achieved, the boost factor and voltage gain of the proposed ADC-qZSI are the largest, which brings a benefit to the low component voltage rating, as follows.

5.3. Component Voltage Rating

Some investigations on capacitor, diode and switch voltage stresses have been conducted, as illustrated in Figure 7. Note that there are a lot of diodes in these topologies, which have unequal voltage stresses, as shown in Table 3. Therefore, simply, the maximum values of diode voltage stresses are only considered in this comparison study. Figure 7a,b show voltage stress comparisons for capacitors C₁ and C₂. The max boost control of the proposed ADC-qZSI produces the smallest capacitors C₁ and C₂ voltage rating compared to others, as shown in Figure 7a,b. Among these topologies, the impedance-source switch voltage stress is equal to the capacitor voltage. Thus, having a lower capacitor voltage rating causes a lower switch voltage rating, as shown in Figure 7c.

Having a higher voltage gain makes the proposed ADC-qZSI able to use a higher modulation index compared to other topologies, as shown in Figure 6b. On the other hand, the boost factor can be calculated as follows:

$$B=G/(1.15\times M)$$

(23)

From (23), it can be seen that the proposed topology with the introduced DPWM method uses a higher modulation index, which leads to requiring a lower boost factor. The max value of diode voltage stress equals the boost factor, as shown in Table 3. Moreover, it is clear that the inverter side switch voltage rating is also equal to the boost factor. As a result, the proposed ADC-qZSI has the lowest diode and inverter side switch voltage stresses among these configurations, as presented in Figure 7d.

6. Simulation and Experimental Verifications

6.1. Simulation Results

The boost operation of the proposed ADC-qZSI has been tested in this section. Both 56 Ω resistive load and 45 Ω–100 mH resistive–inductive load are installed at the output of the inverter for testing. The parameters used in the simulation are listed in

Table 4. Simulation and experimental parameters.

Parameter/Components		Values
Input voltage	Vdc	150 V–400 V
AC output voltage	Vx,RMS	110 VRMS
Output frequency	f0	50 Hz
Switching frequency	fs	10 kHz
Boost inductor	L1, L2	3 mH/20 A
Boost capacitors	C1 and C2	1 mF/400 V
LC filter	Lf and Cf	3 mH and 10 µF

. The inverter is fed by a 150 V DC input voltage which is used to generate 110 V_RMS AC output load voltage. The modulation index M, ST duty ratio D_ST, and extra duty ratio D₀ are 0.81, 0.19, and 0.5, respectively. With these controlling parameters, two capacitor voltages, V_C1 and V_C2 are boosted to 66 V and 132 V for both loads, as shown in Figure 8. As a result, the peak value of DC-link voltage V_PN is 350V, approximately. For resistive load, two inductor currents, I_L1 and I_L2, are continuous, and their values are 4.85 A and 9.57 A, respectively. While they are 3.96 A and 7.83 A because the real power of 45 Ω–100 mH resistive-inductive load is smaller than 56 Ω resistive load for the same 110 V_RMS AC output voltage. The output line-to-line voltage has three voltage levels, which vary from −V_PN to +V_PN. The output load current amplitudes of these loads are the same which is 2.06 A_RMS. However, the current of the resistive-inductive load is a 30-degree lag compared to the current othe f resistive load.

6.2. Experimental Results

A laboratory prototype based on DSP TMS320F28335 has been built to verify the operation of the proposed inverter, as shown in Figure 9. Module six IGBTs SKMGD123D is utilized for the inverter-side circuit. Impedance source network is based on MOSFET 60R060P7, diode VS-60APF12-M3, 1 mF capacitors, and 3 mH inductors. A 56 Ω three-phase output resistive load is considered to test the proposed inverter, which is fed through the tLC filter (3 mH and 10 µF) to mitigate the high-frequency component of the output voltage. The system parameters are listed in Table 4. The proposed ADC-qZSI is verified under buck and boost modes with the range of input DC voltage from 150 V to 400 V. In both cases, the parameters of the inverter are selected to generate 110 V_rms at the output load voltage, in theory.

Firstly, a 150-volt input source is applied to test the inverter in boost mode. The experimental results for the 150-volt input voltage are shown in Figure 10. The impedance source network is utilized to boost the DC-link voltage, V_PN. In this case, the ST duty ratio D_ST, S₀ duty ratio, D₀ and modulation index, M are set as 0.19, 0.5 and 0.81, respectively. With these parameters, the voltages of two capacitors, V_C1 and V_C2 are boosted to 55 V and 105 V, respectively, as shown in Figure 10a. It results in 310 V of the peak value of DC-link voltage, V_PN, and output line-to-line voltage, V_AB, as shown in Figure 10b. As shown in Figure 10a,b, the input current is discontinuous and has an average value of 4.03 A, whereas the two inductor currents, I_L1 and I_L2, are continuous and have average values of 4.08 A and 8.85 A, respectively. The zoom-in waveforms of two inductor currents, switch S₀ drain-source voltage and DC-link voltage are shown in Figure 10c. It shows that two inductor currents are increased linearly in the ST state, which is represented by the zero value of DC link voltage. When S₀ is turned on, the inductor L₂ current is kept constant. The voltage stress of S₀ is equal to the capacitor C₂ voltage. The output load voltage and current waveforms are sinusoidal because of using an LC filter. The RMS values of output load voltage and current are 104 V_RMS and 1.84 A_RMS.

In buck mode, a 400-volt DC input source is applied to test the inverter, the results are shown in Figure 11. The ST duty ratio D_ST, S₀ duty ratio, D₀ and modulation index, M are set as 0, 0.5 and 0.68, respectively. The input voltage is now high enough to produce 110 V_RMS at output load voltage. Therefore, two capacitor voltages are kept at 0 V, approximately, as illustrated in Figure 11a. The DC link voltage is equal to the input voltage. It also results in a 400-volt peak value of output line-to-line voltage, V_AB, as shown in Figure 11b. The waveforms of two inductor currents, switch S₀ drain-source voltage and DC-link voltage are shown in Figure 11c. The voltage stress of S₀ is 40 V, whereas the average values of two inductor L₁ and L₂ currents are 1.43 A and 1.94 A. The DC link voltage is equal to the input voltage. RMS values of output load voltage and current are 109 V_RMS and 1.92 A_RMS, respectively.

Figure 12 shows the experimental results of the proposed inverter under variation of load in two cases: (1) the three-phase load change from 72 Ω to 40 Ω, and (2) the three-phase load change from 40 Ω to 72 Ω. Both cases cause a small effect on capacitor voltages and output load voltages. It is clear that the 40 Ω load causes higher load and device currents than the 72 Ω load. It results in more device loss for case one than for case two, which reduces capacitor voltages, as shown in Figure 12.

7. Conclusions

This paper proposed a new topology of ADC-qZSI by adding one active switch and one diode into the impedance source network. With these devices, one more operating mode is introduced for the proposed inverter besides the conventional ST and non-ST modes. During this extra mode, one inductor voltage is shorted. As a result, the energy of this inductor is maintained, which helps to increase the boost factor and voltage gain of the inverter compared to previous studies of single-stage inverters. Having higher voltage gain leads to the lower voltage rating of capacitors and switching devices. A DPWM control strategy reducing the number of commutations is presented to control this proposed inverter. Under this PWM method, the ST state insertion does not generate any extra commutations and the total switching commutations of the inverter are equal to conventional two-level VSI. Some comparisons between the proposed inverter and other previous single-stage inverters have been conducted to demonstrate these advantages. The simulation and experimental results have been presented to verify the operation of the proposed inverter. Both buck and boost modes are considered to test the inverter.