Two-Phase Volumetric Expanders: A Review of the State-of-the-Art
Abstract
:1. Introduction
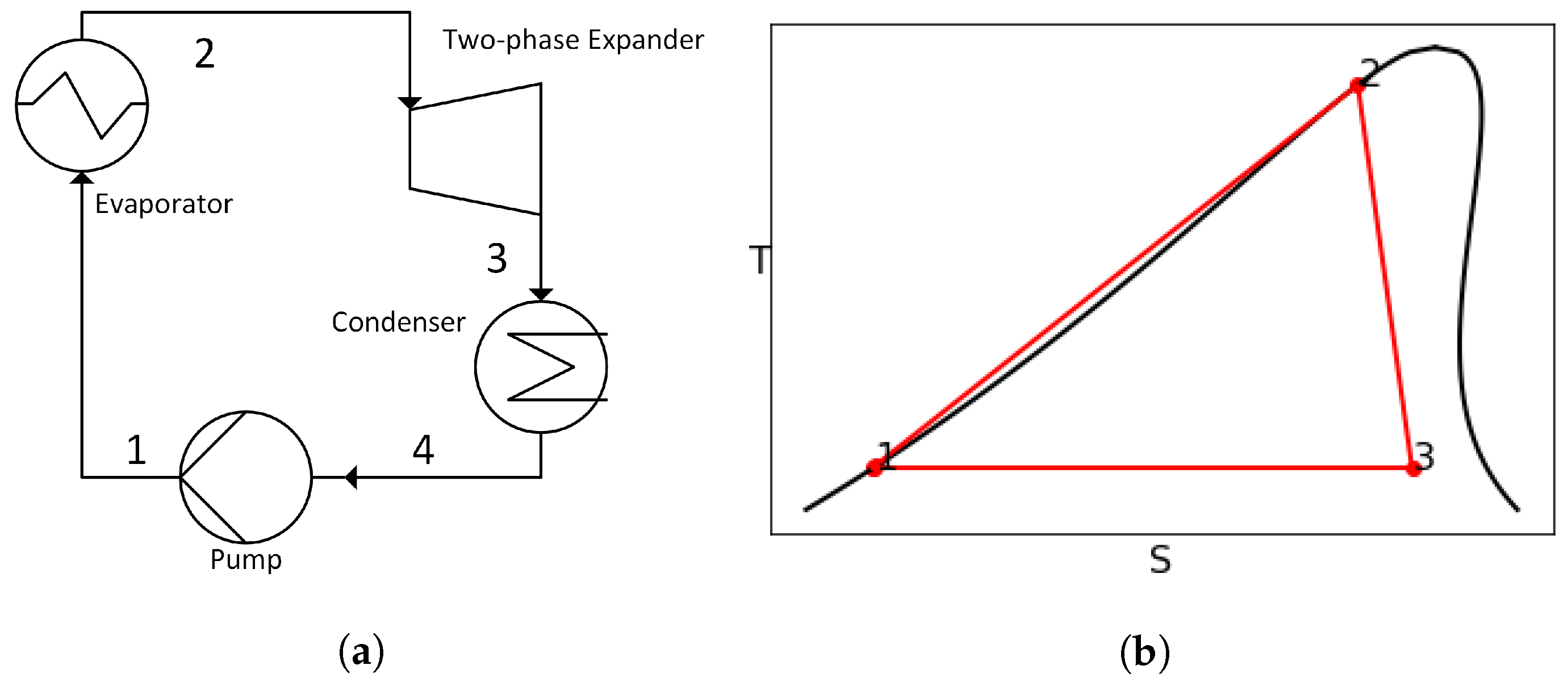
1.1. Two-Phase Expander Applications
1.2. Principles of Flashing
1.3. Expander Types
1.4. Volumetric Expander Types for Two-Phase Expansion
1.5. Positioning of This Review
2. Methods for Modeling Two-Phase Expansion
2.1. Homogeneous Equilibrium Model
2.2. Mixture Model
2.3. Boiling Delay Model
2.4. Homogeneous Relaxation Model
2.5. Conclusions and Comparison
3. Experimental Available Data
3.1. Lysholm Expander
3.2. Static Flash
3.3. Reciprocating Expander
3.4. Conclusions of Two-Phase Experimental Data
4. Modeling of Two-Phase Volumetric Expanders
4.1. Lysholm Expander
4.2. Reciprocating Expander
4.3. Conclusions of Two-Phase Expander Modeling
5. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| BLEVE | Boiling Liquid Expanding Vapor Explosion |
| EOS | Equation of State |
| LNG | Liquefied Natural Gas |
| VPT | Variable Phase Turbine |
| ORC | Organic Rankine Cycle |
| TLC | Trilateral Cycle |
| PEORC | Partial Evaporation Organic Rankine Cycle |
| BVR | Built in Volume Ratio |
| HEM | Homogeneous Equilibrium Model |
| HRM | Homogeneous Relaxation Model |
| WORC | Wet Organic Rankine Cylce |
References
- Cylinder Condensation. J. Am. Soc. Nav. Eng. 1909, 21, 294–297. Available online: https://onlinelibrary.wiley.com/doi/abs/10.1111/j.1559-3584.1909.tb04491.x (accessed on 30 May 2022). [CrossRef]
- Di, J.; Wang, S.S.; Yan, X.J.; Cai, L.X.; Xie, Y.H. Experimental investigation on effect of surface strengthening process and roughness on water droplet erosion behavior in turbomachinery. Tribol. Int. 2020, 153, 106647. [Google Scholar] [CrossRef]
- Eyerer, S.; Dawo, F.; Rieger, F.; Schuster, A.; Aumann, R.; Wieland, C.; Spliethoff, H. Experimental and numerical investigation of direct liquid injection into an ORC twin-screw expander. Energy 2019, 178, 867–878. [Google Scholar] [CrossRef]
- Galoppi, G.; Secchi, R.; Ferrari, L.; Ferrara, G.; Karellas, S.; Fiaschi, D. Radial piston expander as a throttling valve in a heat pump: Focus on the 2-phase expansion. Int. J. Refrig. 2017, 82, 273–282. [Google Scholar] [CrossRef]
- Mahmoud, A.M.; Sherif, S.A.; Lear, W.E. Frictional and internal leakage losses in rotary-vane two-phase refrigerating expanders. J. Energy Resour. Technol. Trans. ASME 2010, 132, 0210071. [Google Scholar] [CrossRef]
- Xia, C.; Zhang, W.; Bu, G.; Wang, Z.; Shu, P. Experimental study on a sliding vane expander in the HFC410A refrigeration system for energy recovery. Appl. Therm. Eng. 2013, 59, 559–567. [Google Scholar] [CrossRef]
- Sumeru, K.; Nasution, H.; Ani, F.N. A review on two-phase ejector as an expansion device in vapor compression refrigeration cycle. Renew. Sustain. Energy Rev. 2012, 16, 4927–4937. [Google Scholar] [CrossRef]
- Ringstad, K.E.; Allouche, Y.; Gullo, P.; Ervik, Å.; Banasiak, K.; Hafner, A. A detailed review on CO2 two-phase ejector flow modeling. Therm. Sci. Eng. Prog. 2020, 20, 100647. [Google Scholar] [CrossRef]
- Panesar, A.S.; Bernagozzi, M. Two-phase expander approach for next generation of heat recovery systems. Int. J. Renew. Energy Dev. 2019, 8, 203–213. [Google Scholar] [CrossRef] [Green Version]
- Lemort, V.; Quoilin, S.; Cuevas, C.; Lebrun, J. Testing and modeling a scroll expander integrated into an Organic Rankine Cycle. Appl. Therm. Eng. 2009, 29, 3094–3102. [Google Scholar] [CrossRef] [Green Version]
- Giuffrida, A. Improving the semi-empirical modelling of a single-screw expander for small organic Rankine cycles. Appl. Energy 2017, 193, 356–368. [Google Scholar] [CrossRef]
- Li, Z.; Lu, Y.; Huang, Y.; Qian, G.; Chen, F.; Yu, X.; Roskilly, A. Comparison study of Trilateral Rankine Cycle, Organic Flash Cycle and basic Organic Rankine Cycle for low grade heat recovery. Energy Procedia 2017, 142, 1441–1447. [Google Scholar] [CrossRef]
- DiPippo, R. Ideal thermal efficiency for geothermal binary plants. Geothermics 2007, 36, 276–285. [Google Scholar] [CrossRef]
- Fischer, J. Comparison of trilateral cycles and organic Rankine cycles. Energy 2011, 36, 6208–6219. [Google Scholar] [CrossRef]
- Hays, L. Demonstration of a Variable Phase Turbine Power System for Low Temperature Geothermal Resources. Energent Corp. 2010, 1–57. [Google Scholar] [CrossRef]
- Lecompte, S.; van den Broek, M.; De Paepe, M. Thermodynamic analysis of the partially evaporating trilateral cycle. In Proceedings of the 2nd International Seminar on ORC Power Systems, Proceedings, Rotterdam, The Netherlands, 7–8 October 2013; p. 4. [Google Scholar]
- Lecompte, S.; Huisseune, H.; van den Broek, M.; De Paepe, M. Methodical thermodynamic analysis and regression models of organic Rankine cycle architectures for waste heat recovery. Energy 2015, 87, 60–76. [Google Scholar] [CrossRef]
- Friedel, L.; Purpst, S. Phase distribution in vessels during depressurisation. Int. J. Heat Fluid Flow 1984, 5, 229–234. [Google Scholar] [CrossRef]
- Wu, W.; Wang, Q.; Zhang, Z.; Wu, Z.; Yang, X.; Xu, L. Influence of evaporating rate on two-phase expansion in the piston expander with cyclone separator. Therm. Sci. 2020, 24, 2077–2088. [Google Scholar] [CrossRef] [Green Version]
- Saury, D.; Harmand, S.; Siroux, M. Experimental study of flash evaporation of a water film. Int. J. Heat Mass Transf. 2022, 45, 3447–3457. [Google Scholar] [CrossRef]
- Wang, C.; Xu, R.; Chen, X.; Jiang, P.; Liu, B. Study on water flash evaporation under reduced pressure. Int. J. Heat Mass Transf. 2019, 131, 31–40. [Google Scholar] [CrossRef]
- Lorenzo, M.D.; Modelling, M.D.L.; Lorenzo, M.D.; Lafon, P. Modelling and Numerical Simulation of Metastable Two-Phase Flows; To Cite This Version: HAL Id: Tel-01889103 Modélisation et Simulation Numérique des Ecoulements Diphasiques Métastables; HAL Open Science: Lyon, France, 2018. [Google Scholar]
- Debenedetti, P.G. Metastable Liquids: Concepts and Principles; Princeton University Press: Princeton, NJ, USA, 1997; Volume 1, pp. 1–400. [Google Scholar]
- Polanco, G.; Holdø, A.E.; Munday, G. General review of flashing jet studies. J. Hazard. Mater. 2010, 173, 2–18. [Google Scholar] [CrossRef] [PubMed]
- Pinhasi, G.; Ullmann, A.; Dayan, A.; Israel, T.A. Modeling of Flashing Two-Phase Flow Gad A. Pinhasi Department of Chemical Engineering and Biotechnology. Rev. Chem. Eng. 2005, 21, 133–264. [Google Scholar] [CrossRef]
- Liao, Y.; Lucas, D. Computational modelling of flash boiling flows: A literature survey. Int. J. Heat Mass Transf. 2017, 111, 246–265. [Google Scholar] [CrossRef]
- Balje´, O.E. A Study on Design Criteria and Matching of Turbomachines: Part A—Similarity Relations and Design Criteria of Turbines. J. Eng. Power 1962, 84, 83–102. [Google Scholar] [CrossRef]
- Francesconi, M.; Dori, E.; Antonelli, M. Analysis of Balje diagrams for a Wankel expander prototype. Appl. Energy 2019, 238, 775–785. [Google Scholar] [CrossRef]
- Narasimhan, A.K.; Wickramaratne, C.; Kamal, R.; Goswami, D.Y.; Singh, P. Mapping scroll expander performance for organic working fluids using dimensionless parameters in Ns-Ds diagram. Energy 2019, 182, 739–752. [Google Scholar] [CrossRef]
- Dumont, O.; Dickes, R.; Lemort, V. Experimental investigation of four volumetric expanders. Energy Procedia 2017, 129, 859–866. [Google Scholar] [CrossRef]
- Imran, M.; Usman, M.; Park, B.S.; Lee, D.H. Volumetric expanders for low grade heat and waste heat recovery applications. Renew. Sustain. Energy Rev. 2016, 57, 1090–1109. [Google Scholar] [CrossRef]
- Taniguchi, H.; Kudo, K.; Giedt, W.H.; Park, I.; Kumazawa, S. Analytical and Experimental Investigation of Two-Phase Flow Screw Expanders for Power Generation. J. Eng. Gas Turbines Power 1988, 110, 628–635. [Google Scholar] [CrossRef]
- Smith, I.K.; Stošić, N.; Aldis, C.A. Development of the trilateral flash cycle system. Part 3: The design of high-efficiency two-phase screw expanders. Proc. Inst. Mech. Eng. Part A J. Power Energy 1996, 210, 75–92. [Google Scholar] [CrossRef]
- Vasuthevan, H.; Brümmer, A. Thermodynamic Modeling of Screw Expander in a Trilateral Flash Cycle. In Proceedings of the International Compressor Engineering, Refrigeration and Air Conditioning, and High Performance Buildings Conferences, Virtual Conference, 23–28 May 2016; pp. 1–10. [Google Scholar]
- Ohman, H.; Lundqvist, P. Srcew expanders in ORC applications, review and a new perspective. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015. [Google Scholar]
- Xia, G.D.; Zhang, Y.Q.; Wu, Y.T.; Ma, C.F.; Ji, W.N.; Liu, S.W.; Guo, H. Experimental study on the performance of single-screw expander with different inlet vapor dryness. Appl. Therm. Eng. 2015, 87, 34–40. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, H.; Wang, F.; Xia, G.; Li, Z.; Zhu, C.; Zhang, H. Numerical investigation of flow behavior and film thickness in the single screw expander. Int. J. Mech. Sci. 2021, 190, 106047. [Google Scholar] [CrossRef]
- Kanno, H.; Shikazono, N. Experimental and modeling study on adiabatic two-phase expansion in a cylinder. Int. J. Heat Mass Transf. 2015, 86, 755–763. [Google Scholar] [CrossRef] [Green Version]
- Zhang, D.; Chong, D.; Yan, J.; Zhang, Y. Study on steam-carrying effect in static flash evaporation. Int. J. Heat Mass Transf. 2012, 55, 4487–4497. [Google Scholar] [CrossRef]
- Spiegler, K.; El-Sayed, Y. The energetics of desalination processes. Desalination 2001, 134, 109–128. [Google Scholar] [CrossRef]
- Mayinger, F. Two-Phase Flow Phenomena with Depressurization-Consequences for the Design and Layout of Safety and Pressure Relief Valves Phgnomene zweiphasiger Striimung bei Druckentlastung-Folgerungen fiir Konstruktion und Auslegung von Sicherheits-und Druckentlast. Chem. Eng. Process. Process. Intensif. 1988, 23, 1–11. [Google Scholar] [CrossRef]
- Downar-Zapolski, P.; Bilickp, Z.; Bolle, L.; Franco, J. The Non-equilibrium relaxation model for one-dimensional flashing liquid flow. Int. J. Multiph. Flow 1996, 22, 473–483. [Google Scholar] [CrossRef]
- Öhman, H.; Lundqvist, P. Experimental investigation of a Lysholm Turbine operating with superheated, saturated and 2-phase inlet conditions. Appl. Therm. Eng. 2013, 50, 1211–1218. [Google Scholar] [CrossRef]
- Bianchi, G.; Kennedy, S.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Two-phase chamber modeling of a twin-screw expander for Trilateral Flash Cycle applications. Energy Procedia 2017, 129, 347–354. [Google Scholar] [CrossRef]
- Bianchi, G.; Kennedy, S.; Zaher, O.; Tassou, S.A.; Miller, J.; Jouhara, H. Numerical modeling of a two-phase twin-screw expander for Trilateral Flash Cycle applications. Int. J. Refrig. 2018, 88, 248–259. [Google Scholar] [CrossRef]
- Smith, I.K. Development of the trilateral flash cycle system: Part 1: Fundamental considerations. Proc. Inst. Mech. Eng. Part A J. Power Energy 1993, 207, 179–194. [Google Scholar] [CrossRef]
- Kanno, H.; Shikazono, N. Modeling study on two-phase adiabatic expansion in a reciprocating expander. Int. J. Heat Mass Transf. 2017, 104, 142–148. [Google Scholar] [CrossRef] [Green Version]
- Kanno, H.; Shikazono, N. Experimental study on two-phase adiabatic expansion in a reciprocating expander with intake and exhaust processes. Int. J. Heat Mass Transf. 2016, 102, 1004–1011. [Google Scholar] [CrossRef] [Green Version]
- Kanno, H.; Hasegawa, Y.; Hayase, I.; Shikazono, N. Experimental Study on Adiabatic Two-Phase Expansion in A Cylinder for trilateral cycle. In Proceedings of the 3rd International Seminar on ORC Power Systems, Brussels, Belgium, 12–14 October 2015. [Google Scholar]
- White, M.T. Investigating the wet-to-dry expansion of organic fluids for power generation. Int. J. Heat Mass Transf. 2022, 192, 122921. [Google Scholar] [CrossRef]
- Banaszkiewicz, M.; Kardaś, D. Numerical calculations of the Moby Dick experiment by means of unsteady relaxation model. J. Theor. Appl. Mech. 1997, 35, 211–232. [Google Scholar]
- Bilicki, Z.; Kwidzilqski, R.; Ali Mohammade, S. Evaluation of the relaxation time of heat and mass exchange in the liquid-vapour bubble flow. Int. J. Heat Mass Transf. 1996, 39, 753–759. [Google Scholar] [CrossRef]
- Wang, Q.; Huang, H.; Xu, L.; Yang, X.; He, Z.; Wu, W. Analysis of the thermodynamic disequilibrium loss of the two-phase expansion process and its influence on the performance of a reciprocating expander. In Proceedings of the IOP Conference Series: Materials Science and Engineering, London, UK, 9–11 September 2019; Institute of Physics Publishing: London, UK, 2019; Volume 604. [Google Scholar] [CrossRef] [Green Version]
- Wang, Q.; Wu, W.; He, Z.; Ziviani, D. Analysis of the intake process and its influence on the performance of a two-phase reciprocating expander. Appl. Therm. Eng. 2019, 160, 113943. [Google Scholar] [CrossRef]
- Lecompte, S.; Van Den Broek, M.; De Paepe, M. Design of an Optical-access Expansion Chamber for Two-phase Expansion. Int. J. Heat Mass Transf. 2012, 86, 755–763. [Google Scholar]
- Lecompte, S.; Van Den Broek, M.; De Paepe, M. Initial Design of an Optical-Access Piston Expansion Chamber for Wet-Expansion. Energy Procedia 2017, 129, 307–314. [Google Scholar] [CrossRef] [Green Version]
- van Heule, X.; Skiadopoulos, A.; Manolakos, D.; De Paepe, M.; Lecompte, S. Modelling and design of a two-phase reciprocating expander for integration in a trilateral flash cycle. In Proceedings of the 6th International Seminar on ORC Power Systems, Virtual Conference, 11–13 October 2021; Technical University of Munich: Munich, Germany, 2021. [Google Scholar]
- Delayed Equilibrium Model (DEM) of Flashing Choked Flows Relevant to LOCA and Implementation in System Codes, Thermal Hydraulics. Int. Conf. Nucl. Eng. 2014, 2B, V02BT09A040. Available online: https://www.researchgate.net/publication/263652479_Delayed_Equilibrium_Model_DEM_of_Flashing_Choked_Flows_Relevant_to_LOCA_and_Implementation_in_System_Codes (accessed on 30 May 2022). [CrossRef]
- Weiss, H.; Steidel, R.; Lundberg, A. Performance Test of a Lysholm Engine. Report. 3 July 1975. Available online: https://digital.library.unt.edu/ark:/67531/metadc1061143/ (accessed on 30 May 2022).
- Steidel, R.F., Jr.; Weiss, H.; Flower, J.E. Performance Characteristics of the Lysholm Engine as Tested for Geothermal Power Applications in the Imperial Valley. J. Eng. Power 1982, 104, 231–240. [Google Scholar] [CrossRef]
- McKay, R. Helical Screw Expander Evaluation Project; Final Report; Jet Propulsion Laboratory, US Department of Energy: La Cañada Flintridge, CA, USA, 1982. [Google Scholar]
- Smith, I.K.; Stosic, N.; Aldis, C.A. Lysholm machines as two-phase expanders. In Proceedings of the International Compressor Engineering Conference, West Lafayette, IN, USA, 19–22 July 1994; Purdue University: West Lafayette, IN, USA, 1994. [Google Scholar]
- Merigoux, J.M.; Pocard, P. Solar Power Units with Screw Expanders; Pergamon Press Inc.: Oxford, UK, 1980; Volume 3, pp. 1293–1317. [Google Scholar]
- Miyatake, O.; Murakami, K.; Kawata, Y.; Fujii, T. Fundamental experiments with flash evaporation. Heat Transf.-Jpn. Res 1973, 2, 89–100. [Google Scholar]
- Zhang, D.; Yan, J.; Liu, Y.; Zhao, B. Preliminary exergy analysis of static flash of pure water. Int. J. Heat Mass Transf. 2015, 86, 377–387. [Google Scholar] [CrossRef]
- Schweizer, F.; Fürst, M.; Wachtmeister, G. Modeling and Validation of a Two-Phase Flow Valve for Expanders in Waste Heat Recovery. J. Therm. Sci. Eng. Appl. 2021, 13, 031026. [Google Scholar] [CrossRef]
- Bianchi, G.; Marchionni, M.; Miller, J.; Tassou, S.A. Modelling and off-design performance optimisation of a trilateral flash cycle system using two-phase twin-screw expanders with variable built-in volume ratio. Appl. Therm. Eng. 2020, 179, 115671. [Google Scholar] [CrossRef]
- Vasuthevan, H.; Brümmer, A. Theoretical investigation of flash vaporisation in a screw expander You may also like Theoretical investigation of flash vaporisation in a screw expander. IOP Conf. Ser. Mater. Sci. Eng. 2017, 232, 012077. [Google Scholar] [CrossRef]
- Steffen, M.; Löffler, M.; Schaber, K. Efficiency of a new Triangle Cycle with flash evaporation in a piston engine. Energy 2013, 57, 295–307. [Google Scholar] [CrossRef]
| Working Fluid | Efficieny | Power | Vapor Quality | |
|---|---|---|---|---|
| [59] (1975) | Water | 49–55% | 16–30 kW | 0.12–0.34 |
| [60] (1982) | Water | 15–53% | 1–60 kW | 0.08–0.27 |
| [61] (1982) | Brine | 45% | 1 MW | 0–0.99 |
| [46] (1993) | R113 | over 70% | 40 kW | - |
| [32] (1988) | R12 | 30–60% | 10 kW | - |
| [43] (2013) | R134a | 73–92% | 50 kW | 0.7–1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
van Heule, X.; De Paepe, M.; Lecompte, S. Two-Phase Volumetric Expanders: A Review of the State-of-the-Art. Energies 2022, 15, 4991. https://doi.org/10.3390/en15144991
van Heule X, De Paepe M, Lecompte S. Two-Phase Volumetric Expanders: A Review of the State-of-the-Art. Energies. 2022; 15(14):4991. https://doi.org/10.3390/en15144991
Chicago/Turabian Stylevan Heule, Xander, Michel De Paepe, and Steven Lecompte. 2022. "Two-Phase Volumetric Expanders: A Review of the State-of-the-Art" Energies 15, no. 14: 4991. https://doi.org/10.3390/en15144991
APA Stylevan Heule, X., De Paepe, M., & Lecompte, S. (2022). Two-Phase Volumetric Expanders: A Review of the State-of-the-Art. Energies, 15(14), 4991. https://doi.org/10.3390/en15144991






