Study on a Two-Dimensional Supersonic Inlet with Inner Profile Adjustment
Abstract
:1. Introduction
2. Inlet Model
2.1. Fixed-Geometry Inlet Scheme
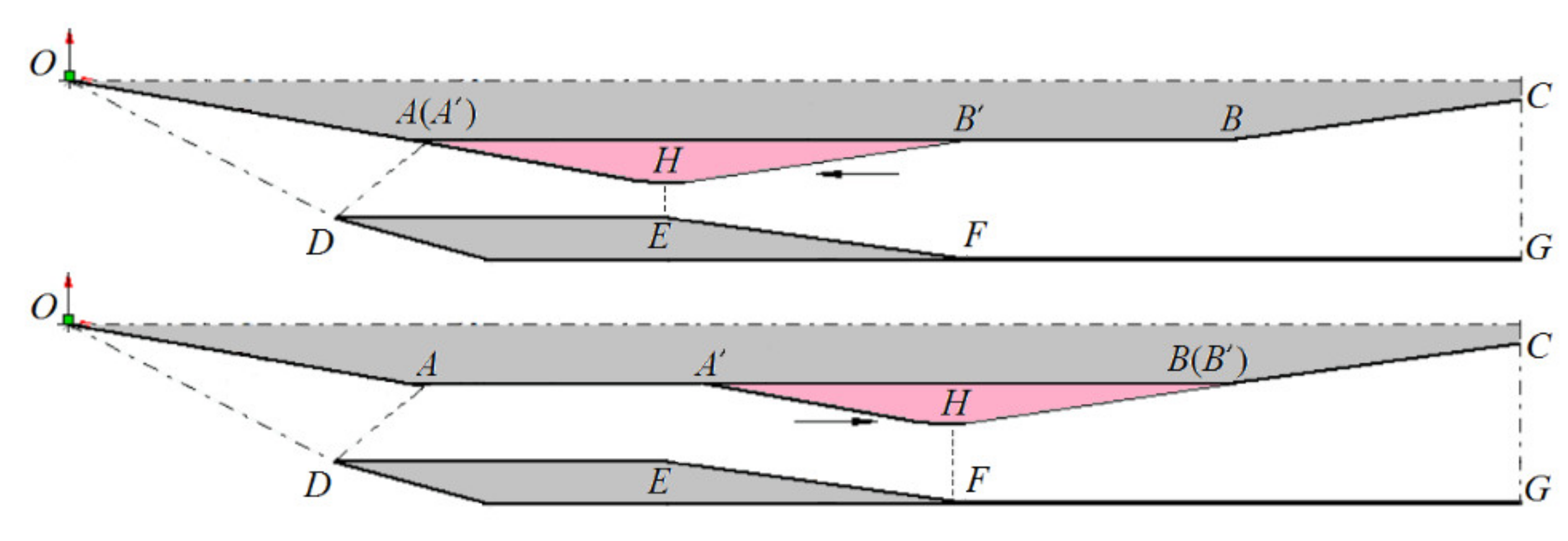
2.2. Adjustable Inlet Scheme
2.3. Design Parameters
3. Theoretical Analysis and Numerical Method
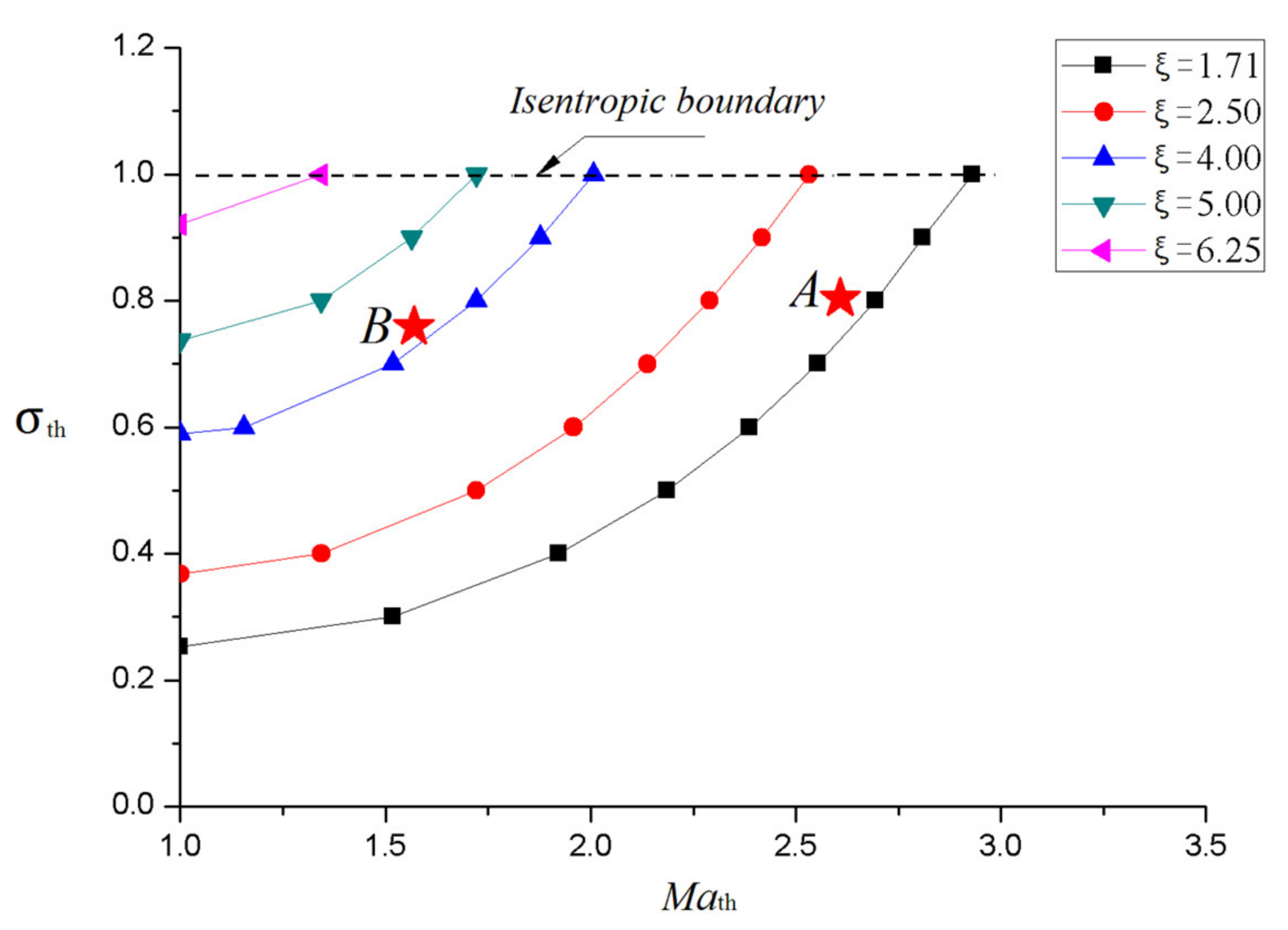
3.1. Resisting Back Pressure Ability
3.2. Total Pressure Recovery
3.3. Numerical Method and Boundary Conditions
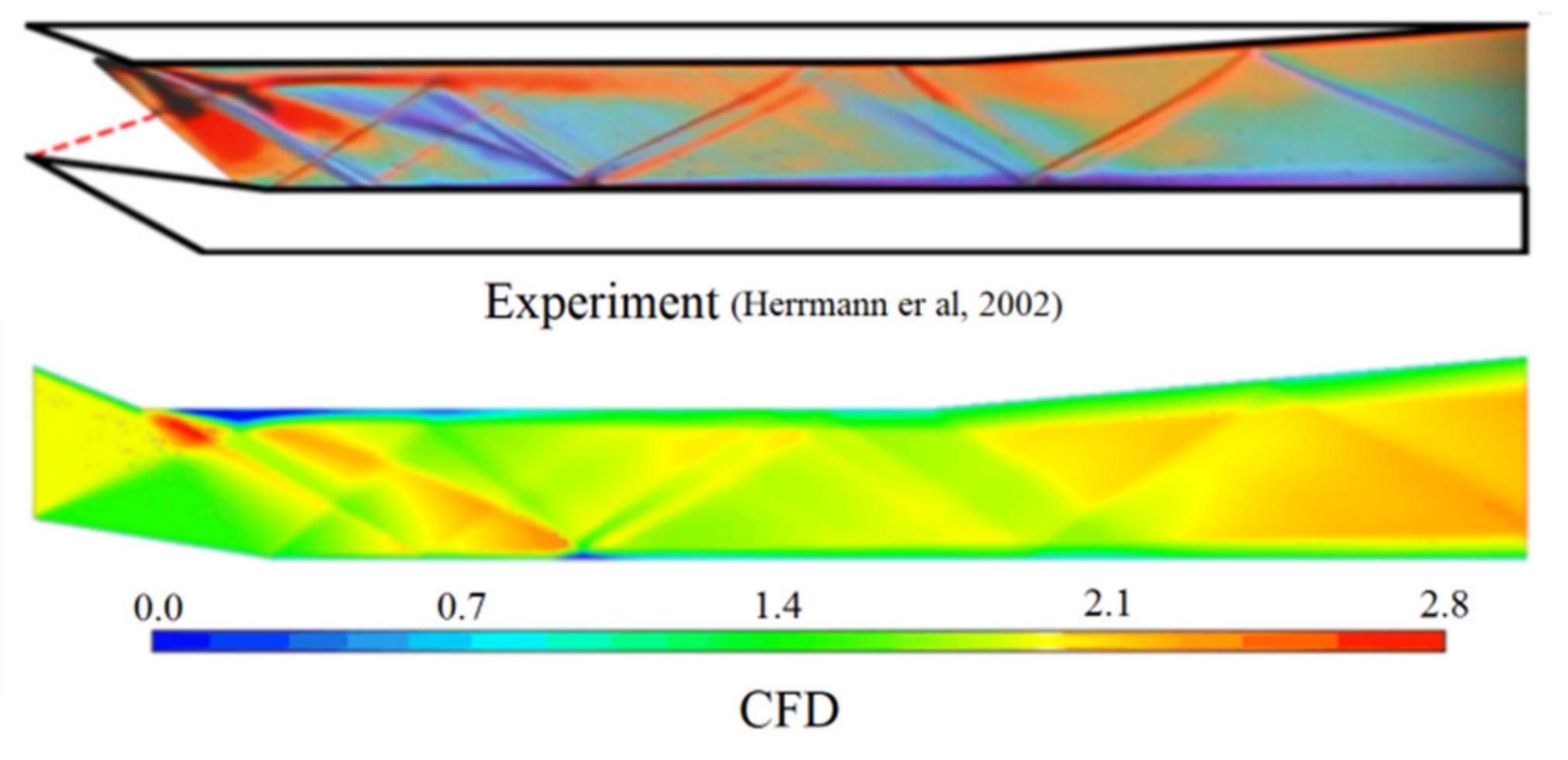
3.4. Verification of the Numerical Methods
4. Inlet Flow Field and Performance Research
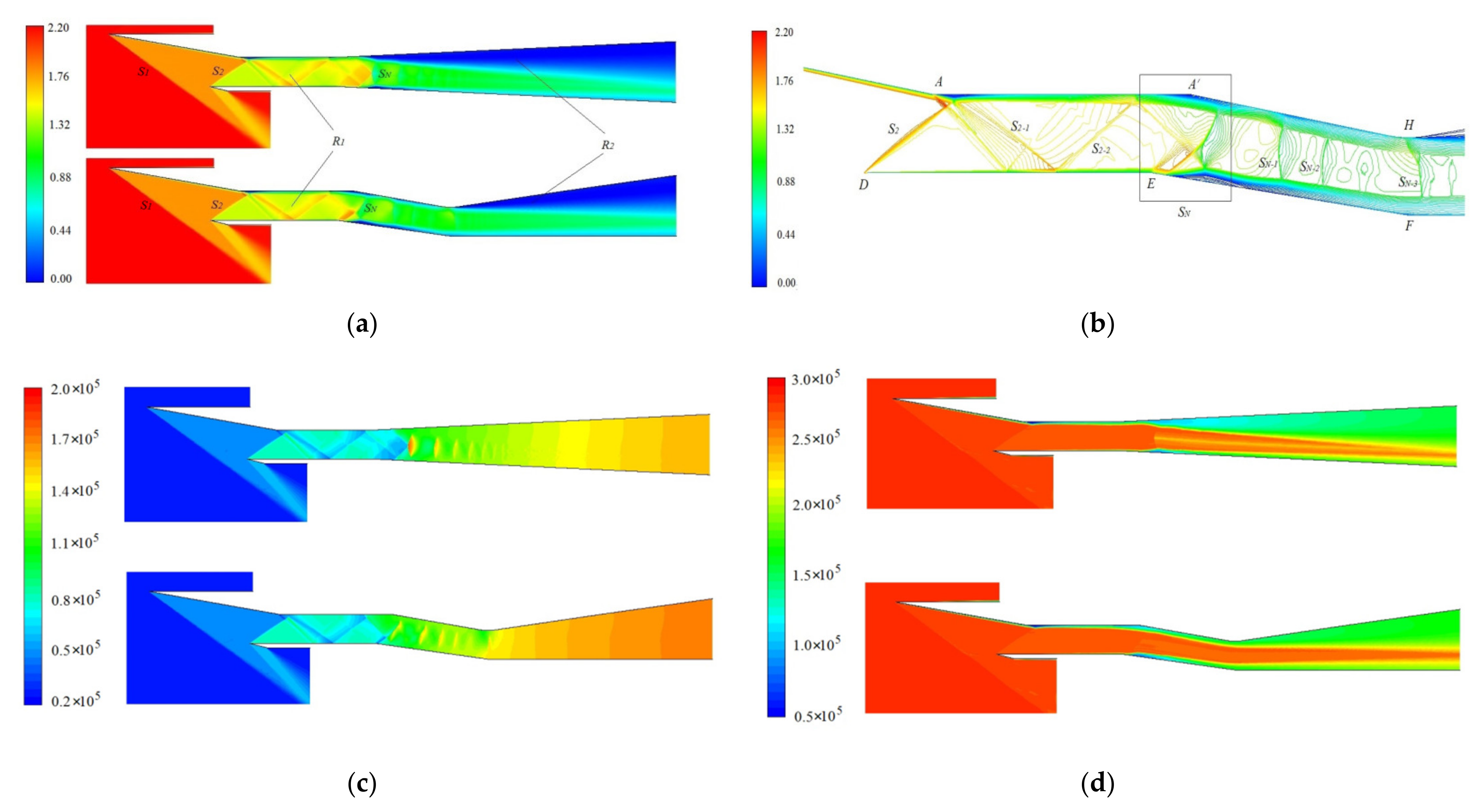
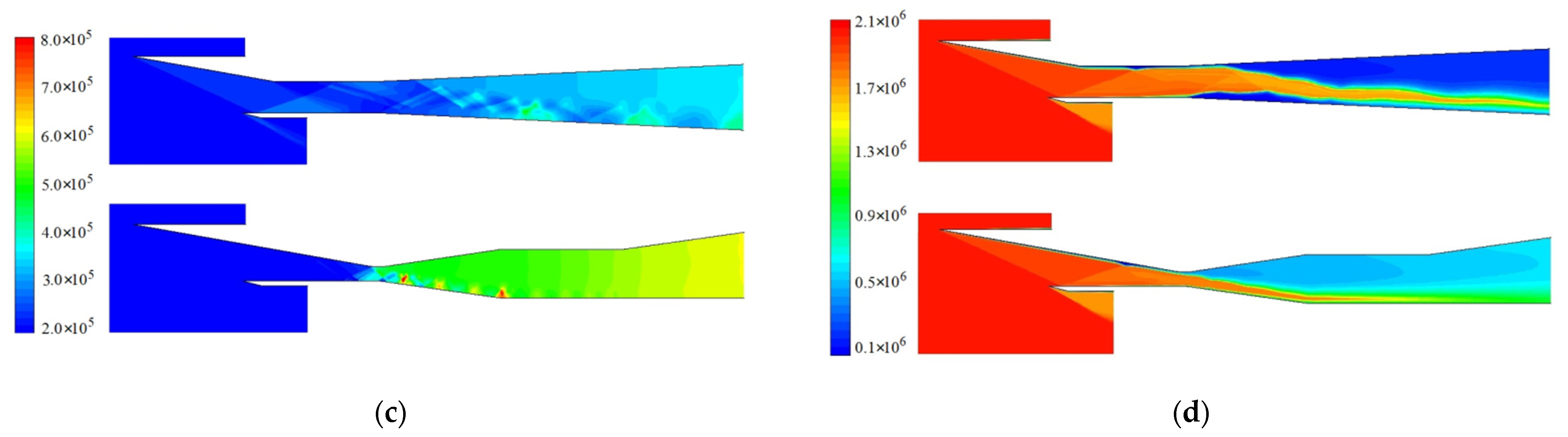
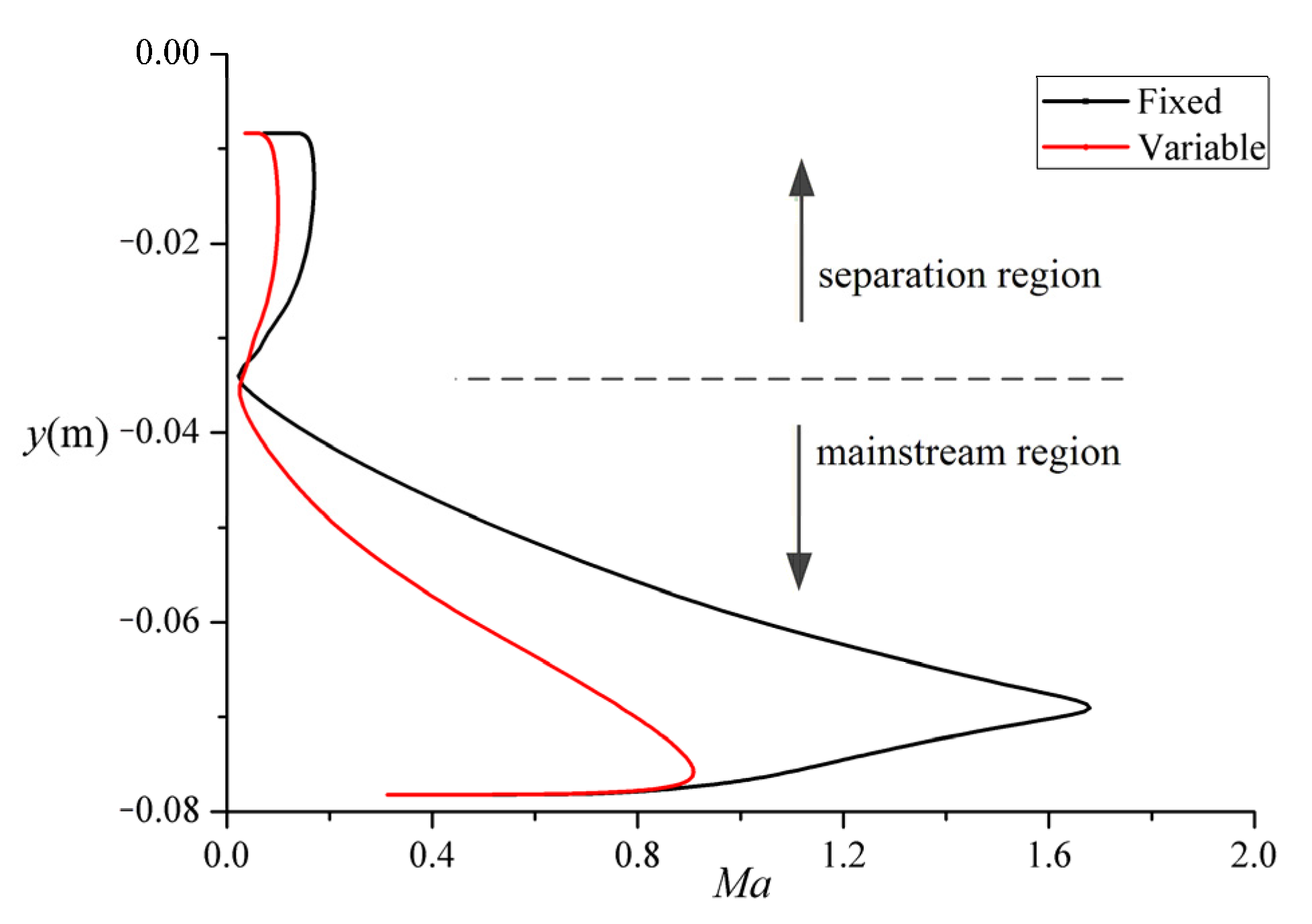
4.1. Results and Analysis in a Low-Speed Self-Starting Mach Number State
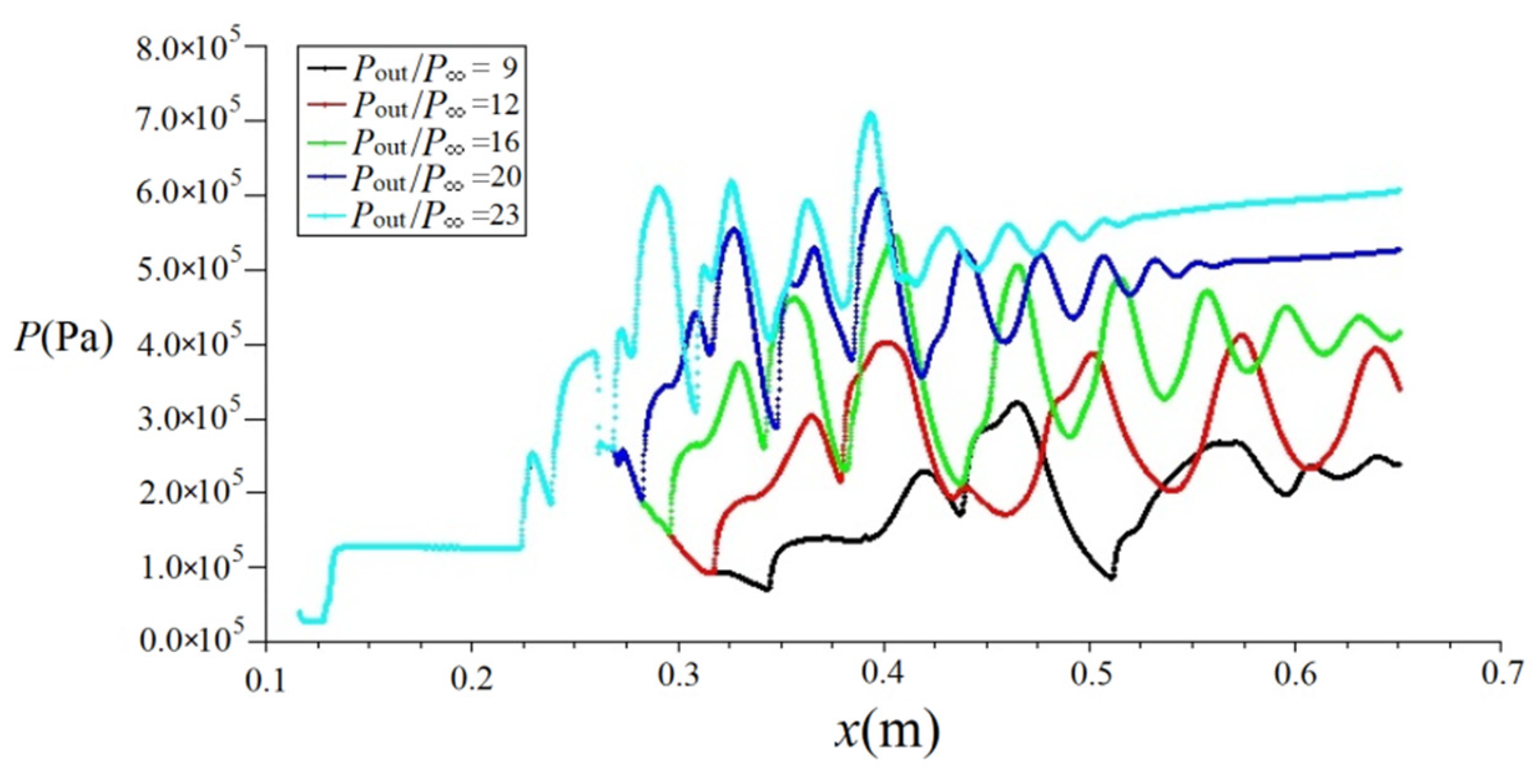
4.2. Results and Analysis at High-Speed Cruise State
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Cai, F.-C.; Chen, F.-M.; Xu, D.-L.; Yang, M. Study on fixed-geometry supersonic inlet design for wide Mach number range application. J. Solid Rocket Technol. 2010, 33, 163–166. [Google Scholar]
- Atkinson, M. Numerical Investigation of a Super-Sonic Inlet Using Bleed and Micro-Ramps to Control Shock-Wave/Boundary Layer Interactions. In Proceedings of the 45th AIAA Aerospace Sciences Meeting and Exhibit, Reno, Nedava, 8–11 January 2007. [Google Scholar]
- Soltani, M.R.; Daliri, A.; Younsi, J.S.; Farahani, M. Effects of Bleed Position on the Stability of a Supersonic Inlet. J. Propuls. Power 2016, 32, 1–14. [Google Scholar] [CrossRef]
- Zhang, Y.C.; Tan, H.J.; Huang, H.X.; Sun, S.; He, X.M.; Cheng, L.; Zhuang, Y. Transient Flow Patterns of Multiple Plasma Synthetic Jetsunder Different Ambient Pressures. Flow Turbul. Combust. 2018, 8, 741–757. [Google Scholar] [CrossRef]
- Huang, H.X.; Tan, H.J.; Sun, S.; Zhuang, Y.C.; Cheng, L. Transient Interaction between Plasma Jet and Supersonic Compression Ramp Flow. Phys. Fluids 2018, 30, 041703. [Google Scholar] [CrossRef]
- Ferrero, A. Control of a supersonic inlet in off-design conditions with plasma actuators and bleed. Aerospace 2020, 7, 32. [Google Scholar] [CrossRef] [Green Version]
- Anderson, B.H.; Tinapple, J.; Surber, L. Optimal Control of Shock Wave Turbulent Boundary Layer Interactions Using Micro-Array Actuation. In Proceedings of the 3rd AIAA Flow Control Conference, San Francisco, CA, USA, 5–8 June 2006. [Google Scholar]
- Zhang, Y.; Tan, H.J.; Tian, F.C.; Zhuang, Y. Control of Incident Shock/Boundary-Layer Interaction by a Two-Dimensional Bump. AIAA J. 2014, 52, 767–776. [Google Scholar] [CrossRef]
- Ramaswamy, D.P.; Schreyer, A.M. Control of shock-induced separation of a turbulent boundary layer using air-jet vortex generators. AIAA J. 2021, 59, 927–939. [Google Scholar] [CrossRef]
- Kaushik, M. Experimental studies on micro-vortex generator controlled shock/boundary-layer interactions in mach 2.2 intake. Int. J. Aeronaut. Space Sci. 2019, 20, 584–595. [Google Scholar] [CrossRef]
- DeBonis, J.R.; Trefny, C.J.; Steffen, C.J. Inlet Development for a Rocket Based Combined Cycle Single Stage to Orbit Vehicle Using Computational Fluid Dynamics. In Proceedings of the 35th Joint Propulsion Conference and Exhibit, Los Angeles, CA, USA, 20–24 June 1999. [Google Scholar]
- Jesse, R.C.; Mark, J.L. An Aerodynamic Redesign of the SR-71 Inlet with Application to Turbine Based Combined Cycle Engines. In Proceedings of the 40th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit, Fort Lauderdale, FL, USA, 11–14 July 2004. [Google Scholar]
- Varvill, R.; Bond, A. The SKYLON space plane. J. Br. Interplanet. Soc. 2004, 57, 22–32. [Google Scholar]
- Laurent, S.; François, F. Development Study of the ATREX Engine for TSTO Spaceplane. In Proceedings of the 10th AIAA/NAL-NASDA-ISAS International Space Planes and Hypersonic Systems and Technologies Conference, Kyoto, Japan, 24–27 April 2001. [Google Scholar]
- Guo, C.W. Research on the Design and Regulation of Variable Axisymmetric Inlet Working under Wide Mach Number; Nanjing University of Aeronautics and Astronautics: Nanjing, China, 2014. [Google Scholar]
- Nan, X.J.; Zhang, H. Design of supersonic axisymmetric variable geometric inlet with zero additional drag. J. Aerosp. Power 2020, 35, 1376–1382. [Google Scholar]
- Falempin, F.; Serre, L. Promethee the French Military Hypersonic Propulsion Program. In Proceedings of the 12th AIAA International Space Planes and Hypersonic Systems and Technologies, Norfolk, VA, USA, 15–19 December 2003. [Google Scholar]
- Bulman, M.; Siebenhaar, A. The strutjet engine-Exploding the myths surrounding high speed airbreathing propulsion. In Proceedings of the Joint Propulsion Conference and Exhibit, San Diego, CA, USA, 22 August 2012. [Google Scholar]
- Jin, Z.G.; Zhang, K.Y. Investigation of a variable geometry scramjet inlet with a rotating cowl operating in a large Mach number range. J. Astronaut. 2010, 31, 1503–1511. [Google Scholar]
- Liu, X.W. Investigation of Wide Applicability Inlet for RBCC Power; Northwestern Polytechnical University: Xi’an, China, 2010. [Google Scholar]
- Zhang, Z.Z.; Liu, P.J.; Qin, F.; Shi, L.; Wang, Y.F. Numerical Investigations on Throat and Lip Adjustments of RBCC Inlet. J. Propuls. Technol. 2018, 39, 1003–1013. [Google Scholar]
- Zhang, J.; Yuan, H.; Wang, Y.; Huang, G. Experiment and numerical investigation of flow control on a supersonic inlet diffuser. Aerosp. Sci. Technol. 2020, 106, 106182. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, L.; Qian, Z. Numerical investigation on the assistant restarting method of variable geometry for high Mach number inlet. Aerosp. Sci. Technol. 2018, 79, 647–657. [Google Scholar] [CrossRef]
- Liu, X.; Shil, L.; Liu, P.; Qin, F.; He, G. Design and numerical investigations on a dual-duct variable geometry RBCC inlet. Int. J. Turbo Jet-Engines 2020, 37, 111–122. [Google Scholar] [CrossRef]
- Dou, L.; Su, P.; Ding, Z. Modeling and nonlinear control for air-breathing hypersonic vehicle with variable geometry inlet. Aerosp. Sci. Technol. 2017, 67, 422–432. [Google Scholar] [CrossRef] [Green Version]
- Francois, F.; Laurent, S. French Flight Testing Program LEA Status in 2009. In Proceedings of the 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, 19–22 October 2009. [Google Scholar]
- Jiang, Z.X. Aerodynamics of Aircraft Internal Flow; Aviation Industry Press: Beijing, China, 1989. [Google Scholar]
- Dong, S.Y. Principle of Solid Rocket Motor; Beijing Institute of Technology Press: Beijing, China, 1996. [Google Scholar]
- Zhu, Z.Q. Applied Computational Fluid Dynamics; Beihang University Press: Beijing, China, 1998. [Google Scholar]
- Tian, X.A.; Wang, C.P.; Cheng, K.M. Numerical analysis of normal shock wave/boundary-layer interactions by using RSM. Acta Aerodyn. Sin. 2013, 31, 156–161. [Google Scholar]
- Herrmann, C.D.; Koschel, W.W. Experimental Investigation of the Internal Compression of a Hypersonic Inlet. In Proceedings of the 38th AIAA/ASME/SAE/ASEE Joint Propulsion Conference & Exhibit, Indianapolis, IN, USA, 7–10 July 2002. [Google Scholar]
- Liu, Z.; Wang, C.; Zhang, K.; Zhao, Z.; Xie, Z. Research on Computational Method of Supersonic Inlet/Isolator Internal Flow. Appl. Sci. 2021, 11, 9272. [Google Scholar] [CrossRef]
- Bao, F.T.; Huang, X.J.; Zhang, Z. Integral Solid Propellant Ramjet Rocket Motor; China Astronautic Publishing House: Beijing, China, 2006. [Google Scholar]






| Parameters | Value |
|---|---|
| /(kg/s) | 1.34 |
| H1/mm | 79.0 |
| H2/mm | 60.0 |
| H3/mm | 33.5 |
| L1/mm | 150.3 |
| L2/mm | 240.6 |
| L3/mm | 110.6 |
| L4/mm | 520.8 |
| L5/mm | 650.0 |
| δ1/(°) | 10.0 |
| δ2/(°) | 10.0 |
| δ3/(°) | 8.4 |
| δ4/(°) | 8.0 |
| δ5/(°) | 8.4 |
| δF/(°) | 27.38 |
| δS2/(°) | 31.80 |
| R/mm | 60 |
| Ma∞ | Model | ξ | Pth | P*th | Pout/P∞ |
|---|---|---|---|---|---|
| 2.2 | Fixed | 1.791 | 73,408 | 255,646 | 4.78 |
| Adjustable | 1.791 | 90,709 | 242,122 | 5.65 | |
| 3.5 | Fixed | 1.791 | 81,872 | 1,627,039 | 7.13 |
| Adjustable | 4.000 | 352,976 | 1,537,187 | 23.86 |
| Math | σth | Mainlet | σinlet | Pth/P∞ | Pout/P∞ | |
|---|---|---|---|---|---|---|
| Fixed | 1.45 | 0.9023 | 0.59 | 0.7318 | 2.77 | 6.0 |
| Adjustable | 1.25 | 0.8545 | 0.58 | 0.7849 | 3.05 | 6.5 |
| Math | σth | Mainlet | σinlet | Pth/P∞ | Pout/P∞ | |
|---|---|---|---|---|---|---|
| Fixed | 2.61 | 0.8038 | 1.11 | 0.3685 | 3.39 | 9 |
| Adjustable | 1.57 | 0.7594 | 0.59 | 0.4030 | 15.48 | 23 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, F.; Huang, G.; Liu, X.; Wu, Z. Study on a Two-Dimensional Supersonic Inlet with Inner Profile Adjustment. Energies 2022, 15, 5057. https://doi.org/10.3390/en15145057
Cai F, Huang G, Liu X, Wu Z. Study on a Two-Dimensional Supersonic Inlet with Inner Profile Adjustment. Energies. 2022; 15(14):5057. https://doi.org/10.3390/en15145057
Chicago/Turabian StyleCai, Feichao, Guanhong Huang, Xiaowei Liu, and Zhihan Wu. 2022. "Study on a Two-Dimensional Supersonic Inlet with Inner Profile Adjustment" Energies 15, no. 14: 5057. https://doi.org/10.3390/en15145057
APA StyleCai, F., Huang, G., Liu, X., & Wu, Z. (2022). Study on a Two-Dimensional Supersonic Inlet with Inner Profile Adjustment. Energies, 15(14), 5057. https://doi.org/10.3390/en15145057






