Study on Dynamic Injection Prediction Model of High-Pressure Common Rail Injector under Thermal Effect
Abstract
:1. Introduction
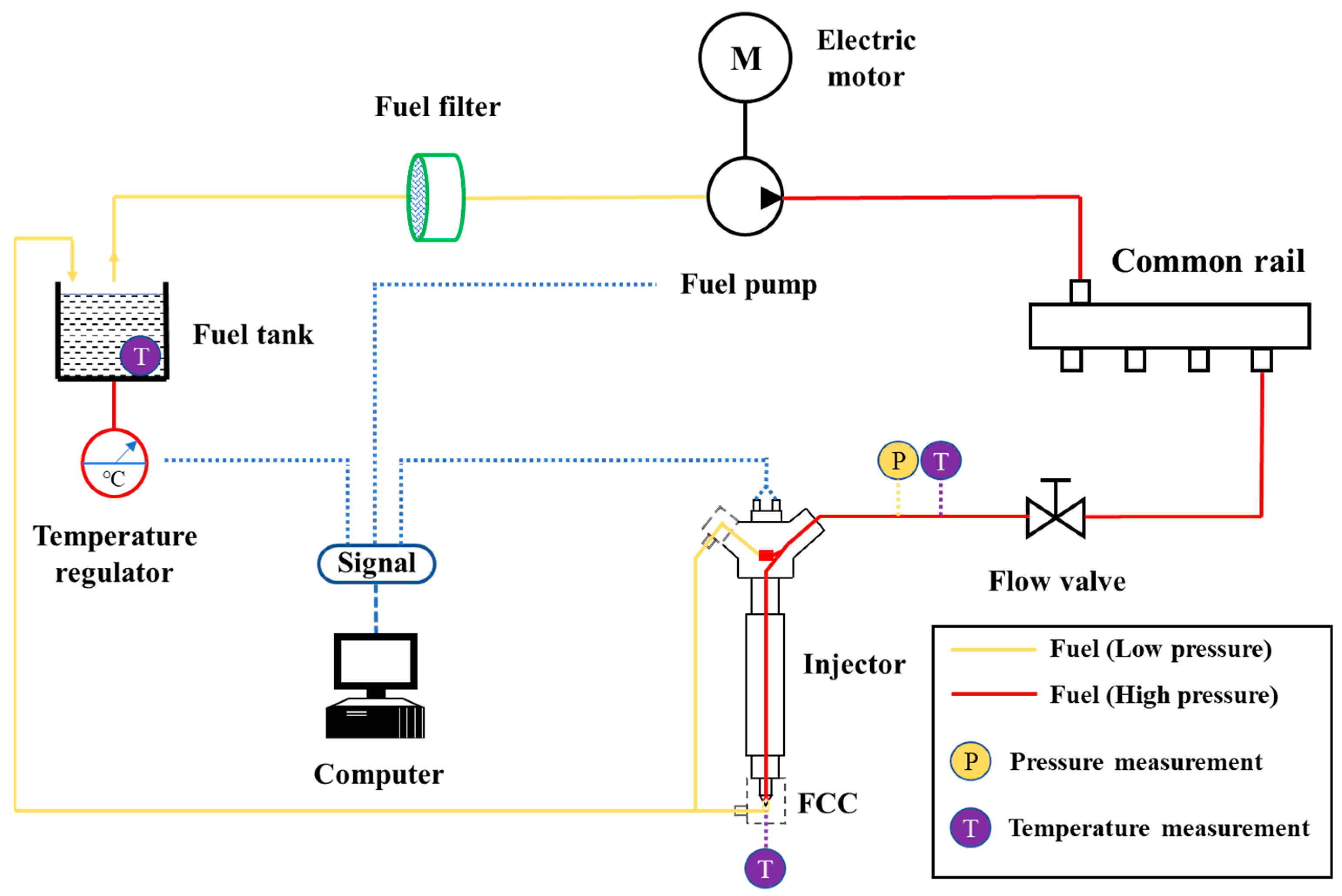
2. Description of the Experimental System
3. Analysis and Discussion
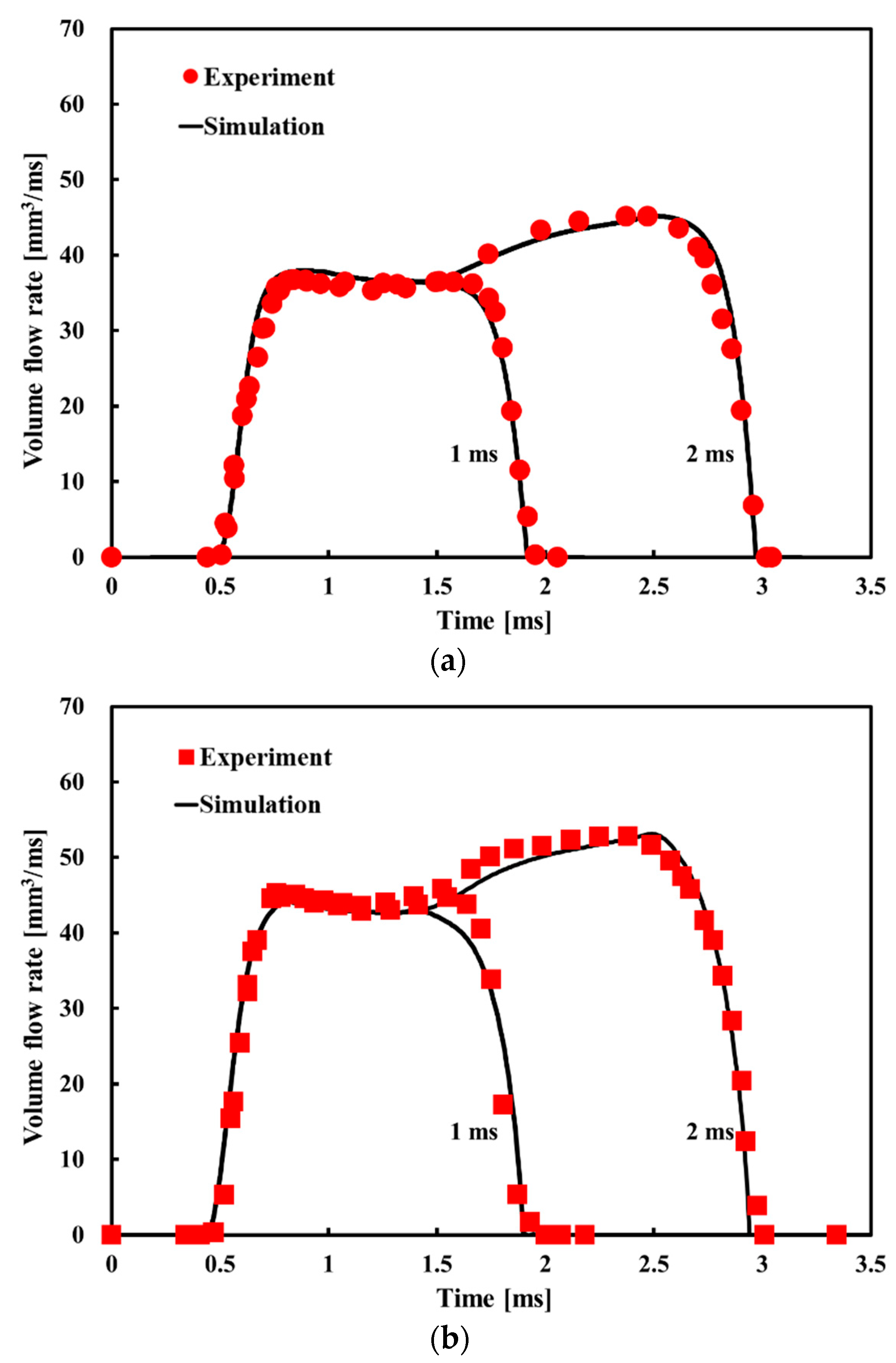
3.1. Development and Verification of the CR Injector Model under Isothermal Flow
3.2. Study on the Simulation Model of CR Injector under Adiabatic Flow
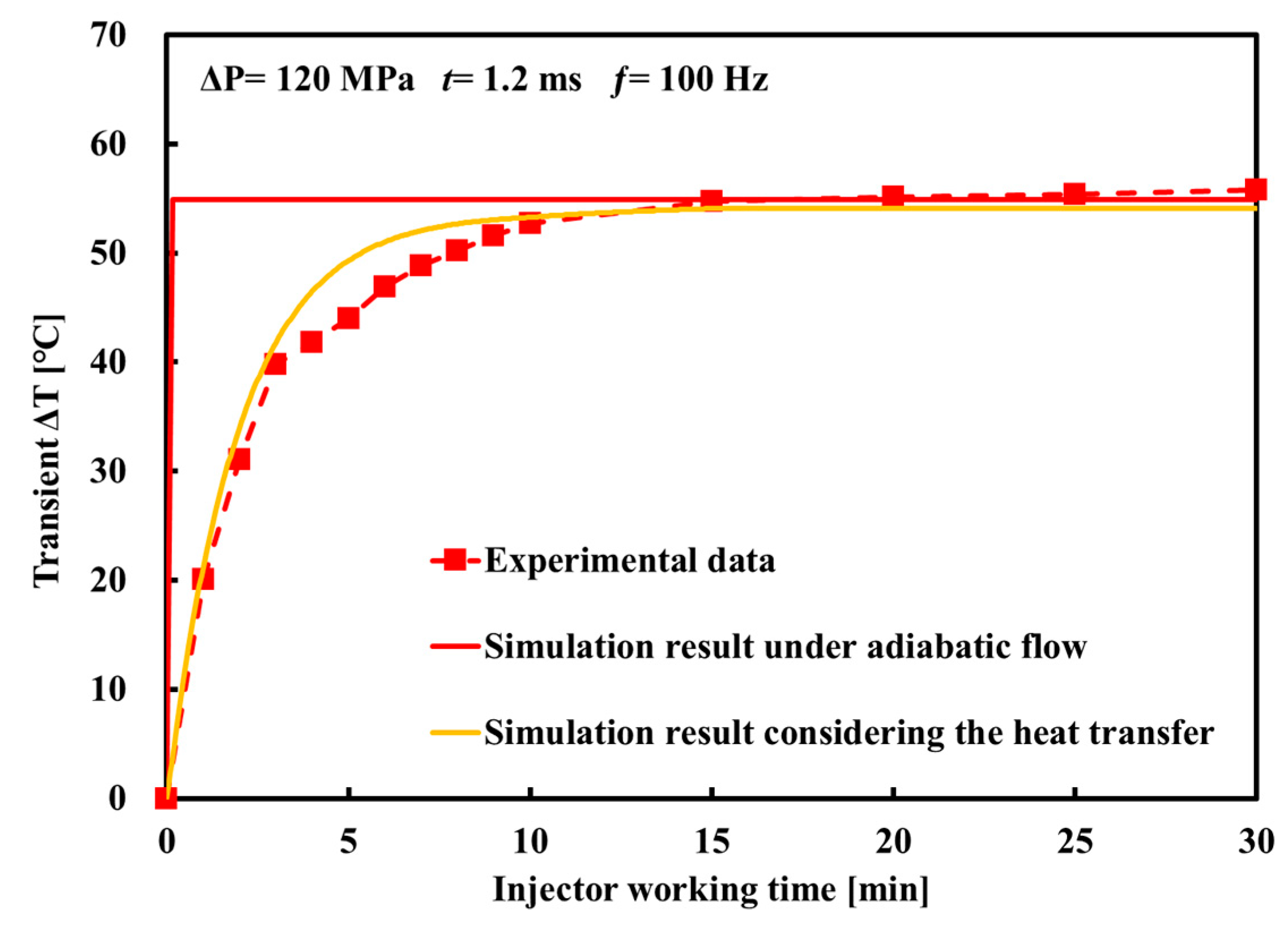
3.3. Study on the Simulation Model of CR Injector under Non-Isothermal Flow Coupled with Heat Transfer
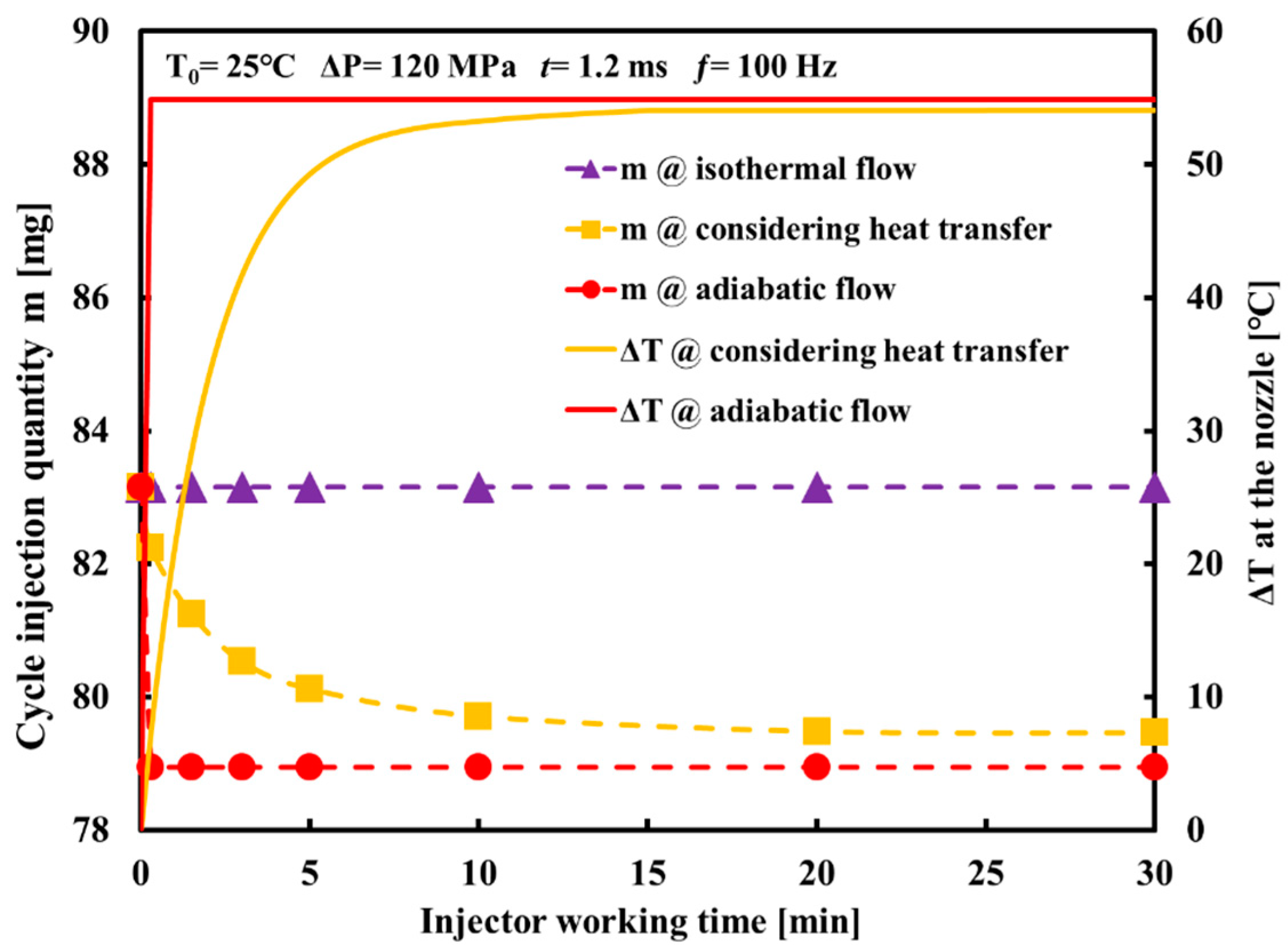
3.4. Influence of Fuel Heating Effects on the Cycle Injection Quantity
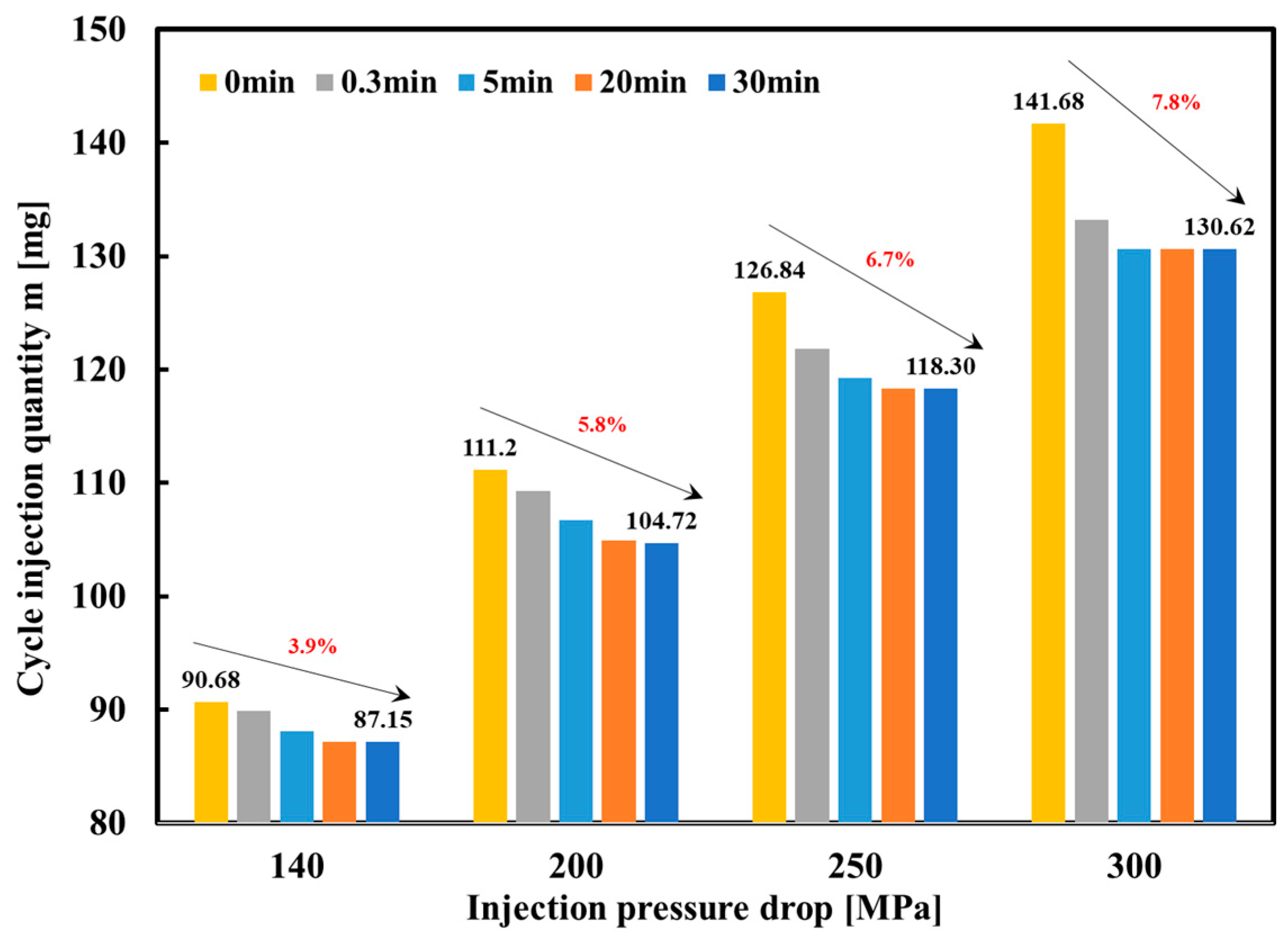
3.5. Influence of Injection Pressure on Cycle Injection Quantity under Thermal Effect
4. Conclusions
- (1)
- The transient ΔT at the nozzle calculated by the adiabatic flow model of the CR injector increases rapidly to the maximum value in a very short time, which differs from the behavior of the experimental ΔT with the fuel injector working time. Therefore, the adiabatic flow model cannot reflect the non-isothermal phenomena that occur during the actual injection process of the injector. The ΔT calculated by the model under non-isothermal flow coupled with heat transfer is in good agreement with the experimental data overall, and it can accurately describe the transient ΔT at the nozzle.
- (2)
- Under the assumption that the fuel in the CR injector is isothermal, the model cannot calculate the cycle injection quantity under the thermal effect in the actual working process. The cycle injection quantity calculated by the adiabatic flow model decreases rapidly owing to the rapid increase in temperature at the beginning of the injector working time, after which it remains unchanged. The cycle injection quantity calculated by the non-isothermal flow model coupled with heat transfer gradually decreases with the injector working time until it stabilizes. The difference in the cycle injection quantity calculated by the two models with the change in injector working time is mainly caused by different thermal phenomena at the nozzle.
- (3)
- As the injection pressure increases, the greater ΔP causes the fuel in the nozzle holes to generate more heat, resulting in a greater reduction in the cycle injection quantity under the action of heat. Therefore, for a high-pressure CR system with high-pressure and ultra-high-pressure injections, it is necessary to consider the influence of heat generation caused by ΔP on the cycle injection quantity when performing precise control of the cycle injection quantity. This conclusion has a guiding role for the control system, achieving precise and flexible control of the injection characteristics.
- (4)
- The experimental data and simulation results in this study demonstrate that the thermal effect at the nozzle of a high-pressure CR injector cannot be ignored, as the heat transfer directly affects the physical properties of the fuel and then reduces the cycle injection quantity. With stricter emission regulations, higher injection pressure requirements will make the thermal effect at the nozzle more obvious, which may significantly affect the injection characteristics. The research methods and results of this paper are informative and instructive. In further research, it is necessary to transform the test bench to realize the experimental measurement of the cycle injection quantity at different injection times under the working state of the injector. The experimental measurement will be mainly carried out in order to compare with the calculation results and prove the significance of this research from an experimental point of view.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Park, S.H.; Yoon, S.H.; Lee, C.S. Effects of multiple-injection strategies on overall spray behavior, combustion, and emissions reduction characteristics of biodiesel fuel. Appl. Energy 2011, 88, 88–98. [Google Scholar] [CrossRef]
- Wang, G.; Yu, W.; Li, X.; Su, Y.; Yang, R.; Wu, W. Experimental and numerical study on the influence of intake swirl on fuel spray and in-cylinder combustion characteristics on large bore diesel engine. Fuel 2019, 237, 209–221. [Google Scholar] [CrossRef]
- Gumus, M.; Sayin, C.; Canakci, M. The impact of fuel injection pressure on the exhaust emissions of a direct injection diesel engine fueled with biodiesel–diesel fuel blends. Fuel 2012, 95, 486–494. [Google Scholar] [CrossRef]
- Theodorakakos, A.; Strotos, G.; Mitroglou, N.; Atkin, C.; Gavaises, M. Friction-induced heating in nozzle hole micro-channels under extreme fuel pressurisation. Fuel 2014, 123, 143–150. [Google Scholar] [CrossRef]
- Strotos, G.; Koukouvinis, P.; Theodorakakos, A.; Gavaises, M.; Bergeles, G. Transient heating effects in high pressure Diesel injector nozzles. Int. J. Heat Fluid Flow 2015, 51, 257–267. [Google Scholar] [CrossRef] [Green Version]
- Zhao, J.; Wei, K.; Yue, P. Investigation of maximum temperature rise on high pressure common rail injector nozzle. SAE Technical Paper 2009, 2019-01-0276. [Google Scholar] [CrossRef]
- Zhang, X.; He, Z.; Wang, Q.; Tao, X.; Zhou, Z.; Xia, X.; Zhang, W. Effect of fuel temperature on cavitation flow inside vertical multi-hole nozzles and spray characteristics with different nozzle geometries. Exp. Therm. Fluid Sci. 2018, 91, 374–387. [Google Scholar] [CrossRef]
- Theodorakakos, A.; Mitroglou, N.; Gavaises, M. Simulation of heating effects in cavitating flows through Diesel fuel injectors caused by extreme fuel pressurisation. In Proceedings of the 8th International Symposium on Cavitation, Singapore, 14–16 August 2012. [Google Scholar]
- Salvador, F.J.; Gimeno, J.; Martín, J.; Carreres, M. Thermal effects on the diesel injector performance through adiabatic 1D modelling. Part I: Model description and assessment of the adiabatic flow hypothesis. Fuel 2020, 260, 116348. [Google Scholar] [CrossRef]
- Payri, R.; Salvador, F.J.; Carreres, M.; Belmar-Gil, M. Thermal effects on the diesel injector performance through adiabatic 1D modelling. Part II: Model validation, results of the simulations and discussion. Fuel 2020, 260, 115663. [Google Scholar] [CrossRef]
- Wang, Z.; Ding, H.; Wyszynski, M.L.; Tian, J.; Xu, H. Experimental study on diesel fuel injection characteristics under cold start conditions with single and split injection strategies. Fuel Processing Technol. 2015, 131, 213–222. [Google Scholar] [CrossRef]
- Salvador, F.J.; Gimeno, J.; Carreres, M.; Crialesi-Esposito, M. Experimental assessment of the fuel heating and the validity of the assumption of adiabatic flow through the internal orifices of a diesel injector. Fuel 2017, 188, 442–451. [Google Scholar] [CrossRef] [Green Version]
- Catania, A.E.; Ferrari, A.; Spessa, E. Temperature variations in the simulation of high-pressure injection-system transient flows under cavitation. Int. J. Heat Mass Transf. 2008, 51, 2090–2107. [Google Scholar] [CrossRef]
- Shi, J.M.; Arafin, M.S. CFD investigation of fuel property effect on cavitating flow in generic nozzle geometries. In Proceedings of the ILASS-Europe 2010, 23rd Annual Conference on Liquid Atomization and Spray Systems, Brno, Czech Republic, 6–8 September 2010. [Google Scholar]
- Giorgi, G.; Ficarella, A.; Tarantino, M. Evaluating cavitation regimes in an internal orifice at different temperatures using frequency analysis and visualization. Int. J. Heat Fluid Flow 2013, 39, 160–172. [Google Scholar] [CrossRef]
- Cao, T.; He, Z.; Si, Z.; L-Seesy, A.I.E.; Guan, W.; Zhou, H.; Wang, Q. Optical experimental study on cavitation development with different patterns in diesel injector nozzles at different fuel temperatures. Exp. Fluids 2020, 61, 185. [Google Scholar] [CrossRef]
- Boudy, F.; Seers, P. Impact of physical properties of biodiesel on the injection process in a common-rail direct injection system. Energy Convers. Manag. 2009, 50, 2905–2912. [Google Scholar] [CrossRef]
- Han, D.; Li, K.; Duan, Y.; Lin, H.; Huang, Z. Numerical study on fuel physical effects on the split injection processes on a common rail injection system. Energy Convers. Manag. 2017, 134, 47–58. [Google Scholar] [CrossRef]
- Boehman, A.L.; Morris, D.; Szybist, J. The Impact of the Bulk Modulus of Diesel Fuels on Fuel Injection Timing. Energy Fuels 2004, 18, 1877–1882. [Google Scholar] [CrossRef]
- Zhao, J.; Lu, X.; Grekhov, L. Experimental study on the fuel heating at the nozzle of the high pressure common-rail injector. Fuel 2021, 283, 119281. [Google Scholar] [CrossRef]
- Yue, P.; Zhao, J.; Wei, K.; Ma, X. The fluid–structure–thermal coupled characteristics of the leakage rate of piston couples interface for common-rail injector. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5826–5835. [Google Scholar] [CrossRef]
- Ndiaye, E.H.I.; Bazile, J.-P.; Nasri, D.; Boned, C.; Daridon, J.L. High pressure thermophysical characterization of fuel used for testing and calibrating diesel injection systems. Fuel 2012, 98, 288–294. [Google Scholar] [CrossRef]
- Chorążewski, M.; Dergal, F.; Sawaya, T.; Mokbel, I.; Grolier, J.-P.E.; Jose, J. Thermophysical properties of Normafluid (ISO 4113) over wide pressure and temperature ranges. Fuel 2013, 105, 440–450. [Google Scholar] [CrossRef]
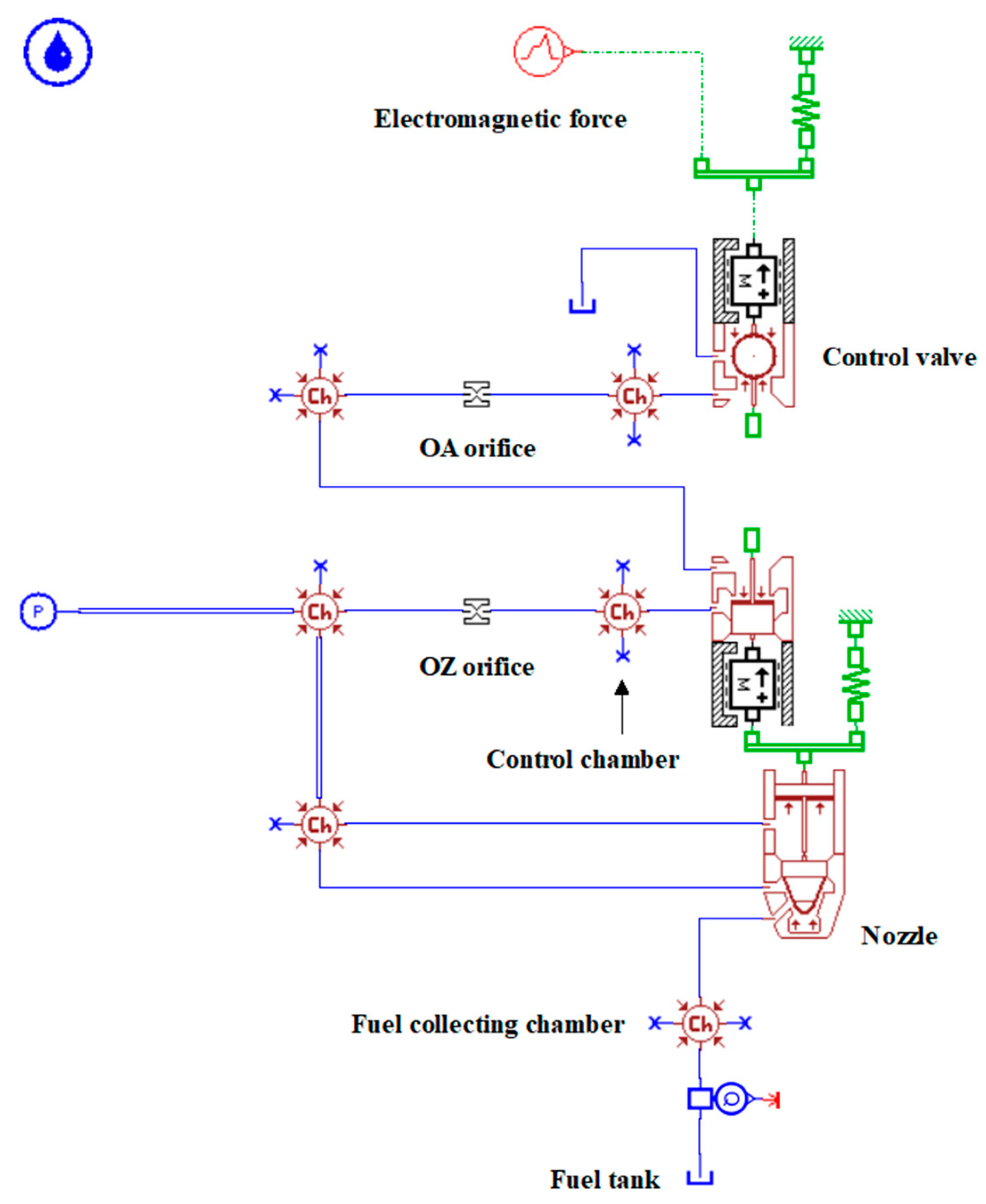
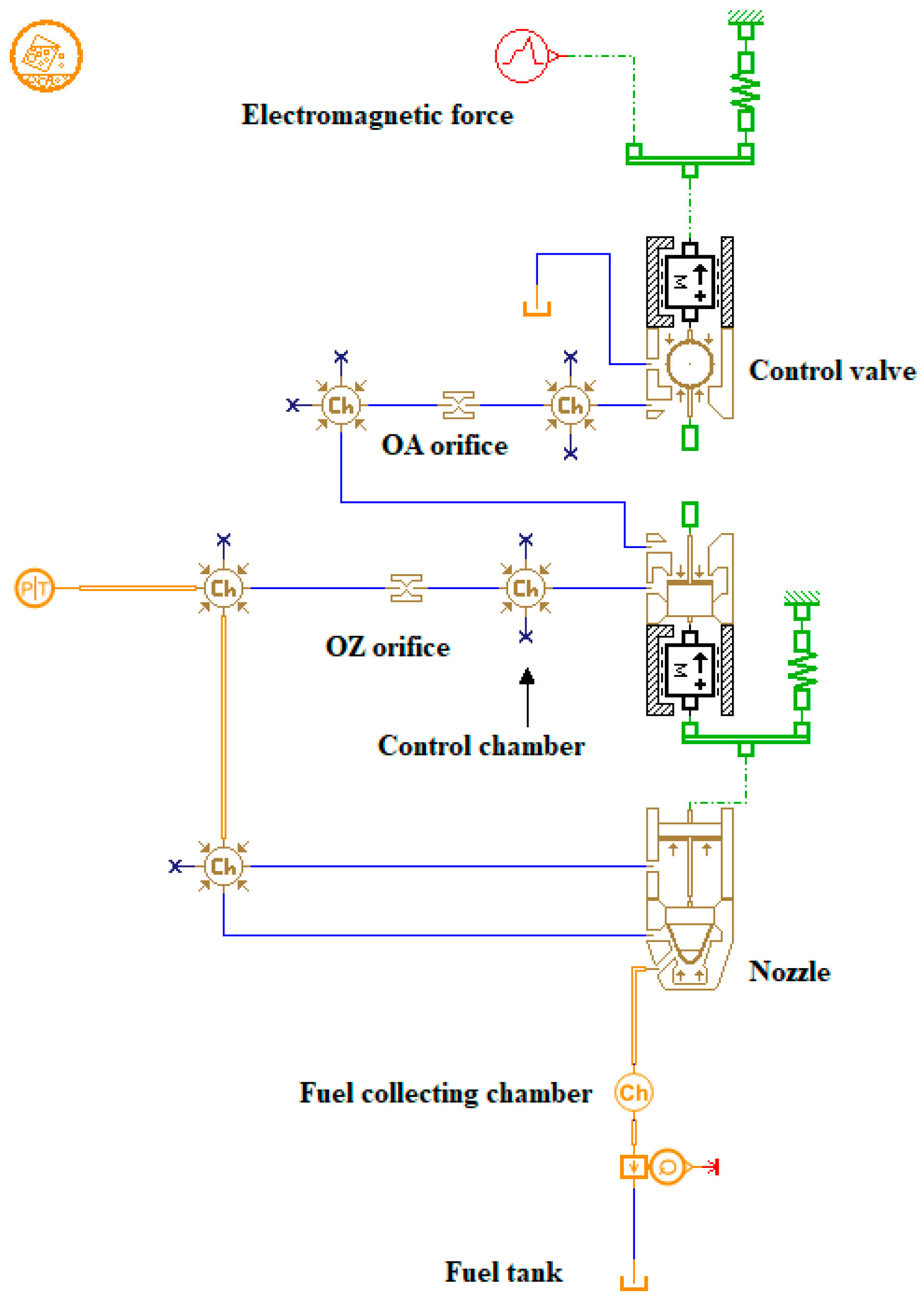
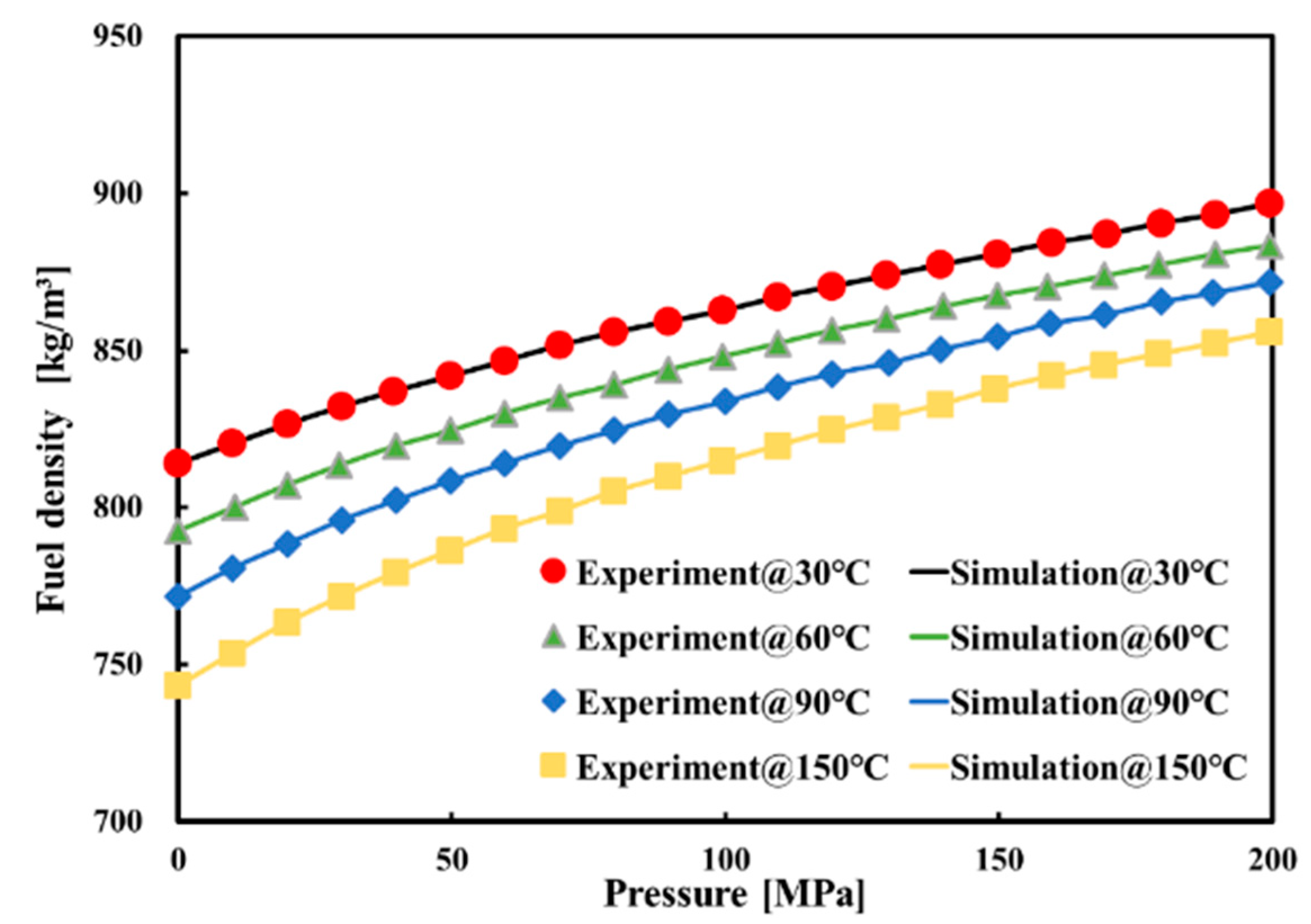
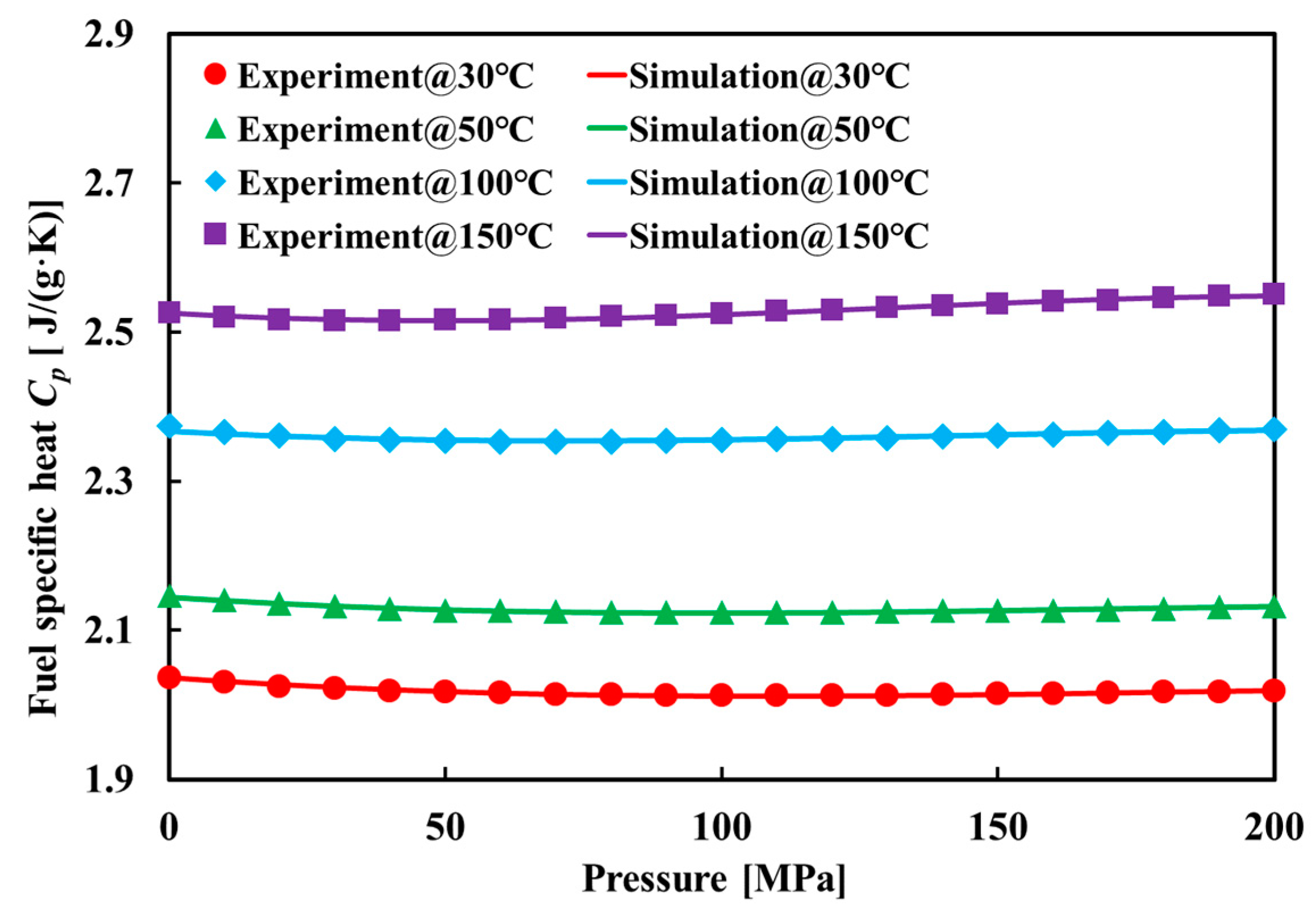
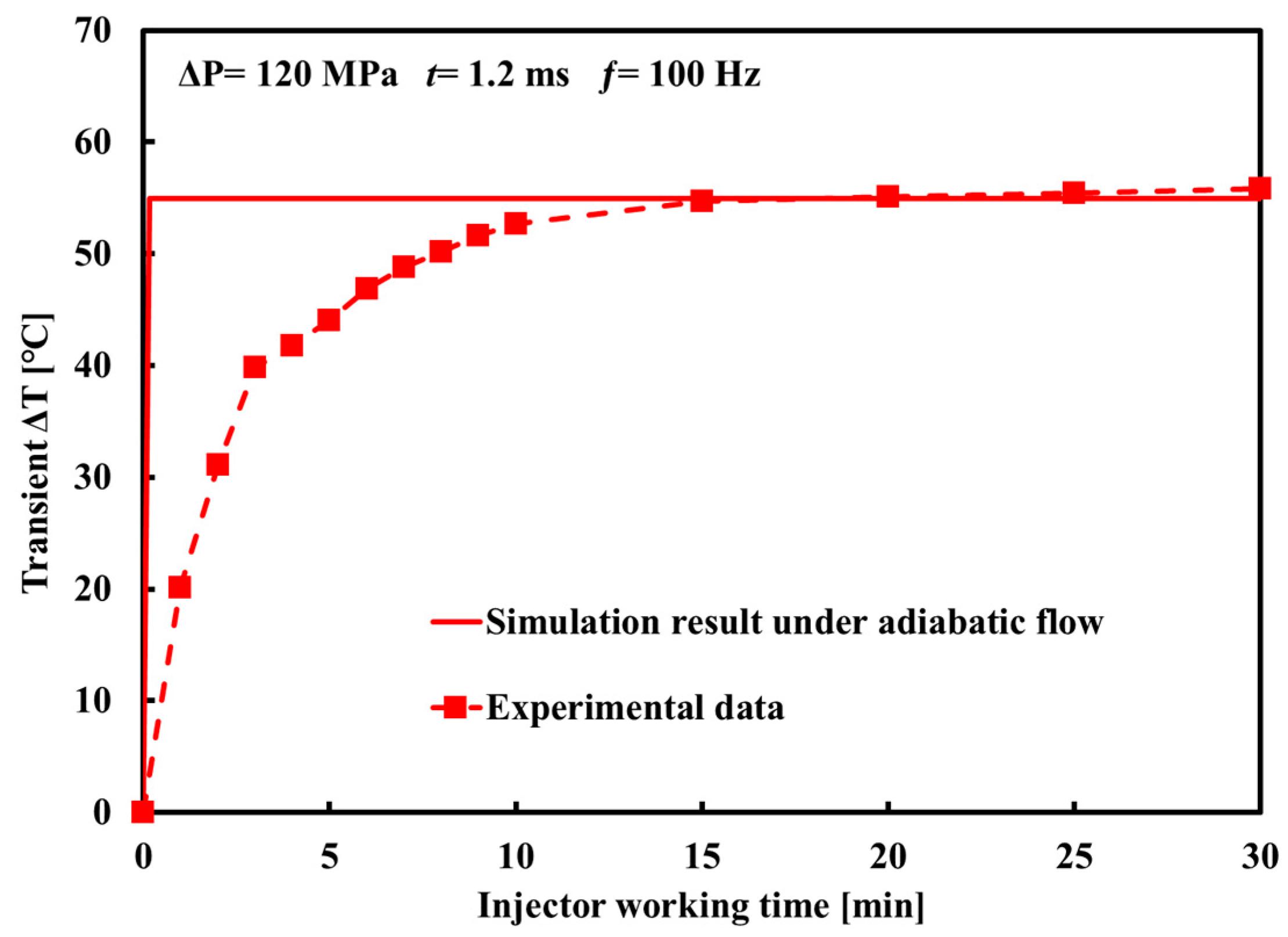
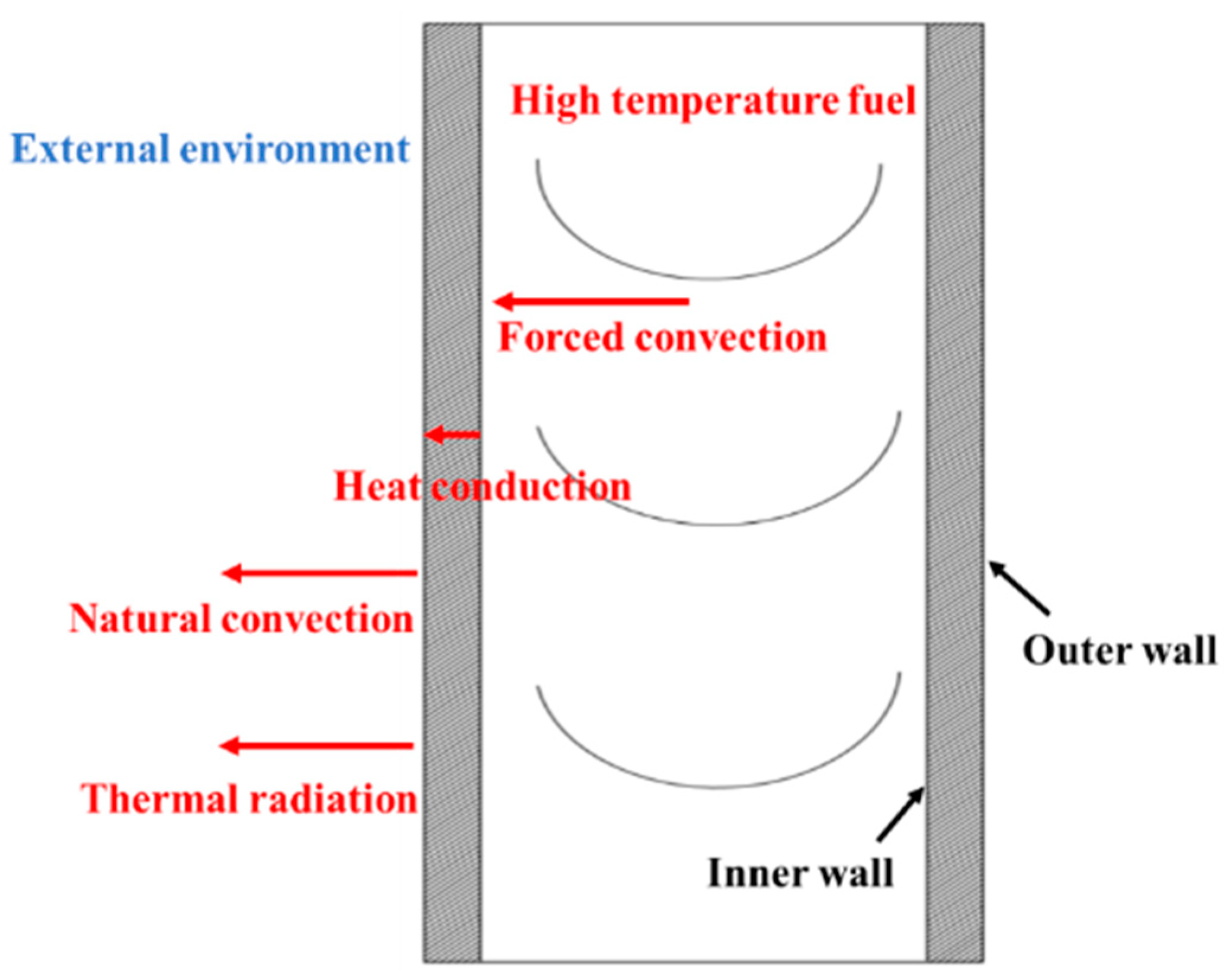
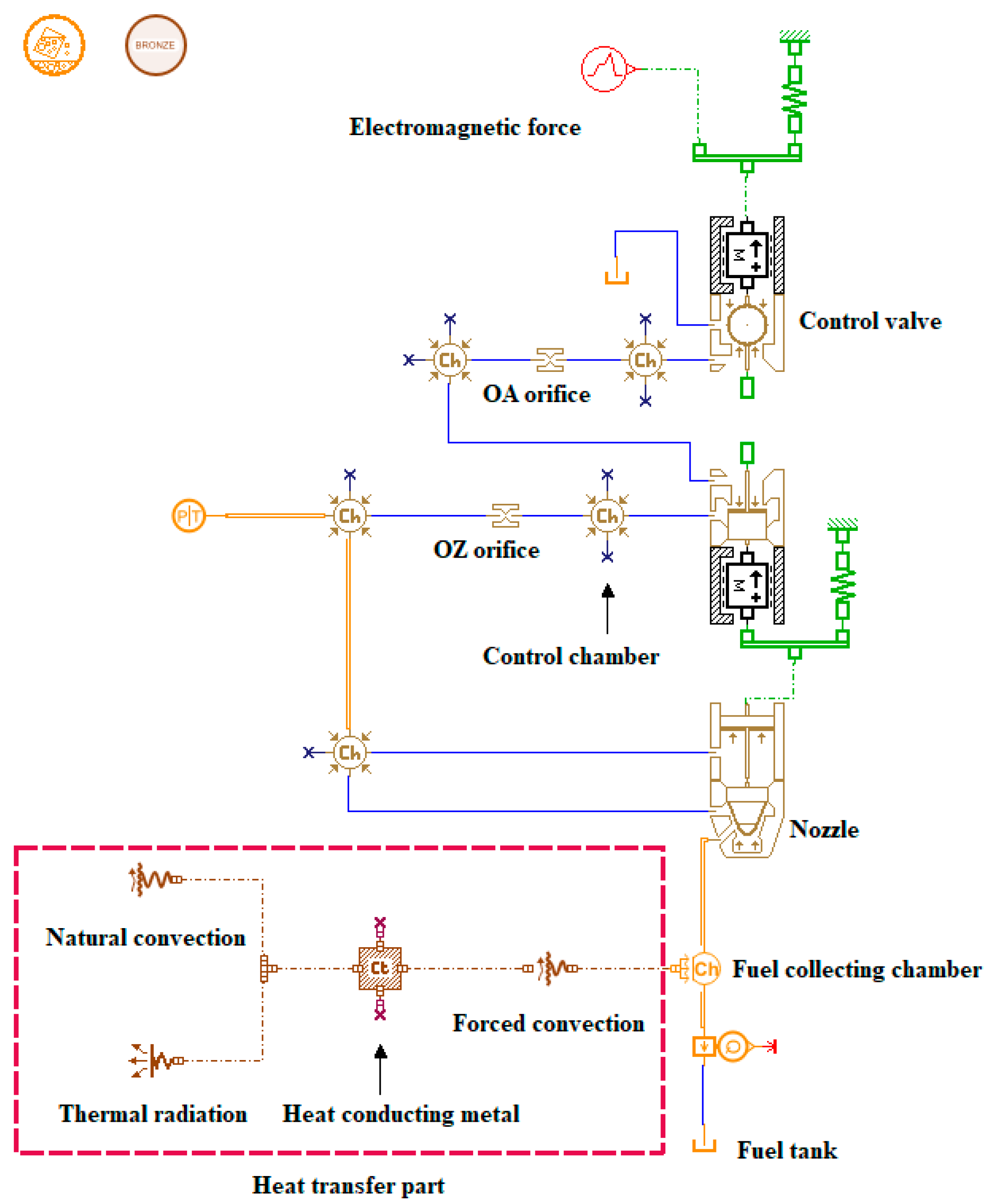
| Parameters (Unit) | Value |
|---|---|
| Ball diameter of control valve (mm) | 1.33 |
| Lift of armature (mm) | 0.07 |
| Diameter of OA orifice (mm) | 0.34 |
| Diameter of OZ orifice (mm) | 0.23 |
| Lift of needle (mm) | 0.25 |
| Diameter of needle (mm) | 4 |
| Pre-tightening force of needle spring (N) | 50 |
| Diameter of nozzle hole (mm) | 0.157 |
| Number of nozzle holes | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Li, Z.; Wu, J.; Liu, J.; Chen, P. Study on Dynamic Injection Prediction Model of High-Pressure Common Rail Injector under Thermal Effect. Energies 2022, 15, 5067. https://doi.org/10.3390/en15145067
Liu Z, Li Z, Wu J, Liu J, Chen P. Study on Dynamic Injection Prediction Model of High-Pressure Common Rail Injector under Thermal Effect. Energies. 2022; 15(14):5067. https://doi.org/10.3390/en15145067
Chicago/Turabian StyleLiu, Zhenming, Ziming Li, Jiechang Wu, Jingbin Liu, and Ping Chen. 2022. "Study on Dynamic Injection Prediction Model of High-Pressure Common Rail Injector under Thermal Effect" Energies 15, no. 14: 5067. https://doi.org/10.3390/en15145067
APA StyleLiu, Z., Li, Z., Wu, J., Liu, J., & Chen, P. (2022). Study on Dynamic Injection Prediction Model of High-Pressure Common Rail Injector under Thermal Effect. Energies, 15(14), 5067. https://doi.org/10.3390/en15145067






