Optimization of Non-Uniform Perforation Parameters for Multi-Cluster Fracturing
Abstract
1. Introduction
2. Mathematical Model of Fracture Propagation
2.1. Rock Deformation with Displacement Discontinuity Method
2.2. Fluid Flow along the Wellbore and the Fracture
3. Numerical Solution
3.1. Discretized Form
3.2. Iterative Scheme
4. Optimization with PSO Method
4.1. PSO Method
4.2. Optimization Scheme
5. Results and Analysis
5.1. Validation of Numerical Model
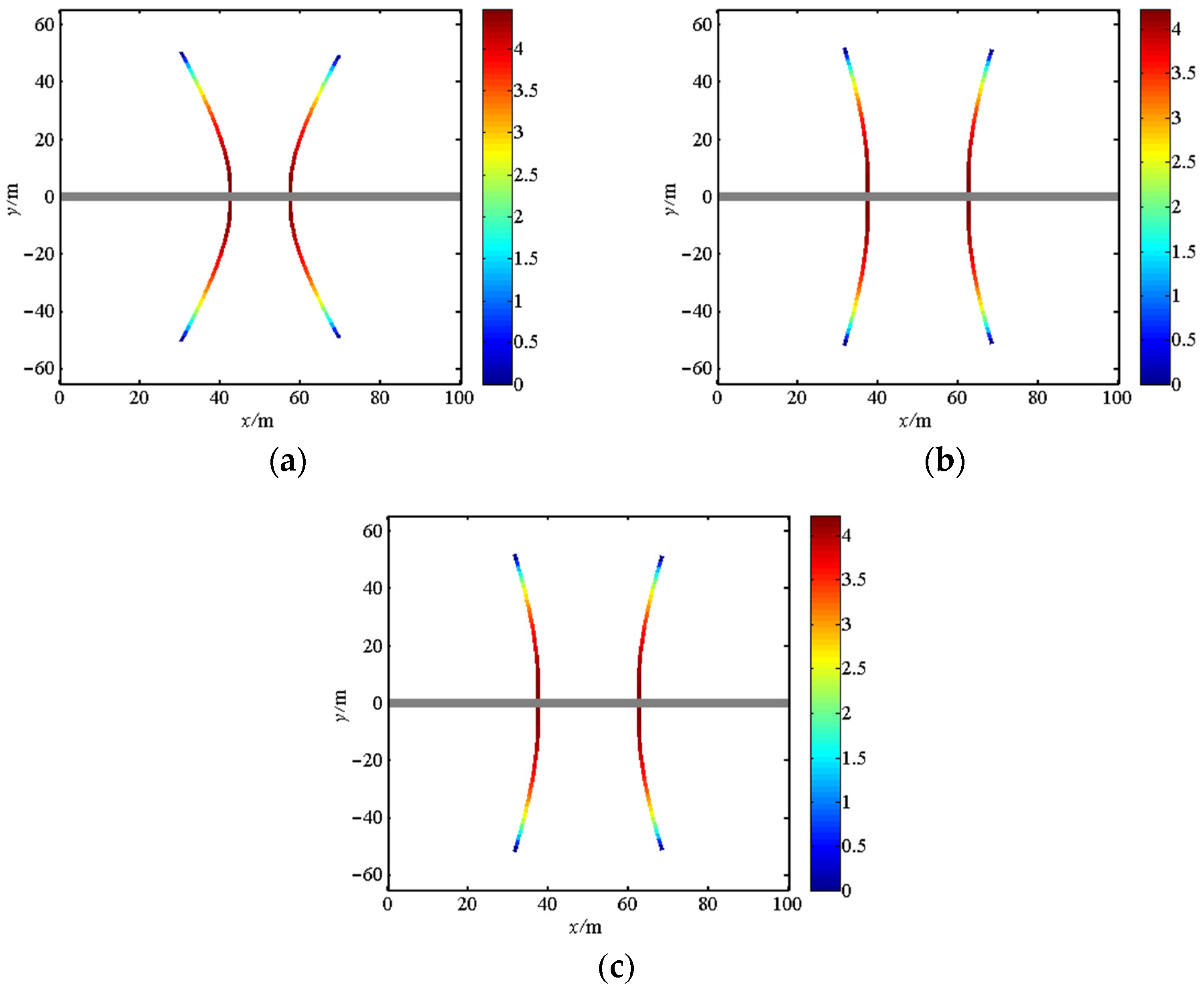
5.2. Propagation of Multiple Hydraulic Fractures
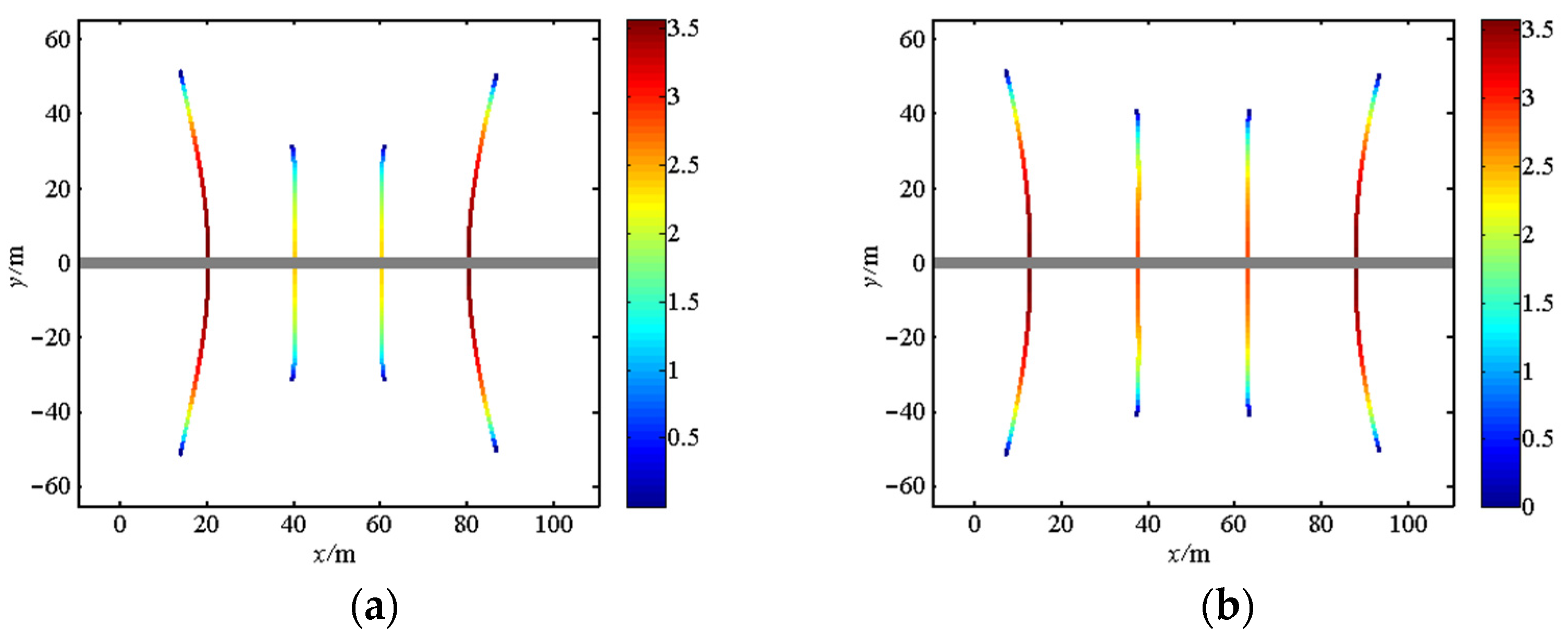
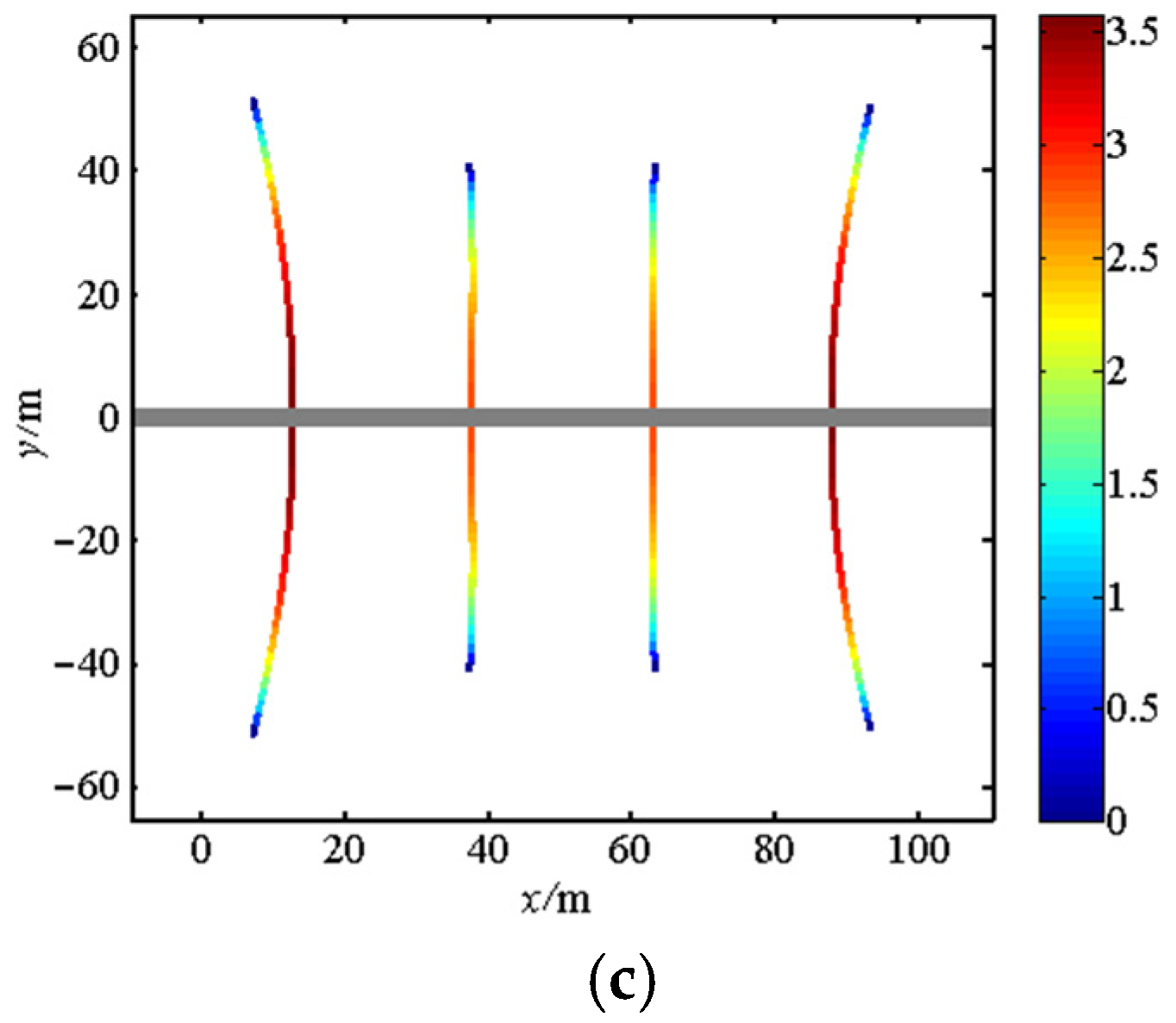
5.3. Optimization of Cluster Spacings
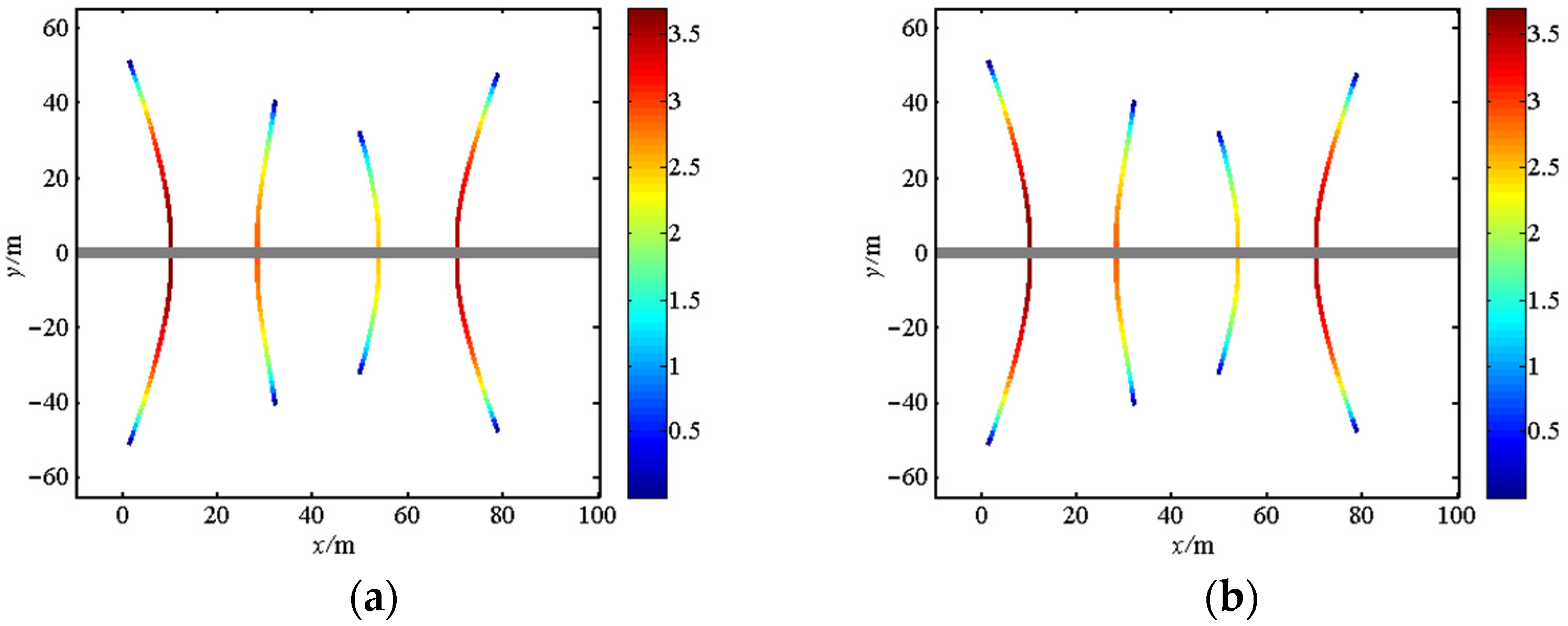
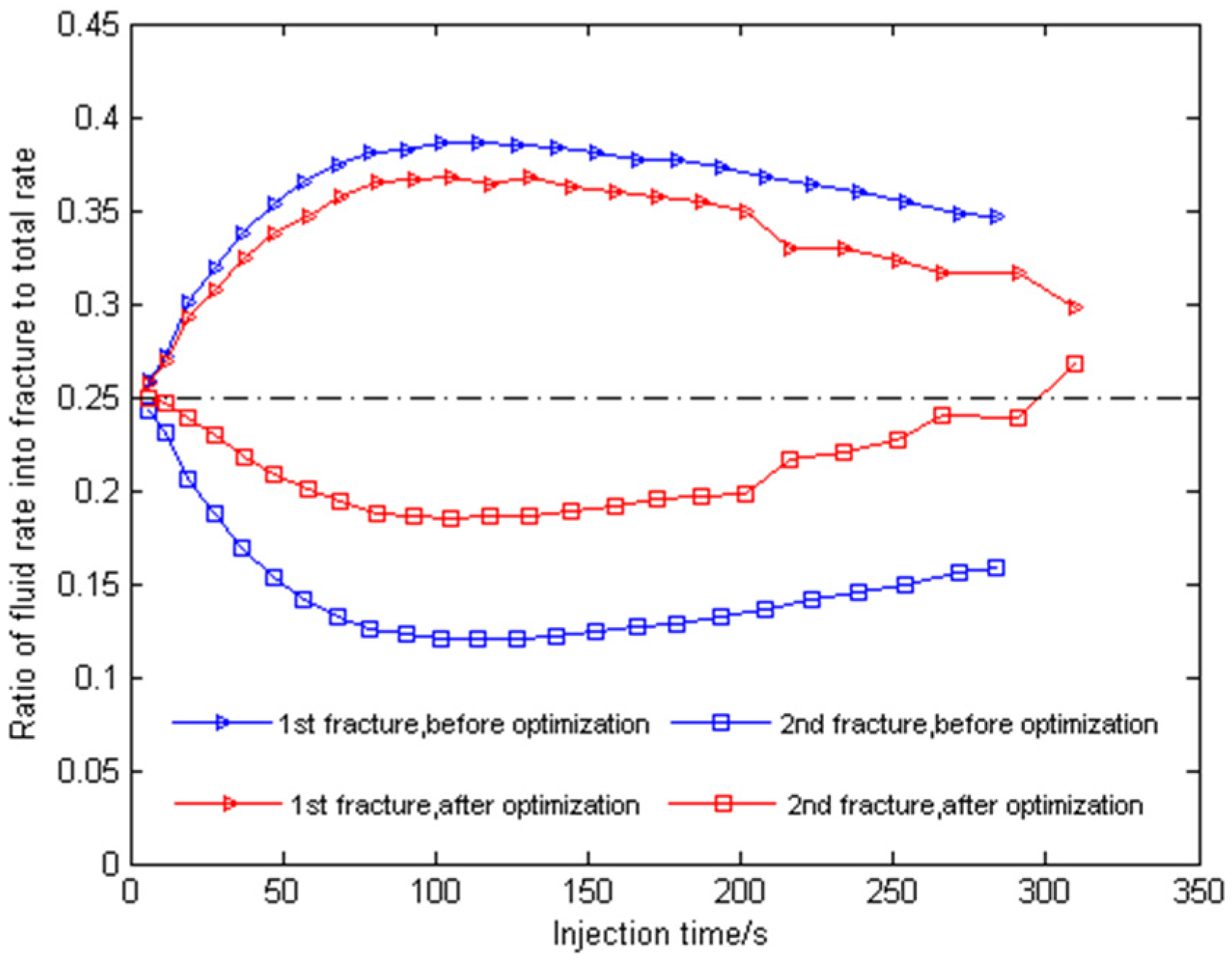
5.4. Optimization of Perforation Parameters
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Crump, J.B.; Conway, M.W. Effects of perforation-entry friction on bottomhole treating analysis. J. Pet. Technol. 1988, 40, 1041–1048. [Google Scholar] [CrossRef]
- Cramer, D.D. The application of limited-entry techniques in massive hydraulic fracturing treatments. In Proceedings of the SPE Production Operations Symposium, Oklahoma City, OK, USA, 8 March 1987. [Google Scholar]
- McDaniel, B.W.; Willett, R.M.; Underwood, P.J. Limited-entry frac applications on long intervals of highly deviated or horizontal wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 3–6 October 1999. [Google Scholar]
- Zhang, Y.; Shao, J.; Liu, Z.; Shi, C. An improved hydromechanical model for particle flow simulation of fractures in fluid-saturated rocks. Int. J. Rock Mech. Min. 2021, 147, 104870. [Google Scholar] [CrossRef]
- Xu, G.; Wong, S.W. Interaction of multiple non-planar hydraulic fractures in horizontal wells. In Proceedings of the International Petroleum Technology Conference, Beijing, China, 26–28 March 2013. [Google Scholar]
- Wu, K.; Olson, J.E. Simultaneous multifracture treatments: Fully coupled fluid flow and fracture mechanics for horizontal wells. SPE J. 2014, 20, 337–346. [Google Scholar] [CrossRef]
- Zhao, J.; Chen, X.; Li, Y.; Fu, B. Simulation of simultaneous propagation of multiple hydraulic fractures in horizontal wells. J. Pet. Sci. Eng. 2016, 147, 788–800. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Numerical investigation of complex hydraulic fracture development in naturally fractured reservoirs. SPE Prod. Oper. 2016, 31, 300–309. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J. Numerical simulation of fracture network generation in naturally fractured reservoirs. J. Nat. Gas Sci. Eng. 2016, 30, 430–443. [Google Scholar] [CrossRef]
- Chen, Z. Finite element modelling of viscosity-dominated hydraulic fractures. J. Petrol. Sci. Eng. 2012, 88, 136–144. [Google Scholar] [CrossRef]
- Chen, Z.; Bunger, A.; Zhang, X.; Jeffrey, R.G. Cohesive zone finite element-based modeling of hydraulic fractures. Acta Mech. Solida Sin. 2009, 22, 443–452. [Google Scholar] [CrossRef]
- Liu, W.; Yao, J.; Zeng, Q. A numerical hybrid model for non-planar hydraulic fracture propagation in ductile formations. J. Petrol. Sci. Eng. 2021, 196, 107796. [Google Scholar] [CrossRef]
- Liu, W.; Zeng, Q.; Yao, J. Poroelastoplastic modeling of complex hydraulic-fracture development in deep shale formations. SPE J. 2021, 26, 2626–2650. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. Numerical study of hydraulic fracture propagation accounting for rock anisotropy. J. Pet. Sci. Eng. 2018, 160, 422–432. [Google Scholar] [CrossRef]
- Liu, P.; Li, J.; Sun, S.; Yao, J.; Zhang, K. Numerical investigation of carbonate acidizing with gelled acid using a coupled thermal-hydrologic-chemical model. Int. J. Therm. Sci. 2021, 160, 1–18. [Google Scholar] [CrossRef]
- Zeng, Q.; Yao, J.; Shao, J. An extended finite element solution for hydraulic fracturing with thermo-hydro-elastic–plastic coupling. Comput. Methods Appl. Mech. Engrg. 2020, 364, 112967. [Google Scholar] [CrossRef]
- Settgast, R.R.; Fu, P.C.; Walsh, S.D.; White, J.A.; Annavarapu, C.; Ryerson, F.J. A fully coupled method for massively parallel simulation of hydraulically driven fractures in 3-dimensions. Int. J. Numer. Anal. Met. 2017, 41, 627–653. [Google Scholar] [CrossRef]
- Zhao, Q.; Lisjak, A.; Mahabadi, O.; Liu, Q.; Grasselli, G. Numerical simulation of hydraulic fracturing and associated microseismicity using finite-discrete element method. J. Rock Mech. Geotech. Eng. 2014, 6, 574–581. [Google Scholar] [CrossRef]
- Yan, C.; Zheng, H.; Sun, G.; Ge, X. Combined finite-discrete element method for simulation of hydraulic fracturing. Rock Mech. Rock Eng. 2016, 49, 1389–1410. [Google Scholar] [CrossRef]
- Zhang, F.; Dontsov, E.; Mack, M. Fully coupled simulation of a hydraulic fracture interacting with natural fractures with a hybrid discrete-continuum method. Int. J. Numer. Anal. Methods Geomech. 2017, 41, 1430–1452. [Google Scholar] [CrossRef]
- Liu, L.; Zhu, W.; Wei, C.; Elsworth, D.; Wang, J. Microcrack-based geomechanical modeling of rock-gas interaction during supercritical CO2 fracturing. J. Petrol. Sci. Eng. 2018, 164, 91–102. [Google Scholar] [CrossRef]
- Guo, T.; Tang, S.; Liu, X.; Zhang, W.; Qu, G. Numerical simulation of hydraulic fracturing of hot dry rock under thermal stress. Eng. Fract. Mech. 2020, 240, 107350. [Google Scholar] [CrossRef]
- Mikelic, A.; Wheeler, M.F.; Wick, T. A phase-field method for propagating fluid-filled fractures coupled to a surrounding porous medium. Multiscale Model. Simul. 2015, 13, 367–398. [Google Scholar] [CrossRef]
- Heider, Y.; Markert, B. A phase-field modeling approach of hydraulic fracture in saturated porous media. Mech. Res. Commun. 2016, 80, 38–46. [Google Scholar] [CrossRef]
- Chukwudozie, C.; Bourdin, B.; Yoshioka, K. A variational phase-field model for hydraulic fracturing in porous media. Comput. Methods Appl. Mech. Engrg. 2019, 347, 957–982. [Google Scholar] [CrossRef]
- Ni, T.; Pesavento, F.; Zaccariotto, M.; Galvanetto, U.; Zhu, Q.; Schrefler, B. Hybrid fem and peridynamic simulation of hydraulic fracture propagation in saturated porous media. Comput. Methods Appl. Mech. Engrg. 2020, 366, 113101. [Google Scholar] [CrossRef]
- Ouchi, H.; Katiyar, A.; Foster, J.; Sharma, M. A peridynamics model for the propagation of hydraulic fractures in naturally fractured reservoirs. SPE J. 2017, 22, 1082–1102. [Google Scholar] [CrossRef]
- Nadimi, S.; Miskovich, I.; McLennan, J. A 3d peridynamic simulation of hydraulic fracture process in a heterogeneous medium. J. Pet. Sci. Eng. 2016, 145, 444–452. [Google Scholar] [CrossRef]
- Yang, Y.; Tang, X.; Zheng, H.; Liu, Q.; Liu, Z. Hydraulic fracturing modeling using the enriched numerical manifold method. Appl. Math. Model. 2018, 53, 462–486. [Google Scholar] [CrossRef]
- Wu, Z.; Wong, L. Extension of numerical manifold method for coupled fluid flow and fracturing problems. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1990–2008. [Google Scholar] [CrossRef]
- Bakhshi, E.; Rasouli, V.; Ghorbani, A.; Fatehi Marji, M.; Damjanac, B.; Wan, X. Lattice numerical simulations of lab-scale hydraulic fracture and natural interface interaction. Rock Mech. Rock Eng. 2019, 52, 1315–1337. [Google Scholar] [CrossRef]
- Samimi, S.; Pak, A. A fully coupled element-free Galerkin model for hydro-mechanical analysis of advancement of fluid-driven fractures in porous media, Int. J. Numer. Anal. Methods Geomech. 2016, 40, 2178–2206. [Google Scholar] [CrossRef]
- Douillet-Grellier, T.; Pramanik, R.; Pan, K.; Albaiz, A.; Jones, B.D.; Pourpak, H.; Williams, J.R. Mesh-free numerical simulation of pressure-driven fractures in brittle rocks. In Proceedings of the SPE Hydraulic Fracturing Technology Conference, The Woodlands, TX, USA, 9–11 February 2016. [Google Scholar]
- Peng, S.; Zhang, Z.; Mou, J.; Zhao, B.; Liu, Z.; Ghassemi, A. Hydraulic fracture simulation with hydro-mechanical coupled discretized virtual internal bond. J. Petrol. Sci. Eng. 2018, 69, 504–517. [Google Scholar] [CrossRef]
- Peirce, A.P.; Bunger, A.P. Interference fracturing: Nonuniform distributions of perforation clusters that promote simultaneous growth of multiple hydraulic fractures. SPE J. 2015, 20, 384–395. [Google Scholar] [CrossRef]
- Chen, X.; Li, Y.; Zhao, J.; Xu, W.; Fu, D. Numerical investigation for simultaneous growth of hydraulic fractures in multiple horizontal wells. J. Nat. Gas Sci. Eng. 2017, 51, 44–52. [Google Scholar] [CrossRef]
- Sun, T.; Zeng, Q.; Xing, H. A model for multiple hydraulic fracture propagation with thermo-hydro-mechanical coupling effects. Energies 2021, 14, 894. [Google Scholar] [CrossRef]
- Wu, K.; Olson, J.E. Mechanisms of simultaneous hydraulic-fracture propagation from multiple perforation clusters in horizontal wells. SPE J. 2016, 21, 1000–1008. [Google Scholar] [CrossRef]
- Zeng, Q.; Liu, Z.; Wang, T.; Gao, Y.; Zhuang, Z. Fully coupled simulation of multiple hydraulic fractures to propagate simultaneously from a perforated horizontal wellbore. Comput. Mech. 2017, 61, 137–155. [Google Scholar] [CrossRef]
- Siebrits, E.; Elbel, J.L.; Hoover, R.S.; Diyashev, I.R.; Griffin, L.G.; Demetrius, S.L.; Wright, C.A.; Davidson, B.M.; Steinsberger, N.P.; Hill, D.G. Refracture reorientation enhances gas production in Barnett shale tight gas wells. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dallas, TX, USA, 1–4 October 2000. [Google Scholar]
- Roussel, N.P.; Sharma, M.M. Optimizing fracture spacing and sequencing in horizontal-well fracturing. SPE Prod. Oper. 2011, 26, 173–184. [Google Scholar] [CrossRef]
- Liu, C.; Liu, H.; Zhang, Y.; Deng, D.; Wu, H. Optimal spacing of staged fracturing in horizontal shale-gas well. J. Pet. Sci. Eng. 2015, 132, 86–93. [Google Scholar] [CrossRef]
- Zeng, Y.; Zhang, X.; Zhang, B. Stress redistribution in multi-stage hydraulic fracturing of horizontal wells in shales. Petrol. Sci. 2015, 12, 628–635. [Google Scholar] [CrossRef][Green Version]
- Yao, J.; Zeng, Q.; Huang, Z.; Sun, H.; Zhang, L. Numerical modeling of simultaneous hydraulic fracturing in the mode of multi-well pads. Sci. China Technol. Sci. 2017, 60, 232–242. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, J.; Hu, Y.; Zhang, S.; Huang, T.; Liu, X. Numerical simulation of multistage fracturing optimization and application in coalbed methane horizontal wells. Eng. Fract. Mech. 2019, 223, 106738. [Google Scholar] [CrossRef]
- Prashanth, S.; Wu, K.; Kwon, S.K. Optimization of simultaneously propagating multiple fractures in hydraulic fracturing to achieve uniform growth using data-based model reduction. Chem Eng. Res. Des. 2018, 136, 675–686. [Google Scholar]
- Wang, Y.; Li, X.; Zhang, B.; Zhao, Z. Optimization of multiple hydraulically fractured factors to maximize the stimulated reservoir volume in silty laminated shale formation, southeastern ordos basin, China. J. Pet. Sci. Eng. 2016, 145, 370–381. [Google Scholar] [CrossRef]
- Zeng, F.; Zhang, Y.; Guo, J.; Zhang, Q.; Zheng, Y. Optimized completion design for triggering a fracture network to enhance horizontal shale well production. J. Pet. Sci. Eng. 2020, 190, 107043. [Google Scholar] [CrossRef]
- Seyed, E.; Kaveh, A.; Hossein, M. Optimization of the horizontal-well multiple hydraulic fracturing operation in a low-permeability carbonate reservoir using fully coupled xfem model. Int. J. Rock Mech. Min. 2019, 114, 33–45. [Google Scholar]
- Xu, S.; Feng, Q.; Wang, S.; Farzam, J.; Li, Y. Optimization of multistage fractured horizontal well in tight oil based on embedded discrete fracture model. Comput. Chem. Eng. 2018, 117, 291–308. [Google Scholar]
- Meyer, B.; Bazan, L.; Jacot, R.; Lattibeaudiere, M. Optimization of multiple transverse hydraulic fractures in horizontal wellbores. In Proceedings of the SPE Unconventional Gas Conference, Pittsburgh, PA, USA, 23–25 February 2010. [Google Scholar]
- Yu, W.; Sepehrnoori, K. Optimization of well spacing for Bakken tight oil reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 25–27 August 2014. [Google Scholar]
- Zhang, H.; Sheng, J. Optimization of horizontal well fracturing in shale gas reservoir based on stimulated reservoir volume. J. Pet. Sci. Eng. 2020, 190, 107059. [Google Scholar] [CrossRef]
- Morozov, A.; Popkov, D.; Duplyakov, V.; Mutalova, R.; Paderin, G. Data-driven model for hydraulic fracturing design optimization: Focus on building digital database and production forecast. J. Pet. Sci. Eng. 2020, 194, 107504. [Google Scholar] [CrossRef]
- Jiang, B.; Li, H.; Zhang, Y.; Wang, Y.; Wang, J.; Patil, S. Multiple fracturing parameters optimization for horizontal gas well using a novel hybrid method. J. Nat. Gas Sci. Eng. 2016, 34, 604–615. [Google Scholar] [CrossRef]
- Kang, C.A.; McClure, M.W.; Reddy, S.; Naidenova, M.; Zdravko, T. Optimizing shale economics with an integrated hydraulic fracturing and reservoir simulator and a bayesian automated history matching and optimization algorithm. In Proceedings of the SPE Hydraulic Fracturing Technology Conference and Exhibition, The Woodlands, TX, USA, 1–3 February 2022. [Google Scholar]
- Willingham, J.D.; Tan, H.C.; Norman, L.R. Perforation Friction Pressure of Fracturing Fluid Slurries. In Proceedings of the Low Permeability Reservoirs Symposium, Denver, CO, USA, 26–28 April 1993. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Mhs95 Sixth International Symposium on Micro Machine & Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Geertsma, J.; De Klerk, F. A rapid method of predicting width and extent of hydraulically induced fractures. J. Petrol. Technol. 1969, 21, 1571–1581. [Google Scholar] [CrossRef]
- Wang, J.; Olson, J.E. Auto-optimization of hydraulic fracturing design with three-dimensional fracture propagation in naturally fractured multi-layer formations. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Virtual, 20–22 July 2020. [Google Scholar]
- Mehrabi, M.; Pei, Y.; Haddad, M.; Javadpour, F.; Sepehrnoori, K. Quasi-static fracture height growth in laminated reservoirs: Impacts of stress and toughness barriers, horizontal well landing depth, and fracturing fluid density. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology Conference, Houston, TX, USA, 26–28 July 2021. [Google Scholar]








| Parameter | Magnitude/Unit | Parameter | Magnitude/Unit |
|---|---|---|---|
| Young’s modulus E | 40 GPa | Fracture height h | 30 m |
| Poisson’s ratio | 0.25 | Fluid viscosity μ | 1 × 10−3 Pa∙s |
| Perforation diameter dp | 0.01 m | Fracturing fluid density ρ | 1.2 × 103 kg/m3 |
| Perforation number np | 60 | Fluid injection rate QT | 0.0405 m3/s |
| Maximum principal stress | 35 MPa | Minimum principal stress | 31 MPa |
| Cluster Number m | Total Spacing ΔS/m | Perforation Number np | Perforation Diameter dp/10−3 m | Variance s2 |
|---|---|---|---|---|
| 3 | 40 | 10, 30, 10 | 7, 15, 7 | 16.23 |
| 50 | 10, 30, 10 | 7, 15, 7 | 0.25 | |
| 4 | 60 | 10, 30, 27, 10 | 7, 11, 15, 7 | 8.31 |
| 70 | 10, 26, 25, 10 | 7, 12, 10, 7 | 0.63 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zeng, Q.; Liu, W.; Yao, J. Optimization of Non-Uniform Perforation Parameters for Multi-Cluster Fracturing. Energies 2022, 15, 5099. https://doi.org/10.3390/en15145099
Zeng Q, Liu W, Yao J. Optimization of Non-Uniform Perforation Parameters for Multi-Cluster Fracturing. Energies. 2022; 15(14):5099. https://doi.org/10.3390/en15145099
Chicago/Turabian StyleZeng, Qingdong, Wenzheng Liu, and Jun Yao. 2022. "Optimization of Non-Uniform Perforation Parameters for Multi-Cluster Fracturing" Energies 15, no. 14: 5099. https://doi.org/10.3390/en15145099
APA StyleZeng, Q., Liu, W., & Yao, J. (2022). Optimization of Non-Uniform Perforation Parameters for Multi-Cluster Fracturing. Energies, 15(14), 5099. https://doi.org/10.3390/en15145099





