Natural Ventilation and Aerosol Particles Dispersion Indoors
Abstract
:1. Introduction
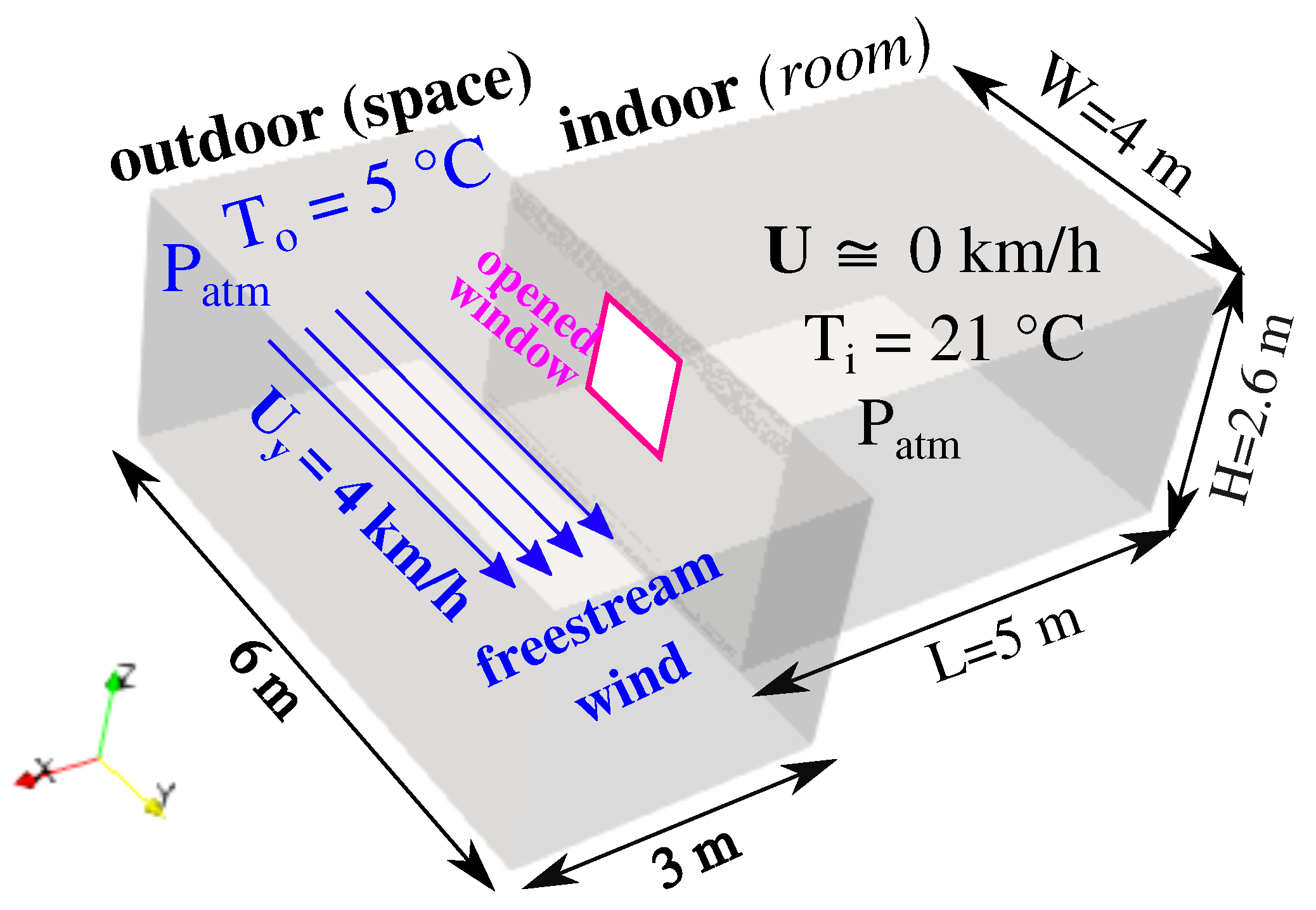
2. Computational Methodology and Problem Setup
- i.
- Natural ventilation due to thermal convection at negligible outdoor wind speed ( km/h), and
- ii.
- Natural ventilation due to thermal convection at a low wind speed of km/h.
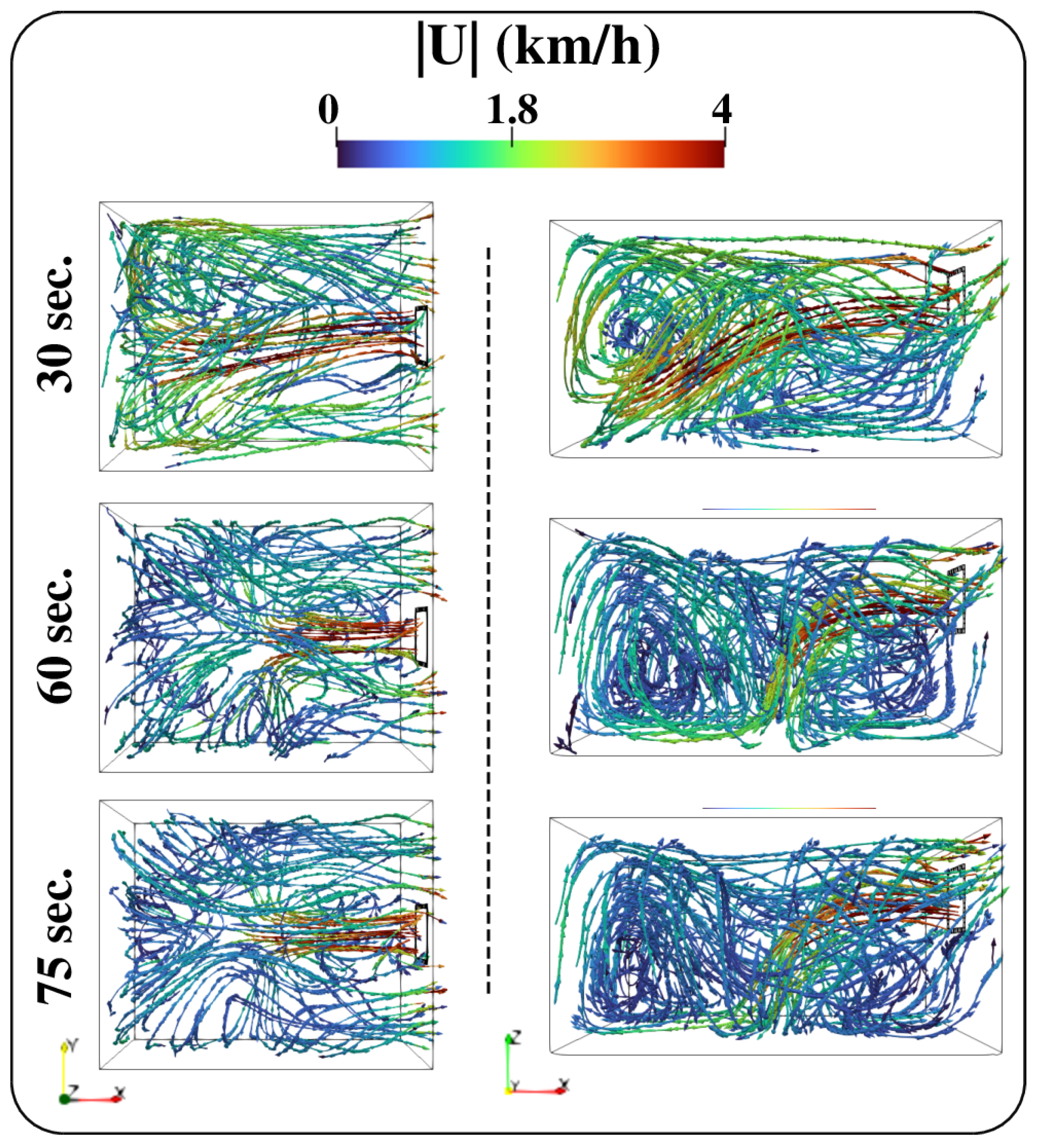
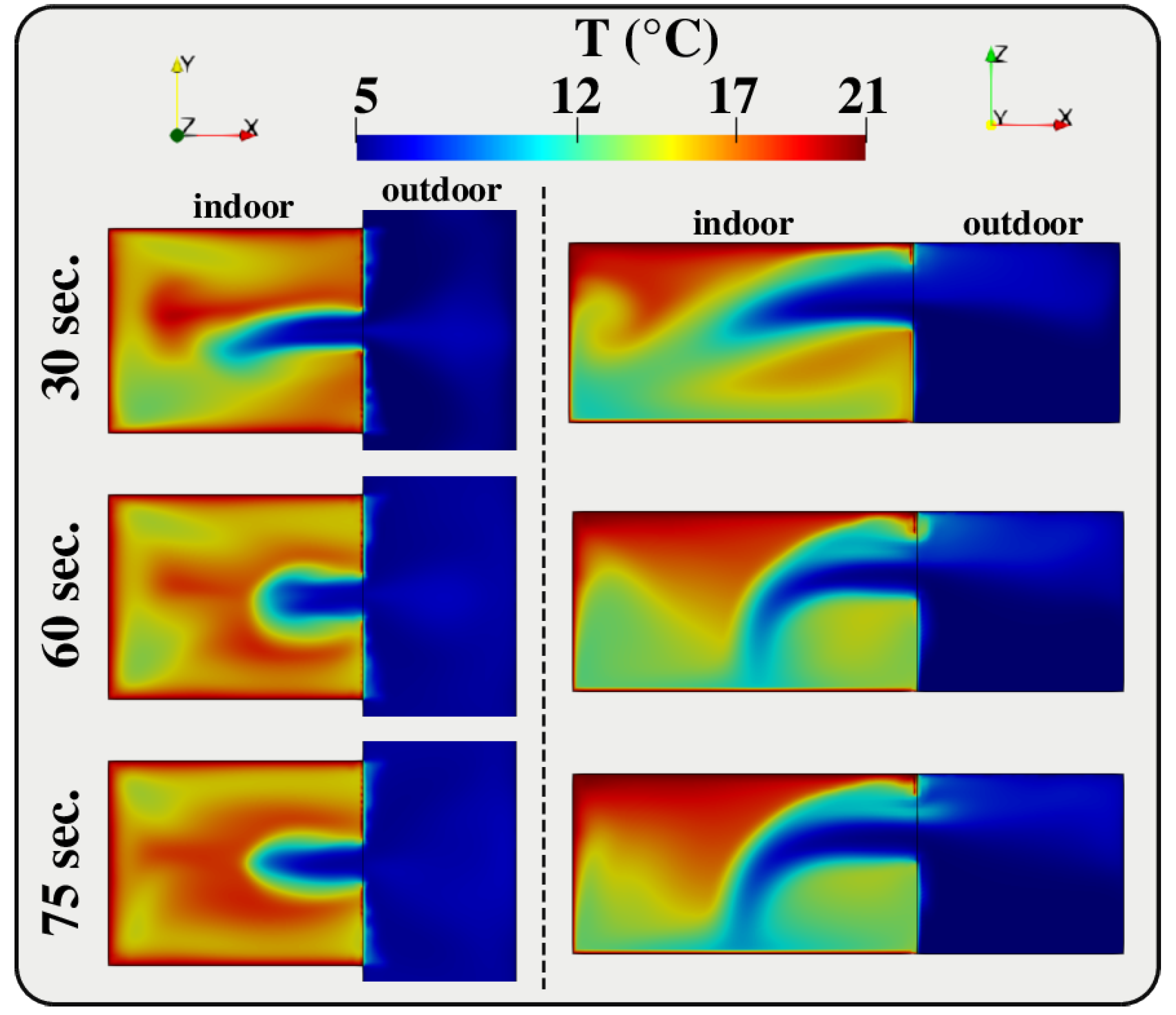
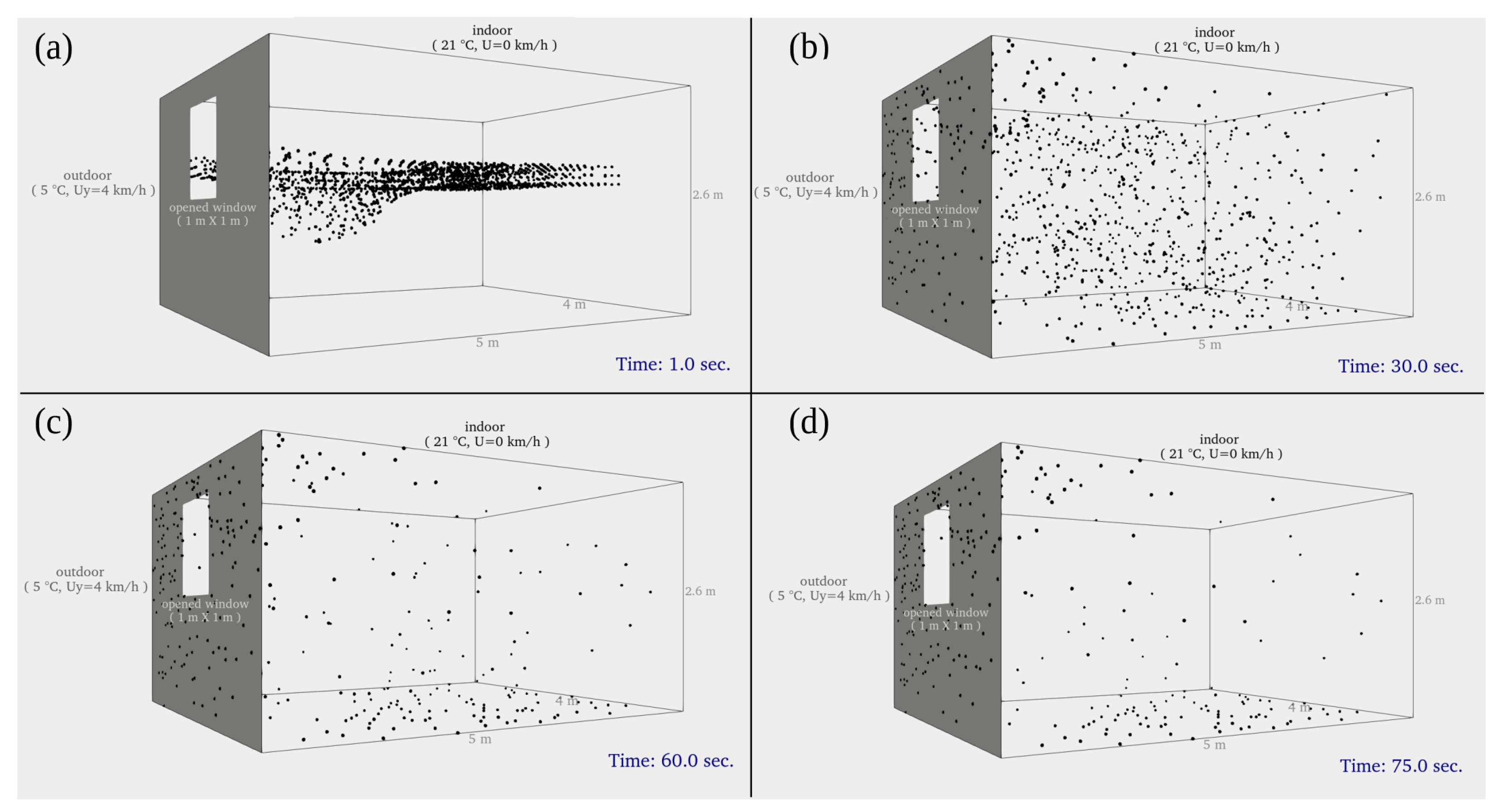
3. Flow Behaviour and Aerosol Particle Transport
4. Conclusions
- For a modest wind speed of airing, 95% of the aerosol particles remain suspended indoors after 75 s, decreasing slowly (slope of −0.03). Removing the particles would need about one hour (for an initial allocation of 3108 aerosol particles).
- Using natural ventilation, we need about 4 h to remove the initial aerosol particles suspended in the room.
- Additionally, considering the average time of viral infection (about 15 min), we should focus on better controlling the spread of hazardous aerosol particulate matter in indoor spaces.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lucci, F.; Frederix, E.; Kuczaj, A.K. AeroSolved: Computational fluid dynamics modeling of multispecies aerosol flows with sectional and moment methods. J. Aerosol Sci. 2022, 159, 105854. [Google Scholar] [CrossRef]
- Janoszek, T.; Lubosik, Z.; Świerczek, L.; Walentek, A.; Jaroszewicz, J. Experimental and CFD Simulations of the Aerosol Flow in the Air Ventilating the Underground Excavation in Terms of SARS-CoV-2 Transmission. Energies 2021, 14, 4743. [Google Scholar] [CrossRef]
- Bekierski, D.; Kostyrko, K.B. The Influence of Outdoor Particulate Matter PM2.5 on Indoor Air Quality: The Implementation of a New Assessment Method. Energies 2021, 14, 6230. [Google Scholar] [CrossRef]
- Sal, R.; Cole, M.; Bobbi, M. Lagrangian 3D CFD Simulation of Turbulent Aerosol Experiments. Trans. Am. Nucl. Soc. 2016, 115, 755–758. [Google Scholar]
- Mead-Hunter, R.; King, A.J.; Kasper, G.; Mullins, B.J. Computational fluid dynamics (CFD) simulation of liquid aerosol coalescing filters. J. Aerosol Sci. 2013, 61, 36–49. [Google Scholar] [CrossRef]
- Yingjie TANG, B.G. Computational fluid dynamics simulation of aerosol transport and deposition. Front. Environ. Sci. Eng. 2011, 5, 362. [Google Scholar] [CrossRef]
- Baoshun Ma, K.R.L. CFD simulation of aerosol deposition in an anatomically based human large-medium airway model. Ann. Biomed. Eng. 2009, 37, 271–285. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. Weather impact on airborne coronavirus survival. Phys. Fluids 2020, 32, 093312. [Google Scholar] [CrossRef]
- Dbouk, T.; Drikakis, D. On pollen and airborne virus transmission. Phys. Fluids 2021, 33, 063313. [Google Scholar] [CrossRef]
- Dbouk, T.; Roger, F.; Drikakis, D. Reducing indoor virus transmission using air purifiers. Phys. Fluids 2021, 33, 103301. [Google Scholar] [CrossRef]
- WHO. World Health Organization. Coronavirus Disease (COVID-19): Ventilation and Air Conditioning. Available online: https://www.who.int/news-room/questions-and-answers/item/coronavirus-disease-COVID-19-ventilation-and-air-conditioning (accessed on 24 December 2021).
- Ding, J.; Yu, C.W.; Cao, S.J. HVAC systems for environmental control to minimize the COVID-19 infection. Indoor Built Environ. 2020, 29, 1195–1201. [Google Scholar] [CrossRef]
- Xu, C.; Luo, X.; Yu, C.; Cao, S.J. The 2019-nCoV epidemic control strategies and future challenges of building healthy smart cities. Indoor Built Environ. 2020, 29, 639–644. [Google Scholar] [CrossRef] [Green Version]
- Chow, W.K.; Chow, C.L. A proposed two-stage quarantine containment scheme against spreading of novel coronavirus (SARS-CoV-2). Indoor Built Environ. 2020, 31, 1202–1209. [Google Scholar] [CrossRef]
- Van-Dijken, F.; Boerstra, A. Implications of COVID-19 pandemic for application of natural ventilation. REHVA J. 2021, 3, 58–63. [Google Scholar]
- Singh, R. Architect’s Role in Airborne Infection Control Through Ventilation Design. IndiaRxiv 2020. [Google Scholar] [CrossRef]
- Foster, A.; Kinzel, M. SARS-CoV-2 transmission in classroom settings: Effects of mitigation, age, and Delta variant. Phys. Fluids 2021, 33, 113311. [Google Scholar] [CrossRef] [PubMed]
- Foster, A.; Kinzel, M. Estimating COVID-19 exposure in a classroom setting: A comparison between mathematical and numerical models. Phys. Fluids 2021, 33, 021904. [Google Scholar] [CrossRef]
- Kim, J.; Hong, Y.; Seong, N.; Kim, D.D. Assessment of ANN Algorithms for the Concentration Prediction of Indoor Air Pollutants in Child Daycare Centers. Energies 2022, 15, 2654. [Google Scholar] [CrossRef]
- Borowski, M.; Zwolińska, K.; Czerwiński, M. An Experimental Study of Thermal Comfort and Indoor Air Quality- A Case Study of a Hotel Building. Energies 2022, 15, 2026. [Google Scholar] [CrossRef]
- Motamedi, H.; Shirzadi, M.; Tominaga, Y.; Mirzaei, P.A. CFD modeling of airborne pathogen transmission of COVID-19 in confined spaces under different ventilation strategies. Sustain. Cities Soc. 2022, 76, 103397. [Google Scholar] [CrossRef]
- Chen, C.Y.; Chen, P.H.; Chen, J.K.; Su, T.C. Recommendations for ventilation of indoor spaces to reduce COVID-19 transmission. J. Formos. Med. Assoc. 2021, 120, 2055–2060. [Google Scholar] [CrossRef] [PubMed]
- Che, W.; Ding, J.; Li, L. Airflow deflectors of external windows to induce ventilation: Towards COVID-19 prevention and control. Sustain. Cities Soc. 2021, 77, 103548. [Google Scholar] [CrossRef] [PubMed]
- Gil-Baez, M.; Lizana, J.; Becerra Villanueva, J.; Molina-Huelva, M.; Serrano-Jimenez, A.; Chacartegui, R. Natural ventilation in classrooms for healthy schools in the COVID era in Mediterranean climate. Build. Environ. 2021, 206, 108345. [Google Scholar] [CrossRef]
- Monge-Barrio, A.; Bes-Rastrollo, M.; Dorregaray-Oyaregui, S.; González-Martínez, P.; Martin-Calvo, N.; López-Hernández, D.; Arriazu-Ramos, A.; Sánchez-Ostiz, A. Encouraging natural ventilation to improve indoor environmental conditions at schools. Case studies in the north of Spain before and during COVID. Energy Build. 2022, 254, 111567. [Google Scholar] [CrossRef]
- Pourfattah, F.; Wang, L.P.; Deng, W.; Ma, Y.F.; Hu, L.; Yang, B. Challenges in simulating and modeling the airborne virus transmission: A state-of-the-art review. Phys. Fluids 2021, 33, 101302. [Google Scholar] [CrossRef]
- Atkinson, J.; Chartier, Y.; Pessoa-Silva, C.; Jensen, P.; Li, Y.; Seto, W. Natural Ventilation for Infection Control in Health-Care Settings; World Health Organization: Geneva, Switzerland, 2009. [Google Scholar]
- Peng, N.N.; Chow, K.W.; Liu, C.H. Computational study on the transmission of the SARS-CoV-2 virus through aerosol in an elevator cabin: Effect of the ventilation system. Phys. Fluids 2021, 33, 103325. [Google Scholar] [CrossRef]
- Narayanan, S.R.; Yang, S. Airborne transmission of virus-laden aerosols inside a music classroom: Effects of portable purifiers and aerosol injection rates. Phys. Fluids 2021, 33, 033307. [Google Scholar] [CrossRef]
- Sinha, K.; Yadav, M.S.; Verma, U.; Murallidharan, J.S.; Kumar, V. Effect of recirculation zones on the ventilation of a public washroom. Phys. Fluids 2021, 33, 117101. [Google Scholar] [CrossRef]
- Park, S.; Choi, Y.; Song, D.; Kim, E.K. Natural ventilation strategy and related issues to prevent coronavirus disease 2019 (COVID-19) airborne transmission in a school building. Sci. Total Environ. 2021, 789, 147764. [Google Scholar] [CrossRef]
- United States Environmental Protection Agency (US-EPA). Indoor Air in Homes and Coronavirus (COVID-19). Available online: https://www.epa.gov/coronavirus/indoor-air-homes-and-coronavirus-COVID-19 (accessed on 24 December 2021).
- Celik, I.B.; Ghia, U.; Roache, P.J.; Freitas, C.J. Procedure for Estimation and Reporting of Uncertainty Due to Discretization in CFD Applications. J. Fluids Eng. 2008, 130, 078001. [Google Scholar] [CrossRef] [Green Version]
- Chatterjee, S.; Murallidharan, J.S.; Agrawal, A.; Bhardwaj, R. Why coronavirus survives longer on impermeable than porous surfaces. Phys. Fluids 2021, 33, 021701. [Google Scholar] [CrossRef] [PubMed]
- Julia, P.; Jillian, L.; Sue, R.K.; Benjamin, W.; Samuel, S.; Heidi, F.; Shannon, M.; Patsy, K.; Natalie, K. COVID-19 in a Correctional Facility Employee Following Multiple Brief Exposures to Persons with COVID-19. MMWR Morb. Mortal. Wkly. Rep. 2020, 69, 1569–1570. [Google Scholar] [CrossRef]





Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dbouk, T.; Drikakis, D. Natural Ventilation and Aerosol Particles Dispersion Indoors. Energies 2022, 15, 5101. https://doi.org/10.3390/en15145101
Dbouk T, Drikakis D. Natural Ventilation and Aerosol Particles Dispersion Indoors. Energies. 2022; 15(14):5101. https://doi.org/10.3390/en15145101
Chicago/Turabian StyleDbouk, Talib, and Dimitris Drikakis. 2022. "Natural Ventilation and Aerosol Particles Dispersion Indoors" Energies 15, no. 14: 5101. https://doi.org/10.3390/en15145101
APA StyleDbouk, T., & Drikakis, D. (2022). Natural Ventilation and Aerosol Particles Dispersion Indoors. Energies, 15(14), 5101. https://doi.org/10.3390/en15145101






