A New 7 kW Air-Core Transformer at 1.5 MHz for Embedded Isolated DC/DC Application
Abstract
:1. Introduction
2. Design of the Proposed Transformer
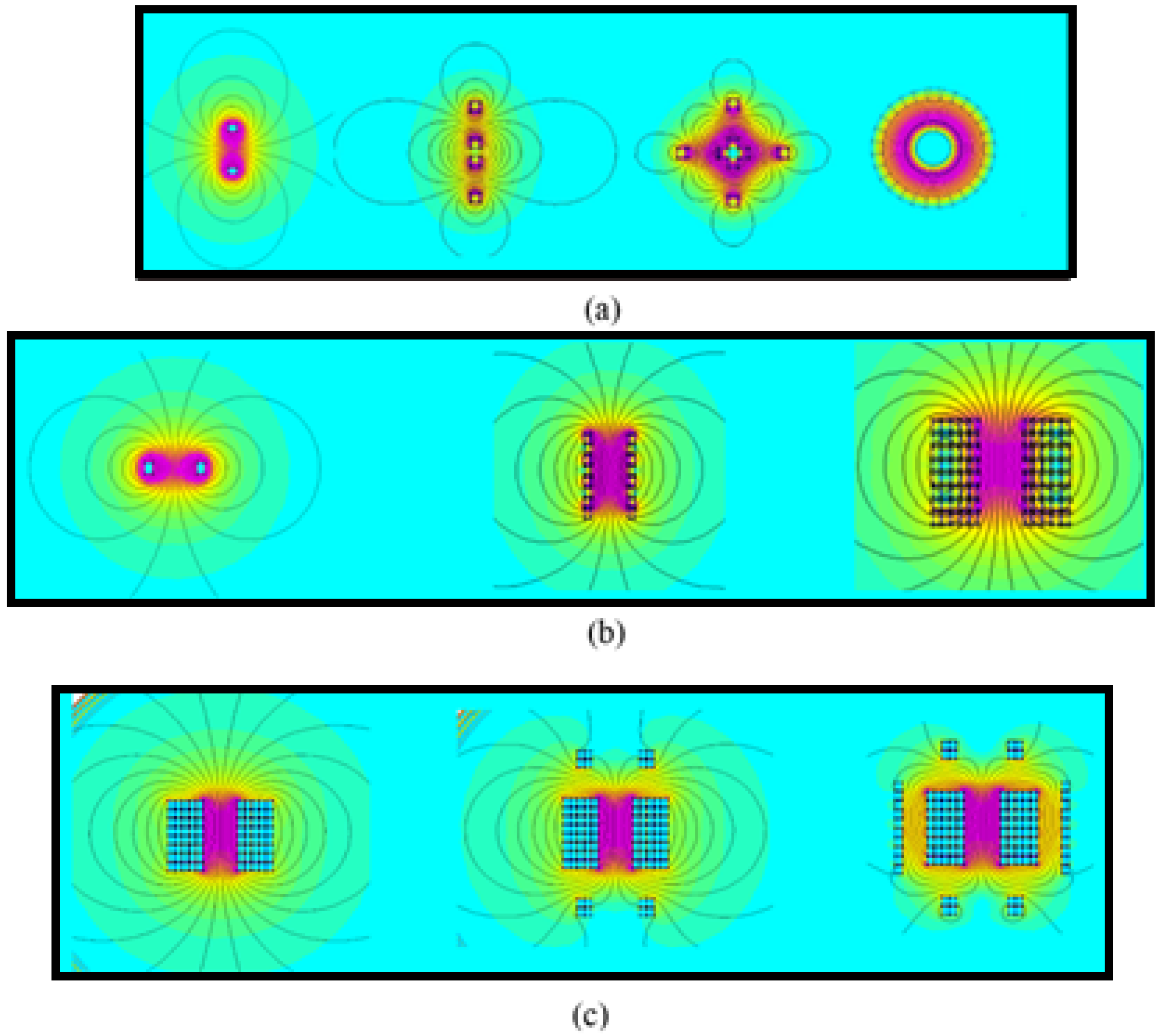
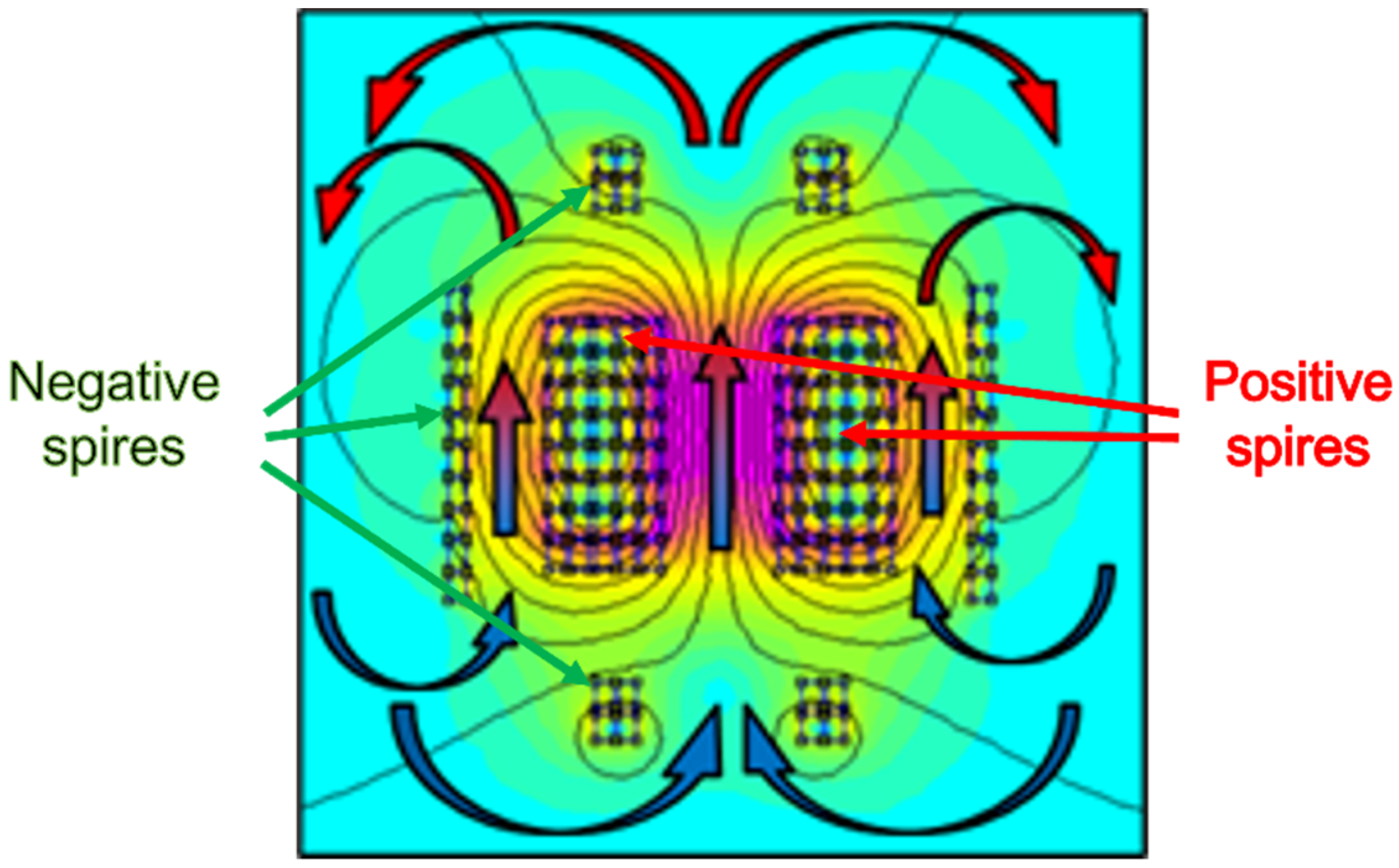
2.1. Magnetic Field Canalization
2.2. Conduction Losses
2.3. Model and Simulation
3. Electromagnetic Calculation
3.1. Electrical Simulation
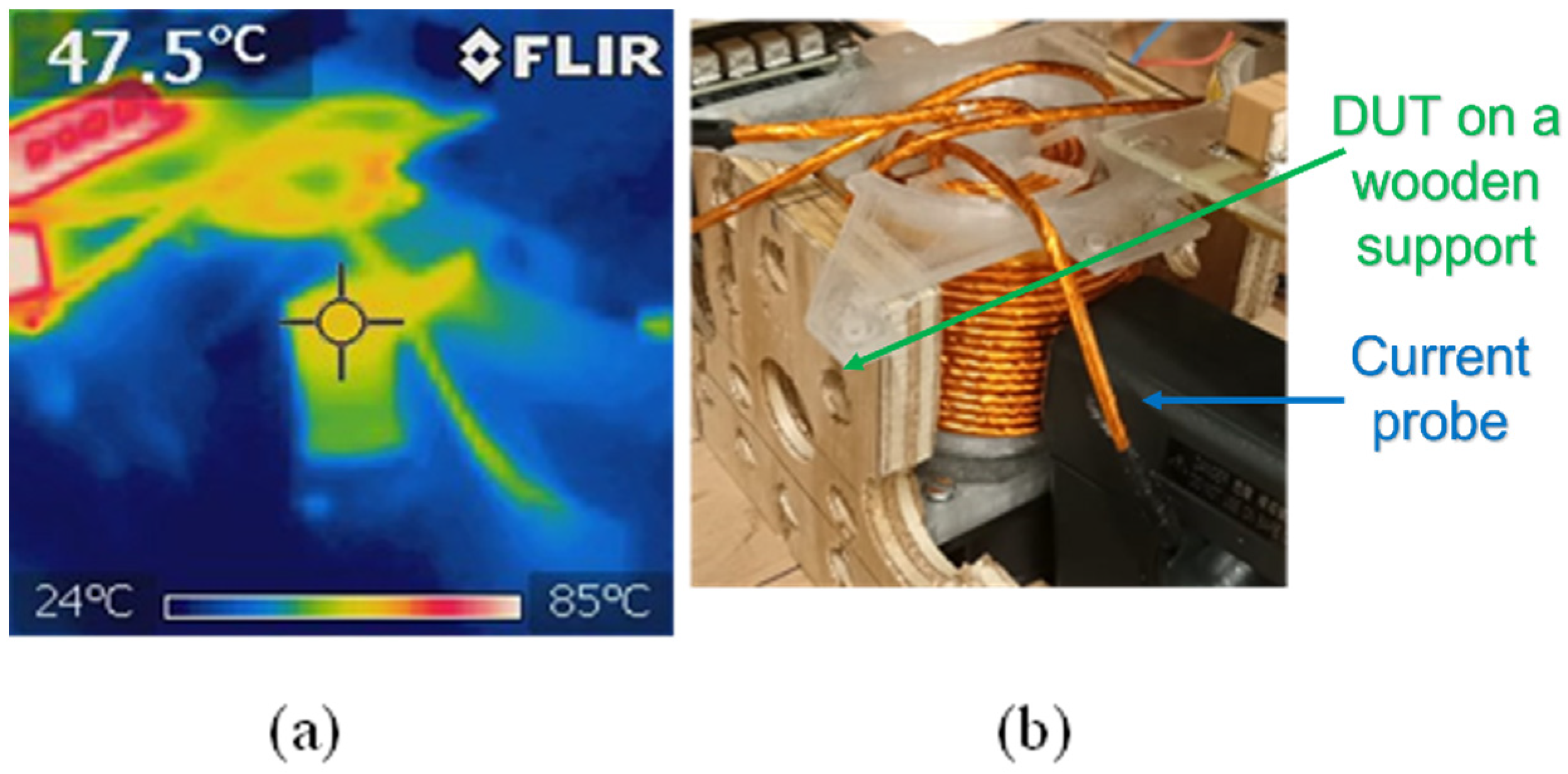
3.2. Test Bench
3.3. Electrical Measurements
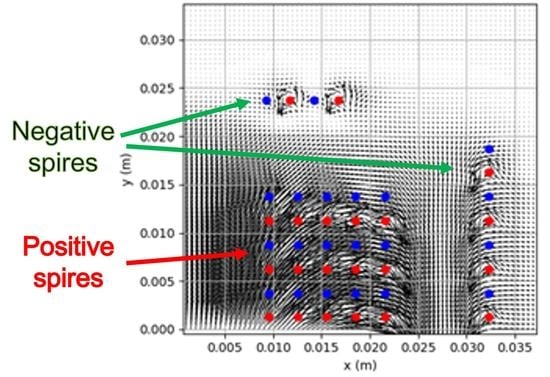
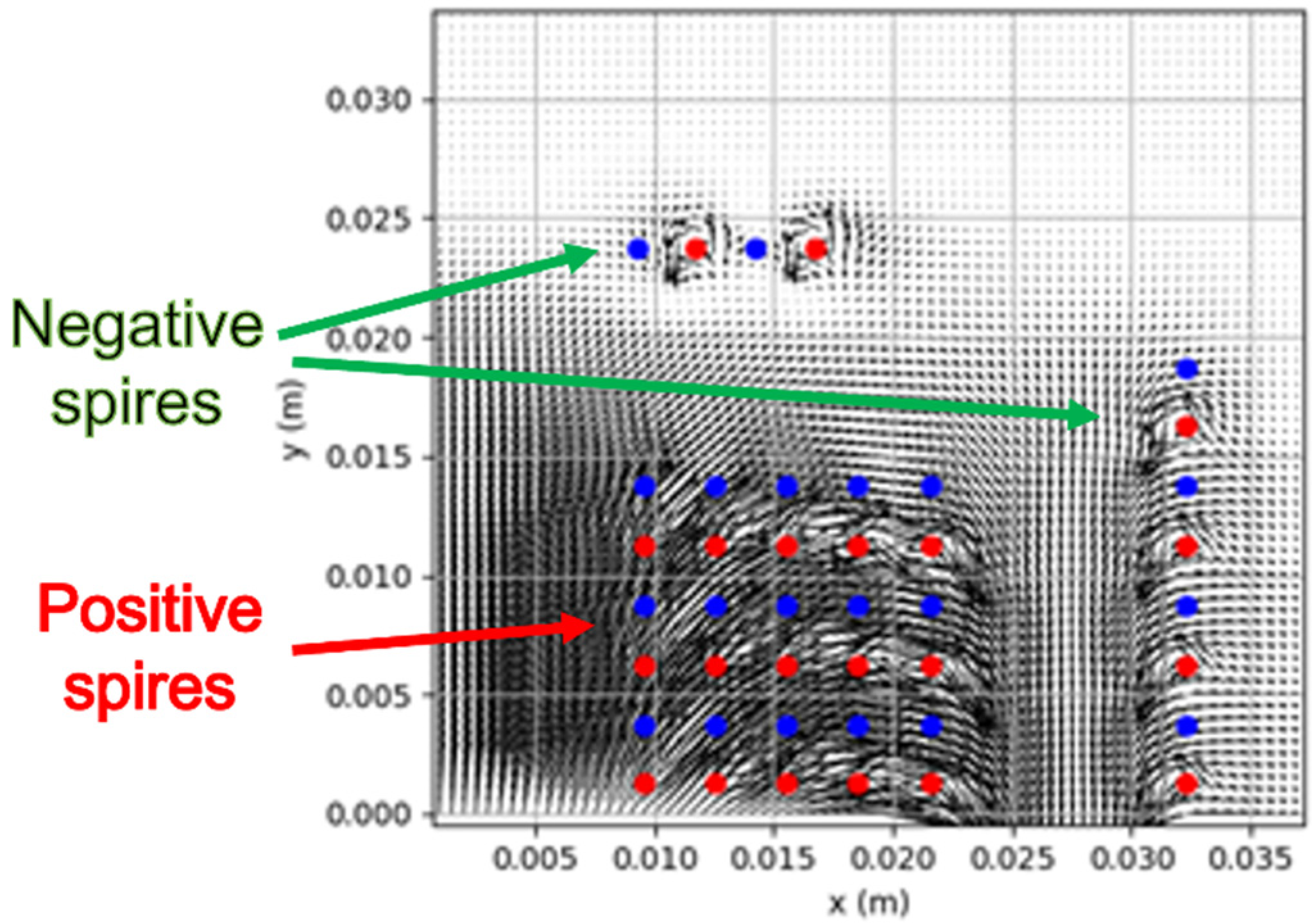
3.4. Magnetic Simulation
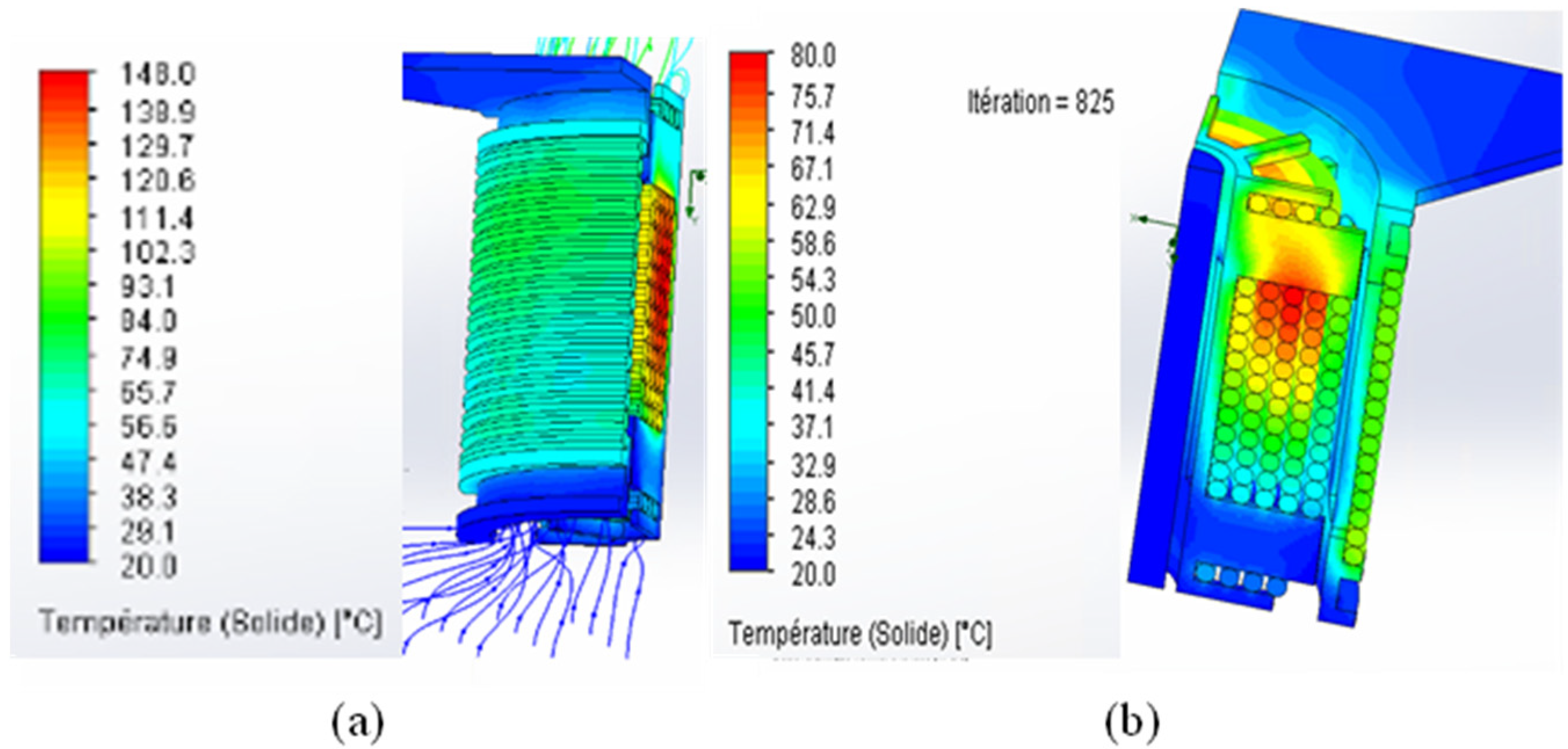
4. Thermal Design
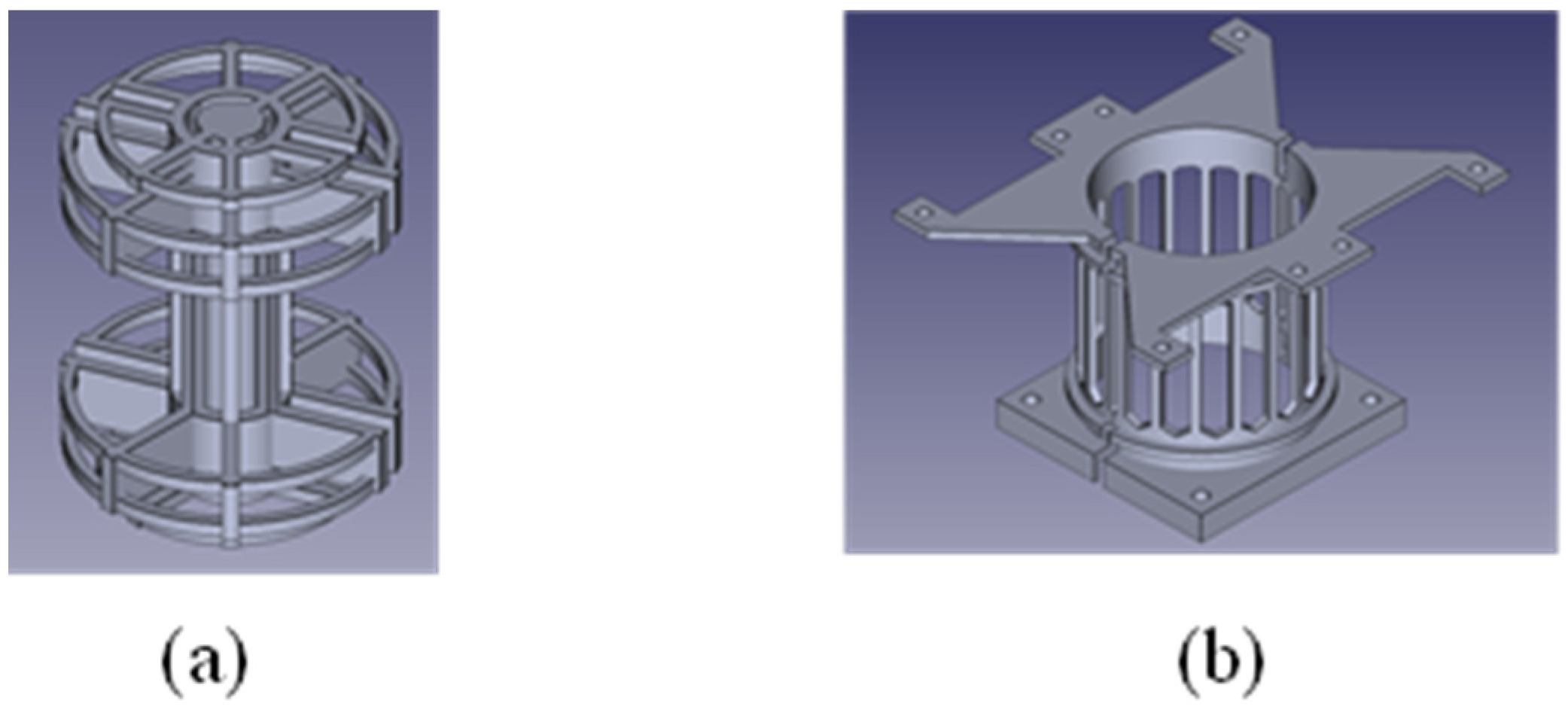
4.1. Support Material Determination
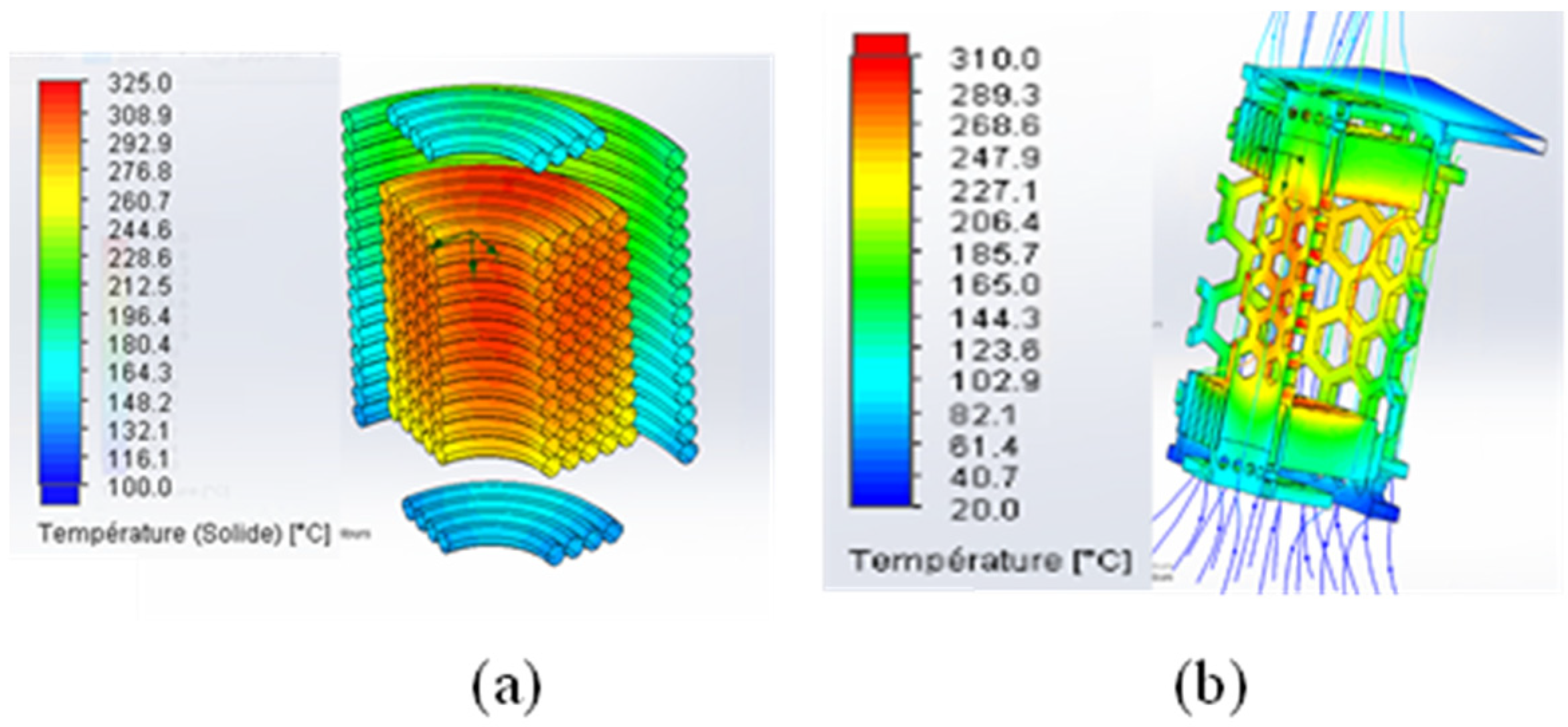
4.2. Natural Convection
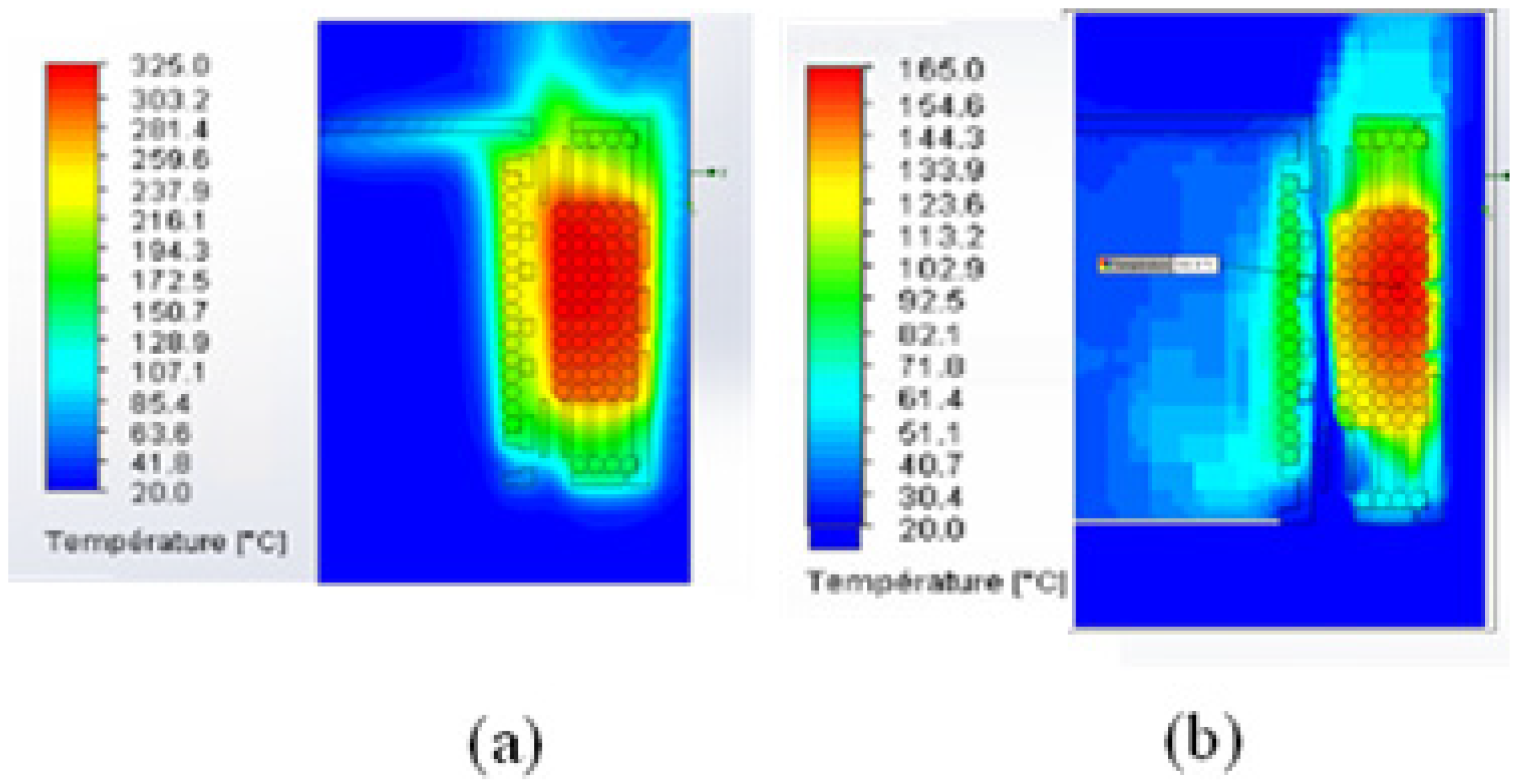
4.3. Air-Forced Convection
4.3.1. Change Material
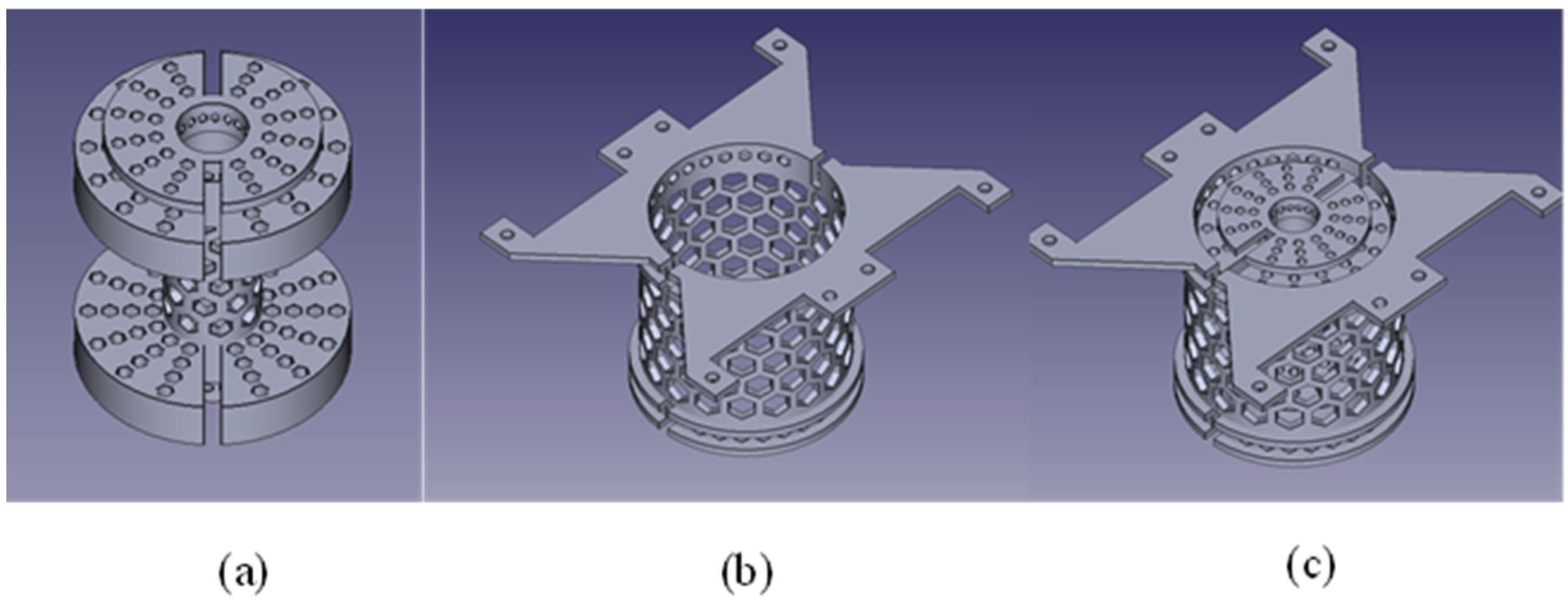
4.3.2. Change the Support Geometry
- The honeycomb configuration is replaced by long vertical corridors increasing the exchange surface in the direction of the fan.
- The above and below parts are the airiest as possible.
- A cylindrical part is added in the middle of the inside hole to force ventilated air to be in contact with the hot surfaces.
- A base is fixed to the fan and confines the air inside the transformer where the temperature is the highest.
4.3.3. Add Spaced Layers
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Jafari, A.; Nikoo, M.S.; Perera, N.; Yildirim, H.K.; Karakaya, F.; Soleimanzadeh, R.; Matioli, E. Comparison of Wide-band-gap Technologies for Soft-Switching Losses at High Frequencies. IEEE Trans. Power Electron. 2020, 35, 12595–12600. [Google Scholar] [CrossRef]
- Ribeiro, K.; Sadarnac, D.; Karimi, C.; Phulpin, T.; Bendani, L. A Bidirectional Three-port Current-fed LC Parallel Resonant Converter. In Proceedings of the 13th IEEE International Conference on Power Electronics and Drive Systems (PEDS 2019), Toulouse, France, 9–12 July 2019. [Google Scholar] [CrossRef]
- Sobrayen, L.; Dehem, P.; Karimi, C.; Phulpin, T.; Sadarnac, D. Modeling and ZVS Constraints of the Hybrid LLC Resonant Converter for MHz Level Operation. In Proceedings of the ECCE, Virtual, Vancouver, BC, Canada, 10–14 October 2021. [Google Scholar]
- Kabbara, W.; Bensetti, M.; Phulpin, T.; Caillierez, A.; Loudot, S.; Sadarnac, D. A Control Strategy to Avoid Drop and Inrush Currents during Transient Phases in a Multi-Transmitters DIPT System. Energies 2022, 15, 2911. [Google Scholar] [CrossRef]
- Nigam, M.; Sullivan, C.R. Multi-layer folded high-frequency toroidal inductor winding. In Proceedings of the IEEE Applied Power Electronics Conference, Austin, TX, USA, 24–28 February 2008; pp. 682–688. [Google Scholar]
- Yildirim, H.K.; Karakaya, F.; Soleimanzadeh, R.; Matioli, E. Design and analysis of different structures of a coreless planar transformer for a flyback converter. In Proceedings of the International Symposium on Power Electronics Power Electronics, Electrical Drives, Automation and Motion, Sorrento, Italy, 20–22 June 2012; pp. 827–831. [Google Scholar] [CrossRef]
- Hui, S.Y.R.; Chung, H.; Tang, S.C. Coreless PCB-based transformers for Power MOSFET/IGBT Gate Drive Circuits. In Proceedings of the PESC97, Record 28th Annual IEEE Power Electronics Specialists Conference, Formerly Power Conditioning Specialists Conference 1970-71, Power Processing and Electronic Specialists Conference 1972, St. Louis, MO, USA, 27 June 1997; Volume 2, pp. 1171–1176. [Google Scholar] [CrossRef]
- Yunas, J.; Yeop, B.; Azrul, M.; Hamzah, A.; Bais, B. Si Monolithic Planar Coreless Inductors for High Frequency Signal Transmission. In Proceedings of the 2013 IEEE International RF and Microwave Conference (RFM), Penang, Malaysia, 9–11 December 2013; pp. 47–50. [Google Scholar] [CrossRef]
- Reggiani, U.; Grandi, G.; Sancineto, G.; Serra, G. Comparison Between Air-Core and Laminated Iron-Core Inductors in Filtering Applications for Switching Converter. In Proceedings of the 7th IEEE International Power Electronics Congress. Technical Proceedings. CIEP 2000 (Cat. No.00TH8529), Acapulco, Mexico, 15–19 October 2000; pp. 9–14. [Google Scholar] [CrossRef]
- Ma, X.; Guo, Y.; Chen, X.; Xiang, Y.; Chen, K.-L. Impact of Coreless Current Transformer Position on Current Measurement. IEEE Trans. Instrum. Meas. 2019, 68, 3801–3809. [Google Scholar] [CrossRef]
- Murgatroyd, P.N. The Optimal Form for Coreless Inductors. IEEE Trans. Magn. 1989, 25, 2670–2677. [Google Scholar] [CrossRef]
- Hsuan, L.; Jiann-Fuh, C. Design process of high-frequency inductor with multiple air-gaps in the dimensional limitation. IET Power Electron. 2021, 16–33. [Google Scholar] [CrossRef]
- Rigot, V.; Phulpin, T.; Sadarnac, D.; Sakly, J. A new design of an air core transformer for Electric Vehicle On-Board Charger. In Proceedings of the 2020 22nd European Conference on Power Electronics and Applications (EPE’20 ECCE Europe), Lyon, France, 7–11 September 2020; pp. 1–9. [Google Scholar]
- Zhang, H.-B.; Cai, M.; He, X.-Y.; Chen, G.-H.; Wu, H.-J. A high self-resonant and quality factor transformer using novel geometry for silicon based RFICs. In Proceedings of the 2013 IEEE International Conference of Electron Devices and Solid-State Circuits, Hong Kong, China, 3–5 June 2013. [Google Scholar]
- Yu, D.; Han, K.S. Self-Inductance of Air-Core Circular Coils with Rectangular Cross Section. IEEE Trans. Magn. 1987, 23, 3916–3921. [Google Scholar] [CrossRef]
- Sadarnac, D. Du Composant Magnétique à L’électronique de Puissance—Analyse Modélisation Conception Dimensionnement des Transformateurs Inductances Convertisseurs—Cours et Exercices Corrigés; Ellipses: Paris, France, 2014. [Google Scholar]
- Vaisambhayana, S.; Dincan, C.; Shuyu, C.; Tripathi, A.; Haonan, T.; Karthikeya, B.R. State of Art survey for design of Medium Frequency High Power Transformer. In Proceedings of the 2016 Asian Conference on Energy, Power and Transportation Electrification (ACEPT), Singapore, 25–27 October 2016. [Google Scholar]
- Dowell, P.L. Effects of eddy currents in transformer windings. Proc. Inst. Electr. Eng. 1966, 113, 1387–1394. [Google Scholar] [CrossRef]
- Meyer, P.; Perriard, Y. Skin and Proximity Effects for Coreless Transformers. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar] [CrossRef]
- Wojda, R.P.; Kazimierczuk, M.K. Winding Resistance and Power Loss of Inductors with Litz and Solid-Round Wires. In Proceedings of the 2016 IEEE International Power Electronics and Motion Control Conference (PEMC), Varna, Bulgaria, 25–28 September 2016; pp. 860–865. [Google Scholar] [CrossRef]
- Rigot, V.; Phulpin, T.; Sakly, J.; Sadarnac, D. An Automotive High-Frequency Coreless Transformer of 11kw Dual Active Bridge Converter. In Proceedings of the PCIM2022, Nuremberg, Germany, 10–12 May 2022. [Google Scholar]
- Taurou, E.; Sadarnac, D.; Karimi, C.; Doffin, H. Design of a transformer for high power density charger—Electric vehicles application. In Proceedings of the 2017 19th European Conference on Power Electronics and Applications (EPE’17 ECCE Europe), Warsaw, Poland, 11–14 September 2017; pp. 1–10. [Google Scholar] [CrossRef]
- Pei, Y.; Le Bihan, Y.; Bensetti, M.; Pichon, L. Comparison of Coupling Coils for Static Inductive Power-Transfer Systems Taking into Account Sources of Uncertainty. Sustainability 2021, 13, 6324. [Google Scholar] [CrossRef]
- Lin, J.; Saunders, R.; Schulmeister, K.; Söderberg, P.; Stuck, B.; Swerdlow, A.; Taki, M.; Veyret, B.; Ziegelberger, G.; Repacholi, M.H. ICNIRP guidelines for limiting exposure to time-varying electric and magnetic fields (1 Hz TO 100 kHz). Health Phys. 2010, 99, 818–836. [Google Scholar] [CrossRef]
- International Commission on Non-Ionizing Radiation Protection. Guidelines for limiting exposure to electromagnetic fields (100 khz to 300 ghz). Health Phys. 2020, 118, 483–524. [Google Scholar] [CrossRef] [PubMed]
- Available online: https://ultimaker.com (accessed on 9 October 2021).
- Hexeb™ “Honeycomb Attributes and Properties” Hexcel Composites 2010-06-01. Available online: https://www.hexcel.com/Products/Honeycomb/ (accessed on 17 July 2022).
- Oftadeh, R.; Haghpanah, B.; Vella, D.; Boudaoud, A.; Vaziri, A. Optimal Fractal-like Hierarchical Honeycombs. Phys. Rev. Lett. 2014, 113, 104301. [Google Scholar] [CrossRef] [PubMed] [Green Version]




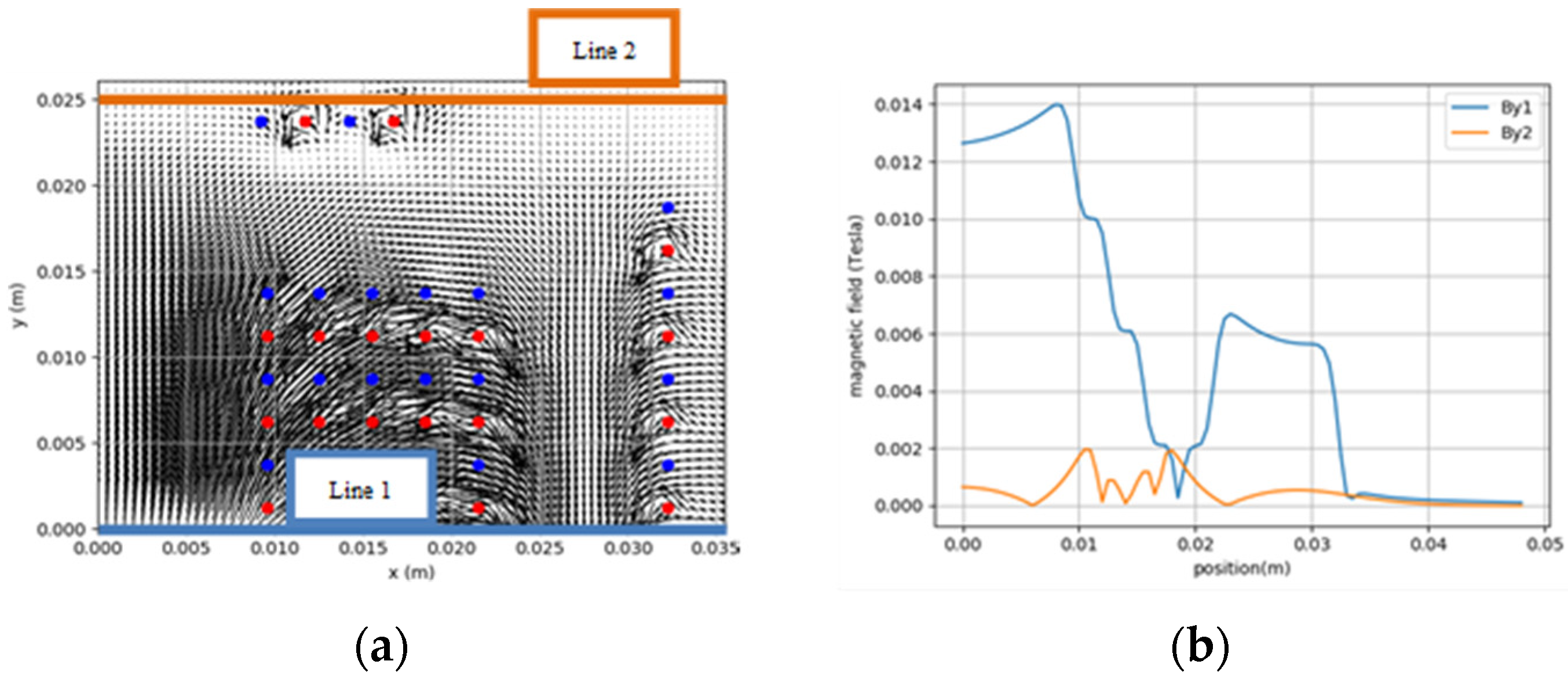
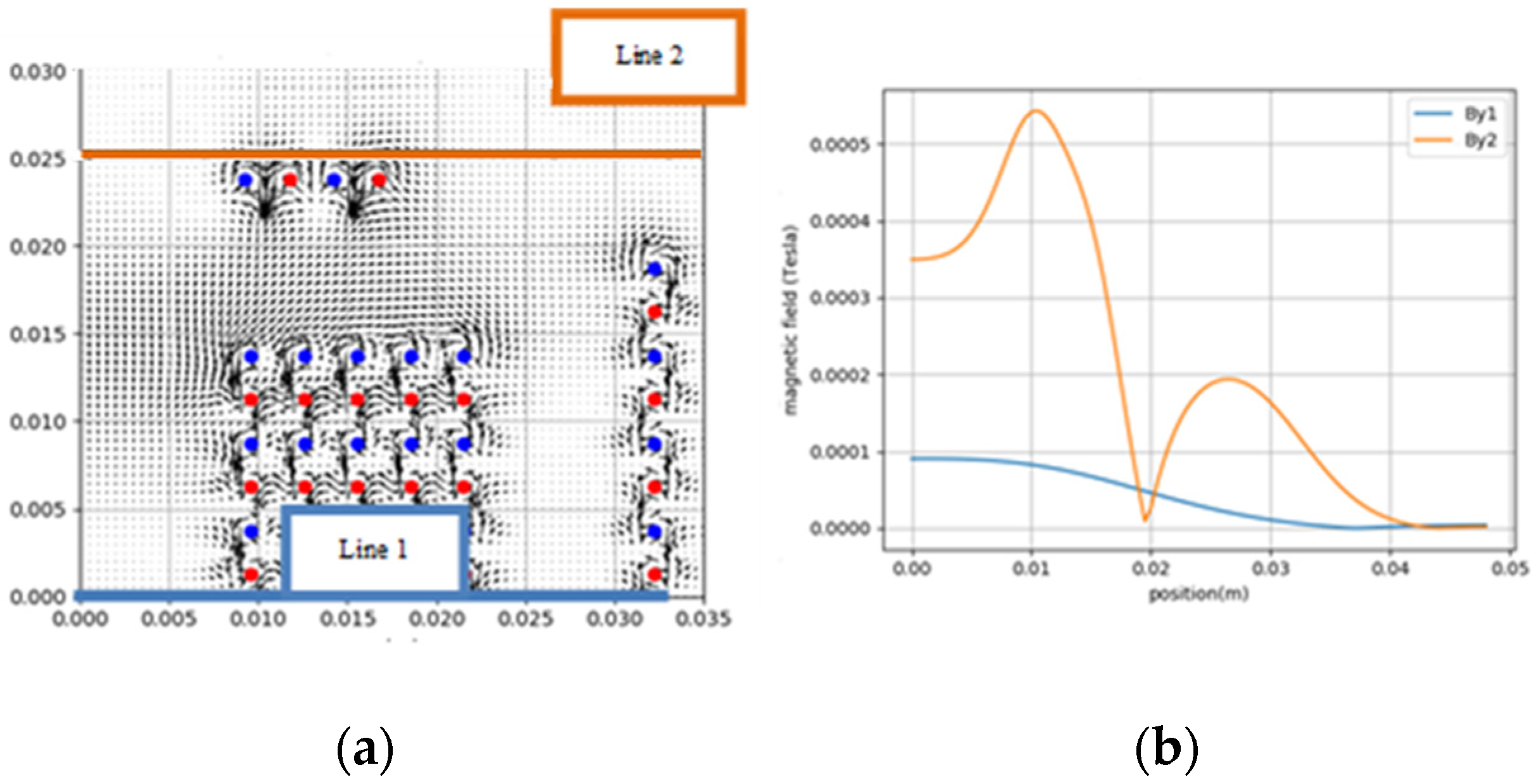

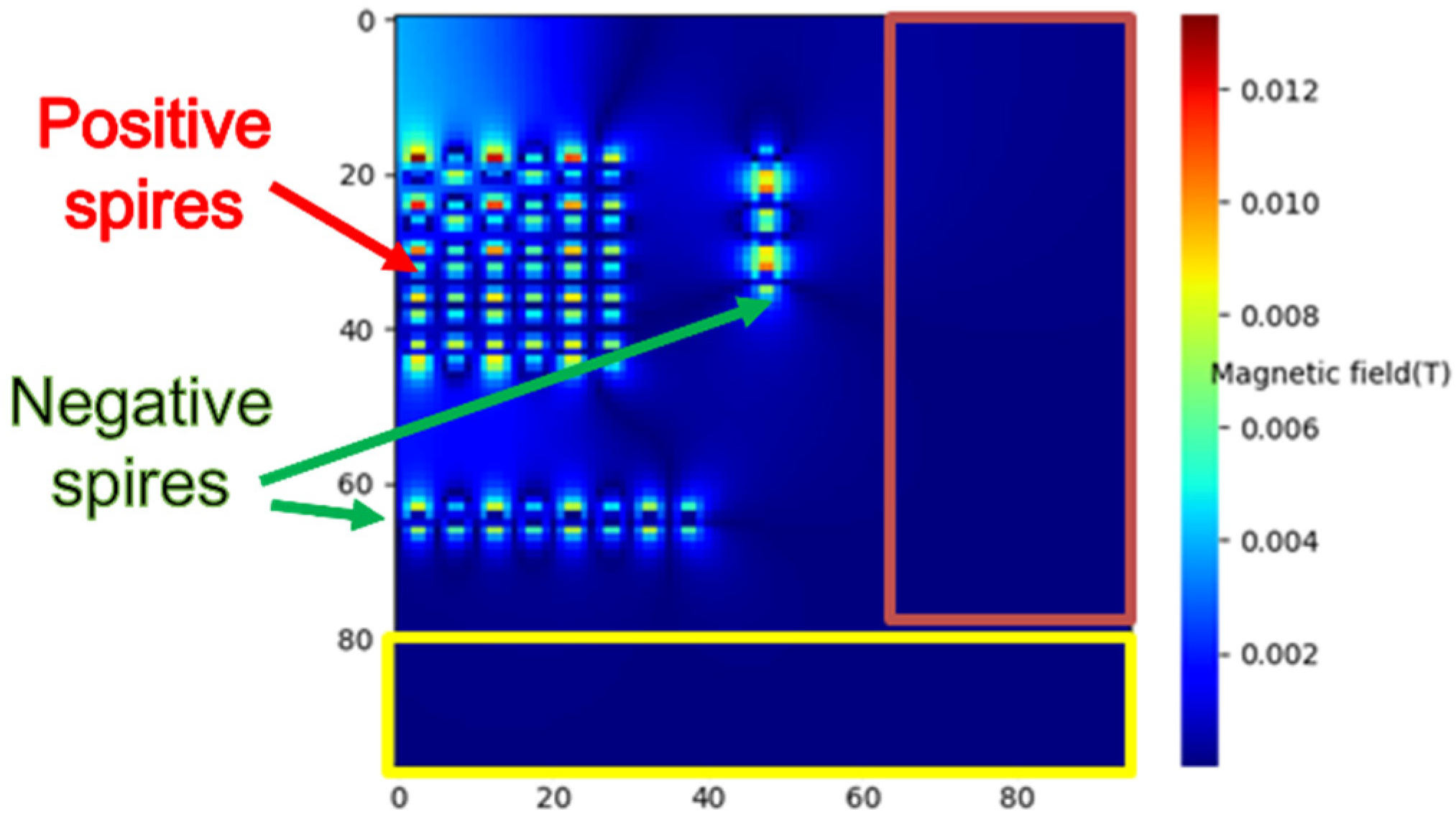
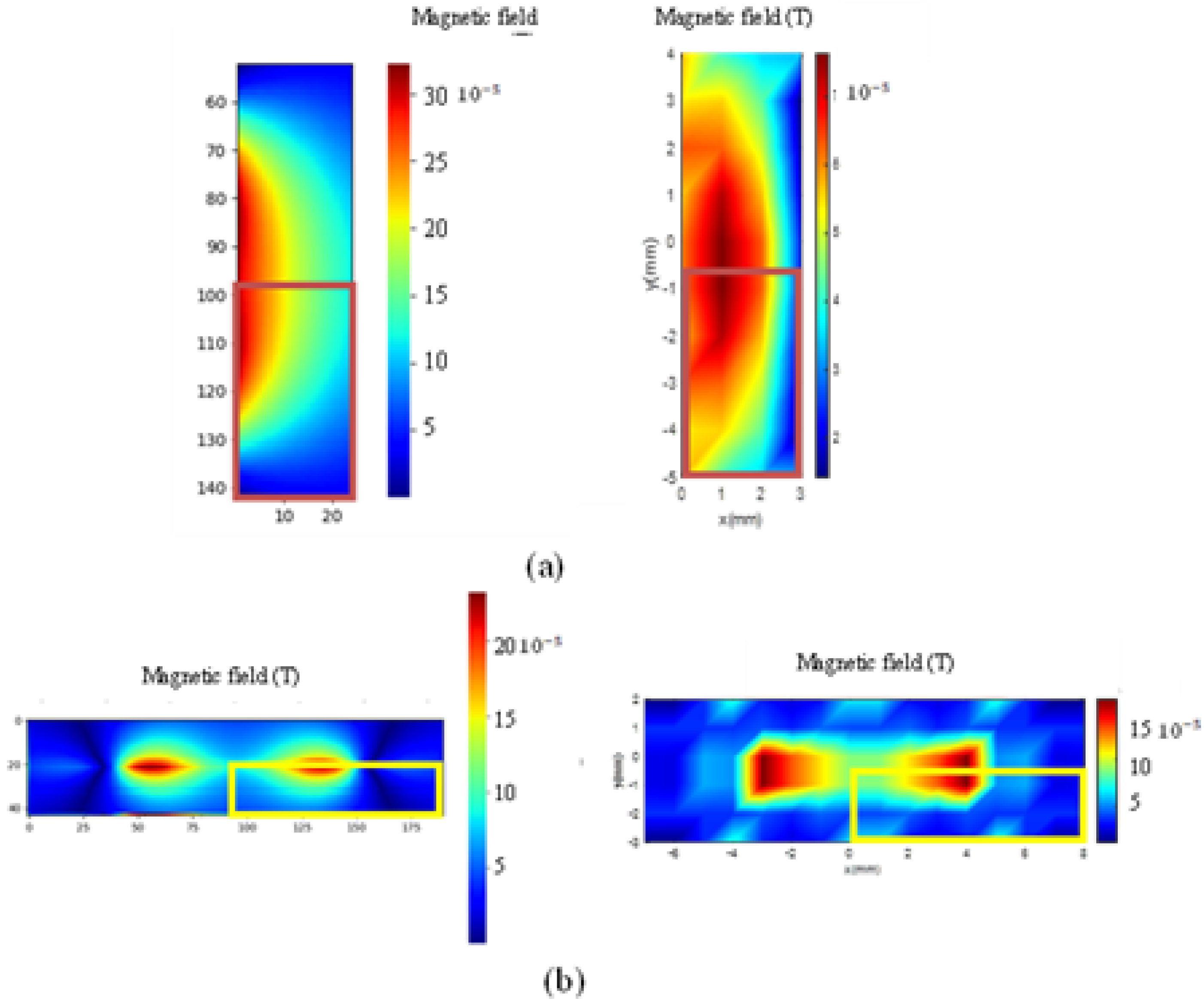

| Inductance | Simple Solenoid (c).1 | Solenoid with Turn Added above and below (c).2 | Solenoid with Magnetic Field Canalized (c).3 |
|---|---|---|---|
| Value | 16.79 µH | 16.77 µH | 15.22 µH |
| Emission | 7.12 mT | 0.13 mT | 0.02 mT |
| Volume | 0.02 L | 0.05 L | 0.10 L |
| Inductance | Tore | Canalized Solenoid |
|---|---|---|
| Value | 15.64 µH | 15.22 µH |
| Emission | 6.2 µT | 20 µT |
| Conductor length | 6.58 m | 5 m |
| Diameter | 0.08 m | 0.05 m |
| Height | 0.05 m | 0.05 m |
| Volume | 0.26 L | 0.10 L |
| Transformer | Number of Turns | Self-Inductance (µH) | Leakage Inductance (µH) | Resistance (mΩ) | Coupling Coefficient |
|---|---|---|---|---|---|
| Simulation | 42 | 19.50 | 2.3 | 225 | 0.88 |
| Experiment | 42 | 20.6 | 1.54 | 248 | 0.93 |
| Material | Impact Resistance (kJ/m2) | Hardness (Shore D) | Glass Transition Temperature (°C) | Thermal Conduction (W K−1 m−1) |
|---|---|---|---|---|
| PLA | 5.14 | 79.8 | 60 | 0.14 |
| ABS | 10.5 | 76 | 85 | 0.17 |
| PET | 7.9 | 76 | 77.4 | 0.15 |
| Nylon | 34.4 | 74 | 50 | 0.25 |
| PC | 3.4 | 78 | 115 | 0.24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigot, V.; Phulpin, T.; Sakly, J.; Sadarnac, D. A New 7 kW Air-Core Transformer at 1.5 MHz for Embedded Isolated DC/DC Application. Energies 2022, 15, 5211. https://doi.org/10.3390/en15145211
Rigot V, Phulpin T, Sakly J, Sadarnac D. A New 7 kW Air-Core Transformer at 1.5 MHz for Embedded Isolated DC/DC Application. Energies. 2022; 15(14):5211. https://doi.org/10.3390/en15145211
Chicago/Turabian StyleRigot, Valentin, Tanguy Phulpin, Jihen Sakly, and Daniel Sadarnac. 2022. "A New 7 kW Air-Core Transformer at 1.5 MHz for Embedded Isolated DC/DC Application" Energies 15, no. 14: 5211. https://doi.org/10.3390/en15145211
APA StyleRigot, V., Phulpin, T., Sakly, J., & Sadarnac, D. (2022). A New 7 kW Air-Core Transformer at 1.5 MHz for Embedded Isolated DC/DC Application. Energies, 15(14), 5211. https://doi.org/10.3390/en15145211