Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”
Abstract
:1. Introduction
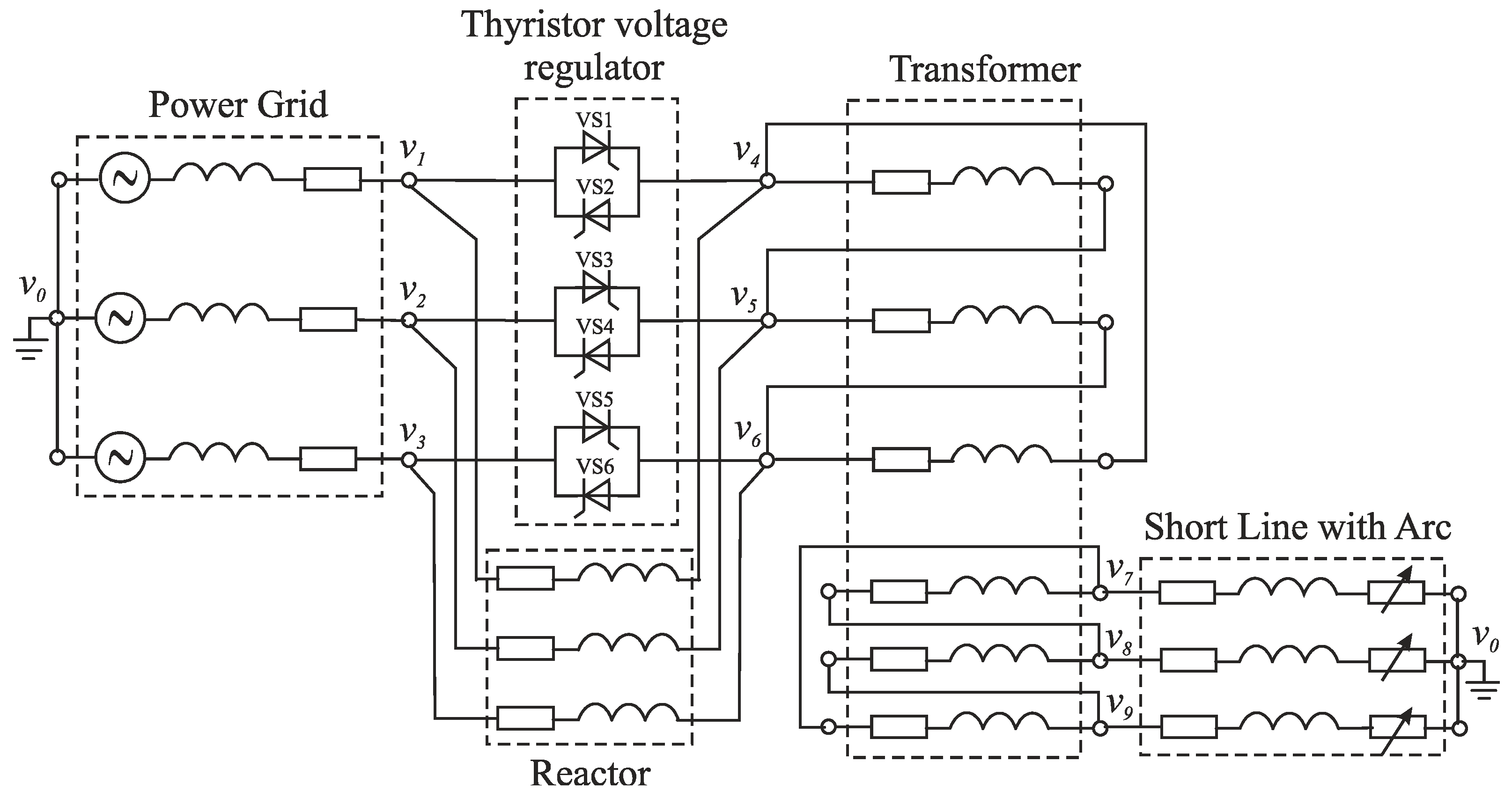
2. Mathematical Model of the Power Circuit and Calculation Algorithm
2.1. Basic Principles of Mathematical Modeling Solution Algorithm
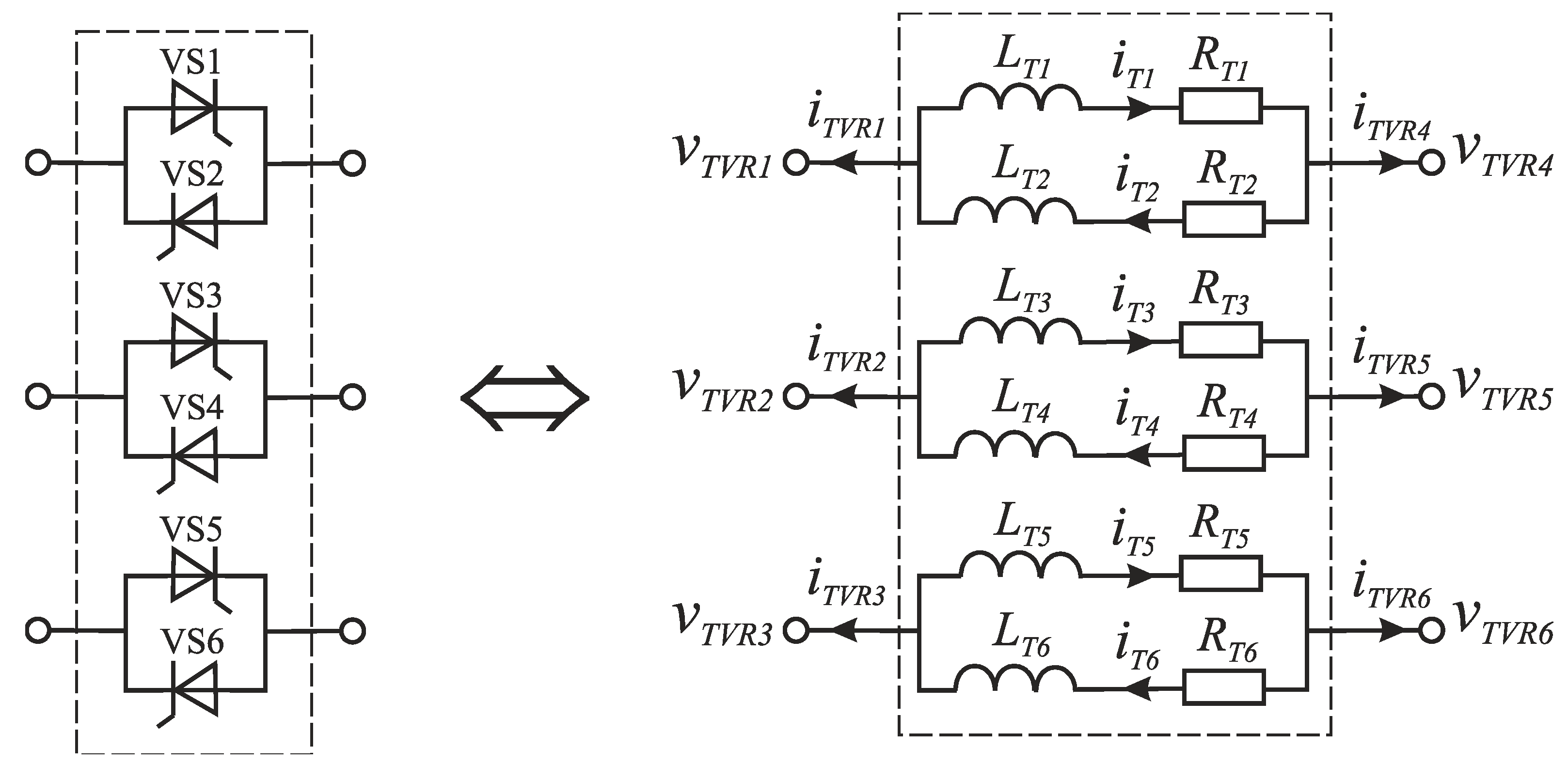
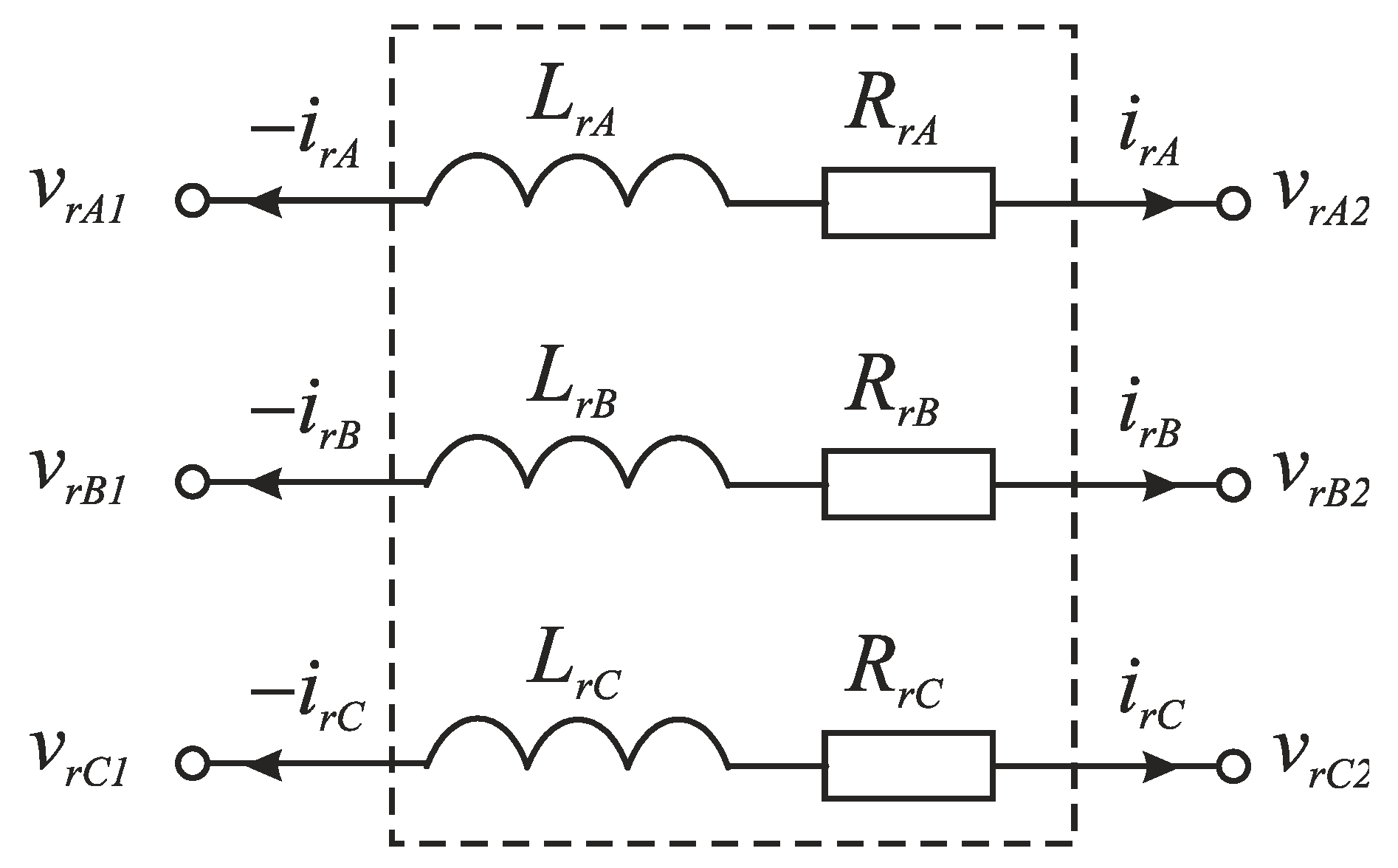
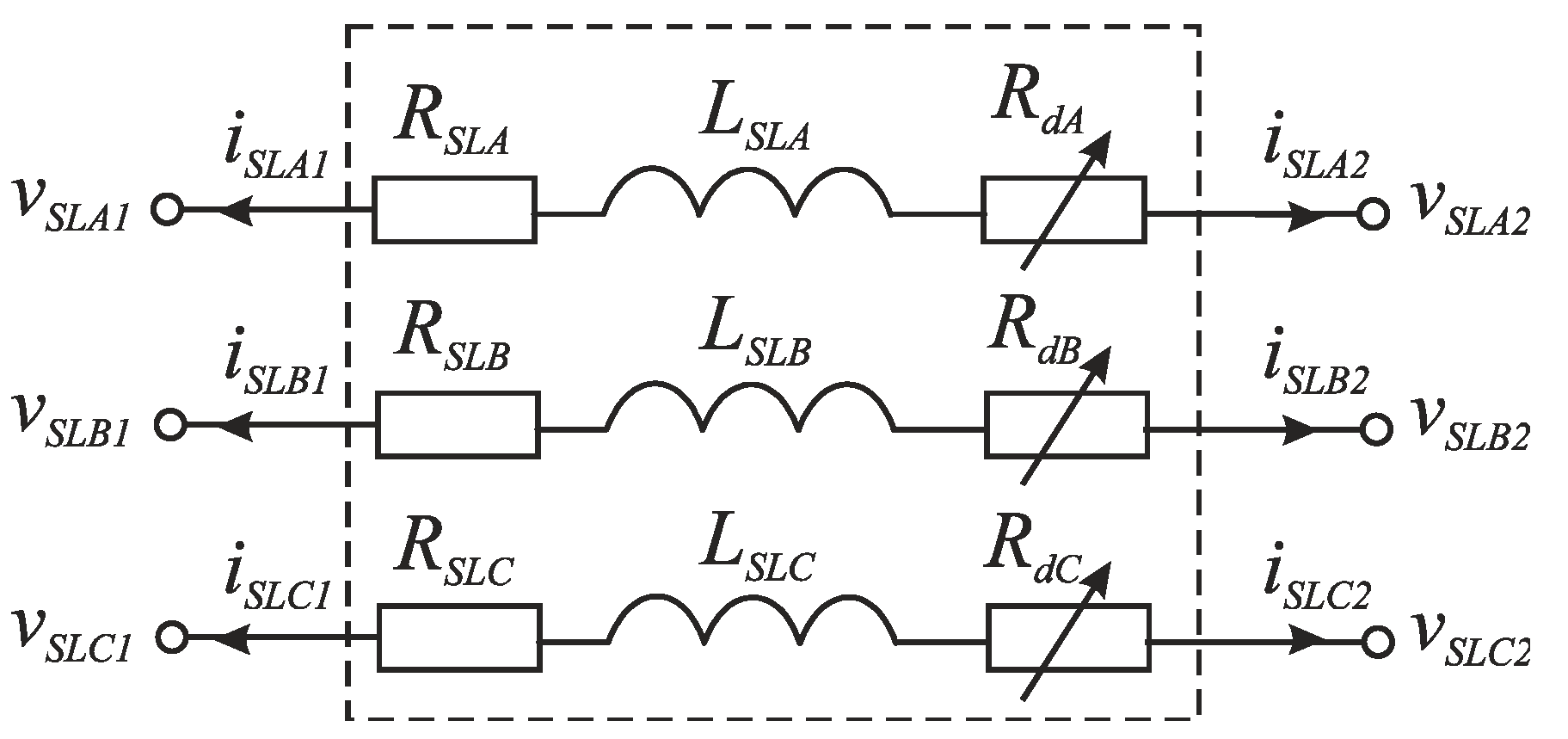
2.2. Mathematical Models of System’s Elements
2.3. The Model Verification
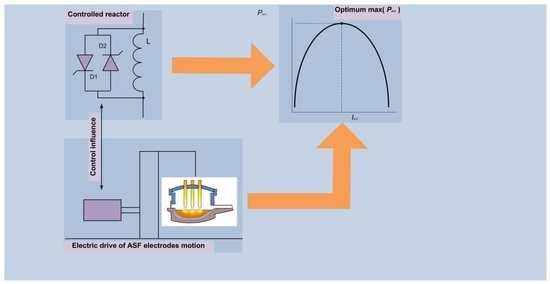
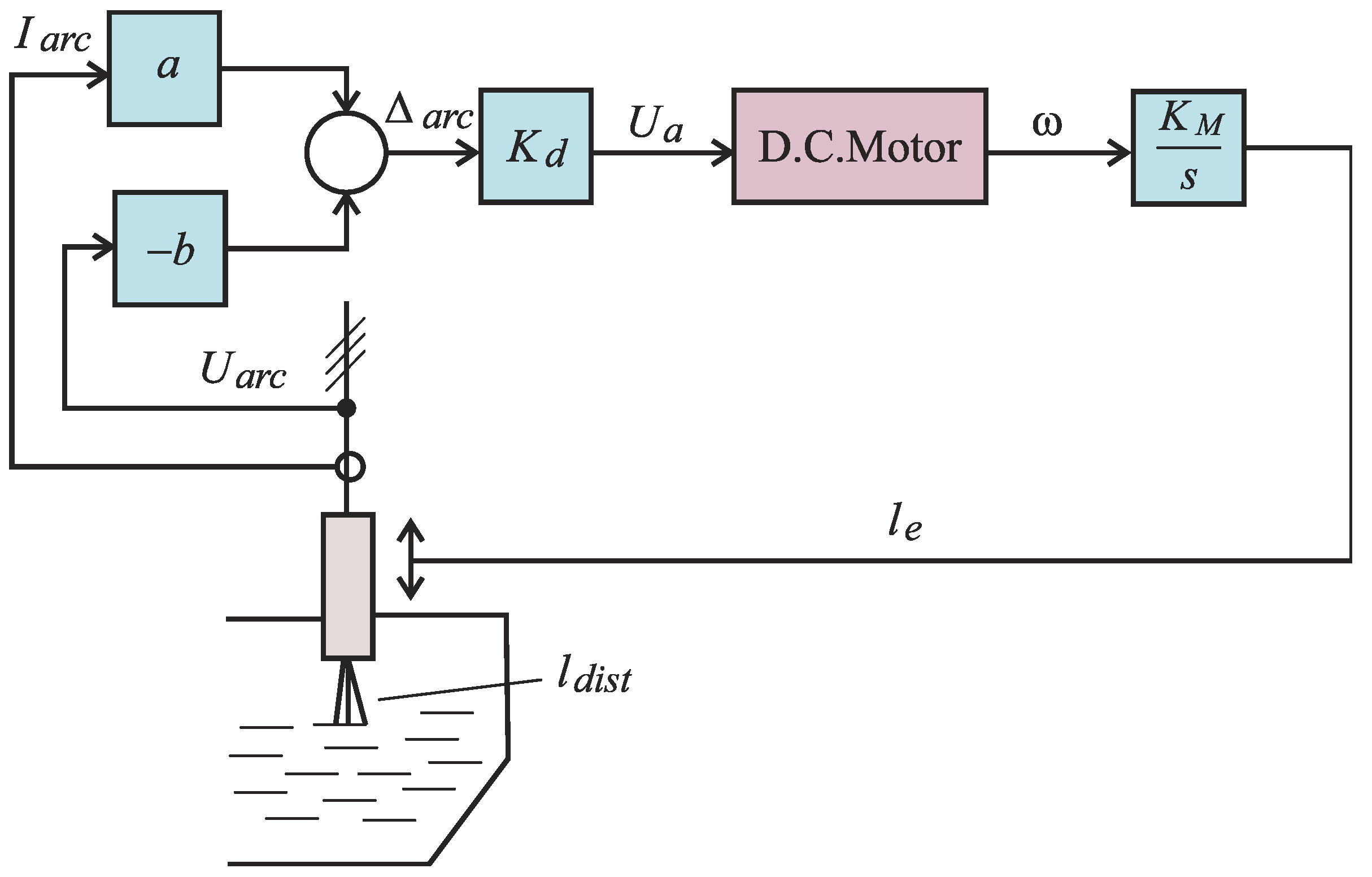
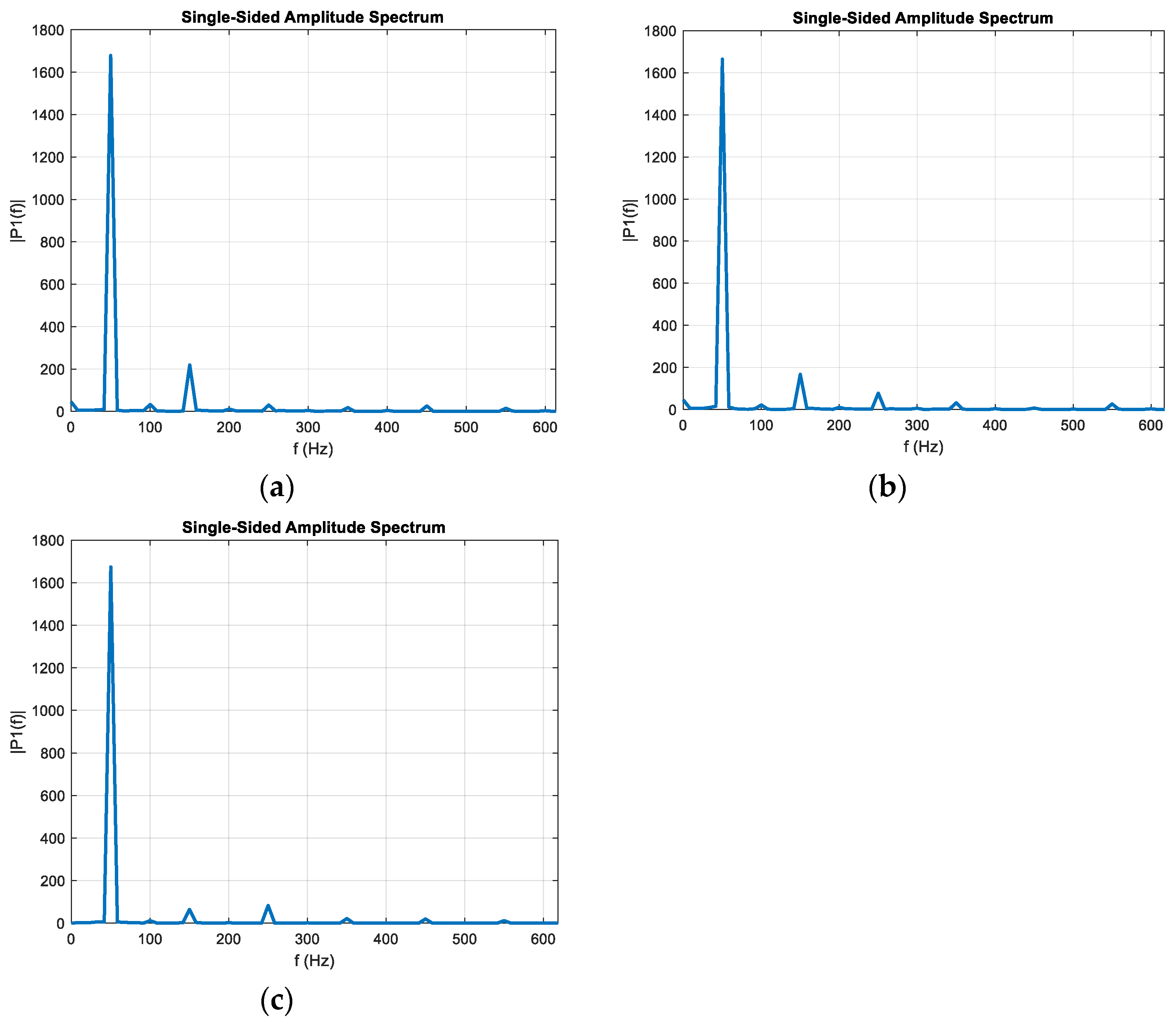
3. The Electrode Movement System
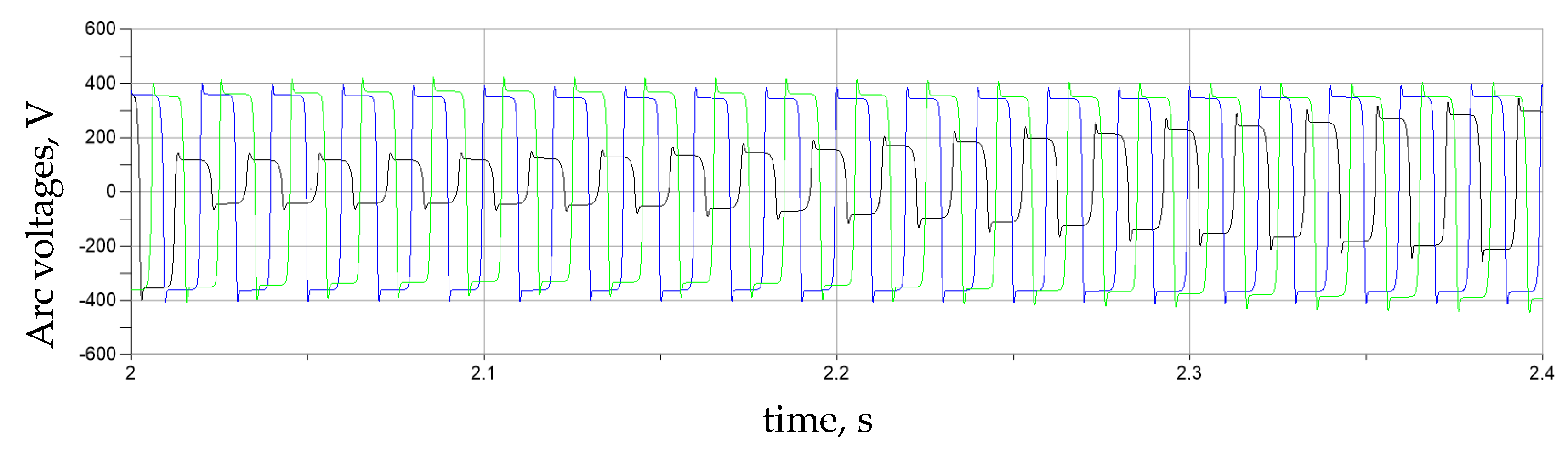
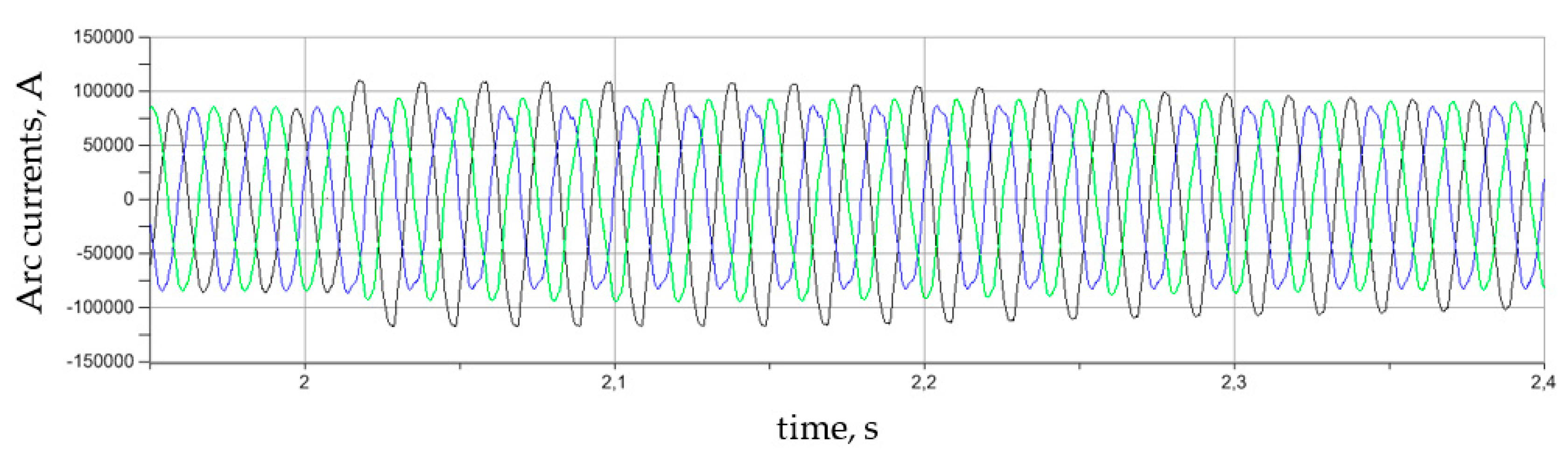
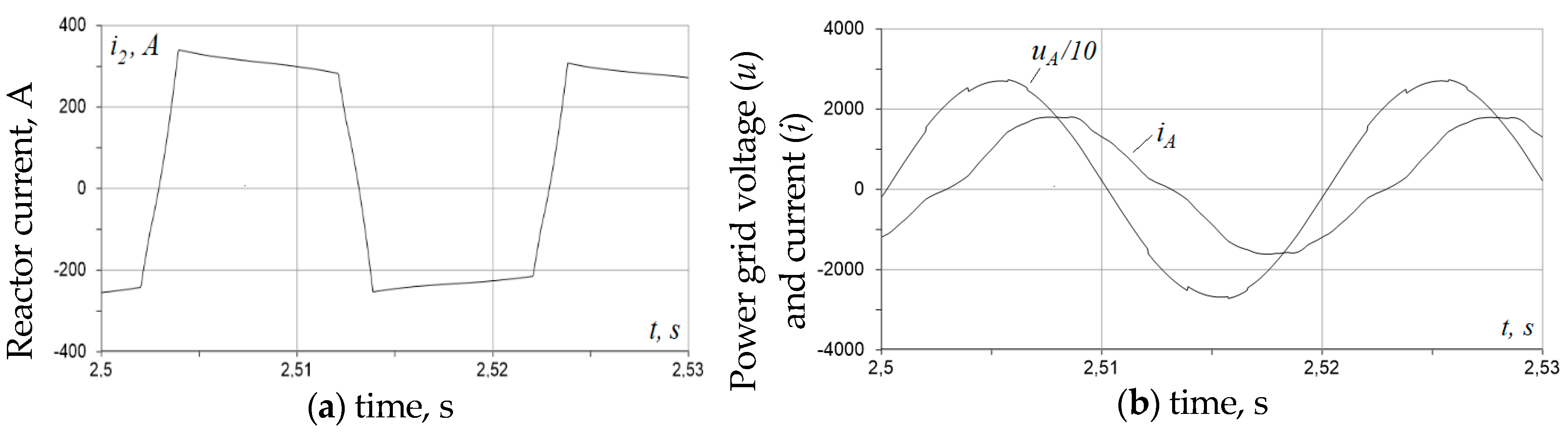
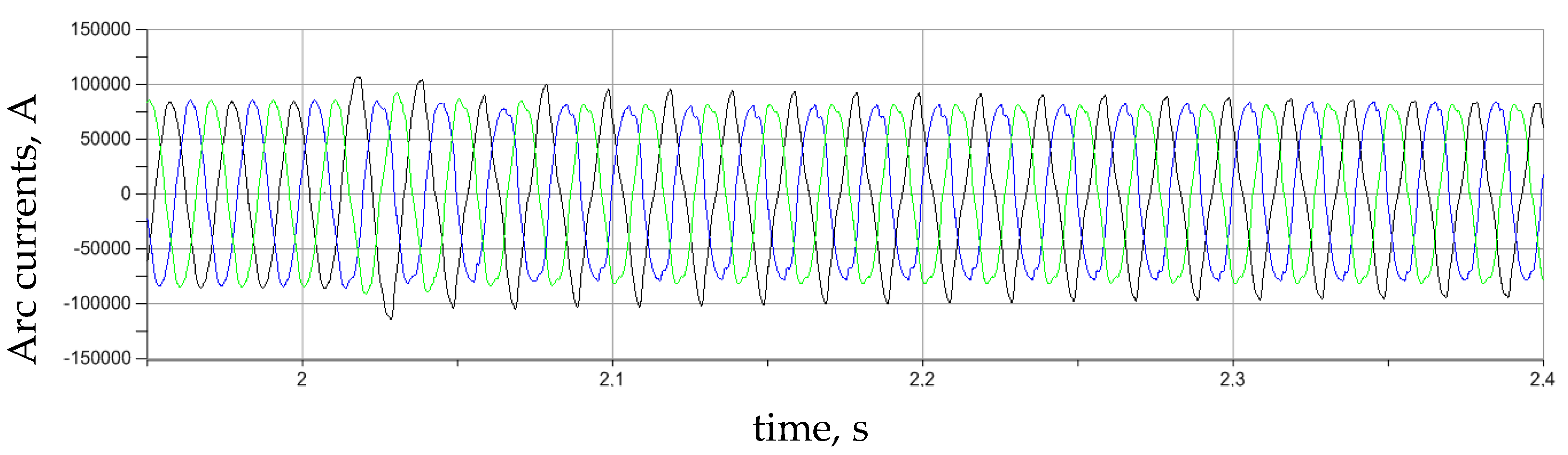
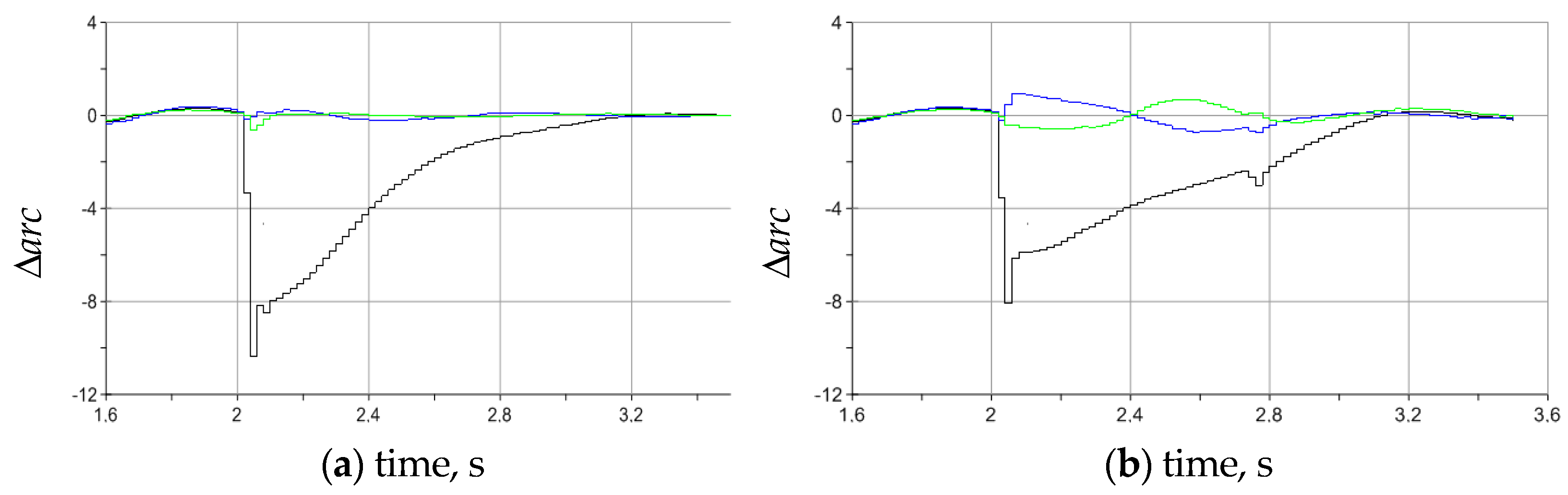
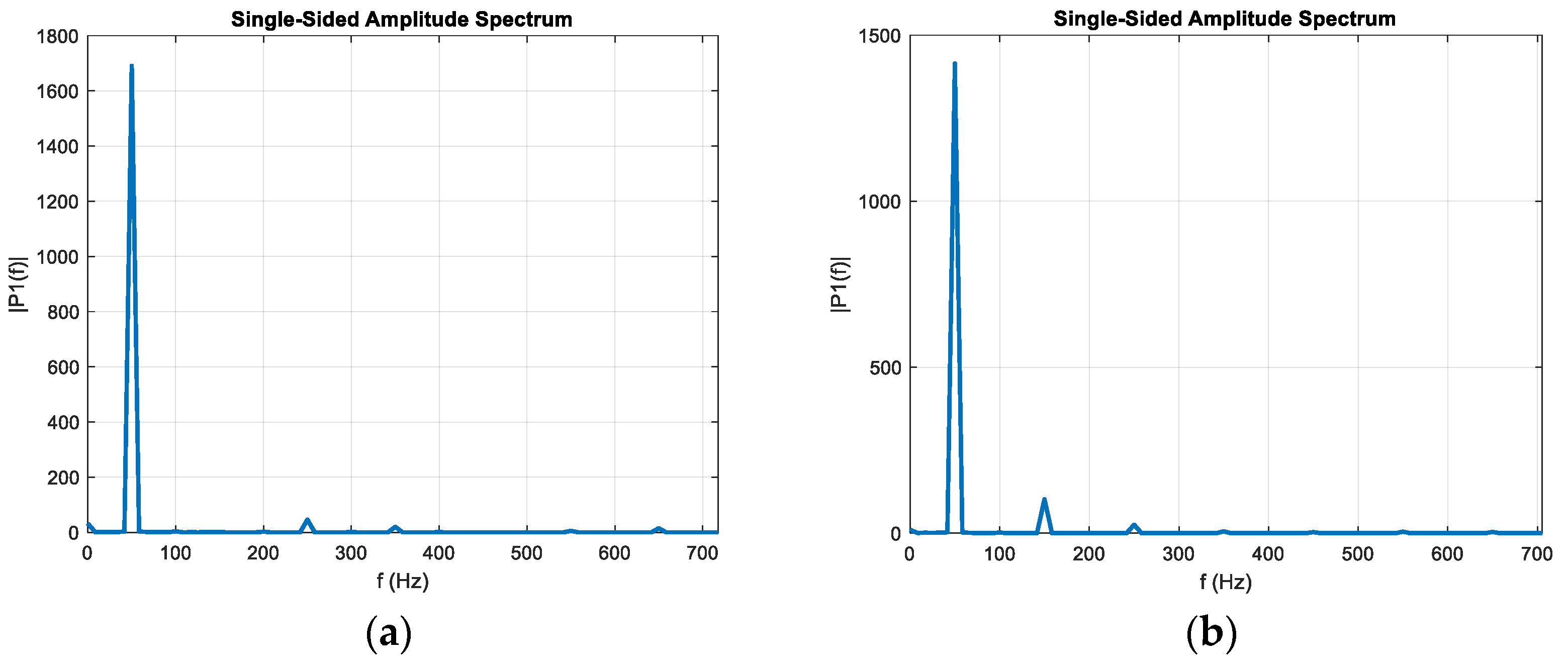
4. Researches Results of Regulation Modes of MTVR
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kim, J.; Sovacool, B.K.; Bazilian, M.; Griffiths, S.; Lee, J.; Yang, M.; Lee, J. Decarbonizing the iron and steel industry: A systematic review of sociotechnical systems, technological innovations, and policy options. Energy Res. Soc. Sci. 2022, 89, 102565. [Google Scholar] [CrossRef]
- Ren, M.; Lu, P.; Liu, X.; Hossain, M.S.; Fang, Y.; Hanaoka, T.; O’Gallachoir, B.; Glynn, J.; Dai, H. Decarbonizing China’s iron and steel industry from the supply and demand sides for carbon neutrality. Appl. Energy 2021, 298, 117209. [Google Scholar] [CrossRef]
- Lee, B.; Sohn, I. Review of Innovative Energy Savings Technology for the Electric Arc Furnace. JOM 2014, 66, 1581–1594. [Google Scholar] [CrossRef]
- Köhle, S.; Madill, J.; Lichterbeck, R. Optimisation of High Voltage AC Electric Arc Furnace Control: Final Report; Directorate-General for Research and Innovation; Publications Office, European Commission: Brussels, Belgium, 2002. [Google Scholar]
- Panoiu, M.; Panoiu, C.; Deaconu, S. Study about the possibility of electrodes motion control in the EAF based on adaptive impedance control. In Proceedings of the 13th International Power Electronics and Motion Control Conference, Poznan, Poland, 1–3 September 2008; pp. 1409–1415. [Google Scholar]
- Lozynskyi, O.; Paranchuk, Y.; Moroz, V.; Stakhiv, P. Computer Model of the Electromechanical System of Moving Electrodes of an Arc Furnace with a Combined Control Law. In Proceedings of the 2019 IEEE 20th International Conference on Computational Problems of Electrical Engineering (CPEE), Lviv-Slavske, Ukraine, 15–18 September 2019; pp. 1–5. [Google Scholar]
- Ghiormez, L.; Prostean, O. Electric arc current control for an electric arc furnace based on fuzzy logic. In Proceedings of the IEEE 10th Jubilee International Symposium on Applied Computational Intelligence and Informatics, Timisoara, Romania, 21–23 May 2015; pp. 359–364. [Google Scholar]
- Parsapoor, A.; Ataei, M.; Kiyoumarsi, A. Adaptive control of the electric arc furnace electrodes using Lyapunov design. In Proceedings of the International Conference on Control, Automation and Systems, Seoul, Korea, 17–20 October 2007; pp. 1617–1622. [Google Scholar]
- Lozynskyi, A.O.; Paranchuk, J.S.; Demkiv, L.I. Investigation of the electrodes movement system of arc furnace fuzzy controller. Tech. Electrodyn. 2014, 2, 73–77. [Google Scholar]
- Paranchuk, Y.; Shabatura, Y.; Kuznyetsov, O. The Electrodes Positioning Control System for the Electric Arc Furnace Basing on Fuzzy Logic. In Proceedings of the IEEE International Conference on Modern Electrical and Energy Systems (MEES), Kremenchuk, Ukraine, 21–24 September 2021; pp. 1–5. [Google Scholar]
- Taslimian, M.; Shabaninia, F.; Vaziri, M.; Vadhva, S. Fuzzy type-2 electrode position controls for an Electric Arc Furnace. In Proceedings of the IEEE 13th International Conference on Information Reuse & Integration (IRI), Las Vegas, NV, USA, 8–10 August 2012; pp. 498–501. [Google Scholar]
- Hong, Z.; Sheng, Y.; Kasuga, J.; Li, M.; Zhao, L. Development of AC Electric Arc-Furnace Control System Based on Fuzzy Neural Network. In Proceedings of the International Conference on Mechatronics and Automation, Luoyang, China, 25–28 June 2006; pp. 2459–2464. [Google Scholar]
- Moghadasian, M.; Alenasser, E. Modelling and Artificial Intelligence-Based Control of Electrode System for an Electric Arc Furnace. Electromagn. Anal. Appl. 2011, 3, 47–55. [Google Scholar] [CrossRef] [Green Version]
- Lozynskyy, O.; Lozynskyi, A.; Paranchuk, Y.; Biletskyi, Y. Optimal control of the electrical mode of an arc furnace on the basis of the three-dimensional vector of phase currents. Math. Modeling Comput. 2019, 6, 69–76. [Google Scholar] [CrossRef]
- Logar, V.; Dovžan, D.; Škrjanc, I. Mathematical Modeling and Experimental Validation of an Electric Arc Furnace. ISIJ Int. 2011, 51, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Hocine, L.; Yacine, D.; Kamel, B.; Samira, K.M. Improvement of electrical arc furnace operation with an appropriate model. Energy 2009, 34, 1207–1214. [Google Scholar] [CrossRef]
- Lozynskyy, A.; Kozyra, J.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Paranchuk, Y.; Kasha, L. A Mathematical Model of Electrical Arc Furnaces for Analysis of Electrical Mode Parameters and Synthesis of Controlling Influences. Energies 2022, 15, 1623. [Google Scholar] [CrossRef]
- Gerling, R.; Louis, T.; Schmeiduch, G.; Sesselmann, R.; Sieber, A. Optimizing the melting process at AC-EAF with neural networks. Metall 1999, 53, 410–418. [Google Scholar]
- Wieczorek, T.; Mązka, K. Modeling of the AC-EAF process using computational intelligence methods. Electrotech. Rev. 2008, 11, 184–188. [Google Scholar]
- Garcia-Segura, R.; Vázquez Castillo, J.; Martell-Chavez, F.; Longoria-Gandara, O.; Ortegón Aguilar, J. Electric Arc Furnace Modeling with Artificial Neural Networks and Arc Length with Variable Voltage Gradient. Energies 2017, 10, 1424. [Google Scholar] [CrossRef]
- Zheng, W.; Xianmin, M. Model Predictive Control Based on Improved DBD Algorithm and Application of Electrode Control in EAF. In Proceedings of the Second International Conference on Intelligent Computation Technology and Automation, Changsha, China, 10–11 October 2009; pp. 806–809. [Google Scholar]
- Martell-Chávez, F.; Ramírez-Argáez, M.; Llamas-Terres, A.; Micheloud-Vernackt, O. Theoretical Estimation of Peak Arc Power to Increase Energy Efficiency in Electric Arc Furnaces. ISIJ Int. 2013, 53, 743–750. [Google Scholar] [CrossRef] [Green Version]
- Łukasik, Z.; Olczykowski, Z. Estimating the Impact of Arc Furnaces on the Quality of Power in Supply Systems. Energies 2020, 13, 1462. [Google Scholar] [CrossRef] [Green Version]
- Olczykowski, Z. Electric Arc Furnaces as a Cause of Current and Voltage Asymmetry. Energies 2021, 14, 5058. [Google Scholar] [CrossRef]
- Olczykowski, Z. Arc Voltage Distortion as a Source of Higher Harmonics Generated by Electric Arc Furnaces. Energies 2022, 15, 3628. [Google Scholar] [CrossRef]
- Pires, I.A.; Cardoso, M.M.G.; Cardoso Filho, B.J. An Active Series Reactor for an Electric Arc Furnace: A Flexible Alternative for Power-Flow Control. IEEE Ind. Appl. Mag. 2016, 22, 53–62. [Google Scholar] [CrossRef]
- Pires, I.A.; Machado, A.; Murta, M.; Cardoso Filho, B.d.J. Experimental results of a Thyristor Switched Series Reactor for Electric Arc Furnaces. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Portland, OR, USA, 2–6 October 2016; pp. 1–5. [Google Scholar]
- Cardoso, M.M.G.; Cardoso Filho, B.J. Thyristor Switched Series Reactor for Electric Arc Furnaces. In Proceedings of the Conference Record of the 2006 IEEE Industry Applications Conference Forty-First IAS Annual Meeting, Tampa, FL, USA, 8–12 October 2006; pp. 124–130. [Google Scholar]
- Samet, H.; Ghanbari, T.; Ghaisari, J. Maximum Performance of Electric Arc Furnace by Optimal Setting of the Series Reactor and Transformer Taps Using a Nonlinear Model. IEEE Trans. Power Deliv. 2015, 30, 764–772. [Google Scholar] [CrossRef]
- Lozinskii, O.Y.; Paranchuk, Y.S. System for the optimum control of the electrical conditions of an arc furnace powered through a controlled reactor. Russ. Metall. 2007, 2007, 737–743. [Google Scholar] [CrossRef]
- Kostyniuk, L.D.; Lozynskyy, A.O.; Lozynskyy, O.Y.; Malyar, A.V.; Marushchak, Y.U.; Paranchuk, Y.S. Situational Control in Arc Steel-Melting Furnaces, Lviv; Lviv Polytechnic Publishing House: Lviv, Ukraine, 2004; p. 382. (In Ukrainian) [Google Scholar]
- Sjarov, M.; Lechler, T.; Fuchs, J.; Brossog, M.; Selmaier, A.; Faltus, F.; Donhauser, T.; Franke, J. The Digital Twin Concept in Industry—A Review and Systematization. In Proceedings of the 25th IEEE International Conference on Emerging Technologies and Factory Automation (ETFA), Vienna, Austria, 8–11 September 2020; pp. 1789–1796. [Google Scholar]
- Classens, K.; Heemels, W.P.M.H.M.; Oomen, T. Digital Twins in Mechatronics: From Model-based Control to Predictive Maintenance. In Proceedings of the IEEE 1st International Conference on Digital Twins and Parallel Intelligence (DTPI), Beijing, China, 15 July–15 August 2021; pp. 336–339. [Google Scholar]
- Brosinsky, C.; Westermann, D.; Krebs, R. Recent and prospective developments in power system control centers: Adapting the digital twin technology for application in power system control centers. In Proceedings of the IEEE International Energy Conference (ENERGYCON), Limassol, Cyprus, 3–7 June 2018; pp. 1–6. [Google Scholar]
- Morello, S.; Gnesda, J.; Dionise, T.J. Arc Furnace Performance Validation: Using Modeling, Monitoring, and Statistical Analysis. IEEE Ind. Appl. Mag. 2019, 25, 95–103. [Google Scholar] [CrossRef]
- Kłosowski, Z.; Cieślik, S. The Use of a Real-Time Simulator for Analysis of Power Grid Operation States with a Wind Turbine. Energies 2021, 14, 2327. [Google Scholar] [CrossRef]
- Kutsyk, A.; Semeniuk, M.; Korkosz, M.; Podskarbi, G. Diagnosis of the Static Excitation Systems of Synchronous Generators with the Use of Hardware-In-the-Loop Technologies. Energies 2021, 14, 6937. [Google Scholar] [CrossRef]
- Kutsyk, A.; Lozynskyy, A.; Vantsevitch, V.; Plakhtyna, O.; Demkiv, L. A Real-Time Model of Locomotion Module DTC Drive for Hardware-In-The-Loop Implementation. Przegląd Elektrotechniczny 2021, 97, 60–65. [Google Scholar] [CrossRef]
- Kavousi-Fard, A.; Khosravi, A.; Nahavandi, S. Reactive Power Compensation in Electric Arc Furnaces Using Prediction Intervals. IEEE Trans. Ind. Electron. 2017, 64, 5295–5304. [Google Scholar] [CrossRef]
- Plakhtyna, O.; Kutsyk, A.; Semeniuk, M.; Kuznyetsov, O. Object-oriented program environment for electromechanical systems analysis based on the method of average voltages on integration step. In Proceedings of the 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Kutna Hora, Czech Republic, 11–13 September 2017; pp. 1–4. [Google Scholar]
- Plakhtyna, O.; Kutsyk, A.; Semeniuk, M. Real-Time Models of Electromechanical Power Systems. Based on the Method of Average Voltages in Integration Step and Their Computer Application. Energies 2020, 13, 2263. [Google Scholar] [CrossRef]
- Plakhtyna, O.; Kutsyk, A.; Lozynskyy, A. Method of average voltages in integration step: Theory and application. Electr. Eng. 2020, 102, 2413–2422. [Google Scholar] [CrossRef]
- Płachtyna, O.; Kłosowski, Z.; Żarnowski, R. Mathematical model of DC drive based on a step-averaged voltage numerical method. Przegląd Elektrotechniczny 2011, 87, 51–56. (In Polish) [Google Scholar]
- Svenchansky, A.D.; Zherdev, I.T.; Kruchinin, A.M. Electric Industrial Furnaces: Arc Furnaces and Special Heating, 2nd ed.; Mironov, Y.M., Svenchanskogo, A.D., Eds.; University Textbook: Singapore, 1981; 296p. [Google Scholar]
- Mironov, Y.M.; Mironova, A.N. Analysis of the influence of the electric inertia of the arc on the characteristics of arc furnaces. Electricity 2017, 5, 62–66. [Google Scholar]




| Operation Mode | Phase A | Phase B | Phase C | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| IA, kA | IA0, kA | IB, kA | IB0, kA | IC, kA | IC0, kA | |||||||
| Mod | Exp | Mod | Exp | Mod | Exp | Mod | Exp | Mod | Exp | Mod | Exp | |
| Switched 3 arcs (symmentrical mode) | 62.7 | 64.5 | - | - | 62.8 | 65.0 | - | - | 63.5 | 66.0 | - | - |
| Onephase short circuit on phase A | 80.0 | 81.0 | −3.8 | −3.2 | 59.2 | 60.0 | 1.7 | 1.5 | 70.0 | 76.0 | 1.4 | 1.65 |
| Control Methode | Standard Deviation Δarc = aIarc − bUarc from 0 |
|---|---|
| Whithout MTVR | 4.64 |
| Control by arc currents | 3.7 |
| Combine control of MTVR | 3.1 |
| Control Method of MTVR | THD, % | ||
|---|---|---|---|
| Phase A | Phase B | Phase C | |
| Current control | 0.19 | 0.198 | 0.2 |
| Combine control | 0.41 | 0.13 | 0.31 |
| Without MTVR | 0.088 | 0.07 | 0.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kozyra, J.; Lozynskyy, A.; Łukasik, Z.; Kuśmińska-Fijałkowska, A.; Kutsyk, A.; Podskarbi, G.; Paranchuk, Y.; Kasha, L. Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”. Energies 2022, 15, 5254. https://doi.org/10.3390/en15145254
Kozyra J, Lozynskyy A, Łukasik Z, Kuśmińska-Fijałkowska A, Kutsyk A, Podskarbi G, Paranchuk Y, Kasha L. Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”. Energies. 2022; 15(14):5254. https://doi.org/10.3390/en15145254
Chicago/Turabian StyleKozyra, Jacek, Andriy Lozynskyy, Zbigniew Łukasik, Aldona Kuśmińska-Fijałkowska, Andriy Kutsyk, Grzegorz Podskarbi, Yaroslav Paranchuk, and Lidiia Kasha. 2022. "Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”" Energies 15, no. 14: 5254. https://doi.org/10.3390/en15145254
APA StyleKozyra, J., Lozynskyy, A., Łukasik, Z., Kuśmińska-Fijałkowska, A., Kutsyk, A., Podskarbi, G., Paranchuk, Y., & Kasha, L. (2022). Combined Control System for the Coordinates of the Electric Mode in the Electrotechnological Complex “Arc Steel Furnace-Power-Supply Network”. Energies, 15(14), 5254. https://doi.org/10.3390/en15145254