Decaying DC Offset Current Mitigation in Phasor Estimation Applications: A Review
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Contributions
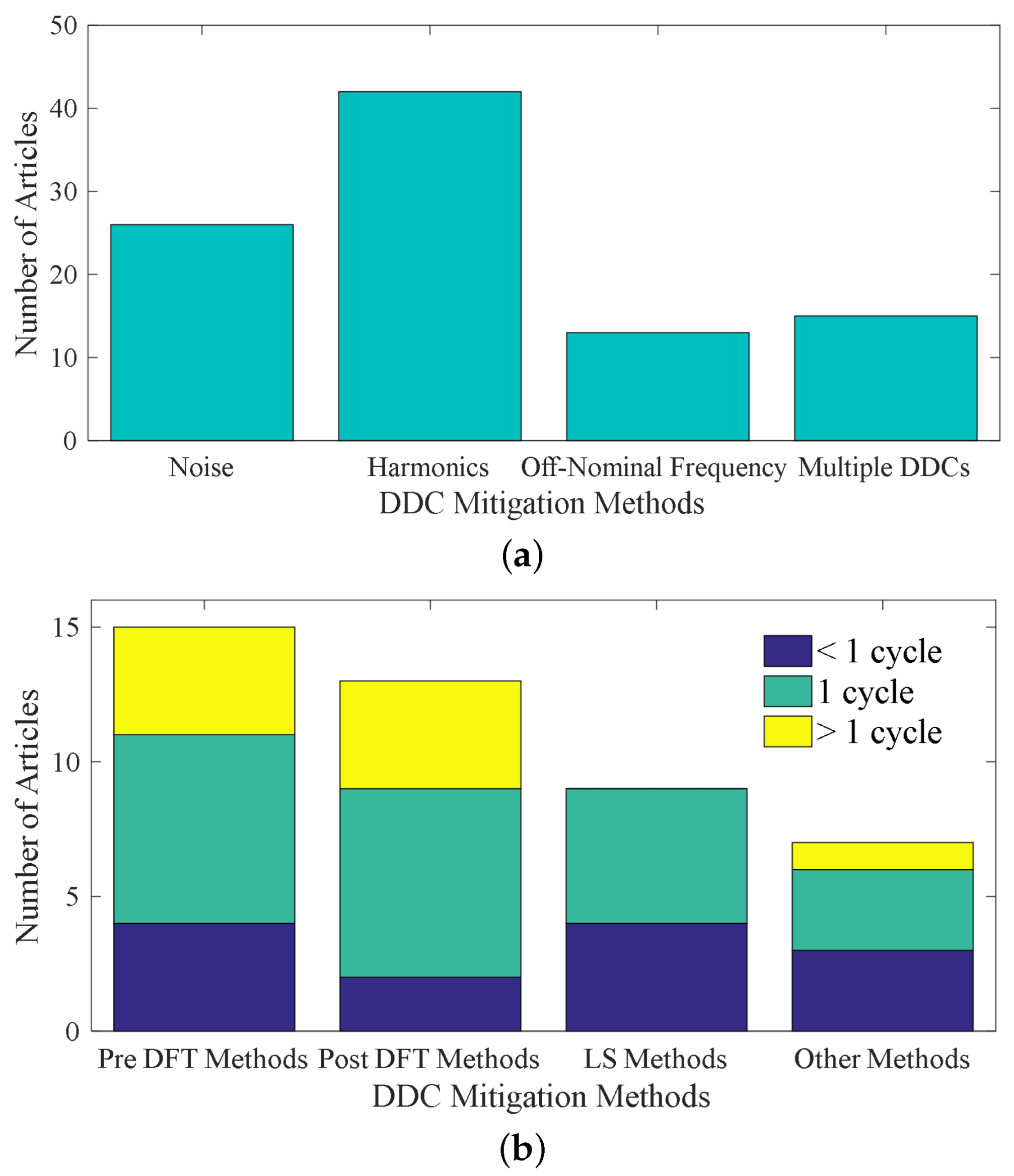
- We present a comprehensive review of DDC estimation methods (including four categories) to present an extensive comparative analysis by addressing the main advantages/disadvantages of each category.
- We provide an overview of the DDC estimation accuracy of different methods in the presence of destructive factors: harmonics, noise, off-nominal frequency (ONF), and multiple DDCs (MDDCs), and nominate the best DDC mitigation methods in each category.
- We investigate some selected schemes to identify their efficiencies through computer simulations.
- We propose guidelines for future research in this field.
1.3. Article Organization
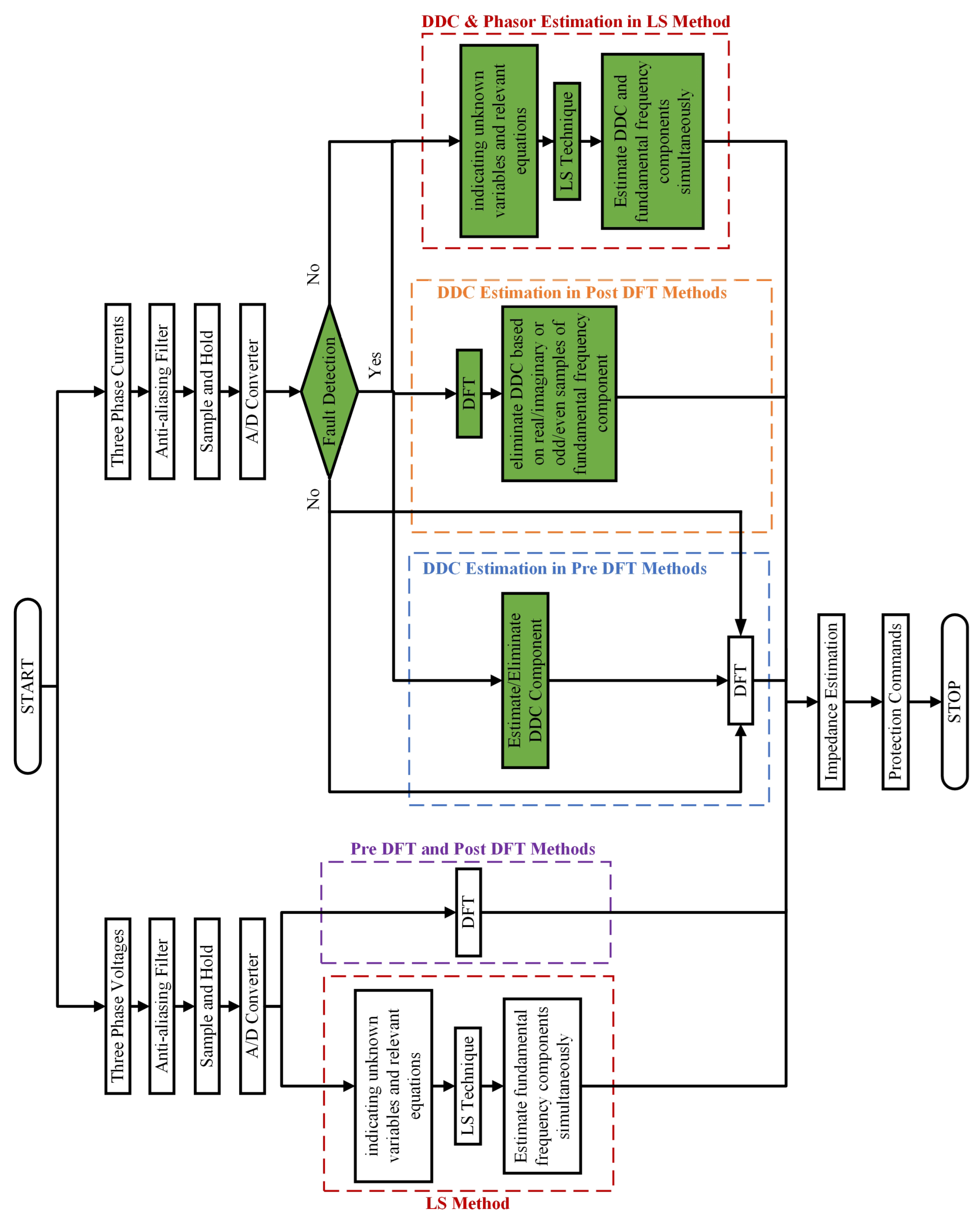
2. DFT Analysis in Current Phasor Estimation
3. Pre-DFT Methods
3.1. A Brief Survey on the DDC Mitigation in Pre-DFT Methods
3.2. Critical Review of Pre-DFT Methods
- Diverse sets of mathematical solutions are open to discovering.
- The majority of methods in this group are simple and suitable for real implementation.
- Sample-based methods use a minimum number of samples for DDC estimation.
- DDC parameters are obtained directly (unlike post-DFT methods).
- Most of the methods are sensitive to noise and need extra filters for noise attenuation.
- MDDC investigations are absent in this category, except for a few methods.
- Harmonics should be discarded before DDC estimation using low-pass filters that add extra delays to the whole process.
4. Post-DFT Methods
4.1. A Brief Survey on the DDC Mitigation in Post-DFT Methods
4.2. Critical Review of Post-DFT Methods
- Most post-DFT methods are applicable in half and FCDFT processes.
- These methods are immune from high-order harmonics, which is a unique feature.
- These methods are applicable in real commercial protection systems due to the existence of conventional DFT-based methods in distance relays.
- Using single or multiple filters increases the delay.
- Recursive approaches are inherently sensitive to noise.
- The computational burden is high due to the recursive solution in this category.
- Non-modeled frequency deviation may cause large errors in DDC estimation.
5. Least-Square Methods
5.1. A Brief Survey on the DDC Mitigation in LS-Based Methods
5.2. Critical Review of LS-Based Methods
- The computational burden is low and suitable for real implementations.
- LS-based methods are straightforward and use a minimum amount of mathematical functions.
- The noise effect can easily be attenuated by using limited extra samples.
- LS-based methods are easily combined with other methods to enhance accuracy.
- Most LS-based methods use approximations for DDC modeling, which decrease accuracy.
- LS-based methods inherently need predefined signals for modeling the problem.
- Utilization of fewer samples in LS-based methods enlarges the noise sensitivity.
- MDDCs were not referred to in LS-based methods.
- Non-linear LS-based methods are not suitable in real-time applications due to higher computational burdens.
6. Other Methods
6.1. A Brief Survey on the DDC Mitigation in Other Methods
6.2. Critical Review of Other Methods
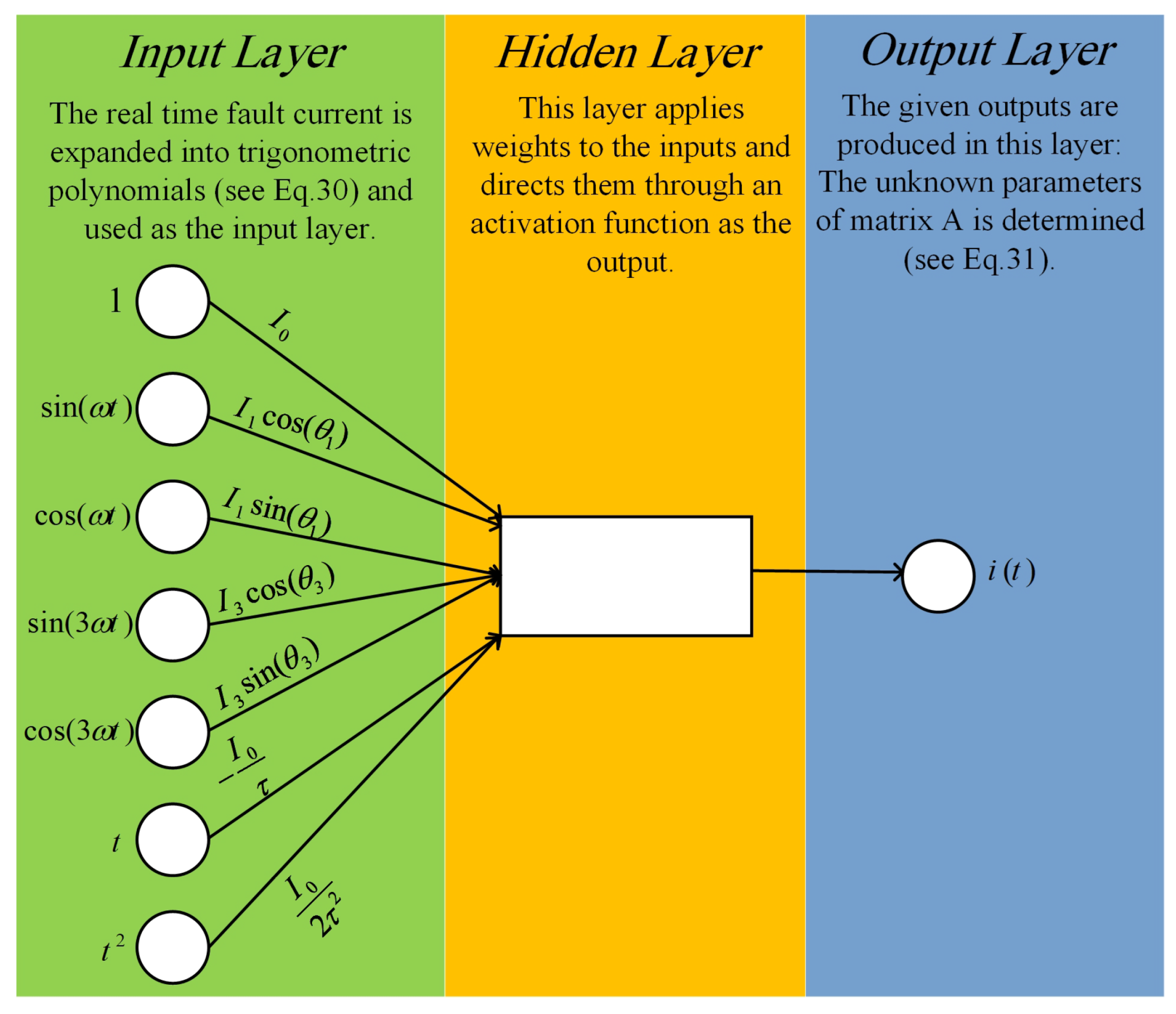
- Precise and extensive data collection can easily increase the accuracy of the ANN and DNN methods.
- DDC estimation can be taken into account in all conditions under the effects of all destructive factors in future attempts through ANN/DNN tools.
- The frequency domain analysis opens up a new prospective in this field.
- ANN and DNN need large training datasets for the phasor estimation in the presence of DDC and impose complexities on the overall system.
- ANN and DNN are inherently offline methods, which need adaptive training data in the case of transient applications.
- ANN and DNN methods depend on power system configurations for fault analysis.
- Multiple filtering adds an extra delay to the phasor estimation.
- Advanced mathematical approaches, such as the ER and Z-domain-based methods, impose large calculation loads on measurement/protection devices.
7. Future Scopes
8. Conclusions
- Applying more complex mathematical approaches did not guarantee a higher efficiency of DDC estimation/elimination. (For instance: method [10] has the lowest RMSE among the simulated methods).
- While the number of samples that were considered for DDC estimation should be minimized to reduce the delay, the noise effect should be taken into account as the main constraint.
- The main drawback of conventional LS-based methods involves the approximation of the exponential term of the DDC. Recent studies attempted to solve this problem but the complexity increased.
- The MDDC estimations were not addressed in the majority of past methods. Thus, it is necessary to include this issue through simplified mathematical solutions, such as pre-DFT methods.
- The most challenging issue in the application of data-based methods involves online training. Therefore, future works in this category should propose a logical procedure to tackle this issue in a proper approach.
- One could potentially investigate a wider range of pre-DFT methods due to their adaptions and ability to cover a broad range of mathematical solutions.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| fault current signal (continuous) | |
| fault current signal (discrete) | |
| DDC amplitude | |
| DDC time constant | |
| k | harmonic order |
| kth harmonic of fault current | |
| T | one cycle time period |
| phase angle of kth harmonic | |
| N | number of samples over a cycle |
| angular frequency | |
| phase angle of fundamental harmonic | |
| time interval | |
| DFT of DDC signal | |
| W | noise signal |
| dq0 fault current signals | |
| auxiliary signal | |
| S1 | summation of current signal samples over a cycle |
| S2 | summation of auxiliary signal samples over a cycle |
| phase angle difference between voltage and current signals |
References
- Jafarpisheh, B.; Madani, S.M.; Mohammad Shahrtash, S. A New DFT-Based Phasor Estimation Algorithm Using High-Frequency Modulation. IEEE Trans. Power Deliv. 2017, 32, 2416–2423. [Google Scholar] [CrossRef]
- Benmouyal, G. Removal of Dc-Offset in Current Waveforms Using Digital Mimic Filtering. IEEE Trans. Power Deliv. 1995, 10, 621–630. [Google Scholar] [CrossRef]
- Hajizadeh, H.; Ahmadi, S.A.; Sanaye-Pasand, M. An Analytical Fast Decaying DC Mitigation Method for Digital Relaying Applications. IEEE Trans. Power Deliv. 2021, 36, 3529–3537. [Google Scholar] [CrossRef]
- Musa, O.; Aksamovic, A. Comparative analysis of algorithms for elimination of exponentially decaying DC component. In Proceedings of the 2012 19th International Conference on Systems, Signals and Image Processing (IWSSIP), Vienna, Austria, 11–13 April 2012; pp. 362–367. [Google Scholar]
- Tajdinian, M.; Samet, H.; Hamedi, A.; Hadaeghi, A.; Bagheri, A.; Allahbakhshi, M.; Seifi, A. Enhancing Immunity of Full-Cycle Discrete Fourier Transform Against Decaying DC Components: A Comparative Analysis. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I CPS Europe), Genova, Italy, 11–14 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Jafarpisheh, B.; Madani, S.M.; Jafarpisheh, S. Improved DFT-Based phasor estimation algorithm using down-sampling. IEEE Trans. Power Deliv. 2018, 33, 3242–3245. [Google Scholar] [CrossRef]
- Schweitzer, E.O.; Hou, D. Filtering for protective relays. In Proceedings of the Communications, Computers and Power in the Modern Environment, Saskatoon, SK, Canada, 17–18 May 1993; pp. 15–23. [Google Scholar] [CrossRef]
- Kirpane, R.; Bedekar, P.P. Removal of DC offset using digital mimic filtering technique. In Proceedings of the 2016 International Conference on Global Trends in Signal Processing, Information Computing and Communication (ICGTSPICC), Jalgaon, India, 22–24 December 2016; pp. 470–475. [Google Scholar] [CrossRef]
- Soliman, S.A.; Alammari, R.A.; El-Hawary, M.E. A new digital transformation for harmonics and DC offset removal for the distance fault locator algorithm. Int. J. Electr. Power Energy Syst. 2004, 26, 389–395. [Google Scholar] [CrossRef]
- Phadke, A.; Hlibka, T.; Ibrahim, M. A digital computer system for EHV substations: Analysis and field tests. IEEE Trans. Power Appar. Syst. 1976, 95, 291–301. [Google Scholar] [CrossRef]
- Guo, Y.; Kezunovic, M.; Chen, D. Simplified algorithms for removal of the effect of exponentially decaying DC-offset on the Fourier algorithm. IEEE Trans. Power Deliv. 2003, 18, 711–717. [Google Scholar] [CrossRef]
- Cho, Y.S.; Lee, C.K.; Jang, G.; Lee, H.J. An innovative decaying DC component estimation algorithm for digital relaying. IEEE Trans. Power Deliv. 2009, 24, 73–78. [Google Scholar] [CrossRef]
- Abdoos, A.A.; Gholamian, S.A.; Farzinfar, M. Accurate and fast DC offset removal method for digital relaying schemes. IET Gener. Transm. Distrib. 2016, 10, 1769–1777. [Google Scholar] [CrossRef]
- Rubeena, R.; Zadeh, M.R.; Bains, T.P.S. An accurate offline phasor estimation for fault location in series-compensated lines. IEEE Trans. Power Deliv. 2014, 29, 876–883. [Google Scholar] [CrossRef]
- Bains, T.P.S.; Dadash Zadeh, M.R. Enhanced Phasor Estimation Technique for Fault Location in Series-Compensated Lines. IEEE Trans. Power Deliv. 2015, 30, 2058–2060. [Google Scholar] [CrossRef]
- Tajdinian, M.; Jahromi, M.Z.; Mohseni, K.; Kouhsari, S.M. An analytical approach for removal of decaying DC component considering frequency deviation. Electr. Power Syst. Res. 2016, 130, 208–219. [Google Scholar] [CrossRef]
- Pazoki, M. A New DC-Offset Removal Method for Distance-Relaying Application Using Intrinsic Time-Scale Decomposition. IEEE Trans. Power Deliv. 2018, 33, 971–980. [Google Scholar] [CrossRef]
- Kumar, B.R.; Kumar, A. Mitigation of the DC offset by a sub-cycle sample method M-Class PMUs. IEEE Trans. Power Deliv. 2019, 34, 1. [Google Scholar] [CrossRef]
- Kumar, B.R.; Mohapatra, A.; Chakrabarti, S. A Novel Sub-Cycle-Based Method for Estimation of Decaying DC Component and Fundamental Phasor. IEEE Trans. Instrum. Meas. 2021, 70, 1–10. [Google Scholar] [CrossRef]
- Afrandideh, S.; Haghjoo, F. A DFT-based phasor estimation method robust to primary and secondary decaying DC components. Electr. Power Syst. Res. 2022, 208, 107907. [Google Scholar] [CrossRef]
- Mohammadi, S.; Rezaei, N.; Mahmoudi, A. A novel analytical method for DC offset mitigation enhancing DFT phasor estimation. Electr. Power Syst. Res. 2022, 209, 108036. [Google Scholar] [CrossRef]
- Gu, J.C.; Yu, S.L. Removal of DC offset in current and voltage signals using a novel Fourier filter algorithm. IEEE Trans. Power Deliv. 2000, 15, 73–79. [Google Scholar] [CrossRef]
- Yu, S.L.; Gu, J.C. Removal of decaying DC in current and voltage signals using a modified fourier filter algorithm. IEEE Trans. Power Deliv. 2001, 16, 372–379. [Google Scholar] [CrossRef]
- Yang, J.Z.; Liu, C.W. Complete elimination of DC offset in current signals for relaying applications. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting. Conference Proceedings (Cat. No.00CH37077), Singapore, 23–27 January 2000; pp. 1933–1938. [Google Scholar] [CrossRef]
- Rosołowski, E.; Izykowski, J.; Kasztenny, B. Adaptive measuring algorithm suppressing a decaying DC component for digital protective relays. Electr. Power Syst. Res. 2001, 60, 99–105. [Google Scholar] [CrossRef]
- Nam, S.R.; Park, J.Y.; Kang, S.H.; Kezunovic, M. Phasor estimation in the presence of DC offset and CT saturation. IEEE Trans. Power Deliv. 2009, 24, 1842–1849. [Google Scholar] [CrossRef]
- Gu, J.C.; Shen, K.Y.; Yu, S.L.; Yu, C.S. Removal of dc offset and subsynchronous resonance in current signals for series compensated transmission lines using a novel Fourier filter algorithm. Electr. Power Syst. Res. 2006, 76, 327–335. [Google Scholar] [CrossRef]
- Yu, C.S. A discrete Fourier transform-based adaptive mimic phasor estimator for distance relaying applications. IEEE Trans. Power Deliv. 2006, 21, 1836–1846. [Google Scholar] [CrossRef]
- Kang, S.H.; Lee, D.G.; Nam, S.R.; Crossley, P.A.; Kang, Y.C. Fourier transform-based modified phasor estimation method immune to the effect of the DC offsets. IEEE Trans. Power Deliv. 2009, 24, 1104–1111. [Google Scholar] [CrossRef]
- Rahmati, A.; Adhami, R. An accurate filtering technique to mitigate transient decaying DC offset. IEEE Trans. Power Deliv. 2014, 29, 966–968. [Google Scholar] [CrossRef]
- Lázaro, J.; Miñambres, J.F.; Zorrozua, M.A. Selective estimation of harmonic components in noisy electrical signals for protective relaying purposes. Int. J. Electr. Power Energy Syst. 2014, 56, 140–146. [Google Scholar] [CrossRef]
- Tajdinian, M.; Seifi, A.R.; Allahbakhshi, M. Half-cycle method for exponentially DC components elimination applicable in phasor estimation. IET Sci. Meas. Technol. 2017, 11, 1032–1042. [Google Scholar] [CrossRef]
- Hwang, J.K.; Song, C.K.; Jeong, M.G. DFT-Based phasor estimation for removal of the effect of multiple DC components. IEEE Trans. Power Deliv. 2018, 33, 2901–2909. [Google Scholar] [CrossRef]
- Kim, W.J.; Kang, S.H. A DC offset removal algorithm based on AR model. J. Int. Counc. Electr. Eng. 2018, 8, 156–162. [Google Scholar] [CrossRef]
- Honorato, T.R.; Silva, K.M. Half-Cycle DFT-Based Phasor Estimation Algorithm for Numerical Digital Relaying. In Proceedings of the 2018 Workshop on Communication Networks and Power Systems (WCNPS), Brasilia, Brazil, 7–9 November 2018; pp. 1–4. [Google Scholar] [CrossRef]
- Liang, Y.; Zhang, Z.; Li, H.; Ding, J.; Wang, G.; Chen, L. A robust and accurate discrete Fourier transform-based phasor estimation method for frequency domain fault location of power transmission lines. IET Gener. Transm. Distrib. 2022, 16, 1990–2002. [Google Scholar] [CrossRef]
- Sachdev, M.S.; Baribeau, M.A. A new algorithm for digital impedance relays. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 2232–2240. [Google Scholar] [CrossRef]
- Girgis, A.A. A new kalman filtering based digital distance relay. IEEE Trans. Power Appar. Syst. 1982, PAS-101, 3471–3480. [Google Scholar] [CrossRef]
- Sachdev, M.S.; Nagpal, M. A recursive least error squares algorithm for power system relaying and measurement applications. IEEE Trans. Power Deliv. 1991, 6, 1008–1015. [Google Scholar] [CrossRef]
- Jafarian, P.; Sanaye-Pasand, M. An adaptive phasor estimation technique based on LES method using forgetting factor. In Proceedings of the 2009 IEEE Power and Energy Society General Meeting (PES ’09), Calgary, AB, Canada, 26–30 July 2009; pp. 1–8. [Google Scholar] [CrossRef]
- Jafarian, P.; Sanaye-Pasand, M. Weighted least error squares based variable window phasor estimator for distance relaying application. IET Gener. Transm. Distrib. 2011, 5, 298–306. [Google Scholar] [CrossRef]
- Hwang, J.K. Least error squared phasor estimation with identification of a decaying DC component. IET Gener. Transm. Distrib. 2018, 12, 1486–1492. [Google Scholar] [CrossRef]
- Min, K.W.; Santoso, S. DC offset removal algorithm for improving location estimates of momentary faults. IEEE Trans. Smart Grid 2018, 9, 5503–5511. [Google Scholar] [CrossRef]
- Achlerkar, P.D.; Panigrahi, B.K. Assessment of DC offset in fault current signal for accurate phasor estimation considering current transformer response. IET Sci. Meas. Technol. 2019, 13, 403–408. [Google Scholar] [CrossRef]
- Kim, W.J.; Nam, S.R.; Kang, S.H. Adaptive phasor estimation algorithm based on a least squares method. Energies 2019, 12, 1387. [Google Scholar] [CrossRef] [Green Version]
- Nam, S.R.; Kang, S.H.; Park, J.K. An analytic method for measuring accurate fundamental frequency components. IEEE Trans. Power Deliv. 2002, 17, 405–411. [Google Scholar] [CrossRef]
- Byeon, G.; Oh, S.; Jang, G. A new DC offset removal algorithm using an iterative method for real-time simulation. IEEE Trans. Power Deliv. 2011, 26, 2277–2286. [Google Scholar] [CrossRef]
- Yusuff, A.A.; Jimoh, A.A.; Munda, J.L. Stationary wavelet transform and single differentiator based decaying DC-offset filtering in post fault measurements. Meas. J. Int. Meas. Confed. 2014, 47, 919–928. [Google Scholar] [CrossRef]
- Da Silva, C.D.; Junior, G.C.; Mariotto, L.; Marchesan, G. Phasor estimation in power systems using a neural network with online training for numerical relays purposes. IET Sci. Meas. Technol. 2015, 9, 836–841. [Google Scholar] [CrossRef]
- Imran, M.; Alsuhaibani, S.A. A Neuro-Fuzzy Inference Model for Diabetic Retinopathy Classification. In Intelligent Data Analysis for Biomedical Applications; Elsevier: Amsterdam, The Netherlands, 2019; pp. 147–172. [Google Scholar] [CrossRef]
- Lana da Silva, C.D.; Cardoso, G.; de Morais, A.P.; Marchesan, G.; Kaehler Guarda, F.G. A continually online trained impedance estimation algorithm for transmission line distance protection tolerant to system frequency deviation. Electr. Power Syst. Res. 2017, 147, 73–80. [Google Scholar] [CrossRef]
- Kim, S.B.; Sok, V.; Kang, S.H.; Lee, N.H.; Nam, S.R. A study on deep neural network-based DC Offset removal for phase estimation in power systems. Energies 2019, 12, 1619. [Google Scholar] [CrossRef] [Green Version]
- Zamora-Mendez, A.; Sotelo-Castañón, J.; Arrieta Paternina, M.R.; Buendia, P.; Torres, C.; Toledo-Santos, C.; Velasco, V.; Zelayal-A, F.; Mejia-Ruiz, G.E. Two effective methods for impedance estimation in distance relays based on the DC offset removal. Electr. Power Syst. Res. 2021, 194, 107102. [Google Scholar] [CrossRef]
- Gautam, S.; Brahma, S.M. Overview of mathematical morphology in power systems—A tutorial approach. In Proceedings of the 2009 IEEE Power Energy Society General Meeting, Calgary, AB, Canada, 26–30 July 2009; pp. 1–7. [Google Scholar] [CrossRef]
- Khodaparast, J. A Review of Dynamic Phasor Estimation by Non-Linear Kalman Filters. IEEE Access 2022, 10, 11090–11109. [Google Scholar] [CrossRef]
- Rao, A.V.K.; Soni, K.M.; Sinha, S.K.; Nasiruddin, I. Dynamic phasor estimation using adaptive artificial neural network. Int. J. Syst. Assur. Eng. Manag. 2021, 12, 310–317. [Google Scholar] [CrossRef]
- Chitsaz, K.; Hajabdollahi, M.; Karimi, N.; Samavi, S.; Shirani, S. Acceleration of Convolutional Neural Network Using FFT-Based Split Convolutions. arXiv 2020, arXiv:2003.12621. [Google Scholar]
- Khodaparast, J.; Fosso, O.; Molinas, M. Phasor Estimation by EMD-Assisted Prony. IEEE Trans. Power Deliv. 2022. [Google Scholar] [CrossRef]

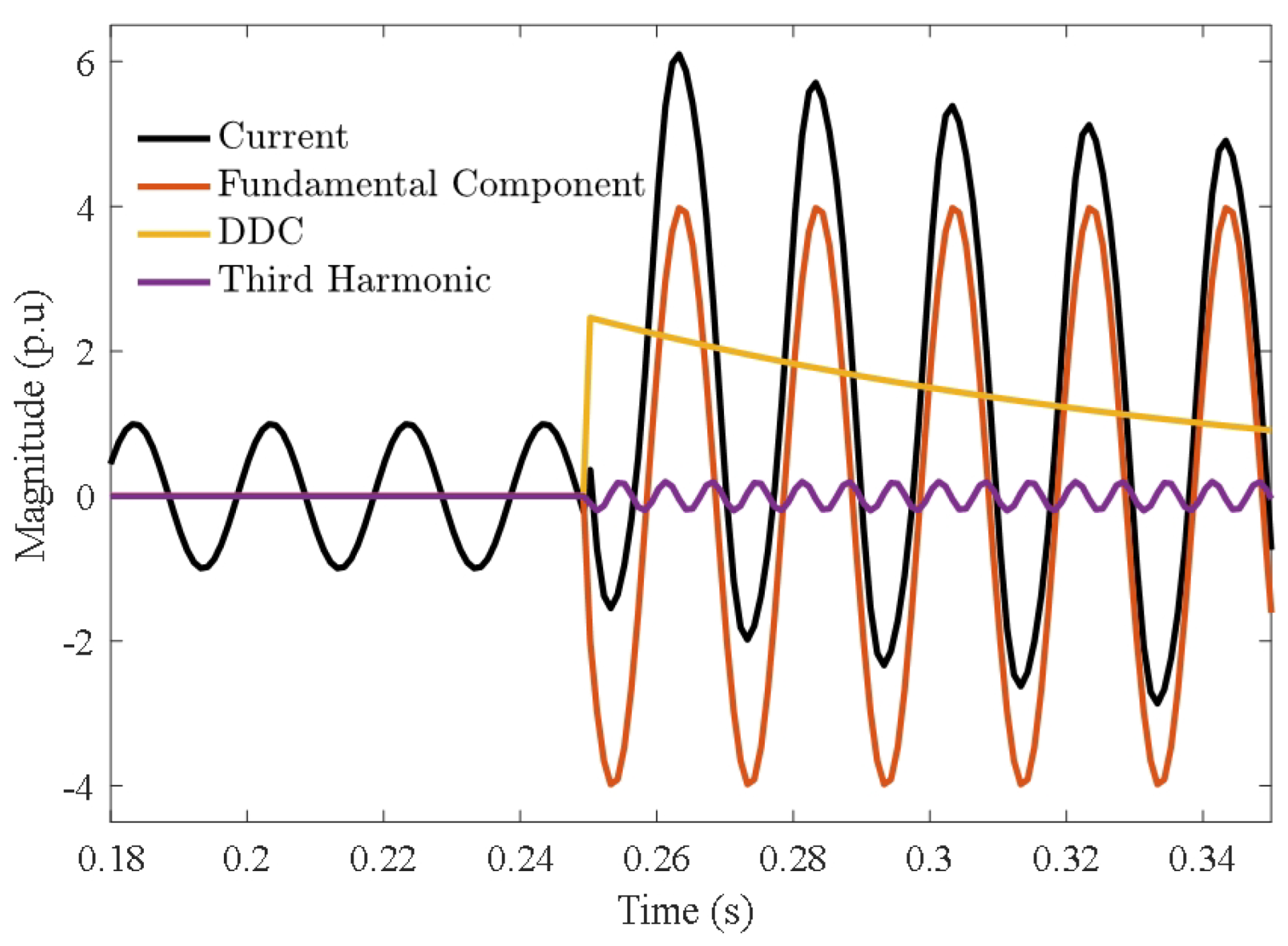

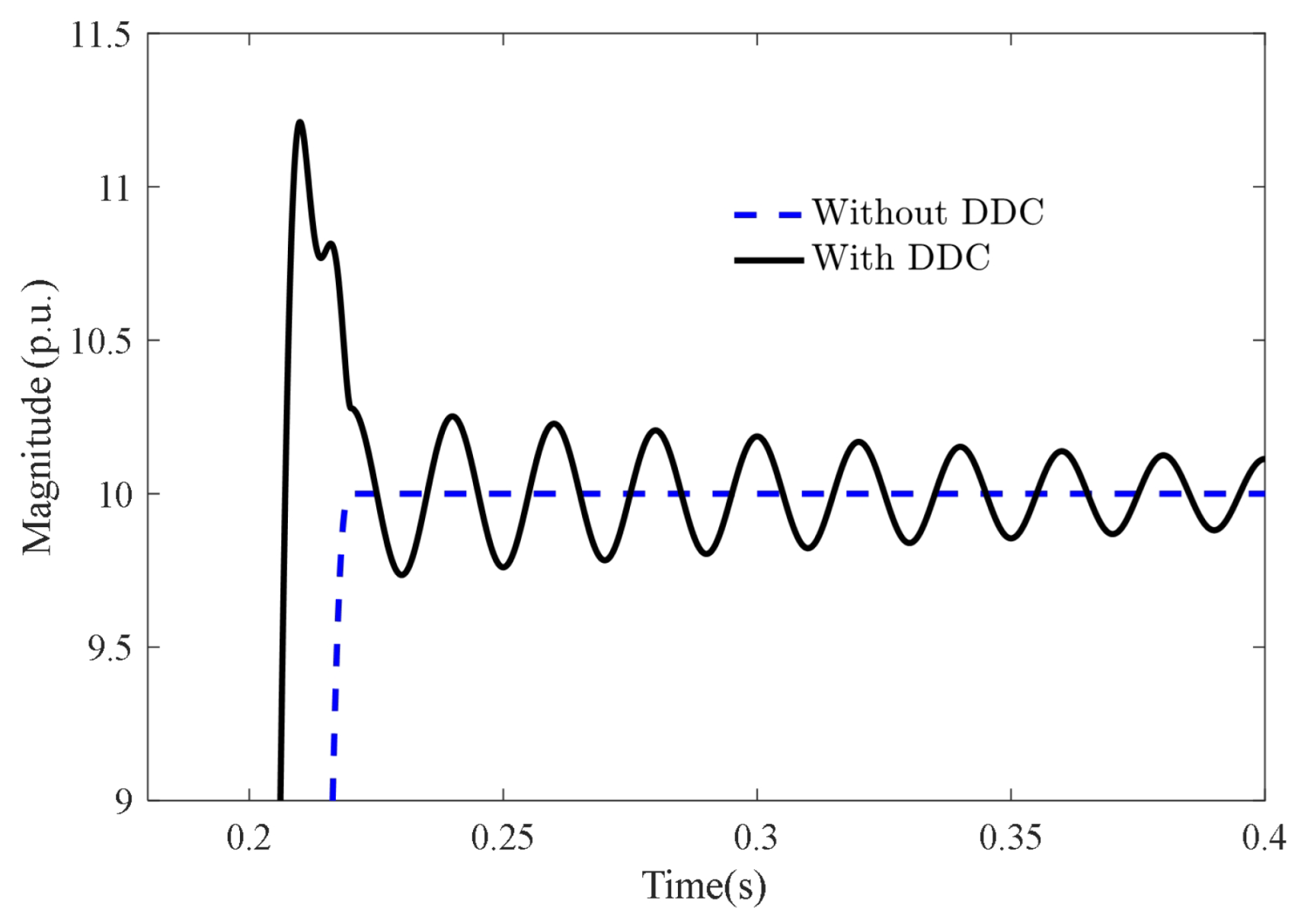
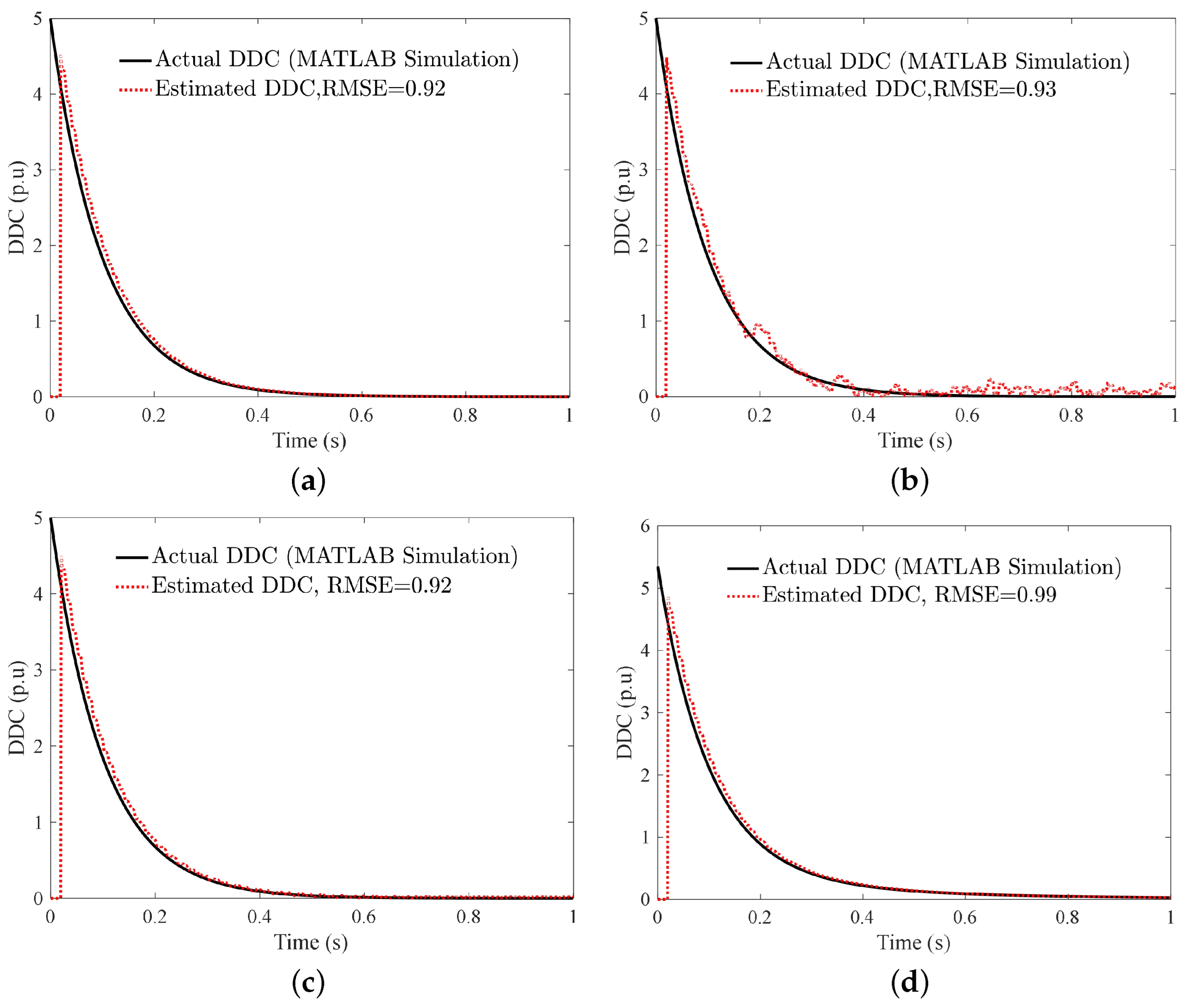
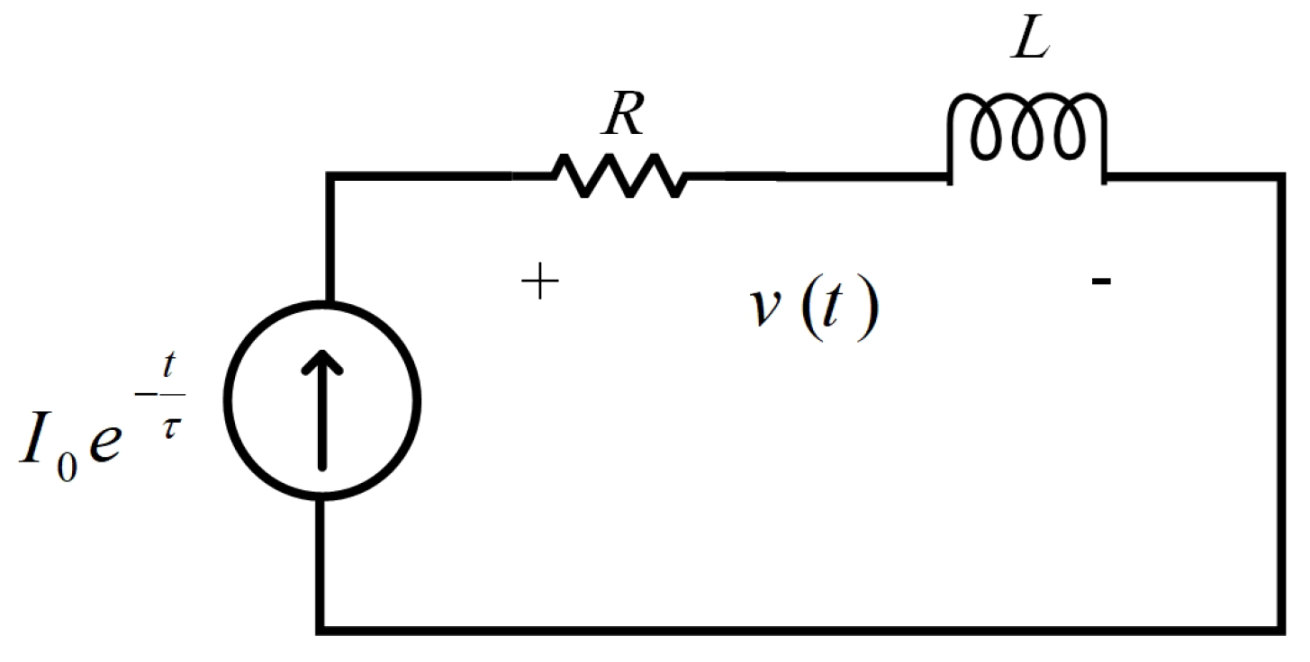
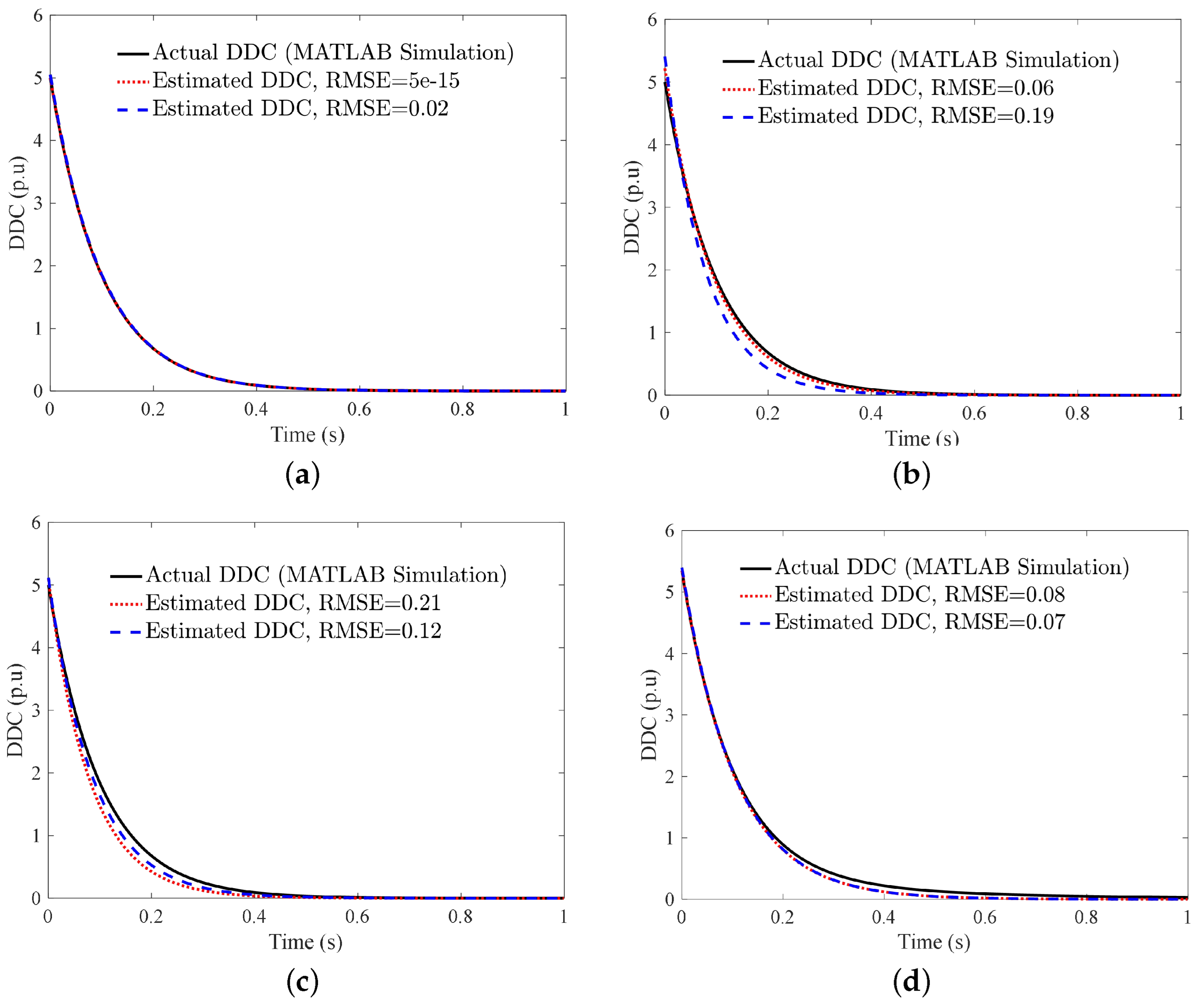
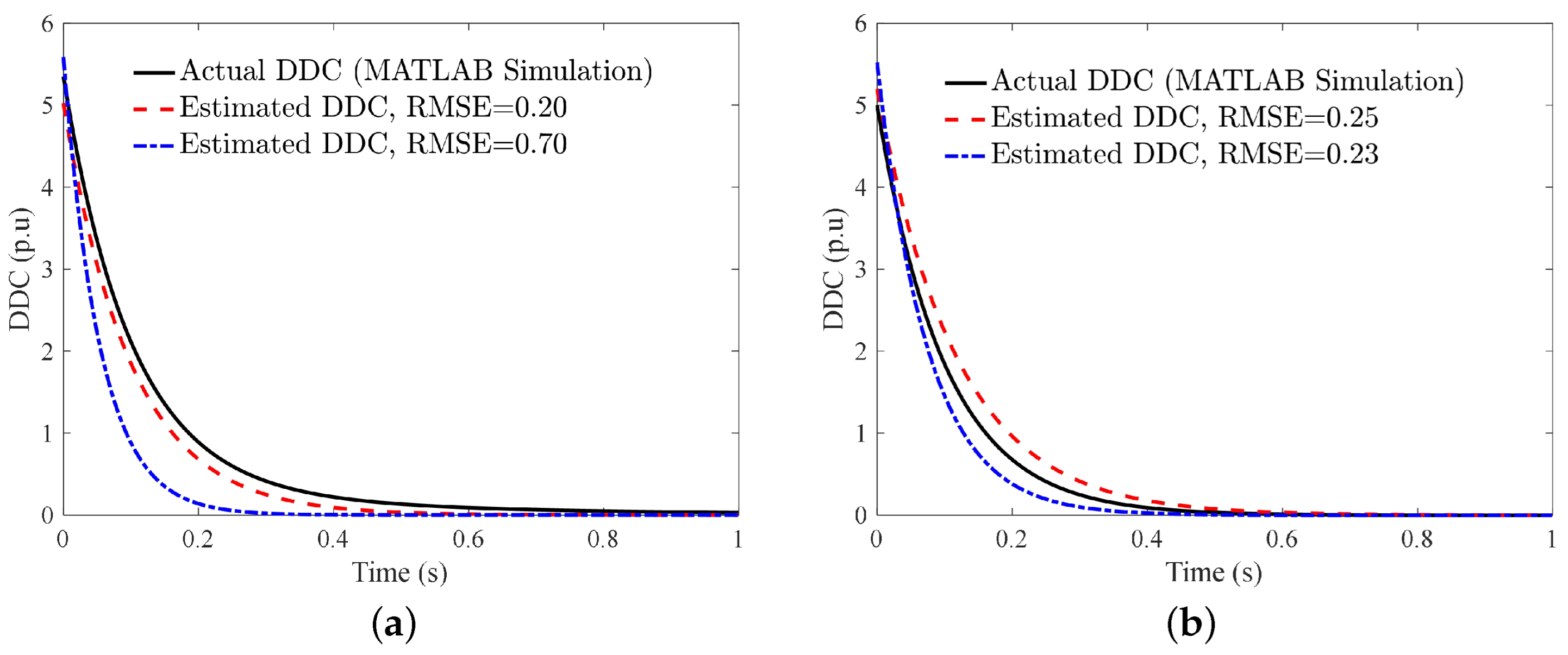
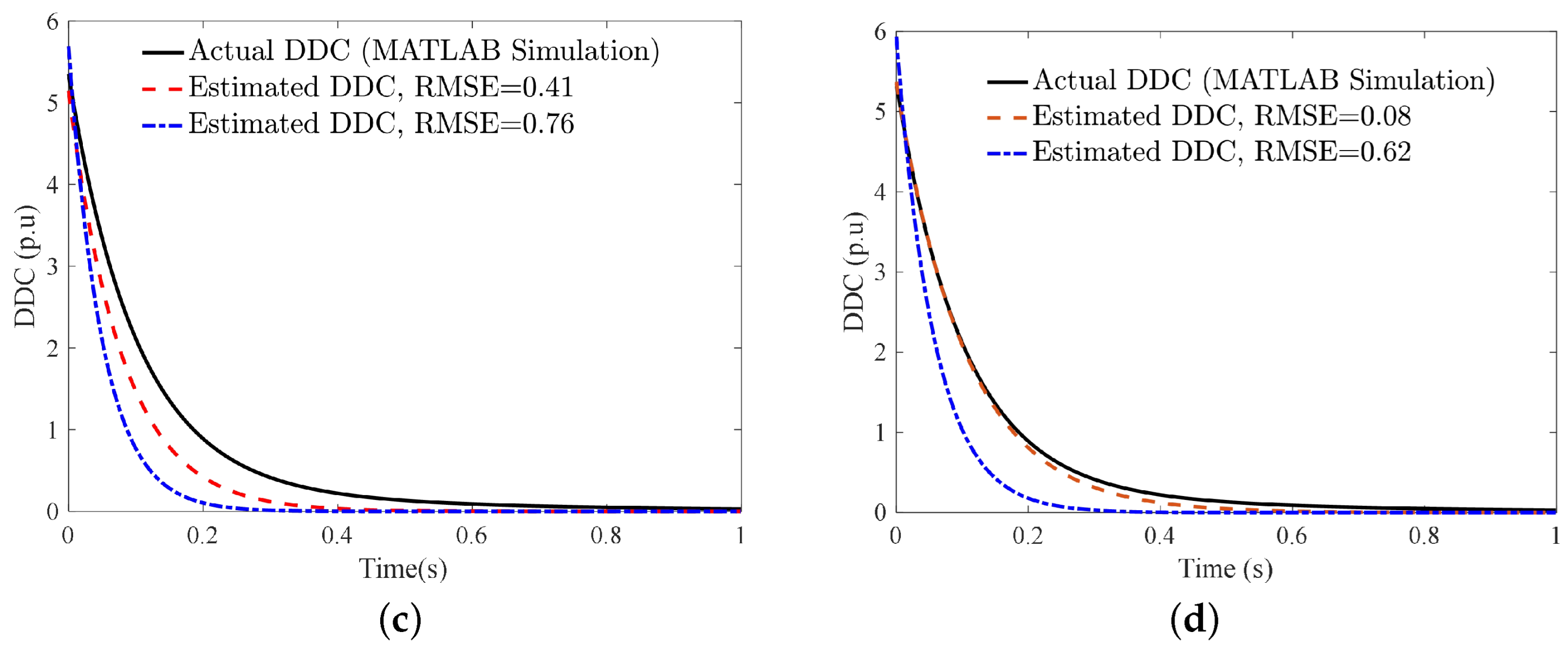


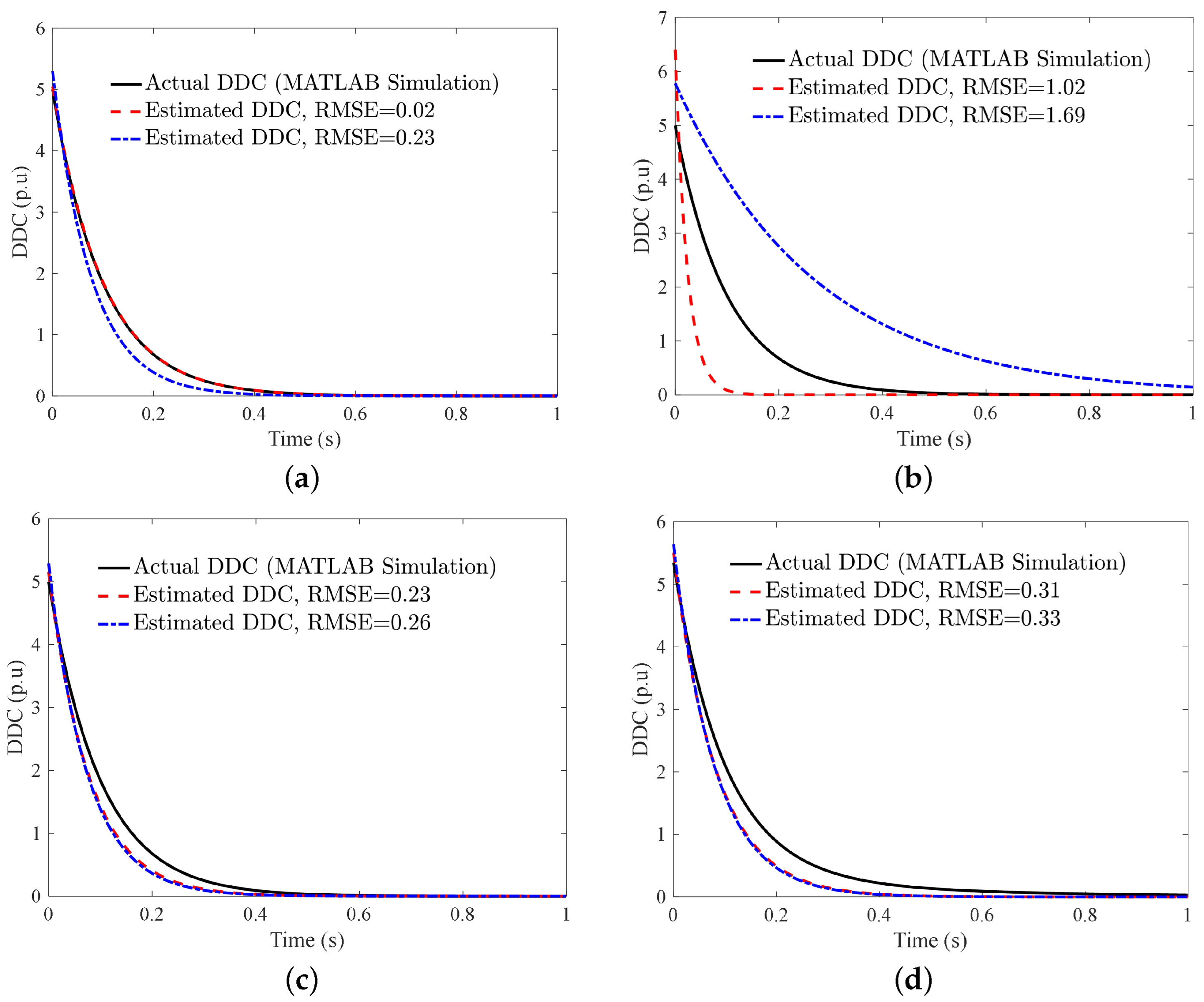
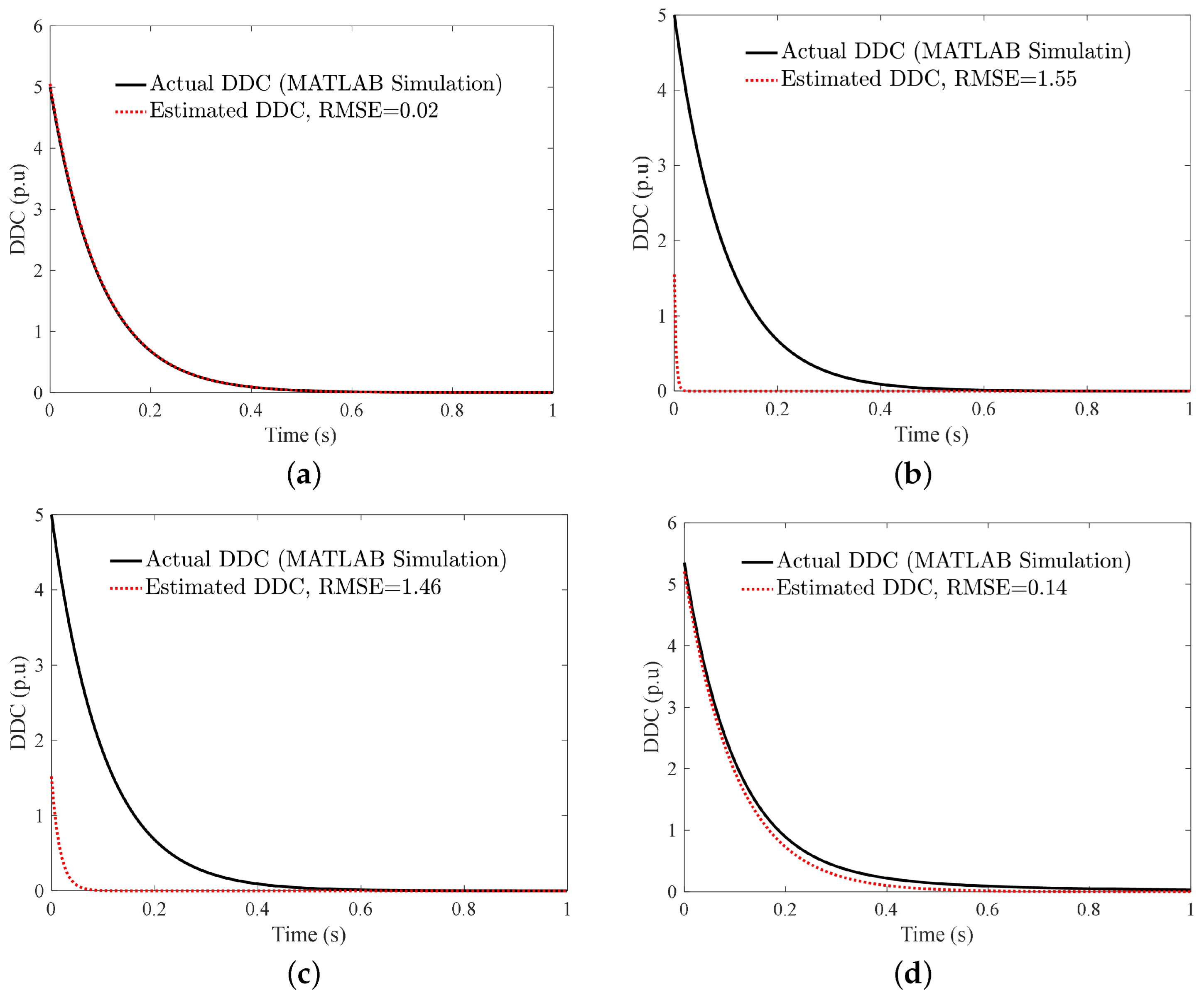
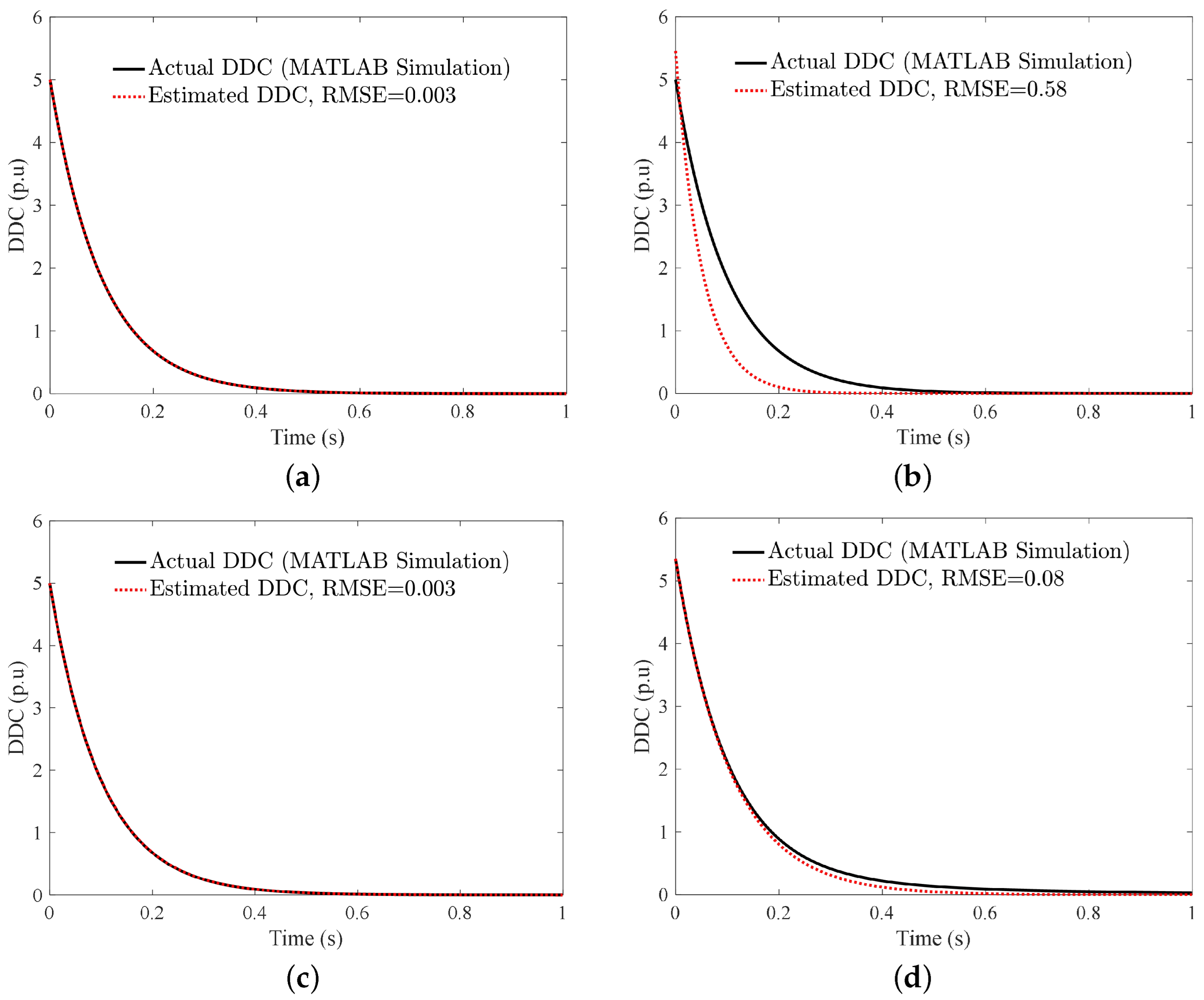
| Parameter | Definition | Value |
|---|---|---|
| Angular frequency | rad/s | |
| DDC amplitude | 5 p.u | |
| Primary DDC time constant | 5 cycles | |
| Secondary DDC time constant | 0.4 s | |
| Fundamental frequency amplitude | 1 p.u | |
| Fundamental frequency angle | rad | |
| Third harmonic amplitude | 0.3 p.u | |
| Third harmonic angle | rad | |
| Frequency deviation | −0.5 Hz | |
| W | White noise | SNR = 4 |
| Method | Noise | Harmonics | Off-Nominal Frequency | Multiple DDCs | Sample Requirements |
|---|---|---|---|---|---|
| [10] | x | ✔ | x | x | 1 cycle |
| [7] | x | ✔ | x | x | 1+1/4 cycle |
| [2] | x | ✔ | x | x | NA |
| [11] | ✔ | x | x | x | 1 cycle |
| [12] | x | ✔ | ✔ | x | 1 cycle +1 sample |
| [14] | ✔ | ✔ | x | x | 1 cycle |
| [13] | ✔ | ✔ | x | x | 1 cycle |
| [15] | ✔ | ✔ | x | x | 1 cycle |
| [16] | x | ✔ | ✔ | ✔ | 1 cycle +2 samples |
| [1] | ✔ | ✔ | ✔ | ✔ | 1 cycle |
| [17] | ✔ | ✔ | ✔ | x | 1 cycle +3 samples |
| [6] | ✔ | ✔ | ✔ | x | 1 cycle |
| [18] | ✔ | ✔ | x | x | 4 samples |
| [3] | ✔ | ✔ | ✔ | ✔ | 1/2 cycle +3 samples |
| [19] | ✔ | ✔ | ✔ | ✔ | half cycle + 2 samples |
| [20] | ✔ | ✔ | ✔ | ✔ | 1 cycle |
| [21] | ✔ | ✔ | ✔ | ✔ | half cycle + 1 sample |
| Method | Noise | Harmonics | Off-Nominal Frequency | Multiple DDCs | Samples Requirement |
|---|---|---|---|---|---|
| [22] | x | ✔ | x | x | 1+1/4 cycle |
| [24] | x | ✔ | x | x | NA |
| [23] | x | ✔ | x | ✔ | 1 cycle |
| [25] | ✔ | ✔ | x | x | 1 cycle +1 sample |
| [27] | x | ✔ | x | x | 1 cycle |
| [26] | x | ✔ | x | x | 1 cycle +2 samples |
| [29] | ✔ | ✔ | x | ✔ | 1 cycle |
| [30] | x | ✔ | ✔ | x | 1 cycle +3 samples |
| [31] | ✔ | ✔ | x | ✔ | 1 cycle |
| [32] | ✔ | ✔ | ✔ | ✔ | 1 cycle |
| [33] | ✔ | ✔ | x | ✔ | 1 cycle |
| [35] | x | ✔ | x | x | 1/2 cycle +3 samples |
| [34] | x | ✔ | x | x | 1/2 cycle +3 samples |
| [36] | ✔ | ✔ | ✔ | ✔ | ≥ 1 cycle |
| Method | Noise | Harmonics | Off-Nominal Frequency | Multiple DDCs | Sample Requirements |
|---|---|---|---|---|---|
| [37] | x | ✔ | x | x | 7 samples |
| [38] | ✔ | ✔ | x | x | 1 cycle |
| [39] | x | ✔ | x | x | 20 samples |
| [40] | x | ✔ | x | x | 1 cycle |
| [41] | x | ✔ | x | x | 1 cycle |
| [42] | ✔ | ✔ | ✔ | ✔ | 7/8 cycle |
| [43] | ✔ | x | x | x | 1 cycle |
| [44] | ✔ | x | x | ✔ | 8 samples |
| [45] | ✔ | ✔ | x | ✔ | 1 cycle |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammadi, S.; Mahmoudi, A.; Kahourzade, S.; Yazdani, A.; Shafiullah, G. Decaying DC Offset Current Mitigation in Phasor Estimation Applications: A Review. Energies 2022, 15, 5260. https://doi.org/10.3390/en15145260
Mohammadi S, Mahmoudi A, Kahourzade S, Yazdani A, Shafiullah G. Decaying DC Offset Current Mitigation in Phasor Estimation Applications: A Review. Energies. 2022; 15(14):5260. https://doi.org/10.3390/en15145260
Chicago/Turabian StyleMohammadi, Sina, Amin Mahmoudi, Solmaz Kahourzade, Amirmehdi Yazdani, and GM Shafiullah. 2022. "Decaying DC Offset Current Mitigation in Phasor Estimation Applications: A Review" Energies 15, no. 14: 5260. https://doi.org/10.3390/en15145260
APA StyleMohammadi, S., Mahmoudi, A., Kahourzade, S., Yazdani, A., & Shafiullah, G. (2022). Decaying DC Offset Current Mitigation in Phasor Estimation Applications: A Review. Energies, 15(14), 5260. https://doi.org/10.3390/en15145260










