A Bidirectional DHC-LT Resonant DC-DC Converter with Research on Improved Fundamental Harmonic Analysis Considering Phase Angle of Load Impedance
Abstract
:1. Introduction
2. Topology Structure and Characteristics
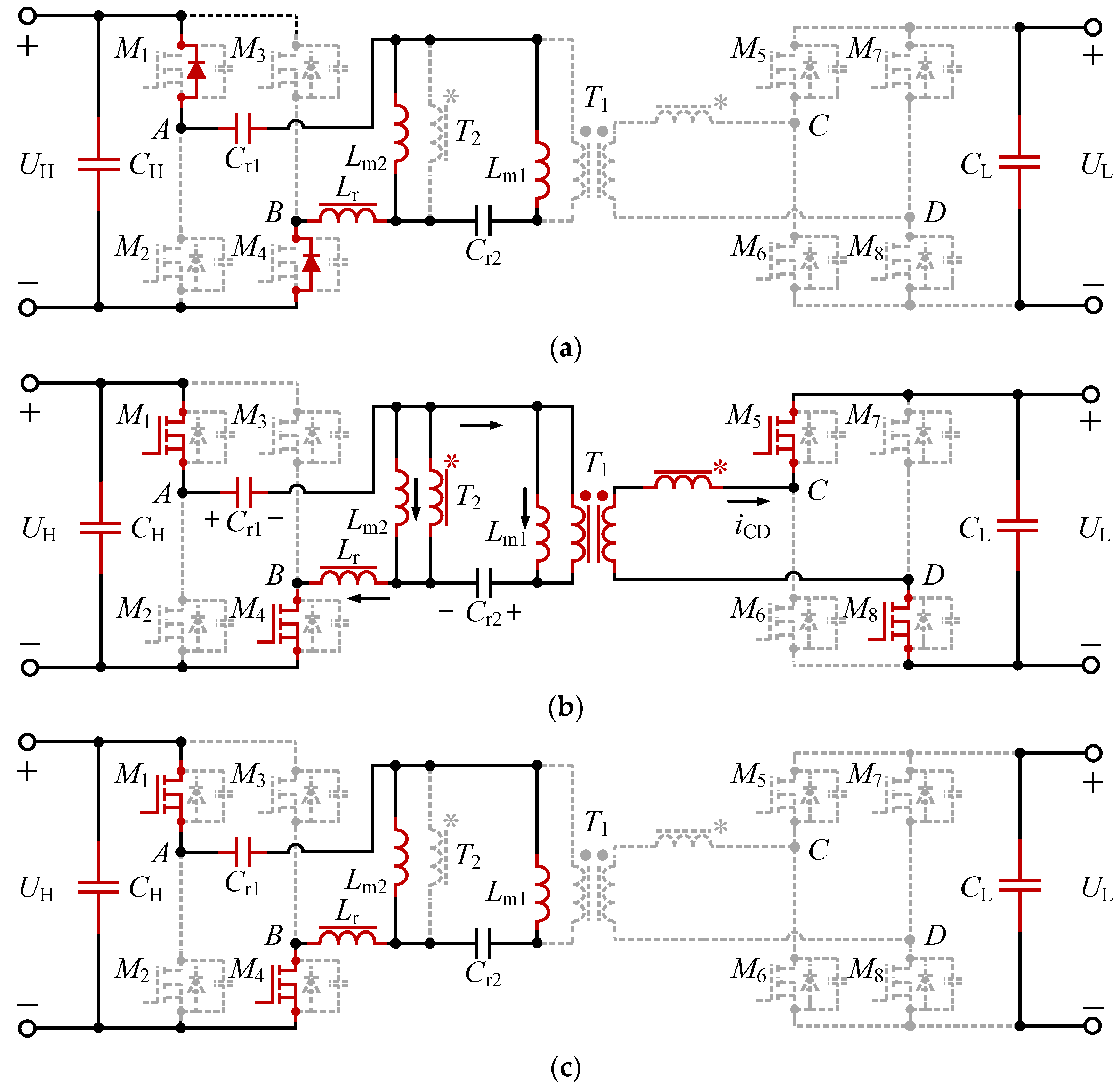
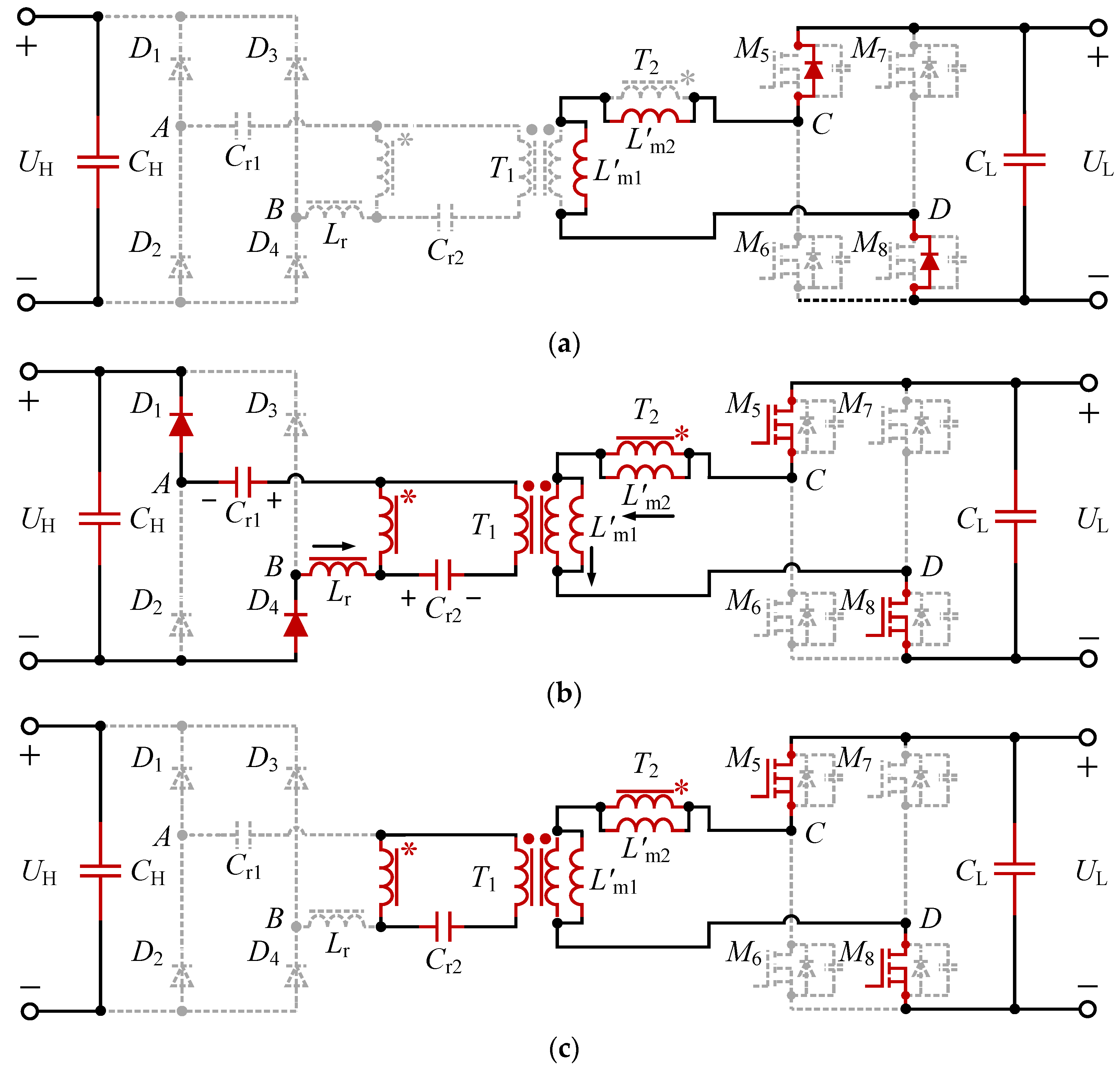
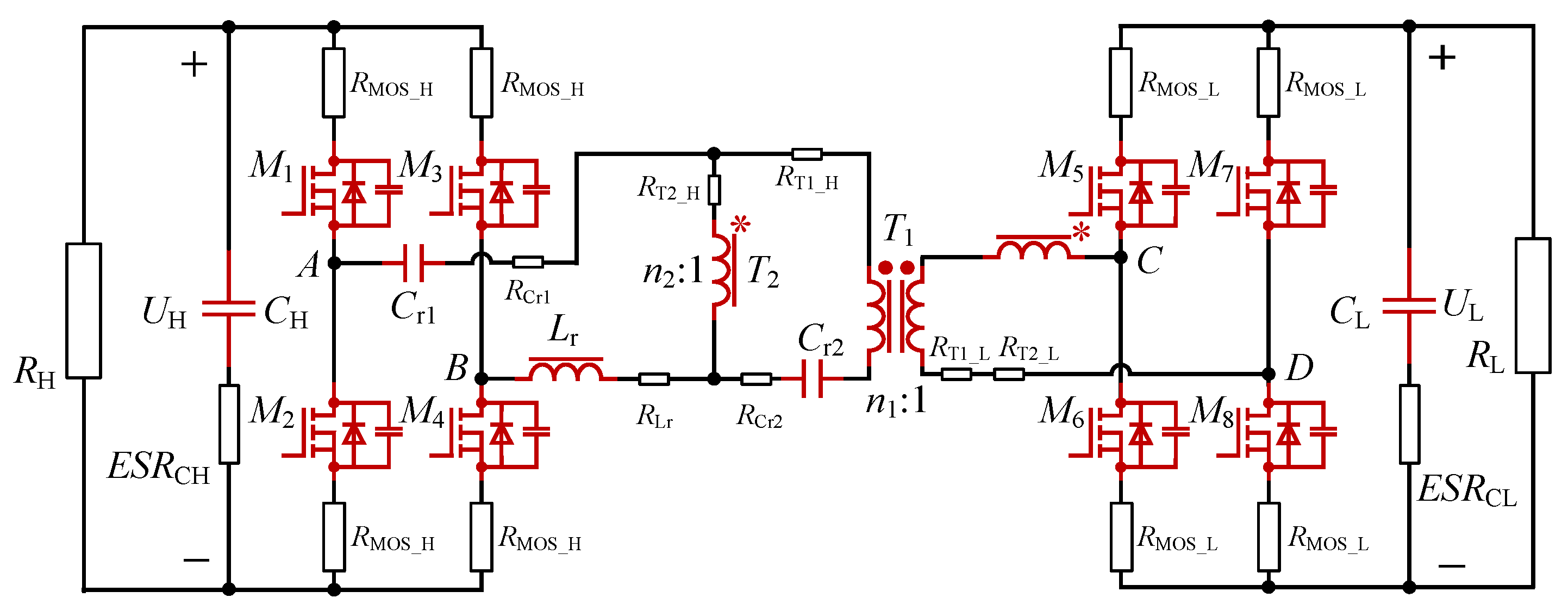
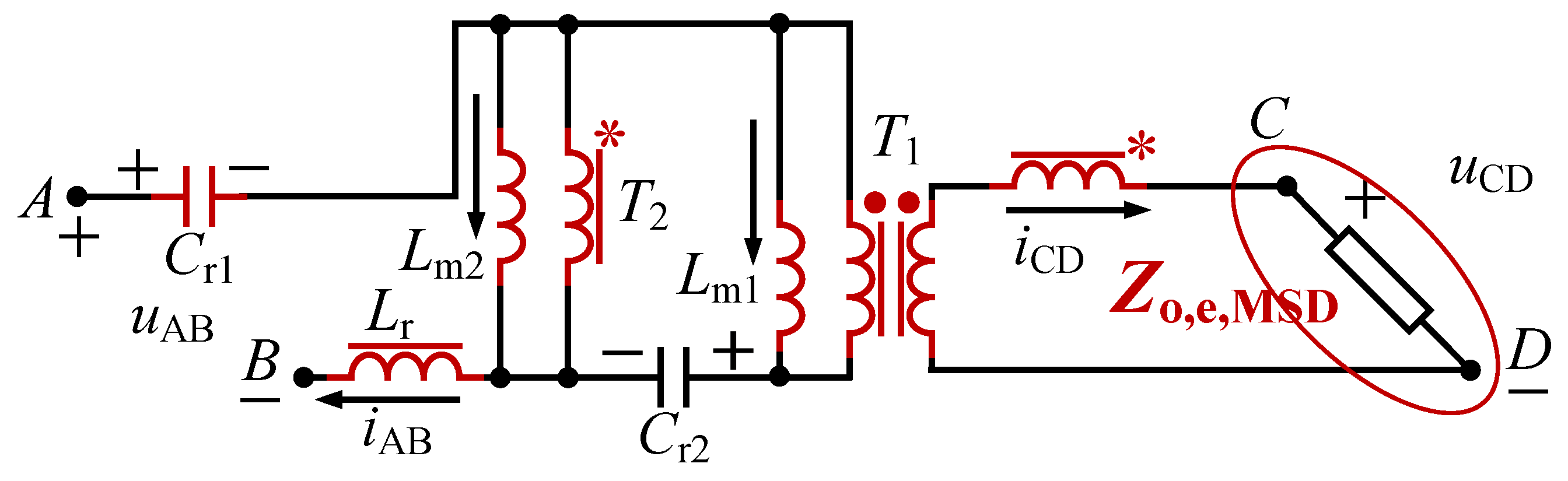
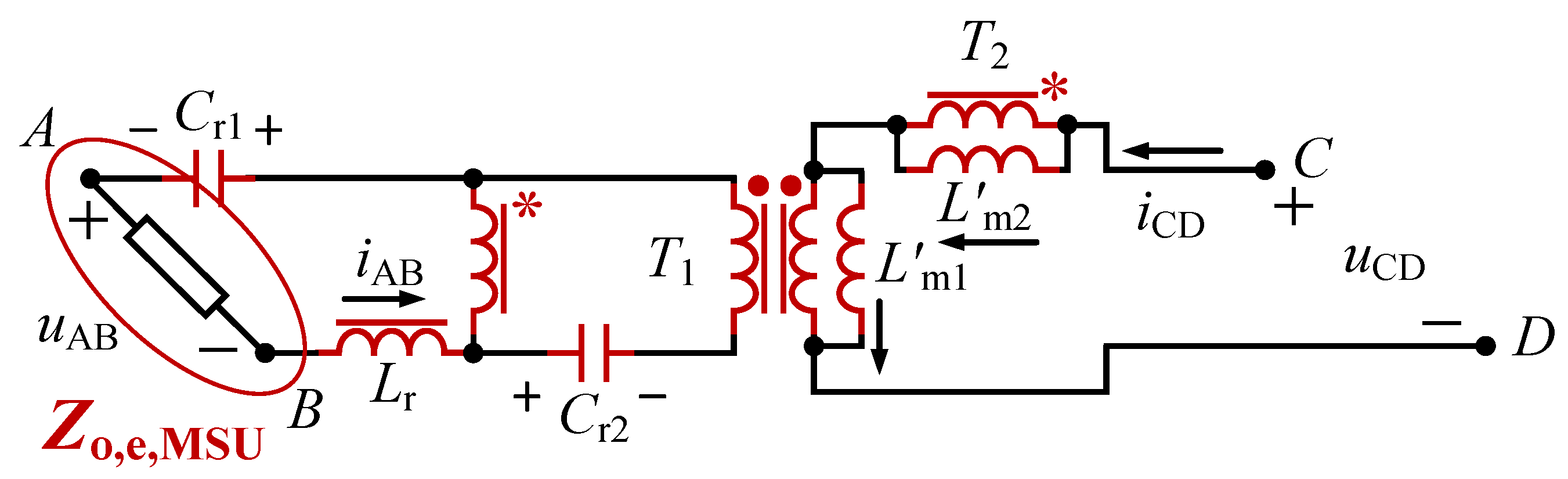
2.1. Topology Structure
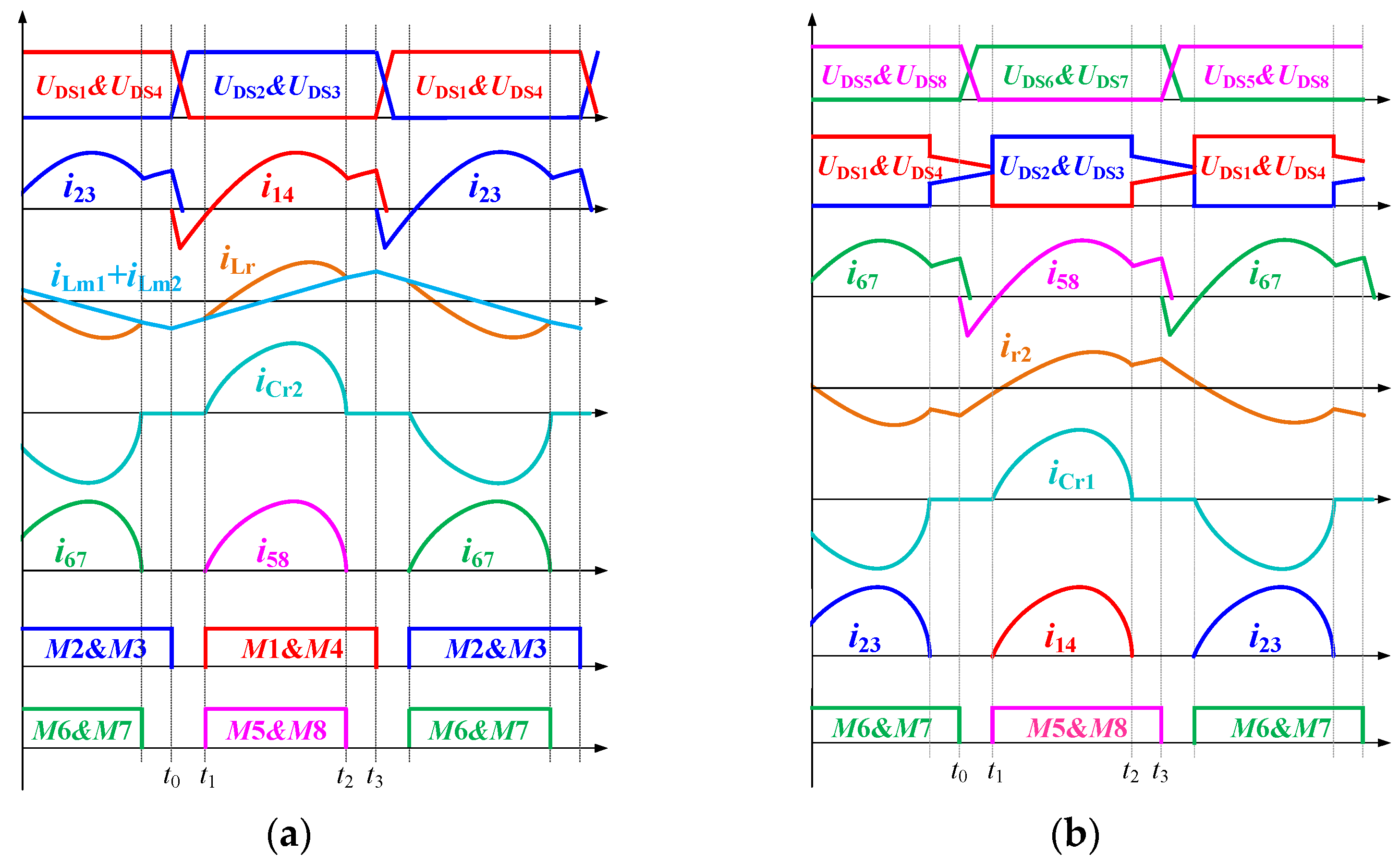
2.2. Operation Principles
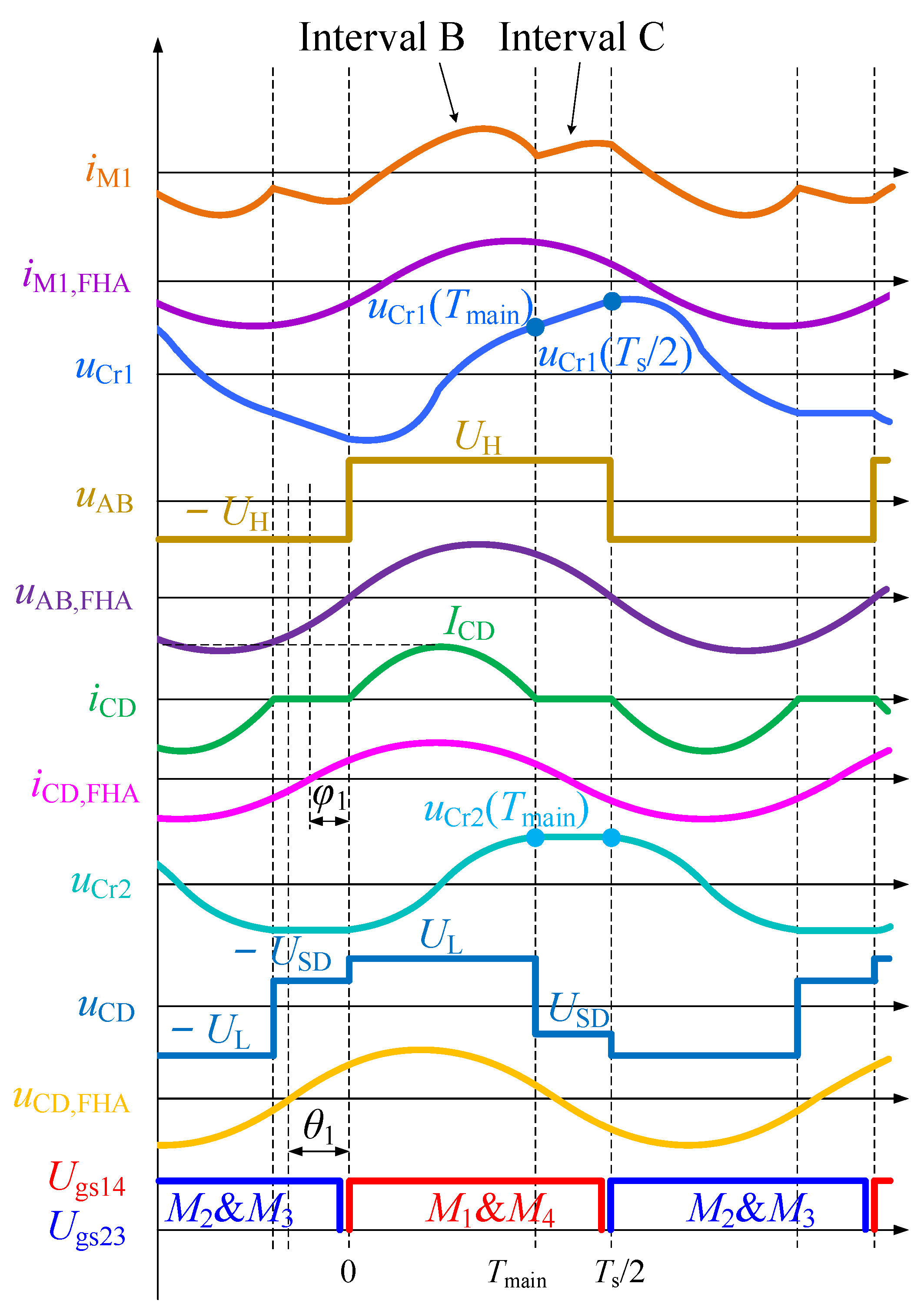
2.2.1. Step-Down Mode
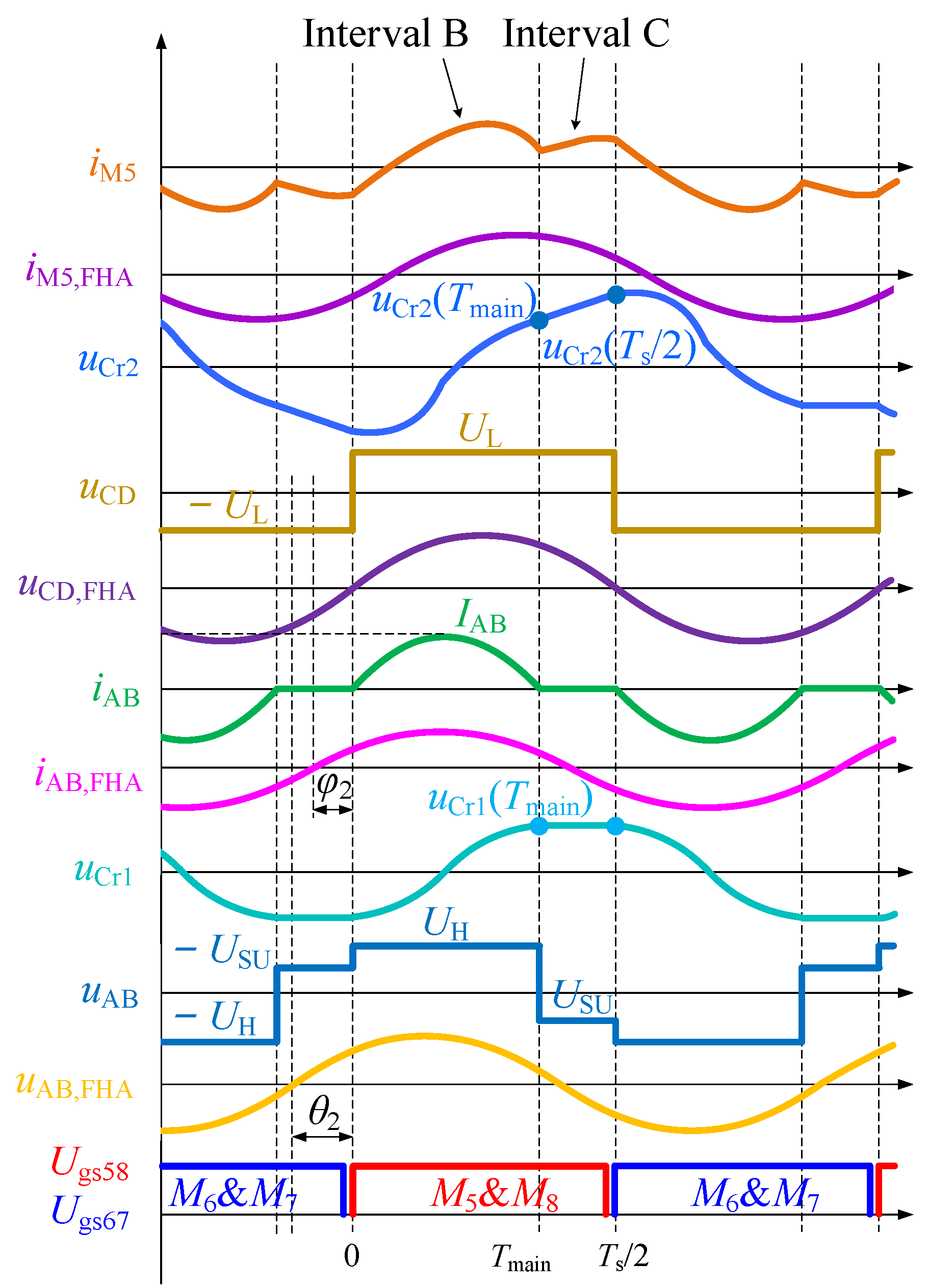
2.2.2. Step-Up Mode
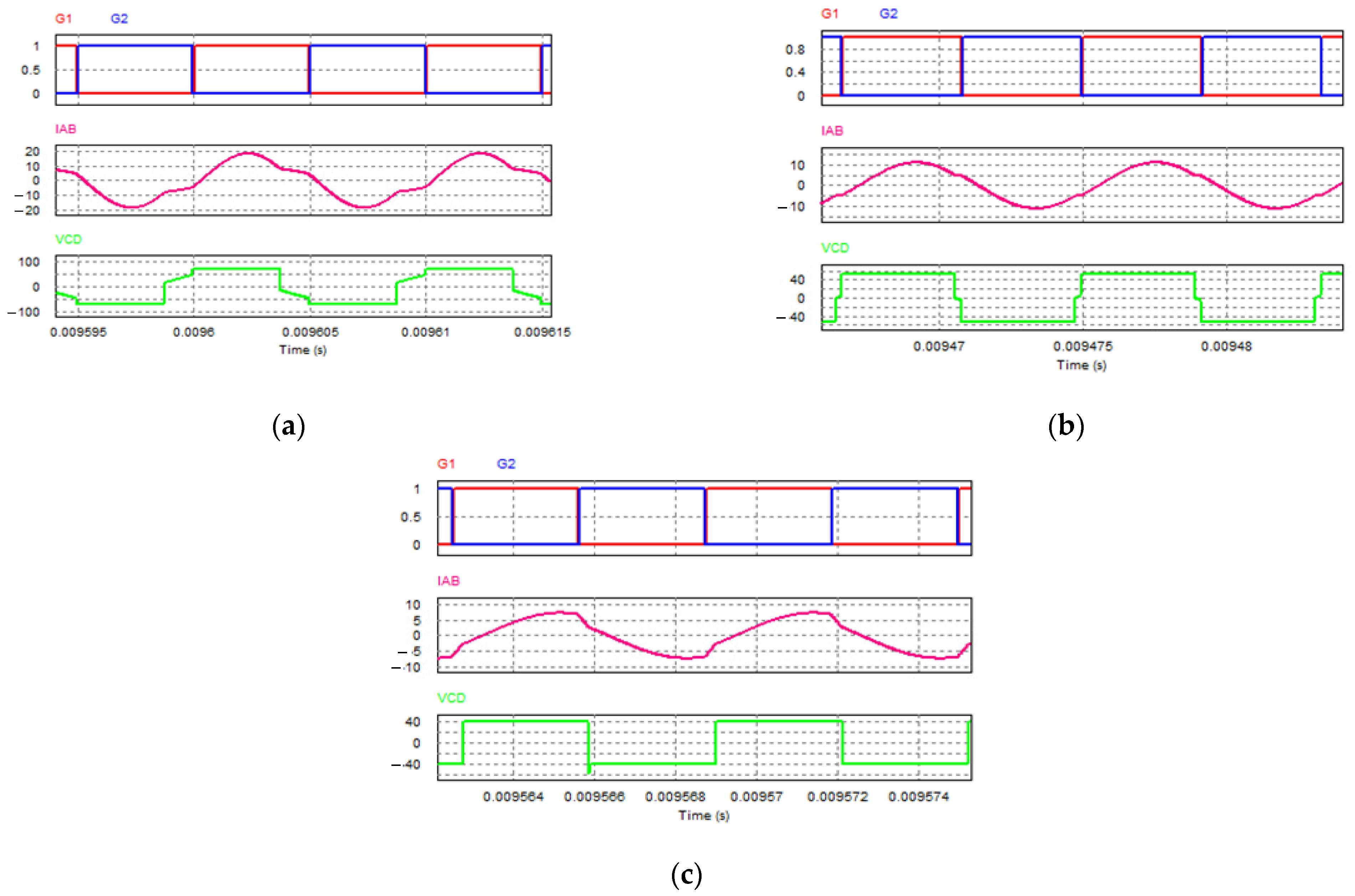
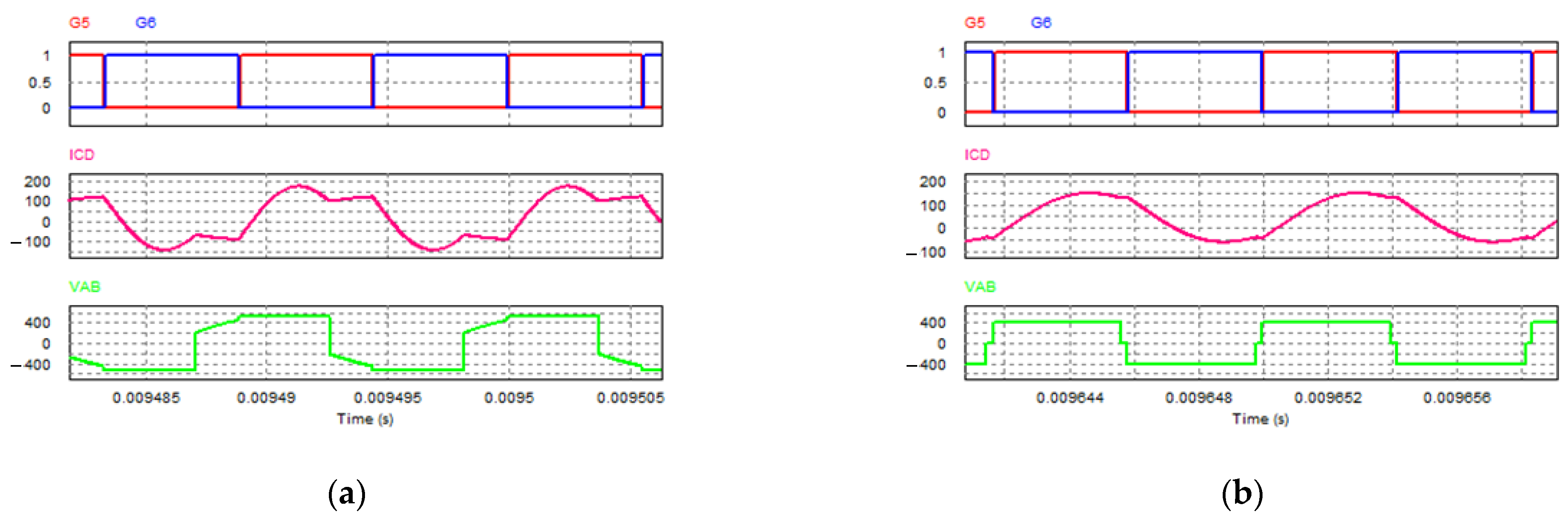
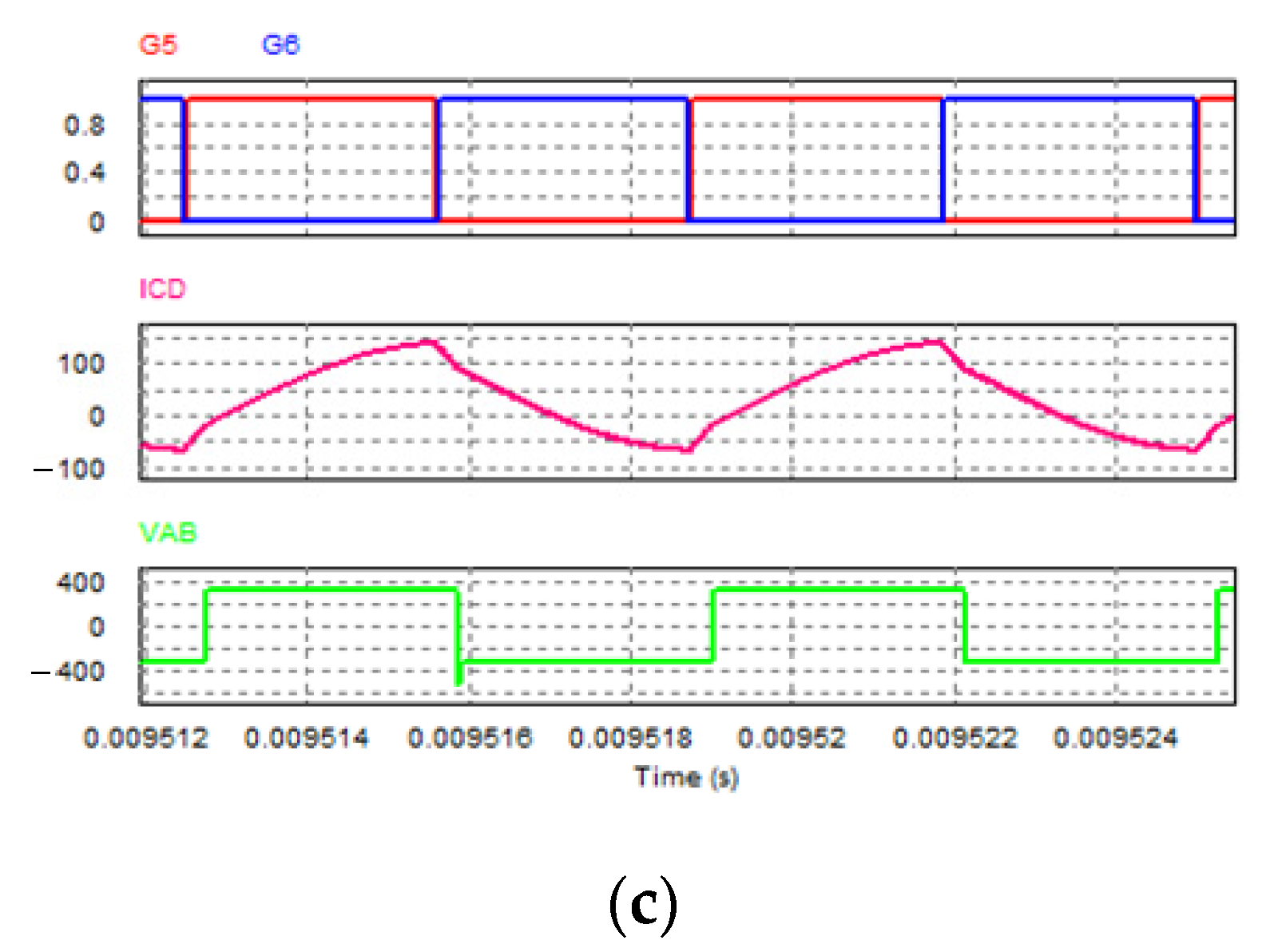
2.3. Simulation Verification
2.4. Small-Signal Modeling
3. Improved FHA with Modification of AC Load Impedance
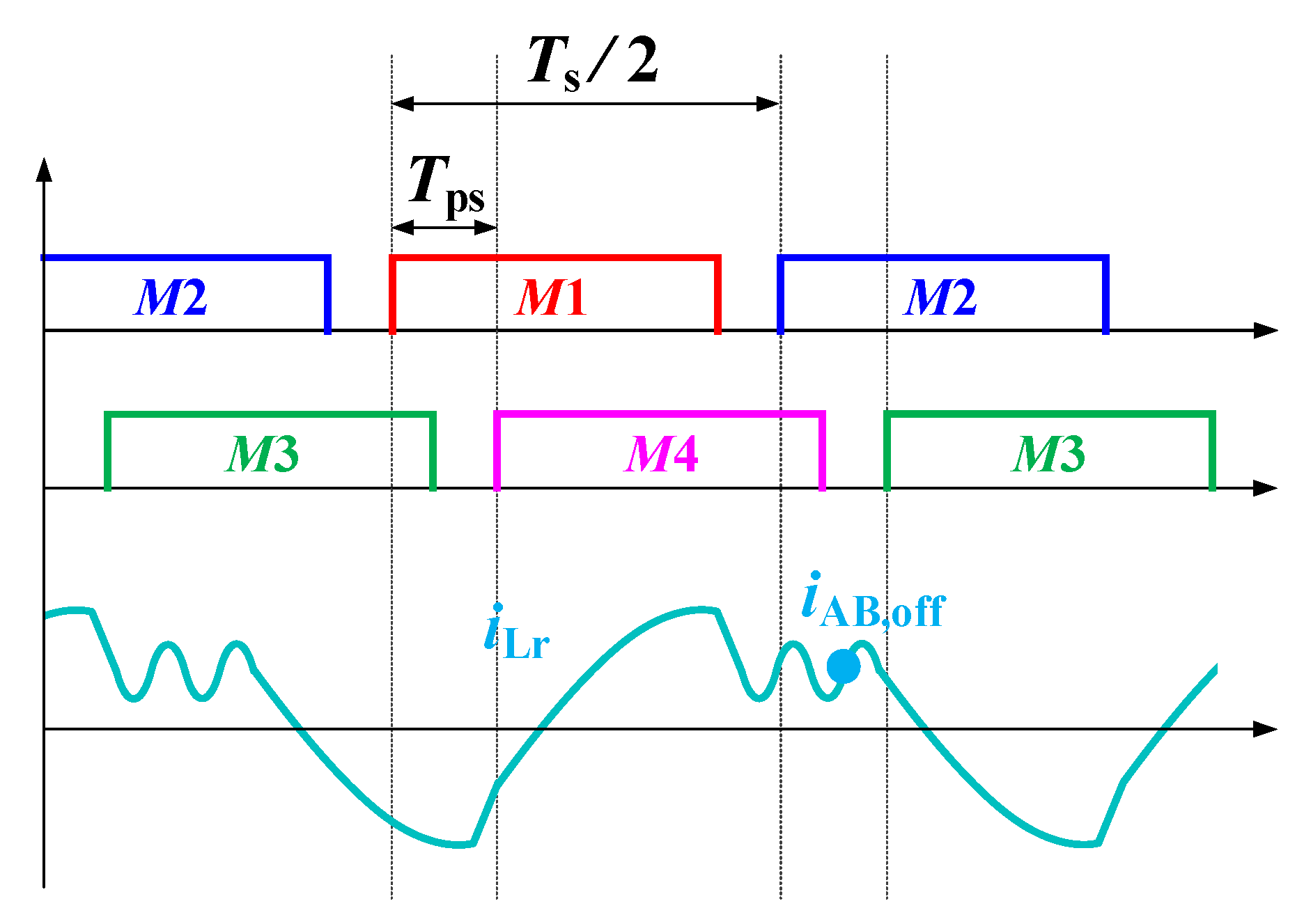
3.1. Improved FHA in Step-Down Mode
Assuming
- (a)
- The main resonance interval (Interval B) lasts half of the main resonant period, and Tmain is equal to 1/2fr.
- (b)
- In Interval C, the voltage between the neutral points of the two arms of the rectifier bridge remains constant, USD. The current flowing through Lm1 remains constant, ILm1, and the current flowing through Lm2 remains constant, ILm2.
- (c)
- The efficiency of the DHC-LT resonant circuit is 100%.
3.2. Improved FHA in Step-Up Mode
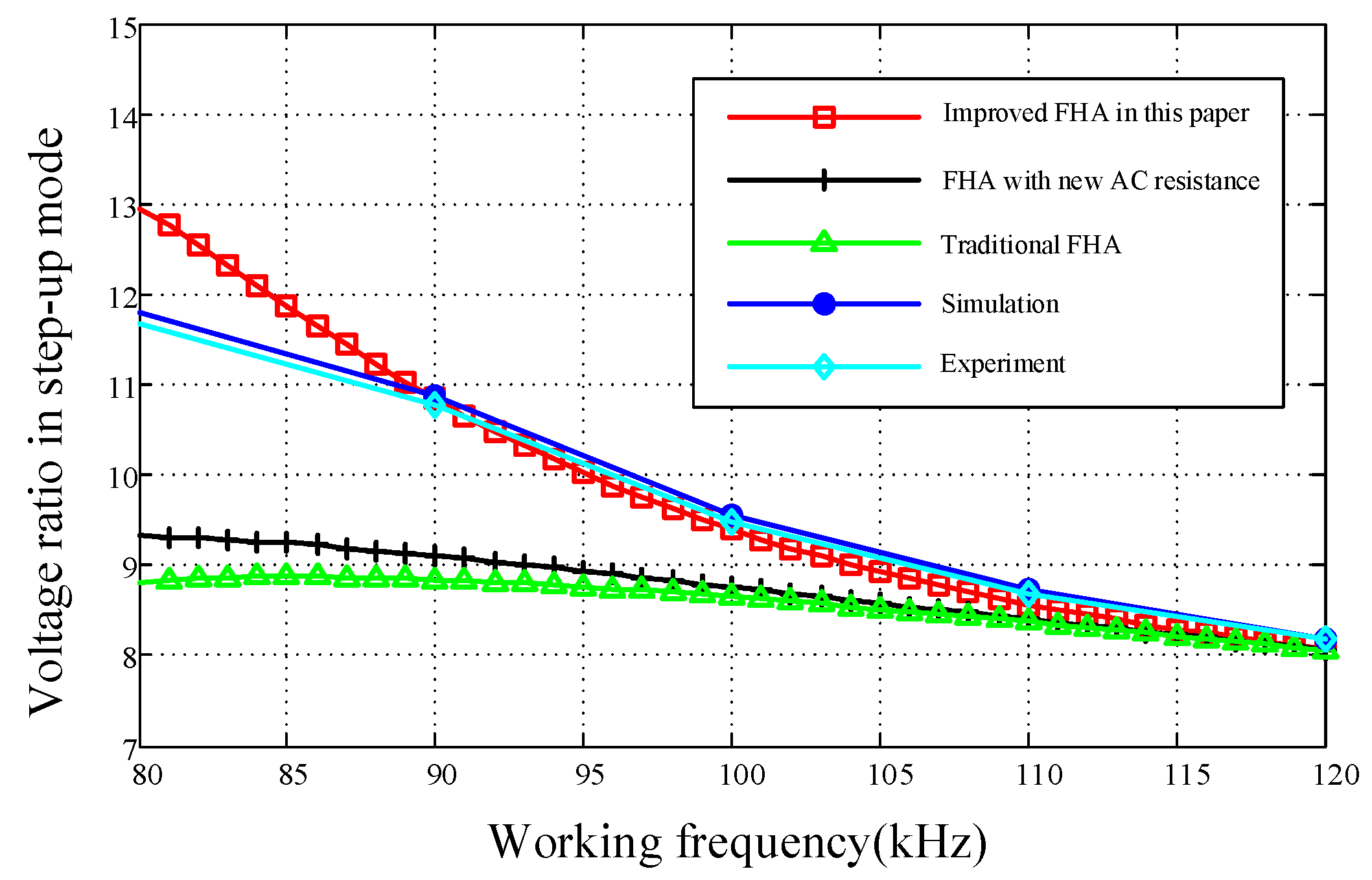
4. Comparison of Different Modeling Approaches
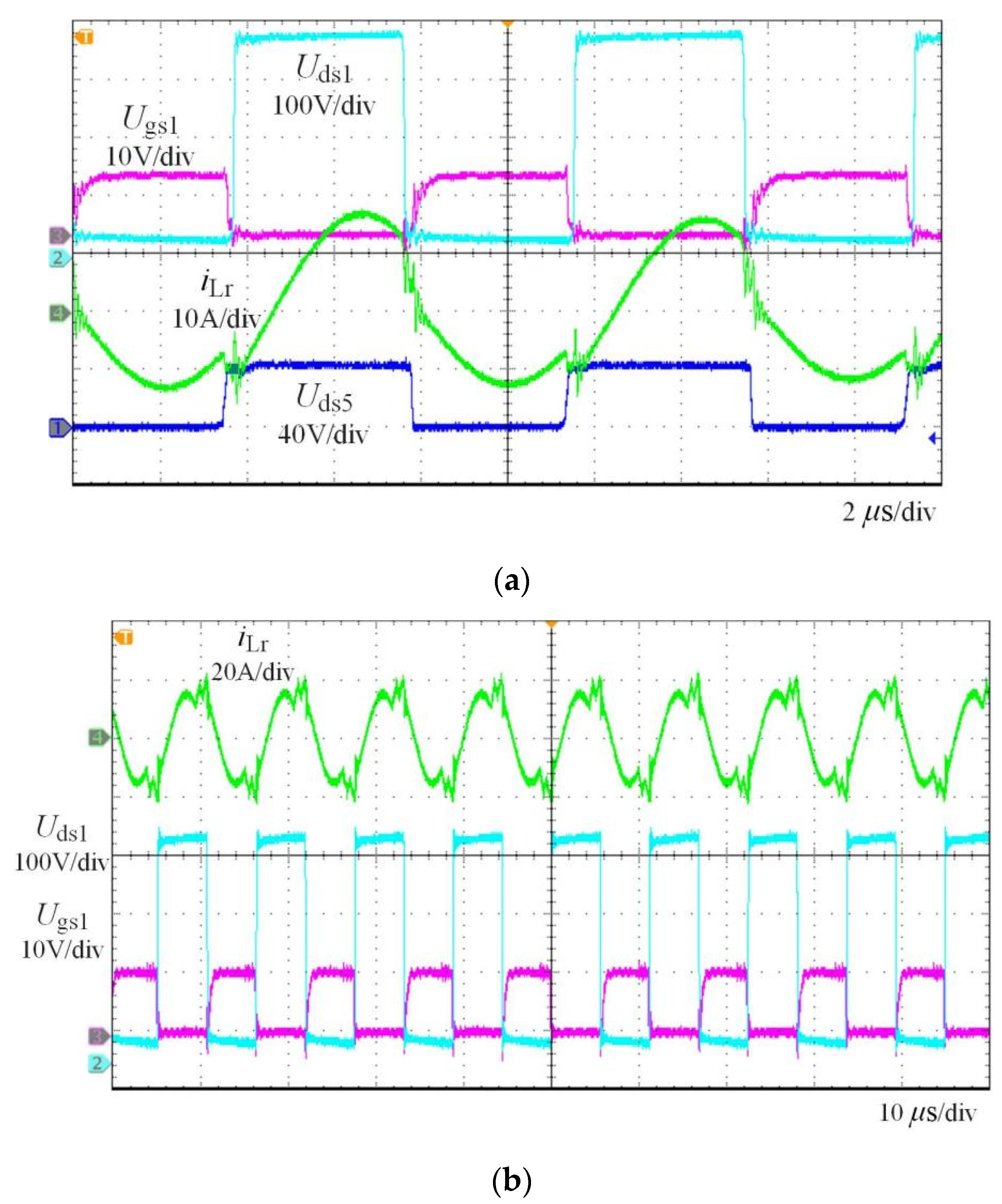
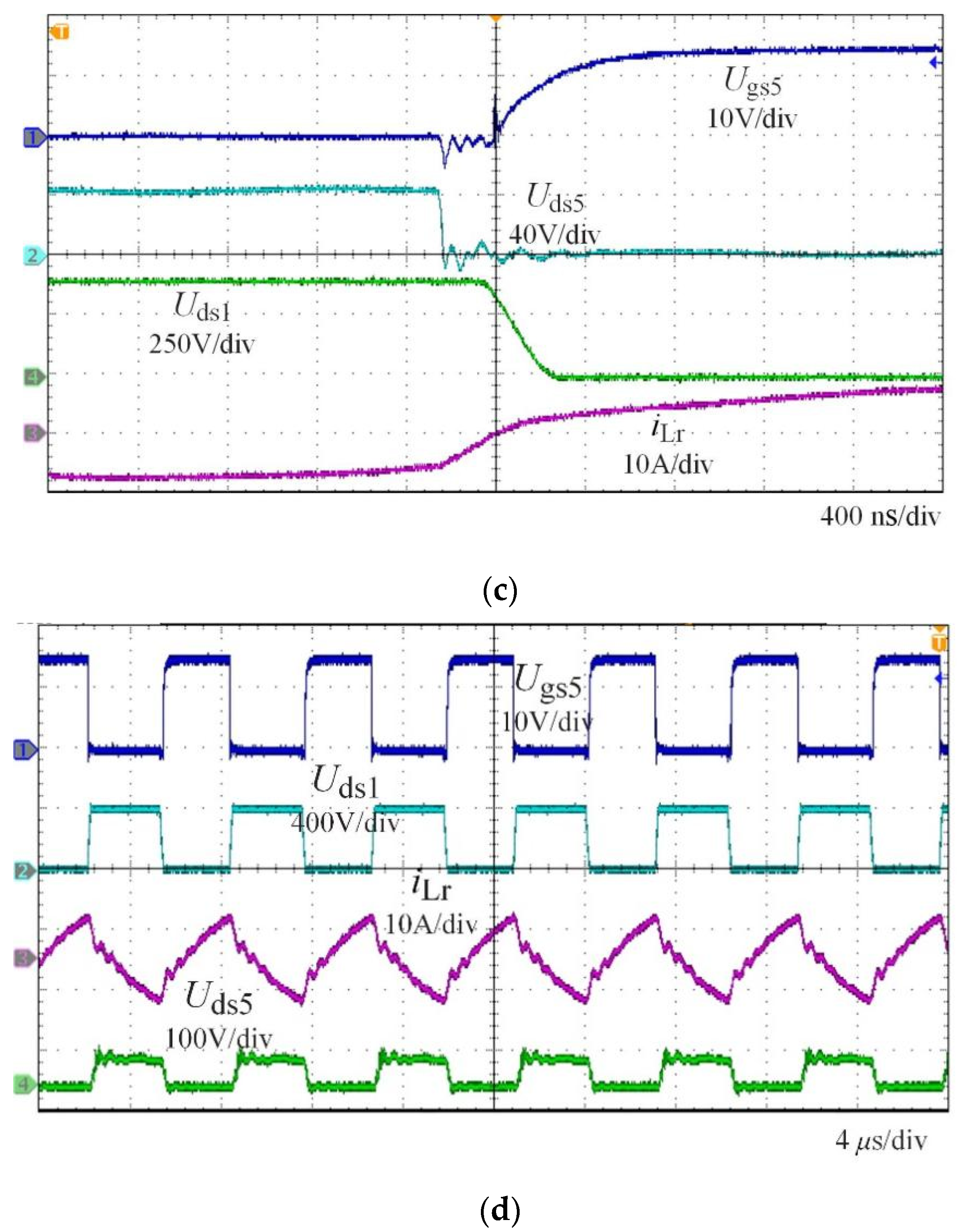
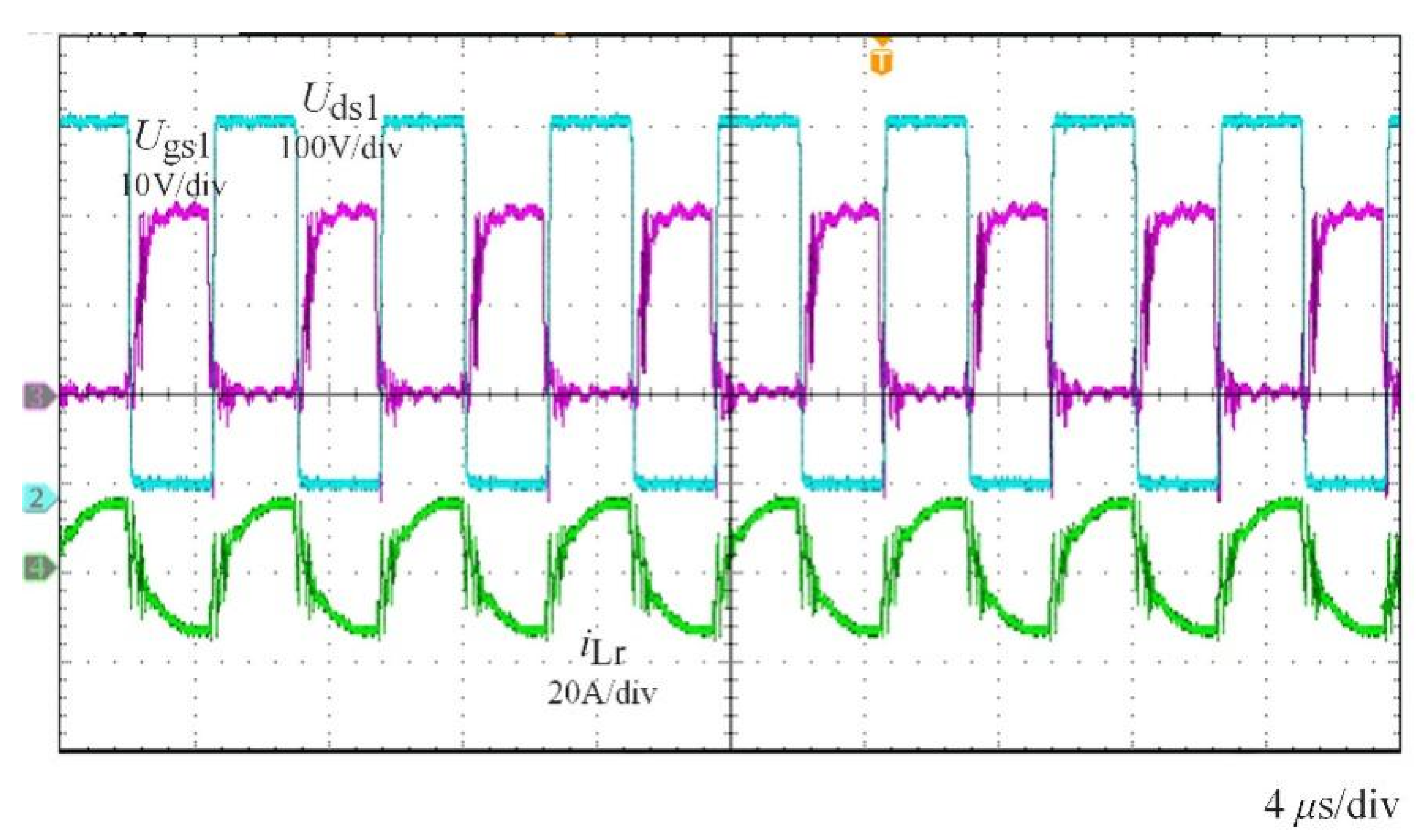
5. Experimental Results
5.1. Experimental Results of Steady-State Operation
5.2. Discussion of Phase-Shift Control
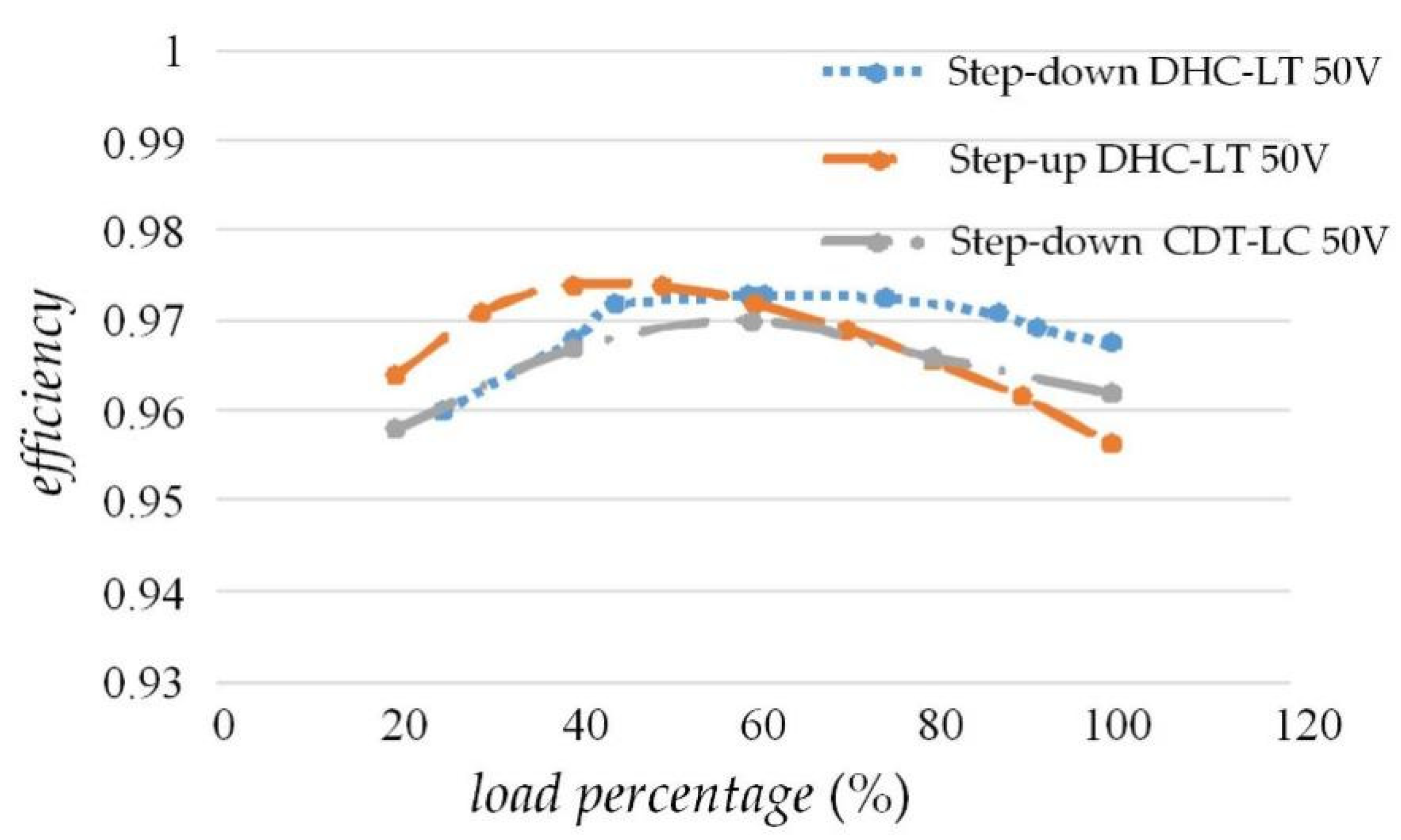
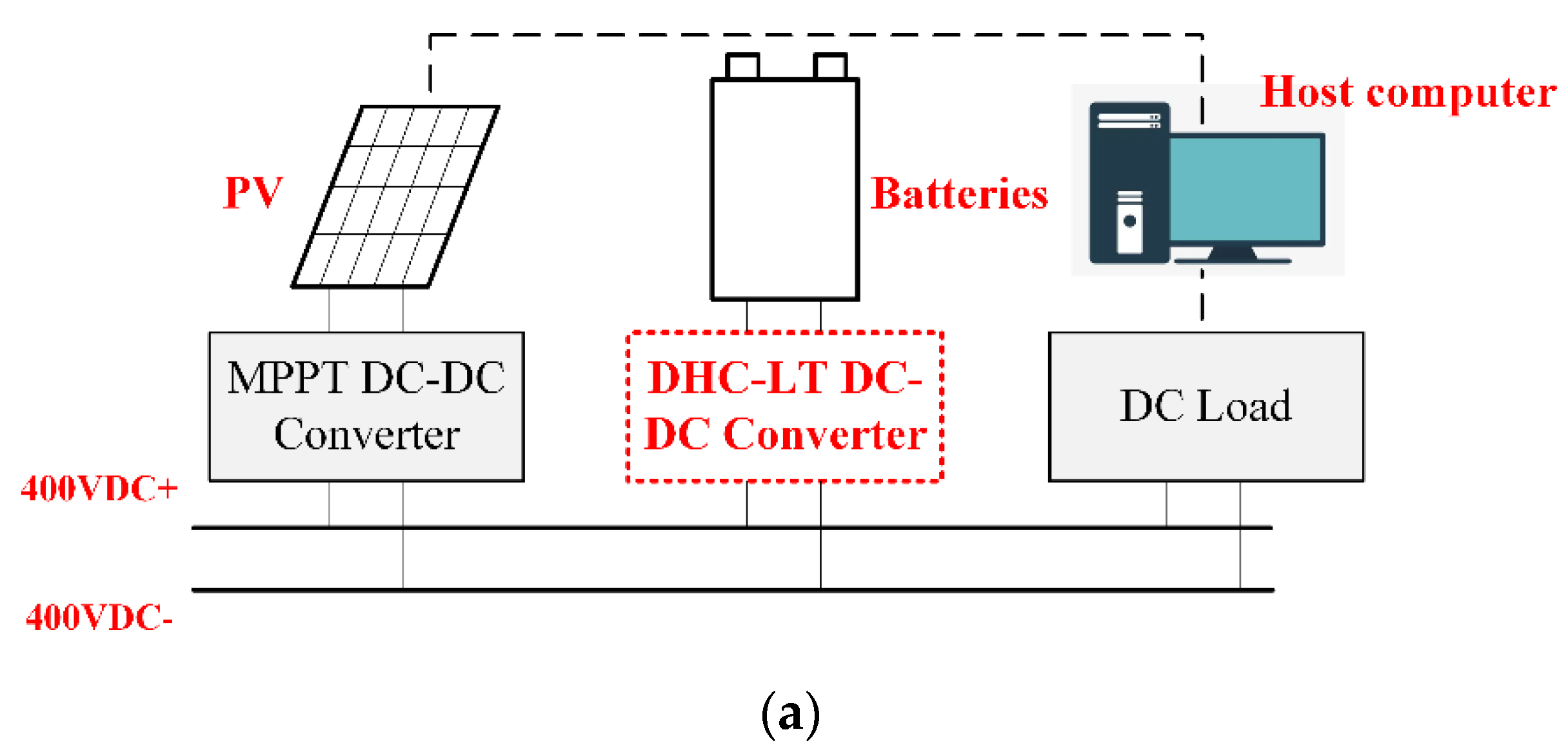
5.3. Verification in Battery/PV System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
- 1.
- Open-loop transfer function of the DHC-LT converter.
- 2.
- Derivation of UCD and ICD in step-down mode.
- 3.
- Derivation of UAB and IAB in step-up mode.
References
- Xu, W.; Chan, N.H.L.; Or, S.W.; Ho, S.L.; Chan, K.W. A New Control Method for a Bi-Directional Phase-Shift-Controlled DC-DC Converter with an Extended Load Range. Energies 2017, 10, 1532. [Google Scholar] [CrossRef] [Green Version]
- Yong, H.; Li, X.; Wu, X.; Li, M.; Wang, Y. Stability Control Design for TAB-Based Three-Port Bidirectional DC/DC Converters in PV-Battery Grid-Connected Applications. In Proceedings of the 46th Annual Conference of the IEEE Industrial Electronics Society (IECON 2020), Singapore, 18–21 October 2020; pp. 3469–3474. [Google Scholar]
- Sha’aban, Y.A.; Ikpehai, A.; Adebisi, B.; Rabie, K.M. Bi-Directional Coordination of Plug-In Electric Vehicles with Economic Model Predictive Control. Energies 2017, 10, 1507. [Google Scholar] [CrossRef] [Green Version]
- Fiaz, M.F.; Calligaro, S.; Iurich, M.; Petrella, R. Analytical Modeling and Control of Dual Active Bridge Converter Considering All Phase-Shifts. Energies 2022, 15, 2720. [Google Scholar] [CrossRef]
- Onar, O.C. A Bidirectional High-Power-Quality Grid Interface With a Novel Bidirectional Noninverted Buck–Boost Converter for PHEVs. IEEE Trans. Veh. Technol. 2012, 61, 2018–2032. [Google Scholar] [CrossRef]
- Chen, B.-Z.; Liao, H.; Chen, L.; Chen, J.-F. Design and Implementation of the Bidirectional DC-DC Converter with Rapid Energy Conversion. Energies 2022, 15, 898. [Google Scholar] [CrossRef]
- Gierczynski, M.; Grzesiak, L.M.; Kaszewski, A. Cascaded Voltage and Current Control for a Dual Active Bridge Converter with Current Filters. Energies 2021, 14, 6214. [Google Scholar] [CrossRef]
- He, P.; Khaligh, A. Comprehensive Analyses and Comparison of 1 kW Isolated DC–DC Converters for Bidirectional EV Charging Systems. IEEE Trans. Transp. Electrif. 2017, 3, 147–156. [Google Scholar] [CrossRef]
- Wang, C.S.; Zhang, S.H.; Wang, Y.F.; Chen, B.; Liu, J.H. A 5-kW Isolated High Voltage Conversion Ratio Bidirectional CLTC Resonant DC–DC Converter With Wide Gain Range and High Efficiency. IEEE Trans. Power Electron. 2019, 34, 340–355. [Google Scholar] [CrossRef]
- Can, E.; Sayan, H.H. Development of fractional sinus pulse width modulation with β gap on three step signal processing. Int. J. Electron. 2022, 1–20. [Google Scholar] [CrossRef]
- Zhao, B.; Song, Q.; Liu, W.; Sun, Y. Overview of Dual-Active-Bridge Isolated Bidirectional DC–DC Converter for High-Frequency-Link Power-Conversion System. IEEE Trans. Power Electron. 2014, 29, 4091–4106. [Google Scholar] [CrossRef]
- Chen, G.; Lee, Y.S.; Hui, S.Y.R.; Xu, D.; Wang, Y. Actively clamped bidirectional flyback converter. IEEE Trans. Ind. Electron. 2000, 47, 770–779. [Google Scholar] [CrossRef]
- Li, H.; Peng, F.Z.; Lawler, J.S. A natural ZVS medium-power bidirectional DC-DC converter with minimum number of devices. IEEE Trans. Ind. Appl. 2015, 39, 525–535. [Google Scholar] [CrossRef] [Green Version]
- Cui, S.; He, D.; Chen, Z.; Habetler, T.G. A Wide Input Voltage Range ZVS Isolated Bidirectional DC-DC Converter for Ultra-capacitor Application in Hybrid and Electric Vehicles. In Proceedings of the 2012 IEEE International Electric Vehicle Conference, Greenville, SC, USA, 4–8 March 2012; pp. 1–6. [Google Scholar]
- Roggia, L.; Costa, P.F.S. Comparative analysis between integrated full-bridge-forward and dual active bridge DC–DC converters. Electron. Lett. 2018, 54, 231–233. [Google Scholar] [CrossRef]
- Núñez, R.O.; Oggier, G.G.; Botterón, F.; Garcia, G.O. Analysis of the Transformer Influence on a Three-Phase Dual Active Bridge DC-DC Converter. IEEE Lat. Am. Trans. 2016, 14, 3048–3055. [Google Scholar] [CrossRef]
- Jin, K.; Liu, C. A Novel PWM High Voltage Conversion Ratio Bidirectional Three-Phase DC/DC Converter With Y–Δ Connected Transformer. IEEE Trans. Power Electron. 2015, 31, 81–88. [Google Scholar] [CrossRef]
- Lee, S.; Park, J.; Choi, S. A Three-Phase Current-Fed Push–Pull DC–DC Converter With Active Clamp for Fuel Cell Applications. IEEE Trans. Power Electron. 2011, 26, 2266–2277. [Google Scholar] [CrossRef]
- Min, J.; Ordonez, M. Bidirectional Resonant CLLC Charger for Wide Battery Voltage Range: Asymmetric Parameters Methodology. IEEE Trans. Power Electron. 2021, 36, 6662–6673. [Google Scholar] [CrossRef]
- Jung, J.H.; Kim, H.S.; Ryu, M.H.; Baek, J.W. Design Methodology of Bidirectional CLLC Resonant Converter for High-Frequency Isolation of DC Distribution Systems. IEEE Trans. Power Electron. 2012, 28, 1741–1755. [Google Scholar] [CrossRef]
- Lin, F.; Zhang, X.; Li, X.; Chaohui, L.; Ma, H. Parameter Design for Symmetrical CLLC-Type DC Transformer Considering Cascaded System Stability and Power Efficiency. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 9, 6219–6231. [Google Scholar] [CrossRef]
- Li, X.; Huang, J.; Ma, Y.; Wang, X.; Yang, J.; Wu, X. Unified Modeling, Analysis, and Design of Isolated Bidirectional CLLC Resonant DC-DC Converters. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 213–223. [Google Scholar] [CrossRef]
- Ibanez, F.; Echeverria, J.M.; Fontan, L. Novel technique for bidirectional series-resonant DC/DC converter in discontinuous mode. IET Power Electron. 2013, 6, 1019–1028. [Google Scholar] [CrossRef]
- Jiang, T.; Zhang, J.; Wu, X.; Sheng, K.; Wang, Y. A Bidirectional LLC Resonant Converter with Automatic Forward and Backward Mode Transition. IEEE Trans. Power Electron. 2014, 30, 757–770. [Google Scholar] [CrossRef]
- Musavi, F.; Craciun, M.; Gautam, D.S.; Eberle, W. Control Strategies for Wide Output Voltage Range LLC Resonant DC–DC Converters in Battery Chargers. IEEE Trans. Veh. Technol. 2014, 63, 1117–1125. [Google Scholar] [CrossRef]
- Çalışkan, E.; Ustun, O. Smart Efficiency Tracking for Novel Switch—LLC Converter for Battery Charging Applications. Energies 2022, 15, 1861. [Google Scholar] [CrossRef]
- Chang, C.; Cheng, C.; Cheng, H. Modeling and Design of the LLC Resonant Converter Used as a Solar-Array Simulator. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 833–841. [Google Scholar] [CrossRef]
- Zhang, S.-H.; Wang, Y.-F.; Chen, B.; Han, F.-Q.; Wang, Q.-C. Studies on a Hybrid Full-Bridge/Half-Bridge Bidirectional CLTC Multi-Resonant DC-DC Converter with a Digital Synchronous Rectification Strategy. Energies 2018, 11, 227. [Google Scholar] [CrossRef] [Green Version]
- Chen, B.; Wang, P.; Wang, Y.F.; Zhang, S.H.; Yang, L.; Ji, R.L. A Bidirectional CDT-LC Resonant DC-DC Converter with a Wide Voltage Range. IEEE Trans. Ind. Electron. 2020, 67, 2009–2020. [Google Scholar] [CrossRef]
- Ma, X.; Wang, P.; Bi, H.; Wang, Z. A Bidirectional LLCL Resonant DC-DC Converter With Reduced Resonant Tank Currents and Reduced Voltage Stress of the Resonant Capacitor. IEEE Access 2020, 8, 125549–125564. [Google Scholar] [CrossRef]
- Liu, T.; Zhou, Z.; Xiong, A.; Zeng, J.; Ying, J. A Novel Precise Design Method for LLC Series Resonant Converter. In Proceedings of the INTELEC 06—Twenty-Eighth International Telecommunications Energy Conference, Providence, RI, USA, 10–14 September 2006; pp. 1–6. [Google Scholar]
- Can, E. The design and experimentation of the new cascaded DC-DC boost converter for renewable energy. Int. J. Electron. 2019, 106, 1374–1393. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Wang, H.; Liu, Y.F.; Sen, P.C. An Accurate Design Algorithm for LLC Resonant Converters—Part I. IEEE Trans. Power Electron. 2016, 31, 5435–5447. [Google Scholar] [CrossRef]
- Hu, Z.; Wang, L.; Qiu, Y.; Liu, Y.F.; Sen, P.C. An Accurate Design Algorithm for LLC Resonant Converters—Part II. IEEE Trans. Power Electron. 2016, 31, 5448–5460. [Google Scholar] [CrossRef]
- Steigerwald, R.L. A Comparison of Half-bridge Resonant Converter Topologies. IEEE Trans. Power Electron. 2002, 3, 174–182. [Google Scholar] [CrossRef]
- Ivensky, G.; Bronshtein, S.; Abramovitz, A. Approximate Analysis of Resonant LLC DC-DC Converter. IEEE Trans. Power Electron. 2011, 26, 3274–3284. [Google Scholar] [CrossRef]
- Liu, J.; Zhang, J.; Zheng, T.Q.; Yang, J. A Modified Gain Model and the Corresponding Design Method for an LLC Resonant Converter. IEEE Trans. Power Electron. 2017, 32, 6716–6727. [Google Scholar] [CrossRef]
- Abdel-Rahim, O.; Alamir, N.; Abdelrahem, M.; Orabi, M.; Kennel, R.; Ismeil, M.A. A Phase-Shift-Modulated LLC-Resonant Micro-Inverter Based on Fixed Frequency Predictive-MPPT. Energies 2020, 13, 1460. [Google Scholar] [CrossRef] [Green Version]





| Component | Model/Value |
|---|---|
| M1,M2,M3,M4 | SRC60R022FB |
| M5,M6,M7,M8 | 2 paralleled FDP2D3N10C |
| Cr1 | 108 nF |
| Cr2 | 36 nF |
| Lm1 | 160 μH |
| n1 | 10 |
| Lm2 | 80 μH |
| n2 | 18 |
| Lr | 40 μH |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, S.; Wu, X.; Zhang, Z.; Zhang, X. A Bidirectional DHC-LT Resonant DC-DC Converter with Research on Improved Fundamental Harmonic Analysis Considering Phase Angle of Load Impedance. Energies 2022, 15, 5281. https://doi.org/10.3390/en15145281
Zhang S, Wu X, Zhang Z, Zhang X. A Bidirectional DHC-LT Resonant DC-DC Converter with Research on Improved Fundamental Harmonic Analysis Considering Phase Angle of Load Impedance. Energies. 2022; 15(14):5281. https://doi.org/10.3390/en15145281
Chicago/Turabian StyleZhang, Shuhuai, Xuezhi Wu, Ziqian Zhang, and Xuejiang Zhang. 2022. "A Bidirectional DHC-LT Resonant DC-DC Converter with Research on Improved Fundamental Harmonic Analysis Considering Phase Angle of Load Impedance" Energies 15, no. 14: 5281. https://doi.org/10.3390/en15145281
APA StyleZhang, S., Wu, X., Zhang, Z., & Zhang, X. (2022). A Bidirectional DHC-LT Resonant DC-DC Converter with Research on Improved Fundamental Harmonic Analysis Considering Phase Angle of Load Impedance. Energies, 15(14), 5281. https://doi.org/10.3390/en15145281







