Coupled FEM and CFD Modeling of Structure Deformation and Performance of PEMFC Considering the Effects of Membrane Water Content
Abstract
:1. Introduction
2. Methods
2.1. FEM Model
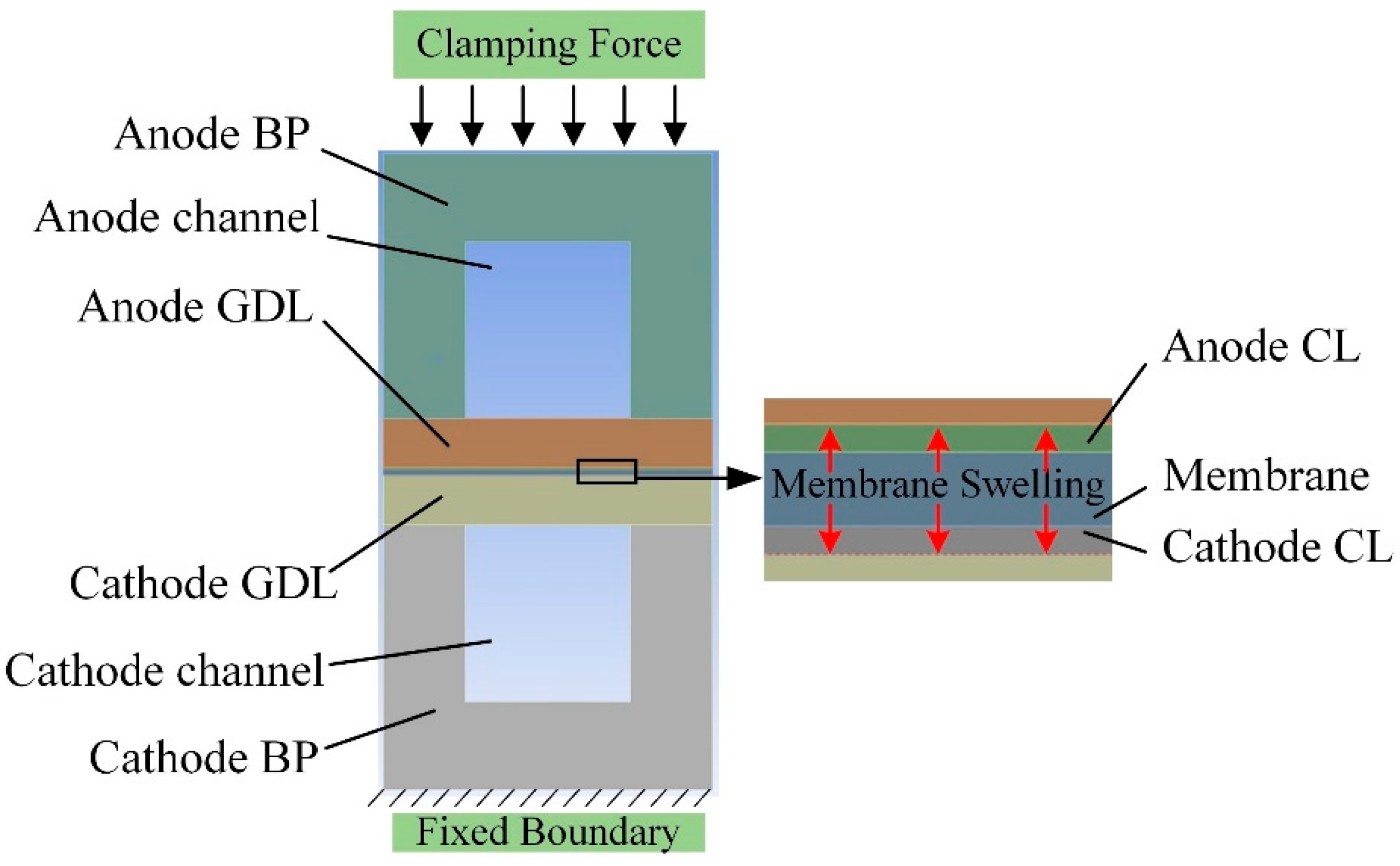
2.1.1. Computational Domain and Assumptions
2.1.2. Mathematical Model
2.1.3. Measurement of Membrane Swelling Expansion Coefficient
2.1.4. Measurement of Young’s Modulus
2.1.5. Boundary Condition
2.1.6. Numerical Procedures
2.2. CFD Model
2.2.1. Computational Domain and Assumptions
2.2.2. Mathematical Model
2.2.3. Boundary Condition
2.2.4. Numerical Procedures
3. Results and Discussion
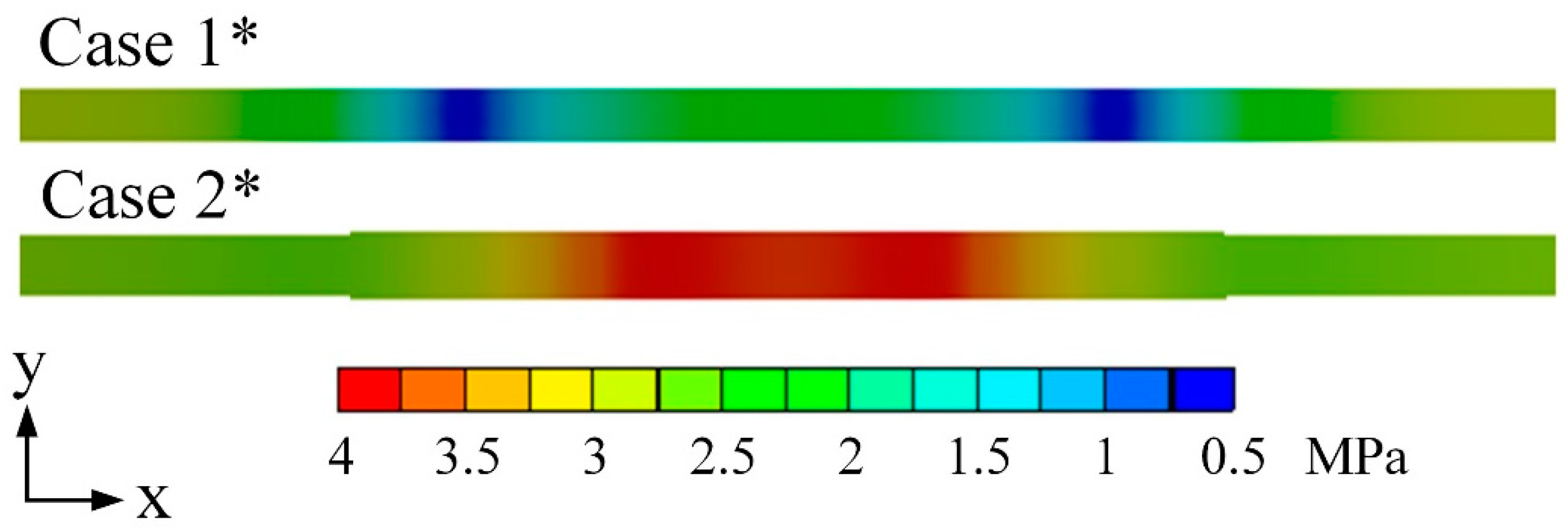
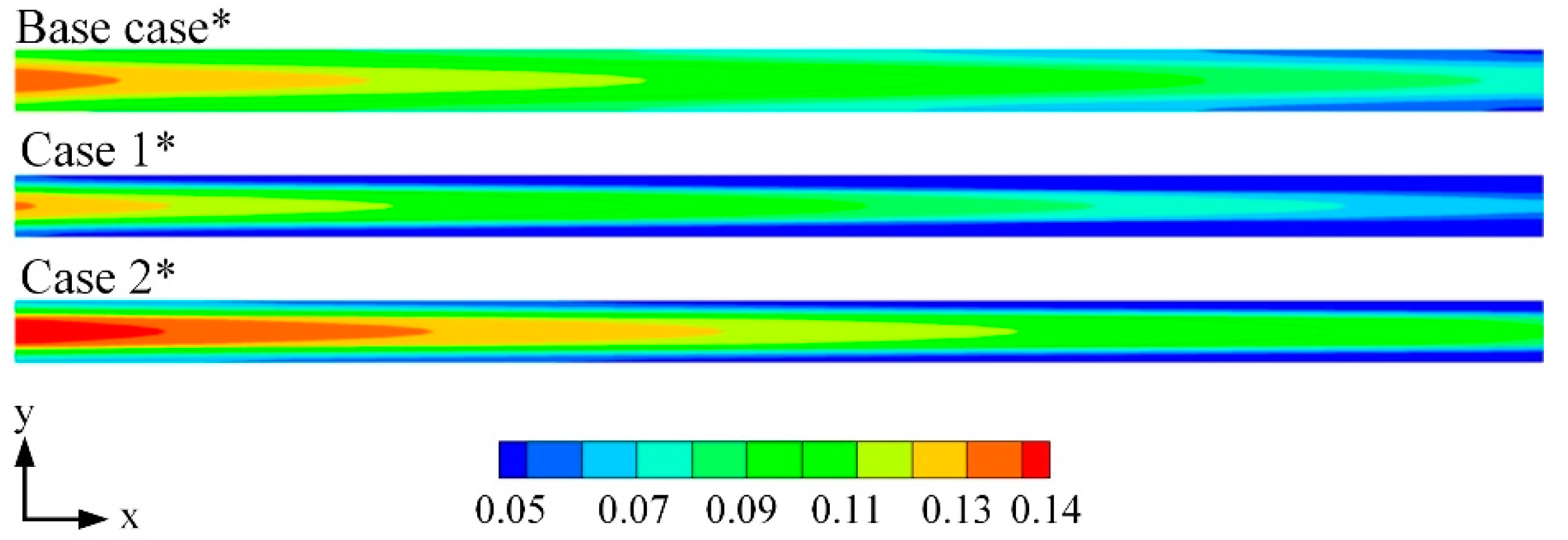
3.1. Model Comparisons
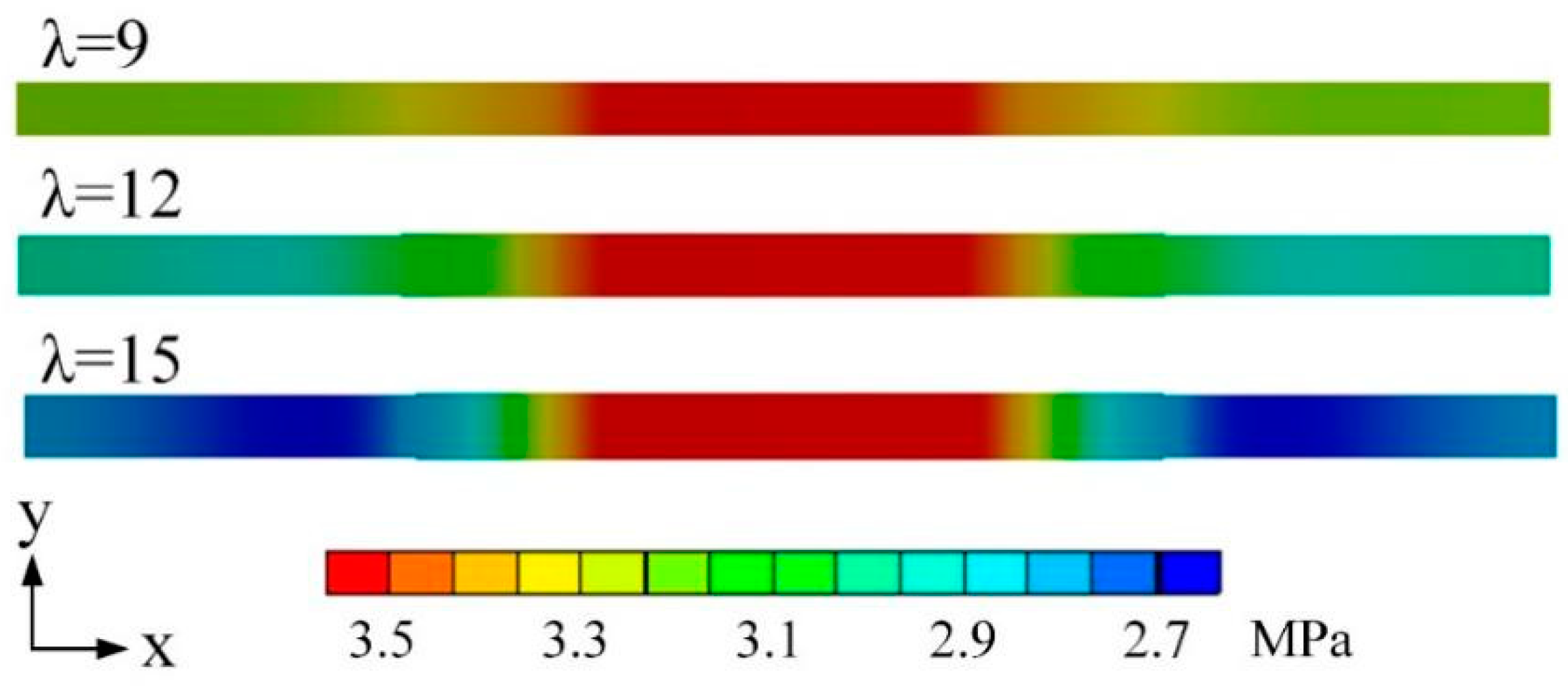
3.2. Effects of Water Content
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FEM | Finite Element Method |
| CFD | Computational Fluid Dynamics |
| PEMFC | Proton Exchange Membrane Fuel Cell |
| CL | Catalyst Layer |
| GDL | Gas Diffusion Layer |
| MEA | Membrane Electrode Assembly |
| RH | Relative Humidity |
| BP | Bipolar Plate |
| CCM | Catalyst Coated Membrane |
| UDFs | User Defined Functions |
| EDC | Effective Diffusion Coefficient |
References
- Pollet, B.G.; Staffell, I.; Shang, J.L. Current status of hybrid, battery and fuel cell electric vehicles: From electrochemistry to market prospects. J. Electrochim. Acta 2012, 84, 235–249. [Google Scholar] [CrossRef]
- Pratt, J.W.; Klebanoff, L.E.; Munoz-Ramos, K.; Akhil, A.A.; Curgus, D.B.; Schenkman, B.L. Proton exchange membrane fuel cells for electrical power generation on-board commercial airplanes. Appl. Energy 2013, 101, 776–796. [Google Scholar] [CrossRef] [Green Version]
- Ouyang, M.; Xu, L.; Li, J.; Lu, L.; Gao, D.; Xie, Q. Performance comparison of two fuel cell hybrid buses with different powertrain and energy management strategies. J. Power Sources 2006, 163, 467–479. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Fan, Y.; He, W.; Guan, J.; Wang, X. Numerical Investigation of Tapered Flow Field Configurations for Enhanced Polymer Electrolyte Membrane Fuel Cell Performance. Appl. Energy 2022, 306, 118021. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, H.; Wang, X.; Qin, Y.; Xing, L. Multi-sub-inlets at cathode flow-field plate for current density homogenization and enhancement of PEM fuel cells in low relative humidity. Energy Convers. Manag. 2022, 252, 115069. [Google Scholar] [CrossRef]
- Tian, Y.D.; Zhu, X.J.; Cao, Y.Y. A study of modeling and control of proton exchange membrane fuel cell stack systems. Chin. J. Power Sources 2004, 28, 656–660. [Google Scholar]
- Su, A.; Ferng, Y.M.; Shih, J.C. CFD investigating the effects of different operating conditions on the performance the characteristics of a high-temperature, P.E.M.F.C. Energy 2010, 35, 16–27. [Google Scholar] [CrossRef]
- Choi, J.E.; Bae, Y.C. Swelling effect of a polymer electrolyte membrane on the development of a semi-empirical cell voltage model. J. Appl. Electrochem. 2009, 39, 1419–1424. [Google Scholar] [CrossRef]
- Toghyani, S.; Nafchi, F.M.; Afshari, E.; Hasanpour, K.; Baniasadi, E.; Atyabi, S.A. Thermal and electrochemical performance analysis of a proton exchange membrane fuel cell under assembly pressure on gas diffusion layer. Int. J. Hydrogen Energy 2018, 43, 4534–4545. [Google Scholar] [CrossRef]
- Zhang, Z.; He, P.; Dai, Y.J.; Jin, P.H.; Tao, W.Q. Study of the mechanical behavior of paper-type GDL in PEMFC based on microstructure morphology. Int. J. Hydrogen Energy 2020, 45, 29379–29394. [Google Scholar] [CrossRef]
- Li, W.Z.; Yang, W.W.; Zhang, W.Y.; Qu, Z.G.; He, Y.L. Three-dimensional modeling of a PEMFC with serpentine flow field incorporating the impacts of electrode inhomogeneous compression deformation. Int. J. Hydrogen Energy 2019, 44, 22194–22209. [Google Scholar] [CrossRef]
- Zhang, H.; Shen, P.K. A brief consideration about the structural evolution of perfluorosulfonic-acid ionomer membranes. Int. J. Hydrogen Energy 2012, 37, 4657–4664. [Google Scholar] [CrossRef]
- Woo, S.H.; Taguet, A.; Otazaghine, B.; Mosdale, A.; Rigacci, A.; Beauger, C. Physicochemical properties of Aquivion/fluorine grafted sepiolite electrolyte membranes for use in PEMFC. Electrochim. Acta 2019, 319, 933–946. [Google Scholar] [CrossRef]
- Zhong, D.; Lin, R.; Jiang, Z.; Zhu, Y.; Liu, D.; Cai, X.; Chen, L. Low temperature durability and consistency analysis of proton exchange membrane fuel cell stack based on comprehensive characterizations. Appl. Energy 2020, 264, 114626. [Google Scholar] [CrossRef]
- Yoon, W.; Huang, X. A multiphysics model of PEM fuel cell incorporating the cell compression effects. J. Electrochem. Soc. 2010, 157, B680–B690. [Google Scholar] [CrossRef]
- Li, Y.; Dillard, D.A.; Lai, Y.H.; Case, S.W.; Ellis, M.W.; Budinski, M.K.; Gittleman, C.S. Experimental measurement of stress and strain in Nafion membrane during hydration cycles. J. Electrochem. Soc. 2011, 159, B173–B184. [Google Scholar] [CrossRef]
- Khattra, N.S.; Karlsson, A.M.; Santare, M.H.; Walsh, P.; Busby, F.C. Effect of time-dependent material properties on the mechanical behavior of PFSA membranes subjected to humidity cycling. J. Power Sources 2012, 214, 365–376. [Google Scholar] [CrossRef] [Green Version]
- Khattra, N.S.; Santare, M.H.; Karlsson, A.M.; Schmiedel, T.; Busby, F.C. Effect of water transport on swelling and stresses in PFSA membranes. Fuel Cells 2015, 15, 178–188. [Google Scholar] [CrossRef]
- Kusoglu, A.; Karlsson, A.M.; Santare, M.H.; Cleghorn, S.; Johnson, W.B. Mechanical response of fuel cell membranes subjected to a hygro-thermal cycle. J. Power Sources 2006, 161, 987–996. [Google Scholar] [CrossRef] [Green Version]
- Taymaz, I.; Benli, M. Numerical study of assembly pressure effect on the performance of proton exchange membrane fuel cell. Energy 2010, 35, 2134–2140. [Google Scholar] [CrossRef]
- Jiao, K.; Li, X. A three-dimensional non-isothermal model of high temperature proton exchange membrane fuel cells with phosphoric acid doped polybenzimidazole membranes. Fuel Cells 2010, 10, 351–362. [Google Scholar] [CrossRef]
- Lu, Z.; Lugo, M.; Santare, M.H.; Karlsson, A.M.; Busby, F.C.; Walsh, P. An experimental investigation of strain rate, temperature and humidity effects on the mechanical behavior of a perfluorosulfonic acid membrane. J. Power Sources 2012, 214, 130–136. [Google Scholar] [CrossRef] [Green Version]
- Zhang, G.B.; Fan, L.H.; Sun, J.; Jiao, K. A 3D model of PEMFC considering detailed multiphase flow and anisotropi transport properties. Int. J. Heat Mass Transf. 2017, 115, 714e24. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, J.; Yang, X.; Du, Q.; Fang, J.H.; Jiao, K. Modeling of high temperature proton exchange membrane fuel cells with novel sulfonated polybenzimidazole membranes. Int. J. Hydrogen Energy 2014, 39, 13671e80. [Google Scholar] [CrossRef]
- Wang, X.; Qin, Y.; Wu, S.; Shangguan, X.; Zhang, J.; Yin, Y. Numerical and experimental investigation of baffle plate arrangement on proton exchange membrane fuel cell performance. J. Power Sources 2020, 457, 228034. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, X.; Shangguan, X.; Zhang, J.; Qin, Y. Numerical investigation on the characteristics of mass transport and performance of PEMFC with baffle plates installed in the flow channel. Int. J. Hydrogen Energy 2018, 43, 8048–8062. [Google Scholar] [CrossRef]
- Yin, Y.; Wang, X.; Zhang, J.; Shangguan, X.; Qin, Y. Influence of sloping baffle plates on the mass transport and performance of PEMFC. Int. J. Energy Res. 2019, 43, 2643–2655. [Google Scholar] [CrossRef]






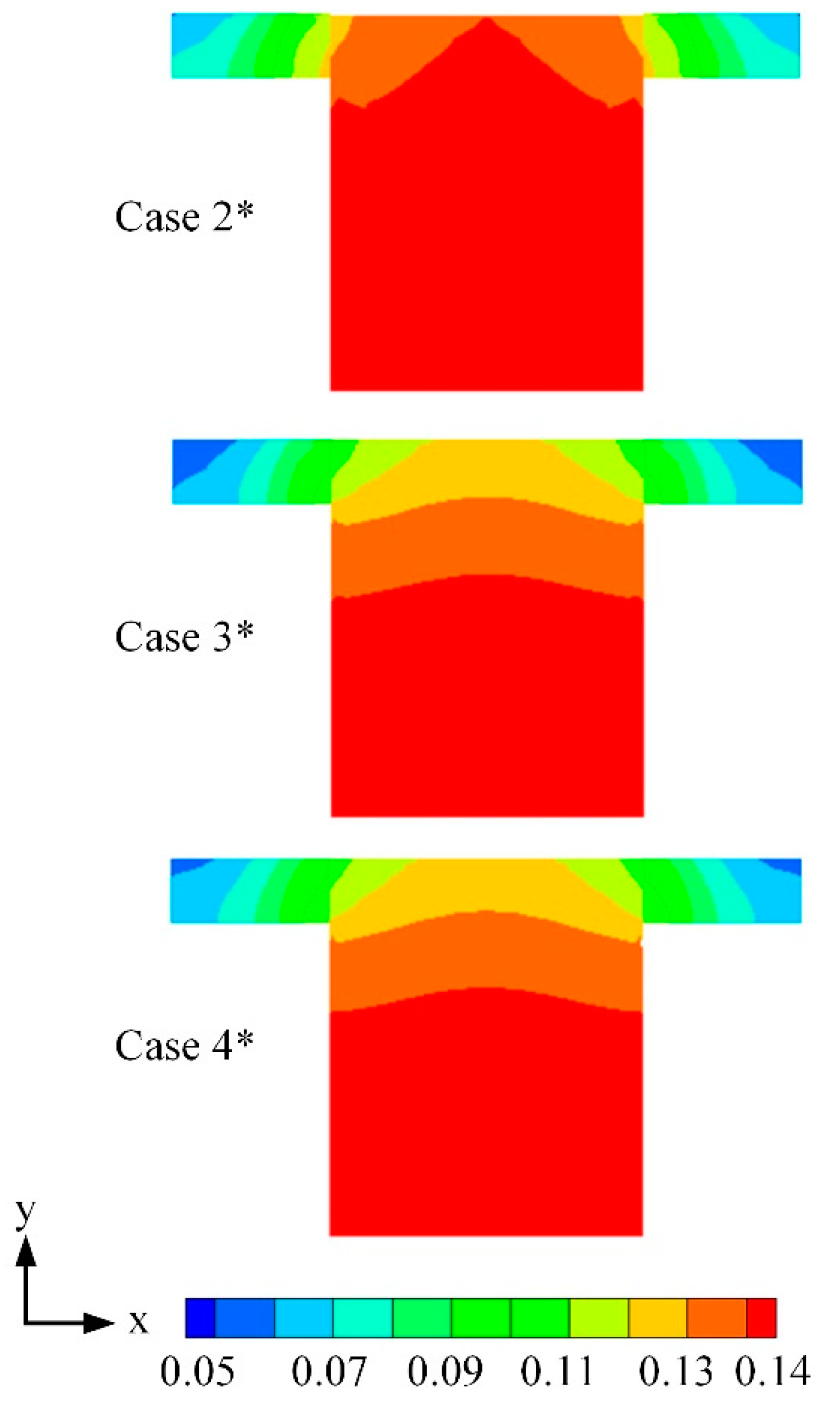
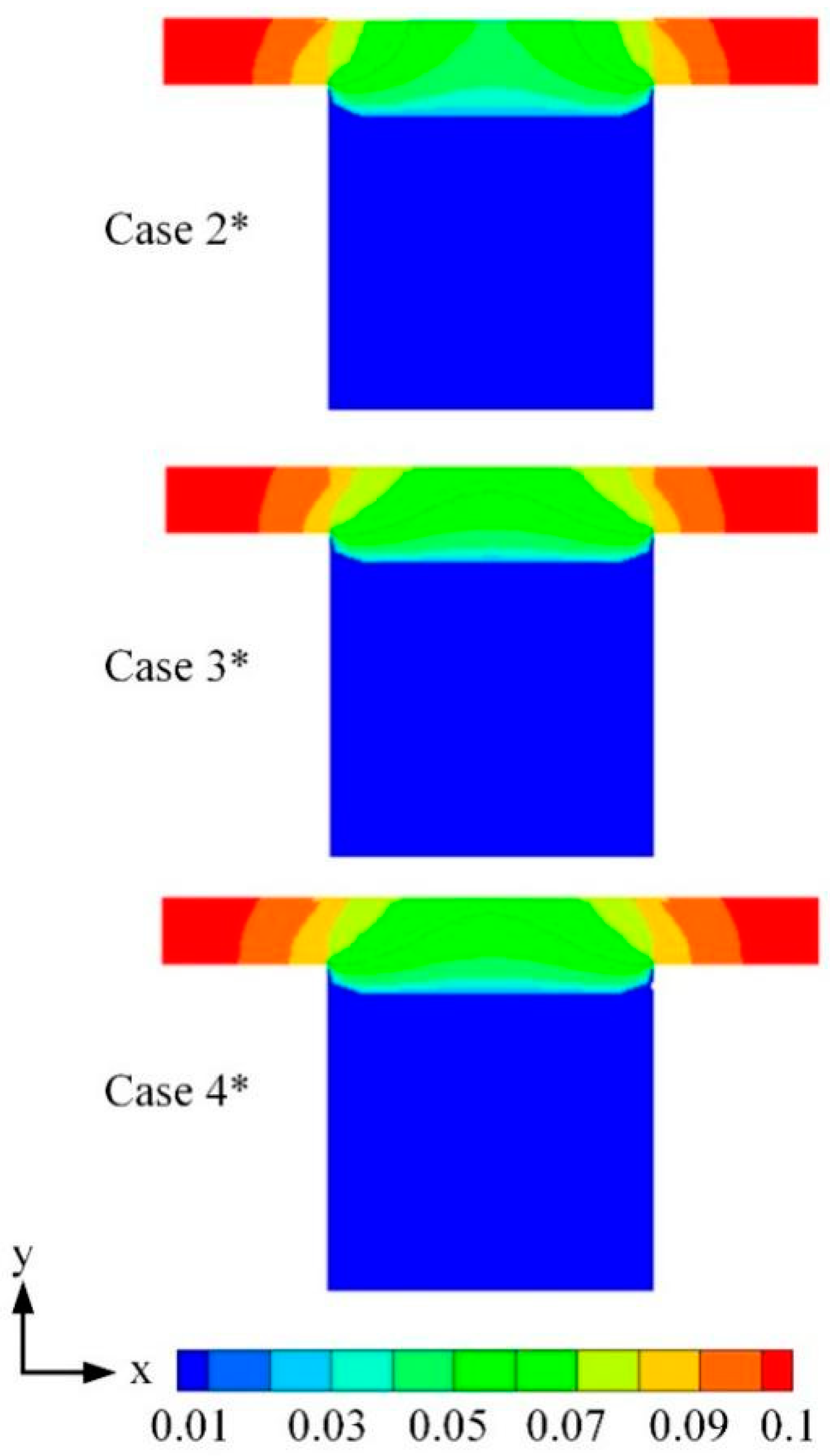
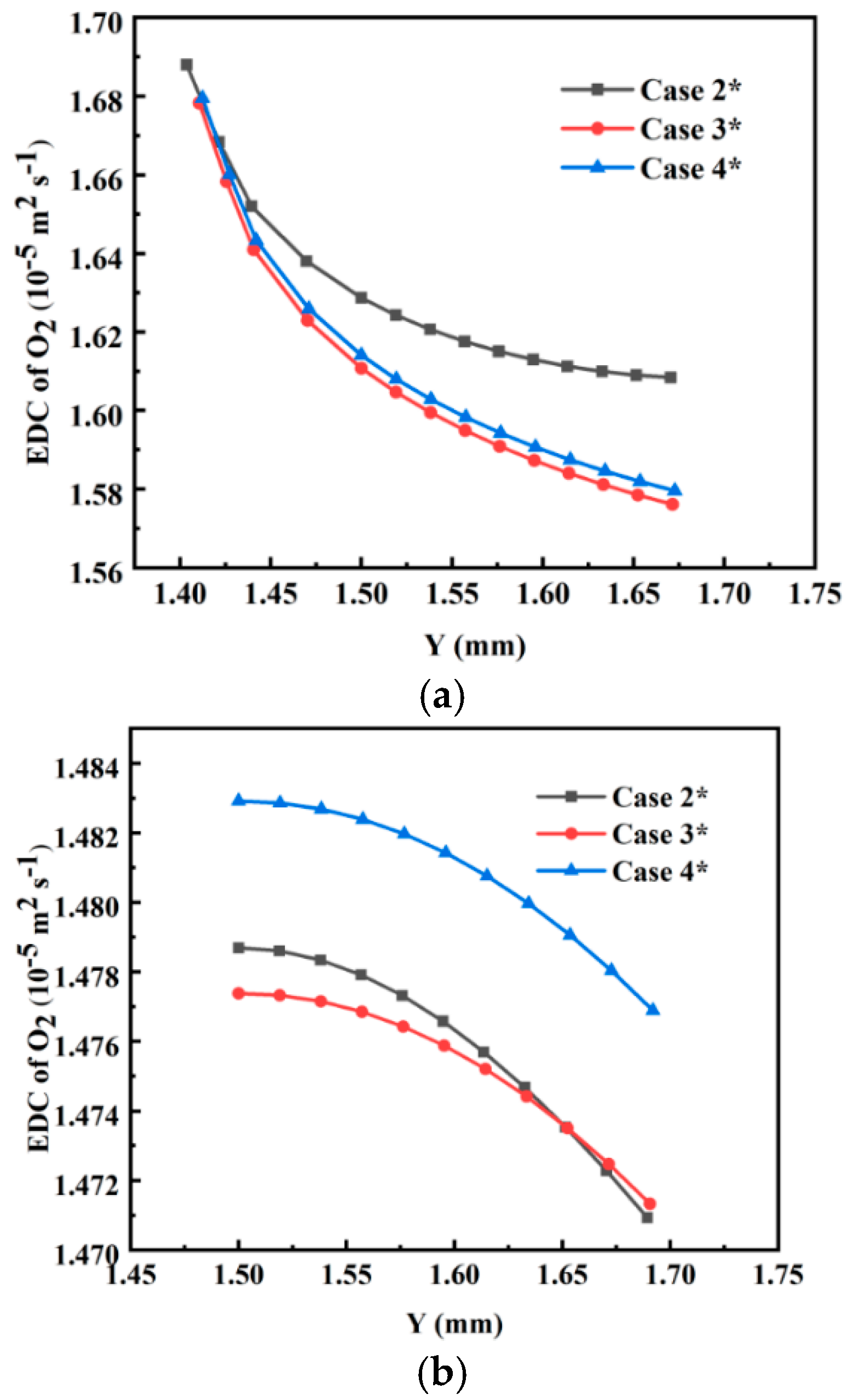
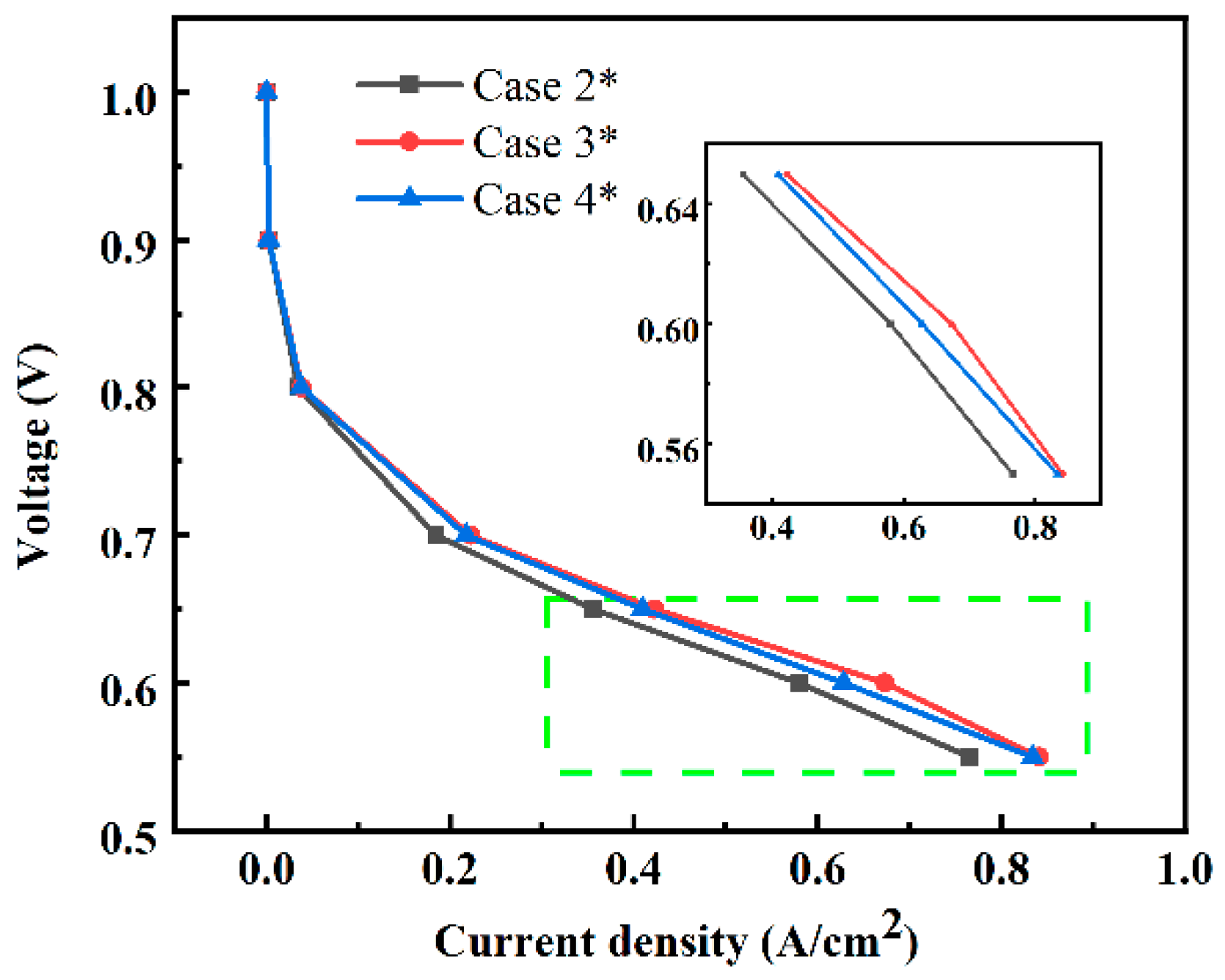
| Time (min) | 0 | 5 | 10 | 20 | 30 | |
|---|---|---|---|---|---|---|
| Parameters | ||||||
| Water content λ | 0 | 0.04274 | 0.05085 | 0.05173 | 0.05128 | |
| Linear strain | 0 | 0.05128 | 0.06050 | 0.06774 | 0.06838 | |
| Parameters | Values | Units |
|---|---|---|
| Anode inlet temperature | 353.15 | K |
| Cathode inlet temperature | 353.15 | K |
| Anode inlet pressure | 101,325 | Pa |
| Cathode inlet pressure | 101,325 | Pa |
| Working voltage | 0.6 | V |
| Anode inlet relative humidity | 100% | — |
| Cathode inlet relative humidity | 100% | — |
| Anode stoichiometric ratio | 1.5 | — |
| Cathode stoichiometric ratio | 3.0 | — |
| Faraday’s constant | 96,487 | C mol−1 |
| Universal gas constant | 8.314 | J mol−1 K−1 |
| Porosity of GDL | 0.6 | — |
| Porosity of CL | 0.3 | — |
| Equivalent weight of dry membrane | 1100 | kg kmol−1 |
| Cases | Base Case* | Case 1* | Case 2* | Case 3* | Case 4* |
|---|---|---|---|---|---|
| Assembly pressure (MPa) | 0 | 1 | 1 | 1 | 1 |
| Water content λ | — | — | 15 | 12 | 9 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dong, Z.; Liu, Y.; Qin, Y. Coupled FEM and CFD Modeling of Structure Deformation and Performance of PEMFC Considering the Effects of Membrane Water Content. Energies 2022, 15, 5319. https://doi.org/10.3390/en15155319
Dong Z, Liu Y, Qin Y. Coupled FEM and CFD Modeling of Structure Deformation and Performance of PEMFC Considering the Effects of Membrane Water Content. Energies. 2022; 15(15):5319. https://doi.org/10.3390/en15155319
Chicago/Turabian StyleDong, Zizhe, Yuwen Liu, and Yanzhou Qin. 2022. "Coupled FEM and CFD Modeling of Structure Deformation and Performance of PEMFC Considering the Effects of Membrane Water Content" Energies 15, no. 15: 5319. https://doi.org/10.3390/en15155319






