Study on Fractal Characteristics of Evolution of Mining-Induced Fissures in Karst Landform
Abstract
:1. Introduction
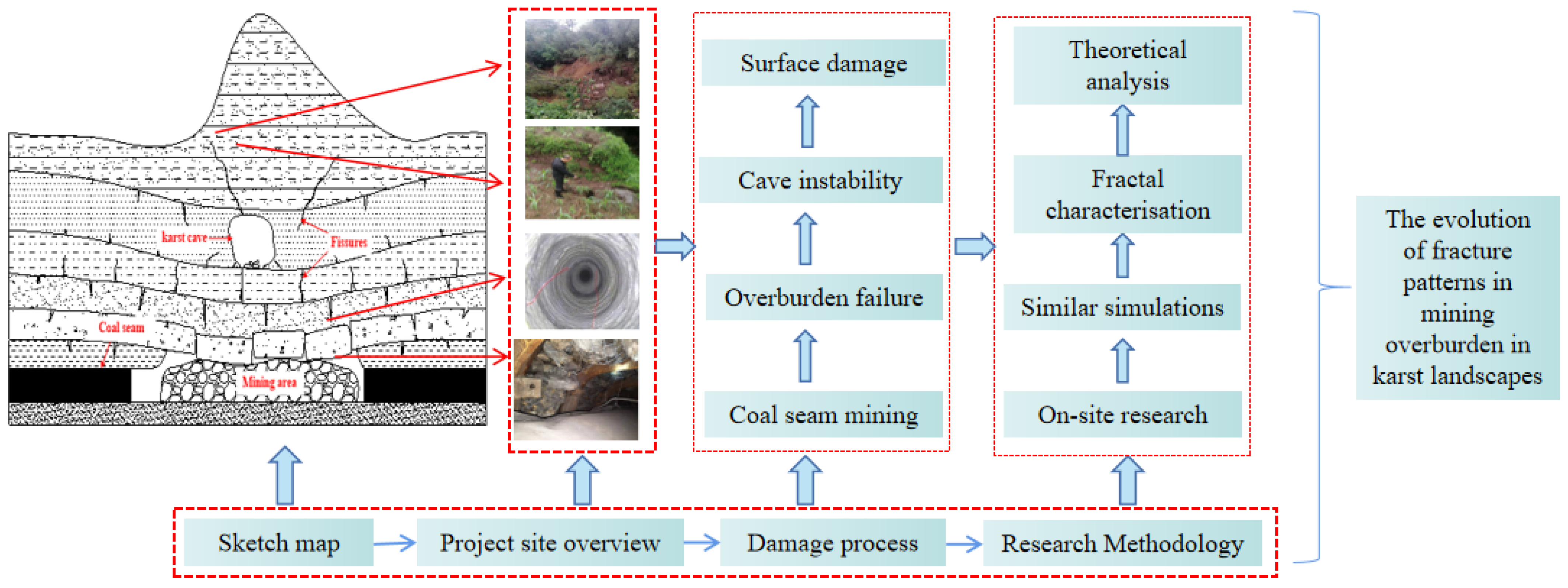
2. Similar Simulation Study on Fracture Evolution Law of Mining Disturbed Rock
2.1. Project Overview and Experimental Design
2.1.1. Similar Materials and Ratio
2.1.2. Simulation Test Platform
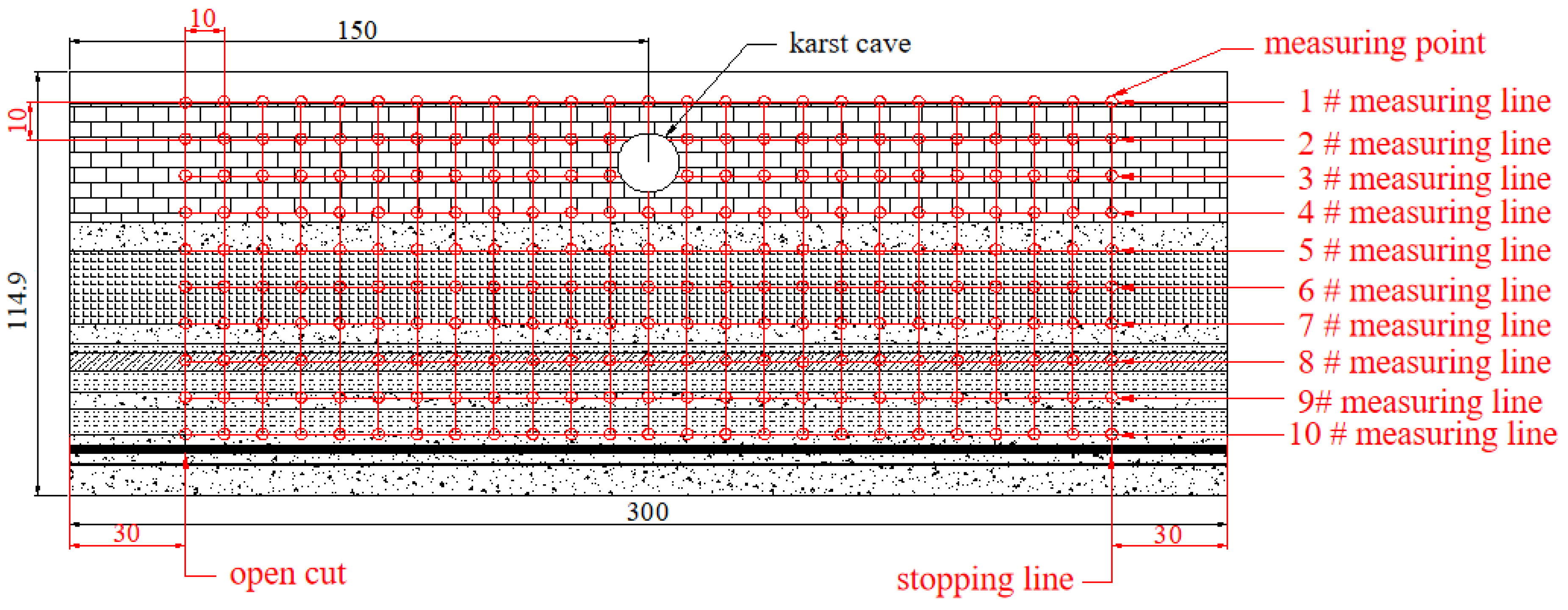
2.1.3. Model Measuring Point Layout
2.2. Evolution Law of Weathered Rock Fissures under Mining Disturbance
2.2.1. Analysis of Dynamic Evolution Process of Fracture Propagation in Rock
- (1)
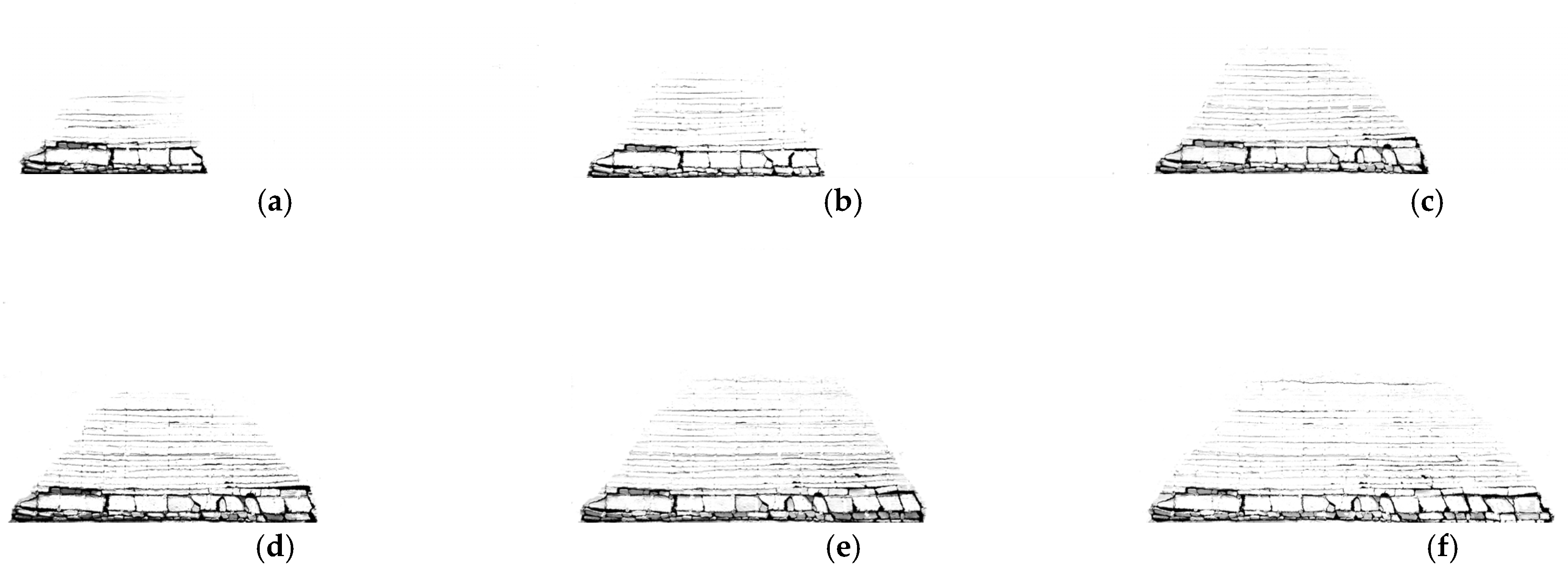
- When the working face advances 24 m, the immediate roof collapses completely, and the caving block is broken, while the upper roof maintains high stability and does not produce obvious cracks; when the working face advances 43 m, the upper roof reaches the ultimate span, and its stability is completely destroyed, resulting in the initial weighting. At this time, a small number of transverse separation cracks are bred above the upper roof. Later, with the periodic instability weighting of the upper roof, the mining-induced cracks continue to expand upward.
- (2)
- When the working face is mined to 138 m, there is a separation fracture below the main key layer. With the increase of the mining width, the fracture channel is expanding, and the separation fracture is more obvious; when the working face advances 156 m, two obvious cracks appear on the left side of the cave, and the mining-induced rock fractures reach the maximum development height of 61 m. However, the cracks do not penetrate the rock strata where the cave is located, indicating that the Changxing limestone-containing rock caves is the main key stratum, and the rock strata are relatively hard, which can effectively prevent the upward development and expansion of the fractures, and the bearing stability is high. At the same time, the mining-induced fractures in the left and lower sides of the cave begin to gradually close.
- (3)
- After the end of working face mining, the development of mining-induced rock fractures stops, the obvious separation zone is formed in the bending zone, and the compaction closed zone is formed below the cave. The vertical fracture fractures above the open cut hole and the coal wall side are more developed. The overall distribution of rock fractures is similar to the ‘platform ladder’ shape.
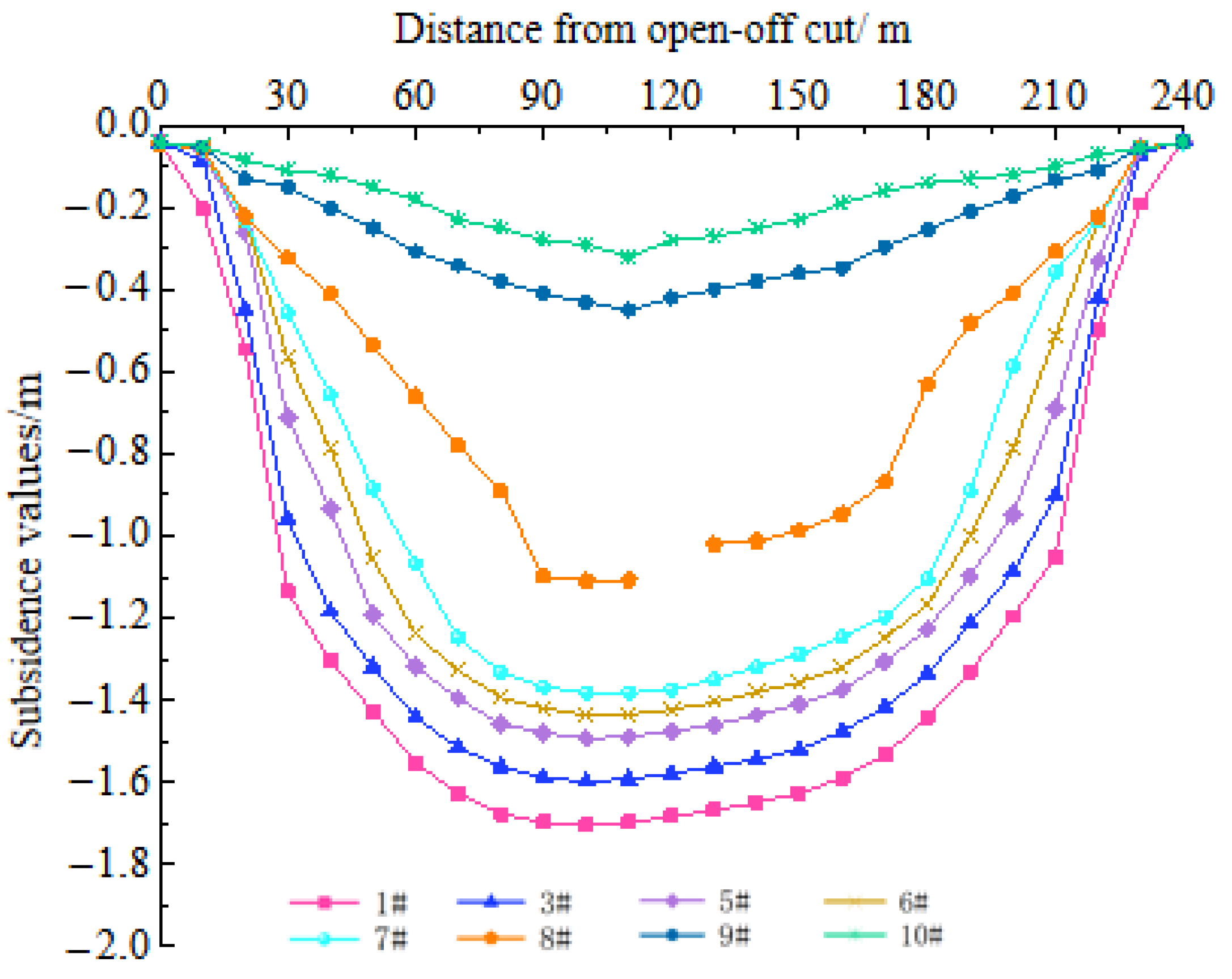
2.2.2. Law of Strata Movement
2.2.3. Variation of Development Height of Separated Fractures
3. Study on Fractal Characteristics of Rock Fracture Evolution under Karst Landform
3.1. Definition of Fractal Dimension
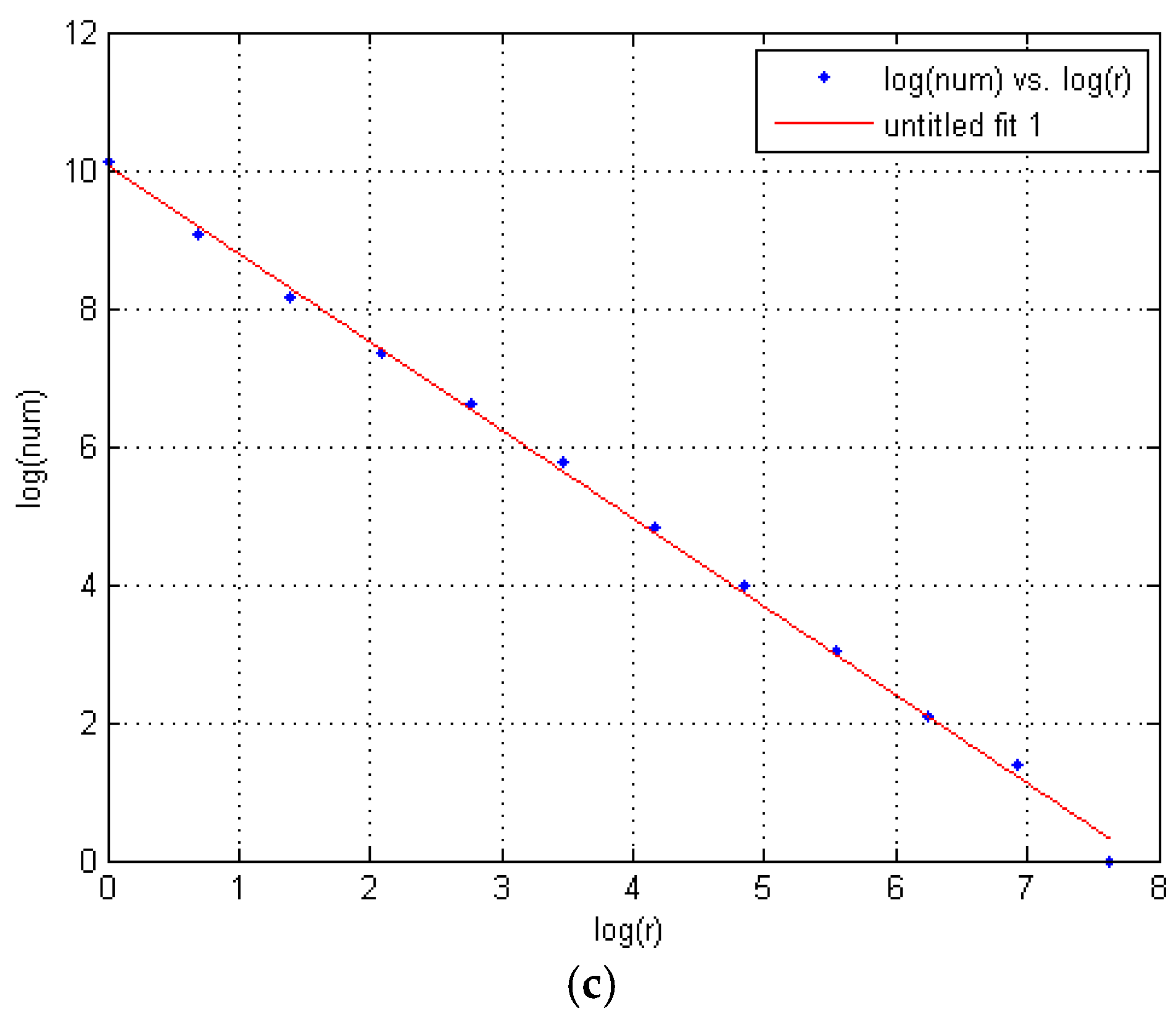
3.2. Calculation Method of Fractal Dimension
3.3. Fractal Characteristics of Mining-Induced Fissure Evolution
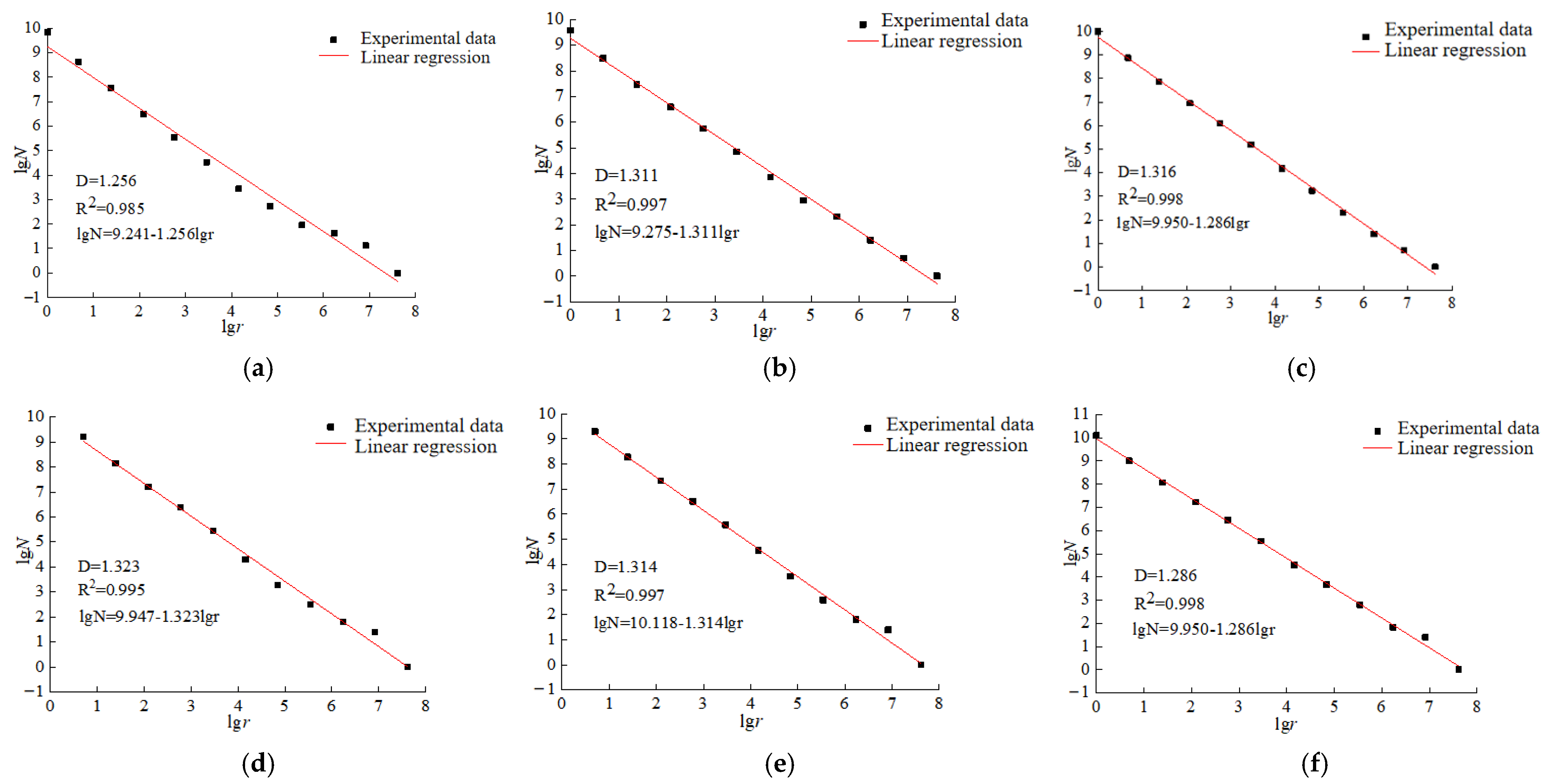
3.3.1. Fractal Dimension Calculation Program
3.3.2. Relationship between Fractal Dimension and Working Face Advancing
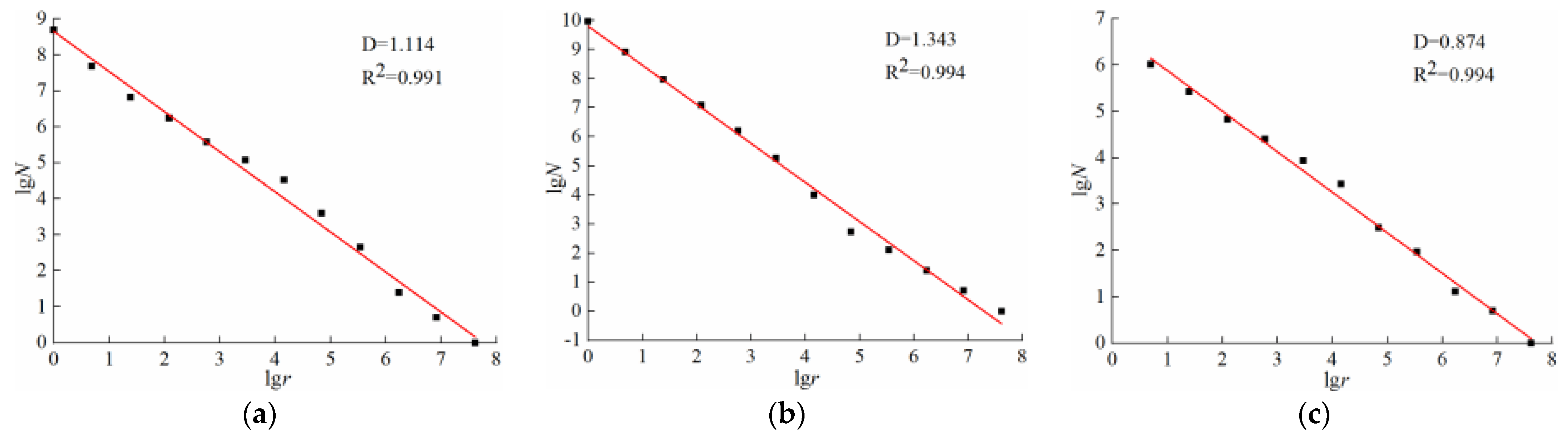
3.3.3. Fractal Characteristics of Three Zones
4. Conclusions
- (1)
- The cave plays a guiding role in the development of mining fractures. Due to the existence of the cave, the integrity of the rock structure is missing, which hinders the transmission of mining stress in the horizontal direction to a certain extent and causes the two sides of the cave to show uncoordinated deformation. The periodic weighting of the upper roof in the cave-affected zone is frequent, and the fragmentation of the fault rock mass becomes larger. The fractures of the upper rock mass are relatively developed, and the fractal dimension of the erosion rock fractures in this region is large.
- (2)
- By calculating the fractal dimension of the two-dimensional image of similar simulated mining-induced fissures, the quantitative characterization and analysis of the mining-induced fissures are carried out. It is concluded that the correlation coefficient of the fractal dimension of the mining-induced fissures under different advancing distances is as high as 0.90, indicating that the mining-induced fissure network of shallow coal seam under karst cave topography has high self-similarity.
- (3)
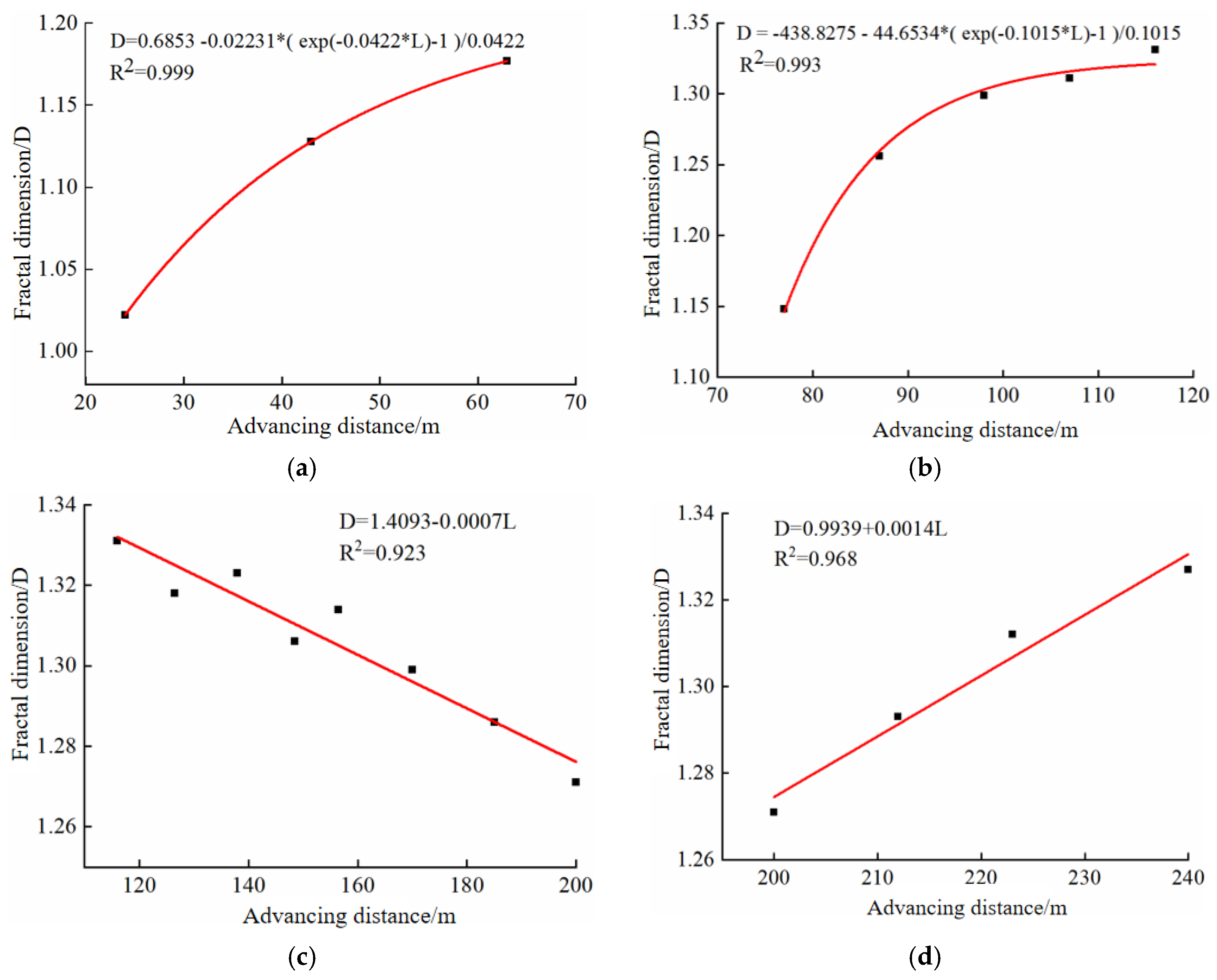
- According to the variation characteristics of fractal dimension with working face, it can be divided into four stages. The first, second, and fourth stages are all ascending stages, and the fractal dimensions of the first and second stages increase exponentially with the correlation coefficients of 0.999 and 0.993, respectively, and the growth rate of the second stage is relatively fast. The fourth stage is linear growth, the slope is 0.0014, and the correlation coefficient is 0.923; the third stage is the dimension reduction stage, where the fractal dimension of fracture network decreases linearly, the slope is −0.0007, and the correlation coefficient is 0.968. The fitting curves of each stage are convergent, and the fitting correlation is high.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Zhao, J. Landslides Distribution and Disaster Analysis in Typical Karst Areas of China-Guizhou as an Example; Shandong Normal University: Jinan, China, 2014. [Google Scholar]
- Xu, H. Geological Theory and Technology for Coalbed Methane Development with Thin and Medium Coal Seam Zones in Guizhou; China University of Mining and Technology: Xuzhou, China, 2012. [Google Scholar]
- Mandelbrot, B.B. The Fractal Geometry of Nature; Freeman: San Francisco, CA, USA, 1982; pp. 25–34. [Google Scholar]
- Xie, H.; Chen, Z. Fractal geometry and fracture of rock. Rock Soil Mech. 1988, 20, 264–271. [Google Scholar]
- Kang, T.; Zhao, Y.; Jin, Z. Fractal study of crack scales distribution in coalmass. J. China Coal Soc. 1995, 20, 393–398. [Google Scholar]
- Yu, G.; Xie, H.; Zhang, Y.; Yang, L.; Su, Z. Test studly of excavation subsidence in jointed rockmass and analysis on damage dynamics. Chin. J. Rock Mech. Eng. 1998, 17, 16. [Google Scholar]
- Xie, H.; Chen, Z.; Wang, J. Fractal study on crack distribution in tunnels for sub-level caving mining. J. China Coal Soc. 1998, 23, 30–35. [Google Scholar]
- Yu, G.; Zhang, C.; Zhao, J. Research and examination-validation of effect of original joints on subsidence range in rock mass. Chin. J. Rock Mech. Eng. 2002, 21, 1478–1482. [Google Scholar]
- Wang, Z.; Zhou, H.; Xie, H. Study on fractal characteristics of mining-induced fracture network evolution of overburden strata in deep mining. Rock Soil Mech. 2009, 30, 2403–2408. [Google Scholar]
- Li, Z.; Ding, X.; Cheng, Z. Study on fractal characteristics of fracture evolution of overlying rock in thin bedrock seam. J. Min. Saf. Eng. 2010, 27, 576–580. [Google Scholar]
- Li, D.; Zhou, H.; Xue, D.; Yi, H.; Gao, H. Relationship between percolation and fractal properties of mining-induced crack network in coal and rock masses. Rock Soil Mech. 2015, 36, 1135–1140. [Google Scholar]
- Wang, G.; Yu, G.; Yu, Y.; Lu, S.; Kang, Y. Study on cracks fractal evolution laws of mining rock mass. J. Min. Saf. Eng. 2012, 29, 859–863. [Google Scholar]
- Majdi, A.; Hassani, F.P.; Nasiri, M.Y. Prediction of the height of destressed zone above the mined panel roof in longwall coal mining. Int. J. Coal Geol. 2012, 98, 62–72. [Google Scholar] [CrossRef]
- Palchik, V. Formation of fractured zones in overburden due to longwall mining. Environ. Geol. 2003, 44, 28–38. [Google Scholar] [CrossRef]
- Rezaei, M.; Asadizadeh, M.; Majdi, A.; Hossaini, M.F. Prediction of representative deformation modulus of longwall panel roof rock strata using Mamdani fuzzy system. Int. J. Min. Sci. Technol. 2015, 25, 23–30. [Google Scholar]
- Li, H.; Wang, W.; Qi, Q.; Zhang, L. Study on fissure development rule of overlying strata influenced by mining based on fractal theory. J. China Coal Soc. 2014, 39, 1023–1031. [Google Scholar]
- Yin, G.; Li, X.; Han, P.; Li, M.; Li, W.; Deng, B. Experimental study on overburden strata fracture evolution law in three dimensional mine-induced stress conditions. J. China Coal Soc. 2016, 41, 406–413. [Google Scholar]
- Wei, J.; Zhang, J.; Jin, Z. Fractal study on the crack mechanism of fissured coal under the influence of mining activities. Ground Press. Strat. Control. 2005, 2, 112–113, 115. [Google Scholar]
- Li, S.; Qin, W.; Li, Z.; Ding, Y. Research on fractal characterization of mined crack network evolution repeated coal mining. J. Liaoning Tech. Univ. 2016, 35, 1384–1389. [Google Scholar]
- Liu, X. Experimental study on fractal law of rock fractures in goaf. J. Taiyuan Univ. Sci. Technol. 2009, 30, 428–431. [Google Scholar]
- Wei, Z.; Li, S.; Lin, H.; Shuang, H.; Ding, Y. Three-dimensional experimental study on evolution characteristics of overburden fractures in fully mechanized mining with large mining height. J. Xi Univ. Sci. Technol. 2020, 40, 589–598. [Google Scholar]
- Lin, H.; Li, S.; Cheng, L.; Wang, H. Experimental Analysis of Dynamic Evolution Model of Mining-Induced Fissure Zone in Overlying Strata. J. Min. Saf. Eng. 2011, 28, 298–303. [Google Scholar]
- Liang, T.; Liu, X.; Wang, S. Fractal study on the crack network evolution and permeability change in mining rock mass. J. China Coal Soc. 2019, 44, 3729–3739. [Google Scholar]
- Guo, L.; Cheng, H.; Peng, S.; Fu, B. Study on Evolution and Subsidence Fractal Characteristics of Overlying Strata in Thick Loose Layers and Thin Bedrocks. Saf. Coal Mines 2020, 51, 59–64, 70. [Google Scholar]
- Ye, Q.; Wang, G.; Jia, Z.; Zheng, C.; Wang, W. Similarity simulation of mining-crack-evolution characteristics of overburden strata in deep coal mining with large dip. J. Pet. Sci. Eng. 2018, 165, 477–487. [Google Scholar] [CrossRef] [Green Version]
- Fang, S.J.; Liang, B.; Sun, W.J.; Shi, Z.-S.; Hao, J.-F.; Wang, B.-F.; Zhang, X.-Y. Study on Stress Evolution Law of Overburden under Repeated Mining in Long-Distance Double Upper Protective Layer. Energies 2022, 15, 4459. [Google Scholar] [CrossRef]
- Liu, X.; Liang, T.; Wang, S.; Nawnit, K. A Fractal Model for Characterizing Hydraulic Properties of Fractured Rock Mass under Mining Influence. Geofluids 2019, 2019, 8391803. [Google Scholar] [CrossRef]
- Zhuo, H.; Qin, B.; Shi, Q.; Li, L. Development law of air leakage fractures in shallow coal seams: A case study in the Shendong Coalfield of China. Environ. Earth Sci. 2018, 77, 772. [Google Scholar] [CrossRef]
- Li, X.; Liu, Z.; Yang, S. Similar Physical Modeling of Roof Stress and Subsidence in Room and Pillar Mining of a Gently Inclined Medium-Thick Phosphate Rock. Adv. Civ. Eng. 2021, 2021, 6686981. [Google Scholar] [CrossRef]
- Zheng, R.; Kan, W.; Ru, L. Study on Overburden’s Destructive Rules Based on Similar Material Simulation. Int. J. Mod. Educ. Comput. Sci. 2011, 3, 54–60. [Google Scholar] [CrossRef]
- Jia, C.Y.; Wang, H.L.; Sun, X.Z.; Liu, K.M.; Zhang, G.B.; Yu, X.B.; Song, X.Y. Similar Material Simulation Test of Overlying Strata Characteristics of Isolated Working Face Mining with Thick-Hard Strata. Geotech. Geol. Eng. 2020, 38, 1121–1132. [Google Scholar] [CrossRef]
- Deng, G.; Xie, H.; Gao, M.; Li, C.; He, Z. Numerical Simulation on the Evolution of Mining-Induced Fracture Network in a Coal Seam and Its Overburden under the Top Coal Caving Method. Adv. Civ. Eng. 2020, 2020, 8833193. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, Y.; Xu, Y.; Zheng, Q.; Wang, Z.; Guo, L. Fracture development and fractal characteristics of overburden rock under repeated mining. Arab. J. Geosci. 2021, 14, 225. [Google Scholar] [CrossRef]
- Cai, J.; Li, X.; Guo, L.; Xue, H.; Xu, B. Fracture Development and Multifield Coupling Evolution Law of Soft Overburden Rock in a Medium-Thick Coal Seam Mine. Geofluids 2022, 2022, 6371887. [Google Scholar] [CrossRef] [PubMed]
- Li, Y.; Peng, J.; Zhang, L.; Zhou, J.; Huang, C.; Lian, M. Quantitative evaluation of impact cracks near the borehole based on 2D image analysis and fractal theory. Geothermics 2022, 100, 102335. [Google Scholar] [CrossRef]
- Mondal, D.; Roy, P.N.S.; Behera, P.K. Use of Correlation Fractal Dimension signatures for understanding the Overlying Strata Dynamics in Longwall Coal Mines. Int. J. Rock Mech. Min. Sci. 2017, 91, 210–221. [Google Scholar] [CrossRef]
- Liang, T.; Liu, X.; Wang, S.; Wang, E.; Li, Q. Study on the Fractal Characteristics of Fracture Network Evolution Induced by Mining. Adv. Civ. Eng. 2018, 2018, 9589364. [Google Scholar] [CrossRef] [Green Version]
- Gao, M.; Xie, J.; Guo, J.; Lu, Y.; He, Z.; Li, C. Fractal evolution and connectivity characteristics of mining-induced crack networks in coal masses at different depths. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 9. [Google Scholar] [CrossRef]
- Jafari, A.; Babadagli, T. Relationship between percolation–fractal properties and permeability of 2-D fracture networks. Int. J. Rock Mech. Min. Sci. 2013, 60, 353–362. [Google Scholar] [CrossRef]
- Yazdi, A.; Hamzehpour, H.; Sahimi, M. Permeability, porosity, and percolation properties of two-dimensional disordered fracture networks. Phys. Rev. E 2011, 84, 046317. [Google Scholar] [CrossRef]
- Huang, D.; Chang, X.; Tan, Y.; Fang, K.; Yin, Y. From rock microstructure to macromechanical properties based on fractal dimensions. Adv. Mech. Eng. 2019, 11, 1687814019836363. [Google Scholar] [CrossRef] [Green Version]
- Zhang, C.; Bai, Q.; Zhu, C. A methodology for determining the size distribution of broken rock masses in longwall mining goaf. Geomech. Geophys. Geo Energy Geo Resour. 2022, 8, 113. [Google Scholar] [CrossRef]
- Sun, B.; Liu, S.; Zeng, S.; Wang, S.; Wang, S. Dynamic characteristics and fractal representations of crack propagation of rock with different fissures under multiple impact loadings. Sci. Rep. 2021, 11, 13071. [Google Scholar] [CrossRef]
- Sun, H.; Liu, X.L.; Zhu, J.B. Correlational fractal characterisation of stress and acoustic emission during coal and rock failure under multilevel dynamic loading. Int. J. Rock Mech. Min. Sci. 2019, 117, 1–10. [Google Scholar] [CrossRef]
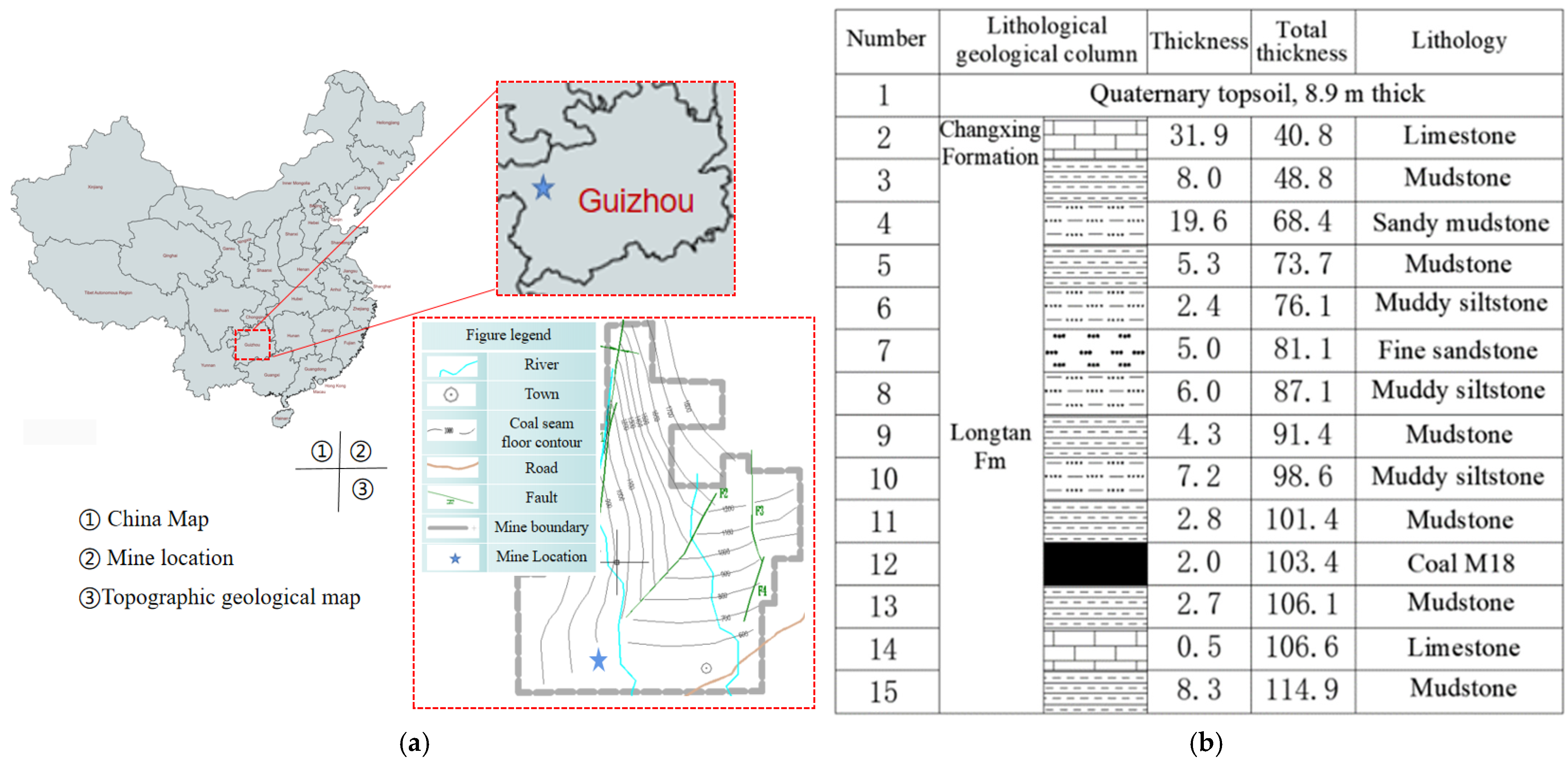






| Number | Lithology | Thickness | Density | Elastic Modulus | Tensile Strength | Poisson Ratio |
|---|---|---|---|---|---|---|
| (m) | (kg/m3) | (GPa) | (MPa) | (GPa) | ||
| 15 | Topsoil layer | 8.9 | 1750 | 0.1 | 0.1 | 0.32 |
| 14 | Changxing Formation | 31.9 | 2430 | 19.9 | 4.4 | 0.20 |
| 13 | Mudstone | 8 | 2450 | 7 | 1.8 | 0.31 |
| 12 | Sandy mudstone | 19.6 | 2595 | 15.3 | 2.54 | 0.22 |
| 11 | Mudstone | 5.3 | 2450 | 7.34 | 2 | 0.31 |
| 10 | Muddy siltstone | 2.4 | 2520 | 14.2 | 1.7 | 0.21 |
| 9 | Fine sandstone | 5 | 2550 | 11.5 | 2.5 | 0.2 |
| 8 | Muddy siltstone | 6 | 2520 | 14.2 | 1.7 | 0.21 |
| 7 | Mudstone | 4.3 | 2550 | 7.34 | 2 | 0.31 |
| 6 | Muddy siltstone | 7.2 | 2600 | 15.6 | 3.9 | 0.23 |
| 5 | Mudstone | 2.8 | 2420 | 8.49 | 1.5 | 0.22 |
| 4 | Coal M18 | 2 | 1400 | 2.5 | 0.6 | 0.25 |
| 3 | Mudstone | 2.7 | 2560 | 8.79 | 2.02 | 0.29 |
| 2 | Limestone | 0.5 | 2700 | 30 | 4.9 | 0.28 |
| 1 | Mudstone | 8.3 | 2640 | 7.87 | 2.37 | 0.29 |
| Number | Lithology | Thickness | Density | Elastic Modulus | Proportion Number | Sand | Lime | Gypsum | Total Material Weight | Water |
|---|---|---|---|---|---|---|---|---|---|---|
| (cm) | (kg/m3) | (GPa) | (kg) | (kg) | (kg) | (kg) | (kg) | |||
| 15 | Topsoil layer | 8.9 | 1094 | 0.00 | - | 127.57 | 9.11 | 9.11 | 145.79 | 16.20 |
| 14 | Changxing Formation | 31.9 | 1519 | 0.12 | 537 | 457.23 | 27.43 | 64.01 | 548.68 | 60.96 |
| 13 | Mudstone | 8 | 1531 | 0.04 | 773 | 114.67 | 11.47 | 4.91 | 131.05 | 14.56 |
| 12 | Sandy mudstone | 19.6 | 1622 | 0.10 | 737 | 280.93 | 12.04 | 28.09 | 321.07 | 35.67 |
| 11 | Mudstone | 5.3 | 1531 | 0.05 | 755 | 75.97 | 5.43 | 5.43 | 86.82 | 9.65 |
| 10 | Muddy siltstone | 2.4 | 1575 | 0.09 | 773 | 34.40 | 3.44 | 1.47 | 39.31 | 4.37 |
| 9 | Fine sandstone | 5 | 1594 | 0.07 | 737 | 71.67 | 3.07 | 7.17 | 81.90 | 9.10 |
| 8 | Muddy siltstone | 6 | 1575 | 0.09 | 773 | 86.00 | 8.60 | 3.69 | 98.29 | 10.92 |
| 7 | Mudstone | 4.3 | 1594 | 0.05 | 755 | 61.63 | 4.40 | 4.40 | 70.44 | 7.83 |
| 6 | Muddy siltstone | 7.2 | 1625 | 0.10 | 637 | 103.20 | 5.16 | 12.04 | 120.40 | 13.38 |
| 5 | Mudstone | 2.8 | 1513 | 0.05 | 773 | 40.13 | 4.01 | 1.72 | 45.87 | 5.10 |
| 4 | Coal M18 | 2 | 875 | 0.02 | 873 | 18.63 | 1.63 | 0.70 | 20.96 | 2.33 |
| 3 | Mudstone | 2.7 | 1600 | 0.05 | 755 | 38.70 | 2.76 | 2.76 | 44.23 | 4.91 |
| 2 | Limestone | 0.5 | 1688 | 0.19 | 537 | 7.17 | 0.43 | 1.00 | 8.60 | 0.96 |
| 1 | Mudstone | 8.3 | 1650 | 0.05 | 737 | 118.97 | 5.10 | 11.90 | 135.96 | 15.11 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gou, R.; Jiang, C.; Liu, Y.; Wang, C.; Li, Y. Study on Fractal Characteristics of Evolution of Mining-Induced Fissures in Karst Landform. Energies 2022, 15, 5372. https://doi.org/10.3390/en15155372
Gou R, Jiang C, Liu Y, Wang C, Li Y. Study on Fractal Characteristics of Evolution of Mining-Induced Fissures in Karst Landform. Energies. 2022; 15(15):5372. https://doi.org/10.3390/en15155372
Chicago/Turabian StyleGou, Rentao, Chengyu Jiang, Yong Liu, Chen Wang, and Yuanlin Li. 2022. "Study on Fractal Characteristics of Evolution of Mining-Induced Fissures in Karst Landform" Energies 15, no. 15: 5372. https://doi.org/10.3390/en15155372
APA StyleGou, R., Jiang, C., Liu, Y., Wang, C., & Li, Y. (2022). Study on Fractal Characteristics of Evolution of Mining-Induced Fissures in Karst Landform. Energies, 15(15), 5372. https://doi.org/10.3390/en15155372







