A Numerical Study on the Energization of the Field Coils of a Full-Size Wind Turbine with Different Types of Flux Pumps
Abstract
:1. Introduction
2. The EcoSwing Field Winding System
3. Design and Characteristics of the Flux Pump Power Supply Systems
3.1. Dynamo Flux Pump
3.2. “Cold Rectifier” Flux Pump
3.3. “Warm Rectifier” Flux Pump
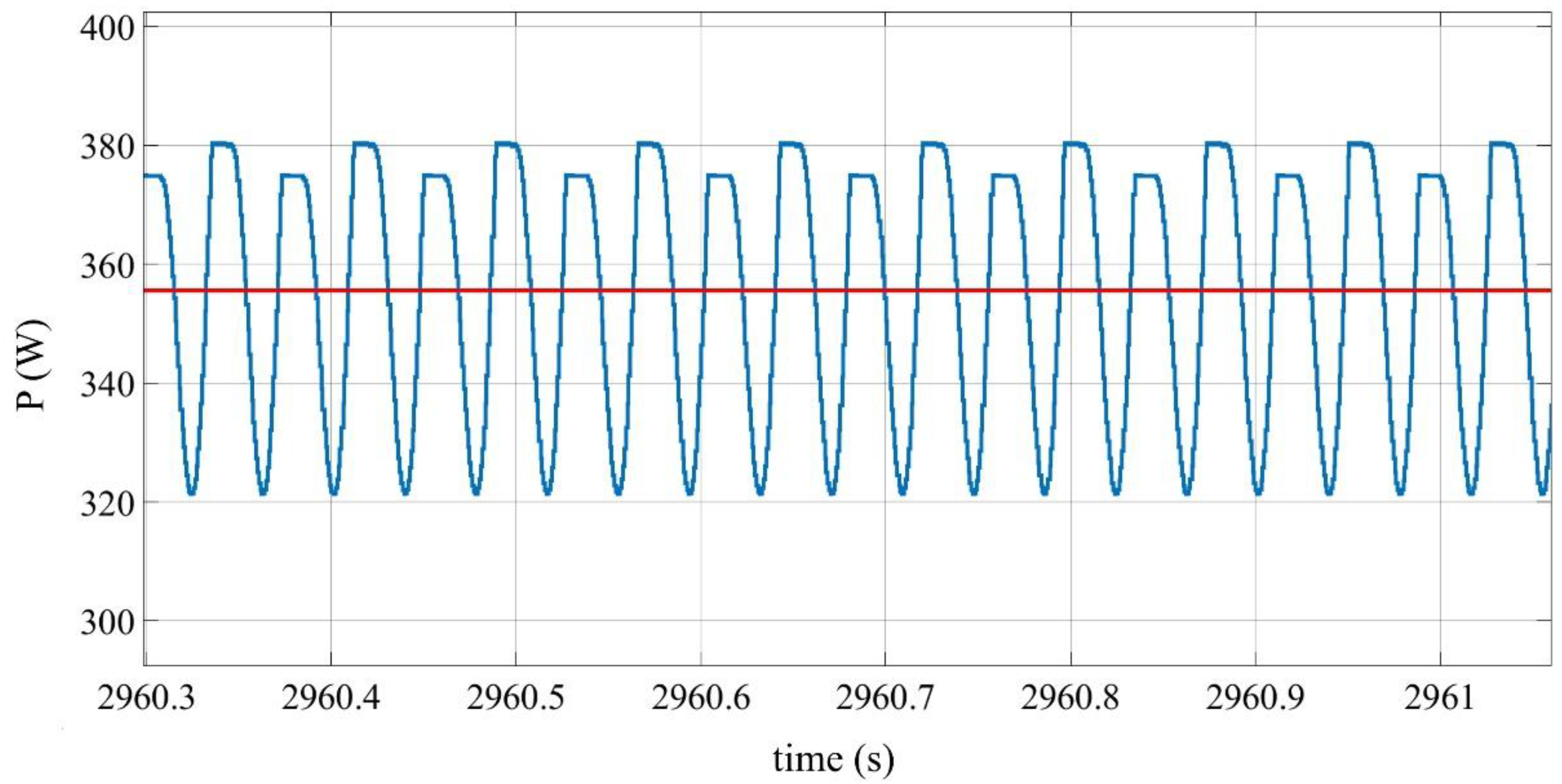
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khalil, M.E. High temperature superconducting generator design for offshore wind turbine application. In Proceedings of the International Conference on Electrical Engineering and Information Communication Technology (ICEEICT), Dhaka, Bangladesh, 21–23 May 2015. [Google Scholar] [CrossRef]
- Lloberas, J.; Sumper, A.; Sanmarti, M.; Granados, X. A review of high temperature superconductors for offshore wind power synchronous generators. Renew. Sustain. Energy Rev. 2014, 38, 404–414. [Google Scholar] [CrossRef]
- Ma, G.; Wang, Z.; Liu, K.; Qian, H.; Wang, C. Potentials of an integrated levitation, guidance, and propulsion system by a superconducting flux linear motor. IEEE Trans. Ind. Electron. 2018, 65, 7548–7557. [Google Scholar] [CrossRef]
- MacManus-Driscoll, J.L.; Wimbush, S.C. Processing and application of high-temperature superconducting coated conductors. Nat. Rev. Mater. 2021, 6, 587–604. [Google Scholar] [CrossRef]
- Bergen, A.; Andersen, R.; Bauer, M.; Boy, H.; Ter Brake, M.; Brutsaert, P.; Bührer, C.; Dhallé, M.; Hansen, J.; ten Kate, H.; et al. Design and in-field testing of the world’s first ReBCO rotor for a 3.6 MW wind generator. Supercond. Sci. Technol. 2019, 32, 125006. [Google Scholar] [CrossRef]
- Frank, M.; Frauenhofer, J.; van Hasselt, P.; Nick, W.; Neumueller, H.W.; Nerowski, G. Long-term operational experience with first Siemens 400 kW HTS machine in diverse configurations. IEEE Trans. Appl. Supercond. 2003, 13, 2120–2123. [Google Scholar] [CrossRef]
- Kalsi, S.S.; Gamble, B.B.; Snitchler, G.; Ige, S.O. The status of HTS ship propulsion motor developments. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006. [Google Scholar] [CrossRef]
- Fair, R.; Lewis, C.; Eugene, J.; Ingles, M. Development of an HTS hydroelectric power generator for the Hirschaid power station. J. Phys. Conf. Ser. 2010, 234, 032008. [Google Scholar] [CrossRef]
- Sivasubramaniam, K.; Zhang, T.; Lokhandwalla, M.; Laskaris, E.T.; Bray, J.W.; Gerstler, B.; Shah, M.R.; Alexander, J.P. Development of a high speed HTS generator for airborne applications. IEEE Trans. Appl. Supercond. 2009, 19, 1656–1661. [Google Scholar] [CrossRef]
- Gamble, B.; Snitchler, G.; Macdonald, T. Full power test of a 36.5 MW HTS propulsion motor. IEEE Trans. Appl. Supercond. 2011, 21, 1083–1088. [Google Scholar] [CrossRef]
- Jha, A.K.; Matsumoto, K. Superconductive RE BCO Thin Films and Their Nanocomposites: The Role of Rare-Earth Oxides in Promoting Sustainable Energy. Front. Phys. 2019, 7, 82. [Google Scholar] [CrossRef]
- Park, Y.G.; Lee, C.Y.; Lee, J.; Nam, S.; Do Chung, Y.; Yoon, Y.S.; Ko, T.K. Experimental analysis on initial current decay characteristics of persistent-mode HTS coil by external alternating magnetic field. IEEE Trans. Appl. Supercond. 2015, 25, 3601204. [Google Scholar] [CrossRef]
- Geng, J.; Zhang, H.; Li, C.; Zhang, X.; Shen, B.; Coombs, T.A. Angular dependence of direct current decay in a closed YBCO double-pancake coil under external AC magnetic field and reduction by magnetic shielding. Supercond. Sci. Technol. 2017, 30, 035022. [Google Scholar] [CrossRef]
- Van de Klundert, L.J.M.; ten Kate, H.H. Fully superconducting rectifiers and flux pumps part 1: Realized methods for flux pumping. Cryogenics 1981, 21, 195–206. [Google Scholar] [CrossRef] [Green Version]
- Coombs, T.A.; Geng, J.; Fu, L.; Matsuda, K. An Overview of Flux Pumps for HTS Coils. IEEE Trans. Appl. Supercond. 2017, 27, 4600806. [Google Scholar] [CrossRef]
- Coombs, T.A. Superconducting flux pumps. J. Appl. Phys. 2019, 125, 230902. [Google Scholar] [CrossRef] [Green Version]
- Wen, Z.; Zhang, H.; Mueller, M. High Temperature Superconducting Flux Pumps for Contactless Energization. Crystals 2022, 12, 766. [Google Scholar] [CrossRef]
- Hoffmann, C.; Pooke, D.; Caplin, A.D. Flux Pump for HTS Magnets. IEEE Trans. Appl. Supercond. 2011, 21, 1628–1631. [Google Scholar] [CrossRef]
- Bumby, C.W.; Pantoja, A.E.; Sung, H.J.; Jiang, Z.; Kulkarni, R.; Badcock, R.A. Through-Wall Excitation of a Magnet Coil by an External-Rotor HTS Flux Pump. IEEE Trans. Appl. Supercond. 2016, 26, 0500505. [Google Scholar] [CrossRef]
- Fu, L.; Matsuda, K.; Lecrevisse, T.; Iwasa, Y.; Coombs, T. A flux pumping method applied to the magnetization of YBCO superconducting coils: Frequency, amplitude and waveform characteristics. Supercond. Sci. Technol. 2016, 29, 04LT01. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Ye, H.; Wang, X.; Gao, Y.; Zhou, Q.; Liu, X.; Lei, Y. Compact Linear-Motor Type Flux Pumps with Different Wavelengths for High-Temperature Superconducting Magnets. IEEE Trans. Appl. Supercond. 2020, 30, 5000305. [Google Scholar] [CrossRef]
- Mataira, R.; Ainslie, M.; Pantoja, A.; Badcock, R.; Bumby, C. Mechanism of the high-Tc superconducting dynamo: Models and experiment. Phys. Rev. Appl. 2020, 14, 024012. [Google Scholar] [CrossRef]
- Geng, J.; Bumby, C.W.; Badcock, R.A. Maximising the current output from a self-switching kA-class rectifier flux pump. Supercond. Sci. Technol. 2020, 33, 045005. [Google Scholar] [CrossRef]
- Gawith, J.D.D.; Geng, J.; Li, C.; Shen, B.; Zhang, X.; Ma, J.; Coombs, T.A. A half-bridge HTS transformer–rectifier flux pump with two AC field-controlled switches. Supercond. Sci. Technol. 2018, 31, 085002. [Google Scholar] [CrossRef]
- Mataira, R.C.; Ainslie, M.D.; Badcock, R.A.; Bumby, C.W. Origin of the DC output voltage from a high-Tc superconducting dynamo. Appl. Phys. Lett. 2019, 114, 162601. [Google Scholar] [CrossRef] [Green Version]
- Ainslie, M.D.; Quéval, L.; Mataira, R.C.; Bumby, C.W. Modelling the frequency dependence of the open-circuit voltage of a high-Tc superconducting dynamo. IEEE Trans. Appl. Supercond. 2021, 31, 4900407. [Google Scholar] [CrossRef]
- Ghabeli, A.; Ainslie, M.; Pardo, E.; Quéval, L.; Mataira, R. Modeling the charging process of a coil by an HTS dynamo-type flux pump. Supercond. Sci. Technol. 2021, 34, 084002. [Google Scholar] [CrossRef]
- Ghabeli, A.; Pardo, E.; Kapolka, M. 3D modeling of a superconducting dynamo-type flux pump. Sci. Rep. 2021, 11, 10296. [Google Scholar] [CrossRef]
- Mataira, R.; Ainslie, M.D.; Badcock, R.; Bumby, C.W. Modeling of stator versus magnet width effects in high-Tc superconducting dynamos. IEEE Trans. Appl. Supercond. 2020, 30, 5204406. [Google Scholar] [CrossRef]
- Ghabeli, A.; Pardo, E. Modeling of airgap influence on DC voltage generation in a dynamo-type flux pump. Supercond. Sci. Technol. 2020, 33, 035008. [Google Scholar] [CrossRef] [Green Version]
- Ainslie, M.; Grilli, F.; Quéval, L.; Pardo, E.; Perez-Mendez, F.; Mataira, R.; Morandi, A.; Ghabeli, A.; Bumby, C.; Brambilla, R. A new benchmark problem for electromagnetic modelling of superconductors: The high-Tc superconducting dynamo. Supercond. Sci. Technol. 2020, 30, 105009. [Google Scholar] [CrossRef] [Green Version]
- Prigozhin, L.; Sokolovsky, V. Two-dimensional model of a high-Tc superconducting dynamo. IEEE Trans. Appl. Supercond. 2021, 31, 5201107. [Google Scholar] [CrossRef]
- Prigozhin, L.; Sokolovsky, V. Fast solution of the superconducting dynamo benchmark problem. Supercond. Sci. Technol. 2021, 34, 065006. [Google Scholar] [CrossRef]
- Sung, H.J.; Go, B.S.; Park, H.; Badcock, R.A.; Park, M.; Yu, I.K. Design, fabrication, and analysis of HTS coils for a 10-kW wind power generator employing a brushless exciter. IEEE Trans. Appl. Supercond. 2017, 27, 5202305. [Google Scholar] [CrossRef]
- Bumby, C.W.; Badcock, R.A.; Sung, H.J.; Kim, K.M.; Jiang, Z.; Pantoja, A.E.; Bernardo, P.; Park, M.; Buckley, R.G. Development of a brushless HTS exciter for a 10 kW HTS synchronous generator. Supercond. Sci. Technol. 2016, 29, 024008. [Google Scholar] [CrossRef]
- Sung, H.J.; Badcock, R.A.; Jiang, Z.; Choi, J.; Park, M.; Yu, I.K. Design and Heat Load Analysis of a 12 MW HTS Wind Power Generator Module Employing a Brushless HTS Exciter. IEEE Trans. Appl. Supercond. 2016, 26, 5205404. [Google Scholar] [CrossRef]
- Tuvdensuren, O.; Sung, H.J.; Go, B.S.; Le, T.T.; Park, M.; Yu, I.K. Structural design and heat load analysis of a flux pump-based HTS module coil for a large-scale wind power generator. J. Phys. Conf. Ser. 2018, 1054, 012084. [Google Scholar] [CrossRef]
- Nam, G.D.; Sung, H.J.; Kim, C.; Lee, J.; Badcock, R.A.; Jiang, Z.; Park, M. Design and Performance Analysis of a Dynamo-Type HTS Flux Pump for a 10 kW Superconducting Generator. IEEE Trans. Appl. Supercond. 2020, 30, 5205005. [Google Scholar] [CrossRef]
- Song, X.; Mijatovic, N.; Kellers, J.; Bührer, C.; Rebsdorf, A.V.; Hansen, J.; Christensen, M.; Krause, J.; Wiezoreck, J.; Pütz, H.; et al. A Full-Size High-Temperature Superconducting Coil Employed in a Wind Turbine Generator Setup. IEEE Trans. Appl. Supercond. 2017, 27, 5201105. [Google Scholar] [CrossRef]
- Song, X.; Buehrer, C.; Mølgaard, A.; Andersen, R.S.; Brutsaert, P.; Bauer, M.; Hansen, J.; Rebsdorf, A.V.; Kellers, J.; Winkler, T.; et al. Commissioning of the World’s First Full-Scale MW-Class Superconducting Generator on a Direct Drive Wind Turbine. IEEE Trans. Energy Convers. 2020, 35, 1697–1704. [Google Scholar] [CrossRef]
- Song, X.; Bührer, C.; Brutsaert, P.; Ammar, A.; Krause, J.; Bergen, A.; Winkler, T.; Dhalle, M.; Hansen, J.; Rebsdorf, A.V.; et al. Ground Testing of the World’s First MW-Class Direct-Drive Superconducting Wind Turbine Generator. IEEE Trans. Energy Convers. 2020, 35, 757–764. [Google Scholar] [CrossRef]
- Song, X.; Bührer, C.; Brutsaert, P.; Krause, J.; Ammar, A.; Wiezoreck, J.; Hansen, J.; Rebsdorf, A.V.; Dhalle, M.; Bergen, A.; et al. Designing and Basic Experimental Validation of the World’s First MW-Class Direct-Drive Superconducting Wind Turbine Generator. IEEE Trans. Energy Convers. 2019, 34, 2218–2225. [Google Scholar] [CrossRef]
- Oomen, M.P.; Leghissa, M.; Ries, G.; Proelss, N.; Neumueller, H.W.; Steinmeyer, F.; Vester, M.; Davies, F. HTS flux pump for cryogen-free HTS magnets. IEEE Trans. Appl. Supercond. 2005, 15, 1465–1468. [Google Scholar] [CrossRef]
- European Commisison. EcoSwing—Energy Cost Optimization using Superconducting Wind Generators—World’s First Demonstration of a 3.6 MW Low-Cost Lightweight DD Superconducting Generator on a Wind Turbine. Available online: https://cordis.europa.eu/project/id/656024 (accessed on 23 June 2022).
- Wiezoreck, J. Cryogenic design of the EcoSwing 3.6 MW superconducting wind generator. In Proceedings of the 2nd International Workshop HTS Applications, Karlsruhe, Germany, 13–15 September 2017. [Google Scholar]
- THEVA. Available online: https://www.theva.de/wp-content/uploads/2018/05/171218_THEVA_Broschuere_Pro-Line_generalproperties.pdf (accessed on 14 July 2022).
- Uglietti, D.; Kitaguchi, H.; Choi, S.; Kiyoshi, T. Angular dependence of critical current in coated conductors at 4.2 K and magnet design. IEEE Trans. Appl. Supercond. 2009, 19, 2909–2912. [Google Scholar] [CrossRef]
- Markiewicz, W.D.; Larbalestier, D.C.; Weijers, H.W.; Voran, A.J.; Pickard, K.W.; Sheppard, W.R.; Jaroszynski, J.; Xu, A.; Walsh, R.P.; Lu, J.; et al. Design of a superconducting 32 T magnet with REBCO high field coils. IEEE Trans. Appl. Supercond. 2011, 22, 4300704. [Google Scholar] [CrossRef]
- Weijers, H.W.; Markiewicz, W.D.; Voran, A.J.; Gundlach, S.R.; Sheppard, W.R.; Jarvis, B.; Johnson, Z.L.; Noyes, P.D.; Lu, J.; Kandel, H.; et al. Progress in the development of a superconducting 32 T magnet with REBCO high field coils. IEEE Trans. Appl. Supercond. 2013, 24, 4301805. [Google Scholar] [CrossRef]
- Allweins, K.; Marzahn, E. Feasibility of HTS dc cables on board a ship. In Proceedings of the 10th EPRI Superconductivity Conference Nexans Deutschl, Tallahassee, FL, USA, 11–13 October 2011. [Google Scholar]
- Morandi, A. HTS dc transmission and distribution: Concepts, applications and benefits. Supercond. Sci. Technol. 2015, 28, 123001. [Google Scholar] [CrossRef]
- Morandi, A.; Gholizad, B.; Stieneker, M.; Stagge, H.; De Doncker, R.W. Technical and Economical Evaluation of DC High-Temperature Superconductor Solutions for the Grid Connection of Offshore Wind Parks. IEEE Trans. Appl. Supercond. 2016, 26, 5402910. [Google Scholar] [CrossRef]
- Masson, P. Power devices design and optimization. In Proceedings of the ASC Short Course, Portland, OR, USA, 7 October 2012. [Google Scholar]
- Bauer, B.; (ThyssenKrupp Transrapid GmbH, München, Bayern, Germany). Personal communication, 2021.
- Oomen, M.P.; Rieger, J.; Leghissa, M.; ten Haken, B.; ten Kate, H.H. Dynamic resistance in a slab-like superconductor with J(B) dependence. Supercond. Sci. Technol. 1999, 12, 382. [Google Scholar] [CrossRef]
- Kails, K.; Zhang, H.; Machura, P.; Mueller, M.; Li, Q. Dynamic loss of HTS field windings in rotating electric machines. Supercond. Sci. Technol. 2020, 33, 045014. [Google Scholar] [CrossRef]
- Jiang, Z.; Bumby, C.W.; Badcock, R.A.; Sung, H.J.; Long, N.J.; Amemiya, N. Impact of flux gap upon dynamic resistance of a rotating HTS flux pump. Supercond. Sci. Technol. 2015, 28, 115008. [Google Scholar] [CrossRef]
- Sung, H.J.; Badcock, R.A.; Go, B.S.; Park, M.; Yu, I.K.; Jiang, Z. Design of a 12-MW HTS wind power generator including a flux pump exciter. IEEE Trans. Appl. Supercond. 2016, 26, 5206205. [Google Scholar]
- Morandi, A.; Russo, G.; Fabbri, M.; Soldati, L. Energy balance, efficiency and operational limits of the dynamo type flux pump. Supercond. Sci. Technol. 2022, 35, 065011. [Google Scholar] [CrossRef]
- Hamilton, K.; Mataira, R.; Geng, J.; Bumby, C.; Carnegie, D.; Badcock, R. Practical Estimation of HTS Dynamo Losses. IEEE Trans. Appl. Supercond. 2020, 30, 4703105. [Google Scholar] [CrossRef]
- Russo, G.; Yazdani-Asrami, M.; Morandi, A.; Scheda, R. Critical surface reconstruction for HTS tapes using Artificial Intelligence techniques. In Proceedings of the Hi-Scale COST Meeting, COST Action CA19108, Bologna, Italy, 15 September 2021. [Google Scholar]
- Robinson Research Institute. Available online: http://htsdb.wimbush.eu/ (accessed on 31 May 2022).
- Strickland, N.M.; Hoffmann, C.; Wimbush, S.C. A 1 kA-class cryogen-free critical current characterization system for superconducting coated conductors. Rev. Sci. Instrum. 2014, 85, 113907. [Google Scholar] [CrossRef]
- Wimbush, S.C.; Strickland, N.M. A Public Database of High-Temperature Superconductor Critical Current Data. IEEE Trans. Appl. Supercond. 2017, 27, 8000105. [Google Scholar] [CrossRef]
- Hamilton, K.; Pantoja, A.E.; Storey, J.G.; Jiang, Z.; Badcock, R.A.; Bumby, C.W. Design and performance of a “squirrel-cage” dynamo-type HTS flux pump. IEEE Trans. Appl. Supercond. 2018, 28, 5205705. [Google Scholar] [CrossRef]
- Nøland, J.K.; Nuzzo, S.; Tessarolo, A.; Alves, E.F. Excitation system technologies for wound-field synchronous machines: Survey of solutions and evolving trends. IEEE Access 2019, 7, 109699–109718. [Google Scholar] [CrossRef]
- Geng, J.; Matsuda, K.; Shen, B.; Zhang, H.; Zhang, X.; Fu, L.; Huang, Z.; Coombs, T.A. HTS Persistent Current Switch Controlled by AC Magnetic Field. IEEE Trans. Appl. Supercond. 2016, 26, 6603304. [Google Scholar] [CrossRef]
- Li, C.; Geng, J.; Gawith, J.; Shen, B.; Zhang, X.; Zhang, H.; Ma, J.; Coombs, T.A. Design for a Persistent Current Switch Controlled by Alternating Current Magnetic Field. IEEE Trans. Appl. Supercond. 2018, 28, 4603205. [Google Scholar] [CrossRef]
- Li, C.; Geng, J.; Shen, B.; Li, X.; Gawith, J.; Ma, J.; Yang, J.; Coombs, T.A. Persistent Current Switch for HTS Superconducting Magnets: Design, Control Strategy, and Test Results. IEEE Trans. Appl. Supercond. 2019, 29, 4900704. [Google Scholar] [CrossRef]
- Abd El-Azeem, S.M.; El-Ghanam, S.M. Comparative study of gallium nitride and silicon carbide MOSFETs as power switching applications under cryogenic conditions. Cryogenics 2020, 107, 103071. [Google Scholar] [CrossRef]
- Tokamak Energy. Available online: https://www.tokamakenergy.co.uk/cryogenic-power-supply/ (accessed on 31 May 2022).
- Kirby, G.; Galvin, T.; Coll, D.; Stevenson, R.; Livesey, P. Varistor Insulation for HTS Magnets. IEEE Trans. Appl. Supercond. 2022, 32, 7700604. [Google Scholar] [CrossRef]
- Yang, S. Cryogenic Characteristics of IGBTs. Doctoral Dissertation, University of Birmingham, Birmingham, UK, 2005. [Google Scholar]
- Rajashekara, K.; Akin, B. A review of cryogenic power electronics-status and applications. In Proceedings of the International Electric Machines & Drives Conference, Chicago, IL, USA, 12–15 May 2013; pp. 899–904. [Google Scholar]
- Rice, J.H.; Geng, J.; Bumby, C.W.; Weijers, H.W.; Wray, S.; Zhang, H.; Schoofs, F.; Badcock, R.A. Design of a 60 kA Flux Pump for Fusion Toroidal Field Coils. IEEE Trans. Appl. Supercond. 2021, 32, 5500205. [Google Scholar] [CrossRef]

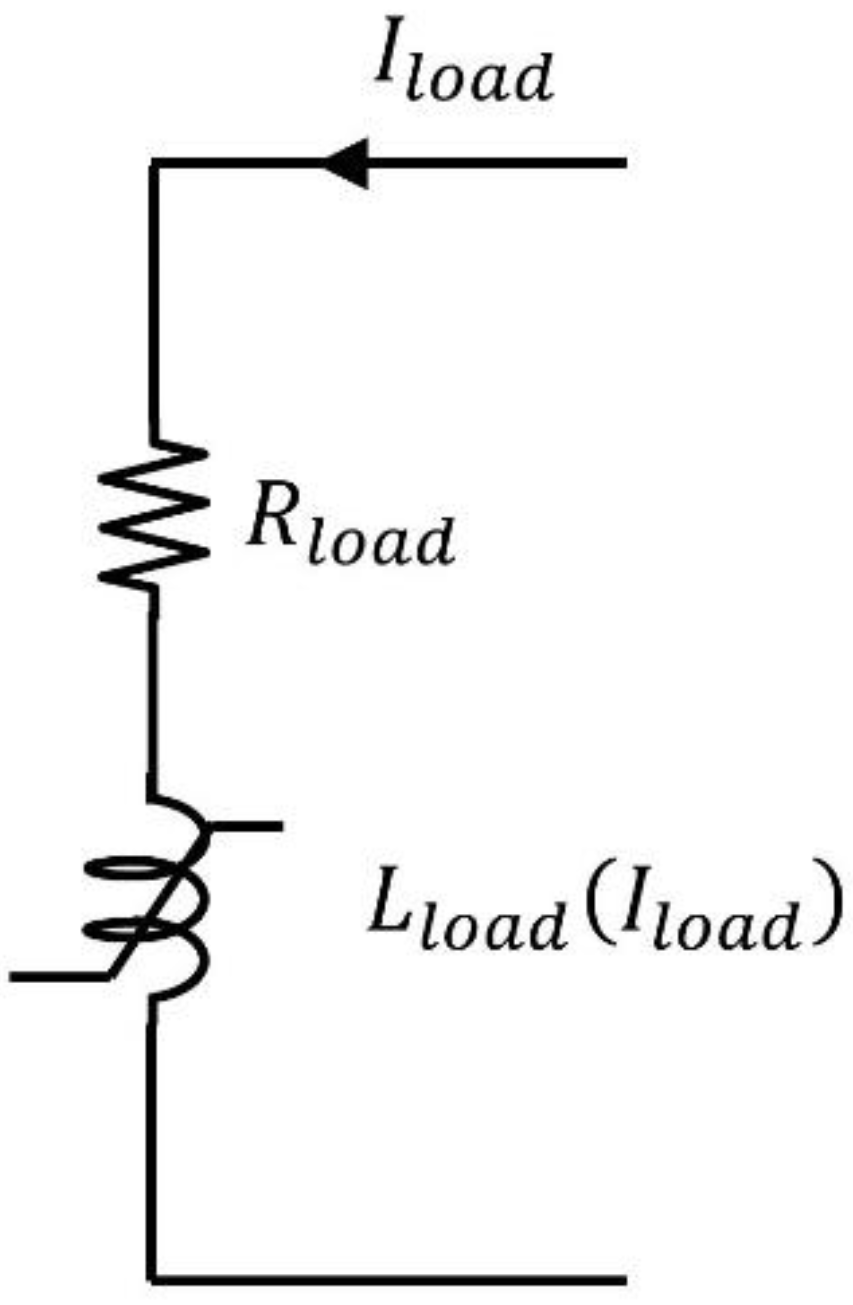


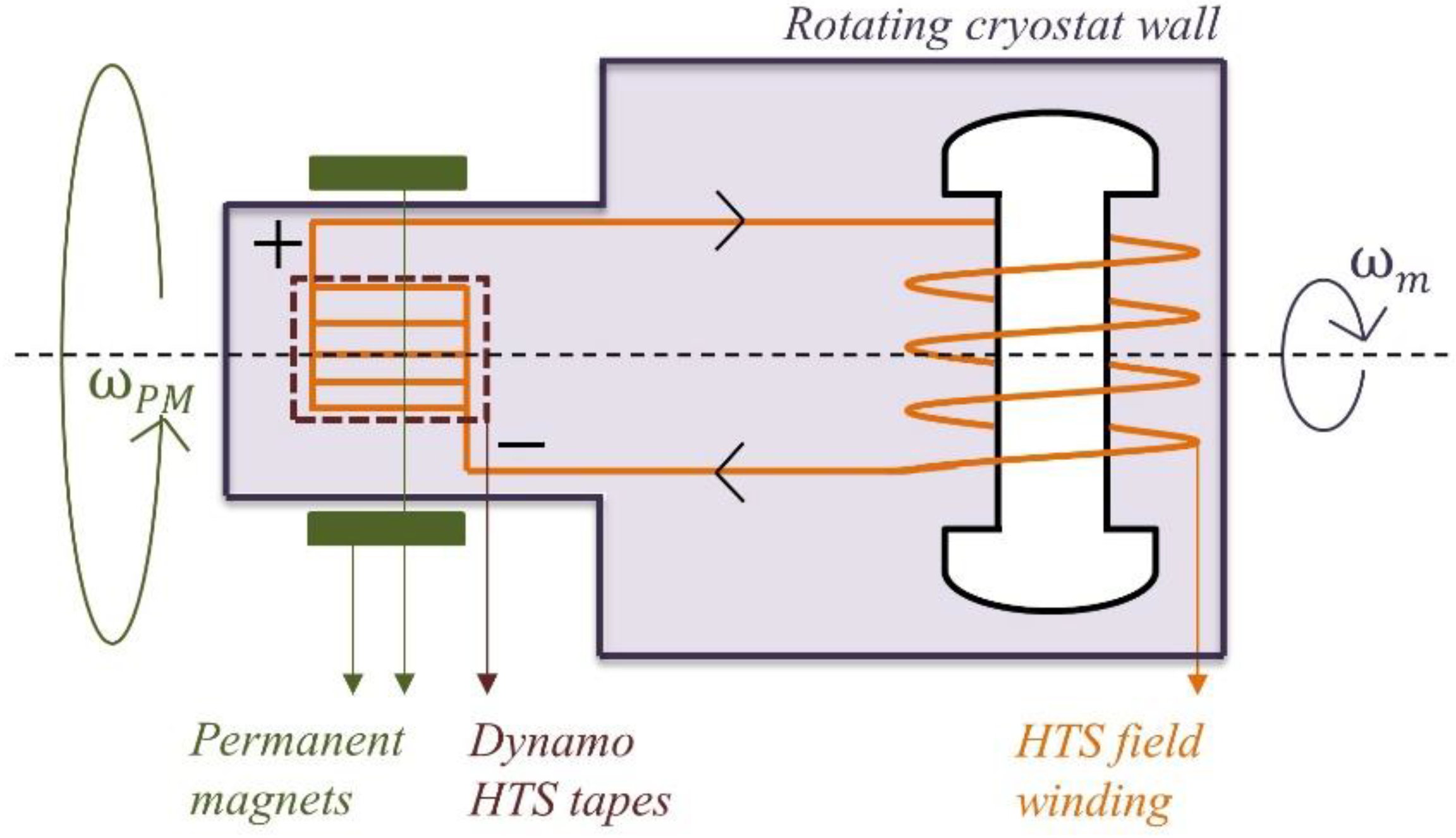
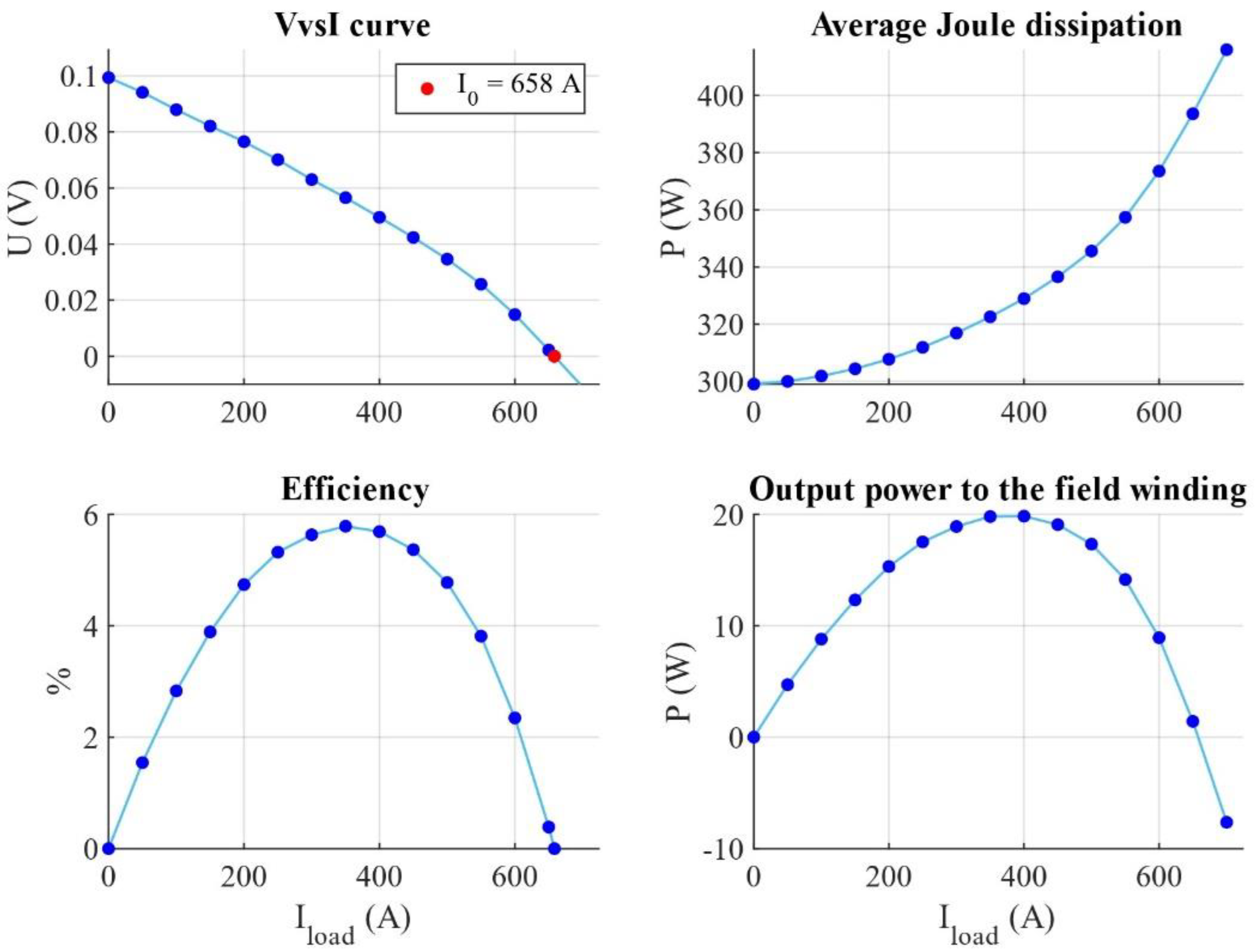
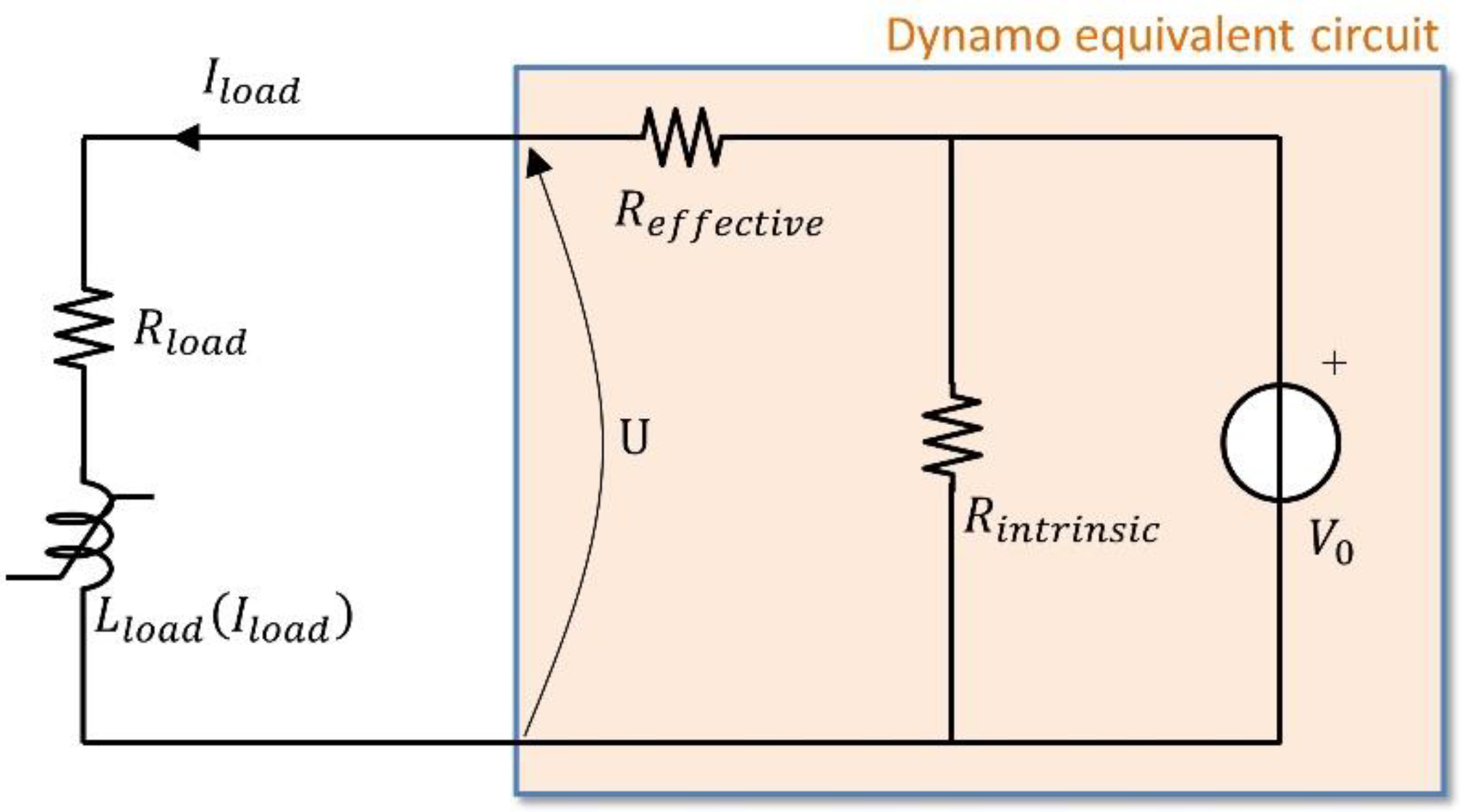

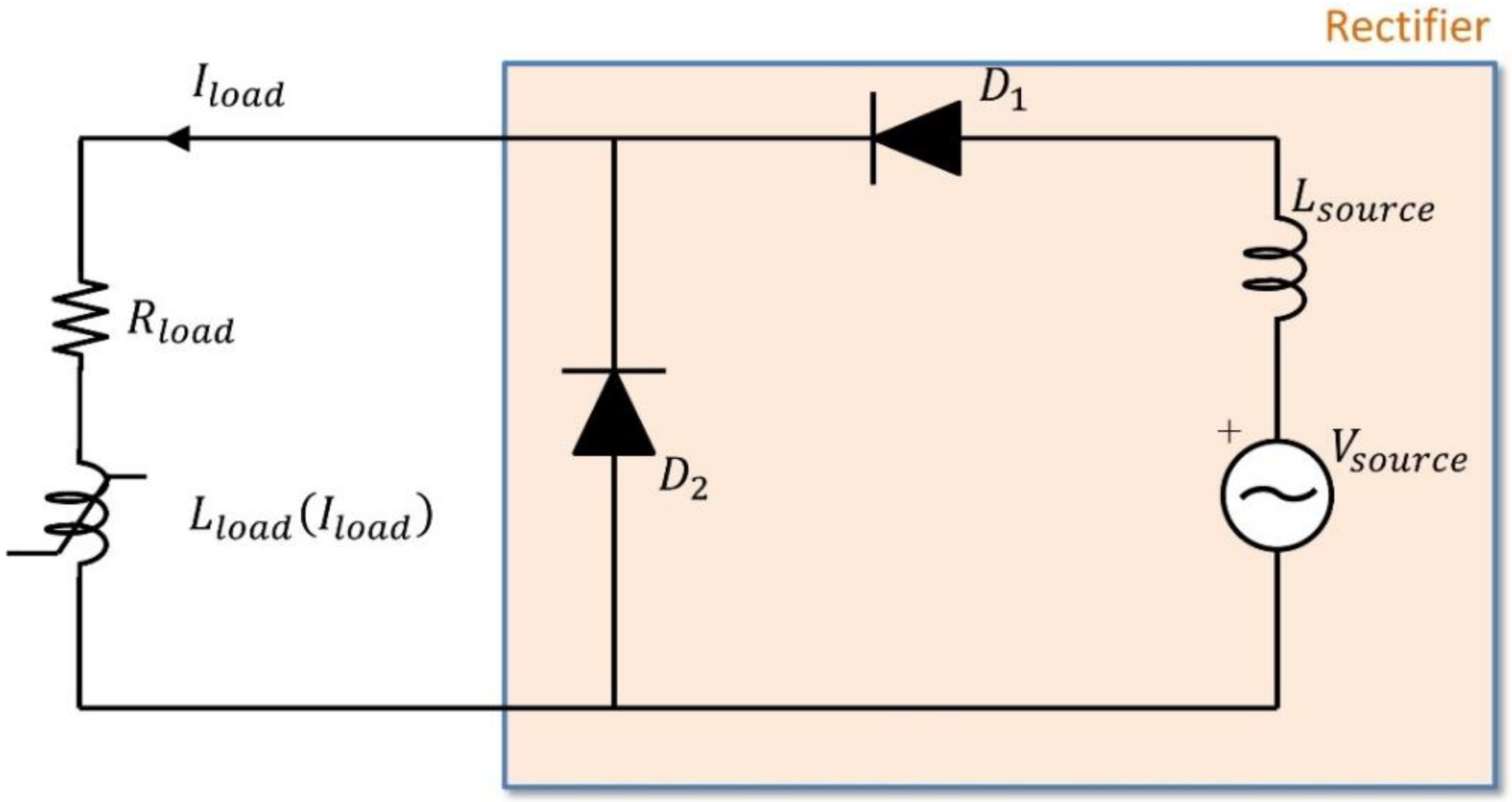

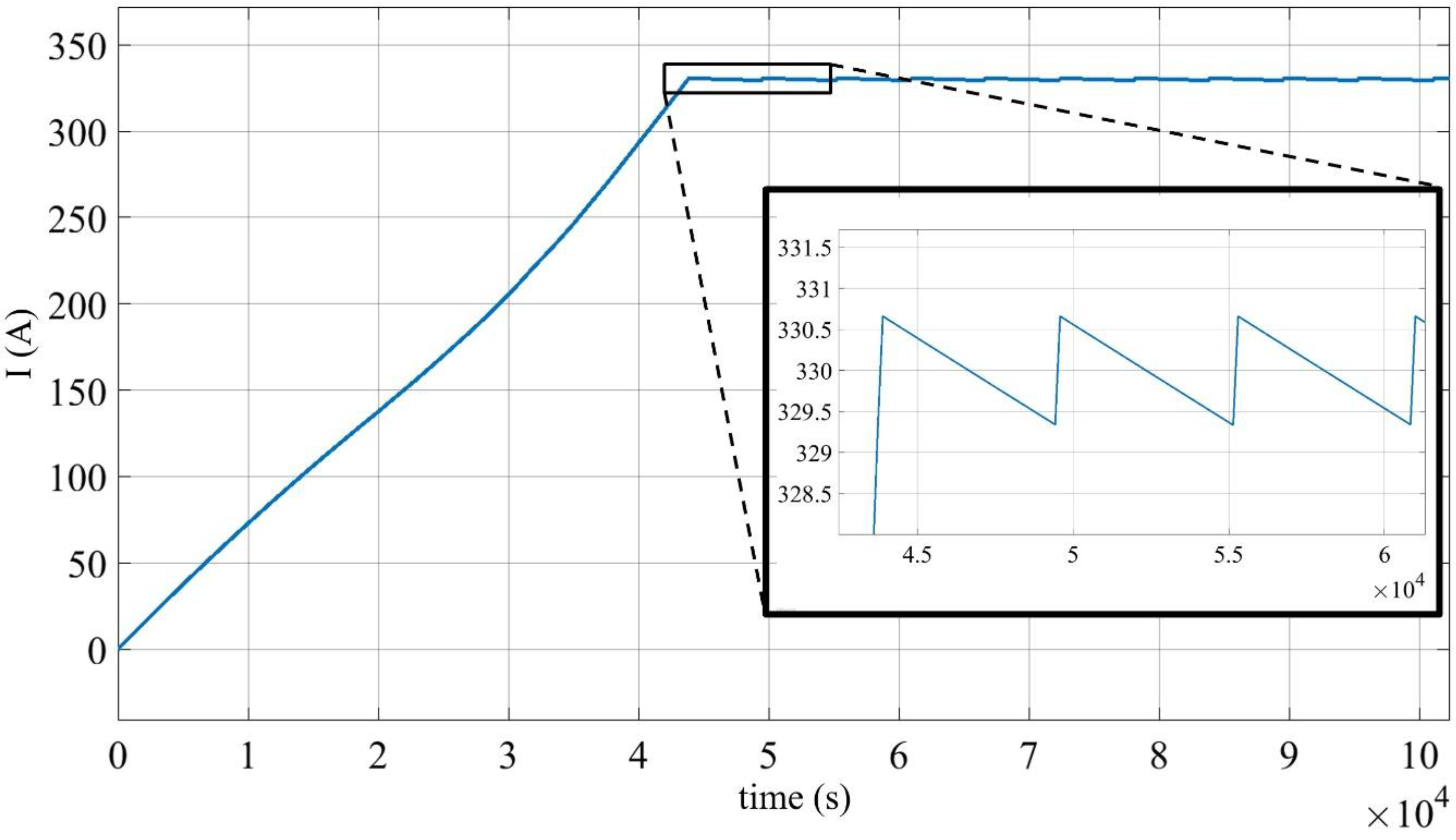
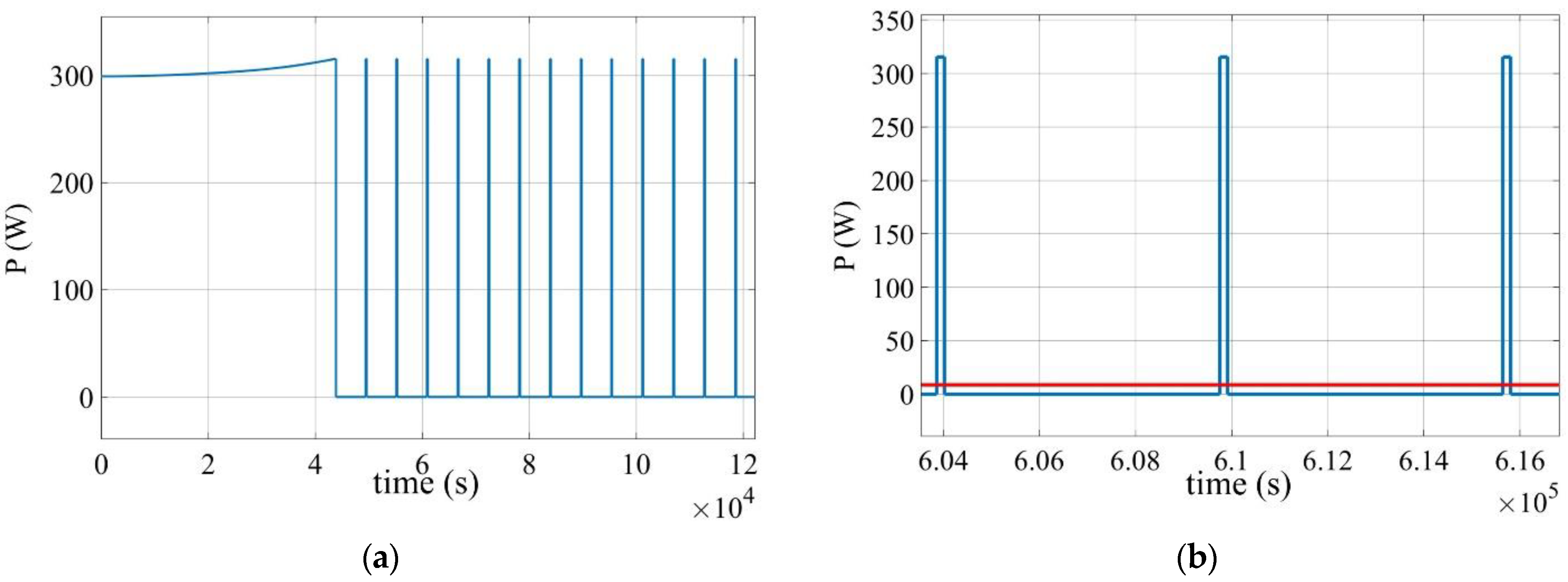
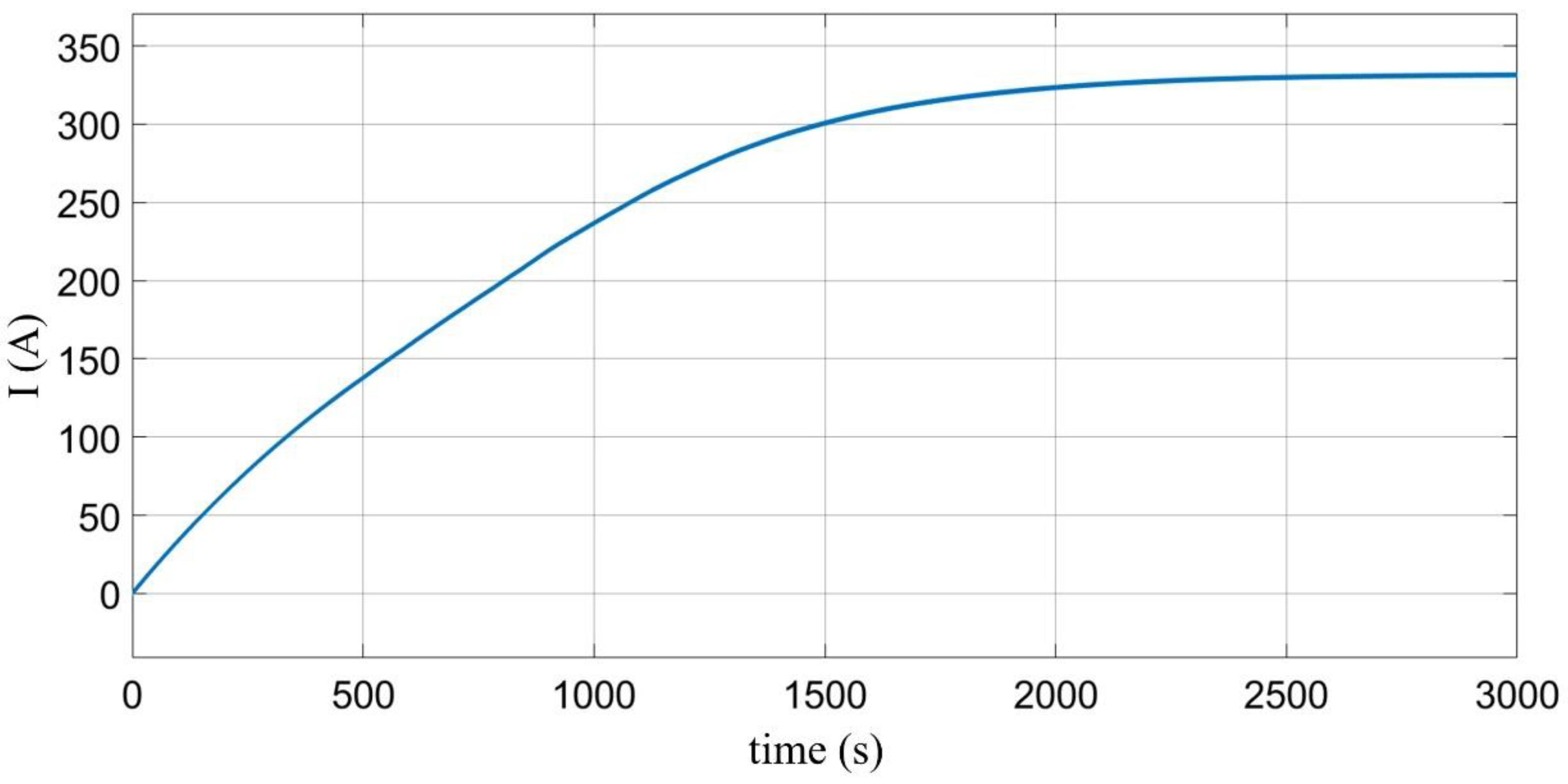
| In—Rated Current | 330 A |
| Ic—Rated current | 1.65 In |
| Number of poles | 40 |
| ωm—Rated speed | 15 rpm |
| Rload—Estimated total resistance of joints | 4.128 µΩ |
| Lload(In)—Inductance at rated current | 10 H |
| Total cooling power requested | 35 kW |
| —Cooling power requested due to current leads heat load | 726 W |
| Number of Permanent Magnets (PM) | 20 |
| Number of HTS tapes | 3 |
| Width of each PM | 6 mm |
| Height of each PM | 12 mm |
| Depth of each PM | 350 mm |
| Remanence of each PM | 1.25 T |
| Width of each HTS tape | 12 mm |
| Thickness of each HTS layer | 1 µm |
| Operating temperature of the HTS tapes | 77 K |
| External radius of the rotor (radial position of tapes) | 300 mm |
| Airgap between the PM and the HTS tape | 5 mm |
| ωr—Relative angular velocity of PMs and tapes | 1500 rpm (0.25 Hz) |
| ωPM—Angular velocity of the PMs in the stationary frame of the rotor | 1485 rpm (24.75 Hz) |
| V0 | 99.4 mV |
| Rinstrinsic | 33.0 µΩ |
| Reffective | 150.9 µΩ |
| Diodes—“on” State Resistance | 1 mΩ |
| Diodes—forward voltage | 0.8 V |
| Diodes—snubber resistance | 500 Ω |
| Diodes—snubber capacitance | 250 nF |
| Vsource—rms value | 12 V |
| Vsource—frequency | 13 Hz |
| Lsource | 1 mH |
| Type of Power Supply | Cooling Power Requested Due to Power Supply (W) | Current Leads | Slip Rings |
|---|---|---|---|
| State of the art | 726 | Yes | Yes |
| “Warm rectifier” flux pump | 1081.5 | Yes | No |
| “Cold rectifier” flux pump | 7821 | No | No |
| Dynamo flux pump | 191 | No | No |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Russo, G.; Morandi, A. A Numerical Study on the Energization of the Field Coils of a Full-Size Wind Turbine with Different Types of Flux Pumps. Energies 2022, 15, 5392. https://doi.org/10.3390/en15155392
Russo G, Morandi A. A Numerical Study on the Energization of the Field Coils of a Full-Size Wind Turbine with Different Types of Flux Pumps. Energies. 2022; 15(15):5392. https://doi.org/10.3390/en15155392
Chicago/Turabian StyleRusso, Giacomo, and Antonio Morandi. 2022. "A Numerical Study on the Energization of the Field Coils of a Full-Size Wind Turbine with Different Types of Flux Pumps" Energies 15, no. 15: 5392. https://doi.org/10.3390/en15155392
APA StyleRusso, G., & Morandi, A. (2022). A Numerical Study on the Energization of the Field Coils of a Full-Size Wind Turbine with Different Types of Flux Pumps. Energies, 15(15), 5392. https://doi.org/10.3390/en15155392







