PV/Battery Grid Integration Using a Modular Multilevel Isolated SEPIC-Based Converter
Abstract
:1. Introduction
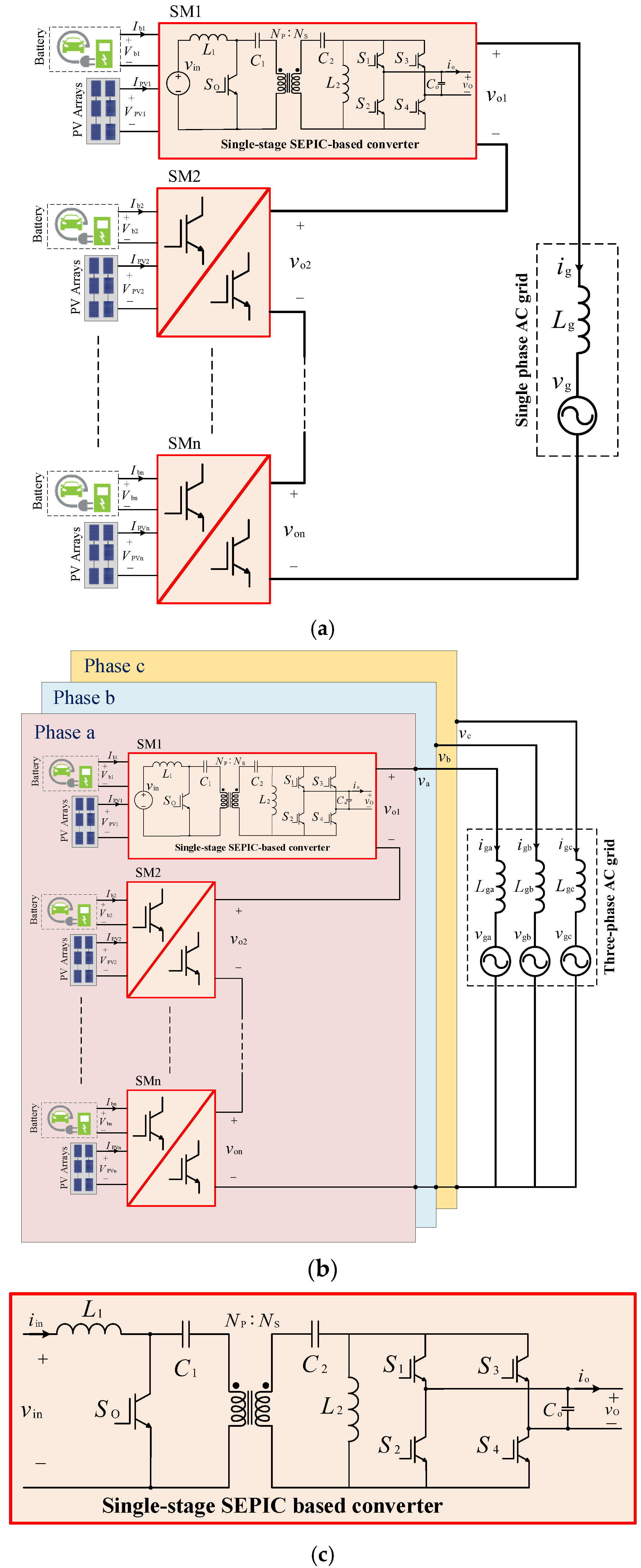
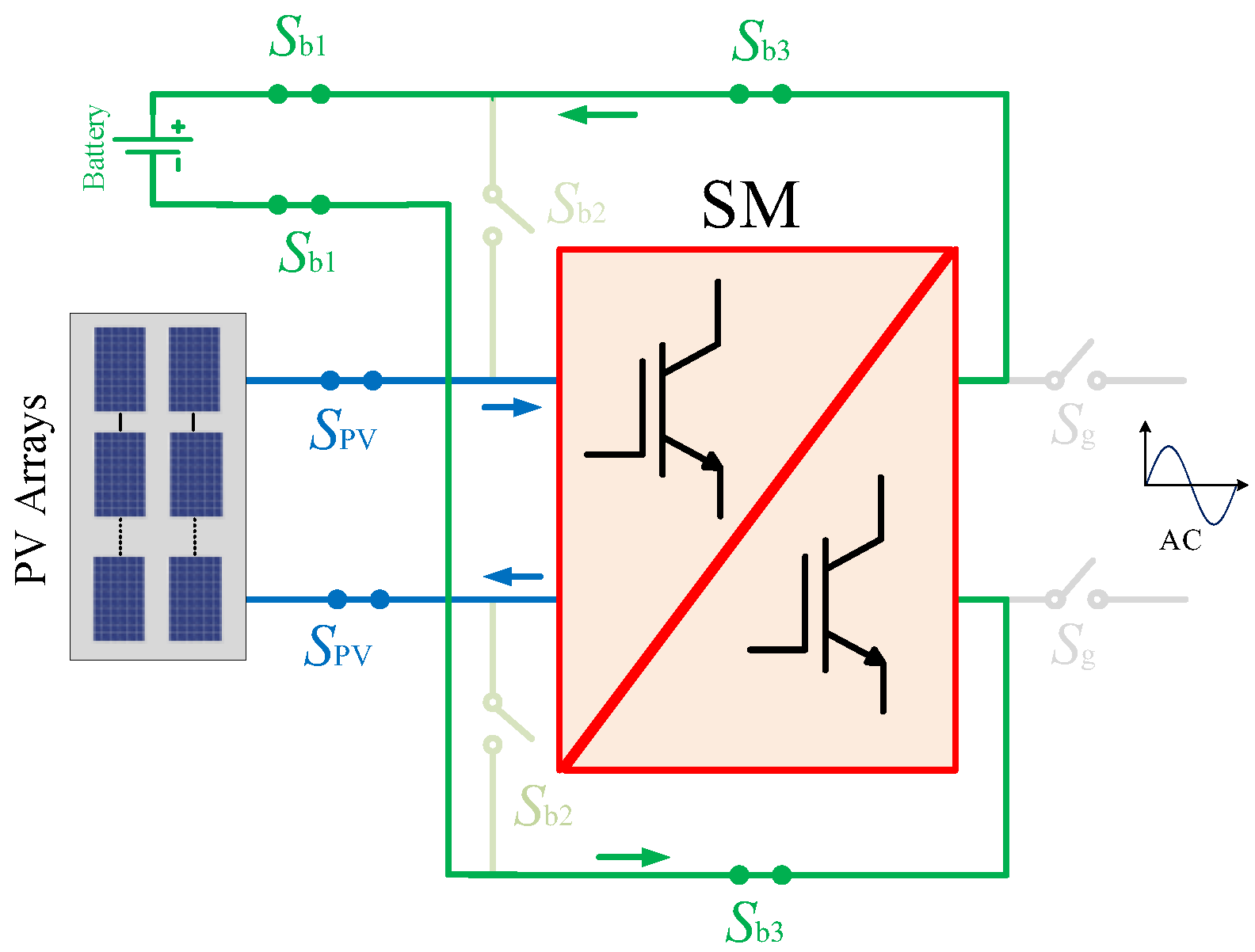
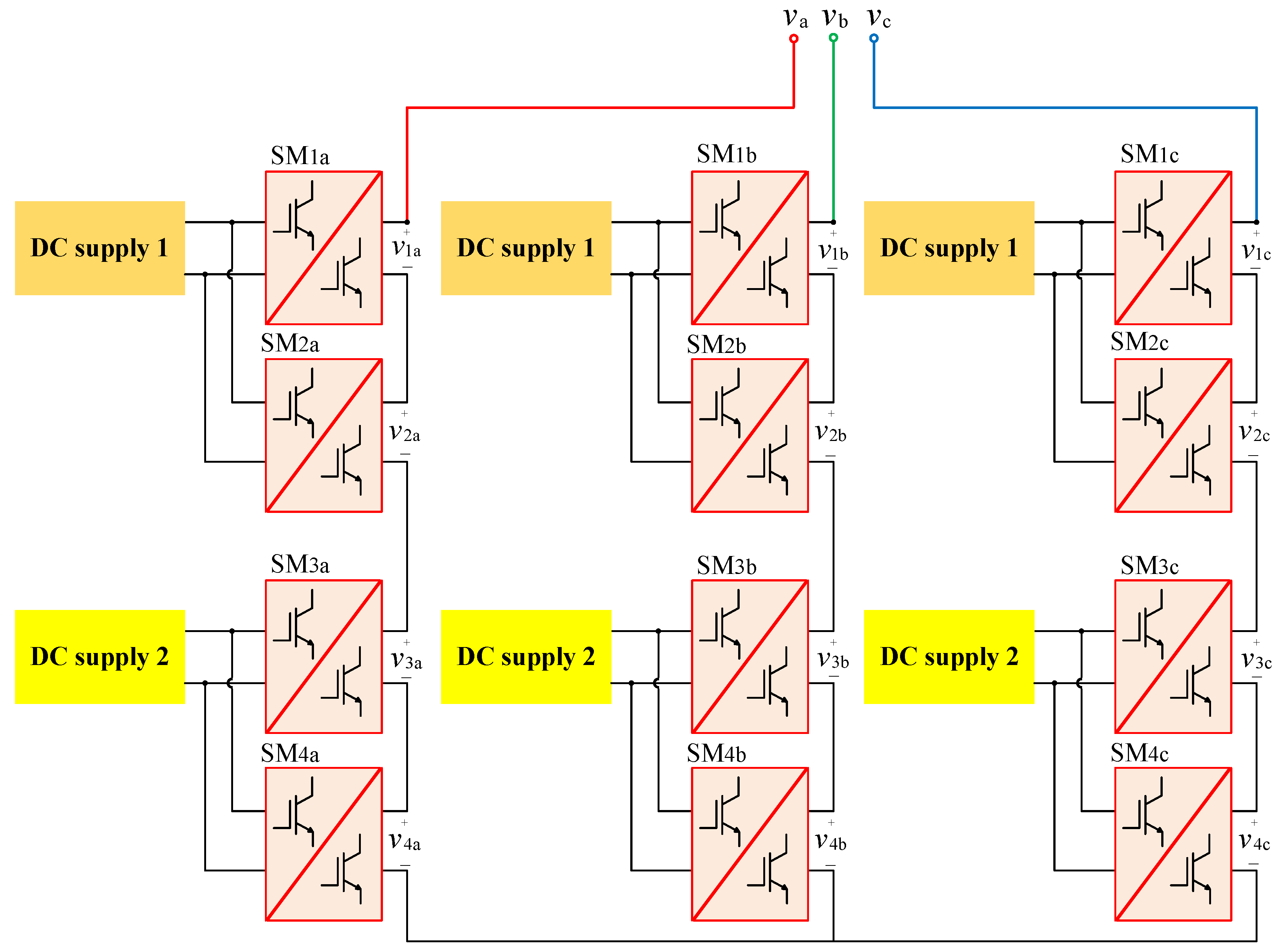
2. The Proposed MMC Topology
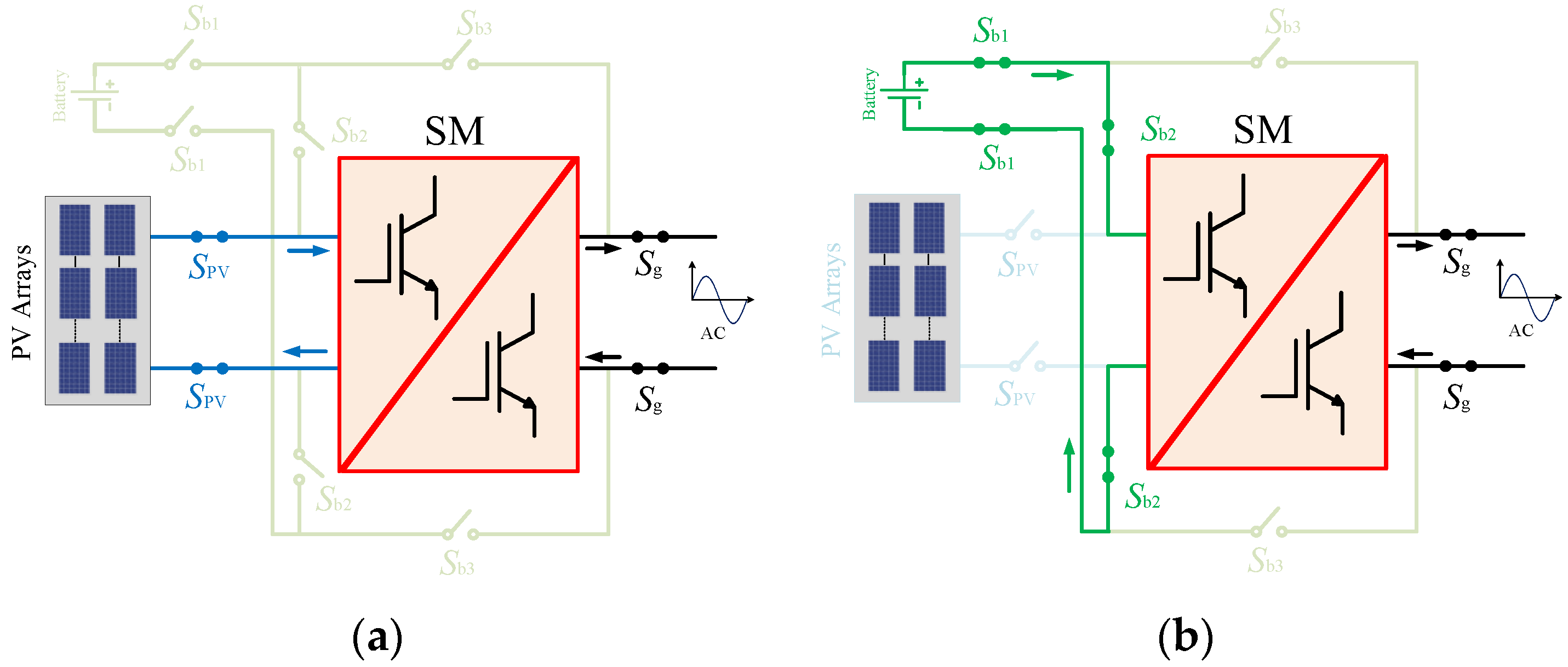
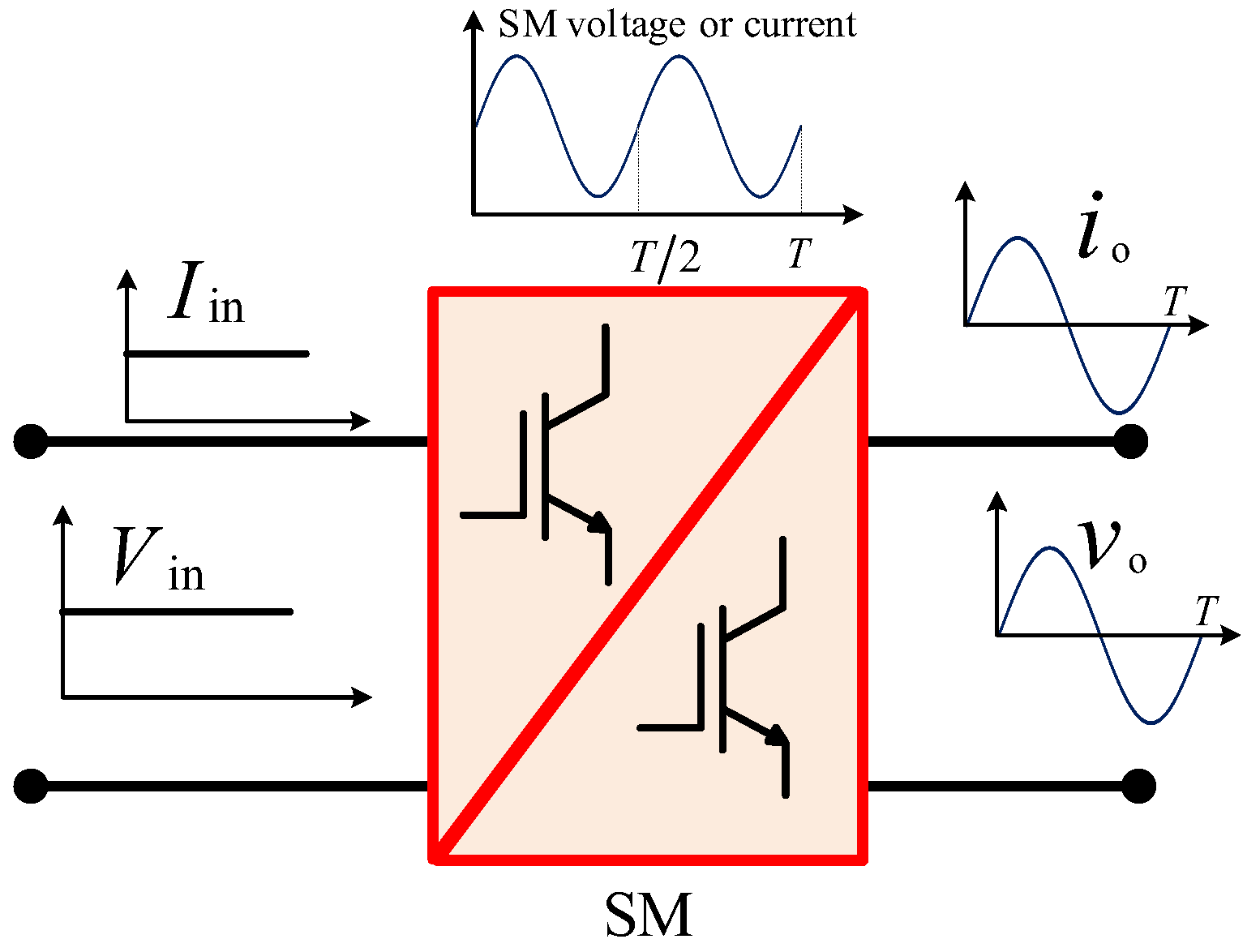
3. System-Level Operation
4. Modes of Operation
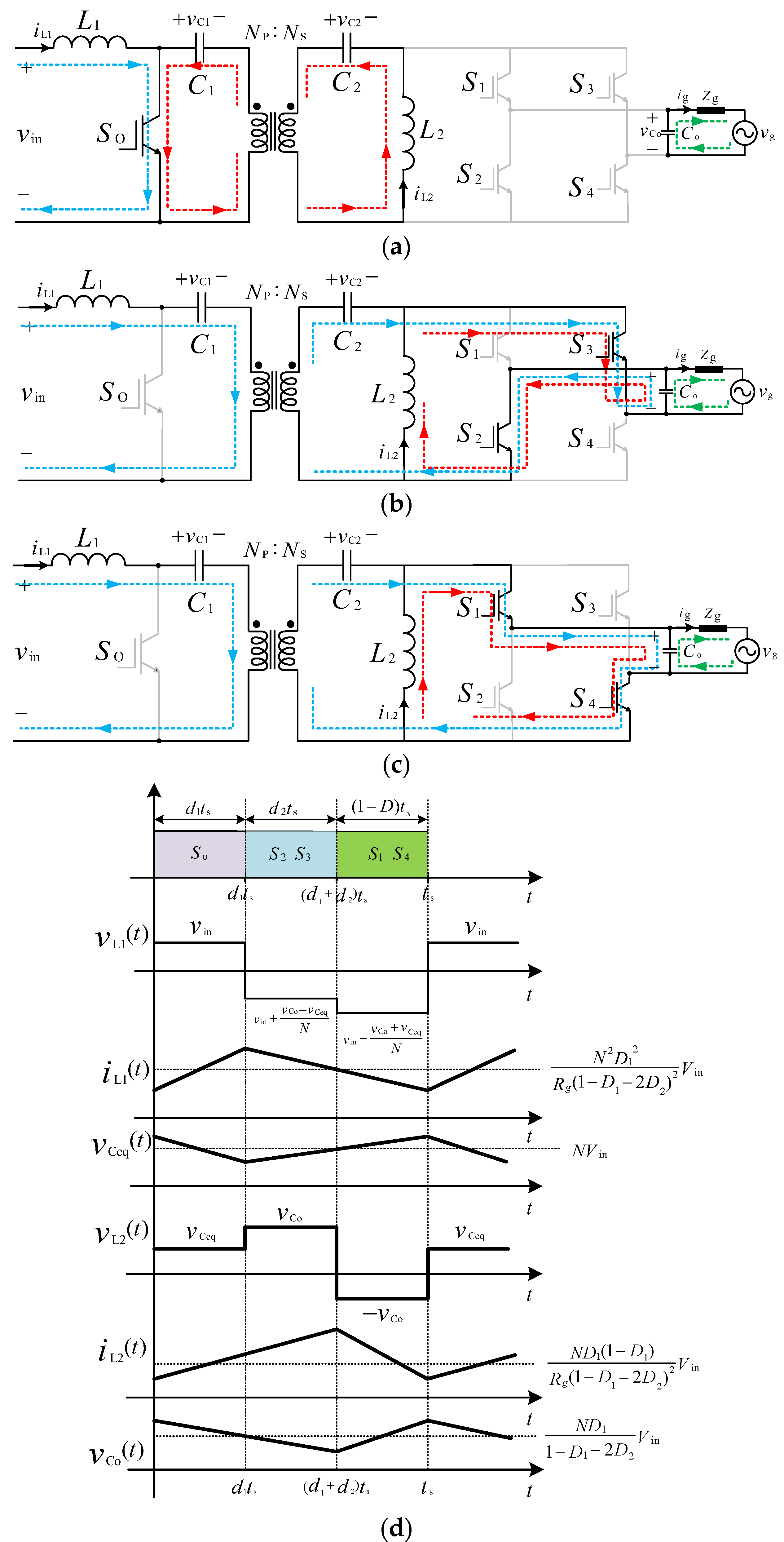
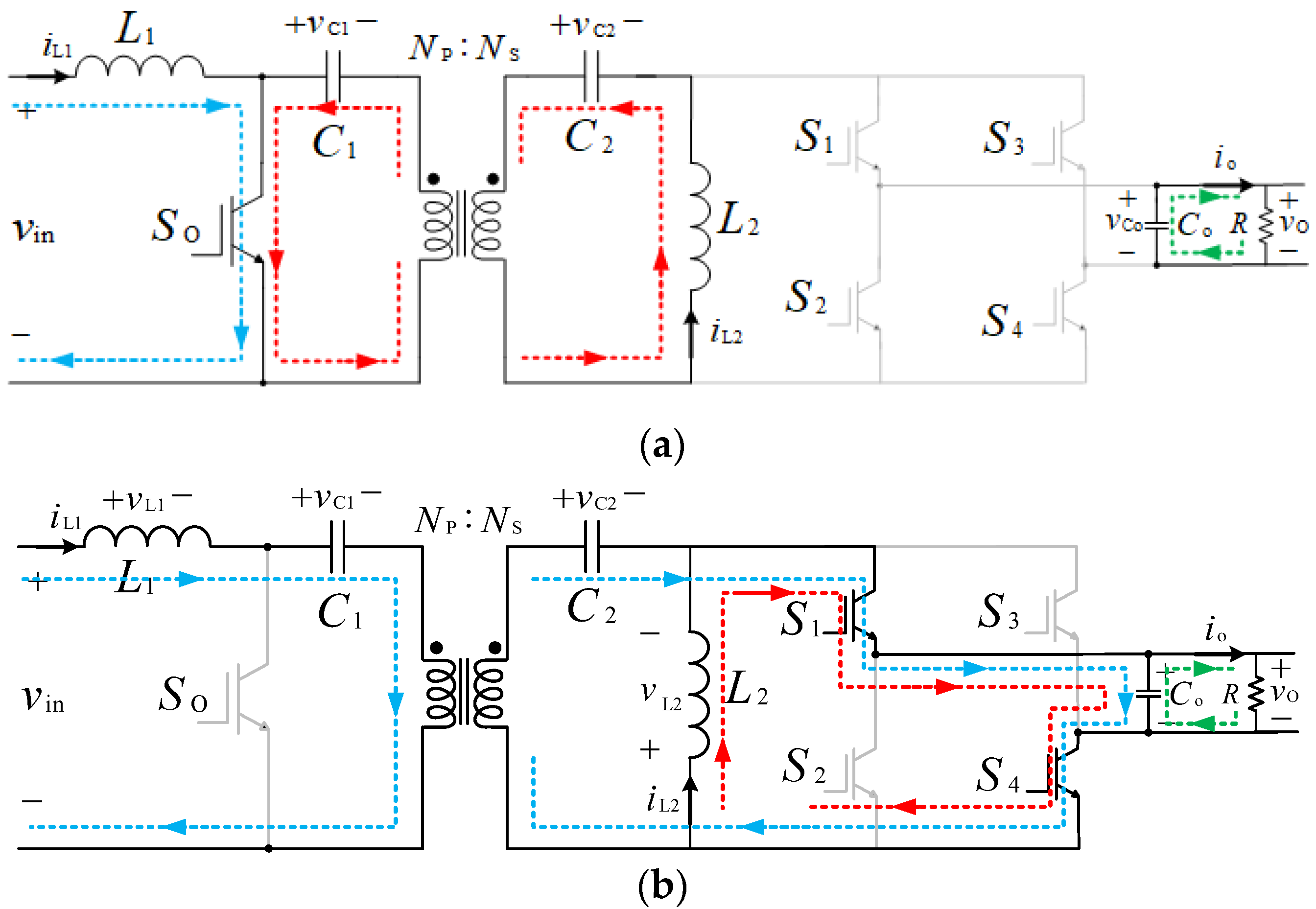
4.1. DC/AC Operation (from PV Modules/Batteries to the AC Grid)
- ▪
- Subinterval 1(0 ≤ t < ton1): During the first subinterval (see Figure 5a), the switch So is turned ON, so the inductor L1 is being charged by the input DC voltage (from either PV modules or the battery packs), and its current iL1 is linearly increasing. The capacitors C1 and C2 discharge into the inductor L2, increasing its current iL2 in a straight line. The output capacitor Co, on the other hand, discharges into the AC grid. This mode will last for ton1 = d1.ts, with d1 and ts being the duty-cycle ratio and the switching time of the SM.
- ▪
- Subinterval 2(ton1 ≤ t < ton1+ ton2): During this subinterval (ton2 = d2·ts), the switch SO is turned OFF. As a result, the inductor L1 discharge into the capacitors C1 and C2, while the inductor L2 is still being charged by turning S2 and S3 ON from the output capacitor Co. Therefore, this subinterval provides the required decoupling between the input and output sides, as shown in Figure 5b.
- ▪
- Subinterval 3(ton1+ ton2 ≤ t < ts): During this subinterval ((1 − d1 − d2)ts), the switch SO is kept in the OFF state, so the inductor L1 is still discharging into the capacitors C1, C2, and Co, increasing their voltages. For the positive half-cycle (vg > 0), the switches S1 and S4 are turned ON. Therefore, the inductor L2 discharges into the output capacitor Co (see Figure 5c).
4.2. DC/DC Operation (Batteries Being Charged by the PV Modules)
- ▪
- Subinterval1 (0 ≤ t < ton): During the first subinterval (see Figure 7a), the switch So is turned ON, resulting in the inductor L1 being charged by the input DC voltage (from the PV module). Concurrently, the capacitors C1 and C2 are discharging into the inductor L2. Therefore, iL1 and iL2 are linearly increasing. The output capacitor Co, on the other hand, discharges into the battery pack. The duration of this period is ton = d·ts, with and ts being the duty-cycle ratio and the switching time of the SM.
- ▪
- Subinterval2 (ton ≤ t < ts): During this subinterval ((1 − d)ts), switch So is turned OFF. Therefore, the inductor L1 discharge into the capacitors C1 and C2, leading them to be charged. Switches S1 and S4 are turned ON to mimic the operation of the typical SEPIC converter and provide a path for the current passing the inductor L2 to flow through the output capacitor Co, increasing its voltage (see Figure 7b).
5. State-Space Modelling of the Proposed SEPIC-Based SM
5.1. DC/AC Operation (from PV Modules/Batteries to the AC Grid)
5.2. The Calculated Duty-Cycle Ratios for Second-Order Harmonic Elimination
5.3. DC/DC Operation (PV Modules to Batteries)
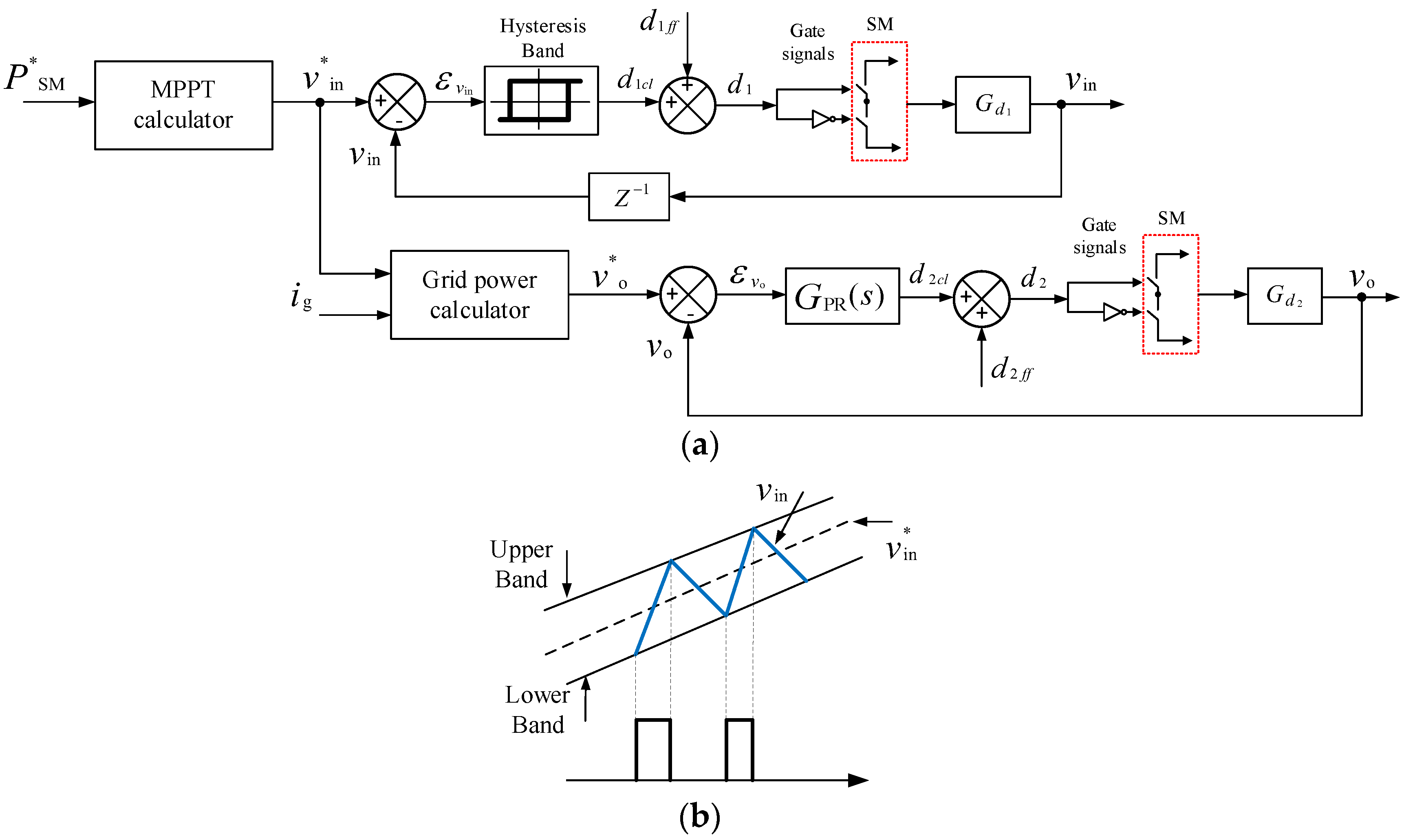
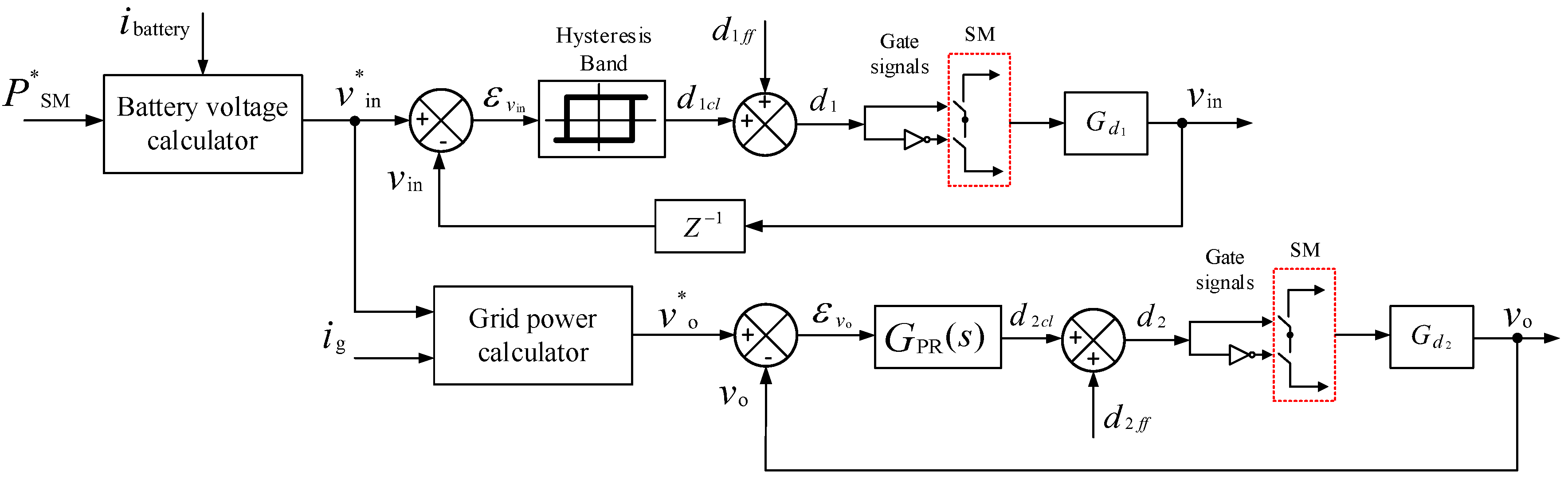
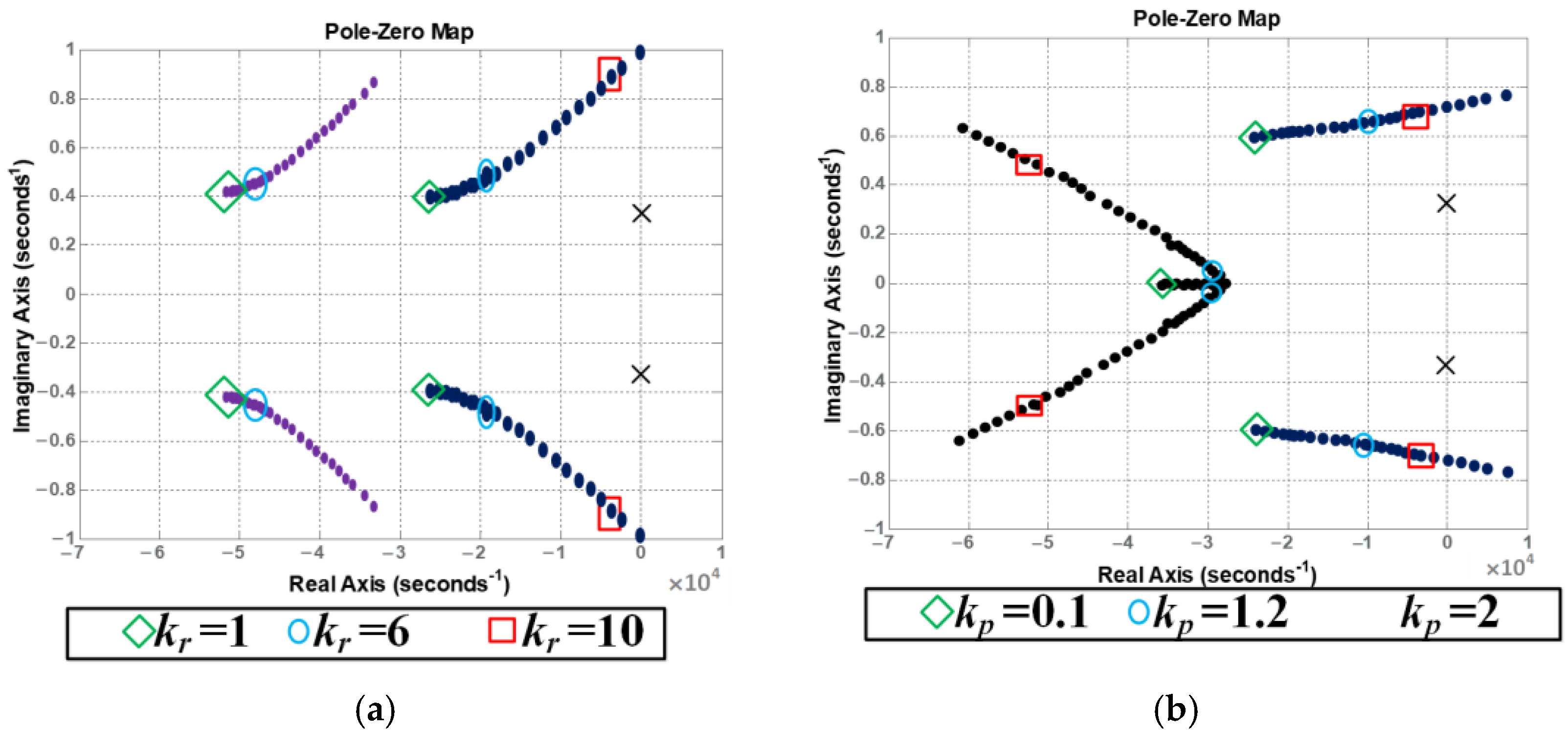
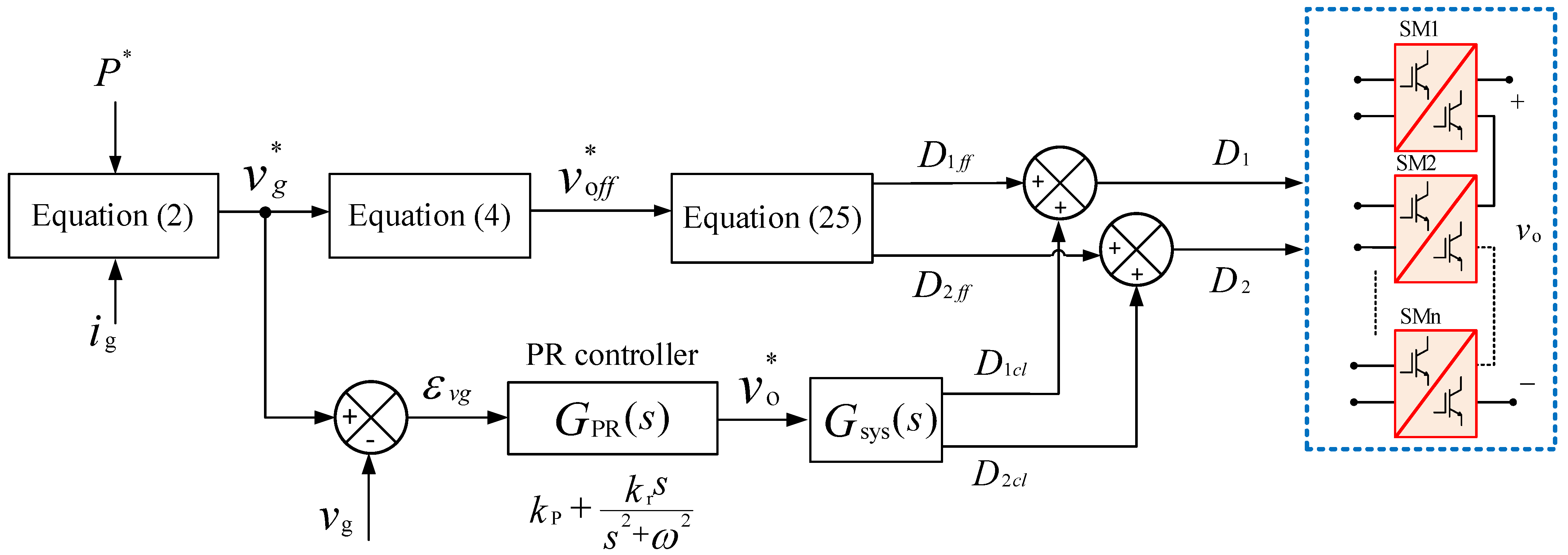
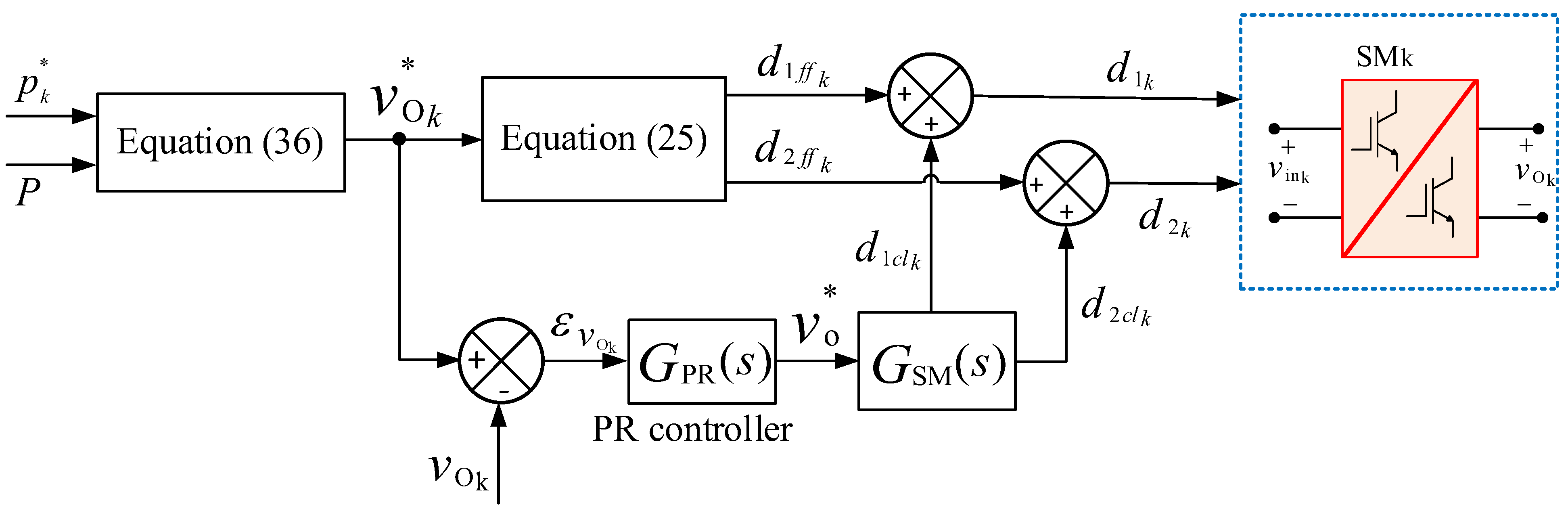
6. Controller Design
6.1. DC/AC Operation (from PV Modules/Batteries to the AC Grid)
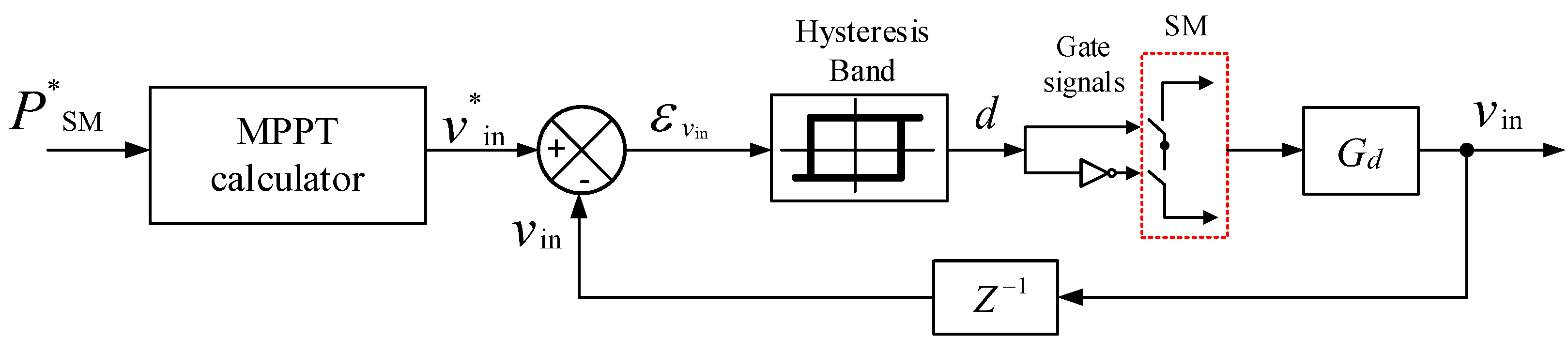
6.2. DC/DC Operation (from PV Modules to Battery Packs)
7. Verification
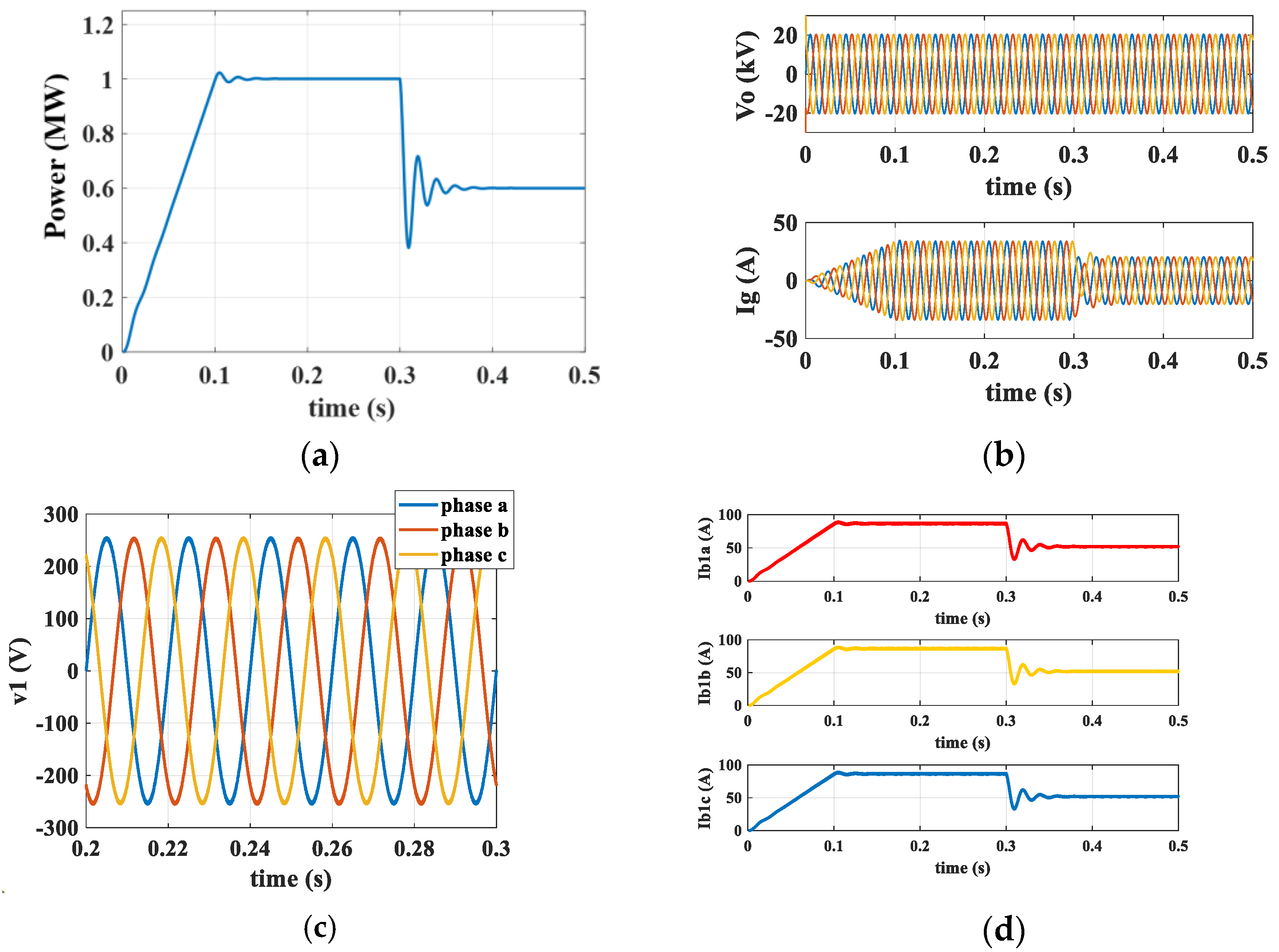
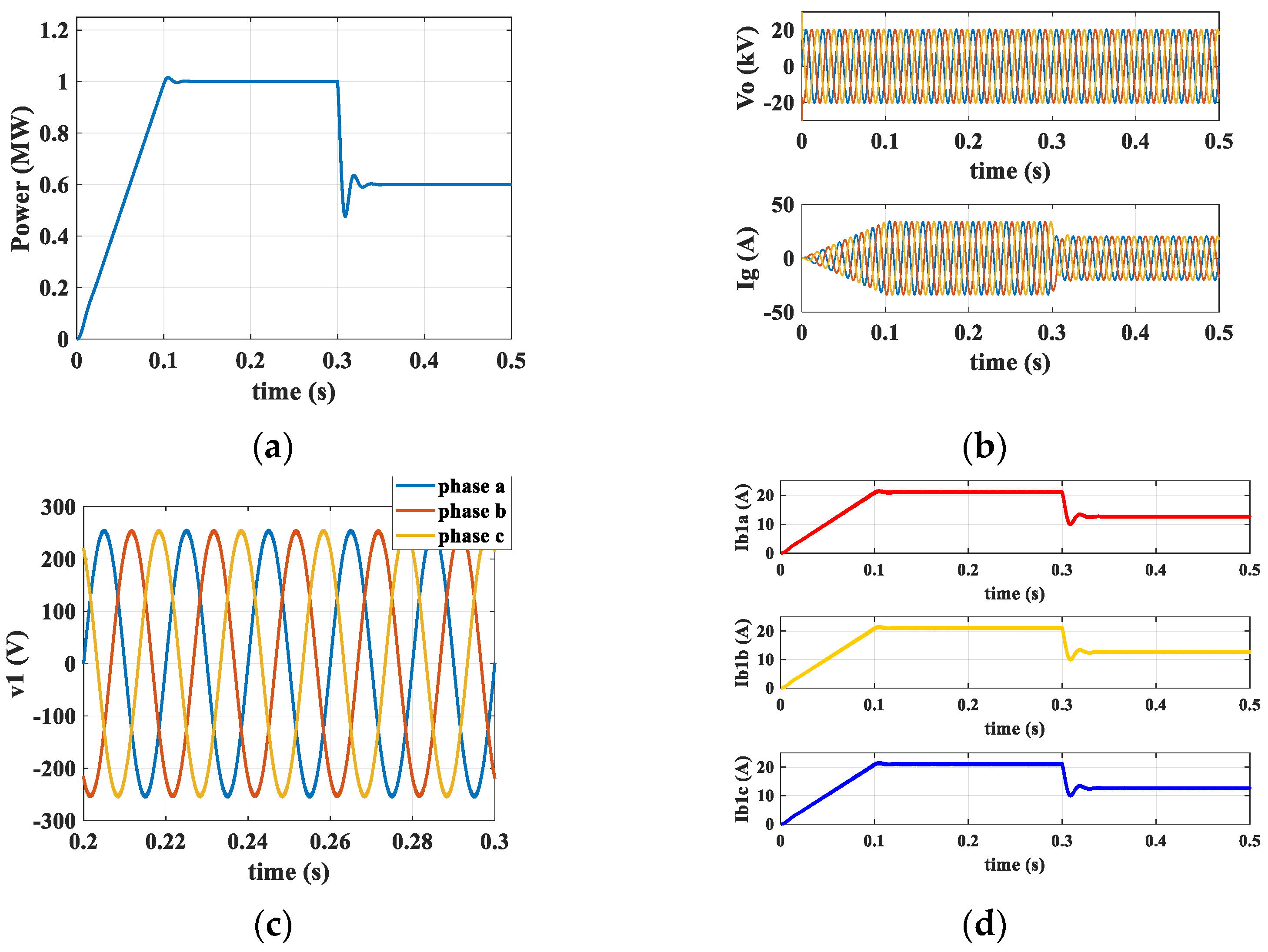
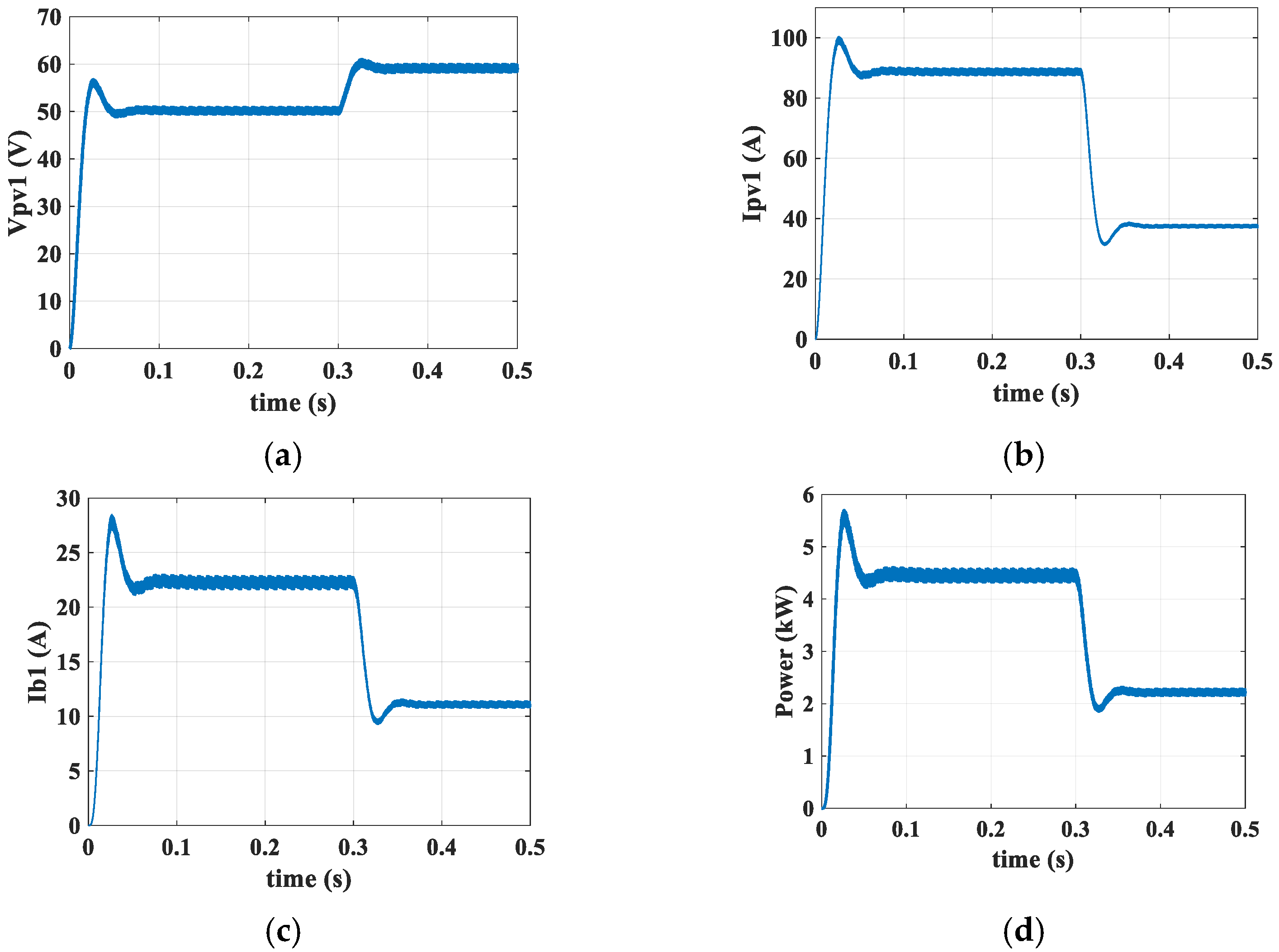
7.1. Simulation Study
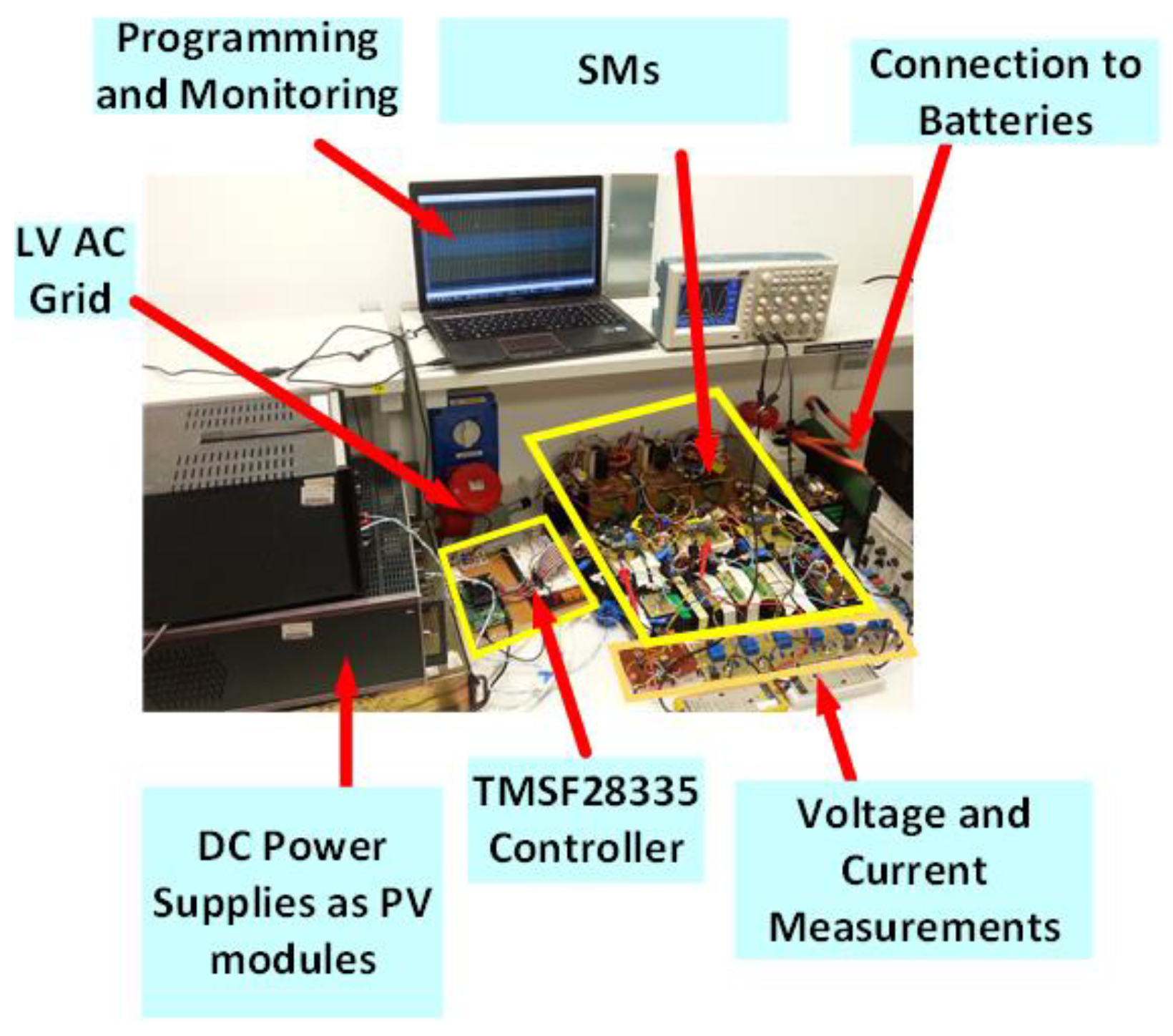
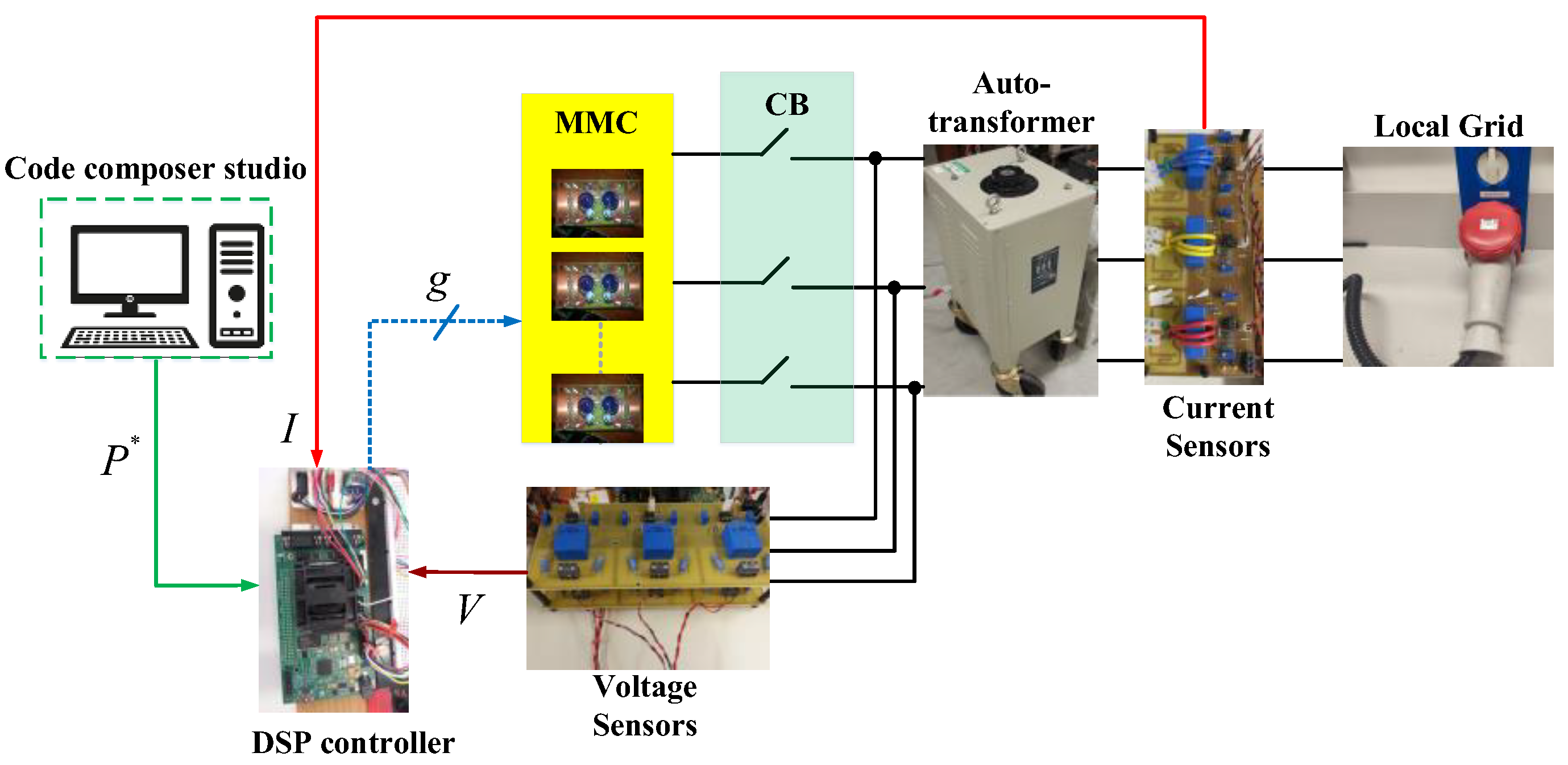
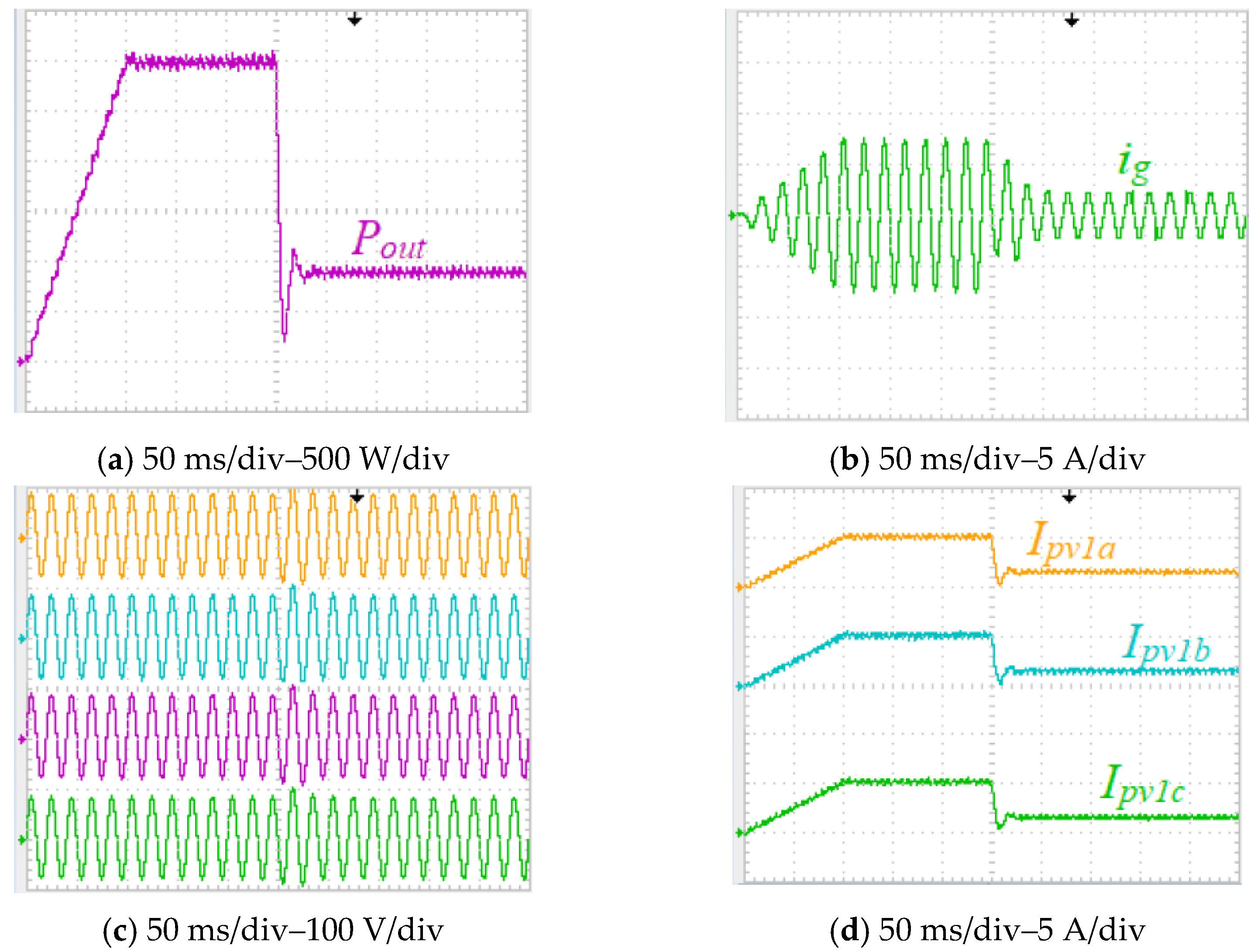
7.2. Experimental Study
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hu, P.; Schmitt, R.R.; Schwarzer, J.; Moore, W.H. Transportation Statistics Annual Report 2021. Available online: https://rosap.ntl.bts.gov/view/dot/59268 (accessed on 21 June 2022).
- Khaligh, A.; D'Antonio, M. Global trends in high-power on-board chargers for electric vehicles. IEEE Trans. Veh. Technol. 2019, 68, 3306–3324. [Google Scholar] [CrossRef]
- Ram, S.K.; Devassy, S.; Verma, B.K.; Mishra, S.; Akbar, S.A. Review on Renewable Energy Based EV Charging System with Grid Support Functionality. In Proceedings of the 2021 7th International Conference on Advanced Computing and Communication Systems (ICACCS), Coimbatore, India, 19–20 March 2021. [Google Scholar]
- Naeem, M.W.; Ahmad, J.; Adnan, M.; Ijaz, K.; Hussain, Z.; Butt, F.A. Control of Grid-tied PV Powered Charging Station for Electric Vehicles. In Proceedings of the 2021 International Conference on Innovative Computing (ICIC), Lahore, Pakistan, 9–10 November 2021. [Google Scholar]
- Adnan, M.; Ahmad, J.; Ali, S.F.; Imran, M. A techno-economic analysis for power generation through wind energy: A case study of Pakistan. Energy Rep. 2021, 7, 1424–1443. [Google Scholar] [CrossRef]
- Shemami, M.S.; Alam, M.S.; Asghar, M.J.; Shariff, S.M. Adaptive Neuro-Fuzzy Inference System (ANFIS) for Optimization of Solar Based Electric Vehicle-to-Home (V2H) Fuzzy Inference System (FIS) Controller. In Proceedings of the 2019 IEEE Transportation Electrification Conference and Expo (ITEC), Detroit, MI, USA, 19–21 June 2019. [Google Scholar]
- Tabari, M.; Yazdani, A. Stability of a dc distribution system for power system integration of plug-in hybrid electric vehicles. IEEE Trans. Smart Grid 2014, 5, 2564–2573. [Google Scholar] [CrossRef]
- Parikh, P.; Patil, S. Active and reactive power control of PV-PHEV fed 3-level Neutral Point Clamped Inverter. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12–14 August 2015. [Google Scholar]
- Rahimi, R.; Habibi, S.; Shamsi, P.; Ferdowsi, M. An Interleaved High Step-Up DC-DC Converter Based on Combination of Coupled Inductor and Built-in Transformer for Photovoltaic-Grid Electric Vehicle DC Fast Charging Systems. In Proceedings of the 2021 IEEE Texas Power and Energy Conference (TPEC), College Station, TX, USA, 2–5 February 2021. [Google Scholar]
- Lei, H.; Hao, R.; You, X.; Li, F. Nonisolated high step-up soft-switching DC–DC converter with interleaving and Dickson switched-capacitor techniques. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 8, 2007–2021. [Google Scholar] [CrossRef]
- Alzahrani, A.; Ferdowsi, M.; Shamsi, P. High-voltage-gain DC–DC step-up converter with bifold Dickson voltage multiplier cells. IEEE Trans. Power Electron. 2019, 34, 9732–9742. [Google Scholar] [CrossRef]
- Zheng, Y.; Xie, W.; Smedley, K.M. Interleaved high step-up converter with coupled inductors. IEEE Trans. Power Electron. 2018, 34, 6478–6488. [Google Scholar] [CrossRef]
- Zheng, Y.; Smedley, K.M. Interleaved high step-up converter integrating coupled inductor and switched capacitor for distributed generation systems. IEEE Trans. Power Electron. 2018, 34, 7617–7628. [Google Scholar] [CrossRef]
- Forouzesh, M.; Shen, Y.; Yari, K.; Siwakoti, Y.P.; Blaabjerg, F. High-efficiency high step-up DC–DC converter with dual coupled inductors for grid-connected photovoltaic systems. IEEE Trans. Power Electron. 2017, 33, 5967–5982. [Google Scholar] [CrossRef]
- Nouri, T.; Kurdkandi, N.V.; Shaneh, M. A novel ZVS high-step-up converter with built-in transformer voltage multiplier cell. IEEE Trans. Power Electron. 2020, 35, 12871–12886. [Google Scholar] [CrossRef]
- Chang, Y.-N.; Cheng, H.-L.; Yen, H.-C.; Chang, C.-H.; Huang, W.-D. An interleaved DC/DC converter with soft-switching characteristic and high step-up ratio. Appl. Sci. 2020, 10, 2167. [Google Scholar] [CrossRef] [Green Version]
- Santos de Carvalho, M.R.; Bradaschia, F.; Rodrigues Limongi, L.; de Souza Azevedo, G.M. Modeling and control design of the symmetrical interleaved coupled-inductor-based boost DC-DC converter with clamp circuits. Energies 2019, 12, 3432. [Google Scholar] [CrossRef] [Green Version]
- Singh, S.A.; Williamson, S.S. Comprehensive review of PV/EV/grid integration power electronic converter topologies for DC charging applications. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2018. [Google Scholar]
- Singh, S.A.; Carli, G.; Azeez, N.A.; Williamson, S.S. A modified Z-source converter based single phase PV/grid inter-connected DC charging converter for future transportation electrification. In Proceedings of the 2016 IEEE Energy Conversion Congress and Exposition (ECCE), Milwaukee, WI, USA, 18–22 September 2016. [Google Scholar]
- Niroomand, M.; Nasr Esfahani, F. Converter Technologies for PV Systems: A Comprehensive Review. In Energy Conversion Systems, Energy Science, Engineering and Technology; Tripathi, S.M., Padmanaban, S., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2021; pp. 1–58. [Google Scholar]
- Alotaibi, S.; Darwish, A. Modular Multilevel Converters for Large-Scale Grid-Connected Photovoltaic Systems: A Review. Energies 2021, 14, 6213. [Google Scholar] [CrossRef]
- Gontijo, G.; Wang, S.; Kerekes, T.; Teodorescu, R. Performance Analysis of Modular Multilevel Converter and Modular Multilevel Series Converter under Variable-Frequency Operation Regarding Submodule-Capacitor Voltage Ripple. Energies 2021, 14, 776. [Google Scholar] [CrossRef]
- Darwish, A.; Abdelsalam, A.K.; Massoud, A.M.; Ahmed, S. Single phase grid connected current source inverter: Mitigation of oscillating power effect on the grid current. In Proceedings of the IET Conference on Renewable Power Generation (RPG 2011), Edinburgh, Scotland, 6–8 September 2011. [Google Scholar]
- Leon, J.I.; Vazquez, S.; Franquelo, L.G. Multilevel converters: Control and modulation techniques for their operation and industrial applications. Proc. IEEE 2017, 105, 2066–2081. [Google Scholar] [CrossRef]
- Yildirim, M.A.; Nowak-Ocłoń, M. Modified Maximum Power Point Tracking Algorithm under Time-Varying Solar Irradiation. Energies 2020, 13, 6722. [Google Scholar] [CrossRef]
- Tobón, A.; Peláez-Restrepo, J.; Villegas-Ceballos, J.P.; Serna-Garcés, S.I.; Herrera, J.; Ibeas, A. Maximum Power Point Tracking of Photovoltaic Panels by Using Improved Pattern Search Methods. Energies 2017, 10, 1316. [Google Scholar] [CrossRef] [Green Version]
- Darwish, A.; Elgenedy, M.A. Current-source modular medium-voltage grid-connected system with high-frequency isolation for photovoltaic applications. IEEE Trans. Energy Convers. 2018, 34, 255–266. [Google Scholar] [CrossRef] [Green Version]
- Badawy, A.D. Current Source dc-dc and dc-ac Converters with Continuous Energy Flow. Ph.D. Thesis, University of Strathclyde, Glasgow, UK, 2015. [Google Scholar]
- Polsky, T.; Horen, Y.; Bronshtein, S.; Baimel, D. Transient and Steady-State Analysis of a SEPIC Converter by an Average State-Space Modelling. In Proceedings of the 2018 IEEE 18th International Power Electronics and Motion Control Conference (PEMC), Budapest, Hungary, 26–30 August 2018. [Google Scholar]
- Niroomand, M.; Nasr Esfahani, F. Control Structures of Grid-Tied Photovoltaic Systems. In Energy Conversion Systems, Energy Science, Engineering and Technology; Tripathi, S.M., Padmanaban, S., Eds.; Nova Science Publishers: Hauppauge, NY, USA, 2021; pp. 59–133. [Google Scholar]





| Parameters | Value |
|---|---|
| Number of modules | n = 80 |
| SM rated power | PSM = 4.2 kW |
| SM inductors | L1 = 0.5 mH L2 = 10 mH |
| SM capacitors | C1 = C2 = 10 μF and Co = 1 μF |
| SM Switching frequency | fs = 50 kHz |
| Transformer turns’ ratio | N = 1 |
| PV module | Grape Solar GS-S-420-KR3 (Pm = 420 W, Vmp = 48.73 V, Imp = 8.62) |
| PV array | 10 parallel × 1 series |
| Battery pack voltage | Vbat = 200 V |
| Grid line-to-line voltage | VO(rms) = 24.5 kV |
| Grid impedance | Lg = 1 mH, rg = 0.5 Ω |
| Grid frequency | f = 50 Hz |
| Parameters | Value |
|---|---|
| Number of modules | n = 4 |
| SM rated power | PSM = 750 W |
| SM inductors | L1 = 1 mH L2 = 10 mH |
| SM capacitors | C1 = C2 = 10 μF and Co = 1 μF |
| SM switching frequency | fs = 20 kHz |
| Transformer turns’ ratio | N = 1 |
| DC supplies | Keysight N8761A Sorensen SGI 100/150 |
| Battery pack voltage | Vbat = 200 V |
| Grid phase voltage | 230 VAC |
| Grid impedance | Lg = 1 mH, rg = 0.5 Ω |
| Grid frequency | f = 50 Hz |
| Battery pack voltage | Vbat = 200 V |
| Grid phase voltage | 230 VAC |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nasr Esfahani, F.; Darwish, A.; Massoud, A. PV/Battery Grid Integration Using a Modular Multilevel Isolated SEPIC-Based Converter. Energies 2022, 15, 5462. https://doi.org/10.3390/en15155462
Nasr Esfahani F, Darwish A, Massoud A. PV/Battery Grid Integration Using a Modular Multilevel Isolated SEPIC-Based Converter. Energies. 2022; 15(15):5462. https://doi.org/10.3390/en15155462
Chicago/Turabian StyleNasr Esfahani, Fatemeh, Ahmed Darwish, and Ahmed Massoud. 2022. "PV/Battery Grid Integration Using a Modular Multilevel Isolated SEPIC-Based Converter" Energies 15, no. 15: 5462. https://doi.org/10.3390/en15155462
APA StyleNasr Esfahani, F., Darwish, A., & Massoud, A. (2022). PV/Battery Grid Integration Using a Modular Multilevel Isolated SEPIC-Based Converter. Energies, 15(15), 5462. https://doi.org/10.3390/en15155462








