A Flexible DC–DC Converter with Multi-Directional Power Flow Capabilities for Power Management and Delivery Module in a Hybrid Electric Aircraft

Abstract

The development of fully electric and hybrid electric aircraft using fuel cells and batteries has lately received much attention since the technology can contribute to achieving an emission-free world. For hybridisation of fuel cells and batteries, the challenge of integrating different voltage sources to supply power to different loads at different voltage levels has to be met. Presently, this is achieved by using a combination of complex passive circuitry and DC–DC converters. In this paper, a new galvanically isolated DC–DC converter topology is proposed; it integrates a battery and fuel cells as input sources and supplies power to a high voltage (HV) and a low voltage (LV) load simultaneously. The converter enables power flow from the sources to the load, as well as between the sources and power flow back towards the battery during recuperation for recharging the battery during flight. The functionality of the converter design is verified using a real-time (RT) hardware-in-the-loop (HiL) test. The proposed concept is easily scalable and can be adopted in any fuel cell and battery drive train of all-electric flights of different sizes.

1. Introduction

As the world is striving to reduce greenhouse gas emissions in all sectors, aviation transport remains a significant polluter of the environment. CO₂ emissions from aviation account for 3% of total emissions in the European Union [1], and they are forecast to rise as air travel grows. The majority of the emissions are generated by commercial aircraft operations. Electric aircraft are seen as an viable option for emission-free travel [2], since renewable energy sources can be integrated in the aircraft. Recently there has been an increased focus on using hybrid drives using Li-ion batteries, and fuel cells [3], which can be paired with to improve the aircraft’s peak power delivery capability. The energy density of hydrogen is approximately three times higher than diesel or gasoline. Due to the superior energy density of fuel cells, they can be used in the low power phases, such as cruise, which is the longest flight phase. During high power demanding phases, such as take-off, the battery can add power to the system to drive the aircraft drive-train.

The concept presented by Hoenicke et al. [4] achieves a fully redundant direct hybrid architecture with a fuel cell and a battery. This concept incorporates several modes of operation like fuel cell only mode, hybrid mode, battery only mode, passive charging mode, and active charging mode. The concept is achieved by using passive diodes, relays and several external DC–DC converters. This architecture decreases the efficiency of the hybrid and introduces considerable weight to the aircraft. Many other concepts offering good weight to volume ratios, efficiencies and safety have already been introduced for electric aircraft [5]. They are dubbed multi-port converter topology and can be used as the main converter for powering the drive trains. Topologies presented in paper [6,7,8], introduce modified buck-boost converters to integrate two or more renewable energy sources without galvanic isolation. Another variation of the non-galvanic multi-port converter is introduced in [9]. This converter can route the power between a battery, an ultracapacitor and a DC load in various ways. Moreover, in more recent works [10,11,12,13,14,15] several multiple galvanically isolated multi-port converters are introduced. These converters mainly use popular bidirectional converter concepts (e.g., Dual-active bridge (DAB)) and extend them to a multi port topology (e.g., triple-active-bridge, quad-active-bridge). Although the dual-active bridge remains a viable topology, the main limitation lies in the fact that they typically do not have good regulation when the input-voltage to the DAB has a wide range. Hence, DABs are ideally more suited for applications like photovoltaic (PV) and Batteries but not for fuel cells ( the voltage output drops drastically when the load current is high).

This work focuses on introducing a novel DC–DC converter that builds upon the concept of [4] and additionally combines the following features into one single converter. On the input side, it integrates the fuel cell and battery into one converter. On the output side, it supplies a HV motor/inverter and LV auxiliary loads like sensors and cooling pumps. For higher safety, the sources and loads are galvanically separated. The name “flexible converter” derives from the ability to seamlessly redirect power to and from different ports of the converter as power transfer in the following directions is possible: Fuel cell to HV and LV load, battery to HV and LV load, fuel cell and battery to HV and LV load, fuel cell to battery (charge) and to HV and LV load, recuperation of HV load to battery (charge) and to LV load, and Fuel cell to battery (charge). This highly integrated DC–DC converter replaces the current state of the art in terms of the number and size of individual components and increases the system efficiency by reducing ohmic and switching losses in the semiconductor switches, which contributes to an overall reduction of component costs and weight.

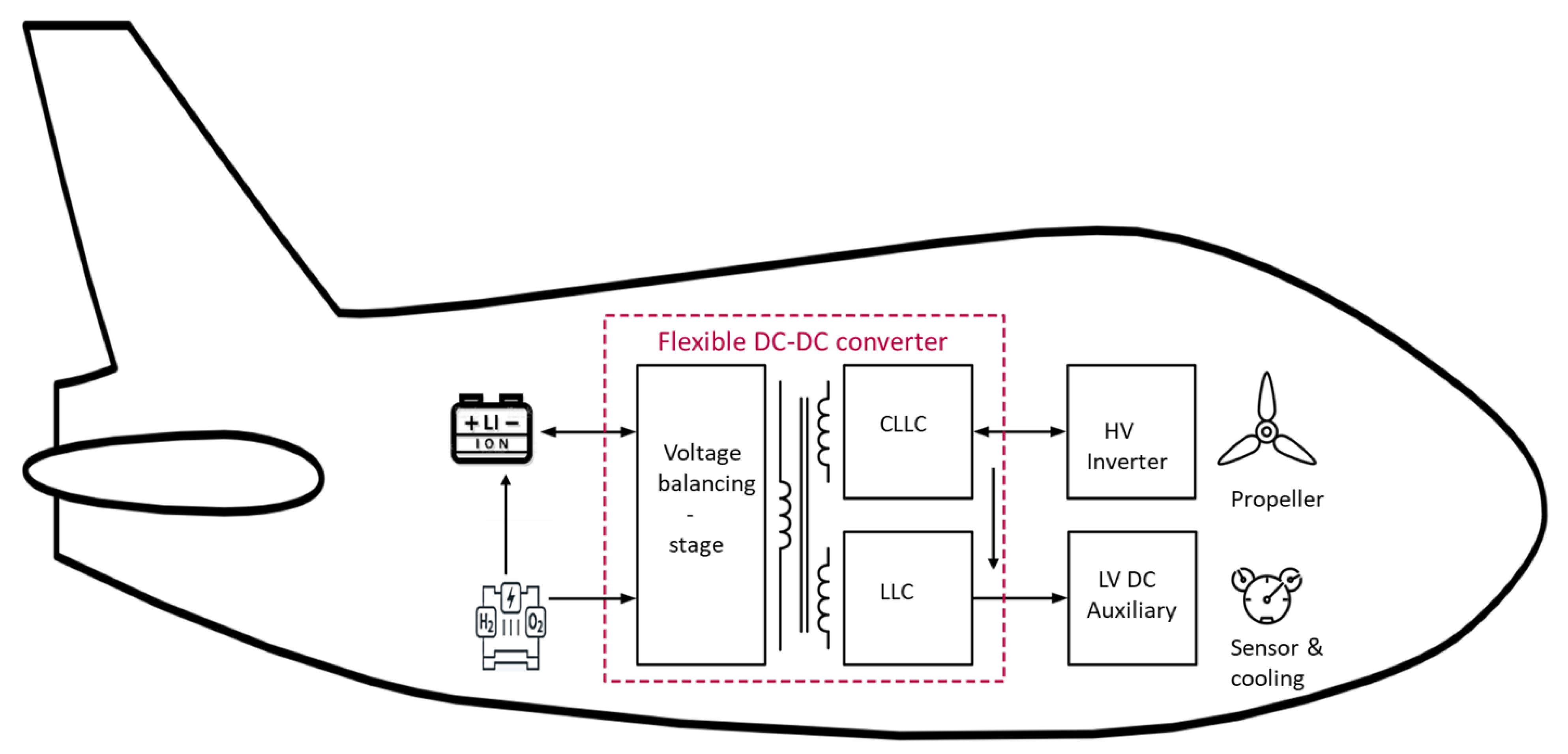
2. Concept and Modes of Operation

The hybrid power-train considered in this paper uses a fuel cell and a Li-ion battery as sources. A HV propeller motor (connected via an inverter) and LV DC auxiliary loads are considered as loads. A flexible DC–DC converter, operates as a power conversion and management interface between the sources and the loads as shown in Figure 1.

The flexible DC–DC selects the best source for the operation in each flight phase and matches the generated and required power based on the flight phase the converter is currently undertaking. A typical flight profile is demonstrated in Figure 2. There are high-power-demanding phases, such as takeoff and climb, and low-power-demanding phases, such as cruising, holding, or descent. During descent power can even be recovered in some cases. The actual figures for peak power demand depend on aircraft design and weight as well as altitude, slope, and flight time. This flexible converter allows each component (battery, fuel cell, and the DC-motor during recuperation) to be connected to the DC-bus separately, allowing for a flexible hybrid system. It is also possible to switch between multiple power modes to achieve optimal power management based on the required power. With this DC–DC converter following modes of operation are possible:

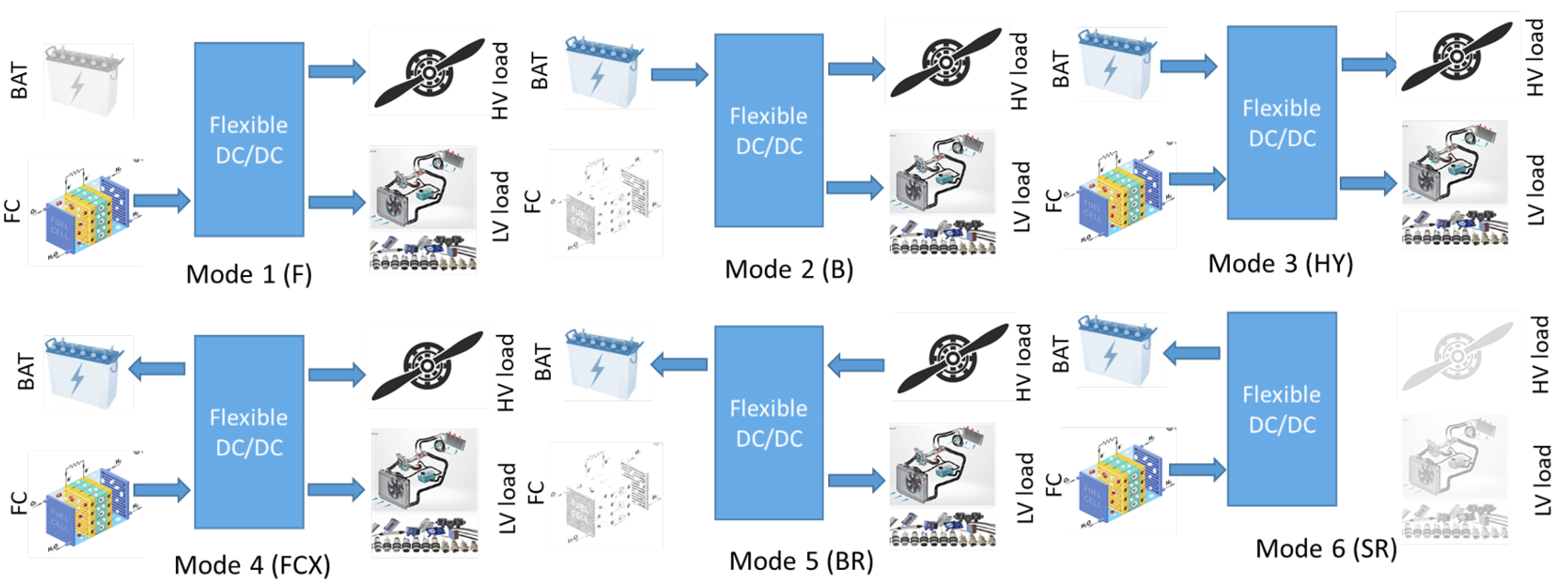
• Mode 1: Fuel cell to loads (F) The aircraft’s principal operation mode is the fuel cell mode. Only the fuel cell provides electricity to the motor and other loads throughout the en-route and holding stages. The fuel cell mode is used if the highest feasible fuel cell power is greater than or equal to the total load power demand. This mode is selected if the fuel cell power alone is sufficient to sustain the required motor power plus losses, and battery charging is not required.
• Mode 2: Battery to load (B) The battery module powers the entire aircraft loads in this mode. This mode is usually regarded as a backup safety mode, in case the fuel cell has a failure. The battery can be used as a redundant backup power source and provide sufficient power to perform an emergency landing. The battery must be sufficiently charged (i.e., high SOC) to use battery-only mode.
• Mode 3: Hybrid mode—Fuel cell and Battery to loads (HY) When the power demand of the loads exceeds the maximum fuel cell power, hybrid mode is used. Fuel cell and battery are simultaneously used to supply power to the loads in this mode. This mode is typically needed during the take-off and climb phase, where peak power demand is very high. At high load current, the voltage output drops significantly, and the fuel cell voltage can be higher or lower than the battery during operation. The voltage output of a Li-ion battery depends on the state of charge and the current but typically varies less than the fuel cell voltage. Hence, this mode necessitates a careful voltage balancing operation.
• Mode 4: Fuel cell to load and Battery Charging (FCX) This mode can be used during cruising or holding phase to recharge the battery during the course of the flight while simultaneously supplying energy to the loads. Similar to hybrid mode, a delicate voltage balancing is needed to match the load and battery voltage.
• Mode 5: Recuperation to Battery (BR) The DC bus voltage generated by the motor during recuperation can be utilized to charge the battery voltage if the battery is not already fully charged (SOC < 100%) while simultaneously supplying energy to the LV loads. This mode uses the braking energy generated by the propeller motor during descent or landing and charges the battery to regain some SOC. Recuperation increases the efficiency of the aircraft as the generated braking energy, instead of being wasted in form of heat in the brakes, is used for charging the batteries.
• Mode 6: Static Battery charging from fuel cell (SR) This mode is reserved for emergency operations and can only be performed when the aircraft is stationary and all loads are entirely powered off. A hypothetical example of usage is the aircraft has an emergency landing, and battery SOC is very low or depleted so that a new take-off is impossible. Using this mode, the fuel cell can charge the battery directly to gain some SOC in the battery.

The different modes of operations are graphically shown in Figure 3.

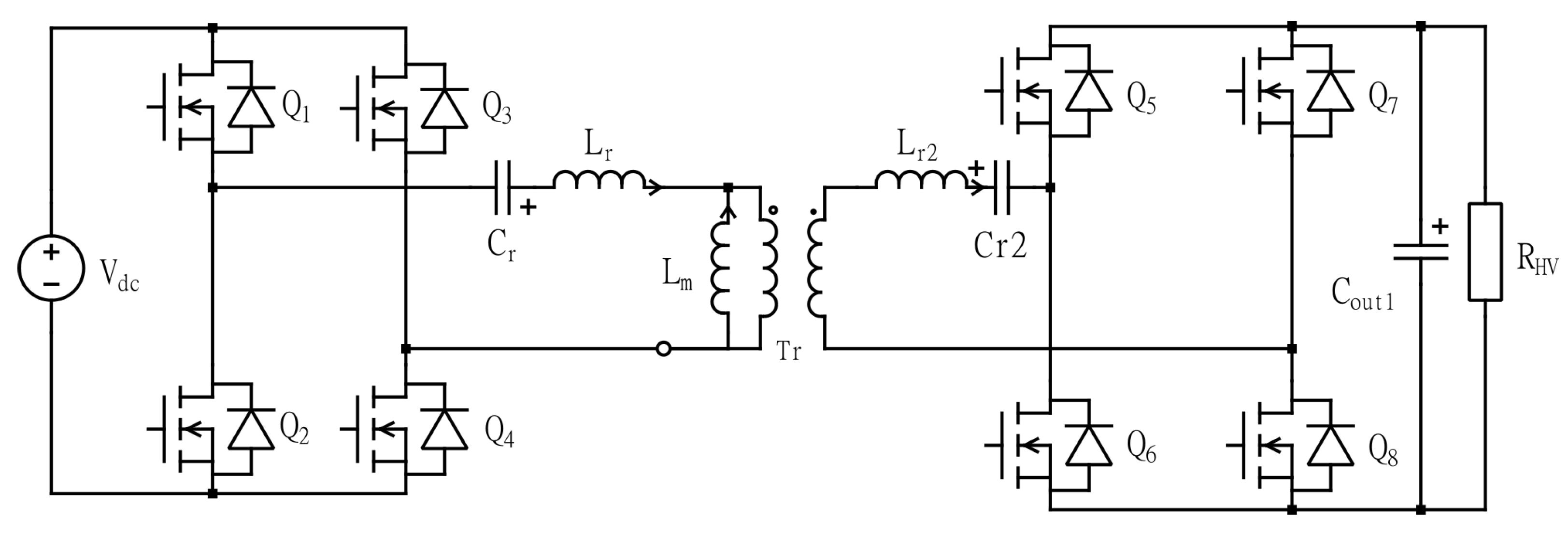
3. Proposed Converter Topology

The proposed flexible converter has two input and two output connections to which multiple power supplies and loads can be connected. This multi-port architecture increases the possibility of compacting and simplifying the entire system. The flexible converter connects multiple power supplies and loads and controls the electric power flow, enabling the energy flow between sources and loads in multiple directions. The proposed converter architecture is shown in Figure 4. The converter is divided into two separate stages to explain the operation principle: the resonant converter stage and the voltage-balancing stage. A DC–link capacitor couples these two stages. The resonant converter stage is bi-directional in nature and is connected to a HV load (inverter and DC motor) and a LV load (auxiliary DC power loads like sensors, cooling pumps). These two stages work in tandem to attain multi-directional power flow. The switches R₁ and R₂ are safety relays, that are used to completely decouple the fuel cell or the battery during a fault or maintenance and will be engaged always during normal operation. The motivation behind the two-stage design is simple. The voltage balancing stage combines two power sources (battery and fuel cell) and boosts their voltage to the target DC-link voltage. Here the concept presented in [9] is reworked and by using different control techniques described later, a voltage balancing system is adopted which can give out a constant DC-link voltage irrespective of the current operating voltage output of the sources. This stage also facilitates 6-way interaction between two sources and the DC link which is also described in Section 3.2. The control strategy also enables soft-switching in the switches during different modes of operations. This reduces the switching losses and cooling requirement of the switches. The resonant converter stage utilizes this DC-link voltage and converts it to a HV and LV DC output. The resonant stage is also designed to achieve soft-switching in every operation mode and is bi-directional in nature. The HV output is capable of supplying power back to the DC-link as well as the LV output using a magnetically coupled transformer.

3.1. Resonant Converter Stage

The resonant converter stage combines two popular resonant converter topologies, CLLC and LLC, into a single converter topology. The CLLC exhibits lower turn-off losses and achieves ZVS turn-on over the entire load range. In contrast, the close competitor in bidirectional capability, the dual-active-bridge (DAB), exhibits much higher turn-off losses and might lose ZVS at light load. Furthermore, when a large leakage inductance is used in DAB, the high RMS current increases losses in the bridges due to large reactive energy between primary and secondary side of the converter. Hence, the CLLC converter shows lower conduction and switching losses than DAB [17], and is more suited to our DC/DC topology.

The hybrid topology combines a unidirectional LLC and a bi-directional CLLC-based converter into one single converter architecture. The LLC converter is used to power the low voltage (LV) loads. Since low voltage loads often consist of sensors, cooling systems, etc., there is no requirement for power recuperation. The CLLC converter is used to power the high voltage loads like the main drive-train and enables recuperation to the primary source. Furthermore, a specially designed transformer magnetically couples the CLLC and LLC so that during the recuperation, the LV output is powered from the recuperation energy, and there is no discontinuity of power supply to the LV loads irrespective of the mode of operation. In the following section, the CLLC and the LLC converter design are discussed.

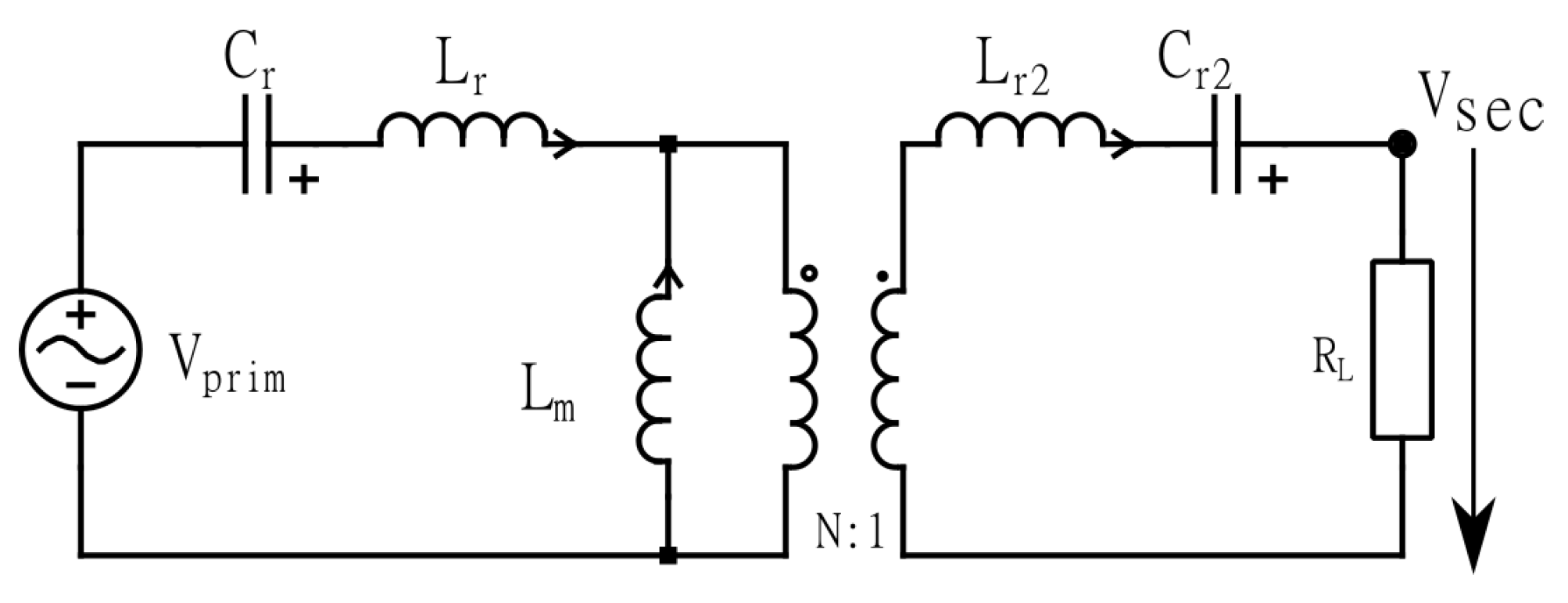
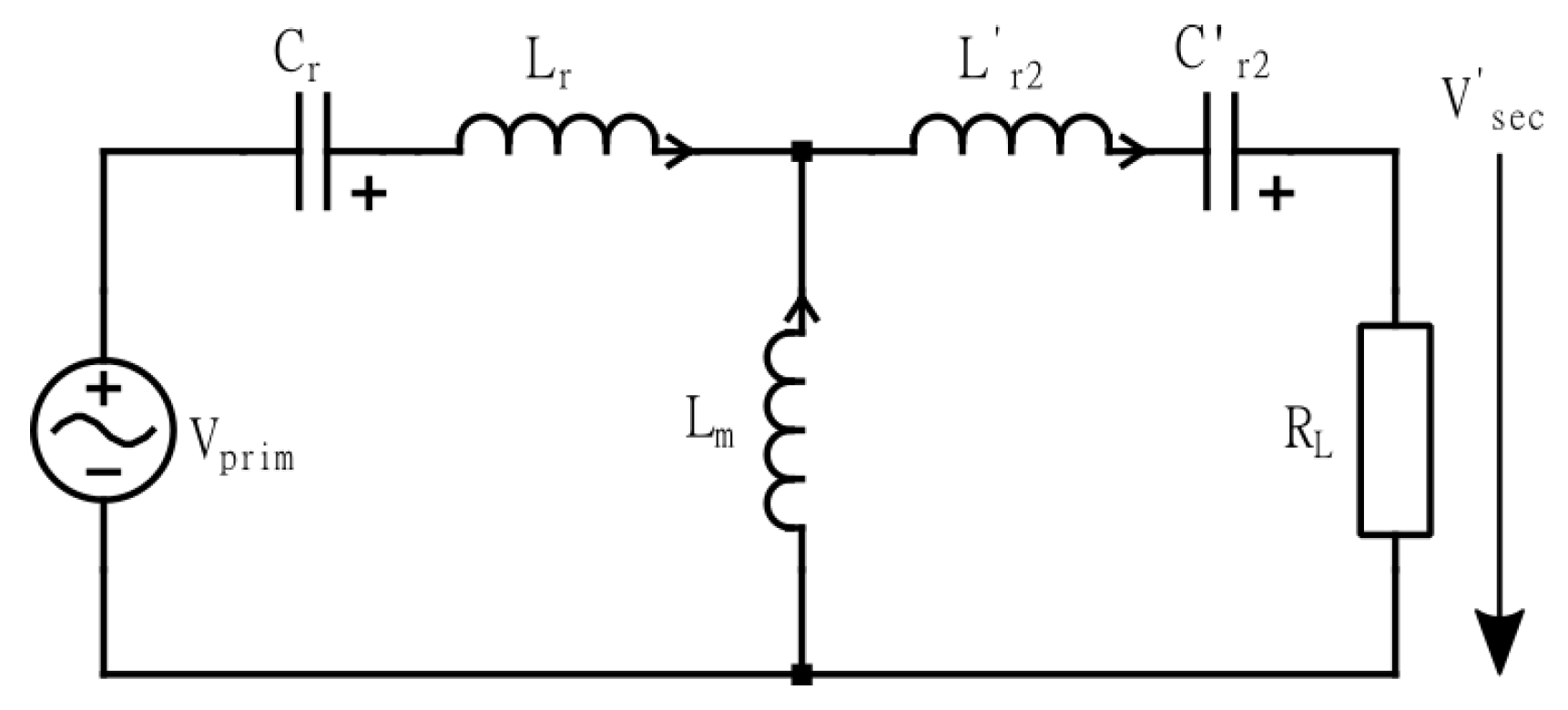
3.1.1. HV Output with CLLC Converter

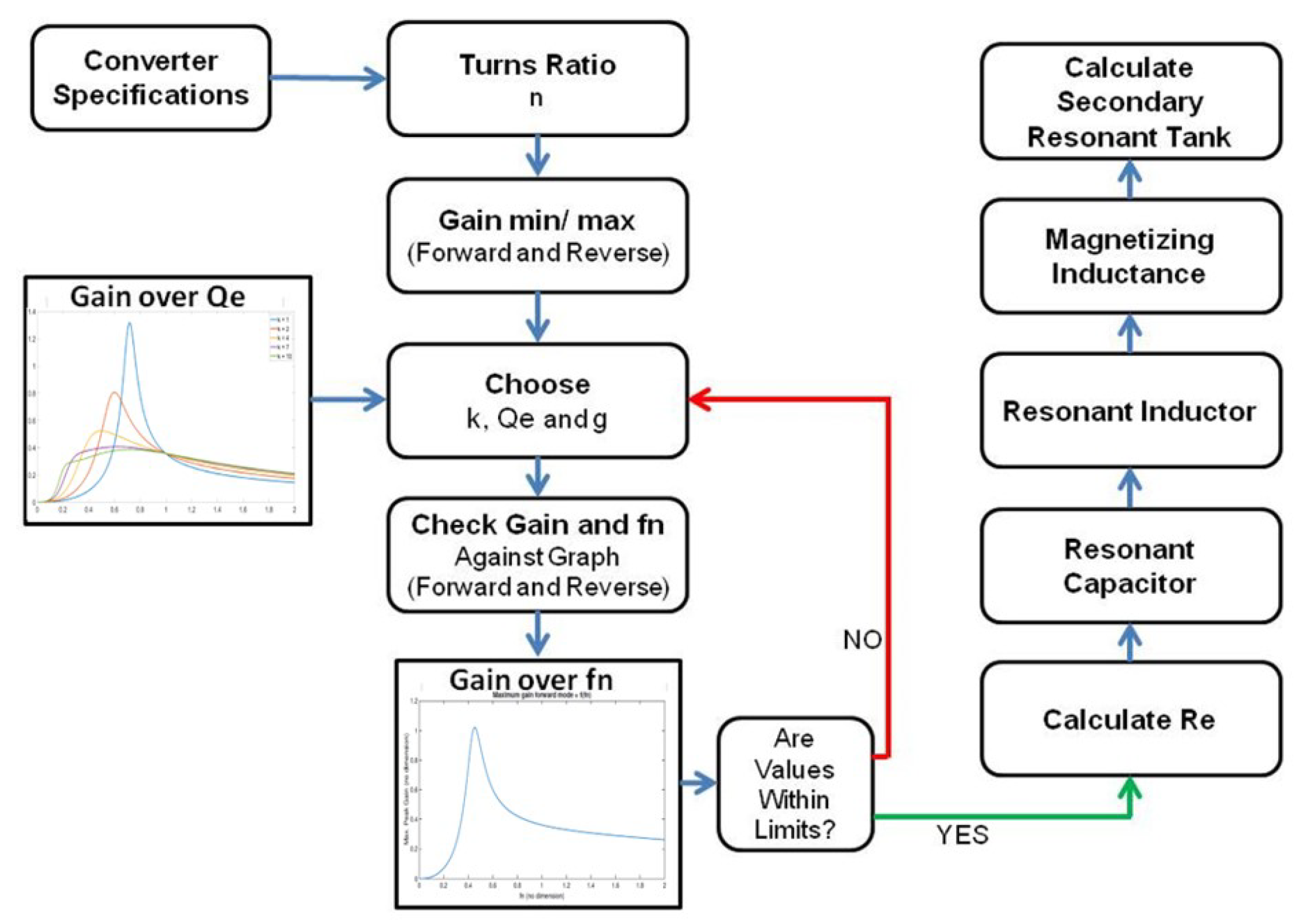
Design Process

The CLLC converter, as shown in Figure 5, consists of several non-linear component. The exact modeling of the converter is extremely difficult. The functionality of the symmetrical CLLC converter is similar to that of an LLC converter. For this reason, the parameters can be dimensioned with a similar design procedure as that of a standard LLC converter. Even though the operation principles of both converter types are similar, there are key differences in the calculation of the converter gain as the CLLC converter can transfer power in both directions. The first harmonic approximation (FHA) analysis [12,18] is highly effective for determining the gain equations for forward and reverse power transfer modes. This technique is based on the assumption that the power transfer from the source to the converter’s load is completely correlated to the fundamental components of voltage and current. Therefore, all current and voltage wave-forms are assumed to be purely sinusoidal. Although this assumption is not entirely accurate, it is very close, mainly when the generated square wave’s switching frequency corresponds to the resonant frequency. If the square wave is different from the series resonance, then, in reality, more frequency components are injected. However, an approximation using the single fundamental harmonic of the square wave can be made while ignoring all of the higher-order harmonics without sacrificing significant accuracy. The equivalent model diagram obtained from the FHA of the CLLC converter is shown in Figure 6.

By referring from the secondary to the primary side or vice versa, the transformer can be replaced by its equivalent T-model in the circuit. The magnetization inductance remains unchanged in this case. The simplified circuit obtained by this simplification in forward mode is shown in Figure 7. Correspondingly, the electrical network for the reverse mode is derived from Figure 8.

The secondary side elements are referred back to primary side and can be determined from the Equations (1)–(3).

$$L_{rs}^{\prime }=L_{rs}·N^2$$

(1)

$$C_{rs}^{\prime }=C_{rs}·N^2$$

(2)

$$R_L^{\prime }=R_L·N^2$$

(3)

Applying Kirchhoff’s Current Law (KCL) and Kirchhoff’s Voltage Law (KVL), the gain Equation (4) is derived:

$$H\left(j{\omega }_F\right)=\frac{V_{sec}^{\prime }}{V_{prim}}=\frac{1}{N}·\frac{[Z_m\left|\right|(Z_{rs}^{\prime }+R_L^{\prime })]·R_L^{\prime }}{Z_{rp}+[Z_M\left|\right|(Z_{rs}^{\prime }+R_L^{\prime })]·(Z_{rs}^{\prime }+R_L^{\prime })}$$

(4)

The real part of the Equation (4) can be represented as (Forward mode gain transfer function) [19]:

$$\begin{array}{c}\hfill D{C}_{f,gain}=\frac{k}{N|\frac{Q_e}{g}[-g(2k+1)f_n+(k+1)(m+1)f_n^{-1}-f_n^{-3}]+j(k+1-f_n^{-2})|}\end{array}$$

(5)

where,

$$k=\frac{L_m}{L_{r1}}$$

(6)

$$f_n=\frac{f_s}{f_r}$$

(7)

$$Q_e=\frac{\sqrt{L_{r1}/C_{r1}}}{R_e}$$

(8)

$$g=\frac{C_{rp}}{C_{rs}}$$

(9)

The parameters inductance ratio (k), quality factor ($Q_e$) and capacitance ratio (g) are dummy parameters that determine the shape of the gain curve as well as the gain of the converter. Each of these parameters is carefully considered for designing the resonant parameters of the converter.

Similarly, the equivalent FHA model for the reverse mode is derived (shown in Figure 8) and the reverse mode gain [19] can be determined as shown in Equation (10).

$$D{C}_{r,gain}=\frac{N·k}{|Q_e[-(2k+1)f_n+(k+1)(g+1)f_n^{-1}-g·f_n^{-3}]+j(k+1-f_n^{-2})|}$$

(10)

The parameter design of the symmetric CLLC converter is an iterative process of constant adjustment and optimization. In this iterative procedure, the resonant tank of the primary side is dimensioned first. To finish the circuit design, the inductance of the secondary side has to be determined. One approach is to set the resonant frequencies on both sides of the transformer to the same value. This results in the Equations (11)–(13) for determining the secondary inductance. In this section, the design steps to derive the resonant parameters are described in brief [20]:

• The first step is to obtain the turns-ratio of the transformer. The turns ratio of the transformer depends on the nominal input voltage (V_in,nom) and the output voltage (V_out,mean). If the forward MOSFET voltage drop and the diode forward voltage drop are ignored, the turns ratio (N) can be obtained from Equation (11).

  $$N=\frac{V_{\mathrm{in},\mathrm{nom}}}{V_{\mathrm{out},\mathrm{mean}}}$$

  (11)
• Next, the maximum voltage gain (M_max) and minimum voltage gain (M_min) is to be decided. Since gain requirements change with the direction of power transfer, two separate gain formulas must be regarded. The voltage gain is the ratio of output voltage and input voltage and is not a fixed value if the converter’s input voltage fluctuates. These two parameters are calculated based on design constraints based in Equation (12):

  $$\begin{array}{c}\hfill M_{\mathrm{f},\max }=\frac{V_{\mathrm{in},\max }}{V_{\mathrm{in},\mathrm{nom}}};M_{\mathrm{f},\min }=\frac{V_{\mathrm{in},\min }}{V_{\mathrm{in},\mathrm{nom}}}\\ \hfill M_{\mathrm{r},\max }=\frac{V_{\mathrm{in},\max }}{V_{\mathrm{in},\mathrm{nom}}};M_{\mathrm{r},\min }=\frac{V_{\mathrm{in},\min }}{V_{\mathrm{in},\mathrm{nom}}}\end{array}$$

  (12)
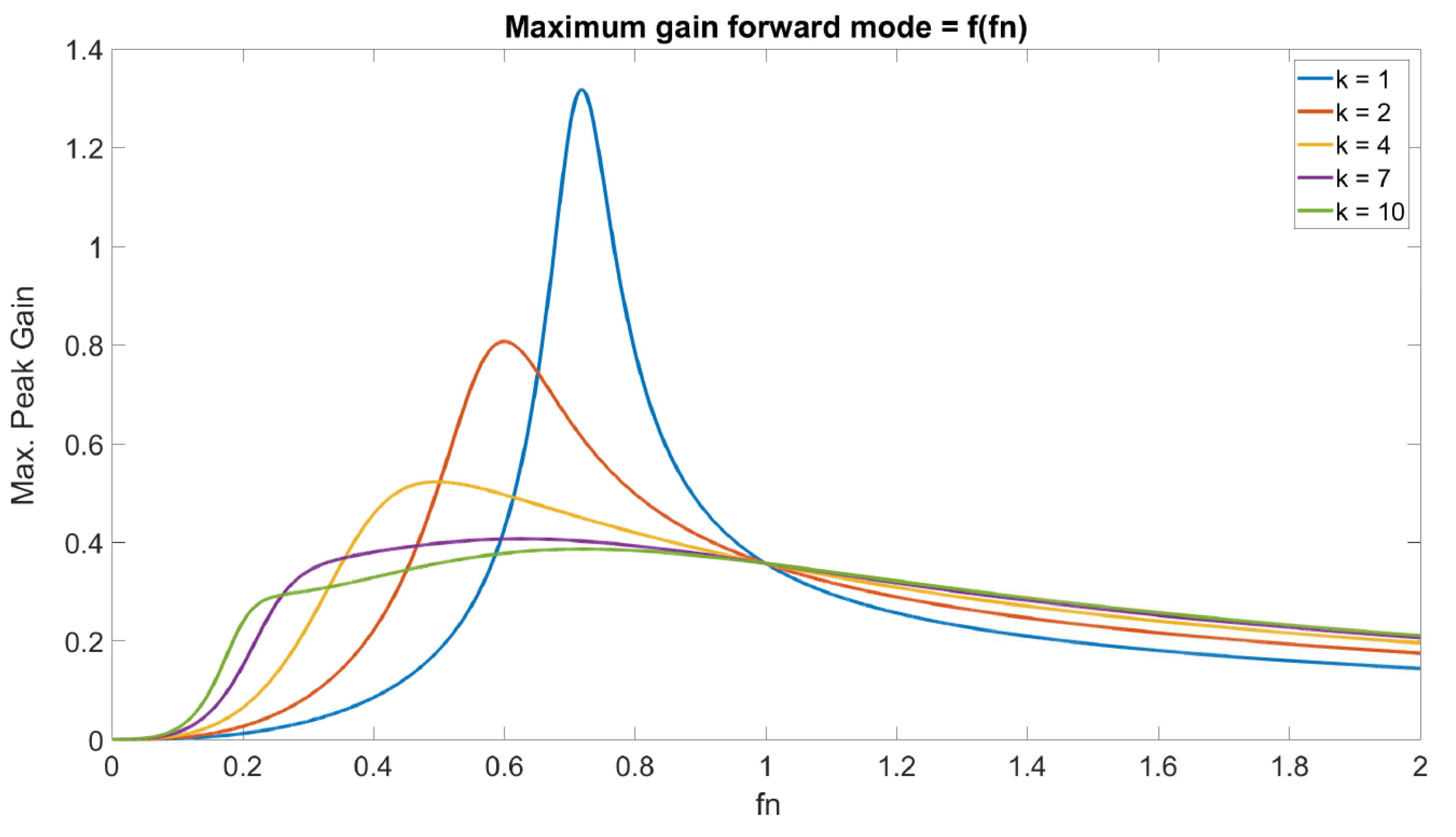
• The parameter k is another critical parameter for the design. It is demarcated by the ratio of the primary magnetization inductance ($L_m$) and the equivalent leakage inductance ($L_r$). The inductance ratio (k) is an important parameter that helps in shaping the gain curve. A small k usually results in considerable magnetization losses inside the transformer. On the other hand, a higher inductance ratio causes a limited gain but offers a broader operating frequency range and enhances efficiency. Figure 9 exhibits the effect of converter gain (in the forward direction) due to variation of parameter k when $Q_e$ and g are assumed constant. Since the focus of the converter is to optimize efficiency, a higher value of k is advised.

  Figure 9. Variation of the gain curve due to variation of parameter k over normalized switching frequency.

  Figure 9. Variation of the gain curve due to variation of parameter k over normalized switching frequency.
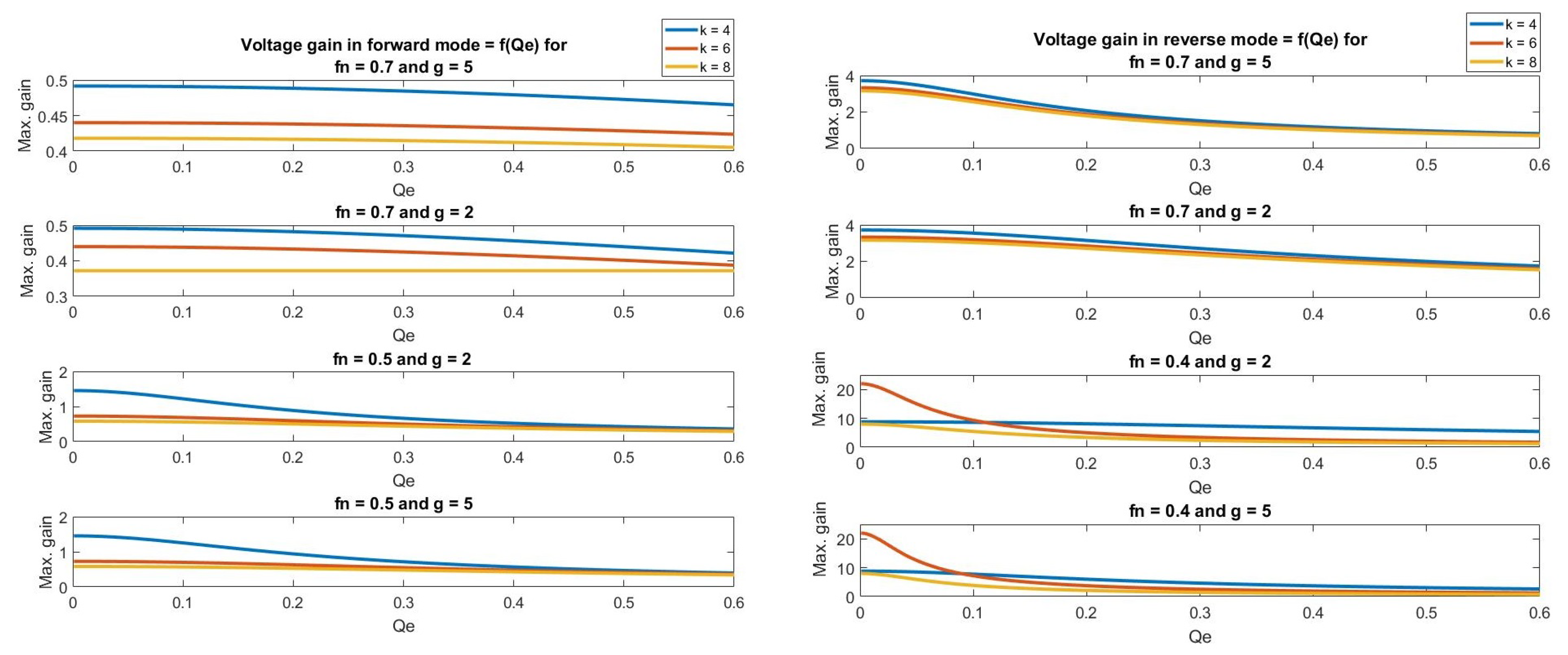
• Subsequently, the value of $Q_e$ is obtained. In order to investigate the effect of $Q_e$ on the gain curve, the gain curve is plotted for a fixed value of $Q_e$ over variable values of K and g for both forward and reverse directions. The result of this analysis is shown in Figure 10. From these curves, the optimal value of $Q_e$ is to be determined from the previously discussed gain requirements that guarantees the required gains conveyed in Equation (12).

  Figure 10. Gain curve for variable values of k and g in (left) forward direction, (right) reverse direction.

  Figure 10. Gain curve for variable values of k and g in (left) forward direction, (right) reverse direction.
• Next, the value of g is to be determined. It can be observed in Figure 10 that the value of the capacity ratio g does not have a significant effect on the gain curve. Nevertheless, at higher frequencies and with a higher value of g, a higher quality factor can be selected since the gradient of the curve is steeper in the lower $Q_e$ region. However, this effect is noticeably reduced at lower switching frequencies. It is advisable to keep the resonance frequencies of the primary and secondary sides in similar values according to the Equation (13), where, $L_{r1}$ is the primary resonance inductance, $L_{r2}$ is the secondary resonance inductance, $C_{r1}$ is the primary resonance capacitance, and $C_{r2}$ is the secondary resonance capacitance.

  $$L_{r2}=\frac{C_{r1}·L_{r1}}{C_{r2}}$$

  (13)
  Hence, the ratio of leakage inductance to the resonant capacitor is kept the same. However, if a large g is chosen, the inductance of the secondary side will have to be significantly reduced. Since, L_rs has a lower limit due to the leakage inductance of the transformer, this constricts the selection of g to a lower value.
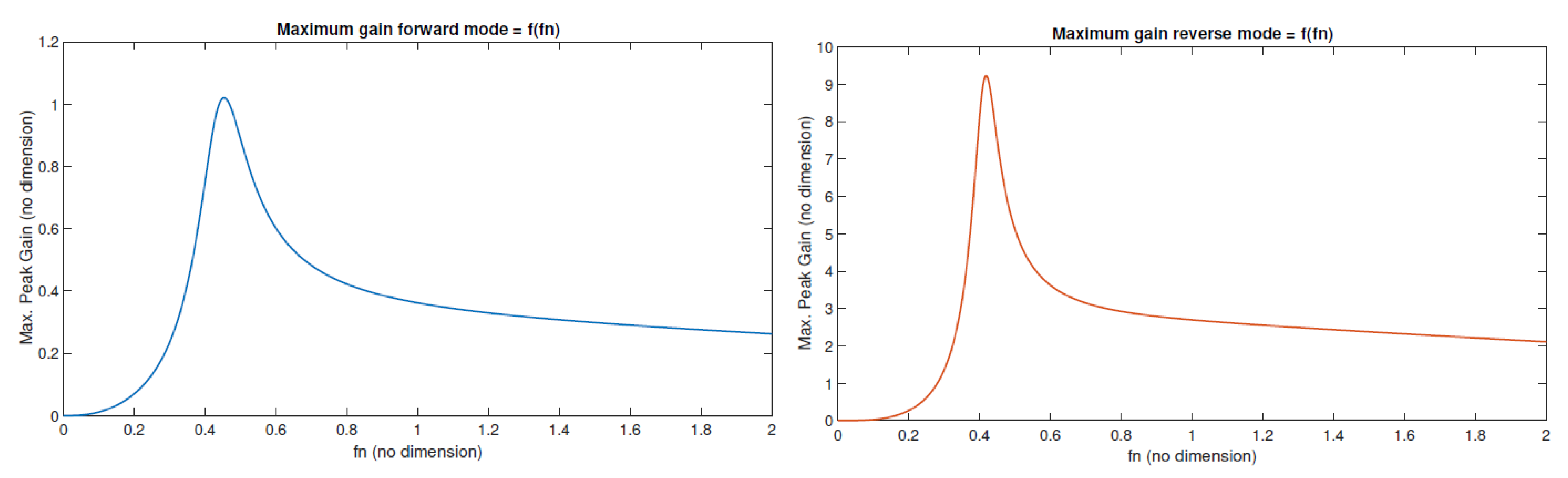
• Finally, forward and reverse gain curves are plotted with the selected values of $Q_e$, k, and g is to validate if the design meets the gain requirement (Figure 11). The resonant tank parameters are calculated using Equations (6)–(9). The overview of the iterative design process is shown in Figure 12.

  Figure 11. Forward and reverse gain from the selected values of $Q_e$, k, and g.

  Figure 11. Forward and reverse gain from the selected values of $Q_e$, k, and g.

  Figure 12. Iterative design flowchart of the CLLC converter design.

  Figure 12. Iterative design flowchart of the CLLC converter design.

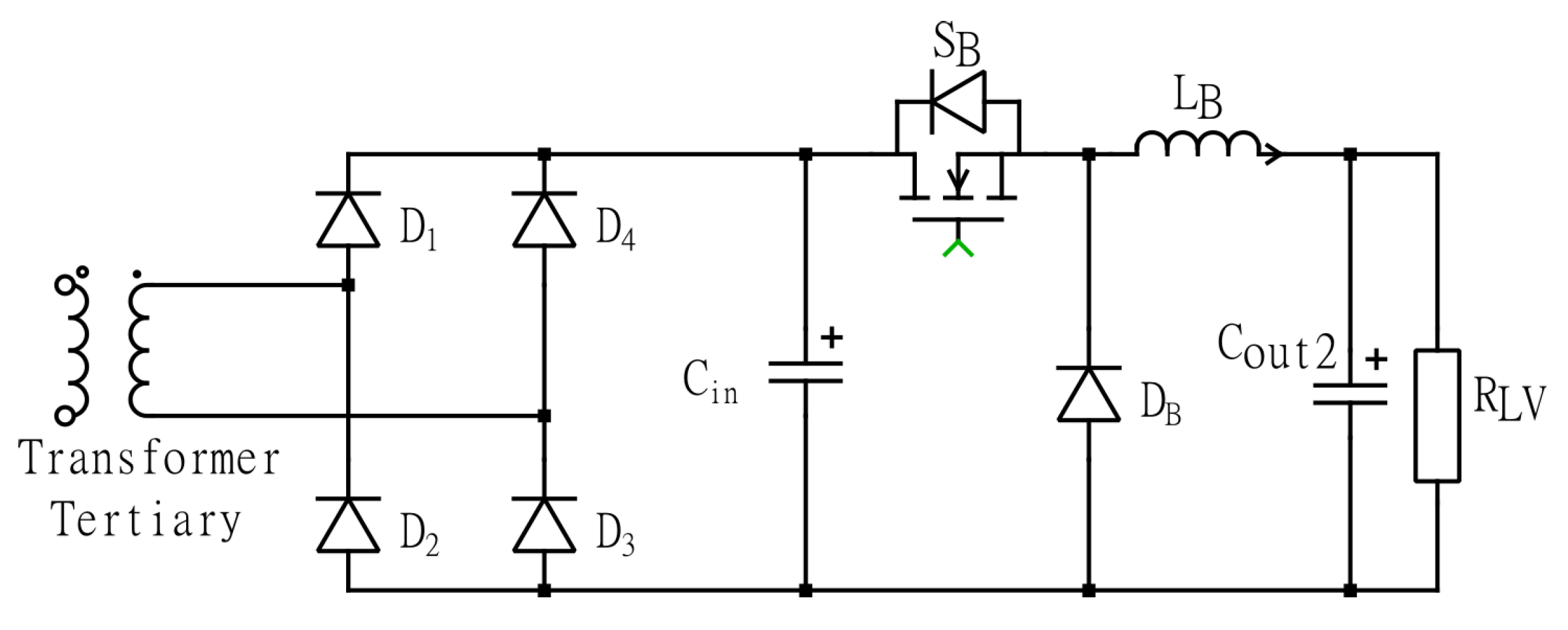
3.1.2. LV Output with LLC Converter and Integrated Buck Converter

In order to supply the onboard instruments with electric power, the circuit is suitably extended. Since high voltages are obtained on both sides of the CLLC converter, it is not advisable to use and directly step down these voltage busses without galvanic isolation. However, obtaining galvanic isolation by using an additional transformer requires additional space, and the entire system becomes heavier and more complex. For this reason, the high-frequency power transformer used in the CLLC converter is further modified to create the possibility of using an LLC converter. The primary side of the LLC converter is already integrated into the CLLC converter. The transformer in the CLLC is designed with a tertiary winding which is magnetically coupled with both the primary and secondary side of the converter. This addition to the circuit does not influence the transfer function as stated in Equations (4) and (10). The only effect it has is that the addition of the LLC branch introduces extra loading on the main LC branch, and hence $Q_e$ value must be adjusted to this extra loading.

An additional advantage of having the aforementioned magnetically coupled transformer is that when the converter is in the reverse recovery mode, the magnetic field of the secondary winding impresses a magnetic field as well as voltage on the tertiary (the LLC) branch of the converter, which can be further utilized to rectify the voltage and achieve a LV DC output. This modification, however, introduces another set of challenges. The magnetic flux inside a transformer used in a bidirectional converter with a large voltage amplification range can vary greatly. The voltage induced in the windings is therefore also variable. A suitable selection of the winding number can ensure that the rectified and smoothed voltage is greater than 28 V, even at the lowest magnetic flux. Furthermore, the transformer must be designed with bigger and bulkier core materials due to a flux density mismatch.

This shortcoming can be overcome by using a buck converter. The voltage can be kept constant at 24 V. With this modification, transformer design can be more optimized for weight and size reduction. This extension offers a constant 24 V in the entire working range and can accommodate voltage fluctuations, especially during the variable voltage of the HV motor during recuperation. The complete secondary side of the LLC converter with an integrated buck-converter for the 24 V power supply is depicted in Figure 13.

For the component selection of the buck converter, it is necessary to know the maximum and minimum input voltage of the buck converter. This data is obtained from simulating the CLLC converter. For the calculation of the buck converter components, the following formulas are used:

$$\begin{array}{c}\hfill \Delta I_L=0.05·I_{out,max,buck}\\ \hfill L_{buck}=\frac{V_{out,buck}·(V_{in,buck}-V_{out,buck})}{\Delta I_L·f_{s,buck}·V_{in,buck}}\\ \hfill C_{out,min}=\frac{\Delta I_L}{8·f_{s,buck}·\Delta V_{out,buck}}\end{array}$$

(14)

3.2. The Voltage Balancing Stage

The voltage balancing stage converts the different voltage levels from two sources and provides a constant voltage across the DC–link capacitor. The topology can also allow battery charging from the DC–link and battery charging directly from the fuel cell. Li-ion batteries often need a constant voltage during charging and should not be subjected to voltages higher than their OCV for a long duration. Therefore, the voltage of the FC, which changes drastically with the load current, needs to be transformed into a voltage closer to the battery’s OCV.

The Voltage-balancing stage is designed on the premise:

• the target DC–link voltage is higher than both battery and fuel cell
• battery voltage can be higher or lower than the fuel cell depending on the operation conditions.

The operation can be explained by considering the green box of the circuit in Figure 4 and its interaction with the DC–link capacitor. The voltage balancing stage modes of operation are explained below. To simplify the discussion and decouple this stage from the resonant converter stage, the DC–link capacitor, when charging, can be thought of as a load, and when it is supplying power back to the battery can be thought of as a constant voltage source in the discussion below.

3.2.1. Battery to DC–Link Capacitor (B2DC) Mode

The battery supplies energy to the DC–link and charges it in this mode. To illustrate the operation in this mode, the switching period is divided into four ($T_1$–$T_4$) time windows [9]. The switching sequences during these time windows are shown in

Table 1. Conduction of switches in different time intervals in B2DC mode.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
Boost mode	$S_2$, $S_3$	$D_1$, $D_4$	$S_1$, $S_4$	$D_1$, $D_4$

.

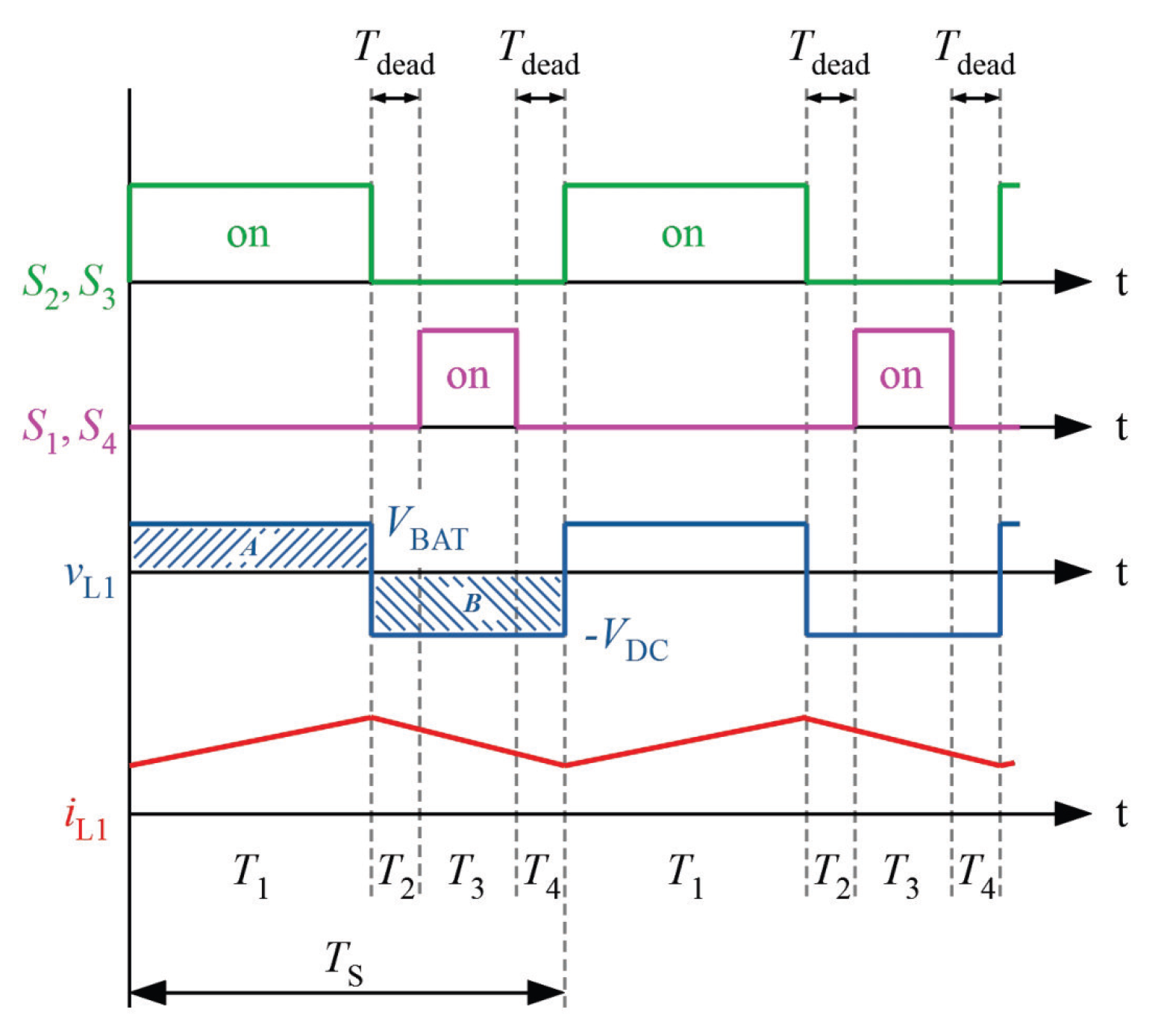
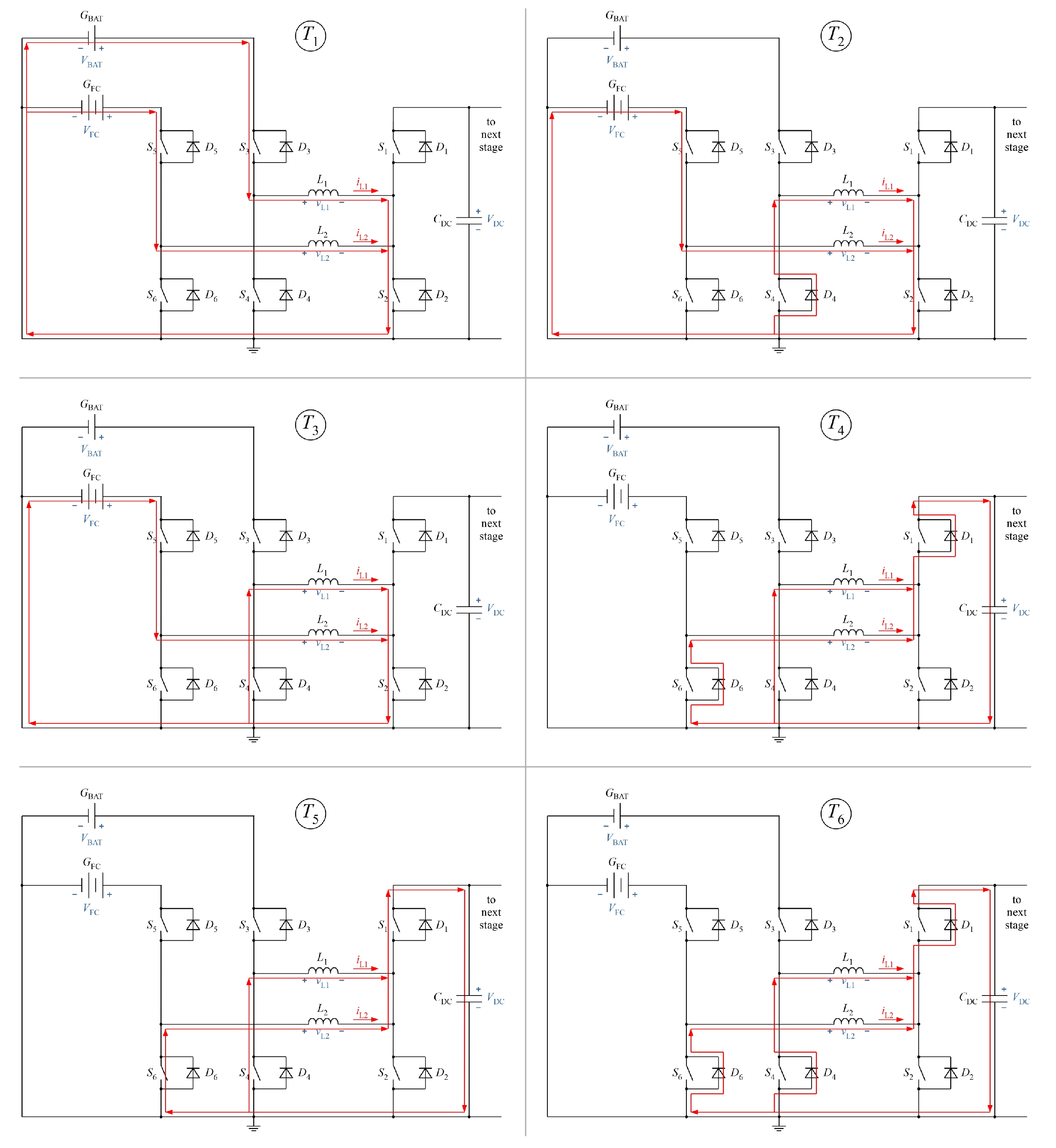
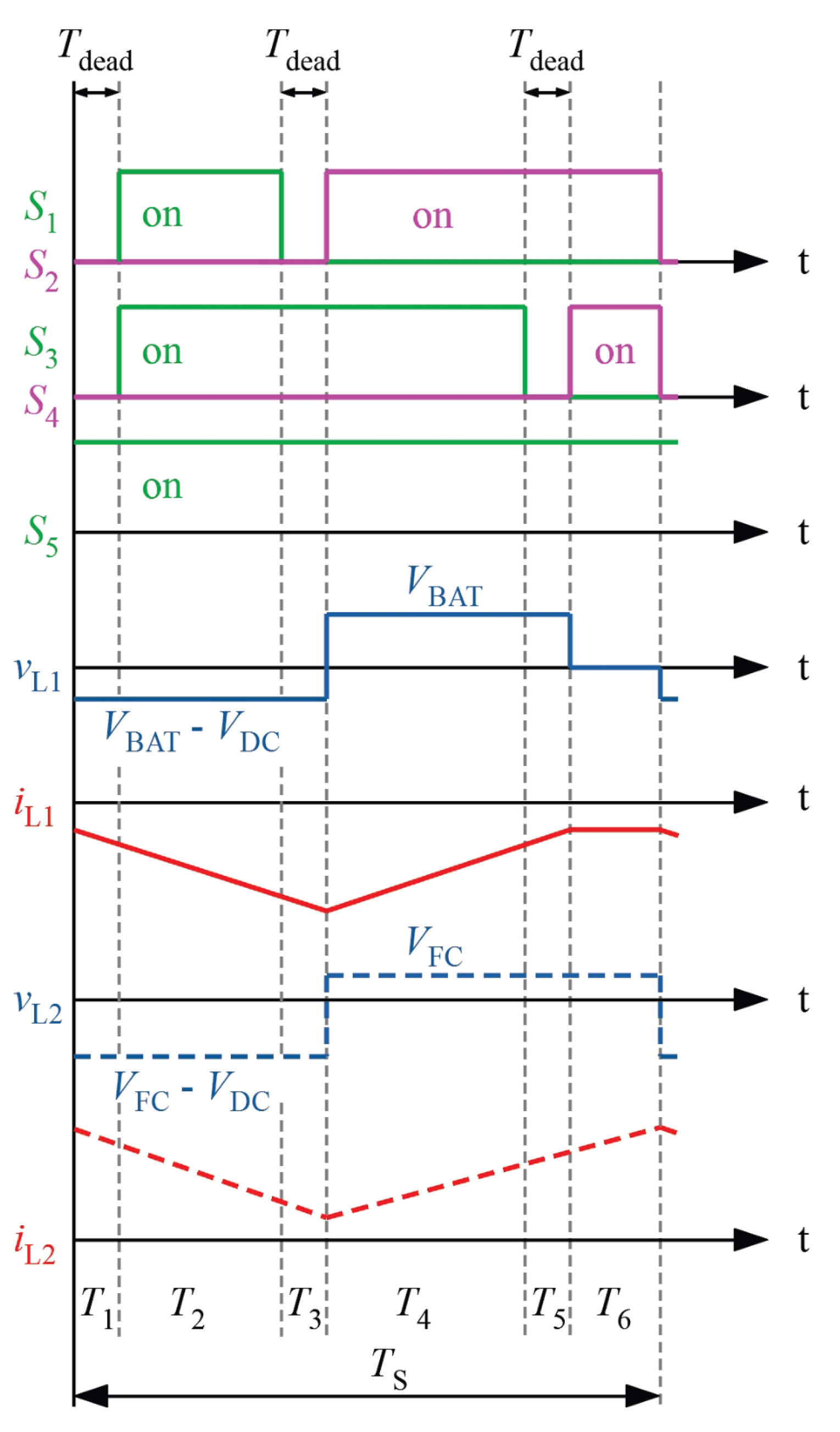
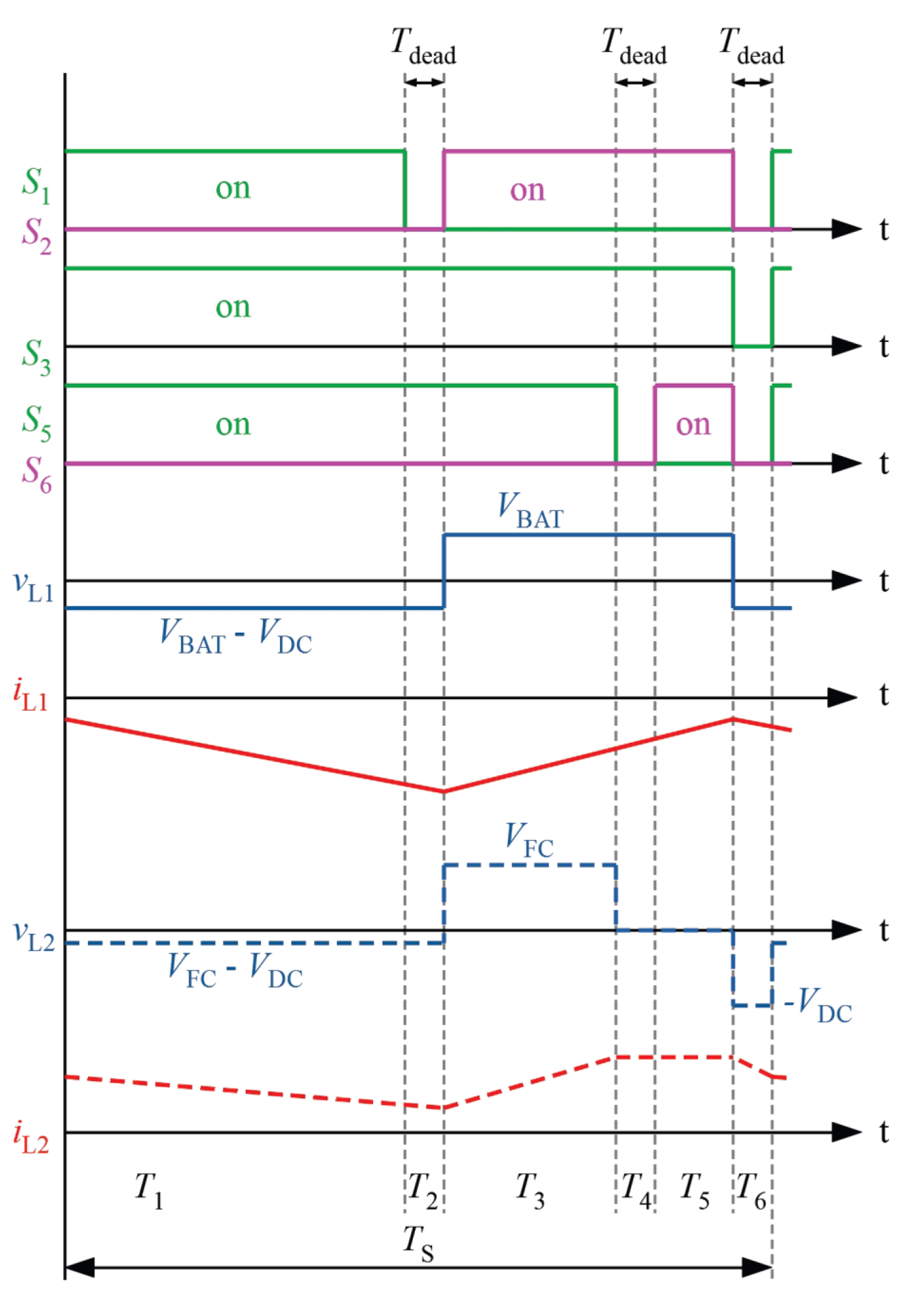
• During $T_1$, the active switches $S_2$ and $S_3$ are both turned-on. In this time interval, inductor $L_1$ is directly charged from the battery, and the current increases through the inductor with a slew rate of $V_{BAT}$/$L_1$, and the current flowing through the $L_1$ rises linearly.
• Time interval $T_2$ is a dead time interval in which all switches are turned-off. As the switches $S_2$ and $S_3$ are no longer conducting, the inductor current i_L1 is forced to commutate through the body diode of $S_1$ ($D_1$) and $S_4$ ($D_4$). This facilities the zero voltage switching of $S_1$ and $S_4$ when turned-on during the next time window. The current through inductor falls at a rate of $-V_{DC}$/$L_1$.
• During $T_3$, the switch pair $S_1$ and $S_4$ are turned-on at ZVS, and conduction losses are minimized.
• During $T_4$ all switches are turned-off and the inductor current commutates back to body diodes $D_1$ and $D_4$ again. Afterward, the $T_1$ sequence is repeated. It is worth mentioning that during $T_1$, $S_2$ and $S_3$ will be inevitably hard-switched. The switching states of the switches and the resulting inductor currents and voltages are shown in Figure 14.

  Figure 14. Active switch states, inductor voltage and inductor current for BAT and DC–link.

  Figure 14. Active switch states, inductor voltage and inductor current for BAT and DC–link.

The co-relation between the battery voltage ($V_{BAT}$) and the DC–link voltage ($V_{DC}$) can be obtained by using volt-second balance method and is shown in Equation (15). Here, the duty cycle (of switch $S_2$, $S_3$) is defined as $D_b$ = $T_1$/$T_S$. The switches $S_1$ and $S_4$ are driven with duty of (1 −$D_b$). This equation is valid as long as the target DC–link voltage is higher than the battery voltage.

$$\begin{array}{c}\hfill V_{BAT}·T_1=V_{DC}·(T_2+T_3+T_4)\\ \hfill V_{BAT}·D_b{T}_S=V_{DC}·(1-D_b)T_S\\ \hfill V_{DC}=\frac{D_b}{1-D_b}·V_{BAT}\end{array}$$

(15)

3.2.2. Fuel Cell to DC–Link Capacitor (FC2DC) Mode

In this mode, the fuel cell supplies energy to the DC–link. The operation principle is very similar to the previous mode. The switching sequences needed for achieving this are shown in

Table 2. Conduction of switches in different time intervals in FC2DC mode.

	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
Boost mode	$S_2$, $S_5$	$D_1$, $D_6$	$S_1$, $S_6$	$D_1$,$D_6$

.

The co-relation between the fuel cell voltage ($V_{FC}$) and the DC–link voltage ($V_{DC}$) can be obtained by using volt-second balance of $L_2$ and is shown in Equation (16) [9]. The duty cycle $D_f$ is defined as $T_1$/$T_S$. The switches $S_2$, $S_5$ are driven with duty $D_f$ and $S_1$, $S_6$ are driven with the duty of (1 −$D_f$). Similar to the previous mode, this equation is also valid as long as the target DC–link voltage is higher than the $FC$ voltage and can accommodate for changes in voltage due to load conditions.

$$V_{DC}=\frac{D_f}{1-D_f}·V_{FC}$$

(16)

3.2.3. Battery and Fuel Cell to DC–Link Capacitor (BFC2DC) Mode

This mode simultaneously transfers power to the DC–link from the battery and fuel cell. Since these two power sources supply power at two different voltage levels, a delicate voltage balancing operation must be carried out, and the voltage must be boosted to the target DC–link voltage. In this mode of operation, both inductor $L_1$ and $L_2$ are utilized to achieve voltage balancing. Due to voltage level mismatch of fuel cell and battery, depending on which source is at a higher voltage level, one inductor needs to be charged for a longer duration than the other within one switching cycle.

The switching states can be illustrated in 6 different time windows ($T_1$–$T_6$) and are depicted in

Table 3. Conduction of switches in different time intervals in BFC2DC mode.

${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$	${\mathit{T}}_5$	${\mathit{T}}_6$
$S_2$, $S_3$, $S_5$	$S_2$, $D_4$, $S_5$	$S_2$, $S_4$, $S_5$	$D_1$, $S_4$, $D_6$	$S_1$, $S_4$, $S_6$	$D_1$, $D_4$, $D_6$

. The current paths inside the voltage-balancing stage during this mode are shown in Figure 15.

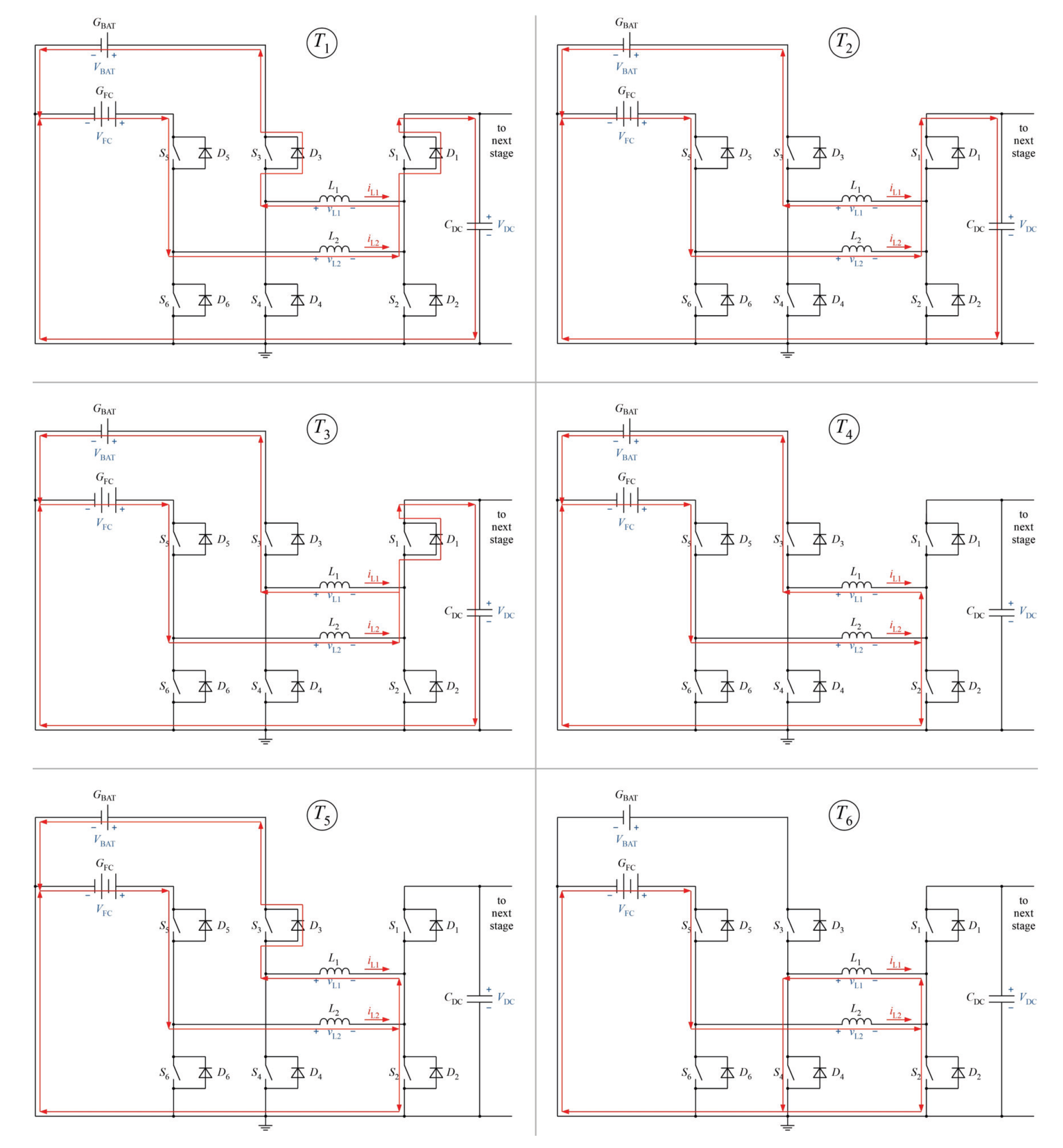
• Time interval $T_1$: During this time interval, inductor $L_1$ and $L_2$ are actively charged. This is achieved by turning-on the switches $S_3$, $S_5$ and $S_2$. Inductor $L_1$ is charged from the battery and the $L_2$ is charged from the fuel cell and a magnetic field builds up inside these inductors. The current through them increases linearly by slew-rates of $V_{BAT}$/$L_1$ and $V_{FC}$/$L_2$, respectively. At the end of the time interval $L_1$ is completely charged.
• Time interval $T_2$: At the beginning of this time interval $S_3$ is turned-off and as a result current automatically commutates through the body diode ($D_4$) of $S_4$. This provides a free wheeling state for current through $L_1$ while $L_2$ keeps on getting charged from the fuel cell.
• Time interval $T_3$: In this time interval, switch $S_4$ is turned-on and is switched on at ZVS, minimizing the switching and conduction losses at $S_4$. At the end of $T_3$, the inductor $L_2$ is also fully charged.
• Time interval $T_4$: In this time interval $S_5$ is turned-off. As a result inductor current through $L_2$ commutates through the body diode of $S_6$ ($D_6$). At the same time the body diode of $S_1$ ($D_1$) is forward biased and both inductors $L_1$ and $L_2$ start transferring energy to the DC–link capacitor.
• Time interval $T_5$: Here, the switches $S_1$ and $S_6$ are both turned-on. The switch $S_4$ which was activated previously at $T_3$ also remains on in this time interval. As a result both switches are turned-on at ZVS and conduction losses are minimized. The energy from $L_1$ and $L_2$ is transferred to the DC–link and as a result the magnetic energy of these inductors falls at a slew-rate $-V_{DC}$/$L_1$ and $-V_{DC}$/$L_2$, respectively.
• Time interval $T_6$: This time interval serves as a mandatory dead time period where all switches are turned off and current is forced to flow through $D_1$, $D_4$ and $D_6$. Afterwards, switching pattern goes back to $T_1$ and the recharging of inductors starts again.

The switching states of the switches and the resulting inductor currents and voltages are shown in Figure 16.

At first, volt-second balance is applied to inductor voltage v_L1. Two duty cycles are defined in this mode: $D_{H1}$ = $T_1$/$T_S$ and $D_{H2}$ = ($T_1$ + $T_2$ + $T_3$)/$T_S$.

$$\begin{array}{c}\hfill V_{BAT}·T_1=V_{DC}·(T_4+T_5+T_6)\\ \hfill V_{BAT}·D_{H1}{T}_S=V_{DC}·(1-D_{H2})T_S\\ \hfill V_{BAT}=\frac{1-D_{H2}}{D_{H1}}·V_{DC}\end{array}$$

(17)

Equation (17) provides the relation between $V_{BAT}$ and $V_{DC}$. Now, the second equation is derived by applying volt-second balance to inductor voltage ${\mathrm{v}}_{L_2}$:

$$\begin{array}{c}\hfill V_{FC}·(T_1+T_2+T_3)=V_{DC}·(T_4+T_5+T_6)\\ \hfill V_{FC}·D_{H2}·T_S=V_{DC}·(1-D_{H2})·T_S\\ \hfill V_{FC}=\frac{1-D_{H2}}{D_{H2}}·V_{DC}\end{array}$$

(18)

Equations (17) and (18) are valid for cases where $V_{FC}$ < $V_{BAT}$ and $V_{FC}$ > $V_{BAT}$. In the later case the inductor $L_2$ will finish charging earlier than $L_1$. However, the underlying principle will be similar in both of the cases.

3.2.4. Fuel Cell to DC–Link and Battery Charging (FC2BDC) Mode

In this mode, the fuel cell supplies energy to the DC–link and simultaneously charges the battery. There are two modes of operation possible based on the battery and fuel cell voltage. The modes of operation are described below:

Fuel Cell Voltage Lower Than the Battery (Boost Mode)

In this mode of operation the following scenario occurs: $V_{FC}$ < $V_{BAT}$ < $V_{DC}$. This mode of operation is called boost mode, because the fuel cell voltage $V_{FC}$ needs to be boosted to two different voltage levels of $V_{BAT}$ and $V_{DC}$ in order to supply energy to the battery as well as the DC–link.

The switching states can be divided in 6 different time windows ($T_1$–$T_6$) and active switches are depicted in

Table 4. Conduction of switches in different time intervals in FC2BDC- Boost mode.

${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$	${\mathit{T}}_5$	${\mathit{T}}_6$
$D_1$, $D_3$, $S_5$	$S_1$, $S_3$, $S_5$	$D_1$, $S_3$, $S_5$	$S_2$, $S_3$, $S_5$	$S_2$, $D_3$, $S_5$	$S_2$, $S_4$, $S_5$

. The current paths inside the voltage-balancing stage during this mode is shown are Figure 17.

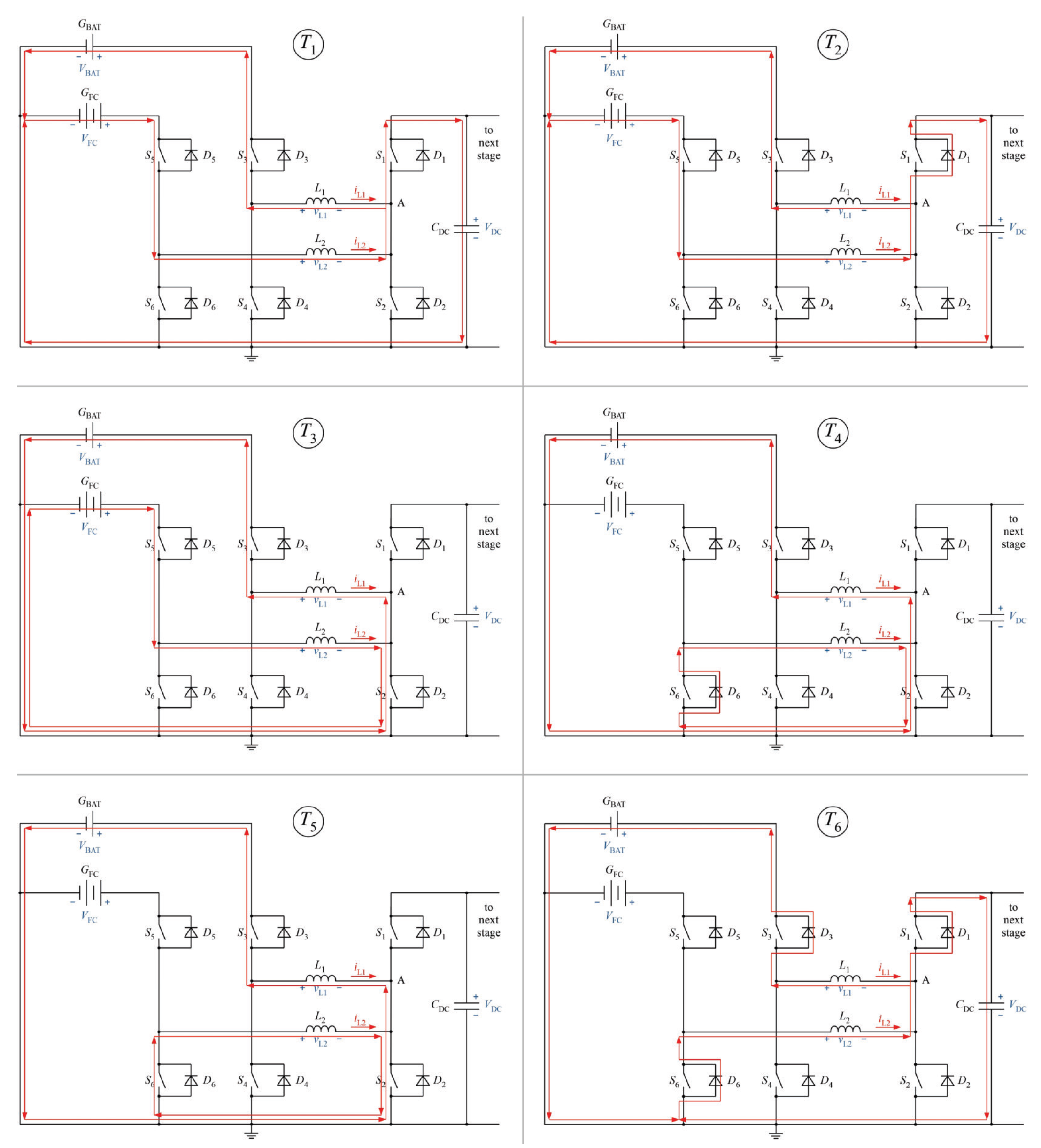
• Time interval $T_1$: During this interval only switch $S_5$ is turned-on. In this time interval the inductor $L_2$ discharges and charges both the battery and the DC–link. The body diode of $S_1$ ($D_1$) and the body diode of $S_3$ ($D_3$) are as a result forward biased.
• Time interval $T_2$: During this interval switch $S_1$ and $S_3$ are also turned–on. Therefore, $S_1$ and $S_3$ are turned–on at ZVS and conduction losses are minimized. In this time-interval, the current from $L_2$ continues to charge both the battery and the DC–link.
• Time interval $T_3$: During this interval $S_1$ is switched off. As a result, current transitions back to the body diode $D_1$ and provides necessary time to completely turn-off $S_1$.
• Time interval $T_4$: During this interval switch $S_2$ is turned-on and current is forced to commutate through switch $S_2$ to ground. In this interval the inductor $L_1$ charges the battery from the magnetic energy stored inside $L_1$ and $L_2$ is charged from the fuel cell.
• Time interval $T_5$: Switch $S_3$ is turned-off and current to the battery is forced to commutate to the body diode of $S_3$ ($D_3$). In this interval $L_2$ is charged from the fuel cell and $L_1$ continues to charge the battery.
• Time interval $T_6$: Finally, $S_2$ and $S_4$ are turned-on providing a free-wheeling path for the inductor current $L_1$. At the end of this time-period, $L_2$ is completely charged and switching-sequence is repeated.

The switching states of the switches and the resulting inductor currents and voltages are shown in Figure 18. To derive the equations describing the voltage relations between $V_{FC}$ to $V_{DC}$ and $V_{BAT}$ to $V_{DC}$, respectively, duty ratios for operational mode FC2BDC-boost are defined as follows: D_X1 = ($T_4+T_5+T_6$)/$T_S$ and D_X2 = $T_6$/$T_S$.

At first, volt-second balance is applied to inductor $L_1$, as shown in Equation (19):

$$\begin{array}{c}\hfill (V_{DC}-V_{BAT})·(T_1+T_2+T_3)=V_{BAT}·(T_4+T_5)\\ \hfill \Rightarrow \frac{V_{DC}}{V_{BAT}}=\frac{T_S-T_6}{T_1+T_2+T_3}\\ \hfill \Rightarrow \frac{V_{DC}}{V_{BAT}}=\frac{1-D_{X2}}{1-D_{X1}}\end{array}$$

(19)

For inductor $L_2$, volt-second balance results in Equation (20):

$$\begin{array}{c}\hfill (V_{DC}-V_{FC})·(T_1+T_2+T_3)=V_{FC}·(T_4+T_5+T_6)\\ \hfill \Rightarrow \frac{V_{DC}}{V_{FC}}=\frac{T_S}{T_1+T_2+T_3}\\ \hfill \Rightarrow \frac{V_{DC}}{V_{FC}}=\frac{1}{1-D_{X1}}\end{array}$$

(20)

Fuel Cell Voltage Is Higher Than the Battery (Buck–Boost Mode)

In this mode of operation the following scenario occurs: $V_{BAT}$ < $V_{FC}$ < $V_{DC}$. This mode of operation is called buck-boost mode, because the Fuel cell voltage $V_{FC}$ needs to be bucked to match the battery’s charging voltage $V_{BAT}$, while it must be boosted to the DC–link voltage level ($V_{DC}$), to supply energy to the battery as well as the DC–link. The commutation path of currents in 6 different time windows ($T_1$–$T_6$) and active switches are depicted in Figure 19 and

Table 5. Conduction of switches in different time intervals in Fuel cell to DC–link and battery charging in buck-boost mode.

${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$	${\mathit{T}}_5$	${\mathit{T}}_6$
$S_1$, $S_3$, $S_5$	$D_1$, $S_3$, $S_5$	$S_2$, $S_3$, $S_5$	$S_2$, $S_3$, $D_6$	$S_2$, $S_3$, $S_6$	$D_1$, $D_3$, $D_6$

, respectively.

During time interval $T_1$, switches $S_1$, $S_3$ and $S_5$ are closed, so the energy which is stored in $L_2$ from the previous operation is transferred to the DC–link and inductor $L_1$. During $T_2$, $S_1$ is turned-off, so that the current commutates through the body diode of $S_1$ ($D_1$). In the next step, $T_3$, switch $S_2$ is gated on, and the charging process of $L_2$ and the discharging process of $L_1$ begins. Current flows from the fuel cell towards ground through $L_2$ and builds up the inductor’s magnetic field. Meanwhile, due to current inertia, the current through $L_1$ has to go on flowing in same direction. Hence, the voltage polarity across $L_1$ reverses, and the current i_L1 transfers the stored energy to the battery and discharges the inductor.

Since in this mode the fuel cell voltage needs to be bucked to reach voltage balancing with the battery voltage, the fuel cell is disconnected from $L_2$ by opening $S_5$ in the time interval $T_4$, and with that the charging process of $L_2$ stops. Therefore, i_L2 commutes to the body diode $D_6$, providing a free-wheeling path for the inductor current. At interval $T_5$, $S_6$ is turned-on at ZVS. When enough energy is transferred from $L_1$ to the battery, the switching sequence goes back to $T_1$ and starts from the beginning. In order to avoid cross conduction, a buffer dead time interval $T_6$ is inserted between $T_5$ and $T_1$, where all active switches are turned-off.

The active switching states and inductor currents and voltages inside the voltage-balancing stage during this mode are shown in Figure 20.

To derive the equations describing the voltage relations between $V_{BAT}$ and $V_{DC}$ or $V_{FC}$ and $V_{DC}$, respectively, duty ratios for operational mode FC2DBC–Buck–Boost are defined as follows: $D_{X3}$ = ($T_3$ + $T_4$ + $T_5$)/$T_S$ and $D_{X4}$ = ($T_1$ + $T_2$ + $T_3$)/$T_S$.

At first, volt-second balance is applied to inductor $L_1$ to obtain the relationship between $V_{DC}$ and $V_{BAT}$, as shown in Equation (21)

$$\begin{array}{c}\hfill (V_{DC}-V_{BAT})·(T_1+T_2+T_6)=V_{BAT}·(T_3+T_4+T_5)\\ \hfill \Rightarrow \frac{V_{DC}}{V_{BAT}}=\frac{T_S}{T_1+T_2+T_6}\\ \hfill \Rightarrow \frac{V_{DC}}{V_{BAT}}=\frac{1}{1-D_{X3}}\end{array}$$

(21)

Next, volt-second balance is applied to inductor $L_2$ to obtain the relationship between $V_{DC}$ and $V_{FC}$ and Equation (22) is obtained.

$$\begin{array}{c}\hfill (V_{DC}-V_{FC})·(T_1+T_2)+V_{DC}·T_6=V_{FC}·T_3\\ \hfill \Rightarrow \frac{V_{DC}}{V_{FC}}=\frac{T_1+T_2+T_3}{T_1+T_2+T_6}\\ \hfill \Rightarrow \frac{V_{DC}}{V_{FC}}=\frac{D_{X4}}{1-D_{X3}}\end{array}$$

(22)

3.2.5. DC–Link Capacitor to Battery (DC2B) Mode

In this mode, energy is transferred from the DC–link to the battery. Since, current flows through inductor $L_1$ in the reverse direction, it is assigned with a negative sign. The switching states can be divided in 4 different time windows ($T_1$–$T_4$) and active switches are depicted in

Table 6. Conduction of switches in different time intervals in DC2B mode.

${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
$S_1$, $S_4$	$D_2$, $D_3$	$S_2$, $S_3$	$D_2$, $D_3$

.

During time interval $T_1$, switches $S_1$ and $S_4$ are closed so that a current can flow from the DC–link through $L_1$ towards ground, charging the inductor $L_1$. When the inductor is sufficiently charged, the switching sequence moves to $T_2$. Here, all of the active switches are opened. As a result, diodes $D_2$ and $D_3$ are forward biased and i_L1. commutes through them, and the energy which is stored in $L_1$ is transferred to the battery. In time interval $T_3$, switches $S_2$ and $S_3$ are turned-on at ZVS to provide a lower-ohmic path to the current that charges the battery. In order to return to the beginning of the switching sequence without risking cross-conduction of active switches, the procedure ends with a dead time interval $T_4$ in which all active switches are turned-off.

The switching states of the switches and the resulting inductor currents and voltages are shown in Figure 21. The equations describing the voltage relations between $V_{BAT}$ and $V_{DC}$ are obtained by applying volt-second balance to the inductor voltage v_L1. This relationship is shown in Equation (23). The duty cycle $D_R$ is defined as ratio of $T_1$ and $T_S$. $S_1$ and $S_4$ are operated at $D_R$, while $S_2$, $S_4$ are operated at duty of (1 −$D_R$).

$$\begin{array}{c}\hfill V_{DC}·T_1=V_{BAT}·(T_2+T_3+T_4)\\ \hfill \Rightarrow \frac{V_{BAT}}{V_{DC}}=\frac{D_R}{1-D_R}\end{array}$$

(23)

3.2.6. Fuel Cell to Battery Charge (FC2B) Mode

This mode is conceptualized for charging the battery from the fuel cell in a unidirectional manner. Based on the operation condition, if the battery voltage is higher than the fuel cell, the fuel cell voltage must be boosted to charge the battery voltage for this mode. However, if the battery voltage is lower than that of the fuel cell, the later source’s voltage must be bucked to a matching battery charging voltage. The voltage-balancing stage can be configured in buck or boost mode to achieve this. For this mode, the active switches $S_1$ and $S_2$ as well as the passive body diodes $D_1$ and $D_2$, as well as the DC–link capacitor are unused, which is why they are omitted in the discussion.

Buck-Mode

Buck mode can be configured using $S_3$ (always on), $S_5$ and $S_6$. Now the converter works as a typical synchronous buck converter. The switching sequence is shown in

Table 7. Conduction of switches in different time intervals in Fuel cell to battery charging.

Mode	${\mathit{T}}_1$	${\mathit{T}}_2$	${\mathit{T}}_3$	${\mathit{T}}_4$
Buck-mode	$S_3$, $S_5$	$S_3$, $D_6$	$S_3$, $S_6$	$S_3$, $D_6$
Boost-mode	$S_4$, $S_5$	$D_3$, $S_5$	$S_3$, $S_5$	$D_3$, $S_5$

. The relation between $V_{FC}$ and $V_{BAT}$ is obtained by the the duty cycle $D_{S_1}$ = $T_1$/$T_S$:

$$V_{BAT}=D_{S_1}·V_{FC}$$

(24)

Boost-Mode

Boost converter is configured using $S_5$ (always closed), $S_3$ and $S_4$. The switching sequence is shown in Table 7. The relation between $V_{FC}$ and $V_{BAT}$ is obtained with the duty cycle D_S2 = $T_1$/$T_S$:

$$V_{BAT}=\frac{1}{1-D_{S_2}}·V_{FC}$$

(25)

4. Experimental Setup and Results

4.1. Experimental Setup

Hardware-in-the-Loop testing has been widely utilized to validate novel control structures for power electronic systems. The underlying concept of HiL testing is high-fidelity real-time simulation. To validate the theoretical analysis, a complete hardware-in-the-loop test bench, as shown in Figure 22 has been used. The real-time simulation is a very popular tool to design and prototype resonant converter and provides very high fidelity results [21,22]. The power converter simulation runs in real-time on the OP4510 real-time simulator from OPAL-RT. Whereas, the complete open-loop control structure has been realized on the LAUNCHXL-F28379D development kit board from Texas Instrument. The simulator’s input/output IOs are mapped to exchange data between controller and simulator. The PWM signals were sampled with digital input at 1 GHz. The converter model was implemented on an FPGA using the eHS solver [23] which is capable of reaching a fixed time-step as low as 135 ns for real-time simulation.

The experimental model loaded to the eHSx128 core is based on the design input parameters and designed converter parameter as shown in

Table 8. Design requirement parameters and designed parameters of the voltage–balancing stage and the resonant converter stage.

Description	Parameter	Value
Design Requirement	Battery Voltage	300–336 V
	Fuel cell Voltage	180–400 V
	HV output voltage (power)	450V (750 W)
	LV output voltage (power)	28 V (250 W)
	DC–link target voltage	450 V ± 5%
Voltage-balancing stage	Inductor $L_1$	4 mH
	Inductor $L_2$	3 mH
	Switching frequency	100 kHz
	$C_{DC}$	100 $\mathsf{\mu }$F
Resonant converter stage	$C_r$	50 nH
	$L_r$	15 $\mathsf{\mu }$H
	$L_m$	200 $\mathsf{\mu }$H
	Transformer turn-ratio	80:29:09
	$C_{r2}$	30 $\mathsf{\mu }$H
	$L_{r2}$	400 $\mathsf{\mu }$H
	Switching frequency	80–250 kHz

. Real-time simulation is carried out in an open-loop with a premise that the battery is at a constant voltage of 330 V and the fuel cell is at 180 V. The calculated duty cycles mentioned in Section 3.2 are shown in

Table 9. Calculated duty cycle and switching frequency chart for fuel cell voltage at 180 V and battery at 330 V.

Switch	${\mathit{S}}_1$	${\mathit{S}}_2$	${\mathit{S}}_3$	${\mathit{S}}_4$	${\mathit{S}}_5$	${\mathit{S}}_6$	${\mathit{S}}_{\mathit{B}}$	CLLC Primary	CLLC Secondary
Mode	Duty	Duty	Duty	Duty	Duty	Duty	Duty	Sw. Frequency	Sw. Frequency
B	40.6%	59.4%	59.4%	40.6%	-	-	20%	175 kHz	-
F	20.8%	79.2%	-	-	79.2%	20.8%	20%	175 kHz	-
HY	27%	73%	38%	62%	73%	27%	20%	175 kHz	-
FCX	39%	61%	51%	49%	100%	0%	20%	175 kHz	-
BR	45%	55%	55%	45%	-	-	47%	-	87.2 kHz
SR	-	-	36.3%	63.7%	100%	-	-	-	-

.

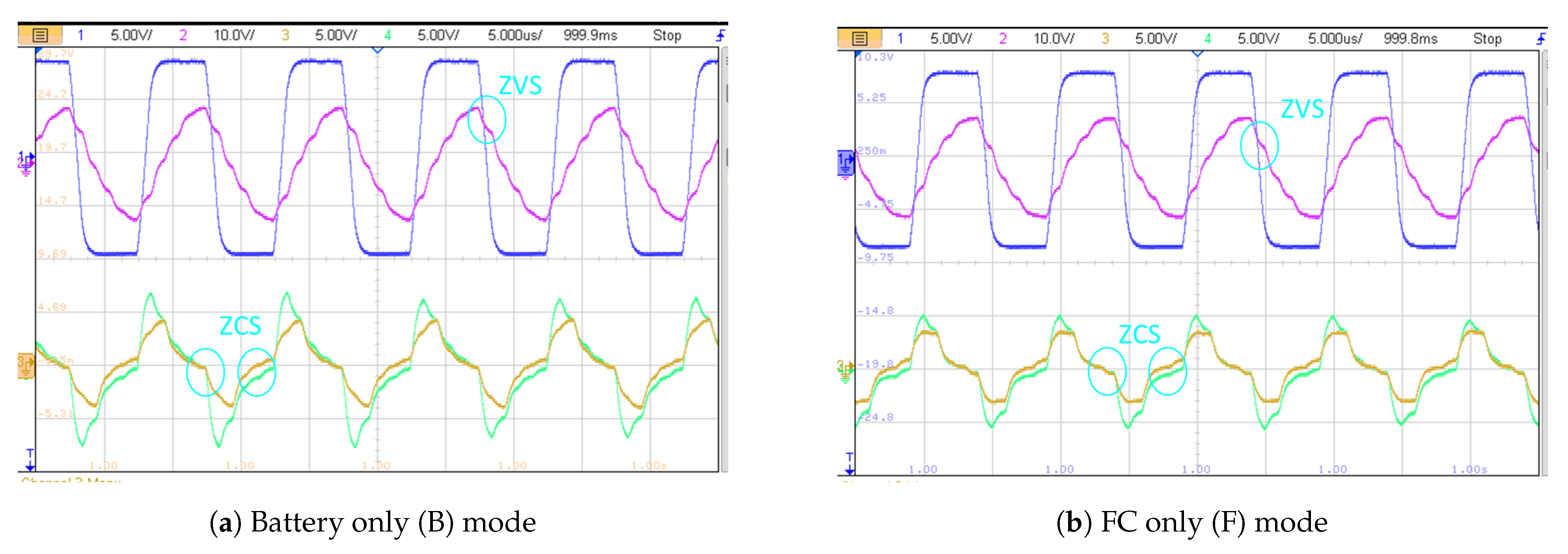
4.2. Experimental Results

To verify the analysis, the proposed converter’s voltage balancing stage is first evaluated for the various modes of operation described in Section 3.2. The resulting voltage and current waveforms of inductor $L_1$ and $L_2$ are shown in Figure 23a–f. Since the IO card of OP4510 is only capable of ±15 V outputs, the voltage and current are scaled to obtain the waveforms. $L_1$ and $L_2$ waveforms for mode F, B, HY, FCX, BR and SR are similar to the theoretical analysis and verify the analysis. Please note in Figure 24d, CH1 and CH2 are swapped with CH3 and CH4, respectively.

Next, the resonant stage key waveforms are verified for all six modes. The switching frequency and buck converter duty cycle for the corresponding mode of operation are shown in the Table 9 and the experimental results are shown in Figure 24a–f. As can be seen from the figures, in mode B, F, HY and FCX, the switch node produces a square waveform, which is impressed on the resonant tank. The resonant current in the primary side is sinusoidal (below resonance frequency) and turns off at ZVS. The secondary current of the CLLC and the tertiary current of the LLC are in a discontinuous mode of operation and are switched at ZCS. During BR mode, the CLLC’s secondary side is energized from the load’s braking energy; hence the secondary side current is now switched at ZVS and the primary side current and LLC secondary current achieve ZCS. Finally, in SR mode, the output loads are not energized, and there is no output obtained. It is worth mentioning that some transitions are slightly distorted as the analogue output of the real-time system is sampled at 100 MHz, and some information is lost.

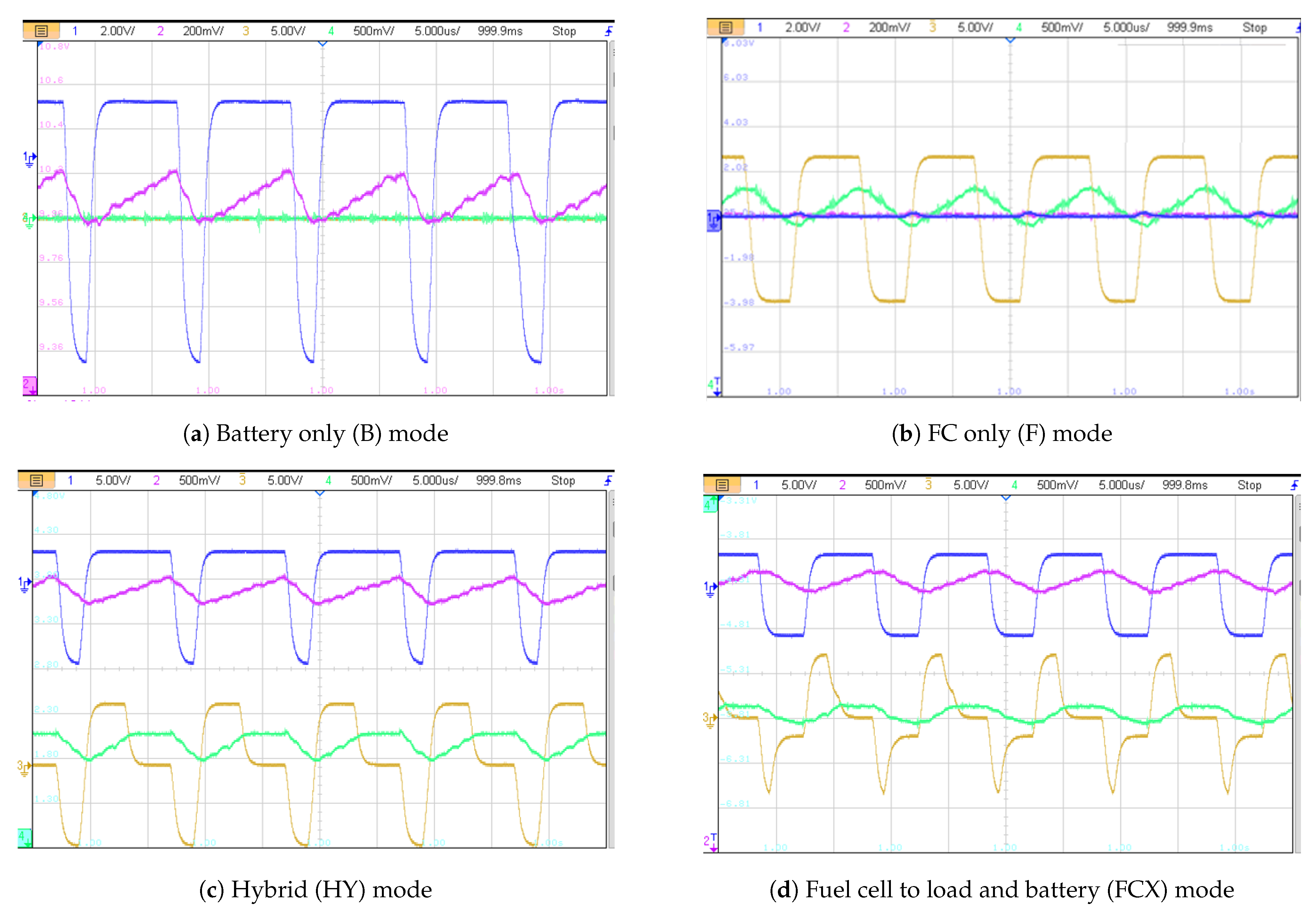
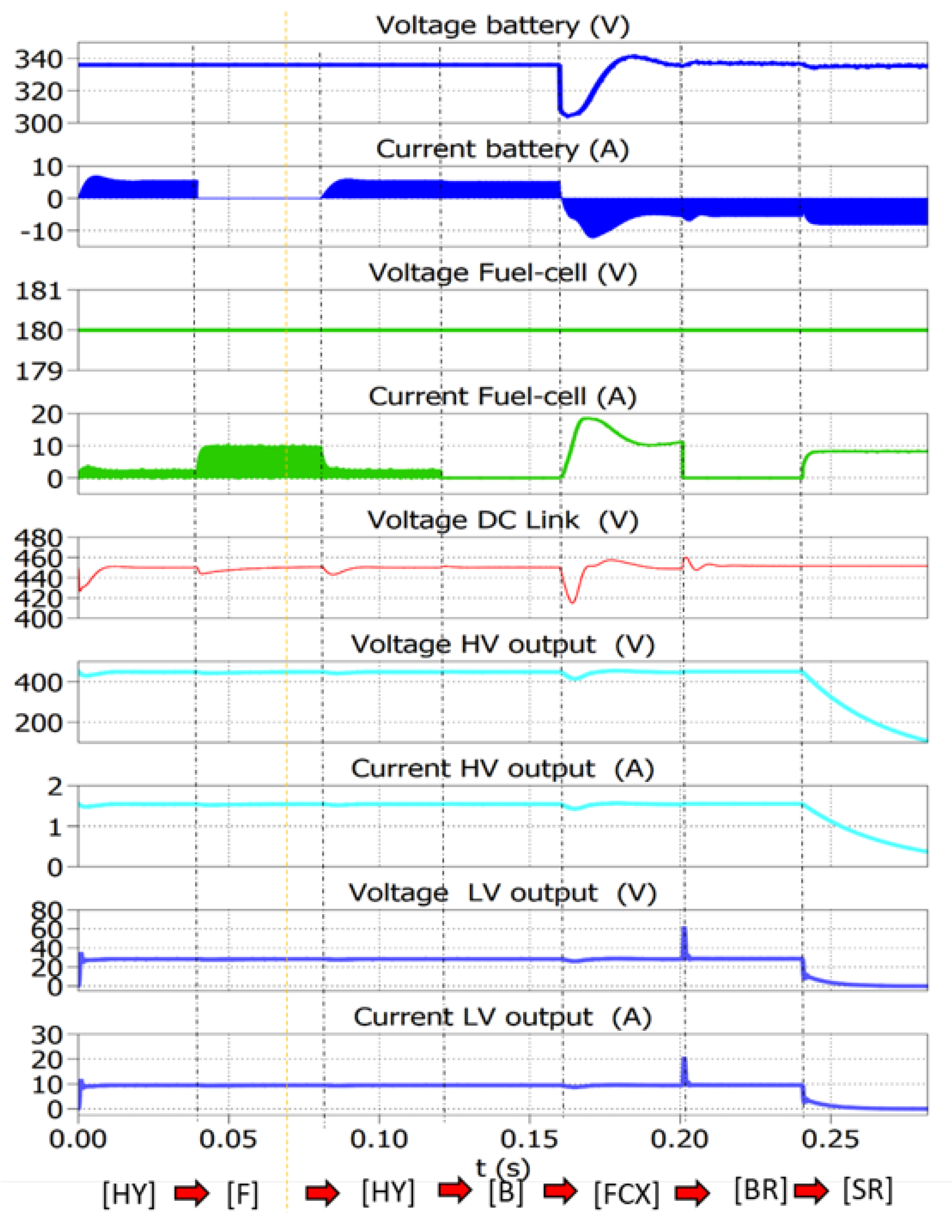
4.3. Mode Transitions

The transitions between different modes of operation are also simulated to check the transients between different states. Here, every 0.04 second the mode of operation is changed in following fashion: HY ⟶ F ⟶ HY ⟶ B ⟶ FCX ⟶ BR ⟶ SR. This is based on a standard flight profile as demonstrated in Figure 2. The results of the simulation are shown in Figure 25. Since the converter is simulated in an open loop, some transient changes are visible during step changes in the duty cycle. This can be further improved by voltage, or current mode closed-loop control and is out of the scope of this paper.

a.

During HY: Current is drawn from both battery and fuel cell. 450 V is obtained at the DC–link and 450 V is obtained at the HV DC output (750 W) while 28 V is obtained at the LV DC output (250 W).

b.

During F: Current is drawn from fuel cell only, and the battery is completely decoupled. 450 V is obtained at the DC–link and 450 V is obtained at the HV DC output (750 W), and 28 V is obtained at LV DC output (250 W).

c.

During HY: Same behaviour as in point a.

d.

During B: Current is drawn only from the battery and the fuel cell is completely decoupled. 450 V is obtained at the DC–link and 450 V is obtained at the HV DC output (750 W) while 28 V is obtained at LV DC output (250 W).

e.

During FCX: Current is drawn from fuel cell only and the battery is charged (negative current). 450 V is obtained at the DC–link and 450 V is obtained at the HV DC output (750 W) while 28 V is obtained at the LV DC output (250 W).

f.

During BR: Current is supplied from the HV DC output of 450 V, and the battery is charged from it (negative current). FC is completely decoupled as it does not support negative current. 450 V is obtained at the DC–link and 28 V is obtained at the LV DC output (250 W).

g.

During SR: Current is drawn from the fuel cell only and the battery is charged from it (negative current). No output voltage is obtained on the HV, and LV outputs as this mode is designed for stationary charging.

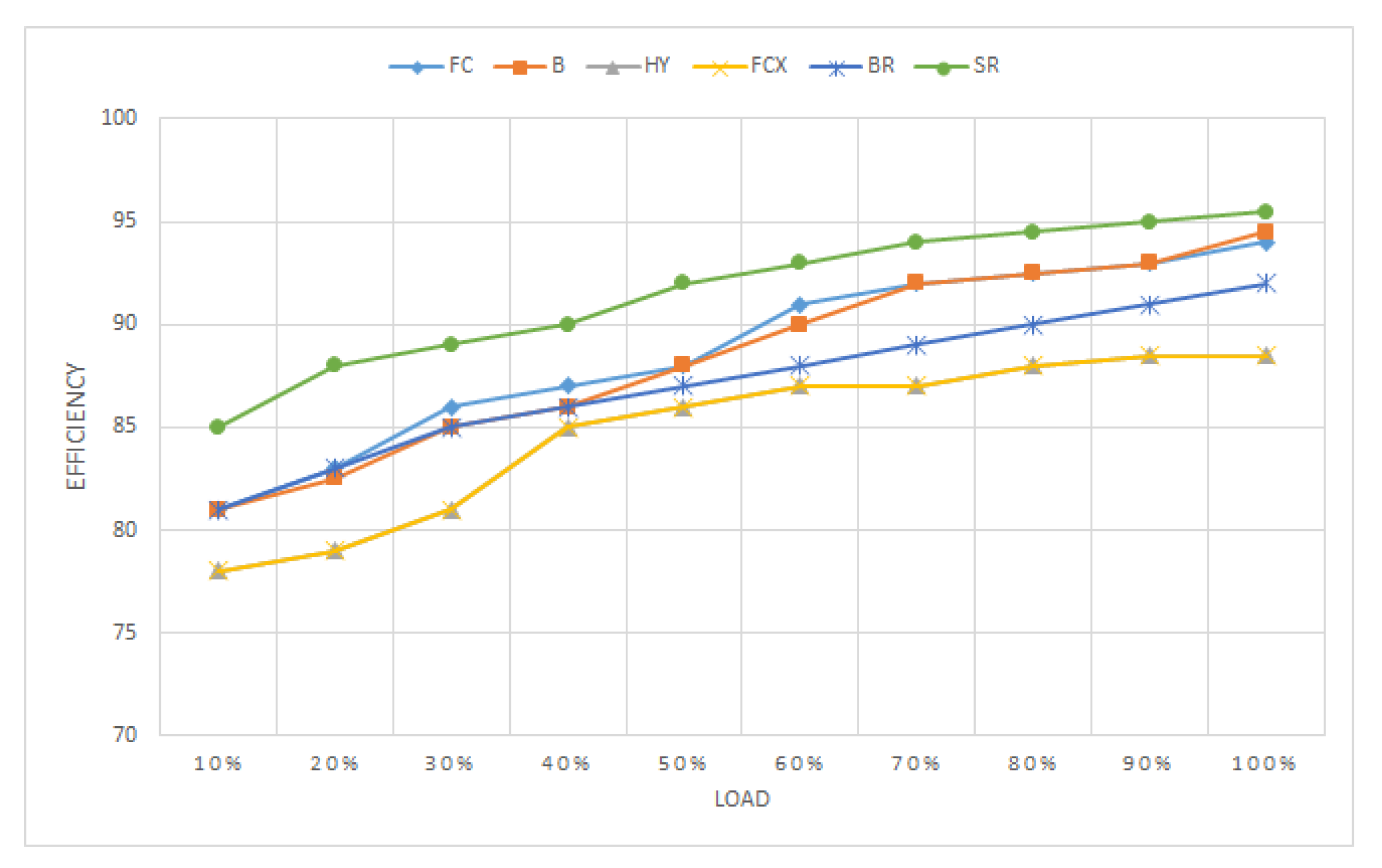
4.4. Efficiency

The efficiency of the converter under different load conditions is measured and shown in Figure 26. At full load, efficiency of the converter lies between 92% and 95% for all modes of operation except the mode FCX. Because the main goal is to confirm the operation, the focus has not been on designing the converter optimally for low load conditions. The efficiency of the converter could be further improved by using synchronous rectification for the LLC secondary and CLLC secondary circuit. This is however, out of the scope of this paper and therefore not discussed.

5. Comparison

In

Table 10. Features comparison of multi–port converters with the proposed converter.

Converter	No. of Switches	Galvanic Isolation	No. of Ports	Mode
				F	B	HY	FCX	BR	SR
[24]	5	no	4	√	√	√	x	√	x
[10]	16	yes	4	√	√	√	x	√	x
[25]	8	yes	4	√	√	√	x	x	x
[26]	8	no	3	√	√	√	√	x	√
[27]	10	no	3	√	√	x	√	x	x
[28]	11	no	3	√	√	x	√	x	√
[4]	29	no	4	√	√	√	√	√	√
Proposed	19	yes	4	√	√	√	√	√	√

, the proposed converter is compared to different multi–port converters in terms of total number of semiconductor switches, number of ports, and supported modes (with assumption that the converters can be modified to fit our application). In comparison to [4,10,24,25,26,27,28], the proposed converter is the only isolated converter that can achieve all six described modes of operation. The converters described in [26,27] are non–isolated converters that are highly undesirable in a hybrid aircraft application, where safety is of utmost importance. The four–port isolated converters described in [10,25], are partially capable of a few of the six required operation modes. However, they are both dual–active–bridge based topologies and as mentioned in Section 3.1, they are not optimal for fuel–cell applications. The concept proposed in [4] is a hybrid drive train that is fully capable of all six modes but the concept consists of diodes and multiple relays to redirect power, which results in a complex control strategy and low efficiency.

6. Conclusions

In this paper, a novel multi–directional galvanically isolated DC–DC converter which uses a battery and a fuel cell as power sources and is capable of supplying the power to a high voltage and a low voltage load is presented. In this converter, battery charging from recuperation or fuel cell is also possible. This paper gives a detailed analysis and operation of the converter for the six described modes. The converter consists of two stages. The resonant stage combines a CLLC and a LLC converter into a hybrid converter. The working principle of the resonant stage and design process is discussed. The voltage balancing stage combines a buck, boost, and buck-boost converter that achieves voltage balancing with careful switching of its six switches from two voltage sources of unequal magnitude. The mathematical relationship between the sources is determined in each mode within the voltage balancing stage. The design of the converter ensures partial soft switching of the buck-boost stage and full soft-switching of the resonant converter stage. Finally, a 1 kW designed prototype is emulated in the OP4510 real-time system, and the results of these experiments are reported, and they closely match the waveforms predicted analytically. This converter is ideal for a hybrid full-electric aircraft, which can take advantage of the different modes of operation and power flow between various sources and loads within the converter independently.