Abstract
(1) Background: Gas hydrates are historically notable due to their prevalence and influence on operational difficulties in the oil and gas industry. Recently, new technologies involving the formation of gas hydrates to accomplish various applications have been proposed. This has created new motivation for the characterization of rheological and mechanical properties and the study of molecular phenomena in gas hydrates systems, particularly in the absence of oil and under pre-nucleation conditions. (2) Methodology: This work reviews advances in research on the promotion, inhibition, rheology, and mechanical properties of gas hydrates obtained through an integrated material synthesis-property characterization-multi-scale theoretical and computational platform at McGill University. (3) Discussion: This work highlights the findings from previous experimental work by our group and identifies some of their inherent physical limitations. The role of computational research methods in extending experimental results and observations in the context of mechanical properties of gas hydrates is presented. (4) Summary and Future perspective: Experimental limitations due to the length and time scales of physical phenomena associated with gas hydrates were identified, and future steps implementing the integrated experimental-computational platform to address the limitations presented here were outlined.
1. Introduction
Gas hydrates are preferentially formed over hexagonal ice during water’s liquid-to-solid phase change in the presence of a gas molecule dissolved in the water. As the phase change begins, water molecules self-organize into a crystal lattice via hydrogen bonds, creating cage structures that can trap gas molecules found in solution [1]. The presence of the gas molecule in the cage stabilizes the lattice energy by dispersing van der Waals forces [2,3]. The gas hydrate crystallizes out of the bulk water system forming a particle mass, which continuously grows while conditions favor hydrate formation and gas molecules are available. First formally described in 1811 by Sir Humphrey Davy [4], increased research motivation came from the occurrence of gas hydrates in oil and gas industry applications identified in the early-mid 20th century [5]. Much of the research that followed focused on the prevention of gas hydrate formation and gave rise to the flow assurance engineering discipline [2].
Recently, several process technologies involving the formation of gas hydrates have been proposed. They take advantage of the physical properties of gas hydrates to help accomplish a process. The high gas-to-liquid volume ratio and the gas selectivity that occurs as gas species are trapped in hydrate cages are two important properties leveraged by the proposed technologies. These include pre- and post-combustion carbon capture from flue gas [6,7,8,9], gas storage and separations [10,11,12,13,14,15], water desalination [16] and treatment [17], or even fruit juice concentration [18]. These new research interests have motivated the study of new gas hydrate promoter additives such as carbon nanofluids [19,20]. Additionally, many of the new process technologies mentioned above involve batch and semi-batch flow systems that are found in (and near) gas hydrate formation conditions. These technologies would benefit from the rheological characterization of gas hydrate systems in the pre-nucleation stage and during hydrate formation. System viscosity information is critical in the design and control of such processes. To this end, rheological phase diagrams of methane and carbon dioxide gas hydrates in pure water have been recently developed [21].
The thermal, mechanical, and interfacial properties of gas hydrates are crucial in expanding the description of gas hydrate formation, as they help describe the structure’s interaction with the environment. These properties of hydrates have been studied for sI and sII hydrates primarily, with sH hydrate studies more recently [22,23,24,25,26,27]. For example, the mechanical properties are critical to determining the strength and flexibility of the structure, and critically understanding the effect of guests on these can determine how suitable the structure is to the desired application [24,28,29]. For example, the Young’s modulus, which is used to describe a structure’s resistance to deformation, was found to be highest for nitrogen-neohexane sH hydrates [30], helping guide further work into the strongest structure. Interfacial properties have also been studied recently to help clarify what exactly is happening at the atomic scale during gas hydrate formation [27,31,32,33,34]. By developing correlations for the surface tension as functions of temperature, physical changes in gas hydrate systems can be predicted prior to an application’s implementation, providing a foundation to the critical applications [27,35]. Other literature has also examined the use of certain surfaces to manipulate the nucleation interface for desired behavior [36,37].
Gas hydrate inhibitor research has previously focused on thermodynamic inhibitors such as ethylene glycol or methanol. However, thermodynamic inhibitors require high volumetric fractions in solution for effective inhibition. This imposes economic and operational constraints as large volumes of inhibitors lower the volumetric transport capacity of process streams and incur high operational costs [2]. Recent work on gas hydrates inhibitors has focused on kinetic hydrate inhibitors (KHIs) as they are effective at lower concentrations (below 1 wt.%) compared to thermodynamics inhibitors [38]. Promising candidates for kinetic hydrate inhibition tend to have the ability to adsorb to the surface of polar hydrate crystal surfaces while also being soluble in water [39,40]. This can be achieved by the activity of hydrophobic and hydrophilic groups, respectively, which makes amphiphilic block copolymers an attractive choice for kinetic hydrate inhibition [41,42]. Some other breakthrough studies on promotion and inhibition include work on the effect of a magnetic field [43,44] on formation, the use of anti-agglomerants [45], the mixed effects of metal nanoparticles on methane hydrate formation [46], and the impact of wax molecules on methane hydrate formation [47,48,49,50,51].
The rheological characterization of gas hydrates requires the use of highly specialized and costly experimental equipment [52,53,54,55,56]. This restricts the ability of such research to be conducted. Additionally, our group has reported experimental limitations (kinetic, diffusion, and heat effect) to high-pressure rheology experiments of pure water gas hydrates [21]. Recent work on the inhibitory and promotional activities of gas hydrates has pointed towards molecular scale phenomena, which can be difficult to describe through experimental methods alone fully [19,41]. A variety of computational research methods can be utilized to solve such problems, including density functional theory (DFT) and molecular dynamics (MD).
This manuscript is intended to inform experimental research groups of the benefits associated with incorporating computational methods to further their research and vice versa—inform computational research groups of inherent limitations faced by experimentalists. This type of cross-discipline information transfer is sometimes lost in literature as experimental and computational research articles are not always presented with each other’s points of view in mind. We provide evidence of these benefits by reviewing the research accomplishments (experimental and computational) based on this integrated platform by our group at McGill University. We further support this by reiterating the main conclusions and limitations we have identified in our experimental research, which point toward molecular time- and length-scale phenomena in gas hydrate systems. Currently, these phenomena are difficult, if not impossible, to be experimentally explored. We begin with a description of experimental equipment and computational methodologies available to our group, followed by research findings regarding gas hydrate nanofluid promoters, polymer inhibitors, interfacial phenomena during hydrate growth, and the characterization of mechanical properties and system rheology. Finally, we conclude with a future perspective on significant research topics on gas hydrates that may be pursued using the presented computational methods, provided the experimental insight, to continue to add to the knowledge base on gas hydrates properties and their applications.
2. Tools and Methods
2.1. Experimental
2.1.1. Gas Hydrate Kinetics
Gas hydrate kinetic experiments require a controlled temperature and pressure environment for reliable measurements. To achieve this, a custom-built stainless steel (316) cylindrical crystallizer reactor was commissioned to be used by all gas hydrate growth kinetics studies presented in this review. It has a volume of 610 mL and is rated to withstand up to 20 MPa. The main chamber has two polycarbonate windows that were used for direct visualization. Liquid and gas phase temperatures and the pressure of the crystallizer were monitored throughout the experiments. A magnetic stirrer was used during hydrate formation at 525 RPM. The entire crystallizer reactor was submerged in a 50/50 volume mixture of ethylene glycol and water which was circulated through a chiller to maintain it at the desired temperature for hydrate formation. Further detailed explanation of experimental procedures and depiction of equipment used can be found elsewhere [19,20,57,58]. This reactor was used to examine the effects of various additives, such as hydrophobic and hydrophilic multi-walled carbon nanotubes (MWCNT), amine-functionalized MWCNT [58], polyvinylpyrrolidone (PVP) [41], amphiphilic block copolymers [42], and hydrophobic and hydrophilic graphene nanoflakes (GNF) [19] on the kinetics of gas hydrate growth.
2.1.2. Nanoparticles Additives
The carbon nanoparticles explored were produced and characterized by the Plasma Processing Lab at McGill University. The graphene nanoflakes were oxygen functionalized via a two-stage process. First, an argon plasma induces homogeneous nucleation of critical carbon clusters in a methane-nitrogen feed, which results in pure graphene sheets. In the second stage, the air is fed to the system, and the oxygen present interacts with the graphene surface and hydrophilic groups such as carboxylic or oxide groups are formed on the surface. The oxygen functionalized graphene nanoflake (O-GNF) produced by this process is 100 × 100 nm with approximately 14% oxygen atomic content. Detailed information on O-GNF production and characterization can be found in U.S. Patent US20160376153A1 and in the work by Legrand et al. [59]. Similarly, oxygen functionalized multi-walled carbon nanotubes (O-MWCNT) were also produced in two stages. The first stage involves the use of acetylene as a carbon source in a gas deposition process which results in MWCNTs deposited on a stainless steel mesh. In the second stage, MWCNTs are exposed to a 20 W capacitively-coupled radio frequency (RF) glow discharge in a gas mixture consisting of argon, ethane, and oxygen. This process causes covalent bonds between hydrophilic oxygen functional groups such as hydroxyl, carboxyl, and carbonyl, and the MWCNT surface. Oxygen makes up approximately 20% of the surface produced on an atomic basis. Alternatively, the second stage can expose the surface to a gas mixture of argon, ethane, and ammonia, which would result in the amine functionalization of the surface with groups that include amine, imine, nitrile, and amide. Detailed descriptions of the production and characterization of MWCNTs are found in work by Hordy et al. [60].
2.1.3. Polymer Additives
Several variations of hydrophobic and hydrophilic polymer structures were investigated to determine their kinetic hydrate inhibitory capacity. Some of the commonly available polymers used to investigate inhibitory activity on gas hydrate growth are polyvinylpyrrolidone (PVP), with average molecular weights of 10,000 g/mol (PVP10), 40,000 g/mol (PVP40), or 360,000 g/mol (PVP360). Additionally, specialized amphiphilic block copolymers were synthesized. The amphiphilic block copolymers were produced with a hydrophilic member constituting of either (1) polyvinyl alcohol (PVA), (2) poly(N-vinylpyrrolidone) (PVP), or (3) poly(vinylcaprolactam) (PVCap) combined with a hydrophobic member of either (a) poly(styrene) or (b) poly(pentafluorstyrene). These were synthesized through a simplified reversible addition-fragmentation chain transfer (RAFT) procedure. The synthesis procedures and polymer characteristics were elaborated at length elsewhere [41,42].
2.1.4. Rheometry
Rheological experiments involving gas hydrates were performed with a custom-built Anton Paar MCR302 shear rheometer equipped with a gas-pressurized high-pressure cell rated to 40 MPag. To our knowledge, this is one of two units found in the world, the only one currently being used for research, the second is kept by the in-house engineering team of Anton Paar. The rheometer uses a magnetic coupled head to induce a rotational force on the measurement geometry. A double-gap measurement geometry was used to record viscosity measurements. The rheometer’s pressure cell was temperature controlled by a circulating current Julabo-F32 chiller with a 50/50 volume mixture of ethylene glycol and water as the thermal fluid. Pressures above those safely available from a gas cylinder (over 10 MPag) were achieved using a Schlumberger DBR positive displacement pump to compress an isolated sample of gas, which was then instantaneously charged into the rheometer at the start of test runs. Further details on experimental procedures and depiction of the equipment can be found elsewhere [21].
2.2. Computational Methods
2.2.1. Molecular Dynamics
Molecular dynamics (MD) simulations are accomplished by the numerical integration of Newton’s equations of motion in a molecular scale system. In a MD simulation, the positions of atoms and how they are bonded are defined in the simulation space. Their positions relative to each other lead to a calculation of their potential energy. The potential energy of the system is determined based on the interactions between the atoms in the system. The total potential energy consists of bonded and non-bonded interactions (Equations (1)–(3)). Generally, bonded interactions such as the bond, bond angle, and dihedral energies are represented by harmonic models (Equation (4)). Non-bonded potential energy arises from electrostatic and van der Waals interactions. Electrostatic potential energy is represented by Coulombic pair-wise interactions (Equation (5)), while van der Waals tends to be represented by the Lennard-Jones (LJ) 12/6 potential (Equation (6)).
In the Equations (1)–(6), , , and , are harmonic force constants, k is Coulomb’s constant, is the distance for zero potential energy in the LJ potential, is the depth of the LJ potential well, is the distance between atoms i and j, and are the partial charges of atoms i and j.
Based on the description above, MD simulations use atom positions to determine the system’s potential energy, the forces imposed between atoms, the resultant accelerations due to the forces imposed, and their instantaneous velocities. The algorithm then takes one unit time step to determine the change in position of all atoms using their calculated instantaneous velocities. This process is repeated to produce trajectories of all atoms in the system through time. The result is a dynamic simulation that can be simulated in the time scale between picoseconds to several hundred nanoseconds. This type of computational methodology is widely used to explore a variety of topics such as material properties [61,62] or interfacial phenomena [63,64,65,66]. For our research group, one of the opportunities associated with the use of molecular dynamics is the ability to explore length and time scales as well as conditions not readily available to experimental work.
The previous description is a simplified explanation of the general steps involved in molecular dynamics simulations. Details on the specific considerations can be found in the classic MD textbook by Rappaport [67]. Moreover, the application of MD normally requires the use of an MD package. Large-scale Atomic/Molecular Massively Parallel Simulator (LAMMPS) is a widely used molecular dynamics package developed and maintained by Sandia National Laboratory and Temple University [68]. It offers a robust and adaptable methodology to implement various force field representations of potential energy (e.g., OLPS [69], CHARMS [70,71], GROMOS [72], AMBER [73]). LAMMPS enables users to simulate using the canonical (NVT), microcanonical (NVE), and isothermal-isobaric (NPT) ensembles, providing a wide range of statistical mechanical tools for the development of physically meaningful estimations of macroscopic properties. Additionally, other auxiliary software packages such as PACKMOL and Moltemplate are important in the development of molecular systems. PACKMOL is a random position generation and optimization algorithm that helps to minimize inter-molecular repulsive forces and thus the potential energy of the system in its initial state [74]. Moltemplate is a python package used to systematically assign force field parameters to all atoms in a molecular simulation [75]. These packages are used together by our group to develop MD simulations capable of modeling molecular scale phenomena in gas hydrate systems.
2.2.2. Density Functional Theory
Density function theory (DFT) is another reliable tool to investigate the properties of gas hydrate systems and validate experimental work. It has proven to be successful in investigating various properties of gas hydrates, including the infrared and Raman spectra of these systems [22,76,77,78,79]. Using DFT to predict material properties provides a first-principles, low-cost approach to the formulation of engineering solutions. Several physical characteristics can be derived from the total energy of the structure, which is computed by solving the time-independent Schrödinger equation. This computation can be performed with various DFT packages, but most commonly used are the Vienna Ab initio Simulation Package (VASP) [80,81,82] and the Spanish Initiative for Electronic Simulations with Thousands of Atoms (SIESTA) [83]. Using periodic boundary conditions, reasonable initial geometric data for the structure, and accurate pseudopotentials, the Kohn–Sham equation can be self-consistently solved. The key difference between these methods involves the basis set: for VASP, plane waves are employed, while for SIESTA, a linear combination of atomic orbitals (LCAO) is used. Our research group found that the norm-conserving pseudopotential composed of a double zeta polarized basis set performed best in SIESTA.
Infrared spectroscopy (IR) is a critical part of fundamental material characterization and description. Deriving material properties from vibration properties can provide a simpler way to determine constant and material properties when compared with direct experiments. Spectra could be measured on site and the material properties of the structure of interest can be derived. Therefore, our group calculated the IR spectra of sII [22,76] and sH [77] gas hydrates in DFT and related them to their material properties. The Vibra utility was utilized with SIESTA to compute the vibration frequencies necessary to obtain the characteristic infrared spectra of the system. This involved an initial geometric relaxation of the unit cell, followed by applying the finite difference method, where each atom of the cell is moved in six different directions (). Then, the force constants and Born charges were calculated and used to construct the dynamical matrices necessary to obtain the IR intensities. The raw intensities were convoluted with a Lorentzian function to obtain a spectrum that would be continuous and comparable to experiments [84].
To move from IR spectra to material properties, it is necessary to make some assumptions. The vibrational frequency of a simple harmonic oscillator is given by [85,86]
where and are the mass of atom 1 and 2, respectively, in kg, k is the bond force constant in N·m, c is the speed of light in cm·s, and is the bond stretching frequency in cm. If the covalent OH bonds and the hydrogen bonds in gas hydrates are considered simple harmonic oscillators, the IR intensities can be input into Equation (7) to solve the bond force constants. With this relationship, a lower frequency is associated with a lower bond strength and a higher frequency with higher bond strength. With the calculated bond force constant now available, the Young’s modulus can be calculated using [87]
where is the equilibrium bond length in m, k is the bond force constant in N·m and E is the Young’s modulus in GPa. Therefore, using Equation (7) in combination with (8), the Young’s modulus of gas hydrates can be established from its infrared spectrum, specifically its hydrogen bond force constant [76,88]. Figure 1 shows a schematic of how theoretical and computational methods integrate a multiscale approach to characterize the material properties of gas hydrates.
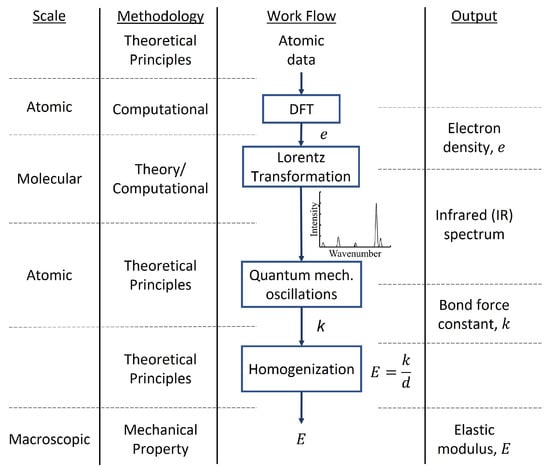
Figure 1.
Workflow diagram illustrating the integration between computational methodologies, the scales of their application, and the output from each methodology.
3. Effects of Additives on Hydrate Growth
3.1. Multi-Walled Carbon Nanotubes
Multi-walled carbon nanotubes are hydrophobic as produced. Once either oxygen or amine becomes functionalized through a plasma process, as described above and detailed in Hordy et al. [60] and Legrand et al. [59], the material becomes hydrophilic. The hydrophilicity affects the material’s ability to form hydrogen bonds in water. The effect of as-produced hydrophobic MWCNT and functionalized hydrophilic MWCNT on the growth kinetics of methane and carbon dioxide gas hydrates were explored. Oxygen functionalized MWCNT were used to examine their effects on methane systems, while amine functionalized MWCNT were used for carbon dioxide systems. The groups found on the surface of MWCNT after amine functionalization can form temporary bonds with carbon dioxide [89,90,91]. This makes this type of functionalization relevant to carbon dioxide gas hydrates systems.
The crystallizer system described above was used to measure system pressures and temperatures to study the growth kinetics of MWCNT-loaded systems. In the case of methane hydrates systems, both the hydrophobic and hydrophilic (oxygen functionalized) MWCNTs enhanced the growth rates of methane hydrates compared to pure water baselines. Hydrophobic MWCNT enhanced growth rates by approximately 6% (5 and 10 ppm MWCNT), while hydrophilic MWCNT enhanced growth rates by as high as 16.3% (0.1 and 10 ppm MWCNT) [57]. Previous research has observed the increase in gas mass uptake into aqueous solutions containing nanoparticles [92,93,94], and that the interfacial area between liquid and gas phases increases in the presence of nanoparticles [94]. This work pointed toward this same effect for the case of MWCNT. The loading of nanoparticles in the system was also observed to affect the growth rate enhancement of hydrates. Concentrations above 1 ppm of hydrophobic MWCNT were found to have enhancement effects, while hydrophilic MWCNT was observed to have two regions of enhancement. At 0.1 ppm, the system experienced maximal enhancement, followed by a decrease at 0.5 and 1 ppm. Finally, the growth rate enhancement continued linearly between 5 and 10 ppm [58]. The two regions of enhancement were attributed to diffusivity enhancement from micro-scale liquid volume displacement from Brownian motion at low loading followed by free mean path limitations overcoming this diffusivity enhancement at high loading [57].
Identical experimental studies were performed to investigate the effects of amine-functionalized MWCNT in carbon dioxide hydrate systems. Both as-produced hydrophobic MWCNT and hydrophilic amine functionalized MWCNT were found to enhance carbon dioxide hydrate growth at lower concentrations, which was attributed to enhanced mass transfer effects [58]. However, for similar loading concentrations, the hydrophilic functionalized MWCNT were observed to enhance hydrate growth to a greater extent than as-produced MWCNT due to its greater affinity to carbon dioxide molecules [58]. Decreases in growth rate enhancements at higher loading concentrations were attributed to heat effect limitations from the nucleation of larger amounts of hydrates. The temperature increase from the exothermic crystallization reaction was found to be high enough to self-limit further hydrate formation. Additionally, it was found that the presence of amine-functionalized MWCNT did not have any considerable effect on the solubility or rate of dissolution of carbon dioxide in water [58]. Generally, the results from hydrophobic and hydrophilic MWCNT studies have pointed towards mass transfer enhancements arising from molecular scale phenomena of nanoparticles on the systems, which can be overcome by increased nanoparticle loading. Insight into the fundamental phenomena involved in these observations may be achieved from computational methods such as molecular dynamics.
3.2. Graphene Nanoflakes
The crystallizer experimental setup described above was also used to investigate the effect of as-produced (hydrophobic) and oxygen functionalized (hydrophilic) graphene nanoflakes (O-GNF) on the growth rates of methane gas hydrates. Similar to the results for the MWCNT studies described above, both hydrophobic and hydrophilic forms of GNF enhanced the methane hydrate growth rates measured compared to measurements performed in pure water baselines [19]. However, the enhancements were much larger than those observed in the presence of MWCNT. Enhancements as great as 101% for as-produced hydrophobic GNF (1 ppm GNF), and as high as 288% for hydrophilic oxygen functionalized GNF (5 ppm O-GNF) were estimated [19]. Both maximums in growth rate enhancements measured were followed by decreased enhancements at higher loading. Nanoparticle loading effects on hydrate growth rate enhancements were attributed to small and large-scale agglomeration effects combined with mean free path limitations. It was reported that hydrophobic as-produced GNF could experience agglomeration at lower loading concentrations in solution and thus result in limited enhancements to hydrate growth [19]. As loading increases, agglomeration is overcome by the increased liquid–gas interfacial area available for mass transfer, which causes gains in the hydrate growth enhancement achieved. However, at the highest loading, large-scale agglomeration becomes the dominant effect resulting in the reduction in the enhancement effect. The use of hydrophilic O-GNF in solution was observed to dramatically increase hydrate growth rates up to 288% in a linear fashion [19]. In the case of hydrophilic O-GNF, agglomeration did not play a big role in the effects observed. Instead, the enhancement was attributed to increased diffusivity and mass transfer at lower concentrations. These effects were negated by reduced free mean paths at mid-range loading concentrations (5 ppm) [19]. Finally, at the highest loading concentration (10 ppm), the free mean path limitations were described to be overcome by the increased O-GNF surface area available to methane.
The results reported for graphene nanoflakes point to similar load effects on hydrate growth rates as the ones described for MWCNT. Hydrophobic and hydrophilic GNF and MWCNT were described to interact differently between themselves and with the system, creating limitations to gas hydrate growth rate. For both types of nanoparticles, the enhancements observed fell under different regions of nanoparticle load effect leading to an overall non-monotonic load effect. Different molecular scale phenomena were used to explain the non-monotonic behavior. Agglomeration, diffusivity, free mean path, and nanoparticle surface area were provided as possible contributors to the detected effect. Most, if not all, of these may be further examined computationally. Due to their scale, molecular dynamics is a promising methodology for further examination of these recently characterized effects.
3.3. Polymer Inhibitors
The initial consideration of kinetic hydrate inhibitors (KHIs) involved commercially available poly(vinylpyrrolidone) (PVP). The efficacy of hydrophobic PVP as a gas hydrate inhibitor was quantified by its effect on methane hydrate growth rate and on the concentration of methane in the liquid phase [95,96]. PVP with different molecular weights were used—10,000 g/mol (PVP10), 40,000 g/mol (PVP40), and 360,000 g/mol (PVP360)—over a range of loading concentrations (0.07 to 20,000 ppmw). PVP was shown to lose inhibitory capacity with increased reactor pressure (increased hydrate pressure driving force) and various molecular weights (polymer chain lengths) were shown to have little impact on the inhibitory activity at a given loading concentration [95]. It was determined that PVP had a negligible effect on methane solubility in water and a significant effect on the supersaturation of methane during hydrate growth [95,96]. The higher liquid concentration was attributed to a reduction in surface area available for hydrate growth due to the uptake of methane by PVP as it adsorbs to the hydrate crystal surface [96].
Amphiphilic molecules have both hydrophilic and hydrophobic subunits or groups and can act as surfactants in solvating a hydrophobic species or material in a hydrophilic solvent. The use of amphiphilic block copolymers as KHIs were explored in various forms. Three types of block copolymers were studied (1) poly(vinyl alcohol) (PVA), (2) poly(vinylpyrrolidone) (PVP), and (3) poly(vinyl caprolactam) (PVCap) hydrophilic base units [41,42]. These base units were combined using a switchable RAFT chain transfer agent (CTA) to attach relatively short poly(styrene) (PS) or poly(pentaflourostyrene) (PPFS) hydrophobic segments. The reduction in methane consumption during the hydrate growth phase was measured for systems inhibited by each block copolymer and compared to base inhibition by commercially available homopolymers PVP and PVA. Details on the experimental setup and procedures are found elsewhere [41,42]. The key results are summarized in Table 1, where columns contain hydrophilic segments while rows contain hydrophobic segments of the copolymer. Values in Table 1 correspond to the block copolymer combination between the segments (e.g., 49% for PVA-PS and 76% for PVP-PPFS). Additionally, Table 1 contains the reduction of methane consumption for hydrophilic PVA, PVP, and PVCap KHIs on the first row.

Table 1.
Reduction in methane gas mole consumption during hydrate growth phase for hydrophilic polymers PVA, PVP, and PVCap, and amphiphilic block copolymer combinations of PVA, PVP, PVCap with PS and PPFS [41,42].
Amphiphilic molecules tend to agglomerate and form micelles when above their critical micelle concentration (CMC) [97]. For instance, in a hydrophilic solvent, the hydrophobic groups in amphiphilic molecules agglomerate to form micelles when above their CMC; likewise, the hydrophilic groups can initiate micelle formation in a hydrophobic solvent. The formation of micelles can obstruct or limit the surfactant activity of amphiphilic molecules and thus reducing their inhibitory capabilities in the context of gas hydrate growth. As such, the CMC is an important characteristic of amphiphilic block copolymers and they were determined for the various block copolymers examined by Rajput et al. [41,42]. There are several methods adequate for measuring CMC of polymer solutions, including density and viscosity, light scattering, and surface potentials [98,99,100,101]. In the work by Rajput et al. [41,42], the zeta surface potential was shown to be a viable method for KHIs [41,42]. Table 2 summarizes the CMCs for the copolymers considered. Block copolymers with lower molecular weights and lower mole fractions of hydrophobic monomers were measured to have higher CMC [41,42]. This is an important consideration when designing new amphiphilic gas hydrate inhibitors.

Table 2.
Critical micelle concentration (CMC) for all amphiphilic block copolymer gas hydrate inhibitors examined by Rajput et al. [41,42].
The mechanism of gas hydrate inhibition by polymers has not been completely characterized but remains best understood as an adsorption process. The inhibitor’s hydrophilic groups adsorb on the surface of the growing hydrate crystal through hydrogen bonding, limiting its surface area available for gas mass diffusion, or the inhibitor’s hydrophobic groups can interact with hydrophobic gas to limit their availability at the hydrate–liquid interface [102]. However, to further characterize the behavior of the liquid–hydrate interface in the presence of inhibitors, molecular dynamics simulations can offer an insight into the molecular scale phenomena that occur. The initial efforts of our group to this end have been the characterization of the gas hydrate interface in the absence of inhibitors. These novel results will be discussed in the following section.
4. Interfacial Effects
The temperature and pressure effects on gas hydrate systems and their precursors form a critical aspect of understanding the crystal’s nucleation and growth. Therefore, our group initially studied these effects on the methane-water interfaces under formation conditions. We could determine the temperature and pressure dependence of interfacial thickness and interfacial tension, with excellent agreement with the experiment [65]. As natural gas is composed of methane, ethane, and propane, we also characterized the water-methane, ethane, and propane gas interface in a similar manner. In this natural gas system, the gases are sequentially adsorbed on the interface in order of size. Moreover, the interfacial tension varied inversely with both pressure and temperature. These results were crucial to guiding our work into more complex systems with gas hydrate crystals [66]. Given the lack of information surrounding sI gas hydrate surface tension and surface energy, some critical questions remained, namely the type of nucleation that occurs [103,104,105,106,107]. We used MD to show that film-shaped nucleation has the lowest work of formation and homogeneous nucleation has the highest work of formation, with the general trend being film-shaped, cap-shaped, lens-shaped, and homogeneous nucleation in work of formation. This was due in part to the formation of a quasi-liquid pre-melting layer that favors lens-shaped over homogeneous nucleation. This detailed nucleation analysis also showed that using ice properties in place of hydrate properties would yield much larger nucleation rates which cause problems in process modeling and behavior prediction in engineering processes [64].
In the MD work, we used the novel NPAT ensemble to maintain a constant cross-sectional area and constant pressure normal to the interface to avoid frequent manual pressure corrections and high-frequency pressure fluctuations that would affect the surface tension [108,109,110]. Additionally, it proved critical to include the effect of elastic deformation of the hydrate structure using the Shuttleworth Equation, shown in Equation (9),
where A is the interfacial area, is the interfacial free energy (assumed to be equal to the surface tension) [111,112], is equal to the interfacial tension calculated based on Bakker’s method, [113] and is the tail correction developed by Blokhuis et al. [114] to account for truncation errors arising from setting a cutoff distance for atomic interactions [114,115,116]. These techniques and corrections led to the production of correlations demonstrating largely linear trends for the temperature dependence of surface tension in methane hydrate-water systems [27]. Direct numerical simulations validated and expanded our results. We used these simulations to compute the excess entropy and enthalpy of the interface to demonstrate that increasing temperature increases structural disorder. The excess surface entropy differed by 0.88% when calculated with direct numerical simulation compared to interfacial theory. The charge distribution, radial pair distribution function, and the hydrogen bond density at the interface confirmed our simulations as well [27]. These simulation results led to concrete engineering applications in environmental and industrial projects. For example, by showing the effect of charge density on interfacial tension, we can provide data to develop methods of controlling nucleation by applying an electric field to the system [117,118,119].
5. Mechanical Properties
The vibrational spectra of structure II [76] and structure H [77] were investigated with DFT and vibrational analysis tools, as they provide information on the structures’ resistance to elastic deformation and stress behavior. Our work showed that there is an agreement between the experimental/theoretical findings for Young’s modulus and the IR-based calculated methods, as shown in Table 3. Differences seen can occur because of the DFT simulations’ exclusion of anharmonic effects coming from the assumption that the bonds behave as harmonic oscillators, the chosen exchange-correlation function, and the fact that DFT performs calculations at zero kelvin while vibrational properties are often temperature dependent.

Table 3.
Equilibrium Hydrogen Bond Length, Force Constants, and Young’s Moduli for sII [24,76] and sH [30,77] Gas Hydrate Systems.
Table 3 shows that guest molecules weaken the hydrogen bonds as seen by the lower hydrogen bond force constants. In turn, the Young’s modulus are lower when compared to the empty structure. The simple harmonic oscillator approximation does not apply to the OH bonds of hydrates, and thus, Young’s modulus is calculated based on the bond force constant of the hydrogen bonds only. Our work also showed that the IR Young’s modulus increases with compression due to the strengthening of the hydrogen bonds [76,77]. The correspondence between the two different methods to calculate Young’s modulus shows the critical role that hydrogen bonds play in the strength of the hydrate structure. Additionally, the guests interact with the backbone via hydrogen bonds and this interaction is what drives the differences between the two final results. As one of the most important mechanical properties, a reliable prediction of Young’s modulus is critical. By showing that DFT can be used to generate spectrographic data, we have provided a methodology that would allow for both the prediction of a spectrum and determination of Young’s modulus from that spectrum, a new method that could be used onsite and in the field to characterize materials.
6. Rheology
As previously mentioned, the opportunity to develop new technologies that do not involve oil in the system has created the need for further characterization of the flow properties of pure water gas hydrate systems. Furthermore, extending the experimental conditions is necessary to explore further regions of the gas hydrate phase diagram. To that end, recent efforts were undertaken to characterize the rheology of methane and carbon dioxide gas hydrate systems in pure water at McGill University. Our research group has used the uniquely capable shear rheometer (described above) to develop novel rheological phase diagrams for methane and carbon dioxide gas hydrates (Figure 2 and Figure 3) [21]. Additionally, the viscosity of pre-nucleation gas hydrate systems were reported. The experimental program extended the previously established maximum pressure in rheological studies involving gas hydrates from 10–15 MPag [52,53,54,55,56] to 30 MPag [21].
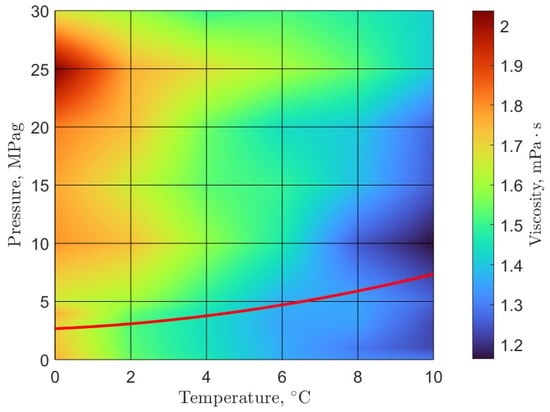
Figure 2.
Rheological phase diagram of methane gas hydrates: the viscosity of pre-nucleation and early hydrate formation systems overlayed with the three-phase hydrate-liquid-gas equilibrium line (red line); equilibrium data from Carroll in Natural Gas Hydrates [3]; figure adapted from Guerra et al. [21].
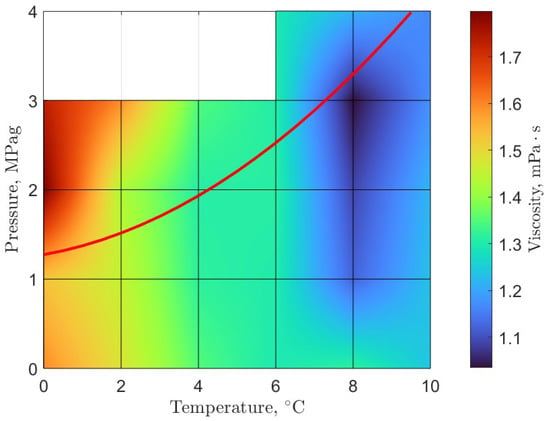
Figure 3.
Rheological phase diagram of carbon dioxide gas hydrates: the viscosity of pre-nucleation and early hydrate formation systems overlayed with the three-phase hydrate-liquid-gas equilibrium line (red line); equilibrium data from Carroll in Natural Gas Hydrates [3]; figure adapted from Guerra et al. [21].
This work found a three-stage gas hydrate formation process characterized by the evolving viscosity of the system. In the initial hydrate growth stage (Figure 4a), an increase in viscosity up to several hundred centipoises was observed. This was followed by a slurry stage (Figure 4b), in which viscosity decreased to as low as 100 cP and varied without a considerable net increase in average viscosity. In the final stage (Figure 4c), the pseudo-stable slurry was overcome by sustained hydrate growth and resulted in an increase in viscosity up to a maximum measurement. The intermediate slurry stage indicated a system state in which hydrate formation seemed to be limited. In addition to this observation, several high-pressure driving force conditions (upwards of 4.1 MPag above equilibrium pressure) failed to form gas hydrates in the 24-h window allowed for hydrate formation. These indicate system limitations to the formation of gas hydrates in the rheometer system. The work categorized these limitations as arising from kinetic, mass diffusion, and heat of crystallization effects [21]. These limitations add to the difficulties involved in the experimental study of gas hydrate rheology. The future development and validation of computational models that can accurately predict viscosity and other transport properties of gas hydrate systems will facilitate the study of such systems and it is currently a focus of research by our group.
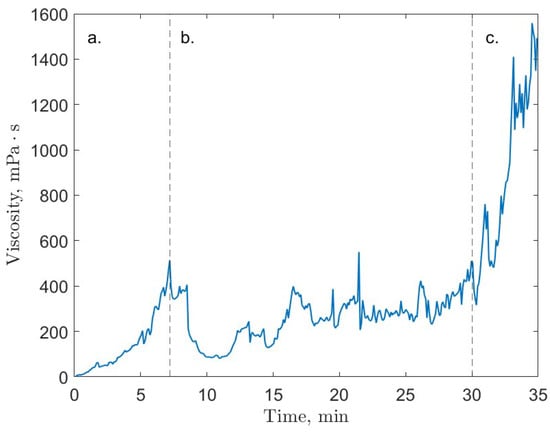
Figure 4.
An example of the three stages of gas hydrate growth as characterized by the system’s viscosity; carbon dioxide test run at 2 °C and 30 MPag; (a) initial growth, (b) slurry stage, (c) final growth; figure adapted from Guerra et al. [21].
7. Summary
7.1. Concluding Remarks
We have presented here several experimental findings where limitations to gas hydrates research associated with (1) experimental conditions and equipment requirements, and (2) the time- and length scales of associated phenomena were identified. Additionally, results from experimental work have suggested molecular scale phenomena as potential causes for macroscopic experimental observations. As the research in the field of gas hydrates advances, computational approaches and theoretical models become important methodologies to continue to expand scientific knowledge in areas such as inhibition and promotion mechanisms, rheology of nanofluid promoted, or polymer inhibited gas hydrate systems, or the mechanical properties of gas hydrates.
We have presented how the integration of experimental and computational methods has successfully modeled phenomena such as interfacial tension effect on the transport of mass, predicted mechanical properties of hydrates, and produced the infrared spectra of sII and sH hydrates from first principles. Computational methods informed by experimental data and previous insight have been crucial to the advancement of gas hydrate research. Molecular dynamics offers a strong computational approach to exploring the molecular length scale, the nanosecond time scale, and various temperature and pressure conditions rooted in the fundamentals of statistical thermodynamics. Density functional theory is a tool well suited for exploring atomic scale phenomena but under theoretical conditions, which are then corrected to real conditions.
The authors would like for this work to inform experimental and computational researchers of the benefits of the interdisciplinary approach in the context of gas hydrate research. Knowledge transfer between groups is not always efficient solely through publication. As presented here, the adoption of computational methods or direct collaboration with experimental groups (or vice versa) can improve the rate at which new discoveries are reported in the gas hydrates field.
7.2. Future Topics to Be Explored
A main theme in this review is the integrated aspect of the experimental and computational platform presented. Experimental results have guided the computational work and discoveries presented above. Based on the research reviewed above, an important new direction of research may be to extend the scope of rheological characterizations of gas hydrate systems beyond experimental limits on conditions and equipment. The results presented in Section 6 indicate molecular length scale phenomena, which can be explored with the help of MD or DFT. We have also recently collected and reported experimental observations on the rheological behavior of high-pressure methane gas hydrate systems promoted by plasma functionalized graphene nanoflakes and multi-walled carbon nanotubes, which have been submitted for publication (presently in the peer-review process). The observed behavior may have molecular scale sources, which may be investigated through MD simulations. Additionally, we are currently experimentally examining the effects of polymer inhibitors, such as PVP, on the viscosity of methane gas hydrate systems, and how they compare to uninhibited systems, with a particular interest in the role of shear rates on the formation of gas hydrates in a shear rheometer.
Moreover, we are currently performing molecular dynamics simulations of methane and carbon dioxide gas hydrate systems in pure water. These efforts intend to validate the estimations of transport properties of such systems from MD simulations by comparison to experimental results [21]. The determination of the performance of various force field potentials in the context of gas hydrate systems under pre-nucleation conditions will also be examined. These MD results may lead to the exploration of alternative forms of force field potentials to be developed for gas hydrate applications by a combination of MD, DFT, and novel machine learning and artificial intelligence techniques to accelerate workflow and further contribute new scientific knowledge.
Author Contributions
Conceptualization, A.G., S.M. and A.D.R.; methodology, A.G. and S.M.; writing—original draft preparation, A.G. and S.M.; writing—review and editing, M.M., P.S. and A.D.R.; visualization, A.G., S.M. and A.D.R.; supervision, A.D.R., P.S. and M.M.; project administration, A.D.R.; funding acquisition, A.D.R., P.S. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
Financial support for the work presented here was received from the Natural Sciences and Engineering Research Council of Canada (NSERC) through the Canada Graduate Scholarship Doctoral (CGS-D) award, NSERC grant number 206269, NSERC grant number 206259, Fonds de Recherche du Québec Nature et technologies (FRQNT) bourse de doctorat en recherche, and from the McGill Engineering Doctoral Award (MEDA).
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Acknowledgments
The authors acknowledge the support from Digital Research Alliance of Canada, Calcul Quebec, and WestGrid through computational resource grants, expertise, and technical support.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| AMBER | Assisted model building with energy refinement |
| CHARMM | Chemistry at Harvard macromolecular mechanics |
| CMC | Critical micelle concentration |
| DFT | Density functional theory |
| GNF | Graphene nanoflakes |
| GROMOS | Groningen molecular simulation |
| IR | Infrared |
| KHI | Kinetic hydrate inhibitor |
| LAMMPS | Large-scale atomic/molecular massively parallel simulator |
| LCAO | Linear combination of atomic orbitals |
| LJ | Lennard–Jones |
| MD | Molecular dynamics |
| MWCNT | Multi-walled carbon nanotubes |
| O-GNF | Oxygen functionalized graphene nanoflakes |
| O-MWCNT | Oxygen functionalized multi-walled carbon nanotubes |
| OPLS | Optimized potentials for liquid simulations |
| PPFS | poly(pentaflourostyrene) |
| PS | poly(styrene) |
| PVA | poly(vinyl alcohol) |
| PVCap | Poly(vinylcaprolactam) |
| PVP | Poly(vinylpyrrolidone) |
| RAFT | Reversible addition-fragmentation chain transfer |
| SIESTA | Spanish initiative for electronic simulations with thousands of atoms |
| VASP | Vienna ab initio simulation package |
References
- Ripmeester, J.A.; Alavi, S. Clathrate Hydrates: Molecular Science and Characterization; Wiley-VCH: Weinheim, Germany, 2022; Available online: https://mcgill.on.worldcat.org/oclc/1301543108 (accessed on 15 June 2022). [CrossRef]
- Sloan, E.; Koh, C. Clathrate Hydrates of Natural Gases, 3rd ed.; Taylor and Francis: Boca Raton, FL, USA, 2008. [Google Scholar]
- Carroll, J. Natural Gas Hydrates: A Guide for Engineers, 3rd ed.; Gulf Professional Publishing: Calgary, AB, Canada, 2014. [Google Scholar]
- Davy, H. On some of the combinations of oxymuriatic gas andoxygene, and on the chemical relations of these principles, to inflammable bodies. Philos. Trans. R. Soc. 1811, 37, 1–35. [Google Scholar]
- Hammerschmidt, E. Formation of gas hydrates in natural gas transmission lines. Ind. Eng. Chem. 1934, 26, 851–855. [Google Scholar] [CrossRef]
- Kang, S.P.; Lee, H. Recovery of CO2 from flue gas using gas hydrate: Thermodynamic verification through phase equilibrium measurements. Environ. Sci. Technol. 2000, 34, 4397–4400. [Google Scholar] [CrossRef]
- Aaron, D.; Tsouris, C. Separation of CO2 from Flue Gas: A Review. Sep. Sci. Technol. 2005, 40, 321–348. [Google Scholar] [CrossRef]
- Linga, P.; Adeyemo, A.; Englezos, P. Medium-Pressure Clathrate Hydrate/Membrane Hybrid Process for Postcombustion Capture of Carbon Dioxide. Environ. Sci. Technol. 2007, 42, 315–320. [Google Scholar] [CrossRef]
- Fan, S.; Li, S.; Wang, J.; Lang, X.; Wang, Y. Efficient capture of CO2 from simulated flue gas by formation of TBAB or TBAF semiclathrate hydrates. Energy Fuels 2009, 23, 4202–4208. [Google Scholar] [CrossRef]
- Eslamimanesh, A.; Mohammadi, A.H.; Richon, D.; Naidoo, P.; Ramjugernath, D. Application of gas hydrate formation in separation processes: A review of experimental studies. J. Chem. Thermodyn. 2012, 46, 62–71. [Google Scholar] [CrossRef]
- Gudmundsson, J.; Parlaktuna, M.; Khokhar, A. Storage of natural gas as frozen hydrate. SPE Prod. Facil. 1994, 9, 69–73. [Google Scholar] [CrossRef]
- Mimachi, H.; Takahashi, M.; Takeya, S.; Gotoh, Y.; Yoneyama, A.; Hyodo, K.; Takeda, T.; Murayama, T. Effect of Long-Term Storage and Thermal History on the Gas Content of Natural Gas Hydrate Pellets under Ambient Pressure. Energy Fuels 2015, 29, 4827–4834. [Google Scholar] [CrossRef]
- Lu, Y.; Lv, X.; Li, Q.; Yang, L.; Zhang, L.; Zhao, J.; Song, Y. Molecular Behavior of Hybrid Gas Hydrate Nucleation: Separation of Soluble H2S from Mixed Gas. Phys. Chem. Chem. Phys. 2022, 24, 9509–9520. [Google Scholar] [CrossRef]
- Gaikwad, N.; Sangwai, J.; Linga, P.; Kumar, R. Separation of Coal Mine Methane Gas Mixture via sII and sH Hydrate Formation. Fuel 2021, 305, 121467. [Google Scholar] [CrossRef]
- Molaghan, P.; Jahanshahi, M.; Ahangari, M.G. H2 and H2S Separation by Adsorption Using Graphene and Zinc Oxide Sheets: Molecular Dynamic Simulations. Phys. B Condens. Matter 2021, 619, 413175. [Google Scholar] [CrossRef]
- Park, K.n.; Hong, S.Y.; Lee, J.W.; Kang, K.C.; Lee, Y.C.; Ha, M.G.; Lee, J.D. A new apparatus for seawater desalination by gas hydrate process and removal characteristics of dissolved minerals (Na+, Mg2+, Ca2+, K+, B3+). Desalination 2011, 274, 91–96. [Google Scholar] [CrossRef]
- Nallakukkala, S.; ur Rehman, A.; Zaini, D.B.; Lal, B. Gas Hydrate-Based Heavy Metal Ion Removal from Industrial Wastewater: A Review. Water 2022, 14, 1171. [Google Scholar] [CrossRef]
- Loekman, S.; Claßen, T.; Seidl, P.; Luzi, G.; Gatternig, B.; Rauh, C.; Delgado, A. Potential Application of Innovative Gas-Hydrate Technology in Fruit Juices Concentration Process. In Proceedings of the 2019 World Congress on Advances in Nano, Bio, Robotics, and Energy (ANBRE19), Jeju Island, Korea, 17–21 September 2019. [Google Scholar]
- McElligott, A.; Uddin, H.; Meunier, J.L.; Servio, P. Effects of Hydrophobic and Hydrophilic Graphene Nanoflakes on Methane Hydrate Kinetics. Energy Fuels 2019, 33, 11705–11711. [Google Scholar] [CrossRef]
- McElligott, A.; Meunier, J.L.; Servio, P. Effects of Hydrophobic and Hydrophilic Graphene Nanoflakes on Methane Dissolution Rates in Water under Vapor–Liquid–Hydrate Equilibrium Conditions. Ind. Eng. Chem. Res. 2021, 60, 2677–2685. [Google Scholar] [CrossRef]
- Guerra, A.; McElligott, A.; Yang Du, C.; Marić, M.; Rey, A.D.; Servio, P. Dynamic viscosity of methane and carbon dioxide hydrate systems from pure water at high-pressure driving forces. Chem. Eng. Sci. 2022, 252, 117282. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. THF Hydrates as Model Systems for Natural Gas Hydrates: Comparing Their Mechanical and Vibrational Properties. Ind. Eng. Chem. Res. 2019, 58, 16588–16596. [Google Scholar] [CrossRef]
- Sloan, E.D. Gas Hydrates: Review of Physical/Chemical Properties. Energy Fuels 1998, 12, 191–196. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. Effect of Guest Size on the Mechanical Properties and Molecular Structure of Gas Hydrates from First-Principles. Cryst. Growth Des. 2017, 17, 6407–6416. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. Structural Properties of sH Hydrate: A DFT Study of Anisotropy and Equation of State. Mol. Simul. 2019, 45, 1524–1537. [Google Scholar] [CrossRef]
- Ghafari, H.; Mohammadi-Manesh, H. The Thermal Properties of Binary Structure sI Clathrate Hydrate from Molecular Dynamics Simulation. Mol. Simul. 2019, 45, 614–622. [Google Scholar] [CrossRef]
- Mirzaeifard, S.; Servio, P.; Rey, A.D. Multiscale Modeling and Simulation of Water and Methane Hydrate Crystal Interface. Cryst. Growth Des. 2019, 19, 5142–5151. [Google Scholar] [CrossRef]
- Schicks, J.M. Gas Hydrates in Nature and in the Laboratory: Necessary Requirements for Formation and Properties of the Resulting Hydrate Phase. ChemTexts 2022, 8, 13. [Google Scholar] [CrossRef]
- Xie, Y.; Zheng, T.; Zhu, Y.J.; Zhong, J.R.; Feng, J.C.; Sun, C.Y.; Chen, G.J. Effects of H2/N2 on CO2 Hydrate Film Growth: Morphology and Microstructure. Chem. Eng. J. 2022, 431, 134004. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. Elastic Properties and Anisotropic Behavior of Structure-H (sH) Gas Hydrate from First Principles. Chem. Eng. Sci. 2020, 227, 115948. [Google Scholar] [CrossRef]
- Bagherzadeh, S.A.; Englezos, P.; Alavi, S.; Ripmeester, J.A. Influence of Hydrated Silica Surfaces on Interfacial Water in the Presence of Clathrate Hydrate Forming Gases. J. Phys. Chem. C 2012, 116, 24907–24915. [Google Scholar] [CrossRef]
- Naeiji, P.; Woo, T.K.; Alavi, S.; Varaminian, F.; Ohmura, R. Interfacial Properties of Hydrocarbon/Water Systems Predicted by Molecular Dynamic Simulations. J. Chem. Phys. 2019, 150, 114703. [Google Scholar] [CrossRef]
- Naeiji, P.; Woo, T.K.; Alavi, S.; Ohmura, R. Molecular Dynamics Simulations of Interfacial Properties of the CO2–Water and CO2–CH4–Water Systems. J. Chem. Phys. 2020, 153, 044701. [Google Scholar] [CrossRef]
- Algaba, J.; Acuña, E.; Míguez, J.M.; Mendiboure, B.; Zerón, I.M.; Blas, F.J. Simulation of the Carbon Dioxide Hydrate-Water Interfacial Energy. J. Colloid Interface Sci. 2022, 623, 354–367. [Google Scholar] [CrossRef]
- Chi, Y.; Xu, Y.; Zhao, C.; Zhang, Y.; Song, Y. In-Situ Measurement of Interfacial Tension: Further Insights into Effect of Interfacial Tension on the Kinetics of CO2 Hydrate Formation. Energy 2022, 239, 122143. [Google Scholar] [CrossRef]
- Hu, P.; Ke, W.; Chen, D. Molecular Mechanism for Methane Hydrate Nucleation on Corroded Iron Surface. Chem. Eng. Sci. 2022, 249, 117303. [Google Scholar] [CrossRef]
- He, Z.; Mi, F.; Ning, F. Molecular Insights into CO2 Hydrate Formation in the Presence of Hydrophilic and Hydrophobic Solid Surfaces. Energy 2021, 234, 121260. [Google Scholar] [CrossRef]
- Koh, C.A. Towards a fundamental understanding of natural gas hydrates. Chem. Soc. Rev. 2002, 31, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Anderson, B.J.; Tester, J.W.; Borghi, G.P.; Trout, B.L. Properties of inhibitors of methane hydrate formation via molecular dynamics simulations. J. Am. Chem. Soc. 2005, 127, 17852–17862. [Google Scholar] [CrossRef]
- Perrin, A.; Musa, O.M.; Steed, J.W. The chemistry of low dosage clathrate hydrate inhibitors. Chem. Soc. Rev. 2013, 42, 1996–2015. [Google Scholar] [CrossRef]
- Rajput, F.; Colantuoni, A.; Bayahya, S.; Dhane, R.; Servio, P.; Maric, M. Poly(styrene/pentafluorostyrene)-block-poly(vinyl alcohol/vinylpyrrolidone) amphiphilic block copolymers for kinetic gas hydrate inhibitors: Synthesis, micellization behavior, and methane hydrate kinetic inhibition. J. Polym. Sci. Part A Polym. Chem. 2018, 56, 2445–2457. [Google Scholar] [CrossRef]
- Rajput, F.; Maric, M.; Servio, P. Amphiphilic Block Copolymers with Vinyl Caprolactam as Kinetic Gas Hydrate Inhibitors. Energies 2021, 14, 341. [Google Scholar] [CrossRef]
- Sun, S.; Li, Y.; Gu, L.; Yang, Z.; Zhao, J. Experimental Study on Carbon Dioxide Hydrate Formation in the Presence of Static Magnetic Field. J. Chem. Thermodyn. 2022, 170, 106764. [Google Scholar] [CrossRef]
- Bazvand, M.; Madani Tehrani, D. Effect of Magnetic Field on Gas Hydrate Formation. Nat. Gas Ind. B 2022. [Google Scholar] [CrossRef]
- Ning, F.; Guo, D.; Din, S.U.; Zhang, H.; Ou, W.; Fang, B.; Liang, Y.; Zhang, L.; Lee, K.; Koh, C.A. The Kinetic Effects of Hydrate Anti-Agglomerants/Surfactants. Fuel 2022, 318, 123566. [Google Scholar] [CrossRef]
- Liu, N.; Li, T.; Liu, T.; Yang, L. Molecular Dynamics Simulations of the Effects of Metal Nanoparticles on Methane Hydrate Formation. J. Mol. Liq. 2022, 356, 118962. [Google Scholar] [CrossRef]
- Liao, Q.; Shi, B.; Li, S.; Song, S.; Chen, Y.; Zhang, J.; Yao, H.; Li, Q.; Gong, J. Molecular Dynamics Simulation of the Effect of Wax Molecules on Methane Hydrate Formation. Fuel 2021, 297, 120778. [Google Scholar] [CrossRef]
- Guo, P.; Song, G.; Ning, Y.; Li, Y.; Wang, W. Investigation on Hydrate Growth at Oil–Water Interface: In the Presence of Wax. Energy Fuels 2021, 35, 11884–11895. [Google Scholar] [CrossRef]
- Song, G.; Ning, Y.; Li, Y.; Wang, W. Investigation on Hydrate Growth at the Oil–Water Interface: In the Presence of Wax and Kinetic Hydrate Inhibitor. Langmuir 2020, 36, 14881–14891. [Google Scholar] [CrossRef] [PubMed]
- Song, G.; Ning, Y.; Guo, P.; Li, Y.; Wang, W. Investigation on Hydrate Growth at the Oil–Water Interface: In the Presence of Wax and Surfactant. Langmuir 2021, 37, 6838–6845. [Google Scholar] [CrossRef] [PubMed]
- Zhang, D.; Huang, Q.; Wang, W.; Li, H.; Zheng, H.; Li, R.; Li, W.; Kong, W. Effects of Waxes and Asphaltenes on CO2 Hydrate Nucleation and Decomposition in Oil-Dominated Systems. J. Nat. Gas Sci. Eng. 2021, 88, 103799. [Google Scholar] [CrossRef]
- Webb, E.B.; Rensing, P.J.; Koh, C.A.; Sloan, E.D.; Sum, A.K.; Liberatore, M.W. High-Pressure Rheology of Hydrate Slurries Formed from Water-in-Oil Emulsions. Energy Fuels 2012, 26, 3504–3509. [Google Scholar] [CrossRef]
- Webb, E.B.; Koh, C.A.; Liberatore, M.W. Rheological Properties of Methane Hydrate Slurries Formed From AOT + Water + Oil Microemulsions. Langmuir 2013, 29, 10997–11004. [Google Scholar] [CrossRef]
- Webb, E.B.; Koh, C.A.; Liberatore, M.W. High Pressure Rheology of Hydrate Slurries Formed from Water-in-Mineral Oil Emulsions. Ind. Eng. Chem. Res. 2014, 53, 6998–7007. [Google Scholar] [CrossRef]
- Pandey, G.; Linga, P.; Sangwai, J.S. High pressure rheology of gas hydrate formed from multiphase systems using modified Couette rheometer. Rev. Sci. Instrum. 2017, 88, 025102. [Google Scholar] [CrossRef] [PubMed]
- Pandey, G.; Sangwai, J.S. High pressure rheological studies of methane hydrate slurries formed from water-hexane, water-heptane, and water-decane multiphase systems. J. Nat. Gas Sci. Eng. 2020, 81, 103365. [Google Scholar] [CrossRef]
- Pasieka, J.; Coulombe, S.; Servio, P. Investigating the effects of hydrophobic and hydrophilic multi-wall carbon nanotubes on methane hydrate growth kinetics. Chem. Eng. Sci. 2013, 104, 998–1002. [Google Scholar] [CrossRef]
- Pasieka, J.; Jorge, L.; Coulombe, S.; Servio, P. Effects of As-Produced and Amine-Functionalized Multi-Wall Carbon Nanotubes on Carbon Dioxide Hydrate Formation. Energy Fuels 2015, 29, 5259–5266. [Google Scholar] [CrossRef]
- Legrand, U.; Mendoza Gonzalez, N.Y.; Pascone, P.; Meunier, J.L.; Berk, D. Synthesis and in-situ oxygen functionalization of deposited graphene nanoflakes for nanofluid generation. Carbon 2016, 102, 216–223. [Google Scholar] [CrossRef]
- Hordy, N.; Coulombe, S.; Meunier, J.L. Plasma Functionalization of Carbon Nanotubes for the Synthesis of Stable Aqueous Nanofluids and Poly(vinyl alcohol) Nanocomposites. Plasma Process. Polym. 2013, 10, 110–118. [Google Scholar] [CrossRef]
- Matus Rivas, O.M.; Rey, A.D. Molecular dynamics on the self-assembly of mesogenic graphene precursors. Carbon 2016, 110, 189–199. [Google Scholar] [CrossRef]
- Matus Rivas, O.M.; Rey, A.D. Molecular dynamics of dilute binary chromonic liquid crystal mixtures. Mol. Syst. Des. Eng. 2017, 2, 223–234. [Google Scholar] [CrossRef]
- Mirzaeifard, S. Analytical and Computational Modeling of Interfacial Properties and Nucleation Process in Methane Hydrates Materials. Ph.D. Thesis, McGill University Libraries, Montreal, QC, Canada, 2020. [Google Scholar]
- Mirzaeifard, S.; Servio, P.; Rey, A.D. Characterization of Nucleation of Methane Hydrate Crystals: Interfacial Theory and Molecular Simulation. J. Colloid Interface Sci. 2019, 557, 556–567. [Google Scholar] [CrossRef]
- Mirzaeifard, S.; Servio, P.; Rey, A.D. Molecular Dynamics Characterization of Temperature and Pressure Effects on the Water-Methane Interface. Colloid Interface Sci. Commun. 2018, 24, 75–81. [Google Scholar] [CrossRef]
- Mirzaeifard, S.; Servio, P.; Rey, A.D. Molecular Dynamics Characterization of the Water-Methane, Ethane, and Propane Gas Mixture Interfaces. Chem. Eng. Sci. 2019, 208, 114769. [Google Scholar] [CrossRef]
- Rapaport, D.C. The Art of Molecular Dynamics Simulation; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Thompson, A.P.; Aktulga, H.M.; Berger, R.; Bolintineanu, D.S.; Brown, W.M.; Crozier, P.S.; in ’t Veld, P.J.; Kohlmeyer, A.; Moore, S.G.; Nguyen, T.D.; et al. LAMMPS—A flexible simulation tool for particle-based materials modeling at the atomic, meso, and continuum scales. Comput. Phys. Commun. 2022, 271, 108171. [Google Scholar] [CrossRef]
- Jorgensen, W.L.; Tirado-Rives, J. The OPLS [optimized potentials for liquid simulations] potential functions for proteins, energy minimizations for crystals of cyclic peptides and crambin. J. Am. Chem. Soc. 1988, 110, 1657–1666. [Google Scholar] [CrossRef] [PubMed]
- Huang, J.; MacKerell Jr, A.D. CHARMM36 all-atom additive protein force field: Validation based on comparison to NMR data. J. Comput. Chem. 2013, 34, 2135–2145. [Google Scholar] [CrossRef] [PubMed]
- MacKerell, A.D., Jr.; Banavali, N.; Foloppe, N. Development and current status of the CHARMM force field for nucleic acids. Biopolymers 2000, 56, 257–265. [Google Scholar] [CrossRef]
- Schuler, L.D.; Daura, X.; van Gunsteren, W.F. An improved GROMOS96 force field for aliphatic hydrocarbons in the condensed phase. J. Comput. Chem. 2001, 22, 1205–1218. [Google Scholar] [CrossRef]
- Maier, J.A.; Martinez, C.; Kasavajhala, K.; Wickstrom, L.; Hauser, K.E.; Simmerling, C. ff14SB: Improving the Accuracy of Protein Side Chain and Backbone Parameters from ff99SB. J. Chem. Theory Comput. 2015, 11, 3696–3713. [Google Scholar] [CrossRef]
- Martínez, L.; Andrade, R.; Birgin, E.G.; Martínez, J.M. PACKMOL: A package for building initial configurations for molecular dynamics simulations. J. Comput. Chem. 2009, 30, 2157–2164. [Google Scholar] [CrossRef] [PubMed]
- Jewett, A.I.; Stelter, D.; Lambert, J.; Saladi, S.M.; Roscioni, O.M.; Ricci, M.; Autin, L.; Maritan, M.; Bashusqeh, S.M.; Keyes, T.; et al. Moltemplate: A Tool for Coarse-Grained Modeling of Complex Biological Matter and Soft Condensed Matter Physics. J. Mol. Biol. 2021, 433, 166841. [Google Scholar] [CrossRef]
- Vlasic, T.M.; Servio, P.D.; Rey, A.D. Infrared Spectra of Gas Hydrates from First-Principles. J. Phys. Chem. B 2019, 123, 936–947. [Google Scholar] [CrossRef]
- Daghash, S.M.; Servio, P.; Rey, A.D. From Infrared Spectra to Macroscopic Mechanical Properties of sH Gas Hydrates through Atomistic Calculations. Molecules 2020, 25, 5568. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Ojamäe, L. CH-Stretching Vibrational Trends in Natural Gas Hydrates Studied by Quantum-Chemical Computations. J. Phys. Chem. C 2015, 119, 17084–17091. [Google Scholar] [CrossRef]
- Liu, Y.; Ojamäe, L. C–C Stretching Raman Spectra and Stabilities of Hydrocarbon Molecules in Natural Gas Hydrates: A Quantum Chemical Study. J. Phys. Chem. A 2014, 118, 11641–11651. [Google Scholar] [CrossRef]
- Blöchl, P.E. Projector Augmented-Wave Method. Phys. Rev. B 1994, 50, 17953–17979. [Google Scholar] [CrossRef] [PubMed]
- Kresse, G.; Furthmüller, J. Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set. Phys. Rev. B 1996, 54, 11169–11186. [Google Scholar] [CrossRef]
- Kresse, G.; Joubert, D. From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method. Phys. Rev. B 1999, 59, 1758–1775. [Google Scholar] [CrossRef]
- Soler, J.M.; Artacho, E.; Gale, J.D.; García, A.; Junquera, J.; Ordejón, P.; Sánchez-Portal, D. The SIESTA Method for Ab Initio Order-N Materials Simulation. J. Phys. Condens. Matter 2002, 14, 2745–2779. [Google Scholar] [CrossRef]
- Fernández-Torre, D.; Escribano, R.; Archer, T.; Pruneda, J.M.; Artacho, E. First-Principles Infrared Spectrum of Nitric Acid and Nitric Acid Monohydrate Crystals. J. Phys. Chem. A 2004, 108, 10535–10541. [Google Scholar] [CrossRef]
- Liu, Y.; Ojamäe, L. Raman and IR Spectra of Ice Ih and Ice XI with an Assessment of DFT Methods. J. Phys. Chem. B 2016, 120, 11043–11051. [Google Scholar] [CrossRef] [PubMed]
- DeKock, R.; Gray, H. Chemical Structure and Bonding; University Science Books: Sausalito, CA, USA, 1989. [Google Scholar]
- Ashby, M.F.; Jones, D.R.H. Engineering Materials 1: An Introduction to Their Properties and Applications, 2nd ed.; Butterworth-Heinemann: Oxford, UK, 1996; Chapter viii; 306p. [Google Scholar]
- Vlasic, T.M.; Servio, P.; Rey, A.D. Atomistic Modeling of Structure II Gas Hydrate Mechanics: Compressibility and Equations of State. AIP Adv. 2016, 6, 085317. [Google Scholar] [CrossRef]
- Yu, C.H.; Huang, C.H.; Tan, C.S. A Review of CO2 Capture by Absorption and Adsorption. Aerosol Air Qual. Res. 2012, 12, 745–769. [Google Scholar] [CrossRef]
- Dai, N.; Mitch, W.A. Influence of Amine Structural Characteristics on N-Nitrosamine Formation Potential Relevant to Postcombustion CO2 Capture Systems. Environ. Sci. Technol. 2013, 47, 13175–13183. [Google Scholar] [CrossRef] [PubMed]
- Chowdhury, F.A.; Yamada, H.; Higashii, T.; Goto, K.; Onoda, M. CO2 Capture by Tertiary Amine Absorbents: A Performance Comparison Study. Ind. Eng. Chem. Res. 2013, 52, 8323–8331. [Google Scholar] [CrossRef]
- Komati, S.; Suresh, A.K. Anomalous enhancement of interphase transport rates by nanoparticles: Effect of magnetic iron oxide on gas-liquid mass transfer. Ind. Eng. Chem. Res. 2010, 49, 390–405. [Google Scholar] [CrossRef]
- Zhu, H.; Shanks, B.H.; Heindel, T.J. Enhancing CO-water mass transfer by functionalized MCM41 nanoparticles. Ind. Eng. Chem. Res. 2008, 47, 7881–7887. [Google Scholar] [CrossRef]
- Olle, B.; Bucak, S.; Holmes, T.C.; Bromberg, L.; Hatton, T.A.; Wang, D.I. Enhancement of oxygen mass transfer using functionalized magnetic nanoparticles. Ind. Eng. Chem. Res. 2006, 45, 4355–4363. [Google Scholar] [CrossRef]
- Posteraro, D.; Verrett, J.; Maric, M.; Servio, P. New insights into the effect of polyvinylpyrrolidone (PVP) concentration on methane hydrate growth. 1. Growth rate. Chem. Eng. Sci. 2015, 126, 99–105. [Google Scholar] [CrossRef]
- Posteraro, D.; Ivall, J.; Maric, M.; Servio, P. New insights into the effect of polyvinylpyrrolidone (PVP) concentration on methane hydrate growth. 2. Liquid phase methane mole fraction. Chem. Eng. Sci. 2015, 126, 91–98. [Google Scholar] [CrossRef]
- Evans, D.F.; Wennerström, H. The Colloidal Domain: Where Physics, Chemistry, Biology, and Technology Meet; Advances in Interfacial Engineering; Wiley: New York, NY, USA, 1999. [Google Scholar]
- Carpena, P.; Aguiar, J.; Bernaola-Galván, P.; Carnero Ruiz, C. Problems Associated with the Treatment of Conductivity Concentration Data in Surfactant Solutions Simulations and Experiments. Langmuir 2002, 18, 6054–6058. [Google Scholar] [CrossRef]
- Bielawska, M.; Jańczuk, B.; Zdziennicka, A. Adhesion work and wettability of polytetrafluorethylene and poly(methyl methacrylate) by aqueous solutions of cetyltrimethylammonium bromide and Triton X-100 mixture with ethanol. J. Colloid Interface Sci. 2013, 404, 201–206. [Google Scholar] [CrossRef]
- Piera, E.; Erra, P.; Infante, M.R. Analysis of cationic surfactants by capillary electrophoresis. J. Chromatogr. A 1997, 757, 275–280. [Google Scholar] [CrossRef]
- Topel, Ö.; Çakır, B.A.; Budama, L.; Hoda, N. Determination of critical micelle concentration of polybutadiene-block-poly(ethyleneoxide) diblock copolymer by fluorescence spectroscopy and dynamic light scattering. J. Mol. Liq. 2013, 177, 40–43. [Google Scholar] [CrossRef]
- Zhang, J.S.; Lo, C.; Couzis, A.; Somasundaran, P.; Wu, J.; Lee, J.W. Adsorption of Kinetic Inhibitors on Clathrate Hydrates. J. Phys. Chem. C 2009, 113, 17418–17420. [Google Scholar] [CrossRef]
- Koop, T.; Murray, B.J. A Physically Constrained Classical Description of the Homogeneous Nucleation of Ice in Water. J. Chem. Phys. 2016, 145, 211915. [Google Scholar] [CrossRef]
- Knott, B.C.; Molinero, V.; Doherty, M.F.; Peters, B. Homogeneous Nucleation of Methane Hydrates: Unrealistic under Realistic Conditions. J. Am. Chem. Soc. 2012, 134, 19544–19547. [Google Scholar] [CrossRef]
- Bai, D.; Chen, G.; Zhang, X.; Sum, A.K.; Wang, W. How Properties of Solid Surfaces Modulate the Nucleation of Gas Hydrate. Sci. Rep. 2015, 5, 12747. [Google Scholar] [CrossRef]
- Koga, T.; Wong, J.; Endoh, M.K.; Mahajan, D.; Gutt, C.; Satija, S.K. Hydrate Formation at the Methane/Water Interface on the Molecular Scale. Langmuir 2010, 26, 4627–4630. [Google Scholar] [CrossRef]
- Zhao, J.; Yang, L.; Liu, Y.; Song, Y. Microstructural Characteristics of Natural Gas Hydrates Hosted in Various Sand Sediments. Phys. Chem. Chem. Phys. PCCP 2015, 17, 22632–22641. [Google Scholar] [CrossRef] [PubMed]
- Biscay, F.; Ghoufi, A.; Malfreyt, P. Adsorption of N-Alkane Vapours at the Water Surface. Phys. Chem. Chem. Phys. 2011, 13, 11308–11316. [Google Scholar] [CrossRef]
- Biscay, F.; Ghoufi, A.; Lachet, V.; Malfreyt, P. Monte Carlo Calculation of the Methane-Water Interfacial Tension at High Pressures. J. Chem. Phys. 2009, 131, 124707. [Google Scholar] [CrossRef]
- Shuttleworth, R. The Surface Tension of Solids. Proc. Phys. Soc. Sect. A 1950, 63, 444–457. [Google Scholar] [CrossRef]
- Vázquez, U.O.M.; Shinoda, W.; Moore, P.B.; Chiu, C.c.; Nielsen, S.O. Calculating the Surface Tension between a Flat Solid and a Liquid: A Theoretical and Computer Simulation Study of Three Topologically Different Methods. J. Math. Chem. 2009, 45, 161–174. [Google Scholar] [CrossRef]
- Binks, B.P.; Clint, J.H. Solid Wettability from Surface Energy Components: Relevance to Pickering Emulsions. Langmuir 2002, 18, 1270–1273. [Google Scholar] [CrossRef]
- Ghiass, M.; Rey, A.D. Interfacial Thermodynamics of Compressible Polymer Solutions. J. Chem. Phys. 2008, 128, 071102. [Google Scholar] [CrossRef] [PubMed]
- Blokhuis, E.; Bedeaux, D.; Holcomb, C.; Zollweg, J. Tail Corrections to the Surface Tension of a Lennard-Jones Liquid-Vapour Interface. Mol. Phys. 1995, 85, 665–669. [Google Scholar] [CrossRef]
- Chapela, G.A.; Saville, G.; Thompson, S.M.; Rowlinson, J.S. Computer Simulation of a Gas–Liquid Surface. Part 1. J. Chem. Soc. Faraday Trans. 2 Mol. Chem. Phys. 1977, 73, 1133–1144. [Google Scholar] [CrossRef]
- Grest, G.S.; Stevens, M.J.; Plimpton, S.J.; Woolf, T.B.; Lehoucq, R.B.; Crozier, P.S.; Ismail, A.E.; Mukherjee, R.M.; Draganescu, A.I. Substructured Multibody Molecular Dynamics; Technical Report; Sandia National Laboratories (SNL): Albuquerque, NM, USA; Livermore, CA, USA, 2006. [Google Scholar] [CrossRef]
- Yan, J.Y.; Patey, G.N. Heterogeneous Ice Nucleation Induced by Electric Fields. J. Phys. Chem. Lett. 2011, 2, 2555–2559. [Google Scholar] [CrossRef]
- Yan, J.Y.; Patey, G.N. Ice Nucleation by Electric Surface Fields of Varying Range and Geometry. J. Chem. Phys. 2013, 139, 144501. [Google Scholar] [CrossRef]
- Luis, D.P.; Herrera-Hernández, E.C.; Saint-Martin, H. A Theoretical Study of the Dissociation of the sI Methane Hydrate Induced by an External Electric Field. J. Chem. Phys. 2015, 143, 204503. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).