An Electromagnetic Var Compensator Suitable for Wind Power Access and Its Control Strategy
Abstract
:1. Introduction
- (1)
- Proposing the topology of an electromagnetic var compensator (EVC) and analyzing its working principle.
- (2)
- Presenting a reactive power compensation control strategy that is suitable for the EVC.
- (3)
- Verifying the feasibility and effectiveness of the proposed topology and reactive power compensation control strategy through simulations.
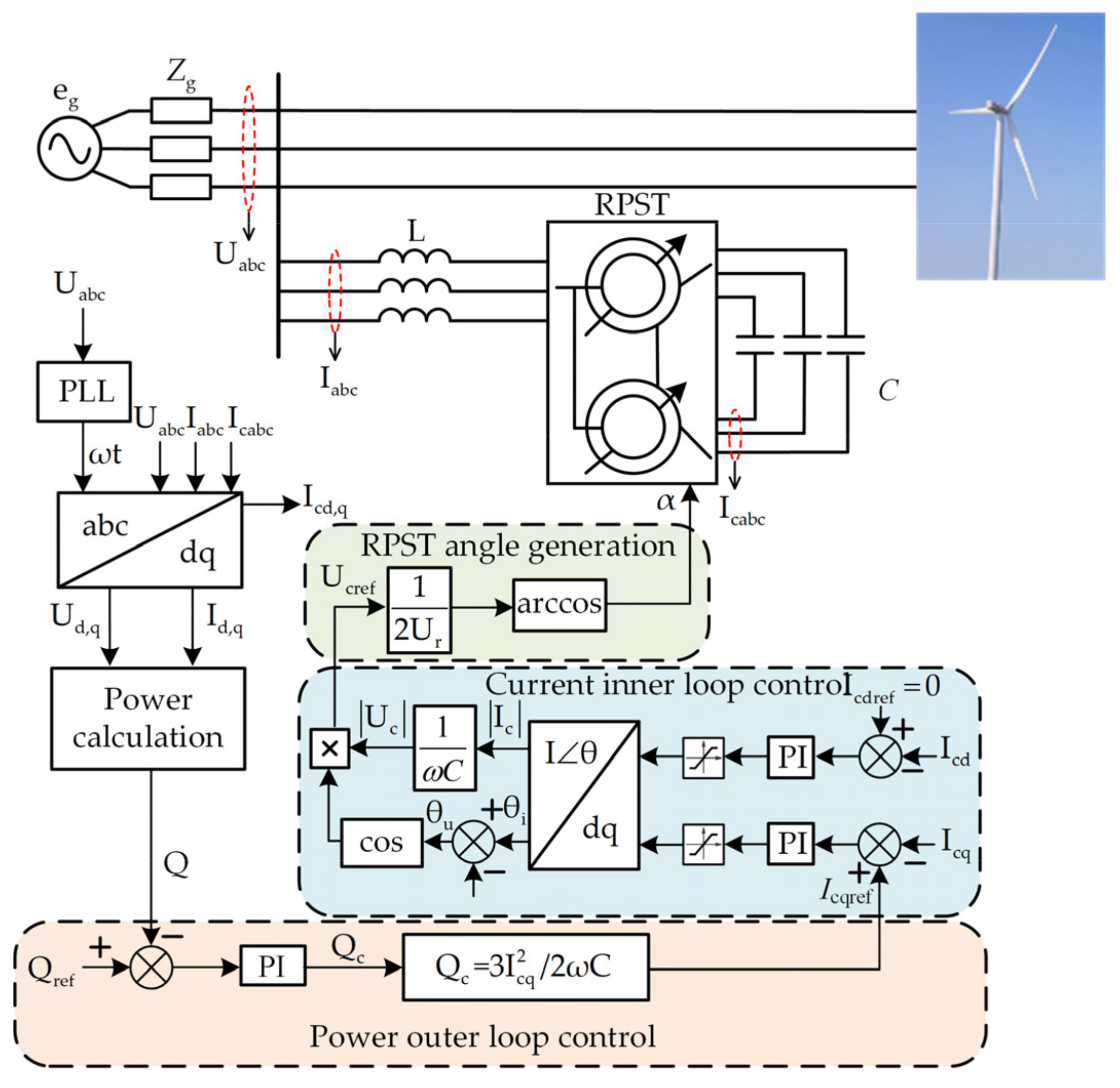
2. Model of the EVC Based on Rotary Phase-Shifting Transformer (RPST)
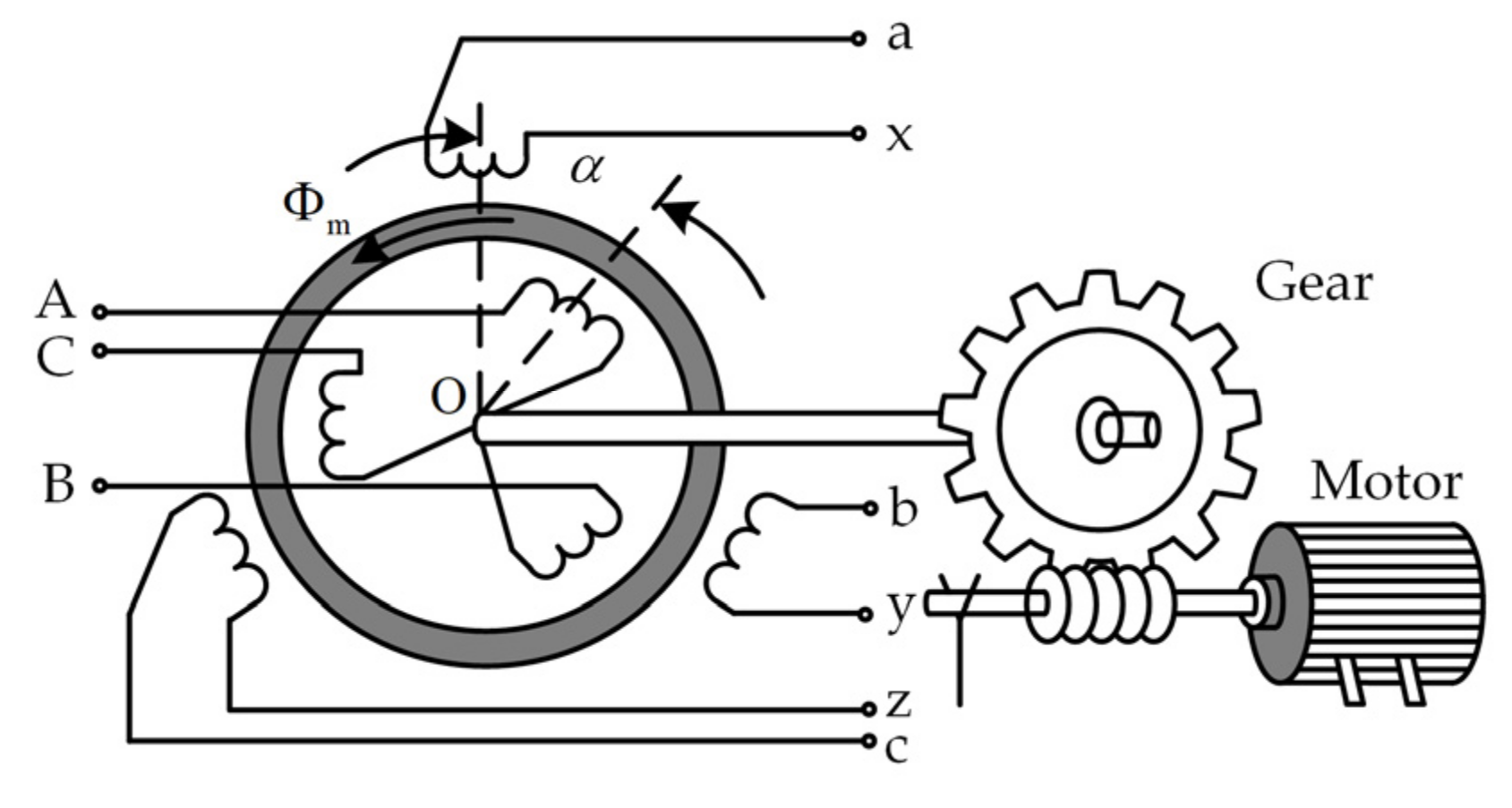
2.1. RPST
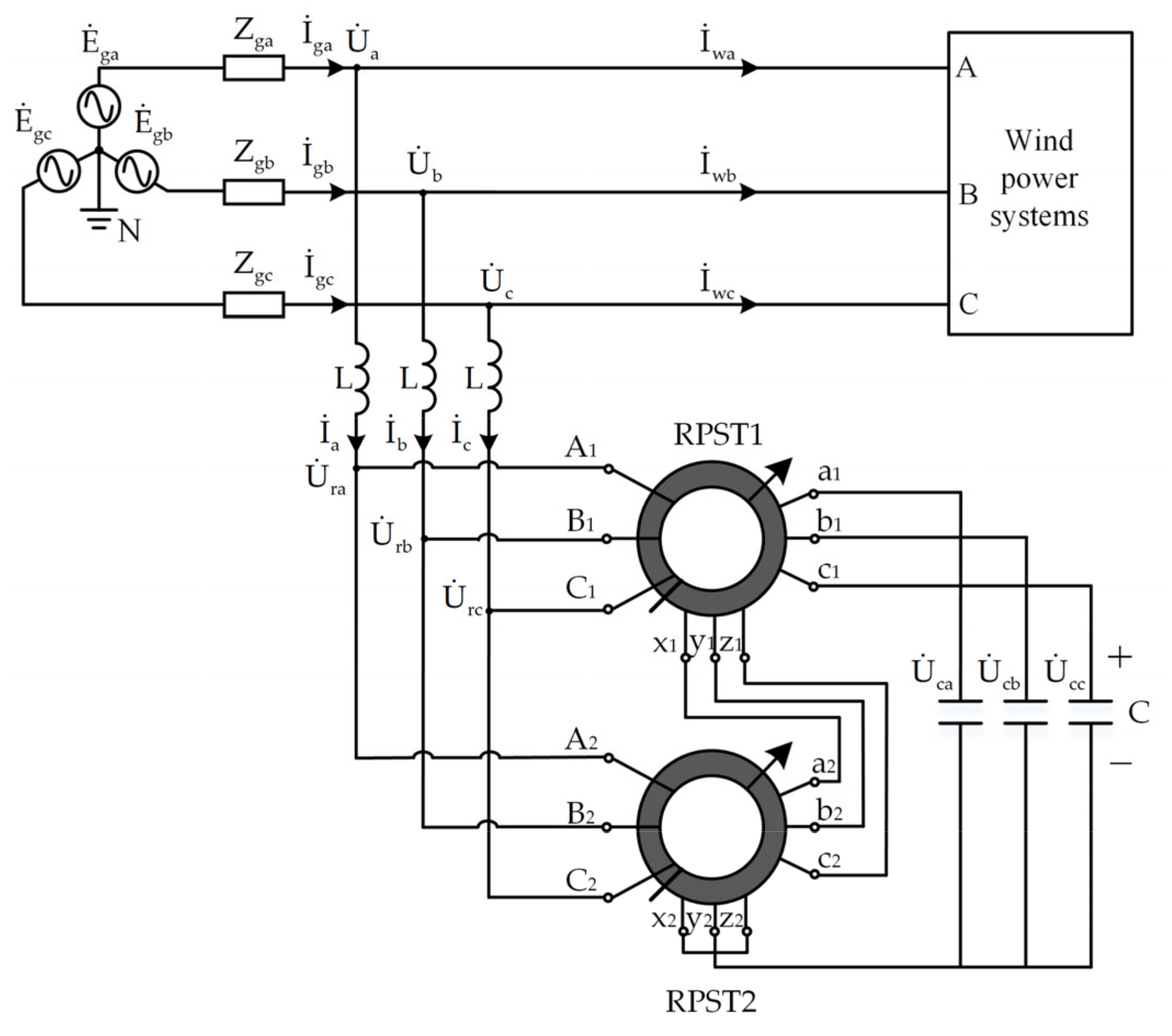
2.2. Topology of the EVC
3. Working Principle of the EVC
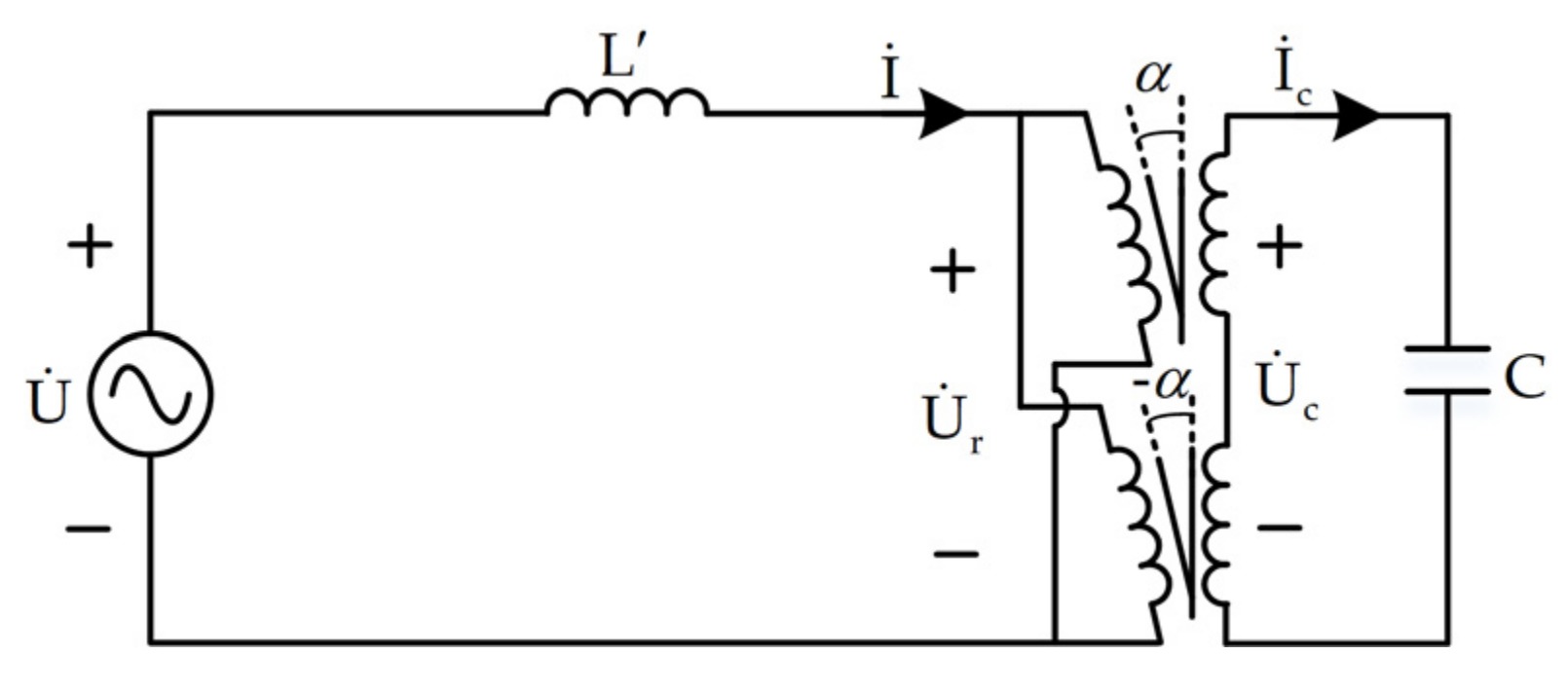
4. Parallel Steady-State Mathematical Model and Control Strategy of the EVC
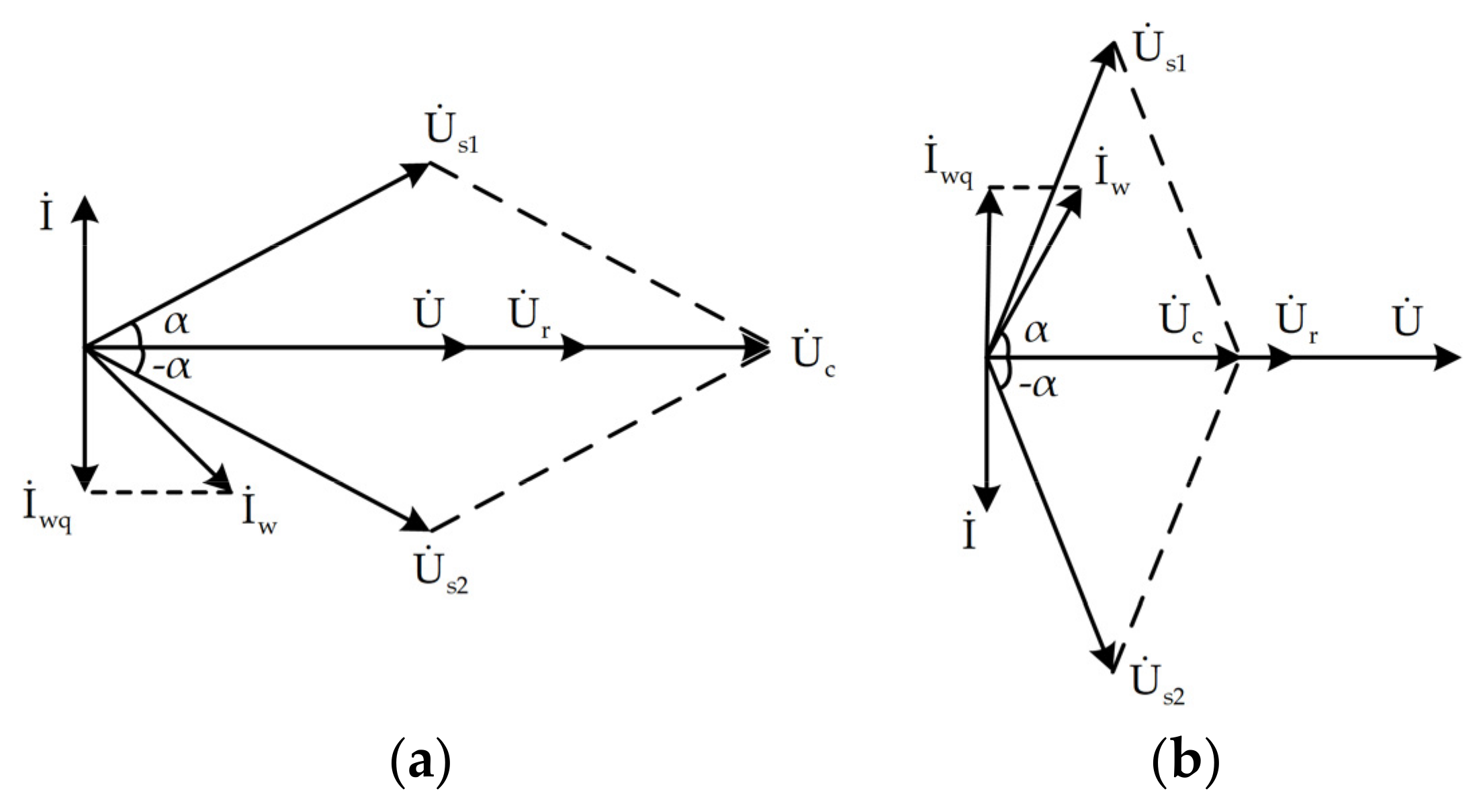
4.1. Parallel Steady-State Mathematical Model of the EVC
4.2. Control Strategy
5. Simulation Analysis
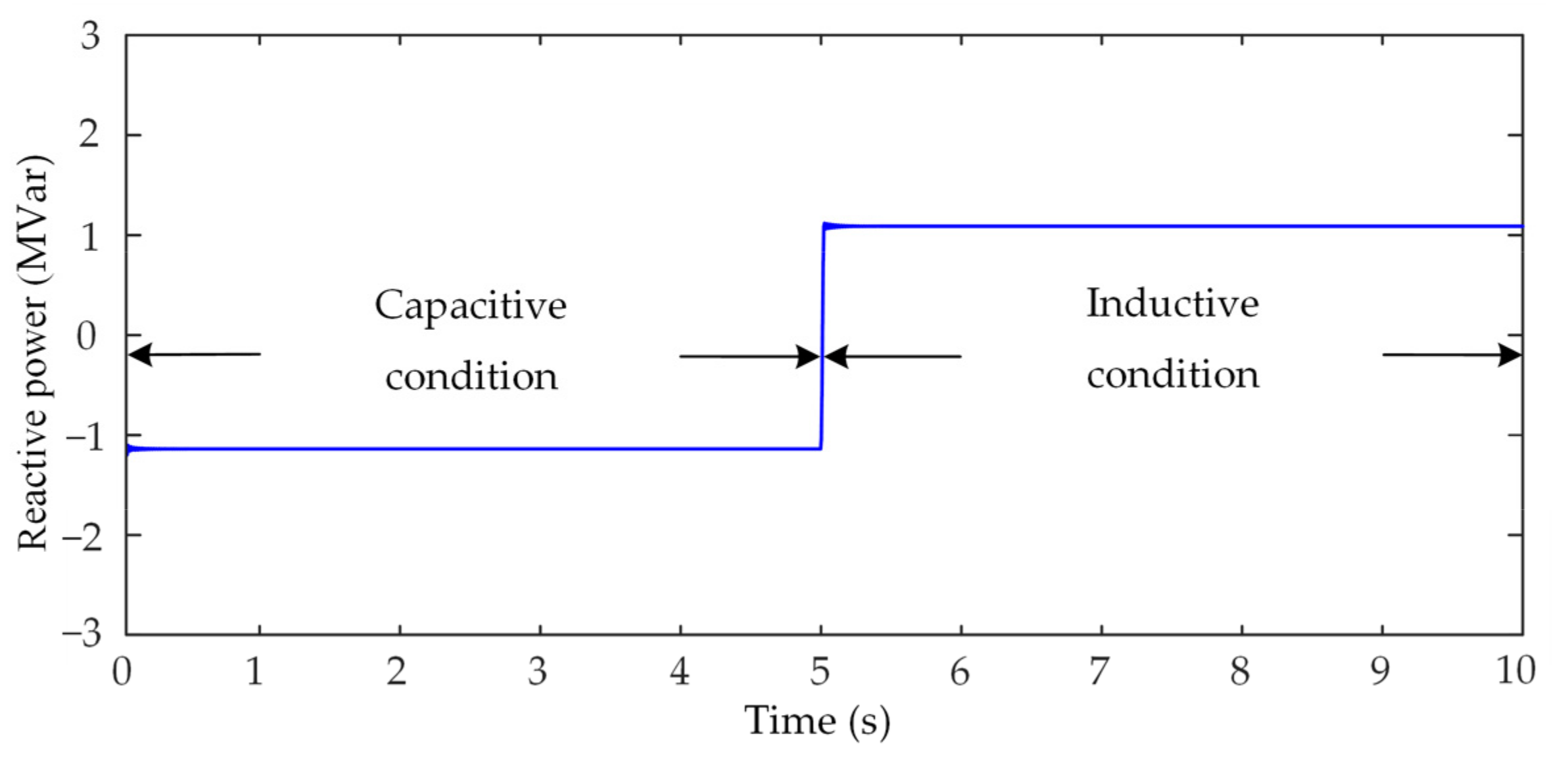
5.1. Adjustment Range of the EVC
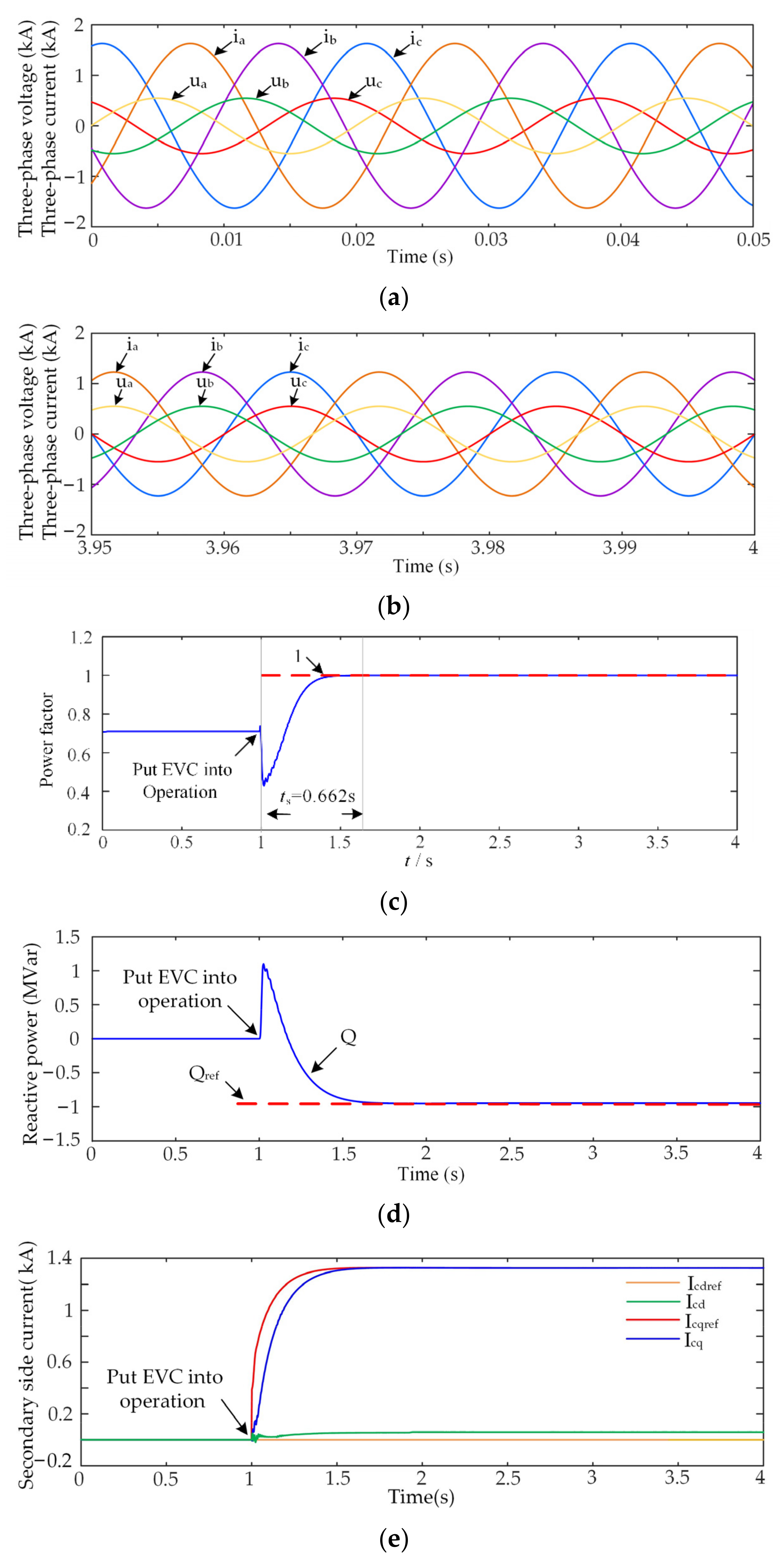
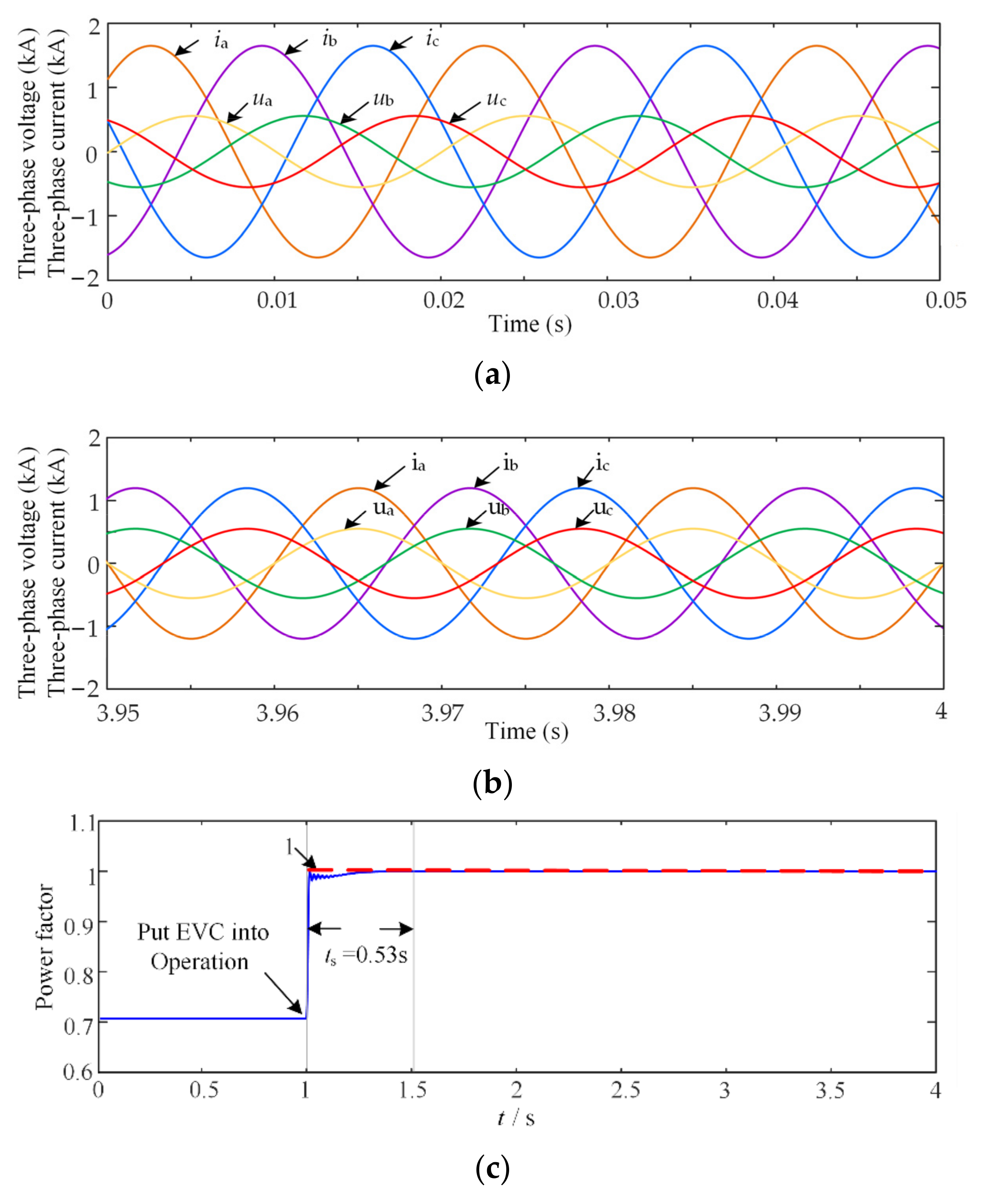
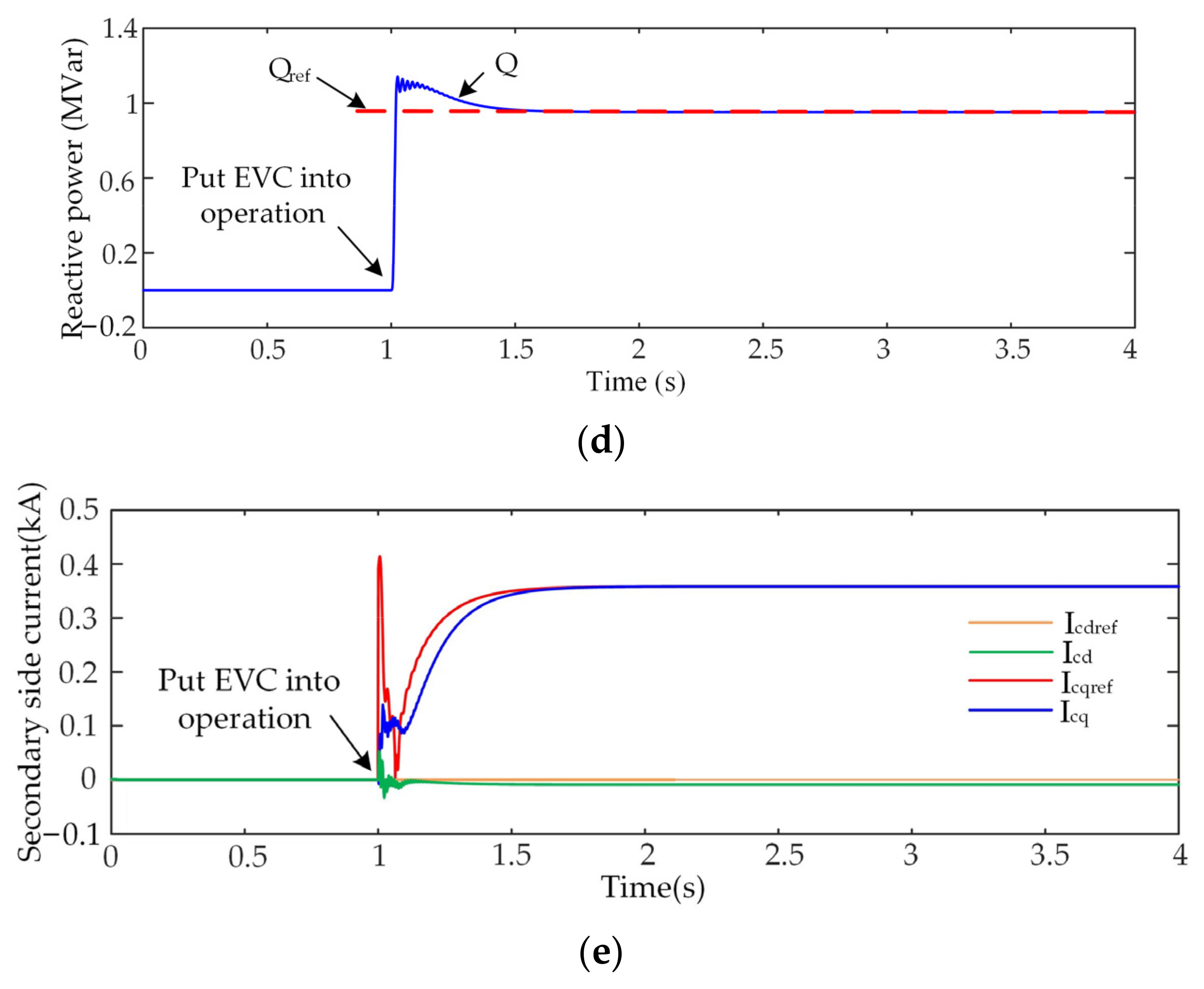
5.2. Adjustment Effect Analysis of the EVC
5.2.1. Capacitive Condition
5.2.2. Inductive Condition
6. Experimental Verification
7. Conclusions
- (1)
- This study proposes a new topology of a shunt reactive power compensation device by replacing the power switching tube bridge of an VSC with RPSTs, which exhibits the features of a simple structure, low costs, no need to provide a separate power supply and isolation transformer, high voltage, and large capacity. The proposed topology can meet the requirements of power systems with a high percentage of wind power for the precise adjustment of reactive power compensation equipment, economic cost, easy operation and maintenance, strong shock resistance, and good tolerance.
- (2)
- Applying the instantaneous reactive power theory, a double closed-loop control strategy for the EVC, including power external and current internal loop controls, is proposed in this work. This strategy exhibits the characteristics of robustness and high control accuracy.
- (3)
- It is verified by simulation that the EVC topology and control strategy proposed in this paper can be applied to the power system with reactive power fluctuation after wind power is connected. The EVC is capable of bidirectional, continuous, and large-capacity compensation. The EVC has the ability to compensate precisely within its rated regulation range, providing new ideas for reactive power compensation devices and their control strategies.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhao, X.; Ma, X.; Chen, B.; Shang, Y.; Song, M. Challenges toward carbon neutrality in China: Strategies and countermeasures. Resour. Conserv. Recycl. 2022, 176, 105959. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, J.; Wu, D.; Fan, G.; Ge, H. Two-phase collaborative optimization and operation strategy for a new distributed energy system that combines multi-energy storage for a nearly zero energy community. Energy Convers. Manag. 2021, 230, 113800. [Google Scholar] [CrossRef]
- Liu, J.; Zhou, Y.; Li, Y.; Lin, G.; Zu, W.; Cao, Y.; Qiao, X.; Sun, C.B.; Cao, Y.; Rehtanz, C. Modelling and analysis of radial distribution network with high penetration of renewable energy considering the time series characteristics. IET Gener. Transm. Distrib. 2020, 14, 2800–2809. [Google Scholar] [CrossRef]
- Liao, H. Review on Distribution Network Optimization under Uncertainty. Energies 2019, 12, 3369. [Google Scholar] [CrossRef] [Green Version]
- Von Appen, J.; Stetz, T.; Braun, M.; Schmiegel, A. Local voltage control strategies for pv storage systems in distribution grids. IEEE Trans. Smart Grid. 2014, 5, 1002–1009. [Google Scholar] [CrossRef]
- Aziz, T.; Ketjoy, N. PV penetration limits in low voltage networks and voltage variations. IEEE Access 2017, 5, 16784–16792. [Google Scholar] [CrossRef]
- Chen, S.X.; Eddy, Y.S.F.; Gooi, H.B.; Wang, M.Q.; Lu, S.F. A centralized reactive power compensation system for LV distribution networks. IEEE Trans. Power Syst. 2014, 30, 274–284. [Google Scholar] [CrossRef]
- Chen, B.; Zhang, C.; Zeng, W.; Xue, G.; Tian, C.; Yuan, J. Electrical magnetic hybrid power quality compensation system for V/V traction power supply system. IET Power Electron. 2015, 9, 62–70. [Google Scholar] [CrossRef]
- Pijarski, P.; Kacejko, P. Methods of simulated annealing and particle swarm applied to the optimization of reactive power flow in electric power systems. Adv. Electr. Comput. Eng. 2018, 18, 43–48. [Google Scholar] [CrossRef]
- Wan, Y.; Murad, M.A.A.; Liu, M.; Milano, F. Voltage frequency control using SVC devices coupled with voltage dependent loads. IEEE Trans. Power Syst. 2019, 34, 1589–1597. [Google Scholar] [CrossRef]
- Duan, C.; Fang, W.; Jiang, L.; Niu, S. FACTS devices allocation via sparse optimization. IEEE Trans. Power Syst. 2016, 31, 1308–1319. [Google Scholar] [CrossRef] [Green Version]
- Ko, W.H.; Gu, J.C. Design and application of a thyristor switched capacitor bank for a high harmonic distortion and fast changing single-phase electric welding machine. IET Power Electron. 2016, 9, 2751–2759. [Google Scholar] [CrossRef]
- Hemmati, R.; Faraji, H.; Beigvand, N.Y. Multi objective control scheme on DFIG wind turbine integrated with energy storage system and FACTS devices: Steady-state and transient operation improvement. Int. J. Electr. Power Energy Syst. 2022, 135, 107519. [Google Scholar] [CrossRef]
- Das, S.; Chatterjee, D.; Goswami, S.K. Tuned-TSC based SVC for reactive power compensation and harmonic reduction in unbalanced distribution system. IET Gener. Transm. Distrib. 2018, 12, 571–585. [Google Scholar] [CrossRef]
- Velásquez, R.M.A.; Lara, J.V.M. Harmonic failure in the filter of static var compensator. Eng. Fail. Anal. 2020, 107, 104207. [Google Scholar] [CrossRef]
- Farivar, G.; Townsend, C.; Hredzak, B.; Pou, J.; Agelidis, V. Passive reactor compensated cascaded H-bridge multilevel LC-StatCom. IEEE Trans. Power Electron. 2017, 32, 8338–8348. [Google Scholar] [CrossRef] [Green Version]
- Abd-Elazim, S.M.; Ali, E.S. Imperialist competitive algorithm for optimal STATCOM design in a multimachine power system. Int. J. Electr. Power Energy Syst. 2016, 76, 136–146. [Google Scholar] [CrossRef]
- Abd-Elazim, S.M.; Ali, E.S. Optimal location of STATCOM in multimachine power system for increasing loadability by cuckoo search algorithm. Int. J. Electr. Power Energy Syst. 2016, 80, 240–251. [Google Scholar] [CrossRef]
- Wei, T.; Mao, C.; Lu, J.; Wang, D.; Wang, Q.; Wu, W. Low cost hybrid reactive power compensator using coordination control strategies. IET Gener. Transm. Distrib. 2016, 10, 1805–1814. [Google Scholar] [CrossRef]
- Shuai, Z.; Luo, A.; Shen, Z.J.; Zhu, W.; Lv, Z.; Wu, C. A dynamic hybrid var compensator and a two-level collaborative optimization compensation method. IEEE Trans. Power Electron. 2009, 24, 2091–2100. [Google Scholar] [CrossRef]
- Li, M.; Li, W.; Zhao, J.; Chen, W.; Yao, W. Three-layer coordinated control of the hybrid operation of static var compensator and static synchronous compensator. IET Gener. Transm. Distrib. 2016, 10, 2185–2193. [Google Scholar] [CrossRef]
- Wang, L.; Chi-Seng, L.; Man-Chung, W. A hybrid-STATCOM with wide compensation range and low DC-link voltage. IEEE Trans. Ind. Electron. 2016, 63, 3333–3343. [Google Scholar] [CrossRef]
- Rahmani, S.; Hamadi, A.; Al-Haddad, K.; Dessaint, L.A. A combination of shunt hybrid power filter and thyristor-controlled reactor for power quality. IEEE Trans. Ind. Electron. 2013, 61, 2152–2164. [Google Scholar] [CrossRef]
- Wang, L.; Lam, C.S.; Wong, M.C. Hybrid structure of static var compensator and hybrid active power filter (SVC//HAPF) for medium-voltage heavy loads compensation. IEEE Trans. Ind. Electron. 2018, 65, 4432–4442. [Google Scholar] [CrossRef]
- Hu, P.; Guerrero, J.M.; He, Z. Design and analysis of a transformerless STATCOM based on hybrid cascaded multilevel converter. Int. J. Electr. Power Energy Syst. 2018, 104, 694–704. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Y.; Wang, Y.; Zhang, D.; Chen, X.; Gong, C. Broadband Impedance Shaping Control Scheme of MMC-based STATCOM for Improving the Stability of the Wind Farm. IEEE Trans. Power Electron. 2021, 36, 10278–10292. [Google Scholar] [CrossRef]
- Lai, J.; Yin, X.; Zhang, Z.; Wang, Z.; Yin, X. System modeling and cascaded passivity based control for distribution transformer integrated with static synchronous compensator. Int. J. Electr. Power Energy Syst. 2019, 113, 1035–1046. [Google Scholar] [CrossRef]
- Wang, C.; Yin, X.; Zhe, Z.; Wen, M. A Novel compensation technology of static synchronous compensator integrated with distribution transformer. IEEE Trans. Power Deliv. 2013, 28, 1032–1039. [Google Scholar] [CrossRef]
- Larsen, E.V. Power Flow Control with Rotary Transformers. U.S. Patent 5,841,267, 24 November 1998. [Google Scholar]
- Haddadi, A.M.; Kazemi, A. Optimal power flow control by rotary power flow controller. Adv. Electr. Comput. Eng. 2011, 11, 79–86. [Google Scholar] [CrossRef]




| Parameter | Value |
|---|---|
| Power voltage es/V | 690 |
| Power Equivalent Impedance Zs/Ω | 0.01 + j1 × 10−5 |
| Inductance L/mH | 0.11 |
| RPST rated capacity/MVA | 2 |
| RPST rated voltage/V | 690 |
| RPST stator side impedance (pu) Zs | 0.01 + j0.11 |
| RPST rotor side impedance (pu) Zr | 0.01 + j0.11 |
| RPST magnetizing inductance (pu) Lm | 3.36 |
| Capacitance C/mF | 3.68 |
| Scale factor of power outer-loop controller Kp_Q | 0.1 |
| Integral factor of power outer-loop controller Ki_Q | 3 |
| Scale factor of active current controller Kp_d | 0.1 |
| Integral factor of active current controller Ki_d | 20 |
| Scaling factor of reactive current controller Kp_q | 0.1 |
| Integral factor of reactive current controller Ki_q | 20 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yan, X.; Guo, Y.; Jia, J.; Aslam, W.; Qi, B.; Wang, Y.; Xu, X. An Electromagnetic Var Compensator Suitable for Wind Power Access and Its Control Strategy. Energies 2022, 15, 5572. https://doi.org/10.3390/en15155572
Yan X, Guo Y, Jia J, Aslam W, Qi B, Wang Y, Xu X. An Electromagnetic Var Compensator Suitable for Wind Power Access and Its Control Strategy. Energies. 2022; 15(15):5572. https://doi.org/10.3390/en15155572
Chicago/Turabian StyleYan, Xiangwu, Yan Guo, Jiaoxin Jia, Waseem Aslam, Bingbao Qi, Yang Wang, and Xiaolin Xu. 2022. "An Electromagnetic Var Compensator Suitable for Wind Power Access and Its Control Strategy" Energies 15, no. 15: 5572. https://doi.org/10.3390/en15155572
APA StyleYan, X., Guo, Y., Jia, J., Aslam, W., Qi, B., Wang, Y., & Xu, X. (2022). An Electromagnetic Var Compensator Suitable for Wind Power Access and Its Control Strategy. Energies, 15(15), 5572. https://doi.org/10.3390/en15155572








