Controlled Islanding under Complete and Partial False Data Injection Attack Uncertainties against Phasor Measurement Units
Abstract
:1. Introduction
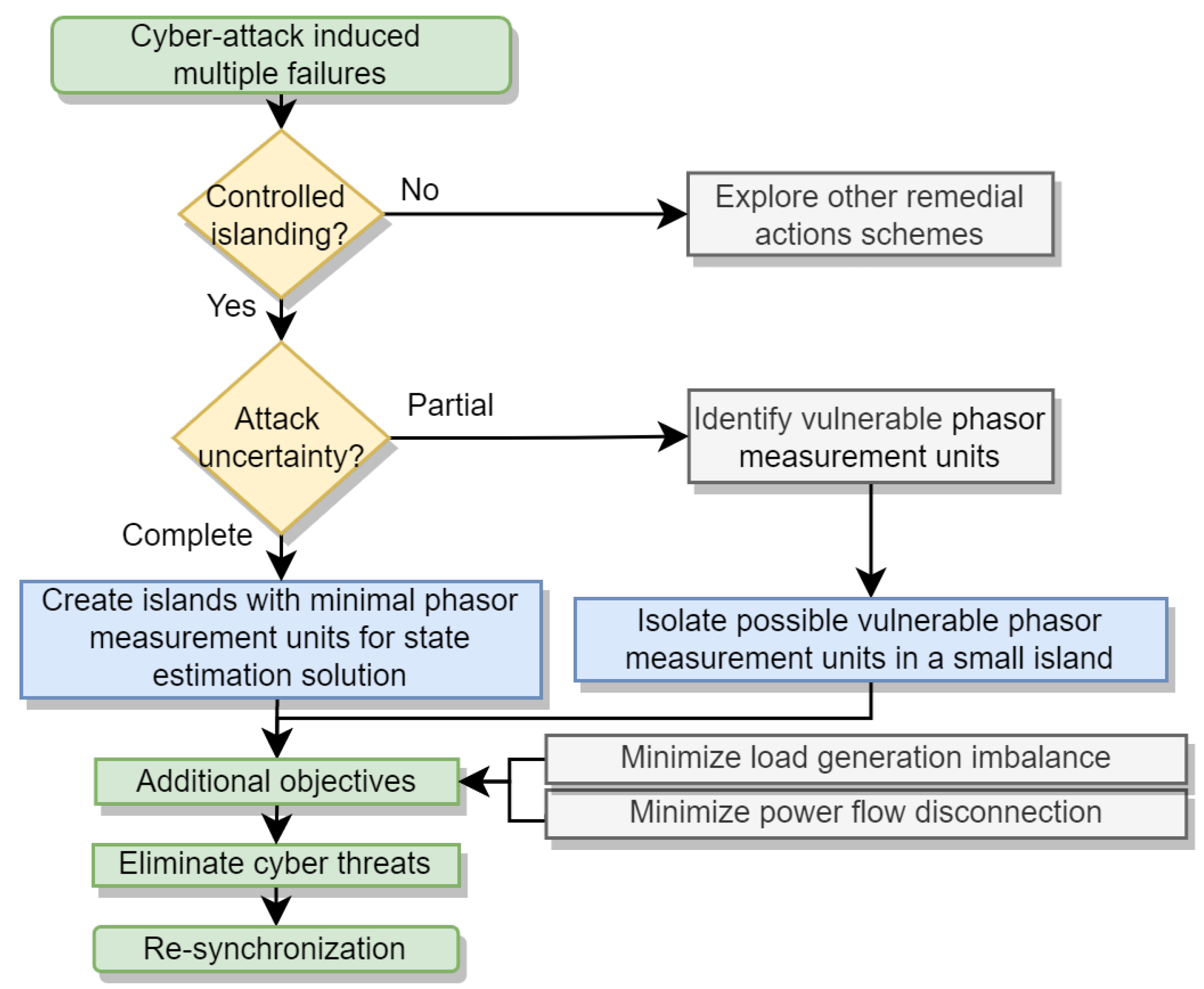
- Incorporating measurement uncertainties: Two new strategies are developed for controlled islanding without or with partial knowledge of false measurements. Controlled islanding is formulated as a multi-objective optimization problem that yields stable and observable islands while ensuring that wrong PMU measurements impact a minimal number of partitions.
- Minimizing the loss of observability: A new method is developed to minimize the loss of observability during the partition process. This approach is efficient when reliable state estimation solutions are sought for the newly-formed islands with minimum PMUs in each island.
- Comprehensive islanding solutions: Trade-offs between different objectives such as island size, observability, load-generation imbalance, and power flow disconnection are investigated using various optimization methods while taking into account the number of islands, generator coherency, and dynamic stability of the system.
2. Background and Motivation
- Scenario 1 under complete uncertainty: maximize the island observability with a minimum number of PMUs; and
- Scenario 2 under partial uncertainty: isolate vulnerable PMUs to a small island.
3. Islanding under Complete Uncertainty
3.1. Objective 1: Maximize Island Observability

3.2. Objective 2: Minimize the Number of Retained PMUs
4. Islanding under Partial Uncertainty
4.1. Objective 1: Isolate PMUs under Attack
4.2. Objective 2: Maximize Island Observability
5. Stability Objectives and Islanding Constraints
5.1. Stability Objectives
5.2. Identifying Coherent Generators
5.3. Partitioning and Connectivity Constraints
6. Multi-Objective Optimization
6.1. Solution Approaches
6.2. Improving Computation Time
7. Case Studies
7.1. Test Case and Parameter Setup
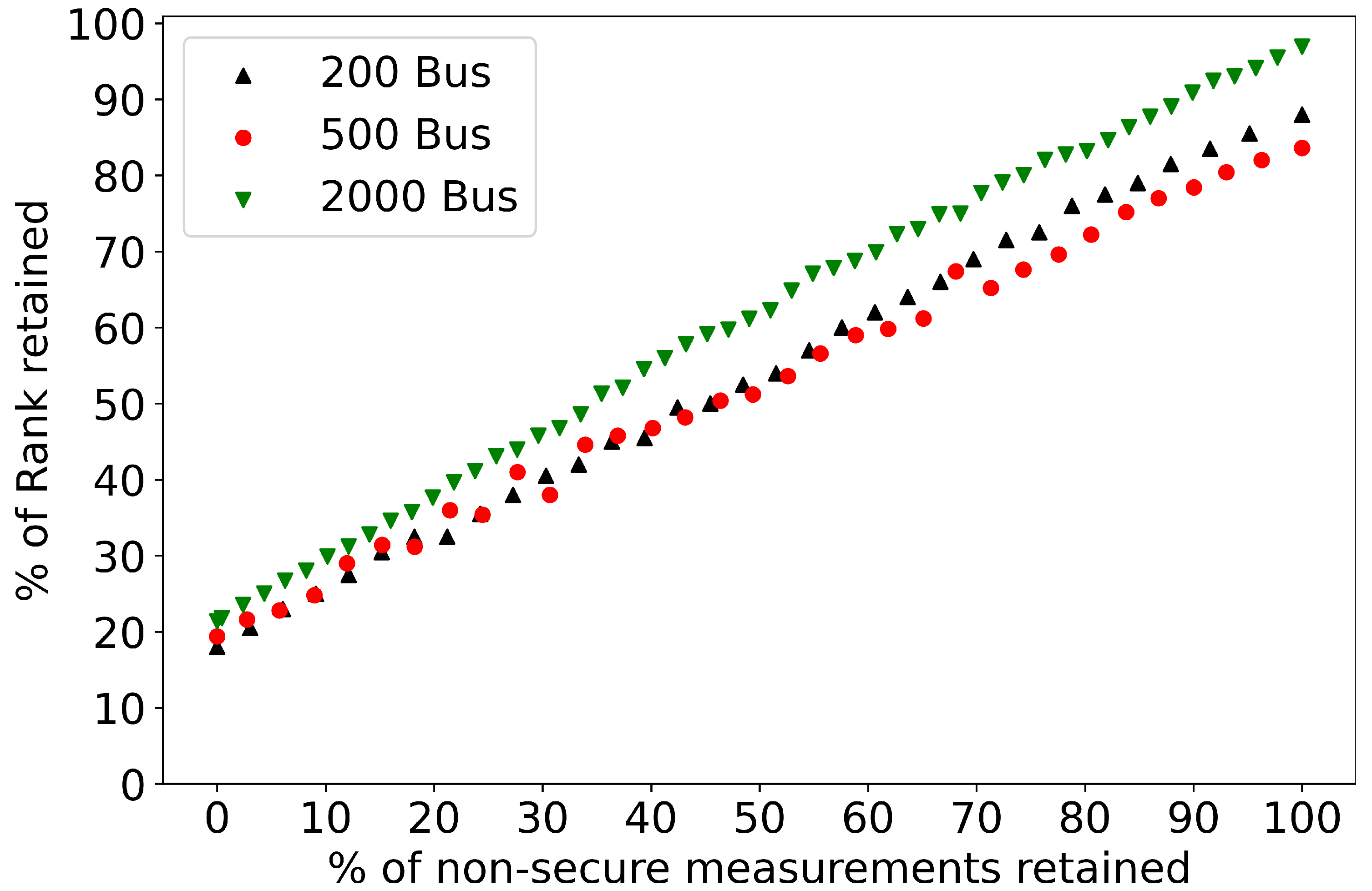
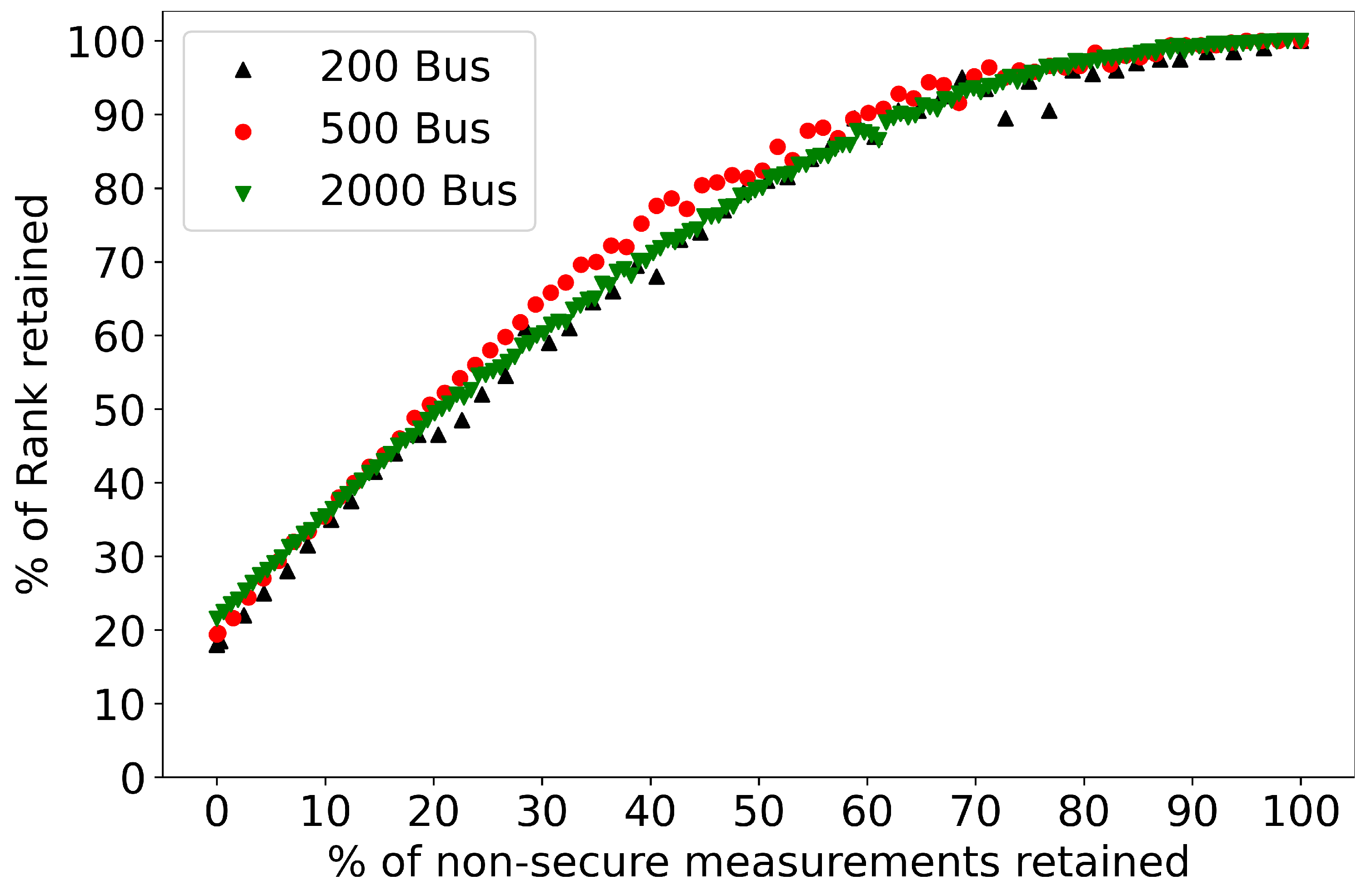
7.2. Performance of Controlled Islanding under Complete Uncertainty
7.2.1. Partitioning into Two Islands
7.2.2. Partitioning into Multiple Islands
7.3. Performance of Controlled Islanding under Partial Uncertainty
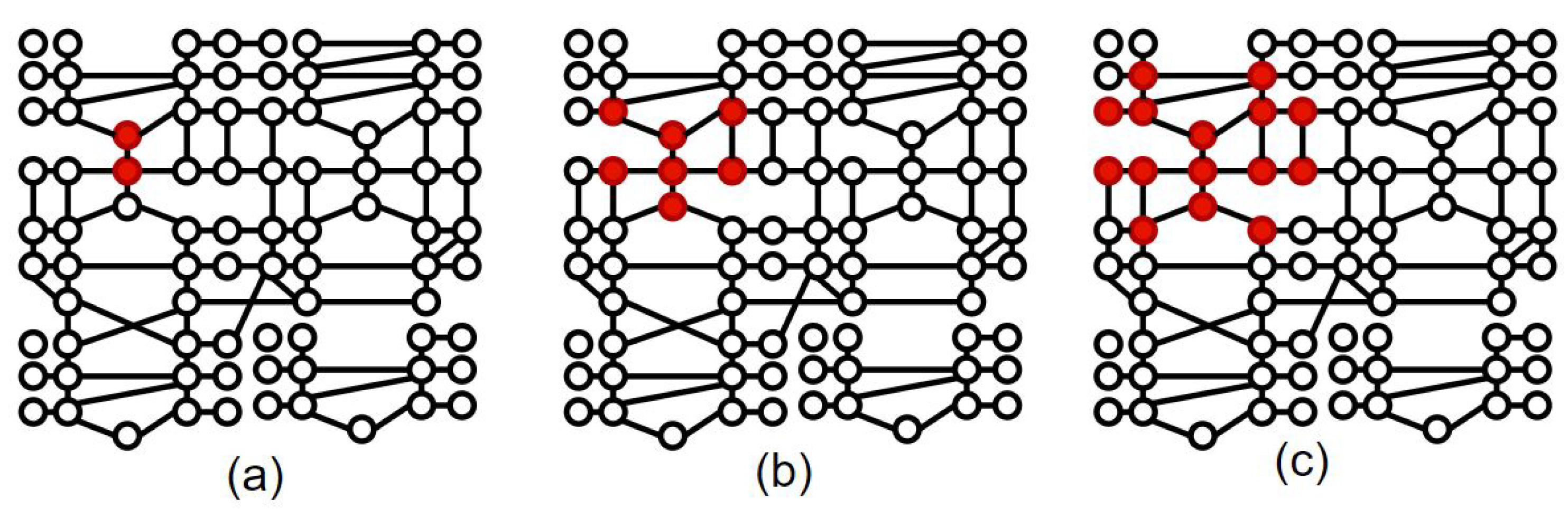
7.3.1. Identification of Attack Buses
7.3.2. Partitioning into Two Islands
7.3.3. Partitioning into Multiple Islands
7.3.4. Effect of Attack Radius R on Size of Vulnerable Island
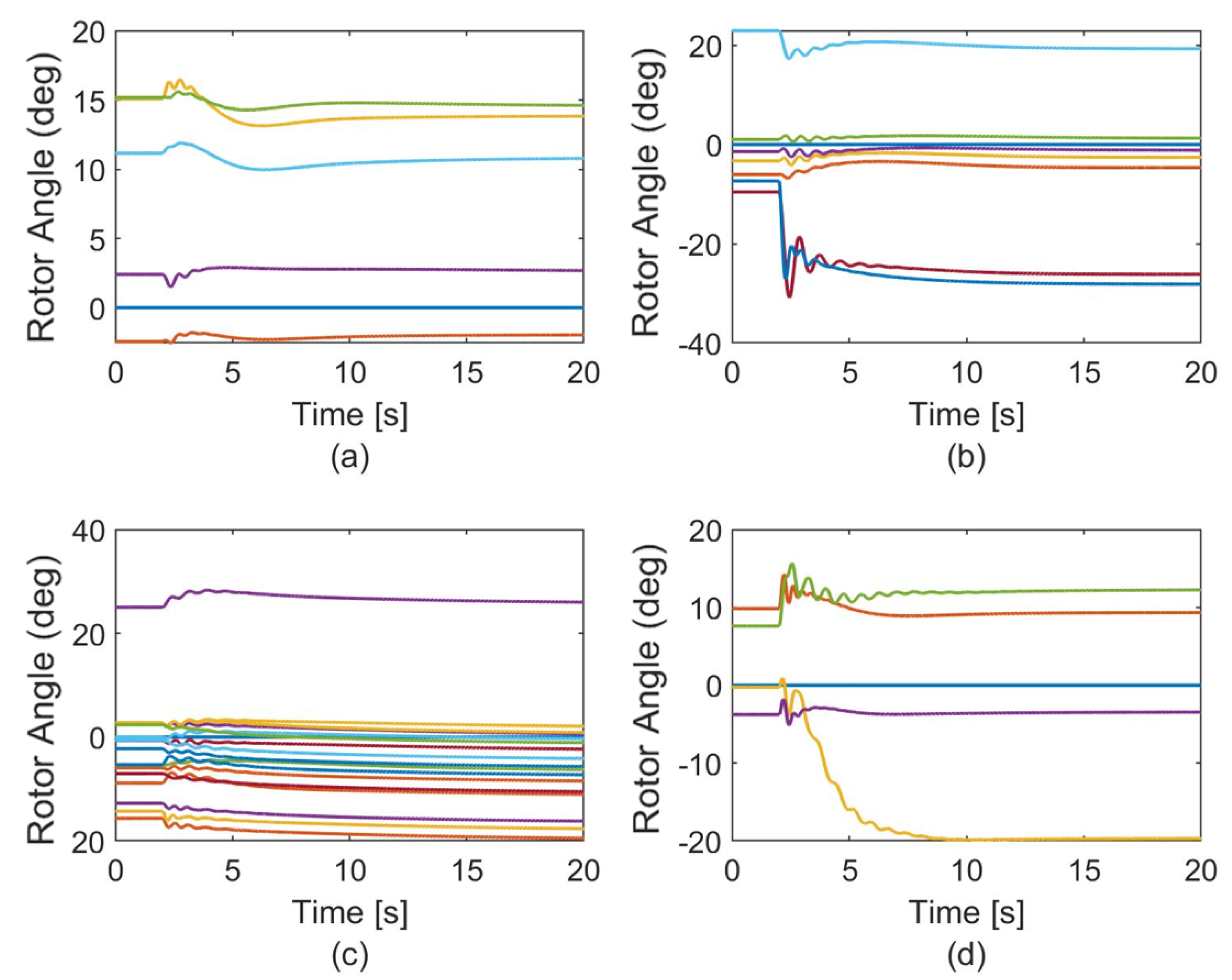
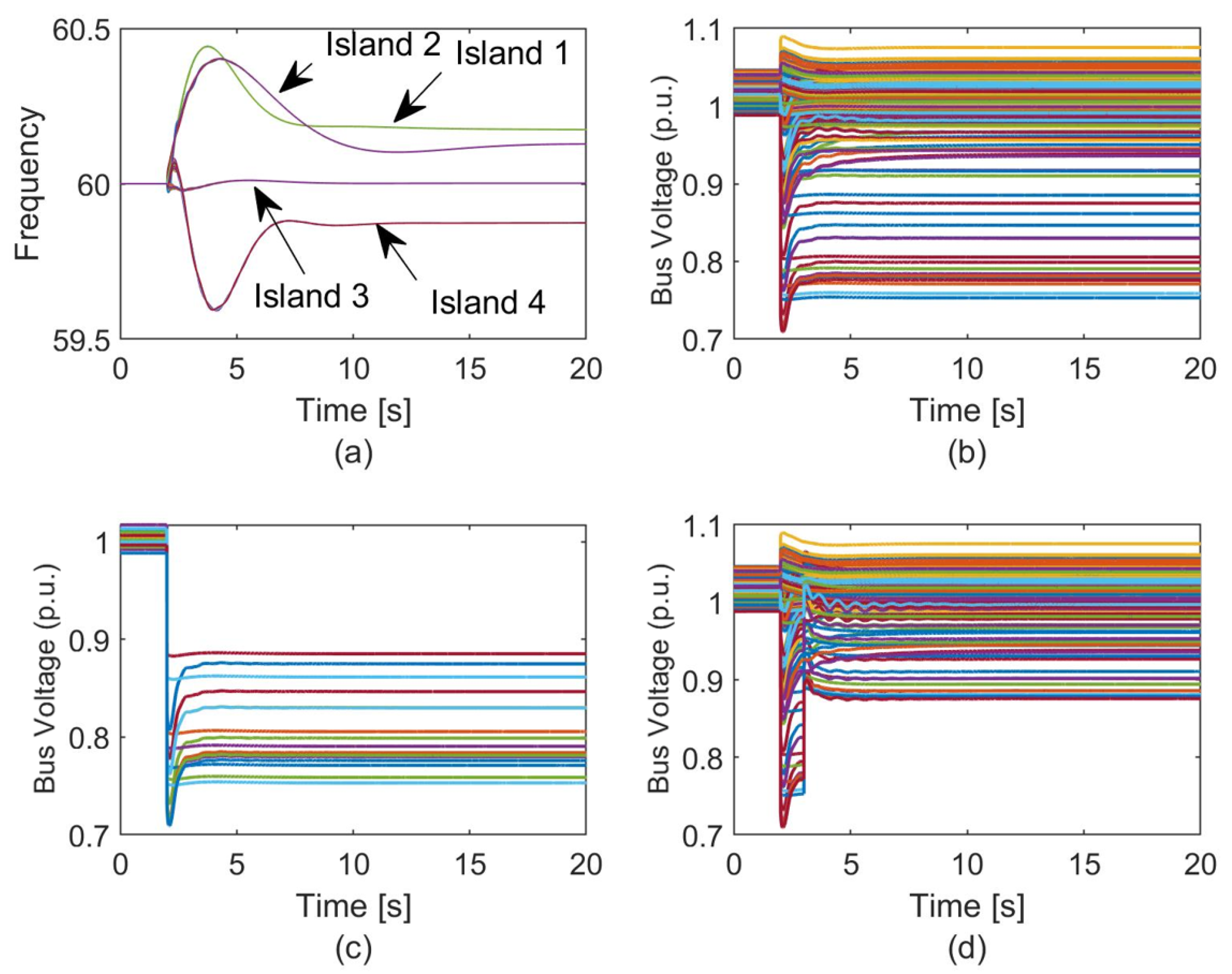
7.4. Dynamic Simulations
7.5. Computation Time
7.6. Comparison of Multiple Solutions
7.7. Limitations
8. Conclusions
- Under complete attack uncertainty with different numbers of PMUs in the original system, it was observed that redundant PMUs played a major role in retaining more observable sections of the newly formed islands.
- Under partial attack uncertainty, it was found that a smaller island was sufficient to isolate all vulnerable PMUs into a single region.
- Various multi-objective optimization methods are compared based on the number of iterations, number of parameters, optimal solution, and the total run time. It was found that the hierarchical approach is particularly attractive in providing acceptable controlled islanding solutions incorporating objective priority and optimal solution degradation when considering multiple competing objectives.
- It was observed that partitioning the power system into multiple smaller islands using the proposed approach created partitions with sufficient steady-state and transient stability margins and maximal observability.
- Lastly, it was found that accurate islanding solutions were obtained when integral constraints on some binary variables were relaxed in the optimization problem and certain objective functions were converted into bounded constraints, thereby reducing computation time.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Set of transmission lines | |
| Set of lines with secure and non-secure PMU measurements, respectively | |
| Set of nodes | |
| Set of source nodes | |
| Net injection measurement at node i | |
| Active powerflow measurement on line | |
| Matrix for topological observability | |
| Observability sub-matrices for secure and non-secure PMU measurements, respectively | |
| System gain matrix | |
| Observability decision matrix | |
| Decision sub-matrix for lines with secure and non-secure measurements, respectively | |
| h | Number of islands |
| Number of nodes and lines, respectively | |
| m | Number of PMU measurements |
| Line connectivity status variable | |
| Node i placement in island h status variable | |
| Coupling variable between and | |
| Line measurement status variable | |
| Linearization variable | |
| Network connectivity flow variable | |
| Slack variable for load-generation balance | |
| Weight associated with non-secure PMU | |
| Weight associated with objective function | |
| Tolerance for optimal solution degradation | |
| Tolerance for bounded constraint | |
| Reference solution for Chebyshev’s method | |
| Reference solution for Benson’s method |
References
- Trodden, P.; Bukhsh, W.; Grothey, A.; McKinnon, K. MILP formulation for controlled islanding of power networks. Int. J. Elec. Power Energy Sys. 2013, 45, 501–508. [Google Scholar] [CrossRef] [Green Version]
- You, H.; Vittal, V.; Wang, X. Slow coherency-based islanding. IEEE Trans. Power Syst. 2004, 19, 483–491. [Google Scholar] [CrossRef]
- Ding, L.; Gonzalez-Longatt, F.M.; Wall, P.; Terzija, V. Two-step spectral clustering controlled islanding algorithm. IEEE Trans. Power Syst. 2012, 28, 75–84. [Google Scholar] [CrossRef] [Green Version]
- Li, J.; Liu, C.C.; Schneider, K.P. Controlled partitioning of a power network considering real and reactive power balance. IEEE Trans. Smart Grid 2010, 1, 261–269. [Google Scholar] [CrossRef]
- Trodden, P.; Bukhsh, W.; Grothey, A.; McKinnon, K. MILP islanding of power networks by bus splitting. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Kyriacou, A.; Demetriou, P.; Panayiotou, C.; Kyriakides, E. Controlled Islanding Solution for Large-Scale Power Systems. IEEE Trans. Power Syst. 2018, 33, 1591–1602. [Google Scholar] [CrossRef]
- Sun, K.; Zheng, D.Z.; Lu, Q. Splitting strategies for islanding operation of large-scale power systems using OBDD-based methods. IEEE Trans. Power Syst. 2003, 18, 912–923. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Vittal, V. Slow coherency based cutset determination algorithm for large power systems. IEEE Trans. Power Syst. 2010, 25, 877–884. [Google Scholar] [CrossRef]
- Ding, T.; Sun, K.; Huang, C.; Bie, Z.; Li, F. Mixed-integer linear programming-based splitting strategies for power system islanding operation considering network connectivity. IEEE Syst. J. 2015, 12, 350–359. [Google Scholar] [CrossRef]
- Zhang, J.; Chu, Z.; Sankar, L.; Kosut, O. False data injection attacks on phasor measurements that bypass low-rank decomposition. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), Dresden, Germany, 23–26 October 2017; pp. 96–101. [Google Scholar]
- Gao, P.; Wang, M.; Chow, J.H.; Ghiocel, S.G.; Fardanesh, B.; Stefopoulos, G.; Razanousky, M.P. Identification of successive “unobservable” cyber data attacks in power systems through matrix decomposition. IEEE Trans. Signal Process. 2016, 64, 5557–5570. [Google Scholar] [CrossRef]
- Zhang, Z.; Gong, S.; Dimitrovski, A.D.; Li, H. Time Synchronization Attack in Smart Grid: Impact and Analysis. IEEE Trans. Smart Grid 2013, 4, 87–98. [Google Scholar] [CrossRef]
- Hug, G.; Giampapa, J.A. Vulnerability assessment of AC state estimation with respect to false data injection cyber-attacks. IEEE Trans. Smart Grid 2012, 3, 1362–1370. [Google Scholar] [CrossRef] [Green Version]
- Musleh, A.S.; Chen, G.; Dong, Z.Y. A Survey on the Detection Algorithms for False Data Injection Attacks in Smart Grids. IEEE Trans. Smart Grid 2019. [Google Scholar] [CrossRef]
- Yuan, L.; Xing, W.; Chen, H.; Zang, B. Security Breaches as PMU Deviation: Detecting and Identifying Security Attacks Using Performance Counters. In Proceedings of the ACM SIGOPS Asia-Pacific Workshop on Systems, Shanghai, China, 11–12 July 2011. [Google Scholar]
- Liu, X.; Li, Z. Local Load Redistribution Attacks in Power Systems With Incomplete Network Information. IEEE Trans. Smart Grid 2014, 5, 1665–1676. [Google Scholar] [CrossRef]
- Che, L.; Liu, X.; Li, Z.; Wen, Y. False data injection attacks induced sequential outages in power systems. IEEE Trans. Power Syst. 2018, 34, 1513–1523. [Google Scholar] [CrossRef]
- Li, Z.; Shahidehpour, M.; Alabdulwahab, A.; Abusorrah, A. Bilevel Model for Analyzing Coordinated Cyber-Physical Attacks on Power Systems. IEEE Trans. Smart Grid 2016, 7, 2260–2272. [Google Scholar] [CrossRef]
- Deng, R.; Zhuang, P.; Liang, H. CCPA: Coordinated Cyber-Physical Attacks and Countermeasures in Smart Grid. IEEE Trans. Smart Grid 2017, 8, 2420–2430. [Google Scholar] [CrossRef]
- Bernstein, A.; Bienstock, D.; Hay, D.; Uzunoglu, M.; Zussman, G. Power grid vulnerability to geographically correlated failures—Analysis and control implications. In Proceedings of the IEEE INFOCOM Conference on Computer Communications, Toronto, ON, Canada, 27 April–2 May 2014; pp. 2634–2642. [Google Scholar]
- NERC. In Special Protection Systems (SPS)/Remedial Action Schemes (RAS): Assessment of Definition, Regional Practices, and Application of Related Standards; North American Electric Reliability Corporation: Atlanta, GA, USA, 2013.
- Basumallik, S.; Eftekharnejad, S.; Johnson, B.K. The impact of false data injection attacks against remedial action schemes. Int. J. Electr. Power Energy Syst. 2020, 123, 106225. [Google Scholar] [CrossRef]
- Wei, F.; Wan, Z.; He, H. Cyber-Attack Recovery Strategy for Smart Grid Based on Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 11, 2476–2486. [Google Scholar] [CrossRef]
- Kushal, T.R.B.; Lai, K.; Illindala, M.S. Risk-based mitigation of load curtailment cyber attack using intelligent agents in a shipboard power system. IEEE Trans. Smart Grid 2018, 10, 4741–4750. [Google Scholar] [CrossRef]
- Zhao, J.; Mili, L.; Wang, M. A generalized false data injection attack against power system nonlinear state estimator and countermeasures. IEEE Trans. Power Syst. 2018, 33, 4868–4877. [Google Scholar] [CrossRef]
- Huang, L.; Sun, Y.; Xu, J.; Gao, W.; Zhang, J.; Wu, Z. Optimal PMU placement considering controlled islanding of power system. IEEE Trans. Power Syst. 2013, 29, 742–755. [Google Scholar] [CrossRef]
- Monticelli, A. State Estimation in Electric Power Systems: A Generalized Approach; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Fazel, S.M. Matrix Rank Minimization with Applications. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 2003. [Google Scholar]
- Gibert, D.; Mateu, C.; Planes, J. The rise of machine learning for detection and classification of malware: Research developments, trends and challenges. J. Netw. Comput. Appl. 2020, 153, 102526. [Google Scholar] [CrossRef]
- Esmalifalak, M.; Liu, L.; Nguyen, N.; Zheng, R.; Han, Z. Detecting Stealthy False Data Injection Using Machine Learning in Smart Grid. IEEE Syst. J. 2017, 11, 1644–1652. [Google Scholar] [CrossRef]
- Bundy, A.; Wallen, L. Breadth-first search. In Catalogue of Artificial Intelligence Tools; Springer: Berlin/Heidelberg, Germany, 1984; p. 13. [Google Scholar]
- Basumallik, S.; Eftekharnejad, S. Dynamic Islanding in Power Systems Based on Real-Time Operating Conditions. In Proceedings of the 2019 North American Power Symposium (NAPS), Wichita, KS, USA, 13–15 October 2019; pp. 1–6. [Google Scholar]
- Chow, J.H.; Peponides, G.; Kokotovic, P.; Avramovic, B.; Winkelman, J. Time-Scale Modeling of Dynamic Networks with Applications to Power Systems; Springer: Berlin/Heidelberg, Germany, 1982; Volume 46. [Google Scholar]
- Antunes, C.H.; Alves, M.J.; Clímaco, J. Multiobjective Linear and Integer Programming; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Cohon, J.L. Multiobjective Programming and Planning; Courier Corporation: Chelmsford, MA, USA, 2004; Volume 140. [Google Scholar]
- Mitchell, J.E. Branch-and-cut algorithms for combinatorial optimization problems. In Handbook of Applied Optimization; 2002; Volume 1, pp. 65–77. Available online: https://homes.di.unimi.it/righini/Didattica/ComplementiRicercaOperativa/MaterialeCRO/2000%20-%20Mitchell%20-%20branch-and-cut.pdf (accessed on 27 June 2020).
- Grotschel, M. Geometric Algorithms and Combinatorial Optimization; Springer Science & Business Media: Berlin/Heidelberg, Germany, 1988. [Google Scholar]
- Birchfield, A.B.; Xu, T.; Gegner, K.M.; Shetye, K.S.; Overbye, T.J. Grid Structural Characteristics as Validation Criteria for Synthetic Networks. IEEE Trans. Power Syst. 2017, 32, 3258–3265. [Google Scholar] [CrossRef]
- PJM. Phasor Measurement Unit (PMU) Placement Plan in RTEP Planning Process 2020. Available online: https://www.pjm.com/-/media/committees-groups/subcommittees/sos/2020/20200713/20200713-item-09-phasor-measurement-unit-placement-plan-in-rtep-planning-process.ashx;asthisisanonlineppt (accessed on 10 February 2021).
- Melhem, Z. Electricity Transmission, Distribution and Storage Systems; Woodhead Publishing Series in Energy; Woodhead Publishing: Sawston, UK, 2013. [Google Scholar]
- U.S. Department of Energy. Synchrophasor Technologies and their Deployment in the Recovery Act Smart Grid Programs, American Recovery and Reinvestment Act of 2009. 2013. Available online: https://www.energy.gov/oe/downloads/synchrophasor-technologies-and-their-deployment-recovery-act-smart-grid-programs-august (accessed on 15 January 2021).
- Xu, B.; Abur, A. Optimal Placement of Phasor Measurement Units for State Estimation; Final Project Report; Power Systems Engineering Research Center: Tempe, AZ, USA, 2005; pp. 5–58. [Google Scholar]
- Lu, C.; Wang, Z.; Ma, M.; Shen, R.; Yu, Y. An optimal PMU placement with reliable zero injection observation. IEEE Access 2018, 6, 54417–54426. [Google Scholar] [CrossRef]
- Kundur, P. Power system stability. In Power System Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 2007; p. 7-1. [Google Scholar]
- Instruction Manuals. SEL-421 Relay 2001. Available online: https://selinc.com/literature/instruction-manuals/?title=421 (accessed on 15 March 2019).
- Schäfer, B.; Witthaut, D.; Timme, M.; Latora, V. Dynamically induced cascading failures in power grids. Nat. Commun. 2018, 9, 1975. [Google Scholar] [CrossRef]
- Vazirani, V.V. Approximation Algorithms; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2013. [Google Scholar]

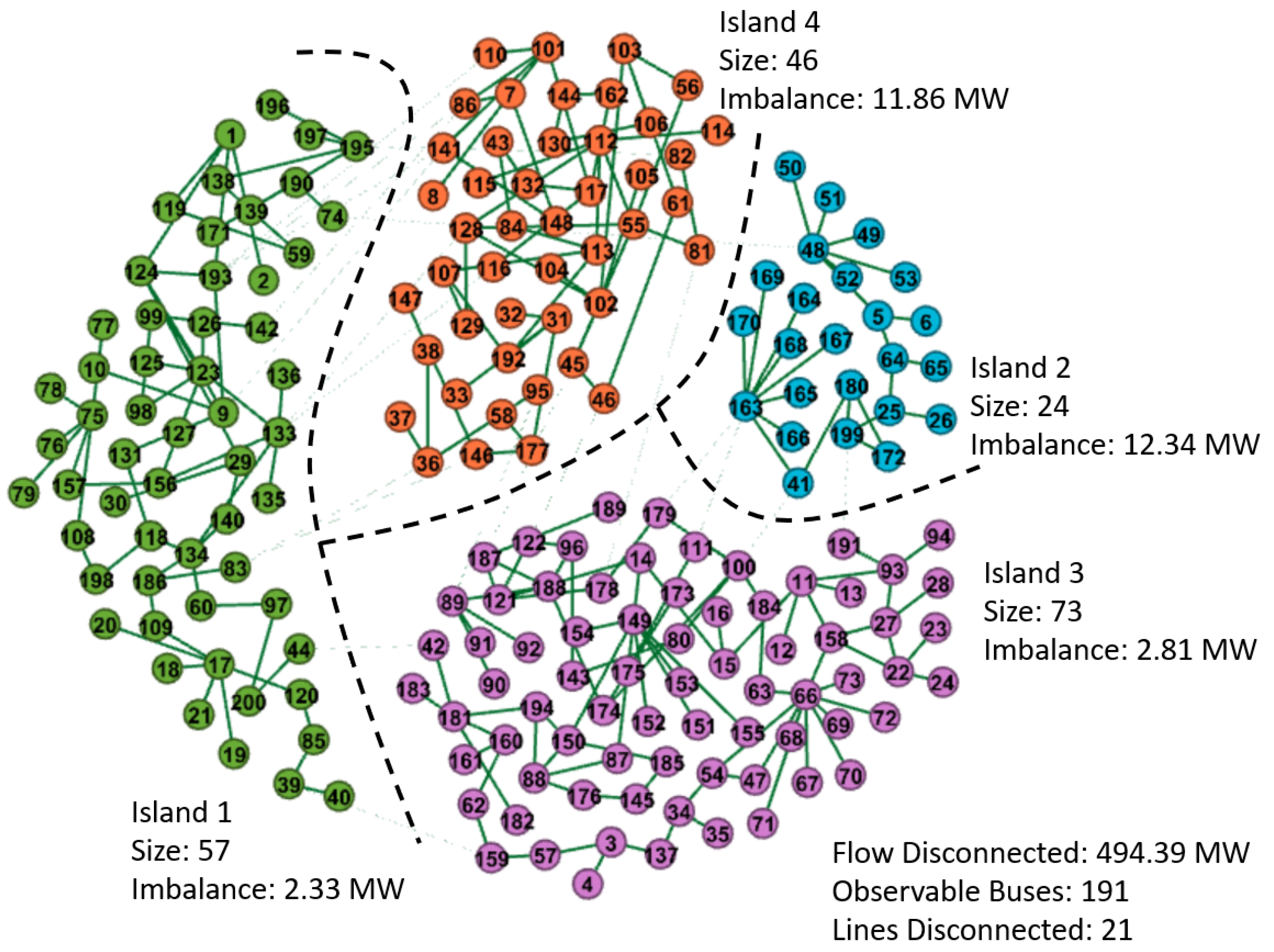
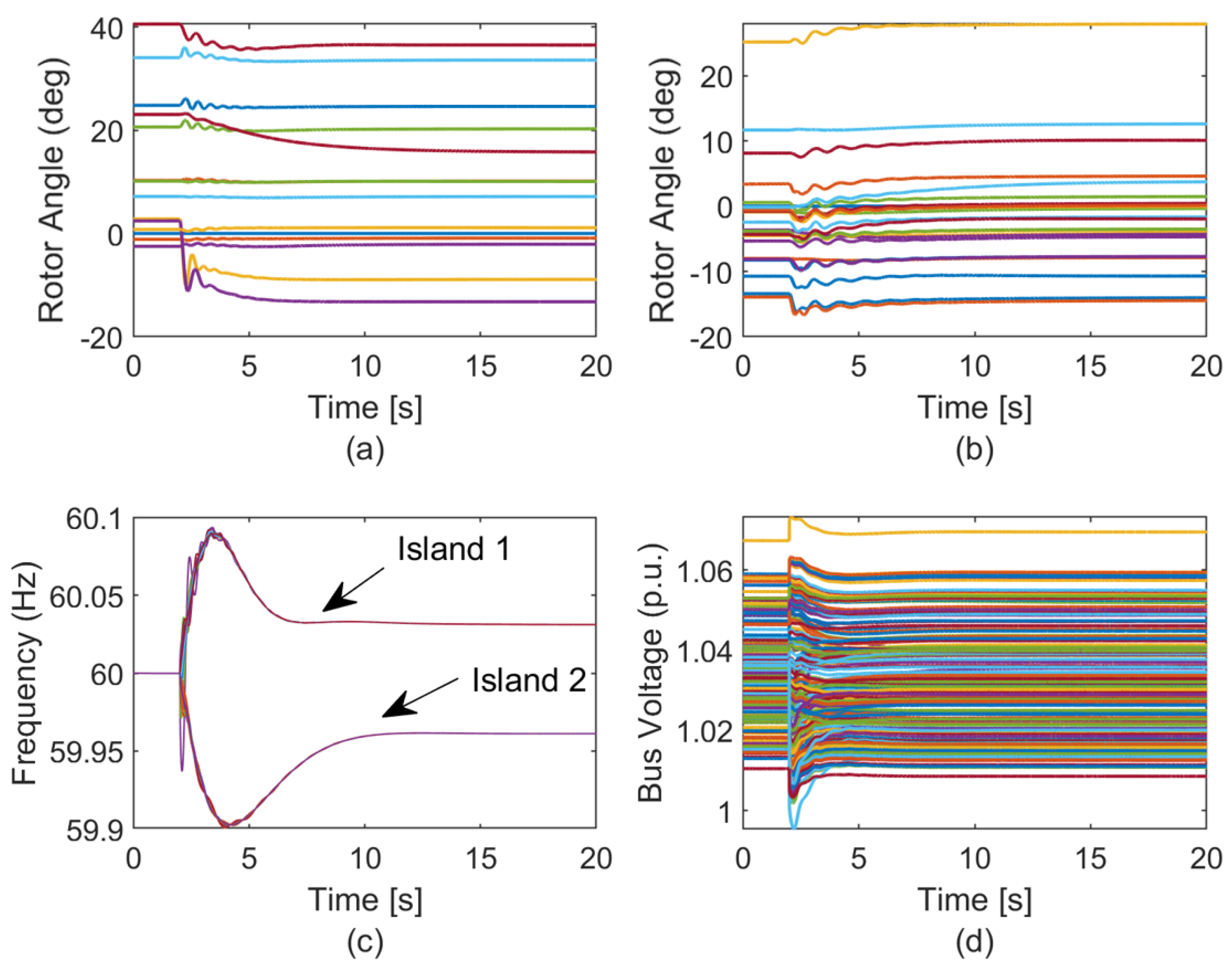

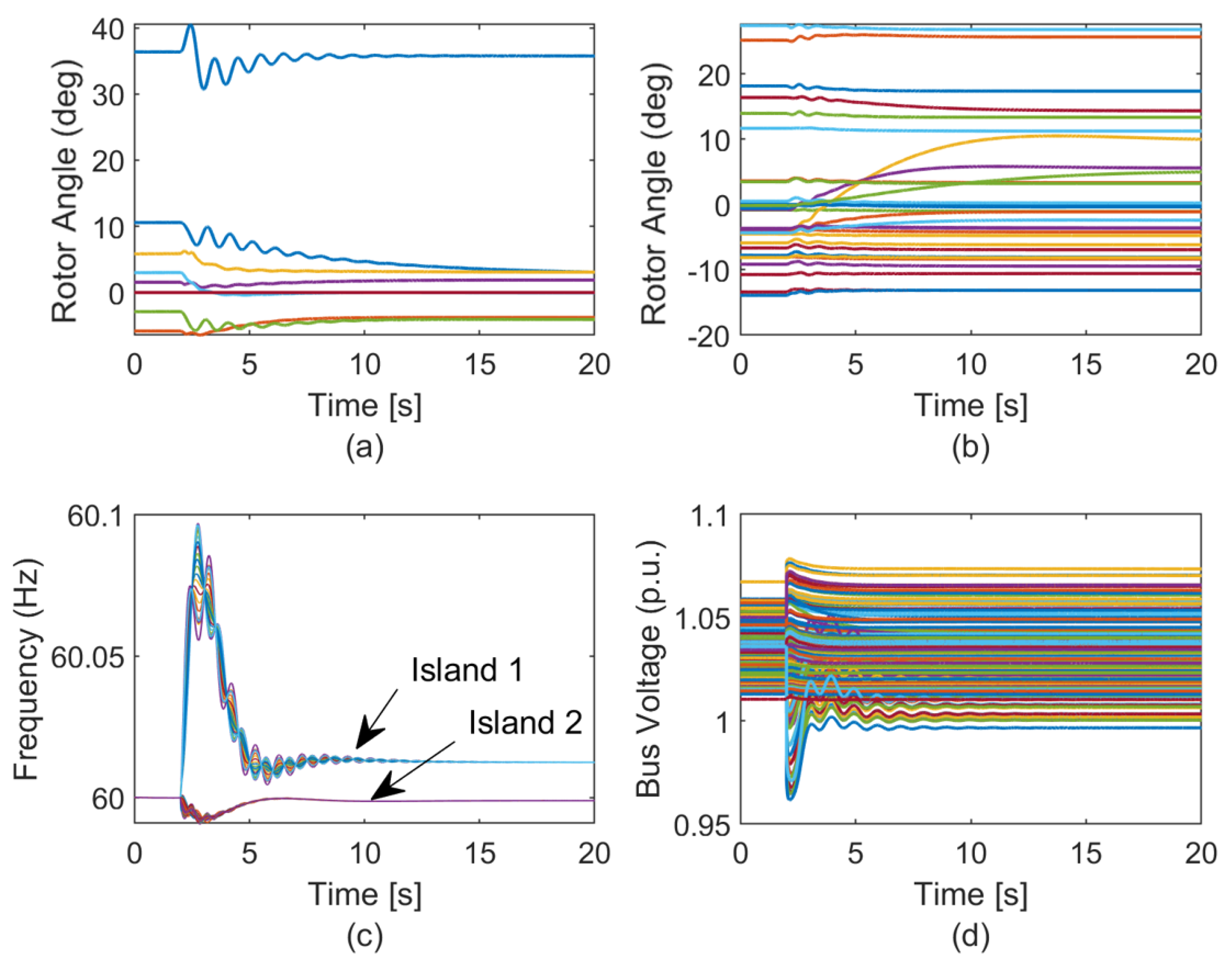
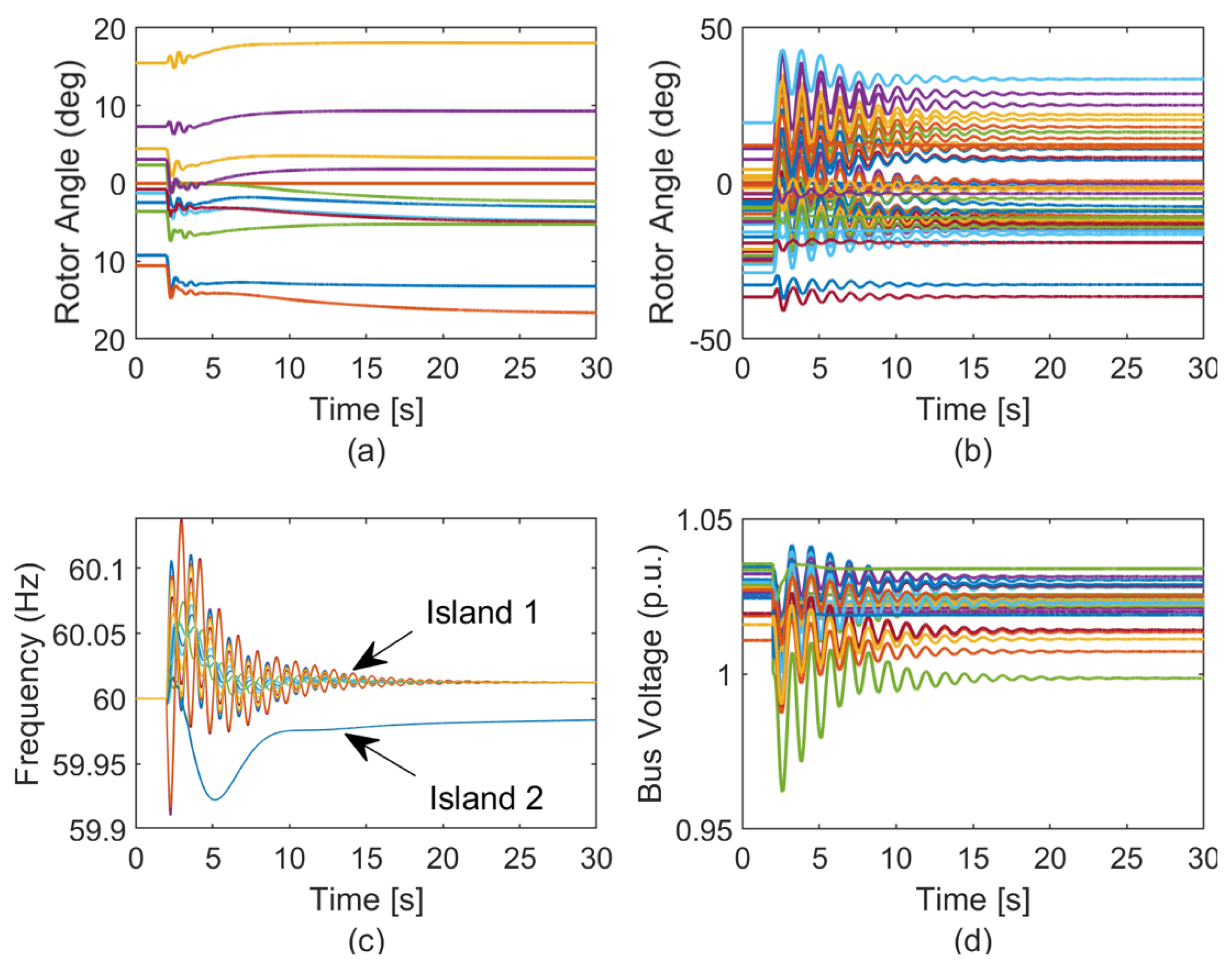

| Solution | Formulation |
|---|---|
| Hierarchical | |
| Weighted-sum | |
| -constraint | |
| Weighted Chebyshev | |
| Benson |
| System | Load | Gen | # Secure | # Non-Secure | # Non-Secure |
|---|---|---|---|---|---|
| (MW) | (MW) | PMUs | PMUs (Obs = 1) | PMUs (Obs = 2) | |
| 200 | 1750 | 1765 | 25 | 46 | 130 |
| 500 | 7750 | 7832 | 63 | 176 | 394 |
| 2000 | 67,109 | 68,728 | 132 | 589 | 1247 |
| System | ||||||
|---|---|---|---|---|---|---|
| 200 | 0.1 | 1 | 1 | 1 | 10 | 40 |
| 500 | 0.01 | 1 | 1 | 1 | 30 | 50 |
| 2000 | 0.01 | 0.1 | 1 | 1 | 50 | 350 |
| System | Rank | Size ( | Imbalance (MW) | Flow Out (MW) |
|---|---|---|---|---|
| 200 | 412 | 29 | 0 | 28.03 |
| 500 | 1000 | 80 | 10 | 400.0 |
| 2000 | 4232 | 303 | 0 | 5373.29 |
| System | Rank | Size () | Imbalance (MW) | Flow Out (MW) |
|---|---|---|---|---|
| 200 | 400 | 50 | 20 | 50 |
| 500 | 1000 | 200 | 350 | 2000 |
| 2000 | 4000 | 400 | 20 | 7000 |
| Optimal Solution [Priority, Degradation] | |||
|---|---|---|---|
| Rank | % Meas Retained | Imbalance (MW) | Flow Out (MW) |
| (Non-Secure) | |||
| 173 [3, 10] | 100 [4, 0] | 445.48 [2, 0] | 294.15 [1, 0] |
| 178 [1, 10] | 100 [4, 0] | 675.52 [2, 0] | 428.09 [3, 0] |
| 163 [3, 10] | 93.33 [4, 0] | 17.57 [1, 0] | 527.98 [2, 0] |
| Optimal Solution [Priority, Degradation] | ||||
|---|---|---|---|---|
| Rank | Size () | Imbalance (MW) | Flow Out (MW) | Time (s) |
| 196 [3, 0] | 42 [2, 0] | 9.80 [4, 0] | 28.03 [1, 0] | 0.27 |
| 197 [3, 0] | 29 [2, 0] | 32.3 [4, 0] | 54.16 [1, 50] | 0.36 |
| 197 [3, 0] | 38 [2, 0] | 0.07 [4, 10] | 35.76 [1, 50] | 0.69 |
| Optimal Solution [Priority, Degradation] | ||||
|---|---|---|---|---|
| Rank | Size () | Imbalance (MW) | Flow Out (MW) | Time (s) |
| 499 [3, 0] | 107 [2, 0] | 649.16 [4, 0] | 649.16 [1, 0] | 0.19 |
| 500 [1, 0] | 196 [3, 0] | 1610.0 [4, 0] | 1465.1 [2, 0] | 0.30 |
| 498 [2, 0] | 11 [1, 0] | 124.22 [4, 0] | 867.36 [3, 0] | 0.15 |
| Optimal Solution [Priority, Degradation] | ||||
|---|---|---|---|---|
| Rank | Size () | Imbalance (MW) | Flow Out (MW) | Time (s) |
| 1979 [4, 0] | 312 [1, 0] | 370.5 [2, 0] | 8519.1 [3, 0] | 511.5 |
| 1980 [4, 0] | 352 [1, 40] | 0.01 [2, 0] | 5650.4 [3, 0] | 131 |
| 1891 [4, 0] | 351 [1, 40] | 8.9 [2, 10] | 5526.9 [3, 0] | 3.4 |
| Scalarization | Rank | Size () | Imbalance (MW) | Flow Out (MW) |
|---|---|---|---|---|
| Weighted-Sum | 197 | 38 | 0.07 | 35.76 |
| -Constraint | 196 | 39 | 2.93 | 34.98 |
| Chebyshev | 197 | 38 | 0.07 | 35.76 |
| Benson | 197 | 38 | 0.07 | 35.76 |
| Scalarization | Rank | Size () | Imbalance (MW) | Flow Out (MW) |
|---|---|---|---|---|
| Weighted-Sum | 499 | 111 | 3.7 | 850.82 |
| -Constraint | 498 | 116 | 12.69 | 847.07 |
| Chebyshev | 498 | 113 | 26.69 | 833.83 |
| Benson | 499 | 111 | 3.7 | 850.82 |
| Scalarization | Rank | Size () | Imbalance (MW) | Flow Out (MW) |
|---|---|---|---|---|
| Weighted-Sum | 1982 | 375 | 2.0 | 5470.56 |
| -Constraint | 1982 | 350 | 24.72 | 5513.70 |
| Chebyshev | 1979 | 340 | 1.85 | 5727.20 |
| Benson | 1980 | 353 | 0.02 | 5501.86 |
| Optimal Solution [Priority, Degradation] | |||||
|---|---|---|---|---|---|
| R | Rank | Size () | Imbalance (MW) | Flow Out (MW) | Time (s) |
| 3 | 198 | 66 | 3.94 | 107.93 | 0.71 |
| 4 | 198 | 85 | 1.82 | 108.99 | 0.57 |
| 5 | 196 | 103 | 2.78 | 126.12 | 0.42 |
| 6 | 196 | 110 | 11.96 | 116.93 | 0.33 |
| 7 | 196 | 120 | 8.74 | 257.32 | 0.27 |
| Optimal Solution [Priority, Degradation] | |||||
|---|---|---|---|---|---|
| R | Rank | Size () | Imbalance (MW) | Flow Out (MW) | Time (s) |
| 2 | 500 | 7 | 153.28 | 385.91 | 3.31 |
| 3 | 497 | 206 | 5.64 | 378.62 | 1.19 |
| 4 | 498 | 254 | 4.02 | 449.39 | 5.16 |
| 5 | 500 | 258 | 19.96 | 1266.38 | 1.68 |
| System | Scenario 1 | Scenario 2 | |||
|---|---|---|---|---|---|
| Hierarchical | Weighted Sum | - Constraint | Chebyshev | Benson | |
| 200-bus | 75.71 | 76.55 | 74.47 | 76.55 | 76.55 |
| 500-bus | 72.38 | 62.16 | 58.59 | 61.20 | 62.14 |
| System | 200-bus | 500-bus | 2000-bus | |||
|---|---|---|---|---|---|---|
| Relaxation | No | Yes | No | Yes | No | Yes |
| Weighted Sum | 0.07 | 0.05 | 0.43 | 0.21 | 69.96 | 0.70 |
| -Constraint | 0.00 | 0.00 | 13.01 | 0.60 | 10.00 | 1.58 |
| Chebyshev | 0.15 | 0.00 | 1.68 | 0.44 | 148.82 | 2.85 |
| Benson | 0.15 | 0.033 | 1.61 | 0.28 | 14.64 | 6.72 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Basumallik, S.; Eftekharnejad, S.; Fardad, M. Controlled Islanding under Complete and Partial False Data Injection Attack Uncertainties against Phasor Measurement Units. Energies 2022, 15, 5723. https://doi.org/10.3390/en15155723
Basumallik S, Eftekharnejad S, Fardad M. Controlled Islanding under Complete and Partial False Data Injection Attack Uncertainties against Phasor Measurement Units. Energies. 2022; 15(15):5723. https://doi.org/10.3390/en15155723
Chicago/Turabian StyleBasumallik, Sagnik, Sara Eftekharnejad, and Makan Fardad. 2022. "Controlled Islanding under Complete and Partial False Data Injection Attack Uncertainties against Phasor Measurement Units" Energies 15, no. 15: 5723. https://doi.org/10.3390/en15155723
APA StyleBasumallik, S., Eftekharnejad, S., & Fardad, M. (2022). Controlled Islanding under Complete and Partial False Data Injection Attack Uncertainties against Phasor Measurement Units. Energies, 15(15), 5723. https://doi.org/10.3390/en15155723






