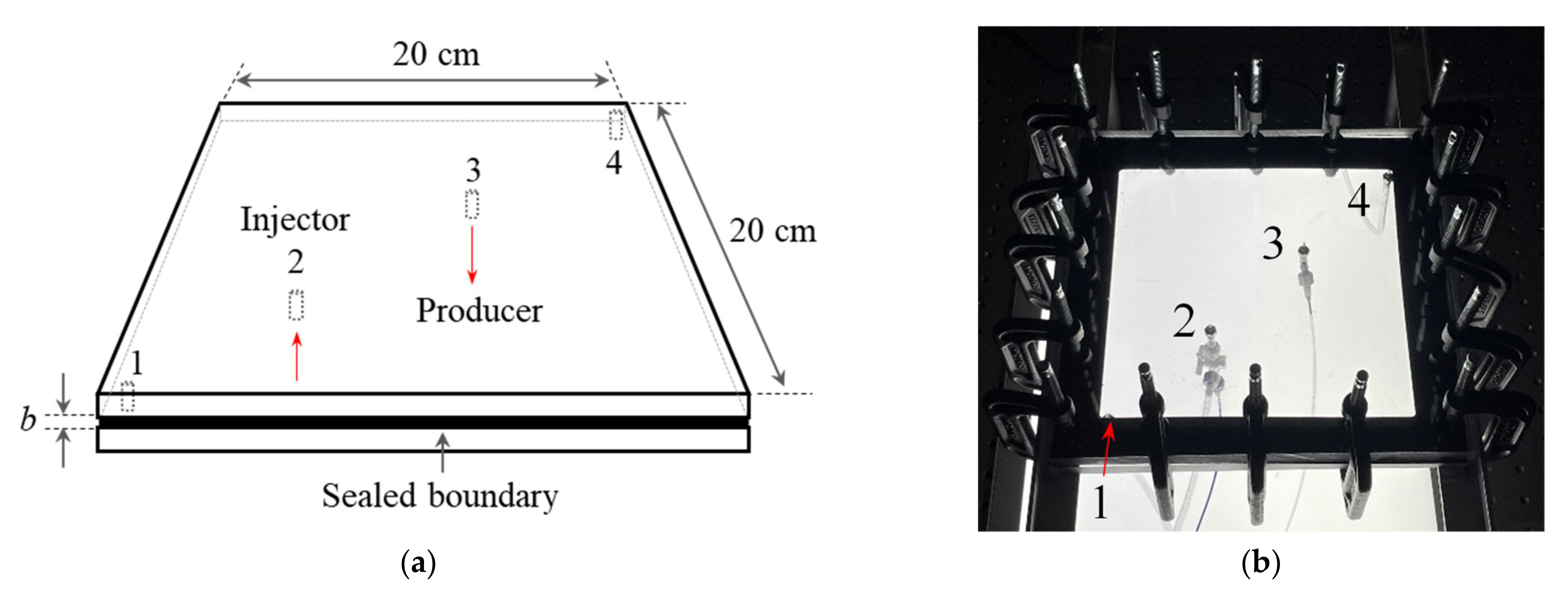
In this section, we will first analyze the flow regimes in miscible displacements at a constant injection rate under the control of constant pressure at outlet. Three new flow regimes are identified and discussed. We then examine how the injection rate affects the VF instabilities and flow regimes. Following that, the impacts of different controls at the production end, i.e., constant pressure vs. constant production rate at outlet, on VF dynamics will be discussed. Both qualitative and quantitative analysis will be performed to better understand the flow dynamics. In most of the following plots for water plumes, only a square of view area incorporating wells 1 to 3 is shown.
3.1. New Flow Regimes
Previous studies on miscible viscous fingering show that flows are first dominated by diffusion at an initial time and then by convection at a later time. Such fingering dynamics result from the competition of these two mechanisms [
20,
21,
36]. The two corresponding regimes are also shown in
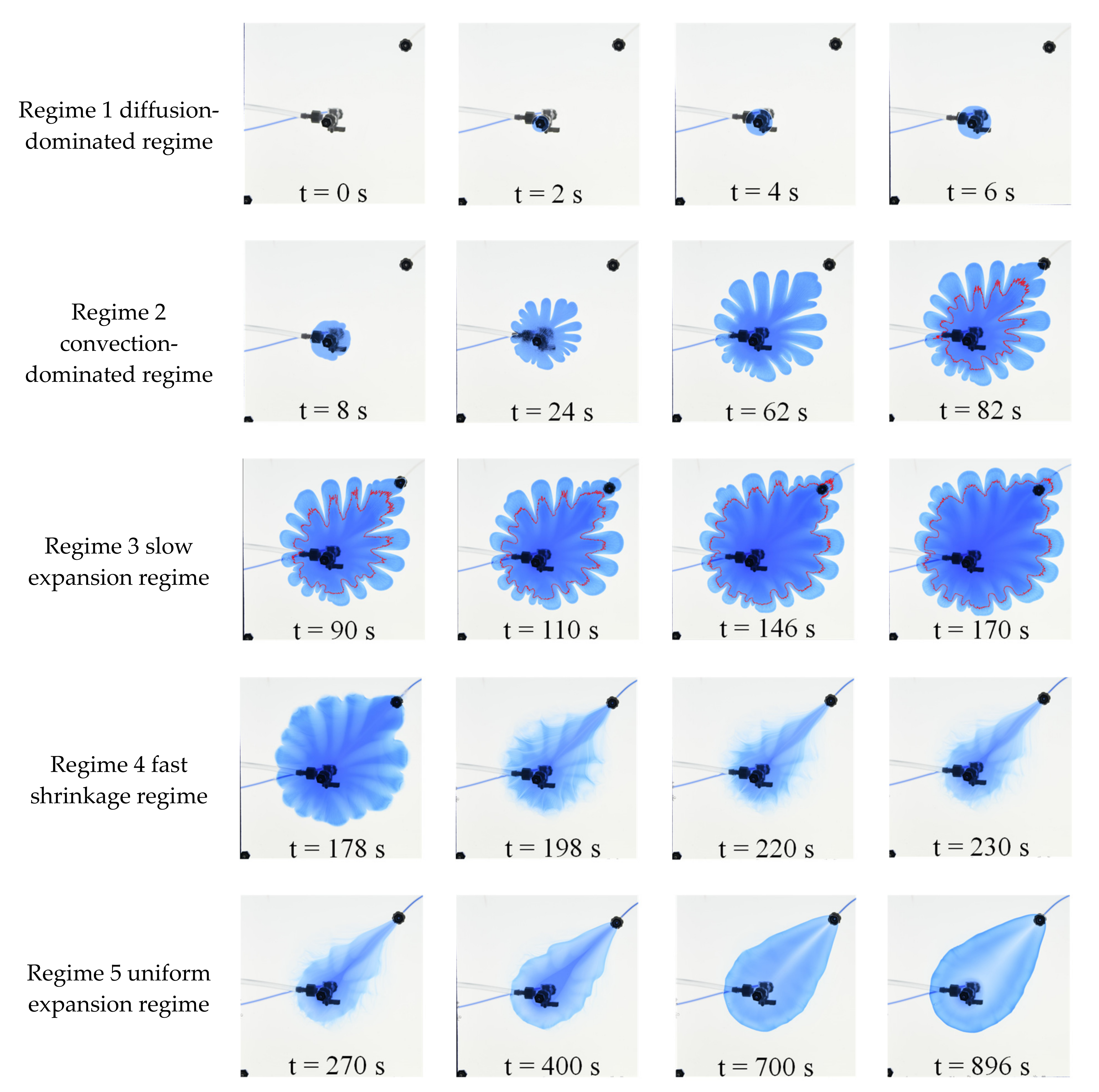
Figure 2 at a constant injection rate of 5.0 mL/min. Regime 1 (diffusion-dominated regime) starts from initial time to t = 6 s prior to the development of viscous fingering. Regime 2 (convection-dominated regime) is from t = 6 s to breakthrough at t = 82 s, with fingering becoming more unstable with time. During these two regimes, only pure glycerol is produced.
Interestingly, as water injection continues, three new flow regimes are observed following the first two regimes, as shown in
Figure 2. Regime 3 starts from breakthrough time t = 82 s when water just reaches to the production well and ends at t = 170 s when the water begins to be produced from the outlet of the tubing. At the end of Regime 3, the water plume reaches the maximum size. This regime seems to be not significantly different from Regime 2 as the water plume continues to expand. However, a careful observation shows that it exhibits different characteristics in terms of fingering structures and dynamics. Specifically, from t = 90 s to t = 170 s, the fingers become shorter with time. The distance between the finger front and the inner water plume (deep blue and highlighted by red outlines) also becomes shorter. This is opposite to the observation in Regime 2. In Regime 3, VF instability is actually suppressed as water is continuously injected. Fingering coalescence happens in the injector-to-producer direction, resulting in a decrease in the count of fingers. In the perpendicular direction, much less fingering coalescence happens, while a minor tip-splitting is observed. Such a slow expansion of water plume is because a proportion of water instantaneously flows out of the Hele–Shaw cell through the production well as water is being injected. Thus, the driving force for water propagation at the water–glycerol interface become weaker compared with that in Regime 2. Overall, the water–glycerol interface grows slowly with stabilized fingers in this new regime. We therefore refer to it as a slow expansion regime.
At t = 170 s, the maximum water plume is achieved. After that, a rapid shrinkage of injected water plume is observed until t = 230 s, which is referred to a fast shrinkage regime. Note that under the control of constant pressure at the outlet, the injection rate is constant, while the pressure at the injector and in the Hele–Shaw continues to increase before water is produced from the outlet. At t = 170 s, the pressure gradient from the injector to outlet is the highest, and the viscosity of fluids along the injector-to-outlet direction is the lowest. According to the Darcy’s law, the production rate will be very fast, resulting in a fast shrinkage of water plume. A clear fluid flow path and backward fingers can be seen at times from t = 198 s to t = 230 s in
Figure 2. In this regime, an irregular pattern of water–glycerol interface is achieved with observed residual water distributed outside of the main water plume.
The fast shrinkage of water plume also creates a connection from injector to producer with minimum resistance for injected water to flow. Consequently, most of the injected water will be directly produced. After a relatively long time after t = 230 s, the irregular pattern of the water plume disappears because of the diffusion of two fluids, while a plume with a stable water–glycerol interface appears. With time, this stable plume expands slowly without any viscous fingering (see
Figure 2 Regime 5, t = 700 s and t = 896 s). Since most of the injected water is preferentially produced through a production well, it will not contribute to the expansion of the water plume. Instead, the expansion of the water plume results from the mixing of two fluids dominated by molecular diffusion. We, therefore, refer to this stage as a uniform expansion regime. An interesting phenomenon in this regime is that there seems to have a higher concentration of glycerol in the injector-to-producer direction.
The VF dynamics and new flow regimes are also examined quantitively in terms of the variations of swept area and interfacial length between two fluids, as depicted in
Figure 3. The software ImageJ is used to determine the interface and their values at different times in each experiment. For immiscible displacements with a clear interface between two fluids, the swept area is expected to increase linearly, as it is proportional to the injection rate and time, regardless of VF instabilities. However, for the miscible case, diffusion plays a role in smoothening the interface of two fluids. For this reason, there is actually no so-called ‘interface’ in miscible displacements. However, for convenience, we use the ‘interface’ or ‘front’ to refer to the evolution of water plume. The variations of swept area also depend on the concentration threshold when determining the interface. As shown in
Figure 3, the swept area of water (red dashed curve) increases linearly from initial time to breakthrough. After that, there is a very slight decrease in the slope from t = 82 s to t = 170 s due to the diffusion. Starting from t = 170 s in Regime 4, a sudden drop in water plume area is observed because of the fast shrinkage of the plume. At the end of Regime 4 at time t = 230 s, a minimum water plume area is achieved, which is followed by the slowly increasing stage of uniform expansion dominated by diffusion.
Interestingly, the variations of interfacial length of water plume exhibit different characteristics compared to the swept area. The interfacial length increases quickly in the first two regimes because of the continuous injection of water and viscous finger instabilities. In the subsequent Regime 3, starting at t = 82 s, it slightly decreases. This is because of the stabilized viscous fingers, as indicated in
Figure 2 from t = 82 s to 170 s (the start and end times of Regime 3, respectively). This is also an important reason why Regime 3 is separated from other regimes. In the fast shrinkage Regime 4, the interfacial length also decreases dramatically. Interestingly, as water flows to the production well quickly, a fluctuation of interfacial length is clearly observed because of the backward fingers in irregular fingering structures, as shown from t = 170 s to 200 s in
Figure 2 and
Figure 3. Such backward fingers take effects in a short time because water quickly flows to the production well and mitigates the irregular structures to some extent. Overall, in Regime 4, the interfacial length decreases with time, and the swept area reaches a minimum value at the end of this regime. The backward fingers do not completely disappear even at the beginning of Regime 5. Instead, the more distorted interfaces lead to an increase in interfacial length (see
Figure 3e at t = 300 s), although the swept area only slightly increases. Eventually, the interfacial length decreases and then increases extremely slowly as more water is injected and as the water plume expands with time.
The present VF dynamics clearly distinguishes itself from that in five-spot geometry [
37], radial geometry [
38], and rectangular geometry [
36]. With the current well location and Hele–Shaw cell geometry, a non-symmetrical fingering pattern is observed, while the five-spot geometry assumes a symmetrical flow pattern. Interestingly, the present work also shows that small fingers can happen at the opposite side of the injector-to-producer direction due to the pressure gradient. The current case is, therefore, more realistic when only two wells exist in the miscible-based processes in subsurface energy and environment systems. Importantly, the new regimes provide more insights into the performance of the ‘life cycle’ miscible displacements.
We further analyze the fractal dimension of viscous fingering for different regimes based on the evolution of interface in
Figure 2 at a water injection rate of 5.0 mL/min. The fractal dimension is obtained by box-counting characterization of the interface depicted by the invading fingers [
39]. The Frac box count plugging in ImageJ is used to determine the fractal dimension for each image. Overall, the value of fractal dimension decreases as flows become more unstable with distorted fingers growing with time, while it increases when flows are stabilized [
40]. Regime 1 (diffusion dominated regime) is neglected because it is too short at 5.0 mL/min. As shown in
Figure 4, the fractal dimension of Regime 2 decreases rapidly as VF becomes more unstable with time. The convective effects are more significant in driving the mixing of two fluids relative to diffusive effects. In contrast, the fractal dimension for Regime 3 generally increases with time, which is consistent with the observation in
Figure 2, where fingers become shorter and wider. This also distinguishes it from Regime 2 and confirms the existence of Regime 3. Following that, a rapid decrease in fractal dimension in Regime 4 is observed, resulting from the quick shrinkage and the backward fingers. The mixing in this regime is caused by the fast co-flowing of fluid mixtures to the outlet. As backward fingers are mitigated by diffusion in Regime 5, the variations of fractal dimension become smooth. Diffusion dominates the mixing of two fluids and the expansion of the water plume.
3.2. Impacts of Water Injection Rate
Displacements with several constant water injection rates are performed.
Figure 5 shows the water plume at the start and end of different flow regimes at a water injection rate of 1.0 mL/min with constant pressure control at the outlet. Five flow regimes can still be seen in the whole displacement processes, which is similar to those at 5.0 mL/min in
Figure 2. However, different characteristics are also observed when the injection rate decreases to 1.0 mL/min. Generally, at a lower injection rate, the VF is less unstable with apparently shorter fingers at a breakthrough time of t = 358 s and at the start of the shrinkage stage t = 476 s. The count of fingers is also less at a lower injection rate. Compared to
Figure 2 where fingers are noticeably stabilized in a slow expansion stage (t = 82 s to 170 s), the stabilizing effect at 1.0 mL/min is however much weaker. At the end of the shrinkage stage at t = 566 s, the size of the water plume at 1.0 mL/min is larger than that of 5.0 mL/min and is less irregular. In fact, when the injection rate is as low as 0.1 mL/min, neither the stabilizing effect nor the shrinkage of water plume is obvious.
The impacts of injection rates are also examined by comparing the VF dynamics when 2.5 mL of water is injected, as depicted in
Figure 6. The Péclet number Pe is defined as
, where q is the volumetric flow rate of injection varying from 0.1 mL/min to 5.0 mL/min. D is the diffusivity between water and glycerol, which is 1.6 × 10
−10 m
2/s [
13,
41]. Overall, at a lower injection rate with a smaller Pe, the water plume is less unstable, and VF mainly develops in the injector-to-producer direction due to the higher pressure gradient in this direction. While on the opposite side of the injector-to-producer direction, the water–glycerol interface propagates stably at a lower injection rate. On the contrary, at a higher injection rate with a larger Pe, small fingers can still develop on the opposite side of the injector-to-producer direction. Another observation is that a larger swept area is achieved at a lower injection rate because of the longer period of time for injecting 2.5 mL water and the smaller water plume. For example, 1800 s is needed to inject 2.5 mL water at an injection rate of 0.1 mL/min. For such a long time, diffusion plays a role in enabling more expansion of the water plume, thus resulting in a larger swept area and less concentration gradient in the water plume.
We further examine water injection rates on the shape of the water plume, as depicted in
Figure 7. When breakthrough happens in
Figure 7a, the flows are apparently more unstable at a higher injection rate because of stronger convection. On the contrary, at a higher injection rate, the minimum size of the water plume at the end of the shrinkage stage is smaller, as shown in
Figure 7b. This is because during the shrinkage stage the stronger convection mobilizes the water plume to the production well quickly under a larger pressure gradient from injector to producer. For the highest injection rate at 5.0 mL/min, the shrinkage rate is so fast that the irregular shape of the water plume is clearly observed with a flow path from the water–glycerol interface to producer, not only along the injection–producer. Water and glycerol are further mixed because of this quick shrinkage. When the injection rate is less than or equal to 0.5 mL/min, the minimum size of the water plume becomes insensitive to the water injection rate. Interestingly, for slower injection rates, some residual glycerol seems to be formed in the injector-to-producer direction indicated by the slight white color. Different from its counterpart at high injection rates, the change of glycerol concentration along the injector–producer direction is not obvious from breakthrough to the end of slow expansion at a low water injection rate. In addition, we have observed the backward fingers in the producer-to-injector direction in
Figure 2,
Figure 6 and
Figure 7. They are caused by the larger pressure gradient at only higher water injection rates.
From the color of water plumes in
Figure 7a, it can be seen that the viscosity of the water plume at a higher injection rate is apparently lower than that at a lower rate when breakthrough happens. This also leads to a large pressure gradient between the injector and producer according to Darcy’s law, which is another reason for the fast shrinkage of the water plume at a higher injection rate.
The influences of water injection rates on VF dynamics can also be quantified by the variations of swept areas, as depicted in
Figure 8. It is clear that the slope of the swept area with time increases with the injection rate of water. Interestingly, the slope of the swept area with the volume of water injected however decreases with the injection rates before the maximum water plume is achieved in
Figure 8b. This is because of the relatively weaker diffusion compared to the increasingly stronger convection at a higher rate. However, at the end of the slow expansion regime, the maximum size of the water plume increases with the injection rate. A non-monotonic relationship between the size of the water plume and injection rates is observed at the end of the shrinkage regime. At a very small injection rate, the shrinkage period is short, and the decrease in water plume is not obvious. Therefore, a larger maximum water plume size in the previous slow expansion stage leads to a larger minimum shrinkage size. However, at the higher injection rate, e.g., 2.0 mL/min and 5.0 mL/min, the stronger convection is favorable for the shrinkage of water plume, resulting in a smaller water plume at the end of the shrinkage regime.
Different water injection rates lead to unstable flows, which can be quantified by the evolution of count of fingers as water is injected to displace glycerol. As shown in
Figure 9, under constant pressure control at the outlet, a higher flow rate induces more fingers because of the stronger convection. The maximum count of fingers is reached at an earlier time for a higher water injection rate. Interestingly, less fluid is needed to reach the maximum count of fingers, as shown in
Figure 9b. Eventually, the count of fingers tends to be zero because of the formation of a stable and smooth interface in the uniform expansion regime.
3.3. Impacts of Control at the Outlet
Experiments with constant production rate control are performed.
Figure 10 depicts the water plume at the beginning and end of the five flow regimes for water injection rates of 5.0 mL/min and 2.0 mL/min, respectively. The main effects occur at the breakthrough and following regimes occur after breakthrough. Because of the constant production rate control at the outlet, the injected water propagates much faster than that under a constant pressure control scenario at the outlet. This is confirmed by a significant reduction in breakthrough time at each injection rate. Furthermore, at 5.0 mL/min, the size of Regime 3 is smaller than that of constant pressure control. The interface of the water plume of Regime 4 is less unstable with fewer backward fingers (see
Figure 10a at t = 132 s vs.
Figure 2 at t = 130 s). For 2.0 mL/min, the duration of a slow expansion regime and fast shrinkage regime is greatly reduced, and the shrinkage regime is not obvious at all. In fact, for water injection rates at 1.0 mL/min, 0.5 mL/min, 0.2 mL/min and 0.1 mL/min, the shrinkage regime and expansion regime are negligible. So, the differences between the two control scenarios at the outlet are not obvious at slow water injection rates.
Figure 11 depicts the variations of swept area with time for the two scenarios with different controls at the outlet. The control with a constant production rate (two-pump scenario) initially shows the same trend of swept area of injected water. As seen in
Figure 11a, the solid and dotted curves nearly overlap for a short time. However, the breakthrough and the time for the maximum size of the water plume occur at an earlier time, when the size of the water plume is much smaller for the two-pump scenario. This indicates that the constant extraction by the additional pump at the outlet may induce an extra pressure gradient from the injector to producer that is favorable for the injected water flowing to the production end. This also suppresses the expansion of the water plume in other directions. At the injection rate of 5.0 mL/min, this results in a much smaller water plume (i.e., 6641 mm
2 vs. 13,060 mm
2). At the injection rate of 2.0 mL/min, the water plume for the two-pump scenario is also much smaller. Both scenarios lead to a comparable size of water plume at the end of the fast shrinkage regime for an injection rate of 5.0 mL/min. At a small injection rate of 2.0 mL/min, the shrinkage regime for the two-pump scenario is however not noticeable. A much larger, stable water plume is observed as water is continuously injected during the following slow expansion regime for the two-pump scenario, as shown in
Figure 10a at t = 132 s and
Figure 10b at t = 220 s.
Although the swept area for different controls at the outlet is significantly different, the interfacial length is however close for the two scenarios at the same injection rate, as shown in
Figure 11b. This is because the scenario with a constant production rate at the outlet (two pumps) does not reduce the VF instabilities too much. Instead, it mainly affects the spreading direction of injected water, with a preferential flow path from the injector to producer. This also results in an early breakthrough time. Another interesting observation in
Figure 11b is that the backward fingering is mitigated to some extent because of the constant production control, which is indicated by the lower fluctuations on the variations of interfacial length vs. time (i.e., the dotted curves in
Figure 11b). At an injection rate of 2.0 mL/min, the backward fingering as well as the fluctuations of interfacial length are much weaker.
Two interesting phenomena were observed through the analysis of the variations of count of fingers with time in
Figure 12. First, at a lower flow rate, a large number of small, uniform fingers are observed (see
Figure 12 at t = 282 s for 0.1 mL/min). Along the injector-to-producer direction (i.e., the main flow direction), these fingers are induced by convection. In contrast, along the producer-to-injector direction and in the transverse direction, the water flow rate is very slow. Spontaneous fingers are formed due to the diffusion and possibly the small but non-zero interfacial tension between two fluids [
42]. Second, the maximum count of fingers is achieved at a water injection rate of 1.0 mL/min for the control of a constant production rate at the outlet, which is different from its counterpart at constant pressure control at the outlet in
Figure 9a. Below this rate, the small, spontaneous fingers tend to merge with each other as water is injected continuously (see 0.1 mL/min vs. 0.2 mL/min in
Figure 13a,b, respectively). In the case of higher flow rates, tip splitting is more obvious. However, the coalesces among these fingers lead to long and wide fingers (see
Figure 13 for 2.0 mL/min and 5.0 mL/min). Therefore, the highest injection rate does not lead to the maximum count of fingers. Eventually, the maximum count of fingers happens at the water injection rate of 1.0 mL/min.
To sum up, the design of experiments, flow regimes, and different controls at the production end in the present work provide new insights to the applications such as oil and gas recovery, geothermal recovery, and CO2 and hydrogen geological storage. More specifically, the design of an injector–producer Hele–Shaw cell and sealed boundary allows examining the post-breakthrough fingering dynamics and flow regimes, which cannot be achieved using the classical radial geometry. The tubing connected to the producer mimics the effect of wellbore on flow dynamics in reservoirs. The different controls on the production end lead to different flow dynamics, which should be considered in the design of field projects. Last but not least, the new design of experiments, i.e., two wells inside the geometry, distinguishes from classical five-spot geometry and expands the capability of the Hele–Shaw cell for studying the non-symmetric flows in a variety of applications.