3D Fracture Propagation Simulation and Pressure Decline Analysis Research for I-Shaped Fracture of Coalbed
Abstract
:1. Introduction
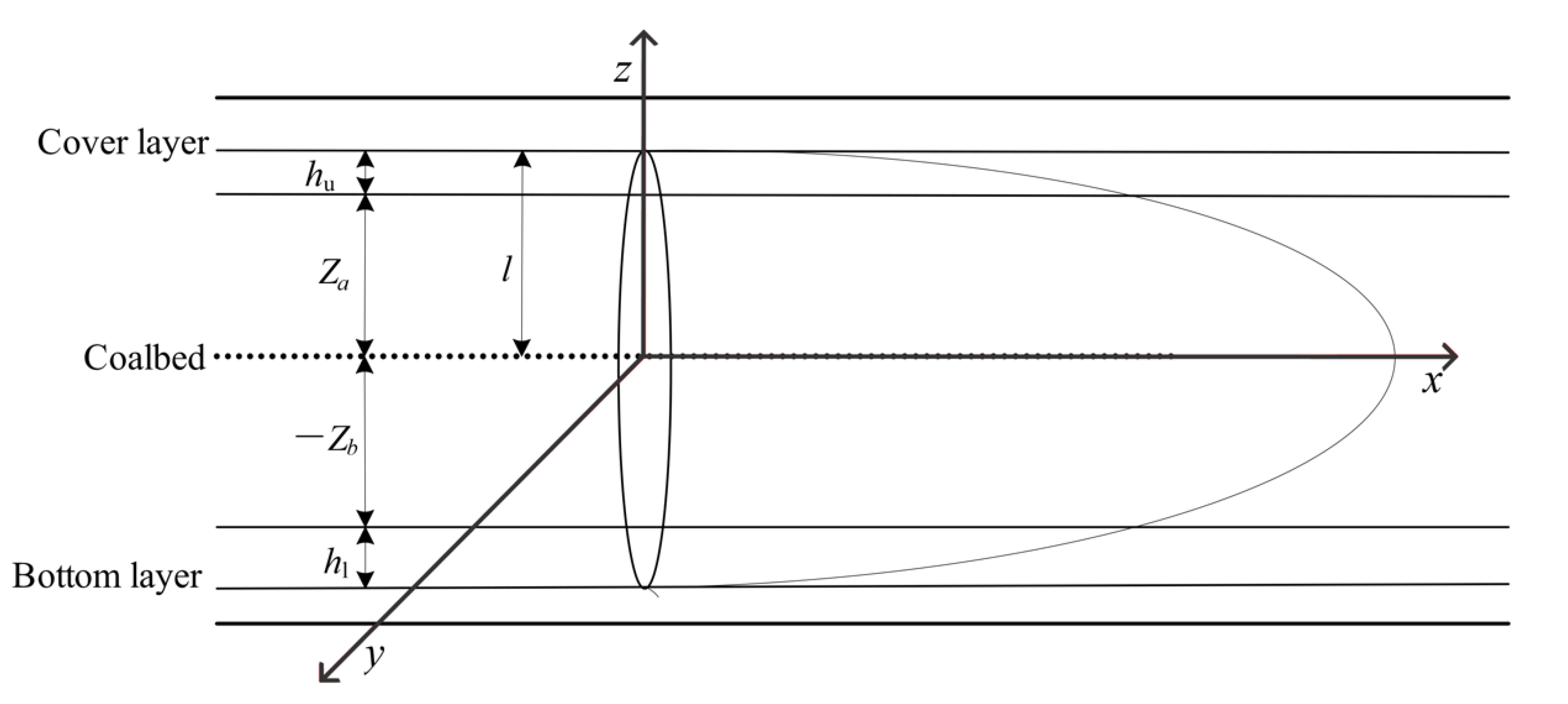
2. I-Shaped Fracture Propagation Simulation Model
- (1)
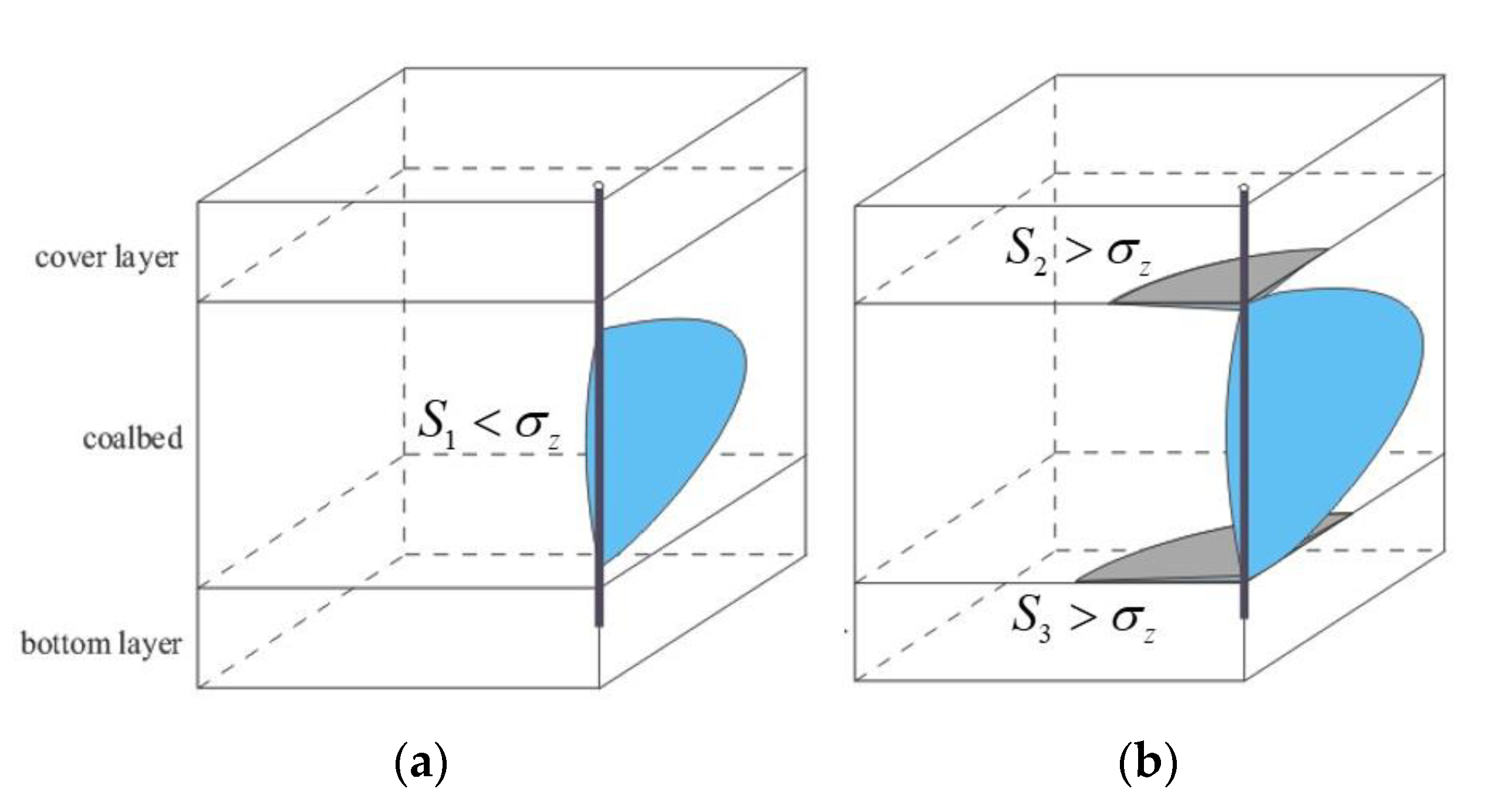
- The hydraulic fracture starts from the coalbed. When the horizontal minimum principal stress of the fractured layer is less than the vertical stress, a vertical fracture is formed in the coalbed (Figure 1a).
- (2)
- Getting along with fracturing, the vertical fracture propagates longitudinally and break through the coal seam boundary. When the horizontal minimum principal stress of the cover and bottom layer is greater than the vertical stress, horizontal fractures are formed in the cover and bottom layer. Thus, an I-shaped fracture is produced (Figure 1b).
2.1. Fracture Propagation Simulation Model of Vertical Components
2.1.1. Continuity Equation
2.1.2. Pressure Drop Equations of the Vertical Component
2.1.3. Fracture Width Equation of the Vertical Component
2.1.4. Fracture Height Equation of Vertical Component
2.2. Model of Horizontal Component
2.2.1. Pressure Drop Equations of the Horizontal Component
2.2.2. Fracture Width Equation of the Horizontal Component
2.3. Material Balance Equation
2.4. Boundary Conditions
2.5. Initial Conditions
2.6. Coupling Conditions
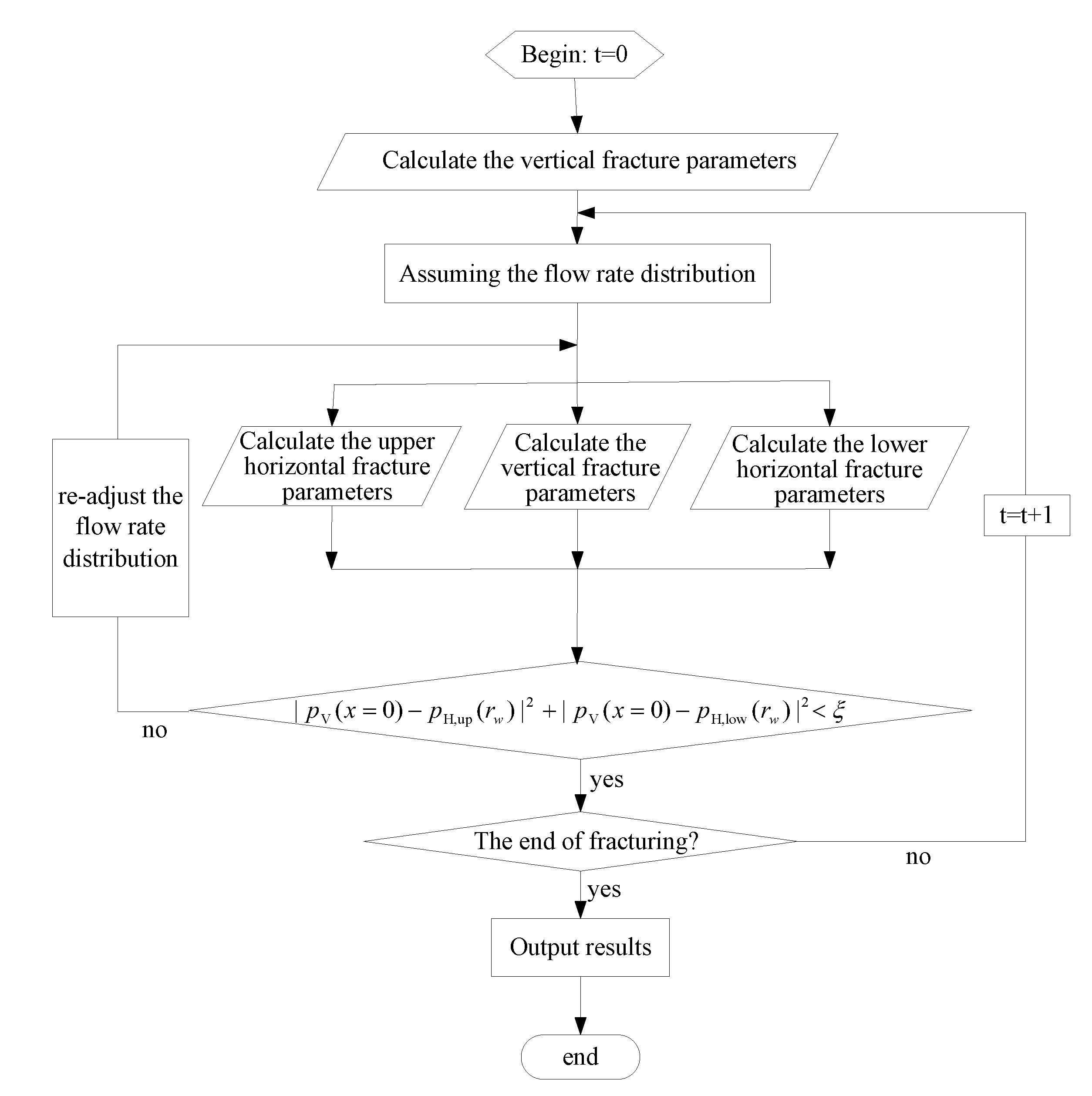
2.7. Numerical Method
3. PDA Model
3.1. PDA Model of Vertical Fracture
3.2. PDA Model of Horizontal Fracture
3.3. Coupling Conditions
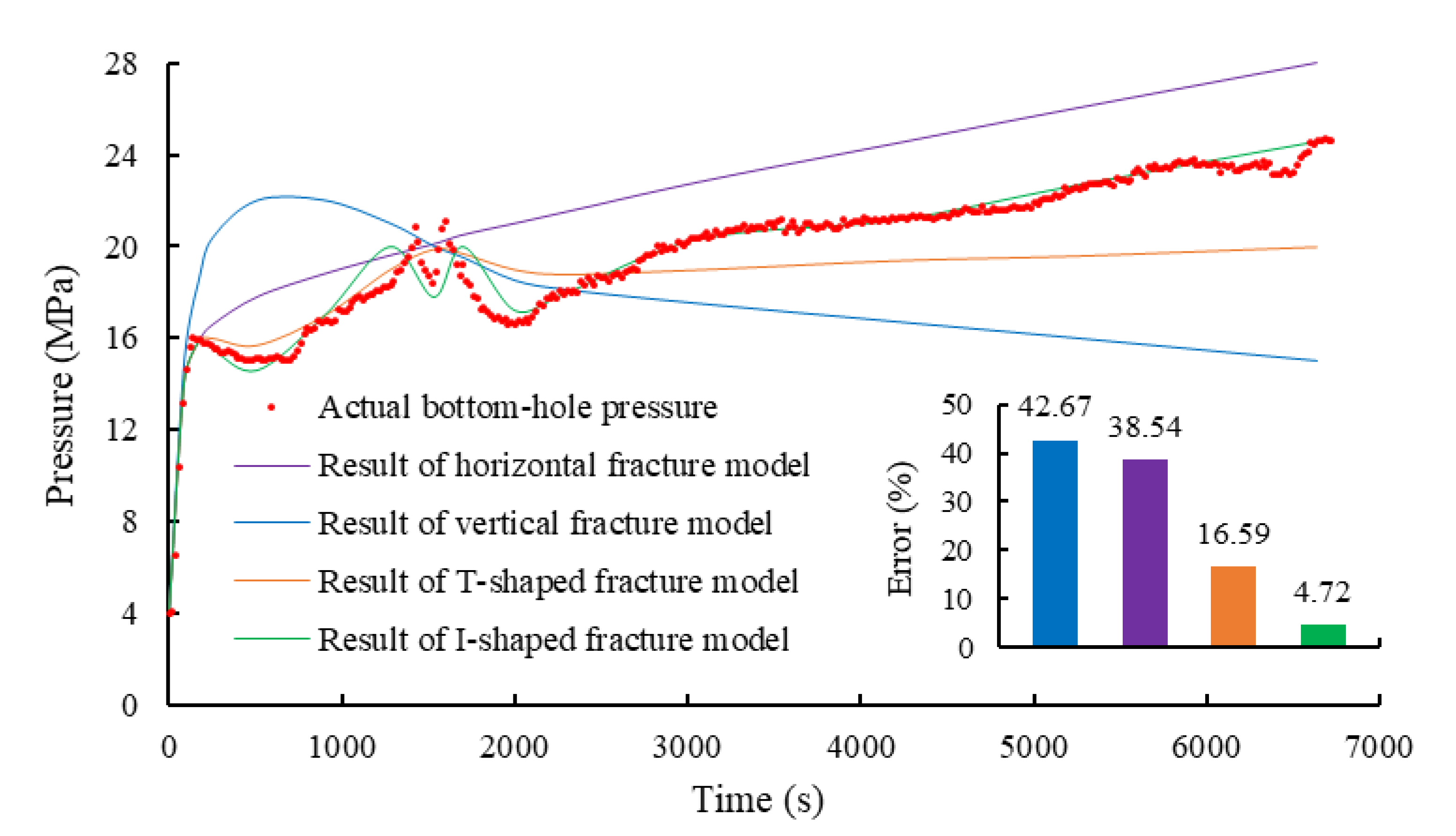
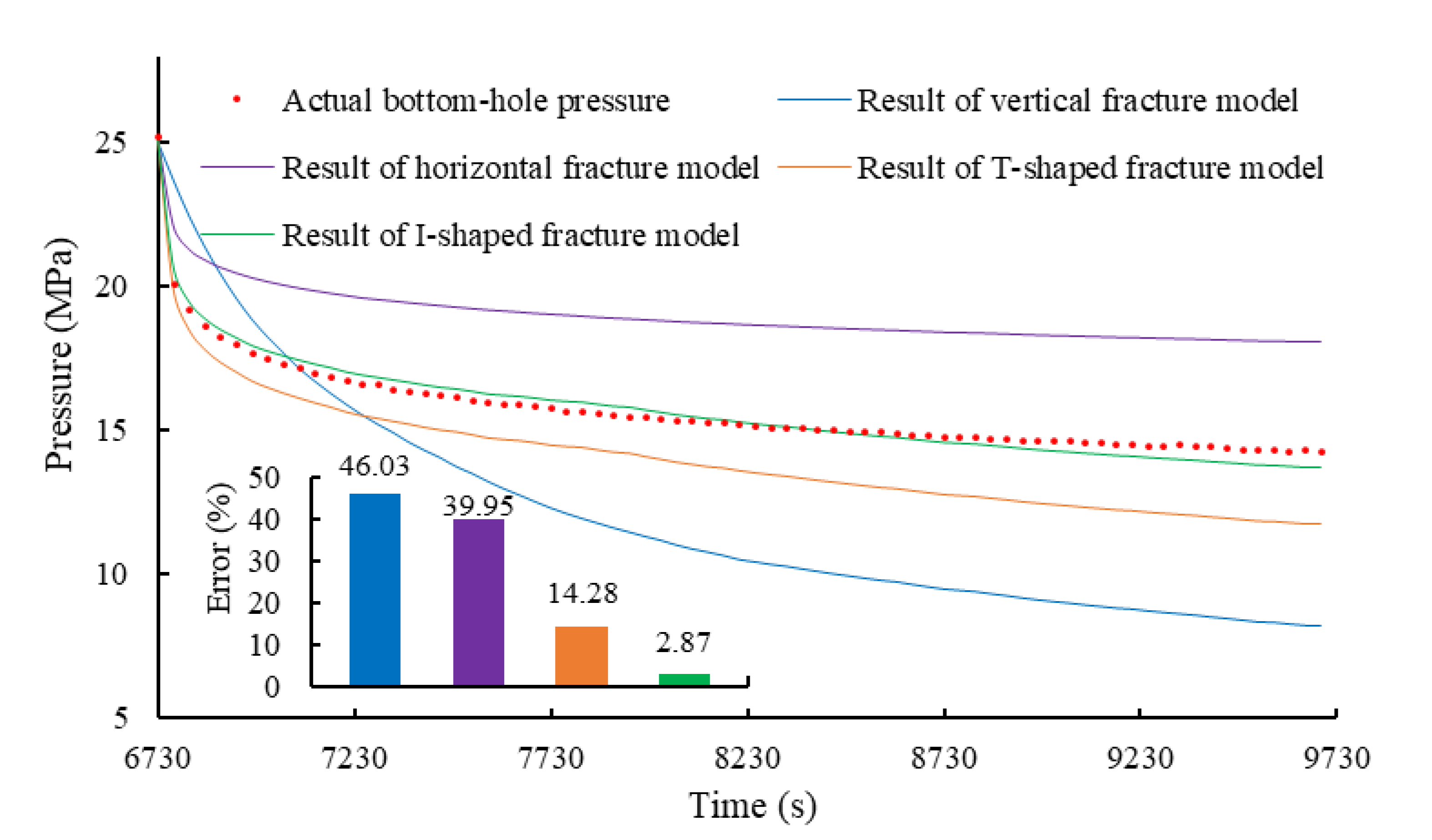
3.4. History Matching of Pseudo Pressure
4. Results and Discussion
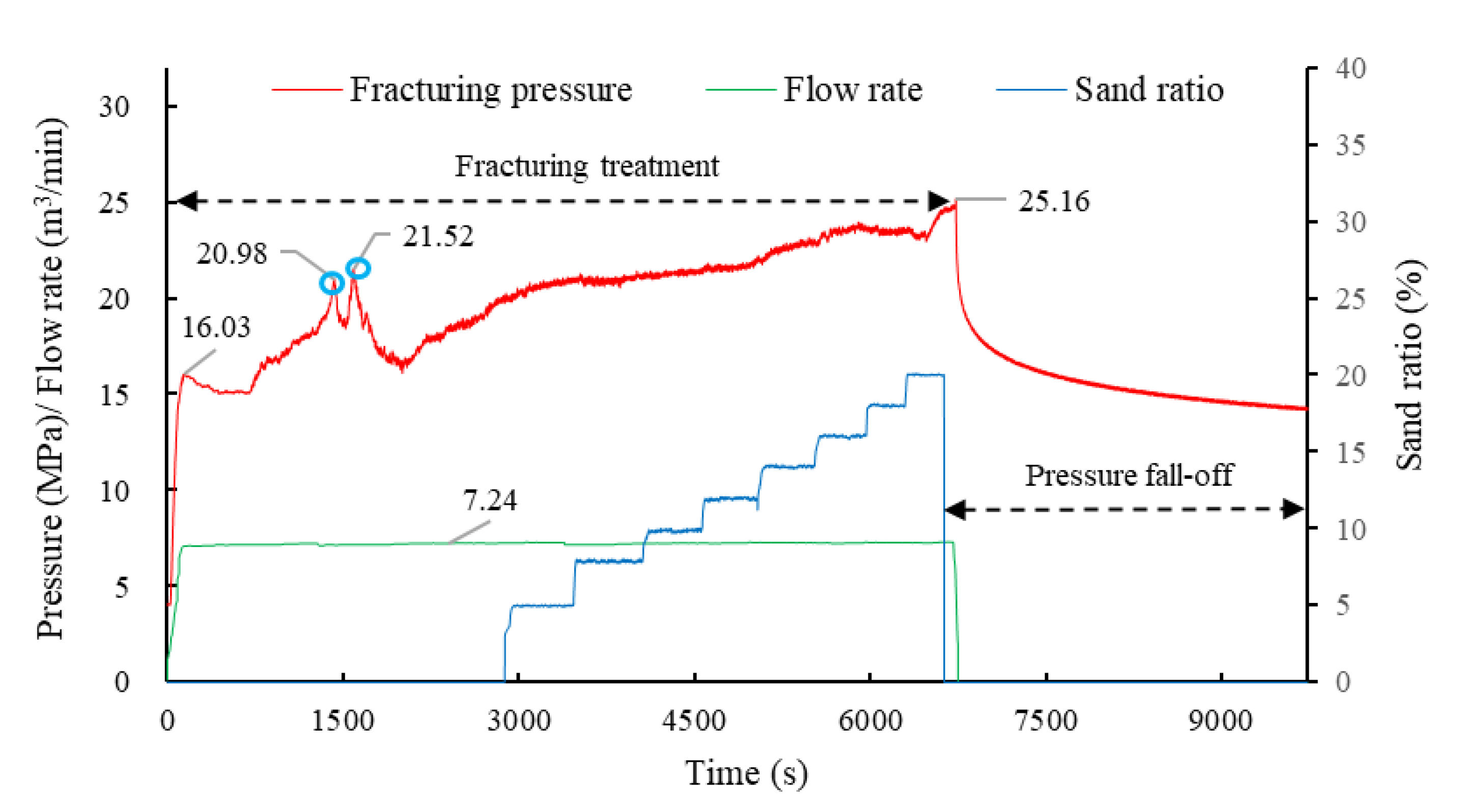
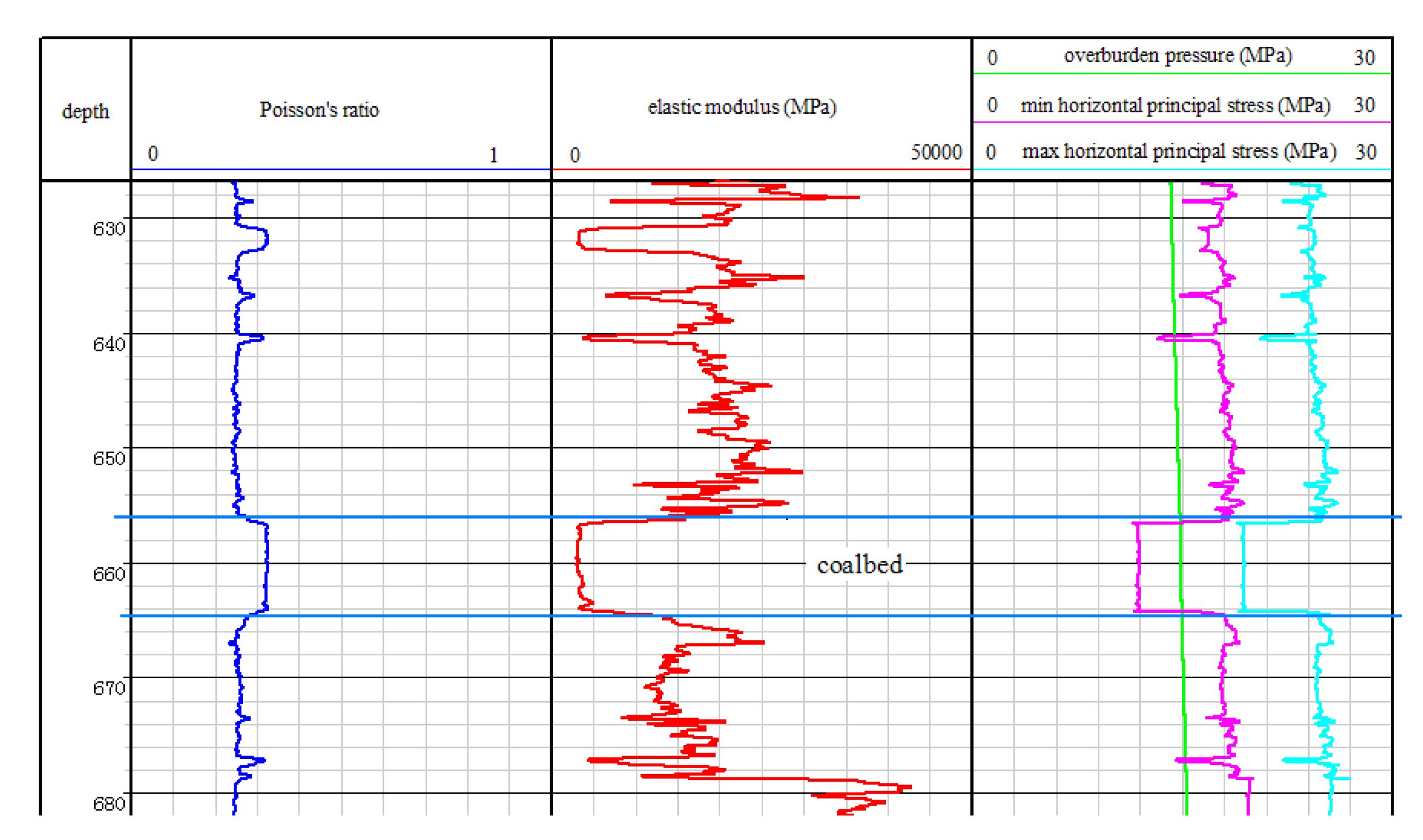
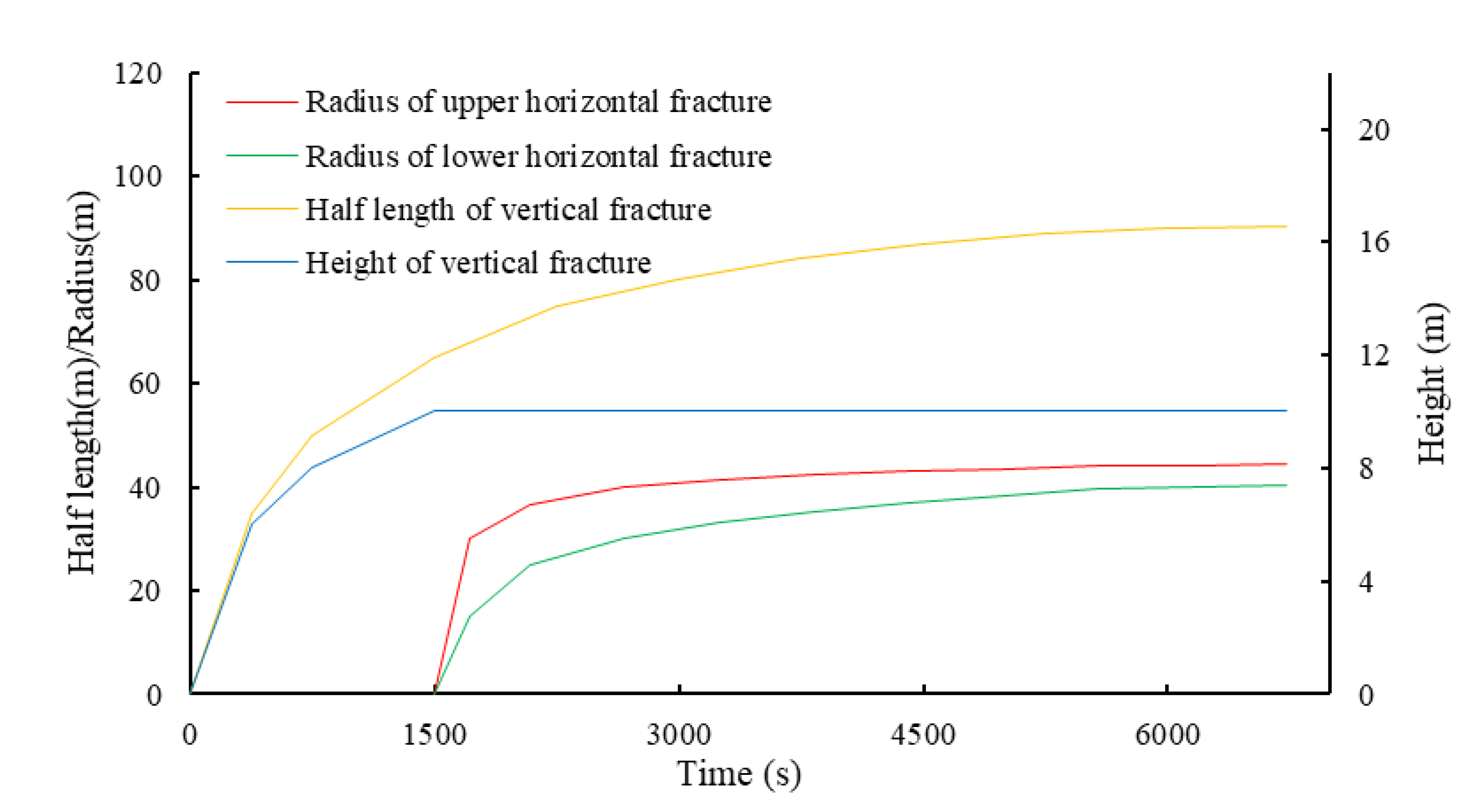
4.1. Results
4.2. Discussion
4.2.1. Influence of Crustal Stress Variation on Fracture Geometry
4.2.2. Influence of Fracturing Fluid on Fracture Geometry
5. Conclusions
- (1)
- The adequate research regarding the fracture propagation mechanism is essential for coal seam fracturing. The I-shaped fracture is often occurred in coal seam fracturing. This paper elaborates its propagation mechanism.
- (2)
- This paper developed the 3D propagation simulation model of I-shaped fracture. Pressure-drop equations of fluid flowing in fractures, fracture width equation, fracture height equation, and continuity equation of fluid flowing in fractures are developed based on the 3D fracture propagation model. Furthermore, the coupling conditions of vertical fracture and horizontal fractures are established based on the flow rate distribution and the bottom-hole pressure equality. Moreover, a satisfactory numerical method of 3D model is developed based on the iterative method. Then, we can obtain the fracture geometries and total fracturing fluid leak-off coefficient.
- (3)
- This paper developed the PDA model of an I-shaped fracture. The coupling conditions and numerical method are similar to a P3D propagation simulation model. Then, we can obtain the leak-off coefficient of post-fracturing fluid, fracture geometries, fracturing fluid efficiency, and fracture closure time, etc.
- (4)
- The proposed models have been applied to a realistic CBM well of the Hancheng area. We obtained the fracture geometries, fracturing fluid efficiency, etc. It is concluded that the established two models are effective tools for the simulation of fracture initiation/propagation and pressure decline of post-fracturing.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| Pressure inside vertical fracture, MPa | |
| Flow rate in vertical fracture, m3/s | |
| Fracturing fluid flow behavior index, m/s0.5 | |
| Fracturing fluid consistency index, MPa·Sn′ | |
| Vertical fracture height, m | |
| Vertical fracture width, m | |
| Channel shape factor, dimensionless | |
| Pressure inside upper horizontal fracture, MPa | |
| Pressure inside lower horizontal fracture, MPa | |
| Flow rate in upper horizontal fracture, m3/s | |
| Flow rate in lower horizontal fracture, m3/s | |
| Average fracture width of upper horizontal fracture, m | |
| Average fracture width of lower horizontal fracture, m | |
| Least horizontal principal stress in coalbed, MPa | |
| Least horizontal principal stress of cover layer, MPa | |
| Least horizontal principal stress of bottom layer, MPa | |
| Half length of vertical component, m | |
| Poisson’s ratio of coalbed, dimensionless | |
| Poisson’s ratio of cover layer, dimensionless | |
| Poisson’s ratio of bottom layer, dimensionless | |
| Young’s modulus of coalbed, MPa | |
| Young’s modulus of cover layer, MPa | |
| Young’s modulus of bottom layer, MPa | |
| Vertical fracture height in bottom layer, m | |
| Vertical fracture height in cover layer, m | |
| Thickness of coalbed, m | |
| Wellbore radius, m | |
| Radial coordinate of horizontal fracture, m | |
| Horizontal fracture radius, m | |
| Upper horizontal fracture radius, m | |
| Lower horizontal fracture radius, m | |
| Maximum fracture width of horizontal fracture, m | |
| Maximum fracture width of upper horizontal fracture, m | |
| Maximum fracture width of lower horizontal fracture, m | |
| Maximum fracture width of coalbed, m | |
| Maximum fracture width of cover layer, m | |
| Maximum fracture width of bottom layer, m | |
| Stress intensity factor of upper fracture tip, dimensionless | |
| Stress intensity factor of lower fracture tip, dimensionless | |
| Cross-section area of fracture, m3 | |
| Total fracturing fluid leak-off coefficient, m/s0.5 | |
| Total fracturing fluid leak-off coefficient of vertical fracture, m/s0.5 | |
| Total fracturing fluid leak-off coefficient of upper horizontal fracture, m/s0.5 | |
| Total fracturing fluid leak-off coefficient of lower horizontal fracture, m/s0.5 | |
| Time of fracturing fluid to reach the given point, s | |
| Time of horizontal fracture began to propagating, s | |
| Half length of fracture, m | |
| Injection rate, m3/s | |
| Bottom-hole pressure of vertical fracture, MPa | |
| Pseudo pressure of vertical fracture, MPa | |
| Vertical fracture height, m | |
| Ratio of average pressure to bottom-hole pressure in vertical fracture, dimensionless | |
| Ratio of average pressure to bottom-hole pressure in upper horizontal fracture, dimensionless | |
| Ratio of average pressure to bottom-hole pressure in lower horizontal fracture, dimensionless | |
| Fracturing time, s | |
| Instantaneous pressure of pump-stopping, MPa | |
| Flow rate of vertical fracture during fracturing treatment, m3/s | |
| Fracturing fluid efficiency, % | |
| Fracture closure time, s | |
| Bottom-hole pressure of upper horizontal fracture, MPa | |
| Pseudo pressure of upper horizontal fracture, MPa | |
| Pseudo pressure of lower horizontal fracture, MPa | |
| Ratio of fracture leak-off area to total fracture area, dimensionless | |
| Fracture closure pressure, MPa | |
| Flow rate of upper horizontal fracture during fracturing treatment, m3/s |
References
- Guo, Z.; Chen, Y.; Zhou, X.; Zeng, F. Inversing fracture parameters using early-time production data for fractured wells. Inverse Probl. Sci. Eng. 2020, 28, 674–694. [Google Scholar] [CrossRef]
- Adachi, J.; Siebrits, E.; Peirce, A.; Desroches, J. Computer simulation of hydraulic fractures. Int. J. Rock Mech. Min. Sci. 2007, 44, 739–757. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, J.; You, Z.; Li, Y.; Zhang, S.; Chen, Y. Prediction of coalbed methane production based on deep learning. Energy 2021, 230, 120847. [Google Scholar] [CrossRef]
- Wang, D.; You, Z.; Johnson, R.L.; Wu, L.; Bedrikovetsky, P.; Aminossadati, S.M.; Leonardi, C. Numerical investigation of the effects of proppant embedment on fracture permeability and well production in Queensland coal seam gas reservoirs. Int. J. Coal Geol. 2021, 242, 103689. [Google Scholar] [CrossRef]
- Wang, T.; Zhou, W.; Chen, J.; Xiao, X.; Li, Y.; Zhao, X. Simulation of hydraulic fracturing using particle flow method and application in a coal mine. Int. J. Coal Geol. 2014, 121, 1–13. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, J.; Sun, X.; Wang, C.; Guo, D.; Hu, H.; Wang, H.; Zeng, Q. A Novel Continuous Fracture Network Model: Formation Mechanism, Numerical Simulation and Field Application. Geofluids 2022, 2022, 1468–8115. [Google Scholar] [CrossRef]
- Feng, Q.; Wu, C.F.; Lei, B. Coal/Rock mechanics features of Qinshui basin and fracturing crack control. Coal Sci. Technol. 2011, 39, 100–103. [Google Scholar]
- Cheng, Y.F.; Wu, B.L.; Dong, B.X.; Li, L.D.; Huang, H.Y. Establishment and application of “T” shape fracture propagation model in hydraulic fracturing of methane well. J. China Coal Soc. 2013, 38, 1430–1434. [Google Scholar]
- Wu, X.; Xi, C.; Wang, G. The mathematic model research of complicated fractures system in coalbed methane wells. Nat. Gas Ind. 2006, 26, 124–126. [Google Scholar]
- Zhang, Z.; Qin, Y.; Yi, T.; You, Z.; Yang, Z. Pore Structure Characteristics of Coal and Their Geological Controlling Factors in Eastern Yunnan and Western Guizhou, China. ACS Omega 2020, 5, 19565–19578. [Google Scholar] [CrossRef]
- Zhang, Z.; Qin, Y.; Wang, G.; Sun, H.; You, Z.; Jin, J.; Yang, Z. Evaluation of Coal Body Structures and Their Distributions by Geophysical Logging Methods: Case Study in the Laochang Block, Eastern Yunnan, China. Nat. Resour. Res. 2021, 30, 2225–2239. [Google Scholar] [CrossRef]
- Guo, Z.; Chen, Y.; Yao, S.; Zhang, Q.; Liu, Y.; Zeng, F. Feasibility Analysis and Optimal Design of Acidizing of Coalbed Methane Wells. J. Energy Resour. Technol. 2019, 141, 082906. [Google Scholar] [CrossRef] [Green Version]
- Guo, D.-L.; Ji, L.-J.; Zhao, J.-Z.; Liu, C.-Q. 3-D Fracture Propagation Simulation and Production Prediction in Coalbed. Appl. Math. Mech. 2001, 22, 385–393. [Google Scholar] [CrossRef]
- Tang, S.; Zhu, B.; Yang, Z. Effect of crustal stress on hydraulic fracturing in coalbed methane wells. J. China Coal Soc. 2011, 36, 65–69. [Google Scholar]
- Garikapati, H.; Verhoosel, C.V.; van Brummelen, E.H.; Zlotnik, S.; Díez, P. Sampling-based stochastic analysis of the PKN model for hydraulic fracturing. Comput. Geosci. 2019, 23, 81–105. [Google Scholar] [CrossRef] [Green Version]
- Liu, Y.; Wang, C.; Zhou, H. Optimization scheme of hydraulic fracturing simulation experiments using mixed-level uniform design method based on the PKN model. J. Phys. Conf. Ser. 2020, 1574, 012165. [Google Scholar] [CrossRef]
- Golovin, S.; Isaev, V.; Baykin, A.; Kuznetsov, D.; Mamontov, A. Hydraulic fracture numerical model free of explicit tip tracking. Int. J. Rock Mech. Min. Sci. 2015, 76, 174–181. [Google Scholar] [CrossRef]
- Nguyen, H.T.; Lee, J.H.; Elraies, K.A. A review of PKN-type modeling of hydraulic fractures. J. Pet. Sci. Eng. 2020, 195, 107607. [Google Scholar] [CrossRef]
- Wrobel, M. On the application of simplified rheological models of fluid in the hydraulic fracture problems. Int. J. Eng. Sci. 2020, 150, 103275. [Google Scholar] [CrossRef]
- Gu, M.; Mohanty, K. Effect of foam quality on effectiveness of hydraulic fracturing in shales. Int. J. Rock Mech. Min. Sci. 2014, 70, 273–285. [Google Scholar] [CrossRef]
- Zia, H.; Lecampion, B.; Zhang, W. Impact of the anisotropy of fracture toughness on the propagation of planar 3D hydraulic fracture. Int. J. Fract. 2018, 211, 103–123. [Google Scholar] [CrossRef]
- Baykin, A.N.; Golovin, S.V. Application of the Fully Coupled Planar 3D Poroelastic Hydraulic Fracturing Model to the Analysis of the Permeability Contrast Impact on Fracture Propagation. Rock Mech. Rock Eng. 2018, 51, 3205–3217. [Google Scholar] [CrossRef]
- Redhaounia, B.; Bédir, M.; Gabtni, H.; Batobo, O.I.; Dhaoui, M.; Chabaane, A.; Khomsi, S. Hydro-geophysical characterization for groundwater resources potential of fractured limestone reservoirs in Amdoun Monts (North-western Tunisia). J. Appl. Geophys. 2016, 128, 150–162. [Google Scholar] [CrossRef]
- Dontsov, E.; Peirce, A. An enhanced pseudo-3D model for hydraulic fracturing accounting for viscous height growth, non-local elasticity, and lateral toughness. Eng. Fract. Mech. 2015, 142, 116–139. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Wu, B.; Jeffrey, R.G.; Connell, L.D.; Zhang, G. A pseudo-3D model for hydraulic fracture growth in a layered rock. Int. J. Solids Struct. 2017, 115-116, 208–223. [Google Scholar] [CrossRef]
- Zia, H.; Lecampion, B. PyFrac: A planar 3D hydraulic fracture simulator. Comput. Phys. Commun. 2020, 255, 107368. [Google Scholar] [CrossRef]
- Skopintsev, A.; Dontsov, E.; Kovtunenko, P.; Baykin, A.; Golovin, S. The coupling of an enhanced pseudo-3D model for hydraulic fracturing with a proppant transport model. Eng. Fract. Mech. 2020, 236, 107177. [Google Scholar] [CrossRef]
- Linkov, A.; Markov, N. Improved pseudo three-dimensional model for hydraulic fractures under stress contrast. Int. J. Rock Mech. Min. Sci. 2020, 130, 104316. [Google Scholar] [CrossRef]
- Wen, M.; Huang, H.; Hou, Z.; Wang, F.; Qiu, H.; Ma, N.; Zhou, S. Numerical simulation of the non-Newtonian fracturing fluid influences on the fracture propagation. Energy Sci. Eng. 2022, 10, 404–413. [Google Scholar] [CrossRef]
- Peirce, A.; Detournay, E. An implicit level set method for modeling hydraulically driven fractures. Comput. Methods Appl. Mech. Eng. 2008, 197, 2858–2885. [Google Scholar] [CrossRef]
- Salimzadeh, S.; Paluszny, A.; Zimmerman, R. Three-dimensional poroelastic effects during hydraulic fracturing in permeable rocks. Int. J. Solids Struct. 2017, 108, 153–163. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Firoozabadi, A. Numerical Simulation of Water Injection in Fractured Media Using the Discrete-Fracture Model and the Galerkin Method. SPE Reserv. Eval. Eng. 2003, 6, 117–126. [Google Scholar] [CrossRef]
- Hossain, M.; Rahman, M. Numerical simulation of complex fracture growth during tight reservoir stimulation by hydraulic fracturing. J. Pet. Sci. Eng. 2008, 60, 86–104. [Google Scholar] [CrossRef]
- Chen, E.; Leung, C.K.; Tang, S.; Lu, C. Displacement discontinuity method for cohesive crack propagation. Eng. Fract. Mech. 2018, 190, 319–330. [Google Scholar] [CrossRef]
- Zvyagin, A.V.; Luzhin, A.A.; Panfilov, D.I.; Shamina, A.A. Numerical method of discontinuous displacements in spatial problems of fracture mechanics. Mech. Solids 2021, 56, 119–130. [Google Scholar] [CrossRef]
- Kim, H.; Onishi, T.; Chen, H.; Datta-Gupta, A. Parameterization of embedded discrete fracture models (EDFM) for efficient history matching of fractured reservoirs. J. Pet. Sci. Eng. 2021, 204, 108681. [Google Scholar] [CrossRef]
- Guo, Z.; Zhao, J.; Li, Y.; Zhao, Y.; Hu, H. Theoretical and experimental determination of proppant-crushing ratio and fracture conductivity with different particle sizes. Energy Sci. Eng. 2022, 10, 177–193. [Google Scholar] [CrossRef]
- Guo, D.; Zhao, J.; Guo, J.; Zeng, X. Three-dimensional model and mathematical fitting method of pressure test data after fracturing. Nat. Gas Ind. 2001, 21, 49–52. [Google Scholar]
- Guo, D.; Wu, G.; Liu, X.; Zhao, J. Analyzing method of pressure decline to identify fracture parameters. Nat. Gas Ind. 2003, 23, 83–85. [Google Scholar]
- Zhao, W.; Ji, G.; Li, K.; Liu, W.; Xiong, L.; Xiao, J. A new pseudo 3D hydraulic fracture propagation model for sandstone reservoirs considering fracture penetrating height. Eng. Fract. Mech. 2022, 264, 108358. [Google Scholar] [CrossRef]
- Ji, L.; Guo, D.; Zhao, J.; Wu, G. 3-D models and its computation of acid fracture simulation. Drill. Prod. Technol. 2000, 23, 39–43. [Google Scholar]
- Guo, D.; Zhang, S.; Li, T.; Pu, X.; Zhao, Y.; Ma, B. Mechanical mechanisms of T-shaped fractures, including pressure decline and simulated 3D models of fracture propagation. J. Nat. Gas Sci. Eng. 2018, 50, 1–10. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value | |
|---|---|---|---|---|
| Young’s modulus (MPa) | Cover layer | 18,000 | Flow state index (dimensionless) | 1 |
| Coalbed | 3000 | Fracturing fluid consistency coefficient (MPa·sn′) | 1 | |
| Bottom layer | 15,000 | Fracturing fluid density (kg/m3) | 1000 | |
| Poisson ratio (dimensionless) | Cover layer | 0.22 | Fracturing fluid volume (m3) | 469.3 |
| Coalbed | 0.31 | Injection rate (m3/min) | 7 | |
| Bottom layer | 0.21 | Coalbed permeability (10−3 μm2) | 0.2 | |
| Coal seam thickness (m) | 8.5 | Coalbed porosity (dimensionless) | 0.03 | |
| Upper Horizontal Fracture Geometry | Lower Horizontal Fracture Geometry | Vertical Fracture Geometry | |||||
|---|---|---|---|---|---|---|---|
| Width (mm) | Radius (m) | Width (mm) | Radius (m) | Width (mm) | Half Length (m) | Height (m) | |
| I-shaped Fracture propagation model | 5.1589 | 40.4279 | 5.3013 | 44.3198 | 6.7478 | 90.1286 | 15 |
| PDA | 5.0461 | 42.2461 | 5.1387 | 43.4789 | 6.2365 | 84.2353 | |
| Parameter | Value | ||||
|---|---|---|---|---|---|
| Crustal stress of cover layer (MPa) | 17.7 | 18.7 | 19.7 | 20.7 | 21.7 |
| Upper horizontal fracture radius (m) | 44.8345 | 43.2174 | 40.4279 | 37.9618 | 36.3447 |
| Vertical fracture half length (m) | 80.3046 | 83.9097 | 90.1286 | 95.6264 | 99.2316 |
| Lower horizontal fracture radius (m) | 39.4889 | 41.2617 | 44.3198 | 47.0233 | 48.7961 |
| Parameter | Value | ||||
|---|---|---|---|---|---|
| Crustal stress of bottom layer (MPa) | 18.4 | 19.4 | 20.4 | 21.4 | 22.4 |
| Upper horizontal fracture radius (m) | 36.4255 | 37.6384 | 40.4279 | 42.8940 | 44.5111 |
| Vertical fracture half length (m) | 81.2059 | 84.6308 | 90.1286 | 96.3475 | 99.0513 |
| Lower horizontal fracture radius (m) | 49.1507 | 47.3779 | 44.3198 | 41.6163 | 39.9321 |
| Parameter | Value | ||||
|---|---|---|---|---|---|
| Fracturing fluid consistency coefficient (MPa·sn’) | 1 | 2 | 3 | 4 | 5 |
| Upper horizontal fracture radius (m) | 40.4279 | 42.3280 | 43.4196 | 44.4303 | 45.3197 |
| Vertical fracture half length (m) | 90.1286 | 94.3646 | 96.7981 | 99.0513 | 101.0342 |
| Lower horizontal fracture radius (m) | 44.3198 | 46.4028 | 47.5995 | 48.7075 | 49.6825 |
| Parameter | Value | ||||
|---|---|---|---|---|---|
| Leak-off coefficient of post-fracturing fluid (m/min0.5) | 0.00100098 | 0.0010854 | 0.001206 | 0.001327 | 0.001447 |
| Upper horizontal fracture radius (m) | 41.9642 | 41.1152 | 40.4279 | 39.6193 | 38.8108 |
| Vertical fracture half length (m) | 93.5535 | 91.6608 | 90.1286 | 88.3260 | 86.5235 |
| Lower horizontal fracture radius (m) | 46.0040 | 45.0732 | 44.3198 | 43.4334 | 42.5470 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Guo, Z.; Zhang, L.; Kang, Y.; You, Z.; Li, S.; Wang, Y.; Zhen, H. 3D Fracture Propagation Simulation and Pressure Decline Analysis Research for I-Shaped Fracture of Coalbed. Energies 2022, 15, 5811. https://doi.org/10.3390/en15165811
Wang C, Guo Z, Zhang L, Kang Y, You Z, Li S, Wang Y, Zhen H. 3D Fracture Propagation Simulation and Pressure Decline Analysis Research for I-Shaped Fracture of Coalbed. Energies. 2022; 15(16):5811. https://doi.org/10.3390/en15165811
Chicago/Turabian StyleWang, Chengwang, Zixi Guo, Lifeng Zhang, Yunwei Kang, Zhenjiang You, Shuguang Li, Yubin Wang, and Huaibin Zhen. 2022. "3D Fracture Propagation Simulation and Pressure Decline Analysis Research for I-Shaped Fracture of Coalbed" Energies 15, no. 16: 5811. https://doi.org/10.3390/en15165811
APA StyleWang, C., Guo, Z., Zhang, L., Kang, Y., You, Z., Li, S., Wang, Y., & Zhen, H. (2022). 3D Fracture Propagation Simulation and Pressure Decline Analysis Research for I-Shaped Fracture of Coalbed. Energies, 15(16), 5811. https://doi.org/10.3390/en15165811







