Modeling of Turbulent Heat-Transfer Augmentation in Gas-Droplet Non-Boiling Flow in Diverging and Converging Axisymmetric Ducts with Sudden Expansion
Abstract
:1. Introduction
2. Mathematical Methods and Numerical Solution
3. Results and Discussion
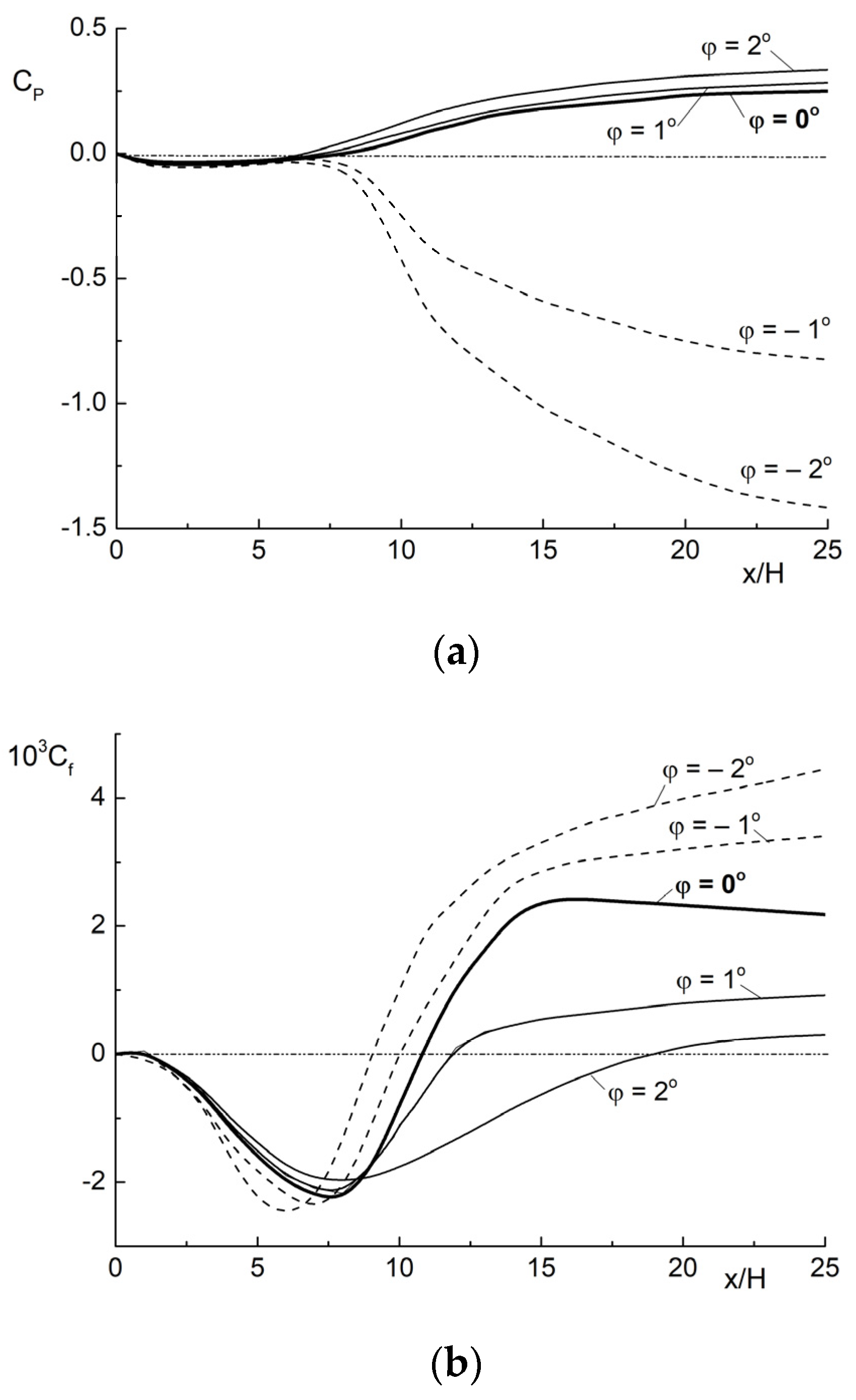
3.1. The Wall Friction and Pressure Coefficients
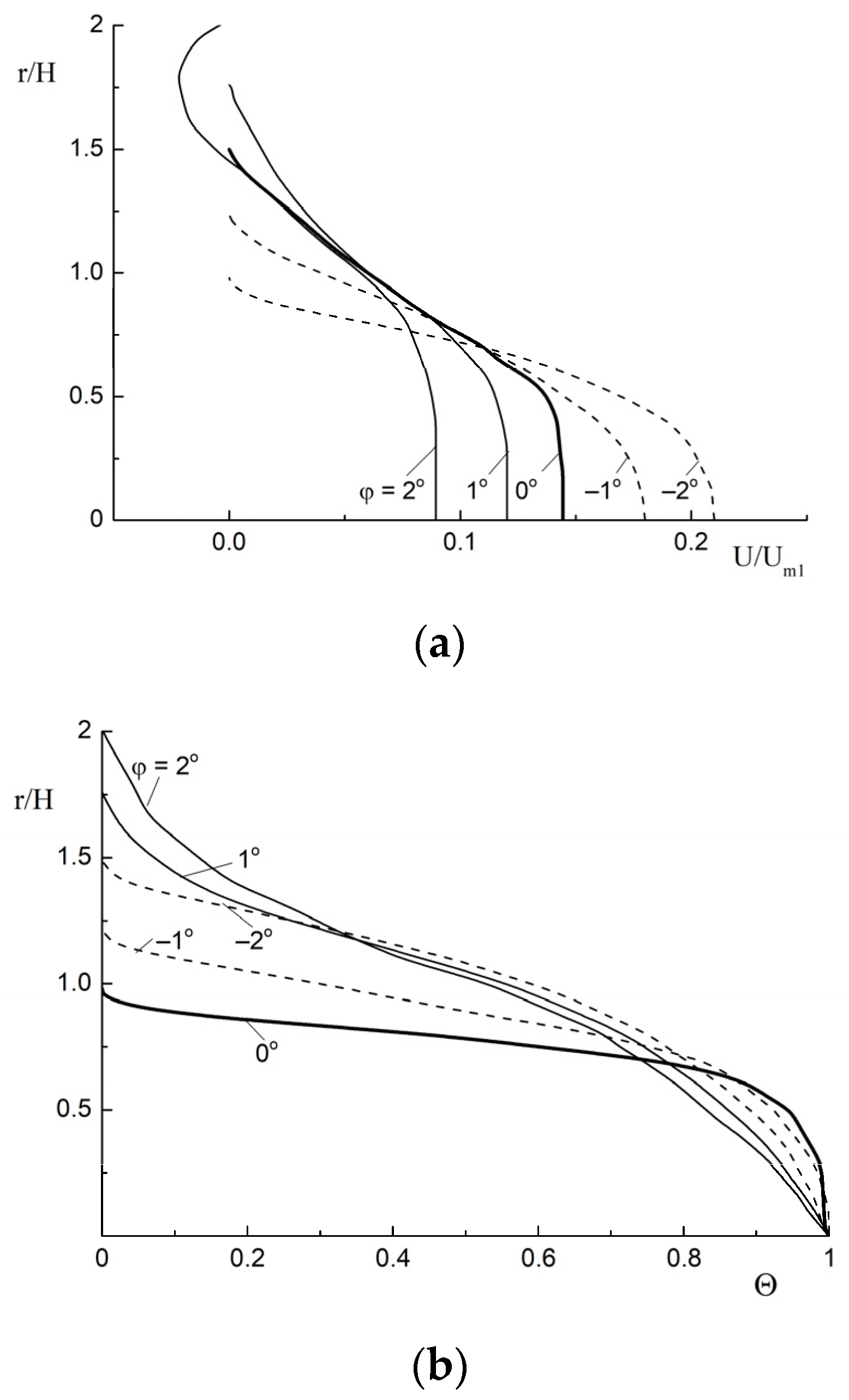
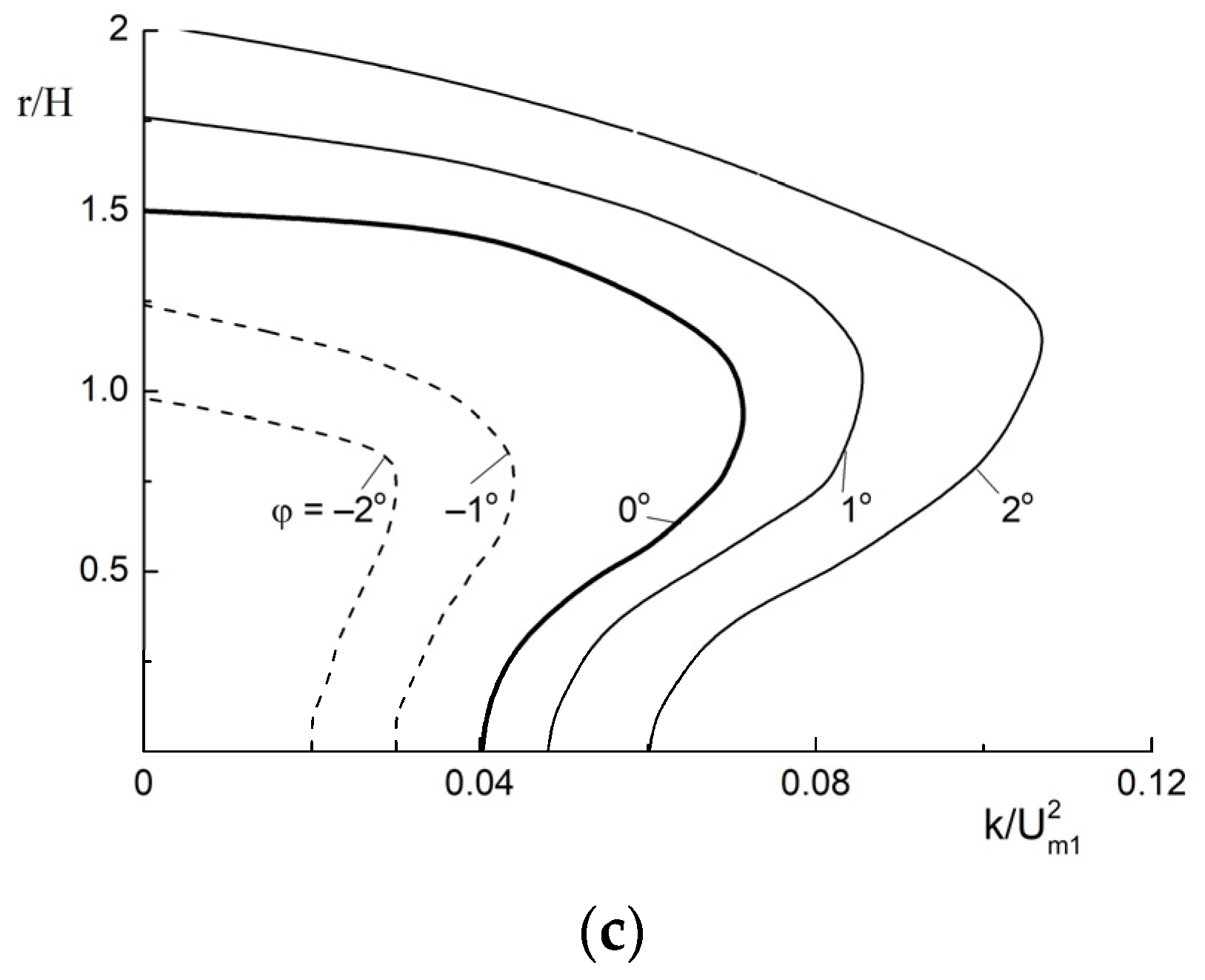
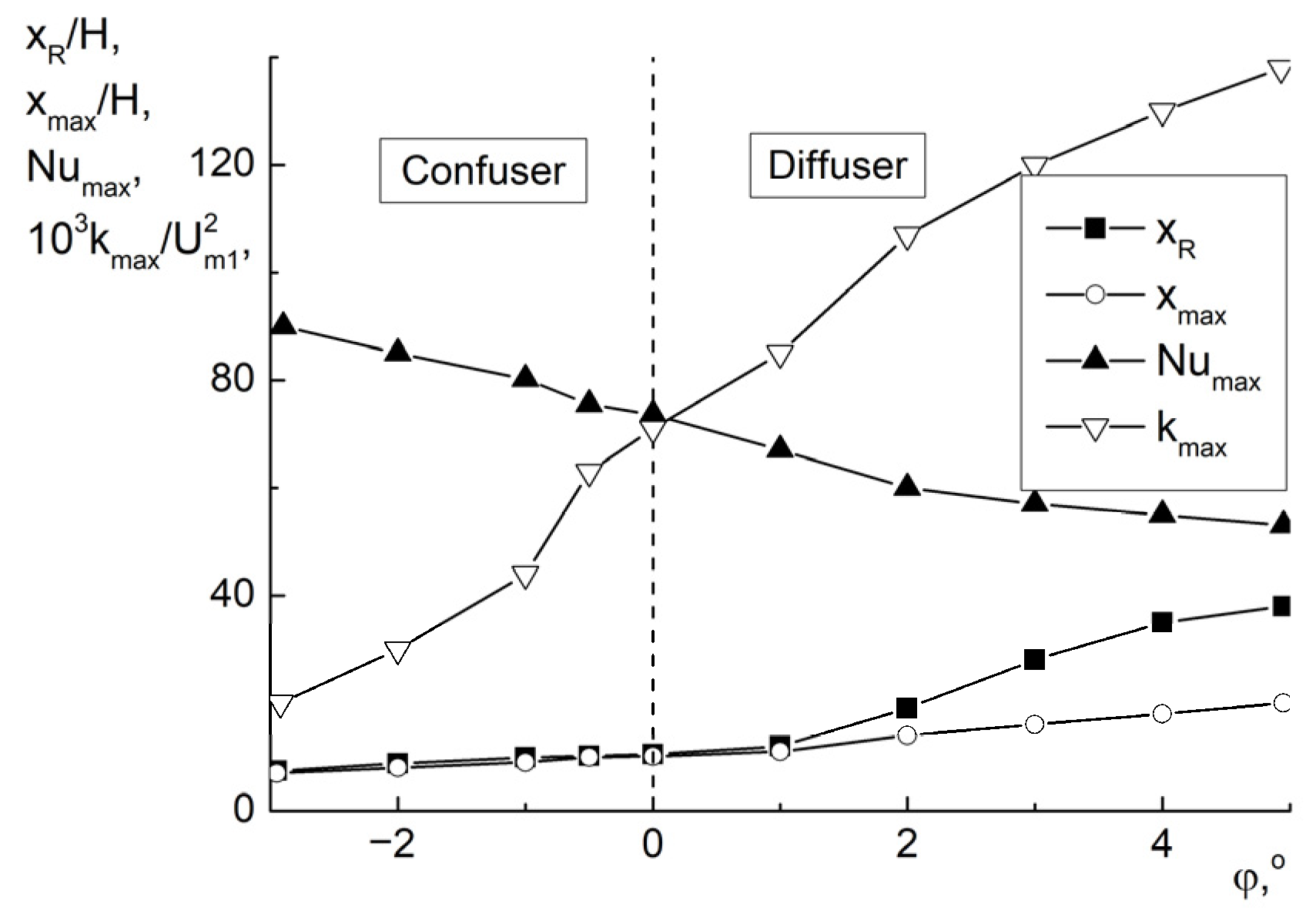
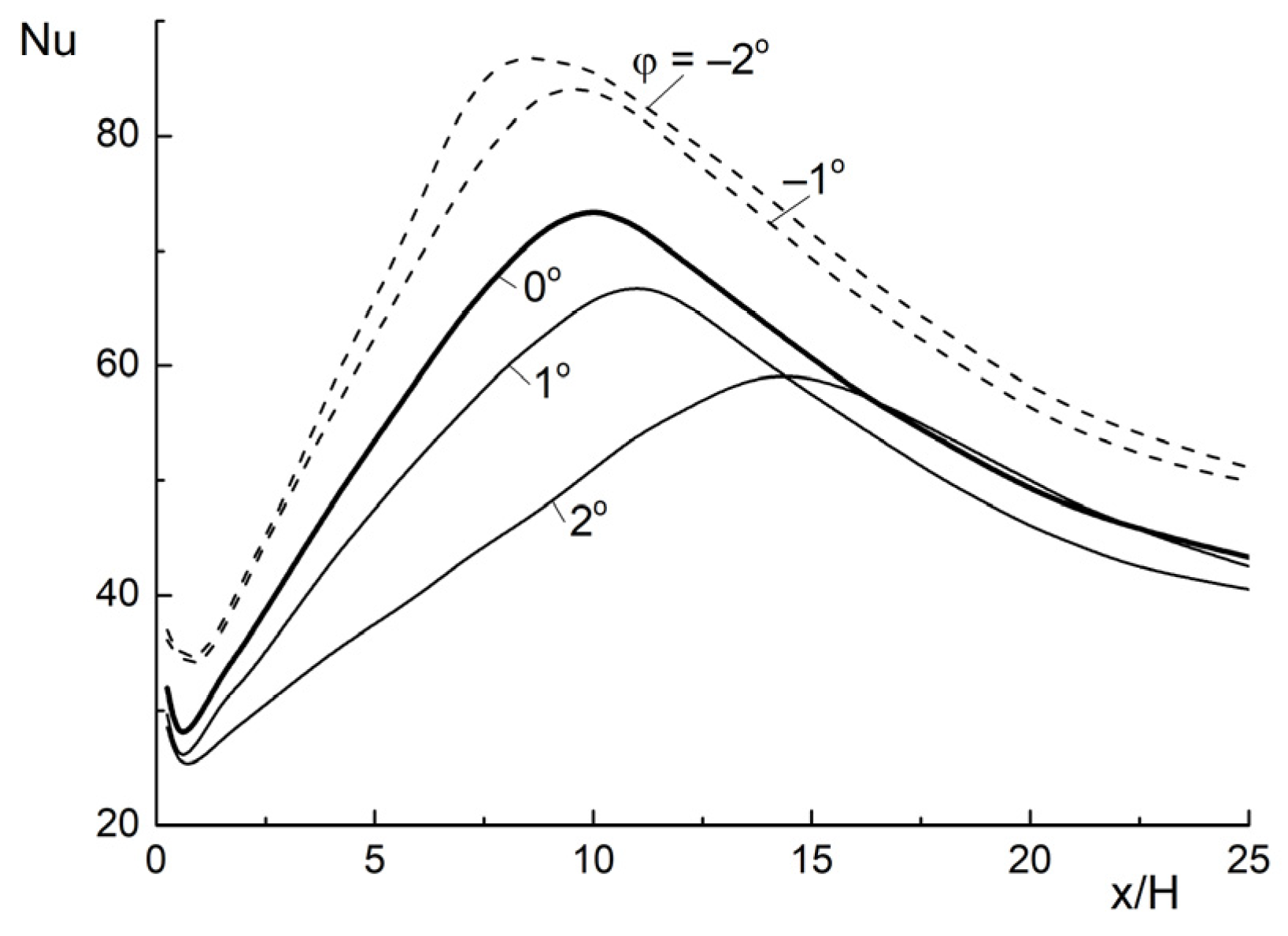
3.2. The Flow Structure in Confuser (FPG) and Diffuser (APG)
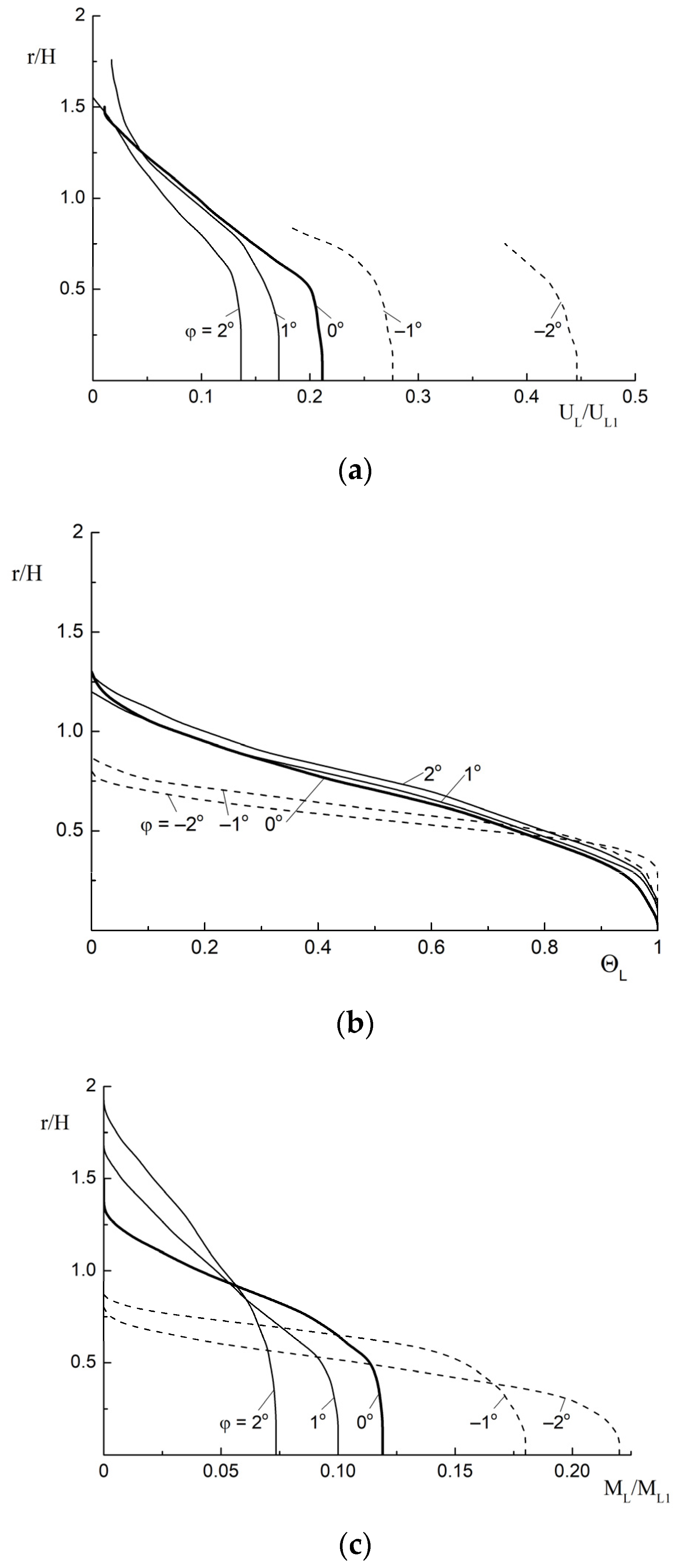
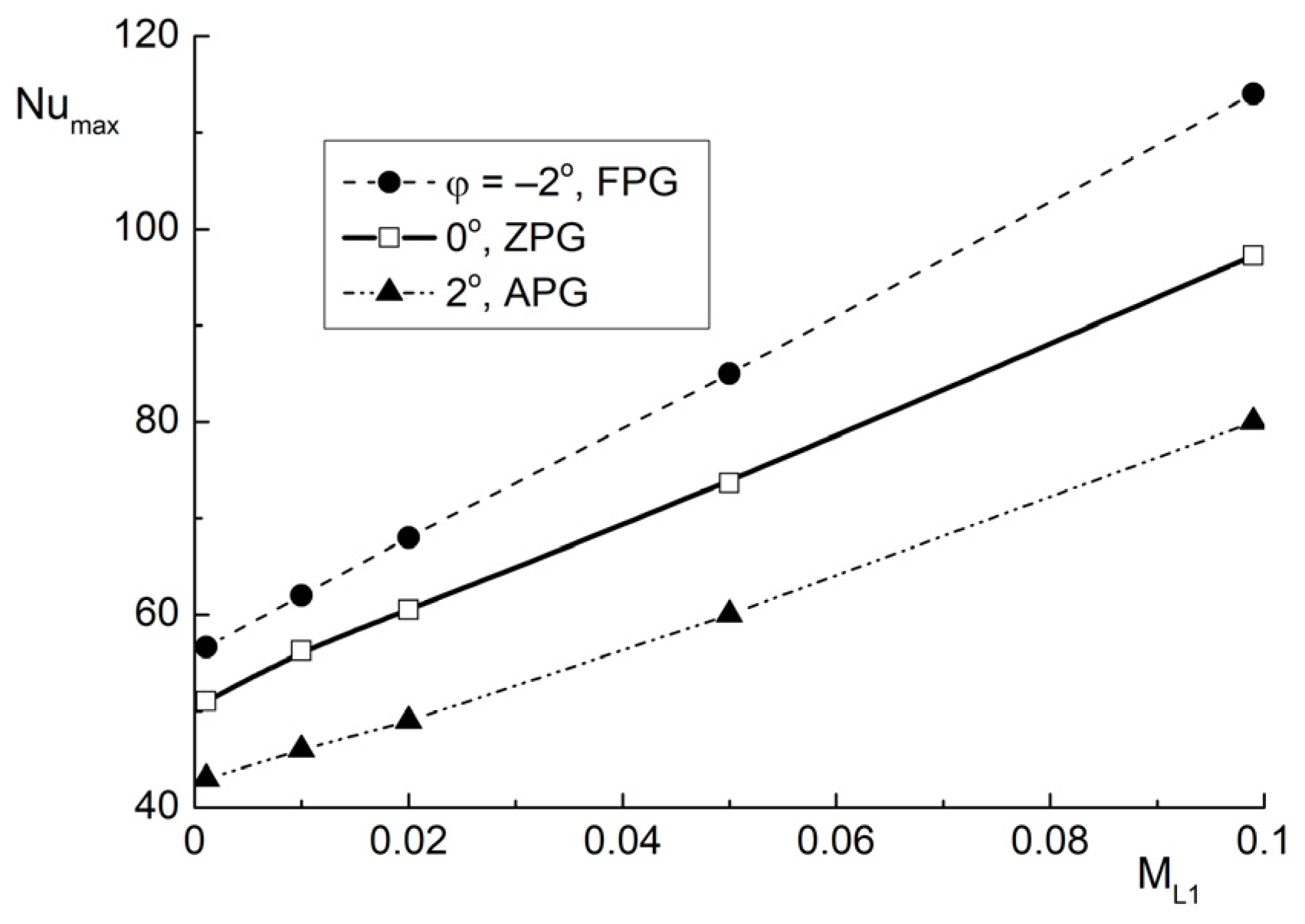
3.3. The Effect of LPG on the Mean Parametrs of the Two-Phase Mist Flow
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| d | droplet diameter |
| H | step height |
| ML | mass fraction |
| Nusselt number | |
| ReH = Um1H/ν | Reynolds number |
| Stk = τ/τf | mean Stokes number |
| T | temperature |
| U | average velocity vector |
| Ui, Uj | mean gas velocities components |
| gas velocity vector seen by the droplet | |
| drift velocity between fluid flow and drops | |
| Weber number | |
| x | streamwise coordinate |
| xmax | location of heat-transfer maximum |
| xR | reattachment length |
| Subscripts | |
| 0 | single-phase fluid (air) flow |
| 1 | initial condition |
| L | liquid |
| m | mean |
| max | maximal value |
| W | wall |
| Greek | |
| Φ | volume fraction |
| λ | thermal conductivity |
| ρ | density |
| ν | kinematic viscosity |
| τ | particle relaxation time |
| τW | wall shear stress |
| φ | diffuser opening angle (φ > 0) or confuser (φ < 0) narrowing angle |
| Acronym | |
| APG | adverse pressure gradient |
| BFS | backward-facing step |
| FPG | favorable pressure gradient |
| LPG | longitudinal pressure gradient |
| CV | control volume |
| SE | sudden expansion |
| ZPG | zero pressure gradient |
References
- Eaton, J.K.; Johnston, J.P. A review of research on subsonic turbulent flow reattachment. AIAA J. 1981, 19, 1093–1100. [Google Scholar] [CrossRef]
- Chen, L.; Asai, K.; Nonomura, T.; Xi, G.N.; Liu, T.S. A review of backward-facing step (BFS) flow mechanisms, heat transfer and control. Thermal Sci. Eng. Progr. 2018, 6, 194–216. [Google Scholar] [CrossRef]
- Klein, A. Review: Effects of inlet conditions on conical-diffuser performance. ASME J. Fluids Eng. 1981, 103, 250–257. [Google Scholar] [CrossRef]
- Azad, R.S. Turbulent flow in a conical diffuser: A review. Exp. Therm. Fluid Sci. 1996, 13, 318–337. [Google Scholar] [CrossRef]
- Apsley, D.D.; Leschziner, M.A. Advanced turbulence modelling of separated flow in a diffuser. Flow Turbul. Combust. 1999, 63, 81–112. [Google Scholar] [CrossRef]
- Driver, D.M.; Seegmiller, H.L. Features of a reattaching turbulent shear layer in divergent channel flow. AIAA J. 1985, 23, 163–171. [Google Scholar] [CrossRef]
- Ra, S.H.; Chang, P.K. Effects of pressure gradient on reattaching flow downstream of a rearward-facing step. J. Aircr. 1990, 27, 93–95. [Google Scholar] [CrossRef]
- Iftekhar, H.; Agelin-Chaab, M. Structure of turbulent flows over forward facing steps with adverse pressure gradient. ASME J. Fluids Eng. 2016, 138, 111202. [Google Scholar] [CrossRef]
- Wang, L.B.; Tao, W.Q.; Wang, Q.W.; Wong, T.T. Experimental study of developing turbulent flow and heat transfer in ribbed convergent/divergent square ducts. Int. J. Heat Fluid Flow 2001, 22, 603–613. [Google Scholar] [CrossRef]
- Terekhov, V.; Dyachenko, A.; Smulsky, Y. The effect of longitudinal pressure gradient on heat transfer in a separated flow behind a sudden expansion of the channel. Heat Transf. Eng. 2020, 41, 1404–1416. [Google Scholar]
- Terekhov, V.I.; Bogatko, T.V. Aerodynamics and heat transfer in a separated flow in an axisymmetric diffuser with sudden expansion. J. Appl. Mech. Techn. Phys. 2015, 56, 471–478. [Google Scholar] [CrossRef]
- Güemes, A.; Sanmiguel Vila, C.; Örlü, R.; Vinuesa, R.; Schlatter, P.; Ianiro, A.; Discetti, S. Flow organization in the wake of a rib in a turbulent boundary layer with pressure gradient. Exp. Therm. Fluid Sci. 2019, 108, 115–124. [Google Scholar] [CrossRef]
- Leont’ev, A.I.; Lushchik, V.G.; Reshmin, A.I. Heat transfer in conical expanding channels. High Temp. 2016, 54, 270–276. [Google Scholar] [CrossRef]
- Lushchik, V.G.; Reshmin, A.I. Heat transfer enhancement in a plane separation-free diffuser. High Temp. 2018, 56, 569–575. [Google Scholar] [CrossRef]
- Lushchik, V.G.; Makarova, M.S.; Reshmin, A.I. Laminarization of flow with heat transfer in a plane channel with a confuser. Fluid Dyn. 2019, 54, 67–76. [Google Scholar] [CrossRef]
- Sakhnov, A.Y. Local laminarization within the mild pressure gradient flow over the heated wall. Int. J. Heat Mass Transf. 2021, 165, 120698. [Google Scholar] [CrossRef]
- Sakhnov, A.Y.; Naumkin, V.S. Velocity overshoot within the accelerated subsonic boundary layer over the heated wall. Int. J. Heat Mass Transf. 2020, 161, 120249. [Google Scholar] [CrossRef]
- Hajaali, A.; Stoesser, T. Flow separation dynamics in three-dimensional asymmetric diffusers. Flow Turbul. Combust. 2022, 108, 973–999. [Google Scholar] [CrossRef]
- Fessler, J.R.; Eaton, J.K. Turbulence modification by particles in a backward-facing step flow. J. Fluid Mech. 1999, 314, 97–117. [Google Scholar] [CrossRef]
- Hishida, K.; Nagayasu, T.; Maeda, M. Augmentation of convective heat transfer by an effective utilization of droplet inertia. Int. J. Heat Mass Transf. 1995, 38, 1773–1785. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Second moment closure modelling of flow, turbulence and heat transfer in droplet-laden mist flow in a ver pipe with sudden expansion. Int. J. Heat Mass Transf. 2013, 66, 210–222. [Google Scholar] [CrossRef]
- Ahmadpour, A.; Noori Rahim Abadi, S.M.A.; Kouhikamali, R. Numerical simulation of two-phase gas–liquid flow through gradual expansions/contractions. Int. J. Multiph. Flow 2016, 79, 31–49. [Google Scholar] [CrossRef]
- Kopparthy, S.; Mansour, M.; Janiga, G.; Thévenin, D. Numerical investigations of turbulent single-phase and two-phase flows in a diffuser. Int. J. Multiph. Flow 2020, 130, 103333. [Google Scholar] [CrossRef]
- Golubkina, I.V.; Osiptsov, A.N. Compressible gas-droplet flow and heat transfer behind a condensation shock in an expanding channel. Int. J. Therm. Sci. 2022, 179, 107576. [Google Scholar] [CrossRef]
- Pakhomov, M.A.; Terekhov, V.I. Gas-droplet flow structure and heat transfer in an axisymmetric diffuser with a sudden expansion. J. Appl. Mech. Techn. Phys. 2020, 61, 787–797. [Google Scholar] [CrossRef]
- Drew, D.A. Mathematical modeling of two-phase flow. Ann. Rev. Fluid Mech. 1983, 15, 261–291. [Google Scholar] [CrossRef]
- Reeks, M.W. On a kinetic equation for the transport of particles in turbulent flows. Phys. Fluids A 1991, 3, 446–456. [Google Scholar] [CrossRef]
- Derevich, I.V.; Zaichik, L.I. Particle deposition from a turbulent flow. Fluid Dyn. 1988, 23, 722–729. [Google Scholar] [CrossRef]
- Wu, H.; Yang, C.; Zhang, Z.; Zhang, Q. Simulation of two-phase flow and syngas generation in biomass gasifier based on two-fluid model. Energies 2022, 15, 4800. [Google Scholar] [CrossRef]
- Zeng, Y.; Xu, W. Investigation on bubble diameter distribution in upward flow by the two-fluid and multi-fluid models. Energies 2021, 14, 5776. [Google Scholar] [CrossRef]
- Fadai-Ghotbi, A.; Manceau, R.; Boree, J. Revisiting URANS computations of the backward-facing step flow using second moment closures. Influence of the numerics. Flow Turbul. Combust. 2008, 81, 395–410. [Google Scholar] [CrossRef]
- Elgobashi, S. On predicting particle-laden turbulent flows. Appl. Scient. Res. 1994, 52, 309–329. [Google Scholar] [CrossRef]
- Lin, S.P.; Reitz, R.D. Drop and spray formation from a liquid jet. Ann. Rev. Fluid Mech. 1998, 30, 85–105. [Google Scholar] [CrossRef]
- Elgobashi, S. An updated classification map of particle-laden turbulent flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow, Fluid Mechanics and Its Applications; Balachandar, S., Prosperetti, A., Eds., Springer: Dordrecht, The Netherlands, 2006; Volume 81, pp. 3–10. [Google Scholar]
- Mukin, R.V.; Zaichik, L.I. Nonlinear algebraic Reynolds stress model for two-phase turbulent flows laden with small heavy particles. Int. J. Heat Fluid Flow 2012, 33, 81–91. [Google Scholar] [CrossRef]
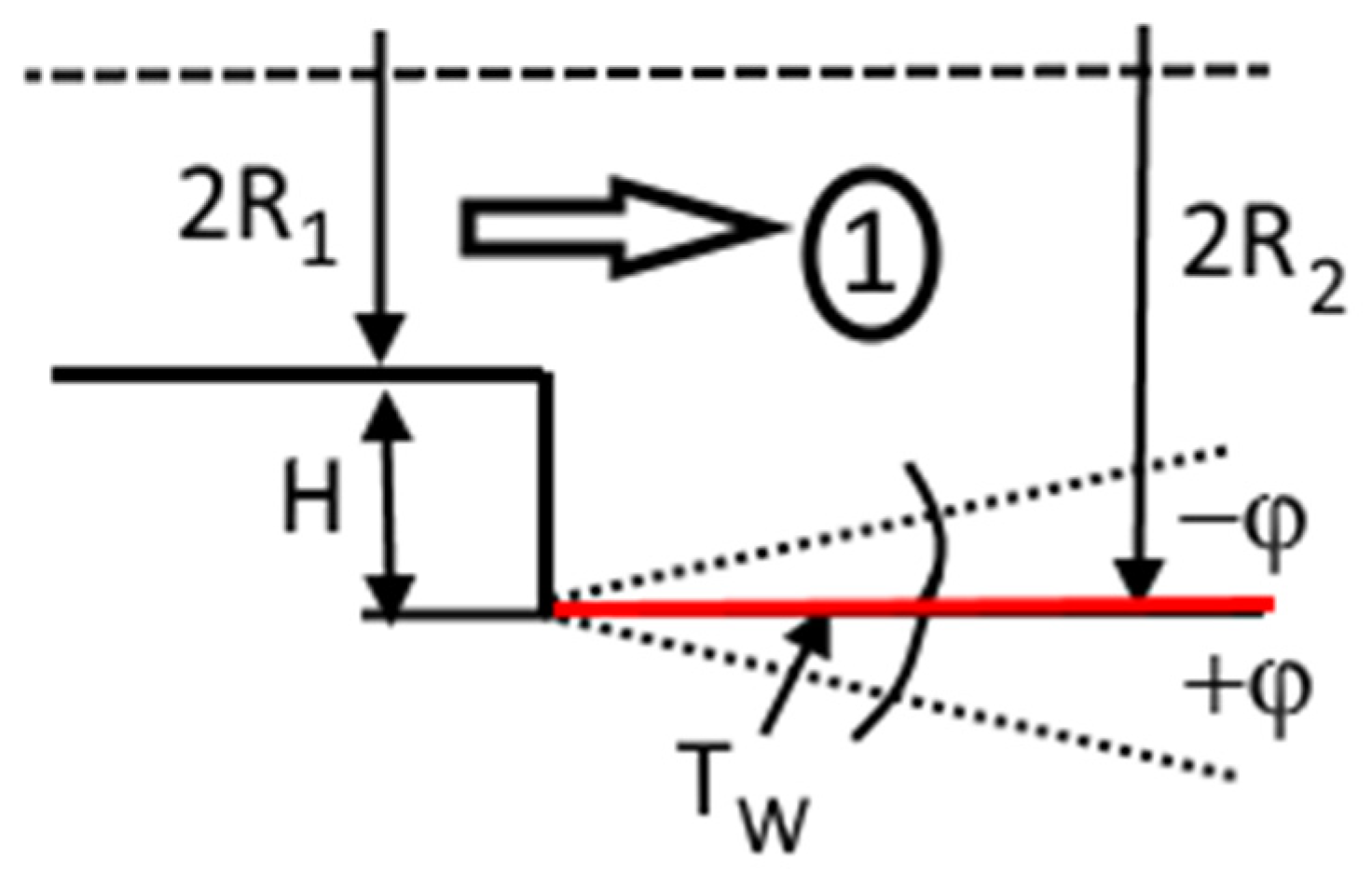
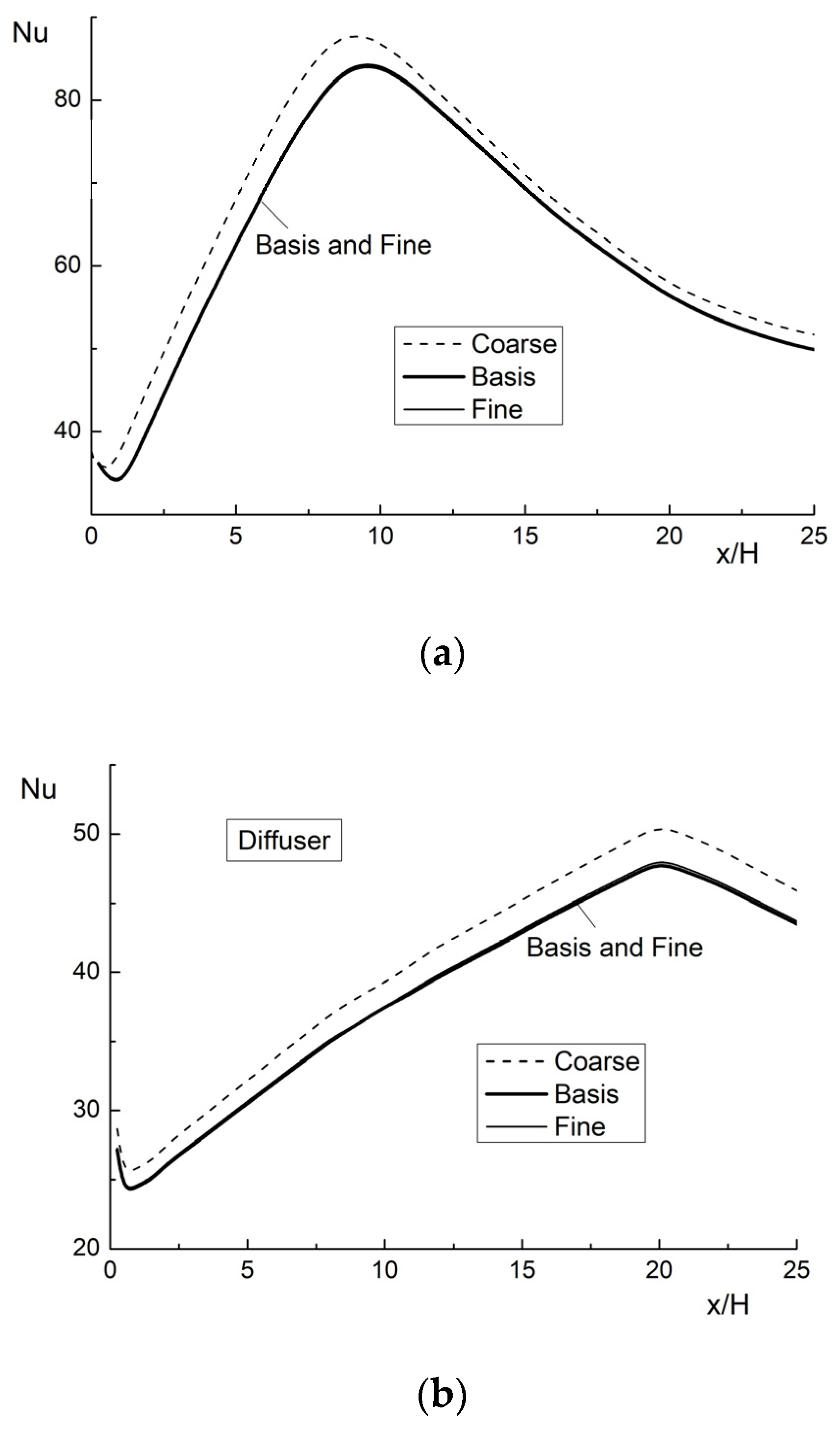
| Flow Type | “Basic” | “Coarse” | “Fine” |
|---|---|---|---|
| Confuser | 550 × 100 | 300 × 50 | 850 × 150 |
| Diffuser | 550 × 200 | 300 × 100 | 850 × 300 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pakhomov, M.A.; Terekhov, V.I. Modeling of Turbulent Heat-Transfer Augmentation in Gas-Droplet Non-Boiling Flow in Diverging and Converging Axisymmetric Ducts with Sudden Expansion. Energies 2022, 15, 5861. https://doi.org/10.3390/en15165861
Pakhomov MA, Terekhov VI. Modeling of Turbulent Heat-Transfer Augmentation in Gas-Droplet Non-Boiling Flow in Diverging and Converging Axisymmetric Ducts with Sudden Expansion. Energies. 2022; 15(16):5861. https://doi.org/10.3390/en15165861
Chicago/Turabian StylePakhomov, Maksim A., and Viktor I. Terekhov. 2022. "Modeling of Turbulent Heat-Transfer Augmentation in Gas-Droplet Non-Boiling Flow in Diverging and Converging Axisymmetric Ducts with Sudden Expansion" Energies 15, no. 16: 5861. https://doi.org/10.3390/en15165861
APA StylePakhomov, M. A., & Terekhov, V. I. (2022). Modeling of Turbulent Heat-Transfer Augmentation in Gas-Droplet Non-Boiling Flow in Diverging and Converging Axisymmetric Ducts with Sudden Expansion. Energies, 15(16), 5861. https://doi.org/10.3390/en15165861






