Voltage Rise Mitigation in PV Rich LV Distribution Networks Using DC/DC Converter Level Active Power Curtailment Method
Abstract
:1. Introduction
2. Problem Analysis and Overview of Proposed Control
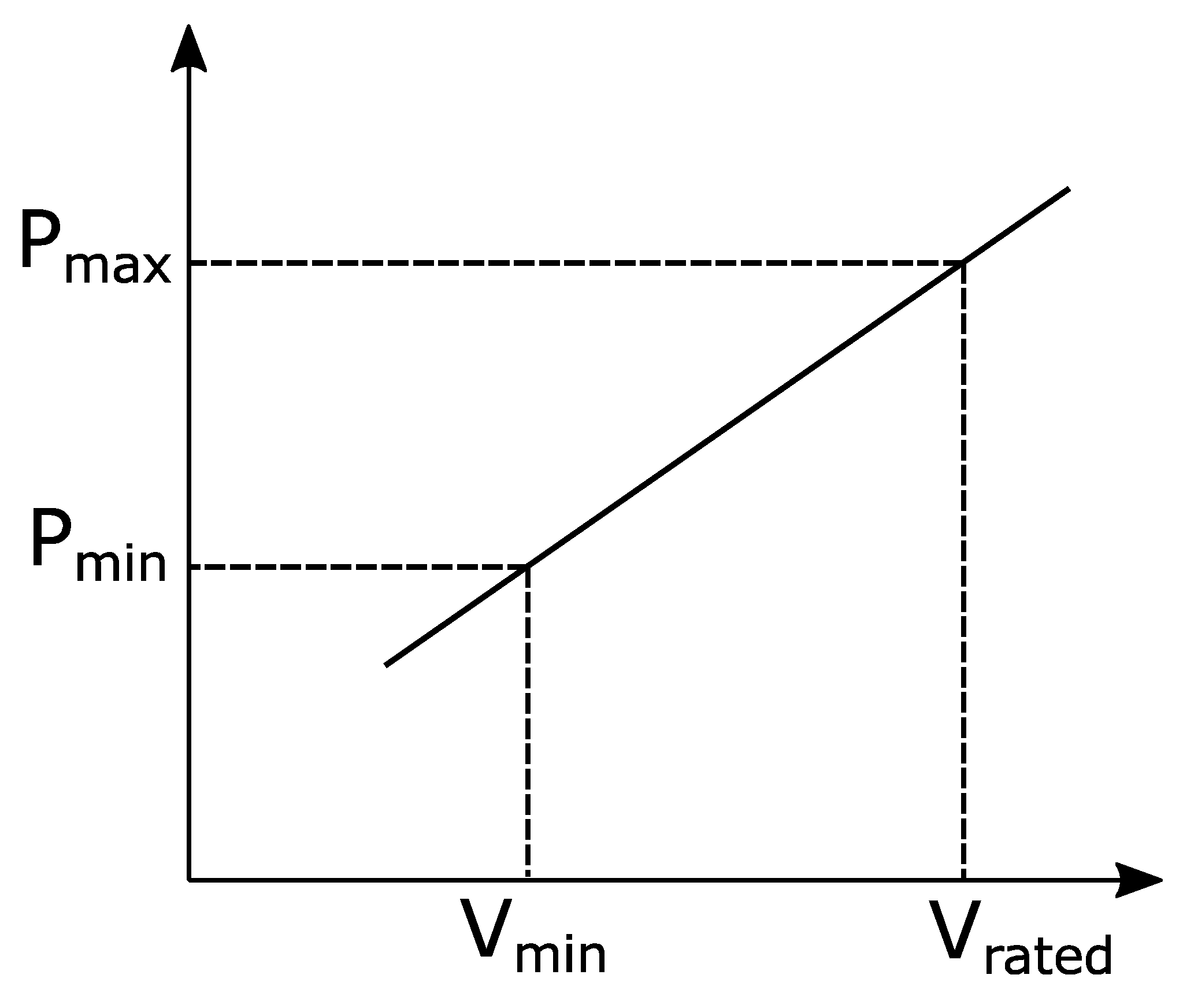
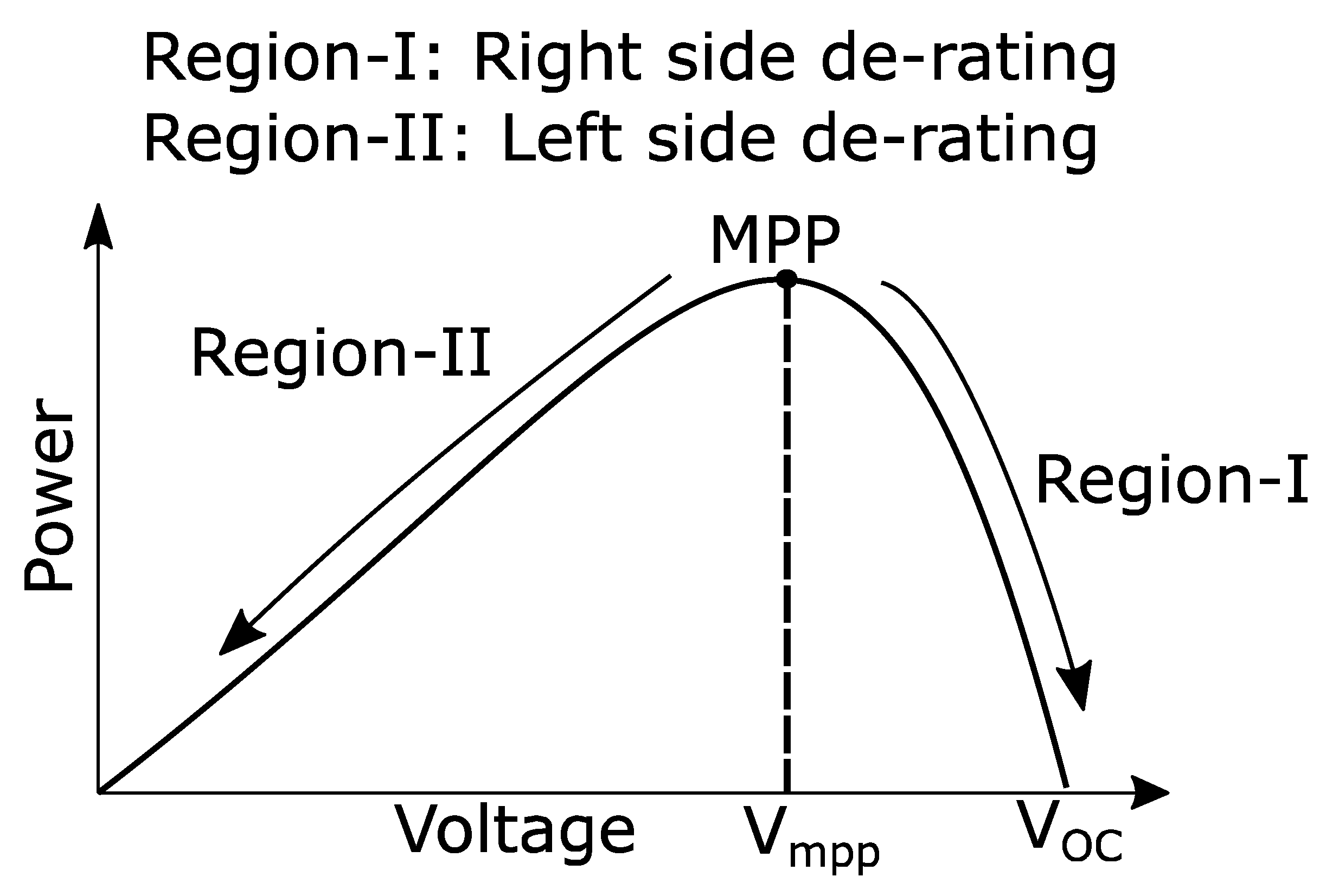
3. De-Rating Based Voltage Control
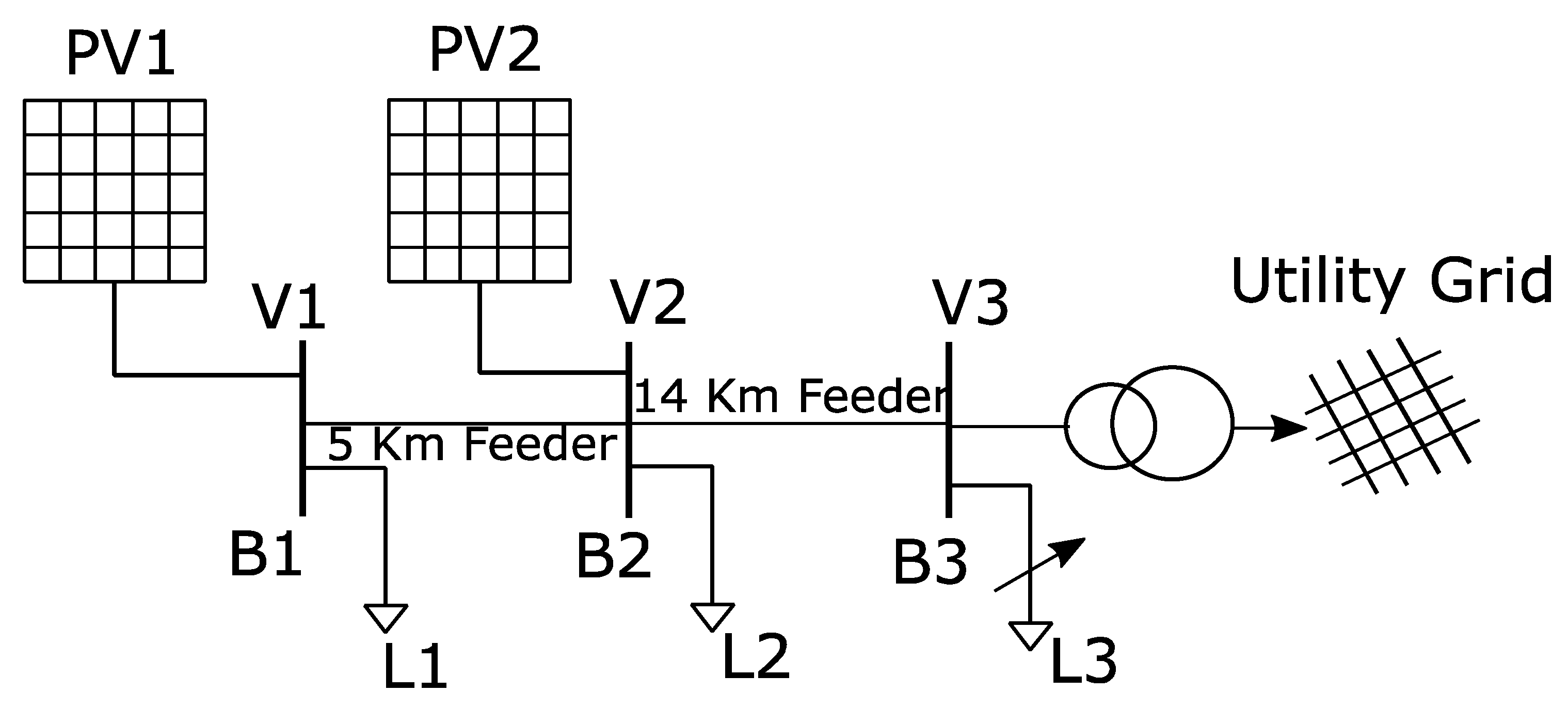
3.1. Description of the Model
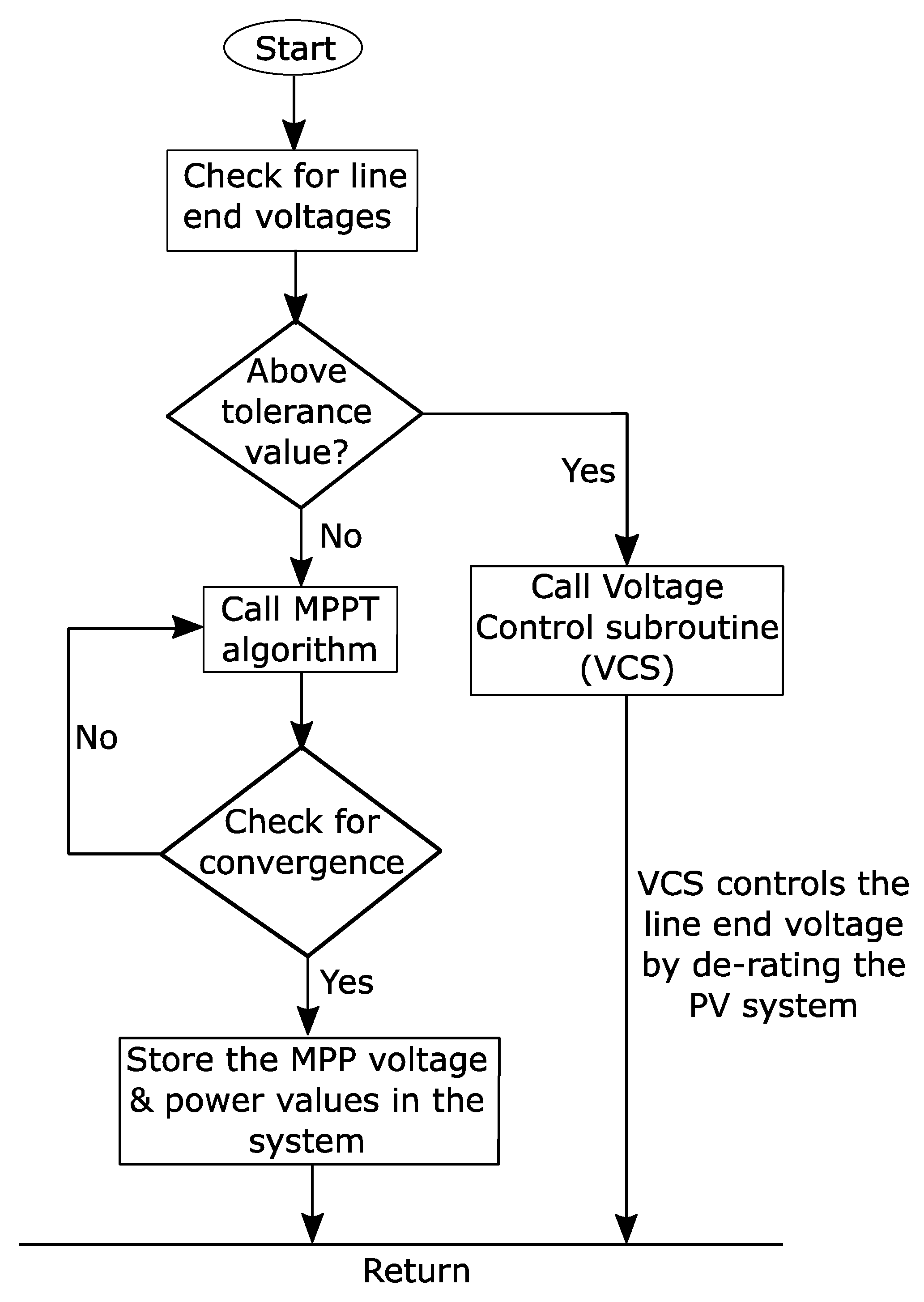
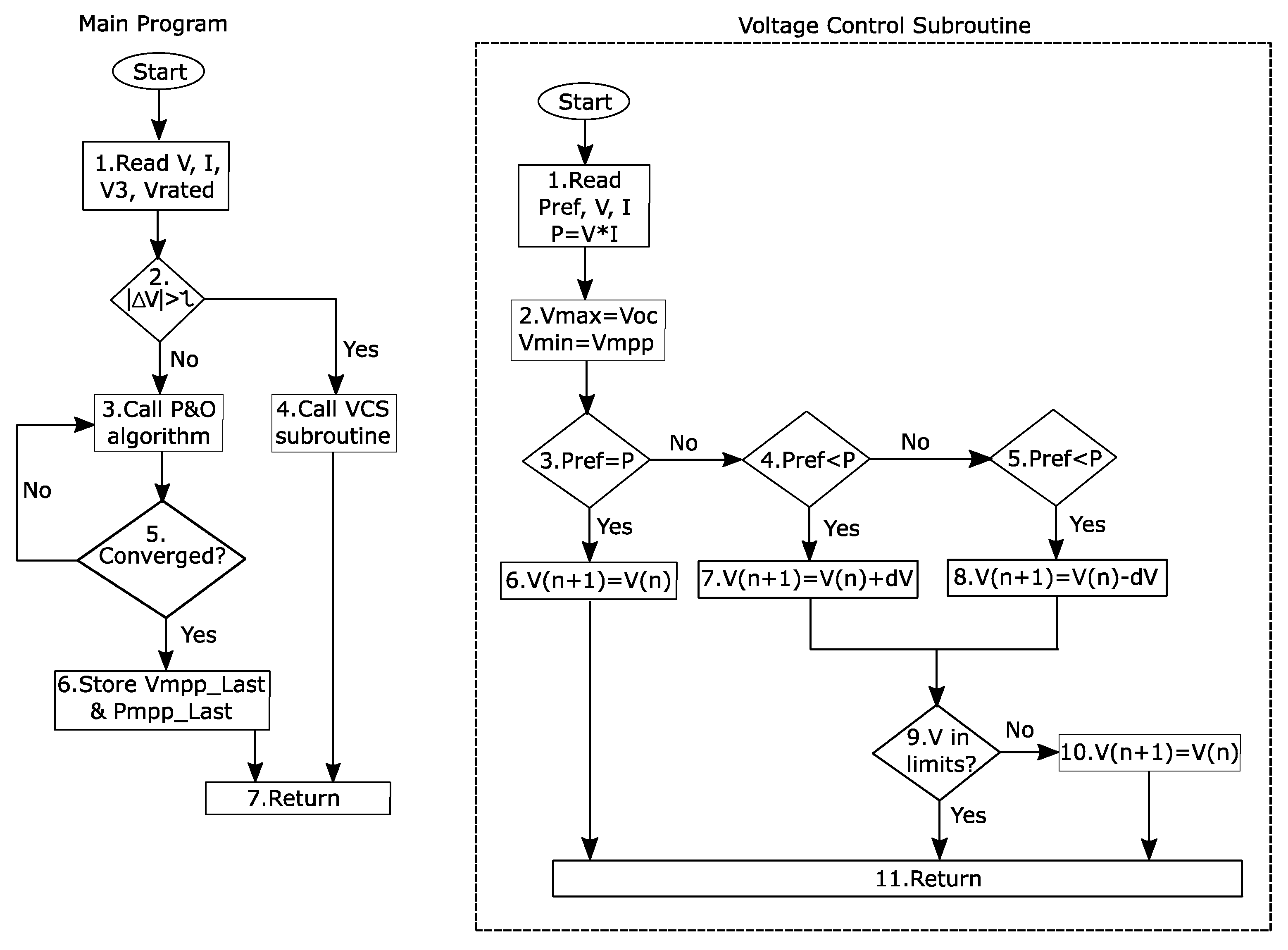
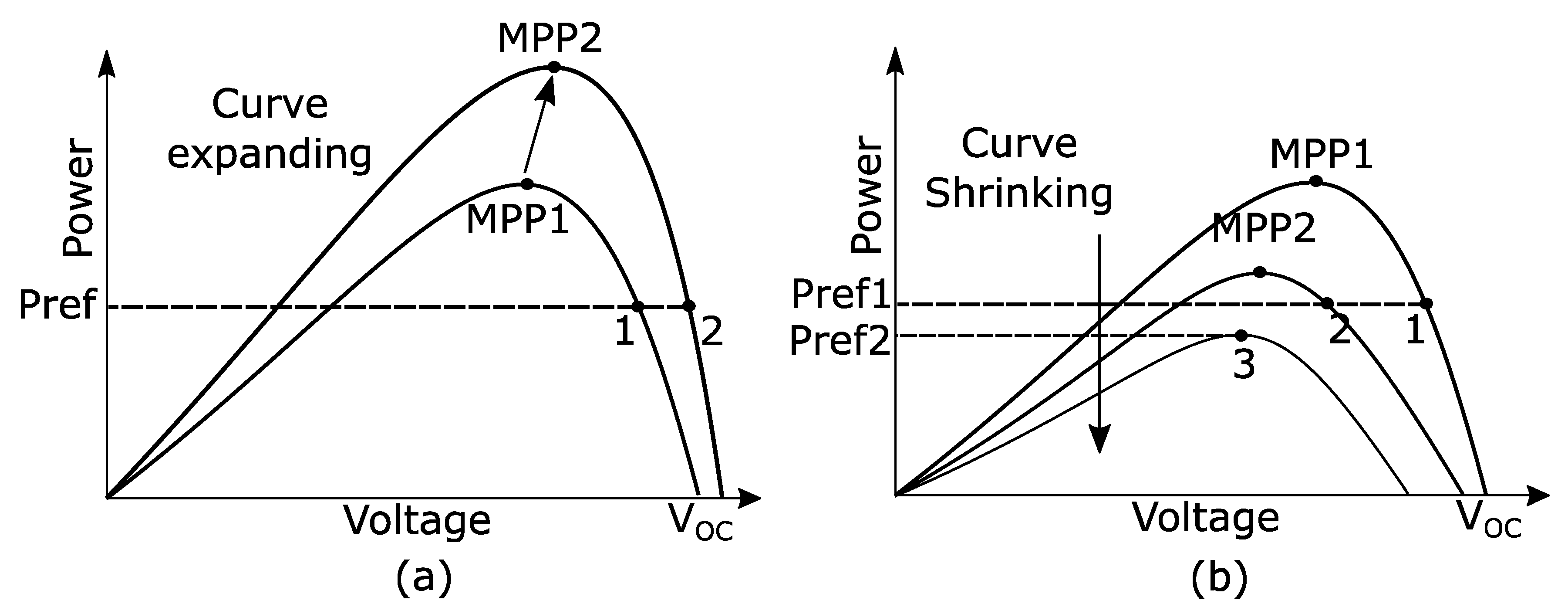
3.2. Voltage Control Algorithm
4. Simulation Results
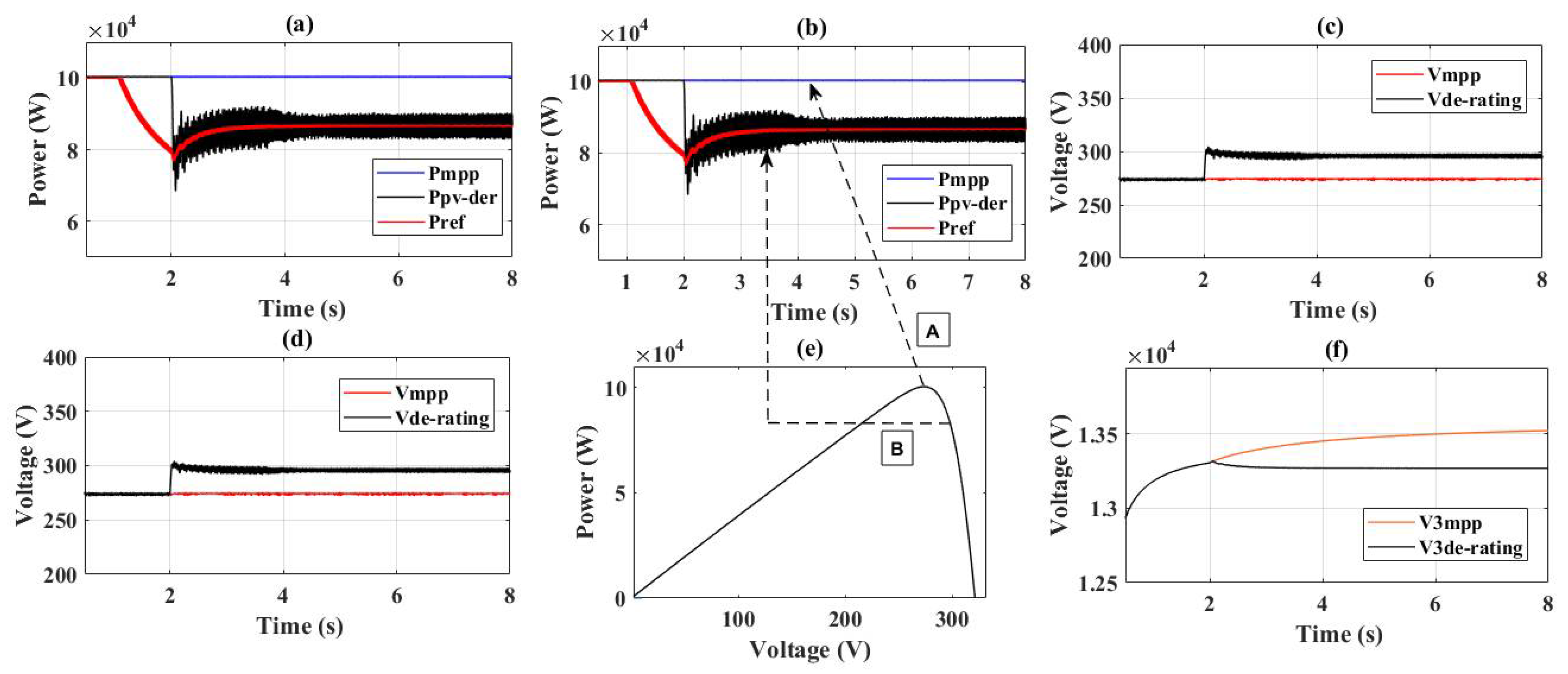
4.1. Case-I: Variable Load and Fixed Irradiance Levels
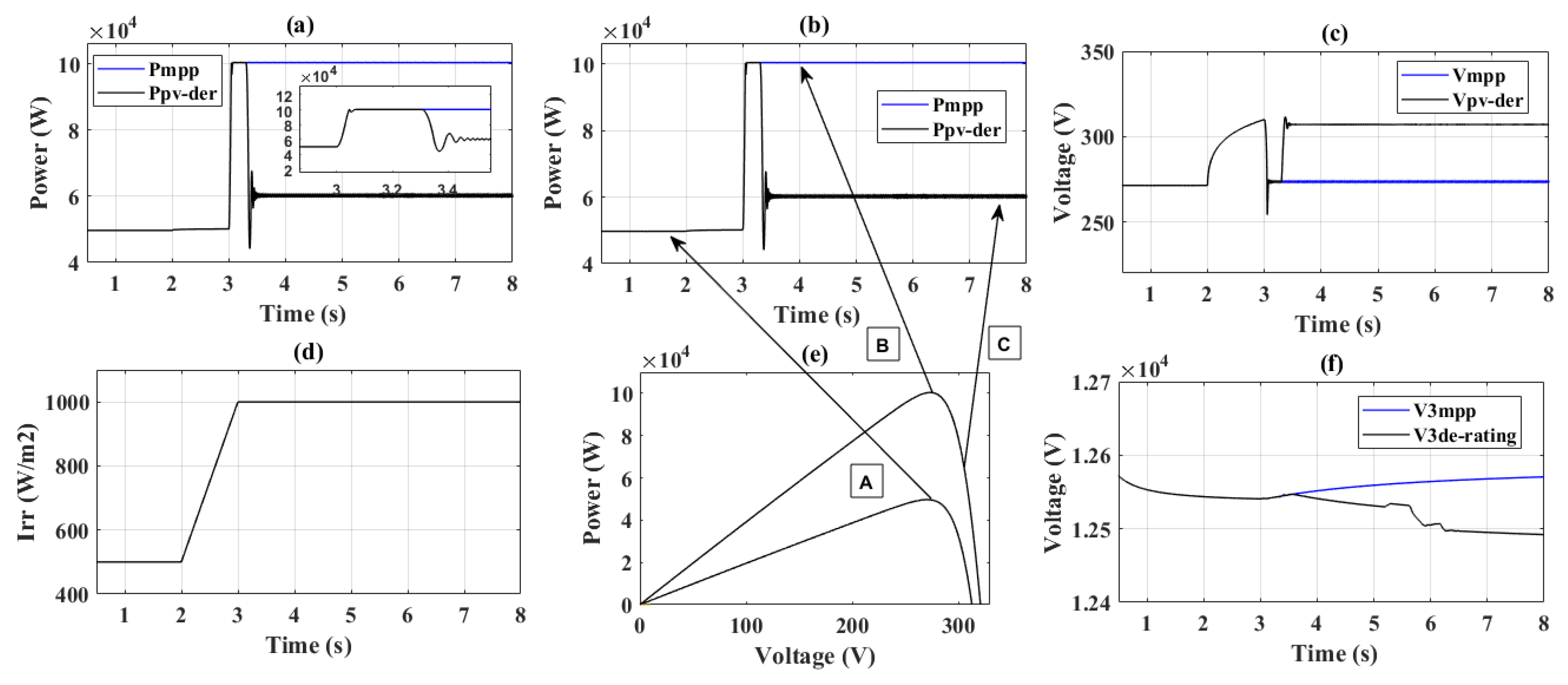
4.2. Case-II: Fixed Load and Variable Irradiance
4.3. Case-III: Variable Load and Variable Irradiance
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Abbreviation | Description |
| PV | Photovoltaic |
| RPC | Reactive power control |
| APC | Active power control |
| LV | Low voltage |
| P–V | Power versus Voltage |
| MPP | Maximum power point |
| MPPT | Maximum power point tracking |
| VCS | Voltage control subroutine |
| VCA | Voltage control algorithm |
| Variables | Description |
| P | Active power |
| Q | Reactive power |
| Vrated | Rated voltage |
| Pref | Reference power |
| Vmpp | Maximum power point voltage |
| V3 | Line end voltage |
| VOC | Open circuit voltage |
| Pmpp | Maximum power point power |
Appendix A
| LV Distribution System | PV System | ||||
|---|---|---|---|---|---|
| Load L1 | P | 2 kW | PV array 1 and 2 | PMPP | 100 kW |
| Q | 0 | VMPP | 260 V | ||
| Vrms/pp | 25 kV | ISC | 400 A | ||
| Load L2 | P | 2 kW | VOC | 320 V | |
| Q | 0 | Dc/dc converter | PV side capacitor | 100 µF | |
| Vrms/pp | 25 e3 | Inverter side capacitor | 6000e µF | ||
| Load L3 | P | 60 kW | Inductor | 5 mH | |
| Q | 4 k Var | PV side T/F 1 and 2 | kVA | 100 | |
| Vrms/pp | 25 kV | VP | 260 V | ||
| Grid side T/F | kVA | 200 | VS | 25 kV | |
| VP | 20 kV | Voltage droop control | k | 0.002 | |
| VS | 25 kV | ||||
References
- Jahangiri, P.; Aliprantis, D.C. Distributed volt/VAr control by PV inverters. IEEE Trans. Power Syst. 2013, 28, 3429–3439. [Google Scholar] [CrossRef]
- Long, C.; Ochoa, L.F. Voltage control of PV-rich LV networks: OLTC-fitted transformer and capacitor banks. IEEE Trans. Power Syst. 2016, 31, 4016–4025. [Google Scholar] [CrossRef]
- Klonari, V.; Toubeau, J.F.; Vandoorn, T.L.; Meersman, B.; de Grève, Z.; Lobry, J.; Vallée, F. Probabilistic framework for evaluating droop control of photovoltaic inverters. Electr. Power Syst. Res. 2015, 129, 1–9. [Google Scholar] [CrossRef]
- Bozalakov, D.V.; Laveyne, J.; Desmet, J.; Vandevelde, L. Overvoltage and voltage unbalance mitigation in areas with high penetration of renewable energy resources by using the modified three-phase damping control strategy. Electr. Power Syst. Res. 2019, 168, 283–294. [Google Scholar] [CrossRef]
- Su, X.; Masoum, M.A.; Wolfs, P.J. Optimal PV inverter reactive power control and real power curtailment to improve performance of unbalanced four-wire LV distribution networks. IEEE Trans. Sustain. Energy 2014, 5, 967–977. [Google Scholar] [CrossRef]
- Dall’Anese, E.; Dhople, S.V.; Johnson, B.B.; Giannakis, G.B. Optimal dispatch of photovoltaic inverters in residential distribution systems. IEEE Trans. Sustain. Energy 2014, 5, 487–497. [Google Scholar] [CrossRef]
- Alam, M.J.; Muttaqi, K.M.; Sutanto, D. A multi-mode control strategy for VAr support by solar PV inverters in distribution networks. IEEE Trans. Power Syst. 2015, 30, 1316–1326. [Google Scholar] [CrossRef]
- Samadi, A.; Eriksson, R.; Rawn, B.; Söder, L. Coordinated active power-Dependent voltage regulation in distribution grids with PV systems. IEEE Trans. Power Deliv. 2014, 29, 1454–1464. [Google Scholar] [CrossRef]
- Olivier, F.; Aristidou, P.; Ernst, D.; Cutsem, T.V. Active management of low-Voltage networks for mitigating overvoltages due to photovoltaic units. IEEE Trans. Smart Grid 2016, 7, 926–936. [Google Scholar] [CrossRef]
- Ali, M.M.V.M.; Babar, M.; Nguyen, P.H.; Cobben, J.F. Overlaying control mechanism for solar PV inverters in the LV distribution network. Electr. Power Syst. Res. 2017, 145, 264–274. [Google Scholar] [CrossRef]
- Haaque, A.N.; Nguyen, P.H.; Vo, T.H.; Bliek, F.W. Agent-based unified approach for thermal and voltage constraint management in LV distribution network. Electr. Power Syst. Res. 2017, 143, 462–473. [Google Scholar] [CrossRef]
- Tonkoski, R.; Lopes, L.A.C.; El-fouly, T.H.M. Coordinated active power curtailment of grid connected PV inverters for overvoltage prevention. IEEE Trans. Sustain. Energy 2011, 2, 139–147. [Google Scholar] [CrossRef]
- Collins, L.; Ward, J.K. Real and reactive power control of distributed PV inverters for overvoltage prevention and increased renewable generation hosting capacity. Renew. Energy 2015, 81, 464–471. [Google Scholar] [CrossRef]
- Mai, T.T.; Haque, A.N.M.M.; Vo, T.; Nguyen, P.H. Coordinated active and reactive power control for overvoltage mitigation in physical LV microgrids. In Proceedings of the 2018 International Conference on Renewable Power Generation, Barcelona, Spain, 25–27 April 2018; pp. 1–6. [Google Scholar]
- Mousavi, S.Y.M.; Jalilian, A.; Savaghebi, M.; Guerrero, J.M. Coordinated control of multifunctional inverters for voltage support and harmonic compensation in a grid-connected microgrid. Electr. Power Syst. Res. 2018, 155, 254–264. [Google Scholar] [CrossRef]
- Ali, M.M.V.M.; Nguyen, P.H.; Kling, W.L.; Chrysochos, A.I.; Papadopoulos, T.A.; Papagiannis, G.K. Fair power curtailment of distributed renewable energy sources to mitigate overvoltages in low-voltage networks. In Proceedings of the IEEE PES Power Tech 2015 Eindhoven, Eindhoven, The Netherlands, 29 June–2 July 2015. [Google Scholar] [CrossRef]
- Weckx, S.; Gonzalez, C.; Driesen, J. Combined central and local active and reactive power control of PV inverters. IEEE Trans. Sustain. Energy 2014, 5, 776–784. [Google Scholar] [CrossRef]
- Alyami, S.; Wang, Y.; Wang, C.; Zhao, J.; Zhao, B. Adaptive real power capping method for fair overvoltage regulation of distribution networks with high penetration of PV systems. IEEE Trans. Smart Grid 2014, 5, 2729–2738. [Google Scholar] [CrossRef]
- Ghasemi, M.A.; Parniani, M. Prevention of distribution network overvoltage by adaptive droop-based active and reactive power control of PV systems. Electr. Power Syst. Res. 2016, 133, 313–327. [Google Scholar] [CrossRef]
- Mai, T.T.; Haque, A.N.M.M.; Nguyen, P.H. Consensus-Based Distributed Control for Overvoltage Mitigation in LV Microgrids. In Proceedings of the IEEE PES Powertech 2019 Milano, Milano, Italy, 23–27 June 2019. [Google Scholar]
- Mai, T.T.; Haque, A.N.M.M.; Vergara, P.P.; Nguyen, P.H.; Pemen, G. Adaptive coordination of sequential droop control for PV inverters to mitigate voltage rise in PV-Rich LV distribution networks. Electr. Power Syst. Res. 2021, 192, 106931. [Google Scholar] [CrossRef]
- Demirok, E.; Gonz´alez, P.C.; Frederiksen, K.H.; Sera, D.; Rodriguez, P.; Teodorescu, R. Local reactive power control methods for overvoltage prevention of distributed solar inverters in low-voltage grids. IEEE J. Photovoltaics 2011, 1, 174–182. [Google Scholar] [CrossRef]
- Zhang, Z.; Dou, C.; Yue, D.; Zhang, B.; Zhao, P. High-economic PV power compensation algorithm to mitigate voltage rise with minimal curtailment. Electr. Power Syst. Res. 2021, 125, 106401. [Google Scholar] [CrossRef]
- Farooqi, A.; Othman, M.M.; Radzi, M.A.M.; Musirin, I.; Noor, S.Z.M.; Abidin, I.Z. Dynamic voltage restorer (DVR) enhancement in power quality mitigation with an adverse impact of unsymmetrical faults. Energy Rep. 2022, 8, 871–882. [Google Scholar] [CrossRef]
- Gholami, K.; Islam, M.R.; Rahman, M.M.; Azizivahed, A.; Fekih, A. State-of-the-art technologies for volt-var control to support the penetration of renewable energy into the smart distribution grids. Energy Rep. 2022, 8, 8630–8651. [Google Scholar] [CrossRef]
- Leon, J.A.; Palacios, C.C.; Salgado, C.V.; Perez, E.H.; Garcia, E.X.M. Particle Swarm Optimization, Genetic Algorithm and Grey Wolf Optimizer Algorithms Performance Comparative for a DC-DC Boost Converter PID Controller. Adv. Sci. Technol. Eng. Syst. J. 2021, 6, 619–625. [Google Scholar] [CrossRef]
- Leon, J.A.; Palacios, C.C.; Salgado, C.V.; Perez, E.H.; Garcia, E.X.M. Optimal PID Parameters Tunning for a DC-DC Boost Converter. In Proceedings of the 2020 IEEE Conference on Technology for Sustainability (SusTech), Santa Ana, CA, USA, 23–25 April 2020. [Google Scholar]
- Chaudhary, P.; Rizwan, M. Voltage regulation mitigation techniques in distribution system with high PV penetration: A review. Renew. Sustain. Energy Rev. 2018, 82, 3279–3287. [Google Scholar] [CrossRef]
- Stetz, T.; Marten, F.; Braun, M. Improved low voltage grid-Integration of photovoltaic systems in germany. IEEE Trans. Sustain. Energy 2013, 4, 534–542. [Google Scholar] [CrossRef]
- Vergara, P.P.; Salazar, M.; Mai, T.T.; Nguyen, P.H.; Slootweg, H. A comprehensive assessment of PV inverters operating with droop control for overvoltage mitigation in LV distribution networks. Renew. Energy 2020, 159, 172–183. [Google Scholar] [CrossRef]
- Verma, P.; Kaur, T.; Kaur, R. Power control strategy of an integrated PV system for active power reserve under dynamic operating conditions. Sustain. Energy Technol. Assess. 2021, 45, 101066. [Google Scholar] [CrossRef]
- Xin, H.; Liu, Y.; Wang, Z.; Gan, D.; Yang, T. A new frequency regulation strategy for photovoltaic systems without energy storage. IEEE Trans. Sust. Energy 2013, 4, 985–993. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, H.; Wang, Z.; Yang, T. Power control strategy for photovoltaic system based on the newton quadratic interpolation. IET Renew. Power Gen. 2014, 8, 611–620. [Google Scholar] [CrossRef]
- Zarina, P.P.; Mishra, S.; Sekhar, P.C. Exploring frequency control capability of a PV system in a hybrid PV-rotating machine-without storage system. Int. J. Elect. Power Energy Syst. 2014, 60, 258–267. [Google Scholar] [CrossRef]
- Rajan, R.; Fernandez, F.M. Power control strategy of photovoltaic plants for frequency regulation in a hybrid power system. Elect. Power Energy Syst. 2019, 110, 171–183. [Google Scholar] [CrossRef]
- Rajan, R.; Fernandez, F.M. Fuzzy based control of grid-connected photovoltaic system for enhancing system inertial response. In Proceedings of the 53rd International Universities Power Engineering Conference (UPEC), Glasgow, UK, 4–7 September 2018; pp. 1–6. [Google Scholar]
- Rajan, R.; Fernandez, F.M. Grid inertia based frequency regulation strategy of photovoltaic system without energy storage. In Proceedings of the International CET Conference on Control, Communication, and Computing (IC4), Trivandrum, India, 5–7 July 2018; pp. 106–111. [Google Scholar]
- Esram, T.; Chapman, P.L. Comparison of Photovoltaic Array Maximum Power Point Tracking Techniques. IEEE Trans. Energy Conv. 2007, 22, 439–448. [Google Scholar] [CrossRef]


| S. No. | Ref. No. | Adopted Control | Power Controlled (P or Q) | Implementation Stage | Critical Remarks | Year of Publication |
|---|---|---|---|---|---|---|
| 1 | [4] | Modified damping based control | P (Active) | Inverter |
| 2019 |
| 2 | [5] | Multi objective optimal power flow | P and Q (both active and reactive) | Inverter |
| 2014 |
| 3 | [6] | Optimal inverter dispatch control | P and Q (both active and reactive) | Inverter |
| 2014 |
| 4 | [7] | Reverse power flow based droop characteristic control | Q (Reactive) | Inverter |
| 2015 |
| 5 | [8] | Active power dependent voltage regulation | Q (Reactive) | Inverter |
| 2014 |
| 6 | [9] | 5-Mode distributed control scheme | P and Q (both active and reactive) | Inverter |
| 2016 |
| 7 | [10] | A power-voltage (P–V) droop control based overvoltage mitigation | P (Active) | Inverter |
| 2017 |
| 8 | [12] | Droop based APC | P (Active) | Inverter |
| 2011 |
| 9 | [13] | P–V and Q-V conjunction control | P and Q (both active and reactive) | Inverter |
| 2015 |
| 10 | [15] | Voltage support technique for VSI | P and Q (both active and reactive) | Inverter |
| 2018 |
| 11 | [16] | Fairness power sharing algorithm | P (Active) | Inverter |
| 2015 |
| 12 | [17] | Optimal reactive power utilization technique for overvoltage compensation | P and Q (both active and reactive) |
| 2014 | |
| 13 | [18] | Fair real power curtailment method | P (Active) | Inverter |
| 2014 |
| 14 | [19] | Adaptive-droop based active and reactive power control | P and Q (both active and reactive) | Unspecified |
| 2016 |
| 15 | [21] | Two-level overvoltage mitigation control | P and Q (both active and reactive) | Inverter |
| 2021 |
| 16 | [23] | Power Compensation algorithm | P and Q (both active and reactive) | NA |
| 2021 |
| 17 | [24] | A new DVR configuration | Q (Reactive) | Inverter |
| 2022 |
| 18 | Proposed method | P (Active) | Dc/dc converter |
|
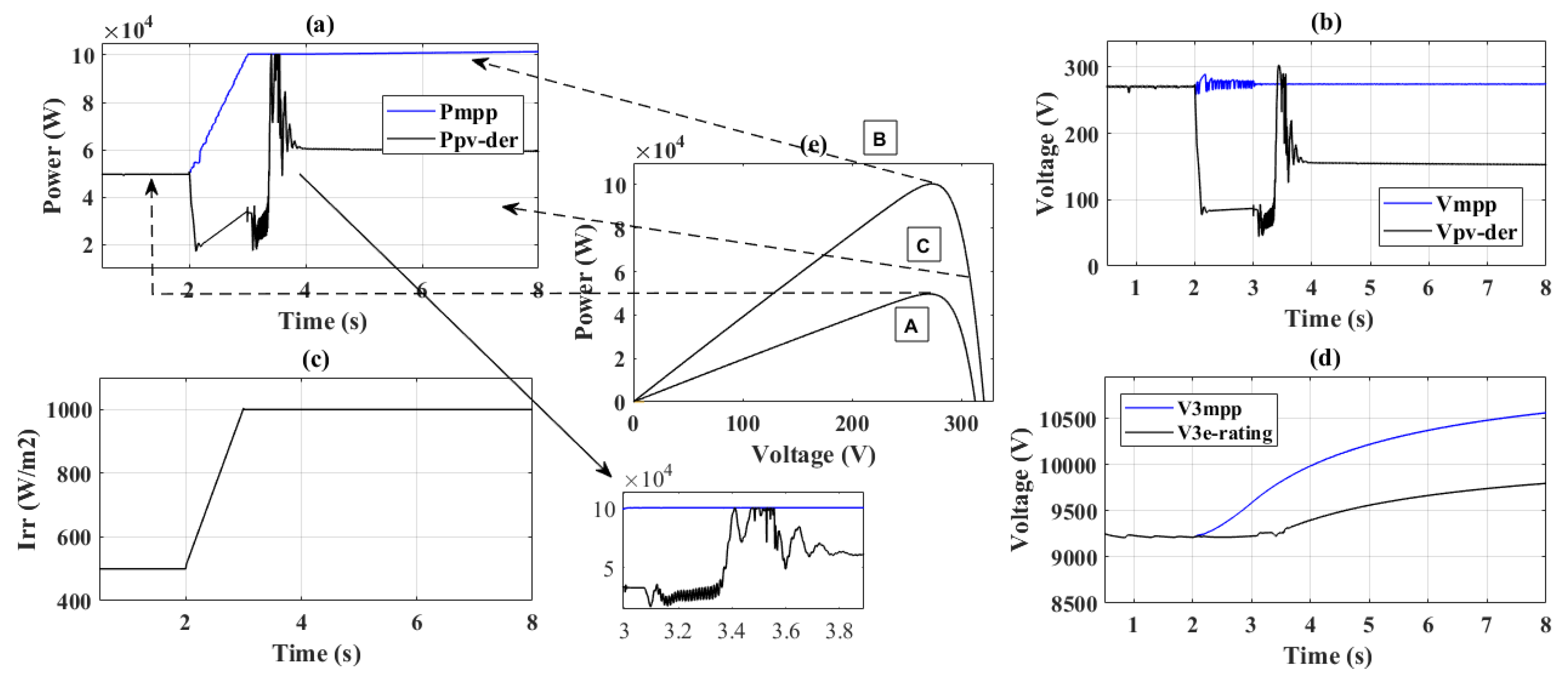
| S. No. | Time (s) | Power (kW)-Figure 8a | Voltage (VPV)-Figure 8c | V3 (kV) MPP-Figure 8f | V3 (kV) De-Rating Figure 8f |
|---|---|---|---|---|---|
| 1 | 1.2 | 100 | 270 | 13.2 | 13.2 |
| 2 | 1.4 | 100 | 270 | 13.2 | 13.2 |
| 3 | 3.5 | 80 | 300 | 13.4 | 13.2 |
| 4 | 4.5 | 86 | 294 | 13.4 | 13.3 |
| 5 | 6.5 | 82 | 296 | 13.5 | 13.3 |
| S. No. | Time (s) | Power (kW)-Figure 9a | Irr. (W/m2)-Figure 9d | Voltage (VPV)-Figure 9c | V3 (kV) MPP-Figure 9f | V3 (kV) De-Rating Figure 9f |
|---|---|---|---|---|---|---|
| 1 | 1.2 | 48 | 500 | 271 | 12.5 | 12.5 |
| 2 | 1.4 | 48 | 500 | 271 | 12.5 | 12.5 |
| 3 | 3.5 | 60 | 1000 | 310 | 12.5 | 12.5 |
| 4 | 4.5 | 60 | 1000 | 310 | 12.56 | 12.53 |
| 5 | 6.5 | 60 | 1000 | 312 | 12.56 | 12.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Verma, P.; Katal, N.; Sharma, B.; Chowdhury, S.; Mehbodniya, A.; Webber, J.L.; Bostani, A. Voltage Rise Mitigation in PV Rich LV Distribution Networks Using DC/DC Converter Level Active Power Curtailment Method. Energies 2022, 15, 5901. https://doi.org/10.3390/en15165901
Verma P, Katal N, Sharma B, Chowdhury S, Mehbodniya A, Webber JL, Bostani A. Voltage Rise Mitigation in PV Rich LV Distribution Networks Using DC/DC Converter Level Active Power Curtailment Method. Energies. 2022; 15(16):5901. https://doi.org/10.3390/en15165901
Chicago/Turabian StyleVerma, Pankaj, Nitish Katal, Bhisham Sharma, Subrata Chowdhury, Abolfazl Mehbodniya, Julian L. Webber, and Ali Bostani. 2022. "Voltage Rise Mitigation in PV Rich LV Distribution Networks Using DC/DC Converter Level Active Power Curtailment Method" Energies 15, no. 16: 5901. https://doi.org/10.3390/en15165901
APA StyleVerma, P., Katal, N., Sharma, B., Chowdhury, S., Mehbodniya, A., Webber, J. L., & Bostani, A. (2022). Voltage Rise Mitigation in PV Rich LV Distribution Networks Using DC/DC Converter Level Active Power Curtailment Method. Energies, 15(16), 5901. https://doi.org/10.3390/en15165901








