Variable Weighting Coefficient of EMF-Based Enhanced Sliding Mode Observer for Sensorless PMSM Drives
Abstract
:1. Introduction
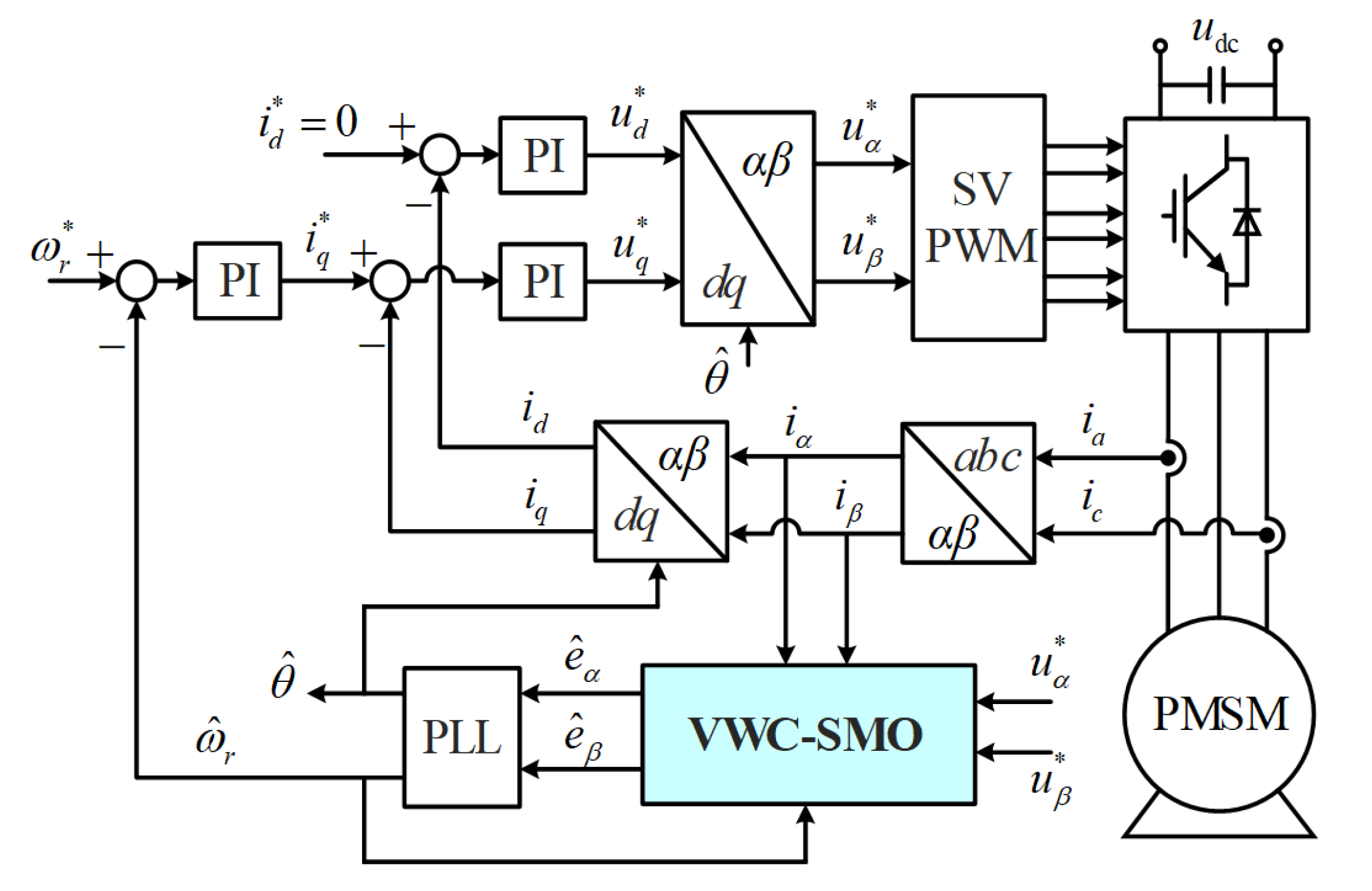
2. SMO-Based Sensorless Control of PMSM
2.1. Field-Oriented Control of Position of Sensorless SPMSM
2.2. SMO-Based Position Estimation
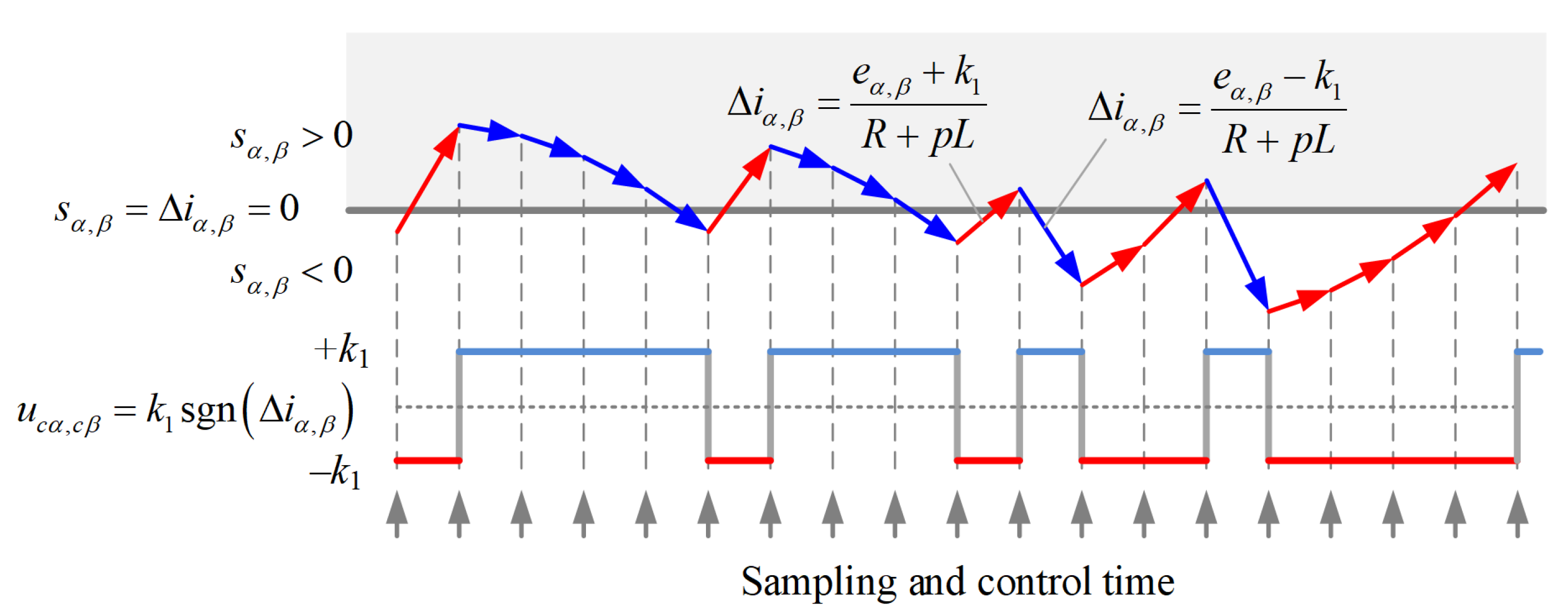
2.3. Asymmetric Approaching Velocity of SMO
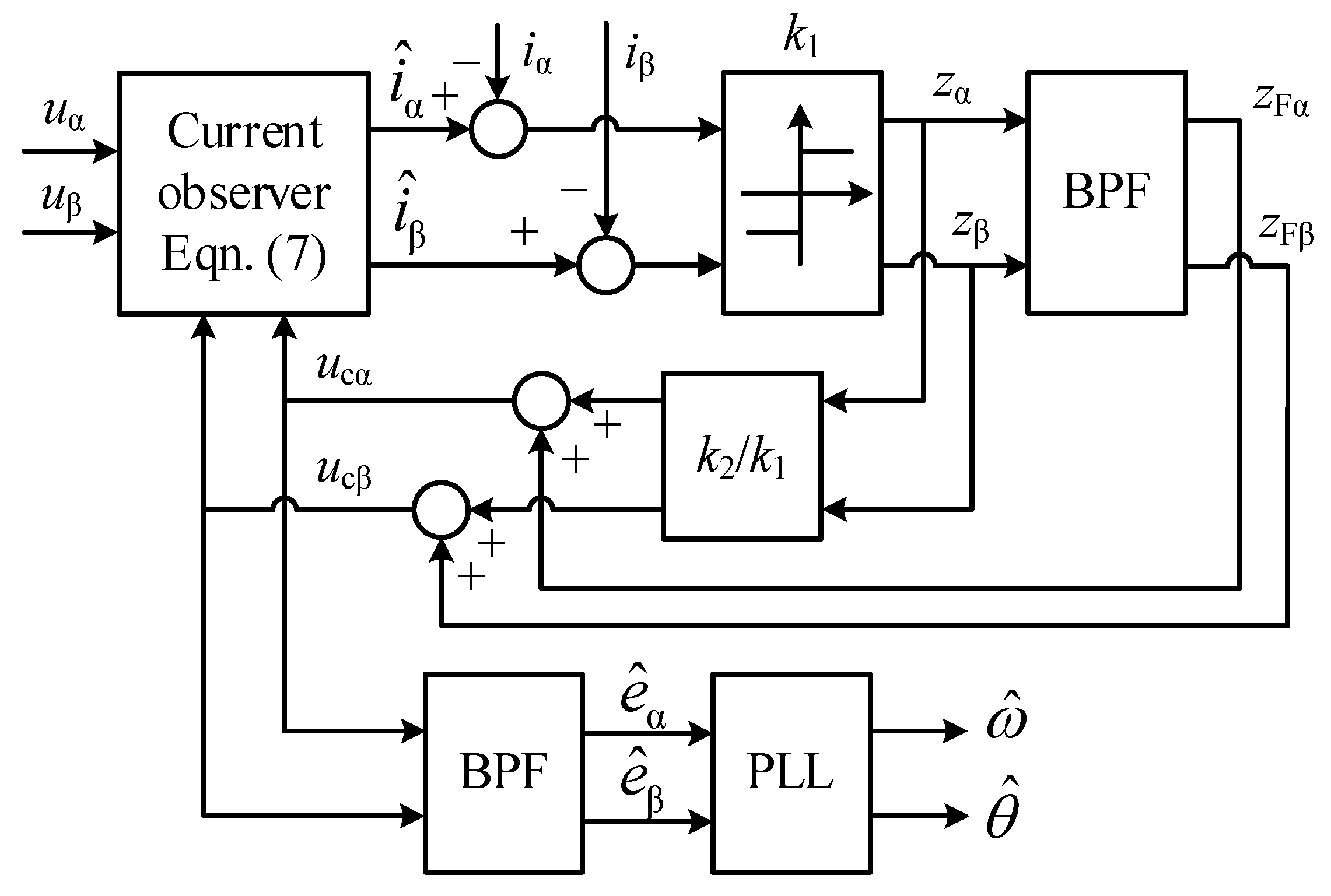
3. Improved SMO Based on Variable Weighting Coefficient of Back EMFS
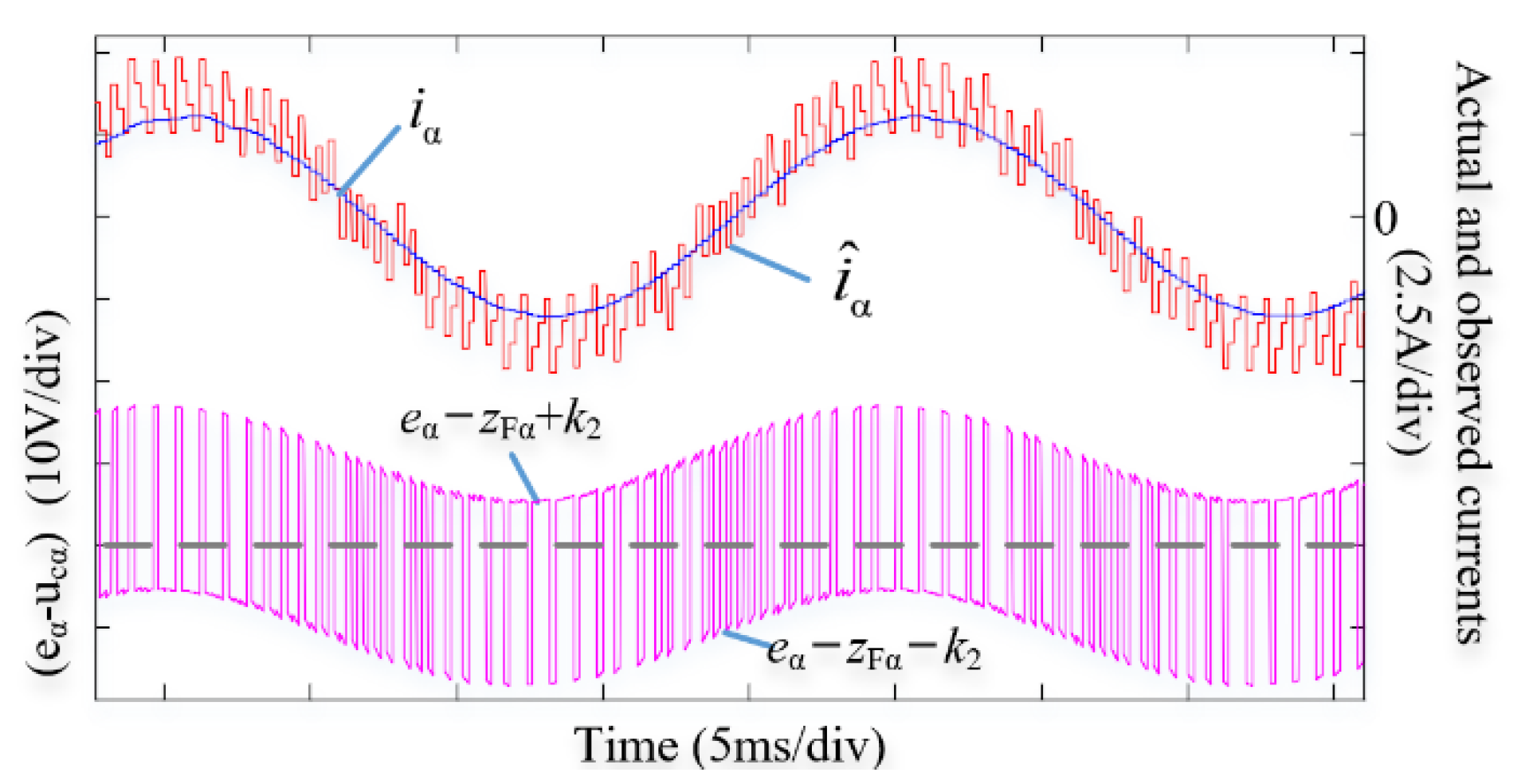
3.1. VWC-SMO
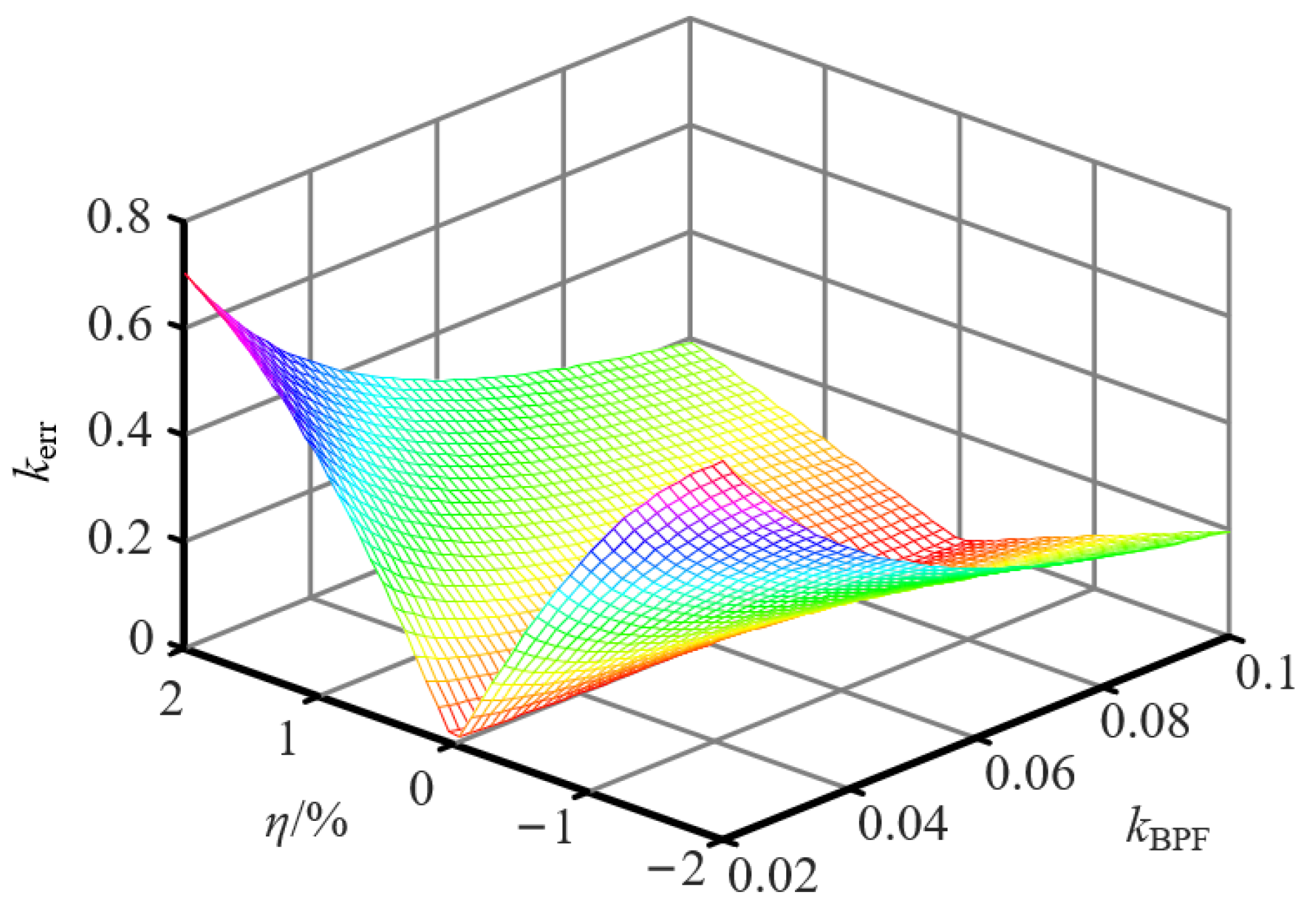
3.2. Parameter Design
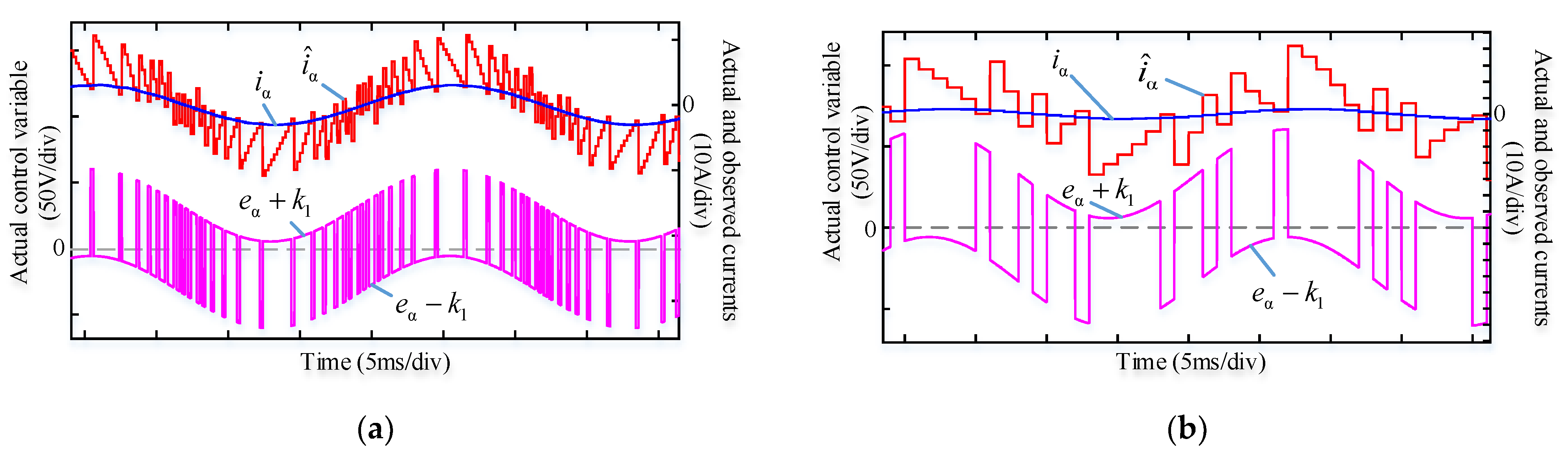
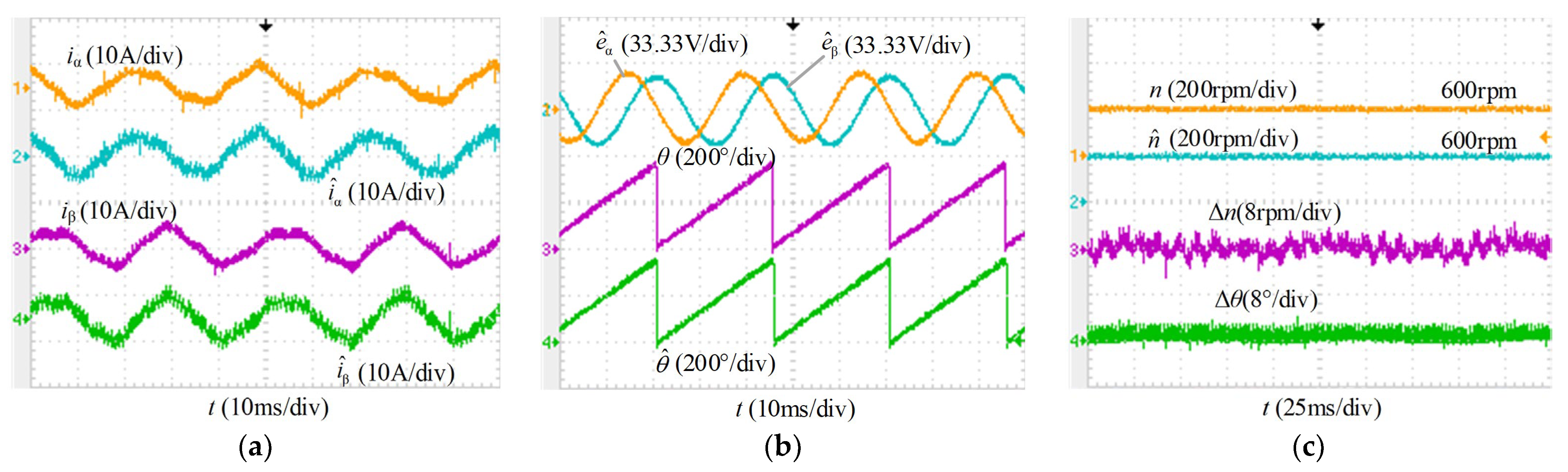
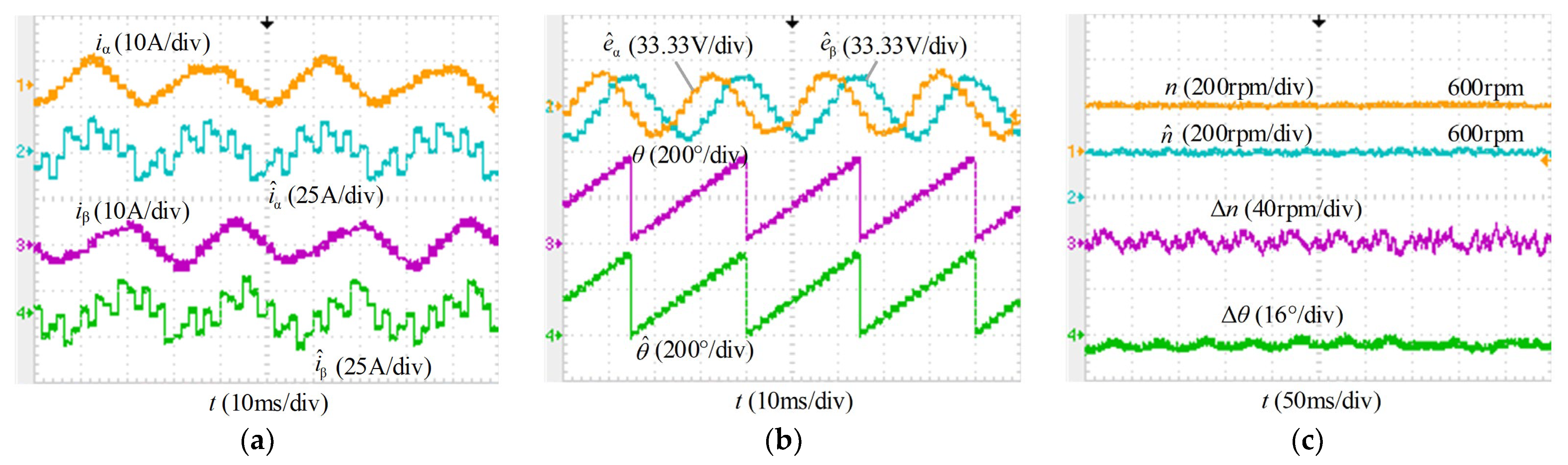
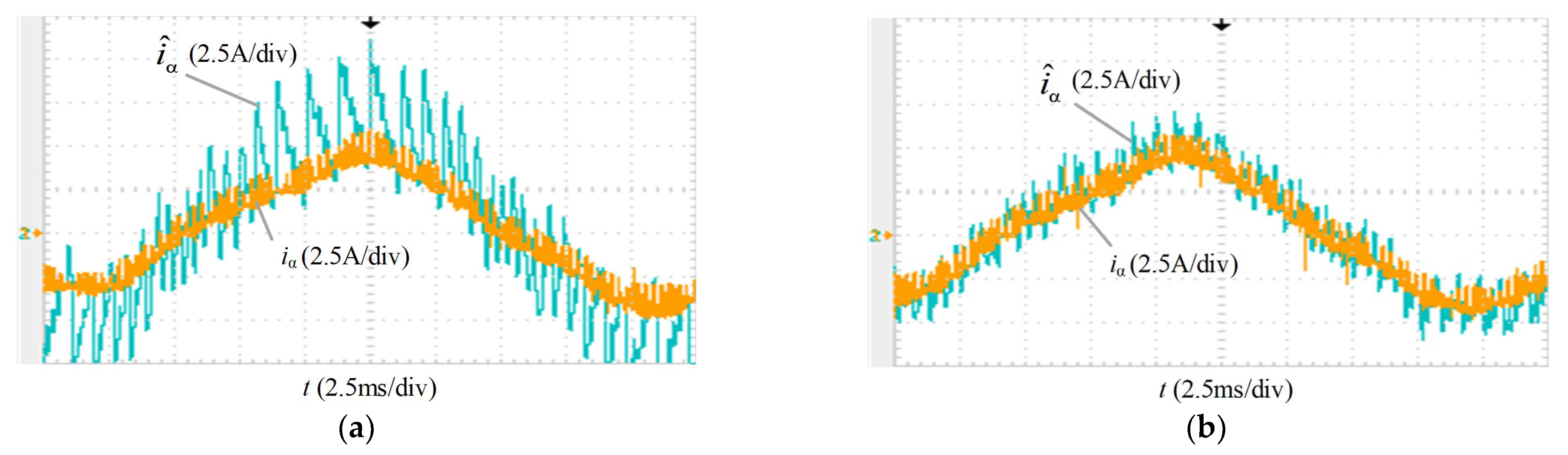
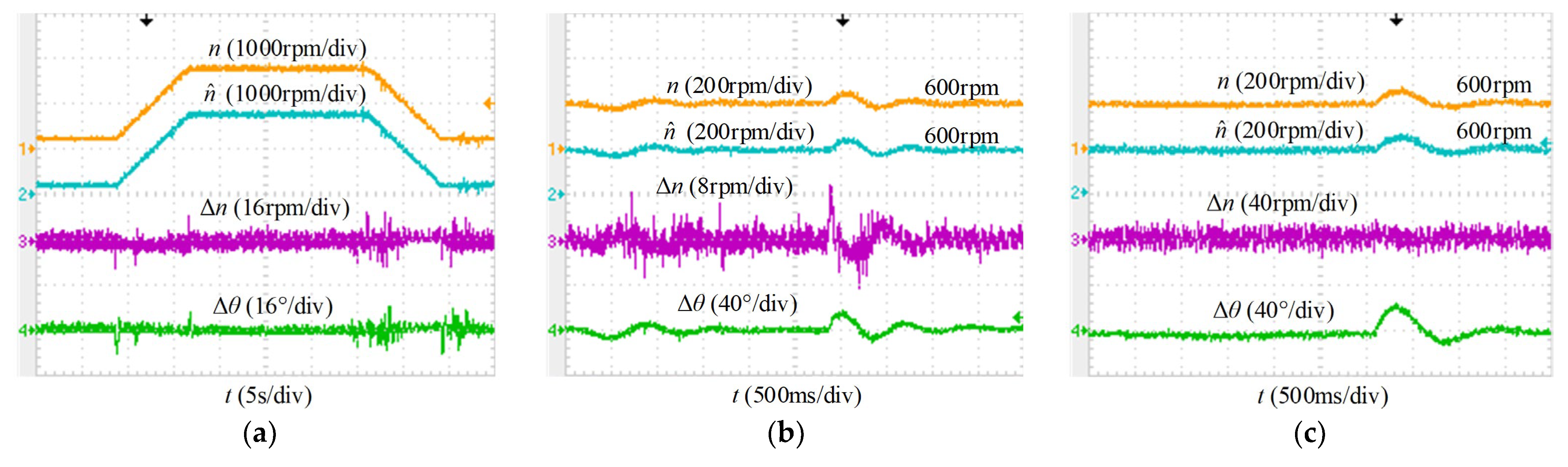
4. Experimental Results
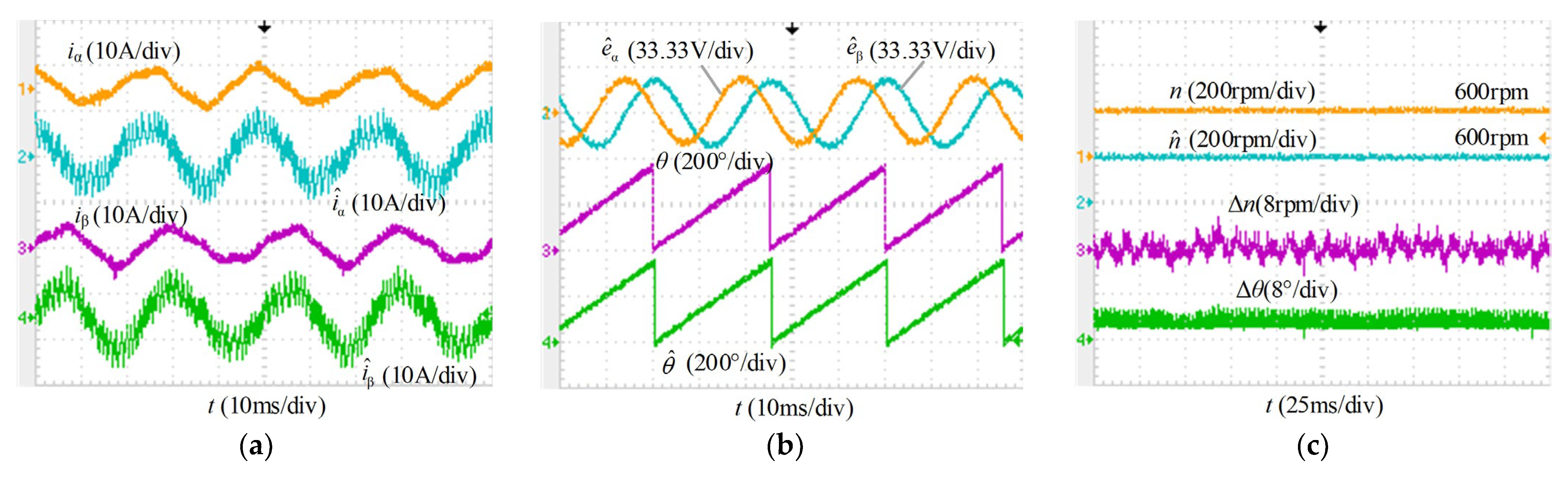
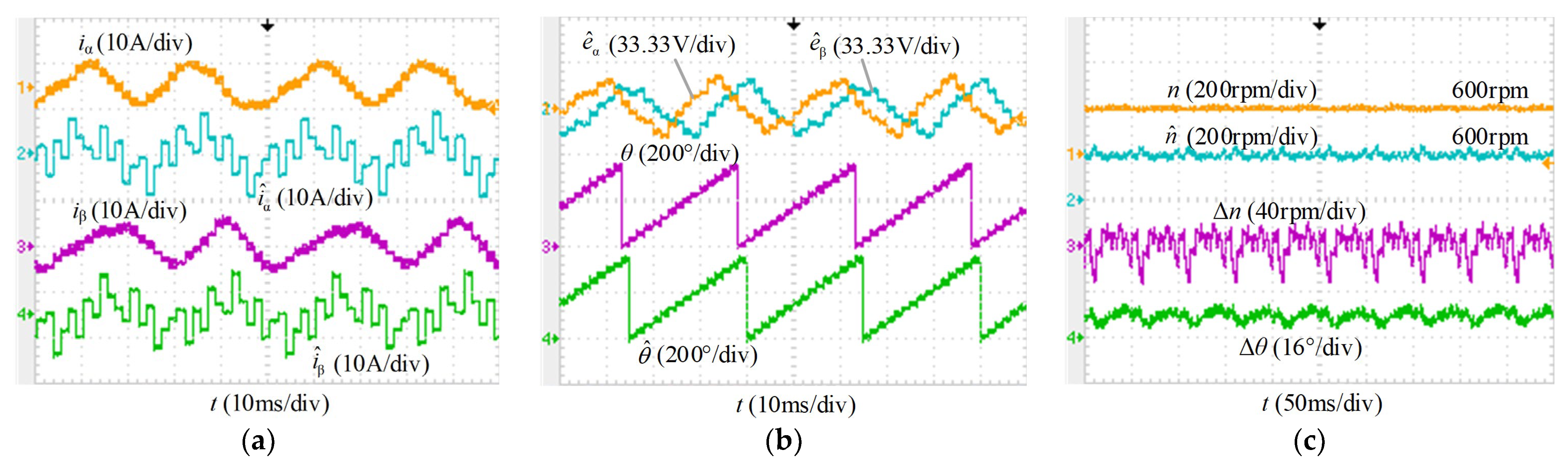
4.1. Steady-State Performance Comparison
4.2. Dynamic Performance of the Proposed VWC-SMO
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, G.; Valla, M.; Solsona, J. Position Sensorless Permanent Magnet Synchronous Machine Drives—A Review. IEEE Trans. Ind. Electron. 2020, 67, 5830–5842. [Google Scholar] [CrossRef]
- Stanica, D.M.; Bizon, N.; Arva, M.C. A brief review of sensorless AC motors control. In Proceedings of the 2021 13th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 1–3 July 2021; pp. 1–7. [Google Scholar]
- Lu, Q.; Wang, Y.; Mo, L.; Zhang, T. Pulsating High Frequency Voltage Injection Strategy for Sensorless Permanent Magnet Synchronous Motor Drives. IEEE Trans. Appl. Supercond. 2021, 31, 1–4. [Google Scholar] [CrossRef]
- Wang, G.; Kuang, J.; Zhao, N.; Zhang, G.; Xu, D. Rotor Position Estimation of PMSM in Low-Speed Region and Standstill Using Zero-Voltage Vector Injection. IEEE Trans. Power Electron. 2018, 33, 7948–7958. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Wang, H.; Xiao, D.; Li, L.; Xu, D. Pseudorandom-Frequency Sinusoidal Injection Based Sensorless IPMSM Drives with Tolerance for System Delays. IEEE Trans. Power Electron. 2019, 34, 3623–3632. [Google Scholar] [CrossRef]
- Kivanc, O.C.; Ozturk, S.B. Sensorless PMSM Drive Based on Stator Feedforward Voltage Estimation Improved with MRAS Multiparameter Estimation. IEEE/ASME Trans. Mechatron. 2018, 23, 1326–1337. [Google Scholar] [CrossRef]
- Ni, Y.; Shao, D. Research of Improved MRAS Based Sensorless Control of Permanent Magnet Synchronous Motor Considering Parameter Sensitivity. In Proceedings of the 2021 IEEE 4th Advanced Information Management, Communicates, Electronic and Automation Control Conference (IMCEC), Chongqing, China, 18–20 June 2021; pp. 633–638. [Google Scholar]
- Andersson, A.; Thiringer, T. Motion Sensorless IPMSM Control Using Linear Moving Horizon Estimation with Luenberger Observer State Feedback. IEEE Trans. Transp. Electrif. 2018, 4, 464–473. [Google Scholar] [CrossRef]
- Zhao, Y.; Qiao, W.; Wu, L. Dead-Time Effect Analysis and Compensation for a Sliding-Mode Position Observer-Based Sensorless IPMSM Control System. IEEE Trans. Ind. Appl. 2015, 51, 2528–2535. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, Y.; Zou, J. Sliding-Mode Sensorless Control of PMSM With Inverter Nonlinearity Compensation. IEEE Trans. Power Electron. 2019, 34, 10206–10220. [Google Scholar] [CrossRef]
- Wang, G.; Zhan, H.; Zhang, G.; Gui, X.; Xu, D. Adaptive Compensation Method of Position Estimation Harmonic Error for EMF-Based Observer in Sensorless IPMSM Drives. IEEE Trans. Power Electron. 2014, 29, 3055–3064. [Google Scholar] [CrossRef]
- Sun, S.; Cheng, H.; Wang, W.; Liu, H.; Mi, S.; Zhou, X. Sensorless DPCC of PMLSM Using SOGI-PLL Based High-Order SMO with Cogging Force Feedforward Compensation. In Proceedings of the 2021 13th International Symposium on Linear Drives for Industry Applications (LDIA), Wuhan, China, 1–3 July 2021; pp. 1–7. [Google Scholar]
- Wang, G.; Li, T.; Zhang, G.; Gui, X.; Xu, D. Position Estimation Error Reduction Using Recursive-Least-Square Adaptive Filter for Model-Based Sensorless Interior Permanent-Magnet Synchronous Motor Drives. IEEE Trans. Ind. Electron. 2014, 61, 5115–5125. [Google Scholar] [CrossRef]
- Wu, X.; Huang, S.; Liu, K.; Lu, K.; Hu, Y.; Pan, W.; Peng, X. Enhanced Position Sensorless Control Using Bilinear Recursive Least Squares Adaptive Filter for Interior Permanent Magnet Synchronous Motor. IEEE Trans. Power Electron. 2020, 35, 681–698. [Google Scholar] [CrossRef]
- Kashif, M.; Murshid, S.; Singh, B. Adaptive Hybrid Generalized Integrator Based SMO for Solar PV Array Fed Encoderless PMSM Driven Water Pump. IEEE Trans. Sustain. Energy 2021, 12, 1651–1661. [Google Scholar] [CrossRef]
- Jian, H.; Song, W. A sliding mode observer of IPMSM combining adaptive synchronous filter and back EMF estimator. In Proceedings of the 2020 7th International Forum on Electrical Engineering and Automation (IFEEA), Hefei, China, 25–27 September 2020; pp. 121–126. [Google Scholar]
- An, Q.; Zhang, J.; An, Q.; Liu, X.; Shamekov, A.; Bi, K. Frequency-Adaptive Complex-Coefficient Filter-Based Enhanced Sliding Mode Observer for Sensorless Control of Permanent Magnet Synchronous Motor Drives. IEEE Trans. Ind. Appl. 2020, 56, 335–343. [Google Scholar] [CrossRef]
- Chen, Z.; Zhang, H.; Zhang, Z. EEMF-based Sensorless control for IPMSM Drives with an Optimized Asymmetric Space Vector Modulation. In Proceedings of the 2019 22nd International Conference on Electrical Machines and Systems (ICEMS), Harbin, China, 11–14 August 2019; pp. 1–5. [Google Scholar]
- Yin, Z.; Zhang, Y.; Cao, X.; Yuan, D.; Liu, J. Estimated Position Error Suppression Using Novel PLL for IPMSM Sensorless Drives Based on Full-Order SMO. IEEE Trans. Power Electron. 2022, 37, 4463–4474. [Google Scholar] [CrossRef]
- Petro, V.; Kyslan, K. A Comparative Study of Different SMO Switching Functions for Sensorless PMSM Control. In Proceedings of the 2021 International Conference on Electrical Drives & Power Electronics (EDPE), Dubrovnik, Croatia, 22–24 September 2021; pp. 102–107. [Google Scholar]
- Liang, D.; Li, J.; Qu, R. Sensorless Control of Permanent Magnet Synchronous Machine Based on Second-Order Sliding-Mode Observer with Online Resistance Estimation. IEEE Trans. Ind. Appl. 2017, 53, 3672–3682. [Google Scholar] [CrossRef]
- Yang, C.; Ma, T.; Che, Z.; Zhou, L. An Adaptive-Gain Sliding Mode Observer for Sensorless Control of Permanent Magnet Linear Synchronous Motors. IEEE Access 2018, 6, 3469–3478. [Google Scholar] [CrossRef]
- Yu, B.; Shen, A.; Chen, B.; Luo, X.; Tang, Q.; Xu, J.; Zhu, M. A Compensation Strategy of Flux Linkage Observer in SPMSM Sensorless Drives Based on Linear Extended State Observer. IEEE Trans. Energy Convers. 2022, 37, 824–831. [Google Scholar] [CrossRef]
- Indriawati, K.; Widjiantoro, B.L.; Rachman, N.R.i. Disturbance Observer-Based Speed Estimator for Controlling Speed Sensorless Induction Motor. In Proceedings of the 2020 3rd International Seminar on Research of Information Technology and Intelligent Systems (ISRITI), Yogyakarta, Indonesia, 10 December 2020; pp. 301–305. [Google Scholar]
- Belkhier, Y.; Shaw, R.N.; Bures, M.; Islam, M.R.; Bajaj, M.; Albalawi, F.; Alqurashi, A.; Ghoneim, S.S. Robust interconnection and damping assignment energy-based control for a permanent magnet synchronous motor using high order sliding mode approach and nonlinear observer. Energy Rep. 2022, 8, 1731–1740. [Google Scholar] [CrossRef]
- Gopinath, G.; Das, S.P. An extended Kalman filter based sensorless permanent magnet synchronous motor drive with improved dynamic performance. In Proceedings of the 2018 IEEE International Conference on Power Electronics, Drives and Energy Systems (PEDES), Chennai, India, 18–21 December 2018; pp. 1–6. [Google Scholar]
- Tondpoor, K.; Saghaiannezhad, S.M.; Rashidi, A. Sensorless Control of PMSM Using Simplified Model Based on Extended Kalman Filter. In Proceedings of the 2020 11th Power Electronics, Drive Systems, and Technologies Conference (PEDSTC), Tehran, Iran, 4–6 February 2020; pp. 1–5. [Google Scholar]
- An, Q.; Zhang, J.; An, Q.; Shamekov, A. Quasi-Proportional-Resonant Controller Based Adaptive Position Observer for Sensorless Control of PMSM Drives Under Low Carrier Ratio. IEEE Trans. Ind. Electron. 2020, 67, 2564–2573. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, G.; Xu, D.; Yu, Y. Discrete-Time Low-Frequency-Ratio Synchronous-Frame Full-Order Observer for Position Sensorless IPMSM Drives. IEEE J. Emerg. Sel. Top. Power Electron. 2017, 5, 870–879. [Google Scholar] [CrossRef]


| Parameter | Symbol | Value |
|---|---|---|
| Rated power | PN (kW) | 3.0 |
| Rated current | IN (A) | 17.8 |
| Rated torque | TeN (N·m) | 14.3 |
| Rated speed | nN (r/min) | 2000 |
| Winding resistance | R (Ω) | 0.1 |
| d-axis inductance | Ld (mH) | 1.5 |
| q-axis inductance | Lq (mH) | 1.5 |
| PM flux linkage | ψf (Wb) | 0.11 |
| Number of pole pairs | np | 4 |
| Rotor inertia | J (kg·m2) | 0.00223 |
| DC link voltage | Udc (V) | 300 |
| Dead time | Td (μs) | 3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, F.; An, Q.; Zhang, J.; Zhao, M.; Li, S. Variable Weighting Coefficient of EMF-Based Enhanced Sliding Mode Observer for Sensorless PMSM Drives. Energies 2022, 15, 6001. https://doi.org/10.3390/en15166001
Cao F, An Q, Zhang J, Zhao M, Li S. Variable Weighting Coefficient of EMF-Based Enhanced Sliding Mode Observer for Sensorless PMSM Drives. Energies. 2022; 15(16):6001. https://doi.org/10.3390/en15166001
Chicago/Turabian StyleCao, Fuqiang, Quntao An, Jianqiu Zhang, Mengji Zhao, and Siwen Li. 2022. "Variable Weighting Coefficient of EMF-Based Enhanced Sliding Mode Observer for Sensorless PMSM Drives" Energies 15, no. 16: 6001. https://doi.org/10.3390/en15166001
APA StyleCao, F., An, Q., Zhang, J., Zhao, M., & Li, S. (2022). Variable Weighting Coefficient of EMF-Based Enhanced Sliding Mode Observer for Sensorless PMSM Drives. Energies, 15(16), 6001. https://doi.org/10.3390/en15166001







