Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump
Abstract
1. Introduction
- 1.
- This study extends the application of data-driven flow sensors to a new research area and optimizes the standard development process for data-driven flow sensors.
- 2.
- An additional data preprocessing step for developing data-driven flow sensors is proposed to deal with the skewed distribution of labeled data. Two different data transformation methods are considered for each of the three commonly-used supervised learning algorithms to analyze the impact of labeled data distribution on model accuracy.
- 3.
- The effect of data size is systematically investigated to design real-world data generation experiments effectively. In the current study, three different data sizes were considered. Three commonly-used supervised learning algorithms for data-driven flow sensor development are investigated for each dataset.
2. Materials and Methods
2.1. Experimental Data Generation
2.1.1. Feature Selection
2.1.2. Data Generating Using Latin Hypercube Sampling
2.2. Data Preprocessing
2.2.1. Fearture Normalization
2.2.2. Label Scaling
2.3. Regression Model Design
2.3.1. Neural Network
2.3.2. Support Vector Regression
2.3.3. Gaussian Regression
2.4. Performance Indicator
2.5. Experiment Setup
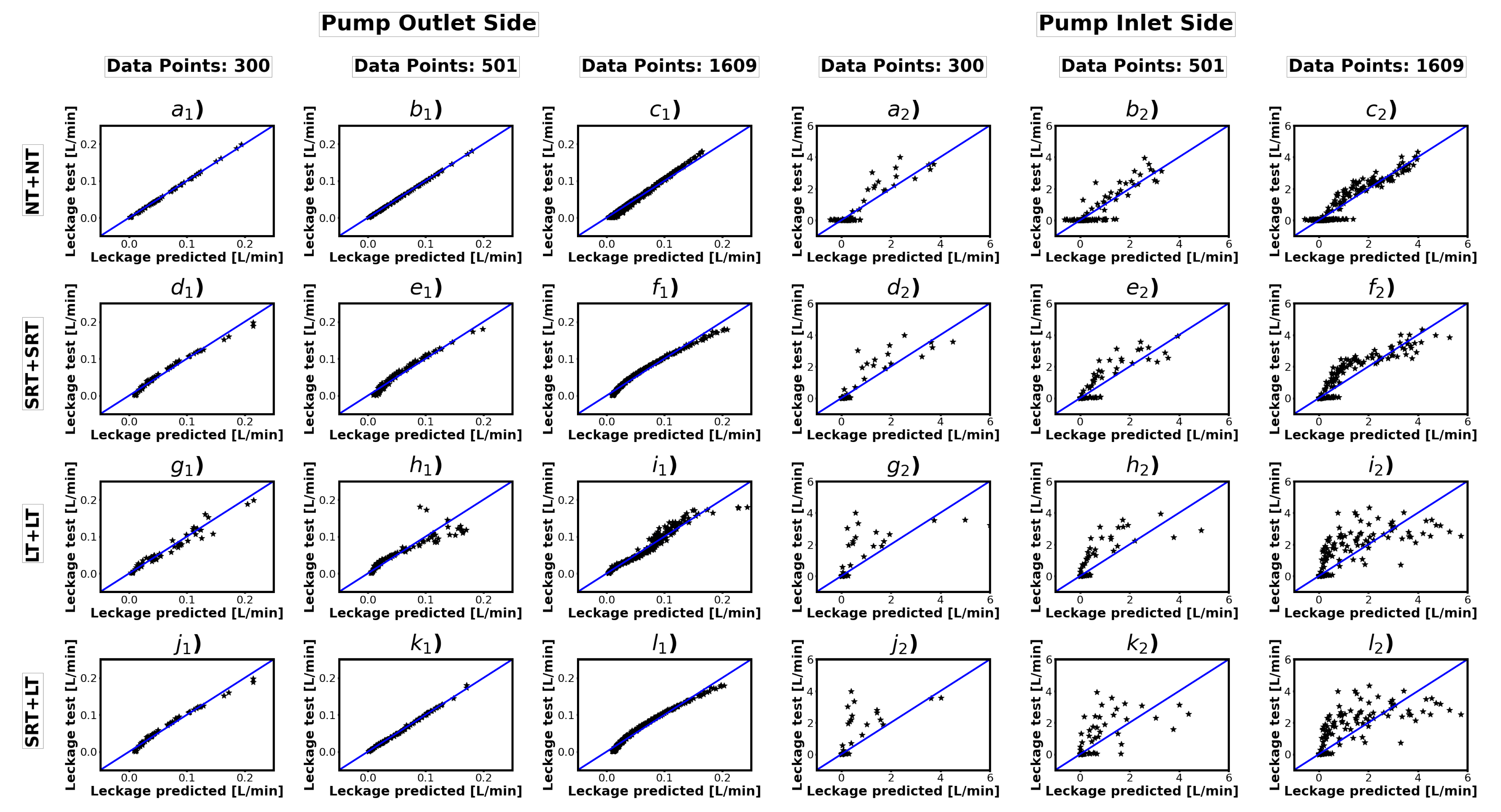
3. Results
4. Discussion
- 1.
- Does the data-driven flow rate sensor model in the current research achieve the equivalent or better performance than the earlier study about the data-driven flow rate sensor?
- 2.
- How does the label distribution affect the performance of the data-driven flow rate sensor?
- 3.
- How does the data amount influence the performance of the data-driven flow rate sensor?
- 1.
- It extends the application area of data-driven flow sensors and is an optimized guideline for developing virtual sensors in methodology.
- 2.
- The impact of data size on the accuracy of developing data-driven flow sensors is systematically investigated. Three different data groups guarantee the model’s accuracy when labeled data are not transformed. Therefore small data can meet the model’s needs when predicting flow rate with a data-driven approach. The application areas of data-driven flow sensors are diverse, and AI models’ performance and data requirements vary significantly from application to application. Consequently, this research cannot provide general guidance for different applications, but the implications of the results of this study play a significant role in guiding us on how to design real-world data generation experiments effectively. In industrial applications, where lack of data volume or expensive data acquisition process is common, it is essential to analyze the problem with simulated data for scenarios before real-world data collection.
- 3.
- We propose an additional data preprocessing step for developing data-driven flow sensors to handle the skewed distribution of labeled data. The results suggest that, especially when using SVR or GP as a training model, the distribution of the labeled data should be analyzed and processed before training the model to obtain better performance.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Geimer, M. Mobile Working Machines; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Gärtner, M. Verlustanalyse am Kolben-Buchse-Kontakt von Axialkolbenpumpen in Schrägscheibenbauweise. Ph.D. Thesis, RWTH Aachen University, Düren, Germany, 2020. [Google Scholar]
- Mohn, G.; Nafz, T. Swash Plate Pumps—The Key to the Future. In Proceedings of the 10th International Fluid Power Conference (10. IFK), Dresden, Germany, 8–10 March 2016; Technical University Dresden: Dresden, Germany, 2016; pp. 139–149. [Google Scholar]
- Xu, B.; Hu, M.; Zhang, J.H.; Mao, Z.B. Distribution Characteristics and Impact on Pump’s Efficiency of Hydro-mechanical Losses of Axial Piston Pump over Wide Operating Ranges. J. Cent. South Univ. 2017, 24, 609–624. [Google Scholar] [CrossRef]
- Haug, S.; Geimer, M. Optimization of Axial Piston Units Based on Demand-driven Relief of Tribological Contacts. In Proceedings of the 10th International Fluid Power Conference (10. IFK), Dresden, Germany, 8–10 March 2016; Technical University Dresden: Dresden, Germany, 2016; pp. 295–306. [Google Scholar]
- Geffroy, S.; Bauer, N.; Mielke, T.; Wegner, S.; Gels, S.; Murrenhoff, H.; Schmitz, K. Optimization of the Tribological Contact of Valve Plate and Cylinder Block within Axial Piston Machines. In Proceedings of the 12th International Fluid Power Conference (12. IFK), Dresden, Germany, 9–11 March 2020; Technical University Dresden: Dresden, Germany, 2020; pp. 389–398. [Google Scholar]
- Geffroy, S.; Wegner, S.; Gels, S.; Schmitz, K. Experimental Investigation of New Design Concepts for the Tribological Contact between the Valve Plate and the Cylinder Block in Axial Piston Machines. In Proceedings of the 17th Scandinavian International Conference on Fluid Power, Linkoping, Sweden, 1–2 June 2021; pp. 104–116. [Google Scholar] [CrossRef]
- Liu, M.; Geimer, M. Estimation and Evaluation of Energy Optimization Potential with Machine Learning Method for Active Hydrostatic Lubrication Control at Cradle Bearing in Axial Piston Pump. In Proceedings of the 13th International Fluid Power Conference (IFK), Aachen, Germany, 13–15 June 2022; RWTH Aachen University: Aachen, Germany, 2022; pp. 539–550. [Google Scholar]
- Manring, N.D. The Discharge Flow Ripple of an Axial-Piston Swash-Plate Type Hydrostatic Pump. J. Dyn. Syst. Meas. Control. 1998, 122, 263–268. [Google Scholar] [CrossRef]
- Ivantysynova, M.; Huang, C. Investigation of the flow in displacement machines considering elastohydrodynamic effect. In Proceedings of the the Fifth JFPS International Symposium on Fluid Power, Nara, Japan, 12–15 November 2002; Volume 1, pp. 219–229. [Google Scholar]
- Li, F.; Wang, D.; Lv, Q.; Haidak, G.; Zheng, S. Prediction on the lubrication and leakage performance of the piston–cylinder interface for axial piston pumps. Proc. Inst. Mech. Eng. Part C J. Mech. Eng. Sci. 2019, 233, 5887–5896. [Google Scholar] [CrossRef]
- Bergada, J.; Kumar, S.; Davies, D.; Watton, J. A complete analysis of axial piston pump leakage and output flow ripples. Appl. Math. Model. 2012, 36, 1731–1751. [Google Scholar] [CrossRef]
- Özmen, Ö.; Sinanoğlu, C.; Caliskan, A.; Badem, H. Prediction of leakage from an axial piston pump slipper with circular dimples using deep neural networks. Chin. J. Mech. Eng. 2020, 33, 28. [Google Scholar] [CrossRef]
- Bikmukhametov, T.; Jäschke, J. First Principles and Machine Learning Virtual Flow Metering: A Literature Review. J. Pet. Sci. Eng. 2020, 184, 106487. [Google Scholar] [CrossRef]
- Al-Qutami, T.A.; Ibrahim, R.; Ismail, I.; Ishak, M.A. Development of Soft Sensor to Estimate Multiphase Flow Rates Using Neural Networks and Early Stopping. Int. J. Smart Sens. Intell. Syst. 2017, 10, 199–222. [Google Scholar] [CrossRef]
- Al-Qutami, T.A.; Ibrahim, R.; Ismail, I. Hybrid Neural Network and Regression Tree Ensemble Pruned by Simulated Annealing for Virtual Flow Metering Application. In Proceedings of the 2017 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuching, Malaysia, 12–14 September 2017; pp. 304–309. [Google Scholar] [CrossRef]
- Shoeibi Omrani, P.; Dobrovolschi, I.; Belfroid, S.; Kronberger, P.; Munoz, E. Improving the Accuracy of Virtual Flow Metering and Back-Allocation through Machine Learning. In Proceedings of the Abu Dhabi International Petroleum Exhibition and Conference, Abu Dhabi, United Arab Emirates, 12–15 November 2018. [Google Scholar] [CrossRef]
- Fortuna, L.; Graziani, S.; Rizzo, A.; Xibilia, M.G. Soft Sensors for Monitoring and Control of Industrial Processes; Springer: London, UK, 2007; Volume 22. [Google Scholar]
- Ahmadi, M.A.; Ebadi, M.; Shokrollahi, A.; Majidi, S.M.J. Evolving Artificial Neural Network and Imperialist Competitive Algorithm for Prediction Oil Flow Rate of the Reservoir. Appl. Soft Comput. 2013, 13, 1085–1098. [Google Scholar] [CrossRef]
- Patil, P.; Sharma, S.C.; Paliwal, V.; Kumar, A. ANN Modelling of Cu Type Pmega Vibration Based Mass Flow Sensor. Procedia Technol. 2014, 14, 260–265. [Google Scholar] [CrossRef][Green Version]
- Patil, P.P.; Sharma, S.C.; Jain, S. Prediction Modeling of Coriolis Type Mass Flow: Sensor Using Neural Network. Instruments Exp. Tech. 2011, 54, 435–439. [Google Scholar] [CrossRef]
- Ghanbarzadeh, S.; Hanafizadeh, P.; Saidi, M.H.; Boozarjomehry, R.B. Intelligent Regime Recognition in Upward Vertical Gas-Liquid Two Phase Flow Using Neural Network Techniques. In Proceedings of the ASME 2010 3rd Joint US-European Fluids Engineering Summer Meeting: Volume 2, Fora, Fluids Engineering Division Summer Meeting, Montreal, QC, Canada, 1–5 August 2010; pp. 293–302. [Google Scholar] [CrossRef]
- AL-Qutami, T.A.; Ibrahim, R.; Ismail, I.; Ishak, M.A. Radial Basis Function Network to Predict Gas Flow Rate in Multiphase Flow. In Proceedings of the the 9th International Conference on Machine Learning and Computing, Singapore, 24–26 February 2017; Association for Computing Machinery: New York, NY, USA, 2017; pp. 141–146. [Google Scholar] [CrossRef]
- Loh, K.; Omrani, P.S.; van der Linden, R. Deep Learning and Data Assimilation for Real-Time Production Prediction in Natural Gas Wells. arXiv 2018, arXiv:1802.05141. [Google Scholar]
- Andrianov, N. A Machine Learning Approach for Virtual Flow Metering and Forecasting. IFAC-PapersOnLine 2018, 51, 191–196. [Google Scholar] [CrossRef]
- AL-Qutami, T.A.; Ibrahim, R.; Ismail, I.; Ishak, M.A. Virtual Multiphase Flow Metering Using Diverse Neural Network Ensemble and Adaptive Simulated Annealing. Exp. Syst. Appl. 2018, 93, 72–85. [Google Scholar] [CrossRef]
- Zheng, G.B.; Jin, N.D.; Jia, X.H.; Lv, P.J.; Liu, X.B. Gas–Liquid Two Phase Flow Measurement Method Based on Combination Instrument of Turbine Flowmeter and Conductance Sensor. Int. J. Multiph. Flow 2008, 34, 1031–1047. [Google Scholar] [CrossRef]
- Wang, L.; Liu, J.; Yan, Y.; Wang, X.; Wang, T. Gas-Liquid Two-Phase Flow Measurement Using Coriolis Flowmeters Incorporating Artificial Neural Network, Support Vector Machine, and Genetic Programming Algorithms. IEEE Trans. Instrum. Meas. 2017, 66, 852–868. [Google Scholar] [CrossRef]
- Chati, Y.S.; Balakrishnan, H. A Gaussian Process Regression Approach to Model Aircraft Engine Fuel Flow Rate. In Proceedings of the 2017 ACM/IEEE 8th International Conference on Cyber-Physical Systems (ICCPS), Pittsburgh, PA, USA, 18–21 April 2017; pp. 131–140. [Google Scholar]
- Ivantysyn, J.; Ivantysynova, M. Hydrostatic Pumps and Motors: Principles, Design, Performance, Modelling, Analysis, Control and Testing, 1st ed.; Akad. Books Internat: New Delhi, India, 2001. [Google Scholar]
- Saad, Z.; Osman, M.K.; Omar, S.; Mashor, M. Modeling and Forecasting of Injected Fuel Flow Using Neural Network. In Proceedings of the 2011 IEEE 7th International Colloquium on Signal Processing and its Applications, Penang, Malaysia, 4–6 March 2011; pp. 243–247. [Google Scholar] [CrossRef]
- Mckay, M.D.; Beckman, R.J.; Conover, W.J. A Comparison of Three Methods for Selecting Values of Input Variables in the Analysis of Output From a Computer Code. Technometrics 2000, 42, 55–61. [Google Scholar] [CrossRef]
- Iman, R.L. Latin Hypercube Sampling. In Encyclopedia of Quantitative Risk Analysis and Assessment; Melnick, E.L., Everitt, B.S., Eds.; John Wiley & Sons, Ltd.: Chichester, UK, 2008. [Google Scholar] [CrossRef]
- Li, X. Numerical Methods for Engineering Design and Optimization; Lecture Notes; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar]
- Kotsiantis, S.B.; Kanellopoulos, D.; Pintelas, P.E. Data preprocessing for supervised leaning. Int. J. Comput. Sci. 2006, 1, 111–117. [Google Scholar]
- Brase, C.H.; Brase, C.P. Understanding Basic Statistics, 4th ed.; Houghton Mifflin: Boston, MA, USA, 2007. [Google Scholar]
- Pedregosa, F.; Varoquaux, G.; Gramfort, A.; Michel, V.; Thirion, B.; Grisel, O.; Blondel, M.; Prettenhofer, P.; Weiss, R.; Dubourg, V.; et al. Scikit-learn: Machine Learning in Python. J. Mach. Learn. Res. 2011, 12, 2825–2830. [Google Scholar]
- Hecht-Nielsen, R. Kolmogorov’s Mapping Neural Network Existence Theorem. In Proceedings of the the International Conference on Neural Networks, San Diego, CA, USA, 21–24 June 1987; IEEE Press: New York, NY, USA, 1987; Volume 3, pp. 11–14. [Google Scholar]
- Ismailov, V. A three layer neural network can represent any multivariate function. arXiv 2020, arXiv:2012.03016. [Google Scholar]
- Cherkassky, V.; Mulier, F. Learning from Data: Concepts, Theory, and Methods; IEEE Press: Piscataway, NJ, USA; Wiley: Hoboken, NJ, USA, 2007. [Google Scholar]
- Hearst, M.; Dumais, S.; Osuna, E.; Platt, J.; Scholkopf, B. Support vector machines. IEEE Intell. Syst. Their Appl. 1998, 13, 18–28. [Google Scholar] [CrossRef]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support-vector networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Schölkopf, B. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2002. [Google Scholar] [CrossRef]
- Rasmussen, C.E.; Williams, C.K.I. Gaussian Processes for Machine Learning, 3rd ed.; Adaptive Computation and Machine Learning; MIT Press: Cambridge, MA, USA, 2008. [Google Scholar]
- Lewis-Beck, C.; Lewis-Beck, M.S. Applied Regression: An Introduction, 2nd ed.; Sage University Papers, Quantitative Applications in the Social Sciences; Sage: Thousand Oaks, CA, USA; London, UK; New Delhi, India, 2016; Volume 22. [Google Scholar]
- Berneti, S.M.; Shahbazian, M. An imperialist competitive algorithm artificial neural network method to predict oil flow rate of the wells. Int. J. Comput. Appl. 2011, 26, 47–50. [Google Scholar]
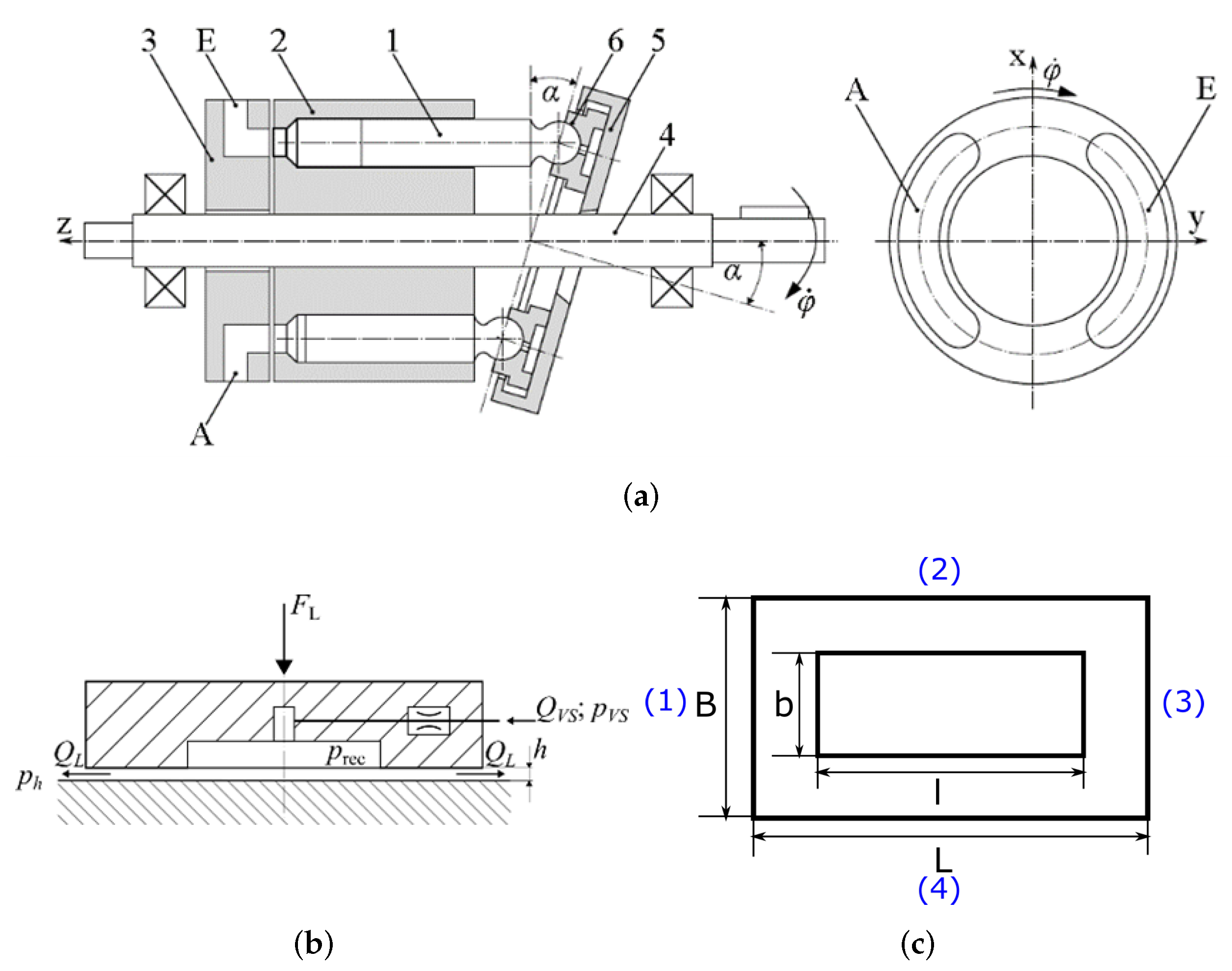
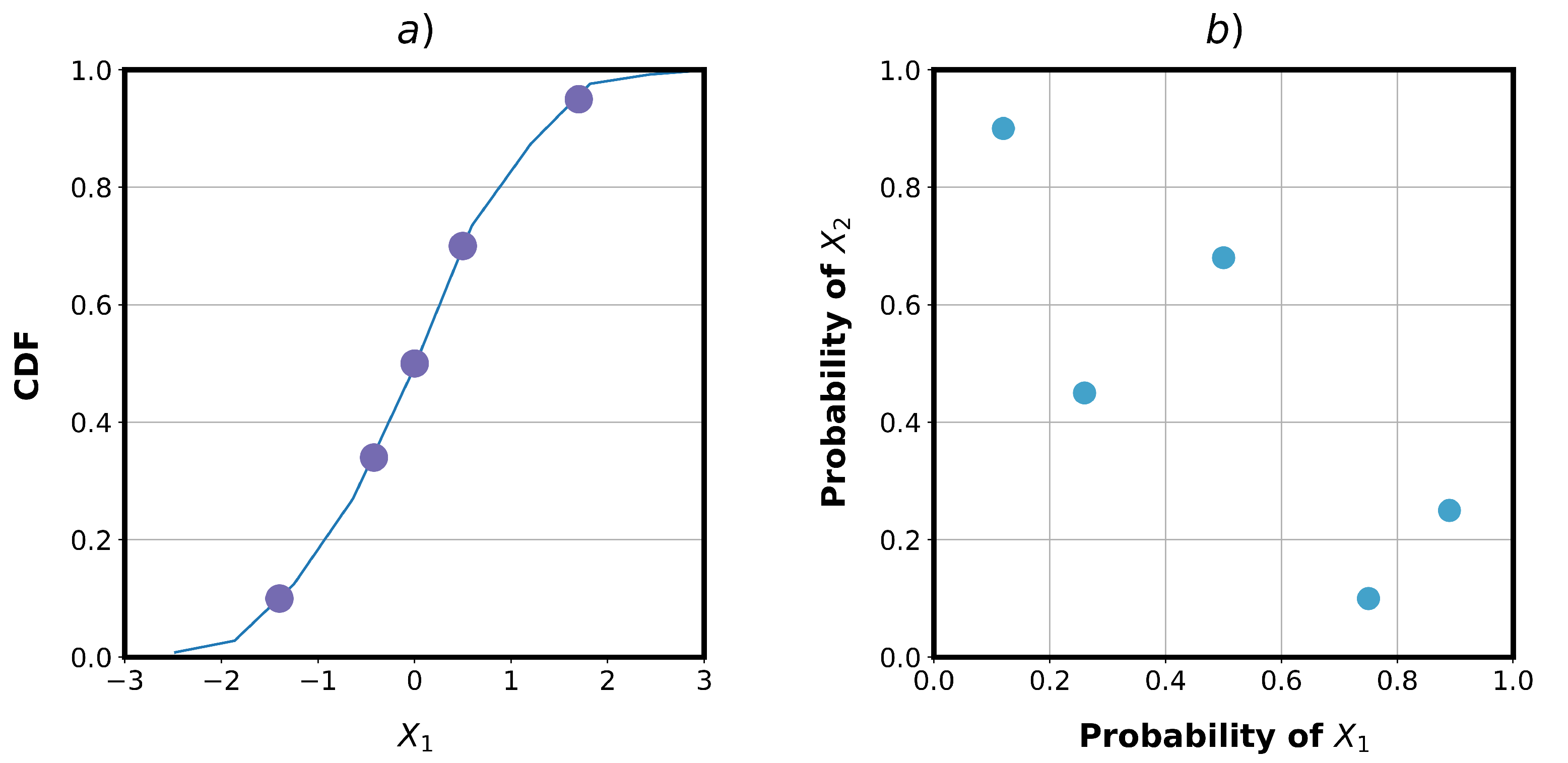
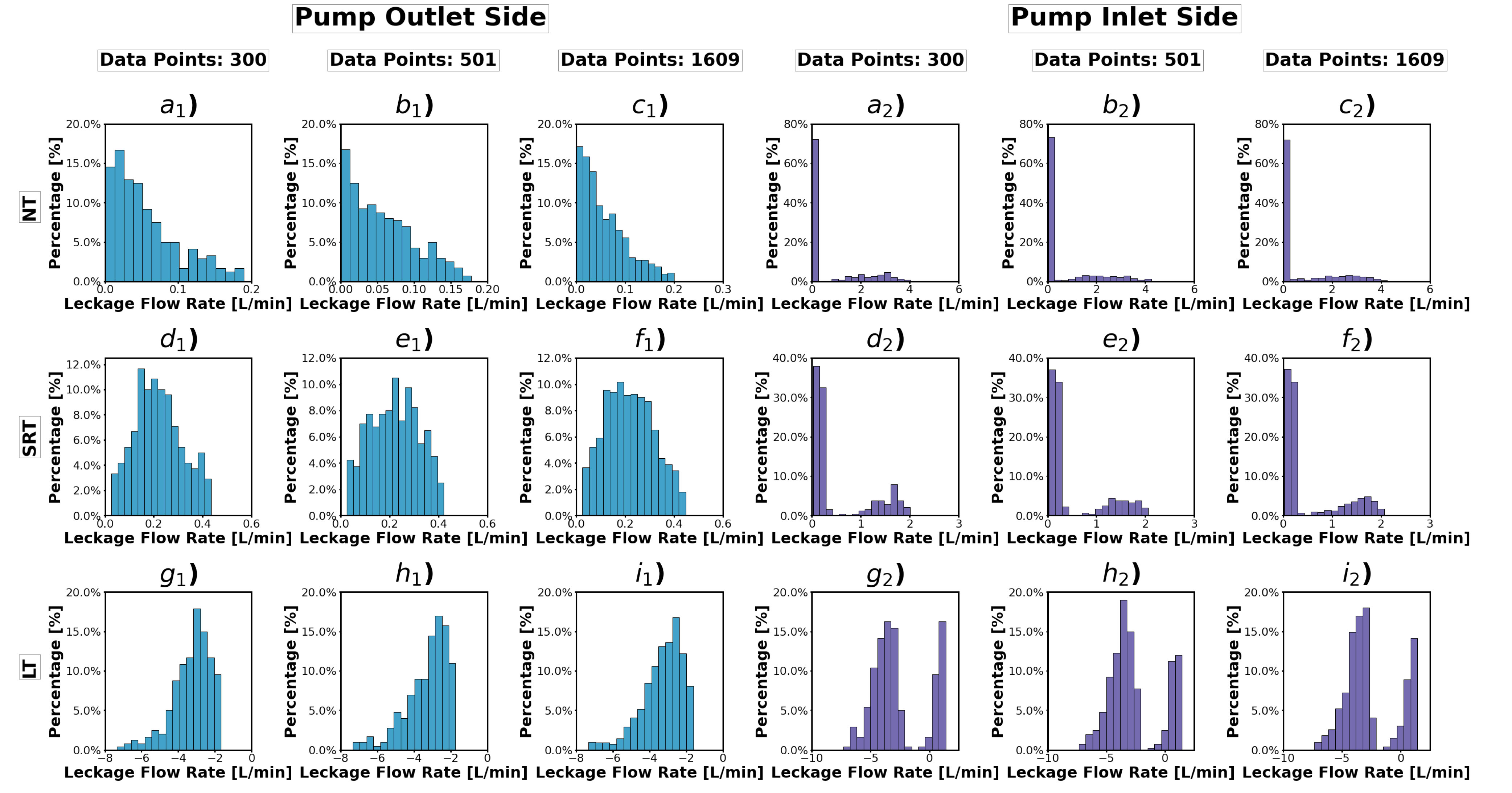

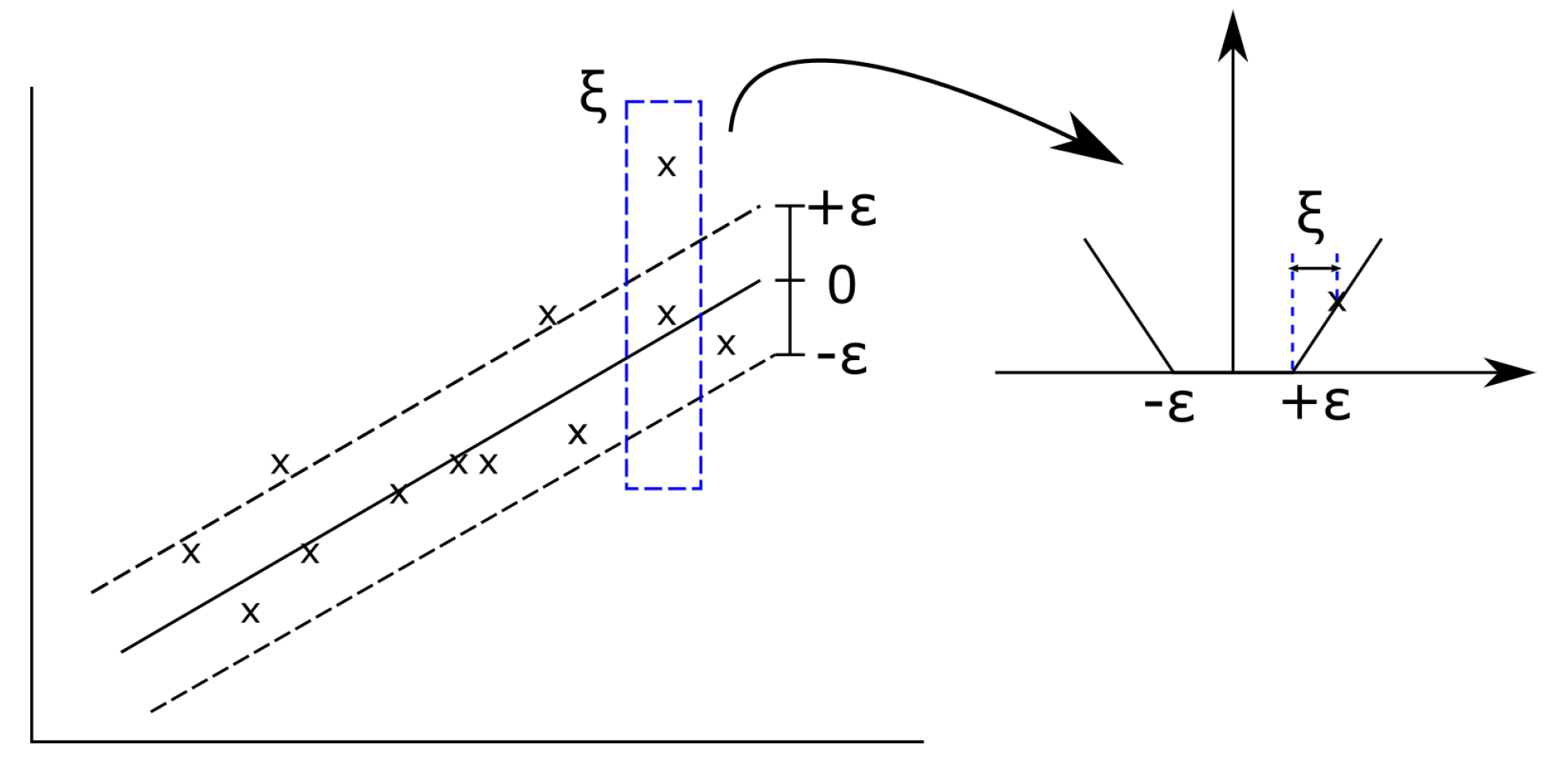


| Pressure at Pump Outlet [bar] | Pressure at Pump Inlet [bar] | Pump Speed [rpm] | Swashplate Postion [%] | Recess Pressure at the Inlet Side in Percent of Outlet Pressure [%] | Recess Pressure at the Outlet Side in Percent of Outlet Pressure [%] |
|---|---|---|---|---|---|
| (10, 315) | (0.8, 60) | (1000, 3000) | (0, 100) | (0, 100) | (0, 80) |
| Experiment Index | Label Scaling | Regression Model | Searched Hyperparameter and Range |
|---|---|---|---|
| 1 | NT + NT | NN | solver: (lbfgs, adam) : (8, 16, 32, 64) : (0.1, 0.01, 0.001, 0.0001) : (0.001, 0.01, 0.05, 0.1) : ((32, 32), (32, 16), (64, 32), 24, 35, 64) |
| 2 | SRT + SRT | NN | solver: (lbfgs, adam) : (8, 16, 32, 64) : (0.1, 0.01, 0.001, 0.0001) : (0.001, 0.01, 0.05, 0.1) : ((32, 32), (32, 16), (64, 32), 24, 35, 64) |
| 3 | LT + LT | NN | solver: (lbfgs, adam) : (8, 16, 32, 64) : (0.1, 0.01, 0.001, 0.0001) : (0.001, 0.01, 0.05, 0.1) : ((32, 32), (32, 16), (64, 32), 24, 35, 64) |
| 4 | SRT + LT | NN | solver: (lbfgs, adam) : (8, 16, 32, 64) : (0.1, 0.01, 0.001, 0.0001) : (0.001, 0.01, 0.05, 0.1) : ((32, 32), (32, 16), (64, 32), 24, 35, 64) |
| 5 | NT + NT | SVR | : (rbf, linear, poly, sigmoid) C: (16, 14, 12, 10, 5, 1, 0.5, 0.1) : (scale, auto) : (0.00001, 0.0001 0.001, 0.01, 0.1, 1) : (2, 3, 5) |
| 6 | SRT + SRT | SVR | : (rbf, linear, poly, sigmoid) C: (16, 14, 12, 10, 5, 1, 0.5, 0.1) : (scale, auto) : (0.00001, 0.0001, 0.001, 0.01, 0.1, 1) : (2, 3, 5) |
| 7 | LT + LT | SVR | : : (rbf, linear, poly, sigmoid) C: (16, 14, 12, 10, 5, 1, 0.5, 0.1) : (scale, auto) : (0.00001, 0.0001, 0.001, 0.01, 0.1, 1) : (2, 3, 5) |
| 8 | SRT + LT | SVR | : (rbf, linear, poly, sigmoid) C: (16, 14, 12, 10, 5, 1, 0.5, 0.1) : (scale, auto) : (0.00001, 0.0001 0.001, 0.01, 0.1, 1) : (2, 3, 5) |
| 9 | NT + NT | GR | : (rbf, 0.1rfb + constant) : (1, 0.5, 0.1, 0.05, 0.01, 0.001, 0.0001, 0.00001, 1 × 10) n: 5, 8, 10, 12, 15, 18, 20) |
| 10 | SRT + SRT | GR | : (rbf, 0.1rfb + constant) : (1, 0.5, 0.1, 0.05, 0.01, 0.001, 0.0001, 0.00001, 1 × 10) n: 5, 8, 10, 12, 15, 18, 20 |
| 11 | LT + LT | GR | : (rbf, 0.1rfb + constant) : (1, 0.5, 0.1, 0.05, 0.01, 0.001, 0.0001, 0.00001, 1 × 10) n: 5, 8, 10, 12, 15, 18, 20 |
| 12 | SRT + LT | GR | : (rbf, 0.1rfb + constant) : (1, 0.5, 0.1, 0.05, 0.01, 0.001, 0.0001, 0.00001, 1 × 10) n: 5, 8, 10, 12, 15, 18, 20) |
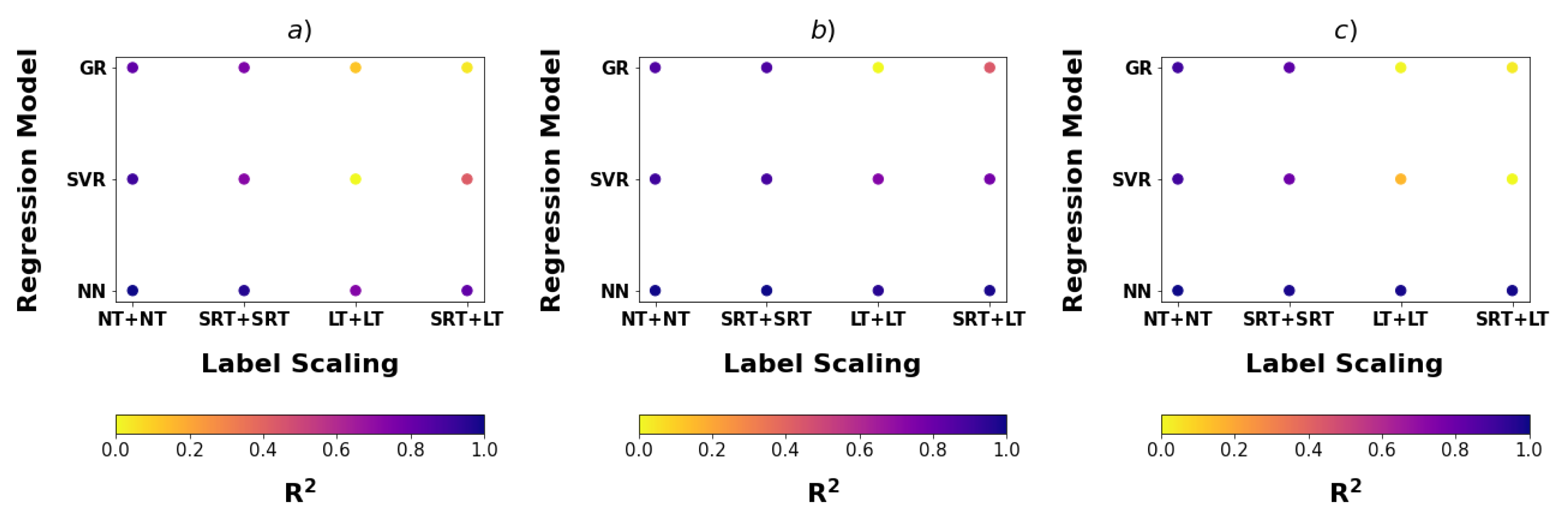
| Experiment Index | Data Points | Label Scaling | Regression Model | Training Score | Test Score |
|---|---|---|---|---|---|
| 1 | 300 | NT + NT | NN | 0.95 | 0.97 |
| 2 | 300 | SRT + SRT | NN | 0.94 | 0.96 |
| 3 | 300 | LT + LT | NN | 0.94 | 0.88 |
| 4 | 300 | SRT + LT | NN | 0.95 | 0.91 |
| 5 | 300 | NT + NT | SVR | 0.87 | 0.94 |
| 6 | 300 | SRT + SRT | SVR | 0.87 | 0.88 |
| 7 | 300 | LT + LT | SVR | 0.85 | 0.63 |
| 8 | 300 | SRT + LT | SVR | 0.89 | 0.77 |
| 9 | 300 | NT + NT | GP | 0.86 | 0.91 |
| 10 | 300 | SRT + SRT | GP | 0.86 | 0.88 |
| 11 | 300 | LT + LT | GR | 0.84 | 0.68 |
| 12 | 300 | SRT + LT | GP | 0.85 | 0.65 |
| 13 | 501 | NT + NT | NN | 0.96 | 0.95 |
| 14 | 501 | SRT + SRT | NN | 0.96 | 0.95 |
| 15 | 501 | LT + LT | NN | 0.96 | 0.93 |
| 16 | 501 | SRT + LT | NN | 0.97 | 0.94 |
| 17 | 501 | NT + NT | SVR | 0.90 | 0.90 |
| 18 | 501 | SRT + SRT | SVR | 0.89 | 0.89 |
| 19 | 501 | LT + LT | SVR | 0.87 | 0.81 |
| 20 | 501 | SRT + LT | SVR | 0.90 | 0.83 |
| 21 | 501 | NT + NT | GP | 0.86 | 0.88 |
| 22 | 501 | SRT + SRT | GP | 0.87 | 0.88 |
| 23 | 501 | LT + LT | GR | 0.87 | 0.41 |
| 24 | 501 | SRT + LT | GP | 0.89 | 0.65 |
| 25 | 1609 | NT + NT | NN | 0.99 | 0.99 |
| 26 | 1609 | SRT + SRT | NN | 0.98 | 0.98 |
| 27 | 1609 | LT + LT | NN | 0.99 | 0.99 |
| 28 | 1609 | SRT + LT | NN | 0.98 | 0.99 |
| 29 | 1609 | NT + NT | SVR | 0.94 | 0.95 |
| 30 | 1609 | SRT + SRT | SVR | 0.92 | 0.90 |
| 31 | 1609 | LT + LT | SVR | 0.90 | 0.61 |
| 32 | 1609 | SRT + LT | SVR | 0.93 | 0.54 |
| 33 | 1609 | NT + NT | GP | 0.93 | 0.95 |
| 34 | 1609 | SRT + SRT | GP | 0.91 | 0.92 |
| 35 | 1609 | LT + LT | GR | 0.89 | 0.54 |
| 36 | 1609 | SRT + LT | GP | 0.89 | 0.55 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, M.; Kim, G.; Bauckhage, K.; Geimer, M. Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump. Energies 2022, 15, 6115. https://doi.org/10.3390/en15176115
Liu M, Kim G, Bauckhage K, Geimer M. Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump. Energies. 2022; 15(17):6115. https://doi.org/10.3390/en15176115
Chicago/Turabian StyleLiu, Minxing, Garyeong Kim, Kai Bauckhage, and Marcus Geimer. 2022. "Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump" Energies 15, no. 17: 6115. https://doi.org/10.3390/en15176115
APA StyleLiu, M., Kim, G., Bauckhage, K., & Geimer, M. (2022). Data-Driven Virtual Flow Rate Sensor Development for Leakage Monitoring at the Cradle Bearing in an Axial Piston Pump. Energies, 15(17), 6115. https://doi.org/10.3390/en15176115







