A Hybrid Adaptive Controller Applied for Oscillating System
Abstract
:1. Introduction
2. Hybrid Speed Controller Applied for the Two-Mass System
2.1. General Overview and Mathematical Description of the Control Structure
| (1) | |
| (2) | |
| (3) |
| (5) | |
| (6) | |
| (7) |
| (14) | |
| (15) | |
| (16) | |
| (17) |
| (20) | |
| (21) | |
| (22) |
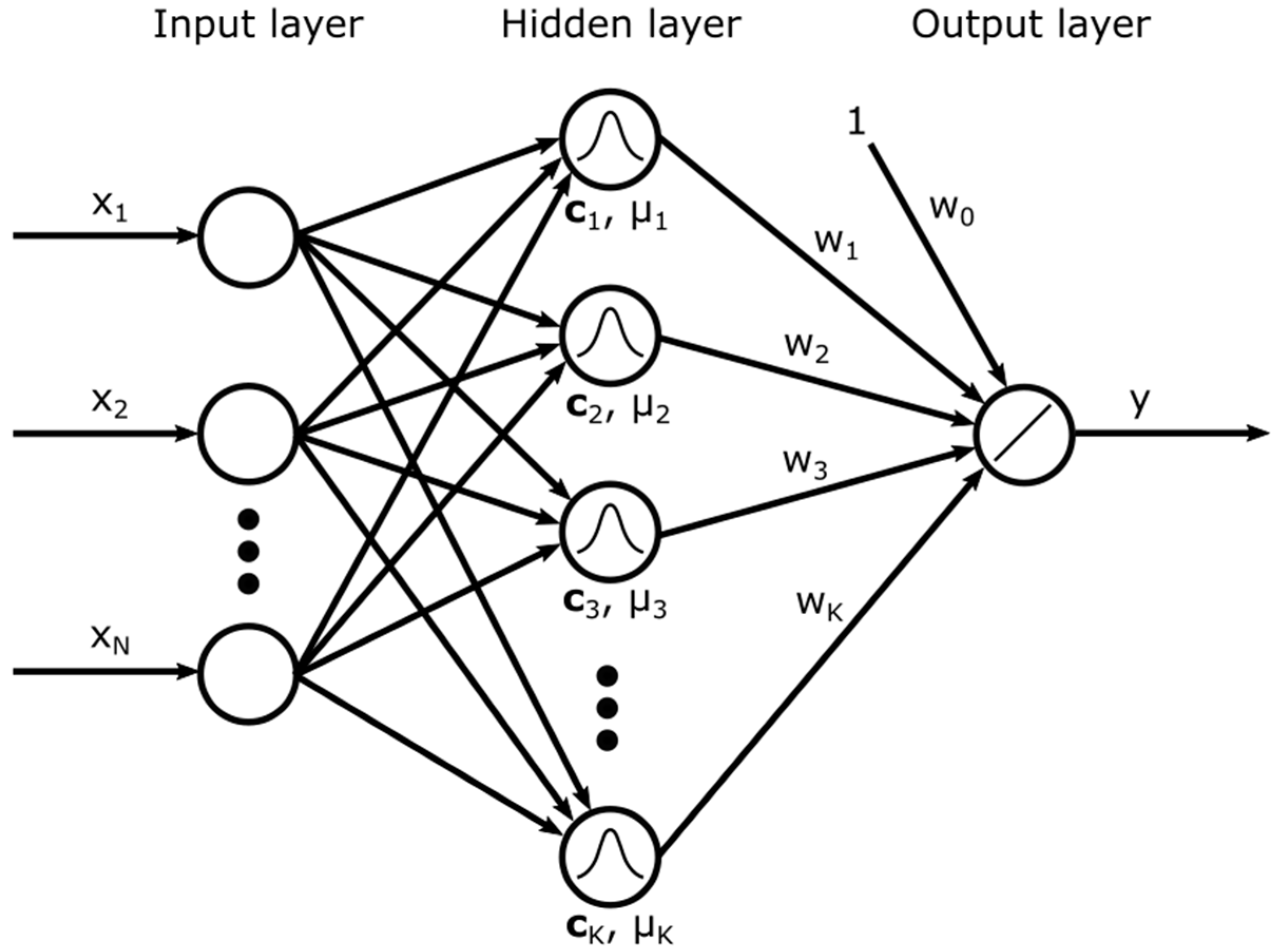
2.2. Radial Basis Function Neural Networks
2.3. Stability Analysis
3. Tests of the Hybrid Controller Applied to the Drive with an Elastic Coupling
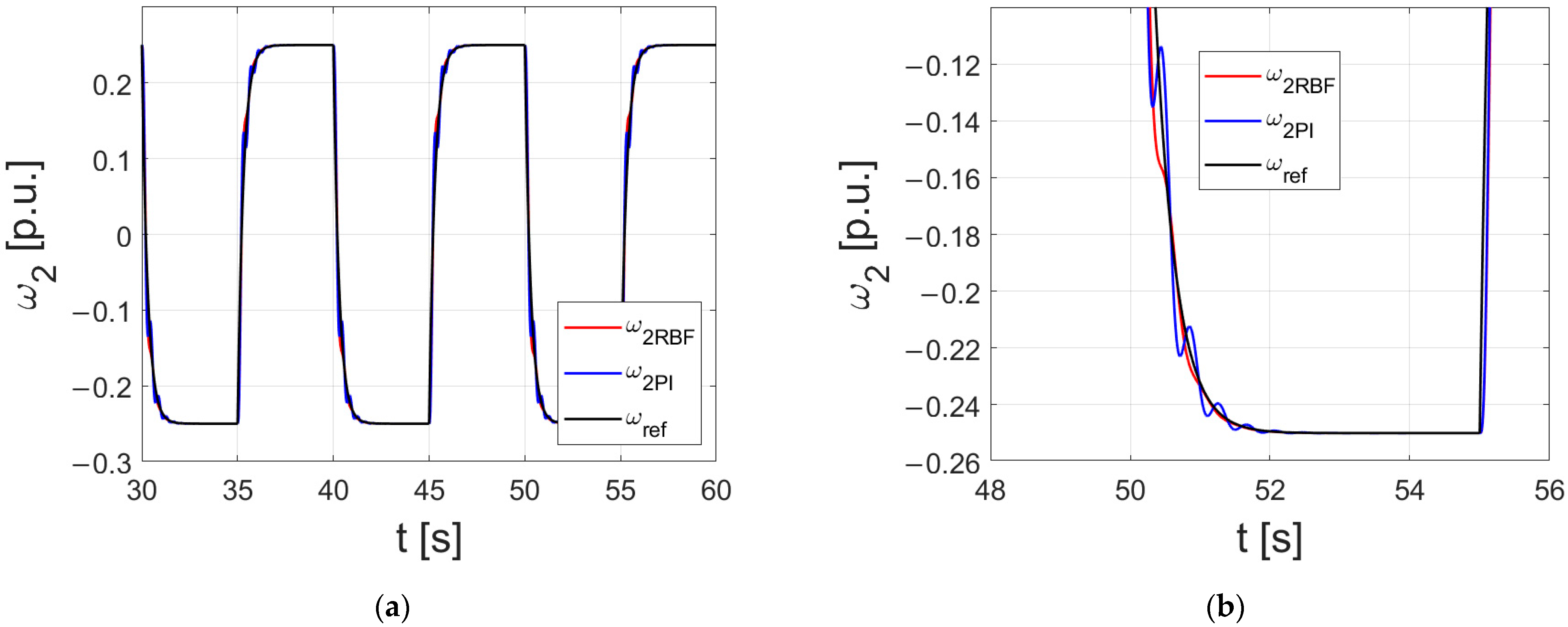
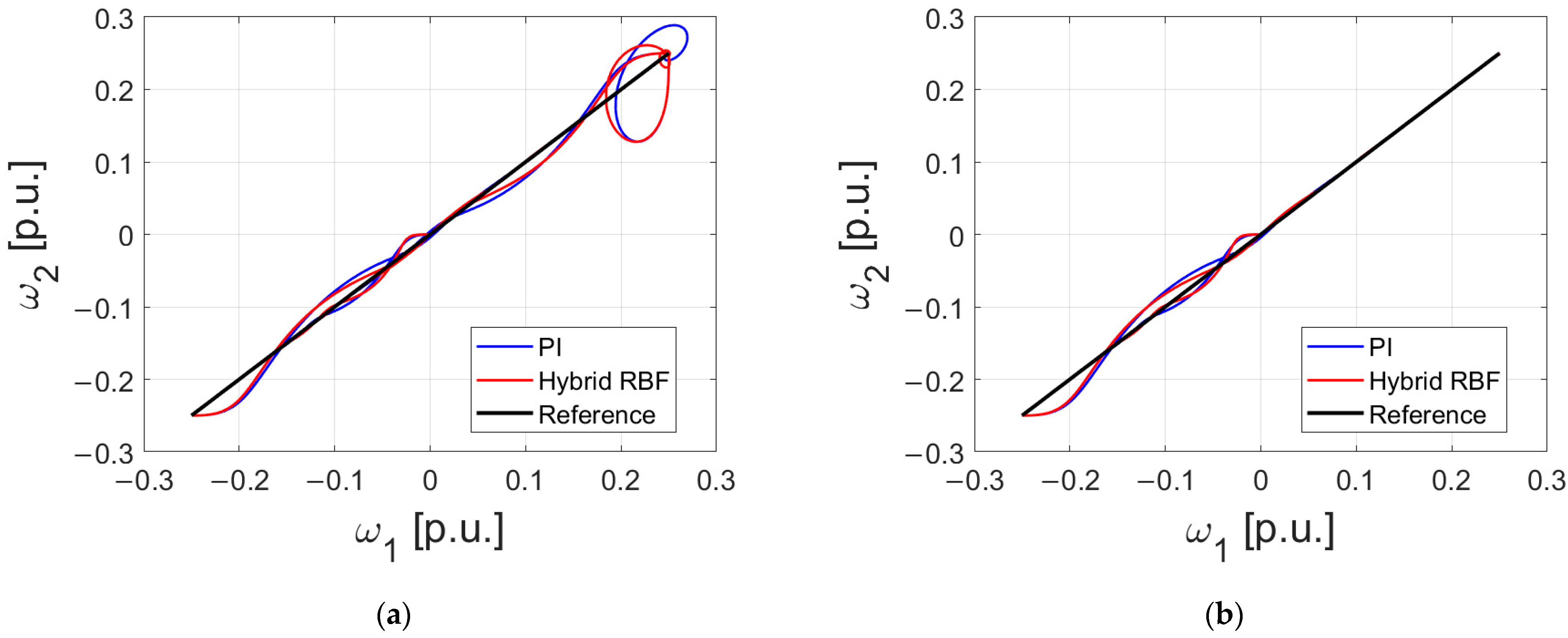
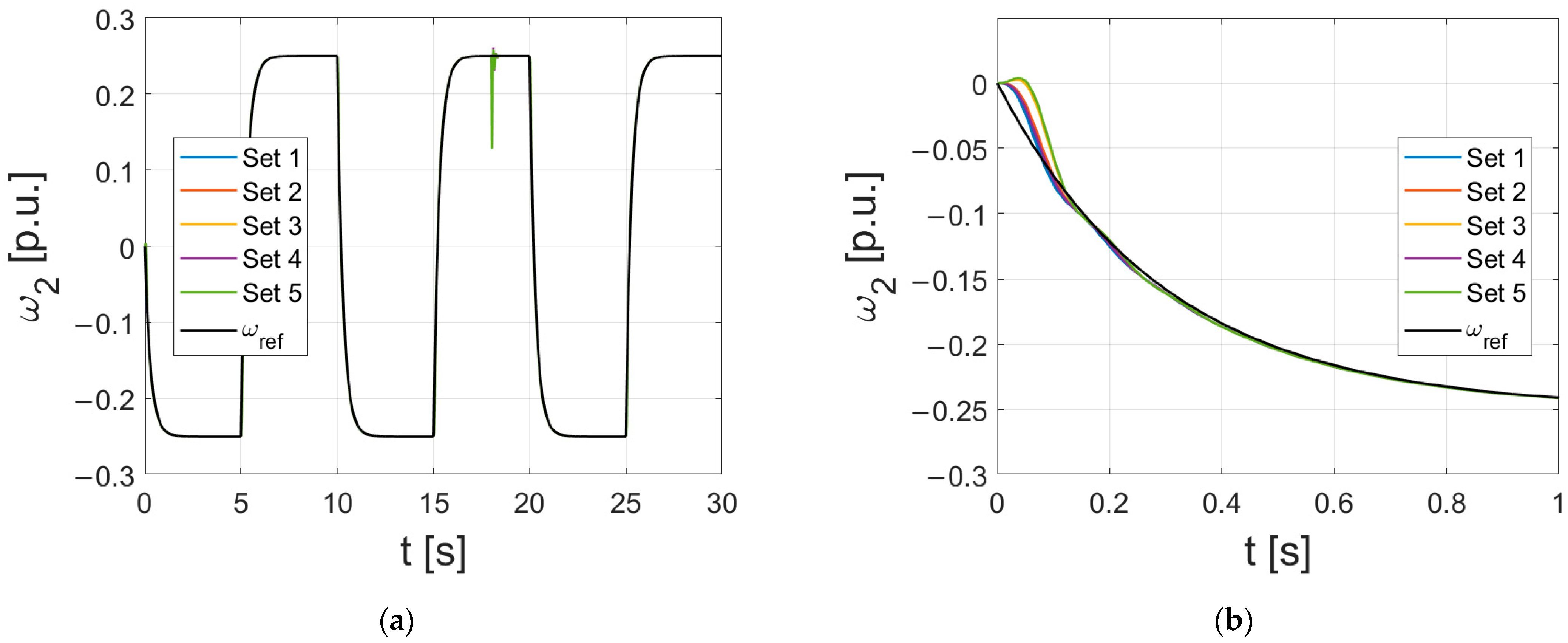
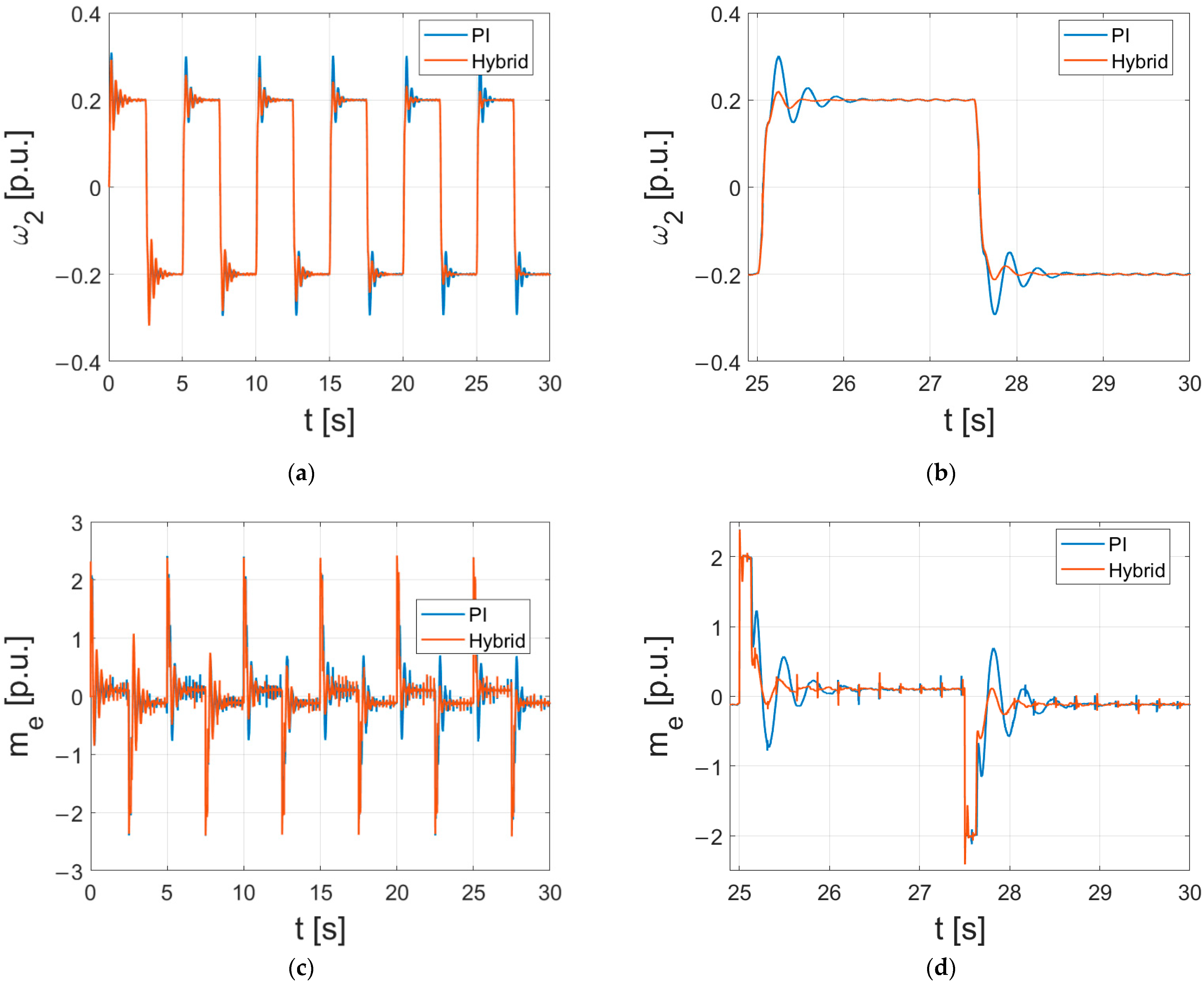
3.1. Simulation Results
3.2. Experimental Results
4. Discussion
- ➢
- The performance of the drive under the presence of disturbances (changes of the parameters of the two-mass system) obtained for the hybrid controller is distinctively improved—a significant reduction in oscillations was achieved. Moreover, the overshoot resulting from switching the direction of rotation was drastically limited (or even eliminated).
- ➢
- Stable operation of the drive was achieved, values of the weights in the output layer of the RBFNN do not disturb the work of the system (it was confirmed with long-time tests).
- ➢
- Initial point of the optimization algorithm (the randomization of the network parameters) does not interfere with the correct tracking of the reference speed.
- ➢
- The features observed in simulations were experimentally confirmed (using a rapid prototyping method).
- ➢
- The considered control strategy with a reduced number of used sensors (the feedback loops are based only on the information about the armature current and the speed of the motor) is by far the most difficult to achieve satisfactory results with.
- ➢
- The practical aspect of the proposed control structure deals with a non-extended (compared to the classical solutions) combination of feedback signals. It leads to a reduced number of sensors. Therefore, cost reduction and an increase in system reliability can be achieved.
- ➢
- The additional part of the controller is applied to achieve model-free compensation. It means that the modification of the time constants or other parameters of the object does not affect the correct work of the controller (additional identification of the system does not need to be performed). Reaction to the disturbances is possible due to the recalculation of the network parameters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Muszynski, R.; Deskur, J. Damping of Torsional Vibrations in High-Dynamic Industrial Drives. IEEE Trans. Ind. Electron. 2010, 57, 544–552. [Google Scholar] [CrossRef]
- Bosetti, H.; Khan, S. Transient Stability in Oscillating Multi-Machine Systems Using Lyapunov Vectors. IEEE Trans. Power Syst. 2018, 33, 2078–2086. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C.; Moriello, L. Optimal Trajectories for Vibration Reduction Based on Exponential Filters. IEEE Trans. Control Syst. Technol. 2016, 24, 609–622. [Google Scholar] [CrossRef]
- Ruf, M. Near time-optimal flexible-joint trajectory planning algorithm for robotic manipulators. In Proceedings of the 2018 IEEE Conference on Control Technology and Applications (CCTA), Copenhagen, Denmark, 21–24 August 2018; pp. 265–272. [Google Scholar] [CrossRef]
- Magee, D.P.; Book, W.J. Optimal Filtering to Minimize the Elastic Behavior in Serial Link Manipulators. In Proceedings of the American Control Conference, Philadelphia, PA, USA, 26 June 1998. [Google Scholar]
- Padron, J.; Kawai, Y.; Yokokura, Y.; Ohishi, K.; Miyazaki, T. Stable torsion torque control based on friction-backlash analogy for two-inertia systems with backlash. IEEJ J. Ind. Appl. 2022, 11, 279–290. [Google Scholar] [CrossRef]
- Chen, Y.; Yang, M.; Sun, Y.; Long, J.; Xu, D.; Blaabjerg, F. A Modified Bi-Quad Filter Tuning Strategy for Mechanical Resonance Suppression in Industrial Servo Drive Systems. IEEE Trans. Power Electron. 2021, 36, 10395–10408. [Google Scholar] [CrossRef]
- Preitl, S.; Precup, R.E.; Solyom, S.; Kovacs, L. Development of Conventional and Fuzzy Controllers for Output Coupled Drive Systems and Variable Inertia. IFAC Proc. Vol. 2001, 34, 261–269. [Google Scholar] [CrossRef]
- Hung, J.Y. Control of Industrial Robots that Have Transmission Elasticity. IEEE Trans. Ind. Electron. 1991, 38, 421–427. [Google Scholar] [CrossRef]
- Ruderman, M.; Iwasaki, M. Sensroless Torsion Control of Elastic-Joint Robots With Hysteresis and Friction. IEEE Trans. Ind. Electron. 2016, 63, 1889–1899. [Google Scholar] [CrossRef]
- Dhaouadi, R.; Kubo, K.; Tobise, M. Two-Degree-of-Freedom Robust Speed Controller For High Performance Rolling Mill Drives. In Proceedings of the Conference Record of the 1992 IEEE Industry Applications Society Annual Meeting, Houston, TX, USA, 4–9 October 1992; pp. 400–407. [Google Scholar] [CrossRef]
- Orlowska-Kowalska, T.; Kaminski, M. Application of the OBD method for optimization of neural state variable estimators of the two-mass drive system. Neurocomputing 2009, 72, 3034–3045. [Google Scholar] [CrossRef]
- Åström, K.; Hägglund, T. PID Controllers: Theory, Design, and Tuning, 2nd ed.; The Instrumentation, Systems, and Automation Society: Research Triangle Park, NC, USA, 1995; pp. 111–116. [Google Scholar]
- Zhang, G.; Furusho, J. Speed Control of Two-Inertia System by PI/PID Control. IEEE Trans. Ind. Electron. 2000, 47, 603–609. [Google Scholar] [CrossRef]
- Zhang, G. Comparison of Control Schemes for Two-Inertia System. In Proceedings of the IEEE 1999 International Conference on Power 373 Electronics and Drive Systems. PEDS’99, Hong Kong, China, 27–29 July 1999; pp. 573–578. [Google Scholar] [CrossRef]
- Saarakkala, S.E.; Hinkkanen, M. State-Space Speed Control of Two-Mass Mechanical Systems: Analytical Tuning and Experimental Evaluation. IEEE Trans. Ind. Appl. 2014, 50, 3428–3437. [Google Scholar] [CrossRef]
- Pacas, J.M.; John, T.; Eutebach, T. Automatic Identification and Damping of Torsional Vibrations in High-Dynamic-Drives. In Proceedings of the 2000 IEEE International Symposium on Industrial Electronics ISIE’2000, Cholula, Puebla, Mexico, 4–8 December 2000; pp. 201–206. [Google Scholar] [CrossRef]
- Szabat, K.; Orlowska-Kowalska, T. Vibration Suppression in a Two-Mass Drive System Using PI Speed Controller and Additional Feedbacks-Comparative Study. IEEE Trans. Ind. Electron. 2007, 54, 1193–1206. [Google Scholar] [CrossRef]
- Derugo, P.; Szabat, K. Damping of Torsional Vibrations of Two-Mass System Using Adaptive Low Computational Cost Fuzzy PID Controller. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, Australia, 9–12 June 2015; pp. 1162–1165. [Google Scholar] [CrossRef]
- Xing, Y.; Wang, X.; Yang, D.; Zhang, Z. Sensorless Control of Permanent Magnet Synchronous Motor Based on Model Reference Adaptive System. In Proceedings of the 2017 10th International Symposium on Computational Intelligence and Design (ISCID), Hangzhou, China, 9–10 December 2017; pp. 20–23. [Google Scholar] [CrossRef]
- Vazifehdan, M.; Zarchi, H.A.; Khoshhava, M.A. Sensorless Vector Control of Induction Machines via Sliding Mode based Model Reference Adaptive System. In Proceedings of the 2020 28th Iranian Conference on Electrical Engineering (ICEE), Tabriz, Iran, 4–6 August 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Mohanalakshimi, J.; Suresh, H.N. Sensorless Speed Estimation and Vector Control of an Induction Motor Drive Using Model Reference Adaptive Control. In Proceedings of the 2015 International Conference on Power and Advanced Control Engineering (ICPACE), Bengaluru, India, 12–14 August 2015; pp. 377–382. [Google Scholar] [CrossRef]
- Nandana, J.; Anas, A.S. An Efficient Speed Control Method for Two Mass Drive Systems using ADALINE. In Proceedings of the 2015 International Conference on Smart Technologies and Management for Computing, Communication, Controls, Energy and Materials (ICSTM), Avadi, India, 6–8 May 2015; pp. 418–423. [Google Scholar] [CrossRef]
- Lukichev, D.V.; Demidova, G.L.; Brock, S. Fuzzy Adaptive PID Control for Two-Mass Servo-Drive System with Elasticity and Friction. In Proceedings of the 2015 IEEE 2nd International Conference on Cybernetics (CYBCONF), Gdynia, Poland, 24–26 June 2015; pp. 443–448. [Google Scholar] [CrossRef]
- Li, D.; Zhang, Z.; Liu, P.; Wang, Z.; Zhang, L. Battery Fault Diagnosis for Electric Vehicles Based on Voltage Abnormality by Combining the Long Short-Term Memory Neural Network and the Equivalent Circuit Model. IEEE Trans. Power Electron. 2022, 36, 1303–1315. [Google Scholar] [CrossRef]
- Wolkiewicz, M.; Kowalski, C.T. Incipient stator fault detector based on neural networks end symmetrical components analysis for induction motor drives. In Proceedings of the 2016 13th Selected Issues of Electrical Engineering and Electronics (WZEE), Rzeszow, Poland, 4–8 May 2016; pp. 1–7. [Google Scholar] [CrossRef]
- Quintero-Manriquez, E.; Sanchez, E.N.; Felix, R.A. Induction motor torque control via discrete-time neural sliding mode. In Proceedings of the 2016 International Joint Conference on Neural Networks (IJCNN), Vancouver, BC, Canada, 24–29 July 2016; pp. 2756–2761. [Google Scholar] [CrossRef]
- Azizi, S.; Asemani, M.H.; Vafamand, N.; Mobayen, S.; Fekih, A. Adaptive Neural Network Linear Parameter-Varying Control of Shipboard Direct Current Microgrids. IEEE Access 2022, 10, 75825–75834. [Google Scholar] [CrossRef]
- Chan, V.M.; Hernández-Vargas, E.A.; Sánchez, E.N. Neural inverse optimal control applied to design therapeutic options for patients with COVID-19. In Proceedings of the 2021 International Joint Conference on Neural Networks (IJCNN), Shenzhen, China, 18–22 July 2021; pp. 1–7. [Google Scholar] [CrossRef]
- Nebeluk, R.; Lawrynczuk, M. Fast Nonlinear Model Predictive Control Using a Custom Cost-Function: Preliminary Results. In Proceedings of the 2022 30th Mediterranean Conference on Control and Automation (MED), Vouliagmeni, Greece, 28 June–1 July 2022; pp. 13–18. [Google Scholar] [CrossRef]
- Du, G.; Liang, Y.; Gao, B.; Al Otaibi, S.; Li, D. A Cognitive Joint Angle Compensation System Based on Self-Feedback Fuzzy Neural Network With Incremental Learning. IEEE Trans. Ind. Inform. 2021, 17, 2928–2937. [Google Scholar] [CrossRef]
- Quintero-Manriquez, E.; Sanchez, E.N.; Harley, R.G.; Li, S.; Felix, R.A. Neural Inverse Optimal Control Implementation for Induction Motors via Rapid Control Prototyping. IEEE Trans. Power Electron. 2019, 34, 5981–5992. [Google Scholar] [CrossRef]
- Kaminski, M.; Orlowska-Kowalska, T. FPGA Implementation of ADALINE-Based Speed Controller in a Two-Mass System. IEEE Trans. Ind. Inform. 2013, 9, 1301–1311. [Google Scholar] [CrossRef]
- Li, D.; Liu, P.; Zhang, Z.; Zhang, L.; Deng, J.; Wang, Z.; Dorell, D.G.; Li, W.; Sauer, D.U. Battery Thermal Runaway Fault Prognosis in Electric Vehicles Based on Abnormal Heat Generation and Deep Learning Algorithms. IEEE Trans. Power Electron. 2022, 37, 8513–8525. [Google Scholar] [CrossRef]
- Roy, S.; Menapace, W.; Oei, S.; Luijten, B.; Fini, E.; Saltori, C.; Huijben, I.; Chennakeshava, N.; Mento, F.; Sentelli, A.; et al. Deep Learning for Classification and Localization of COVID-19 Markers in Point-of-Care Lung Ultrasound. IEEE Trans. Med. Imaging 2020, 39, 2676–2687. [Google Scholar] [CrossRef]
- Skowron, M.; Orlowska-Kowalska, T.; Kowalski, C.T. Detection of Permanent Magnet Damage of PMSM Drive Based on Direct Analysis of the Stator Phase Currents Using Convolutional Neural Network. IEEE Trans. Ind. Electron. 2022, 69, 13665–13675. [Google Scholar] [CrossRef]
- Niu, F.; Tian, L.; Li, Y.Y.R.; Norman, T.L. Studies on flow instability of helical tube steam generator with Nyquist criterion. Nucl. Eng. Des. 2014, 266, 63–69. [Google Scholar] [CrossRef]
- El-Marhomy, A.A.; Abdel-Sattar, N.E. Stability analysis of rotor-bearing systems via Routh-Hurwitz criterion. Appl. Energy 2004, 77, 287–308. [Google Scholar] [CrossRef]
- Stanisławski, R. Modified Mikhailov stability criterion for continuous-time noncommensurate fractional-order systems. J. Frankl. Inst. 2022, 359, 1677–1688. [Google Scholar] [CrossRef]
- Nguyen, P.T.H.; Stüdli, S.; Braslavsky, J.H.; Middleton, R.H. Lyapunov stability of grid-connected wind turbines with permanent magnet synchronous generator. Eur. J. Control 2022, 65, 100615. [Google Scholar] [CrossRef]
- Hara, K.; Hashimoto, S.; Funato, H.; Kamiyama, K. Robust comparison between state feedback-based speed control systems with and without state observers in resonant motor drives. Proc. Second Int. Conf. Power Electron. Drive Syst. 1997, 1, 371–376. [Google Scholar] [CrossRef]
- Meng, X.; Rozycki, P.; Qiao, J.; Wilamowski, B.M. Nonlinear system modeling using RBF Networks for industrial application. IEEE Trans. Industr. Inform. 2018, 14, 931–940. [Google Scholar] [CrossRef]
- Zhang, P.; Zhou, X.; Pelliccione, P.; Leung, H. RBF-MLMR: A Multi-Label Metamorphic Relation Prediction Approach Using RBF Neural Network. IEEE Access 2017, 5, 21791–21805. [Google Scholar] [CrossRef]
- Liu, Z.; Guo, Y.; Gao, M.; Zhao, X.; Zhang, Y. Fuzzy Neural Network Blind Equalization Algorithm Based on Radial Basis Function. In Proceedings of the 2009 International Conference on Intelligent Human-Machine Systems and Cybernetics, Hangzhou, China, 26–27 August 2009; pp. 280–283. [Google Scholar] [CrossRef]
- Bose, B.K. Modern Power Electronics and AC Drives; Prentice Hall PTR: Upper Saddle River, NJ, USA, 2002; pp. 625–658. [Google Scholar]
- Wu, W.; Zhong, S.; Zhou, G. A study on PID intelligent optimization based on radial basis function neural networks. In Proceedings of the 2013 3rd International Conference on Consumer Electronics, Communications and Networks, Xianning, China, 20–22 November 2013; pp. 57–60. [Google Scholar] [CrossRef]
- Simoncini, V. Computational Methods for Linear Matrix Equations. SIAM Rev. 2016, 58, 377–441. [Google Scholar] [CrossRef] [Green Version]


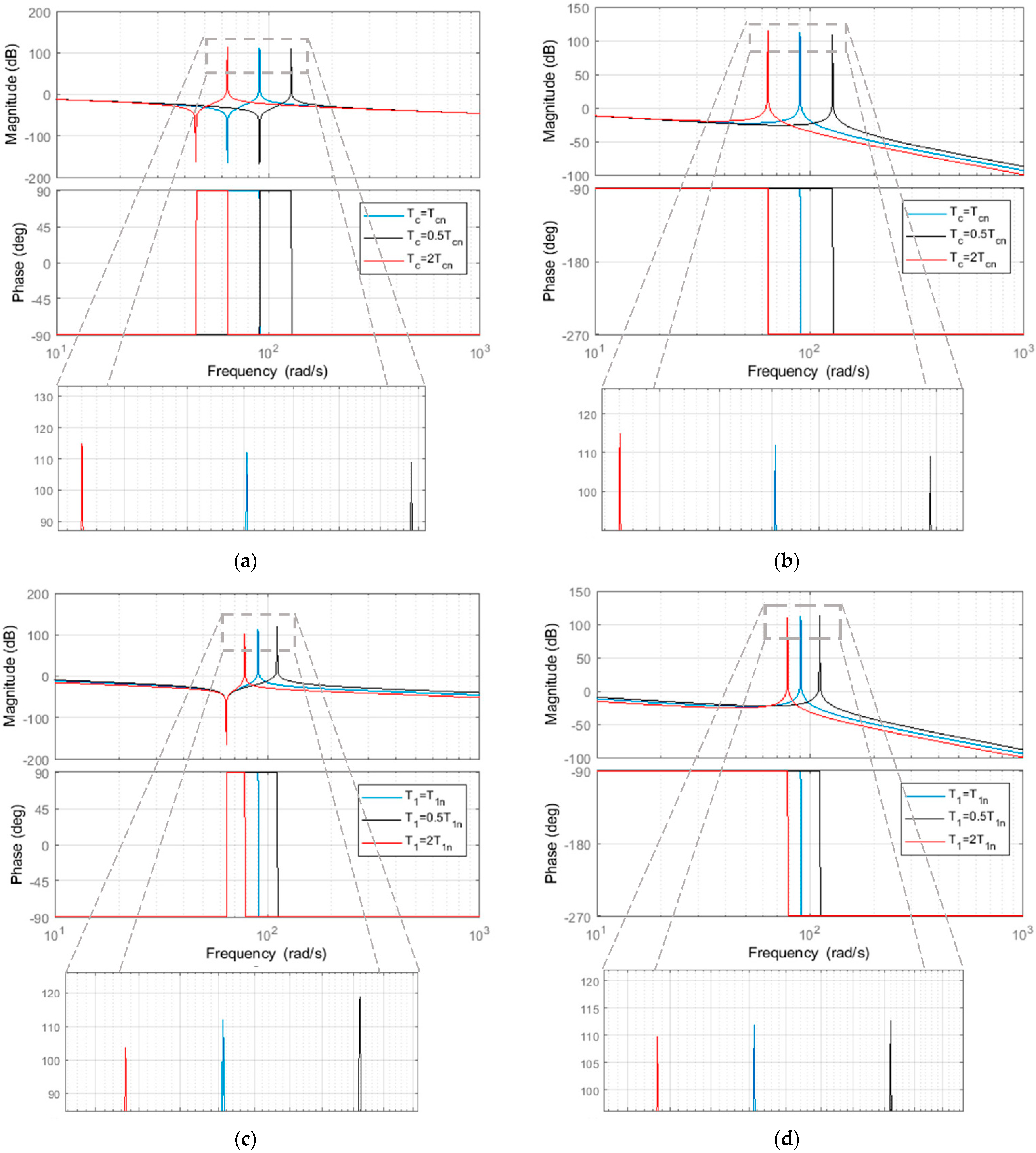









| Parameter | Symbol | Value | Unit |
|---|---|---|---|
| Nominal power | PN | 500 | W |
| Nominal angular speed | nN | 1450 | min−1 |
| Motor mechanical time constant | T1 | 0.203 | s |
| Load mechanical time constant | T2 | 0.203 | s |
| Shaft mechanical time constant | Tc | 0.0026 | s |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stanislawski, R.; Tapamo, J.-R.; Kaminski, M. A Hybrid Adaptive Controller Applied for Oscillating System. Energies 2022, 15, 6265. https://doi.org/10.3390/en15176265
Stanislawski R, Tapamo J-R, Kaminski M. A Hybrid Adaptive Controller Applied for Oscillating System. Energies. 2022; 15(17):6265. https://doi.org/10.3390/en15176265
Chicago/Turabian StyleStanislawski, Radoslaw, Jules-Raymond Tapamo, and Marcin Kaminski. 2022. "A Hybrid Adaptive Controller Applied for Oscillating System" Energies 15, no. 17: 6265. https://doi.org/10.3390/en15176265
APA StyleStanislawski, R., Tapamo, J.-R., & Kaminski, M. (2022). A Hybrid Adaptive Controller Applied for Oscillating System. Energies, 15(17), 6265. https://doi.org/10.3390/en15176265