Automatic Determination of Rock-Breaking Target Poses for Impact Hammers

Abstract

This paper describes a system for the automatic determination of rock-breaking target poses for impact hammers used in underground mines. The rock-breaking target pose is defined as the position and angle at which the impact hammer must strike a rock in order to break it. The automatic determination of this pose is essential for the autonomous operation of an impact hammer. The proposed system takes as input sensor data composed of point clouds and images, and automatically determines a rock-breaking target pose. The system consists of a rock segmentation subsystem that receives the sensor data and identifies and individualizes the rocks/boulders present above the grizzly, and a rock-breaking target pose generation and evaluation subsystem that receives the rock information produced by the rock segmentation subsystem, and generates a list of rock-breaking target pose candidates, it evaluates them, and it selects the best candidate as the rock-breaking target pose. The system is evaluated using real data. The reported experiments show the system’s capability to generate appropriate target poses.

1. Introduction

Mining operations are progressively moving towards using autonomous and/or tele-operated equipment, because this improves their safety, productivity and reliability. This is especially important in underground mining, where workers are exposed to risks such as rock falls, mud rushes and continued exposure to dust [1]. All these hazards have been steadily increasing as underground mining operations go deeper, geo-mechanical conditions become more extreme and the time to enter and leave the mines becomes longer [2]. Consequently, great effort has been invested in improving the automation level of underground mining machines, especially those that operate in high-risk areas [1], such as load–haul–dump (LHD) machines, also known as scoop trams; and impact hammers, also known as rock breakers, rock-breaking manipulators, rock-breaking hammers or pedestal-mounted breaker booms [3].

Impact hammers are used to break rocks that are too large to pass through the steel grates, called grizzlies, placed on top of ore passes, which are vertical tunnels connecting different production levels. Thus, the material loaded and transported by the LHDs is dumped onto the grizzlies and fragmented, when needed, by impact hammers (see Figure 1).

In modern underground mines, impact hammers are usually tele-operated from a control room located in a safe place, often several kilometers away from the operation area. The tele-operation of the hammers is a complex task which requires skilled operators, not only because they must control these hammers effectively, but because they must do so by relying on visual information provided by cameras: there is latency produced by encoding, transmitting and decoding this information; there is often poor visibility of the environment (mainly because of the presence of dust and poor illumination); and the visualization interfaces that are commonly available to the operators fail to properly characterize the 3D nature of the environment.

In order to improve this situation, assistive tele-operation systems for impact hammers (e.g., [3]) and autonomous control systems for impact hammers (e.g., [4]), are under development. A common problem to be solved in both kinds of applications is the automatic determination of the position where the hammer must impact the rock, and the angle of such an impact. In other words, it is essential to be able to automatically determine the so-called rock-breaking target pose, either for the autonomous operation of the hammer, or to provide this information to the operator. To the best of our knowledge, this problem has not been addressed properly in most of the literature [3,5,6,7,8]. In [4] a simple rock-breaking target pose methodology is proposed, but it does not take into account the orientation of the end-effector with respect to the rock surface or the shape of the rock, obtaining sub-optimal results in the proof-of-concept test when attempting to break the rocks.

Thus, the main goal of this paper is to describe a system for the automatic determination of rock-breaking target poses for impact hammers. The system takes as input sensor data composed of images and point clouds, and automatically determines a rock-breaking target pose. The system is composed of a rock segmentation subsystem that receives the sensor data and identifies and individualizes the rocks/boulders present above the grizzly, and a rock-breaking target pose generation and evaluation subsystem that receives the rock information produced by the rock segmentation subsystem, and generates a list of rock-breaking target pose candidates. It evaluates them and it selects the best candidate. The system is evaluated using real data.

To the best of our knowledge, autonomous impact hammers are not commercially openly available, so this work improves the state of the art in this topic by providing the following main contributions:

• The design of algorithms for generating rock-breaking target poses and assessing them, which are based on the way this task is performed by human operators in mining sites. This information was obtained from good practice manuals and from interviews with operators.
• A rock segmentation procedure that is the result of merging the segmentation obtained by processing the point-cloud data and the detection of rocks obtained by image processing techniques.
• The adaptation of image processing techniques used for image segmentation (e.g., flooding or watershed) to segment point-cloud data.
• Incorporating to the end-effector’s target pose a criterion of a range of contact angles in which the hammer and the rock minimize the slippage due to impact.

This paper is organized as follows: In Section 2, the proposed system for determining the rock-breaking target pose is described. In Section 3, the results obtained when evaluating the system using both simulated and real data, are presented. In Section 4, we analyze the obtained results. In Section 5 the conclusions derived from this work are drawn. Finally, in Section 6 a patent derived from this work is mentioned.

2. Proposed System for Determining the Rock-Breaking Target Pose for Impact Hammers

2.1. General System Description

The proposed system implements a method that, based on sensor data composed of point clouds and images, automatically determines a rock-breaking target pose for an impact hammer, so that it can fragment oversized rocks within a pile of material. This system consists of two subsystems: a subsystem that performs rock segmentation, and a subsystem that generates and evaluates rock-breaking target poses. The rock segmentation subsystem receives sensor data (point clouds and images) and identifies and individualizes the rocks present above the grizzly. The rock-breaking target pose generation and evaluation subsystem receives sensor data and the rock’s identification produced by the rock segmentation subsystem, and generates a list of rock-breaking target pose candidates, which are then evaluated to finally deliver the best candidate. Both subsystems may operate permanently and continuously, i.e., they are suited for constantly analyzing the environment, and determining the next rock-breaking target pose for the hammer.

Both subsystems are composed of several components, each of them performing different tasks. The overall system may be depicted by the diagram displayed in Figure 2. In this section each of these modules and their interactions are going to be described in detail.

2.2. Rock Segmentation Subsystem

As mentioned above, the rock segmentation subsystem receives sensor data (point clouds and images), and through a series of logical and mathematical operations identifies and individualizes the rocks/boulders above the grizzly. This subsystem consists of the following modules: Sensing and Data Acquisition; Point Cloud Generation; Rock Segmentation using Point Clouds; Rock Detection using Images; and Rock Segmentation based on Fused Data (see Figure 2).

2.2.1. Sensing and Data Acquisition

To determine the rock-breaking target poses, it is necessary to generate a representation in which each rock in a given rock pile is properly individualized. This individualization, referred to as instance segmentation, should provide a three-dimensional representation of the rocks, which would allow the hammer to strike them. To achieve this goal, 3D points and images are captured by sensors, allowing the generation of a 3D model of the workspace, as well as a characterization of the colors and textures present in the environment. Although the system may work with different range sensors and cameras, the current implementation uses two 3D LIDAR sensors (laser scanners), and two visible spectrum cameras.

The sensors must be properly positioned to capture a large percentage of the grizzly and the material above it. The data from these sensors are processed by an industrial computer, which performs the various operations required to implement the rock segmentation and rock-breaking target pose determination subsystems.

2.2.2. Point Cloud Generation

The raw captured point cloud contains points corresponding to the material on the ore pass, the impact hammer and the mine infrastructure. For this reason, the first stage of the segmentation process consists of eliminating the captured points associated to the mine infrastructure and the impact hammer, so a point cloud containing only data of the material above the ore pass’s grizzly is obtained. To achieve this, a bounding box representing the working volume is defined, which allows eliminating all the points outside of it. Then, the points belonging to the impact hammer are eliminated using a model that represents its simplified geometry given its current configuration. This model is obtained using geometric primitives which, along with the measurements of the arm encoders, represent, approximately, the physical space that the impact hammer is currently using.

Then, the points that belong to the mine infrastructure (such as the floor, the grizzly, railings, and other adjacent structures) are eliminated using a previously constructed environment model. This model corresponds to a voxel representation of the empty grizzly and its surroundings (although, already limited by the workspace bounding box used to filter points). The environment model is generated prior to system operation and ensuring that the grill is free of material. This generation process starts by removing points that are outside the working volume, then the remaining points are integrated and merged into a single point cloud. Next, outlier points are removed using a predefined cluster filtering process [9]. Finally, this point cloud is stored for use in the operation. Using this model, it is possible to classify the points that correspond to the mine infrastructure as those points located within the voxels of the constructed model.

The points that belong to the constructed environment model are then separated from the rest of the point cloud. The remaining points are combined to represent in a unique and simplified way the information provided by the LIDARs. To achieve this, the measurements obtained from the LIDARs are temporally integrated using a time window of 1 s. This not only makes the obtained point cloud of the environment denser, but also allows filtering spurious measurements.

Finally, the resolution of the data is reduced to allow faster processing. To accomplish this, the data are subsampled using voxels, where the spatial locations of all the points contained within a given voxel, $p_1,p_2,...,p_k$, are represented by a single centroid point, $c_P$. These centroids are defined by Equation (1), that is, their coordinates are the average coordinates of the points contained inside their corresponding voxel.

$$c_P=\frac{1}{k}\sum _{i=1}^k{p}_i$$

(1)

The result of applying all the steps described in this section is a point cloud containing a representation of the material above the grizzly.

2.2.3. Rock Segmentation Using Point Clouds

In order to segment each rock in the point cloud, a version of the watershed method adapted to point clouds defining a surface is applied (see details in [10]). This new version of the method allows applying the concept of “descent” and initial labeling on a point cloud, and performing a surface analysis without having to convert this point cloud to a polygon mesh, which is the way these types of methods are often applied (e.g., [11,12]). In general, using surface processing with polygonal meshes is convenient when an object is well defined, and it is required to generate a 3D visualization of it. Since in this case the information obtained from the surface is more relevant than the visualization itself, it is more convenient to use the point cloud directly, which is what the proposed method does. Furthermore, by not requiring a polygon mesh and directly processing a point cloud, this method avoids the construction of additional data structures, which could increase its processing cost.

In the proposed method, an initial labeling is performed by first identifying the convex surface points that are most similar to rocks. These points are called seeds. To obtain these seeds, it is first necessary to obtain the normal vector associated to each point. To obtain these normal vectors, a plane at the location of each point is estimated using the least squares algorithm.

Then, the so-called “height value” of each point is calculated, which determines what the initial labels will be, and how these labels will be propagated. The “height value” is determined by a height function. In traditional watershed segmentation algorithms, the Z-axis value or the surface curvature is usually used to segment point clouds. In our case, the height function is defined using the deviation between the normal component of the plane at the location of a given point, and a desired orientation. We are interested in finding the points whose planes have a normal component ${\left(n_x,n_y,n_z\right)}^{⊺}$ that is aligned with the Z-axis direction. Given the aforementioned, the height function $H\left(p\right)$ is defined by Equation (2), that is, as the dot product between the normal of the plane (associated to a point), and the unit vector $\overrightarrow{r}={\left(0,0,1\right)}^{⊺}$.

$$H\left(p\right)=\overrightarrow{r}·{\left(n_x,n_y,n_z\right)}^{⊺}$$

(2)

With this function, a higher height value is assigned to points that belong to flattened geometric “peaks” in the point cloud. If the Z-axis were used directly, as in more commonly used height functions, the height values would be higher for metric peaks. This is not convenient when segmenting rocks, as they often come in different sizes, and consequentially, may possess widely different maximum heights when positioned above the grizzly.

With the above, a binary labeling of the points is performed by using the function defined by Equation (3), where $H_t$ is a predefined threshold value.

$$L\left(p\right)=\left\{\begin{array}{cc}1\hfill & \mathrm{if}H\left(p\right)>H_t,\hfill \\ 0\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(3)

Afterwards, the morphological operations of dilation and erosion are applied on the binary labels assigned to the point cloud, “connecting” the labels of points that are close to each other, according to a predefined proximity radius. These morphological operations effectively remove small connected components of labeled points, whilst combining connected components that are close to one another. Finally, the resulting labels are clustered into new labels according to the proximity of their corresponding points, and these groups are individualized by re-labeling the points that conform them. These new labels are codified using natural numbers starting from 2 and up until $N_l$, depending on the number of groups.

When the flooding or watershed descent stage is carried out, a propagation of the labels from the seeds to points of lower height value is performed, which allows delimiting the points of contact between different rocks. Within this stage, a series of adaptations are made to apply a standard flooding 3D methodology [11] to our context in a meaningful manner.

First, a different height function is utilized for the descent stage. This new function will be referred to as $H_{\mathrm{descent}}\left(p\right)$. This switch between height functions is based on the fact that the requirements for both stages (labeling, and descent) are different. In the initial labeling, the height function is designed to detect rocks using a single cut threshold, so it is convenient to generate seeds associated to geometric peaks, prioritizing their overall shape, and ignoring their metric height. On the other hand, for the descent stage, the objective is to propagate points (starting from the detected seeds) in a way such as to correctly limit the separations between different rocks. In this sense, using the same labeling criterion for this task would not be convenient, as it is not possible to reliably model a surface as a single plane at these intersections. If we consider the Z-axis values of the points in these intersections, however, their minimum value approximates reasonably well the boundary between different rocks. Therefore, $H_{\mathrm{descent}}\left(p\right)$ is defined by Equation (4) as in standard watershed algorithms, that is, it assigns height values according to the points’ Z-axis coordinate.

$$H_{\mathrm{descent}}\left(p\right)=p_z$$

(4)

Although this criterion does not generalize well in cases where a rock rests above another, in our application context this is not a problem: we are only concerned with segmenting rocks that are at the upper level of the material in the grizzly, since these are the rocks that take precedence at the time of the fragmentation.

In the flooding process, a hierarchical ranking of the height values is performed, assigning a certain height level, $N\left(p\right)$, to each point. Afterwards, a propagation of labels by the proximity of the points and their height level is carried out.

The height level of a point, $N\left(p\right)$, is assigned according to Equation (5), where $\Delta H_{\mathrm{descent}}$ is a predefined resolution parameter. $\Delta H_{\mathrm{descent}}$ is actually the same resolution parameter that is utilized in the voxelization process performed over the LIDAR data, as described in Section 2.2.2.

$$N\left(p\right)=⌈\frac{H_{\mathrm{descent}}\left(p\right)}{\Delta H_{\mathrm{descent}}}⌉$$

(5)

After $N\left(p\right)$ is computed, the points are analyzed from highest to lowest hierarchy. If a point already has a label, the label is propagated to neighbor points in the next (inferior) level of hierarchy. On the contrary, if a point has no associated label, then it takes the label of the nearest labeled point. When doing this, the distance used in the neighbor search process is greater than the one used in the descending stage. This allows propagating the label to the nearest local maximum (or catchment basins of the surface) that are incorrectly generated by noisy Z values of the points. Label propagation by level allows labels to propagate uniformly through all points within the same hierarchy, thus producing the flooding effect of watershed for a point cloud.

Finally, the system labels the points that were not processed by associating them to the label of the nearest point to them. As a result, a segmented point cloud is obtained in which each point has a label that corresponds to a given rock instance. Figure 3 illustrates the result of applying the described process on a point cloud obtained from a scene where several rocks are present.

2.2.4. Rock Detection Using Images

Rocks are detected using a convolutional neural network called RockyCenterNet [13]. RockyCenterNet is based on CenterNet [14], which is a one-stage object detector in which center points are estimated, and then the other properties of a detection, such as bounding boxes’ widths and heights, are regressed. Unlike CenterNet and most object detectors, RockyCenterNet uses ellipses to enclose a rock’s bounds, enabling a better description of the shape of the rocks than a classical approach based on bounding boxes. According to the evaluation reported in [13], RockyCenterNet is a suitable choice for detecting rocks in mining applications when real-time operation and a good approximation of a rock’s shape are needed.

2.2.5. Rock Segmentation Based on Fused Data

By using RockyCenterNet, rocks detected in the images are represented by ellipses, which in turn are represented by a coordinate and a set of parameters in the image space: a central position ${\left(x_I,y_I\right)}^{⊺}$, and a major axis $a_I$, a minor axis $b_I$, and an orientation ${\theta }_I$. Each ellipse is projected onto the point cloud containing the rocks already segmented, generating a new coordinate and set of parameters in the point cloud’s space, according to the camera reference system: a centroid ${\left(x_P,y_P,z_P\right)}^{⊺}$, a major axis $a_P$, a minor axis $b_P$, and an orientation ${\theta }_P$. The centroids lie on the rock surface, and are calculated by intersecting a ray generated by the pinhole camera model of the cameras with the point cloud. The points ${\left(x_r,y_r,z_r\right)}^{⊺}$ that conform this ray are defined by Equation (6), where ${\left(f_x,f_y,c_x,c_y\right)}^{⊺}$ are parameters of the intrinsic matrix of the camera model [15]. The intersection is obtained using an octree voxel representation of the cloud spacing [16], and then recursively searching for the voxel closest to the ray.

$$\left(\begin{array}{c}{x}_r\\ y_r\\ z_r\end{array}\right)=z_r\left(\begin{array}{c}\left(x_I-c_x\right)/f_x\\ \left(y_I-c_y\right)/f_y\\ 1\end{array}\right)$$

(6)

Once the centroids ${\left(x_P,y_P,z_P\right)}^{⊺}$ have been calculated, the other parameters of the ellipse in the point cloud space are computed according to Equations (7)–(9), with $f_a$ and $f_b$ defined by Equations (10) and (11), respectively.

$$\begin{array}{cc}\hfill a_P& =a_I·z_P/f_a\hfill \end{array}$$

(7)

$$\begin{array}{cc}\hfill b_P& =b_I·z_P/f_b\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill {\theta }_P& ={\theta }_I\hfill \end{array}$$

(9)

$$\begin{array}{cc}\hfill f_a& =\sqrt{f_x^{2}co{s}^2\left({\theta }_I\right)+f_y^{2}si{n}^2\left({\theta }_I\right)}\hfill \end{array}$$

(10)

$$\begin{array}{cc}\hfill f_b& =\sqrt{f_x^{2}si{n}^2\left({\theta }_I\right)+f_y^{2}co{s}^2\left({\theta }_I\right)}\hfill \end{array}$$

(11)

Each properly segmented rock should contain a single centroid. Consequently, segmented rocks containing more than one centroid should be subdivided into smaller rocks. To subdivide a rock, the ellipse closest to each of the points on the rock is found, and assigned to that point.

This process goes as follows: For all segmented rocks, and each ellipse on its surface, the normal of the rock in the ellipse’s centroid point is calculated, and then the depth of the centroid is corrected so that it is placed near the estimated center of the rock. Next, the Mahalanobis distance $d(p_j,c)$ between the point $p_j={\left(x_j,y_j,z_j\right)}^{⊺}$ of the cloud and the corrected centroid $c={\left(x_P,y_P,z_P\right)}^{⊺}$ of the ellipse is calculated according to Equation (12). The covariance matrix C is defined by Equation (13) where the ellipse parameters defined in Equations (7) and (8) are used as its first two diagonal components, and their product as its third diagonal component.

$$d(p_j,c)=\sqrt{{\left(p_j-c\right)}^{⊺}{C}^{-1}\left(p_j-c\right)}$$

(12)

$$C=\left(\begin{array}{ccc}{a}_P^2& 0& 0\\ 0& b_P^2& 0\\ 0& 0& a_P{b}_P\end{array}\right)$$

(13)

After the Mahalanobis distance for all ellipses and points is calculated, each point on the rock is associated with the ellipse that has the smallest distance to it. Finally, all the points associated to the same ellipse are clustered together. The result of the previous step is a set of clusters, each of them associated with a given ellipse.

Some of these point clusters may have a wrong ellipse assignment, as until this point no spacial information regarding their location is utilized. To detect these wrong assignments, it is verified that there are no different clusters associated with the same ellipse by performing the following additional checks:

• If an ellipse has only one associated cluster, that cluster is considered as correctly assigned.
• If an ellipse has multiple associated clusters, only the largest cluster is considered as correctly assigned, while the others are merged to the largest.
• The remaining clusters (which have associated ellipses but were not considered as correctly assigned) are disintegrated by reassigning their points to the nearest correctly assigned clusters.

The result of applying the point cloud correction using the ellipses is exemplified in Figure 4.

2.3. Subsystem for Generation and Evaluation of Rock Breaking Target Poses

This subsystem generates a set of feasible and hierarchized rock-breaking target poses. The resulting poses from this process should be such that a fracture would likely occur if the hammer’s end effector aligns to them when impacting on rocks. Furthermore, the order in which these poses would be assigned as targets for the impact hammer should minimize the time that leaving the grizzly without material would take. To accomplish its objectives, this subsystem follows a set of flexible rules and criteria to select and prioritize the rock breaking target poses. These rules are based on good practice manuals and mine operators’ feedback.

To generate a finite set of poses, the material’s surface is divided into equidistant sub-regions on an $XY$ plane parallel to the grizzly. The system then processes each of these sub-region to validate if it would be feasible to position the impact hammer’s end effector on this region, considering both the material’s surface geometry and the hammer’s kinematic constraints. Afterwards, for each reachable region, a rock breaking target pose is generated. Finally, an evaluation and ranking of the generated poses is performed.

The following processing stages summarize the overall subsystem functioning:

• Generation of sub-regions.
• Validation of sub-regions.
• Generation and Hierarchization of rock breaking target poses.

The interaction between each stage is illustrated in Figure 5. In the following, each of these stages is described in detail.

2.3.1. Generation of Sub-Regions

As a first step, the segmented point cloud is processed to define a set of sub-regions. To generate these sub-regions, the points in the segmented point cloud are grouped according to their position in a plane parallel to the grizzly. This plane is divided in cells using a virtual grid. For each cell, the points that are at the upper level of the voxel representation of the segmented point cloud are grouped together. Figure 6 illustrates the virtual grid above the grizzly, whilst Figure 7 shows a representation of the projection of the segmented point cloud onto the $XY$ plane’s grid cells.

To make a proper analysis of the breaking success related to each sub-region, it is necessary that these regions ensure that the tip of the chisel makes contact only with the points within the sub-region. In general, the chisel of an impact hammer that would be typically used in mining facilities is a steel cylinder with a diameter between 8 cm and 12 cm, ending in a rounded tip. Considering the most extreme case in which the wear on the tip is maximum, the tip of the hammer would cover the area of a circle with a radius of 6 cm. For this reason, each sub-region is represented as a square of size 12 cm × 12 cm. This design decision ensures that, from a three-dimensional perspective, the contact area between the hammer’s end effector and a rock is always less than the area covered by a given sub-region.

The generation of the sub-regions is obtained using the following method:

• To evaluate whether or not a rock would pass through the grizzly, a rough estimation of its enveloping volume is made. This allows identifying the rocks that, due to their large dimensions, would not be able to easily pass through the grizzly (i.e., the rocks that the system would target during the crushing process). To estimate the rock’s enveloping volume, a 3D bounding box is constructed for each rock, using their respective point cloud. A graphic example of these bounding boxes is illustrated in Figure 8.
• The rocks that would likely pass through the grizzly (because of their low volume) are managed differently by the system, and are not considered during the rock breaking target poses’ search. For instance, there might be rocks that possess a size and shape such that, although they could pass directly through the grizzly, are stuck. These cases are often dealt with by operators by redistributing the material on the grizzly.
  Another possible scenario that is managed differently is when rocks that, due to lack of visibility, are wrongly classified as “small”. This case could happen, for instance, due to occlusions between rocks. These rocks are not considered for the breaking rock target pose generation, since, if they are small, they will likely fall through the grizzly after a material redistribution (performed by the hammer or due to more material being put on the grizzly) and if they are just occluded, it is likely that also because of redistributions of the material they will eventually become completely visible, and thus subject to being a target for the impact hammer.
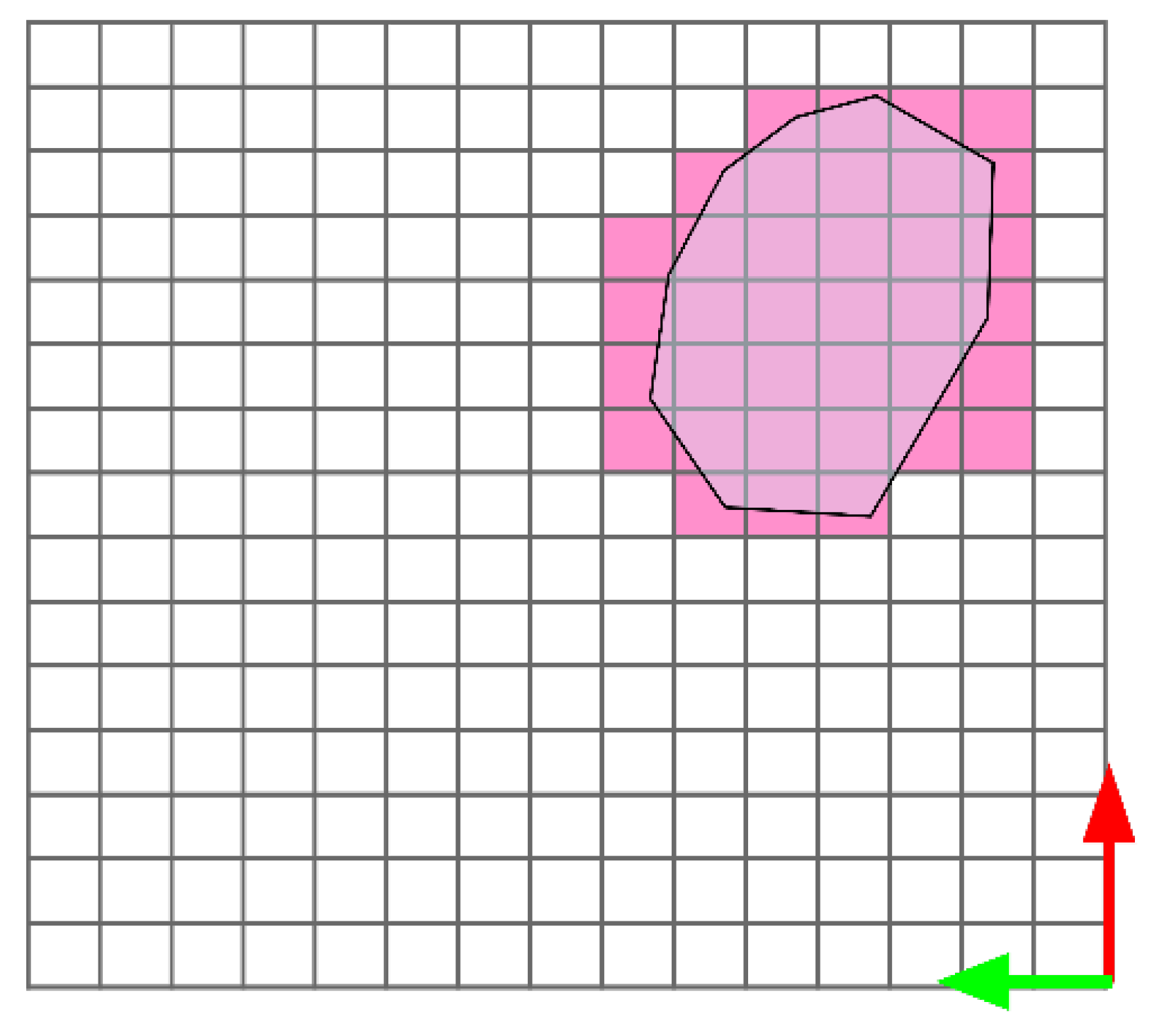
• All the rocks that would not pass through the grizzly (because of their estimated volume) are considered for the breaking rock target pose search. In these cases, the rocks’ corresponding points are grouped considering their position projected in the virtual $XY$ grid cells (described previously). Thus, each of these groups of points is a sub-region associated with a particular rock. An example of these groupings is illustrated in Figure 9.
• Finally, the generated sub-regions that posses a low number of points, or whose points belong to different rocks, are discarded.

2.3.2. Validation of Sub-Regions

Each generated sub-region is analyzed to determine whether or not it would be possible to find a rock breaking target pose within it, according to a set of rules. A sub-region would be discarded if at least one of these rule is not fulfilled. It is convenient to evaluate each rule considering its complexity to minimize the usage of system resources (that is, simpler rules should be evaluated before more complex rules).

For the proposed system design, three rules are considered:

• Rule 1: A vertical orientation of the impact hammer’s end effector has to be maintained.
• Rule 2: The hammers’ end effector should try to break the rocks by hitting them on low curvature regions.
• Rule 3: If a rock is very large, the attempts to break it should start by trying to hit it at its “edges”.

The first rule seeks to ensure that the rock breaking is always done in a vertical orientation (that is, parallel to the Z axis). This is relevant because, when this rule is fulfilled, the impact force goes in the opposite direction of the force with which the rocks are supported on the grizzly. This allows the rock to be held firmly when pressure is applied to it. To evaluate this rule mathematically, the normal component of the surface within the sub-region, $\overrightarrow{n}$, is compared to the desired vertical component (that is, with the unit vector $\overrightarrow{r}={\left(0,0,1\right)}^{⊺}$) to obtain the angular error $ϵ$ between the computed normal vector and $\overrightarrow{r}$. If this angular difference is greater than a predefined tolerance, the rule is considered to be not satisfied. The angular error $ϵ$, in radians, is defined according to Equation (14).

$$ϵ=\arccos \left(\overrightarrow{n}·\overrightarrow{r}\right)$$

(14)

In Figure 10 examples of applying “Rule 1” using different tolerances is illustrated.

The second rule seeks to ensure that the impact hammer does not slip when positioned on a rock. To accomplish this, the curvatures $\rho$ of the surfaces conformed by the points within each sub-region are calculated. If a given curvature exceeds a predefined threshold, this rule is considered to be not satisfied.

The curvature of a given point may be computed along with the normals utilized to evaluate the first rule. To obtain these curvatures, the eigenvalues of the covariance matrix of the neighbor points (relative to the point for which $\overrightarrow{n}$ and/or $\rho$ is being computed) are utilized, thus characterizing the curvature according to Equation (15).

$$\rho =\frac{{\lambda }_0}{{\lambda }_0+{\lambda }_1+{\lambda }_2},{\lambda }_0<{\lambda }_1<{\lambda }_2$$

(15)

In Figure 11 an example of applying “Rule 2” using different curvature thresholds is illustrated.

Finally, the third rule seeks to ensure two conditions that would allow a large rock to be fractured properly. Considering that the effort required to break a large rock by percuting on its geometric center would likely be greater than the effort required to break it by percuting near its edges, the operator manual we used as reference suggests that “large” rocks should be split from their edges to their center. To comply with this guideline, the system selects sub-regions that are not too far from the rocks’ borders. On the other hand, trying to break rocks by percuting too near to their borders would probably be inefficient, as the largest resulting rocks would have a size similar to their related original rock, thus requiring several rock breaking attempts to significantly reduce their size.

Considering both scenarios, the system tries to select sub-regions that are in a certain distance range from the rocks’ borders. To handle this, the position of each sub-region in relation to the edge of a rock is evaluated. If the distance of the sub-region to the borders is outside a range of 30 cm to 60 cm, then the region is discarded.

To calculate the distance of a sub-region to the rock’s borders, the distance between the center of the sub-regions and the point associated to its nearest rock edge is measured. This measurement is performed by projecting both the sub-regions and the rock’s edges to a $XY$ plane.

To find the rocks’ borders, the 2D concave hull algorithm is utilized in the aforementioned $XY$. This allows finding each rocks’ “enveloping points”. Figure 12 shows the effect of applying this method on a 2D point cloud.

There are cases when the rocks present narrow regions that should to be considered as possible rock breaking points because it would be easier to achieve a rock fracture if percuting on them. The “Rule 3”, however, may consider that all the points contained in these narrow regions are too near to the rocks’ borders. For this reason, the system also detects all the narrow regions of as given rock, and uses a lower threshold tolerance on them. This way, sub-regions that would belong to these narrow areas are not discarded.

To find the narrow regions, the system calculates the border-to-border distance on the second eigenvector coordinate system of the rock’s cloud distribution. This way, a region is classified as “narrow” if its border-to-border distance is below a certain threshold. An example of this procedure is illustrated in Figure 13.

With all of the above, Figure 14 shows an example of applying Rule 3 and all its considerations.

2.3.3. Generation and Hierarchization of Rock Breaking Target Poses

A rock breaking pose from each sub-region is generated and then hierarchized. To generate a pose, the sub-region’s center, projected in the $XY$ plane, is assigned as the pose’s position. The pose’s orientation is always predefined as vertical, i.e., with an orientation parallel to ${\left(0,0,-1\right)}^{⊺}$.

To prioritize the obtained target poses, different criteria are combined. This criteria, however, may vary according to the operation state of the rock crushing process (e.g., the system might start by attempting to break the largest rock, but if this rock leaves residues after being fractured, then the following target might be an accessible rock residue instead of another rock). It is also possible to modify the system’s behavior considering a user’s priorities (e.g., it may be preferred by the user to clear a given quadrant of the grizzly if that quadrant is, for instance, utilized to discharge more material).

Currently, three hierarchization criteria are integrated into the system, and they are sequentially executed. These criteria are based on operation manuals and feedback provided by experienced operators, and are the following:

• Criterion 1: Picking the most accessible pose (that is, the pose that can be reached in the shortest possible time).
• Criterion 2: Attempting to break the largest rock.
• Criterion 3: Attempting to clear a specific grizzly’s quadrant.

The purpose of Criterion 1 is to reduce the time that would take the impact hammer to reach the target pose starting from its current pose. To obtain an estimation of this time, it is necessary to know the current configuration of the impact hammer, and to have an inverse kinematics model of it. This allows generating trajectory plans for the hammer (from its pose to a target pose), and consequentially, getting an estimate of the time that it would take the hammer to follow such trajectories.

The result of applying this criterion is a list of ordered target poses according to the time it would take the impact hammer to reach them. The ordering goes from shortest to longest time. Different results obtained after applying Criterion 1 are illustrated in Figure 15.

Criterion 2 is related to starting the breaking rocks’ process addressing the most critical case, since the rock with the largest dimension is the one that produces the greatest spatial obstruction on the grizzly. This criterion is in charge of finding the rock with the largest volume, and keeping track of the target poses associated with that rock, ignoring the rest. Naturally, it is convenient to use this criterion in combination with Criterion 1 for ranking the breaking poses associated with the preferred, largest, rock. An example of this combination is illustrated in Figure 16.

Besides prioritizing a specific quadrant to target rocks, Criterion 3 may establish a termination condition for the operation, as in some cases it is not desired to completely clear the grizzly, but rather to only clear a region to allow the unloading of more material. This is because the process of clearing the grizzly prevents LHDs from unloading material in the ore pass, which in turn, may slow the whole operation, therefore diminishing the production throughput of the mine.

In the rock breaking operation, the grizzly is usually divided into four quadrants within the $XY$ plane. Operating on a given quadrant allows limiting the use of the hammer to that specific quadrant, which is also convenient when trying to reduce the use of the impact hammer whilst ensuring that the grizzly is never completely full. To implement this criterion, all the poses that correspond to a rock outside of the selected quadrant are discarded. An example of using this criterion is illustrated in Figure 17.

3. Experiments

3.1. Experimental Configuration

The proposed system was implemented and continuously tested in simulations during development, using Gazebo [17] and ROS [18]. Furthermore, using ROS allowed us to seamlessly integrate the resulting software to real-world environments for validation.

To evaluate the system, experiments in the real world were conducted. We constructed a scaled experimental setup conformed by a hydraulic mini-excavator (a Bobcat E10 which we modified), a scaled steel grizzly, and four sensors: two Livox MID-40 LiDARs, and two Arecont AV 5225P MIR cameras. This setup is displayed in Figure 18.

Although several scenarios simulating real mining sites’ conditions were built for Gazebo, to adjust the system’s parameters for this setting, and to model the mini-excavator itself, we replicated the real world’s experimental configuration in the simulator, as shown in Figure 19.

To evaluate the performance of the developed system (and its different modules), rocks that would not pass through the grizzly are positioned in several configurations, and both the segmentation of rocks and the generation of target rock-breaking poses are assessed. Although the system may use cameras to detect rocks using visual information, and in this manner, improve the performed instance segmentation, we do not use this part of the system for the real world experiments. In the constructed scenario, the visual cameras are only used to evaluate the system’s performance and rate the generated rock-breaking target poses.

The hydraulic mini-excavator and the scaled steel grizzly have, approximately, a 1:2 scale with respect to a typical impact hammer used in mining sites. Furthermore, the grizzly has 16 cells for which small sized material could pass. Let us assign a pair of indices to each of these cells, counting rows and columns from 1 to 4, as illustrated in Figure 20.

Given the aforementioned, the experiments described in

Table 1. Experimental configurations used to conduct the evaluation of the developed system, in the real world.

Experimental Configuration		Description
1 rock	(i, j)	A single rock is sequentially positioned above the grizzly in a single cell (i, j), for (i, j) ∈ {(1, 1), (1, 4), (4, 1), (4, 4), (2, 2), (2, 3), (3, 2), (3, 3)}.
4 rocks	corners	Four rocks that do not overlap are positioned in the corners of the grizzly, that is, in (1, 1), (1, 4), (4, 1), and (4, 4).
	center	Four rocks that do not overlap are positioned around the center of the grizzly, that is, in (2, 2), (2, 3), (3, 2) and (3, 3).
	center + overlap	Four rocks are again positioned around the center of the grizzly, but this time they overlap.
5 rocks	upper/bottom row	The rocks are sequentially positioned in the upper row, lower row, leftmost
	leftmost/rightmost column	column, and rightmost column of the grizzly. They overlap.
5 to 6 rocks + clutter	upper/bottom row	The same four settings as in the “5 rocks” case are considered (that is, overlapping rocks are sequentially positioned in the upper row, lower row, leftmost
	leftmost/rightmost column	column, and right most column of the grizzly), however, this time small rocks cluttering the environment are present.
8 rocks	center + corners	Eight rocks are positioned in both the corners and the center of the grizzly, without overlap.
	center + overlap	Eight rocks are positioned around the center of the grizzly, overlapping each other.
8 to 9 rocks + clutter	center + corners	The same two configurations for eight rocks are considered, that is, rocks positioned in the corners and center of the grizzly, without overlapping, and
	center + overlap	then near the center of the grizzly, overlapping each other, however, this time small rocks are added to the environment.

were conducted.

To quantitatively measure the system’s performance, the following metrics are considered:

• For the rocks’ segmentation: Precision and recall, measured as if we were detecting rocks. The metrics typically used for segmentation tasks using images (such as the intersection over union) are not utilized, as manually labeling ground truths for the point clouds processed by the system would be highly prone to error.
• For the rocks’ instance segmentation: The number of correctly and incorrectly individualized rocks is measured.
• For the generation of rock-breaking target poses: An average score over the generated poses (limiting the generated poses to a maximum of 10), and an average score over only the highest priority pose are considered. The scores are 1 (bad), 2 (could be improved), and 3 (good), and the evaluation is performed by humans who are knowledgeable about good practices for rock-breaking mining operations. We will refer to the average score over all the generated rock-breaking poses as “Overall Rock-breaking Pose score” (ORP score) and to the average score for the highest priority pose as “Best Rock-breaking Pose score” (BRP score).

3.2. Evaluation Results

According to the configurations described in Table 1, we positioned rocks in the grizzly of the scaled real environment. For each configuration, the proposed system was run and we captured its output, that is, the point cloud containing the rocks’ segmentation (and instance segmentation), and the set of generated target breaking-rock poses. The obtained data were labeled and scored to generate the results presented in

Table 2. Performance metrics for the experiments conducted in the real world. ORP score: Overall Rock-breaking Pose score. BRP score: Best Rock-breaking Pose score.

Experimental Configuration		Segmentation		Instance Segmentation		Rock-Breaking Pose Evaluation
		Precision	Recall	Correct	Incorrect	ORP Score	BRP Score
1 rock	(1,1)	1.0	1.0	1	0	3.00	3.00
	(1,4)	1.0	1.0	1	0	1.67	1.67
	(4,1)	1.0	1.0	1	0	3.00	3.00
	(4,4)	1.0	1.0	1	0	3.00	2.67
	(2,2)	1.0	1.0	1	0	3.00	3.00
	(2,3)	1.0	1.0	1	0	3.00	2.67
	(3,2)	1.0	1.0	1	0	3.00	3.00
	(3,3)	1.0	1.0	1	0	3.00	3.00
4 rocks	corners	1.0	1.0	4	0	2.67	3.00
	center	1.0	1.0	4	0	2.67	3.00
	center + overlap 1	1.0	1.0	0	4	2.33	2.33
	center + overlap 2	1.0	1.0	1	3	2.67	2.67
5 rocks	upper row	1.0	1.0	0	5	3.00	3.00
	bottom row	1.0	1.0	1	4	1.67	1.00
	leftmost column	1.0	1.0	3	2	2.33	2.33
	rightmost column	1.0	1.0	3	2	2.00	2.33
5 to 6 rocks + clutter	upper row	1.0	1.0	1	4	2.33	2.00
	bottom row	1.0	1.0	1	4	2.33	3.00
	leftmost column	1.0	1.0	1	5	2.67	3.00
	rightmost column	1.0	1.0	0	6	2.33	2.67
8 rocks	center + corners 1	1.0	1.0	8	0	2.67	3.00
	center + corners 2	1.0	1.0	8	0	2.67	2.33
	center + corners 3	1.0	1.0	8	0	2.67	3.00
	center + overlap 1	1.0	1.0	3	5	2.33	3.00
	center + overlap 2	1.0	1.0	2	6	2.33	3.00
	center + overlap 3	1.0	1.0	2	6	3.00	3.00
8 to 9 rocks + clutter	center + corners 1	1.0	1.0	5	4	3.00	3.00
	center + corners 2	1.0	1.0	4	5	2.33	3.00
	center + corners 3	1.0	1.0	2	7	3.00	3.00
	center + overlap 1	1.0	1.0	1	7	3.00	3.00
	center + overlap 2	1.0	1.0	1	7	2.33	3.00
	center + overlap 3	1.0	1.0	2	7	2.67	3.00

. A summary of the scores provided by experts, regarding the generated target poses’ quality, is presented in

Table 3. Summary of the performance metrics for the target poses’ quality. ORP score: Overall Rock-breaking Pose score. BRP score: Best Rock-breaking Pose score.

Experimental Configuration		Rock-Breaking Pose Evaluation
		ORP Score	BRP Score
1 rock	8 trials	2.83	2.75
4 rocks	4 trials	2.59	2.75
5 rocks	4 trials	2.25	2.17
5 to 6 rocks + clutter	4 trials	2.42	2.67
8 rocks	6 trials	2.61	2.89
8 to 9 rocks + clutter	6 trials	2.72	3.0

. Finally, some examples of the performed experiments are shown in Figure 21.

4. Discussion

The obtained results, presented in Table 2, provide information that allows characterizing the system’s overall performance, as well as its strengths and weaknesses. As the proposed system performs several operations (each of them with a given output), we will divide the analysis based on its segmentation, instance segmentation, and rock-breaking pose generation performance.

4.1. Segmentation

The data presented in Table 2 show that the system’s segmentation performance is approximately perfect. This result is expected, as the segmentation process is fundamentally a background subtraction method, where the points corresponding to the rocks are separated from those that belong to an environment model that is constructed when no material above the grizzly is present.

Following this approach results in an almost perfect segmentation, where the main challenge corresponds to the creation of the environment model, the parameterization of the workspace to filter unwanted LIDAR measurements, the correct construction of the simplified geometric model of the impact hammer, and the calibration of the sensors.

Taking into account that the environment model and the workspace are relatively easy to construct, the main weakness of the segmentation subsystem is that it depends on the grizzly not moving relative to the LIDARs, and the impact hammer’s encoders providing correct measurements, that is, it mainly relies on proper sensor calibration.

4.2. Instance Segmentation

The data show that the instance segmentation performance for all the experiments when no overlapping between rocks occurs is correct (that is, experimental configurations “1 rock”, “4 rocks corners and center”, and “8 rocks center + corners”). This result showcases that the instance segmentation subsystem easily differentiates rocks when they are represented by disconnected clusters of points.

When there are overlapping rocks (be these the rocks that should be targeted by the impact hammer, or small sized boulders that have not passed through the grizzly), the instance segmentation subsystem fails to achieve a good performance. This behavior may be explained due to the difficulty of differentiating rock instances by only relying on the information provided by the rocks’ segmented point cloud.

However, it is important to remark that the main objective of the developed system is not to accurately represent each rock, but to characterize them with enough accuracy to select the best possible rock-breaking pose (which is, conceptually, one of the tasks the operators of impact hammers currently perform).

In addition, even though a correct instance segmentation is difficult to achieve when overlapping occurs, since the rock’s segmentation is approximately perfect (refer to Section 4.1), no information regarding where the rocks are located is lost for the target rock-breaking poses generation step.

4.3. Rock-Breaking Pose Generation

The obtained results show that, in most cases, the rock-breaking target poses generated by the system are appropriate, both when rating all of them (ORP score) and when only rating the highest priority pose (BRP score). It is important to remember that the goal of the proposed system is to determine a rock-breaking target pose for the hammer. This is achieved in most cases.

Furthermore, by inspecting the results presented in Table 2, it is noted that the BRP score is, in general, higher than the ORP score. As the criteria to prioritize a target rock-breaking pose over other poses are related to factors such as the impact hammer’s end effector pose, or a quadrant, the variation on the rocks’ overall shape (product of a bad instance segmentation), or the presence of multiple rocks (resulting in a scenario where it would be difficult to determine which rock should be fragmented first), it is not going to necessarily negatively alter the quality of the generated highest priority pose, as its priority largely depends on factors based on geometric measures and overall rock segmentation, and not on a proper rock individualization.

We recognize, however, that there might be situations where the quality of the target rock-breaking poses would be affected by a bad instance segmentation. This could happen, for instance, when small boulders artificially make a potential target rock appear larger than what it really is. This might result in target poses being generated near the edge of the rock that needs to be fragmented, or worse yet, on top of the small boulders.

The BRP being in general rated higher than the ORP is also a positive metric for the developed system, since it is the highest rated pose the only pose that the impact hammer would attempt to break. After this attempt, the system would be run again to obtain an updated characterization of the environment and select the best possible target rock-breaking pose, attempt to break the associated rock, and repeat the cycle.

5. Conclusions

In this paper we presented a system for generating and selecting rock-breaking target poses for impact hammers. The system and its components were described, and a real-world performance evaluation was conducted to assess its capabilities. It was found that the proposed system can generate rock-breaking target poses for the rock-breaking task performed by impact hammers in mining operations in a reliable way, complying with standard rules of operation and different criteria to prioritize poses.

6. Patents

This research has a PCT patent application on WIPO under the title “METHOD AND SYSTEM FOR DETERMINING AND SELECTING ROCK BREAKING TARGET POSES FOR A ROCK BREAKER” (application number: PCT/IB2021/059373) [10].