Reinforcement Learning: Theory and Applications in HEMS
Abstract
:1. Introduction
2. Home Energy Management Systems
2.1. Networking and Communication
2.2. Sensors and Controller Platforms
2.3. Control Algorithms
3. Overview of Reinforcement Learning
3.1. Deep Neural Networks
3.2. Reinforcement Learning
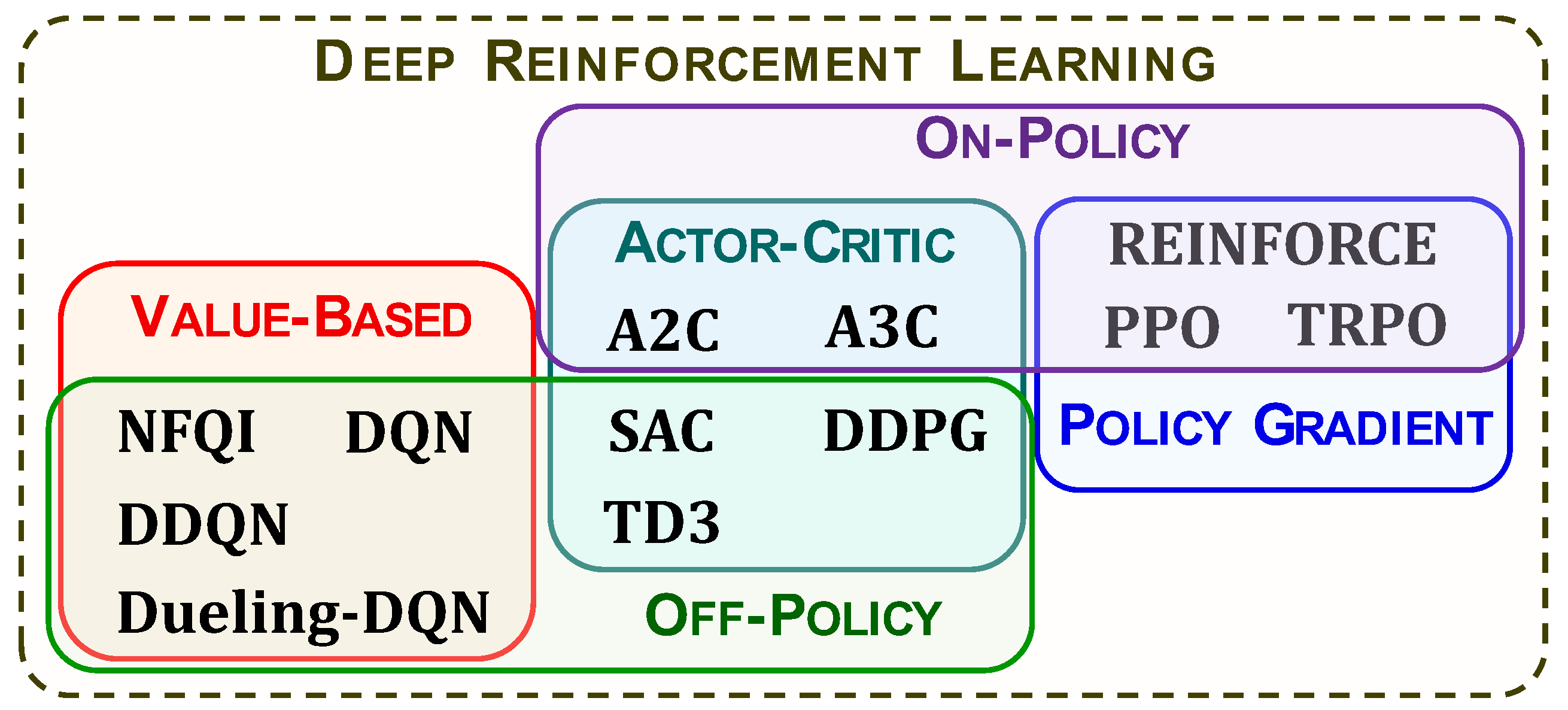
3.3. Taxonomy of Algorithms
4. Value-Based Reinforcement Learning
4.1. Tabular Q-Learning
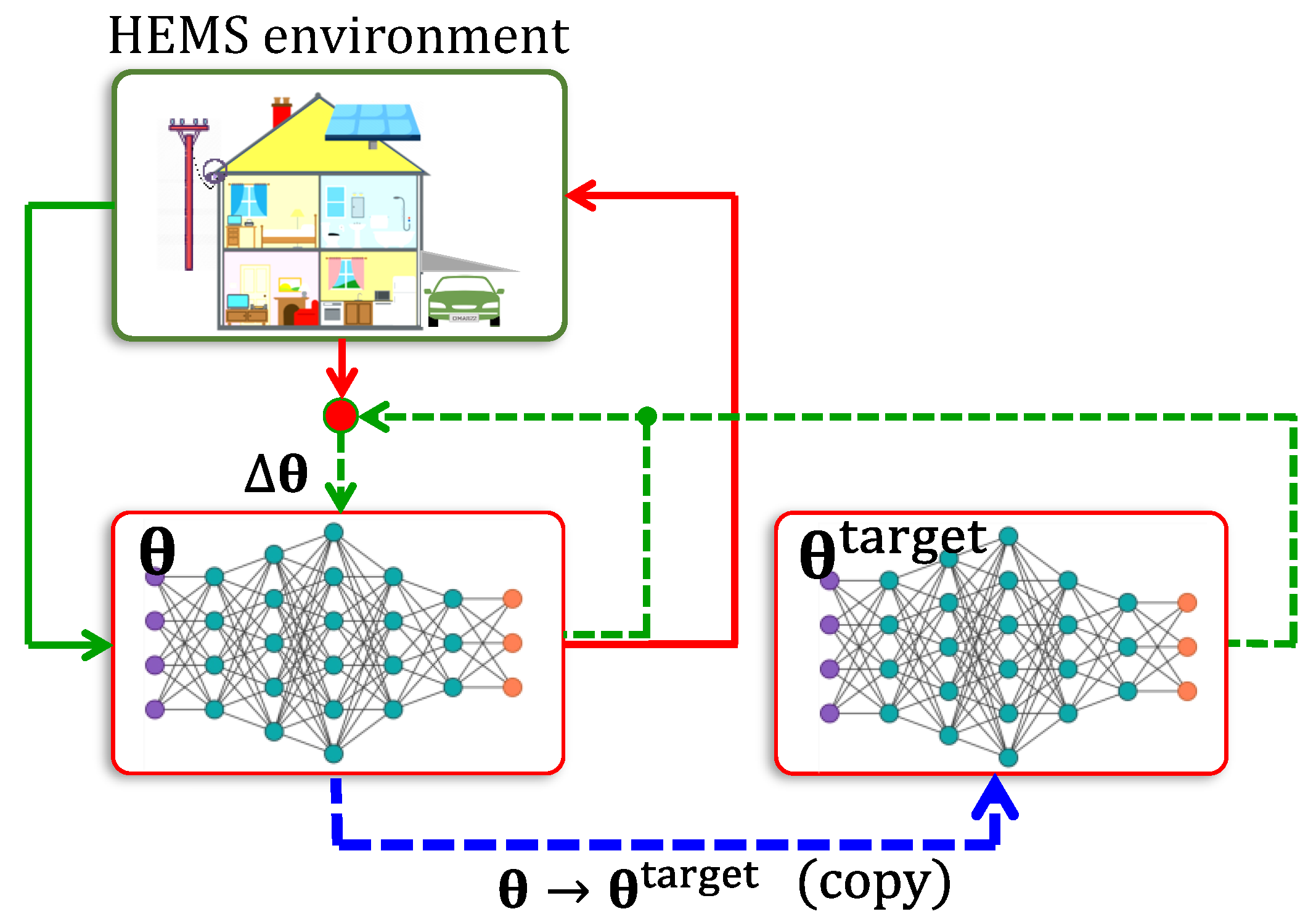
4.2. Deep Q-Networks
- (i)
- A different DNN for each action is maintained, so that the total of DNNs in this arrangement is . The state (encoded appropriately using the state’s features), serves as the common input to all the DNNs.
- (ii)
- A single DNN with separate inputs for state and action is maintained and its output is . While this manner of storing Q-values requires the use of only a single DNN, in order to obtain , the actions must be applied sequentially to it.
5. Policy-Based and Actor–Critic Reinforcement Learning
5.1. Deep Policy Networks
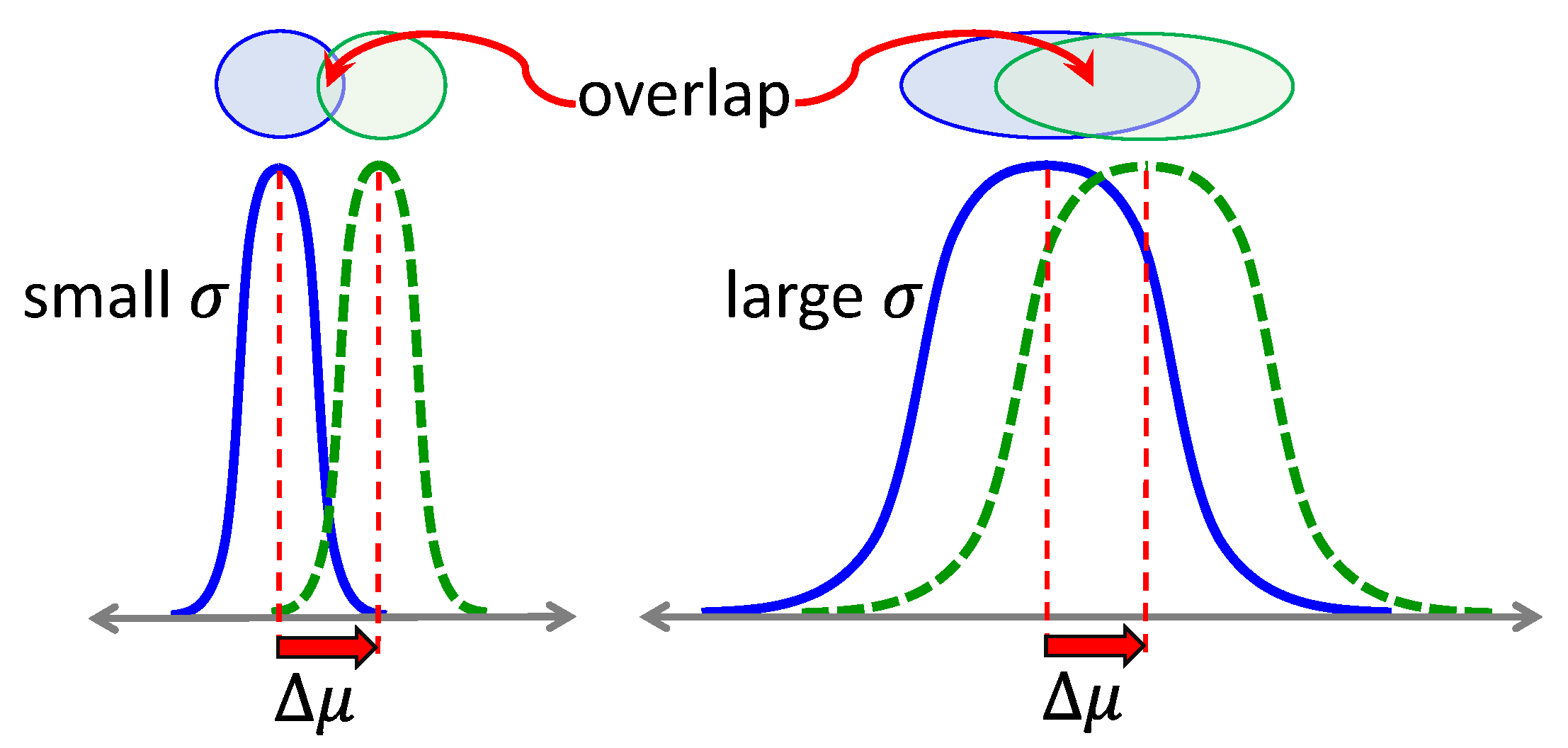
5.2. Natural Gradient Methods
5.3. Off-Policy Methods
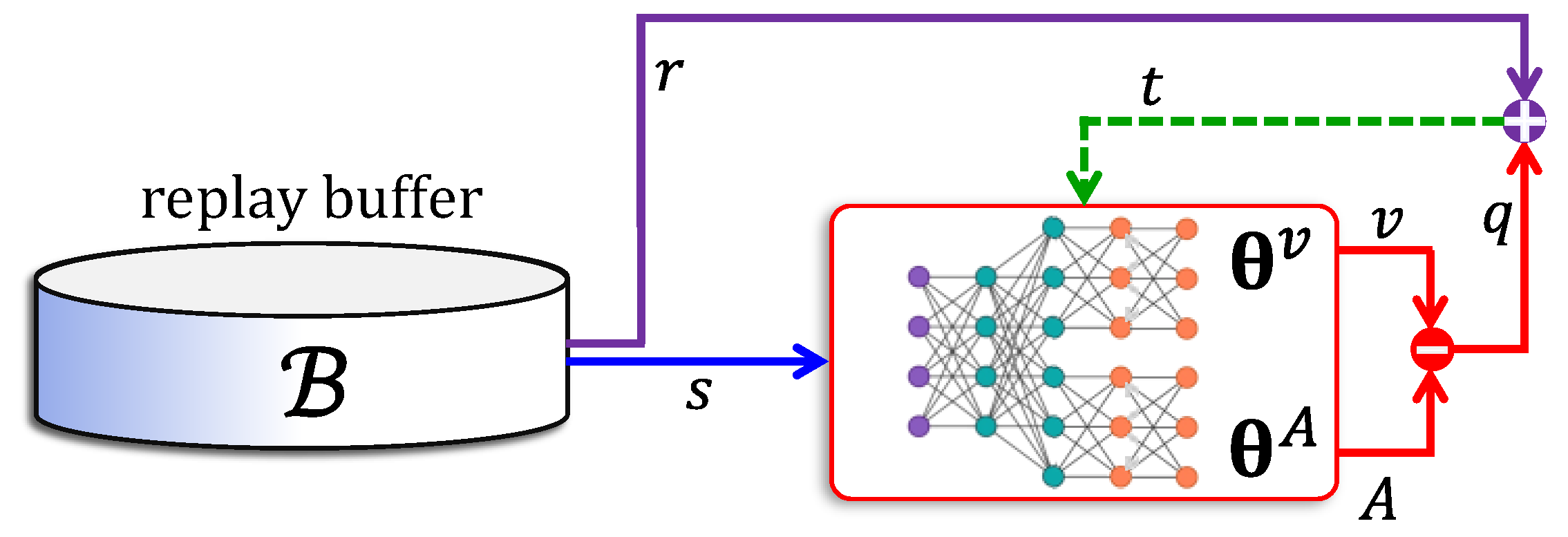
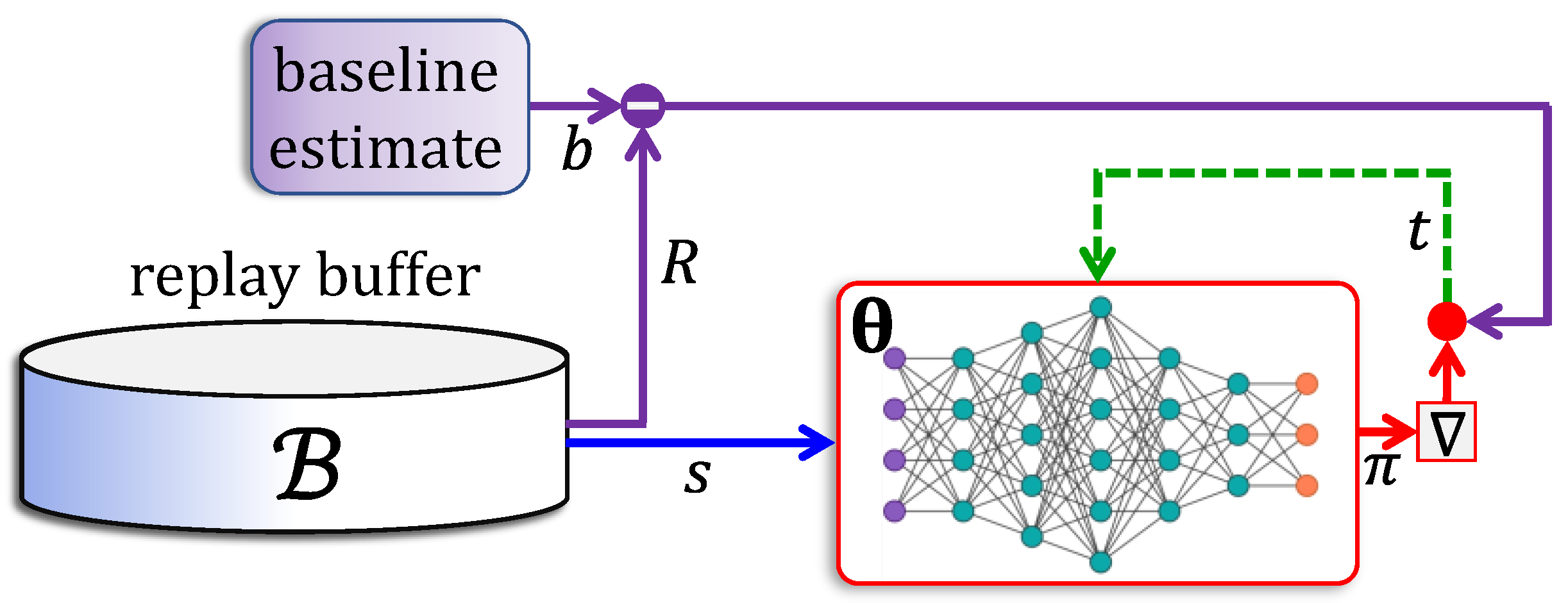
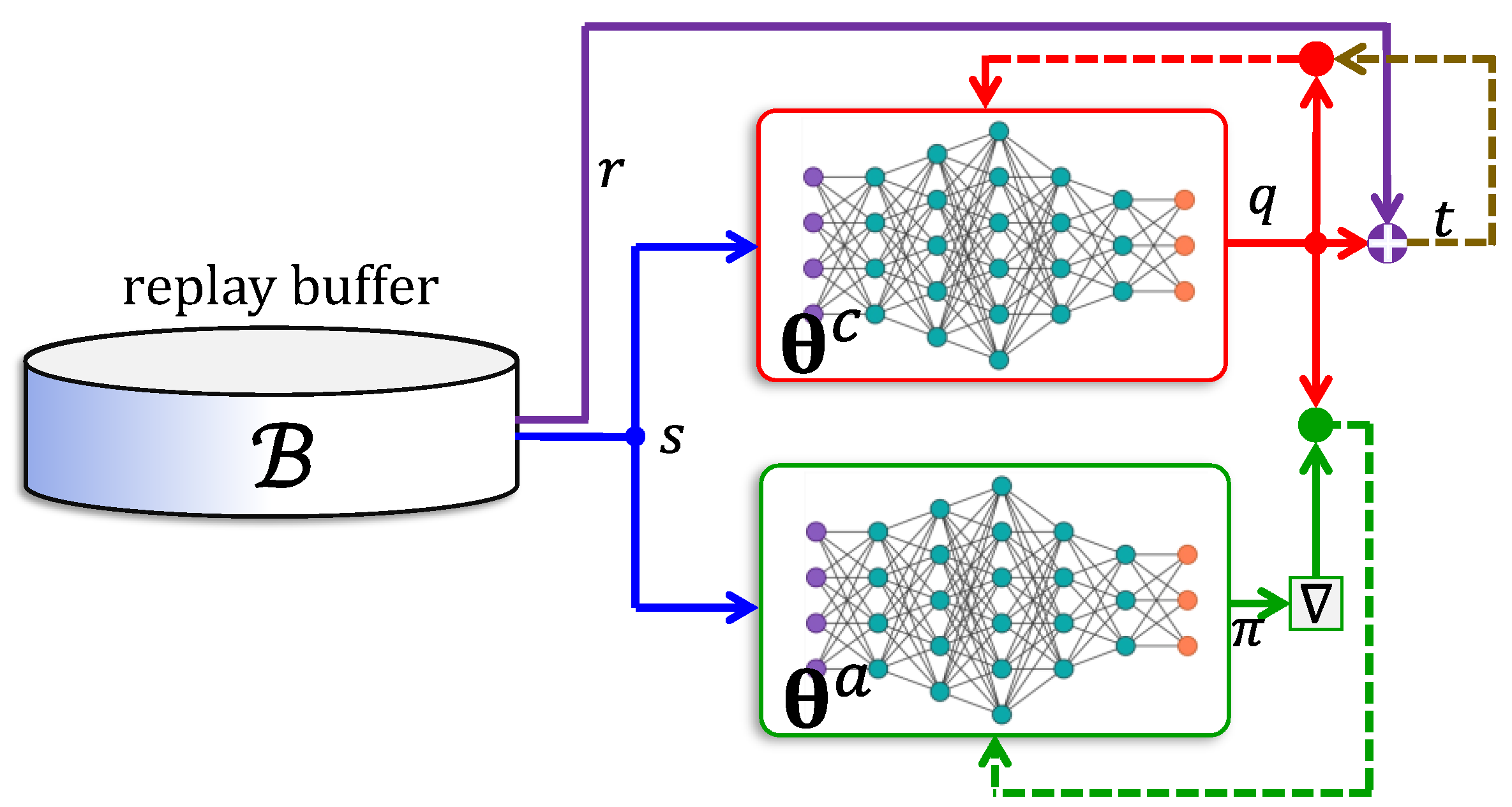
5.4. Actor–Critic Networks
- (i)
- The actor network uses an advantage function , which is the difference between a return value and the value of state . Accordingly, the critic is trained to approximate the value function.
- (ii)
- The reward is computed using a -step lookahead feature, where the log-gradient is weighted using the sum of the next rewards.
- (i)
- can be sampled for several different actions and be assigned the action corresponding to the sample maximum [96].
- (ii)
- A convex approximation of around can be devised and obtained over the approximate function [97].
- (iii)
- A separate off-policy policy network can be used to learn the optimal policy [98].
6. Use of Reinforcement Learning in Home Energy Management Systems
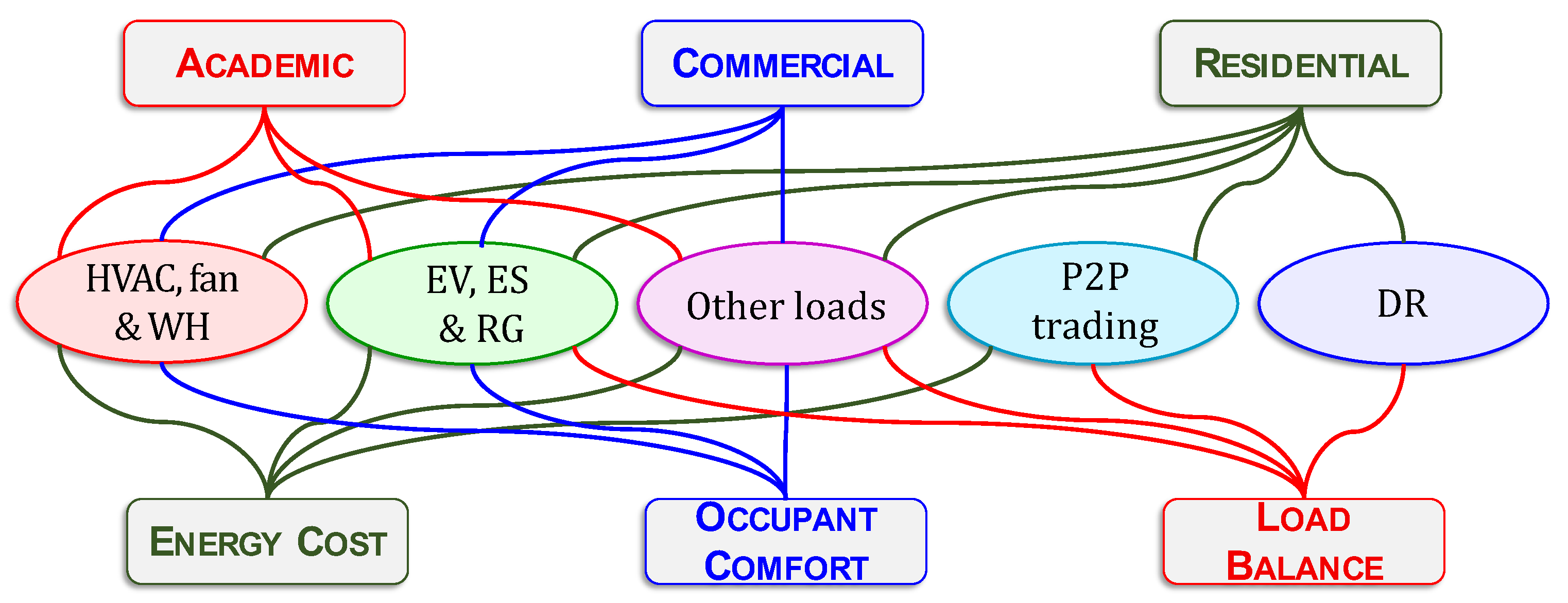
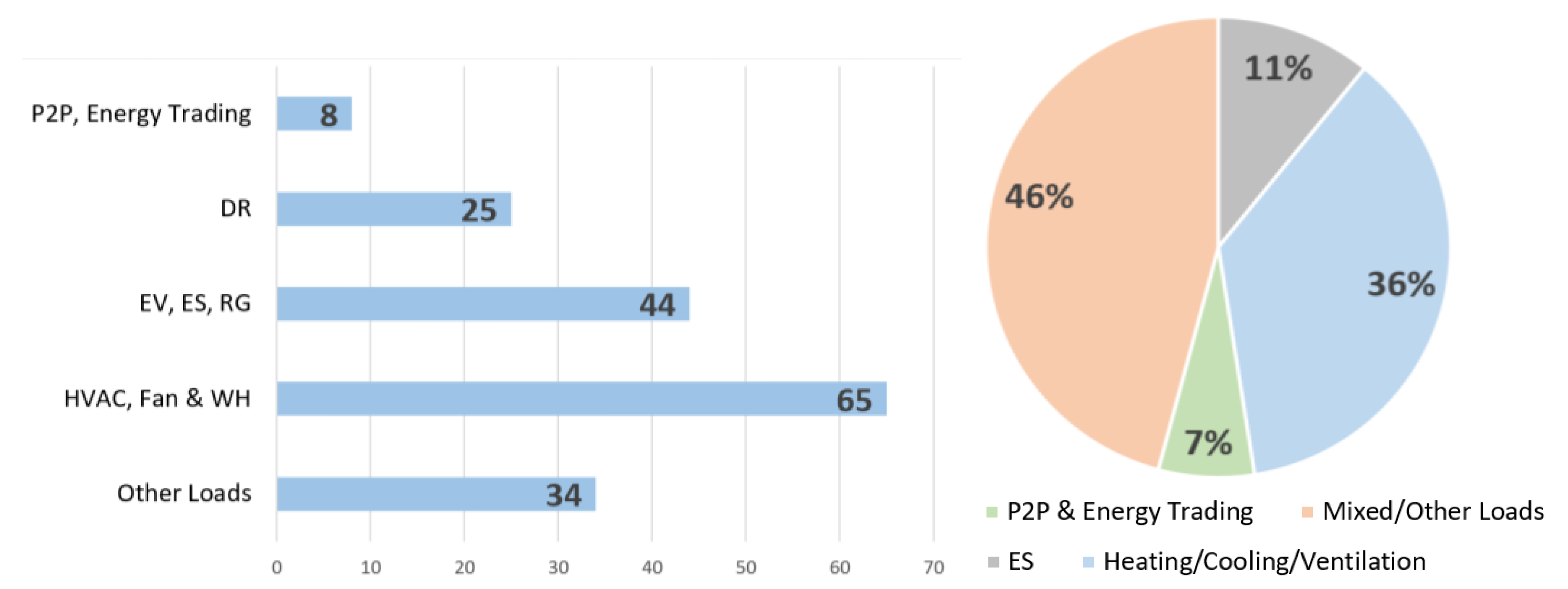
6.1. Application Classes
- (i)
- Heating, Ventilation and Air Conditioning, Fans and Water Heaters: Heating, ventilation, and air conditioning (HVAC) systems alone are responsible for about half of the total electricity consumption [48,101,102,103,104]. In this survey, HVAC, fans and water heaters (WH) have been placed under a single category. Effective control of these loads is a major research topic in HEMS.
- (ii)
- Electric Vehicles, Energy Storage, and Renewable Generation: The charging of electric vehicles (EVs) and energy storage (ES) devices, i.e., batteries are studied in the literature as in [105,106]. Wherever applicable, EV and ES must be charged in coordination with renewable generation (RG) such as solar panels and wind turbines. The aim is to make decisions in order to save energy costs, while addressing comfort and other consumer requirements. Thus, EV, ES, and RG have been placed under a single class for the purpose of this survey.
- (iii)
- Other Loads: Suitable scheduling of several home appliances such as dishwasher, washing machine, etc., can be achieved through HEMS to save energy usage or cost. Lighting schedules are important in buildings with large occupancy. These loads have been lumped into a single class.
- (iv)
- Demand Response: With the rapid proliferation of green energies into homes and buildings, and these sources merged into the grid, demand response (DR) has acquired much research significance in HEMS. DR programs help in load balancing, by scheduling and/or controlling shiftable loads and in incentivizing participants [107,108] to do so through HEMS. RL for DR is one of the classes in this survey.
- (v)
- Peer-to-Peer Trading: Home energy management has been used to maximize the profit for the prosumers by trading the electricity with each other directly in peer-to-peer (P2P) trading or indirectly through a third party as in [109]. Currently, theoretical research on automated trading is receiving significant attention. P2P trading is the fifth and final application category to have been considered in this survey.
6.2. Objectives and Building Types
- (i)
- Energy Cost: The cost of using any electrical device by the consumer and in most of the cases it is proportionally related to its energy consumption. In this paper we use the terms ‘cost’ and ‘consumption’ interchangeably.
- (ii)
- Occupant Comfort: the main factor that can affect the occupant’s comfort is the thermal comfort, which depends mainly on the room temperature and humidity.
- (iii)
- Load Balance: Power supply companies try to achieve load balance by reducing the power consumption of consumers at peak periods to match the station power supply. The consumers are motivated to participate in such programs by price incentives.
- (i)
- Residential: for the purpose of this survey, individual homes, residential communities, as well as apartment complexes fall under this type of building.
- (ii)
- Commercial: these buildings include offices, office complexes, shops, malls, hotels, as well as industrial buildings.
- (iii)
- Academic: academic buildings range from schools, university classrooms, buildings, research laboratories, up to entire campuses.
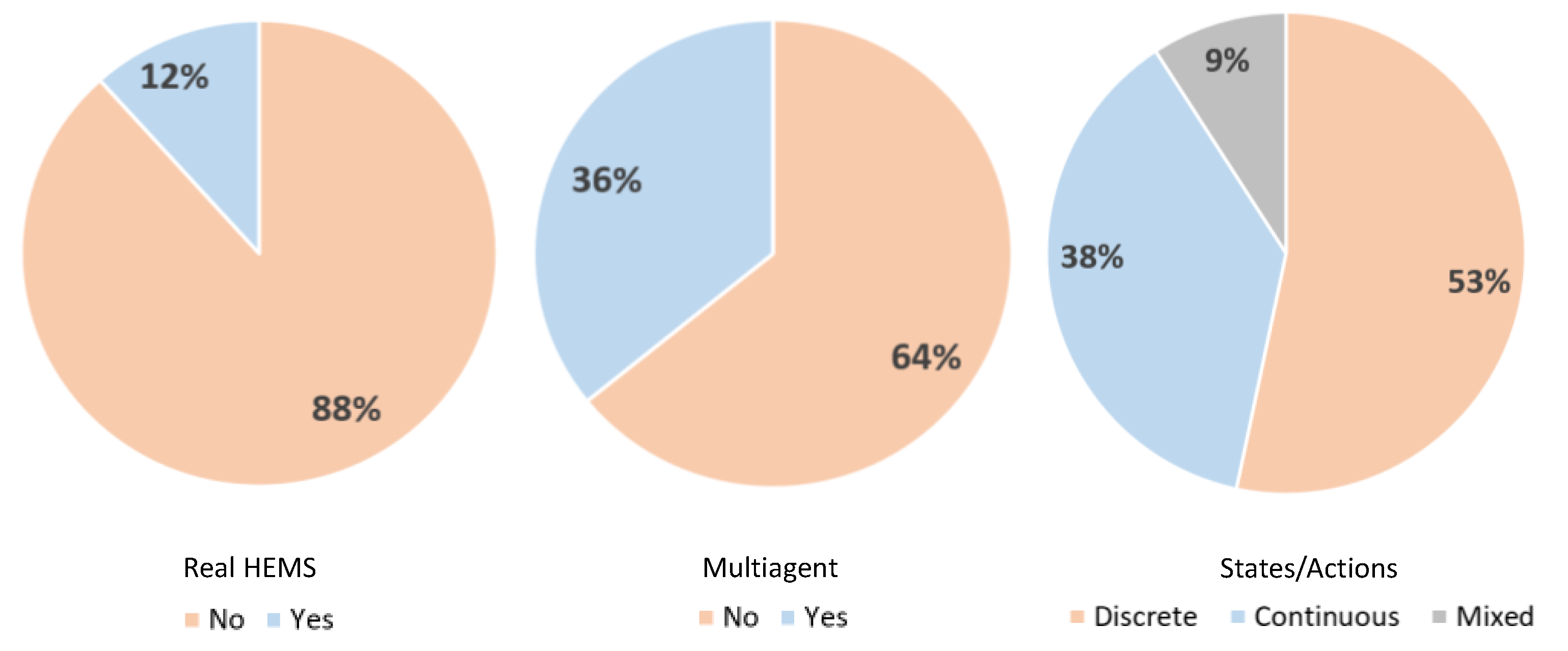
6.3. Deployment, Multi-Agents, and Discretization
7. Reinforcement Learning Algorithms in Home Energy Management Systems
8. Conclusions
- (i)
- Although 66% of all articles used deep RL, many articles used tabular learning. This may indicate that only simplified application were considered.
- (ii)
- Around 53% of all articles used discrete states and actions. This is another indication that the HEMS scenarios may have been simplified.
- (iii)
- Around 12% of all approaches covered in this survey were deployed in the real world, their use being limited to simulation platforms only.
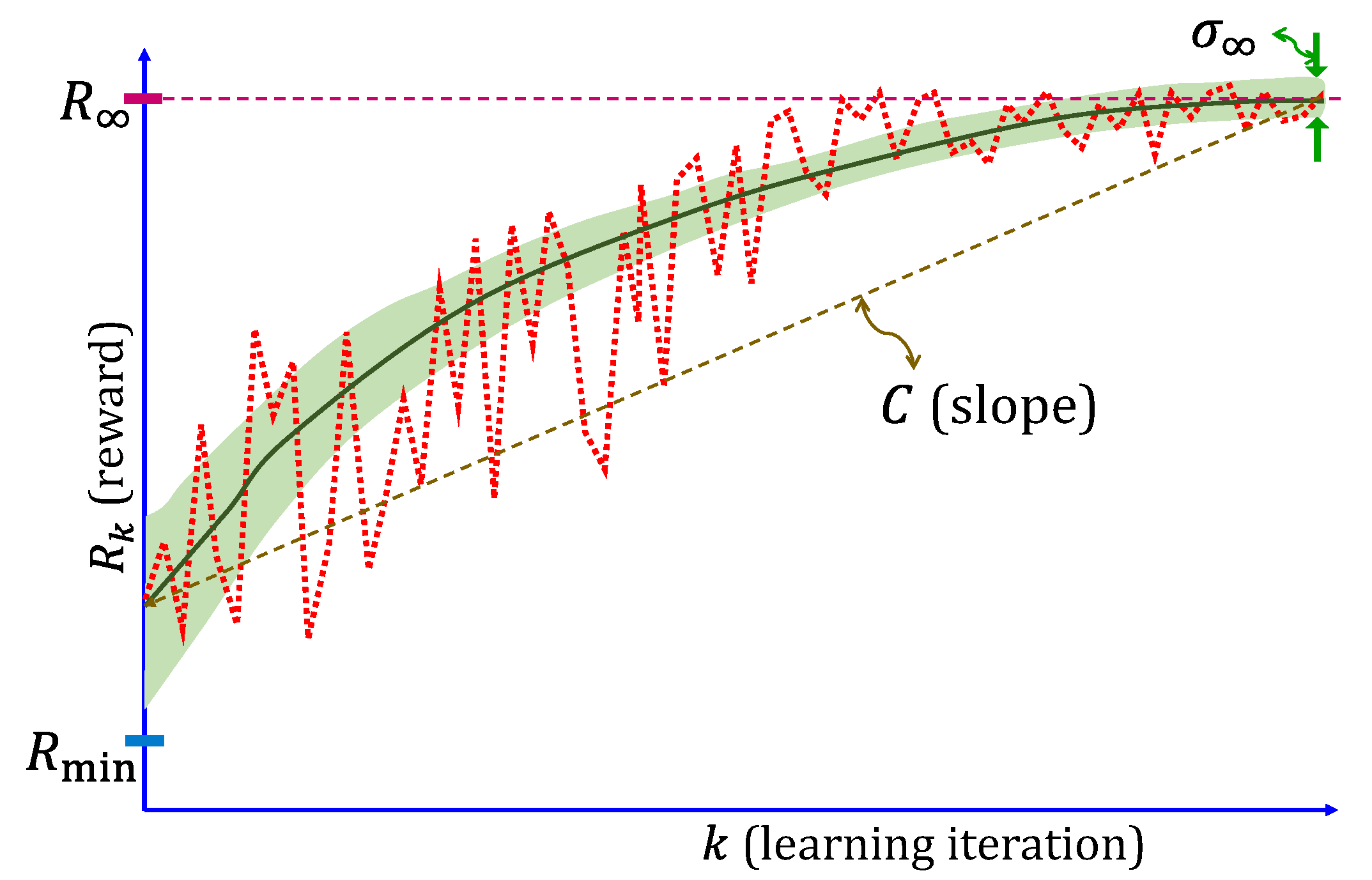
- (i)
- Saturation reward (): the expected reward must be relatively high at saturation.
- (ii)
- Variance at saturation (): the reward must not have excessive variance at saturation.
- (iii)
- Exploitation risk (): The minimum possible reward must not be so low that the environment is adversely affected. This is the risk associated with exploration and tends to occur during the initial exploratory stages of the RL training.
- (iv)
- Convergence rate (): the number of iterations before the reward starts to saturate should not be large.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- U.S. Energy Information Administration. Electricity Explained: Use of Electricity. 14 May 2021. Available online: www.eia.gov/energyexplained/electricity/use-of-electricity.php (accessed on 10 April 2022).
- Center for Sustainable Systems. U.S. Energy System Factsheet. Pub. No. CSS03-11; Center for Sustainable Systems, University of Michigan: Ann Arbor, MI, USA, 2021; Available online: https://css.umich.edu/publications/factsheets/energy/us-energy-system-factsheet (accessed on 10 April 2022).
- Shakeri, M.; Shayestegan, M.; Abunima, H.; Reza, S.S.; Akhtaruzzaman, M.; Alamoud, A.; Sopian, K.; Amin, N. An intelligent system architecture in home energy management systems (HEMS) for efficient demand response in smart grid. Energy Build. 2017, 138, 154–164. [Google Scholar] [CrossRef]
- Leitão, J.; Gil, P.; Ribeiro, B.; Cardoso, A. A survey on home energy management. IEEE Access 2020, 8, 5699–5722. [Google Scholar] [CrossRef]
- Shareef, H.; Ahmed, M.S.; Mohamed, A.; Al Hassan, E. Review on Home Energy Management System Considering Demand Responses, Smart Technologies, and Intelligent Controllers. IEEE Access 2018, 6, 24498–24509. [Google Scholar] [CrossRef]
- Mahapatra, B.; Nayyar, A. Home energy management system (HEMS): Concept, architecture, infrastructure, challenges and energy management schemes. Energy Syst. 2019, 13, 643–669. [Google Scholar] [CrossRef]
- Dileep, G. A survey on smart grid technologies and applications. Renew. Energy 2020, 146, 2589–2625. [Google Scholar] [CrossRef]
- Zafar, U.; Bayhan, S.; Sanfilippo, A. Home energy management system concepts, configurations, and technologies for the smart grid. IEEE Access 2020, 8, 119271–119286. [Google Scholar] [CrossRef]
- Alanne, K.; Sierla, S. An overview of machine learning applications for smart buildings. Sustain. Cities Soc. 2022, 76, 103445. [Google Scholar] [CrossRef]
- Aguilar, J.; Garces-Jimenez, A.; R-Moreno, M.D.; García, R. A systematic literature review on the use of artificial intelligence in energy self-management in smart buildings. Renew. Sustain. Energy Rev. 2021, 151, 111530. [Google Scholar] [CrossRef]
- Himeur, Y.; Ghanem, K.; Alsalemi, A.; Bensaali, F.; Amira, A. Artificial intelligence based anomaly detection of energy consumption in buildings: A review, current trends and new perspectives. Appl. Energy 2021, 287, 116601. [Google Scholar] [CrossRef]
- Barto, A.G.; Sutton, R.S.; Anderson, C.W. Neuronlike elements that can solve difficult learning control problems. IEEE Trans. Syst. Man Cybern. 1983, 13, 835–846. [Google Scholar] [CrossRef]
- Tesauro, G. TD-Gammon, a self-teaching backgammon program, achieves master-level play. Neural Comput. 1994, 6, 215–219. [Google Scholar] [CrossRef]
- Peters, J.; Schaal, S. Reinforcement learning of motor skills with policy gradients. Neural Netw. 2008, 21, 682–697. [Google Scholar] [CrossRef]
- Mnih, V.; Kavukcuoglu, K.; Silver, D.; Rusu, A.A.; Veness, J.; Bellemare, M.G.; Graves, A.; Riedmiller, M.; Fidjeland, A.K.; Ostrovski, G.; et al. Human-level control through deep reinforcement learning. Nature 2015, 518, 529–533. [Google Scholar] [CrossRef]
- Silver, D.; Huang, A.; Maddison, C.J.; Guez, A.; Sifre, L.; van den Driessche, G.; Schrittwieser, J.; Antonoglou, I.; Panneershelvam, V.; Lanctot, M.; et al. Mastering the game of Go with deep neural networks and tree search. Nature 2016, 529, 484–489. [Google Scholar] [CrossRef]
- Silver, D.; Schrittwieser, J.; Simonyan, K.; Antonoglou, I.; Huang, A.; Guez, A.; Hubert, T.; Baker, L.; Lai, M.; Bolton, A.; et al. Mastering the game of Go without human knowledge. Nature 2017, 550, 354–359. [Google Scholar] [CrossRef]
- Arulkumaran, K.; Deisenroth, M.P.; Brundage, M.; Bharath, A.A. A brief survey of deep reinforcement learning. IEEE Signal Process. Mag. 2017, 34, 26–38. [Google Scholar] [CrossRef]
- François-Lavet, V.; Henderson, P.; Islam, R.; Bellemare, M.G.; Pineau, J. An introduction to deep reinforcement learning. Found. Trends Mach. Learn. 2018, 11, 219–354. [Google Scholar] [CrossRef]
- Silver, D.; Singh, S.; Precup, D.; Sutton, R.S. Reward is enough. Artif. Intell. 2021, 299, 103535. [Google Scholar] [CrossRef]
- Goertzel, B. Artificial General Intelligence; Pennachin, C., Ed.; Springer: New York, NY, USA, 2007; Volume 2. [Google Scholar]
- Zhang, T.; Mo, H. Reinforcement learning for robot research: A comprehensive review and open issues. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211007305. [Google Scholar] [CrossRef]
- Bhagat, S.; Banerjee, H.; Tse, Z.T.H.; Ren, H. Deep reinforcement learning for soft, flexible robots: Brief review with impending challenges. Robotics 2019, 8, 4. [Google Scholar] [CrossRef] [Green Version]
- Lee, C.; An, D. AI-Based Posture Control Algorithm for a 7-DOF Robot Manipulator. Machines 2022, 10, 651. [Google Scholar] [CrossRef]
- Shakhatreh, H.; Sawalmeh, A.H.; Al-Fuqaha, A.; Dou, Z.; Almaita, E.; Khalil, I.; Othman, N.S.; Khreishah, A.; Guizani, M. Unmanned Aerial Vehicles (UAVs): A survey on civil applications and key research challenges. IEEE Access 2019, 7, 48572–48634. [Google Scholar] [CrossRef]
- Zeng, F.; Wang, C.; Ge, S.S. A survey on visual navigation for artificial agents with deep reinforcement learning. IEEE Access 2020, 8, 135426–135442. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, W.; Yu, R.; Zhang, Y. Motion planning for mobile robots-focusing on deep reinforcement learning: A systematic review. IEEE Access 2021, 9, 69061–69081. [Google Scholar] [CrossRef]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.-C.; Kim, D.I. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Zhang, G.; Li, Y.; Niu, Y.; Zhou, Q. Anti-jamming path selection method in a wireless communication network based on Dyna-Q. Electronics 2022, 11, 2397. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, J.; Wang, H.; Shen, X.; Wang, B.; Dong, Y. Deep reinforcement learning-based adaptive modulation for underwater acoustic communication with outdated channel state information. Remote Sens. 2022, 14, 3947. [Google Scholar] [CrossRef]
- Ullah, Z.; Al-Turjman, F.; Mostarda, L. Cognition in UAV-aided 5G and beyond communications: A survey. IEEE Trans. Cogn. Commun. Netw. 2020, 6, 872–891. [Google Scholar] [CrossRef]
- Nguyen, T.T.; Reddi, V.J. Deep reinforcement learning for cyber security. arXiv 2019, arXiv:1906.05799. [Google Scholar] [CrossRef] [PubMed]
- Alavizadeh, H.; Alavizadeh, H.; Jang-Jaccard, J. Deep Q-Learning Based Reinforcement Learning Approach for Network Intrusion Detection. Computers 2022, 11, 41. [Google Scholar] [CrossRef]
- Jin, Z.; Zhang, S.; Hu, Y.; Zhang, Y.; Sun, C. Security state estimation for cyber-physical systems against DoS attacks via reinforcement learning and game theory. Actuators 2022, 11, 192. [Google Scholar] [CrossRef]
- Zhu, H.; Cao, Y.; Wang, W.; Jiang, T.; Jin, S. Deep reinforcement learning for mobile edge caching: Review, new features, and open issues. IEEE Netw. 2018, 32, 50–57. [Google Scholar] [CrossRef]
- Liu, Y.; Wu, F.; Lyu, C.; Li, S.; Ye, J.; Qu, X. Deep dispatching: A deep reinforcement learning approach for vehicle dispatching on online ride-hailing platform. Transp. Res. Part E Logist. Transp. Rev. 2022, 161, 102694. [Google Scholar] [CrossRef]
- Liu, S.; See, K.C.; Ngiam, K.Y.; Celi, L.A.; Sun, X.; Feng, M. Reinforcement learning for clinical decision support in critical care: Comprehensive review. J. Med. Internet Res. 2020, 22, e18477. [Google Scholar] [CrossRef]
- Elavarasan, D.; Vincent, P.M.D. Crop yield prediction using deep reinforcement learning model for sustainable agrarian applications. IEEE Access 2020, 8, 86886–86901. [Google Scholar] [CrossRef]
- Garnier, P.; Viquerat, J.; Rabault, J.; Larcher, A.; Kuhnle, A.; Hachem, E. A review on deep reinforcement learning for fluid mechanics. Comput. Fluids 2021, 225, 104973. [Google Scholar] [CrossRef]
- Cheng, L.-C.; Huang, Y.-H.; Hsieh, M.-H.; Wu, M.-E. A novel trading strategy framework based on reinforcement deep learning for financial market predictions. Mathematics 2021, 9, 3094. [Google Scholar] [CrossRef]
- Kim, S.-H.; Park, D.-Y.; Lee, K.-H. Hybrid deep reinforcement learning for pairs trading. Appl. Sci. 2022, 12, 944. [Google Scholar] [CrossRef]
- Zhu, T.; Zhu, W. Quantitative trading through random perturbation Q-network with nonlinear transaction costs. Stats 2022, 5, 546–560. [Google Scholar] [CrossRef]
- Zhang, D.; Han, X.; Deng, C. Review on the research and practice of deep learning and reinforcement learning in smart grids. CSEE J. Power Energy Syst. 2018, 4, 362–370. [Google Scholar] [CrossRef]
- Zhang, Z.; Zhang, D.; Qiu, R.C. Deep reinforcement learning for power system applications: An overview. CSEE J. Power Energy Syst. 2020, 6, 213–225. [Google Scholar] [CrossRef]
- Jogunola, O.; Adebisi, B.; Ikpehai, A.; Popoola, S.I.; Gui, G.; Gacanin, H.; Ci, S. Consensus algorithms and deep reinforcement learning in energy market: A review. IEEE Internet Things J. 2021, 8, 4211–4227. [Google Scholar] [CrossRef]
- Perera, A.T.D.; Kamalaruban, P. Applications of reinforcement learning in energy systems. Renew. Sustain. Energy Rev. 2021, 137, 110618. [Google Scholar] [CrossRef]
- Chen, X.; Qu, G.; Tang, Y.; Low, S.; Li, N. Reinforcement learning for selective key applications in power systems: Recent advances and future challenges. IEEE Trans. Smart Grid 2022, 13, 2935–2958. [Google Scholar] [CrossRef]
- Mason, K.; Grijalva, S. A review of reinforcement learning for autonomous building energy management. Comput. Electr. Eng. 2019, 78, 300–312. [Google Scholar] [CrossRef]
- Wang, Z.; Hong, T. Reinforcement learning for building controls: The opportunities and challenges. Appl. Energy 2020, 269, 115036. [Google Scholar] [CrossRef]
- Han, M.; May, R.; Zhang, X.; Wang, X.; Pan, S.; Yan, D.; Jin, Y.; Xu, L. A review of reinforcement learning methodologies for controlling occupant comfort in buildings. Sustain. Cities Soc. 2019, 51, 101748–101762. [Google Scholar] [CrossRef]
- Yu, L.; Qin, S.; Zhang, M.; Shen, C.; Jiang, T.; Guan, X. A review of deep reinforcement learning for smart building energy management. IEEE Internet Things J. 2021, 8, 12046–12063. [Google Scholar] [CrossRef]
- Zhang, H.; Seal, S.; Wu, D.; Bouffard, F.; Boulet, B. Building energy management with reinforcement learning and model predictive control: A survey. IEEE Access 2022, 10, 27853–27862. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Nagy, Z. Reinforcement learning for demand response: A review of algorithms and modeling techniques. Appl. Energy 2019, 235, 1072–1089. [Google Scholar] [CrossRef]
- Ali, H.O.; Ouassaid, M.; Maaroufi, M. Chapter 24: Optimal appliance management system with renewable energy integration for smart homes. Renew. Energy Syst. 2021, 533–552. [Google Scholar] [CrossRef]
- Sharda, S.; Singh, M.; Sharma, K. Demand side management through load shifting in IoT based HEMS: Overview, challenges and opportunities. Sustain. Cities Soc. 2021, 65, 102517. [Google Scholar] [CrossRef]
- Danbatta, S.J.; Varol, A. Comparison of Zigbee, Z-Wave, Wi-Fi, and Bluetooth wireless technologies used in home automation. In Proceedings of the 7th International Symposium on Digital Forensics and Security (ISDFS), Barcelos, Portugal, 10–12 June 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Withanage, C.; Ashok, R.; Yuen, C.; Otto, K. A comparison of the popular home automation technologies. In Proceedings of the 2014 IEEE Innovative Smart Grid Technologies - Asia (ISGT ASIA), Kuala Lumpur, Malaysia, 20–23 May 2014; 2014; pp. 600–605. [Google Scholar] [CrossRef]
- Van de Kaa, G.; Stoccuto, S.; Calderón, C.V. A battle over smart standards: Compatibility, governance, and innovation in home energy management systems and smart meters in the Netherlands. Energy Res. Soc. Sci. 2021, 82, 102302. [Google Scholar] [CrossRef]
- Rajasekhar, B.; Tushar, W.; Lork, C.; Zhou, Y.; Yuen, C.; Pindoriya, N.M.; Wood, K.L. A survey of computational intelligence techniques for air-conditioners energy management. IEEE Trans. Emerg. Top. Comput. Intell. 2020, 4, 555–570. [Google Scholar] [CrossRef]
- Huang, C.; Zhang, H.; Wang, L.; Luo, X.; Song, Y. Mixed deep reinforcement learning considering discrete-continuous hybrid action space for smart home energy Management. J. Mod. Power Syst. Clean Energy 2022, 10, 743–754. [Google Scholar] [CrossRef]
- Yu, L.; Xie, W.; Xie, D.; Zou, Y.; Zhang, D.; Sun, Z.; Zhang, L.; Zhang, Y.; Jiang, T. Deep reinforcement learning for smart home energy management. IEEE Internet Things J. 2020, 7, 2751–2762. [Google Scholar] [CrossRef]
- Das, S. Deep Neural Networks. YouTube, 31 January 2022 [Video File]. Available online: www.youtube.com/playlist?list=PL_4Jjqx0pZY-SIO8jElzW0lNpzjcunOx4 (accessed on 1 April 2022).
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016; Available online: https://www.deeplearningbook.org/ (accessed on 1 August 2022).
- Achiam, J. Open AI, Part 2: Kinds of RL Algorithms. 2018. Available online: spinningup.openai.com/en/latest/spinningup/rl_intro2.html (accessed on 1 August 2022).
- Bellman, R. Dynamic Programming; Rand Corporation: Santa Monica, CA, USA, 1957. [Google Scholar]
- Bellman, R. A Markovian decision process. J. Math. Mech. 1957, 6, 679–684. [Google Scholar] [CrossRef]
- Howard, R. Dynamic Programming and Markov Processes; MIT Press: Cambridge, MA, USA, 1960. [Google Scholar]
- Castronovo, M.; Maes, F.; Fonteneau, R.; Ernst, D. Learning exploration/exploitation strategies for single trajectory reinforcement learning. Eur. Workshop Reinf. Learn. PMLR 2013, 24, 1–10. [Google Scholar]
- Fan, J.; Wang, Z.; Xie, Y.; Yang, Z. A theoretical analysis of deep Q-learning. Learn. Dyn. Control PMLR 2020, 120, 486–489. [Google Scholar]
- Sutton, R.S.; Barto, A.G. Reinforcement Learning: An Introduction; Bradford Books; MIT Press: Cambridge, MA, USA, 1998; revised 2018. [Google Scholar]
- Watkins, C.J.C.H. Learning from Delayed Rewards. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 1989. [Google Scholar]
- Rummery, G.A.; Niranjan, M. On-line Q-Learning Using Connectionist Systems; Technical Report; Department of Engineering, University of Cambridge: Cambridge, UK, 1994; Volume 37. [Google Scholar]
- Williams, R.J. Simple statistical gradient-following algorithms for connectionist reinforcement learning. Mach. Learn. 1992, 8, 229–256. [Google Scholar] [CrossRef] [Green Version]
- Riedmiller, M. Neural fitted Q iteration-first experiences with a data efficient neural reinforcement learning method. In Proceedings of the European Conference on Machine Learning, Porto, Portugal, 3–7 October 2005; Springer: Berlin/Heidelberg, Germany, 2005; pp. 317–328. [Google Scholar]
- Lin, L. Self-improving reactive agents based on reinforcement learning, planning and teaching. Mach. Learn. 1992, 8, 293–321. [Google Scholar] [CrossRef]
- Schaul, T.; Quan, J.; Antonoglou, I.; Silver, D. Prioritized experience replay. arXiv 2015, arXiv:1511.05952. [Google Scholar]
- Hasselt, H. Double Q-learning. Adv. Neural Inf. Processing Syst. 2010, 23, 2613–2621. [Google Scholar]
- Pentaliotis, A. Investigating Overestimation Bias in Reinforcement Learning. Ph.D. Thesis, University of Groningen, Groningen, The Netherlands, 2020. Available online: https://www.ai.rug.nl/~mwiering/Thesis-Andreas-Pentaliotis.pdf (accessed on 1 April 2022).
- Van Hasselt, H.; Guez, A.; Silver, D. Deep reinforcement learning with double Q learning. In Proceedings of the 30th AAAI Conference on Artificial Intelligence, Phoenix, Arizona, USA, 12–17 February 2016; Volume 30. [Google Scholar]
- Fujimoto, S.; Hoof, H.; Meger, D. Addressing function approximation error in actor-critic methods. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1587–1596. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Abbeel, P.; Levine, S. Soft actor-critic: Off-policy maximum entropy deep reinforcement learning with a stochastic actor. In Proceedings of the International Conference on Machine Learning, Stockholm, Sweden, 10–15 July 2018; pp. 1861–1870. [Google Scholar]
- Jiang, H.; Xie, J.; Yang, J. Action Candidate Driven Clipped Double Q-learning for discrete and continuous action tasks. arXiv 2022, arXiv:2203.11526. [Google Scholar]
- Wang, Z.; Schaul, T.; Hessel, M.; van Hasselt, H.; Lanctot, M.; de Freitas, N. Dueling network architectures for deep reinforcement learning. In Proceedings of the 33rd International Conference on Machine Learning, New York, NY, USA, 19–24 June 2016; Volume 48, pp. 1995–2003. [Google Scholar]
- Sutton, R.S.; McAllester, D.A.; Singh, S.P.; Mansour, Y. Policy gradient methods for reinforcement learning with function approximation. Adv. Neural Inf. Processing Syst. 2020, 12, 1057–1063. [Google Scholar]
- Sutton, R.S.; Singh, S.; McAllester, D. Comparing Policy Gradient Methods for Reinforcement Learning with Function Approximation. 2000. Available online: http://incompleteideas.net/papers/SSM-unpublished.pdf (accessed on 1 August 2022).
- Ciosek, K.; Whiteson, S. Expected policy gradients for reinforcement learning. arXiv 2018, arXiv:1801.03326. [Google Scholar]
- Thomas, P.S.; Brunskill, E. Policy gradient methods for reinforcement learning with function approximation and action-dependent baselines. arXiv 2017, arXiv:1706.06643. [Google Scholar]
- Weaver, L.; Tao, N. The optimal reward baseline for gradient-based reinforcement learning. In Proceedings of the 17th Conference on Uncertainty in Artificial Intelligence, Washington, DC, USA, 2–5 August 2001; pp. 538–545. [Google Scholar]
- Costa, S.I.R.; Santos, S.A.; Strapasson, J.E. Fisher information distance: A geometrical reading. Discret. Appl. Math. 2015, 197, 59–69. [Google Scholar] [CrossRef]
- Kakade, S. A natural policy gradient. Adv. Neural Inf. Processing Syst. 2002, 14, 1057–1063. [Google Scholar]
- Schulman, J.; Levine, S.; Abbeel, P.; Jordan, M.; Moritz, P. Trust region policy optimization. In Proceedings of the 32nd International Conference on Machine Learning, Lille, France, 6–11 July 2015; Volume 37, pp. 1889–1897. [Google Scholar]
- Schulman, J.; Wolski, F.; Dhariwal, P.; Radford, A.; Klimov, O. Proximal policy optimization algorithms. arXiv 2017, arXiv:1707.06347. [Google Scholar]
- Konda, V.R.; Tsitsiklis, J.N. On actor-critic algorithms. SIAM J. Control. Optim. 2003, 42, 1143–1166. [Google Scholar] [CrossRef]
- Mnih, V.; Badia, A.P.; Mirza, M.; Graves, A.; Lillicrap, T.; Harley, T.; Silver, D.; Kavukcuoglu, K. Asynchronous methods for deep reinforcement learning. Int. Conf. Mach. Learn. PMLR 2016, 48, 1928–1937. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2017, arXiv:1509.02971v6. [Google Scholar]
- Kalashnikov, D.; Irpan, A.; Pastor, P.; Ibarz, J.; Herzog, A.; Jang, E.; Quillen, D.; Holly, E.; Kalakrishnan, M.; Vanhoucke, V.; et al. Scalable deep reinforcement learning for vision-based robotic manipulation. In Proceedings of the Conference on Robot Learning, Zürich, Switzerland, 15 June 2018; pp. 651–673. [Google Scholar]
- Wang, Z.; Bapst, V.; Heess, N.; Mnih, V.; Munos, R.; Kavukcuoglu, K.; de Freitas, N. Sample efficient actor-critic with experience replay. arXiv 2016, arXiv:1611.01224. [Google Scholar]
- Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D.; Riedmiller, M. Deterministic policy gradient algorithms. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 387–395. [Google Scholar]
- Meng, L.; Gorbet, R.; Kulić, D. The effect of multi-step methods on overestimation in deep reinforcement learning. In Proceedings of the 25th International Conference on Pattern Recognition (ICPR), Milan, Italy, 10–15 January 2021; pp. 347–353. [Google Scholar]
- Haarnoja, T.; Zhou, A.; Hartikainen, K.; Tucker, G.; Ha, S.; Tan, J.; Kumar, V.; Zhu, H.; Gupta, A.; Abbeel, P.; et al. Soft actor-critic algorithms and applications. arXiv 2018, arXiv:1812.05905. [Google Scholar]
- Esrafilian-Najafabadi, M.; Haghighat, F. Occupancy-based HVAC control systems in buildings: A state-of-the-art review. Build. Environ. 2021, 197, 107810. [Google Scholar] [CrossRef]
- Jia, L.; Wei, S.; Liu, J. A review of optimization approaches for controlling water-cooled central cooling systems. Build. Environ. 2021, 203, 108100. [Google Scholar] [CrossRef]
- Yu, L.; Sun, Y.; Xu, Z.; Shen, C.; Yue, D.; Jiang, T.; Guan, X. Multi-Agent Deep Reinforcement Learning for HVAC Control in Commercial Buildings. IEEE Trans. Smart Grid 2021, 12, 407–419. [Google Scholar] [CrossRef]
- Noye, S.; Martinez, R.M.; Carnieletto, L.; de Carli, M.; Aguirre, A.C. A review of advanced ground source heat pump control: Artificial intelligence for autonomous and adaptive control. Renew. Sustain. Energy Rev. 2022, 153, 111685. [Google Scholar] [CrossRef]
- Paraskevas, A.; Aletras, D.; Chrysopoulos, A.; Marinopoulos, A.; Doukas, D.I. Optimal Management for EV Charging Stations: A Win–Win Strategy for Different Stakeholders Using Constrained Deep Q-Learning. Energies 2022, 15, 2323. [Google Scholar] [CrossRef]
- Ren, M.; Liu, X.; Yang, Z.; Zhang, J.; Guo, Y.; Jia, Y. A novel forecasting based scheduling method for household energy management system based on deep reinforcement learning. Sustain. Cities Soc. 2022, 76, 103207. [Google Scholar] [CrossRef]
- Alfaverh, F.; Denaï, M.; Sun, Y. Demand Response Strategy Based on Reinforcement Learning and Fuzzy Reasoning for Home Energy Management. IEEE Access 2020, 8, 39310–39321. [Google Scholar] [CrossRef]
- Antonopoulos, I.; Robu, V.; Couraud, B.; Kirli, D.; Norbu, S.; Kiprakis, A.; Flynn, D.; Elizondo-Gonzalez, S.; Wattam, S. Artificial intelligence and machine learning approaches to energy demand-side response: A systematic review. Renew. Sustain. Energy Rev. 2020, 130, 109899. [Google Scholar] [CrossRef]
- Chen, T.; Su, W. Indirect Customer-to-Customer Energy Trading with Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 4338–4348. [Google Scholar] [CrossRef]
- Bourdeau, M.; Zhai, X.q.; Nefzaoui, E.; Guo, X.; Chatellier, P. Modeling and forecasting building energy consumption: A review of data-driven techniques. Sustain. Cities Soc. 2019, 48, 101533. [Google Scholar] [CrossRef]
- Ma, N.; Aviv, D.; Guo, H.; Braham, W.W. Measuring the right factors: A review of variables and models for thermal comfort and indoor air quality. Renew. Sustain. Energy Rev. 2021, 135, 110436. [Google Scholar] [CrossRef]
- Xu, J.; Mahmood, H.; Xiao, H.; Anderlini, E.; Abusara, M. Electric Water Heaters Management via Reinforcement Learning with Time-Delay in Isolated Microgrids. IEEE Access 2021, 9, 132569–132579. [Google Scholar] [CrossRef]
- Lork, C.; Li, W.; Qin, Y.; Zhou, Y.; Yuen, C.; Tushar, W.; Saha, T.K. An uncertainty-aware deep reinforcement learning framework for residential air conditioning energy management. Appl. Energy 2020, 276, 115426. [Google Scholar] [CrossRef]
- Correa-Jullian, C.; Droguett, E.L.; Cardemil, J.M. Operation scheduling in a solar thermal system: A reinforcement learning-based framework. Appl. Energy 2020, 268, 114943. [Google Scholar] [CrossRef]
- Hao, J.; Gao, D.W.; Zhang, J.J. Reinforcement Learning for Building Energy Optimization Through Controlling of Central HVAC System. IEEE Open Access J. Power Energy 2020, 7, 320–328. [Google Scholar] [CrossRef]
- Lu, S.; Wang, W.; Lin, C.; Hameen, E.C. Data-driven simulation of a thermal comfort-based temperature set-point control with ASHRAE RP884. Build. Environ. 2019, 156, 137–146. [Google Scholar] [CrossRef]
- Liu, M.; Peeters, S.; Callaway, D.S.; Claessens, B.J. Trajectory Tracking with an Aggregation of Domestic Hot Water Heaters: Combining Model-Based and Model-Free Control in a Commercial Deployment. IEEE Trans. Smart Grid 2019, 10, 5686–5695. [Google Scholar] [CrossRef] [Green Version]
- Saifuddin, M.R.B.M.; Logenthiran, T.; Naayagi, R.T.; Woo, W.L. A Nano-Biased Energy Management Using Reinforced Learning Multi-Agent on Layered Coalition Model: Consumer Sovereignty. IEEE Access 2019, 7, 52542–52564. [Google Scholar] [CrossRef]
- Zhou, S.; Hu, Z.; Gu, W.; Jiang, M.; Zhang, X. Artificial intelligence based smart energy community management: A reinforcement learning approach. CSEE J. Power Energy Syst. 2019, 5, 1–10. [Google Scholar] [CrossRef]
- Ojand, K.; Dagdougui, H. Q-Learning-Based Model Predictive Control for Energy Management in Residential Aggregator. IEEE Trans. Autom. Sci. Eng. 2022, 19, 70–81. [Google Scholar] [CrossRef]
- Wang, Y.; Lin, X.; Pedram, M. A Near-Optimal Model-Based Control Algorithm for Households Equipped with Residential Photovoltaic Power Generation and Energy Storage Systems. IEEE Trans. Sustain. Energy 2016, 7, 77–86. [Google Scholar] [CrossRef]
- Kim, S.; Lim, H. Reinforcement Learning Based Energy Management Algorithm for Smart Energy Buildings. Energies 2018, 11, 2010. [Google Scholar] [CrossRef]
- Shang, Y.; Wu, W.; Guo, J.; Ma, Z.; Sheng, W.; Lv, Z.; Fu, C. Stochastic dispatch of energy storage in microgrids: An augmented reinforcement learning approach. Appl. Energy 2020, 261, 114423. [Google Scholar] [CrossRef]
- Kofinas, P.; Dounis, A.I.; Vouros, G.A. Fuzzy Q-Learning for multi-agent decentralized energy management in microgrids. Appl. Energy 2018, 219, 53–67. [Google Scholar] [CrossRef]
- Park, J.Y.; Dougherty, T.; Fritz, H.; Nagy, Z. LightLearn: An adaptive and occupant centered controller for lighting based on reinforcement learning. Build. Environ. 2019, 147, 397–414. [Google Scholar] [CrossRef]
- Korkidis, P.; Dounis, A.; Kofinas, P. Computational Intelligence Technologies for Occupancy Estimation and Comfort Control in Buildings. Energies 2021, 14, 4971. [Google Scholar] [CrossRef]
- Zhang, X.; Lu, R.; Jiang, J.; Hong, S.H.; Song, W.S. Testbed implementation of reinforcement learning-based demand response energy management system. Appl. Energy 2021, 297, 117131. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Yu, M. Demand Response for Home Energy Management Using Reinforcement Learning and Artificial Neural Network. IEEE Trans. Smart Grid 2019, 10, 6629–6639. [Google Scholar] [CrossRef]
- Remani, T.; Jasmin, E.A.; Ahamed, T.P.I. Residential Load Scheduling With Renewable Generation in the Smart Grid: A Reinforcement Learning Approach. IEEE Syst. J. 2019, 13, 3283–3294. [Google Scholar] [CrossRef]
- Khan, M.; Seo, J.; Kim, D. Real-Time Scheduling of Operational Time for Smart Home Appliances Based on Reinforcement Learning. IEEE Access 2020, 8, 116520–116534. [Google Scholar] [CrossRef]
- Ahrarinouri, M.; Rastegar, M.; Seifi, A.R. Multiagent Reinforcement Learning for Energy Management in Residential Buildings. IEEE Trans. Ind. Inform. 2021, 17, 659–666. [Google Scholar] [CrossRef]
- Chen, S.-J.; Chiu, W.-Y.; Liu, W.-J. User Preference-Based Demand Response for Smart Home Energy Management Using Multiobjective Reinforcement Learning. IEEE Access 2021, 9, 161627–161637. [Google Scholar] [CrossRef]
- Xu, X.; Jia, Y.; Xu, Y.; Xu, Z.; Chai, S.; Lai, C.S. A Multi-Agent Reinforcement Learning-Based Data-Driven Method for Home Energy Management. IEEE Trans. Smart Grid 2020, 11, 3201–3211. [Google Scholar] [CrossRef]
- Fang, X.; Wang, J.; Song, G.; Han, Y.; Zhao, Q.; Cao, Z. Multi-Agent Reinforcement Learning Approach for Residential Microgrid Energy Scheduling. Energies 2019, 13, 123. [Google Scholar] [CrossRef]
- Wan, Y.; Qin, J.; Yu, X.; Yang, T.; Kang, Y. Price-Based Residential Demand Response Management in Smart Grids: A Reinforcement Learning-Based Approach. IEEE/CAA J. Autom. Sin. 2022, 9, 123–134. [Google Scholar] [CrossRef]
- Lu, R.; Hong, S.H.; Zhang, X. A Dynamic pricing demand response algorithm for smart grid: Reinforcement learning approach. Appl. Energy 2018, 220, 220–230. [Google Scholar] [CrossRef]
- Wen, Z.; O’Neill, D.; Maei, H. Optimal Demand Response Using Device-Based Reinforcement Learning. IEEE Trans. Smart Grid 2015, 6, 2312–2324. [Google Scholar] [CrossRef] [Green Version]
- Lu, R.; Hong, S.H. Incentive-based demand response for smart grid with reinforcement learning and deep neural network. Appl. Energy 2019, 236, 937–949. [Google Scholar] [CrossRef]
- Kong, X.; Kong, D.; Yao, J.; Bai, L.; Xiao, J. Online pricing of demand response based on long short-term memory and reinforcement learning. Appl. Energy 2020, 271, 114945. [Google Scholar] [CrossRef]
- Hurtado, L.A.; Mocanu, E.; Nguyen, P.H.; Gibescu, M.; Kamphuis, R.I.G. Enabling Cooperative Behavior for Building Demand Response Based on Extended Joint Action Learning. IEEE Trans. Ind. Inform. 2018, 14, 127–136. [Google Scholar] [CrossRef]
- Barth, D.; Cohen-Boulakia, B.; Ehounou, W. Distributed Reinforcement Learning for the Management of a Smart Grid Interconnecting Independent Prosumers. Energies 2022, 15, 1440. [Google Scholar] [CrossRef]
- Ruelens, F.; Iacovella, S.; Claessens, B.; Belmans, R. Learning Agent for a Heat-Pump Thermostat with a Set-Back Strategy Using Model-Free Reinforcement Learning. Energies 2015, 8, 8300–8318. [Google Scholar] [CrossRef]
- Ruelens, F.; Claessens, B.J.; Vandael, S.; de Schutter, B.; Babuška, R.; Belmans, R. Residential Demand Response of Thermostatically Controlled Loads Using Batch Reinforcement Learning. IEEE Trans. Smart Grid 2017, 8, 2149–2159. [Google Scholar] [CrossRef]
- Ruelens, F.; Claessens, B.J.; Quaiyum, S.; de Schutter, B.; Babuška, R.; Belmans, R. Reinforcement Learning Applied to an Electric Water Heater: From Theory to Practice. IEEE Trans. Smart Grid 2018, 9, 3792–3800. [Google Scholar] [CrossRef]
- Han, M.; May, R.; Zhang, X.; Wang, X.; Pan, S.; Da, Y.; Jin, Y. A novel reinforcement learning method for improving occupant comfort via window opening and closing. Sustain. Cities Soc. 2020, 61, 102247. [Google Scholar] [CrossRef]
- Kazmi, H.; Suykens, J.; Balint, A.; Driesen, J. Multi-agent reinforcement learning for modeling and control of thermostatically controlled loads. Appl. Energy 2019, 238, 1022–1035. [Google Scholar] [CrossRef]
- Xu, S.; Chen, X.; Xie, J.; Rahman, S.; Wang, J.; Hui, H.; Chen, T. Agent-based modeling and simulation for the electricity market with residential demand response. CSEE J. Power Energy Syst. 2021, 7, 368–380. [Google Scholar] [CrossRef]
- Reka, S.S.; Venugopal, P.; Alhelou, H.H.; Siano, P.; Golshan, M.E.H. Real Time Demand Response Modeling for Residential Consumers in Smart Grid Considering Renewable Energy with Deep Learning Approach. IEEE Access 2021, 9, 56551–56562. [Google Scholar] [CrossRef]
- Kontes, G.; Giannakis, G.I.; Sánchez, V.; de Agustin-Camacho, P.; Romero-Amorrortu, A.; Panagiotidou, N.; Rovas, D.V.; Steiger, S.; Mutschler, C.; Gruen, G. Simulation-Based Evaluation and Optimization of Control Strategies in Buildings. Energies 2018, 11, 3376. [Google Scholar] [CrossRef]
- Jia, Q.; Chen, S.; Yan, Z.; Li, Y. Optimal Incentive Strategy in Cloud-Edge Integrated Demand Response Framework for Residential Air Conditioning Loads. IEEE Trans. Cloud Comput. 2022, 10, 31–42. [Google Scholar] [CrossRef]
- Macieira, P.; Gomes, L.; Vale, Z. Energy Management Model for HVAC Control Supported by Reinforcement Learning. Energies 2021, 14, 8210. [Google Scholar] [CrossRef]
- Vázquez-Canteli, J.R.; Ulyanin, S.; Kämpf, J.; Nagy, Z. Fusing TensorFlow with building energy simulation for intelligent energy management in smart cities. Sustain. Cities Soc. 2019, 45, 243–257. [Google Scholar] [CrossRef]
- Zhou, T.; Lin, M. Deadline-Aware Deep-Recurrent-Q-Network Governor for Smart Energy Saving. IEEE Trans. Netw. Sci. Eng. 2021. [Google Scholar] [CrossRef]
- Claessens, B.J.; Vrancx, P.; Ruelens, F. Convolutional Neural Networks for Automatic State-Time Feature Extraction in Reinforcement Learning Applied to Residential Load Control. IEEE Trans. Smart Grid 2018, 9, 3259–3269. [Google Scholar] [CrossRef]
- Tuchnitz, F.; Ebell, N.; Schlund, J.; Pruckner, M. Development and Evaluation of a Smart Charging Strategy for an Electric Vehicle Fleet Based on Reinforcement Learning. Appl. Energy 2021, 285, 116382. [Google Scholar] [CrossRef]
- Tittaferrante, A.; Yassine, A. Multiadvisor Reinforcement Learning for Multiagent Multiobjective Smart Home Energy Control. IEEE Trans. Artif. Intell. 2022, 3, 581–594. [Google Scholar] [CrossRef]
- Zhong, S.; Wang, X.; Zhao, J.; Li, W.; Li, H.; Wang, Y.; Deng, S.; Zhu, J. Deep reinforcement learning framework for dynamic pricing demand response of regenerative electric heating. Appl. Energy 2021, 288, 116623. [Google Scholar] [CrossRef]
- Wei, P.; Xia, S.; Chen, R.; Qian, J.; Li, C.; Jiang, X. A Deep-Reinforcement-Learning-Based Recommender System for Occupant-Driven Energy Optimization in Commercial Buildings. IEEE Internet Things J. 2020, 7, 6402–6413. [Google Scholar] [CrossRef]
- Liang, Z.; Huang, C.; Su, W.; Duan, N.; Donde, V.; Wang, B.; Zhao, X. Safe Reinforcement Learning-Based Resilient Proactive Scheduling for a Commercial Building Considering Correlated Demand Response. IEEE Open Access J. Power Energy 2021, 8, 85–96. [Google Scholar] [CrossRef]
- Deng, X.; Zhang, Y.; Zhang, Y.; Qi, H. Towards optimal HVAC control in non-stationary building environments combining active change detection and deep reinforcement learning. Build. Environ. 2022, 211, 108680. [Google Scholar] [CrossRef]
- Wei, T.; Ren, S.; Zhu, Q. Deep Reinforcement Learning for Joint Datacenter and HVAC Load Control in Distributed Mixed-Use Buildings. IEEE Trans. Sustain. Comput. 2021, 6, 370–384. [Google Scholar] [CrossRef]
- Chen, T.; Su, W. Local Energy Trading Behavior Modeling with Deep Reinforcement Learning. IEEE Access 2018, 6, 62806–62814. [Google Scholar] [CrossRef]
- Suanpang, P.; Jamjuntr, P.; Jermsittiparsert, K.; Kaewyong, P. Autonomous Energy Management by Applying Deep Q-Learning to Enhance Sustainability in Smart Tourism Cities. Energies 2022, 15, 1906. [Google Scholar] [CrossRef]
- Blad, C.; Bøgh, S.; Kallesøe, C. A Multi-Agent Reinforcement Learning Approach to Price and Comfort Optimization in HVAC-Systems. Energies 2021, 14, 7491. [Google Scholar] [CrossRef]
- Yang, T.; Zhao, L.; Li, W.; Wu, J.; Zomaya, A.Y. Towards healthy and cost-effective indoor environment management in smart homes: A deep reinforcement learning approach. Appl. Energy 2021, 300, 117335. [Google Scholar] [CrossRef]
- Heidari, A.; Maréchal, F.; Khovalyg, D. An occupant-centric control framework for balancing comfort, energy use and hygiene in hot water systems: A model-free reinforcement learning approach. Appl. Energy 2022, 312, 118833. [Google Scholar] [CrossRef]
- Valladares, W.; Galindo, M.; Gutiérrez, J.; Wu, W.; Liao, K.; Liao, J.; Lu, K.; Wang, C. Energy optimization associated with thermal comfort and indoor air control via a deep reinforcement learning algorithm. Build. Environ. 2019, 155, 105–117. [Google Scholar] [CrossRef]
- Dmitrewski, A.; Molina-Solana, M.; Arcucci, R. CntrlDA: A building energy management control system with real-time adjustments. Application to indoor temperature. Build. Environ. 2022, 215, 108938. [Google Scholar] [CrossRef]
- Mathew, A.; Jolly, M.J.; Mathew, J. Improved residential energy management system using priority double deep Q-learning. Sustain. Cities Soc. 2021, 69, 102812. [Google Scholar] [CrossRef]
- Ruelens, F.; Claessens, B.J.; Vrancx, P.; Spiessens, F.; Deconinck, G. Direct load control of thermostatically controlled loads based on sparse observations using deep reinforcement learning. CSEE J. Power Energy Syst. 2019, 5, 423–432. [Google Scholar] [CrossRef]
- Chemingui, Y.; Gastli, A.; Ellabban, O. Reinforcement Learning-Based School Energy Management System. Energies 2020, 13, 6354. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, Y.; Bernstein, A.; Chintala, R.; Graf, P.; Jin, X.; Biagioni, D. Two-Stage Reinforcement Learning Policy Search for Grid-Interactive Building Control. IEEE Trans. Smart Grid 2022, 13, 1976–1987. [Google Scholar] [CrossRef]
- Yang, L.; Sun, Q.; Zhang, N.; Li, Y. Indirect Multi-energy Transactions of Energy Internet with Deep Reinforcement Learning Approach. IEEE Trans. Power Syst. 2022. [Google Scholar] [CrossRef]
- Guo, C.; Wang, X.; Zheng, Y.; Zhang, F. Real-time optimal energy management of microgrid with uncertainties based on deep reinforcement learning. Energy 2022, 238, 121873. [Google Scholar] [CrossRef]
- Jung, S.; Jeoung, J.; Kang, H.; Hong, T. Optimal planning of a rooftop PV system using GIS-based reinforcement learning. Appl. Energy 2021, 298, 117239. [Google Scholar] [CrossRef]
- Li, H.; Wan, Z.; He, H. Real-Time Residential Demand Response. IEEE Trans. Smart Grid 2020, 11, 4144–4154. [Google Scholar] [CrossRef]
- Gao, G.; Li, J.; Wen, Y. DeepComfort: Energy-efficient thermal comfort control in buildings via reinforcement learning. IEEE Internet Things J. 2020, 7, 8472–8484. [Google Scholar] [CrossRef]
- Du, Y.; Zandi, H.; Kotevska, O.; Kurte, K.; Munk, J.; Amasyali, K.; Mckee, E.; Li, F. Intelligent multi-zone residential HVAC control strategy based on deep reinforcement learning. Appl. Energy 2021, 281, 116117. [Google Scholar] [CrossRef]
- Kodama, N.; Harada, T.; Miyazaki, K. Home Energy Management Algorithm Based on Deep Reinforcement Learning Using Multistep Prediction. IEEE Access 2021, 9, 153108–153115. [Google Scholar] [CrossRef]
- Svetozarevic, B.; Baumann, C.; Muntwiler, S.; di Natale, L.; Zeilinger, M.N.; Heer, P. Data-driven control of room temperature and bidirectional EV charging using deep reinforcement learning: Simulations and experiments. Appl. Energy 2022, 307, 118127. [Google Scholar] [CrossRef]
- Zenginis, I.; Vardakas, J.; Koltsaklis, N.E.; Verikoukis, C. Smart Home’s Energy Management through a Clustering-based Reinforcement Learning Approach. IEEE Internet Things J. 2022, 9, 16363–16371. [Google Scholar] [CrossRef]
- Chung, H.-M.; Maharjan, S.; Zhang, Y.; Eliassen, F. Distributed Deep Reinforcement Learning for Intelligent Load Scheduling in Residential Smart Grids. IEEE Trans. Ind. Inform. 2021, 17, 2752–2763. [Google Scholar] [CrossRef]
- Qiu, D.; Ye, Y.; Papadaskalopoulos, D.; Strbac, G. Scalable coordinated management of peer-to-peer energy trading: A multi-cluster deep reinforcement learning approach. Appl. Energy 2021, 292, 116940. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Wu, X.; Strbac, G.; Ward, J. Model-Free Real-Time Autonomous Control for a Residential Multi-Energy System Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2020, 11, 3068–3082. [Google Scholar] [CrossRef]
- Li, W.; Tang, M.; Zhang, X.; Gao, D.; Wang, J. Operation of Distributed Battery Considering Demand Response Using Deep Reinforcement Learning in Grid Edge Control. Energies 2021, 14, 7749. [Google Scholar] [CrossRef]
- Touzani, S.; Prakash, A.K.; Wang, Z.; Agarwal, S.; Pritoni, M.; Kiran, M.; Brown, R.; Granderson, J. Controlling distributed energy resources via deep reinforcement learning for load flexibility and energy efficiency. Appl. Energy 2021, 304, 117733. [Google Scholar] [CrossRef]
- Zhou, X.; Lin, W.; Kumar, R.; Cui, P.; Ma, Z. A data-driven strategy using long short term memory models and reinforcement learning to predict building electricity consumption. Appl. Energy 2022, 306, 118078. [Google Scholar] [CrossRef]
- Lu, R.; Li, Y.-C.; Li, Y.; Jiang, J.; Ding, Y. Multi-agent deep reinforcement learning based demand response for discrete manufacturing systems energy management. Appl. Energy 2020, 276, 115473. [Google Scholar] [CrossRef]
- Desportes, L.; Fijalkow, I.; Andry, P. Deep Reinforcement Learning for Hybrid Energy Storage Systems: Balancing Lead and Hydrogen Storage. Energies 2021, 14, 4706. [Google Scholar] [CrossRef]
- Zou, Z.; Yu, X.; Ergan, S. Towards optimal control of air handling units using deep reinforcement learning and recurrent neural network. Build. Environ. 2020, 168, 106535. [Google Scholar] [CrossRef]
- Liu, B.; Akcakaya, M.; Mcdermott, T.E. Automated Control of Transactive HVACs in Energy Distribution Systems. IEEE Trans. Smart Grid 2021, 12, 2462–2471. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Gao, G.; Wen, Y.; Jin, G.; Christopoulos, G. Toward Intelligent Multizone Thermal Control with Multiagent Deep Reinforcement Learning. IEEE Internet Things J. 2021, 8, 11150–11162. [Google Scholar] [CrossRef]
- Miao, Y.; Chen, T.; Bu, S.; Liang, H.; Han, Z. Co-Optimizing Battery Storage for Energy Arbitrage and Frequency Regulation in Real-Time Markets Using Deep Reinforcement Learning. Energies 2021, 14, 8365. [Google Scholar] [CrossRef]
- Du, Y.; Wu, D. Deep Reinforcement Learning from Demonstrations to Assist Service Restoration in Islanded Microgrids. IEEE Trans. Sustain. Energy 2022, 13, 1062–1072. [Google Scholar] [CrossRef]
- Qiu, D.; Dong, Z.; Zhang, X.; Wang, Y.; Strbac, G. Safe reinforcement learning for real-time automatic control in a smart energy-hub. Appl. Energy 2022, 309, 118403. [Google Scholar] [CrossRef]
- Bahrami, S.; Chen, Y.C.; Wong, V.W.S. Deep Reinforcement Learning for Demand Response in Distribution Networks. IEEE Trans. Smart Grid 2021, 12, 1496–1506. [Google Scholar] [CrossRef]
- Ye, Y.; Tang, Y.; Wang, H.; Zhang, X.-P.; Strbac, G. A Scalable Privacy-Preserving Multi-Agent Deep Reinforcement Learning Approach for Large-Scale Peer-to-Peer Transactive Energy Trading. IEEE Trans. Smart Grid 2021, 12, 5185–5200. [Google Scholar] [CrossRef]
- Deltetto, D.; Coraci, D.; Pinto, G.; Piscitelli, M.S.; Capozzoli, A. Exploring the Potentialities of Deep Reinforcement Learning for Incentive-Based Demand Response in a Cluster of Small Commercial Buildings. Energies 2021, 14, 2933. [Google Scholar] [CrossRef]
- Brandi, S.; Fiorentini, M.; Capozzoli, A. Comparison of online and offline deep reinforcement learning with model predictive control for thermal energy management. Autom. Constr. 2022, 135, 104128. [Google Scholar] [CrossRef]
- Hu, W.; Wen, Y.; Guan, K.; Jin, G.; Tseng, K.J. iTCM: Toward Learning-Based Thermal Comfort Modeling via Pervasive Sensing for Smart Buildings. IEEE Internet Things J. 2018, 5, 4164–4177. [Google Scholar] [CrossRef]
- Coraci, D.; Brandi, S.; Piscitelli, M.S.; Capozzoli, A. Online Implementation of a Soft Actor-Critic Agent to Enhance Indoor Temperature Control and Energy Efficiency in Buildings. Energies 2021, 14, 997. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, B.; Liu, H.; Sun, H.; Pan, Z.; Guo, Q. Exploiting the Flexibility Inside Park-Level Commercial Buildings Considering Heat Transfer Time Delay: A Memory-Augmented Deep Reinforcement Learning Approach. IEEE Trans. Sustain. Energy 2022, 13, 207–219. [Google Scholar] [CrossRef]
- Zhu, D.; Yang, B.; Liu, Y.; Wang, Z.; Ma, K.; Guan, X. Energy management based on multi-agent deep reinforcement learning for a multi-energy industrial park. Appl. Energy 2022, 311, 118636. [Google Scholar] [CrossRef]
- Qin, Y.; Ke, J.; Wang, B.; Filaretov, G.F. Energy optimization for regional buildings based on distributed reinforcement learning. Sustain. Cities Soc. 2022, 78, 103625. [Google Scholar] [CrossRef]
- Pinto, G.; Deltetto, D.; Capozzoli, A. Data-driven district energy management with surrogate models and deep reinforcement learning. Appl. Energy 2021, 304, 117642. [Google Scholar] [CrossRef]
- Pinto, G.; Piscitelli, M.S.; Vázquez-Canteli, J.R.; Nagy, Z.; Capozzoli, A. Coordinated energy management for a cluster of buildings through deep reinforcement learning. Energy 2021, 229, 120725. [Google Scholar] [CrossRef]
- Pinto, G.; Kathirgamanathan, A.; Mangina, E.; Finn, D.P.; Capozzoli, A. Enhancing energy management in grid-interactive buildings: A comparison among cooperative and coordinated architectures. Appl. Energy 2022, 310, 118497. [Google Scholar] [CrossRef]
- Zhang, Z.; Ma, C.; Zhu, R. Thermal and Energy Management Based on Bimodal Airflow-Temperature Sensing and Reinforcement Learning. Energies 2018, 11, 2575. [Google Scholar] [CrossRef]
- Hosseinloo, A.H.; Ryzhov, A.; Bischi, A.; Ouerdane, H.; Turitsyn, K.; Dahleh, M.A. Data-driven control of micro-climate in buildings: An event-triggered reinforcement learning approach. Appl. Energy 2020, 277, 115451. [Google Scholar] [CrossRef]
- Taboga, V.; Bellahsen, A.; Dagdougui, H. An Enhanced Adaptivity of Reinforcement Learning-Based Temperature Control in Buildings Using Generalized Training. IEEE Trans. Emerg. Top. Comput. Intell. 2022, 6, 255–266. [Google Scholar] [CrossRef]
- Lee, S.; Choi, D.-H. Federated Reinforcement Learning for Energy Management of Multiple Smart Homes with Distributed Energy Resources. IEEE Trans. Ind. Inform. 2022, 18, 488–497. [Google Scholar] [CrossRef]
- Zhang, X.; Biagioni, D.; Cai, M.; Graf, P.; Rahman, S. An Edge-Cloud Integrated Solution for Buildings Demand Response Using Reinforcement Learning. IEEE Trans. Smart Grid 2021, 12, 420–431. [Google Scholar] [CrossRef]
- Chen, T.; Bu, S.; Liu, X.; Kang, J.; Yu, F.R.; Han, Z. Peer-to-Peer Energy Trading and Energy Conversion in Interconnected Multi-Energy Microgrids Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Smart Grid 2022, 13, 715–727. [Google Scholar] [CrossRef]
- Woo, J.H.; Wu, L.; Park, J.-B.; Roh, J.H. Real-Time Optimal Power Flow Using Twin Delayed Deep Deterministic Policy Gradient Algorithm. IEEE Access 2020, 8, 213611–213618. [Google Scholar] [CrossRef]
- Fu, C.; Zhang, Y. Research and Application of Predictive Control Method Based on Deep Reinforcement Learning for HVAC Systems. IEEE Access 2021, 9, 130845–130852. [Google Scholar] [CrossRef]
- Ye, Y.; Qiu, D.; Wang, H.; Tang, Y.; Strbac, G. Real-Time Autonomous Residential Demand Response Management Based on Twin Delayed Deep Deterministic Policy Gradient Learning. Energies 2021, 14, 531. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, D.; Gooi, H.B. Optimization strategy based on deep reinforcement learning for home energy management. CSEE J. Power Energy Syst. 2020, 6, 572–582. [Google Scholar] [CrossRef]
- Mocanu, E.; Mocanu, D.C.; Nguyen, P.H.; Liotta, A.; Webber, M.E.; Gibescu, M.; Slootweg, J.G. On-Line Building Energy Optimization Using Deep Reinforcement Learning. IEEE Trans. Smart Grid 2019, 10, 3698–3708. [Google Scholar] [CrossRef]
- Shuai, H.; He, H. Online Scheduling of a Residential Microgrid via Monte-Carlo Tree Search and a Learned Model. IEEE Trans. Smart Grid 2021, 12, 1073–1087. [Google Scholar] [CrossRef]
- Biemann, M.; Scheller, F.; Liu, X.; Huang, L. Experimental evaluation of model-free reinforcement learning algorithms for continuous HVAC control. Appl. Energy 2021, 298, 117164. [Google Scholar] [CrossRef]
- Homod, R.Z.; Togun, H.; Hussein, A.K.; Al-Mousawi, F.N.; Yaseen, Z.M.; Al-Kouz, W.; Abd, H.J.; Alawi, O.A.; Goodarzi, M.; Hussein, O.A. Dynamics analysis of a novel hybrid deep clustering for unsupervised learning by reinforcement of multi-agent to energy saving in intelligent buildings. Appl. Energy 2022, 313, 118863. [Google Scholar] [CrossRef]
- Ceusters, G.; Rodríguez, R.C.; García, A.B.; Franke, R.; Deconinck, G.; Helsen, L.; Nowé, A.; Messagie, M.; Camargo, L.R. Model-predictive control and reinforcement learning in multi-energy system case studies. Appl. Energy 2021, 303, 117634. [Google Scholar] [CrossRef]
- Dorokhova, M.; Martinson, Y.; Ballif, C.; Wyrsch, N. Deep reinforcement learning control of electric vehicle charging in the presence of photovoltaic generation. Appl. Energy 2021, 301, 117504. [Google Scholar] [CrossRef]
- Ernst, D.; Glavic, M.; Capitanescu, F.; Wehenkel, L. Reinforcement learning versus model predictive control: A comparison on a power system problem. IEEE Trans. Syst. Man Cybern. Part B (Cybern.) 2008, 39, 517–529. [Google Scholar] [CrossRef]
- Li, S.; Liu, Y.; Qu, X. Model controlled prediction: A reciprocal alternative of model predictive control. IEEE/CAA J. Autom. Sin. 2022, 9, 1107–1110. [Google Scholar] [CrossRef]
- Jordan, S.; Chandak, Y.; Cohen, D.; Zhang, M.; Thomas, P. Evaluating the performance of reinforcement learning algorithms. In Proceedings of the International Conference on Machine Learning, Virtual, 13–18 July 2020; pp. 4962–4973. [Google Scholar]






| Reference | Application | Objective | Building Type | Algorithm |
|---|---|---|---|---|
| [112] | HVAC, Fans, WH | Cost | Residential | Q-Learning |
| [113] | Cost and Comfort | |||
| [114,115] | Other | Academic | ||
| [116] | Comfort | Mixed/NA | ||
| [117] | Other | |||
| [109,118] | P2P Trading | Cost | ||
| [119,120] | Residential | |||
| [121] | EV, ES, and RG | |||
| [122,123] | Mixed/NA | |||
| [124] | Other | Residential | ||
| [125,126] | Other/Mixed | Cost and Comfort | Commercial | |
| [127] | Academic | |||
| [107,128,129,130,131,132] | Residential | |||
| [133] | Other | |||
| [134,135] | Cost | |||
| [136] | Mixed/NA | |||
| [137] | Cost and Comfort | |||
| [138,139] | Cost and Load Balance | |||
| [140] | Other | |||
| [141] | P2P Trading | Cost | Distributed RL | |
| [142,143,144] | HVAC, Fans, WH | Cost and Comfort | Residential | Other (FQI) |
| [145] | Comfort | Commercial | Q-Learn. and SARSA | |
| [146] | Cost and Comfort | Residential | SARSA | |
| [147] | Other/Mixed | Cost and Load Balance | Policy Learning | |
| [148] | Other | |||
| [149] | Cost and Comfort | Commercial | Model Based RL | |
| [150] | HVAC, Fans, WH | Cost | Residential | Other (CARLA) |
| [151] | Cost and Comfort | Commercial | Other (Context. RL) |
| Reference | Application | Objective | Building Type | Algorithm |
|---|---|---|---|---|
| [152,153] | Other/Mixed | Cost | Residential | DQN |
| [154] | Cost and Load Balance | |||
| [105] | EV, ES, and RG | Cost | ||
| [155] | Other | |||
| [156] | Cost and Comfort | |||
| [157] | HVAC, Fans, WH | Cost | ||
| [158] | Other/Mixed | Commercial | ||
| [159] | Cost and Comfort | |||
| [160,161] | HVAC, Fans, WH | Mixed/NA | ||
| [162,163] | Other/Mixed | Cost | ||
| [164,165,166] | HVAC, Fans, WH | Cost and Comfort | Residential | DDQN |
| [167] | Academic | |||
| [168] | Comfort | Commercial | ||
| [169] | Other/Mixed | Cost and Load Balance | Residential | |
| [106] | Cost and Comfort | Dueling-DQN | ||
| [170] | HVAC, Fans, WH | Cost | Other (FQI-LSTM, FQI-CNN) |
| Reference | Application | Objective | Building Type | Algorithm |
|---|---|---|---|---|
| [171] | HVAC, Fans, WH | Cost and Comfort | Academic | PPO |
| [172] | Commercial | |||
| [173] | P2P Trading | Other | Mixed/NA | |
| [174] | EV, ES, and RG | |||
| [175] | Other/Mixed | Cost | ||
| [176] | Cost and Comfort | Residential | TRPO |
| Reference | Application | Objective | Building Type | Algorithm |
|---|---|---|---|---|
| [177,178] | HVAC, Fans, WH | Cost and Comfort | Residential | DDPG |
| [61,179,180,181] | Other/Mixed | |||
| [182,183] | Cost and Load Balance | |||
| [184] | Cost | |||
| [185] | EV, ES, and RG | |||
| [186] | Other/Mixed | Cost and Comfort | Academic | |
| [187] | Other | |||
| [188,189] | EV, ES, and RG | Commercial | ||
| [190,191,192] | HVAC, Fans, WH | Cost and Comfort | Mixed/NA | |
| [193,194,195] | EV, ES, and RG | Other | ||
| [196,197] | Other/Mixed | Cost and Load Balance | Residential | SAC |
| [198,199] | HVAC, Fans, WH | Cost | Commercial | |
| [103,200,201,202] | Cost and Comfort | |||
| [203] | Other/Mixed | |||
| [204] | Academic | |||
| [205,206,207] | HVAC, Fans, WH | Cost and Load Balance | Mixed/NA | |
| [208,209,210] | Cost and Comfort | |||
| [211] | Other/Mixed | Residential | A2C | |
| [212] | HVAC, Fans, WH | Cost | Commercial | A3C |
| [213] | P2P Trading | Mixed/NA | TD3 | |
| [214] | HVAC, Fans, WH | |||
| [215] | Cost and Comfort | |||
| [216] | Other/Mixed | Residential |
| Reference | Application | Objective | Building Type | Algorithm |
|---|---|---|---|---|
| [60] | Other/Mixed | Cost and Comfort | Residential | DQN, DDPG |
| [217] | DQN, DDQN | |||
| [218] | Cost and Load Balance | DQN, DPG | ||
| [219] | P2P Trading | Other (Model-Based DRL) | ||
| [220] | HVAC, Fans, WH | Cost and Comfort | Academic | SAC, TD3, TRPO, PPO |
| [221] | Mixed/NA | Other (Clustering DRL) | ||
| [222] | EV, ES, and RG | PPO, TD3 | ||
| [223] | Cost and Load Balance | Commercial | DDPG, DDQN, DQN |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al-Ani, O.; Das, S. Reinforcement Learning: Theory and Applications in HEMS. Energies 2022, 15, 6392. https://doi.org/10.3390/en15176392
Al-Ani O, Das S. Reinforcement Learning: Theory and Applications in HEMS. Energies. 2022; 15(17):6392. https://doi.org/10.3390/en15176392
Chicago/Turabian StyleAl-Ani, Omar, and Sanjoy Das. 2022. "Reinforcement Learning: Theory and Applications in HEMS" Energies 15, no. 17: 6392. https://doi.org/10.3390/en15176392
APA StyleAl-Ani, O., & Das, S. (2022). Reinforcement Learning: Theory and Applications in HEMS. Energies, 15(17), 6392. https://doi.org/10.3390/en15176392







