Harmonic Compensation via Grid-Tied Three-Phase Inverter with Variable Structure I&I Observer-Based Control Scheme
Abstract
:1. Introduction
- Solving power quality issues in three-phase systems using a photovoltaic grid-tied inverter.
- The development of a sliding mode control scheme that provides the grid tied PV inverter with the capability to compensate reactive power, to mitigate harmonic distortion and to balance the three-phase currents.
- The reference currents are calculated using the DQ0 reference frame transformation. The resulting reference signals provide the controller with information required to compensate for reactive power, harmonic distortion, and unbalance voltage.
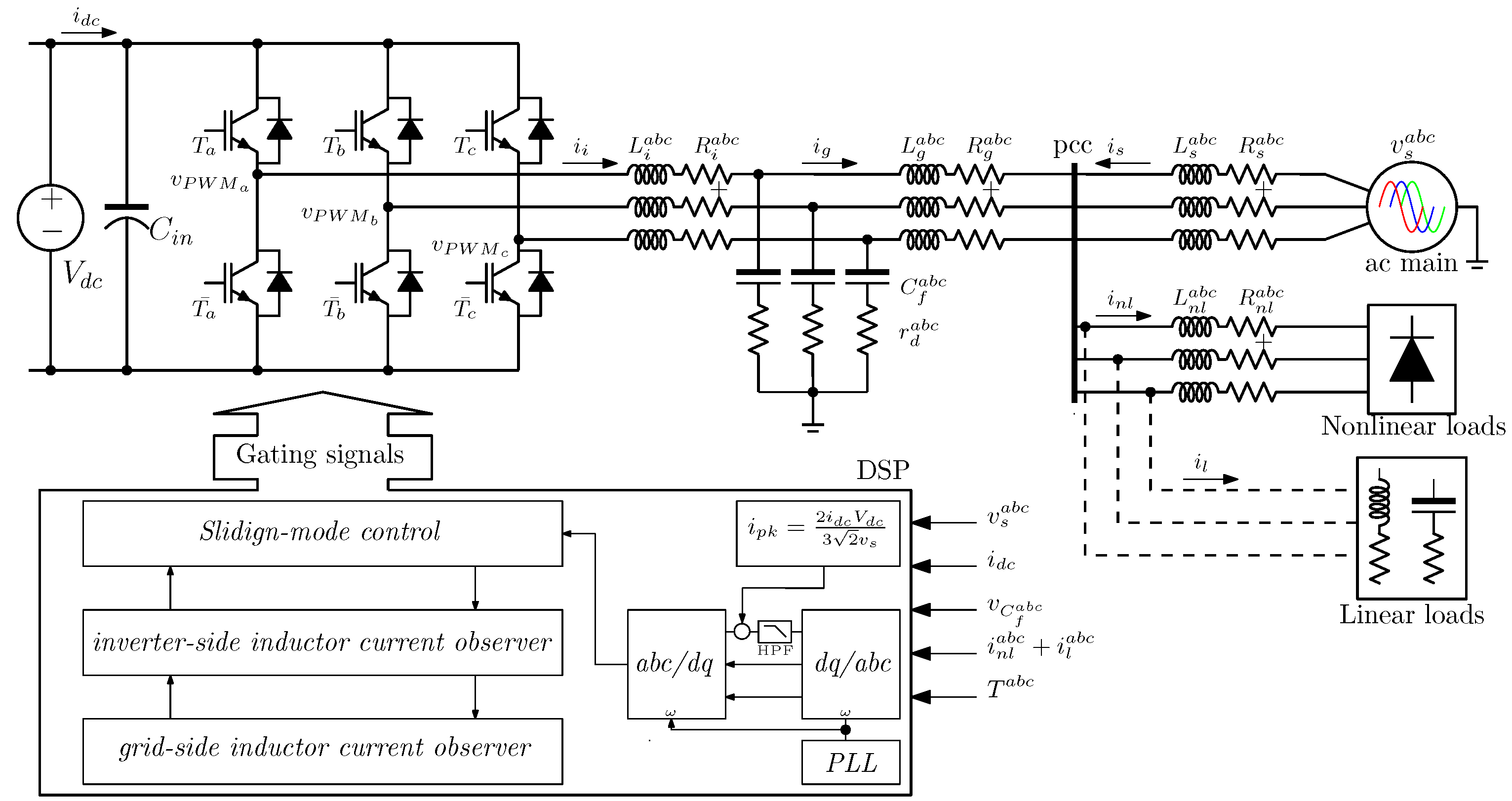
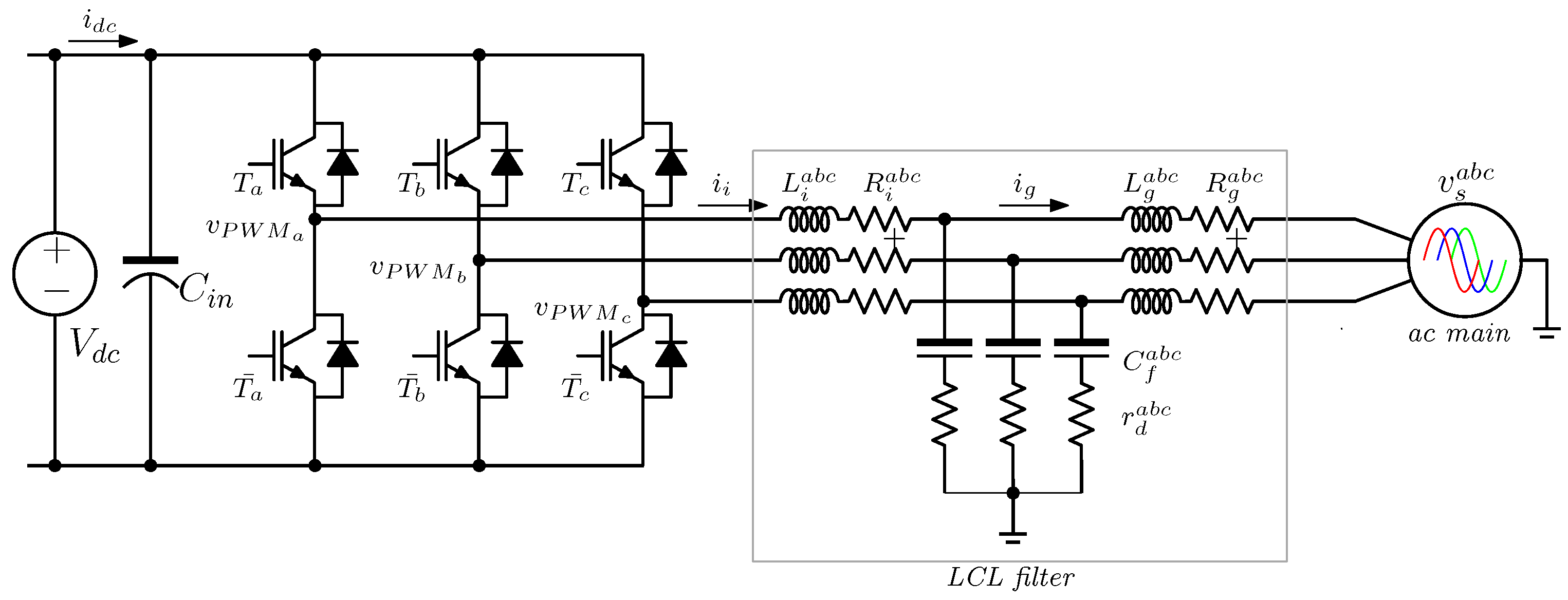
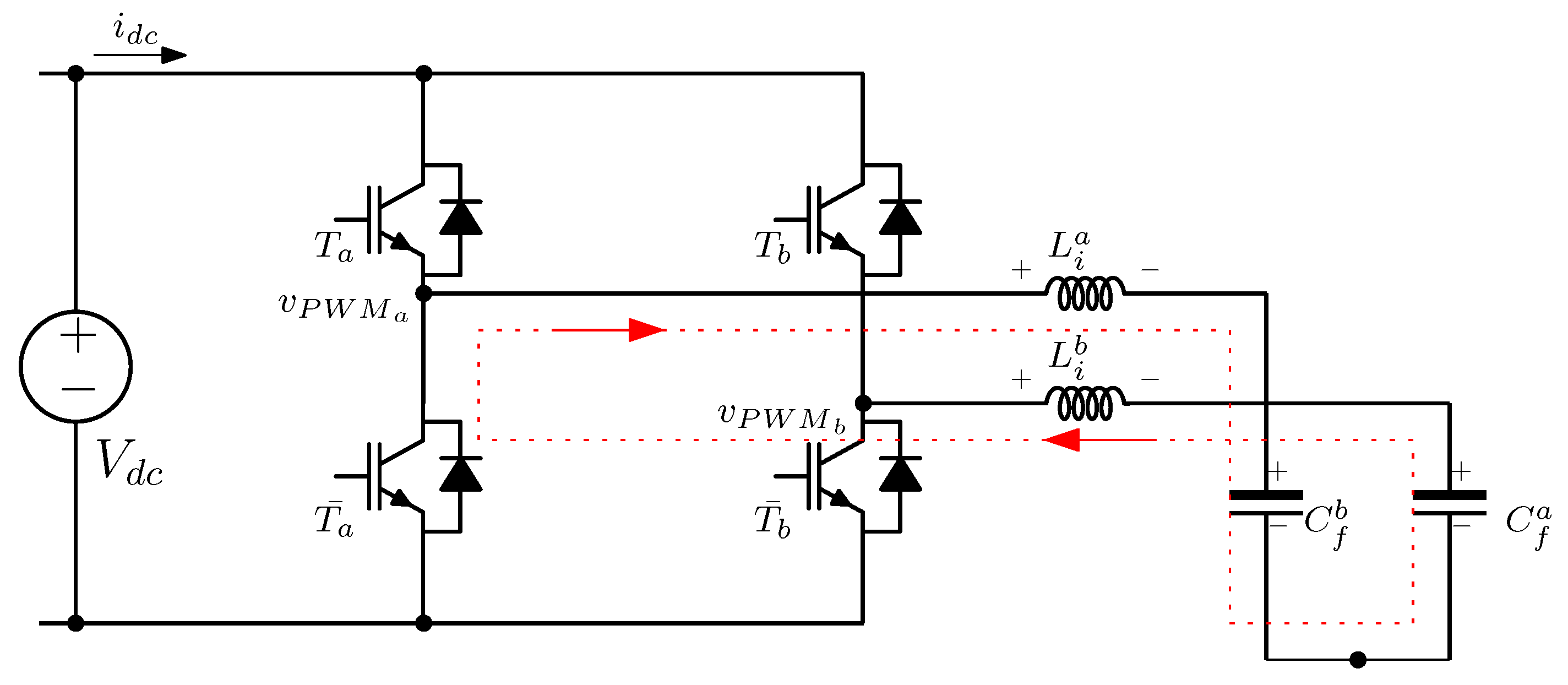
2. Power Stage Description
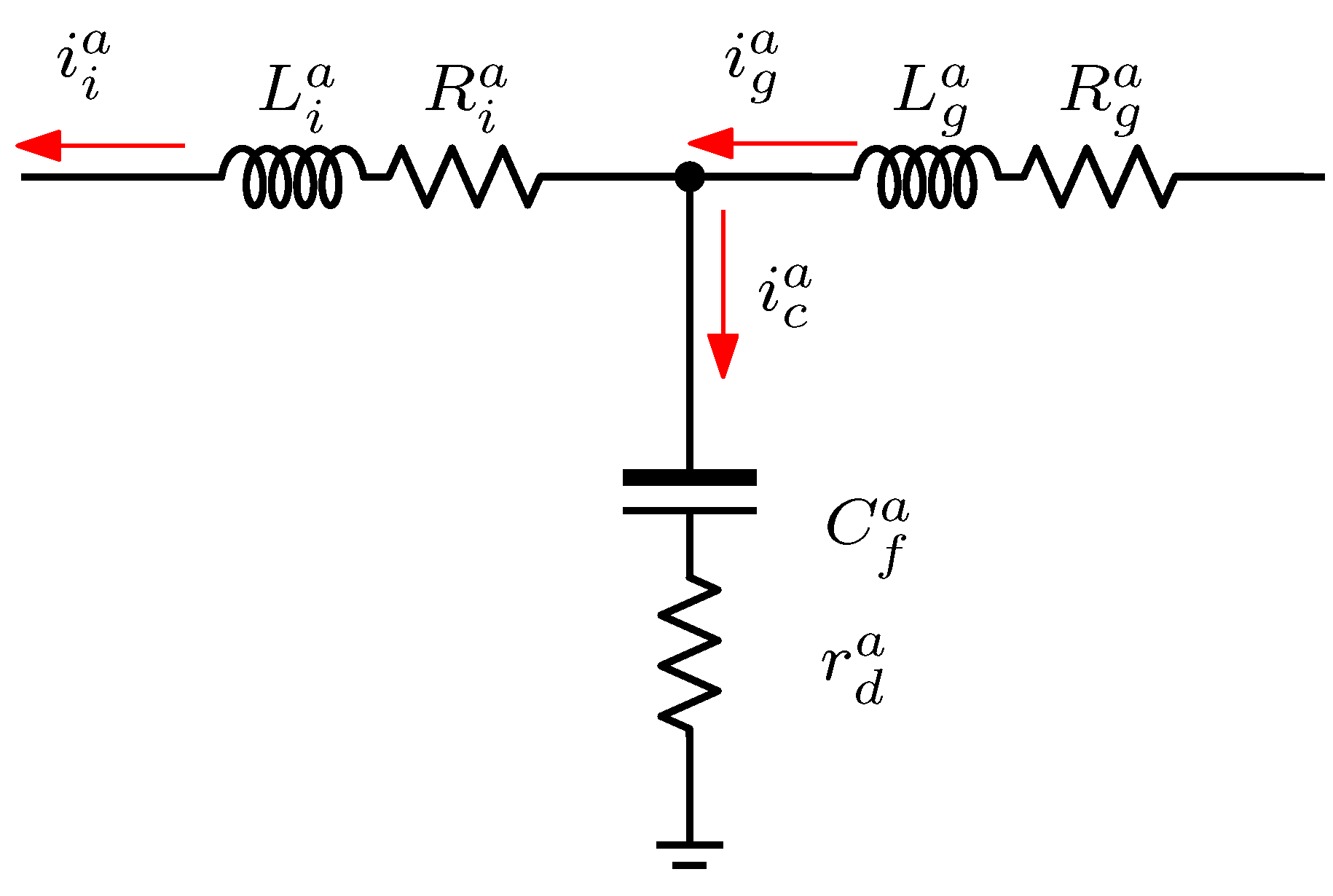
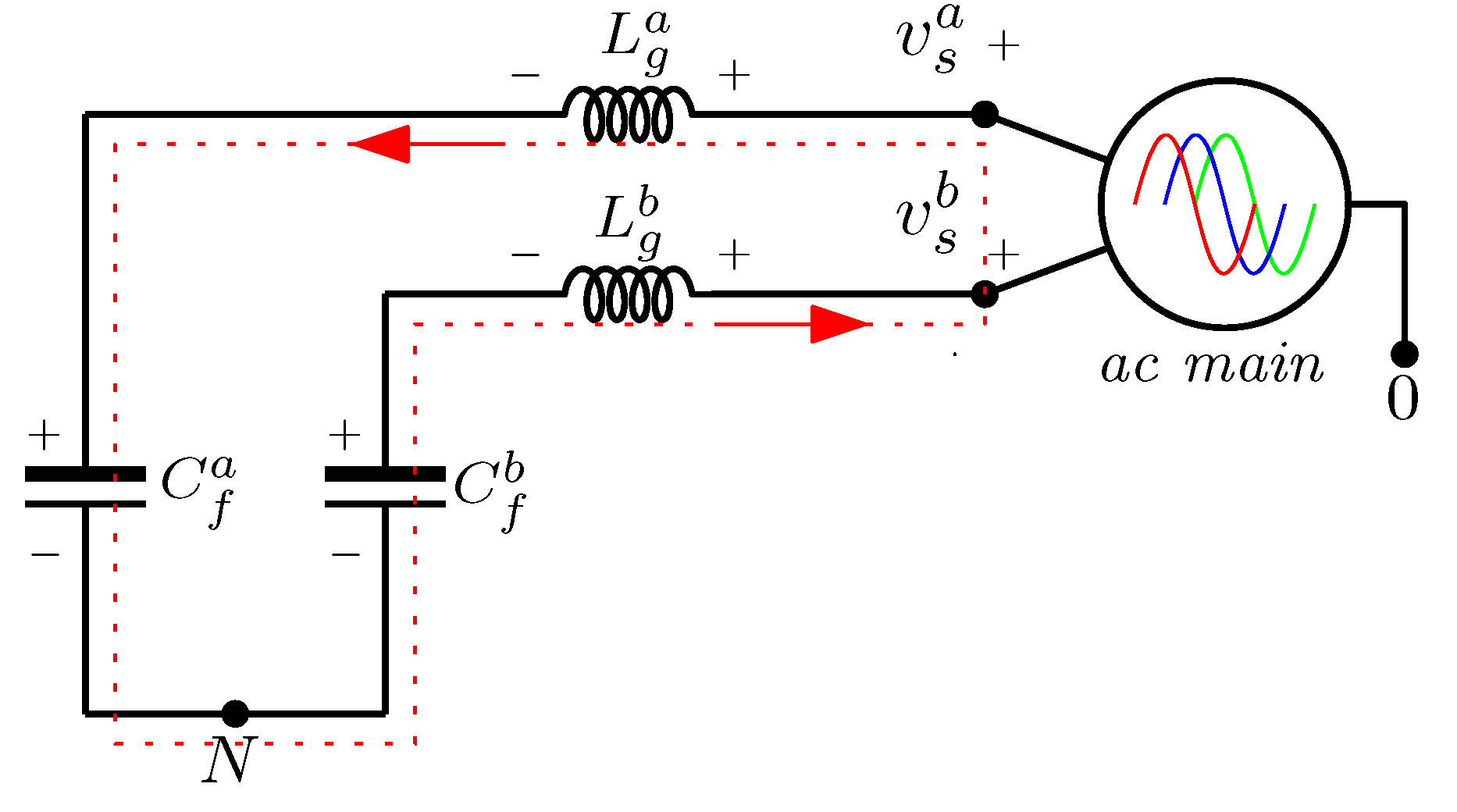
2.1. Mathematical Modeling of Power Converter
- Parasitic resistances associated to the inductors are zero,
- Damping resistances in series capacitors are zero,
- Voltages are balanced (i.e., ),
- Currents are balanced (i.e., ).
2.2. LCL Filter Tuning
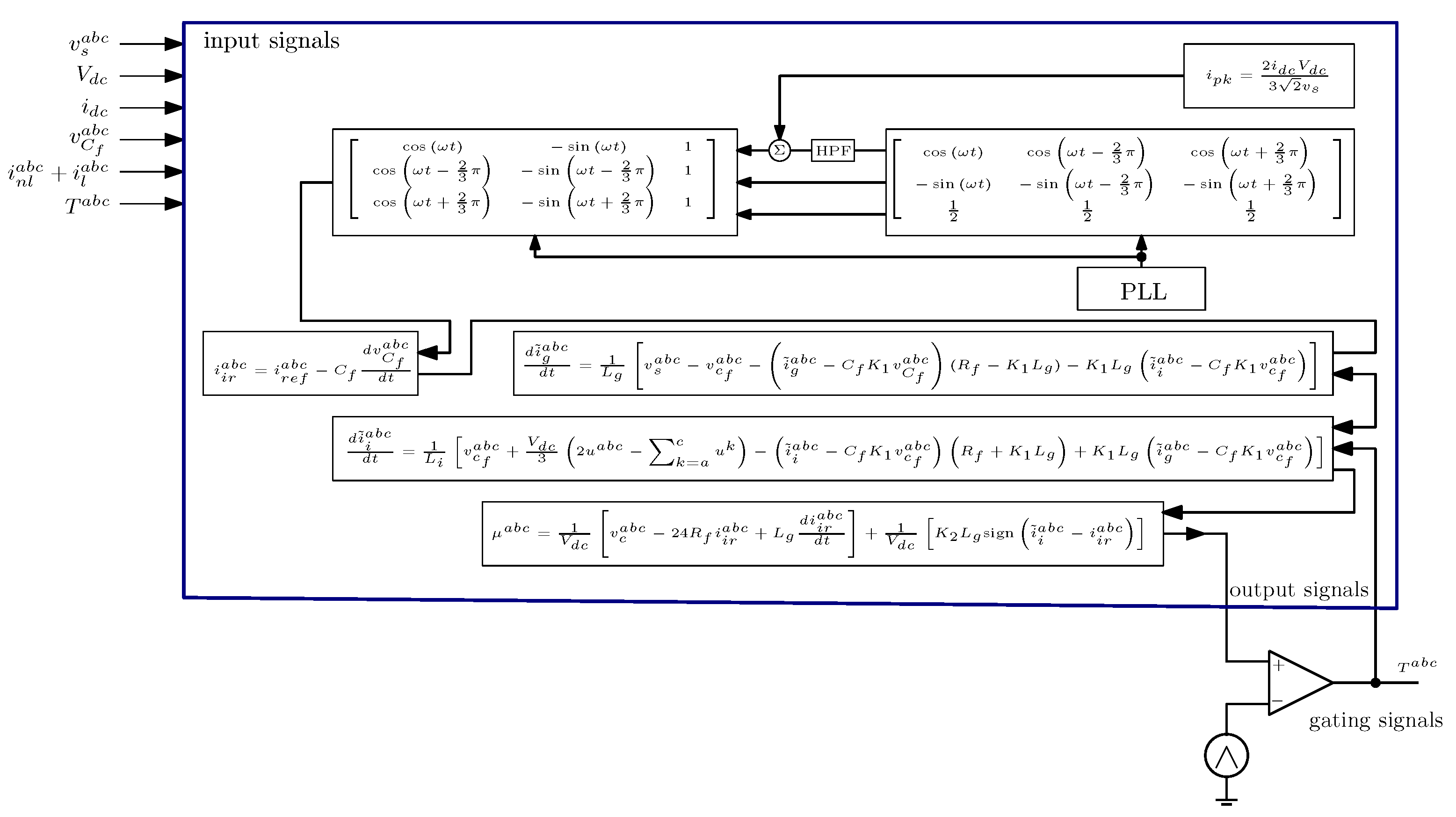
3. Controller Design
3.1. Sliding Mode Controller Design
3.2. Reference Calculation
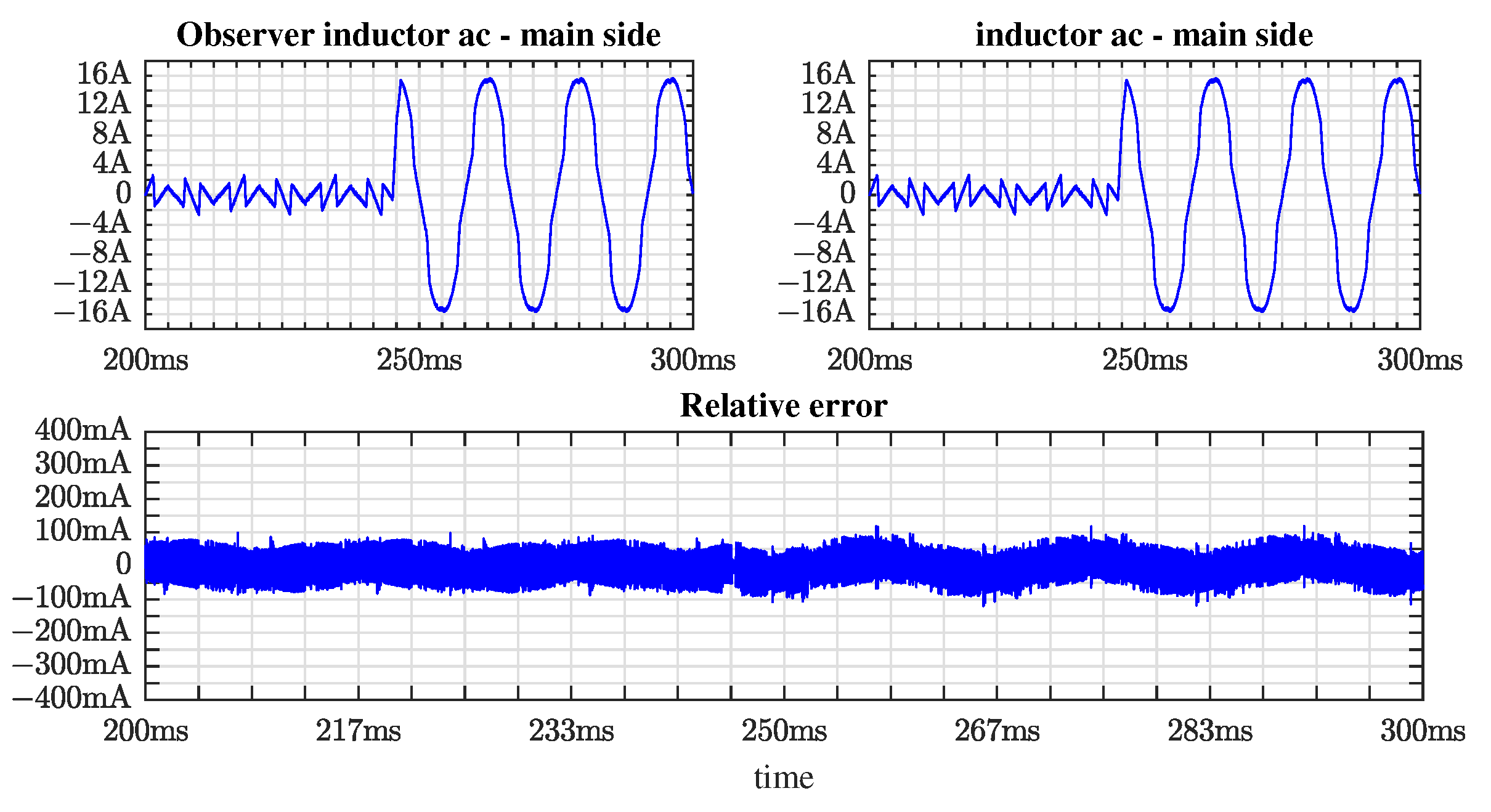
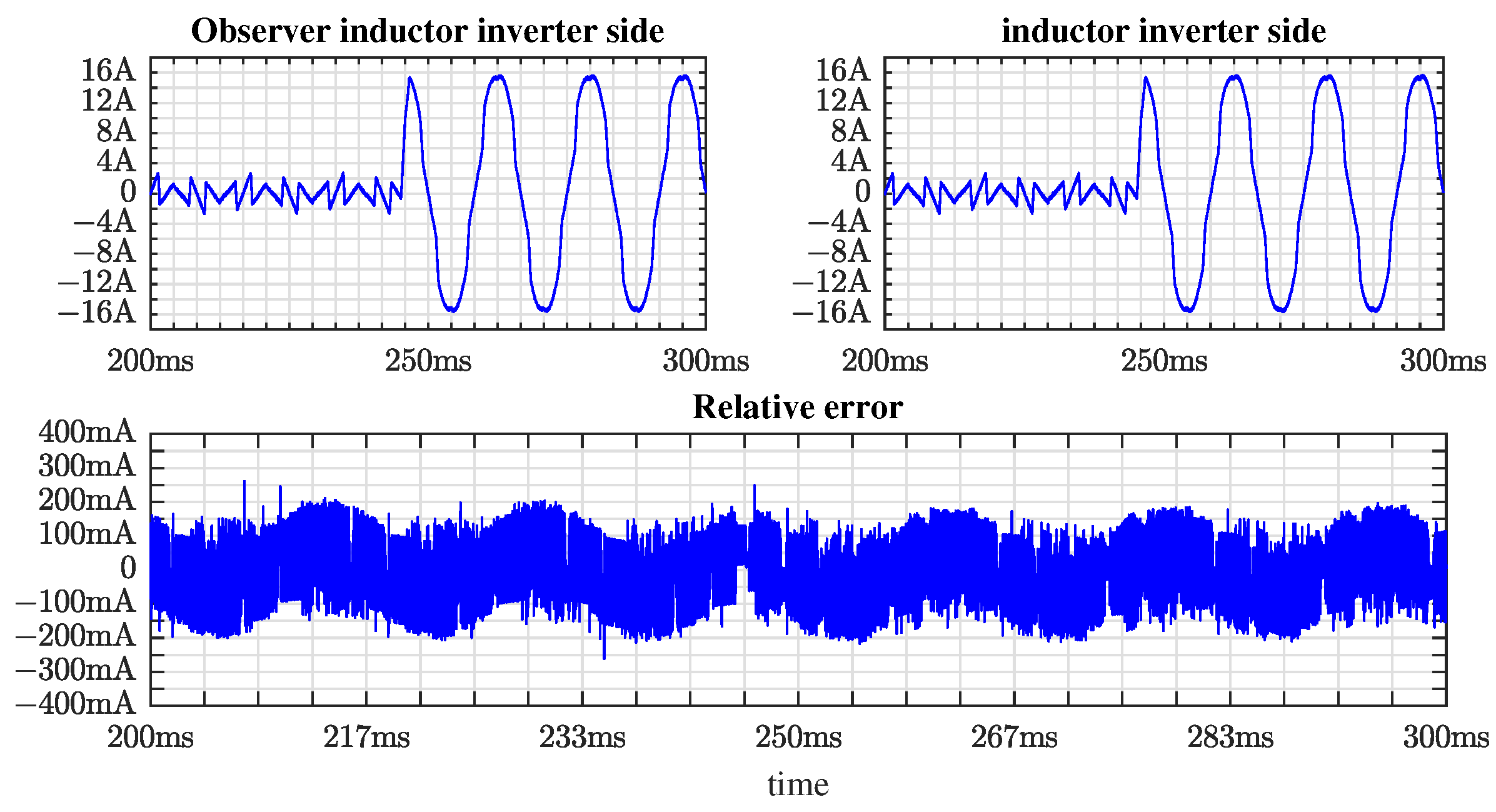
3.3. Inductor Current Estimator
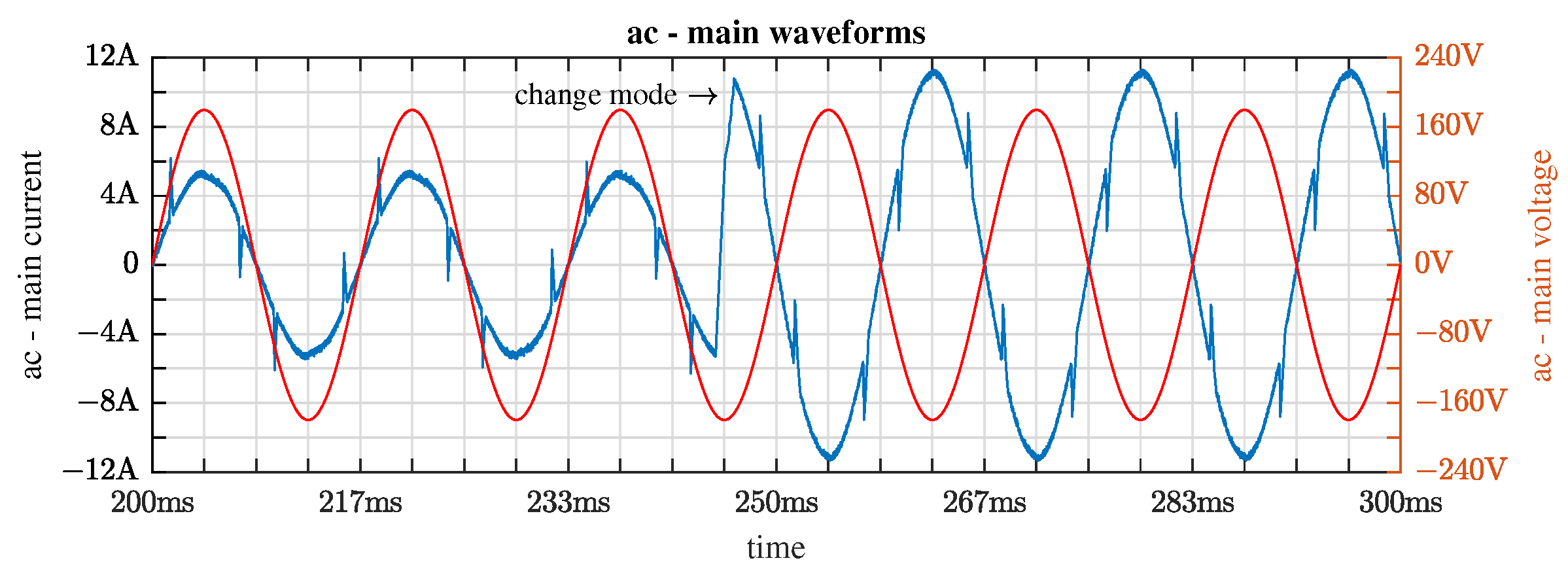
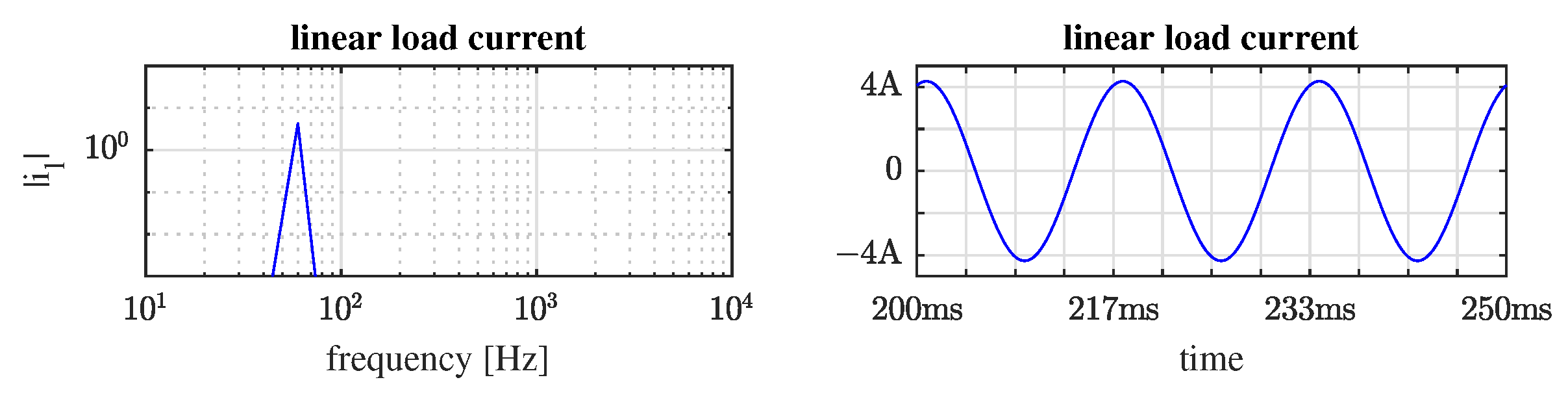
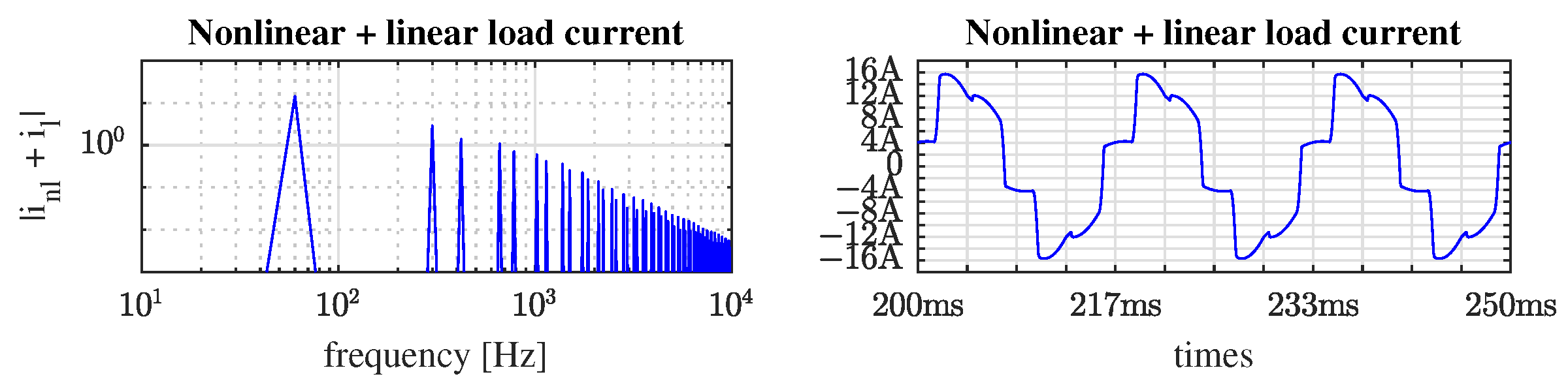
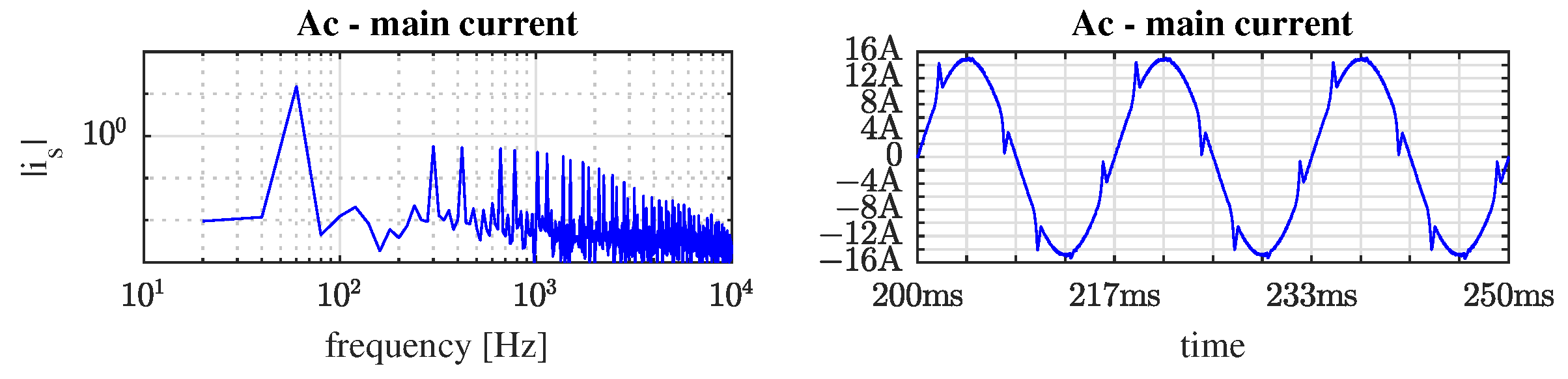
4. Simulation Results
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Energy Agency. Renewables 2018: Analysis and Forecasts to 2O23; Market Report Series; IEA: Paris, France, 2018; Available online: https://www.iea.org/reports/renewables-2018 (accessed on 10 January 2021).
- El Ghaly, A.; Tarnini, M.; Moubayed, N.; Chahine, K. A Filter-Less Time-Domain Method for Reference Signal Extraction in Shunt Active Power Filters. Energies 2022, 15, 5568. [Google Scholar] [CrossRef]
- Nicolae, P.M.; Nicolae, I.D.; Nicolae, M.S. Some Considerations Regarding the Measurement of the Compensation Efficiency in Three-Phase Systems. Energies 2022, 15, 5004. [Google Scholar] [CrossRef]
- Pichan, M.; Seyyedhosseini, M.; Hafezi, H. A New DeadBeat-Based Direct Power Control of Shunt Active Power Filter With Digital Implementation Delay Compensation. IEEE Access 2022, 10, 72866–72878. [Google Scholar] [CrossRef]
- Li, P.; Huo, L.; Guo, Y.; An, G.; Guo, X.; Li, Z.; Sun, H. Modulation and Control Strategy of 3CH4 Combined Current Source Grid-Connected Inverter. Energies 2022, 15, 4219. [Google Scholar] [CrossRef]
- Shieh, J.J.; Hwu, K.I.; Li, Y.Y. A Single-Voltage-Source Class-D Boost Multi-Level Inverter with Self-Balanced Capacitors. Energies 2022, 15, 4082. [Google Scholar] [CrossRef]
- Desai, A.A.; Mikkili, S.; Senjyu, T. Novel H6 Transformerless Inverter for Grid Connected Photovoltaic System to Reduce the Conduction Loss and Enhance Efficiency. Energies 2022, 15, 3789. [Google Scholar] [CrossRef]
- Singh, A.; Parida, S. A review on distributed generation allocation and planning in deregulated electricity market. Renew. Sustain. Energy Rev. 2018, 82, 4132–4141. [Google Scholar] [CrossRef]
- Kalair, A.; Abas, N.; Kalair, A.; Saleem, Z.; Khan, N. Review of harmonic analysis, modeling and mitigation techniques. Renew. Sustain. Energy Rev. 2017, 78, 1152–1187. [Google Scholar] [CrossRef]
- Kharrazi, A.; Sreeram, V.; Mishra, Y. Assessment techniques of the impact of grid-tied rooftop photovoltaic generation on the power quality of low voltage distribution network—A review. Renew. Sustain. Energy Rev. 2020, 120, 109643. [Google Scholar] [CrossRef]
- Basso, T.; DeBlasio, R. IEEE P1547-series of standards for interconnection. In Proceedings of the 2003 IEEE PES Transmission and Distribution Conference and Exposition (IEEE Cat. No.03CH37495), Dallas, TX, USA, 7–12 September 2003; Volume 2, pp. 556–561. [Google Scholar] [CrossRef] [Green Version]
- Khosravi, N.; Abdolmohammadi, H.; Bagheri, S.; Miveh, M. Improvement of harmonic conditions in the AC/DC microgrids with the presence of filter compensation modules. Renew. Sustain. Energy Rev. 2021, 143, 110898. [Google Scholar] [CrossRef]
- Li, D.; Wang, T.; Pan, W.; Ding, X.; Gong, J. A comprehensive review of improving power quality using active power filters. Electr. Power Syst. Res. 2021, 199, 107389. [Google Scholar] [CrossRef]
- Gusman, L.; Pereira, H.; Callegari, J.; Cupertino, A. Design for reliability of multifunctional PV inverters used in industrial power factor regulation. Int. J. Electr. Power Energy Syst. 2020, 119, 105932. [Google Scholar] [CrossRef]
- Ravinder, K.; Bansal, H.O. Investigations on shunt active power filter in a PV-wind-FC based hybrid renewable energy system to improve power quality using hardware-in-the-loop testing platform. Electr. Power Syst. Res. 2019, 177, 105957. [Google Scholar] [CrossRef]
- Kashif, M.; Hossain, M.; Zhuo, F.; Gautam, S. Design and implementation of a three-level active power filter for harmonic and reactive power compensation. Electr. Power Syst. Res. 2018, 165, 144–156. [Google Scholar] [CrossRef]
- Souza, R.R.; Moreira, A.B.; Barros, T.A.; Ruppert, E. A proposal for a wind system equipped with a doubly fed induction generator using the Conservative Power Theory for active filtering of harmonics currents. Electr. Power Syst. Res. 2018, 164, 167–177. [Google Scholar] [CrossRef]
- Sahli, A.; Krim, F.; Laib, A.; Talbi, B. Model predictive control for single phase active power filter using modified packed U-cell (MPUC5) converter. Electr. Power Syst. Res. 2020, 180, 106139. [Google Scholar] [CrossRef]
- Kryonidis, G.C.; Kontis, E.O.; Papadopoulos, T.A.; Pippi, K.D.; Nousdilis, A.I.; Barzegkar-Ntovom, G.A.; Boubaris, A.D.; Papanikolaou, N.P. Ancillary services in active distribution networks: A review of technological trends from operational and online analysis perspective. Renew. Sustain. Energy Rev. 2021, 147, 111198. [Google Scholar] [CrossRef]
- Ghosh, S.; Rahman, S.; Pipattanasomporn, M. Distribution Voltage Regulation Through Active Power Curtailment With PV Inverters and Solar Generation Forecasts. IEEE Trans. Sustain. Energy 2017, 8, 13–22. [Google Scholar] [CrossRef]
- Mai, T.T.; Haque, A.N.M.; Vergara, P.P.; Nguyen, P.H.; Pemen, G. Adaptive coordination of sequential droop control for PV inverters to mitigate voltage rise in PV-Rich LV distribution networks. Electr. Power Syst. Res. 2021, 192, 106931. [Google Scholar] [CrossRef]
- Hannan, M.A.; Ghani, Z.A.; Hoque, M.M.; Ker, P.J.; Hussain, A.; Mohamed, A. Fuzzy Logic Inverter Controller in Photovoltaic Applications: Issues and Recommendations. IEEE Access 2019, 7, 24934–24955. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Y.; Liang, R.; Geng, T.; Zhang, W. Adaptive Current Control for Grid-Connected Inverter with Dynamic Recurrent Fuzzy-Neural-Network. Energies 2022, 15, 4163. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding mode control, implementation and performance analysis of standalone PV fed dual inverter. Sol. Energy 2017, 155, 1178–1187. [Google Scholar] [CrossRef]
- Kumar, N.; Saha, T.K.; Dey, J. Sliding-Mode Control of PWM Dual Inverter-Based Grid-Connected PV System: Modeling and Performance Analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 435–444. [Google Scholar] [CrossRef]
- Wai, R.J.; Wang, W.H. Grid-Connected Photovoltaic Generation System. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 953–964. [Google Scholar] [CrossRef]
- Fernao Pires, V.; Martins, J.; Hao, C. Dual-inverter for grid-connected photovoltaic system: Modeling and sliding mode control. Sol. Energy 2012, 86, 2106–2115. [Google Scholar] [CrossRef]
- Hassine, I.M.B.; Naouar, M.W.; Mrabet-Bellaaj, N. Model Predictive-Sliding Mode Control for Three-Phase Grid-Connected Converters. IEEE Trans. Ind. Electron. 2017, 64, 1341–1349. [Google Scholar] [CrossRef]
- Tan, S.C.; Lai, Y.M.; Tse, C.K. General Design Issues of Sliding-Mode Controllers in DC-DC Converters. IEEE Trans. Ind. Electron. 2008, 55, 1160–1174. [Google Scholar] [CrossRef]
- Dhar, S.; Dash, P. A new backstepping finite time sliding mode control of grid connected PV system using multivariable dynamic VSC model. Int. J. Electr. Power Energy Syst. 2016, 82, 314–330. [Google Scholar] [CrossRef]
- Reveles-Miranda, M.; Sánchez-Florez, D.F.; Cruz-Chan, J.R.; Ordoñez López, E.E.; Flota-Bañuelos, M.; Pacheco-Catalán, D. The Control Scheme of the Multifunction Inverter for Power Factor Improvement. Energies 2018, 11, 1662. [Google Scholar] [CrossRef] [Green Version]
- Reveles-Miranda, M.; Flota-Bañuelos, M.; Chan-Puc, F.; Ramirez-Rivera, V.; Pacheco-Catalán, D. A Hybrid Control Technique for Harmonic Elimination, Power Factor Correction, and Night Operation of a Grid-Connected PV Inverter. IEEE J. Photovoltaics 2020, 10, 664–675. [Google Scholar] [CrossRef]
- Said-Romdhane, M.; Naouar, M.; Slama-Belkhodja, I.; Monmasson, E. Simple and systematic LCL filter design for three-phase grid-connected power converters. Math. Comput. Simul. 2015, 130, 181–193. [Google Scholar] [CrossRef]
- Normand-Cyrot, D.; Fossard, A.J. Nonlinear Systems: Modeling and Estimation; Springer Science & Business Media: Berlin, Germany, 1995. [Google Scholar]
- Hoon, Y.; Mohd Radzi, M.A.; Hassan, M.K.; Mailah, N.F. A Dual-Function Instantaneous Power Theory for Operation of Three-Level Neutral-Point-Clamped Inverter-Based Shunt Active Power Filter. Energies 2018, 11, 1592. [Google Scholar] [CrossRef]
- Ding, X.; Xue, R.; Zheng, T.; Kong, F.; Chen, Y. Robust Delay Compensation Strategy for LCL-Type Grid-Connected Inverter in Weak Grid. IEEE Access 2022, 10, 67639–67652. [Google Scholar] [CrossRef]
- Guzman, R.; de Vicuña, L.G.; Morales, J.; Castilla, M.; Miret, J. Model-Based Control for a Three-Phase Shunt Active Power Filter. IEEE Trans. Ind. Electron. 2016, 63, 3998–4007. [Google Scholar] [CrossRef] [Green Version]





| Description | Parameter | Value |
|---|---|---|
| Ac-main voltage | 127 V | |
| Dc-link | 450 V | |
| Grid frequency | 60 Hz | |
| Frequency modulation index | 200 | |
| Power load | 1 kW | |
| Dc-link capacitor | 2400 F | |
| Filter capacitor | 137.01 nF | |
| Inductor parasitic resistances | , | 100 m |
| Damping filter resistance | 139 | |
| Filter inductance, inverter-side | 32 mH | |
| Filter inductance, grid-side | 1.9 mH | |
| Observer gain | ||
| Sliding mode controller gain | 0.65 |
| Without APF | With APF | |||||
|---|---|---|---|---|---|---|
| 1 | 13.812 | 13.812 | 22.611 | 16.344 | 15.944 | 15.257 |
| 5 | 9.551 | 9.551 | 9.273 | 0.378 | 0.625 | 0.657 |
| 7 | 4.015 | 4.015 | 2.875 | 0.104 | 0.117 | 0.149 |
| 11 | 0.391 | 0.391 | 0.439 | 0.118 | 0.155 | 0.177 |
| 13 | 0.585 | 0.574 | 0.165 | 0.119 | 0.087 | 0.062 |
| 17 | 0.167 | 0.167 | 0.194 | 0.036 | 0.009 | 0.043 |
| 23 | 0.221 | 0.221 | 0.142 | 0.031 | 0.040 | 0.031 |
| 25 | 0.100 | 0.100 | 0.070 | 0.027 | 0.027 | 0.014 |
| THD | THD | |||||
| 75.21% | 75.21% | 42.97% | 2.61% | 4.19% | 4.62% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Flota-Bañuelos, M.; Miranda-Vidales, H.; Fernández, B.; Ricalde, L.J.; Basam, A.; Medina, J. Harmonic Compensation via Grid-Tied Three-Phase Inverter with Variable Structure I&I Observer-Based Control Scheme. Energies 2022, 15, 6419. https://doi.org/10.3390/en15176419
Flota-Bañuelos M, Miranda-Vidales H, Fernández B, Ricalde LJ, Basam A, Medina J. Harmonic Compensation via Grid-Tied Three-Phase Inverter with Variable Structure I&I Observer-Based Control Scheme. Energies. 2022; 15(17):6419. https://doi.org/10.3390/en15176419
Chicago/Turabian StyleFlota-Bañuelos, Manuel, Homero Miranda-Vidales, Bernardo Fernández, Luis J. Ricalde, A. Basam, and J. Medina. 2022. "Harmonic Compensation via Grid-Tied Three-Phase Inverter with Variable Structure I&I Observer-Based Control Scheme" Energies 15, no. 17: 6419. https://doi.org/10.3390/en15176419
APA StyleFlota-Bañuelos, M., Miranda-Vidales, H., Fernández, B., Ricalde, L. J., Basam, A., & Medina, J. (2022). Harmonic Compensation via Grid-Tied Three-Phase Inverter with Variable Structure I&I Observer-Based Control Scheme. Energies, 15(17), 6419. https://doi.org/10.3390/en15176419








