Mapping Methodology for Self and Mutual Inductance Profiles in IPT Systems
Abstract
:1. Introduction
2. Magnetic Coupler
2.1. Fundamentals
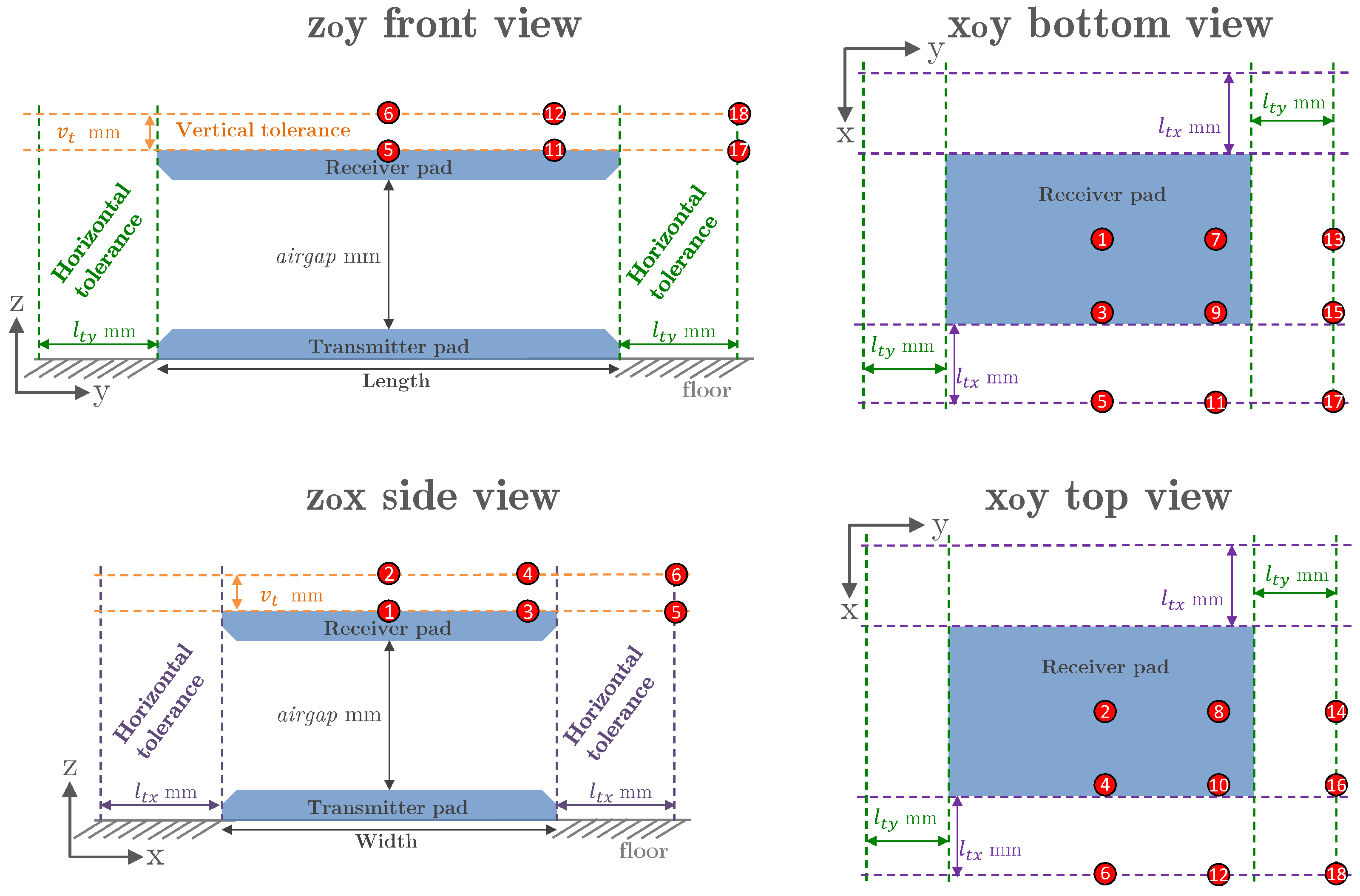
2.2. Geometry
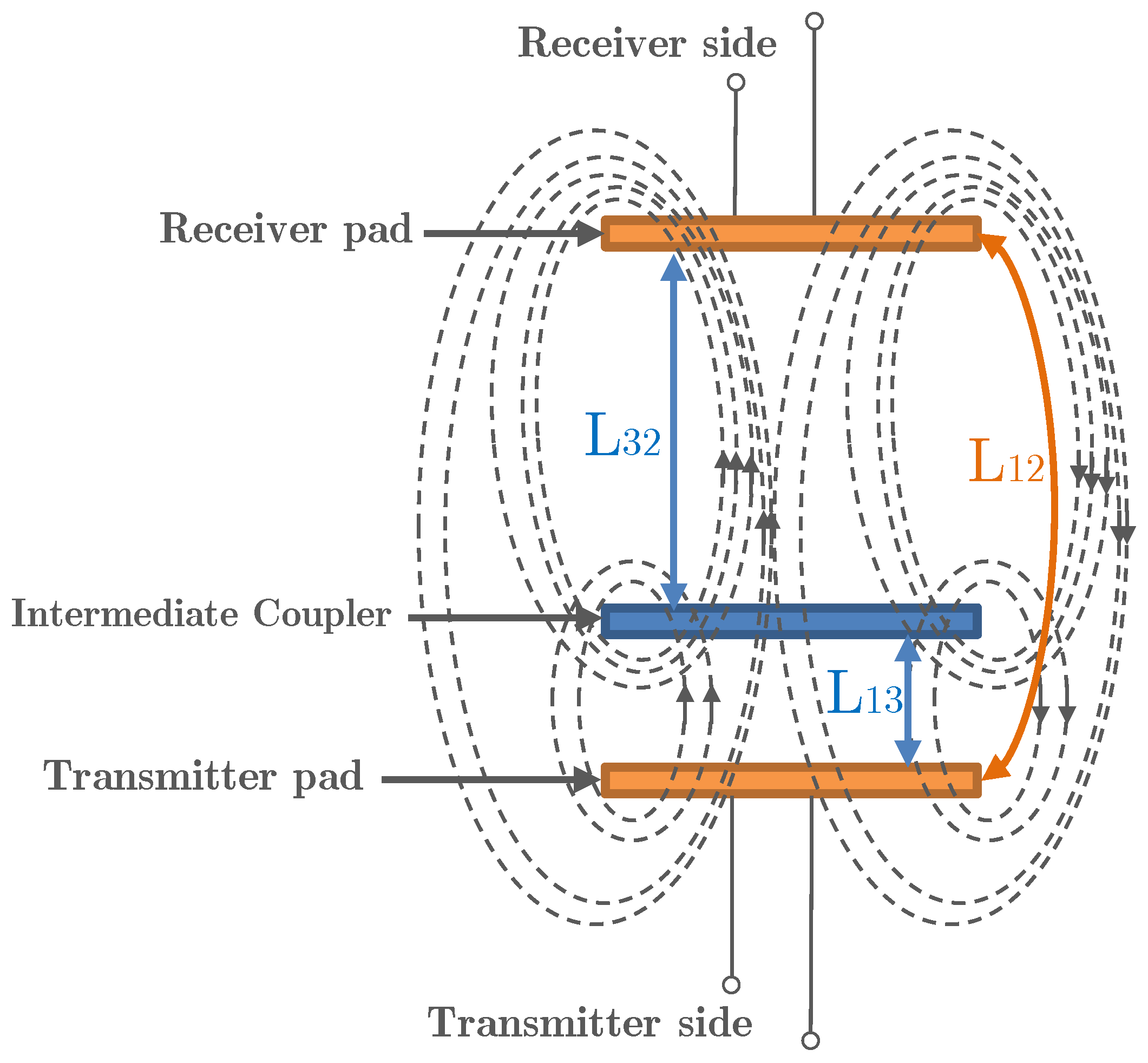
3. Characterization of MC
3.1. Mutual Inductance Profiling
3.1.1. Methodology
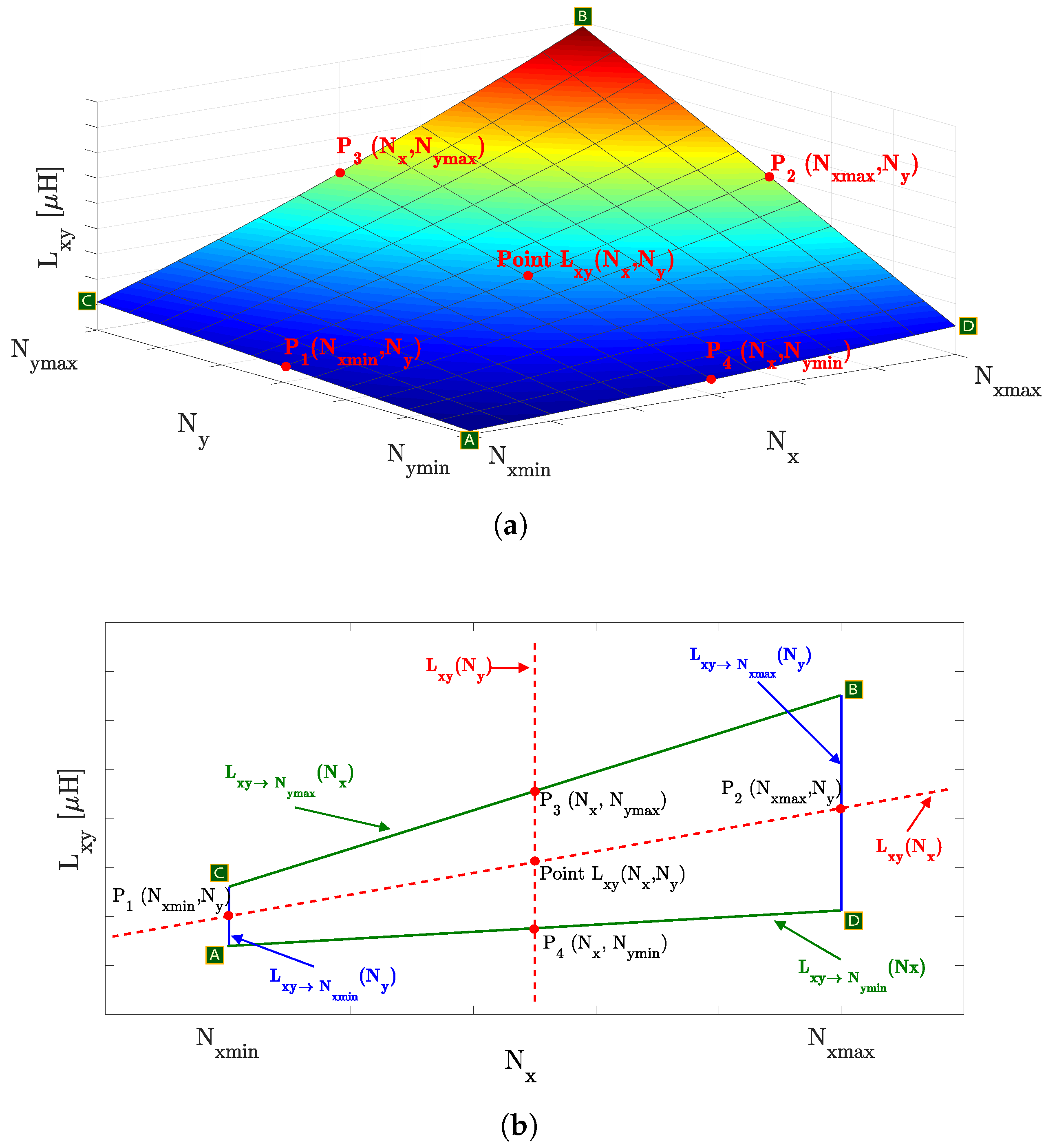
- Profile of : Figure 6 illustrates the surface of with a fixed value of and , using the FEA results from A to D, identified by the alphabetic numbered green squares. Figure 6b depicts a 2D plane, view from the axis of Figure 6a. The value of for specific values of and , exemplified by the red dot labeled as in Figure 6b, can be identified by either linear functions or , illustrated by the red dashed lines, which intersect at the desired value. The slope and intercept of are determined using points and . The values of and are obtained using line equations and for the desired , respectively. The desired value of is then found using equation for the desired . This process is repeated times to create the surface illustrated in Figure 6a. The profiling of is replicated for all charging positions .
- Replace and with desired values in surface function , determined in step 1, and repeat the process for all simulated . The new values of already take into consideration the effect of the selected set of turns.
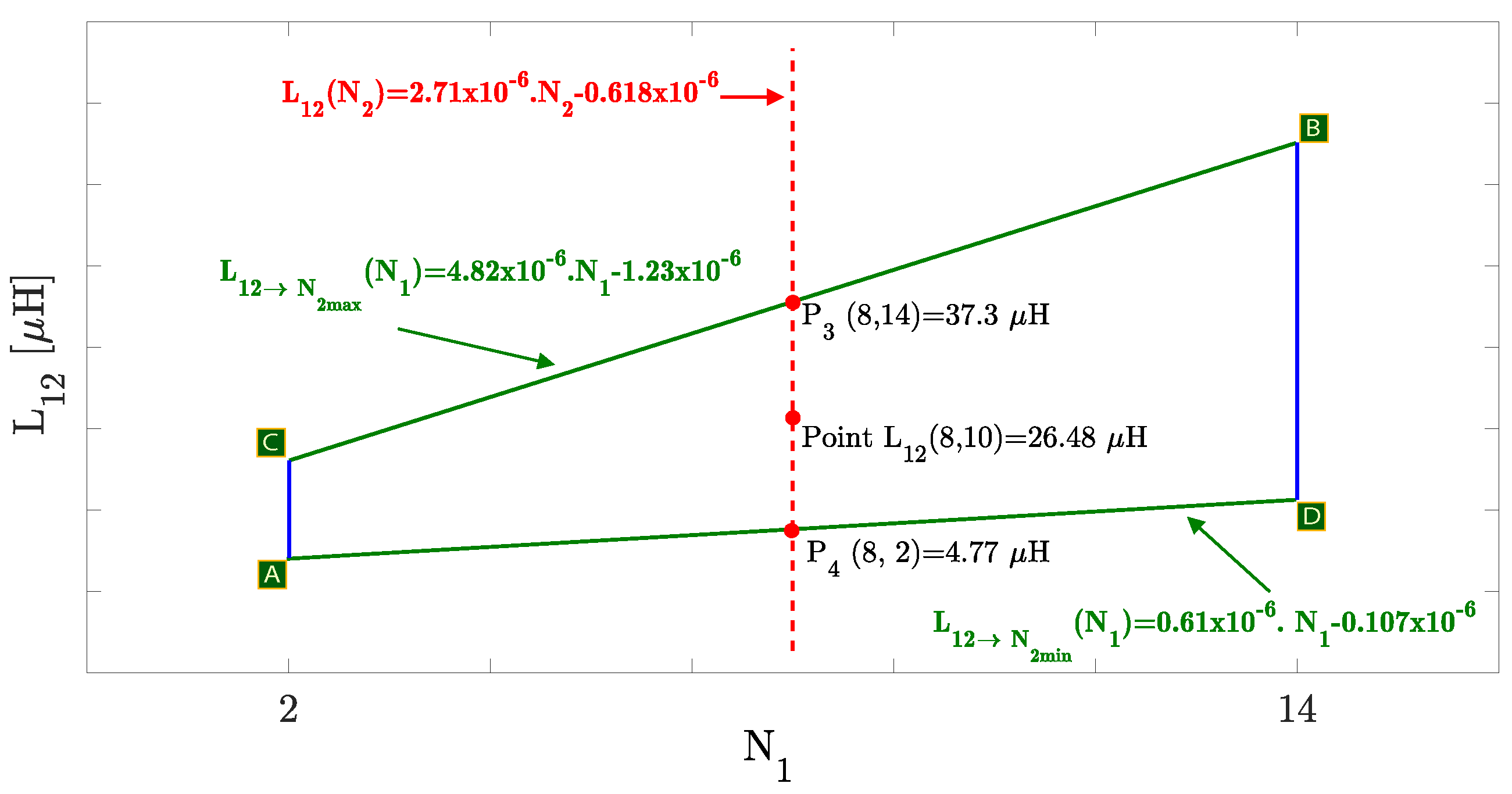
- Profile of : Use the values found in Step 2 for 1 and 2 to determine the constants and in (7). Repeat the process for the remaining with the same lateral displacements but different air gap values, i.e., ( 3, 4), ( 5, 6), …, ( 17, 18). A total of three equations are determined for circular-shaped MCs and nine equations for non-circular MCs. The equations are identified from to in Figure 7a.
- Replace in equations to with the desired value to determine in points to , as illustrated in Figure 7a. The new values take into account the effect of the selected set of turns and air gap values.
- Profile of : Use the values found in Step 4 that have the same and values, such as to , to determine the Gaussian constants , and in (8). Repeat the process (if applicable) for the set of points to and to . A total of one or three equations is determined according to the shape of the MC. Circular-shaped MCs are only evaluated in relation to or and only one equation is needed, whereas the remaining MCs require a total of three equations. Figure 7b illustrates the labeled equations from to .
- Replace in equations to with the desired value to determine in the points to , represented in Figure 7b with the color green. The new values already take into account the effect of , , and .
- Replace in equation with the desired value to determine for a set of turns, , and values. Steps 7 and 8 are only required for non-circular shaped MCs.
- Profile of : Repeat Step 2 to Step 8 for every combination of , , , and to create the volume illustrated in Figure 4.
3.2. Self-Inductance Profiling
- Replace with the desired value equation , determined in step 1, and repeat the process for the remaining equations. The new values of already take into consideration the effect of the selected number of turns;
- Profile of : Replicate Step 3 to Step 9 of the methodology described in Section 3.1 to model the effect of air gap and lateral displacements in .
3.3. Development to Three-Coil Systems
4. Case Study
4.1. Specifications and FEA Simulations
4.2. Self and Mutual Inductance Profiling
4.3. Performance and Runtime
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Acronyms | |
| BPP | Bipolar pad |
| CFLP | Concrete ferrite-less pad |
| FLCP | Ferrite-less circular pad |
| IPT | Inductive Power Transfer |
| CP | Circular pad |
| DDP | Double D pad |
| IC | Intermediate coupler |
| MC | Magnetic Coupler |
| Symbol | |
| Transmitter coil self-inductance | |
| Intermediary coil self-inductance | |
| Mutual inductance bet. and | |
| Mutual inductance bet. and | |
| Mutual inductance bet. and | |
| Open-circuit voltage | |
| No-load active power | |
| Switching angular frequency | |
| Lateral displacement along x axis | |
| Vertical distance between coils | |
| FEA Simulation with specific | |
| Receiver coil self-inductance | |
| Intermediary capacitance | |
| Mutual coupling bet. and | |
| Mutual coupling bet. and | |
| Mutual coupling bet. and | |
| Open-circuit current | |
| No-load reactive power | |
| Number of turns in x coil | |
| Lateral displacement along y axis | |
| Charging position |
References
- Bandyopadhyay, S.; Venugopal, P.; Dong, J.; Bauer, P. Comparison of Magnetic Couplers for IPT-Based EV Charging Using Multi-Objective Optimization. IEEE Trans. Veh. Technol. 2019, 68, 5416–5429. [Google Scholar] [CrossRef]
- Bosshard, R.; Iruretagoyena, U.; Kolar, J.W. Comprehensive Evaluation of Rectangular and Double-D Coil Geometry for 50 kW/85 kHz IPT System. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1406–1415. [Google Scholar] [CrossRef]
- Budhia, M.; Boys, J.T.; Covic, G.A.; Huang, C.Y. Development of a Single-Sided Flux Magnetic Coupler for Electric Vehicle IPT Charging Systems. IEEE Trans. Ind. Electron. 2013, 60, 318–328. [Google Scholar] [CrossRef]
- Zaheer, A.; Covic, G.A.; Kacprzak, D. A Bipolar Pad in a 10-kHz 300-W Distributed IPT System for AGV Applications. IEEE Trans. Ind. Electron. 2014, 61, 3288–3301. [Google Scholar] [CrossRef]
- Zhong, W.X.; Zhang, C.; Liu, X.; Hui, S.Y.R. A Methodology for Making a Three-Coil Wireless Power Transfer System More Energy Efficient Than a Two-Coil Counterpart for Extended Transfer Distance. IEEE Trans. Power Electron. 2015, 30, 933–942. [Google Scholar] [CrossRef]
- Kamineni, A.; Covic, G.A.; Boys, J.T. Analysis of Coplanar Intermediate Coil Structures in Inductive Power Transfer Systems. IEEE Trans. Power Electron. 2015, 30, 6141–6154. [Google Scholar] [CrossRef]
- Moon, S.; Kim, B.C.; Cho, S.Y.; Ahn, C.H.; Moon, G.W. Analysis and Design of a Wireless Power Transfer System with an Intermediate Coil for High Efficiency. IEEE Trans. Ind. Electron. 2014, 61, 5861–5870. [Google Scholar] [CrossRef]
- Li, Y.; Xu, Q.; Lin, T.; Hu, J.; He, Z.; Mai, R. Analysis and Design of Load-Independent Output Current or Output Voltage of a Three-Coil Wireless Power Transfer System. IEEE Trans. Transp. Electrif. 2018, 4, 364–375. [Google Scholar] [CrossRef]
- Marques, E.G.; Mendes, A.M.S. Optimization of transmitter magnetic structures for roadway applications. In Proceedings of the 2017 IEEE Applied Power Electronics Conference and Exposition (APEC), Tampa, FL, USA, 36–30 March 2017; pp. 959–965. [Google Scholar] [CrossRef]
- Jiwariyavej, V.; Imura, T.; Hori, Y. Coupling Coefficients Estimation of Wireless Power Transfer System via Magnetic Resonance Coupling Using Information from Either Side of the System. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 191–200. [Google Scholar] [CrossRef]
- Chow, J.P.W.; Chung, H.S.H.; Cheng, C.S. Use of Transmitter-Side Electrical Information to Estimate Mutual Inductance and Regulate Receiver-Side Power in Wireless Inductive Link. IEEE Trans. Power Electron. 2016, 31, 6079–6091. [Google Scholar] [CrossRef]
- Su, Y.; Chen, L.; Wu, X.; Hu, A.P.; Tang, C.; Dai, X. Load and Mutual Inductance Identification from the Primary Side of Inductive Power Transfer System With Parallel-Tuned Secondary Power Pickup. IEEE Trans. Power Electron. 2018, 33, 9952–9962. [Google Scholar] [CrossRef]
- Marques, E.G.; Mendes, A.M.S.; Perdigão, M.S.; Costa, V.S. Design Methodology of a Three Coil IPT System with Parameters Identification for EVs. IEEE Trans. Veh. Technol. 2021, 70, 7509–7521. [Google Scholar] [CrossRef]
- Acero, J.; Carretero, C.; Lope, I.; Alonso, R.; Lucia, Ó.; Burdio, J.M. Analysis of the Mutual Inductance of Planar-Lumped Inductive Power Transfer Systems. IEEE Trans. Ind. Electron. 2013, 60, 410–420. [Google Scholar] [CrossRef]
- Wei, G.; Jin, X.; Wang, C.; Feng, J.; Zhu, C.; Matveevich, M.I. An Automatic Coil Design Method with Modified AC Resistance Evaluation for Achieving Maximum Coil Coil Efficiency in WPT Systems. IEEE Trans. Power Electron. 2020, 35, 6114–6126. [Google Scholar] [CrossRef]
- Nagendra, G.R.; Covic, G.A.; Boys, J.T. Determining the physical size of inductive couplers for IPT EV systems. In Proceedings of the 2014 IEEE Applied Power Electronics Conference and Exposition—APEC, Fort Worth, TX, USA, 16–20 March 2014; pp. 3443–3450. [Google Scholar]
- Song, K.; Ma, B.; Yang, G.; Jiang, J.; Wei, R.; Zhang, H.; Zhu, C. A Rotation-Lightweight Wireless Power Transfer System for Solar Wing Driving. IEEE Trans. Power Electron. 2019, 34, 8816–8830. [Google Scholar] [CrossRef]
- Tejeda, A.; Covic, G.A.; Boys, J.T. Novel single-sided ferrite-less magnetic coupler for roadway EV charging. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 3148–3153. [Google Scholar]
- Tejeda, A.; Carretero, C.; Boys, J.T.; Covic, G.A. Ferrite-Less Circular Pad with Controlled Flux Cancelation for EV Wireless Charging. IEEE Trans. Power Electron. 2017, 32, 8349–8359. [Google Scholar] [CrossRef]
- Zhang, W.; White, J.C.; Abraham, A.M.; Mi, C.C. Loosely Coupled Transformer Structure and Interoperability Study for EV Wireless Charging Systems. IEEE Trans. Power Electron. 2015, 30, 6356–6367. [Google Scholar] [CrossRef]
- Mohammad, M.; Choi, S.; Islam, M.Z.; Kwak, S.; Baek, J. Core Design and Optimization for Better Misalignment Tolerance and Higher Range Wireless Charging of PHEV. IEEE Trans. Transp. Electrif. 2017, 3, 445–453. [Google Scholar] [CrossRef]
- Zhang, W.; Wong, S.C.; Tse, C.K.; Chen, Q. An Optimized Track Length in Roadway Inductive Power Transfer Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 598–608. [Google Scholar] [CrossRef]





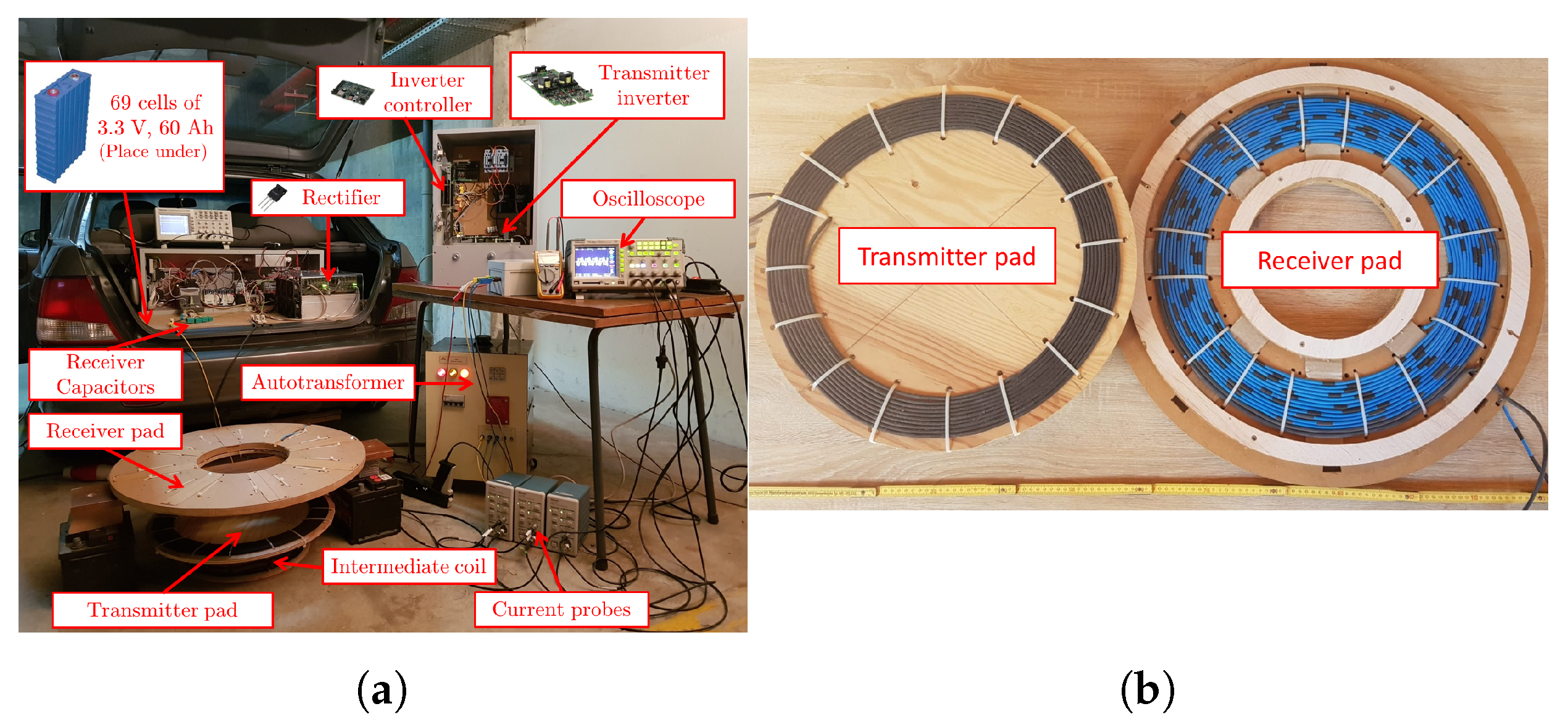
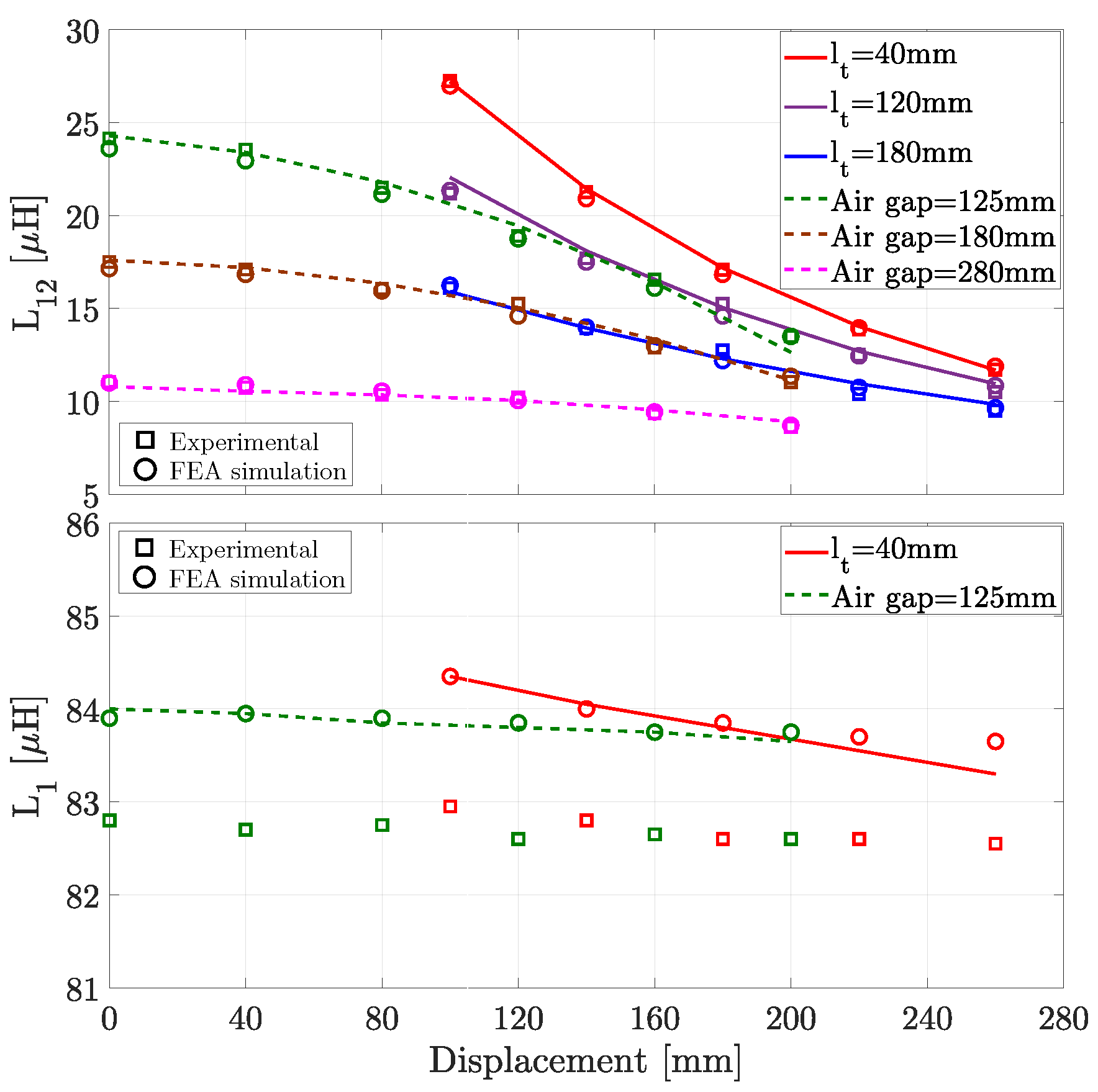
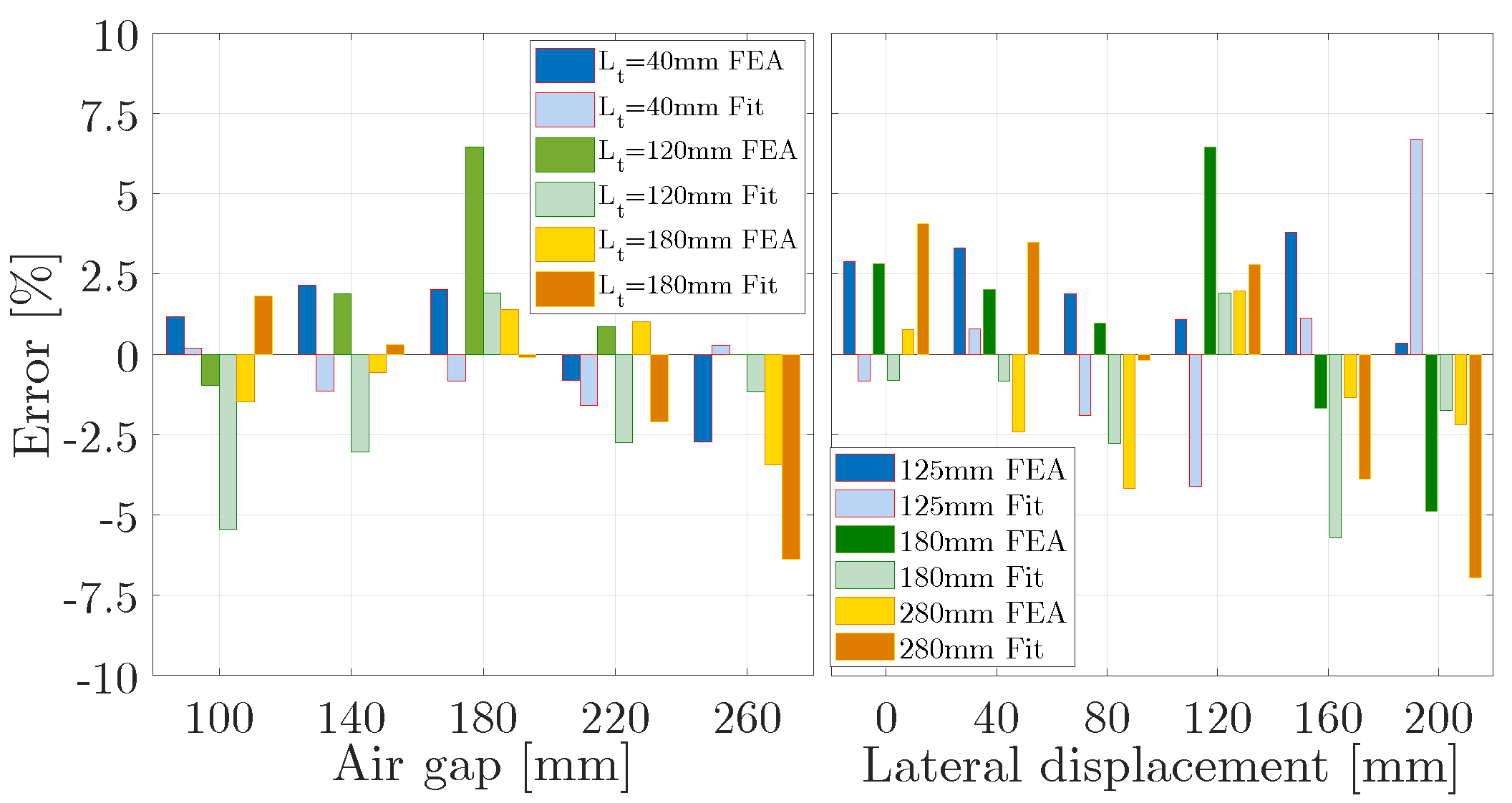
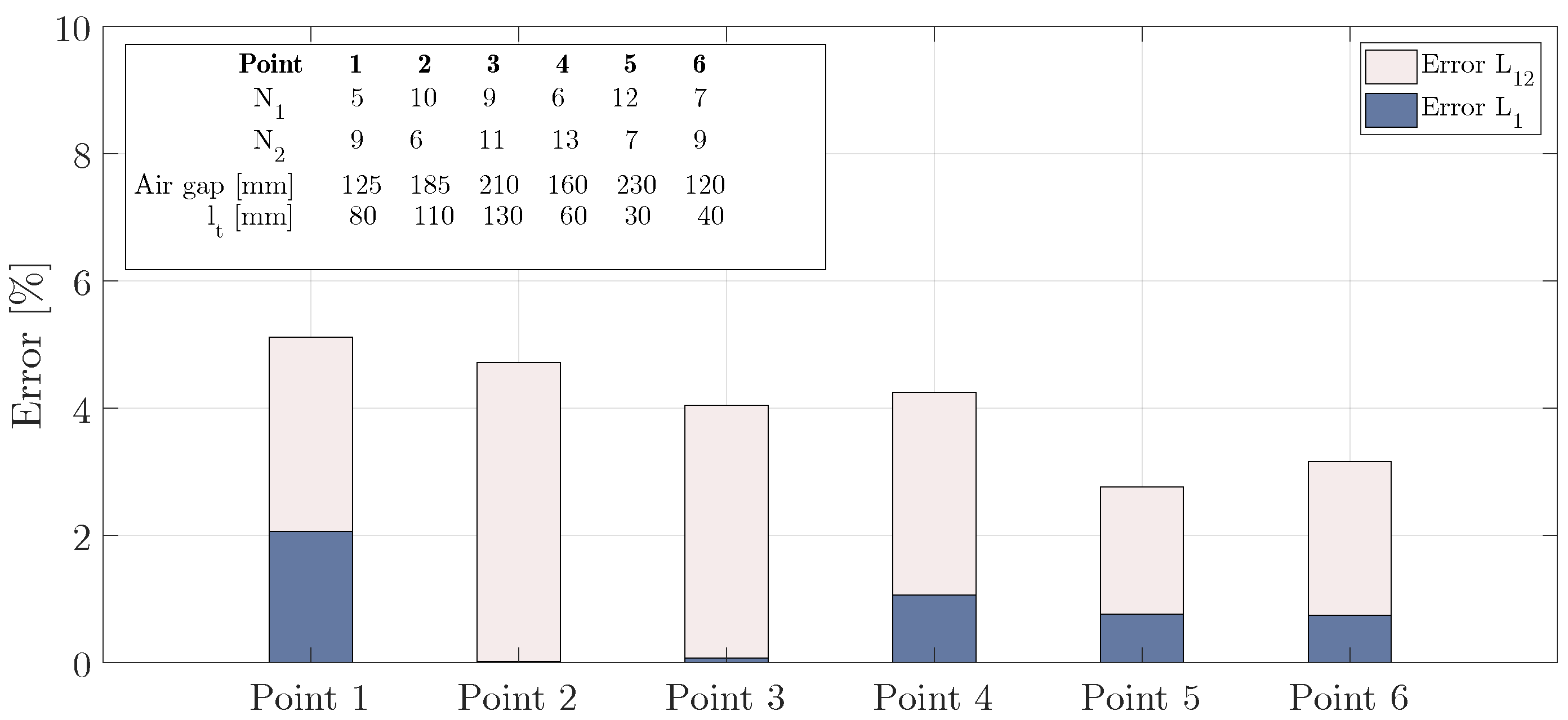
| Specifications and Constraints | Value |
|---|---|
| Normal frequency operation () | 85 kHz |
| [100–250 mm] | |
| lateral tolerance () | [0–150 mm] |
| Maximum , , | 30 A |
| Maximum MC size () | 800 mm |
| known | ||||
|---|---|---|---|---|
| MC | ||||
| CP | 6 | 1 | 2 | 12 |
| BPP | 18 | 1 | 2 | 36 |
| FLCP | 6 | 1 | 3 | 18 |
| unknown | ||||
| CP | 6 | 5 | 2 | 60 |
| BPP | 18 | 5 | 2 | 180 |
| FLCP | 6 | 7 | 3 | 126 |
| Scenarios | A | B | C | D | E | Unit | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1.12 | 4.32 | 66.2 | 160 | 8.4 | 4.33 | 8.48 | 161 | 19.9 | 56.8 | [H] |
| 2 | 0.34 | 4.23 | 21.9 | 155 | 2.7 | 4.23 | 2.73 | 155 | 6.3 | 55.3 | |
| 3 | 0.95 | 4.31 | 57.6 | 159 | 7.28 | 4.3 | 7.36 | 159 | 17.1 | 56.5 | |
| 4 | 0.31 | 4.22 | 20.4 | 155 | 2.51 | 4.23 | 2.53 | 155 | 5.84 | 55.2 | |
| 5 | 0.63 | 4.26 | 40.2 | 157 | 5.02 | 4.27 | 5.03 | 157 | 11.6 | 55.9 | |
| 6 | 0.24 | 4.22 | 16.5 | 155 | 1.99 | 4.22 | 2.01 | 155 | 4.63 | 55.3 | |
| Pos 1 | Pos 2 | Pos 3 | Unit |
|---|---|---|---|
| H | |||
| Pos4 | Pos5 | Pos6 | |
| H |
| Pos 1 | Pos 2 | Pos 3 | Unit |
|---|---|---|---|
| H | |||
| Pos4 | Pos5 | Pos6 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Marques, E.G.; Mendes, A.M.S.; Perdigão, M.; Costa, V.S. Mapping Methodology for Self and Mutual Inductance Profiles in IPT Systems. Energies 2022, 15, 6450. https://doi.org/10.3390/en15176450
Marques EG, Mendes AMS, Perdigão M, Costa VS. Mapping Methodology for Self and Mutual Inductance Profiles in IPT Systems. Energies. 2022; 15(17):6450. https://doi.org/10.3390/en15176450
Chicago/Turabian StyleMarques, Emanuel G., André M. S. Mendes, Marina Perdigão, and Valter S. Costa. 2022. "Mapping Methodology for Self and Mutual Inductance Profiles in IPT Systems" Energies 15, no. 17: 6450. https://doi.org/10.3390/en15176450
APA StyleMarques, E. G., Mendes, A. M. S., Perdigão, M., & Costa, V. S. (2022). Mapping Methodology for Self and Mutual Inductance Profiles in IPT Systems. Energies, 15(17), 6450. https://doi.org/10.3390/en15176450







