Numerical Study on Behaviors of the Sloshing Liquid Oxygen Tanks
Abstract
:1. Introduction
2. Establishment and Verification of the Sloshing Model
2.1. Problem Description
- (1)
- The tank was treated as a rigid vessel, the thermal insulation layer was not considered, and the specific heat flux was set uniformly on the tank walls.
- (2)
- Liquid oxygen was considered incompressible, and the variation of density with temperature was based on the Boussinesq approximation. Furthermore, the vapor was treated as real gas using the Soave–Redlich–Kwong model.
- (3)
- The non-slip boundary was employed on the tank wall.
2.2. Numerical Model
- (1)
- Governing equations:
- (2)
- The algebraic interface area density (AIAD) model:
- (3)
- Heat and mass transfer model:
2.3. Numerical Implementation
2.4. Initial and Boundary Conditions
2.5. Mesh Independence Validation
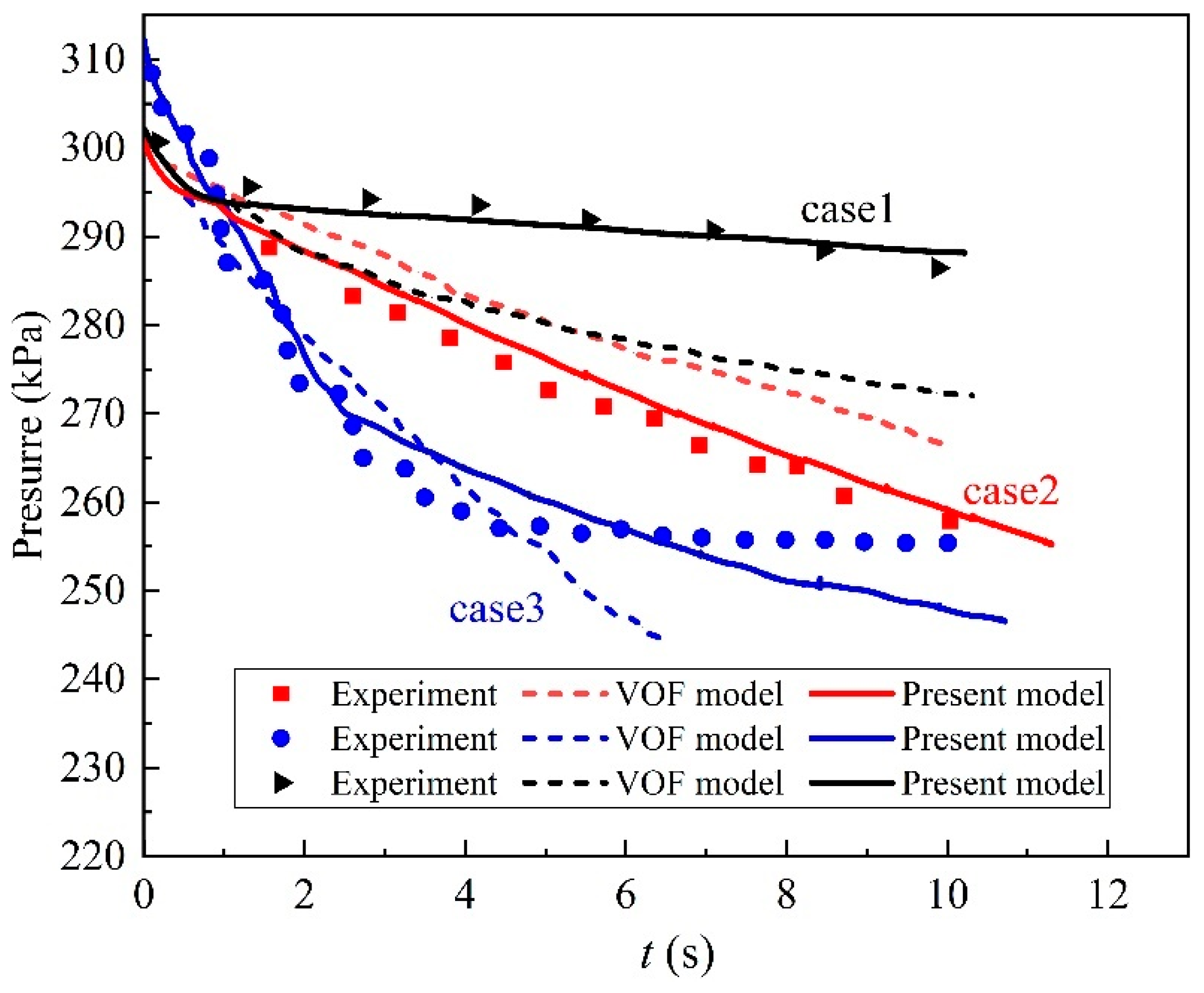
2.6. Validation of CFD Model
3. Results and Discussion
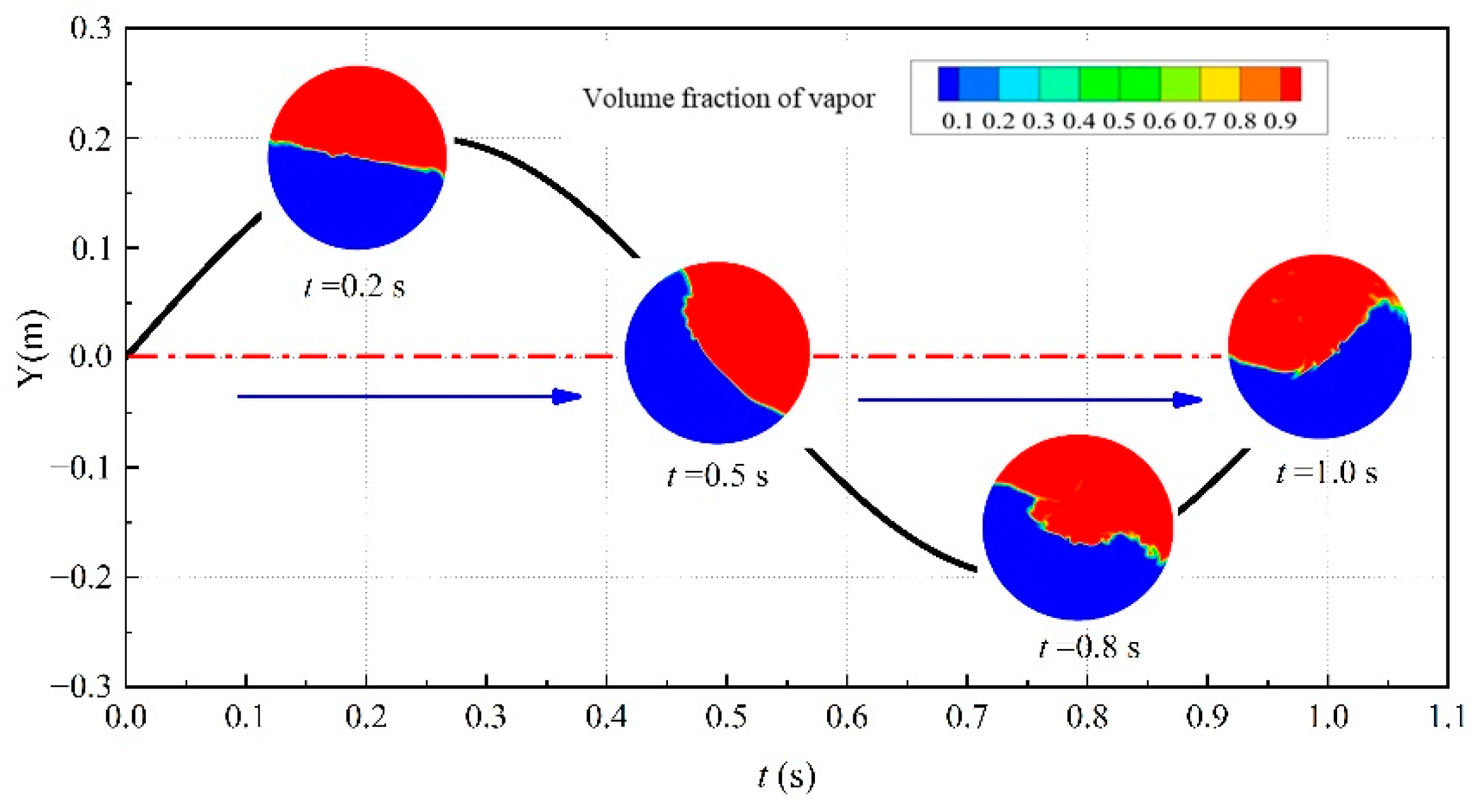
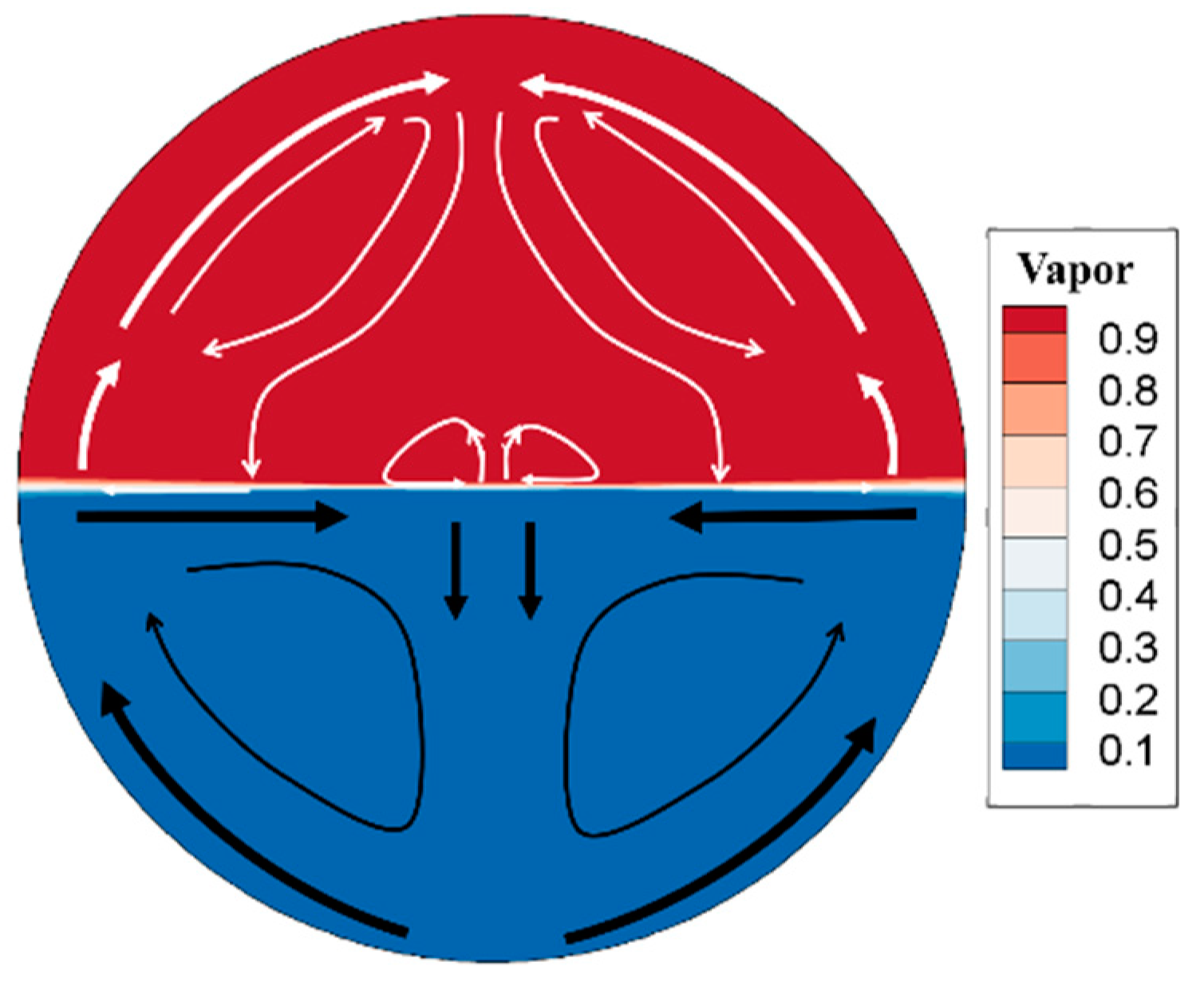
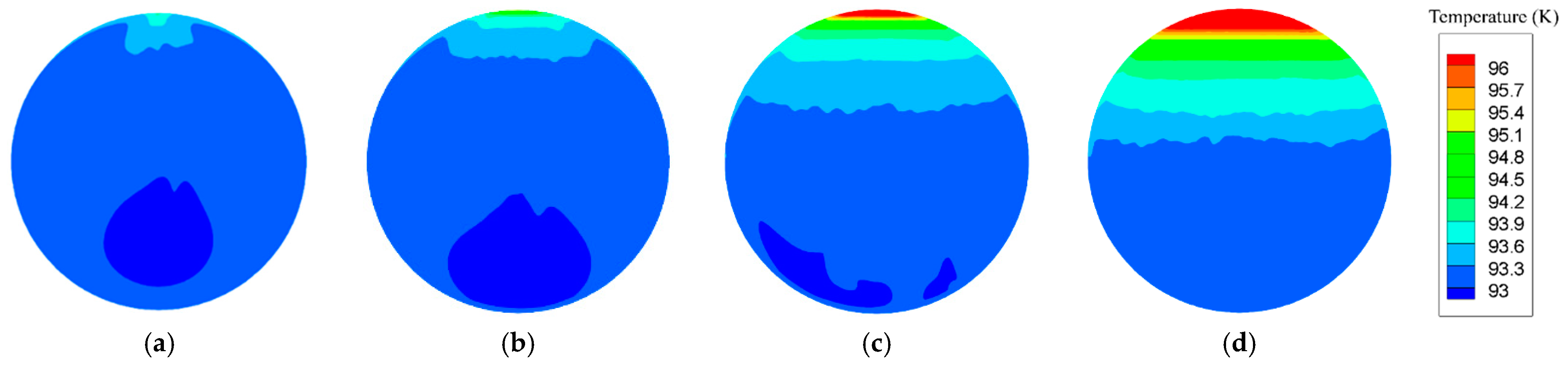
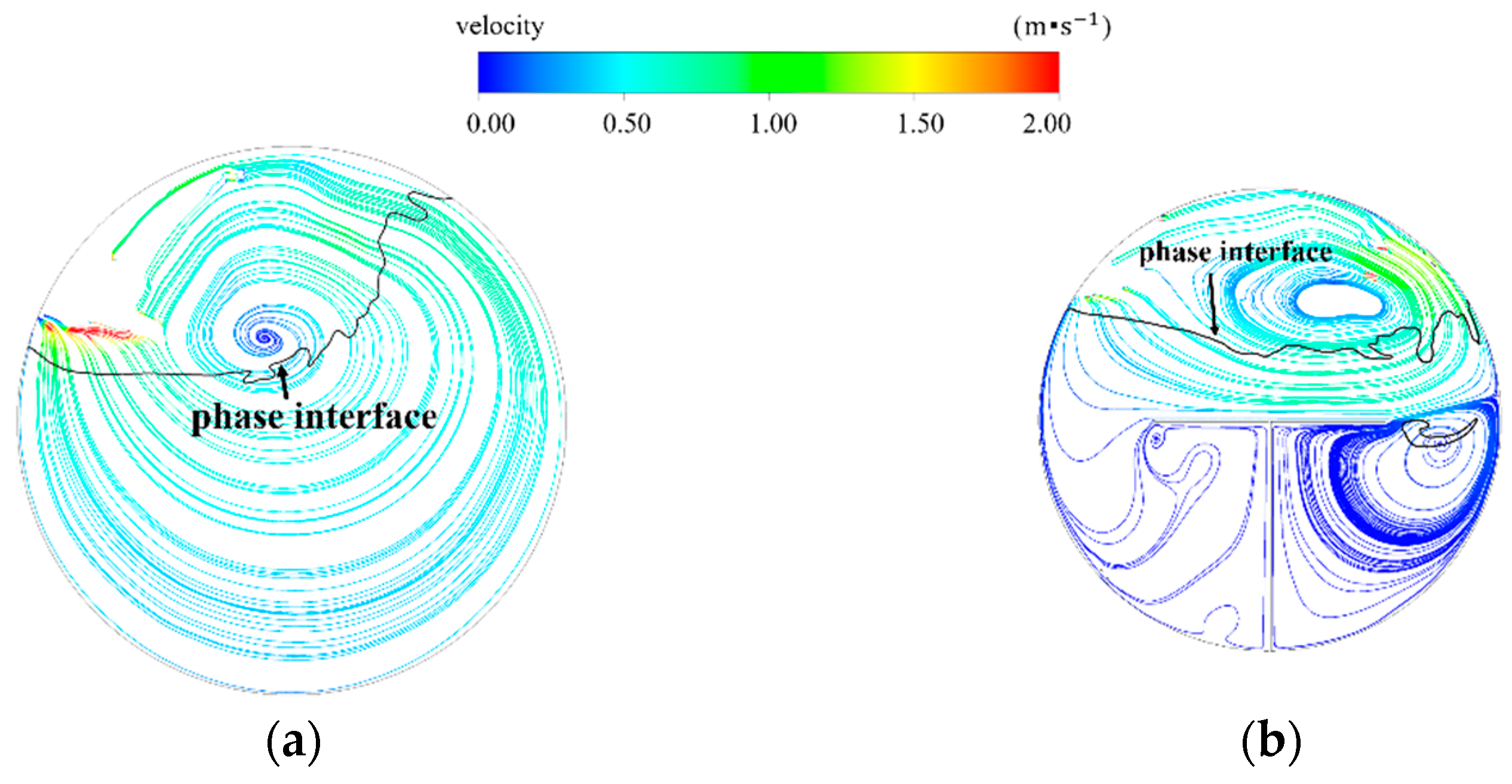
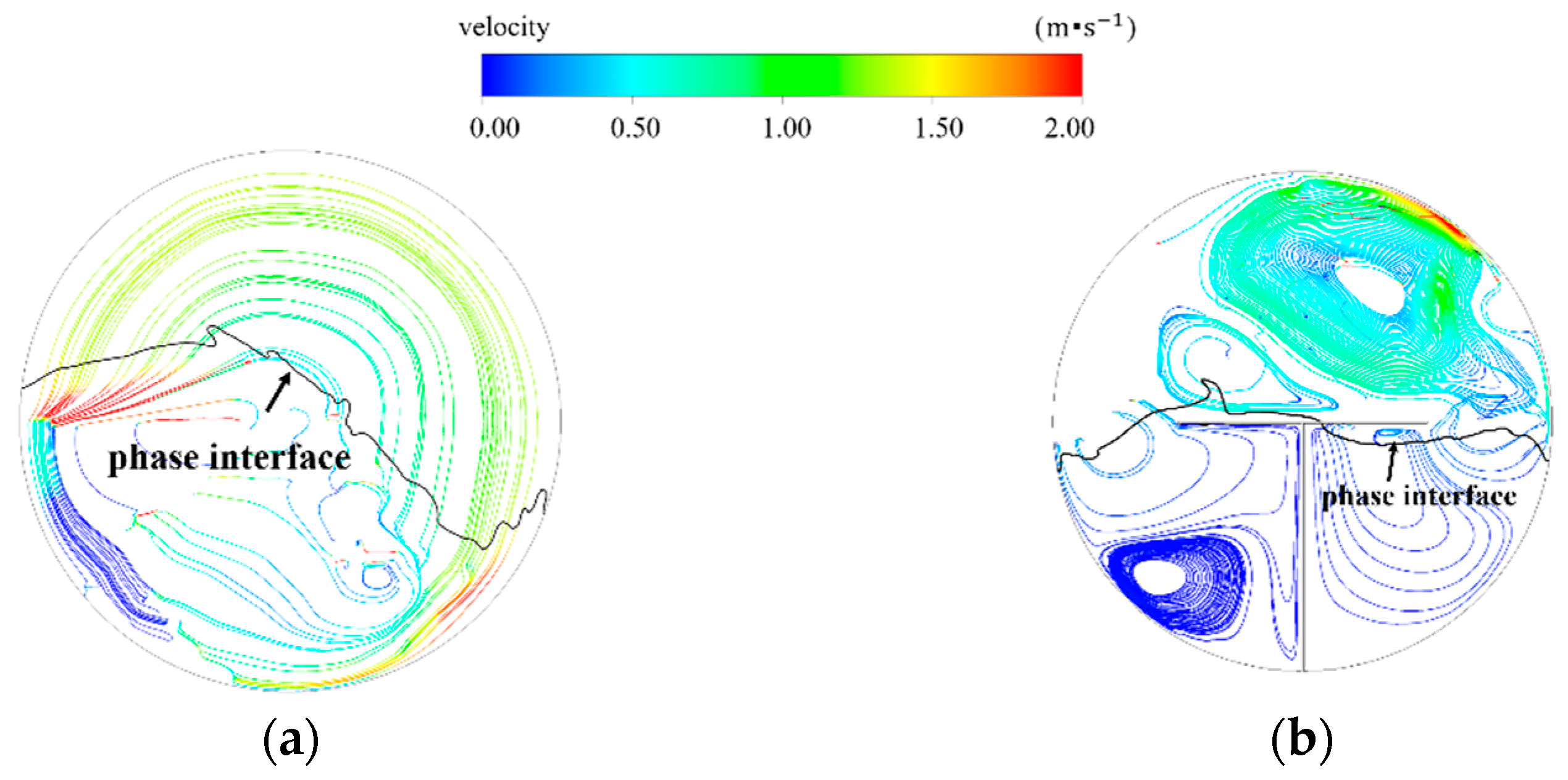
3.1. Interfacial Behaviors
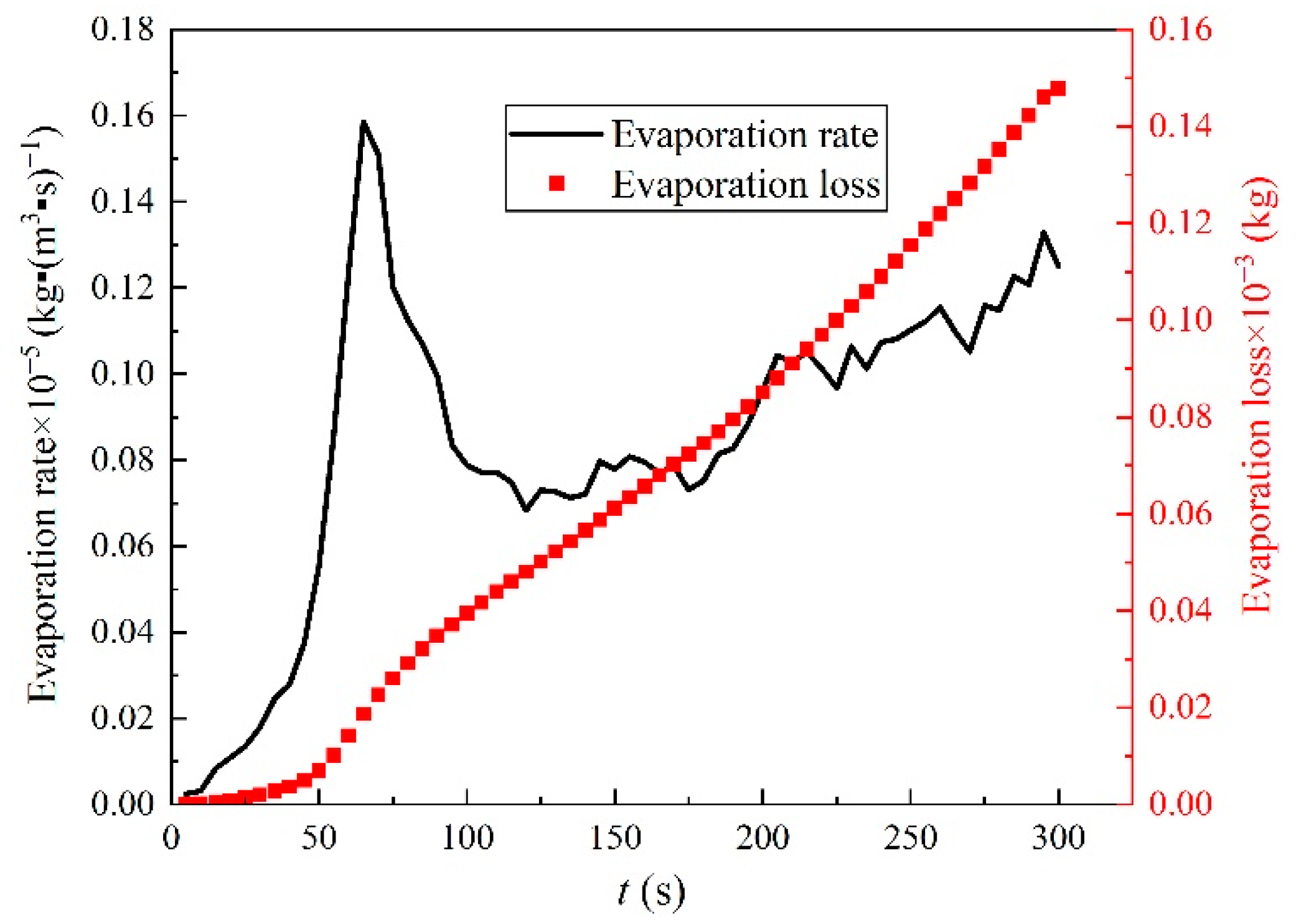
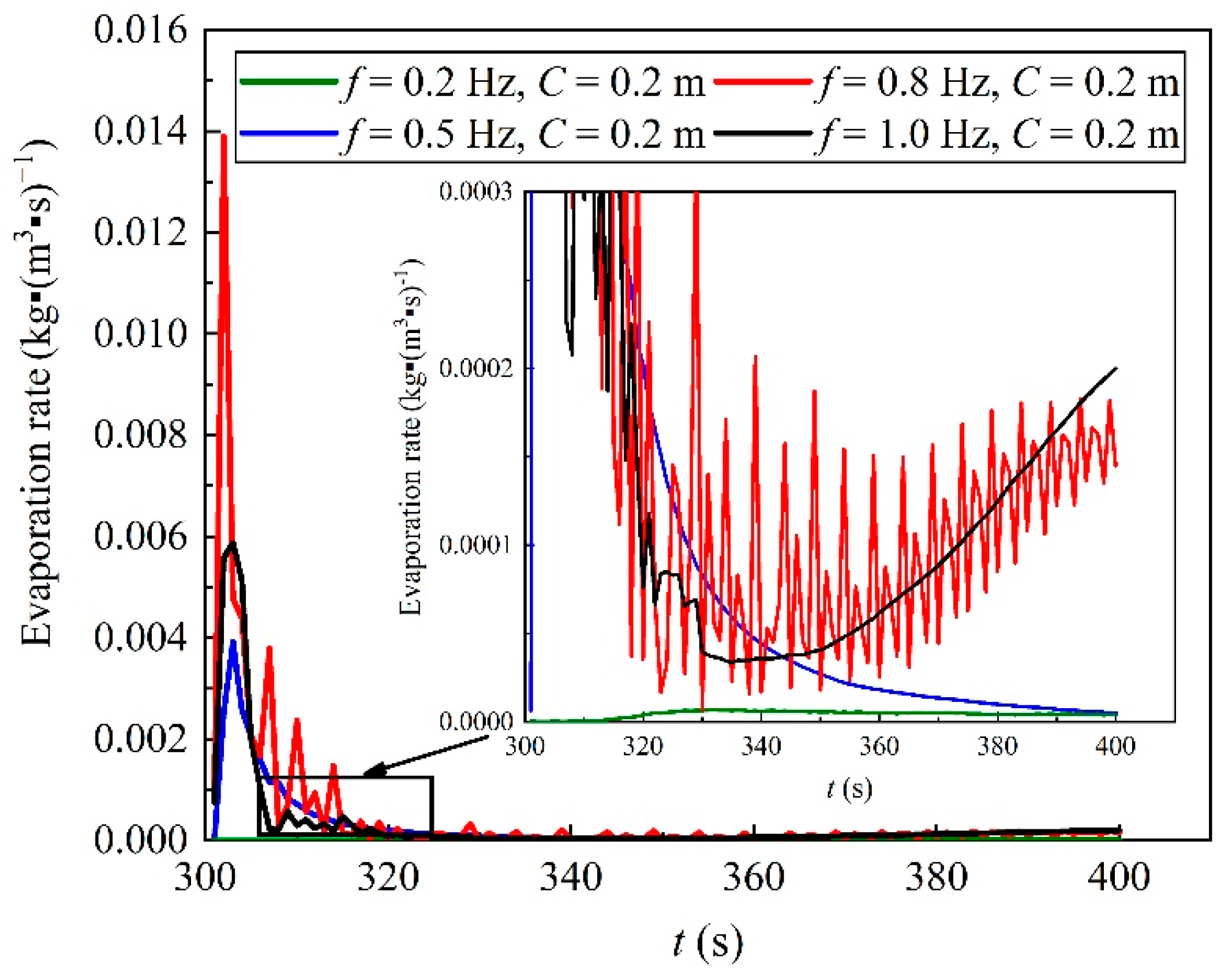
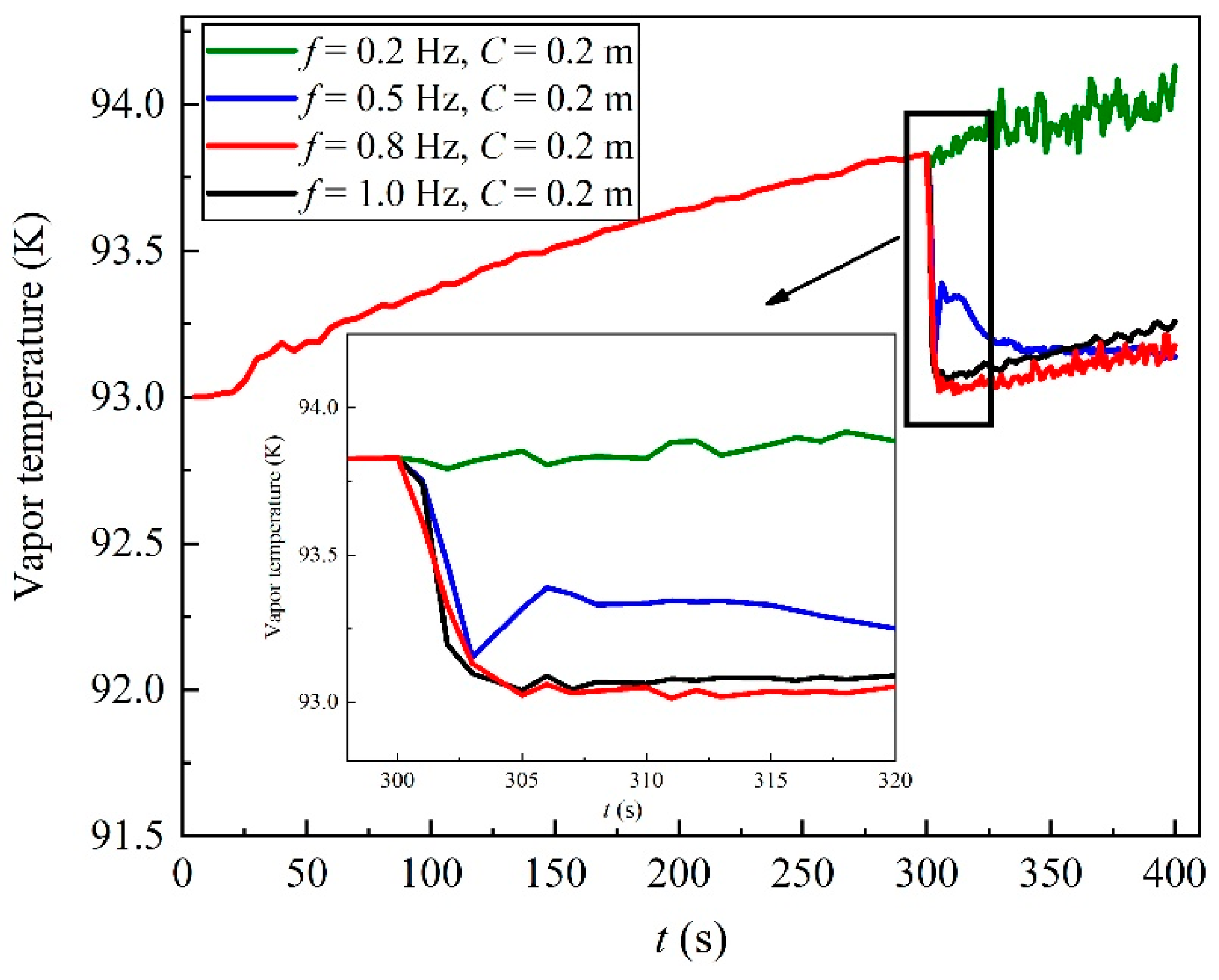
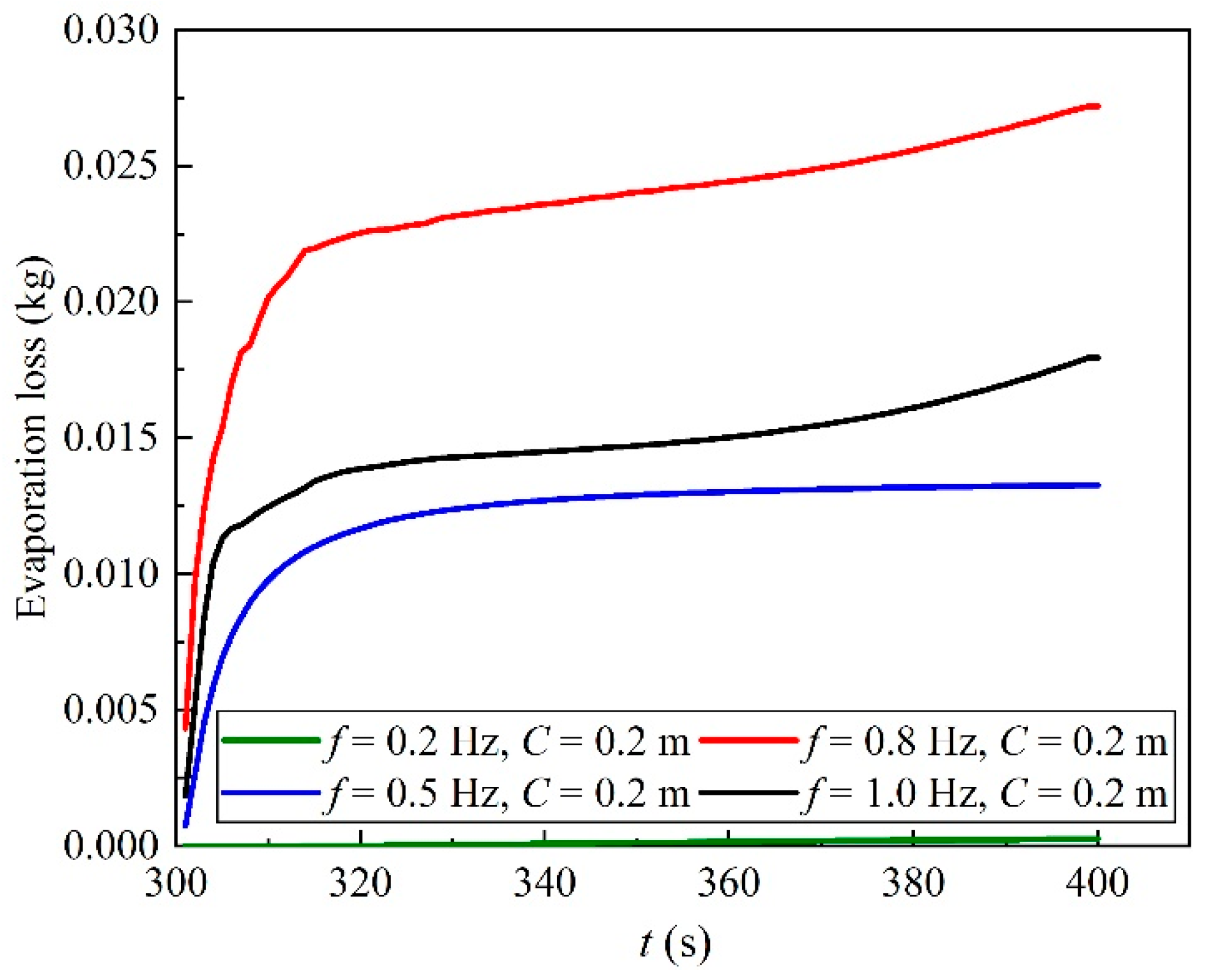
3.2. Evaporation Characteristics of Liquid Oxygen
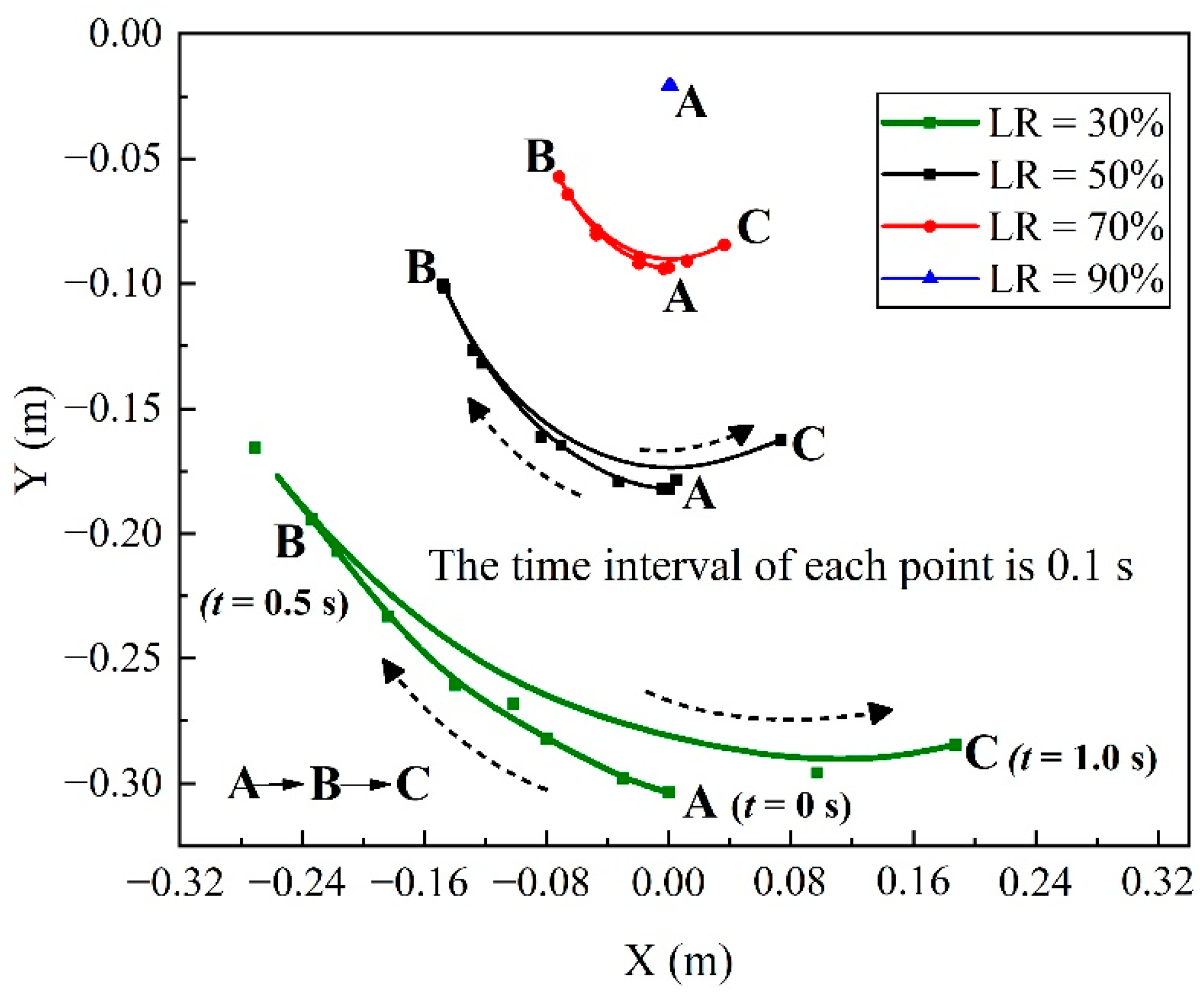
3.3. Anti-Sloshing Performance of T-Shaped Baffle
4. Conclusions
- (1)
- The evaporation rate is significantly promoted once the sloshing condition is imposed. It is attributed to the sharp pressure loss and the conversion of kinetic energy into friction heat.
- (2)
- Thermal destratification and vapor explosion stimulated by sloshing jointly promote evaporation. The evaporation loss under the vapor–liquid coupling excitation is approximately 120 times that of the evaporation loss under the low-frequency sloshing. This phenomenon may induce structural vibrations and pose a safety hazard.
- (3)
- The T-shaped baffle behaves with an ascendant anti-sloshing performance when the baffle height approaches the liquid level. The generation of tip vortices and the enhancement of the wall shearing effect contribute to the energy loss and act as the motion damping factors. However, the momentum increment is incurred by the acceleration of the liquid above the baffle. The anti-sloshing performance of the T-shaped baffle is determined by the optimal weight of the energy loss and increased momentum.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Duan, Z.; Sun, H.; Cheng, C.; Tang, W.; Xue, H. A moving-boundary based dynamic model for predicting the transient free convection and thermal stratification in liquefied gas storage tank. Int. J. Therm. Sci. 2021, 160, 106690. [Google Scholar] [CrossRef]
- Zheng, Y.; Chen, J.; Shang, Y.; Chang, H.; Chen, H.; Shu, S. Numerical analysis of the influence of wall vibration on heat transfer with liquid hydrogen boiling flow in a horizontal tube. Int. J. Hydrogen Energy 2017, 42, 30804–30812. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, Z. An overview of liquid–vapor phase change, flow and heat transfer in mini-and micro-channels. Int. J. Therm. Sci. 2014, 86, 227–245. [Google Scholar] [CrossRef]
- Davy, G.; Reyssat, E.; Vincent, S.; Mimouni, S. Euler–Euler simulations of condensing two-phase flows in mini-channel: Combination of a sub-grid approach and an interface capturing approach. Int. J. Multiph. Flow 2022, 149, 103964. [Google Scholar] [CrossRef]
- Zhang, W.; Ke, P.; Yang, C.; Zhou, C. Progress of computability of multi-scale interface problems in gas-liquid two-phase flow. CIESC J. 2014, 65, 4645–4654. [Google Scholar]
- Hoehne, T.; Lucas, D. Numerical simulations of counter-current two-phase flow experiments in a PWR hot leg model using an interfacial area density model. Int. J. Heat Fluid Flow 2011, 32, 1047–1056. [Google Scholar] [CrossRef]
- Höhne, T.; Vallée, C. Experiments and numerical simulations of horizontal two-phase flow regimes using an interfacial area density model. J. Comput. Multiph. Flows 2010, 2, 131–143. [Google Scholar] [CrossRef]
- Dalla Barba, F.; Scapin, N.; Demou, A.D.; Rosti, M.E.; Picano, F.; Brandt, L. An interface capturing method for liquid-gas flows at low-Mach number. Comput. Fluids 2021, 216, 104789. [Google Scholar] [CrossRef]
- Chen, Y.G.; Djidjeli, K.; Price, W.G. Numerical simulation of liquid sloshing phenomena in partially filled containers. Comput. Fluids 2009, 38, 830–842. [Google Scholar] [CrossRef]
- Liu, C.; Wang, J.; Wan, D. CFD Computation of Wave Forces and Motions of DTC Ship in Oblique Waves. Int. J. Offshore Polar Eng. 2018, 28, 154–163. [Google Scholar] [CrossRef]
- Sanapala, V.S.; Velusamy, K.; Patnaik, B.S.V. CFD simulations on the dynamics of liquid sloshing and its control in a storage tank for spent fuel applications. Ann. Nucl. Energy 2016, 94, 494–509. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, H. Numerical simulation of 3D sloshing flow in partially filled LNG tank using a coupled level-set and volume-of-fluid method. Ocean Eng. 2015, 104, 10–30. [Google Scholar] [CrossRef]
- Boniou, V.; Schmitt, T.; Vié, A. Comparison of interface capturing methods for the simulation of two-phase flow in a unified low-Mach framework. Int. J. Multiphase Flow 2022, 149, 103957. [Google Scholar] [CrossRef]
- Liu, Z.; Feng, Y.; Lei, G.; Li, Y. Hydrodynamic performance on sloshing process in a liquid oxygen tank under intermittent excitation. Cryogenics 2019, 98, 92–101. [Google Scholar] [CrossRef]
- Liu, Z.; Li, C. Influence of slosh baffles on thermodynamic performance in liquid hydrogen tank. J. Hazard. Mater. 2018, 346, 253–262. [Google Scholar] [CrossRef] [PubMed]
- Liu, Z.; Li, Y. Thermal physical performance in liquid hydrogen tank under constant wall temperature. Renew. Energy 2019, 130, 601–612. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Y.; Zhou, G. Study on thermal stratification in liquid hydrogen tank under different gravity levels. Int. J. Hydrogen Energy 2018, 43, 9369–9378. [Google Scholar] [CrossRef]
- Kumar, S.P.; Prasad, B.; Venkatarathnam, G.; Ramamurthi, K.; Murthy, S.S. Influence of surface evaporation on stratification in liquid hydrogen tanks of different aspect ratios. Int. J. Hydrogen Energy 2007, 32, 1954–1960. [Google Scholar] [CrossRef]
- Roh, S.; Son, G.; Song, G.; Bae, J. Numerical study of transient natural convection in a pressurized LNG storage tank. Appl. Therm. Eng. 2013, 52, 209–220. [Google Scholar] [CrossRef]
- Wu, S.; Ju, Y. Numerical study of the boil-off gas (BOG) generation characteristics in a type C independent liquefied natural gas (LNG) tank under sloshing excitation. Energy 2021, 223, 120001. [Google Scholar] [CrossRef]
- Grotle, E.L.; Aesoy, V. Dynamic modelling of the thermal response enhanced by sloshing in marine LNG fuel tanks. Appl. Therm. Eng. 2018, 135, 512–520. [Google Scholar] [CrossRef]
- Zuo, Z.; Jiang, W.; Pan, P.; Qin, X.; Huang, Y. Quasi-equilibrium evaporation characteristics of oxygen in the liquid–vapor interfacial region. Int. Commun. Heat Mass Transf. 2021, 129, 105697. [Google Scholar] [CrossRef]
- Xue, M.; Lin, P.; Zheng, J.; Ma, Y.; Yuan, X.; Nguyen, V. Effects of perforated baffle on reducing sloshing in rectangular tank: Experimental and numerical study. China Ocean Eng. 2013, 27, 615–628. [Google Scholar] [CrossRef]
- Brar, G.S.; Singh, S. An experimental and CFD analysis of sloshing in a tanker. Procedia Technol. 2014, 14, 490–496. [Google Scholar] [CrossRef]
- Nayak, S.K.; Biswal, K.C. Fluid damping in rectangular tank fitted with various internal objects—An experimental investigation. Ocean Eng. 2015, 108, 552–562. [Google Scholar] [CrossRef]
- Panigrahy, P.K.; Maity, S.U.K. Experimental studies on sloshing behavior due to horizontal movement of liquids in baffled tanks. Ocean Eng. 2009, 36, 213–222. [Google Scholar] [CrossRef]
- Akyildiz, H.; Uenal, N.E.; Aksoy, H. An experimental investigation of the effects of the ring baffles on liquid sloshing in a rigid cylindrical tank. Ocean Eng. 2013, 59, 190–197. [Google Scholar] [CrossRef]
- Unal, U.O.; Bilici, G.; Akyildiz, H. Liquid sloshing in a two-dimensional rectangular tank: A numerical investigation with a T-shaped baffle. Ocean Eng. 2019, 187, 106181–106183. [Google Scholar] [CrossRef]
- Brackbill, J.U.; Kothe, D.B.; Zemach, C. A continuum method for modeling surface tension. J. Comput. Phys. 1992, 100, 335–354. [Google Scholar] [CrossRef]
- Marshall, W.R.; Ranz, W.E. Evaporation from Drops—Part I. Chem. Eng. Prog. 1952, 48, 141–146. [Google Scholar]
- Ranz, W.R. Evaporation from drops Part II. Chem. Eng. Prog. 1952, 48, 173–180. [Google Scholar]
- Lee, W.H. Pressure iteration scheme for two-phase flow modeling. In Mutiphase Transport: Fundamentals, Reactor Safety, Applications, Proceedings of the Multi-Phase Flow and Heat Transfer Symposium-Workshop, Miami Beach, FL, USA 16–18 April 1979; Hemisphere Publishing Corp.: Washington, DC, USA, 1980; pp. 407–432. [Google Scholar]
- Grotle, E.L.; Æsøy, V. Numerical simulations of sloshing and the thermodynamic response due to mixing. Energies 2017, 10, 1338. [Google Scholar] [CrossRef] [Green Version]
- Scurlock, R.G. Surface Evaporation of Cryogenic Liquids, Including LNG and LPG. In Stratification, Rollover and Handling of LNG, LPG and Other Cryogenic Liquid Mixtures; Springer: Cham, Switzerland, 2016; pp. 41–62. [Google Scholar]
- Ma, X.; Tian, M.; Zhang, G.; Leng, X. Numerical investigation on gas-liquid two-phase flow-induced vibration in a horizontal tube. J. Vib. Shock 2016, 35, 204–210. [Google Scholar]




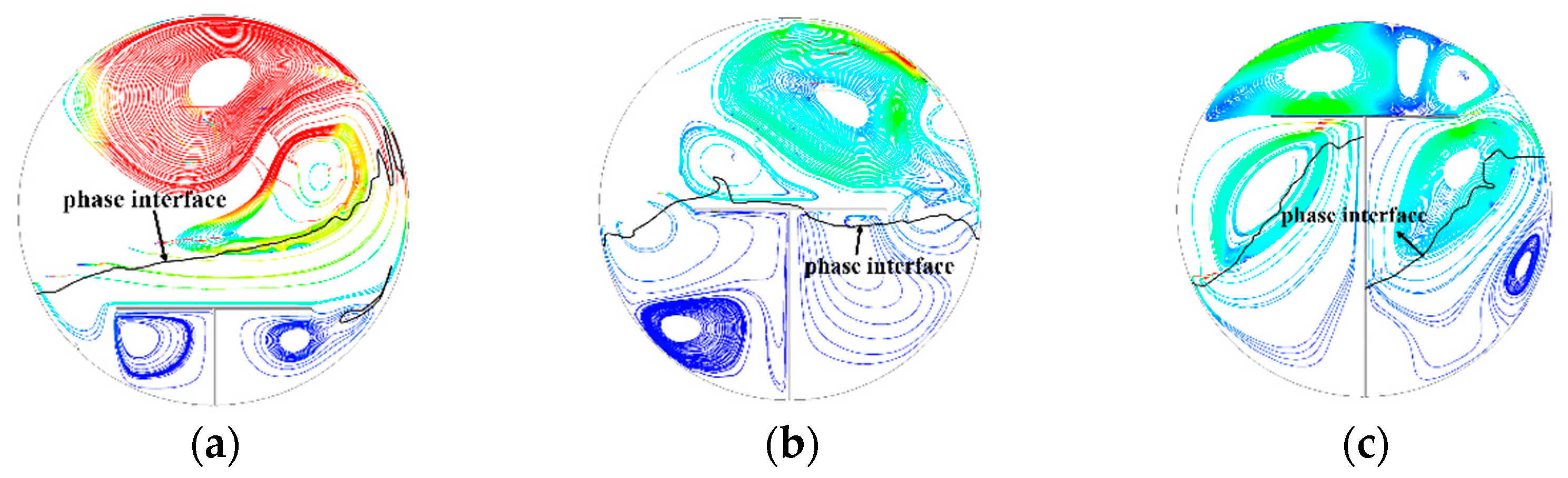
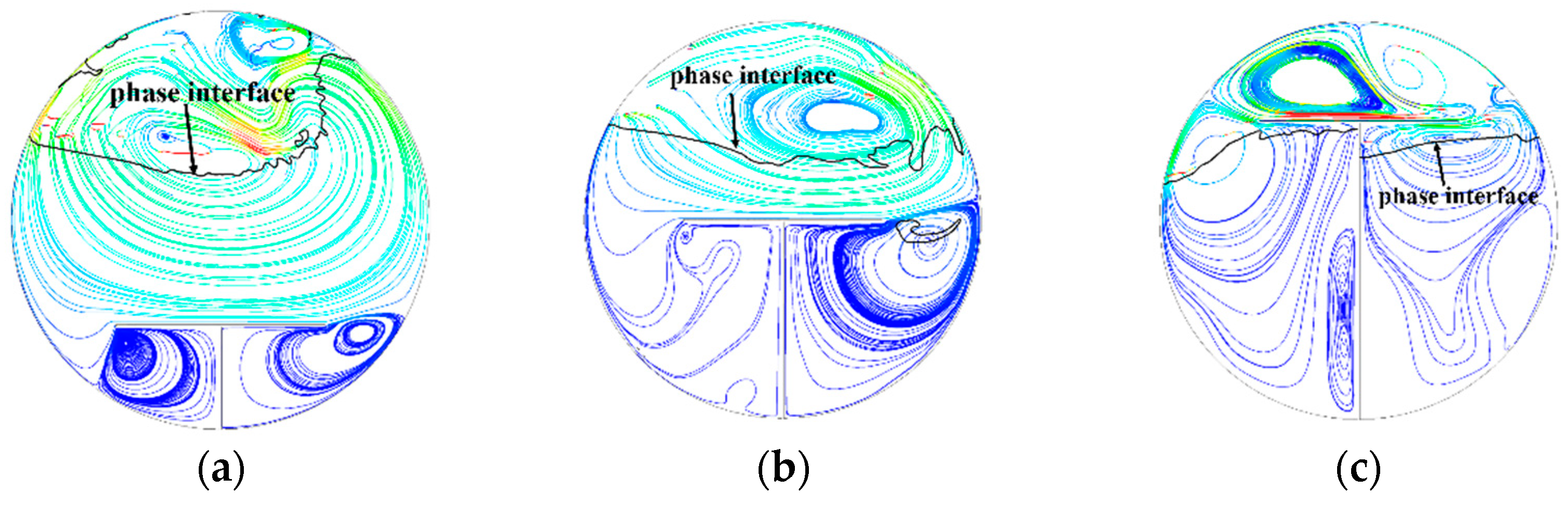
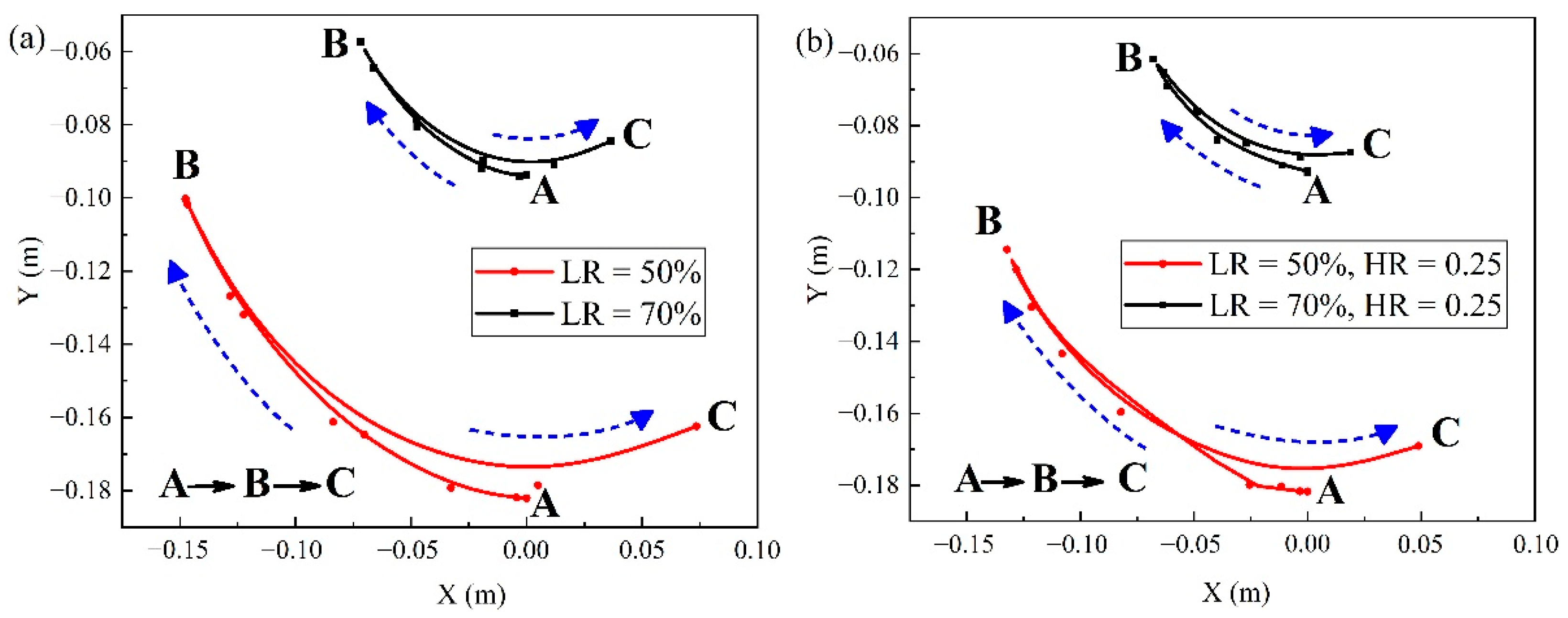

| No. | Case | LR | Type of Baffle | HR | No. | Case | LR | Type of Baffle | HR |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0.5LR | 50% | none | - | 6 | 0.7LR | 70% | none | - |
| 2 | 0.5LR0.25HR | 50% | T-shaped | 0.25 | 7 | 0.7LR0.25HR | 70% | T-shaped | 0.25 |
| 3 | 0.5LR0.5HR | 50% | T-shaped | 0.50 | 8 | 0.7LR0.5HR | 70% | T-shaped | 0.50 |
| 4 | 0.5LR0.75HR | 50% | T-shaped | 0.75 | 9 | 0.7LR0.75HR | 70% | T-shaped | 0.75 |
| 5 | 0.9LR | 90% | none | - | 10 | 0.3LR | 30% | none | - |
| Materials | |||||
|---|---|---|---|---|---|
| Oxygen-liquid | 1127.1 | 1707.9 | 0.14677 | 1.8 × 10−4 | 0.0045085 |
| Oxygen-vapor | 5.802 | 975.9 | 0.00847 | 7.2 × 10−6 | 0.0121 |
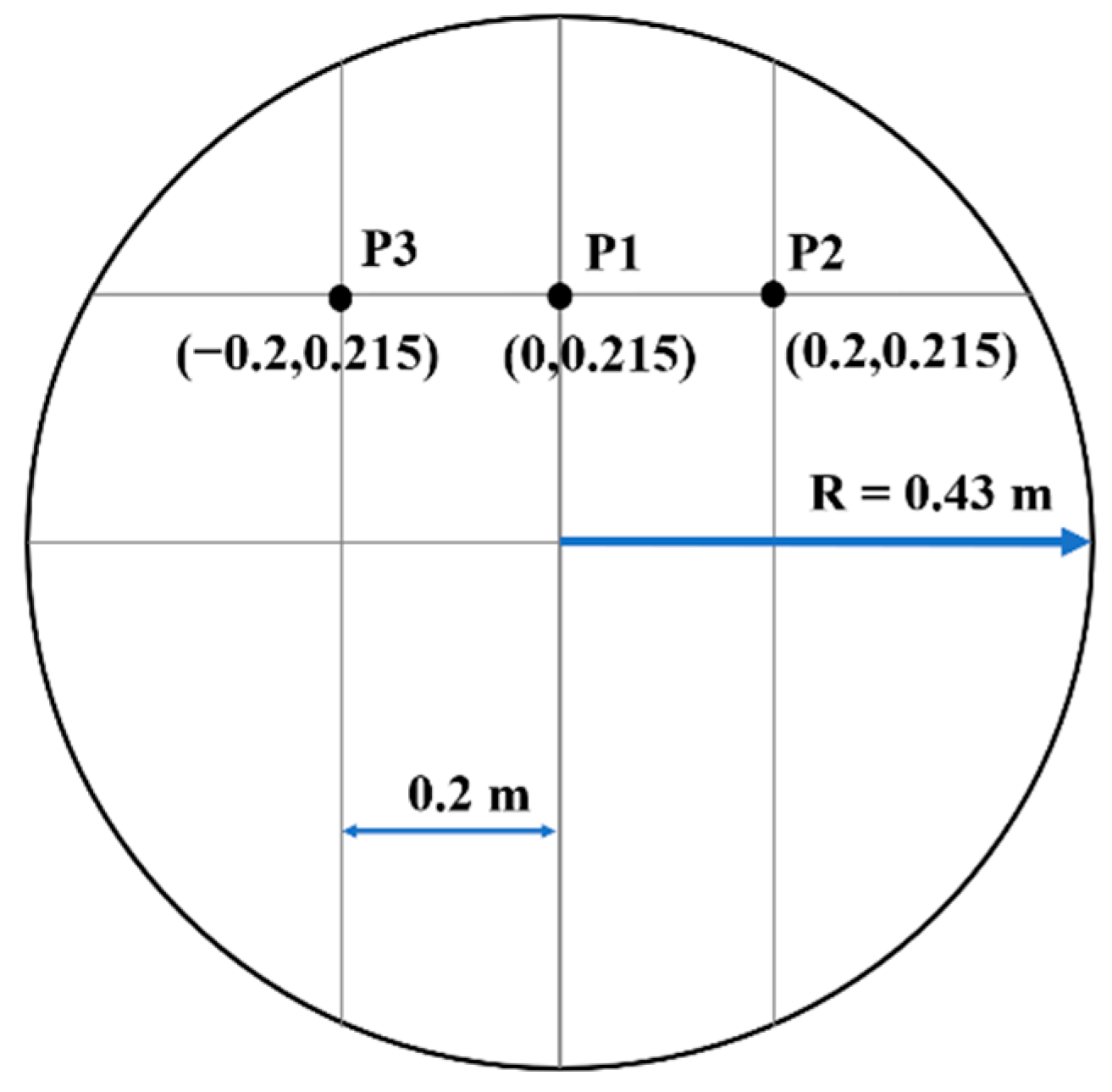
| Monitor | Coordinates | Monitor | Coordinates | Monitor | Coordinates |
|---|---|---|---|---|---|
| P1 | (0, 0.215) | P2 | (0.2, 0.215) | P3 | (−0.2, 0.215) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Chen, H.; Gao, X.; Pan, X.; Huang, Q.; Xie, J.; Chen, J. Numerical Study on Behaviors of the Sloshing Liquid Oxygen Tanks. Energies 2022, 15, 6457. https://doi.org/10.3390/en15176457
Zhang H, Chen H, Gao X, Pan X, Huang Q, Xie J, Chen J. Numerical Study on Behaviors of the Sloshing Liquid Oxygen Tanks. Energies. 2022; 15(17):6457. https://doi.org/10.3390/en15176457
Chicago/Turabian StyleZhang, Hanyue, Hong Chen, Xu Gao, Xi Pan, Qingmiao Huang, Junlong Xie, and Jianye Chen. 2022. "Numerical Study on Behaviors of the Sloshing Liquid Oxygen Tanks" Energies 15, no. 17: 6457. https://doi.org/10.3390/en15176457
APA StyleZhang, H., Chen, H., Gao, X., Pan, X., Huang, Q., Xie, J., & Chen, J. (2022). Numerical Study on Behaviors of the Sloshing Liquid Oxygen Tanks. Energies, 15(17), 6457. https://doi.org/10.3390/en15176457





