Development of a Control-Oriented Ignition Delay Model for GCI Combustion
Abstract
:1. Introduction
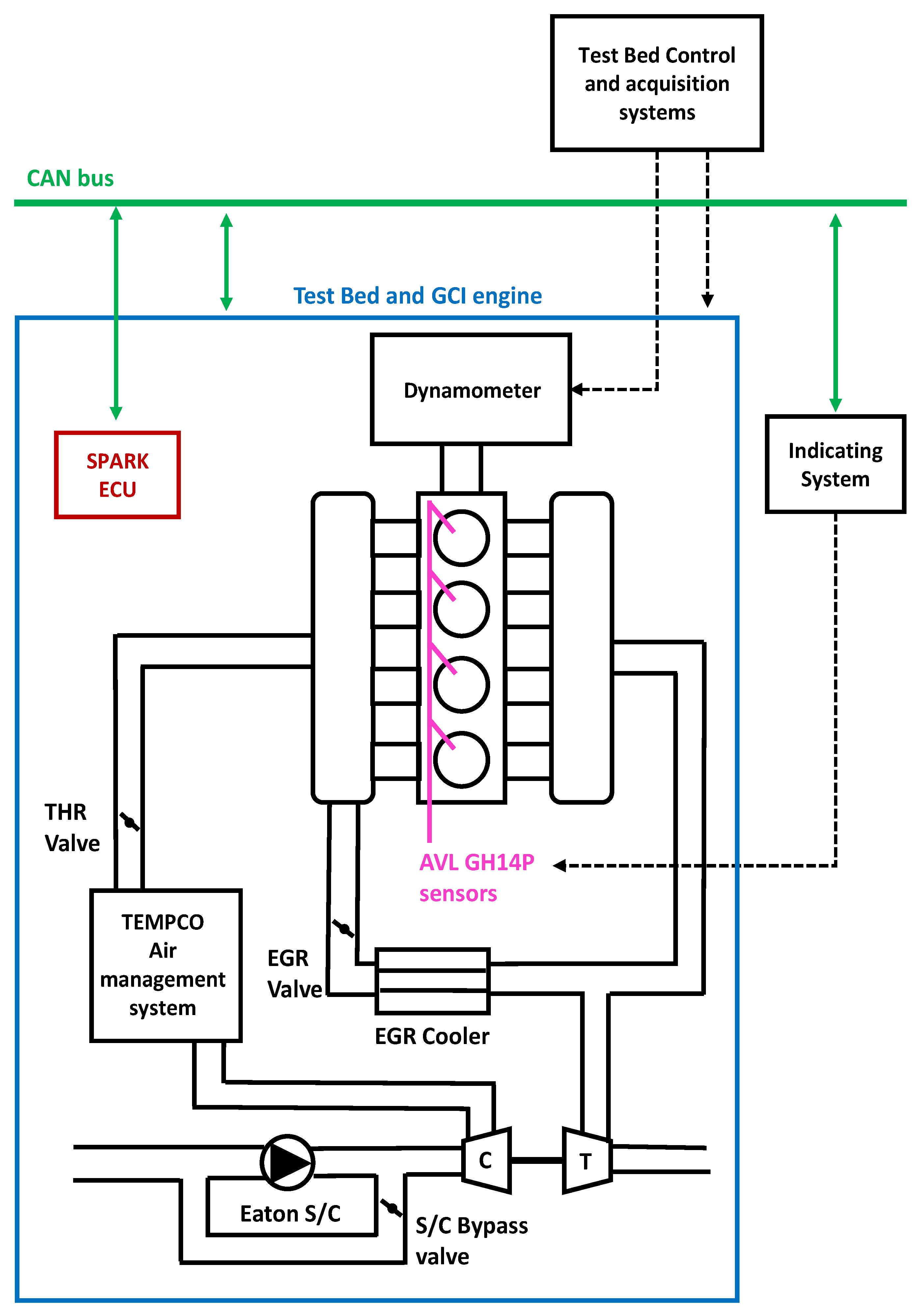
2. Experimental Layout
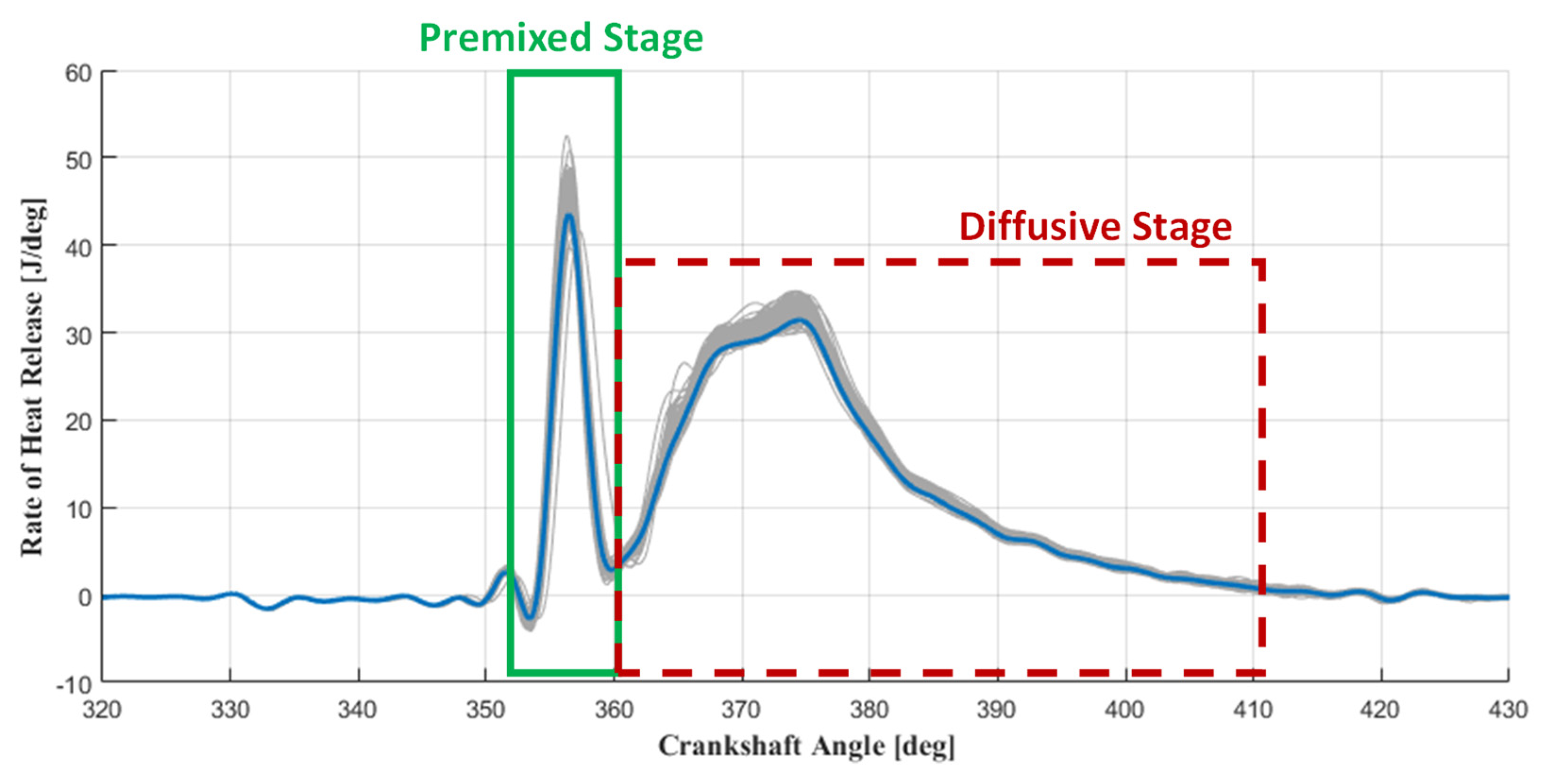
3. Ignition Delay Analysis for GCI Combustion
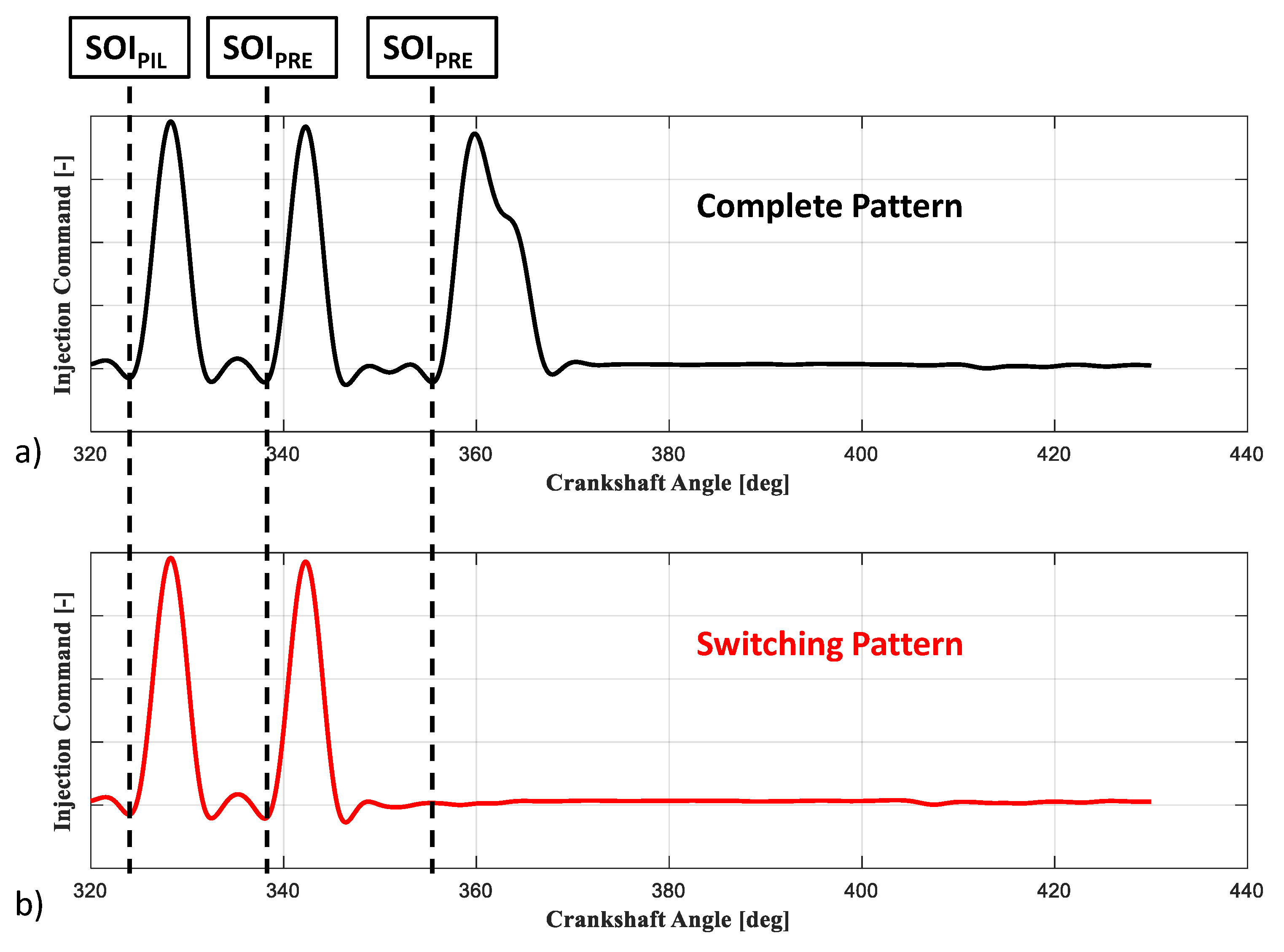
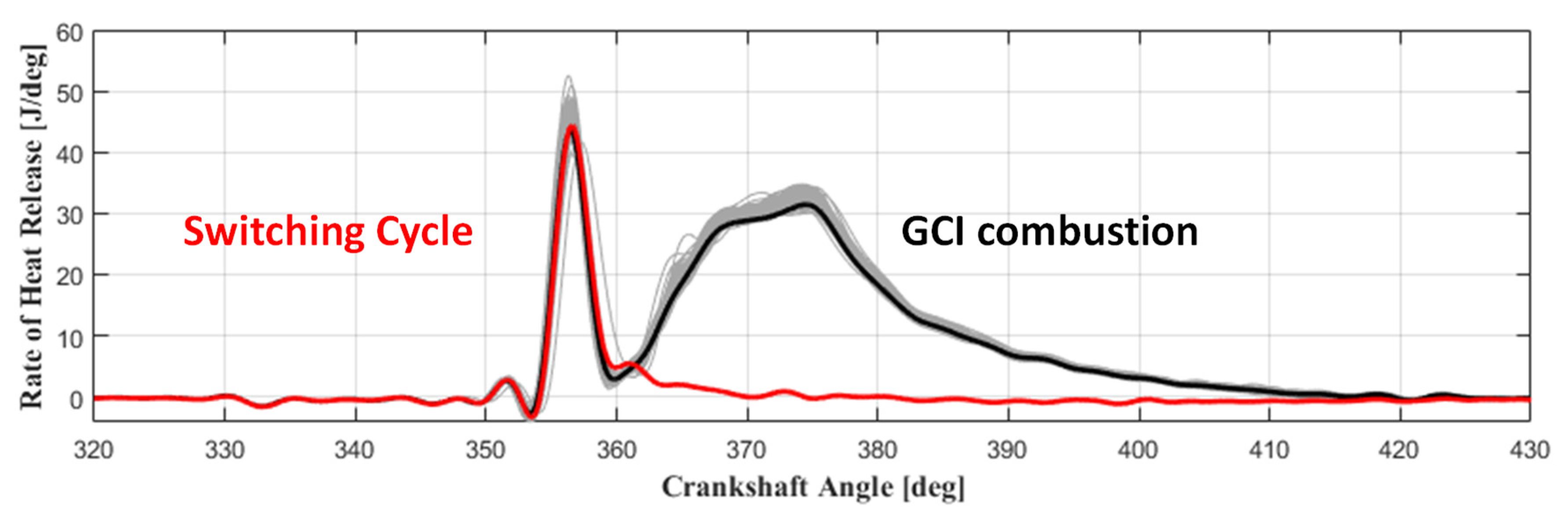
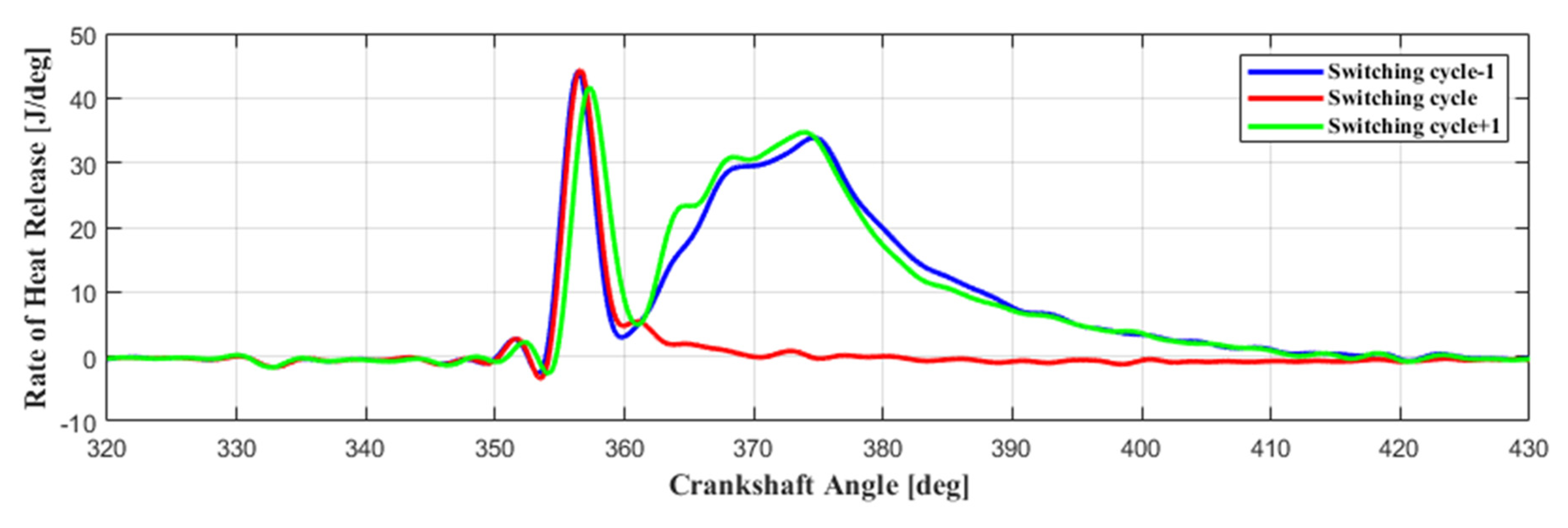
3.1. Switching Pattern Methodology
3.2. Ignition Delay Sensitivity Analysis
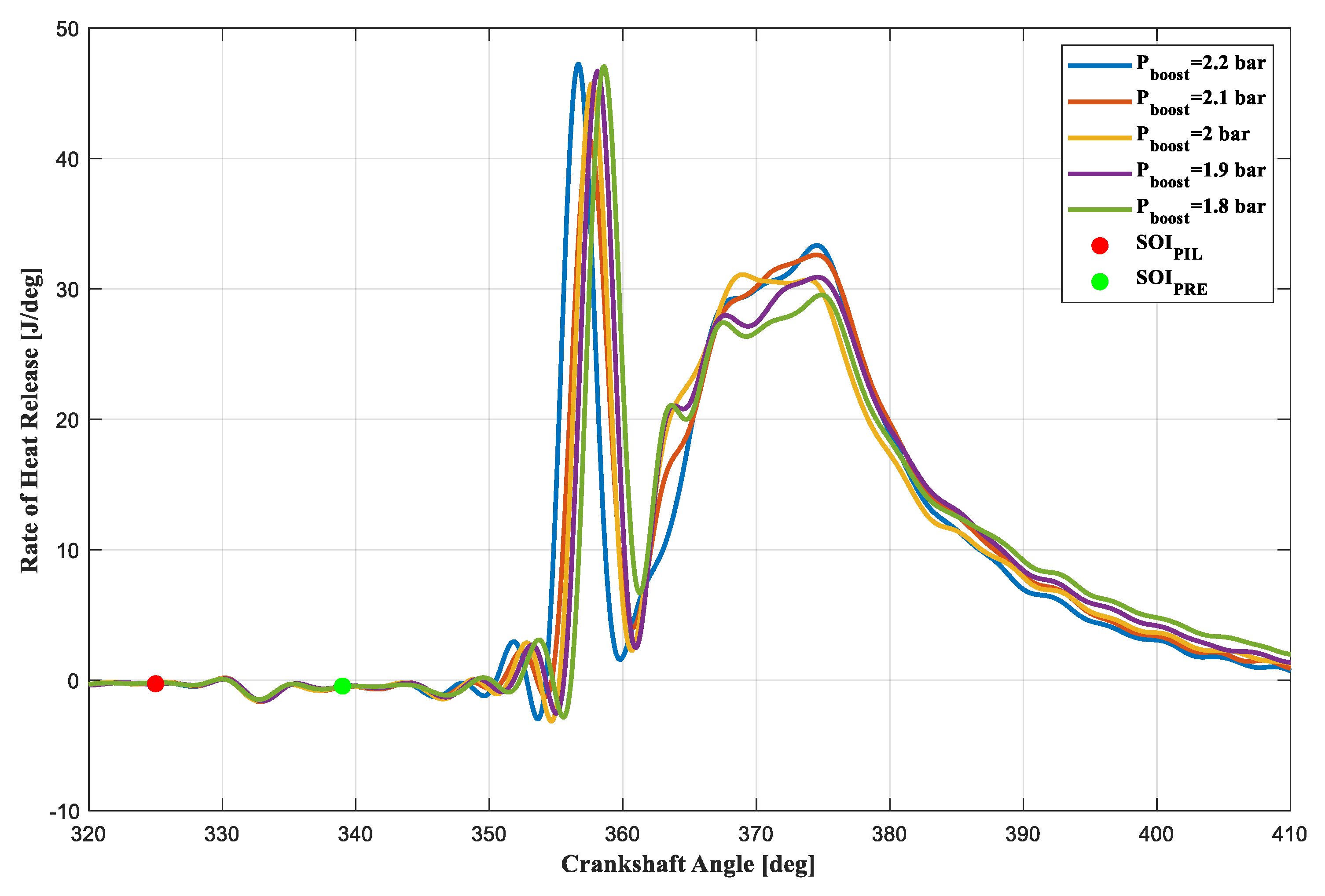
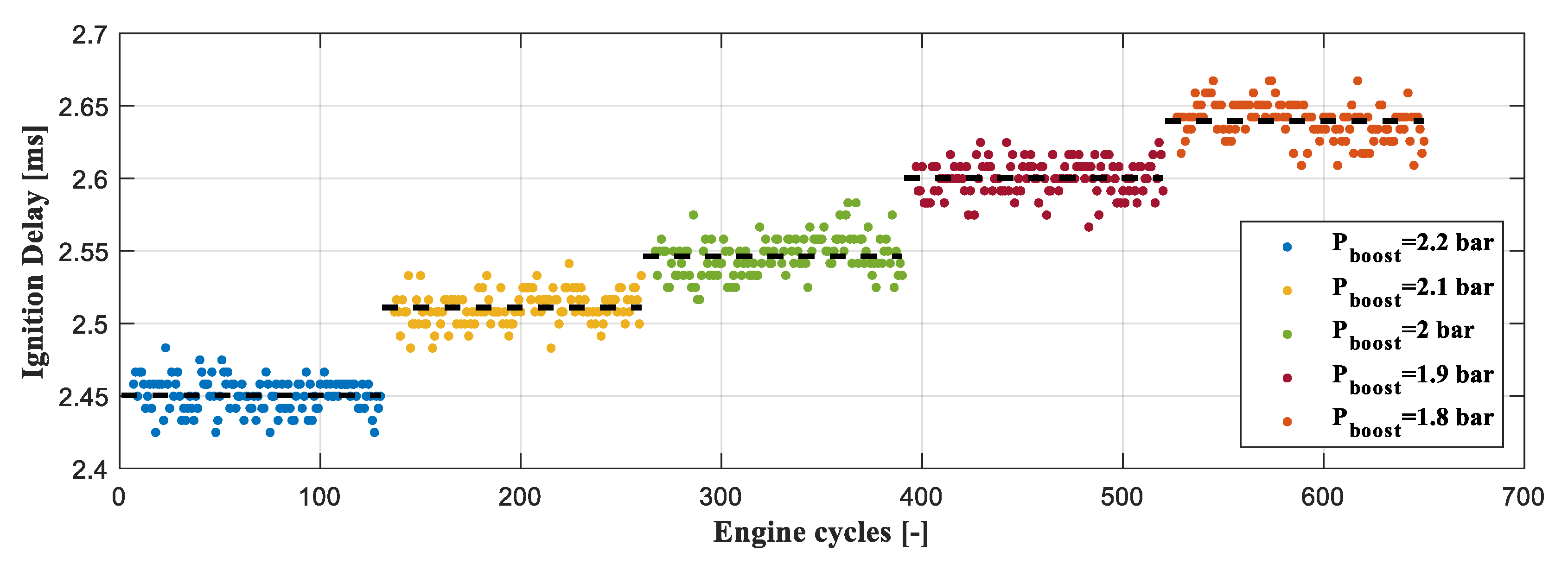
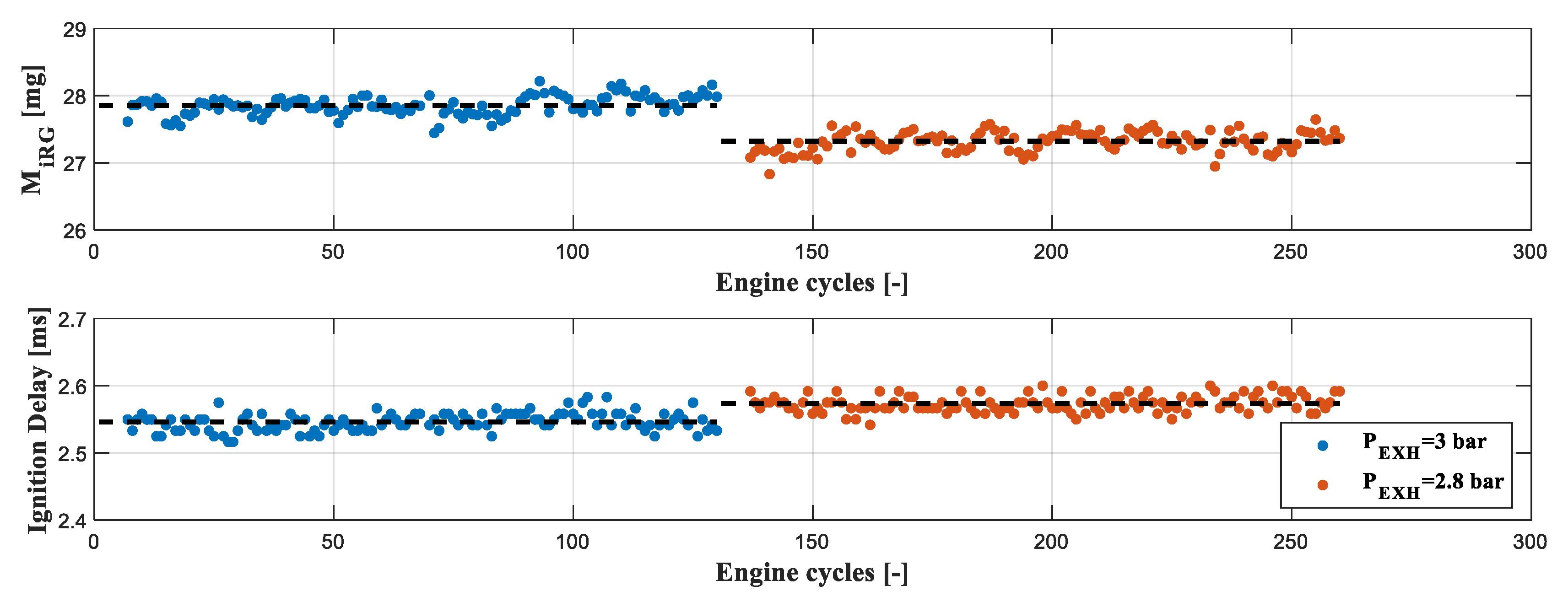
3.2.1. Gasoline Pressure
3.2.2. Injection Phasing
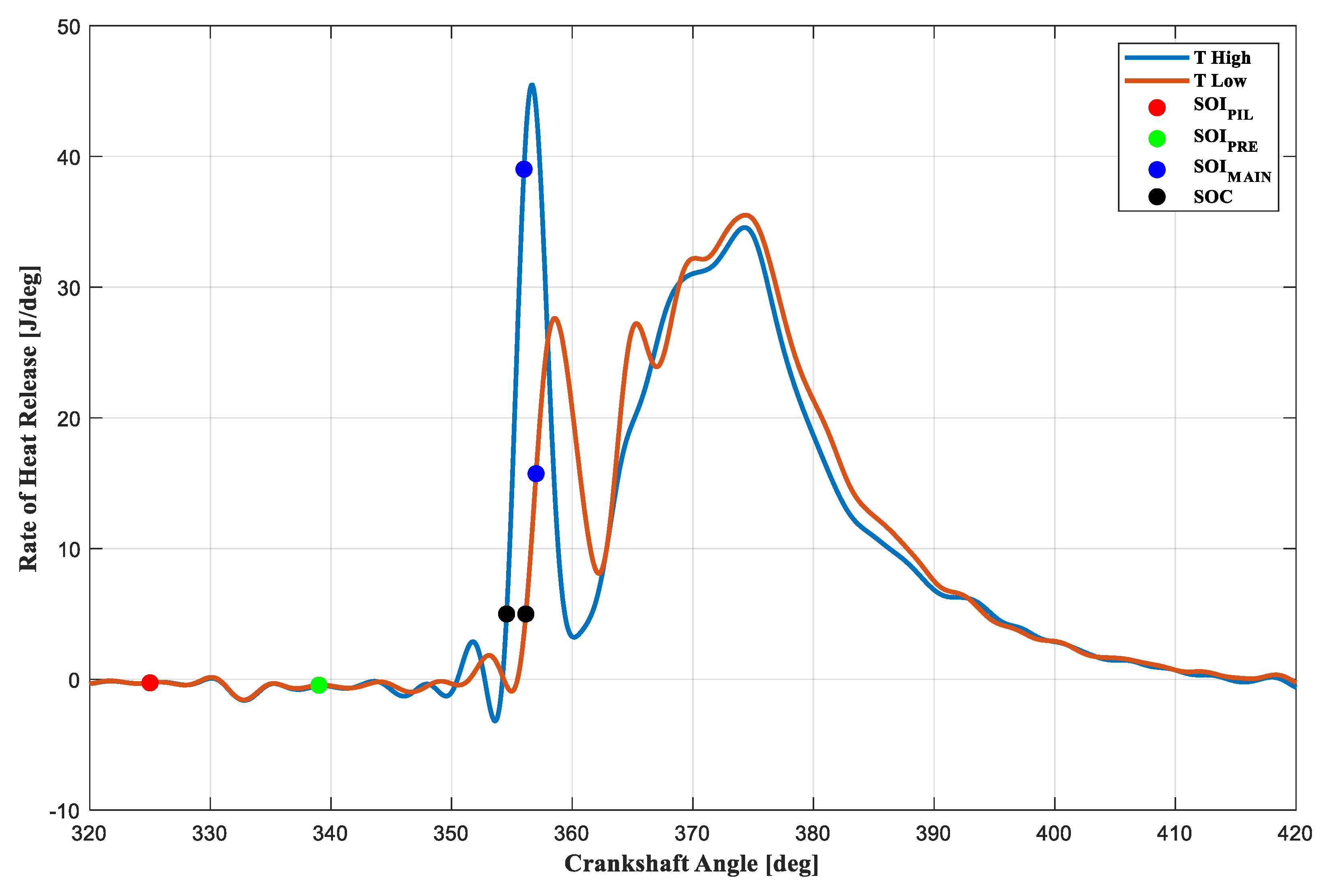
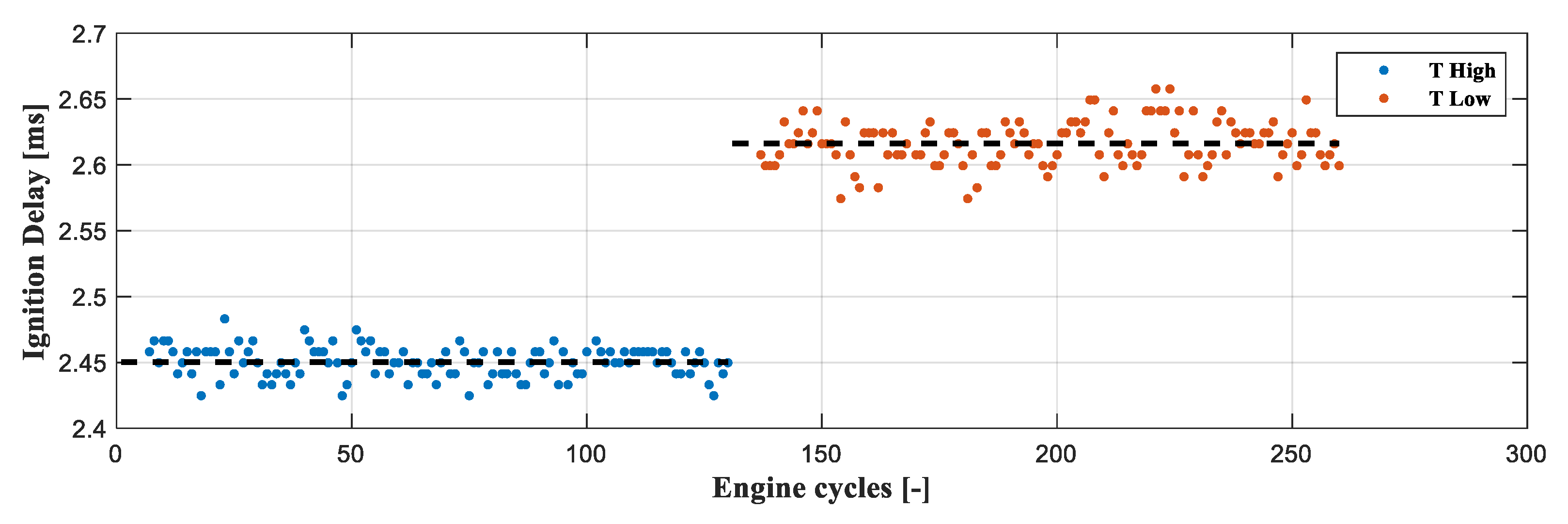
3.2.3. Intake Temperature
3.2.4. Intake Pressure
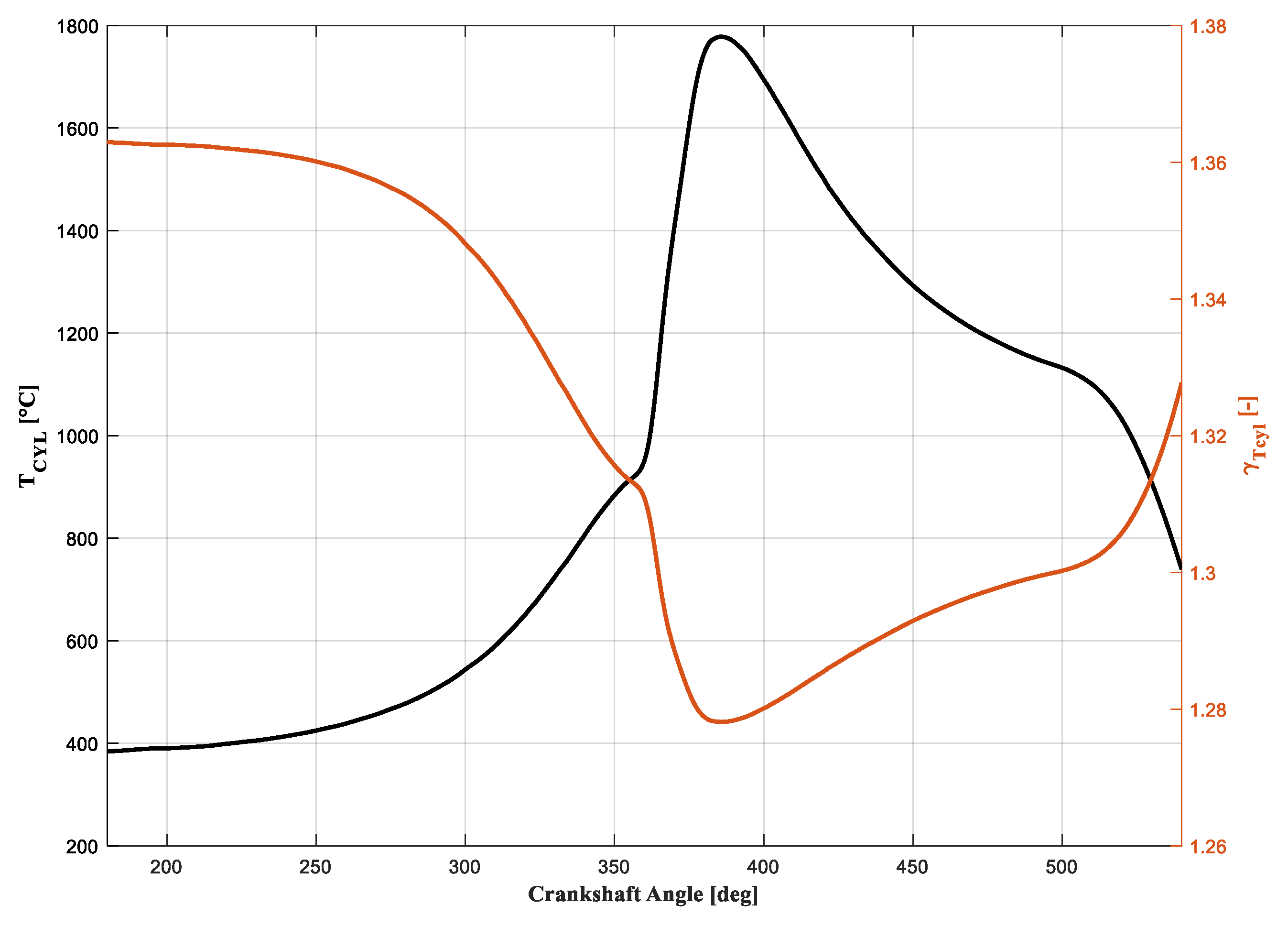
3.2.5. Mass and Temperature of Residual Gases Trapped in the Combustion Chamber
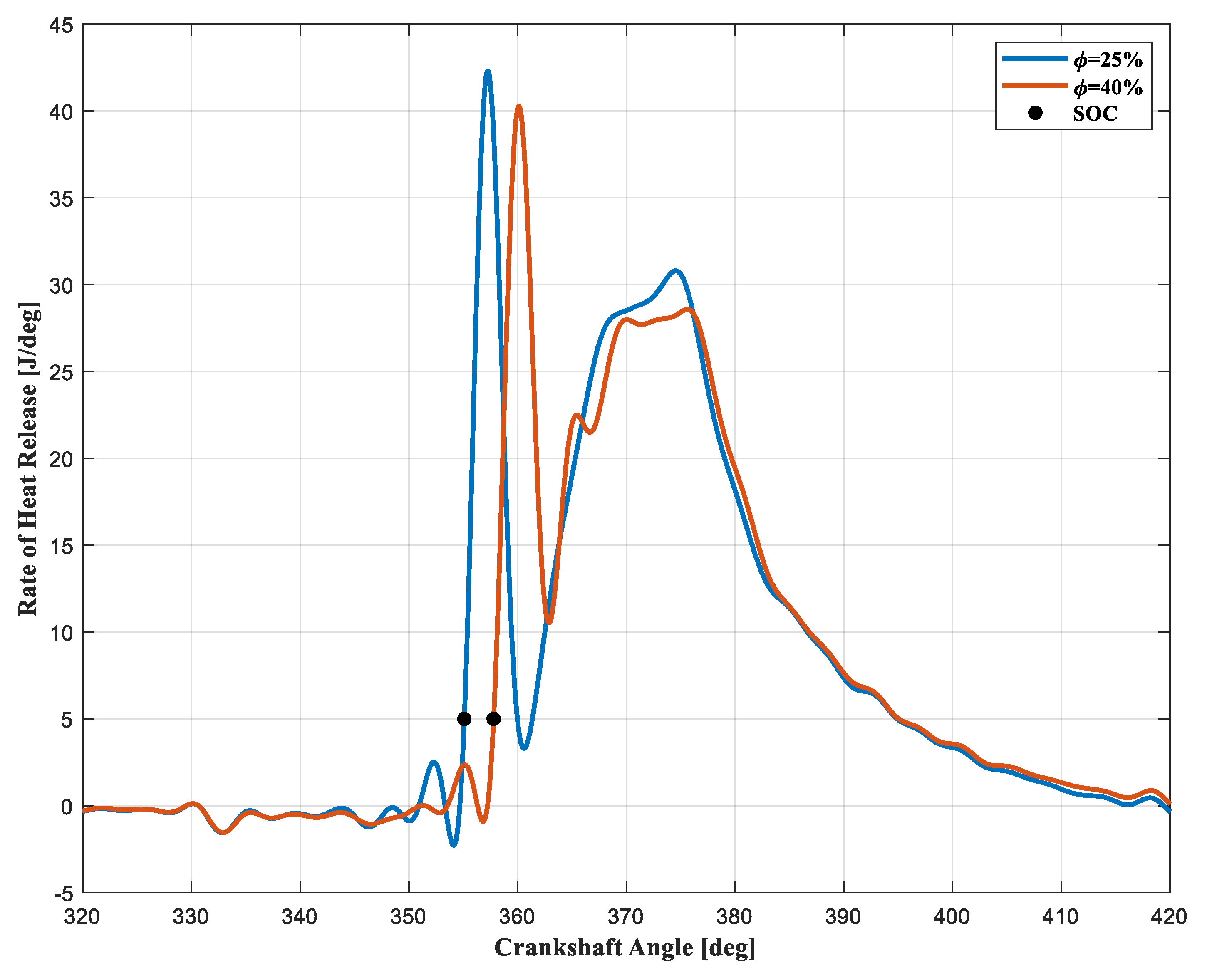
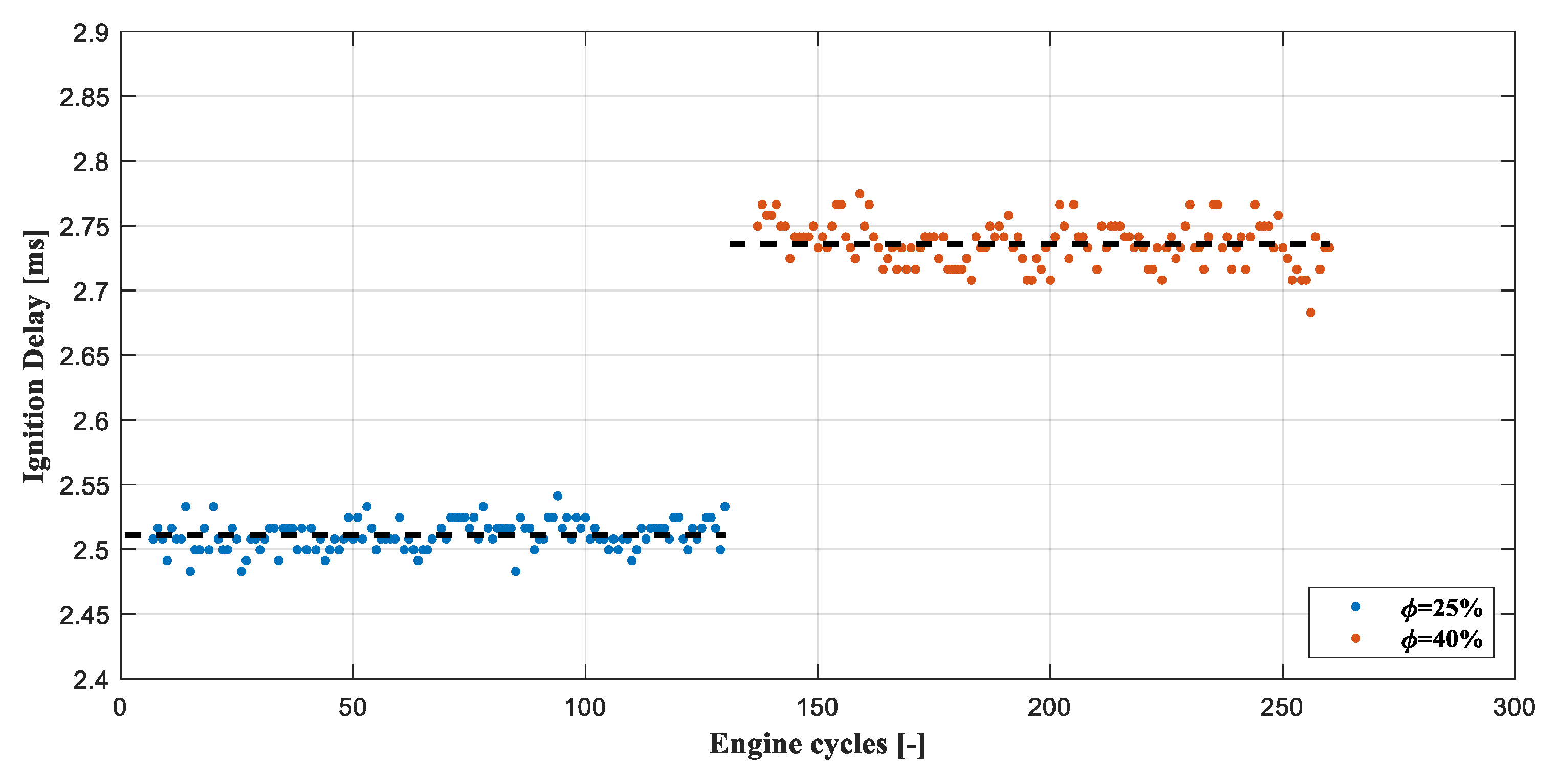
3.2.6. Air Humidity
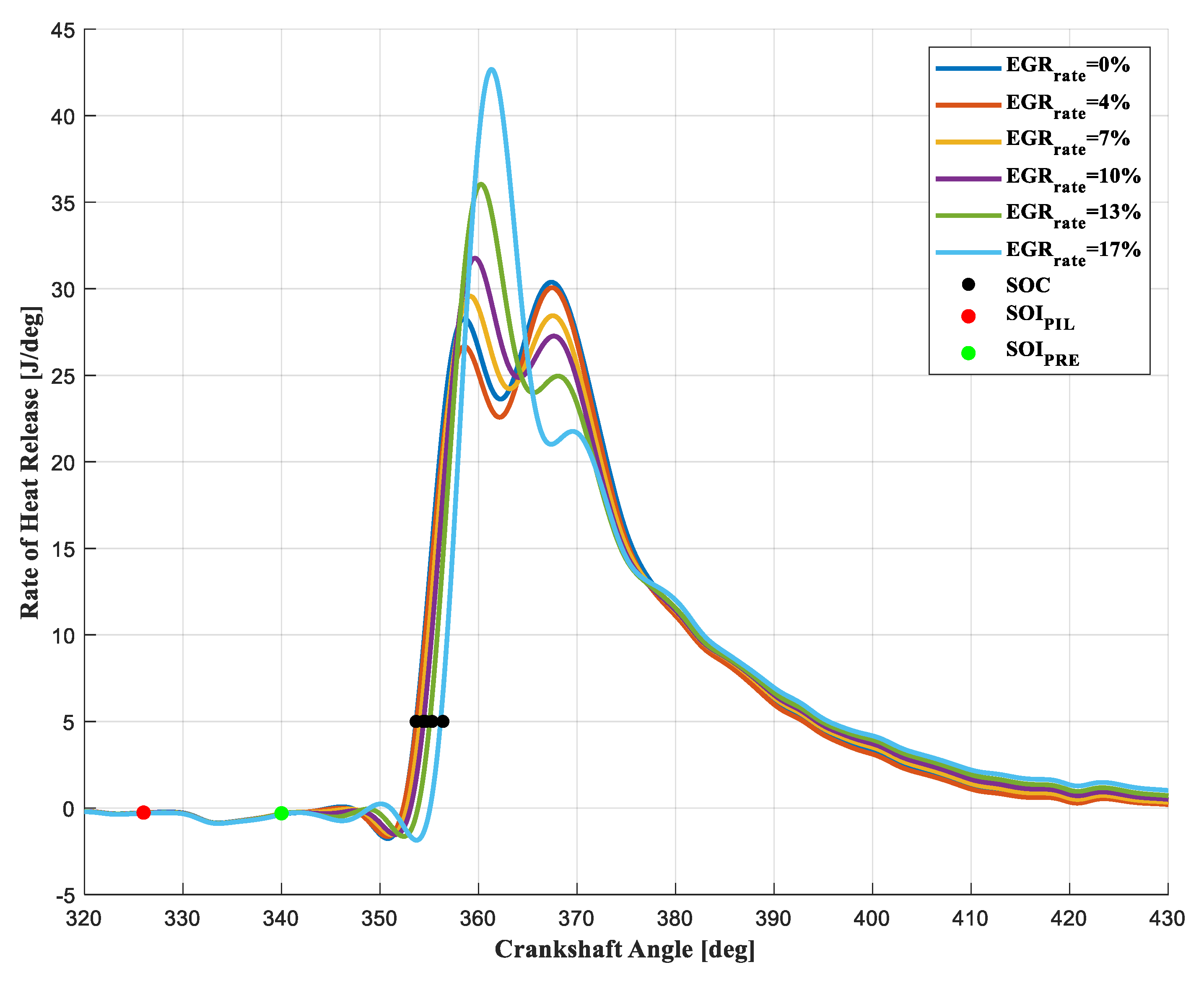
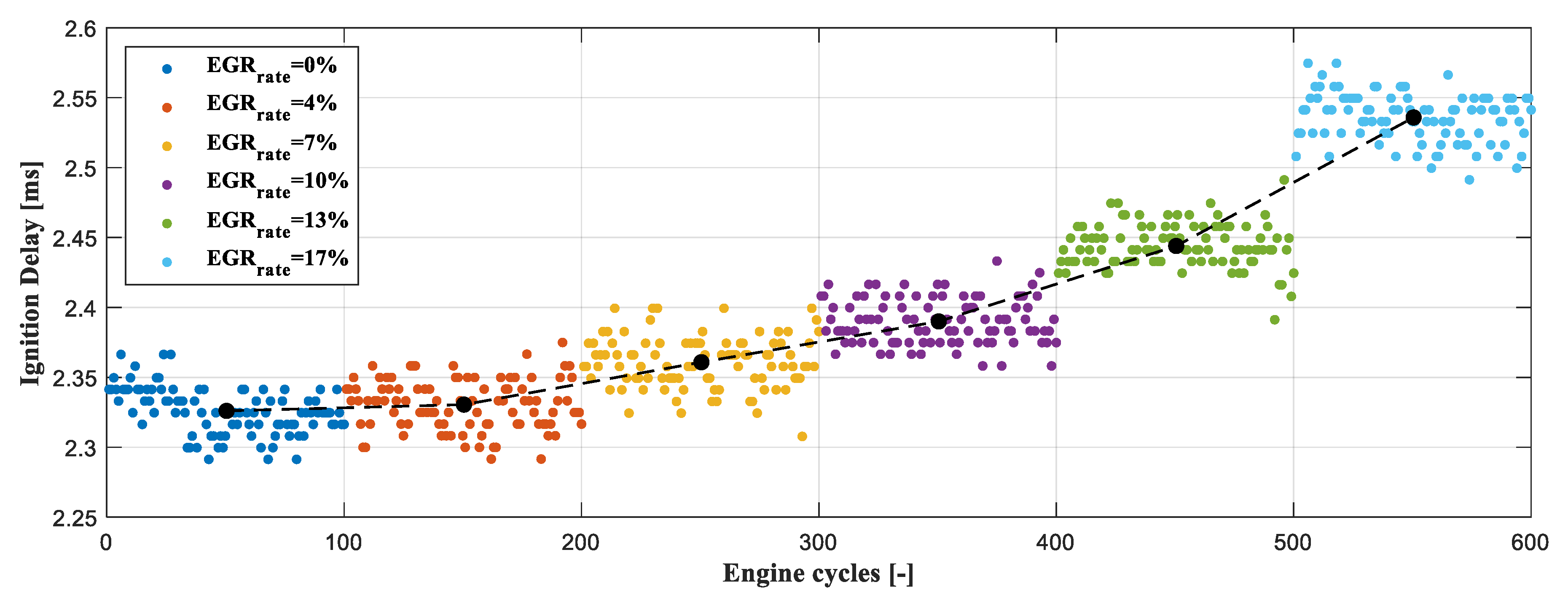
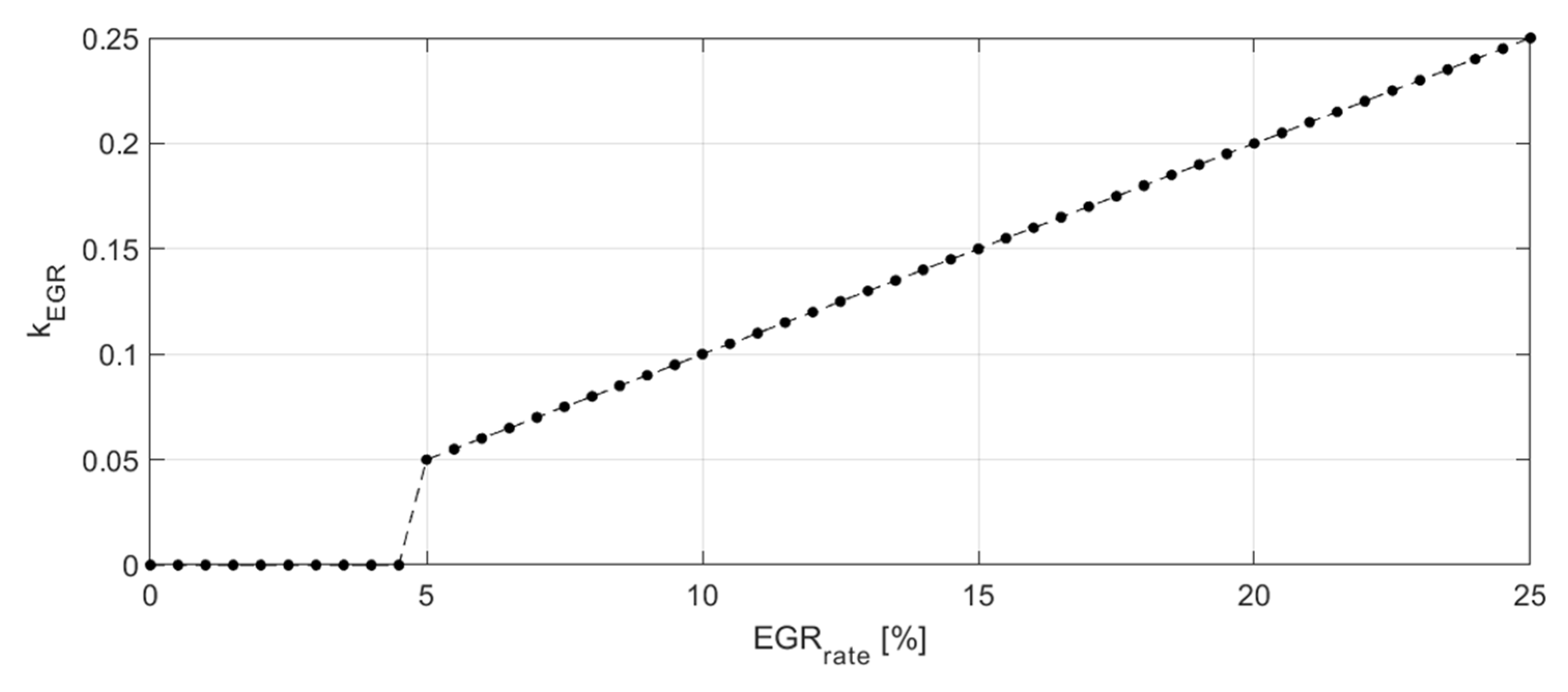
3.2.7. EGR Rate
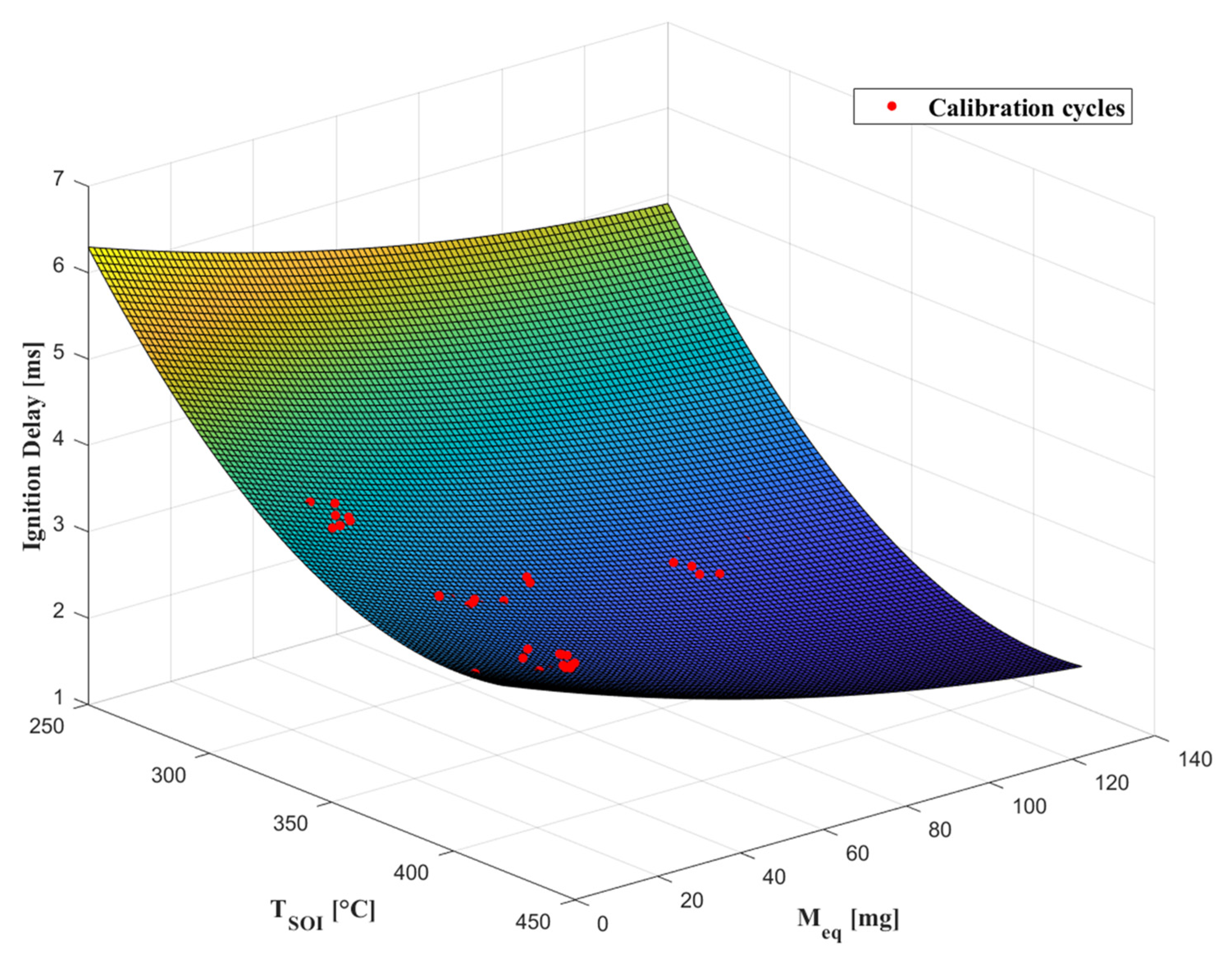
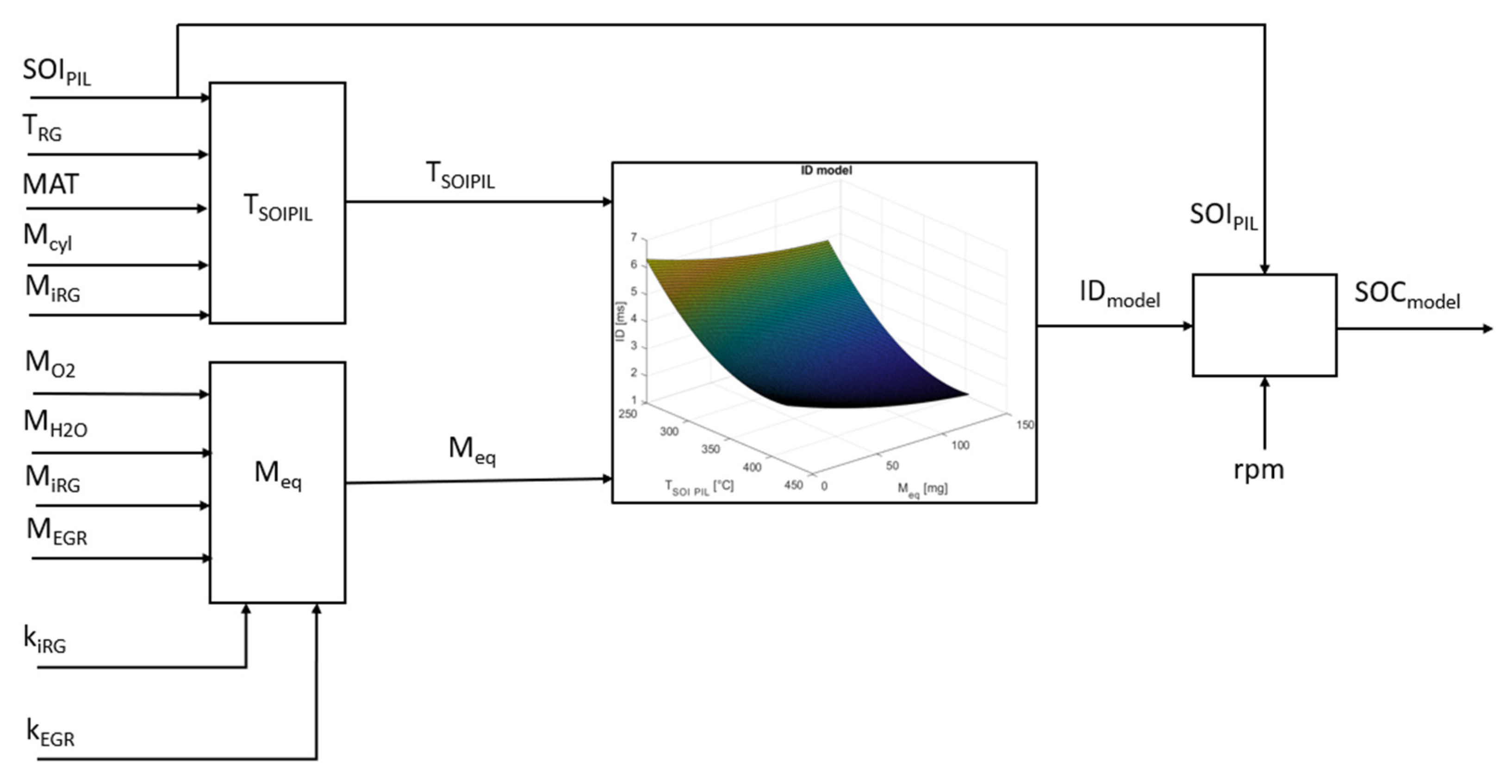
4. Control-Oriented Ignition Delay Model: Development and Calibration
5. Control-Oriented Ignition Delay Model: Results
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| BEVs | Battery Electric Vehicles |
| CAN | Controller Area Network |
| CA50 | Center of combustion |
| CDC | Conventional Diesel Combustion |
| CL | Closed-Loop |
| CO2 | Carbone dioxide |
| Mixture Activation Energy | |
| ECU | Electronic Control Unit |
| EGR | Exhaust Gas Recirculated |
| EGRrate | Mixture dilution Factor |
| ETmain | Energizing Time |
| EVO | Exhaust valve opening |
| FCEVs | Fuel Cell Electric Vehicles |
| GCI | Gasoline partially premixed Compression Ignition combustion |
| HCCI | Homogeneous Charge Compression Ignition |
| ICE | Internal Combustion Engine |
| ID | Ignition Delay |
| Measured Ignition delay | |
| Estimated Ignition delay | |
| IMEP | Indicated Mean Effective Pressure |
| LTCs | Low-Temperature Combustions |
| Amount of fresh Charge | |
| Exhaust Gases Mass | |
| Equivalent Mass (Chemical–Physical Index) | |
| Water Vapor Mass | |
| Oxygen Mass | |
| Oxygen Mass | |
| Residual Gas Mass | |
| Dry Air Mass | |
| N2 | Nitrogen |
| NOx | Nitrogen Oxides |
| O2 | Oxygen |
| Pboost | Boost pressure |
| Pexh | In-cylinder pressure averaged during exhaust stroke |
| PInt | In-cylinder pressure averaged during intake stroke |
| R | Specific Gas Constant |
| Air Specific Gas Constant | |
| Universal Gas Constant | |
| RMS | Root Mean Square Error |
| RoHR | Rate of Heat Release |
| RON | Research Octane Number |
| RPM | Revolutions per Minute |
| S/C | Supercharger |
| SOC | Start of Combustion |
| SOI | Start of Injection |
| Start of Injection angle for Pilot injection | |
| Start of Injection angle for Pre-injection | |
| Start of Injection angle for Main injection | |
| T | Mixture Temperature |
| Gas Temperature during combustion process (from cylinder pressure signal) | |
| Exhaust gas Temperature (from the cylinder pressure signal) | |
| Mixture Temperature at Intake Valve Closing Timing | |
| Manifold Air Temperature | |
| Residual Gases Temperature | |
| Charge Temperature at SOI | |
| Mixture Temperature at | |
| TDC | Top Dead Center |
| V | Cylinder Volume |
| Vcc | Combustion chamber volume |
| Vcyl | Maximum geometrical volume of the cylinder |
| VIVC | Volume at Intake Valve Closing angle |
| Volume at | |
| VGT | Variable Geometry Turbine |
| aTDC | After Top Dead Center |
| bTDC | Before Top Dead Center |
| dP | Derivative pressure |
| dV | Derivative volume |
| cp | Heat capacity at constant pressure |
| cv | Heat capacity at constant volume |
| dp | Pressure derivative |
| ID model error | |
| ID model coefficient for External EGR | |
| ID model coefficient for Residuals | |
| Mass of fresh air | |
| Test cell pressure | |
| Partial pressure of water vapor in the air–water mixture | |
| Air saturation pressure | |
| In-cylinder pressure | |
| Mass fraction of water vapor | |
| ΔV1 | Re-expansion reduction volume contribution |
| γ | Adiabatic index |
| Adiabatic index of mixture during compression stroke | |
| Adiabatic index of mixture during expansion stroke | |
| Angular position at which RoHR reaches 5 J/deg | |
| Relative humidity | |
| Local Air–fuel Ratio |
References
- Available online: https://www.evgo.com/ev-drivers/types-of-evs (accessed on 20 January 2022).
- Available online: https://thedriven.io/2018/08/28/what-is-a-fuel-cell-electric-vehicle (accessed on 20 January 2022).
- Available online: https://www.unep.org/resources/emissions-gap-report-2021 (accessed on 25 January 2022).
- Murya, R.K. Characteristics and Control of Low Temperature Combustion Engines; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Dernotte, J.; Dec, J.; Ji, C. Investigation of the Sources of Combustion Noise in HCCI Engines. SAE Int. J. Engines 2014, 7, 730–761. [Google Scholar] [CrossRef]
- Saxena, S.; Bedoya, I.D. Fundamental phenomena affecting low temperature combustion and HCCI engines, high load limits and strategies for extending these limits. Prog. Energy Combust. Sci. 2013, 39, 457–488. [Google Scholar] [CrossRef]
- Ganesh, D.; Nagarajan, G.; Ibrahim, M.M. Study of performance, combustion and emission characteristics of diesel homogeneous charge compression ignition (HCCI) combustion with external mixture formation. Fuel 2008, 87, 3497–3503. [Google Scholar] [CrossRef]
- Sellnau, M.; Foster, M.; Moore, W.; Sinnamon, J.; Hoyer, K.; Klemm, W. Pathway to 50% Brake Thermal Efficiency Using Gasoline Direct Injection Compression Ignition; SAE Technical Paper 2019-01-1154; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Ravaglioli, V.; Ponti, F.; Silvagni, G.; Moro, D.; Stola, F.; De Cesare, M. Performance Assessment of Gasoline PPC in a Light-Duty CI Engine; SAE Technical Paper 2022-01-0456; SAE International: Warrendale, PA, USA, 2022. [Google Scholar] [CrossRef]
- Li, C.; Yin, L.; Shamun, S.; Tuner, M.; Johansson, B.; Solsjö, R.; Bai, X.S. Transition from HCCI to PPC: The Sensitivity of Combustion Phasing to the Intake Temperature and the Injection Timing with and without EGR; SAE Technical Paper 2016-01-0767; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Stola, F.; Ravaglioli, V.; Silvagni, G.; Ponti, F.; De Cesare, M. Analysis of the Effects of Injection Pressure Variation in Gasoline Partially Premixed Combustion; SAE Technical Paper 2021-01-0517; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Belgiorno, G.; Dimitrakopoulos, N.; Di Blasio, G.; Beatrice, C.; Tunestål, P.; Tunér, M. Effect of the engine calibration parameters on gasoline partially premixed combustion performance and emissions compared to conventional diesel combustion in a light-duty Euro 6 engine. Appl. Energy 2018, 228, 2221–2234. [Google Scholar] [CrossRef]
- Stola, F.; Ravaglioli, V.; Silvagni, G.; Ponti, F.; De Cesare, M. Injection Pattern Investigation for Gasoline Partially Premixed Combustion Analysis; SAE Technical Paper 2019-24-0112; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Silvagni, G.; Ravaglioli, V.; Ponti, F.; Corti, E.; Raggini, L.; Scocozza, G.; Stola, F.; De Cesare, M. Development of a Predictive Pressure Waves Model for High-Pressure Common Rail Injection Systems. SAE Int. J. Engines 2022, 15. [Google Scholar] [CrossRef]
- Hernandez, J.J.; Sanz-Argent, J.; Carot, J.M.; Jabaloyes, J.M. Ignition delay time correlations for a diesel fuel with application to engine combustion modelling. Int. J. Engine Res. 2010, 11, 199–206. [Google Scholar] [CrossRef]
- Heywood, J. Internal Combustion Engine Fundamentals; McGraw-Hill Education: New York, NY, USA, 1988. [Google Scholar]
- Lee, Y.; Lee, S.; Min, K. Ignition Delay Model of Multiple Injections in CI Engines; SAE Technical Paper 2019-24-0071; SAE International: Warrendale, PA, USA, 2019. [Google Scholar] [CrossRef]
- Ravaglioli, V.; Ponti, F.; Silvagni, G.; De Cesare, M. Development of a Methodology for the Investigation of Residual Gases Effects on Gasoline Compression Ignition. In Proceedings of the ASME 2020 Internal Combustion Engine Division Fall Technical Conference, Virtual, Online, 4–6 November 2020; V001T04A006. ASME: New York, NY, USA, 2020. [Google Scholar] [CrossRef]
- Ravaglioli, V.; Ponti, F.; Silvagni, G.; Moro, D.; Stola, F.; De Cesare, M. Investigation of Gasoline Partially Premixed Combustion with External Exhaust Gas Recirculation. SAE Int. J. Engines 2022, 15. [Google Scholar] [CrossRef]
- Matsuura, K.; Iida, N. Effect of Temperature-Pressure Time History on Auto-Ignition Delay of Air-Fuel Mixture; SAE Technical Paper 2018-01-1799; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- An, Y.; Ali, M.J.; Vallinayagam, R.; AlRamadan, A.; Sim, J.; Chang, J.; Im, H.; Johansson, B. Compression Ignition of Low Octane Gasoline under Partially Premixed Combustion Mode; SAE Technical Paper 2018-01-1797; SAE International: Warrendale, PA, USA, 2018. [Google Scholar] [CrossRef]
- Ponti, F.; Ravaglioli, V.; Cavina, N.; De Cesare, M. Diesel Engine Combustion Sensing Methodology Based on Vibration Analysis. ASME J. Eng. Gas Turbines Power 2014, 136, 111503. [Google Scholar] [CrossRef]
- Oh, S.; Min, K.; Sunwoo, M. Real-time start of a combustion detection algorithm using initial heat release for direct injection diesel engines. Appl. Therm. Eng. 2015, 89, 332–345. [Google Scholar] [CrossRef]
- Luján, J.; Bermúdez, V.; Guardiola, C.; Abbad, A. A methodology for combustion detection in diesel engines through in-cylinder pressure derivative signal. Mech. Syst. Signal Process. 2010, 24, 2261–2275. [Google Scholar] [CrossRef]
- Dempsey, A.B.; Curran, S.J.; Wagner, R.M. A perspective on the range of gasoline compression ignition combustion strategies for high engine efficiency and low NOx and soot emissions: Effects of in-cylinder fuel stratification. Int. J. Engine Res. 2016, 17, 897–917. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, M.; Atkinson, W.; Schmidt, H.; Lee, S.Y.; Naber, J.; Tzanetakis, T.; Sim, J. Experimental Investigation of the Compression Ignition Process of High Reactivity Gasoline Fuels and E10 Certification Gasoline using a High-Pressure Direct Injection Gasoline Injector; SAE Technical Paper 2020-01-0323; SAE International: Warrendale, PA, USA, 2020. [Google Scholar] [CrossRef]
- Liu, J.; Wang, H.; Zheng, Z.; Mao, B.; Li, L.; Yao, M. Effects of Pilot Injection Strategy on Combustion and Emission Characteristics in Gasoline Compression Ignition. Energy Procedia 2017, 142, 1267–1273. [Google Scholar] [CrossRef]
- Yazdani, A.; Naber, J.; Shahbakhti, M.; Dice, P.; Glugla, C.; Cooper, S.; McEwan, D.; Huberts, G. Air Charge and Residual Gas Fraction Estimation for a Spark-Ignition Engine Using In-Cylinder Pressure; SAE Technical Paper 2017-01-0527; SAE International: Warrendale, PA, USA, 2017. [Google Scholar] [CrossRef]
- Sinnamon, J.F.; Sellnau, M.C. A New Technique for Residual Gas Estimation and Modelling in Engines; SAE Technical Paper 2008-01-0093; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef]
- Chang, Y.; Mendrea, B.; Sterniak, J.; Bohac, S.V. Effect of Ambient Temperature and Humidity on Combustion and Emissions of a Spark-Assisted Compression Ignition Engine. ASME J. Eng. Gas Turbines Power 2017, 139, 051501. [Google Scholar] [CrossRef]
- Badra, J.; Elwardany, A.; Sim, J.; Viollet, Y.; Im, H.G.; Chang, J. Effects of In-Cylinder Mixing on Low Octane Gasoline Compression Ignition Combustion; SAE Technical Paper 2016-01-0762; SAE International: Warrendale, PA, USA, 2016. [Google Scholar] [CrossRef]
- Kumar, P.; Sellnau, M. EGR System Optimization for Light-Duty Gasoline Compression Ignition (GCI) Engine; SAE Technical Paper 2021-01-0515; SAE International: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Kassa, M.; Hall, C.; Ickes, A.; Wallner, T. In-Cylinder Oxygen Mass Fraction Estimation Method for Minimizing Cylinder-to-Cylinder Variations; SAE Technical Paper 2015-01-0874; SAE International: Warrendale, PA, USA, 2015. [Google Scholar] [CrossRef]
- Vojtisek-Lom, M.; Kotek, M. Estimation of Engine Intake Air Mass Flow using a generic Speed-Density method. J. Middle Eur. Constr. Des. Cars 2014, 12, 7–15. [Google Scholar]
- Pipitone, E.; Beccari, A.; Beccari, S. Reliable TDC Position Determination: A Comparison of Different Thermodynamic Methods through Experimental Data and Simulations; SAE Technical Paper 2008-36-0059; SAE International: Warrendale, PA, USA, 2008. [Google Scholar] [CrossRef] [Green Version]


| Engine Parameter | Values |
|---|---|
| Displaced volume | 1248 cc |
| Maximum Torque | 200 Nm @ 1500 rpm |
| Maximum Power | 70 kW @ 3800 rpm |
| Injection System | Common Rail, Multi-Jet |
| Bore | 69.6 mm |
| Stroke | 82 mm |
| Compression ratio | 16.8:1 |
| Number of Valves | 4 per cylinder |
| Architecture | L4 |
| Firing Order | 1-3-4-2 |
| Engine Parameter | High-Temperature Condition | Low-Temperature Condition |
|---|---|---|
| Engine speed [rpm] | 2000 | 2000 |
| IMEP [bar] | 12 | 12 |
| Boost pressure [bar] | 2.2 | 2.2 |
| Exhaust pressure [bar] | 3 | 3 |
| Intake temperature [°C] | 77 | 50 |
| CA50 [ca. deg aTDC] | 12 | 12 |
| SOI Pil, SOI Pre, SOI Main [deg bTDC] | [35, 21, 4] | [35, 21, 3] |
| Injection pressure [bar] | 500 | 500 |
| ETmain [μs] | 686 | 683 |
| Engine Parameter | Calibrated Values |
|---|---|
| Engine speed [rpm] | 2000 |
| IMEP [bar] | 12 |
| Boost pressure [bar] | Sweep from 2.2 to 1.8 |
| Exhaust pressure [bar] | 3 |
| Intake temperature [°C] | 74 |
| CA50 [ca. deg aTDC] | 12 |
| SOI Pil, SOI Pre, SOI Main [deg bTDC] | [35, 21, CL] |
| Injection pressure [bar] | 500 |
| Engine Parameter | High Exhaust Pressure | Low Exhaust Pressure |
|---|---|---|
| Engine speed [rpm] | 2000 | 2000 |
| IMEP [bar] | 12 | 12 |
| Boost pressure [bar] | 2 | 2 |
| Exhaust pressure [bar] | 3 | 2.8 |
| Intake temperature [°C] | 73 | 73 |
| MFB50 [ca. deg aTDC] | 12 | 12 |
| SOI Pil, SOI Pre, SOI Main [deg bTDC] | [35, 21, 4] | [35, 21, 4] |
| Injection pressure [bar] | 500 | 500 |
| ETmain [μs] | 695 | 699 |
| Engine Parameter | Low Relative Humidity | High Relative Humidity |
|---|---|---|
| Engine speed [rpm] | 2000 | 2000 |
| IMEP [bar] | 12 | 12 |
| Boost pressure [bar] | 2.1 | 2.1 |
| Exhaust pressure [bar] | 3 | 3 |
| Intake temperature [°C] | 73 | 73 |
| Relative humidity [–] | 25% | 40% |
| CA50 [ca. deg aTDC] | 12 | 12 |
| SOI Pil, SOI Pre, SOI Main [deg bTDC] | [34, 20, 4] | [35, 21, 4] |
| Injection pressure [bar] | 500 | 500 |
| ETmain [μs] | 695 | 699 |
| Engine Parameter | Calibrated Values |
|---|---|
| Engine speed [rpm] | 2000 |
| IMEP [bar] | 12 |
| Boost pressure [bar] | 1.6 |
| EGR rate [%] | 0-4-7-10-13-17 |
| Exhaust pressure at 0% of EGR rate [bar] | 3 |
| Intake temperature [°C] | 45 |
| CA50 [ca. deg aTDC] | 8 |
| SOI Pil, SOI Pre, SOI Main [deg bTDC] | [34, 20, CL] |
| Injection pressure [bar] | 500 |
| Variable Name | Relation with the ID | |
|---|---|---|
| Thermodynamic variables | ||
| Chemical–Physical variables | ||
| Model Parameter | Calibrated Values |
|---|---|
| a | 25.69 |
| b | 0.1127 |
| c | 0.01435 |
| d | |
| e | |
| f |
| Engine Speed [rpm] | IMEP [bar] | CA50 [deg aTDC] | Boost Pressure [barA] | Intake Temperature [°C] | Exhaust Pressure [mbarA] | SOI Pil [deg bTDC] | SOI Pre [deg bTDC] | Relative Humidity [%] |
|---|---|---|---|---|---|---|---|---|
| 2000 | 8 | 9 | 1.8 | 75 | 3.1 | 34 | 20 | 46 |
| 2000 | 9 | 12 | 1.7–1.6 | 70 | 2.5 | 43 | 29 | 38 |
| 2000 | 9 | 12 | [1.9:0.1:1.6] | 70 | 2.7 | 43 | 29 | 38 |
| 2000 | 12 | 12 | 2.1 | 72 | 3 | 35 | 21 | 40 |
| 2000 | 12 | 12 | 2.1 | 72 | 2.8 | 35 | 21 | 38 |
| 2000 | 12 | 12 | [2.2:0.1:1.8] | 74 | 3 | 35 | 21 | 25 |
| 2000 | 9 | 12 | [1.9:0.1:1.6] | 60 | 2.7 | 43 | 35 | 35 |
| 2000 | 9 | 12 | 1.8–1.7 | 60 | 2.5 | 43 | 35 | 35 |
| 2000 | 12 | 12 | 2.1 | 50 | 3 | 35 | 37 | 37 |
| 2000 | 12 | 12 | 2.1 | 50 | 2.8 | 35 | 37 | 37 |
| 2000 | 12 | 12 | [2.2:0.1:1.9] | 50 | 3 | 35 | 21 | 21 |
| 2000 | 12 | 12 | [2.1:0.1:1.7] | 50 | 2.8 | 35 | 21 | 21 |
| 2000 | 14 | 12 | [2.2:0.1:2] | 52 | 3 | 35 | 20 | 20 |
| 2000 | 14 | 12 | [2.1:0.1:1.8] | 52 | 2.8 | 35 | 20 | 20 |
| Engine Speed [rpm] | IMEP [bar] | CA50 [deg aTDC] | Boost Pressure [barA] | Intake Temperature [°C] | Exhaust Pressure [mbarA] | SOI Pil [deg bTDC] | SOI Pre [deg bTDC] | Relative Humidity [%] |
|---|---|---|---|---|---|---|---|---|
| 2000 | 8 | 14 | 1.5 | 40 | 1.9 | 32 | 18 | 44 |
| 2000 | 8 | 14 | 1.6 | 40 | 2.2 | 32 | 18 | 45 |
| 2000 | 12 | 14 | 1.6 | 46 | 1.8 | 34 | 20 | 44 |
| 2000 | 12 | 14 | 1.7 | 46 | 2 | 34 | 20 | 49 |
| 2000 | 14 | 14 | 1.9 | 43 | 2.2 | 35 | 21 | 45 |
| 2000 | 14 | 14 | 2 | 49 | 2.4 | 35 | 21 | 40 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Silvagni, G.; Ravaglioli, V.; Falfari, S.; Ponti, F.; Mariani, V. Development of a Control-Oriented Ignition Delay Model for GCI Combustion. Energies 2022, 15, 6470. https://doi.org/10.3390/en15176470
Silvagni G, Ravaglioli V, Falfari S, Ponti F, Mariani V. Development of a Control-Oriented Ignition Delay Model for GCI Combustion. Energies. 2022; 15(17):6470. https://doi.org/10.3390/en15176470
Chicago/Turabian StyleSilvagni, Giacomo, Vittorio Ravaglioli, Stefania Falfari, Fabrizio Ponti, and Valerio Mariani. 2022. "Development of a Control-Oriented Ignition Delay Model for GCI Combustion" Energies 15, no. 17: 6470. https://doi.org/10.3390/en15176470
APA StyleSilvagni, G., Ravaglioli, V., Falfari, S., Ponti, F., & Mariani, V. (2022). Development of a Control-Oriented Ignition Delay Model for GCI Combustion. Energies, 15(17), 6470. https://doi.org/10.3390/en15176470










