Deviation from Darcy Law in Porous Media Due to Reverse Osmosis: Pore-Scale Approach
Abstract
:1. Introduction
2. Numerical Analysis
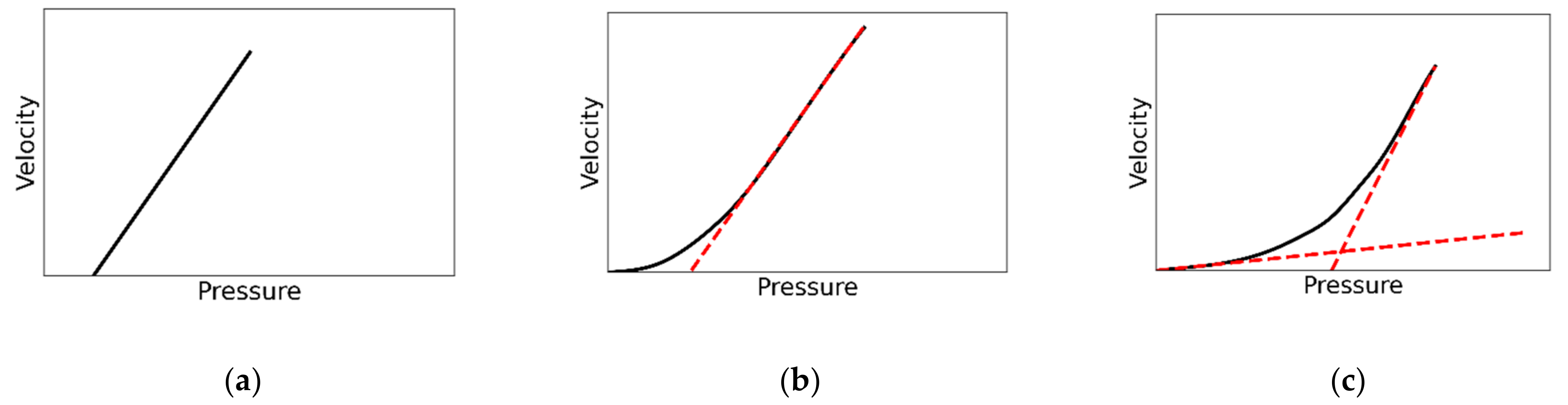
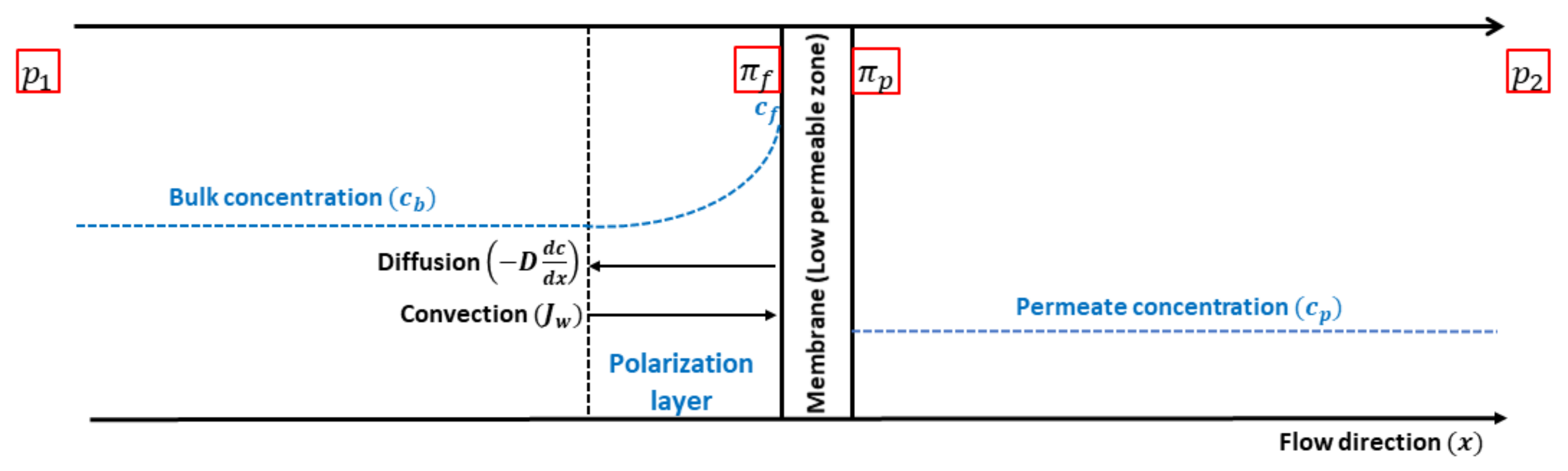
2.1. Theory
2.2. Computational Domain
2.3. Governing Equations and Boundary Conditions
3. Results and Discussion
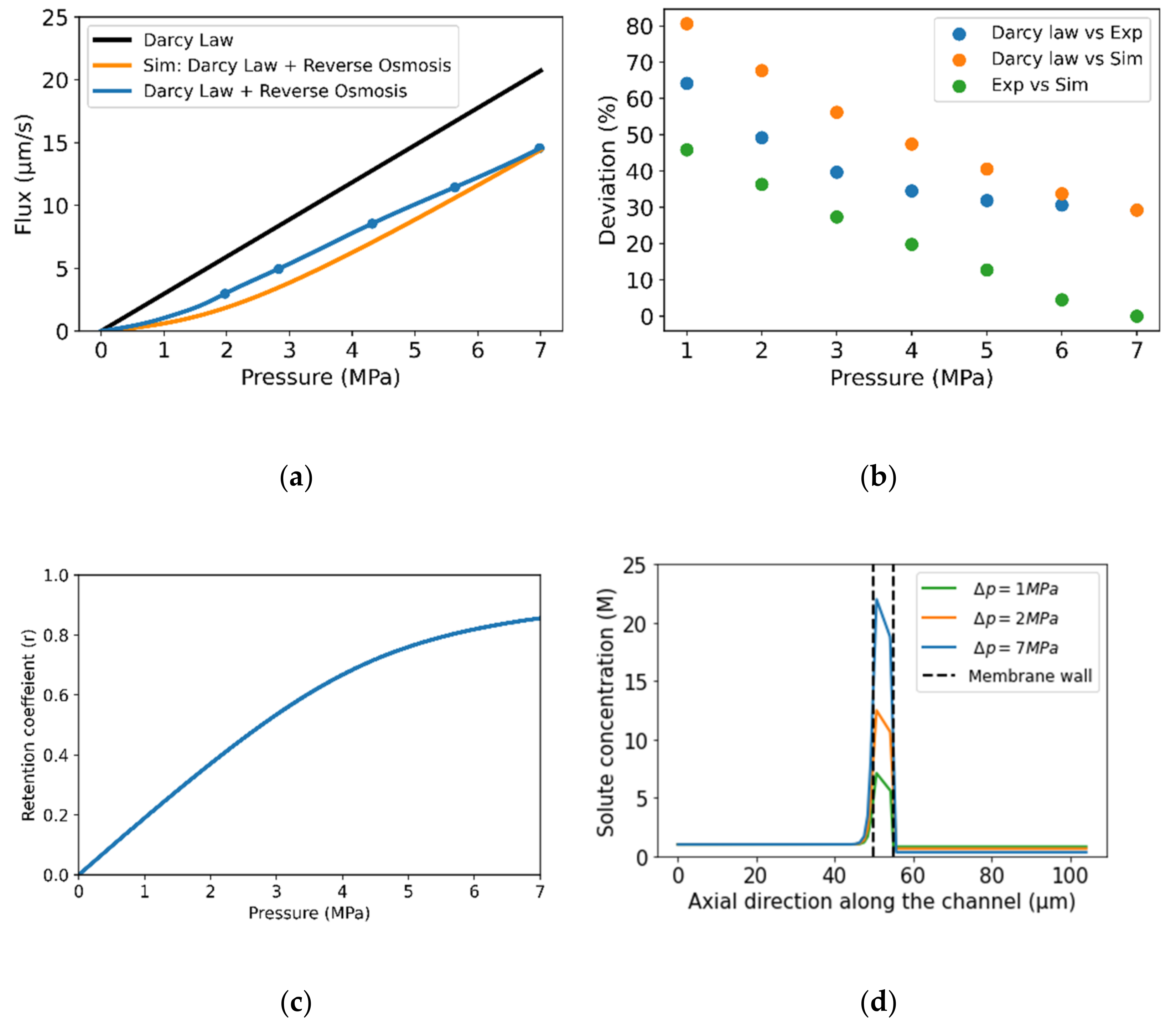
3.1. Model Validation
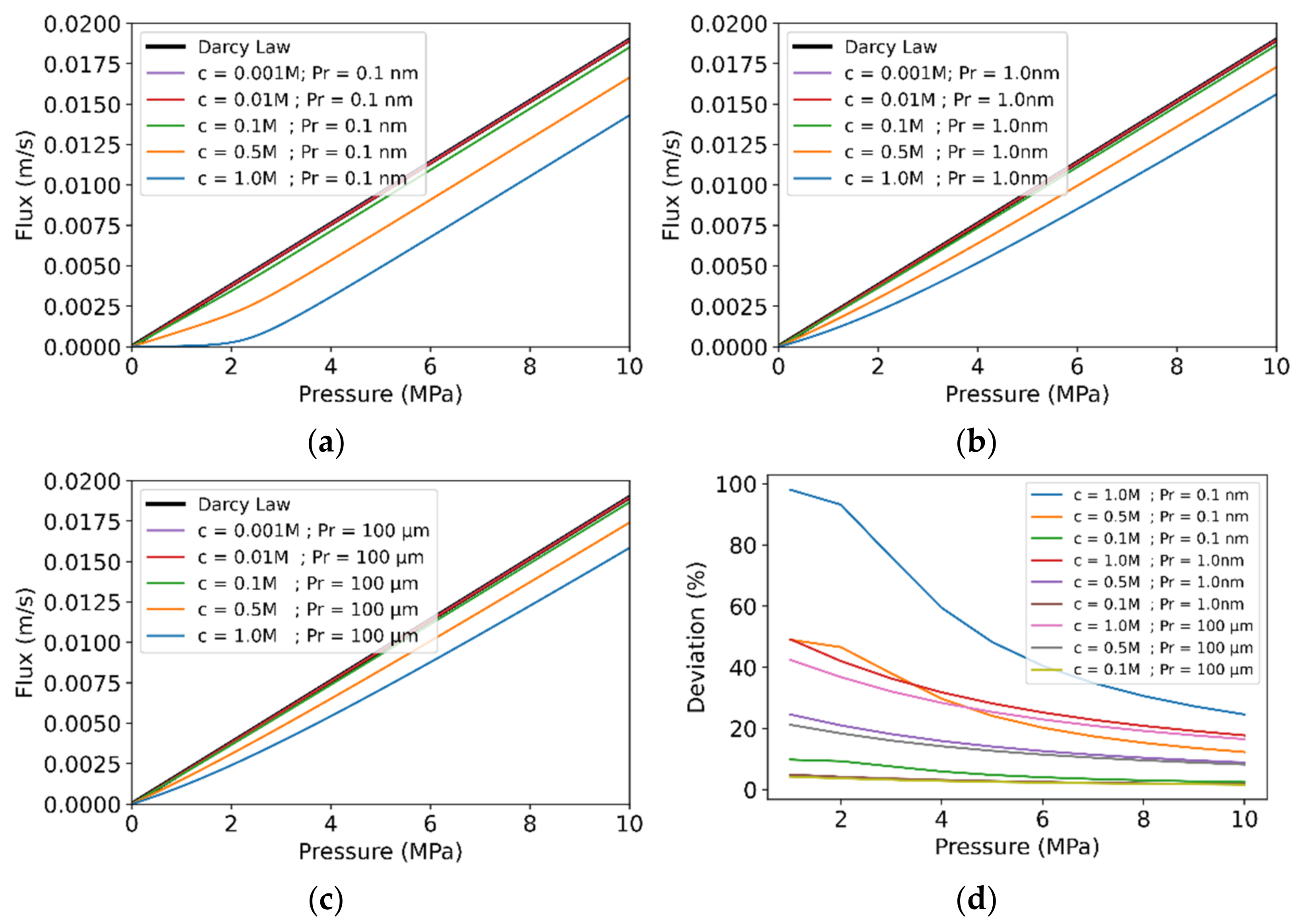
3.2. Effect of Pore Radius and Bulk Concentration
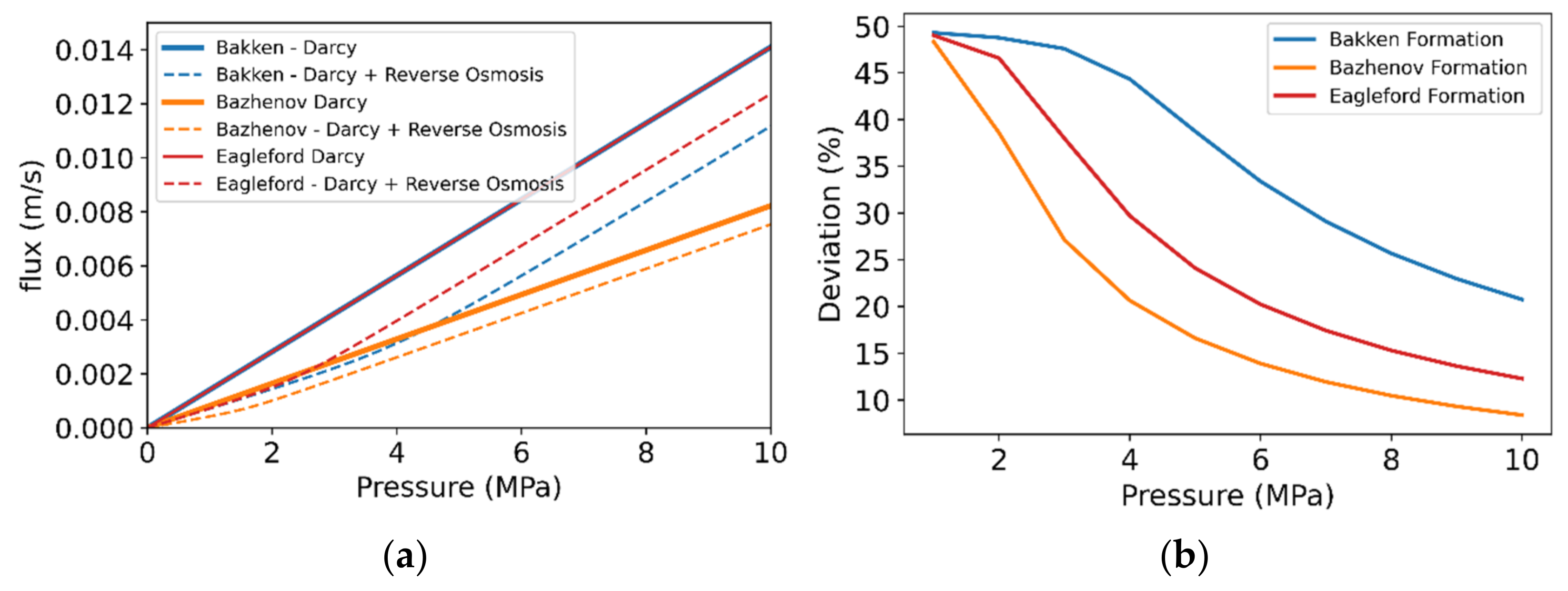
3.3. Case-Study: Extent of Deviation from the Darcy Law for Different Tight/Shale Formations
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kundu, P.; Kumar, V.; Mishra, I.M. Experimental and numerical investigation of fluid flow hydrodynamics in porous media: Characterization of pre-Darcy, Darcy and non-Darcy flow regimes. Powder Technol. 2016, 303, 278–291. [Google Scholar] [CrossRef]
- Veyskarami, M.; Hassani, A.H.; Ghazanfari, M.H. Modeling of non-Darcy flow through anisotropic porous media: Role of pore space profiles. Chem. Eng. Sci. 2016, 151, 93–104. [Google Scholar] [CrossRef]
- Bratsun, D.; Siraev, R. Controlling mass transfer in a continuous-flow microreactor with a variable wall relief. Int. Commun. Heat Mass Transf. 2020, 113, 104522. [Google Scholar] [CrossRef]
- Sunjoto, S. The inventions technology on water resources to support environmental engineering based infrastructure. In Proceedings of the 5th International Conference on Education, Concept, and Application of Green Technology, Semarang, Indonesia, 5–6 October 2016; AIP Publishing LLC: Melville, NY, USA, 2017. [Google Scholar] [CrossRef]
- Satter, A.; Iqbal, G.M. Reservoir rock properties. In Reservoir Engineering; Elsevier: Amsterdam, The Netherlands, 2016; pp. 29–79. [Google Scholar] [CrossRef]
- Sun, S.; Zhang, T. Recent progress in multiscale and mesoscopic reservoir simulation. In Reservoir Simulations; Elsevier: Amsterdam, The Netherlands, 2020; pp. 205–258. [Google Scholar] [CrossRef]
- U.S. EIA. Annual Energy Outlook 2017 with Projections to 2050; Technical Report 8; EIA: Washington, DC, USA, 2017. [Google Scholar]
- Wang, S. Shale gas exploitation: Status, problems and prospect. Nat. Gas Ind. B 2018, 5, 60–74. [Google Scholar] [CrossRef]
- Yan, B.; Killough, J.E.; Wang, Y.; Cao, Y. Novel Approaches for the Simulation of Unconventional Reservoirs. In Proceedings of the Unconventional Resources Technology Conference, Denver, CO, USA, 12–14 August 2013. [Google Scholar] [CrossRef]
- Huang, Y.; Yang, Z.; He, Y.; Wang, X. An overview on nonlinear porous flow in low permeability porous media. Theor. Appl. Mech. Lett. 2013, 3, 022001. [Google Scholar] [CrossRef]
- Wang, D.; Wang, G. Dynamics of ion transport and electric double layer in single conical nanopores. J. Electroanal. Chem. 2016, 779, 39–46. [Google Scholar] [CrossRef]
- Wang, H.; Su, Y.; Wang, W.; Sheng, G.; Li, H.; Zafar, A. Enhanced water flow and apparent viscosity model considering wettability and shape effects. Fuel 2019, 253, 1351–1360. [Google Scholar] [CrossRef]
- Maknickas, A.; Skarbalius, G.; Džiugys, A.; Misiulis, E. Nano-scale water Poiseuille flow: MD computational experiment. In Proceedings of the AIP Conference Proceedings; AIP Publishing: Melville, NY, USA, 2020. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Zhu, C.; Zhang, J. Visualizing Gas Diffusion Behaviors in Three-Dimensional Nanoporous Media. Energy Fuels 2021, 35, 2075–2086. [Google Scholar] [CrossRef]
- Bai, B.; Zhu, R.; Wu, S.; Yang, W.; Gelb, J.; Gu, A.; Zhang, X.; Su, L. Multi-scale method of Nano(Micro)-CT study on microscopic pore structure of tight sandstone of Yanchang Formation, Ordos Basin. Pet. Explor. Dev. 2013, 40, 354–358. [Google Scholar] [CrossRef]
- Orlov, D.; Ebadi, M.; Muravleva, E.; Volkhonskiy, D.; Erofeev, A.; Savenkov, E.; Balashov, V.; Belozerov, B.; Krutko, V.; Yakimchuk, I.; et al. Different methods of permeability calculation in digital twins of tight sandstones. J. Nat. Gas Sci. Eng. 2021, 87, 103750. [Google Scholar] [CrossRef]
- Wyckoff, R.D.; Botset, H.G.; Muskat, M.; Reed, D.W. The Measurement of the Permeability of Porous Media for Homogeneous Fluids. Rev. Sci. Instrum. 1933, 4, 394–405. [Google Scholar] [CrossRef]
- King, F.H. Principles and Conditions of the Movements of Ground Water; US Government Printing Office: Washington, DC, USA, 1899; Volume 647.
- Churaev, N.V. Physical and Chemical Transport Processes in Porous Bodies.Pdf. 1990. Available online: https://www.studmed.ru/churaev-nv-fizikohimiya-processov-massoperenosa-v-poristyh-telah_b19eb202c34.html (accessed on 11 November 2021).
- Swartzendruber, D. Non-Darcy flow behavior in liquid-saturated porous media. J. Geophys. Res. 1962, 67, 5205–5213. [Google Scholar] [CrossRef]
- Dudgeon, C.R. An experimental study of the flow of water through coarse granular media. La Houille Blanche 1966, 52, 785–801. [Google Scholar] [CrossRef]
- Zeng, B.; Cheng, L.; Li, C. Low velocity non-linear flow in ultra-low permeability reservoir. J. Pet. Sci. Eng. 2011, 80, 1–6. [Google Scholar] [CrossRef]
- Lv, C.; Wang, J.; Sun, Z. An experimental study on starting pressure gradient of fluids flow in low permeability sandstone porous media. Pet. Explor. Dev. 2002, 29, 86–89. [Google Scholar]
- Han, X.; Wang, E.; Liu, Q. Non-Darcy flow of single-phase water through low permeability rock. J. Tsinghua Univ. 2004, 44, 804–807. [Google Scholar]
- Xu, S.; Yue, X.A. Experimental research on nonlinear flow characteristics at low velocity. J. China Univ. Pet. 2007, 31, 60–63. [Google Scholar]
- Xu, J.; Cheng, L.; Zhou, Y.; Ma, L. A new method for calculating kickoff pressure gradient in low permeability reservoirs. Pet. Explor. Dev. 2007, 34, 594. [Google Scholar]
- Siddiqui, F.; Soliman, M.Y.; House, W.; Ibragimov, A. Pre-Darcy flow revisited under experimental investigation. J. Anal. Sci. Technol. 2016, 7, 2. [Google Scholar] [CrossRef] [Green Version]
- Basak, P. Non-Darcy Flow and its Implications to Seepage Problems. J. Irrig. Drain. Div. 1977, 103, 459–473. [Google Scholar] [CrossRef]
- Soni, J.; Islam, N.; Basak, P. An experimental evaluation of non-Darcian flow in porous media. J. Hydrol. 1978, 38, 231–241. [Google Scholar] [CrossRef]
- Kececioglu, I.; Jiang, Y. Flow Through Porous Media of Packed Spheres Saturated with Water. J. Fluids Eng. 1994, 116, 164–170. [Google Scholar] [CrossRef]
- Klinkenberg, L. The Permeability of Porous Media to Liquids and Gases. API-41-200. All Days. 1941. Available online: https://faculty.ksu.edu.sa/sites/default/files/klinkenbergspaper-1941.pdf (accessed on 11 November 2021).
- Santoso, R.K.; Fauzi, I.; Hidayat, M.; Swadesi, B.; Aslam, B.M.; Marhaendrajana, T. Study of Non-Newtonian fluid flow in porous media at core scale using analytical approach. Geosyst. Eng. 2017, 21, 21–30. [Google Scholar] [CrossRef]
- Panfilov, M.; Fourar, M. Physical splitting of nonlinear effects in high-velocity stable flow through porous media. Adv. Water Resour. 2006, 29, 30–41. [Google Scholar] [CrossRef]
- Hayes, R.E.; Afacan, A.; Boulanger, B. An equation of motion for an incompressible Newtonian fluid in a packed bed. Transp. Porous Media 1995, 18, 185–198. [Google Scholar] [CrossRef]
- Whitaker, S. The equations of motion in porous media. Chem. Eng. Sci. 1966, 21, 291–300. [Google Scholar] [CrossRef]
- Crestel, E.; Kvasničková, A.; Santanach-Carreras, E.; Bibette, J.; Bremond, N. Motion of oil in water induced by osmosis in a confined system. Phys. Rev. Fluids 2020, 5, 104003. [Google Scholar] [CrossRef]
- Naeem, M.H.T.; Dehaghani, A.H.S. Evaluation of the performance of oil as a membrane during low-salinity water injection focusing on type and concentration of salts. J. Pet. Sci. Eng. 2020, 192, 107228. [Google Scholar] [CrossRef]
- Adler, P.M.; Malevich, A.E.; Mityushev, V.V. Nonlinear correction to Darcy’s law for channels with wavy walls. Acta Mech. 2013, 224, 1823–1848. [Google Scholar] [CrossRef]
- Javadi, M.; Sharifzadeh, M.; Shahriar, K.; Mehrjooei, M. Non-linear fluid flow through rough-walled fractures. In Proceedings of the ISRM Regional Symposium-EUROCK 2009, Cavtat, Croatia, 29–31 October 2009; OnePetro: Richardson, TX, USA, 2009. [Google Scholar]
- Qian, J.; Chen, Z.; Zhan, H.; Guan, H. Experimental study of the effect of roughness and Reynolds number on fluid flow in rough—Walled single fractures: A check of local cubic law. Hydrol. Processes 2010, 25, 614–622. [Google Scholar] [CrossRef]
- Kutiĺek, M. Non-Darcian Flow of Water in Soils—Laminar Region. Dev. Soil Sci. 1972, 2, 327–340. [Google Scholar] [CrossRef]
- Shannon, M.A.; Bohn, P.W.; Elimelech, M.; Georgiadis, J.G.; Mariñas, B.J.; Mayes, A.M. Science and technology for water purification in the coming decades. Nanosci. Technol. A Collect. Rev. Nat. J. 2008, 452, 301–310. [Google Scholar] [CrossRef] [PubMed]
- Greenlee, L.F.; Lawler, D.F.; Freeman, B.D.; Marrot, B.; Moulin, P. Reverse osmosis desalination: Water sources, technology, and today’s challenges. Water Res. 2009, 43, 2317–2348. [Google Scholar] [CrossRef] [PubMed]
- Li, D.; Wang, H. Recent developments in reverse osmosis desalination membranes. J. Mater. Chem. 2010, 20, 4551. [Google Scholar] [CrossRef]
- Shafi, H.Z.; Khan, Z.; Yang, R.; Gleason, K.K. Surface modification of reverse osmosis membranes with zwitterionic coating for improved resistance to fouling. Desalination 2015, 362, 93–103. [Google Scholar] [CrossRef]
- Whitworth, T.M. Clay membranes. In Encyclopedia of Earth Science; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999; pp. 83–85. [Google Scholar] [CrossRef]
- Hung, L.Y.; Lue, S.J.; You, J.H. Mass-transfer modeling of reverse-osmosis performance on 0.5–2% salty water. Desalination 2011, 265, 67–73. [Google Scholar] [CrossRef]
- Mai, Z.; Gui, S.; Fu, J.; Jiang, C.; Ortega, E.; Zhao, Y.; Tu, W.; Mickols, W.; der Bruggen, B.V. Activity-derived model for water and salt transport in reverse osmosis membranes: A combination of film theory and electrolyte theory. Desalination 2019, 469, 114094. [Google Scholar] [CrossRef]
- Fritz, S.J. Ideality of Clay Membranes in Osmotic Processes: A Review. Clays Clay Miner. 1986, 34, 214–223. [Google Scholar] [CrossRef]
- Kharaka, Y.K.; Berry, F.A. Simultaneous flow of water and solutes through geological membranes—I. Experimental investigation. Geochim. Et Cosmochim. Acta 1973, 37, 2577–2603. [Google Scholar] [CrossRef]
- Shackelford, C.D.; Meier, A.; Sample-Lord, K. Limiting membrane and diffusion behavior of a geosynthetic clay liner. Geotext. Geomembr. 2016, 44, 707–718. [Google Scholar] [CrossRef]
- Neuzil, C.E.; Person, M. Reexamining ultrafiltration and solute transport in groundwater. Water Resour. Res. 2017, 53, 4922–4941. [Google Scholar] [CrossRef]
- De Marsily, G. Stochastic Description of Flow in Porous Media. In Encyclopedia of Physical Science and Technology; Elsevier: Amsterdam, The Netherlands, 2003; pp. 95–104. [Google Scholar] [CrossRef]
- Gill, W.N.; Tien, C.; Zeh, D.W. Concentration Polarization Effects in a Reverse Osmosis System. Ind. Eng. Chem. Fundam. 1965, 4, 433–439. [Google Scholar] [CrossRef]
- Song, L.; Liu, C. A total salt balance model for concentration polarization in crossflow reverse osmosis channels with shear flow. J. Membr. Sci. 2012, 401–402, 313–322. [Google Scholar] [CrossRef]
- Liu, C.; Audra, M.; Ken, R.; Lianfa, S. Modeling of Concentration Polarization in a Reverse Osmosis Channel with Parabolic Crossflow. Water Environ. Res. 2014, 86, 56–62. [Google Scholar] [CrossRef]
- Gekas, V.; Hallström, B. Mass transfer in the membrane concentration polarization layer under turbulent cross flow. J. Membr. Sci. 1987, 30, 153–170. [Google Scholar] [CrossRef]
- Gherasim, C.V.; Cuhorka, J.; Mikulášek, P. Analysis of lead(II) retention from single salt and binary aqueous solutions by a polyamide nanofiltration membrane: Experimental results and modelling. J. Membr. Sci. 2013, 436, 132–144. [Google Scholar] [CrossRef]
- Hadi, S.; Mohammed, A.A.; Al-Jubouri, S.M.; Abd, M.F.; Majdi, H.S.; Alsalhy, Q.F.; Rashid, K.T.; Ibrahim, S.S.; Salih, I.K.; Figoli, A. Experimental and Theoretical Analysis of Lead Pb2 and Cd2 Retention from a Single Salt Using a Hollow Fiber PES Membrane. Membranes 2020, 10, 136. [Google Scholar] [CrossRef]
- Kim, S.; Hoek, E.M. Modeling concentration polarization in reverse osmosis processes. Desalination 2005, 186, 111–128. [Google Scholar] [CrossRef]
- Hassan, A.R.; Abdull, N.; Ismail, A.F. A Theoretical Approach on Membrane Characterization: The Deduction of Fine Structural Details of Asymmetric Nanofiltration Membranes. Desalination 2007, 206, 107–126. [Google Scholar] [CrossRef]
- Song, L. Thermodynamic modeling of solute transport through reverse osmosis membrane. Chem. Eng. Commun. 2000, 180, 145–167. [Google Scholar] [CrossRef]
- Safiddine, L.; Zafour, H.-Z.; Rao, U.M.; Fofana, I. Regeneration of Transformer Insulating Fluids Using Membrane Separation Technology. Energies 2019, 12, 368. [Google Scholar] [CrossRef]
- Renard, P.; de Marsily, G. Calculating equivalent permeability: A review. Adv. Water Resour. 1997, 20, 253–278. [Google Scholar] [CrossRef]
- Tanganov, B. About sizes of the hydrated salt ions—The components of sea water. Eur. J. Nat. Hist. 2013, 1, 36–37. [Google Scholar]
- Laliberté, M.; Cooper, W.E. Model for Calculating the Density of Aqueous Electrolyte Solutions. J. Chem. Amp Eng. Data 2004, 49, 1141–1151. [Google Scholar] [CrossRef]
- Zhang, H.-L.; Han, S.-J. Viscosity and Density of Water Sodium Chloride Potassium Chloride Solutions at 298.15 K. J. Chem. Amp Eng. Data 1996, 41, 516–520. [Google Scholar] [CrossRef]
- Hawthorne, S.B.; Jin, L.; Kurz, B.A.; Miller, D.J.; Grabanski, C.B.; Sorensen, J.A.; Pekot, L.J.; Bosshart, N.W.; Smith, S.A.; Burton-Kelly, M.E.; et al. Integrating Petrographic and Petrophysical Analyses with CO2 Permeation and Oil Extraction and Recovery in the Bakken Tight Oil Formation. In Proceedings of the SPE Unconventional Resources Conference, Calgary, AB, Canada, 16 February 2017. [Google Scholar] [CrossRef]
- Karimi, S.; Kazemi, H. Characterizing Pores and Pore-Scale Flow Properties in Middle Bakken Cores. SPE J. 2017, 23, 1343–1358. [Google Scholar] [CrossRef]
- Ramiro-Ramirez, S.; Flemings, P.B.; Bhandari, A.R.; Jimba, O.S. Steady-State Liquid Permeability Measurements in Samples from the Bakken Formation, Williston Basin, USA. In Proceedings of the SPE Annual Technical Conference and Exhibition, Dubai, UAE, 22 September 2021. [Google Scholar] [CrossRef]
- Karsanina, M.V.; Volkov, V.V.; Konarev, P.V.; Belokhin, V.S.; Bayuk, I.O.; Korost, D.V.; Gerke, K.M. Rapid Rock Nanoporosity Analysis Using Small Angle Scattering Fused with Imaging Data Based on Stochastic Reconstructions. In Proceedings of the SPE Russian Petroleum Technology Conference, Moscow, Russia, 22 October 2019. [Google Scholar] [CrossRef]
- Cho, Y.; Eker, E.; Uzun, I.; Yin, X.; Kazemi, H. Rock Characterization in Unconventional Reservoirs: A Comparative Study of Bakken, Eagle Ford, and Niobrara Formations. In SPE Low Perm Symposium; OnePetro: Richardson, TX, USA, 2016. [Google Scholar] [CrossRef]
- Yan, L.; Aslannejad, H.; Hassanizadeh, S.M.; Raoof, A. Impact of water salinity differential on a crude oil droplet constrained in a capillary: Pore-scale mechanisms. Fuel 2020, 274, 117798. [Google Scholar] [CrossRef]
- Yin, Y.; Qu, Z.; Prodanović, M.; Landry, C.J. Identifying the dominant transport mechanism in single nanoscale pores and 3D nanoporous media. Fundam. Res. 2022. [Google Scholar] [CrossRef]


| Boundary | Condition | Parameter |
|---|---|---|
| Inlet | Velocity | |
| Inlet | Bulk concentration | |
| Outlet | Pressure | |
| Channel wall | No-flow, No-slip |
| Parameter | Unit | Zone A | Zone B | Zone C |
|---|---|---|---|---|
| Permeability | ||||
| Width | 5 | 5 | 5 | |
| Length | 50 | 5 | 50 | |
| Fluid viscosity | 0.001 | 0.001 | 0.001 | |
| Fluid density | 1000 | 1000 | 1000 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dorhjie, D.B.; Yusupov, R.; Krutko, V.; Cheremisin, A. Deviation from Darcy Law in Porous Media Due to Reverse Osmosis: Pore-Scale Approach. Energies 2022, 15, 6656. https://doi.org/10.3390/en15186656
Dorhjie DB, Yusupov R, Krutko V, Cheremisin A. Deviation from Darcy Law in Porous Media Due to Reverse Osmosis: Pore-Scale Approach. Energies. 2022; 15(18):6656. https://doi.org/10.3390/en15186656
Chicago/Turabian StyleDorhjie, Desmond Batsa, Roman Yusupov, Vladislav Krutko, and Alexey Cheremisin. 2022. "Deviation from Darcy Law in Porous Media Due to Reverse Osmosis: Pore-Scale Approach" Energies 15, no. 18: 6656. https://doi.org/10.3390/en15186656







