Optimization Design of the Organic Rankine Cycle for an Ocean Thermal Energy Conversion System
Abstract
1. Introduction
2. Model and Method
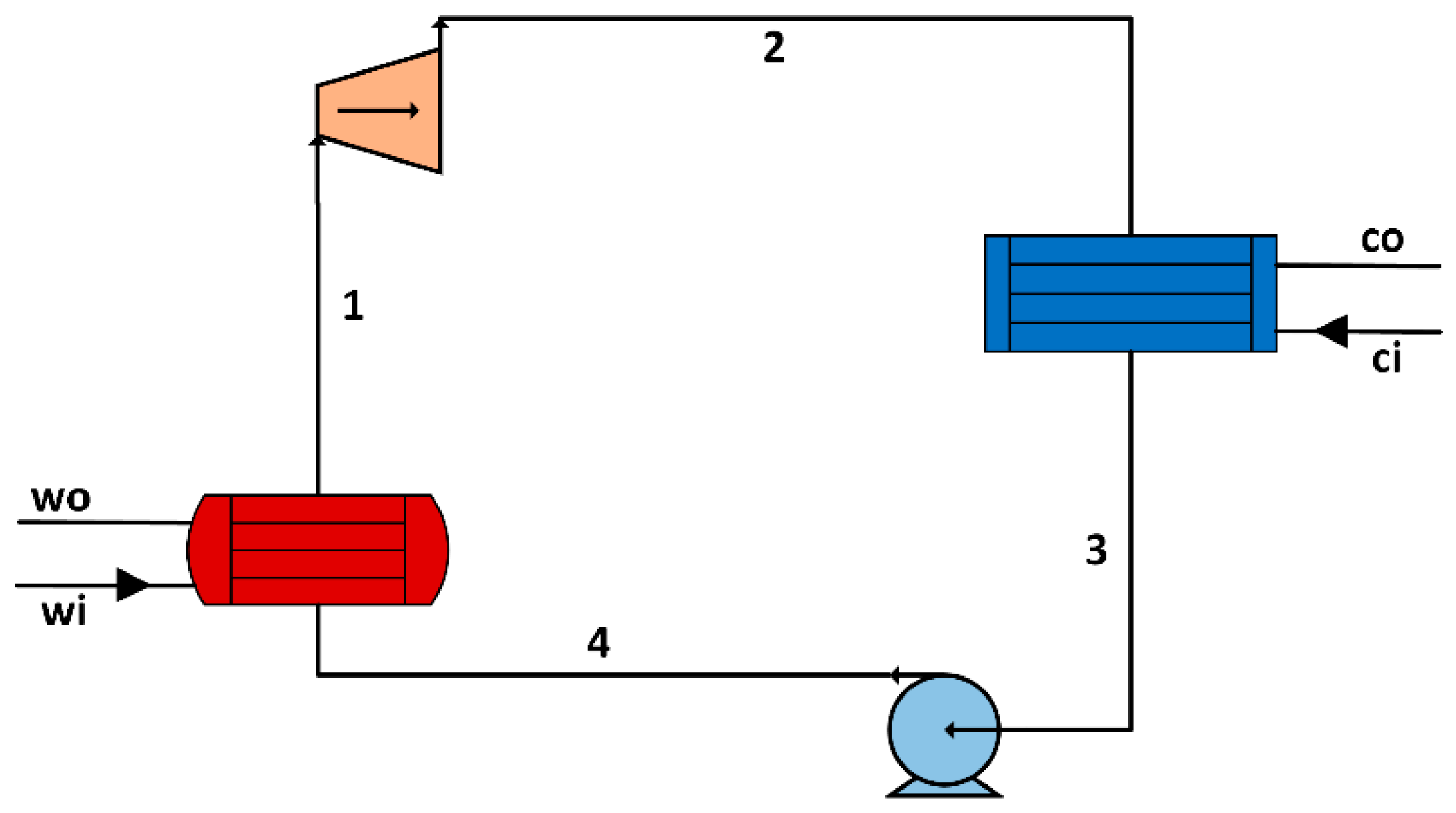
2.1. System Description
2.2. Mathematical Model
2.2.1. Power Calculation
- (1)
- The turbine output electric power
- (2)
- The electric power consumption of the working fluid pump
- (3)
- The electric power consumption of the seawater pump
- (4)
- The net output power of the OTEC plant
2.2.2. Heat Transfer Area Calculation
- (1)
- Heat transfer area of the evaporator
- (2)
- Heat transfer area of the condenser
2.2.3. Method
- (1)
- the objective functions
- (2)
- The constraints on the decision variable range
- (3)
- the evaluation indexes
3. Results
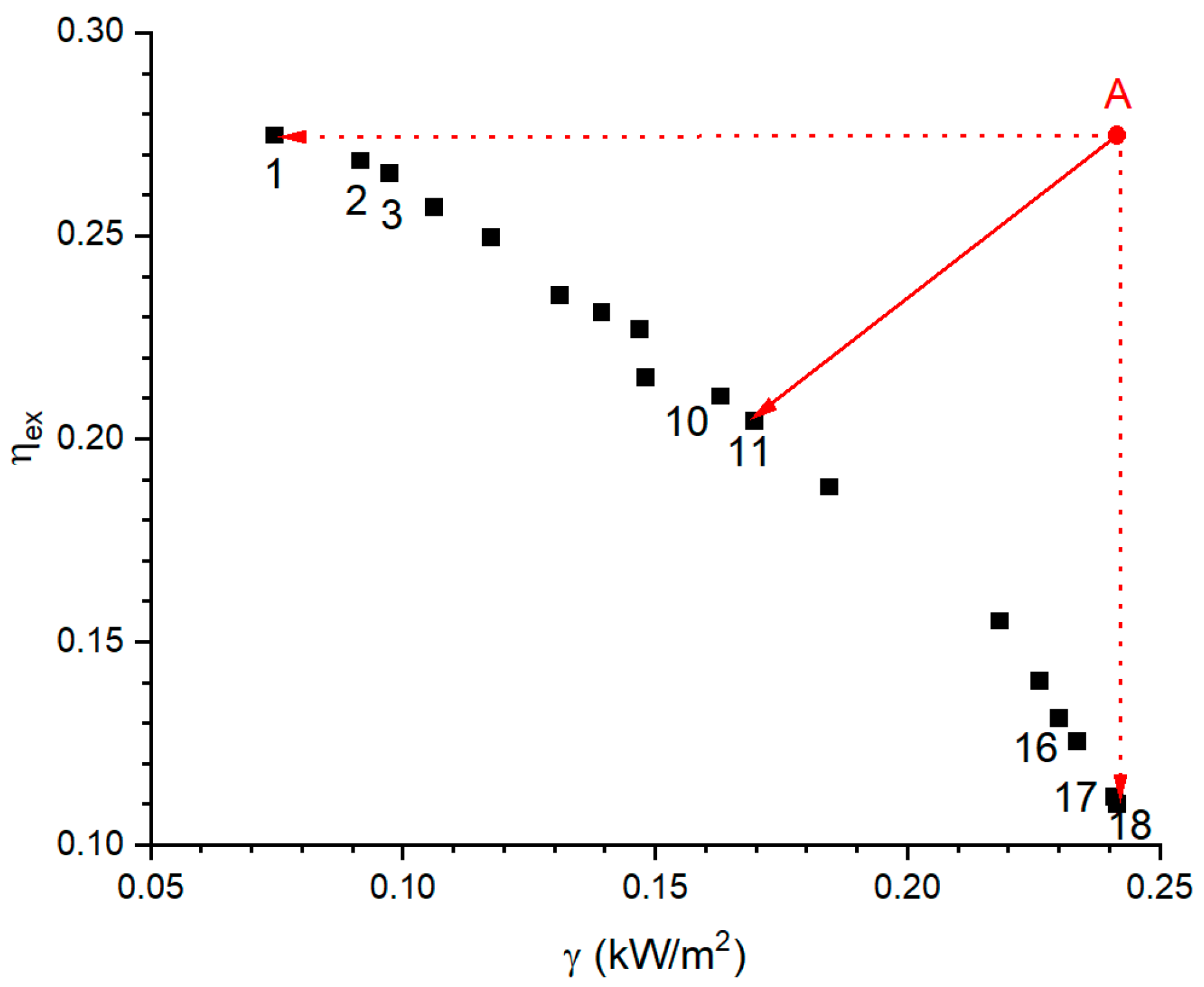
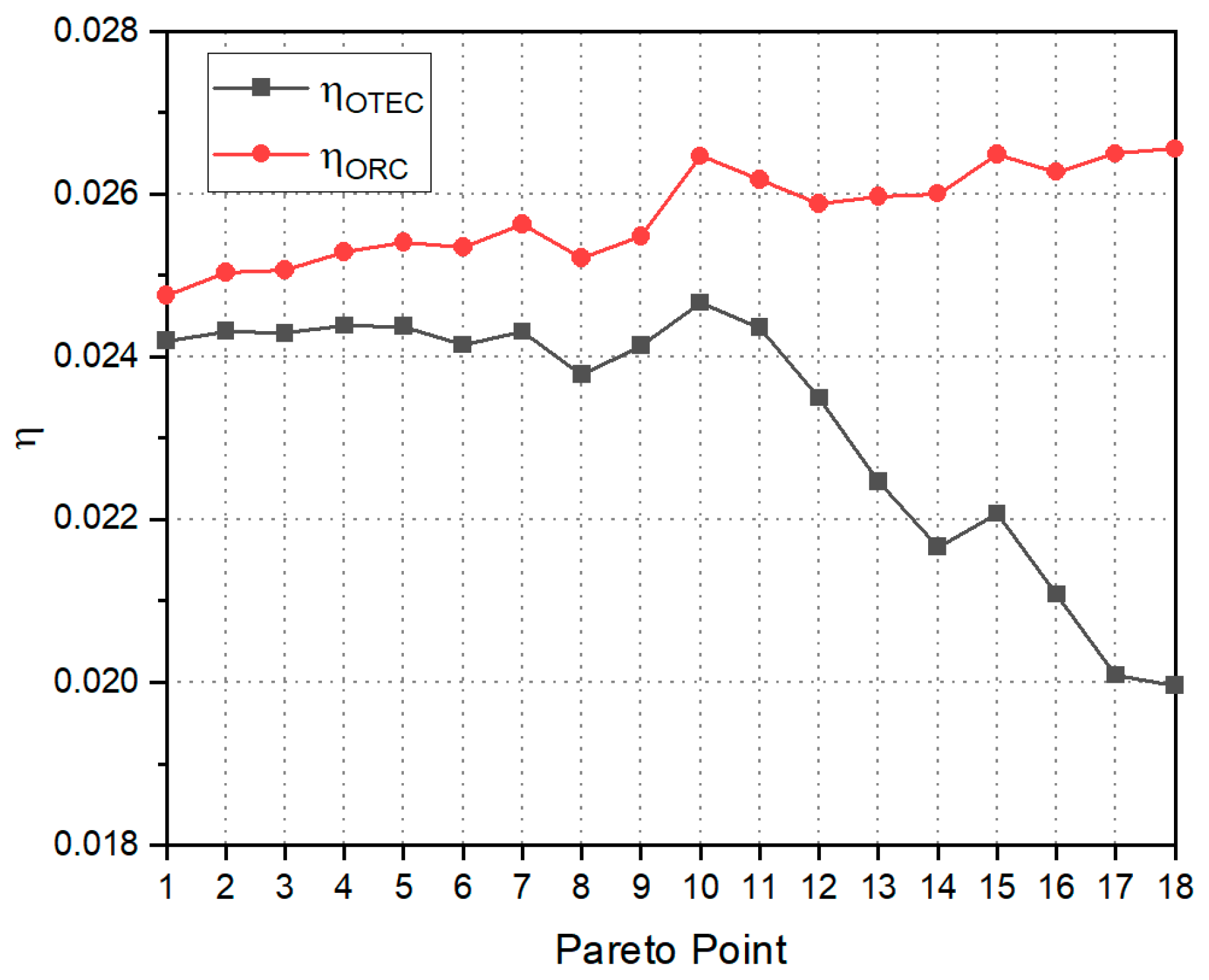
3.1. The Optimization Design Results
3.2. The Effects of Decision Parameters on the Performance of the OTEC
- The effects of evaporating temperature and condensing temperature
- The effect of the pinch-point temperature difference
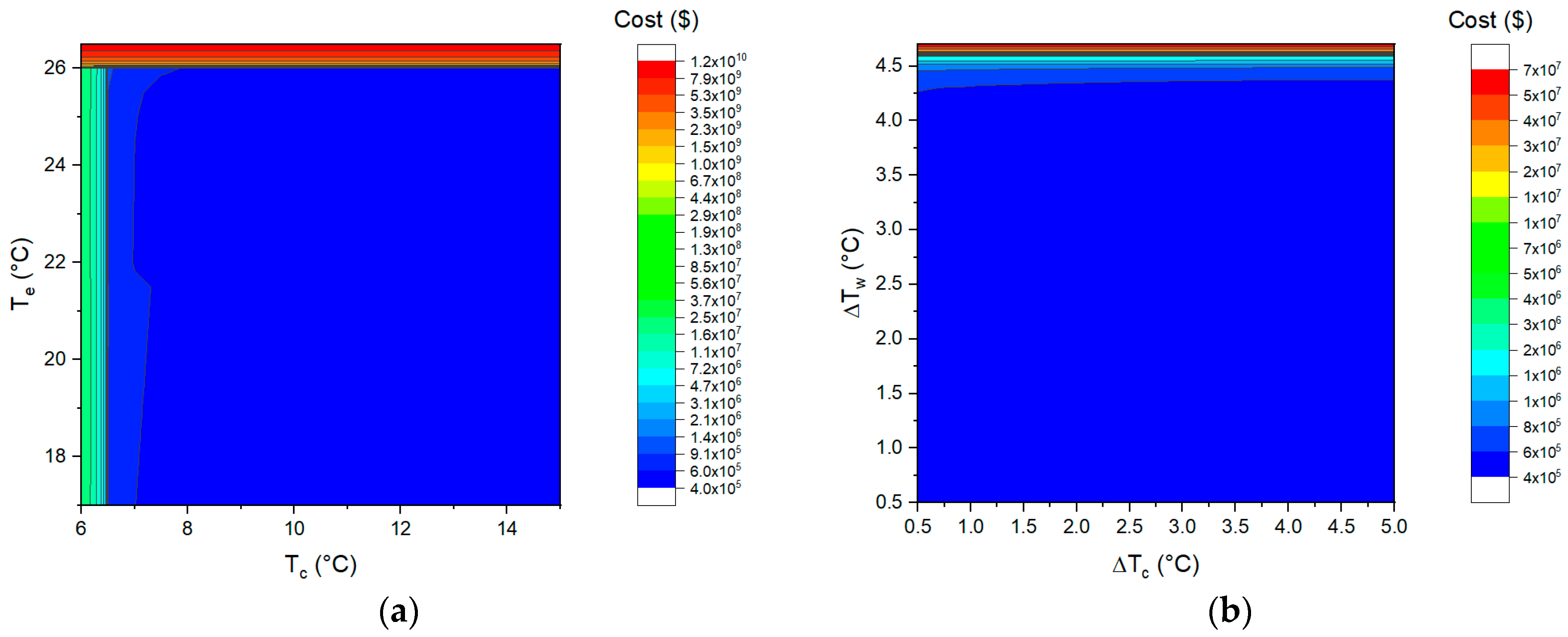
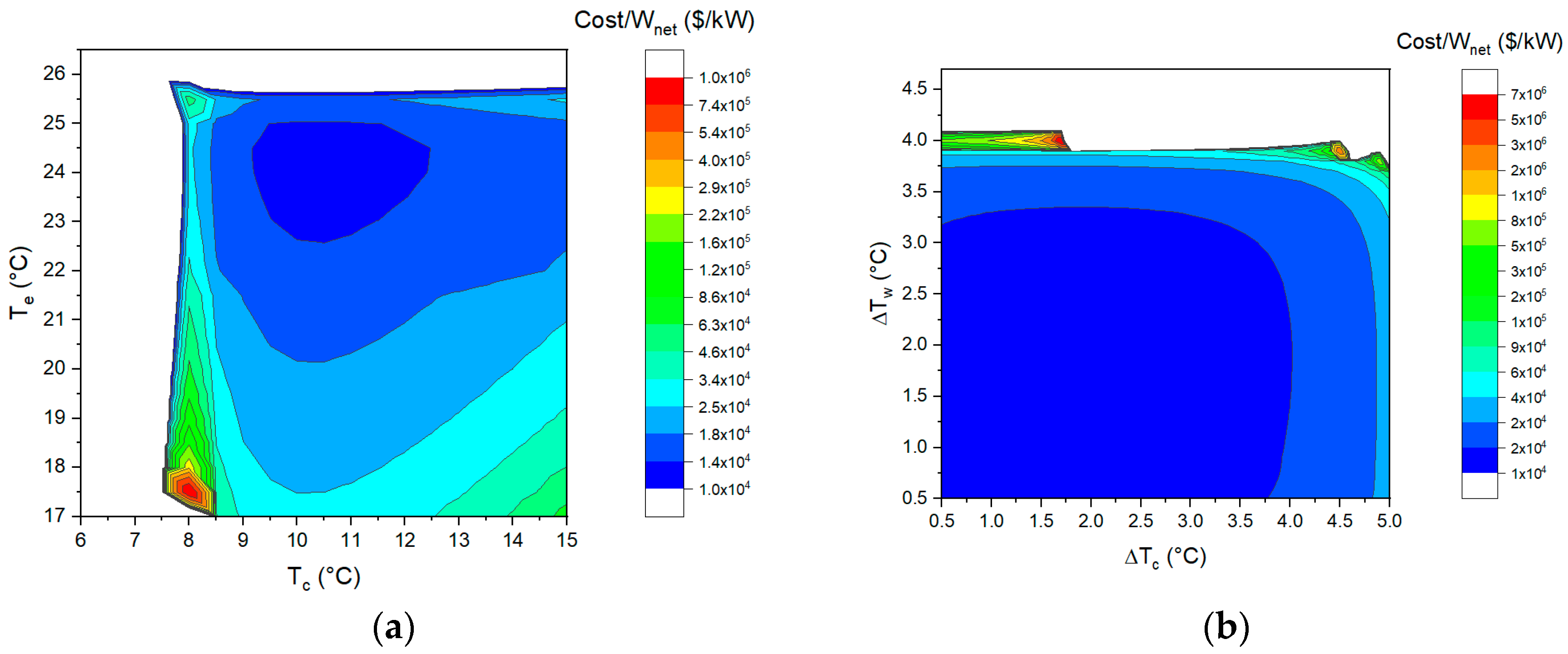
- The effect of the four decision parameters on the investment cost
4. Conclusions
- (1)
- The exergy efficiency, the net output power per unit area, the net thermal efficiency, and the net output power increase first and then decrease with the increase in evaporating temperature or condensing temperature.
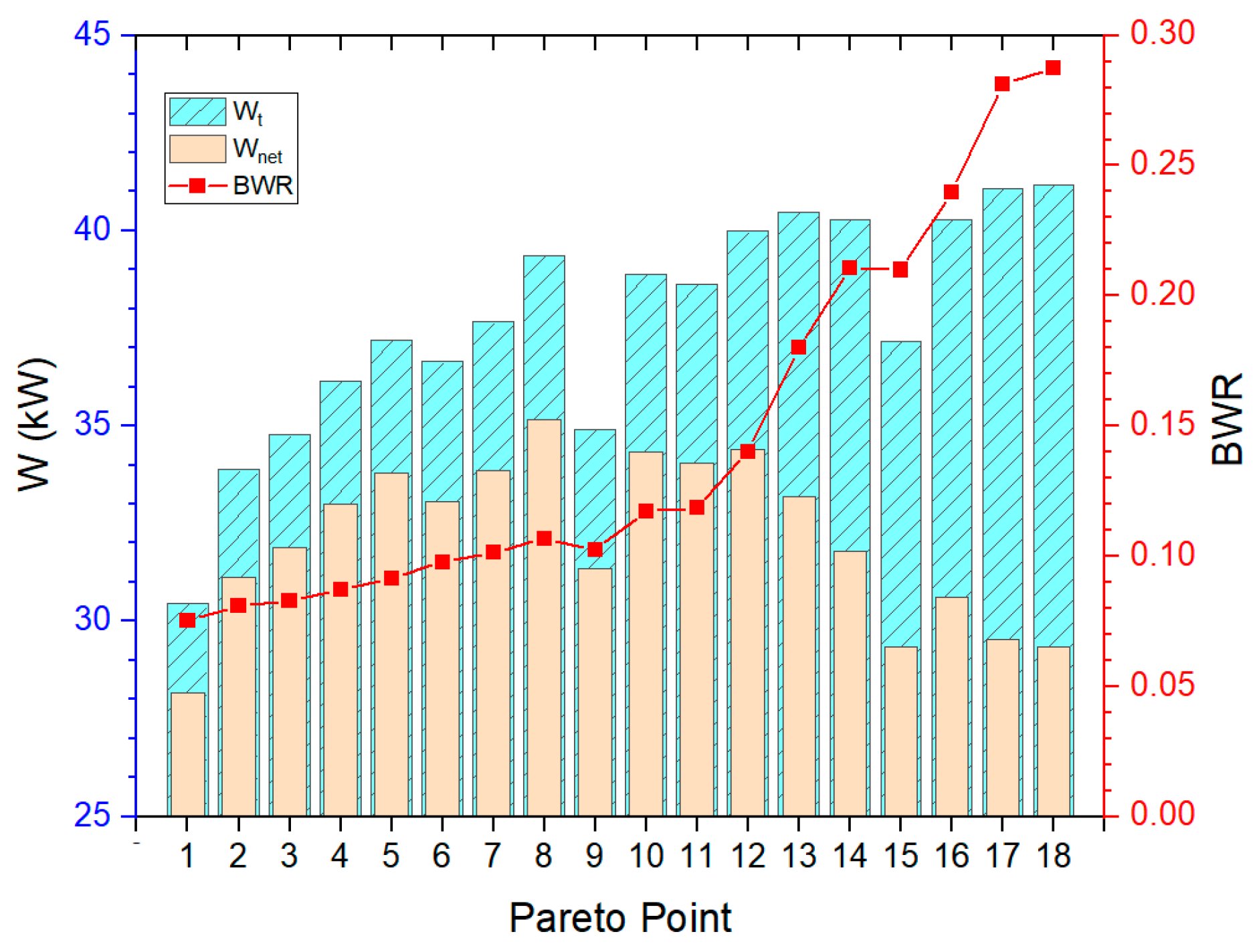
- (2)
- The back work ratio (BWR) is seriously affected by the condensing temperature. Increasing the condensing temperature can decrease the BWR value; however, the net output power is not necessarily large when the BWR is small.
- (3)
- The parameters directly related to the pinch-point temperature difference are, mainly, the flow rate of the seawater, the area of the heat exchanger, and the seawater pump power consumption. A small pinch-point temperature difference is beneficial for the performance parameters (the exergy efficiency, the thermal efficiency of the OTEC, the net output power, the net output power per unit seawater flow rate, and the back work ratio).
- (4)
- The investment cost is not very sensitive to the pinch-point temperature difference and evaporating temperature and condensing temperature over wide ranges. The effects of evaporating temperature and condensing temperature on the investment cost per unit net output power are roughly similar to those on the net output power per unit heat exchange area. However, the change in the investment cost per unit net output power with the pinch-point temperature difference is mainly determined by the change trend of the net output power.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
| Pareto Point | BWR | WPSF | Cost | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| kg/s | °C | °C | °C | °C | kW/m2 | % | % | % | % | kJ/kg | kW | kg/s | × 105 USD | |
| 1 | 5.993 | 23.46 | 12.50 | 0.53 | 0.51 | 0.075 | 27.47 | 2.420 | 2.476 | 7.529 | 0.288 | 28.17 | 33.74 | 4.909 |
| 2 | 6.585 | 23.43 | 12.34 | 0.69 | 0.56 | 0.092 | 26.84 | 2.432 | 2.504 | 8.093 | 0.281 | 31.14 | 38.09 | 4.926 |
| 3 | 6.748 | 23.37 | 12.27 | 0.80 | 0.57 | 0.097 | 26.54 | 2.429 | 2.507 | 8.287 | 0.278 | 31.89 | 39.43 | 4.927 |
| 4 | 6.950 | 23.23 | 12.03 | 1.09 | 0.59 | 0.106 | 25.70 | 2.438 | 2.529 | 8.716 | 0.268 | 33.01 | 42.01 | 4.928 |
| 5 | 7.112 | 23.21 | 11.96 | 1.21 | 0.75 | 0.117 | 24.95 | 2.438 | 2.541 | 9.151 | 0.261 | 33.79 | 44.42 | 4.877 |
| 6 | 7.027 | 23.20 | 11.98 | 1.06 | 1.42 | 0.131 | 23.53 | 2.415 | 2.534 | 9.780 | 0.257 | 33.06 | 48.17 | 4.681 |
| 7 | 7.134 | 23.03 | 11.69 | 1.36 | 1.25 | 0.139 | 23.12 | 2.431 | 2.563 | 10.132 | 0.251 | 33.85 | 49.96 | 4.708 |
| 8 | 7.586 | 23.02 | 11.86 | 1.50 | 1.28 | 0.147 | 22.69 | 2.378 | 2.522 | 10.671 | 0.242 | 35.17 | 51.91 | 4.766 |
| 9 | 6.651 | 22.88 | 11.61 | 2.09 | 1.24 | 0.148 | 21.50 | 2.414 | 2.548 | 10.250 | 0.222 | 31.34 | 47.10 | 4.495 |
| 10 | 7.117 | 23.24 | 11.50 | 1.48 | 1.78 | 0.163 | 21.04 | 2.467 | 2.647 | 11.713 | 0.230 | 34.33 | 56.13 | 4.614 |
| 11 | 7.157 | 23.38 | 11.77 | 1.86 | 1.66 | 0.170 | 20.44 | 2.436 | 2.617 | 11.868 | 0.207 | 34.04 | 52.80 | 4.579 |
| 12 | 7.497 | 23.13 | 11.67 | 1.71 | 2.35 | 0.185 | 18.82 | 2.349 | 2.588 | 14.002 | 0.208 | 34.39 | 63.49 | 4.560 |
| 13 | 7.562 | 23.09 | 11.60 | 2.69 | 2.51 | 0.218 | 15.51 | 2.247 | 2.596 | 18.016 | 0.156 | 33.19 | 67.02 | 4.473 |
| 14 | 7.510 | 22.93 | 11.43 | 2.56 | 3.09 | 0.226 | 14.03 | 2.166 | 2.600 | 21.053 | 0.154 | 31.80 | 78.06 | 4.411 |
| 15 | 6.791 | 22.86 | 11.14 | 3.27 | 2.71 | 0.230 | 13.11 | 2.207 | 2.649 | 21.001 | 0.130 | 29.36 | 69.26 | 4.247 |
| 16 | 7.432 | 23.23 | 11.58 | 2.98 | 3.00 | 0.234 | 12.56 | 2.108 | 2.627 | 23.979 | 0.122 | 30.62 | 73.12 | 4.394 |
| 17 | 7.503 | 22.84 | 11.11 | 3.32 | 3.08 | 0.241 | 11.18 | 2.009 | 2.650 | 28.117 | 0.114 | 29.53 | 84.02 | 4.408 |
| 18 | 7.503 | 22.84 | 11.09 | 3.30 | 3.14 | 0.242 | 11.01 | 1.996 | 2.656 | 28.741 | 0.113 | 29.34 | 85.94 | 4.408 |
References
- Zhang, J.; Tang, Z.; Qian, F. A review of recent advances and key technologies in ocean thermal energy conversion. J. Hohai Univ. 2019, 47, 55–64. [Google Scholar]
- Wang, C.; Lu, W. Analysis Method and Reserve Assessment of Ocean Energy Resources; Ocean Press: Beijing, China, 2009; p. 171. [Google Scholar]
- Vera, D.; Baccioli, A.; Jurado, F.; Desideri, U. Modeling and optimization of an ocean thermal energy conversion system for remote islands electrification. Renew. Energy 2020, 162, 1399–1414. [Google Scholar] [CrossRef]
- Shen, W. Analysis of Thermodynamic Cycle in Ocean Thermal Energy Conversion (OTEC) System; China University of Petroleum (East China): Qingdao, China, 2012. [Google Scholar]
- Kalina, A.I. Generation of Energy by Means of a Working Fluid, and Regeneration of a Working Fluid. U.S. Patent US04346561A, 31 August 1982. [Google Scholar]
- Uehara, H.; Ikegami, Y.; Fukugawa, H.; Uto, M. Performance Analysis of OTEC System Using Kalina Cycle. Thermodynamic Characteristics of Cycle. Trans. Jpn. Soc. Mech. Eng. Part B 1994, 60, 3519–3525. [Google Scholar] [CrossRef]
- Uehara, H.; Ikegami, Y.; Nishida, T. Performance Analysis of OTEC System Using a Cycle with Absorption and Extraction Processes. Trans. Jpn. Soc. Mech. Eng. Ser. B 1998, 64, 2750–2755. [Google Scholar] [CrossRef]
- Satoru, G.; Yoshiki, M.; Takenao, S.; Takeshi, Y.; Yasuyuki, I.; Masatoshi, N. Construction of simulation model for OTEC plant using Uehara cycle. Electr. Eng. Jpn. 2011, 176, 1–13. [Google Scholar]
- Liu, W.M.; Chen, F.Y.; Wang, Y.Q.; Jiang, W.J. Progress of Closed-Cycle OTEC and Study of a New Cycle of OTEC. Adv. Mater. Res. 2012, 354–355, 275–278. [Google Scholar] [CrossRef]
- White, H.J. Mini-OTEC. Int. J. Ambient. Energy 1980, 1, 75–88. [Google Scholar] [CrossRef]
- Negara, R.B.; Koto, J. Potential of 100 kW of Ocean Thermal Energy Conversion in Karangkelong, Sulawesi Utara, Indonesia. Int. J. Environ. Res. Clean Energy 2017, 5, 1–10. [Google Scholar]
- Yang, M.H.; Yeh, R.H. Analysis of optimization in an OTEC plant using organic Rankine cycle. Renew. Energy 2014, 68, 25–34. [Google Scholar] [CrossRef]
- Uehara, H.; Ikegami, Y. Optimization of a Closed-Cycle OTEC System. Trans Asme J. Sol. Energy Eng. 1990, 112, 247–256. [Google Scholar] [CrossRef]
- Bernardoni, C.; Binotti, M.; Giostri, A. Techno-economic analysis of closed OTEC cycles for power generation. Renew. Energy 2018, 132, 1018–1033. [Google Scholar] [CrossRef]
- Najafi, A.; Rezaee, S.; Torabi, F. Multi-objective optimization of ocean thermal energy conversion power plant via genetic algorithm. In Proceedings of the 2011 IEEE Electrical Power and Energy Conference, Winnipeg, MB, Canada, 3–5 October 2011. [Google Scholar]
- Zhang, S.R.; Sun, Y.S.; Wang, M.T.; Jang, L.X.; Liu, Q.Y. Multi-objective function optimization study on ocean thermal energy organic rankine cycle systems. Renew. Energy Resour. 2017, 35, 621–626. [Google Scholar]
- Wang, M.; Zhao, Y.; Zhang, H.; Wang, B. Multi-objective Optimization of OTEC Rankine Cycle based on PSO Algorithm. Chin. J. Sol. Energy 2019, 40, 2716–2724. [Google Scholar]
- Hettiarachchi, H.; Golubovic, M.; Worek, W.M. Optimum design criteria for an Organic Rankine cycle using low-temperature geothermal heat sources. Energy 2007, 32, 1698–1706. [Google Scholar] [CrossRef]
- Wang, J.; Yan, Z.; Man, W. Multi-objective optimization of an organic Rankine cycle (ORC) for low grade waste heat recovery using evolutionary algorithm. Energy Convers. Manag. 2013, 71, 146–158. [Google Scholar] [CrossRef]
- Ahmadi, P.; Dincer, I.; Rosen, M.A. Thermoeconomic multi-objective optimization of a novel biomass-based integrated energy system. Energy 2014, 68, 958–970. [Google Scholar] [CrossRef]
- Jiang, L.; Zhu, Y.D.; Jin, V.; Yu, L.J. Comprehensive Evaluation Method of ORC System Performance Based on the Multi-Objective Optimization. Adv. Mater. Res. 2014, 997, 721–727. [Google Scholar] [CrossRef]
- Sun, F.; Ikegami, Y.; Jia, B.; Arima, H. Optimization design and exergy analysis of organic rankine cycle in ocean thermal energy conversion. Appl. Ocean. Res. 2012, 35, 38–46. [Google Scholar] [CrossRef]
- Song, Z.; Ye, L.; Yang, B.; Yisen, Z.; Qingwei, Z.; Xiaoyong, W.; Min, D.; Jie, M.; Hao, X. An assessment of ocean thermal energy conversion resources in the South China Sea. In Proceedings of the OCEANS 2016–Shanghai, Shanghai, China, 10–13 April 2016. [Google Scholar]
- Jitsuhara, S.; Ikegami, Y.; Uehara, H. Optimization of Design Conditions for OTEC. In the Case of Annual Operation Performance. Trans. Jpn. Soc. Mech. Eng. Part B 1994, 60, 641–648. [Google Scholar] [CrossRef][Green Version]
- Giostri, A.; Romei, A.; Binotti, M. Off-design performance of closed OTEC cycles for power generation. Renew. Energy 2021, 170, 1353–1366. [Google Scholar] [CrossRef]
- Gorgy, E.; Eckels, S. Convective boiling of R-134a on enhanced-tube bundles. Int. J. Refrig. 2016, 68, 145–160. [Google Scholar] [CrossRef]
- Thome, J.R. Engineering Data Book III; Wolverine Tube Inc.: Decatur, AL, USA, 2004; Volume 5, pp. 17–25. [Google Scholar]
- Kedzierski, M.A.; Carr, M.A.; Brown, J.S. Measurement and Prediction of Vapor-Space Condensation of Refrigerants on Trapezoidal-Finned and Turbo-C Geometries. J. Enhanc. Heat Transf. 2013, 20, 59–71. [Google Scholar] [CrossRef]
- Tong, J.; Zhao, Z. Thermal Engineering Foundation; Higher Education Press: Beijing, China, 2009; p. 246. [Google Scholar]
- Huber, J.B. Shell-Side Condensation of HFC-134a and HCFC-123 on Enhanced-Tube Bundles; Iowa State University: Ames, IA, USA, 1994. [Google Scholar]
- Available online: https://ww2.mathworks.cn/help/gads/gamultiobj-algorithm.html (accessed on 25 August 2022).
- Turton, R. Analysis, Synthesis and Design of Chemical Processes; (Appendix A); Prentice Hall International: Hoboken, NJ, USA, 2008. [Google Scholar]
- Borugadda, V.B.; Kamath, G.; Dalai, A.K. Techno-economic and life-cycle assessment of integrated Fischer-Tropsch process in ethanol industry for bio-diesel and bio-gasoline production. Energy 2020, 195, 116985.1–116985.6. [Google Scholar] [CrossRef]







| Parameters | Symbol | Value |
|---|---|---|
| Deep seawater temperature | 4 °C | |
| Surface seawater temperature | 28 °C | |
| Diameter of seawater pipe | 0.35 m | |
| Length of deep seawater pipe | 3000 m | |
| Length of surface seawater pipe | 200 m | |
| Design isentropic efficiency of turbine | 0.8 | |
| Design efficiency of generator | 0.9 | |
| Design efficiency of working fluid pump | 0.6 | |
| Design efficiency of seawater pump | 0.8 | |
| Type of heat transfer pipe in evaporator | Turbo BII | |
| Number of heat transfer pipes in evaporator | 478 | |
| Type of heat transfer pipe in condenser | Turbo CII | |
| Number of heat transfer pipes in condenser | 478 | |
| Working fluid | R134a |
| Point | Pressure (kPa) | Temperature (°C) | Enthalpy (kJ/kg) | Entropy (kJ/kg K) | Phase |
|---|---|---|---|---|---|
| 1 | 631.09 | 23.24 | 411.43 | 1.7169 | Saturated vapor |
| 2 | 435.78 | 11.73 | 405.37 | 1.7222 | Superheated, 0.23 °C |
| 3 | 435.78 | 11.50 | 215.64 | 1.0557 | Saturated liquid |
| 4 | 631.09 | 11.67 | 215.91 | 1.0561 | Subcooled, 11.57 °C |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, X.; Liu, Y.; Chen, Y.; Zhang, L. Optimization Design of the Organic Rankine Cycle for an Ocean Thermal Energy Conversion System. Energies 2022, 15, 6683. https://doi.org/10.3390/en15186683
Yang X, Liu Y, Chen Y, Zhang L. Optimization Design of the Organic Rankine Cycle for an Ocean Thermal Energy Conversion System. Energies. 2022; 15(18):6683. https://doi.org/10.3390/en15186683
Chicago/Turabian StyleYang, Xiaowei, Yanjun Liu, Yun Chen, and Li Zhang. 2022. "Optimization Design of the Organic Rankine Cycle for an Ocean Thermal Energy Conversion System" Energies 15, no. 18: 6683. https://doi.org/10.3390/en15186683
APA StyleYang, X., Liu, Y., Chen, Y., & Zhang, L. (2022). Optimization Design of the Organic Rankine Cycle for an Ocean Thermal Energy Conversion System. Energies, 15(18), 6683. https://doi.org/10.3390/en15186683






