Influencing Factors of Shear Wave Radiation of a Dipole Source in a Fluid-Filled Borehole
Abstract
:1. Introduction
2. Theory and Methods
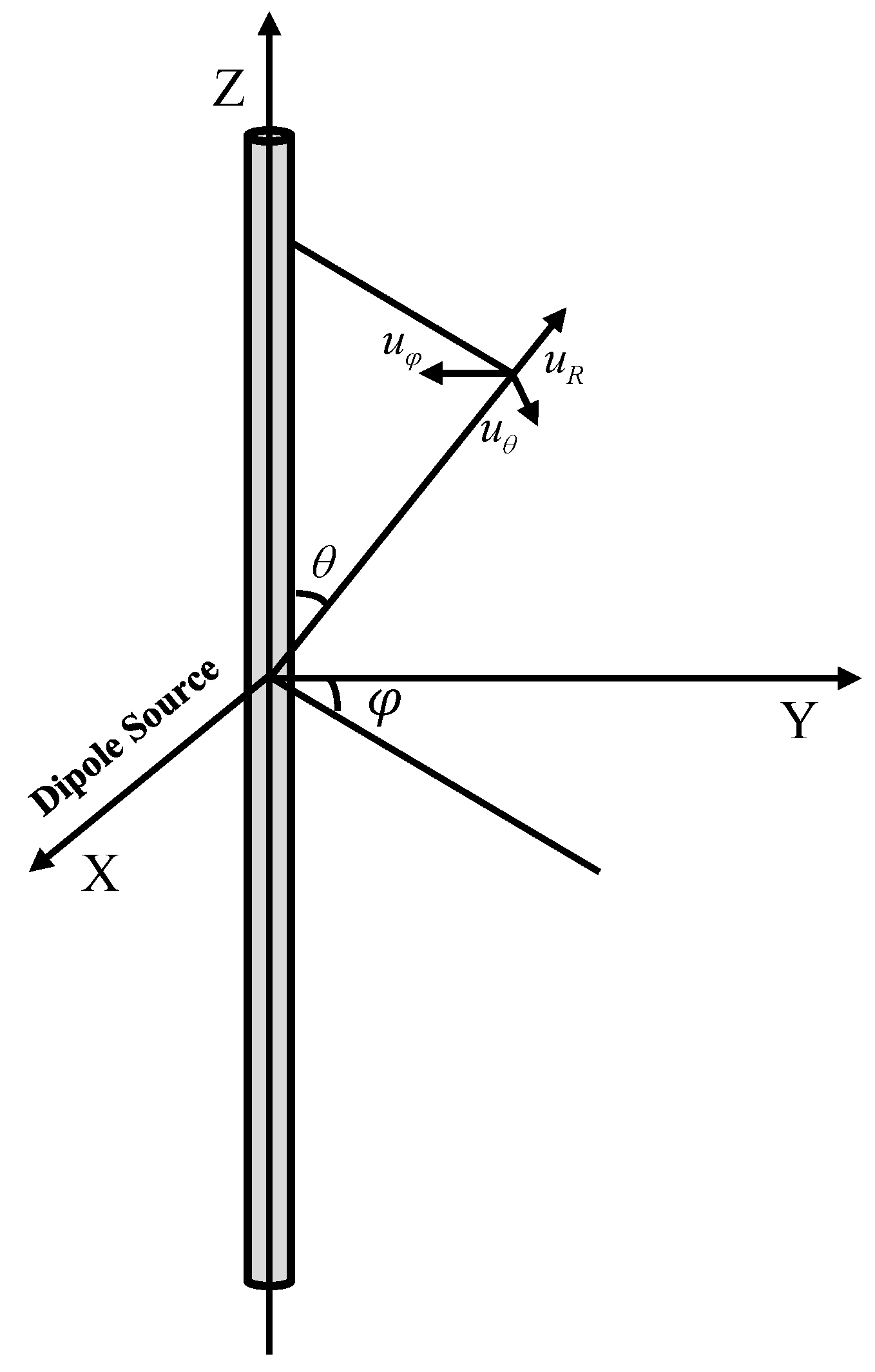
2.1. Theory of Dipole-Source Radiation in a Fluid-Filled Borehole
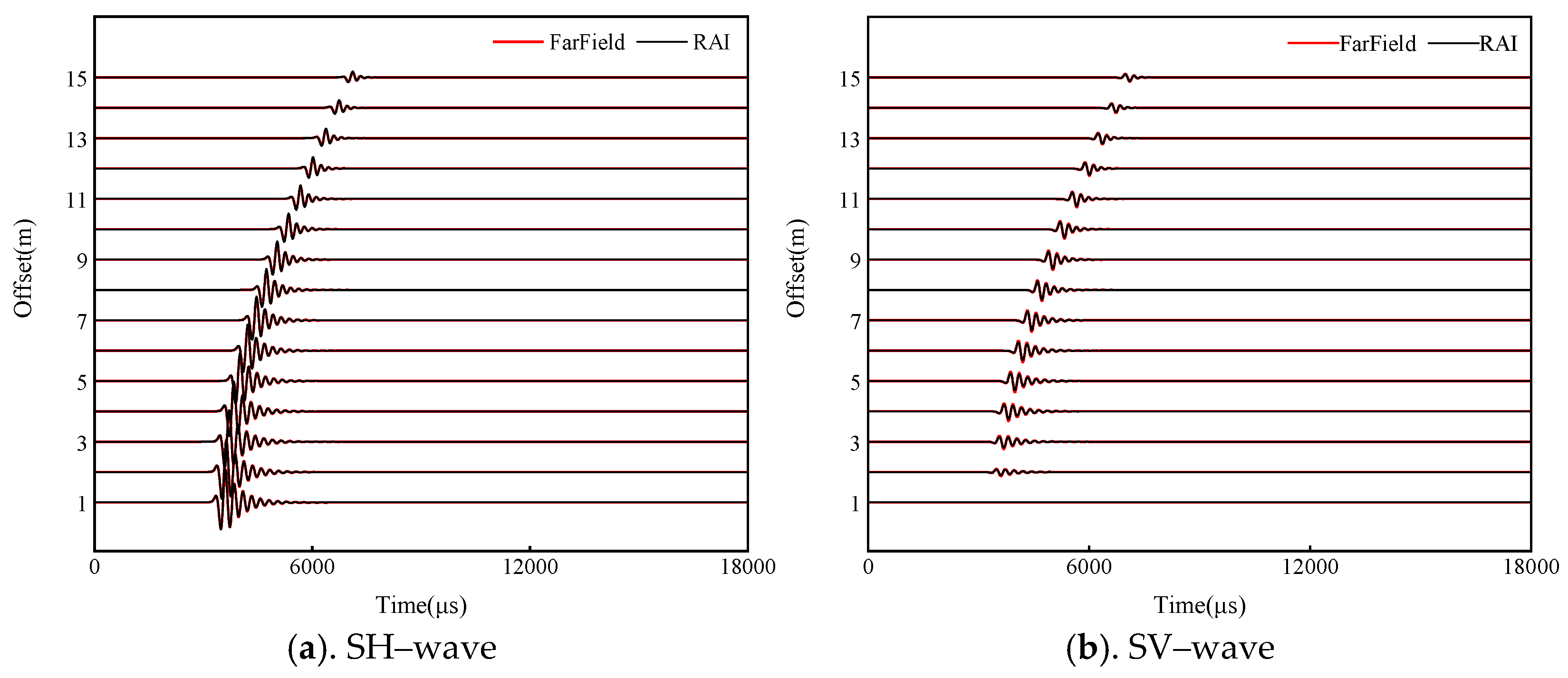
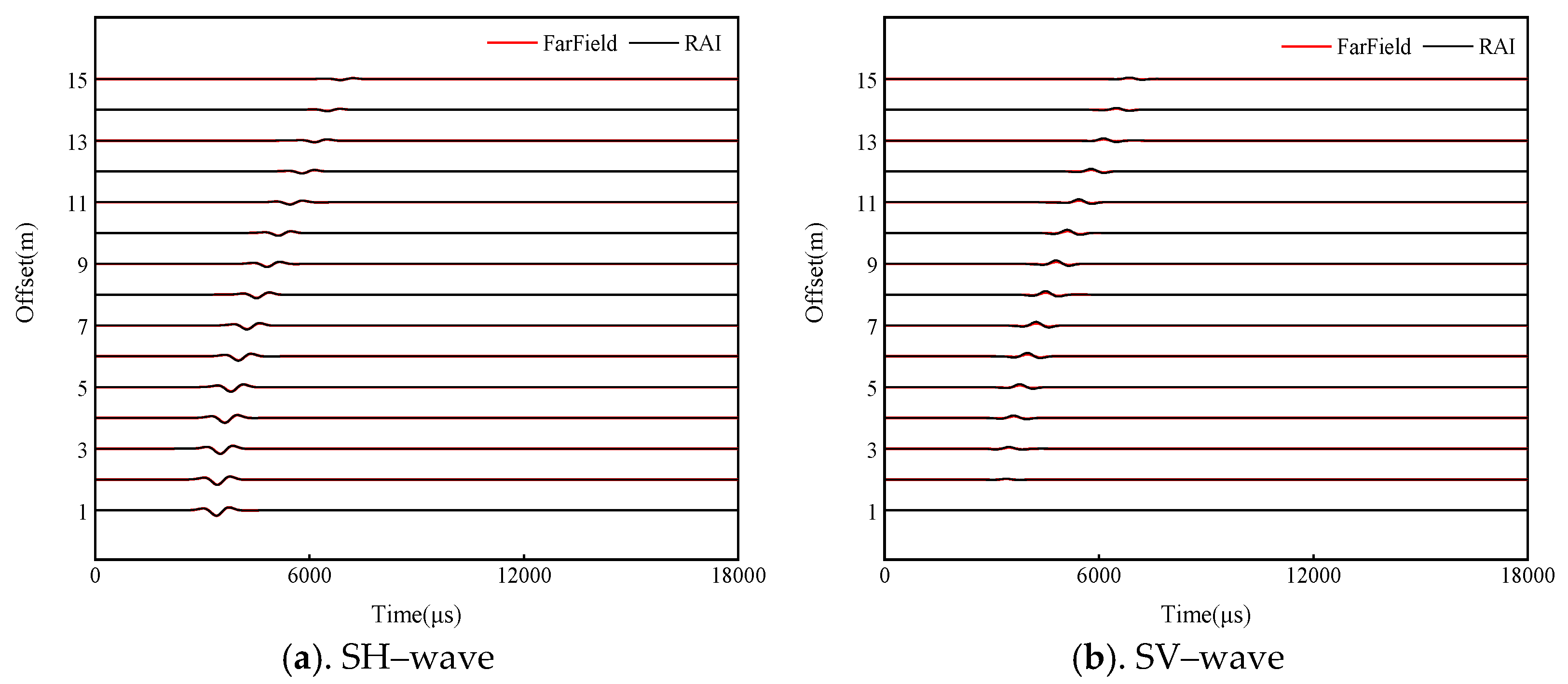
2.2. Verification of the Far-Field Asymptotic Solution
3. Results Analysis of Numerical Simulation
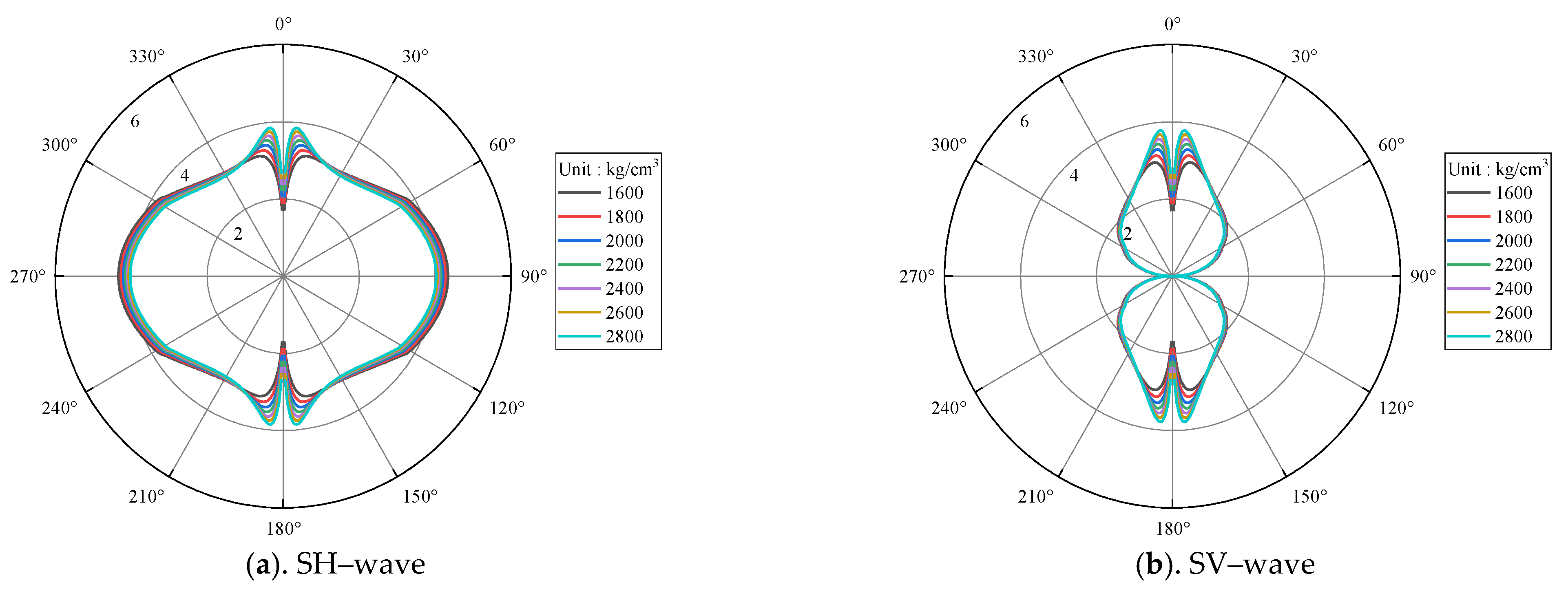
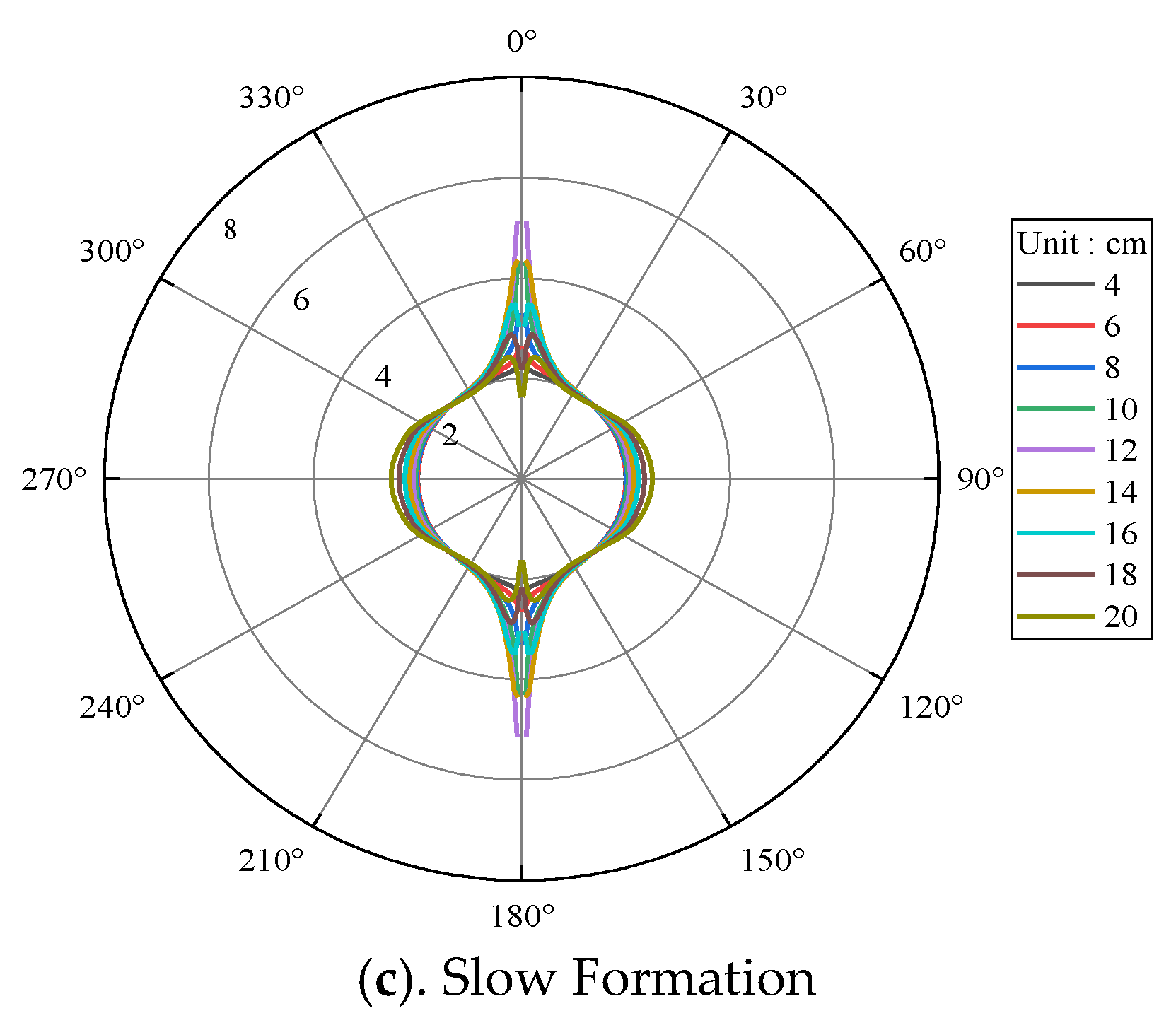
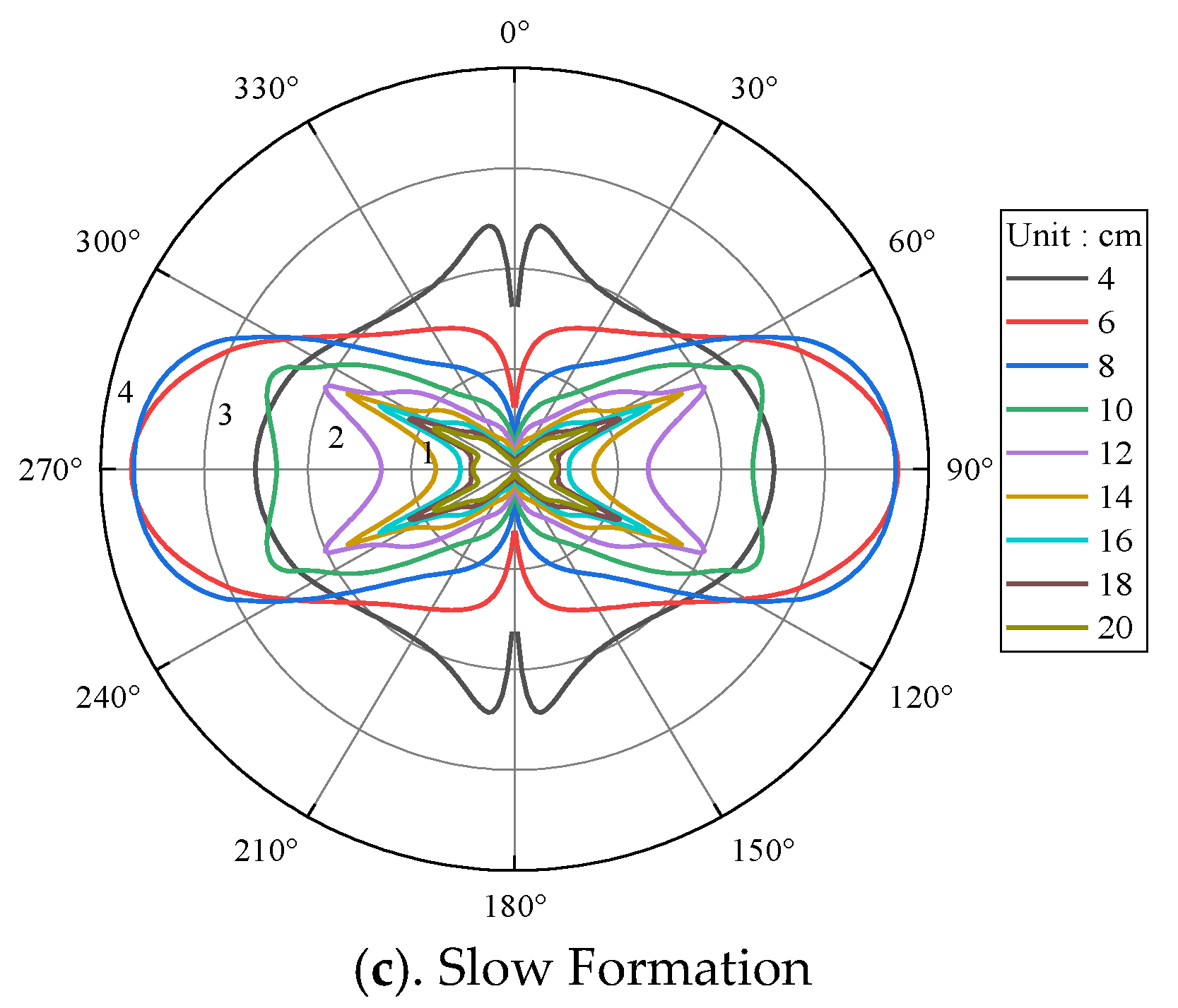
3.1. Formation Elastic Parameters
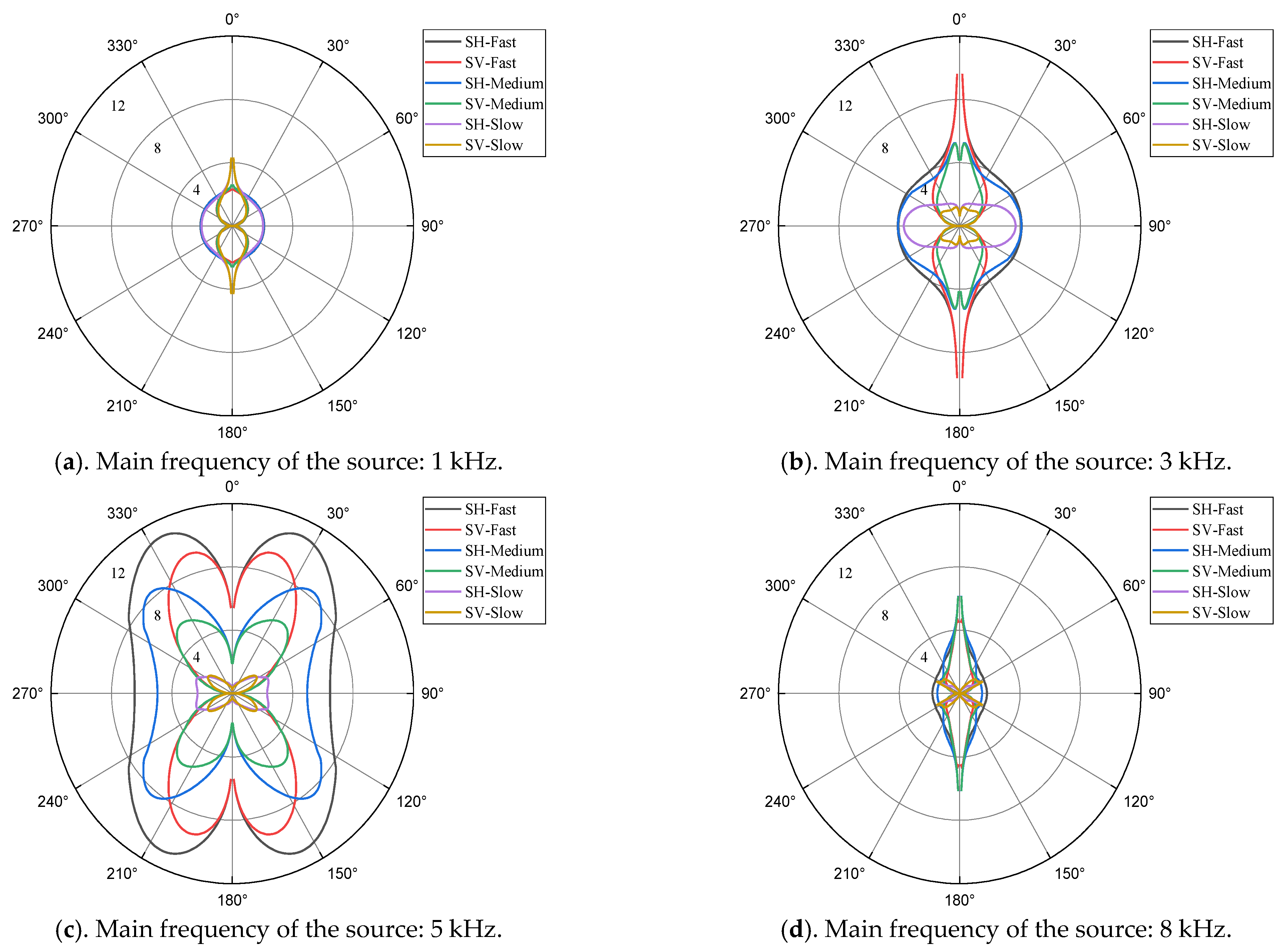
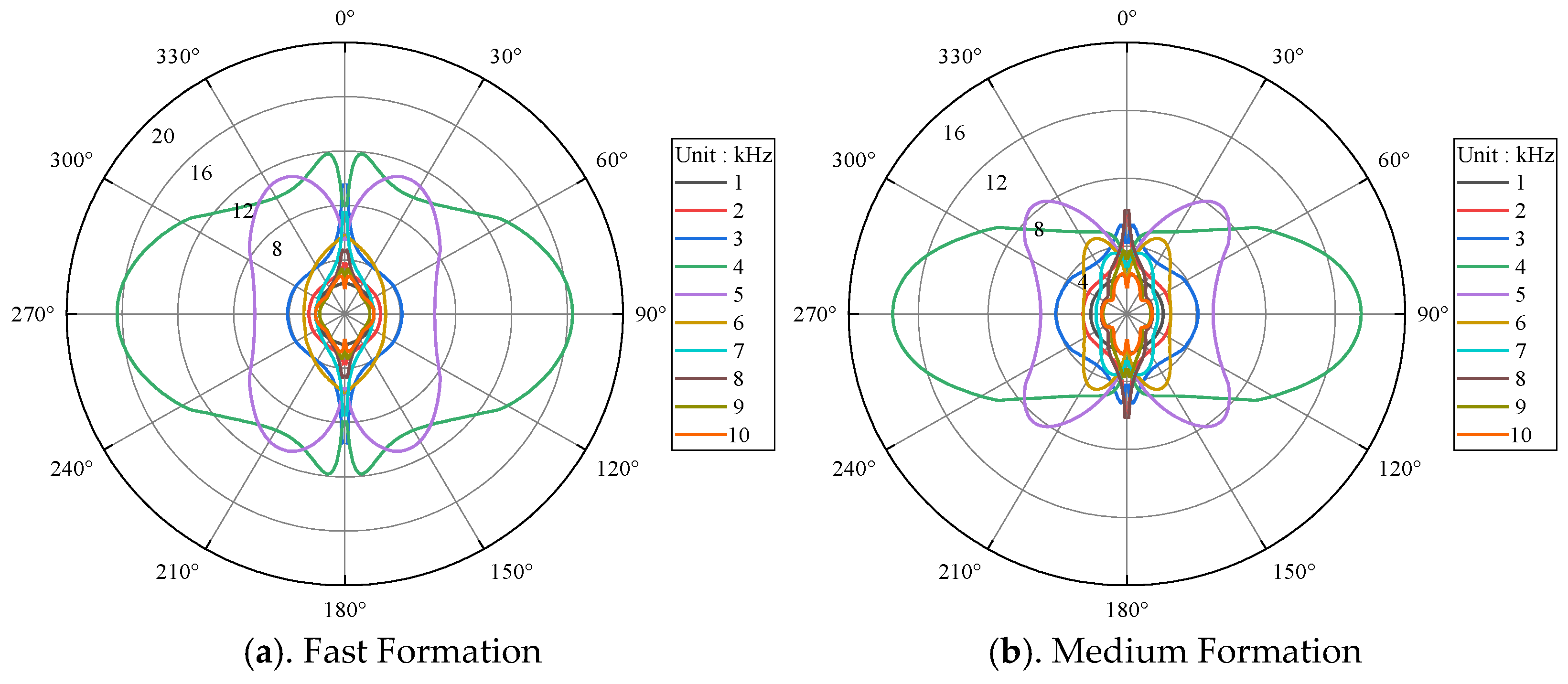
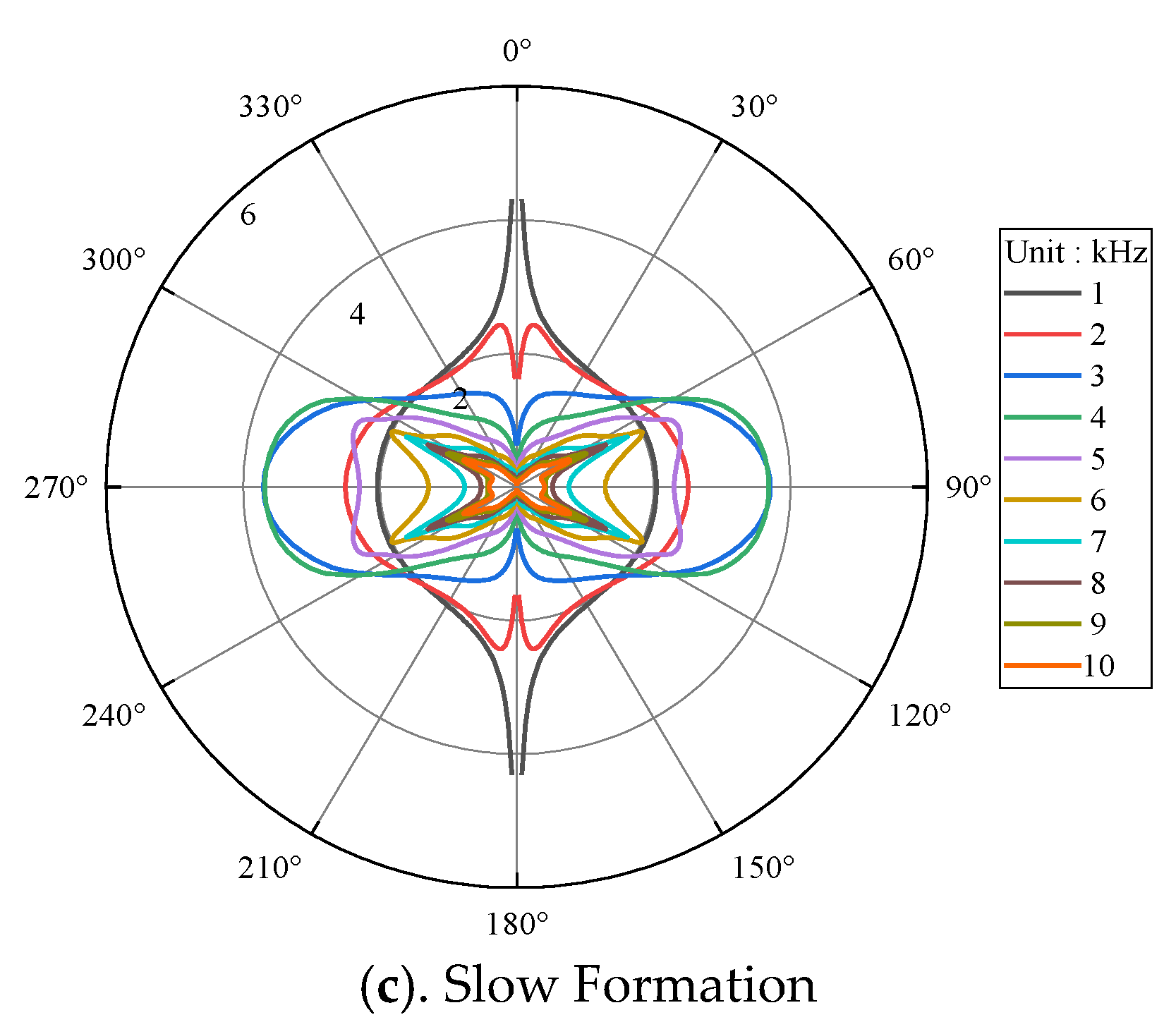
3.2. Main Frequency of the Dipole Source
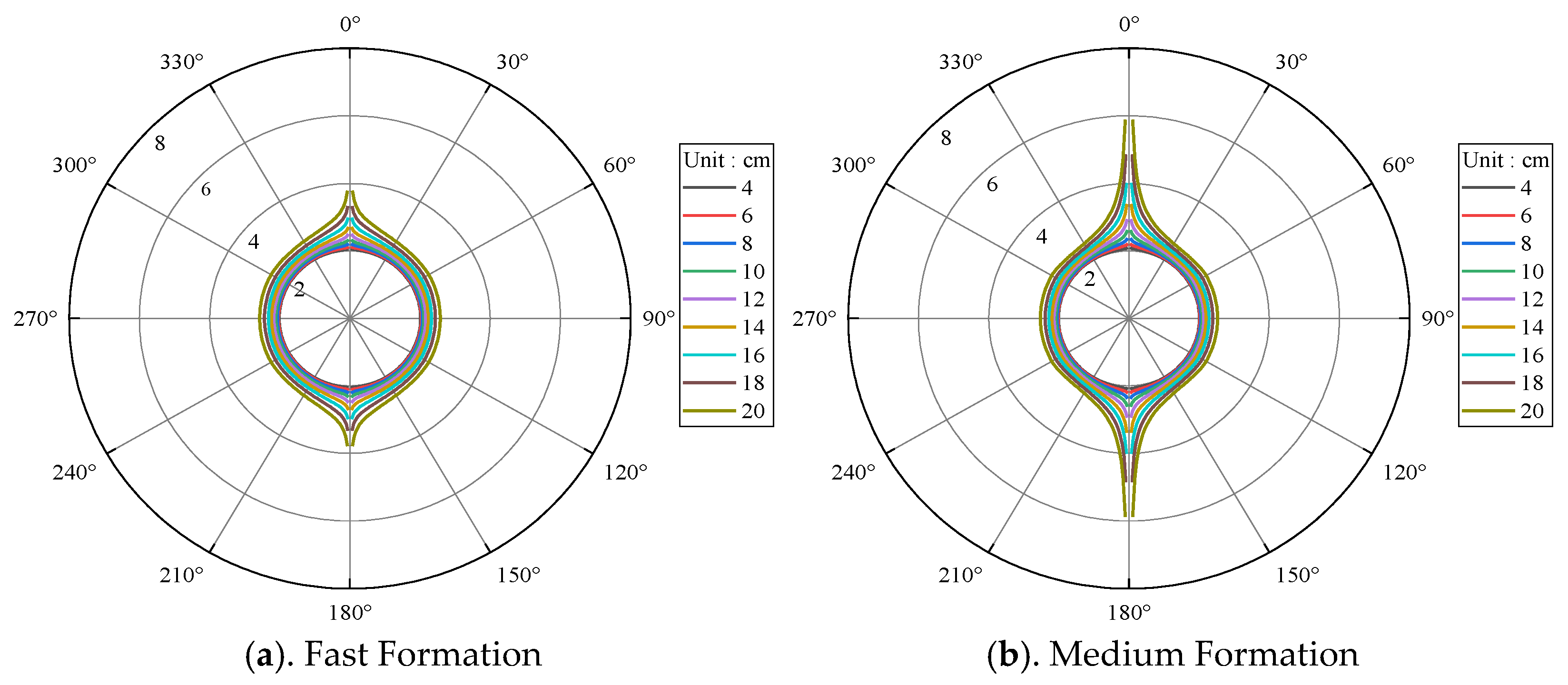
3.3. Borehole Radius
4. Conclusions
- The radiation of the shear waves by a dipole-source is insensitive to formation density and compressional wave velocity, but very sensitive to shear wave velocity. The shear wave velocity of the formation not only affects the shear wave amplitude radiated to the formation by the dipole source, but also affects the amplitude of the shear waves at different positions in space.
- The borehole modulation on the dipole-source radiation is weak at low frequency (lower than 1 kHz). However, it cannot be neglected at high frequency (higher than 3 kHz). The optimal main frequencies of the source in different formations are very close, which is good for the application of this technology under different conditions.
- The borehole modulation on the dipole-source radiation depends on the relative size of the shear wave wavelength and the borehole radius. The larger the ratio of the borehole radius to the shear wave wavelength, the stronger the modulation on the dipole-source radiation. Therefore, the variations of the dipole-source radiation patterns of the shear waves with the borehole radius are similar to that with the main frequency of the source under certain conditions.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hornby, B.E. Imaging of near-borehole structure using full waveform sonic data. Geophysics 1989, 54, 747–757. [Google Scholar] [CrossRef]
- Yamamoto, H.; Watanabe, S.; Koelman, J.M.V.; Geel, J.; Brie, A.; Fujii, K.; Coates, R. Borehole Acoustic Reflection Survey Experiments in Horizontal Wells for Accurate Well Positioning. In Proceedings of the SPE CIM International Conference on Horizontal Well Technology, Calgary, AB, Canada, 6–8 November 2000. [Google Scholar]
- Chai, X.Y.; Zhang, W.R.; Wang, G.Q.; Liu, J.D.; Xu, M.; Liu, D.D.; Song, C.L. Application of Remote Exploration Acoustic Reflection Imaging Logging Technique in Fractured Reservoir. Well Logging Technol. 2009, 33, 539–543. [Google Scholar]
- Zheng, Y.B.; Tang, X.M. Imaging near-borehole structure using acoustic logging data with pre-stack F−K migration. In Proceedings of the SEG Annual Meeting, Houston, TX, USA, 6–11 November 2005. [Google Scholar]
- Li, J.X.; Tao, G.; Zhang, K. Borehole sonic reflection imaging by finite difference reverse time migration. In Proceedings of the SEG Annual Meeting, Houston, TX, USA, 23–27 September 2013. [Google Scholar]
- Tang, X.M.; Glassman, H.; Patterson, D. Single-well acoustic imaging in anisotropic formations. Geophysics 2008, 73, 109–113. [Google Scholar] [CrossRef]
- Li, J.X.; Tao, G.; Kristopher, A.I. Borehole Reverse Time Migration in Anisotropic Medium. In Proceedings of the SEG Annual Meeting, New Orleans, LA, USA, 18−23 October 2015. [Google Scholar]
- Zhang, G. Forward Modeling and Efficient Processing Algorithms of Remote Detection Acoustic Logging. Ph.D. Thesis, Peking University, Beijing, China, 2016. [Google Scholar]
- Li, N.; Xiao, C.W.; Wu, L.H.; Shi, Y.J.; Wu, H.L.; Feng, Q.F.; Zhang, C.S.; Xie, B.; Zhao, T.P. The Innovation and Development of Log Evaluation for Complex Carbonate Reservoir in China. Well Logging Technol. 2014, 38, 1–10. [Google Scholar]
- Haldorsen, J.; Voskamp, A.; Thorsen, R.; Vissapragada, B.; Williams, S.; Fejerskov, M. Borehole Acoustic Reflection Survey for High Resolution Imaging. In Proceedings of the SEG Annual Meeting, New Orleans, LA, USA, 1−6 October 2006. [Google Scholar]
- Tang, X.M.; Douglas, J.P. Single-well S-wave imaging using multicomponent dipole acoustic-log data. Geophysics 2009, 74, 211–223. [Google Scholar] [CrossRef]
- Tang, X.M.; Patterson, D. Shear-wave imaging using cross-dipole acoustic logging tool. In Proceedings of the SEG Annual Meeting, Houston, TX, USA, 25–30 October 2009. [Google Scholar]
- Wei, Z.T.; Tang, X.M. Numerical simulation of radiation, reflection, and reception of elastic waves from a borehole dipole source. Geophysics 2012, 77, 253–261. [Google Scholar] [CrossRef]
- Cao, J.J.; Tang, X.M.; Wei, Z.T. Radiation of an acoustic dipole source in open and cased borehole with application to single-well shear-wave imaging. Chin. J. Geophys. 2014, 57, 1683–1692. [Google Scholar]
- Cao, J.J.; Tang, X.M.; Su, Y.D.; Wei, Z.T.; Zhuang, C.X. Radiation characteristics of the single-well imaging field in while-drilling logging using an acoustic dipole source. Chin. J. Geophys. 2016, 59, 3503–3512. [Google Scholar]
- Tang, X.M.; Cao, J.J.; Wei, Z.T. Radiation and reception of elastic waves from a dipole source in open and cased boreholes. J. China Univ. Pet. 2013, 37, 57–64. [Google Scholar]
- White, J.E. Use of reciprocity theorem for computation of low-frequency radiation patterns. Geophysics 1960, 25, 613–624. [Google Scholar] [CrossRef]
- Meredith, J.A. Numerical and analytical modelling of downhole seismic sources: The near and far field. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1990. [Google Scholar]
- Tang, X.M.; Cao, J.J.; Wei, Z.T. Shear-wave radiation, reception, and reciprocity of a borehole dipole source: With application to modeling of shear-wave reflection survey. Geophysics 2014, 79, 43–50. [Google Scholar] [CrossRef]
- Cao, J.J.; Tang, X.M.; Su, Y.D.; Wei, Z.T. Radiation efficiency of a multipole acoustic source in a fluid-filled borehole. Chin. J. Geophys. 2016, 59, 757–766. [Google Scholar]
- Cao, J.J.; Tang, X.M.; Su, Y.D. Radiation characteristics of a multipole acoustic source in an open borehole. Tech. Acoust. 2016, 35, 487–492. [Google Scholar]
- Cao, J.J.; Tang, X.M.; Su, Y.D.; Lee, S.Q. Radiation characteristics of an acoustic dipole source for single-well imaging. In Proceedings of the SEG Annual Meeting, Dallas, TX, USA, 16–21 October 2016. [Google Scholar]



| Fluid | 1500 | 0 | 1000 | 0.1 |
| Fast Formation | 6220 | 3455 | 2710 | - |
| Medium Formation | 3600 | 1920 | 2250 | - |
| Slow Formation | 2800 | 1200 | 2150 | - |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, H.; Wang, C.; Liu, Y.; Xia, S.; Fu, H.; Yuan, Y.; Bie, K.; Li, X. Influencing Factors of Shear Wave Radiation of a Dipole Source in a Fluid-Filled Borehole. Energies 2022, 15, 6789. https://doi.org/10.3390/en15186789
Wang H, Wang C, Liu Y, Xia S, Fu H, Yuan Y, Bie K, Li X. Influencing Factors of Shear Wave Radiation of a Dipole Source in a Fluid-Filled Borehole. Energies. 2022; 15(18):6789. https://doi.org/10.3390/en15186789
Chicago/Turabian StyleWang, Hao, Caizhi Wang, Yingming Liu, Shouji Xia, Haicheng Fu, Ye Yuan, Kang Bie, and Xincheng Li. 2022. "Influencing Factors of Shear Wave Radiation of a Dipole Source in a Fluid-Filled Borehole" Energies 15, no. 18: 6789. https://doi.org/10.3390/en15186789
APA StyleWang, H., Wang, C., Liu, Y., Xia, S., Fu, H., Yuan, Y., Bie, K., & Li, X. (2022). Influencing Factors of Shear Wave Radiation of a Dipole Source in a Fluid-Filled Borehole. Energies, 15(18), 6789. https://doi.org/10.3390/en15186789




