Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan
Abstract
:1. Introduction
2. Materials and Methods
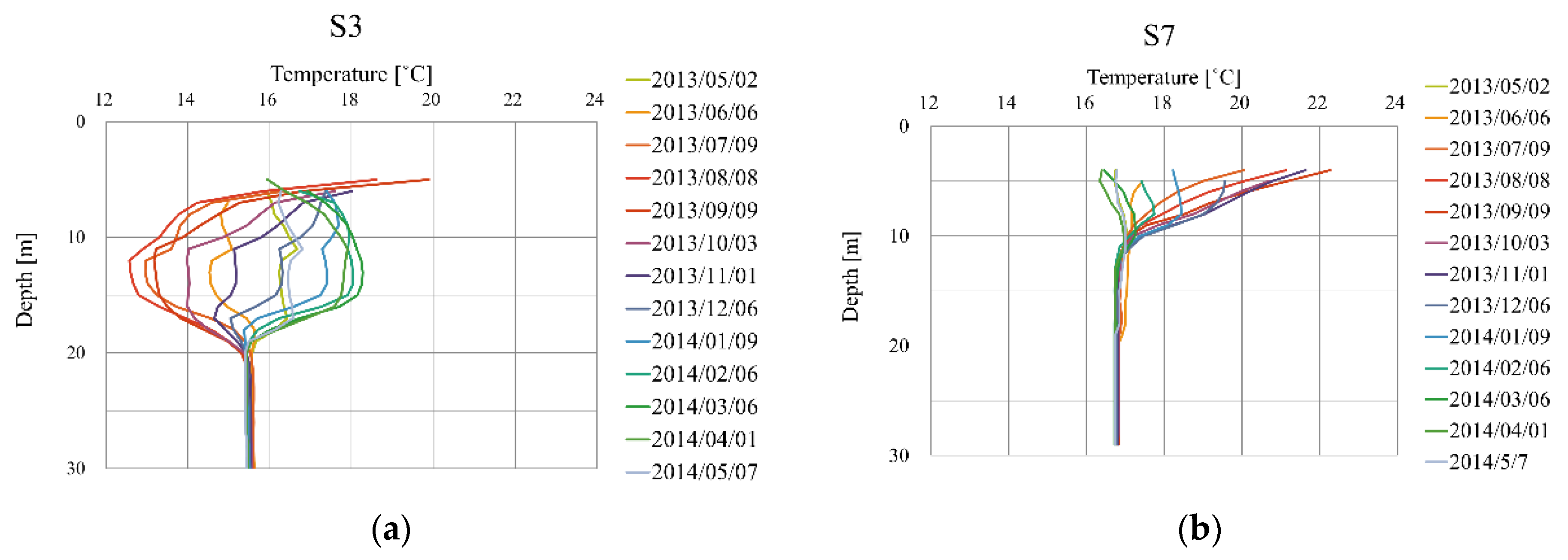
2.1. Site Description
2.2. Regional Simulation Model Settings
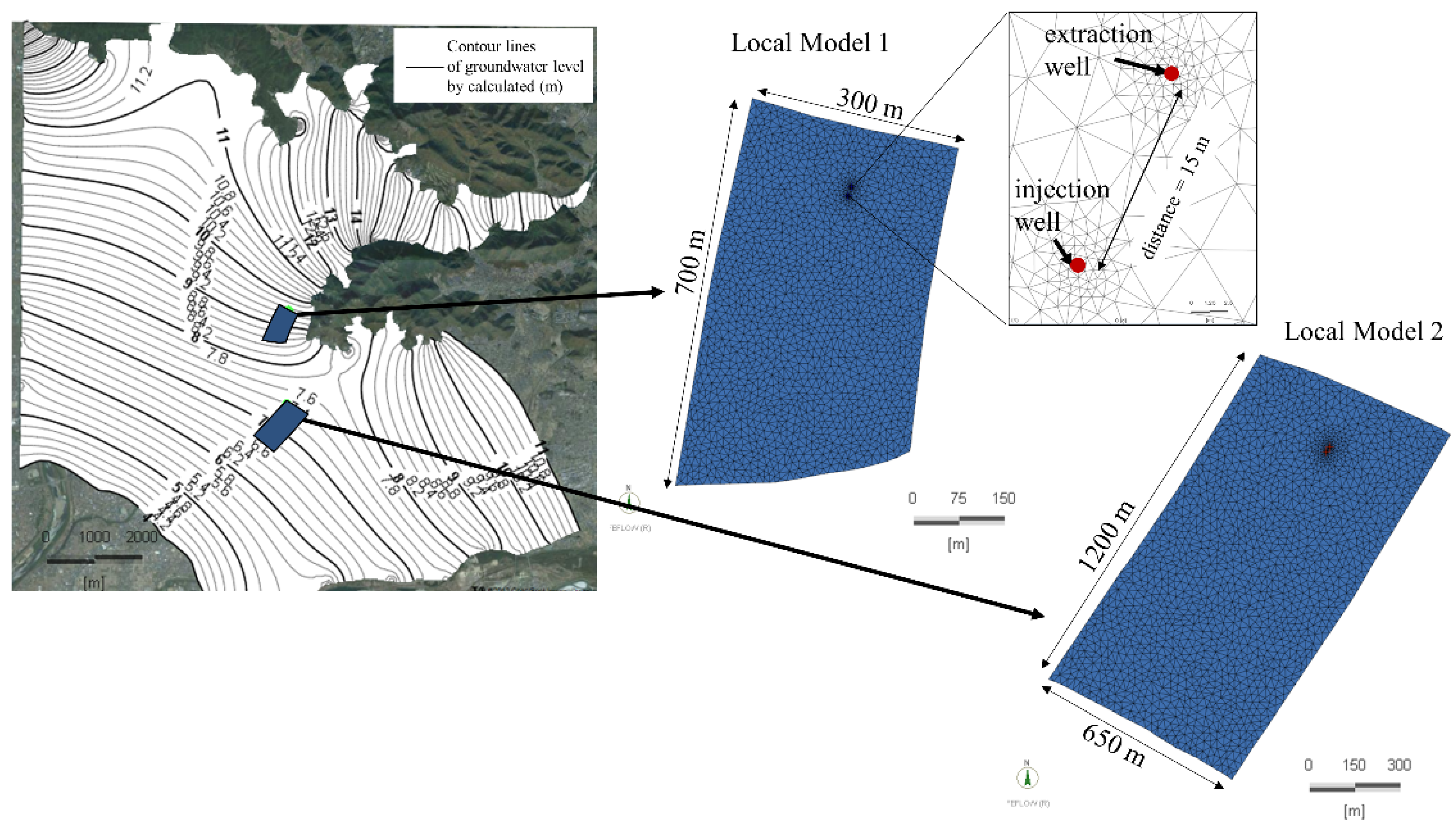
2.3. Local Simulation Model Settings
3. Results
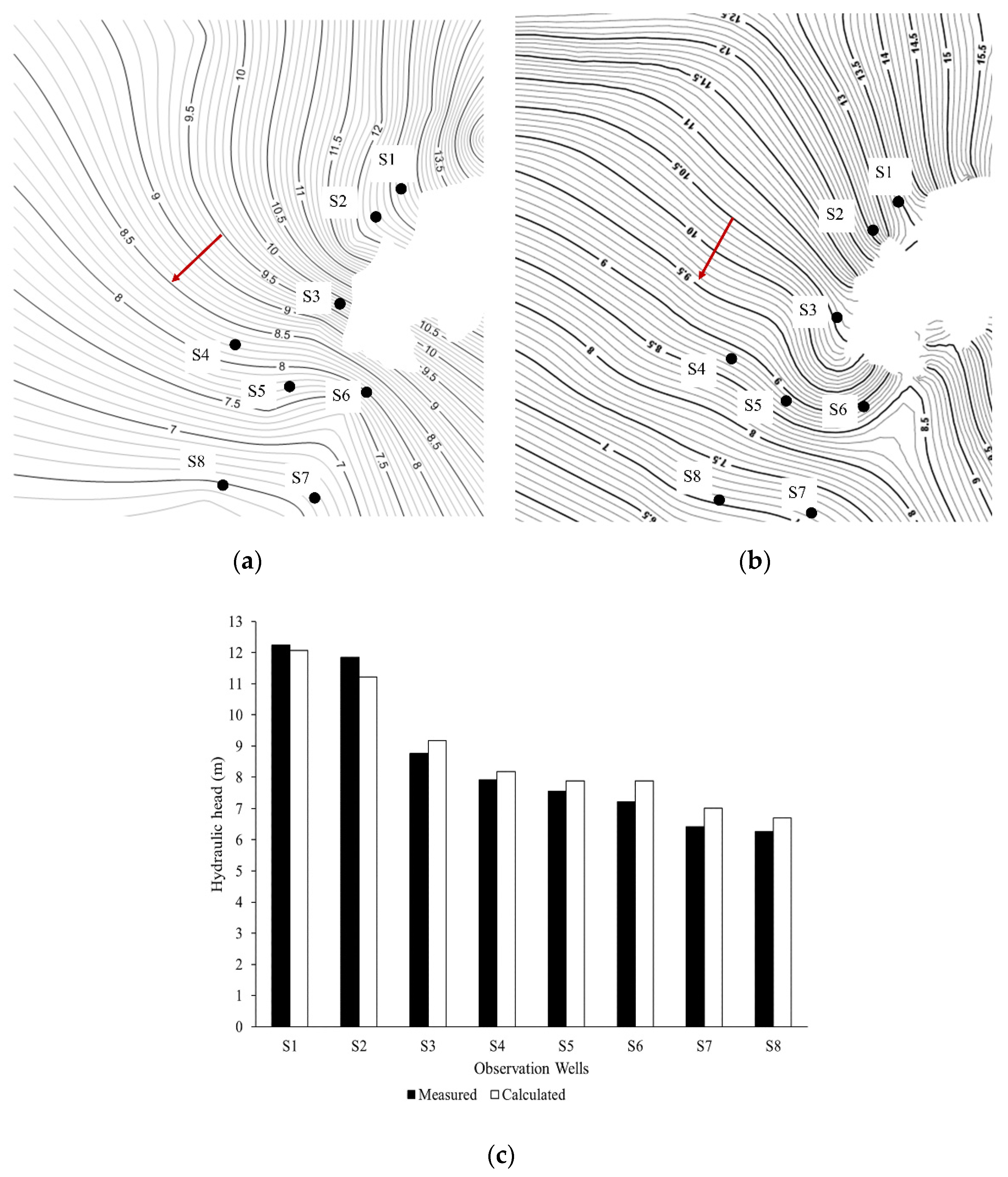
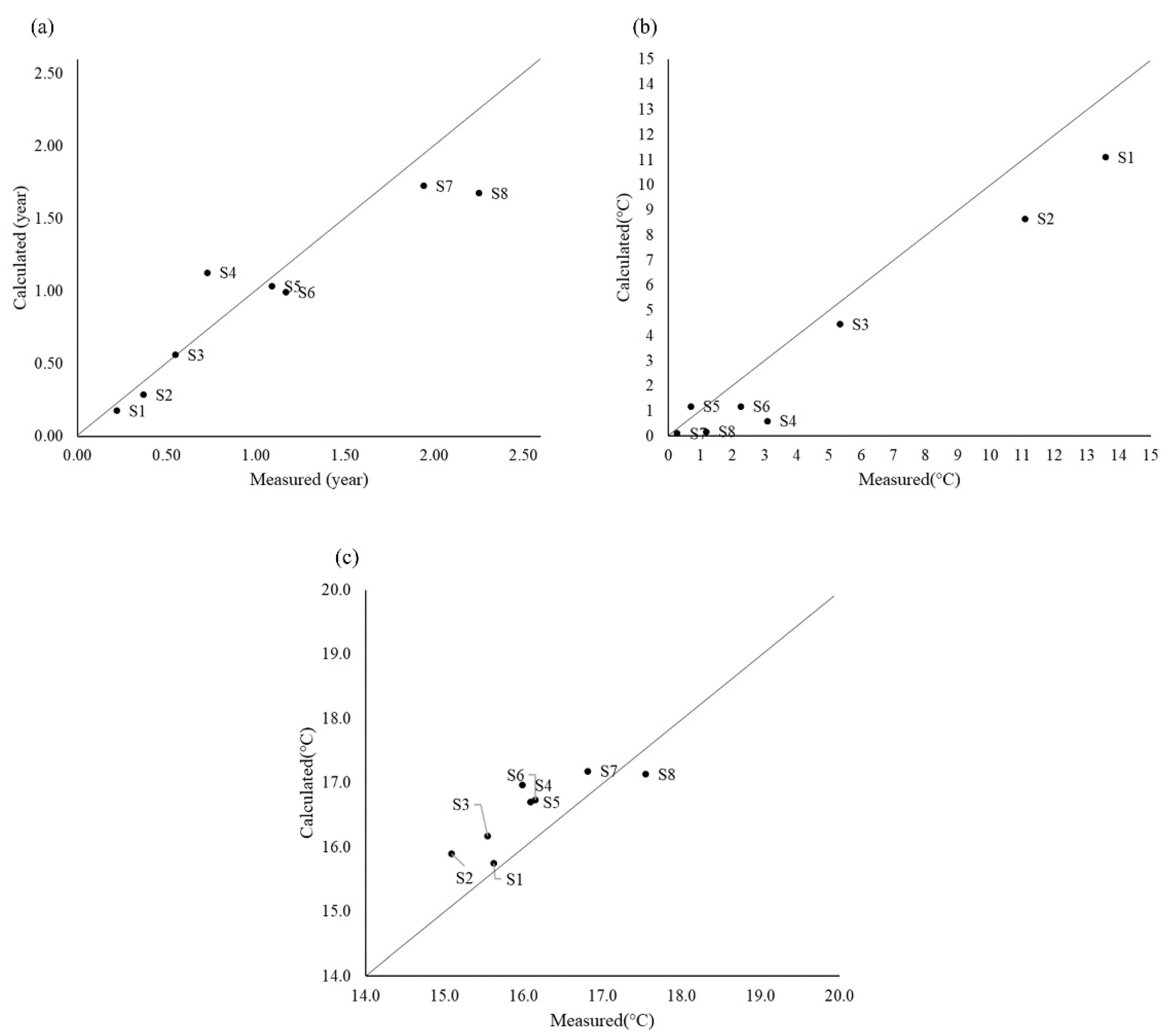
3.1. Regional Simulation
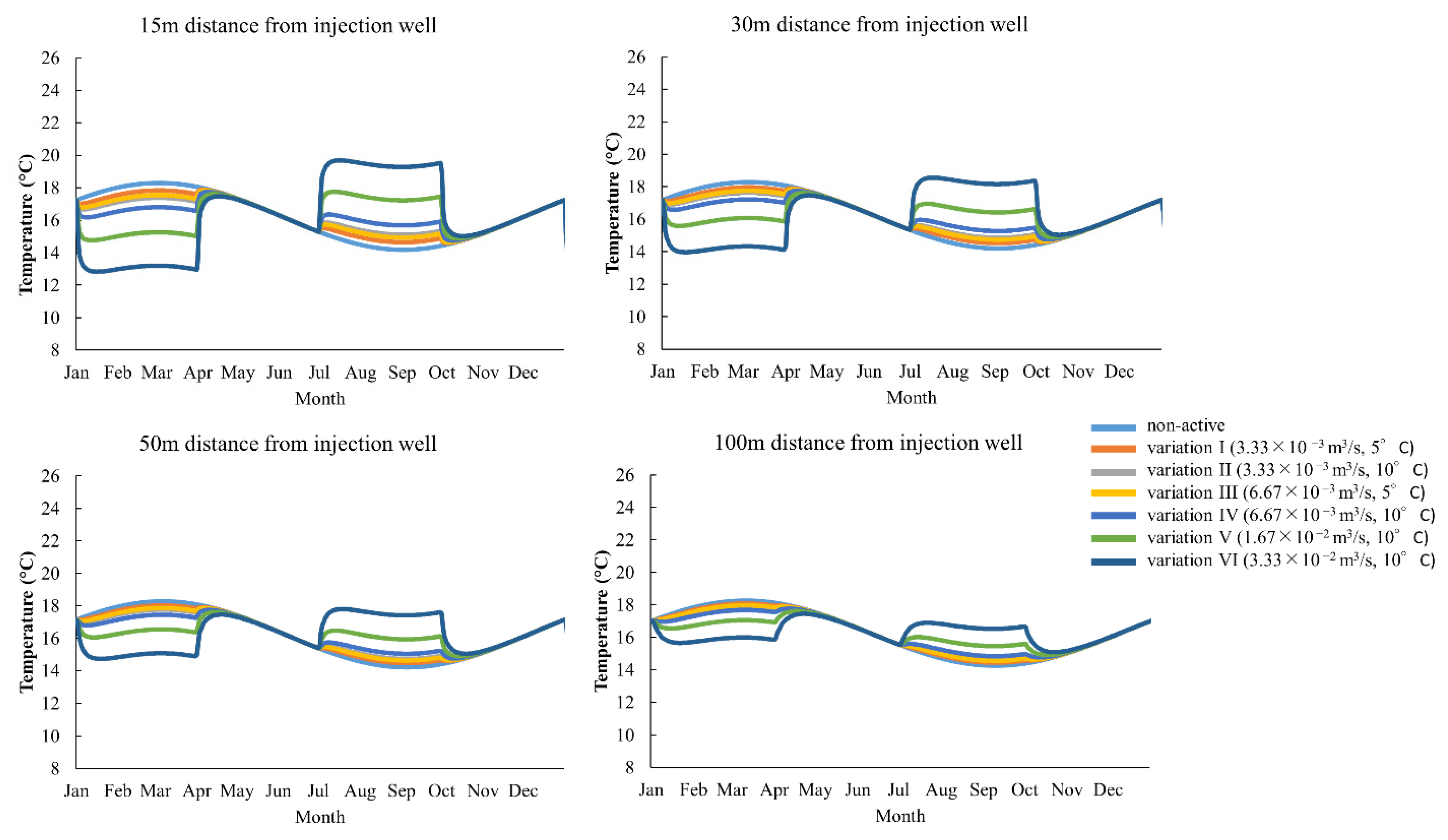
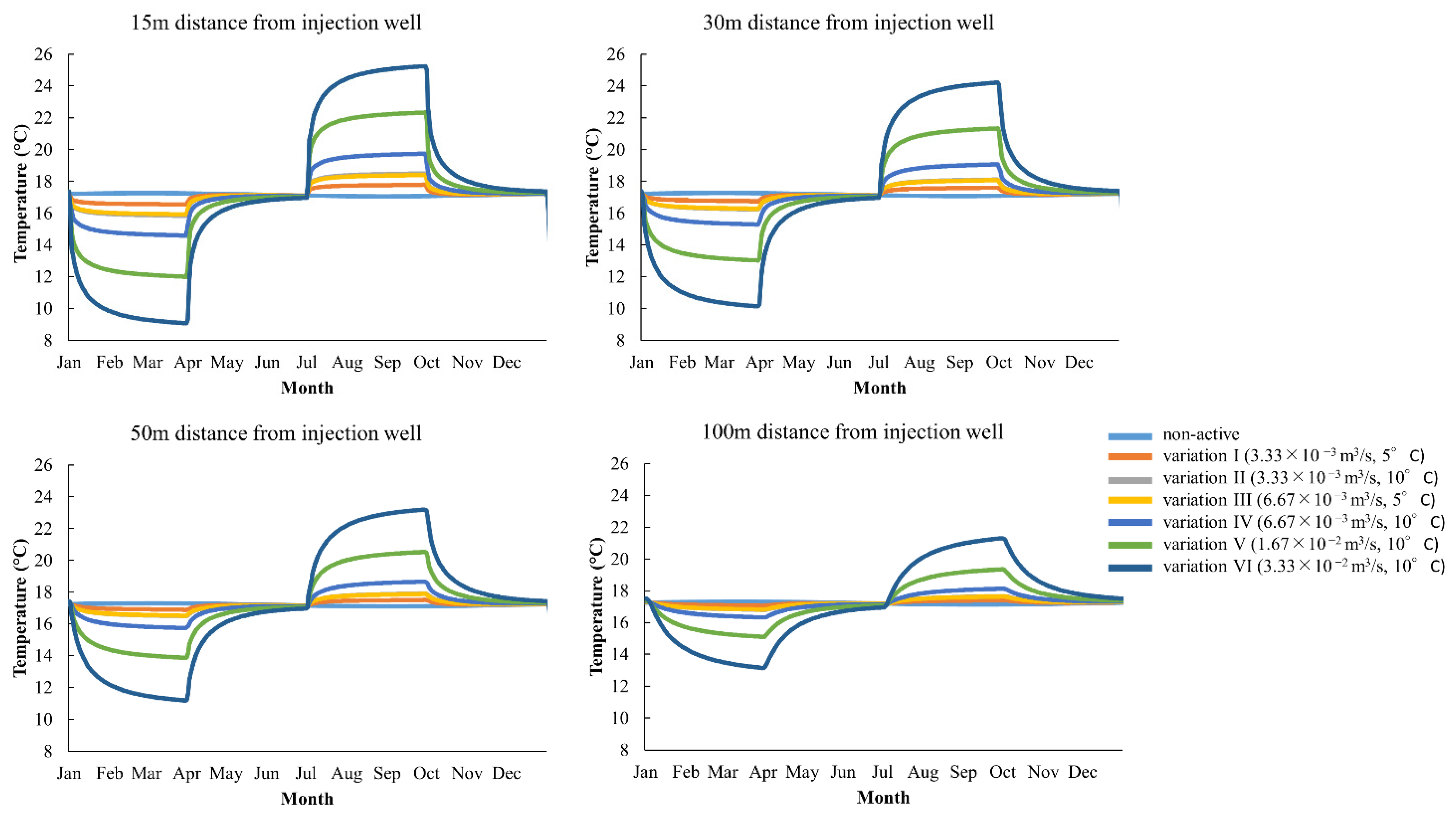
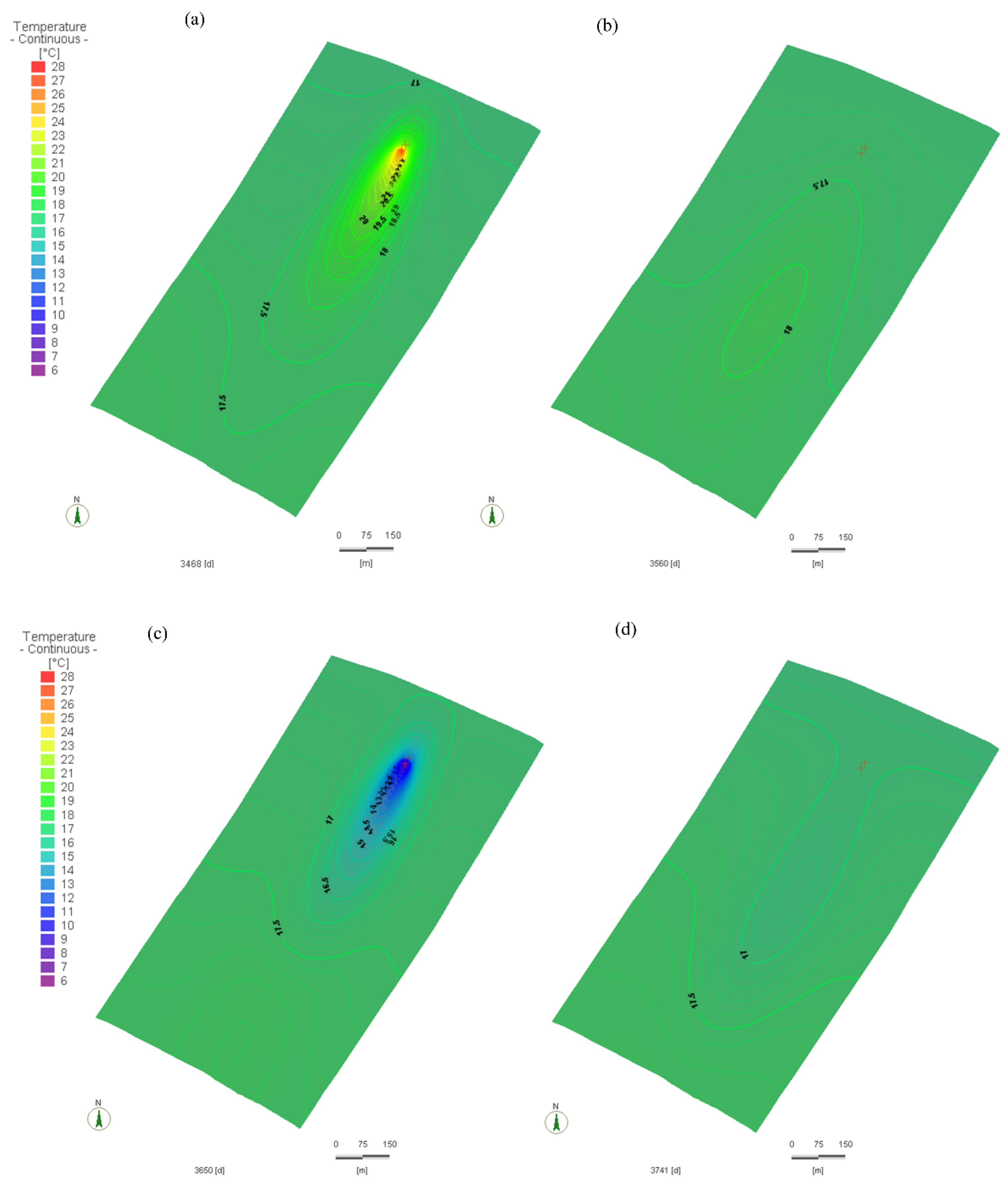
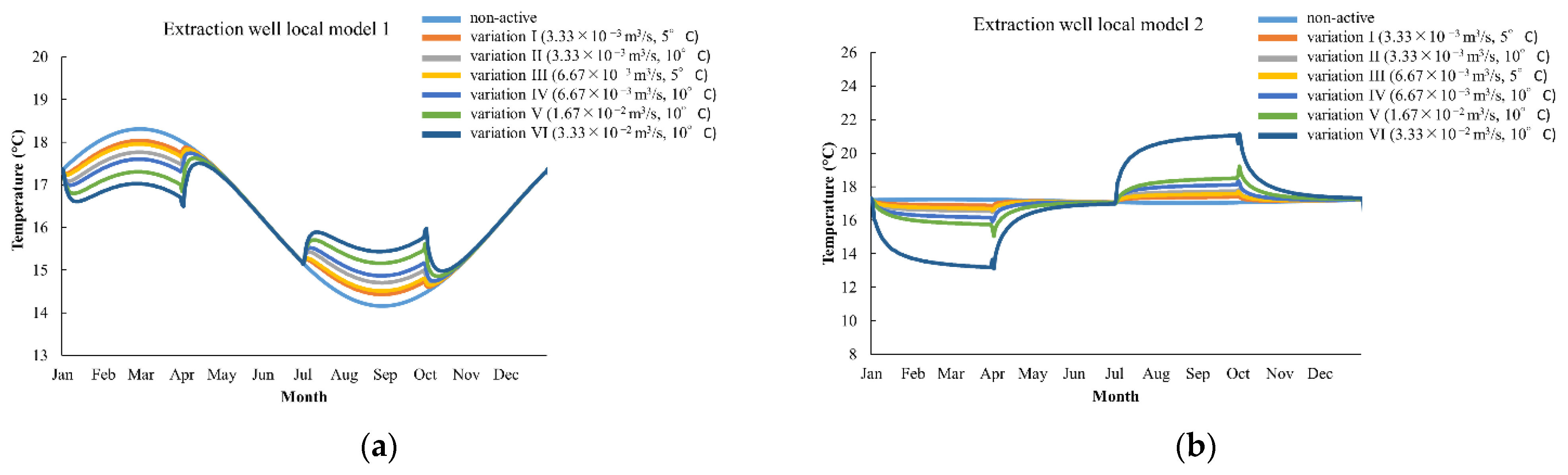
3.2. Local Simulation and Open-Loop Operation
4. Discussion
4.1. Regional Simulation
4.2. Comparison between Local Models 1 and 2
4.3. Geothermal Heat Pump Use in the Alluvial Fan
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sanner, B.; Karytsas, C.; Mendrinos, D.; Rybach, L. Current status of ground source heat pumps and underground thermal energy storage in Europe. Geothermics 2003, 32, 579–588. [Google Scholar] [CrossRef]
- Haehnlein, S.; Bayer, P.; Blum, P. International legal status of the use of shallow geothermal energy. Renew. Sustain. Energy Rev. 2010, 14, 2611–2625. [Google Scholar] [CrossRef]
- Blum, P.; Campillo, G.; Munch, W.; Kolbel, T. CO2 savings of ground source heat pump systems—A regional analysis. Renew. Energy 2010, 35, 122–127. [Google Scholar] [CrossRef]
- Lo Russo, S.; Gnavi, L.; Roccia, E.; Taddia, G.; Verda, V. Groundwater Heat Pump (GWHP) System Modeling and Thermal Affected Zone (TAZ) Prediction Reliability: Influence of Temporal Variations in Flow Discharge and Injection Temperature. Geothermics 2014, 51, 103–112. [Google Scholar] [CrossRef]
- Casasso, A.; Sethi, R. Assessment and minimization of potential environmental impacts of ground source heat pump (GSHP) systems. Water 2019, 11, 1573. [Google Scholar] [CrossRef]
- Meng, B.; Vienken, T.; Kolditz, O.; Shao, H. Evaluating the Thermal Impacts and Sustainability of Intensive Shallow Geothermal Utilization on a Neighborhood Scale: Lessons Learned from a Case Study. Energy Convers. Manag. 2019, 199, 111913. [Google Scholar] [CrossRef]
- Freedman, V.L.; Waichler, S.R.; Mackley, R.D.; Horner, J.A. Assessing the Thermal Environmental Impacts of an Groundwater Heat Pump in Southeastern Washington State. Geothermics 2012, 42, 65–77. [Google Scholar] [CrossRef]
- Pophillat, W.; Bayer, P.; Teyssier, E.; Blum, P.; Attard, G. Impact of Groundwater Heat Pump Systems on Subsurface Temperature under Variable Advection, Conduction and Dispersion. Geothermics 2020, 83, 101721. [Google Scholar] [CrossRef]
- Piga, B.; Casasso, A.; Pace, F.; Godhio, A.; Sethi, R. Thermal Impact Assessments of Groundwater Heat Pumps (GWHPs): Rigorous vs. Simplified Models. Energies 2017, 10, 1385. [Google Scholar] [CrossRef]
- Ohtani, T.; Mizuno, T.; Kouda, A.; Kojima, S. Seasonal Change of Underground Temperature and its Geothermal Utilization in Gifu City, Japan. In Proceedings of the World Geothermal Congress, Melbourne, Australia, 19–25 April 2015; pp. 19–25. [Google Scholar]
- Banks, D. Thermogeological assessment of open-loop well-doublet schemes: A review and synthesis of analytical approaches. Hydrogeol. J. 2009, 17, 1149–1155. [Google Scholar] [CrossRef]
- Lo Russo, S.; Taddia, G.; Baccino, G.; Verda, V. Different design scenarios related to an open loop groundwater heat pump in a large building: Impact on subsurface and primary energy consumption. Energy Build. 2011, 43, 347–357. [Google Scholar] [CrossRef]
- Pophillat, A.; Attard, G.; Bayer, B.; Hecht-Mendez, J. Analytical solutions for predicting thermal plumes of groundwater heat pump systems. Renew. Energy 2020, 147, 2696–2707. [Google Scholar] [CrossRef]
- Gifu Prefecture, Gifu City, Teikoku Construction Consultant. Report on feasibility study of geothermal heat pumps. 2011; 201p.
- Neton, M.J.; Dorsch, J.; Olson, C.D.; Young, S.C. Architecture and Directional Scales of Heterogeneity in Alluvial-Fan Aquifers. J. Sediment. Res. 1994, 64B, 245–257. [Google Scholar] [CrossRef]

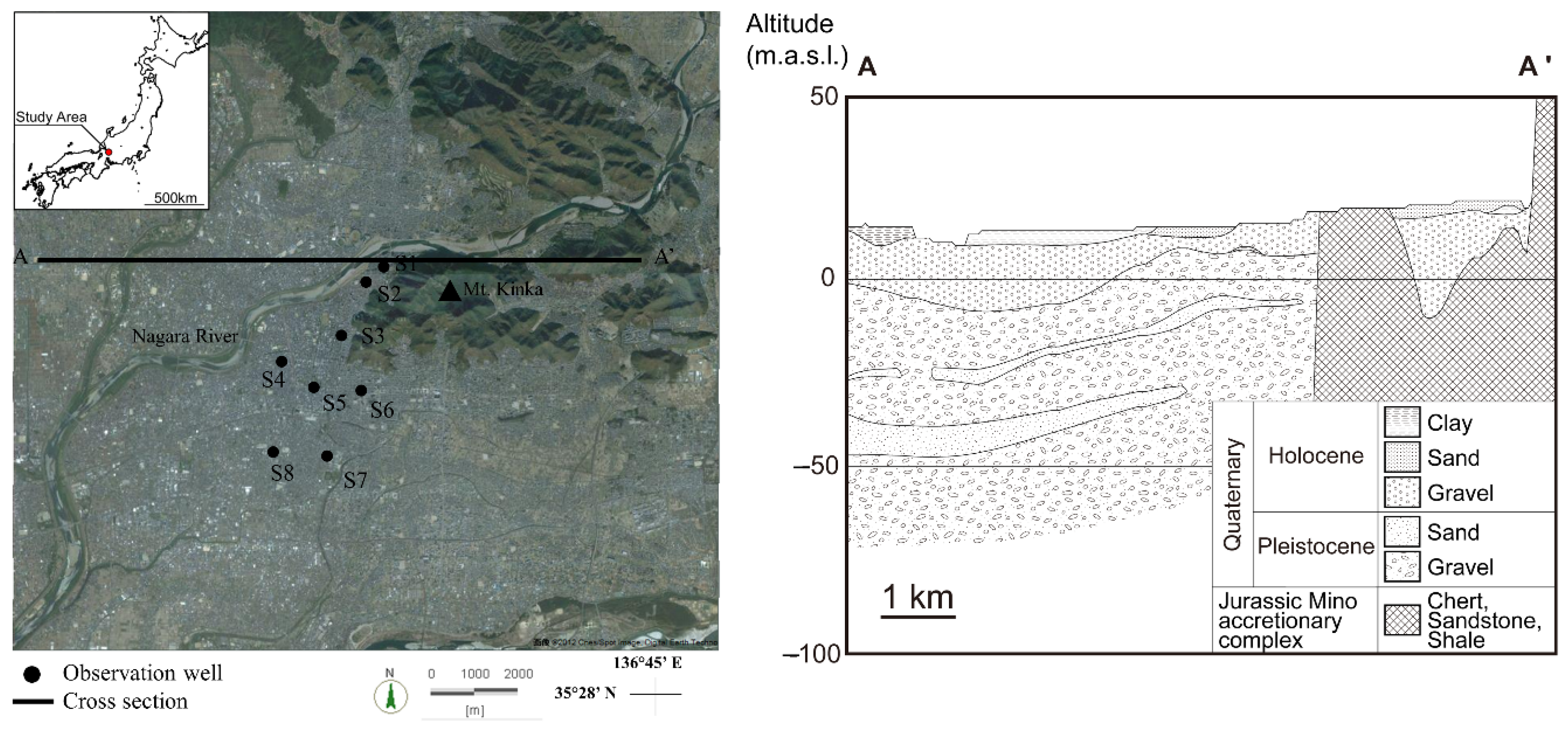







| Layer | Geological Layers | Thickness of Each Layer (m) | Flow | Heat Transport | |
|---|---|---|---|---|---|
| Conductivity (m/s) | Porosity (%) | Dispersivity (m) | |||
| 1–2 | Clay (Holocene) | 1–4 | 1 × 10−6 | 30 | 90 (longitudinal) 9 (transverse) |
| 3–14 | Gravel (Holocene) | 1 | 7 × 10−2 | ||
| 15–20 | Gravel (Pleistocene) | 1 | 1 × 10−4 | ||
| 21 | Sand (Pleistocene) | 2–6 | 5 × 10−5 | ||
| 22–27 | Gravel (Pleistocene) | 2–3 | 1 × 10−4 | ||
| 28–30 | Gravel (Pleistocene) | <50 | |||
| 31 | Chert, Sandstone, Shale (Jurassic Mino Accretionary Complex) | <250 | 1 × 10−8 | 10 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Permanda, R.; Ohtani, T. Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan. Energies 2022, 15, 6816. https://doi.org/10.3390/en15186816
Permanda R, Ohtani T. Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan. Energies. 2022; 15(18):6816. https://doi.org/10.3390/en15186816
Chicago/Turabian StylePermanda, Randa, and Tomoyuki Ohtani. 2022. "Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan" Energies 15, no. 18: 6816. https://doi.org/10.3390/en15186816
APA StylePermanda, R., & Ohtani, T. (2022). Thermal Impact by Open-Loop Geothermal Heat Pump Systems in Two Different Local Underground Conditions on the Alluvial Fan of the Nagara River, Gifu City, Central Japan. Energies, 15(18), 6816. https://doi.org/10.3390/en15186816









