Reward–Penalty vs. Deposit–Refund: Government Incentive Mechanisms for EV Battery Recycling
Abstract
:1. Introduction
2. Literature Review
2.1. EV Battery Recycling
2.2. Closed-Loop Supply Chain Incentives
2.3. Trade-In Strategy
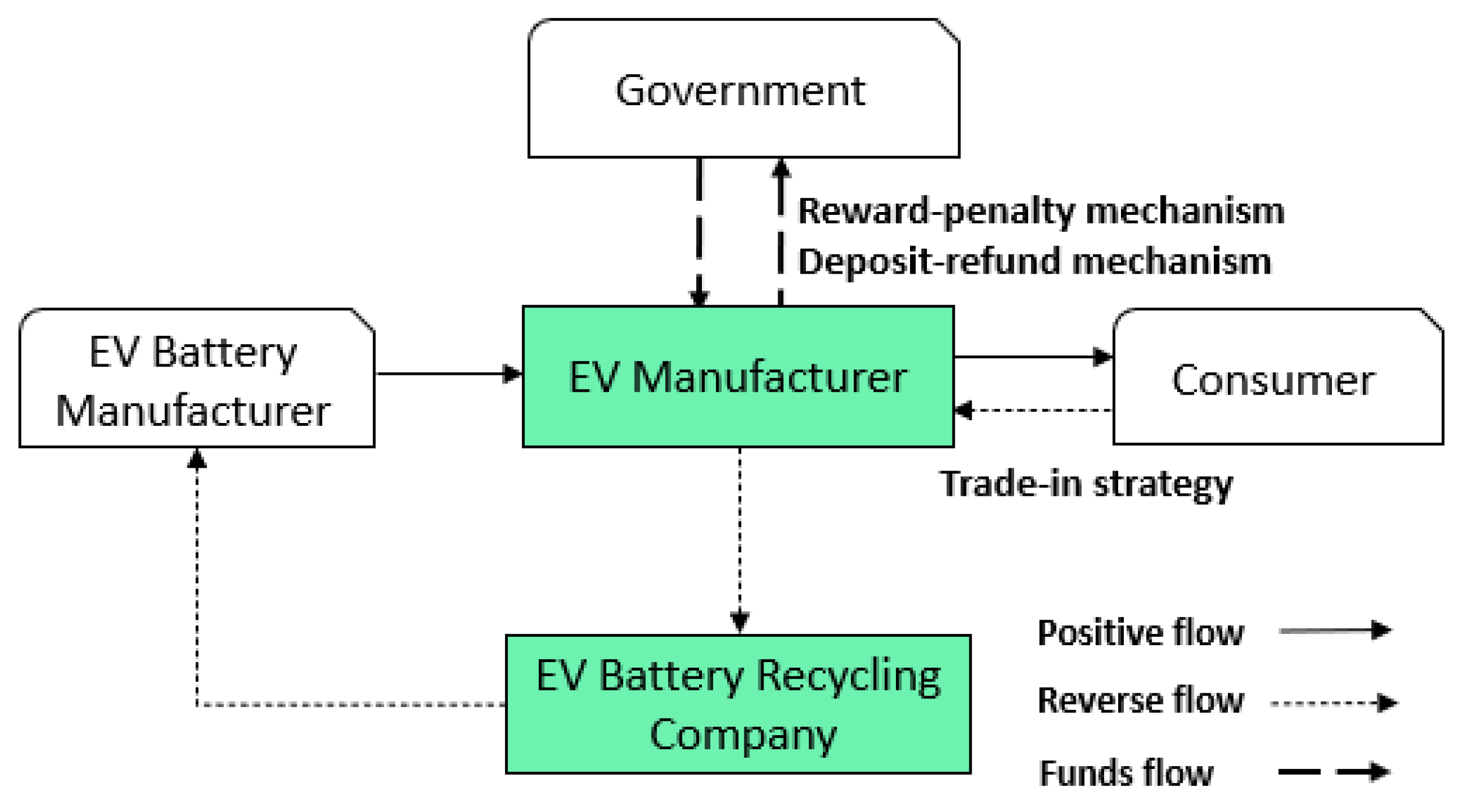
3. Stackelberg Game Model
4. Equilibrium Analysis
4.1. Reward–Penalty Mechanism
4.2. Deposit–Refund Mechanism
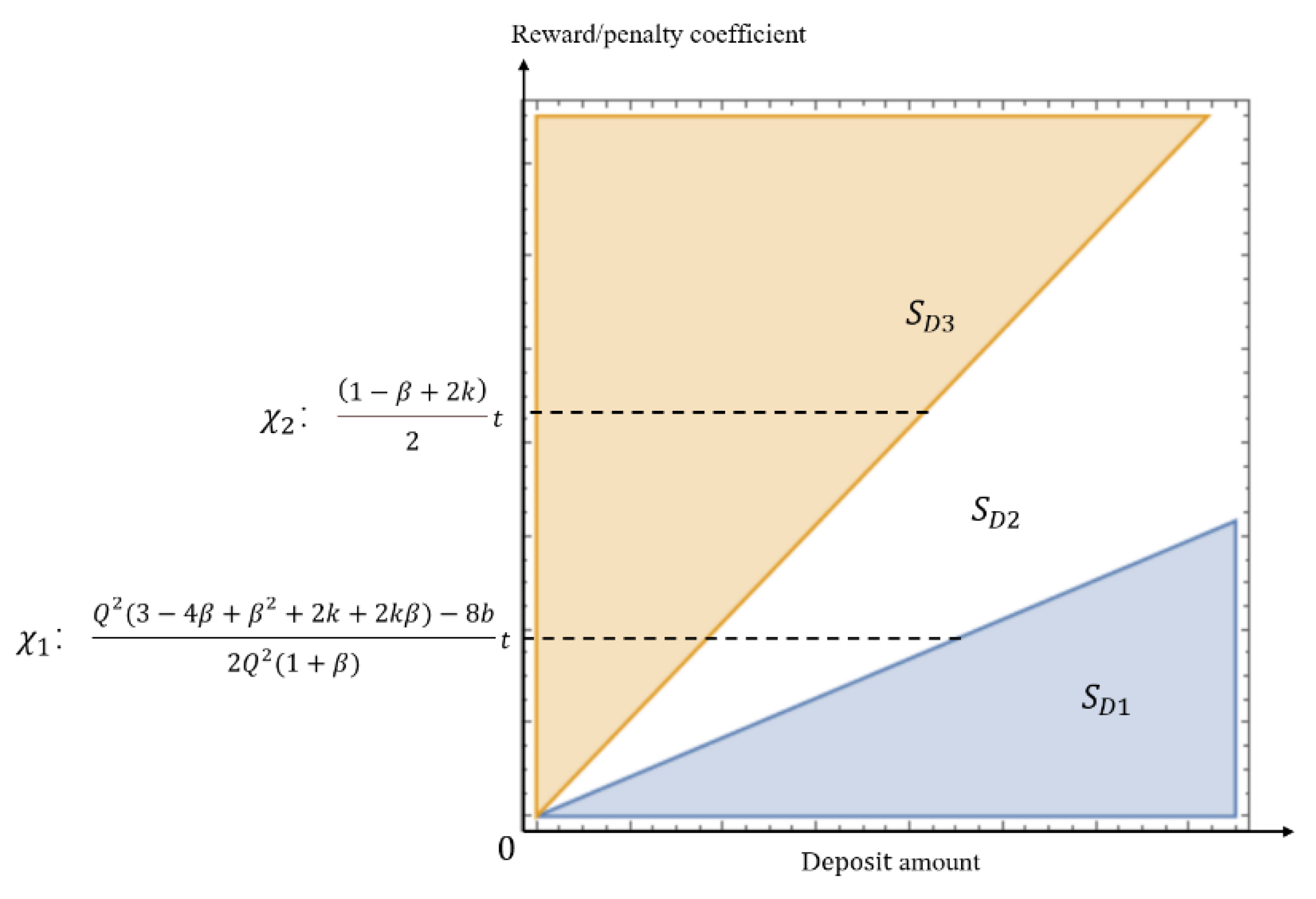
5. Comparisons and Analysis
5.1. Sales of the New Batteries
5.2. Collection and Recycling of Waste Batteries
5.3. Social Welfare
6. Numerical Study
6.1. Data Collection
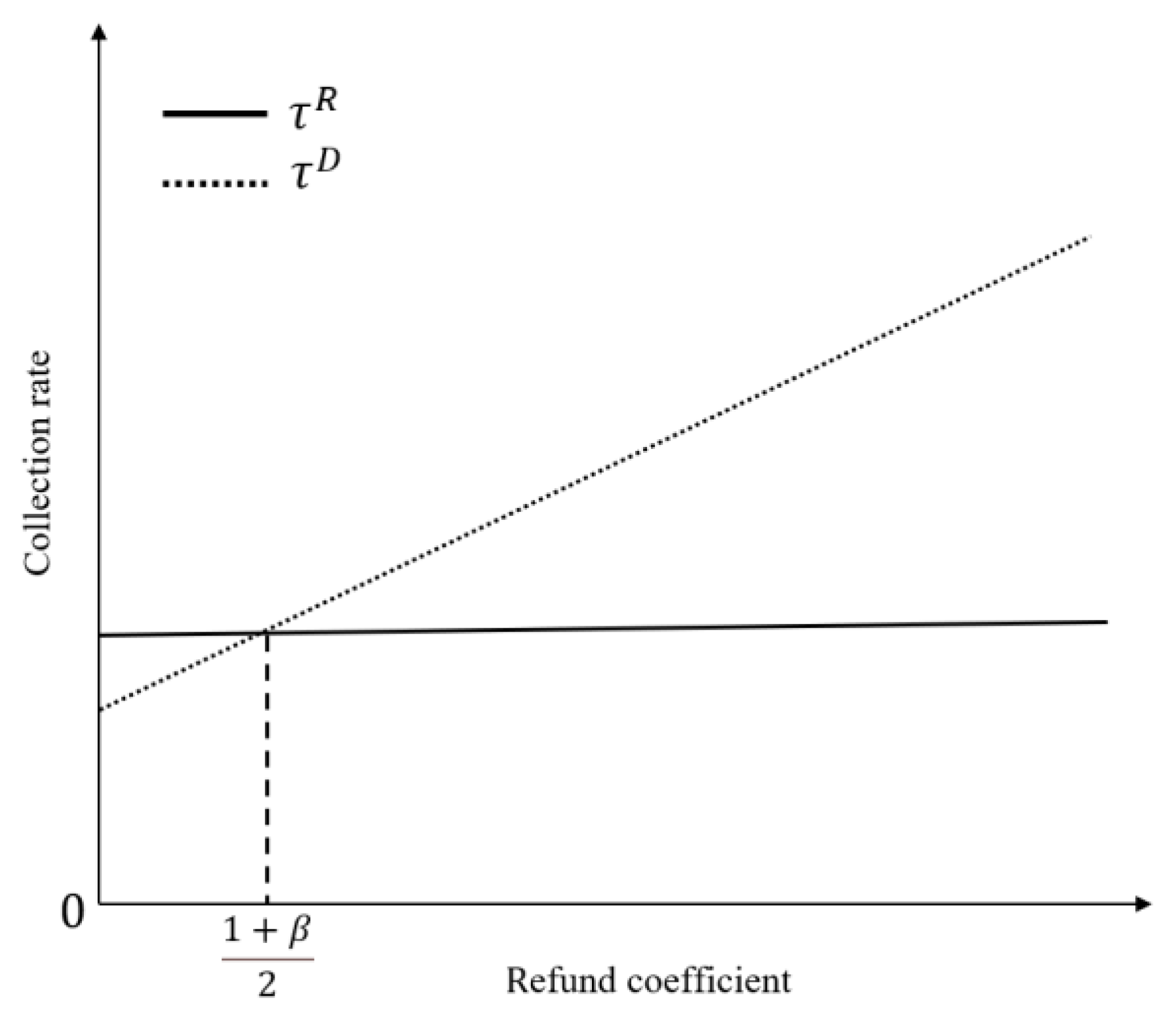
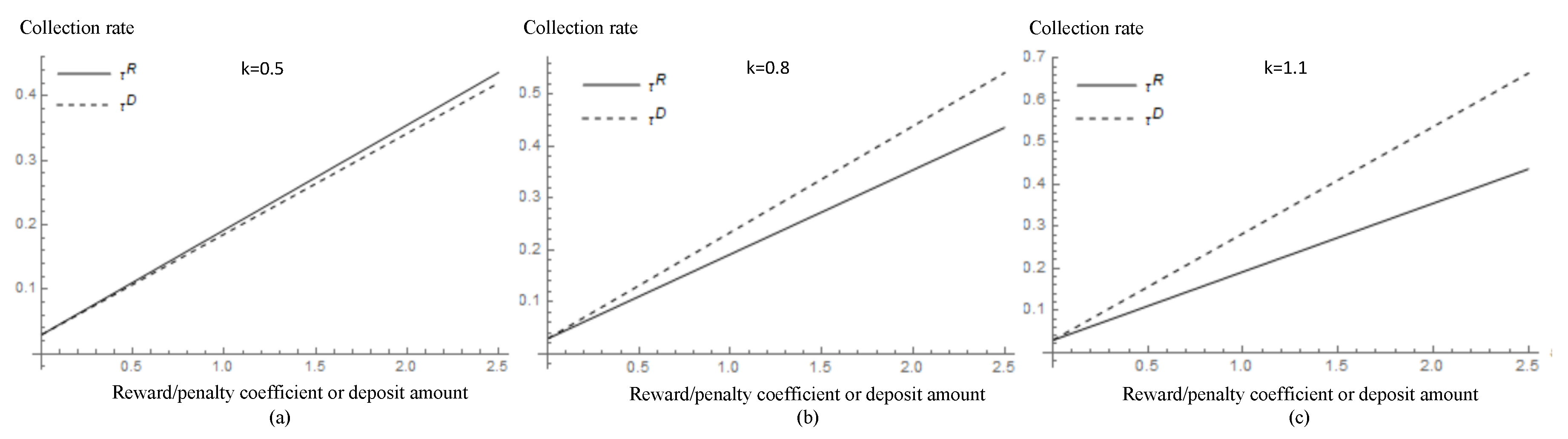
6.2. Collection Rate Analyses
6.3. Profit Analyses for the EV Manufacturer and the Recycling Enterprise
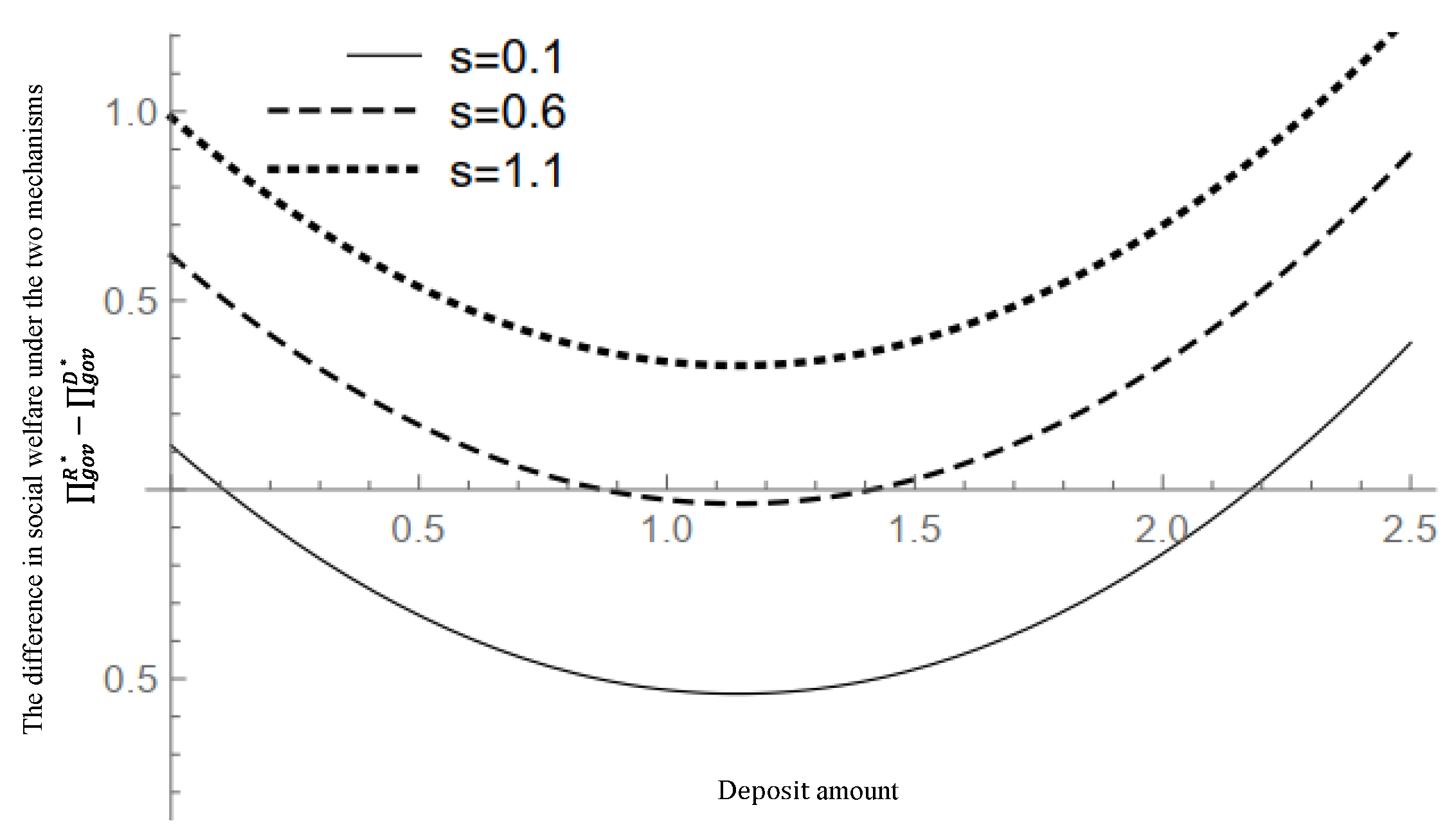
6.4. Social Welfare Analyses
7. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Y.; Wen, Z.; Li, Q.; Li, S. Research on Energy Management Strategies for Electric Vehicles. In Proceedings of the 2011 Asia-Pacific Power and Energy Engineering Conference, Shanghai, China, 27–29 March 2012; pp. 1–4. [Google Scholar]
- Hu, X.; Wang, H.; Tang, X. Cyber-Physical Control for Energy-Saving Vehicle Following With Connectivity. IEEE Trans. Ind. Electron. 2017, 64, 8578–8587. [Google Scholar] [CrossRef]
- Pei, H.; Hu, X.; Yang, Y.; Tang, X.; Hou, C.; Cao, D. Configuration optimization for improving fuel efficiency of power split hybrid powertrains with a single planetary gear. Appl. Energy 2018, 214, 103–116. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Q.; Li, Y.; Li, H.; Pan, X.; McLellan, B. The social-economic-environmental impacts of recycling retired EV batteries under reward-penalty mechanism. Appl. Energy 2019, 251, 113313. [Google Scholar] [CrossRef]
- Gu, X.; Ieromonachou, P.; Zhou, L.; Tseng, M.-L. Optimising quantity of manufacturing and remanufacturing in an electric vehicle battery closed-loop supply chain. Ind. Manag. Data Syst. 2018, 118, 283–302. [Google Scholar] [CrossRef]
- Saxena, S.; Le Floch, C.; MacDonald, J.; Moura, S. Quantifying EV battery end-of-life through analysis of travel needs with vehicle powertrain models. J. Power Sources 2015, 282, 265–276. [Google Scholar] [CrossRef]
- China Internet Data and Information Network. New Energy Vehicle Battery Circular Economy Potential Study. Available online: http://www.199it.com/archives/1188970.html (accessed on 12 January 2021).
- Administration, N.E. Speed up to Solve the Problem of Power Battery Industry. Available online: http://www.nea.gov.cn/2018-09/10/c_137457800.htm (accessed on 10 September 2018).
- Union, E. Disposal of Spent Batteries and Accumulators. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=LEGISSUM:l21202 (accessed on 9 June 2020).
- Walls, M. Deposit-Refund Systems in Practice and Theory. Resour. Future Discuss. Pap. 2011, 11–47. [Google Scholar] [CrossRef]
- Li, X.; Mu, D.; Du, J.; Cao, J.; Zhao, F. Game-based system dynamics simulation of deposit-refund scheme for electric vehicle battery recycling in China. Resour. Conserv. Recycl. 2020, 157, 104788. [Google Scholar] [CrossRef]
- Tang, Y.; Zhang, Q.; Li, Y.; Wang, G.; Li, Y. Recycling mechanisms and policy suggestions for spent electric vehicles’ power battery -A case of Beijing. J. Clean. Prod. 2018, 186, 388–406. [Google Scholar] [CrossRef]
- Wang, J.; Li, W.; Nozomu, M.; Adachi, T. Closed-loop supply chain under different channel leaderships: Considering different deposit–refund systems practically applied in China. J. Mater. Cycles Waste Manag. 2021, 23, 1765–1776. [Google Scholar] [CrossRef]
- Li, L.; Dababneh, F.; Zhao, J. Cost-effective supply chain for electric vehicle battery remanufacturing. Appl. Energy 2018, 226, 277–286. [Google Scholar] [CrossRef]
- Harper, G.; Sommerville, R.; Kendrick, E.; Driscoll, L.; Slater, P.; Stolkin, R.; Walton, A.; Christensen, P.; Heidrich, O.; Lambert, S.; et al. Recycling lithium-ion batteries from electric vehicles. Nature 2019, 575, 75–86. [Google Scholar] [CrossRef]
- Ciez, R.E.; Whitacre, J.F. Examining different recycling processes for lithium-ion batteries. Nat. Sustain. 2019, 2, 148–156. [Google Scholar] [CrossRef]
- Beaudet, A.; Larouche, F.; Amouzegar, K.; Bouchard, P.; Zaghib, K. Key Challenges and Opportunities for Recycling Electric Vehicle Battery Materials. Sustainability 2020, 12, 5837. [Google Scholar] [CrossRef]
- Kannan, G.; Sasikumar, P.; Devika, K. A genetic algorithm approach for solving a closed loop supply chain model: A case of battery recycling. Appl. Math. Model. 2010, 34, 655–670. [Google Scholar] [CrossRef]
- Wang, L.; Wang, X.; Yang, W. Optimal design of electric vehicle battery recycling network–from the perspective of electric vehicle manufacturers. Appl. Energy 2020, 275, 115328. [Google Scholar] [CrossRef]
- Li, Y.; Xu, F.; Zhao, X. Governance mechanisms of dual-channel reverse supply chains with informal collection channel. J. Clean. Prod. 2017, 155, 125–140. [Google Scholar] [CrossRef]
- Gu, X.; Ieromonachou, P.; Zhou, L.; Tseng, M.-L. Developing pricing strategy to optimise total profits in an electric vehicle battery closed loop supply chain. J. Clean. Prod. 2018, 203, 376–385. [Google Scholar] [CrossRef]
- Qiao, Q.; Zhao, F.; Liu, Z.; Hao, H. Electric vehicle recycling in China: Economic and environmental benefits. Resour. Conserv. Recycl. 2018, 140, 45–53. [Google Scholar] [CrossRef]
- Ma, W.-M.; Zhao, Z.; Ke, H. Dual-channel closed-loop supply chain with government consumption-subsidy. Eur. J. Oper. Res. 2013, 226, 221–227. [Google Scholar] [CrossRef]
- Wang, W. Deposit-refund System of a Closed-loop Supply Chain under Competition between Manufacturers. Chin. J. Manag. Sci. 2021, 29, 179–188. [Google Scholar] [CrossRef]
- Wang, Y.; Chang, X.; Chen, Z.; Zhong, Y.; Fan, T. Impact of subsidy policies on recycling and remanufacturing using system dynamics methodology: A case of auto parts in China. J. Clean. Prod. 2014, 74, 161–171. [Google Scholar] [CrossRef]
- Liu, H.; Lei, M.; Deng, H.; Leong, G.K.; Huang, T. A dual channel, quality-based price competition model for the WEEE recycling market with government subsidy. Omega 2016, 59, 290–302. [Google Scholar] [CrossRef]
- Zhou, W.; Zheng, Y.; Huang, W. Competitive advantage of qualified WEEE recyclers through EPR legislation. Eur. J. Oper. Res. 2017, 257, 641–655. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, Y.; Fan, L.; He, L.; Da, Q. Research on the premium and penalty mechanism of the reverse supply chain considering various goals of government. Chin. J. Manag. Sci. 2015, 23, 68–76. [Google Scholar] [CrossRef]
- Zhang, H.; Zheng, Y.; Cao, J.; Qiu, Y. Has government intervention effectively encouraged the use of waste cooking oil as an energy source? Comparison of two Chinese biofuel companies. Energy 2017, 140, 708–715. [Google Scholar] [CrossRef]
- Li, X.; Zuo, H. Impacts of government double intervention on dual-sale-channel closed-loop supply chain. Syst. Eng. Theory Pract. 2017, 37, 2600–2610. [Google Scholar]
- Wang, W.; Ding, J.; Sun, H. Reward-penalty mechanism for a two-period closed-loop supply chain. J. Clean. Prod. 2018, 203, 898–917. [Google Scholar] [CrossRef]
- Song, X.; Geng, Y.; Dong, H.; Chen, W. Social network analysis on industrial symbiosis: A case of Gujiao eco-industrial park. J. Clean. Prod. 2018, 193, 414–423. [Google Scholar] [CrossRef]
- Linderhof, V.; Oosterhuis, F.H.; van Beukering, P.J.; Bartelings, H. Effectiveness of deposit-refund systems for household waste in the Netherlands: Applying a partial equilibrium model. J. Environ. Manag. 2018, 232, 842–850. [Google Scholar] [CrossRef]
- Bohm, P. Deposit-Refund Systems: Theory and Applications to Environmental, Conservation, and Consumer Policy; Resources for the Future, Inc.: Washington, DC, USA, 1981. [Google Scholar]
- Buffington, J. The viability of a “Voluntary Refund-Deposit System” for Aluminum can Recycling in the US. In Light Metals 2014; Springer: Berlin/Heidelberg, Germany, 2014; pp. 913–918. [Google Scholar]
- Gong, Y.; Chen, M.; Wang, Z.; Zhan, J. With or without deposit-refund system for a network platform-led electronic closed-loop supply chain. J. Clean. Prod. 2020, 281, 125356. [Google Scholar] [CrossRef]
- Xie, T.; Zhang, J.; Wang, F. Decision-Making Models and Effects of Deposit-Refund System for E-Waste in China. Oper. Reserch Manag. Sci. 2017, 26, 182–189. [Google Scholar]
- Zhang, F.; Zhang, R. Trade-in remanufacturing, customer purchasing behavior, and government policy. Manuf. Serv. Oper. Manag. 2018, 20, 601–616. [Google Scholar] [CrossRef]
- Dou, G.; Choi, T.-M. Does implementing trade-in and green technology together benefit the environment? Eur. J. Oper. Res. 2021, 295, 517–533. [Google Scholar] [CrossRef]
- Park, S.; Mowen, J.C. Replacement purchase decisions: On the effects of trade-ins, hedonic versus utilitarian usage goal, and tightwadism. J. Consum. Behav. Int. Res. Rev. 2007, 6, 123–131. [Google Scholar] [CrossRef]
- Liu, J.; Zhai, X.; Chen, L. Optimal pricing strategy under trade-in program in the presence of strategic consumers. Omega 2018, 84, 1–17. [Google Scholar] [CrossRef]
- Ray, S.; Boyaci, T.; Aras, N. Optimal prices and trade-in rebates for durable, remanufacturable products. Manuf. Serv. Oper. Manag. 2005, 7, 208–228. [Google Scholar] [CrossRef]
- Miao, Z.; Fu, K.; Xia, Z.; Wang, Y. Models for closed-loop supply chain with trade-ins. Omega 2017, 66, 308–326. [Google Scholar] [CrossRef]
- Hu, S.; Ma, Z.-J.; Sheu, J.-B. Optimal prices and trade-in rebates for successive-generation products with strategic consumers and limited trade-in duration. Transp. Res. Part E Logist. Transp. Rev. 2019, 124, 92–107. [Google Scholar] [CrossRef]
- Miao, Z.; Mao, H.; Fu, K.; Wang, Y. Remanufacturing with trade-ins under carbon regulations. Comput. Oper. Res. 2018, 89, 253–268. [Google Scholar] [CrossRef]
- Ferrer, G.; Swaminathan, J.M. Managing New and Remanufactured Products. Manag. Sci. 2006, 52, 15–26. [Google Scholar] [CrossRef]
- Wei, J.; Zhao, J. Pricing and remanufacturing decisions in two competing supply chains. Int. J. Prod. Res. 2014, 53, 258–278. [Google Scholar] [CrossRef]
- Hong, X.; Govindan, K.; Xu, L.; Du, P. Quantity and collection decisions in a closed-loop supply chain with technology licensing. Eur. J. Oper. Res. 2017, 256, 820–829. [Google Scholar] [CrossRef]
- Luo, C.; Leng, M.; Tian, X.; Wang, S. Subsidizing purchases of public interest products: A duopoly analysis under a subsidy scheme. Oper. Res. Lett. 2017, 45, 543–548. [Google Scholar] [CrossRef]
- Esenduran, G.; Kemahlıoğlu-Ziya, E.; Swaminathan, J.M. Impact of Take-Back Regulation on the Remanufacturing Industry. Prod. Oper. Manag. 2017, 26, 924–944. [Google Scholar] [CrossRef]
- Administration, N.E. Interim Measures to Encourage the Purchase and Use of New EVs in Shanghai. Available online: http://www.nea.gov.cn/2014-05/23/c_133356393.htm (accessed on 23 May 2014).
- Development and Reform Commission of Shenzhen Municipality. Finance Support Policy for the Promotion of New Energy Vehicle in Shenzhen. Available online: http://fgw.sz.gov.cn/zwgk/qt/tzgg/content/post_4584163.html (accessed on 18 January 2019).
- Network, P.A. What is the Capacity of Electric Vehicle Power Battery? Available online: https://www.pcauto.com.cn/jxwd/1596/15963515.html (accessed on 9 May 2019).
- High-Tech Lithium Battery. THE Price of Power Battery System Will Drop to 1.5 yuan/wh within 4 Years. Available online: https://www.gg-lb.com/asdisp2-65b095fb-25053-.html (accessed on 26 October 2016).
- Xie, J. Pareto Equilibrium of New Energy Vehicle Power Battery Recycling Based on Extended Producer Responsibility. Chin. J. Manag. Sci. 2022, 28, 1–12. [Google Scholar] [CrossRef]
- News, G. Subsidies Will be Available for the Purchase of Home Appliances Trade-in. Available online: http://www.gxnews.com.cn/staticpages/20190622/newgx5d0d8566-18440517.shtml (accessed on 22 June 2019).

| Symbols | Description |
|---|---|
| The selling price per unit for the new EV batteries | |
| The recycling price per unit for the waste EV batteries | |
| Potential market demand of the new EV batteries | |
| The residual value per unit for the waste EV batteries | |
| The EV manufacturer’s effort cost coefficient for trade-in strategy | |
| The purchasing cost per unit for the new EV batteries | |
| The recycling cost per unit for the waste EV batteries | |
| The sale quantity of the new EV batteries | |
| Potential volume of the waste EV batteries | |
| The collection rate baseline set by the government () | |
| The actual collection rate of the EV manufacturer | |
| The trade-in discount set by the EV manufacturer | |
| The reward/penalty coefficient with the reward–penalty mechanism () | |
| The deposit amount per unit for the new EV batteries with deposit–refund mechanism () | |
| The refund coefficient with the deposit–refund mechanism () | |
| The environmental benefits of recycling a waste EV battery | |
| The environmental damage caused by a waste EV battery that is not recycled | |
| The profit of the EV manufacturer with the reward–penalty mechanism | |
| The profit of the recycling enterprise with the reward–penalty mechanism | |
| Government’s concern for social welfare with the reward–penalty mechanism | |
| The profit of the EV manufacturer with the deposit–refund mechanism | |
| The profit of the recycling enterprise with the deposit–refund mechanism | |
| Government’s concern for social welfare with the deposit–refund mechanism |
| Variable Range | |||
|---|---|---|---|
| τ | |||
| Parameter | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Value | 2.61 | 2.9 | 6.75 | 20% | 7.2 | 0.034 | 0.08 | 0.5 | [0, 2.5] | [0, 2.5] |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hao, H.; Xu, W.; Wei, F.; Wu, C.; Xu, Z. Reward–Penalty vs. Deposit–Refund: Government Incentive Mechanisms for EV Battery Recycling. Energies 2022, 15, 6885. https://doi.org/10.3390/en15196885
Hao H, Xu W, Wei F, Wu C, Xu Z. Reward–Penalty vs. Deposit–Refund: Government Incentive Mechanisms for EV Battery Recycling. Energies. 2022; 15(19):6885. https://doi.org/10.3390/en15196885
Chicago/Turabian StyleHao, Hao, Wenxian Xu, Fangfang Wei, Chuanliang Wu, and Zhaoran Xu. 2022. "Reward–Penalty vs. Deposit–Refund: Government Incentive Mechanisms for EV Battery Recycling" Energies 15, no. 19: 6885. https://doi.org/10.3390/en15196885
APA StyleHao, H., Xu, W., Wei, F., Wu, C., & Xu, Z. (2022). Reward–Penalty vs. Deposit–Refund: Government Incentive Mechanisms for EV Battery Recycling. Energies, 15(19), 6885. https://doi.org/10.3390/en15196885






