Method and a Device for Testing the Friction Force in Precision Pairs of Injection Apparatus of the Self-Ignition Engines
Abstract
:1. Introduction
2. Friction Power Losses
2.1. Friction Power Losses in Piston Internal Combustion Engines
2.2. Friction Power Losses in Injection Apparatus
3. Tests of Friction Force in Injectors of Combustion Engines
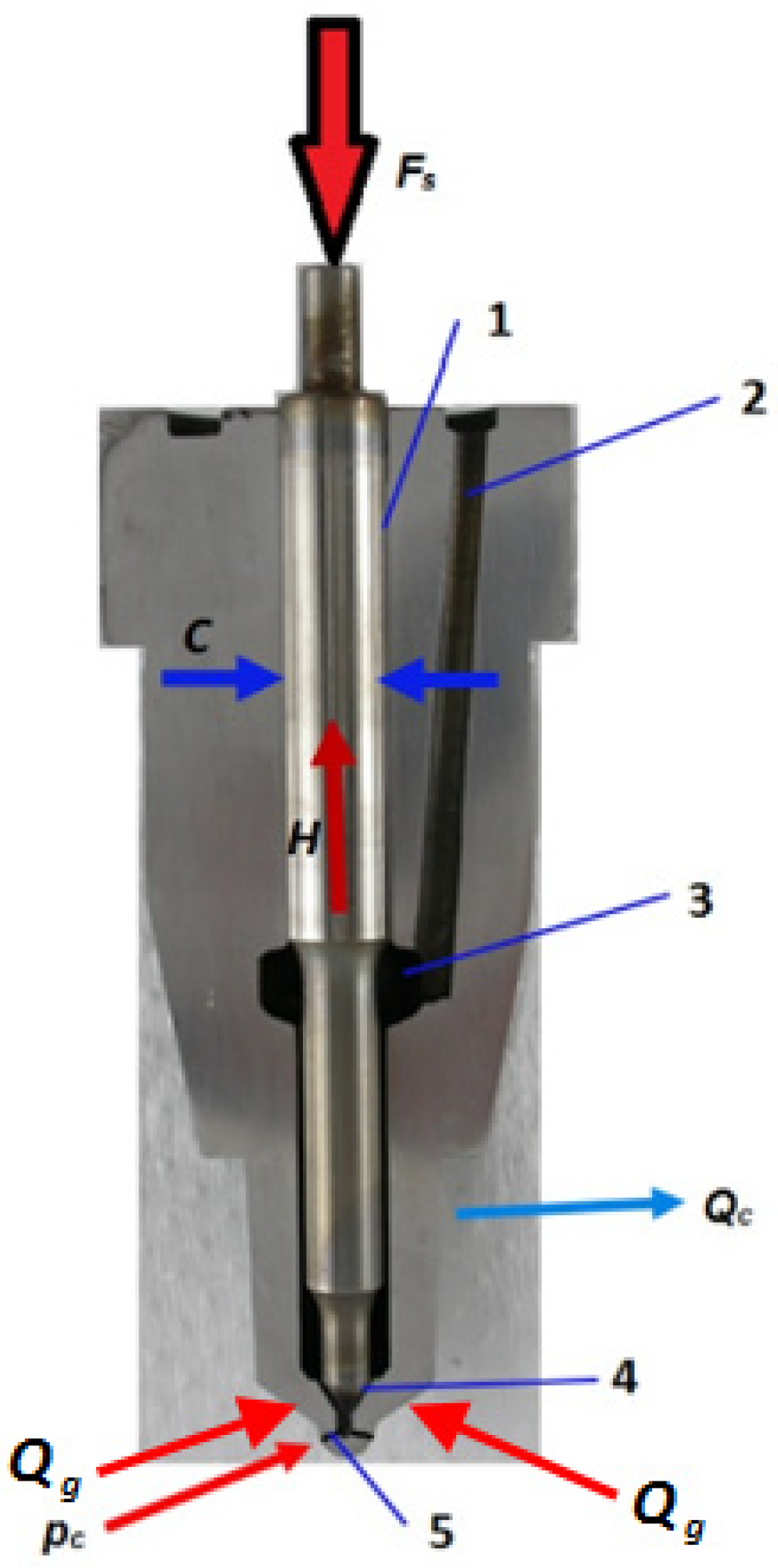
4. Test Method
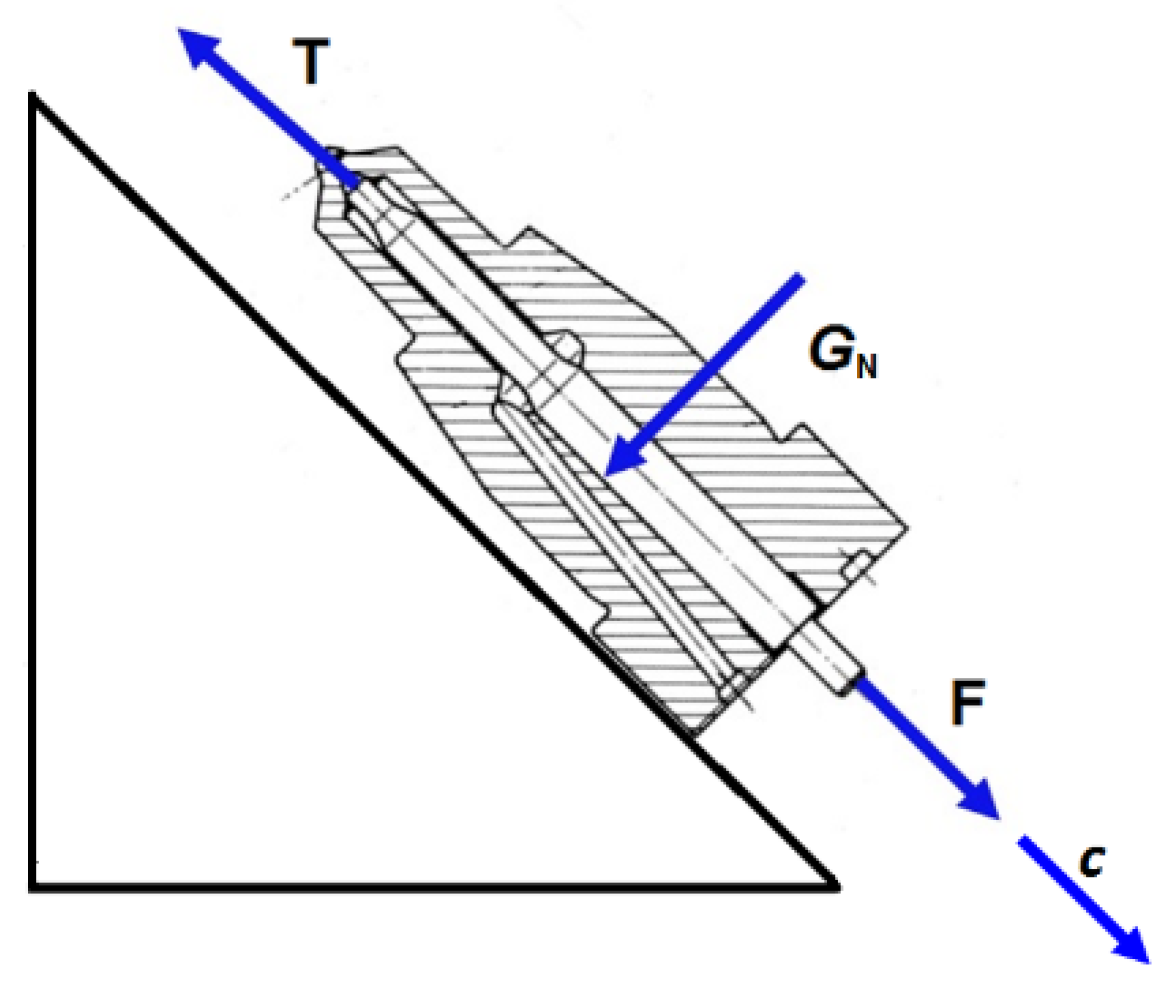
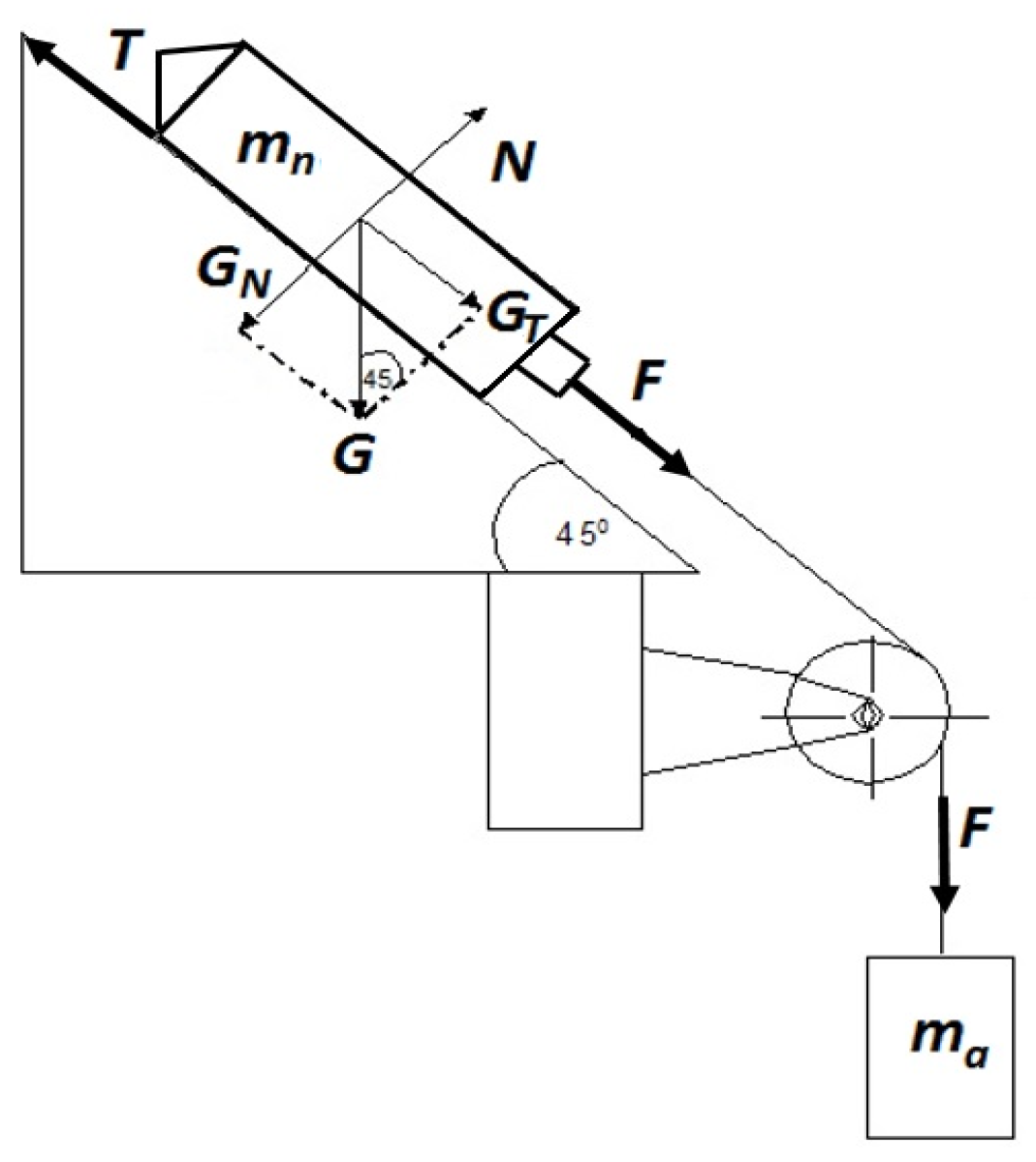
4.1. Measurement Method
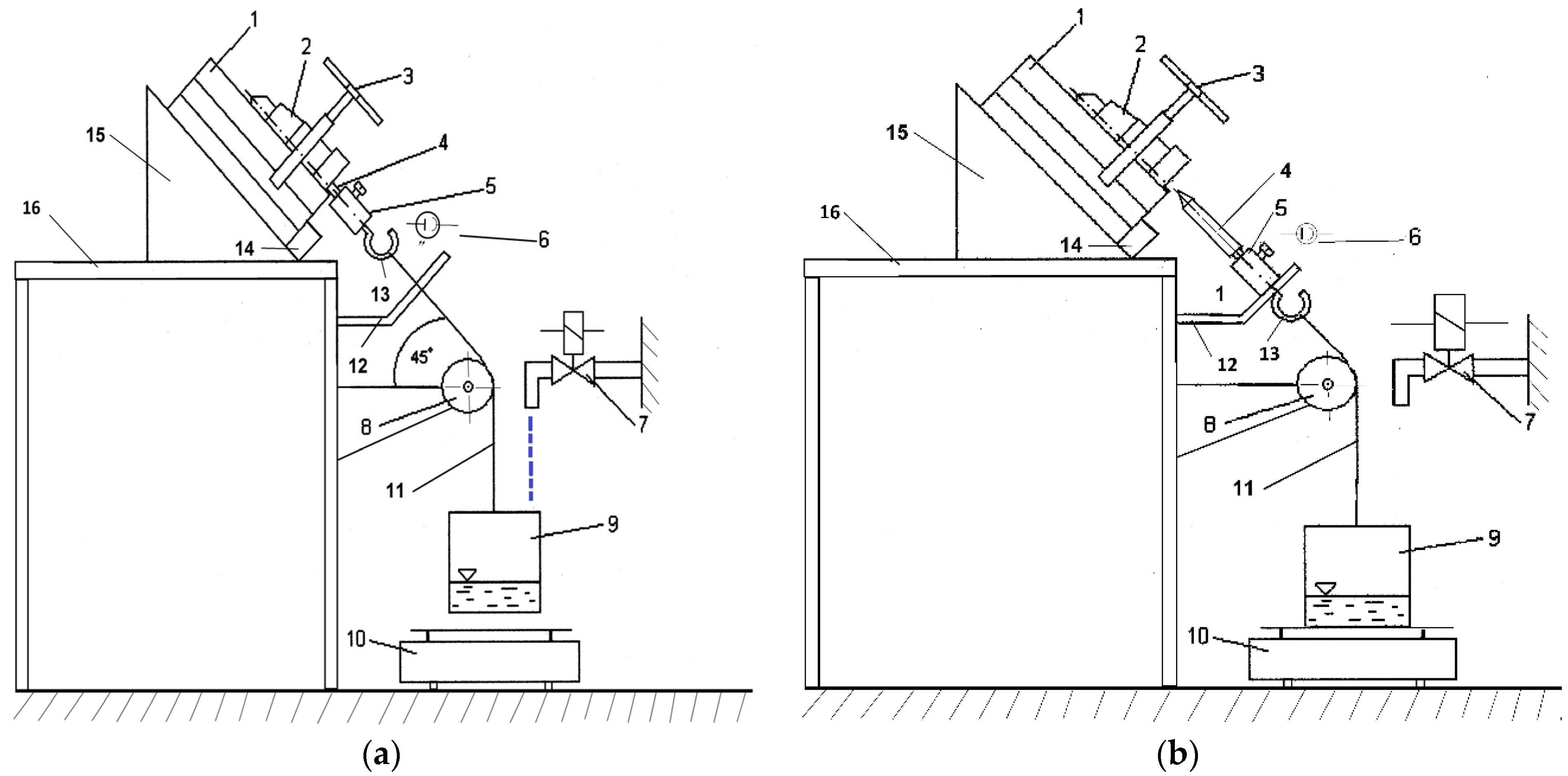
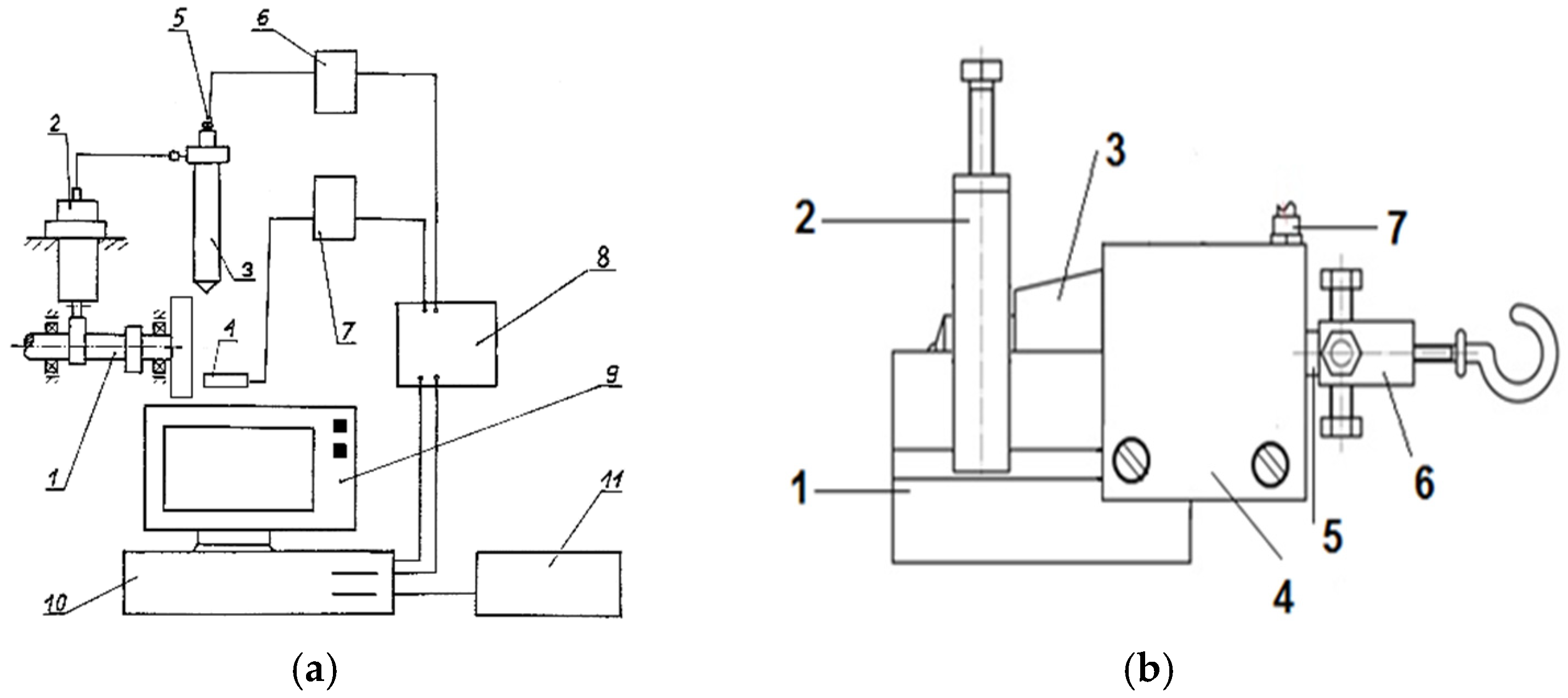
4.2. Measurement Stands
4.3. Estimating Measurement Errors
5. Sample Test Results
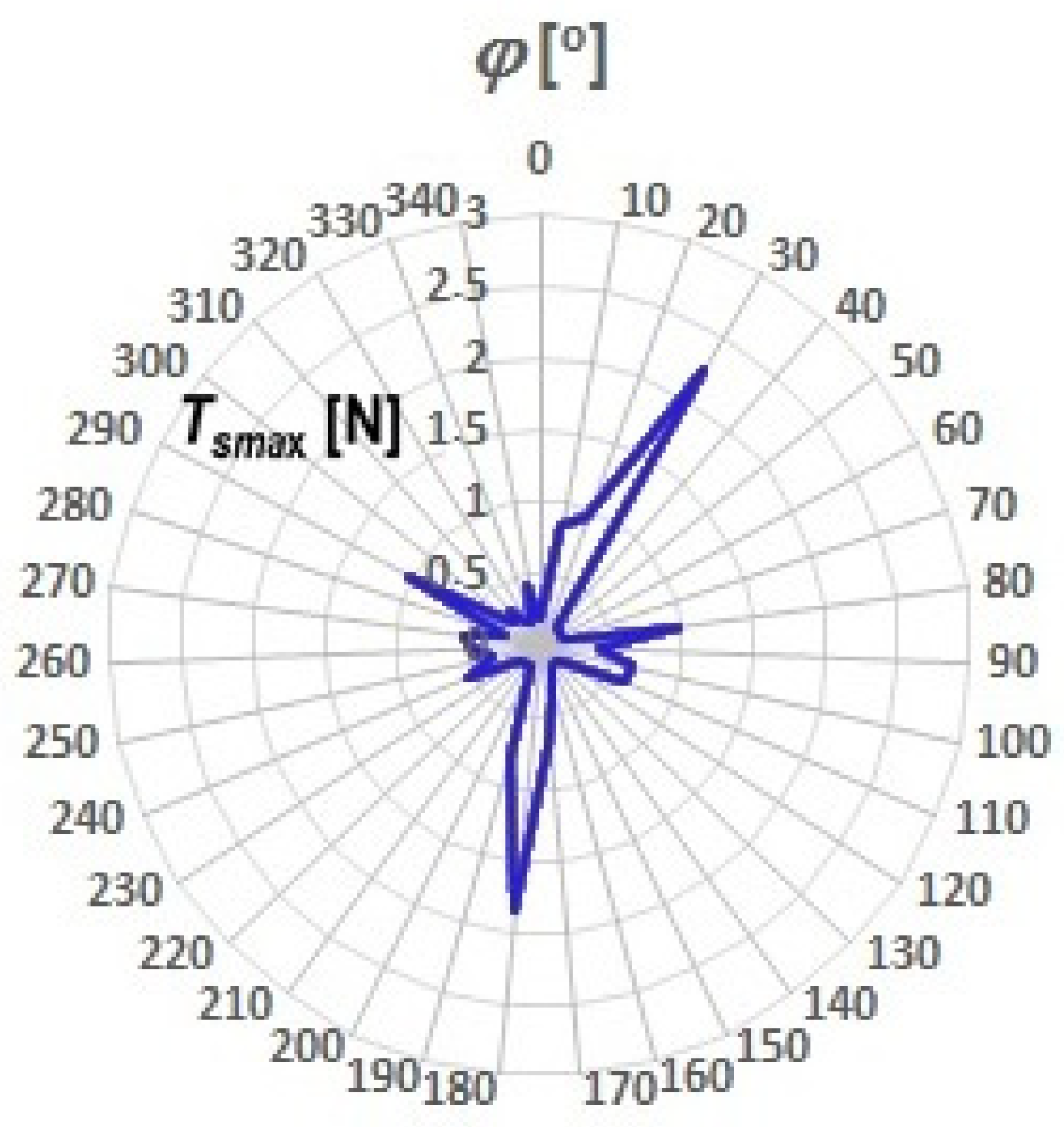
5.1. Results of Measurements of the Maximum Static Friction Force
5.2. Results of Measurements of Dynamic Static Friction Force
5.3. Influence of Various Factors on the Values of the Maximum Friction Force
6. Conclusions
7. Patents
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| a | acceleration of the injector needle | mn | mass of the needle |
| E | energy stream supplied to the engine in the fuel | N | pressure force perpendicular to the surface |
| Ee | useful energy stream | s | the dimension of the needle nozzle perpendicular to the longitudinal axis |
| Eco | cooling losses | Td | dynamic friction force |
| Eo | outlet losses | Ts | static friction force |
| Ein | energy stream of incomplete combustion losses in self-ignition engines | Tsmax | maximum static friction force |
| Eh | stream of energy lost to the environment through heat exchange | Tsmaxa | average maximum static friction force |
| Eo | outlet losses | Nmax | frictional power |
| Em | energy flux lost to mechanical losses | α | the angle of the inclined plane |
| Er | the flux of the rest of the energy losses and the heat-balance error | relative maximum error of the signal processing | |
| c | needle-movement speed | φ | angle of position of the body and the nozzle needle |
| g | acceleration of gravity | μd(c) | motion-friction coefficient |
| h | needle lift | μs | the coefficient of static friction |
| LT | friction work | σ(Ts) | random absolute root means square error of the static friction force in time τ |
| ma | additional mass | random relative error of the static frictional force |
References
- Yan, R.; Wang, S.; Du, Y. Development of a two-stage ship fuel consumption prediction and reduction model for a dry bulk ship. Transp. Res. 2020, 138, 101930. [Google Scholar] [CrossRef]
- Wong, V.W.; Tung, S.C. Overview of automotive engine friction and reduction trends-effects of surface, material, and lubricant-additive technologies. Friction 2016, 4, 1–28. [Google Scholar] [CrossRef]
- Li, R.; Meng, X.H.; Xie, Y.B. A new coupling tribodynamic model of crosshead slipper-guide system and piston skirt-liner system of low-speed marine diesel engines. Tribol. Int. 2018, 117, 189–205. [Google Scholar] [CrossRef]
- Delprete, C.; Gastaldi, C.; Giorio, L. A minimal input engine friction model for power loss prediction. Lubricants 2022, 10, 94. [Google Scholar] [CrossRef]
- Monieta, J. Selection of diagnostic symptoms and injection subsystems of marine reciprocating internal combustion engines. Appl. Sci. 2019, 9, 1540. [Google Scholar] [CrossRef]
- Monieta, J. Research on the friction force of the needle in the nozzle body of marine diesel engines in the presence of a lubricating medium that account position changes. Tribologia 2012, 2, 41–57. [Google Scholar]
- Monieta, J.; Lorek, Ł. Researches of friction force of injector nozzles in injector bodies of marine diesel engines in the presence of lubricating compound. J. Pol. CIMAC 2008, 3, 111–121. [Google Scholar]
- Monieta, J.; Kasyk, L. Optimization of design and technology of injector nozzles in terms of minimizing energy losses on friction in compression ignition engines. Appl. Sci. 2021, 11, 7341. [Google Scholar] [CrossRef]
- Bielawski, P. Diagnosing machines with the use of friction. Diagnostics 2003, 29, 15–20. [Google Scholar]
- Fadel, C.; Chalhoub, N.G.; Kfoury, G.A. Direct measurement of the piston-assembly friction force in a single cylinder engine under motoring conditions. In Proceedings of the 1st Annual Dynamic Systems and Control Conference 2008, Ann Arbor, MI, USA, 20–22 October 2008; pp. 20–22. [Google Scholar] [CrossRef]
- Karczewski, M.; Szczęch, L. Investigation of internal resistance of a diesel engine. Sci. J. PNA 2013, 193, 27–49. [Google Scholar]
- Aydin, Z.; Savas, Ö.; Parlak, A.; Keskin, I.; Ünlügençoglu, K. Effects of fuel contamination to marine lubricant. Acta Phys. Pol. 2016, 129, 1–4. [Google Scholar] [CrossRef]
- Truhan, J.J.; Qu, J.; Blau, P.J. The effect of lubricating oil condition on the friction and wear of piston ring and cylinder liner materials in a reciprocating bench test. Wear 2005, 259, 1048–1055. [Google Scholar] [CrossRef]
- Ruddy, B.L.; Dowson, D.; Economus, P.N. A theoretical analysis of the twin land type of oil-control piston ring. J. Mech. Eng. Sci. 1981, 23, 51–62. [Google Scholar] [CrossRef]
- Livanos, G.A.; Kyrtatos, N.P. Friction model of a marine diesel engine piston assembly. Tribol. Int. 2007, 40, 1441–1453. [Google Scholar] [CrossRef]
- Vølund, A. Measurement and Calculation of Frictional Loss in Large Two-Stroke Engines. Ph.D. Thesis, Technical University of Denmark, Lyngby, Denmark, 2003; pp. 1–200. [Google Scholar]
- Knauder, C.; Allmaier, H.; Sander, D.E.; Sams, T. Investigations of the friction losses of different engine concepts. Lubricants 2019, 7, 39. [Google Scholar] [CrossRef]
- Wang, Z.J.; Shuai, S.J.; Li, Z.J.; Yu, W.B. A Review of Energy Loss Reduction Technologies for Internal Combustion Engines to Improve Brake Thermal Efficiency. Energies 2021, 14, 6656. [Google Scholar] [CrossRef]
- Abril, S.O.; Rojas, J.P.; Florez, E.N. Numerical methodology for determining the energy losses in auxiliary systems and friction processes applied to low displacement diesel engines. Lubricants 2020, 8, 103. [Google Scholar] [CrossRef]
- Idzior, M. A Study of Combustion Ignition Engine Injector Nozzle Parameters in the Aspect of Operating Properties. Scientific Dissertations, Poznan University of Technology, Poznan, Poland, 2004; pp. 51–139. [Google Scholar]
- Stöeckli, M.; Affolter, P.; Otto, H. Durability and long-term stability of electronic fuel injection systems for Diesel, HFO and gas engines. In Proceedings of the 25th CIMAC Congress 2007, Viena, Austria, 21–24 May 2007; pp. 1–9. [Google Scholar]
- Włodarski, J.K. Reciprocating Internal Combustion Engines—Tribological Processes; Publishing House of Communication and Communications: Warsaw, Poland, 1982; pp. 56–63. [Google Scholar]
- Baratta, M.; Catania, A.E.; Pesce, F.C. CNG Injector Nozzle Design and Flow Prediction. In Proceedings of the ASME 2010 Internal Combustion Engine Division Fall Technical Conference, San Antonio, TX, USA, 12–15 September 2010; pp. 795–800. [Google Scholar] [CrossRef]
- Włodarski, J.K. Operating States of Marine Combustion Engines; Maritime University of Gdynia Publisher: Gdynia, Poland, 2001; pp. 159–178. [Google Scholar]
- Hebda, M. Friction, Lubrication and Wear Processes of Machines; Publisher of the Institute of Sustainable Technologies: Warsaw, Poland; Radom, Poland, 2007; pp. 155–455. [Google Scholar]
- Drozdowski, J. A Study on Thermal Loads, Cavitation and Reliability of Marine Diesel Engine Fuel Injectors. Study 30; Maritime University Szczecin: Szczecin, Poland, 1998; pp. 33–84. [Google Scholar]
- Daimler, C.; Güttler, J.; Hora, P. Einspritzdüse für in Einspritzsystem sowie ein Erfahren zur Herstellung einer Einspritzdüse eines Einspritzsystem eines Kraftfahrzeuges. Deutschland Patent 10256590, 3 June 2004. [Google Scholar]
- Monieta, J.; Łukomski, M. Methods and means of estimation of technical state features of the marine diesel engines injector nozzles type Sulzer 6AL20/24. Sci. J. Marit. Univ. Szczec. 2005, 5, 383–392. [Google Scholar]
- Theodorakakos, A.; Strotos, G.; Mitroglou, N.; Atkin, C.; Gavaises, M. Friction-induced heating in nozzle hole micro-channels under extreme fuel pressurisation. Fuel 2014, 123, 143–150. [Google Scholar] [CrossRef]
- Strotos, G.; Koukouvinis, P.; Theodorakakos, A.; Gavaises, M.; Bergeles, G. Transient heating effects in high pressure Diesel injector nozzles. Int. J. Heat Fluid Flow 2015, 51, 257–267. [Google Scholar] [CrossRef]
- Vidal, A.; Kolovos, K.; Gold, M.R.; Pearson, R.; Koukouvinis, P.; Gavaises, M. Preferential cavitation and friction-induced heating of multi-component Diesel fuel surrogates up to 450 MPa. Int. J. Heat Mass Transf. 2021, 166, 120744. [Google Scholar] [CrossRef]
- Szczerek, M.; Tuszyński, W. Tribological Studies. Seizure; ITeE: Radom, Poland, 2000; pp. 7–142. [Google Scholar]
- Yasunori, K. Fuel Injection Nozzle. U.S. Patent 20020109021A1, 15 August 2002. [Google Scholar]
- Yasunori, K.; Takashi, I. Fuel Injection Nozzle with a Member to Reduce the Frictional Force Developed between Parts during the Clamping. EP Patent 1236887A3, 14 January 2004. [Google Scholar]
- Holmberg, K.; Andersson, P.; Nylund, N.O.; Mäkelä, K.; Erdemir, A. Global energy consumption due to friction in trucks and buses. Tribol. Int. 2014, 78, 94–114. [Google Scholar] [CrossRef]
- Zabelin, P. Internal Combustion Engine Efficiency. U.S. Patent 20140318507A1, 30 October 2014. [Google Scholar]
- Longwic, R.; Sander, P.; Górski, K.; Jańczuk, B.; Zdziennicka, A.; Szymczyk, K. The new concept of using rapeseed oil as a fuel to power diesel engines. Rail Transp. Tech. 2013, 10, 2877–2899. [Google Scholar]
- Lopez, J.J.; Salvador, F.J.; de la Garza, O.A. Characterization of the pressure losses in a common rail diesel injector. Proc. Inst. Mech. Eng. 2012, 226, 1697–1706. [Google Scholar] [CrossRef] [Green Version]
- Ciornei, F.C.; Alaci, S.; Romanu, I.C.; Mihai, I.; Lazar, V.C. Aspects concerning the friction for the motion on an inclined plane of an axisymmetric body. Mater. Sci. Eng. 2019, 477, 1–10. [Google Scholar] [CrossRef]
- Dudziak, M.; Domek, G.; Kołodziej, A.; Talaśka, K. Contact problems between the hub and the shaft with a three-angular shape of cross-section for different angular positions. Procedia Eng. 2014, 96, 50–58. [Google Scholar] [CrossRef]
- Piaseczny, L. Repair Technology of Marine Internal Combustion Engines; Maritime Publisher: Gdansk, Poland, 1992; pp. 352–414. [Google Scholar]
- Farth, A.; Volgt, A.; Spickenreuther, M. Method for Setting the Nozzle Opening Pressure for an Injection Nozzle and Arrangement for Carrying out the Method. U.S. Patent 6976389 B2, 13 June 2002. [Google Scholar]
- Vinogradov, M.; Dorfman, V. Method and Device for Measuring Forces. U.S. Patent WO2003036249A1, 1 May 2003. [Google Scholar]
- Kelemenova, T.; Dovica, M.; Bozek, P.; Koláriková, I.; Benedik, O.; Virgala, I.; Prada, E.; Mikova, L.; Kot, L.; Kelemen, M. Specific problems in measurement of coefficient of friction using variable incidence tribometer. Symmetry 2020, 12, 1235. [Google Scholar] [CrossRef]





| Engine Type | AL20/24D | L16/24 |
|---|---|---|
| Number of spray holes | 7, 9 | 8 |
| Spray-hole diameter [mm] | 0.23; 0.25 | 0.29 |
| Spray angle [°] | 159 | 145 |
| Needle lift [mm] | 0.50 | 0.40 |
| Needle sealing-cone angle [mm] | 7, 8 | 6 |
| Needle length without pin [mm] | 39.3 | 75.7 |
| License | Sulzer | MAN B&W |
| ma kg | mn kg | Ga N | GT N | Tsmax N | Tsmaxa N |
|---|---|---|---|---|---|
| 0.2068 | 0.02522 | 2.028 | 0.1748 | 2.203 | 2.097 |
| 0.2408 | 0.02512 | 2.361 | 0.1742 | 2.536 | |
| 0.1638 | 0.02512 | 1.606 | 0.1742 | 1.780 | |
| 0.1728 | 0.02512 | 1.694 | 0.1742 | 1.869 | |
| 0 | 0.02670 | 0 | 0.1852 | 0.1852 | 0.1852 |
| 0 | 0.02670 | 0 | 0.1852 | 0.1852 | |
| 0 | 0.02670 | 0 | 0.1852 | 0.1852 | |
| 0 | 0.02670 | 0 | 0.1852 | 0.1852 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monieta, J. Method and a Device for Testing the Friction Force in Precision Pairs of Injection Apparatus of the Self-Ignition Engines. Energies 2022, 15, 6898. https://doi.org/10.3390/en15196898
Monieta J. Method and a Device for Testing the Friction Force in Precision Pairs of Injection Apparatus of the Self-Ignition Engines. Energies. 2022; 15(19):6898. https://doi.org/10.3390/en15196898
Chicago/Turabian StyleMonieta, Jan. 2022. "Method and a Device for Testing the Friction Force in Precision Pairs of Injection Apparatus of the Self-Ignition Engines" Energies 15, no. 19: 6898. https://doi.org/10.3390/en15196898
APA StyleMonieta, J. (2022). Method and a Device for Testing the Friction Force in Precision Pairs of Injection Apparatus of the Self-Ignition Engines. Energies, 15(19), 6898. https://doi.org/10.3390/en15196898







