Energy Absorption Characteristics of Bio-Inspired Honeycomb Column Thin-Walled Structure under Low Strain Rate Uniaxial Compression Loading
Abstract
:1. Introduction
- The proposed BHTSs improved the mechanical performance of the conventional HS, increased the SEA of the manufacturing structure, reduced the mass of the stressed structure and the use of manufacturing materials, which saved resources.
- The application of AM to the manufacture of complex cellular structures not only solves the problem of manufacturing such specimens by traditional industrial methods but also improves material utilization and saves energy.
- In the numerical simulation of BHTSs, specific studies have been made in response to some scholars underestimating the SRE of aluminum alloy materials under low velocity uniaxial compression loading and do not consider the failure behavior of materials.
- The results obtained can provide new ideas and a theoretical basis for the rational design of additive manufacturing porous biomorphic materials, and they have potential application prospects in the fields of protective equipment [8,9], resource utilization efficiency [28,29] and energy saving and emission reduction [30]. In addition, Table 1 lists some other contributions in these research areas.
2. Materials and Methods
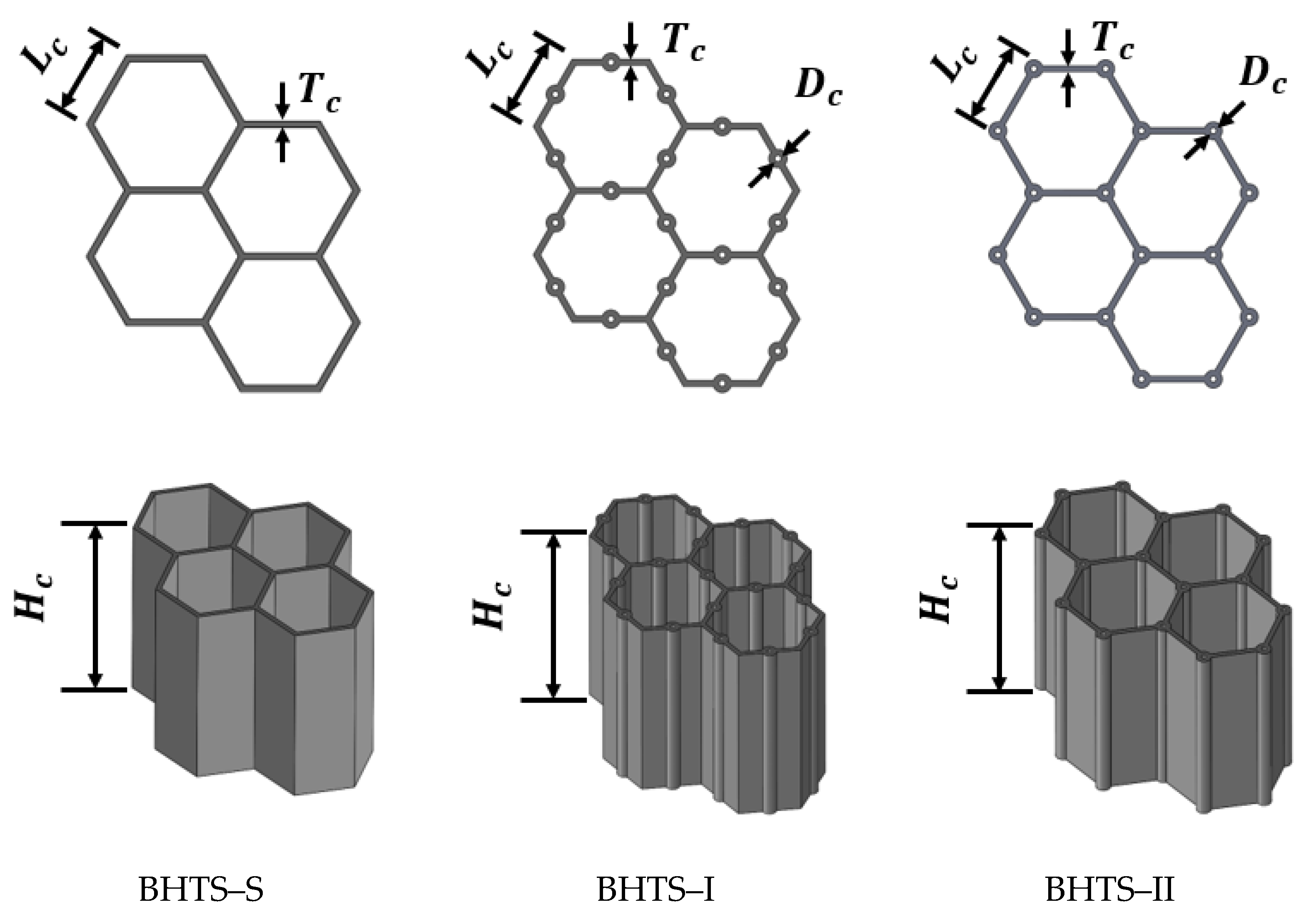
2.1. The Design of BHTSs
2.2. Mechanical Properties of the Base Material for the BHTSs
2.3. Out-of-Plane Uniaxial Compression Test
2.4. Assessment of the EA Performance
2.5. Finite Element Model (FEM)
3. Results and Discussions
3.1. Deformation and Failure Modes
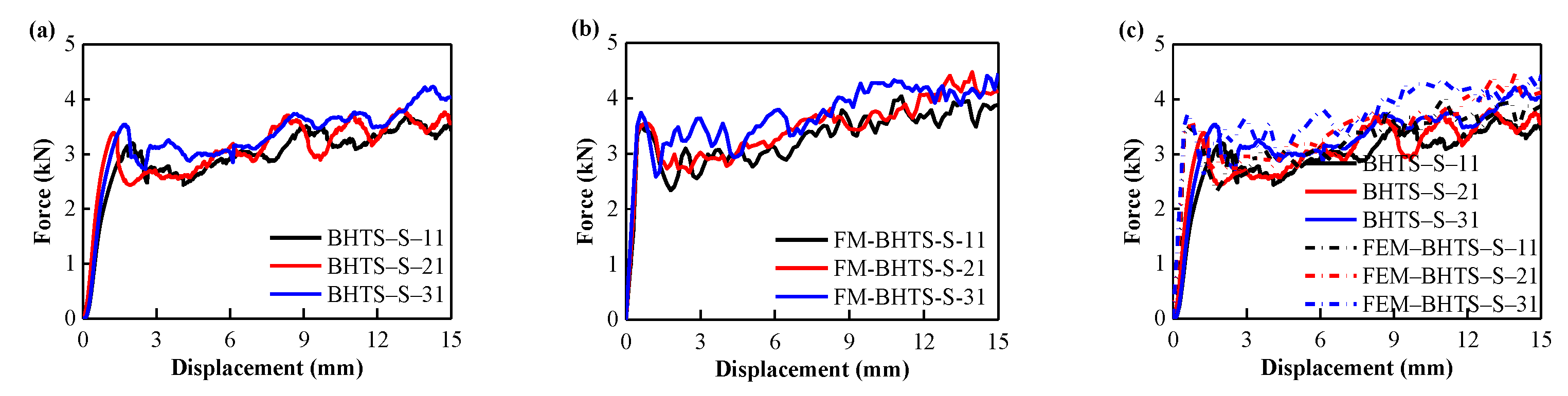
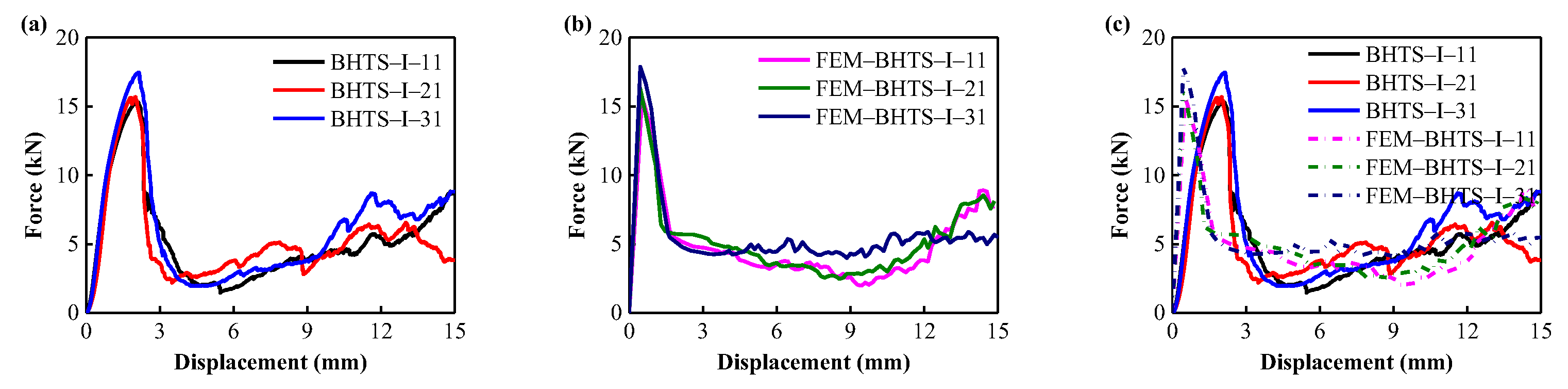
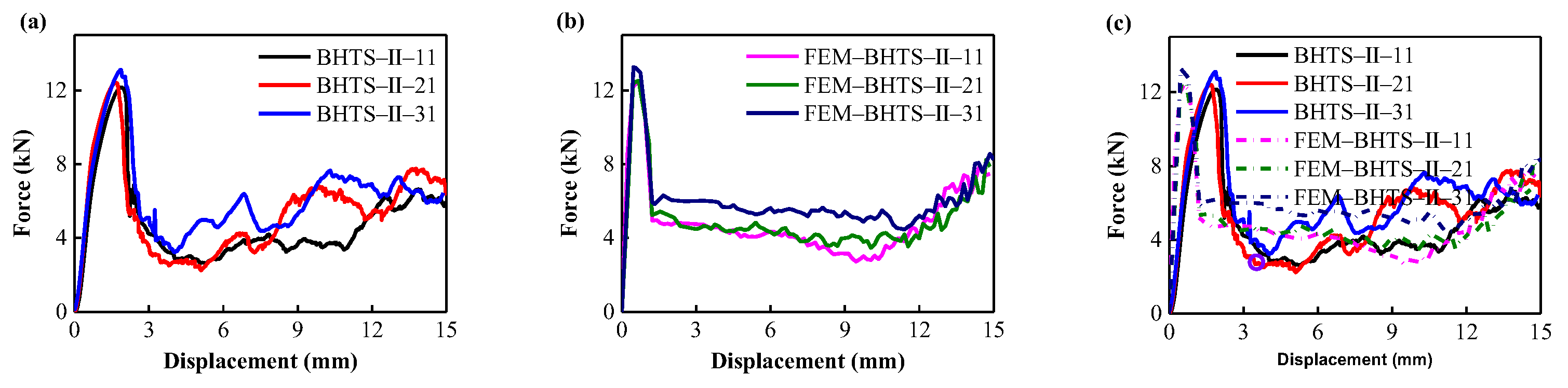
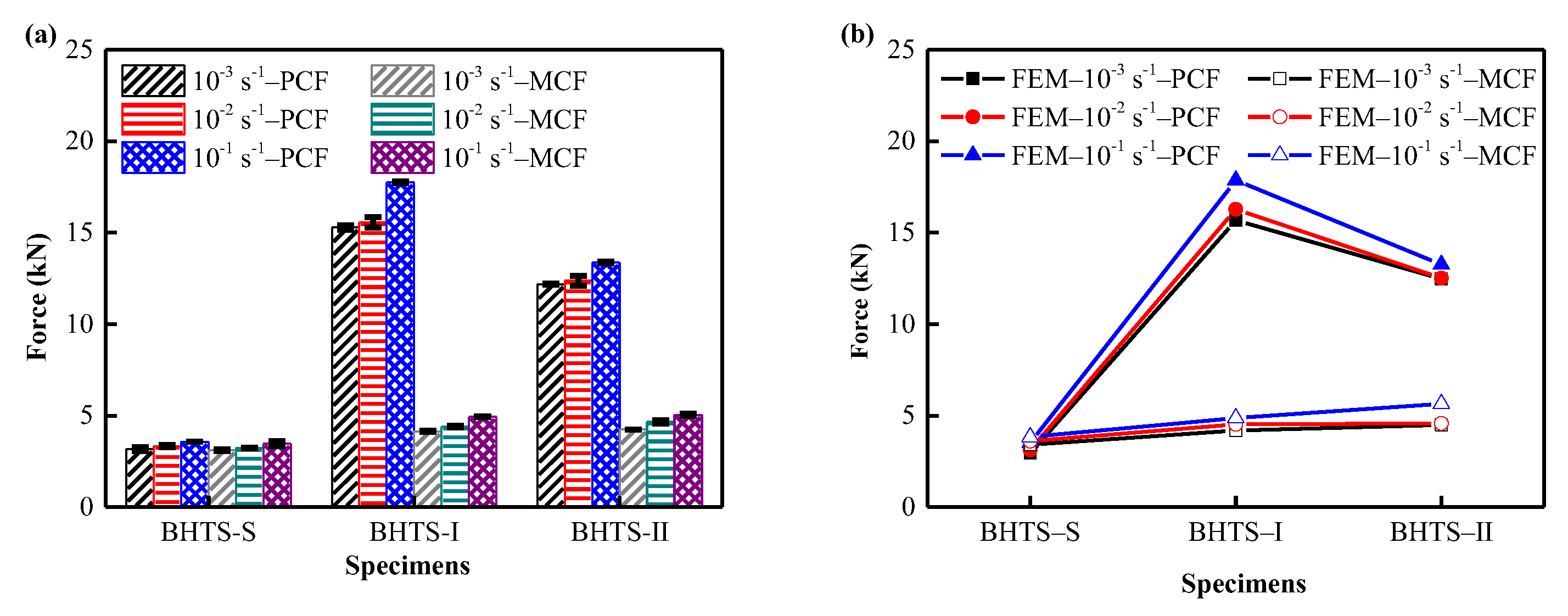
3.2. Validation of the FEM
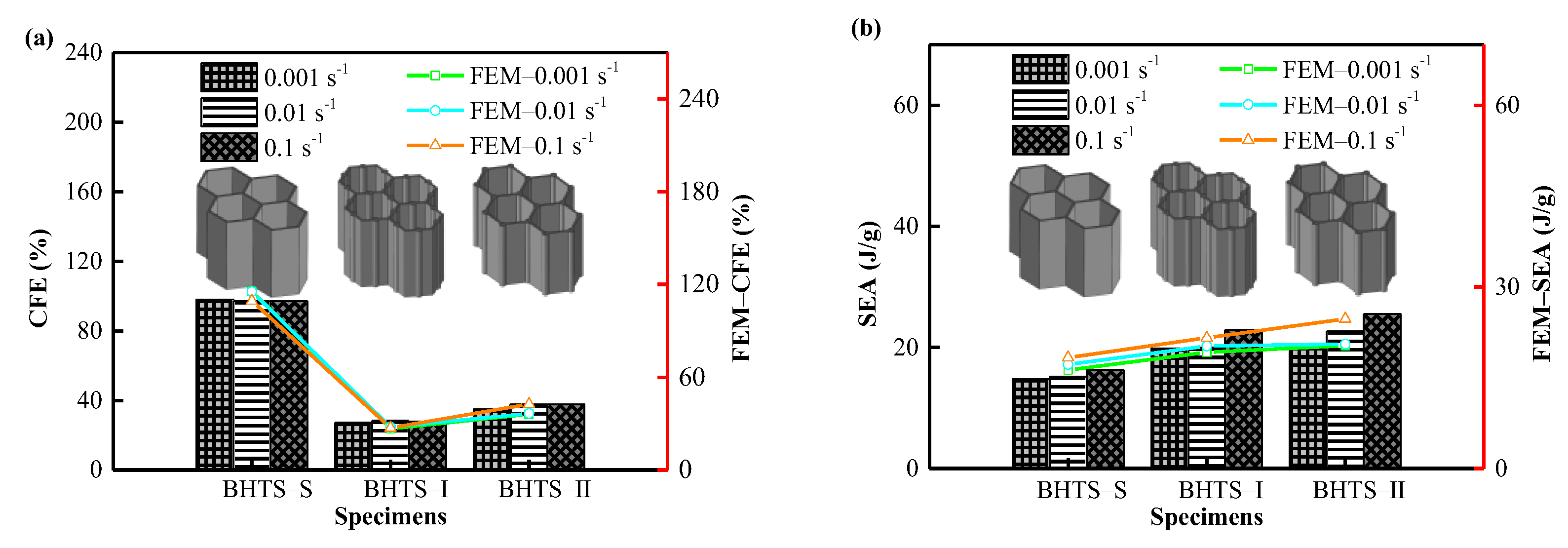
3.3. Mechanical Properties and EA Performance
3.4. Comparison of EA Characteristics of BHTSs
4. Conclusions
- The designed cross-sectional shape had a very significant effect on the BHTS, and the bionic structure of the beetle elytra greatly enhanced the mean crushing force and energy absorption properties of the honeycomb structure.
- The comparison of energy absorption characteristics of BHTS by test shows that the strain rate effect has a significant effect on the energy absorption capacity of BHTS under axial impact load.
- The finite element simulation results are in good agreement with the experimental results. This research method can provide an important reference for the design, manufacture and modeling of materials based on BHTS.
- The finite element simulation and lightweight BHTSs design concept used in the design process of BHTSs greatly reduce the material consumption in the design stage; the additive manufacturing with high utilization rate of materials used in the test process optimizes the use efficiency of materials, conforms to the concept of energy saving and emission reduction, and has potential promotion value.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Notations
| Cell wall thickness | Initial yield stress | ||
| Column height | Strain rate | ||
| Cell side length | Hardening parameter | ||
| Column diameter | , | Strain rate parameter | |
| True strain | Effective plastic strain | ||
| Engineering strain | Plastic hardening modulus | ||
| True stress | Plastic strain | ||
| Engineering stress | Elastic modulus | ||
| Spherical stress tensor | Tangent modulus |
References
- He, W.; Yao, L.; Meng, X.; Sun, G.; Xie, D.; Liu, J. Effect of structural parameters on low-velocity impact behavior of aluminum honeycomb sandwich structures with CFRP face sheets. Thin-Walled Struct. 2019, 137, 411–432. [Google Scholar] [CrossRef]
- Riccio, A.; Raimondo, A.; Saputo, S.; Sellitto, A.; Battaglia, M.; Petrone, G. A numerical study on the impact behaviour of natural fibres made honeycomb cores. Compos. Struct. 2018, 202, 909–916. [Google Scholar] [CrossRef]
- Sun, M.; Wowk, D.; Mechefske, C.; Kim, I.Y. An analytical study of the plasticity of sandwich honeycomb panels subjected to low-velocity impact. Compos. Part B Eng. 2019, 168, 121–128. [Google Scholar] [CrossRef]
- Zhang, J.; Ye, Y.; Qin, Q.; Wang, T. Low-velocity impact of sandwich beams with fibre-metal laminate face-sheets. Compos. Sci. Technol. 2018, 168, 152–159. [Google Scholar] [CrossRef]
- Siivola, J.T.; Minakuchi, S.; Takeda, N. Unloading response prediction of indentation loaded foam core sandwich structures using extended foam material model with tensile hardening. Compos. Part B Eng. 2016, 84, 71–82. [Google Scholar] [CrossRef]
- Feng, D.; Aymerich, F. Damage prediction in composite sandwich panels subjected to low-velocity impact. Compos. Part A Appl. Sci. Manuf. 2013, 52, 12–22. [Google Scholar] [CrossRef]
- di Caprio, F.; Cristillo, D.; Saputo, S.; Guida, M.; Riccio, A. Crashworthiness of wing leading edges under bird impact event. Compos. Struct. 2019, 216, 39–52. [Google Scholar] [CrossRef]
- Ufodike, C.O.; Wang, H.; Ahmed, M.F.; Dolzyk, G.; Jung, S. Design and modeling of bamboo biomorphic structure for in-plane energy absorption improvement. Mater. Des. 2021, 205, 109736. [Google Scholar] [CrossRef]
- Ufodike, C.O. Exploring the Wood Material Properties and Structures for Engineering Application; Florida Agricultural and Mechanical University: Tallahassee, FL, USA, 2020. [Google Scholar]
- du Plessis, A.; Broeckhoven, C.; Yadroitsava, I.; Yadroitsev, I.; Hands, C.H.; Kunju, R.; Bhate, D. Beautiful and functional: A review of biomimetic design in additive manufacturing. Addit. Manuf. 2019, 27, 408–427. [Google Scholar] [CrossRef]
- Zhang, Q.; Yang, X.; Li, P.; Huang, G.; Feng, S.; Shen, C.; Han, B.; Zhang, X.; Jin, F.; Xu, F. Bioinspired engineering of honeycomb structure–Using nature to inspire human innovation. Prog. Mater. Sci. 2015, 74, 332–400. [Google Scholar] [CrossRef]
- Hao, P.; Du, J. Energy absorption characteristics of bio-inspired honeycomb column thin-walled structure under impact loading. J. Mech. Behav. Biomed. Mater. 2018, 79, 301–308. [Google Scholar] [CrossRef] [PubMed]
- Naleway, S.E.; Porter, M.M.; McKittrick, J.; Meyers, M.A. Structural design elements in biological materials: Application to bioinspiration. Adv. Mater. 2015, 27, 5455–5476. [Google Scholar] [CrossRef] [PubMed]
- Naleway, S.E.; Taylor, J.R.; Porter, M.M.; Meyers, M.A.; McKittrick, J. Structure and mechanical properties of selected protective systems in marine organisms. Mater. Sci. Eng. C 2016, 59, 1143–1167. [Google Scholar] [CrossRef]
- Xiang, J.; Du, J.; Li, D.; Liu, K. Aerodynamic performance of the locust wing in gliding mode at low Reynolds number. J. Bionic Eng. 2016, 13, 249–260. [Google Scholar] [CrossRef]
- Chen, J.; Dai, G.; Xu, Y.; Iwamoto, M. Basic study of biomimetic composite materials in the forewings of beetles. Mater. Sci. Eng. A 2008, 483, 625–628. [Google Scholar] [CrossRef]
- Sun, M.; Liang, A.; Watson, G.S.; Watson, J.A.; Zheng, Y.; Jiang, L. Compound Microstructures and Wax Layer of Beetle Elytral Surfaces and Their Influence on Wetting Properties. PLoS ONE 2012, 7, e46710. [Google Scholar] [CrossRef]
- Chen, J.; He, C.; Gu, C.; Liu, J.; Mi, C.; Guo, S. Compressive and flexural properties of biomimetic integrated honeycomb plates. Mater. Des. 2014, 64, 214–220. [Google Scholar] [CrossRef]
- Sun, J.; Ling, M.; Wang, Y.; Chen, D.; Zhang, S.; Tong, J.; Wang, S. Quasi-static and dynamic nanoindentation of some selected biomaterials. J. Bionic Eng. 2014, 11, 144–150. [Google Scholar] [CrossRef]
- Chen, J.; Xie, J.; Zhu, H.; Guan, S.; Wu, G.; Noori, M.N.; Guo, S. Integrated honeycomb structure of a beetle forewing and its imitation. Mater. Sci. Eng. C 2012, 32, 613–618. [Google Scholar] [CrossRef]
- Clark, A.J.; Triblehorn, J.D. Mechanical properties of the cuticles of three cockroach species that differ in their wind-evoked escape behavior. PeerJ 2014, 2, e501. [Google Scholar] [CrossRef] [Green Version]
- Lomakin, J.; Huber, P.A.; Eichler, C.; Arakane, Y.; Kramer, K.J.; Beeman, R.W.; Kanost, M.R.; Gehrke, S.H. Mechanical properties of the beetle elytron, a biological composite material. Biomacromolecules 2011, 12, 321–335. [Google Scholar] [CrossRef]
- Sun, J.-Y.; Tong, J.; Ma, Y.-H. Nanomechanical behaviours of cuticle of three kinds of beetle. J. Bionic Eng. 2008, 5, 152–157. [Google Scholar] [CrossRef]
- Xiang, J.; Du, J. Energy absorption characteristics of bio-inspired honeycomb structure under axial impact loading. Mater. Sci. Eng. A 2017, 696, 283–289. [Google Scholar] [CrossRef]
- Guo, F.; Fei, Q.; Li, Y.; Gupta, N. Dynamic Out-of-Plane Compressive Failure Mechanism of Carbon/Carbon Composite: Strain Rate Effect on the Defect Propagation and Microstructure Failure. J. Eng. Mater. Technol. 2021, 143, 1–31. [Google Scholar]
- Rosenthal, I.; Stern, A.; Frage, N. Strain rate sensitivity and fracture mechanism of AlSi10Mg parts produced by selective laser melting. Mater. Sci. Eng. A 2017, 682, 509–517. [Google Scholar] [CrossRef]
- Hadadzadeh, A.; Amirkhiz, B.S.; Odeshi, A.; Li, J.; Mohammadi, M. Role of hierarchical microstructure of additively manufactured AlSi10Mg on dynamic loading behavior. Addit. Manuf. 2019, 28, 1–13. [Google Scholar] [CrossRef]
- Sharma, P.; Said, Z.; Kumar, A.; Nižetić, S.; Pandey, A.; Hoang, A.T.; Huang, Z.; Afzal, A.; Li, C.; Le, A.T.; et al. Recent advances in machine learning research for nanofluid-based heat transfer in renewable energy system. Energy Fuels 2022, 36, 6626–6658. [Google Scholar] [CrossRef]
- Said, Z.; Sharma, P.; Elavarasan, R.M.; Tiwari, A.K.; Rathod, M.K. Exploring the specific heat capacity of water-based hybrid nanofluids for solar energy applications: A comparative evaluation of modern ensemble machine learning techniques. J. Energy Storage 2022, 54, 105230. [Google Scholar] [CrossRef]
- Yadav, D.; Singh, R.; Kumar, A.; Sarkar, B. Reduction of Pollution through Sustainable and Flexible Production by Controlling By-Products. J. Environ. Inform. 2022. [Google Scholar] [CrossRef]
- Gu, C.L.; He, C.L.; Liu, J.X.; Chen, J.X. Trial Manufacture of Bionic Honeycomb Plates and their bending properties. In Applied Mechanics and Materials; Trans Tech Publ: Stafa-Zurich, Switzerland, 2014; Volume 461, pp. 101–107. [Google Scholar]
- Xiang, J.; Du, J.; Li, D.; Zhen, C. Functional morphology and structural characteristics of wings of the ladybird beetle, Coccinella septempunctata (L.). Microsc. Res. Tech. 2016, 79, 550–556. [Google Scholar] [CrossRef]
- Saufi, S.; Zuhri, M.Y.M.; Dezaki, M.L.; Sapuan, S.M.; Ilyas, R.A.; As’Arry, A.; Ariffin, M.K.A.; Bodaghi, M. Compression Behaviour of Bio-Inspired Honeycomb Reinforced Starfish Shape Structures Using 3D Printing Technology. Polymers 2021, 13, 4388. [Google Scholar] [CrossRef] [PubMed]
- Dubicki, A.; Zglobicka, I.; Kurzydłowski, K.J. Investigation of Energy-Absorbing Properties of a Bio-Inspired Structure. Metals 2021, 11, 881. [Google Scholar] [CrossRef]
- China National Standardization Administration Committee. Test Method for Flatwise Compression Properties of Sandwich Constructions or Cores; China Standard Publishing House: Beijing, China, 2005. (In Chinese) [Google Scholar]
- Ha, N.S.; Pham, T.M.; Tran, T.T.; Hao, H.; Lu, G. Mechanical properties and energy absorption of bio-inspired hierarchical circular honeycomb. Compos. Part B Eng. 2022, 236, 109818. [Google Scholar] [CrossRef]
- Hamid, W.L.H.W.A.; Aminanda, Y.; Dawood, M.S. Experimental Investigation on the Energy Absorption Capability of Foam-Filled Nomex Honeycomb Structure. In Applied Mechanics and Materials; Trans Tech Publ: Stafa-Zurich, Switzerland, 2013; Volume 393, pp. 460–466. [Google Scholar]
- Ahangar, P.; Cooke, M.E.; Weber, M.H.; Rosenzweig, D.H. Current biomedical applications of 3D printing and additive manufacturing. Appl. Sci. 2019, 9, 1713. [Google Scholar] [CrossRef]
- Gibson, I.; Rosen, D.; Stucker, B.; Khorasani, M. Development of additive manufacturing technology. In Additive Manufacturing technologies; Springer: Berlin/Heidelberg, Germany, 2021; pp. 23–51. [Google Scholar]
- Dizon, J.R.C.; Espera, A.H., Jr.; Chen, Q.; Advincula, R.C. Mechanical characterization of 3D-printed polymers. Addit. Manuf. 2018, 20, 44–67. [Google Scholar] [CrossRef]
- Laurençon, M.; de Resseguier, T.; Loison, D.; Baillargeat, J.; Ngnekou, J.D.; Nadot, Y. Effects of additive manufacturing on the dynamic response of AlSi10Mg to laser shock loading. Mater. Sci. Eng. A 2019, 748, 407–417. [Google Scholar] [CrossRef]
- Ahmed, N.; Xue, P.; Zafar, N. Dynamic axial crushing of bitubular tubes with curvy polygonal inner-tube sections. Int. J. Comput. Mater. Sci. Eng. 2017, 6, 1750024. [Google Scholar] [CrossRef]
- Palanivelu, S.; van Paepegem, W.; Degrieck, J.; Kakogiannis, D. Parametric study of crushing parameters and failure patterns of pultruded composite tubes using cohesive elements and seam, Part I: Central delamination and triggering modelling. Polym. Test. 2010, 29, 729–741. [Google Scholar] [CrossRef]
- Tran, T.; Ton, T. Lateral crushing behaviour and theoretical prediction of thin-walled rectangular and square tubes. Compos. Struct. 2016, 154, 374–384. [Google Scholar] [CrossRef]
- Dong, J.-H.; Wang, Y.-J.; Jin, F.-N.; Fan, H.-L. Crushing behaviors of buckling-induced metallic meta-lattice structures. Def. Technol. 2022, 18, 1301–1310. [Google Scholar] [CrossRef]
- Lee, J.-H.; Wang, L.; Boyce, M.C.; Thomas, E.L. Periodic bicontinuous composites for high specific energy absorption. Nano Lett. 2012, 12, 4392–4396. [Google Scholar] [CrossRef] [PubMed]
- Ryzińska, G.; David, M.; Prusty, G.; Tarasiuk, J.; Wroński, S. Effect of fibre architecture on the specific energy absorption in carbon epoxy composite tubes under progressive crushing. Compos. Struct. 2019, 227, 111292. [Google Scholar] [CrossRef]
- Yin, H.; Huang, X.; Scarpa, F.; Wen, G.; Chen, Y.; Zhang, C. In-plane crashworthiness of bio-inspired hierarchical honeycombs. Compos. Struct. 2018, 192, 516–527. [Google Scholar] [CrossRef]
- Available online: http://lsdyna.ru/wp-content/uploads/2018/10/LS-DYNA-KEYWORD-USERS-MANUAL-VOL2.pdf./ (accessed on 12 September 2022).
- Jones, N. Structural Impact; Cambridge University Press: Cambridge, UK, 2011. [Google Scholar]
- Wan, Y.; Zhu, L.; Fang, H.; Liu, W.; Mao, Y. Experimental testing and numerical simulations of ship impact on axially loaded reinforced concrete piers. Int. J. Impact Eng. 2019, 125, 246–262. [Google Scholar] [CrossRef]
- Wang, H.; Yang, B.; Chen, K.; Elchalakani, M. Parametric analysis and simplified approach for steel-framed subassemblies with reverse channel connection under falling-debris impact. Eng. Struct. 2020, 225, 111263. [Google Scholar] [CrossRef]
- Gunes, R.; Arslan, K. Development of numerical realistic model for predicting low-velocity impact response of aluminium honeycomb sandwich structures. J. Sandw. Struct. Mater. 2016, 18, 95–112. [Google Scholar] [CrossRef]
- Xie, S.; Jing, K.; Zhou, H.; Liu, X. Mechanical properties of Nomex honeycomb sandwich panels under dynamic impact. Compos. Struct. 2020, 235, 111814. [Google Scholar] [CrossRef]
- Available online: http://lsdyna.ru/wp-content/uploads/2018/10/LS-DYNA-KEYWORD-USERS-MANUAL-VOL1.pdf./ (accessed on 12 September 2022).
- Grant, M.; Boyd, S. CVX: Matlab Software for Disciplined Convex Programming, Version 2.0 Beta. Available online: http://cvxr.com/cvx (accessed on 20 September 2020).








| Authors | Major Findings | Research Gaps |
|---|---|---|
| Chen et al. (2008) [16] | The microstructures and bio-structure design techniques in the forewing of the Allomyrina dichotoma beetle were examined. | Not verified by test. |
| Chen et al. (2012) [20] | Based on the research of the beetle forewing structure, a method of constructing honeycomb panel in integral form was designed. | No model test study. |
| Chen et al. (2014) [18] | Compression and bending properties of a novel bionic integrated honeycomb panel were studied. | Manufacturing accuracy needs to be improved. |
| Sun et al. (2014) [19] | Investigation of the viscoelastic behavior of some biomaterials (nacre, cattle horn and beetle cuticle) at lamellar length scales using quasi-static and dynamic nanoindentation techniques in the materials’ Transverse Direction (TD) and Longitudinal Direction (LD). | No corresponding engineering structures were designed and tested. |
| Clark and Triblehorn. (2014) [21] | The structure and material properties of insect cuticle were studied. | No model test study. |
| Gu et al. (2014) [31] | The bionic honeycomb panel was trial-produced, and its mechanical properties were discussed. | Manufacturing accuracy needs to be improved. |
| Xiang et al. (2016) [32] | Surface morphology and the cross-sectional microstructure of the wings were presented. | Not verified by test. |
| Rosenthal et al. (2016) [26] | Strain-rate-sensitive behavior of SLM-AlSi10Mg aluminum alloy in the strain rate range of 2.77 × 10−6–2.77 × 10−1. | No numerical model was established. |
| Xiang and Du. (2017) [24] | Two BHTS were proposed. | SRE and material failure not considered. |
| Hao and Du. (2018) [12] | Three BHTS were proposed. | SRE and material failure not considered. |
| Hadadzadeh et al. (2019) [27] | Aluminum alloy AlSi10Mg is strain rate sensitive in the strain-rate range of 800 s–1 and 3200 s–1. | No numerical model was established. |
| Guo et al. (2021) [25] | The out-of-plane compressive behavior of carbon/carbon composites is sensitive to strain rate in the strain rate range of 0.0001 s–1 and 1000 s–1. | The designed structure is not based on bionic principles. |
| Saufi et al. (2021) [33] | The EA capacity and high strength of the bionic structure were studied by fused deposition modeling technology. | SRE not considered. |
| Dubicki et al. (2021) [34] | The structure of the simulated diatom truncated body retains its similarity to natural shells, and 3D printing and compression tests were performed to develop new energy-absorbing materials using bionic methods. | SRE not considered. |
| Present study | Two BHTS models with different filling modes proposed by Hao and Du were used to fabricated SLM-AlSi10Mg specimens by AM technology. The comparative study was carried out under three different low strain rates of 0.001 s−1, 0.01 s−1 and 0.1 s−1, the failure mode and EA were evaluated. A reasonable numerical model were established by using explicit finite element software LS-DYNA. | |
| Specimen Label | Column Height | Cell Side Length | ||
|---|---|---|---|---|
| BHTS–S | 0.5 | 20.0 | 6.0 | / |
| BHTS–I | 0.5 | 20.0 | 6.0 | 0.5 |
| BHTS–II | 0.5 | 20.0 | 6.0 | 0.5 |
| Density | Young’s Modulus | Poisson’s Ratio | Initial Yield Strength |
|---|---|---|---|
| 2670 kg/m3 | 69 ± 5 GPa | 0.3 | 220 ± 10 MPa |
| Panel Number | Type | Strain Rate | ||
|---|---|---|---|---|
| 0.001 s−1 | 0.01 s−1 | 0.1 s−1 | ||
| 1 | Specimen | BHTS–S–11 | BHTS–S–21 | BHTS–S–31 |
| FEM | FEM-BHTS–S | FEM-BHTS–S | FEM-BHTS–S | |
| 2 | Specimen | BHTS–I–11 | BHTS–I–21 | BHTS–I–31 |
| FEM | FEM-BHTS–I | FEM-BHTS–I | FEM-BHTS–I | |
| 3 | Specimen | BHTS–II–11 | BHTS–II–21 | BHTS–II–31 |
| FEM | FEM-BHTS–II | FEM-BHTS–II | FEM-BHTS–II | |
| (a) | |||||||||||||||||
| Group Number | Detail | Specimen | Velocity/Specimen Length | Velocity (mm/s) | Mass (g) | PCF (kN) | MCF (kN) | ||||||||||
| 1 | BHTS–S | 11 | 10−3 | 0.02 | 3.02 | 3.20 | 3.13 | ||||||||||
| 12 | 10−3 | 0.02 | 2.97 | 3.15 | 3.09 | ||||||||||||
| 21 | 10−2 | 0.2 | 3.03 | 3.38 | 3.24 | ||||||||||||
| 22 | 10−2 | 0.2 | 3.03 | 3.27 | 3.21 | ||||||||||||
| 31 | 10−1 | 2 | 3.01 | 3.53 | 3.48 | ||||||||||||
| 32 | 10−1 | 2 | 3.03 | 3.61 | 3.45 | ||||||||||||
| 2 | BHTS–I | 11 | 10−3 | 0.02 | 3.85 | 15.30 | 4.19 | ||||||||||
| 12 | 10−3 | 0.02 | 3.88 | 15.26 | 4.09 | ||||||||||||
| 21 | 10−2 | 0.2 | 3.88 | 15.67 | 4.36 | ||||||||||||
| 22 | 10−2 | 0.2 | 3.85 | 15.44 | 4.43 | ||||||||||||
| 31 | 10−1 | 2 | 3.87 | 17.46 | 4.89 | ||||||||||||
| 32 | 10−1 | 2 | 3.85 | 18.04 | 4.99 | ||||||||||||
| 3 | BHTS–II | 11 | 10−3 | 0.02 | 3.63 | 12.13 | 4.19 | ||||||||||
| 21 | 10−3 | 0.02 | 3.66 | 12.24 | 4.29 | ||||||||||||
| 21 | 10−2 | 0.2 | 3.62 | 12.34 | 4.68 | ||||||||||||
| 22 | 10−2 | 0.2 | 3.62 | 12.40 | 4.65 | ||||||||||||
| 31 | 10−1 | 2 | 3.64 | 13.09 | 5.16 | ||||||||||||
| 32 | 10−1 | 2 | 3.61 | 13.64 | 4.94 | ||||||||||||
| (b) | |||||||||||||||||
| Group Number | Detail | Specimen | CFE (%) | EA (J) | SEA (J/g) | Average Value | |||||||||||
| PCF (kN) | MCF (kN) | CFE (%) | EA (J) | SEA (J/g) | |||||||||||||
| 1 | BHTS–S | 11 | 97.81 | 44.29 | 14.67 | 3.18 | 3.11 | 97.96 | 44.13 | 14.74 | |||||||
| 12 | 98.10 | 43.96 | 14.80 | ||||||||||||||
| 21 | 95.86 | 45.95 | 15.17 | 3.33 | 3.23 | 97.02 | 45.90 | 15.15 | |||||||||
| 22 | 98.17 | 45.85 | 15.13 | ||||||||||||||
| 31 | 98.58 | 49.21 | 16.35 | 3.57 | 3.47 | 97.08 | 49.12 | 16.27 | |||||||||
| 32 | 95.57 | 49.03 | 16.18 | ||||||||||||||
| 2 | BHTS–I | 11 | 27.39 | 77.89 | 20.23 | 15.28 | 4.14 | 27.10 | 76.63 | 19.83 | |||||||
| 12 | 26.81 | 75.37 | 19.43 | ||||||||||||||
| 21 | 27.84 | 78.14 | 20.14 | 15.56 | 4.40 | 28.27 | 77.10 | 19.95 | |||||||||
| 22 | 28.70 | 76.05 | 19.75 | ||||||||||||||
| 31 | 28.03 | 90.02 | 23.26 | 17.75 | 4.94 | 27.84 | 88.39 | 22.90 | |||||||||
| 32 | 27.64 | 86.75 | 22.53 | ||||||||||||||
| 3 | BHTS–II | 11 | 34.50 | 71.84 | 19.79 | 12.19 | 4.24 | 34.78 | 73.17 | 20.08 | |||||||
| 21 | 35.06 | 74.50 | 20.36 | ||||||||||||||
| 21 | 37.89 | 81.66 | 22.56 | 12.37 | 4.67 | 37.71 | 81.99 | 22.65 | |||||||||
| 22 | 37.53 | 82.31 | 22.74 | ||||||||||||||
| 31 | 39.41 | 92.22 | 25.34 | 13.37 | 5.05 | 37.83 | 92.45 | 25.51 | |||||||||
| 32 | 36.25 | 92.68 | 25.67 | ||||||||||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xia, H.; Sun, Q.; Liu, Y. Energy Absorption Characteristics of Bio-Inspired Honeycomb Column Thin-Walled Structure under Low Strain Rate Uniaxial Compression Loading. Energies 2022, 15, 6957. https://doi.org/10.3390/en15196957
Xia H, Sun Q, Liu Y. Energy Absorption Characteristics of Bio-Inspired Honeycomb Column Thin-Walled Structure under Low Strain Rate Uniaxial Compression Loading. Energies. 2022; 15(19):6957. https://doi.org/10.3390/en15196957
Chicago/Turabian StyleXia, Hongxiang, Quansheng Sun, and Yancheng Liu. 2022. "Energy Absorption Characteristics of Bio-Inspired Honeycomb Column Thin-Walled Structure under Low Strain Rate Uniaxial Compression Loading" Energies 15, no. 19: 6957. https://doi.org/10.3390/en15196957





