Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions
Abstract
1. Introduction


| AM Advantages | AM Disadvantages |
|---|---|
|
|
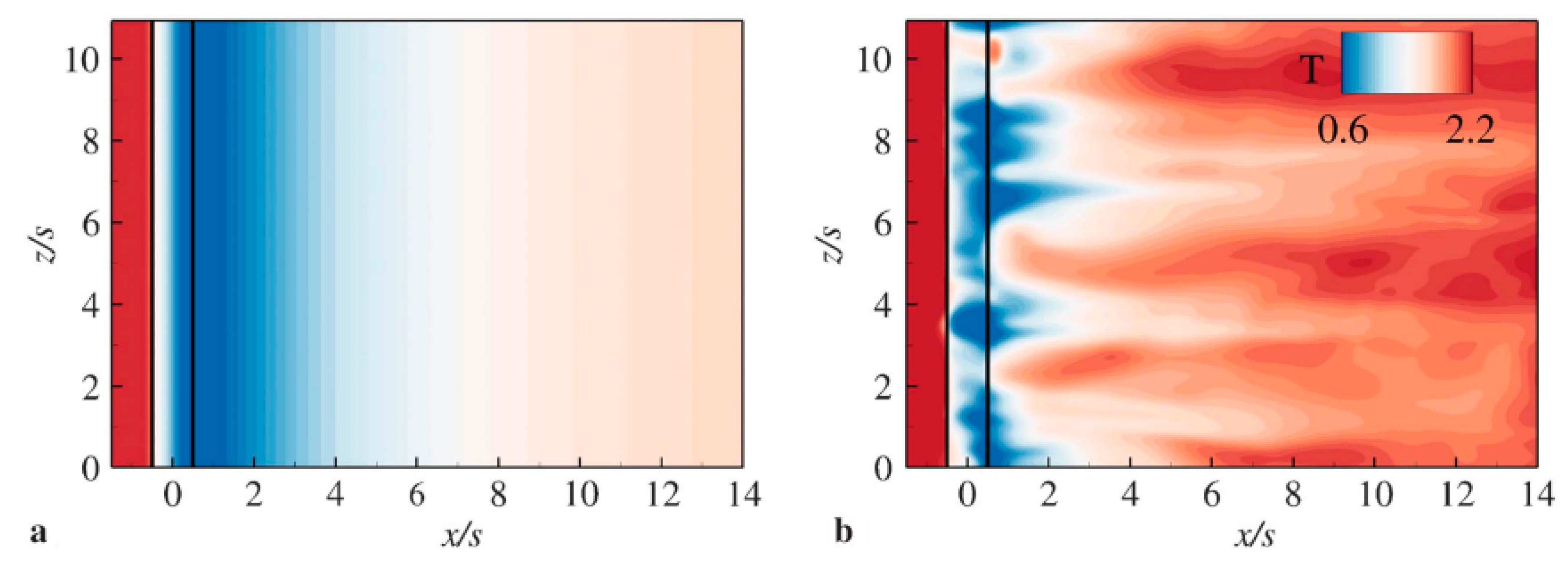
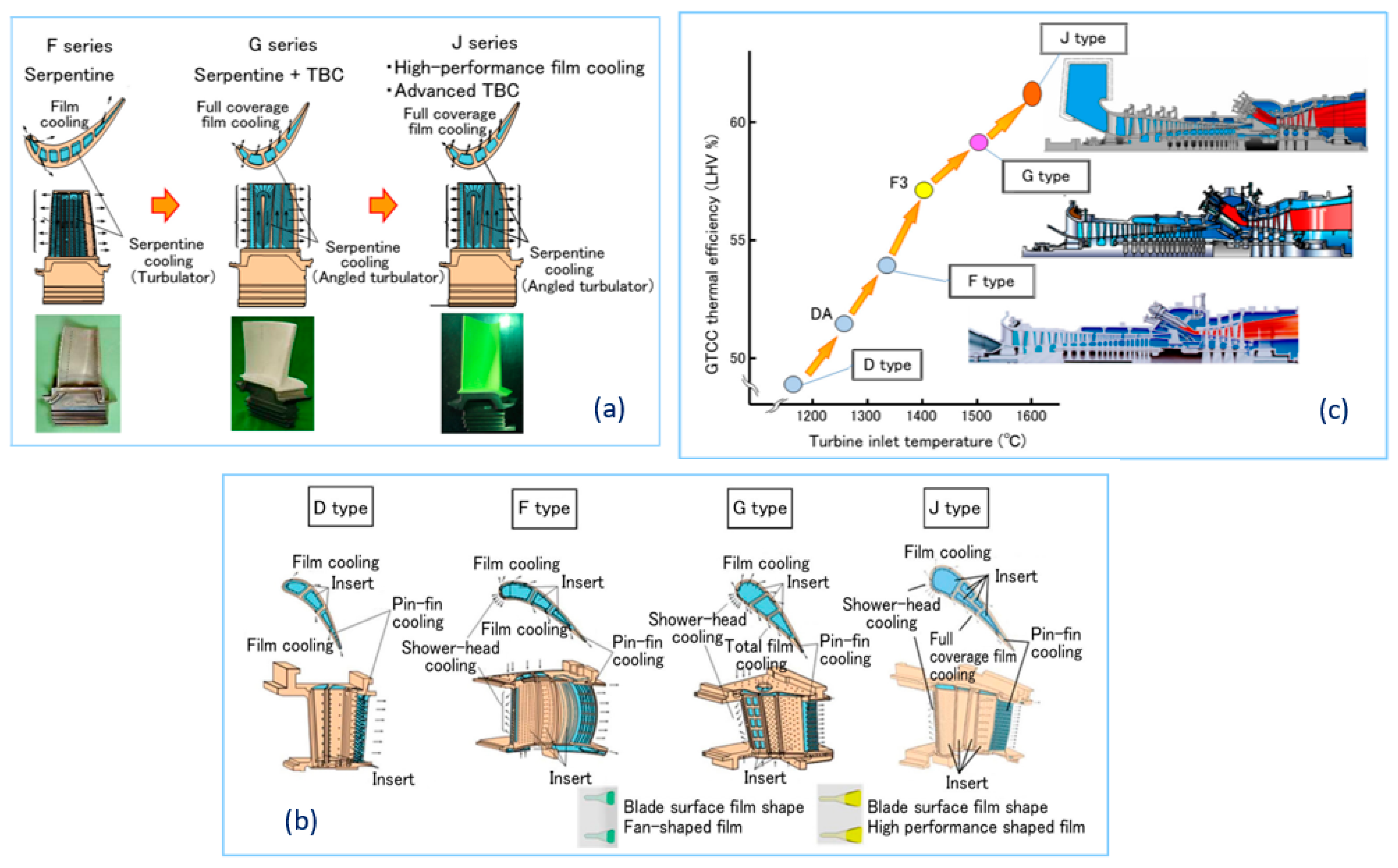
2. Historical Perspective of Film-Cooling Performance
2.1. Hole Positioning and Film Exit Configurations
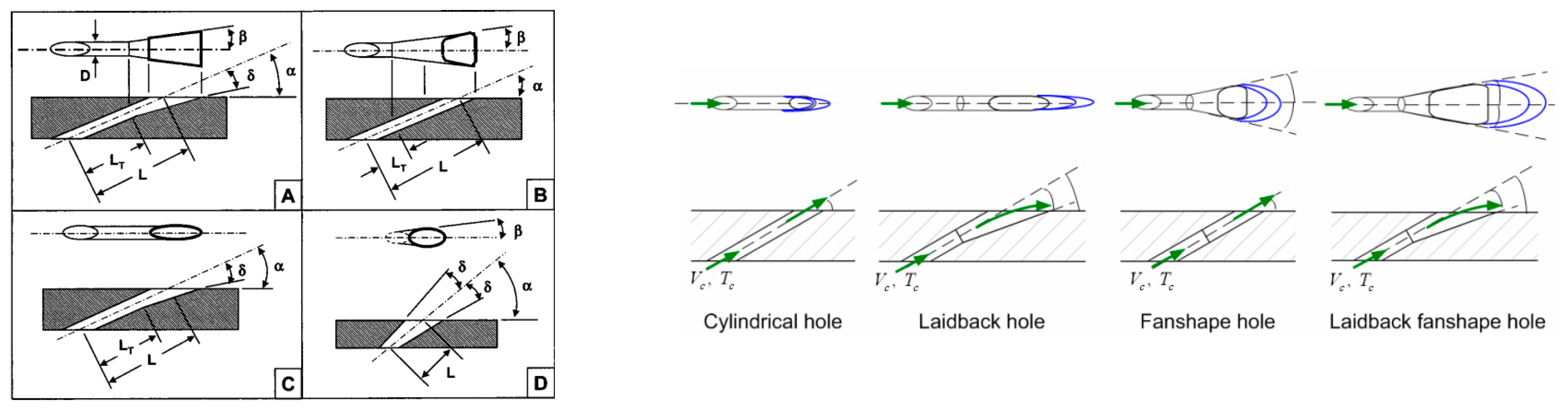

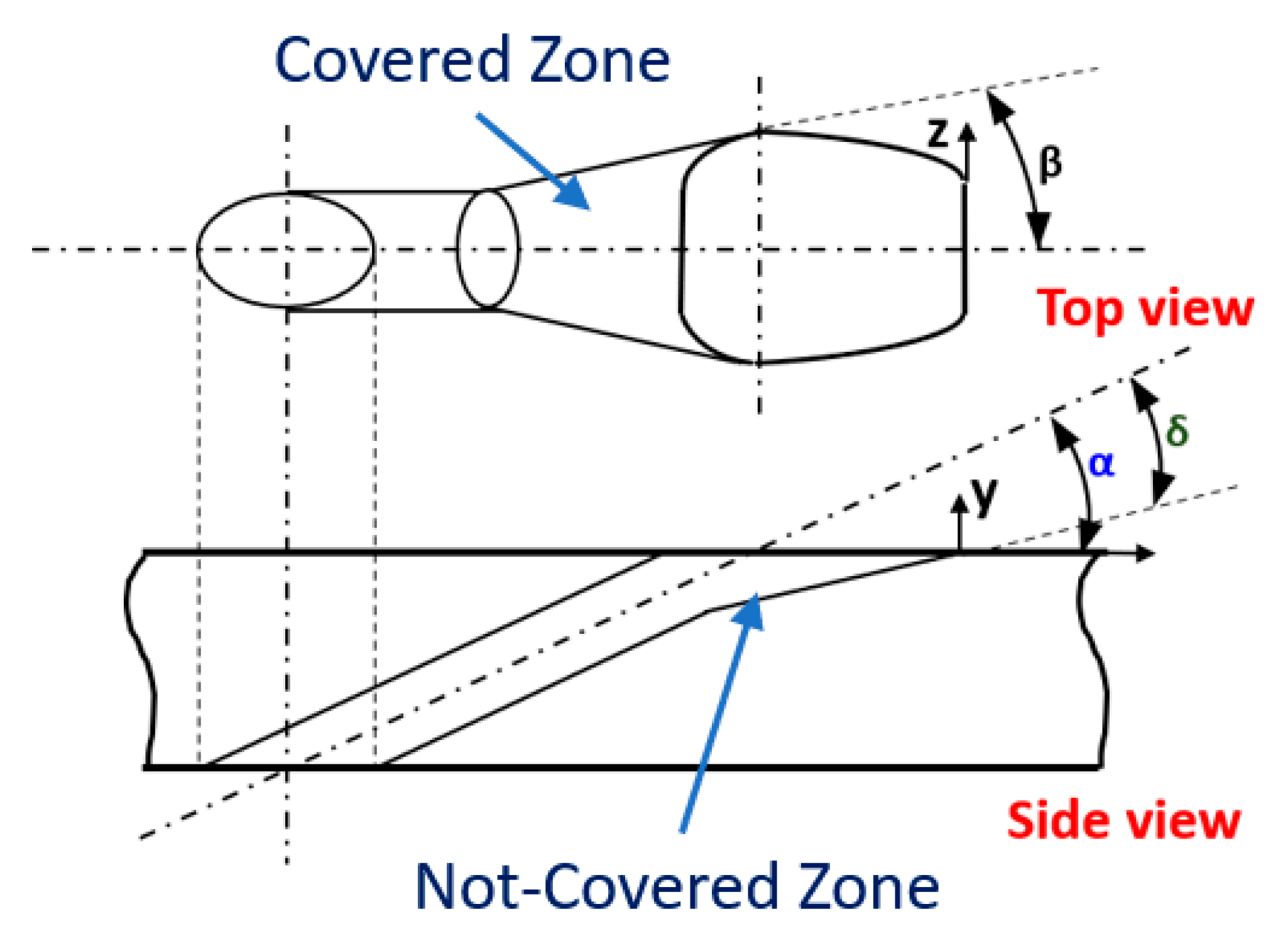
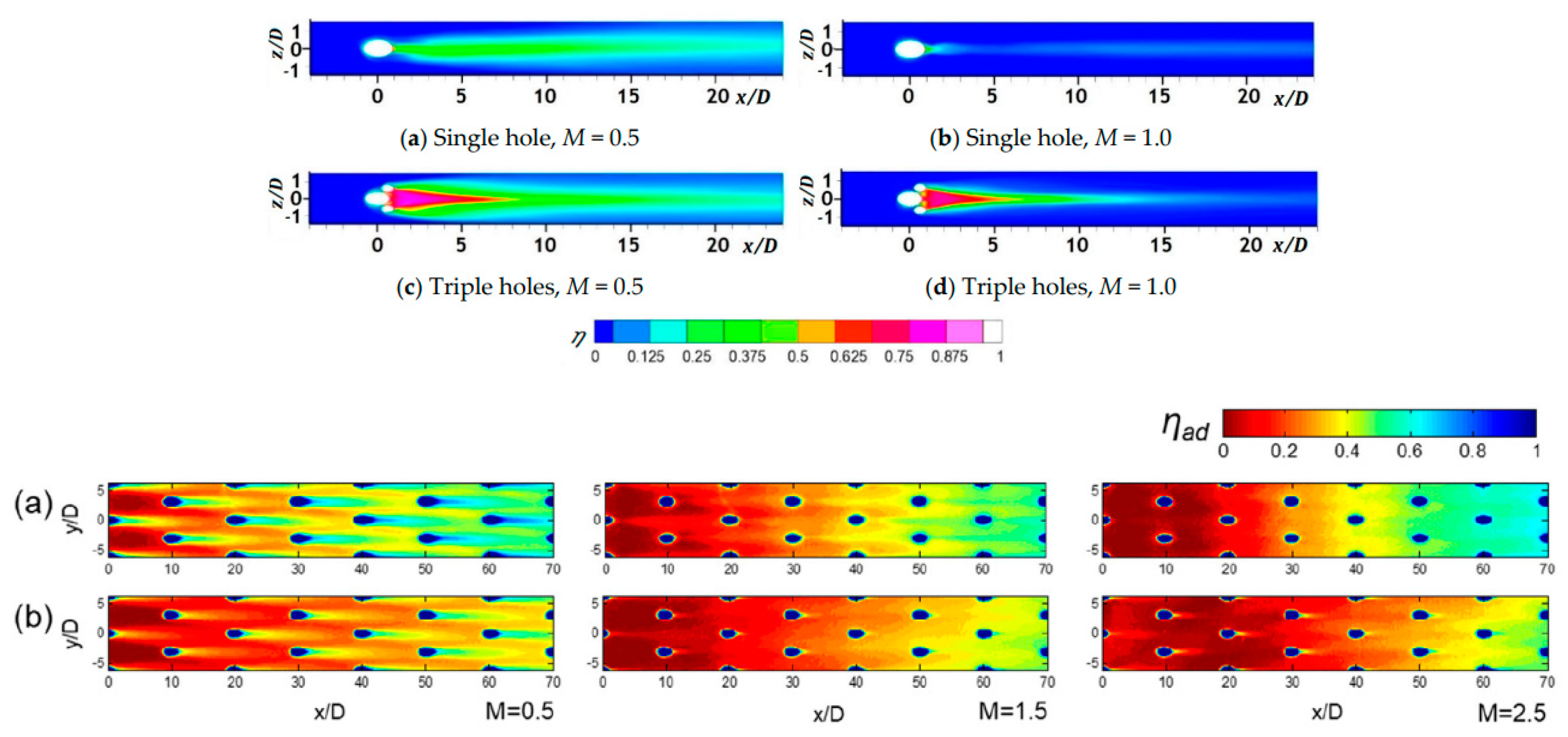
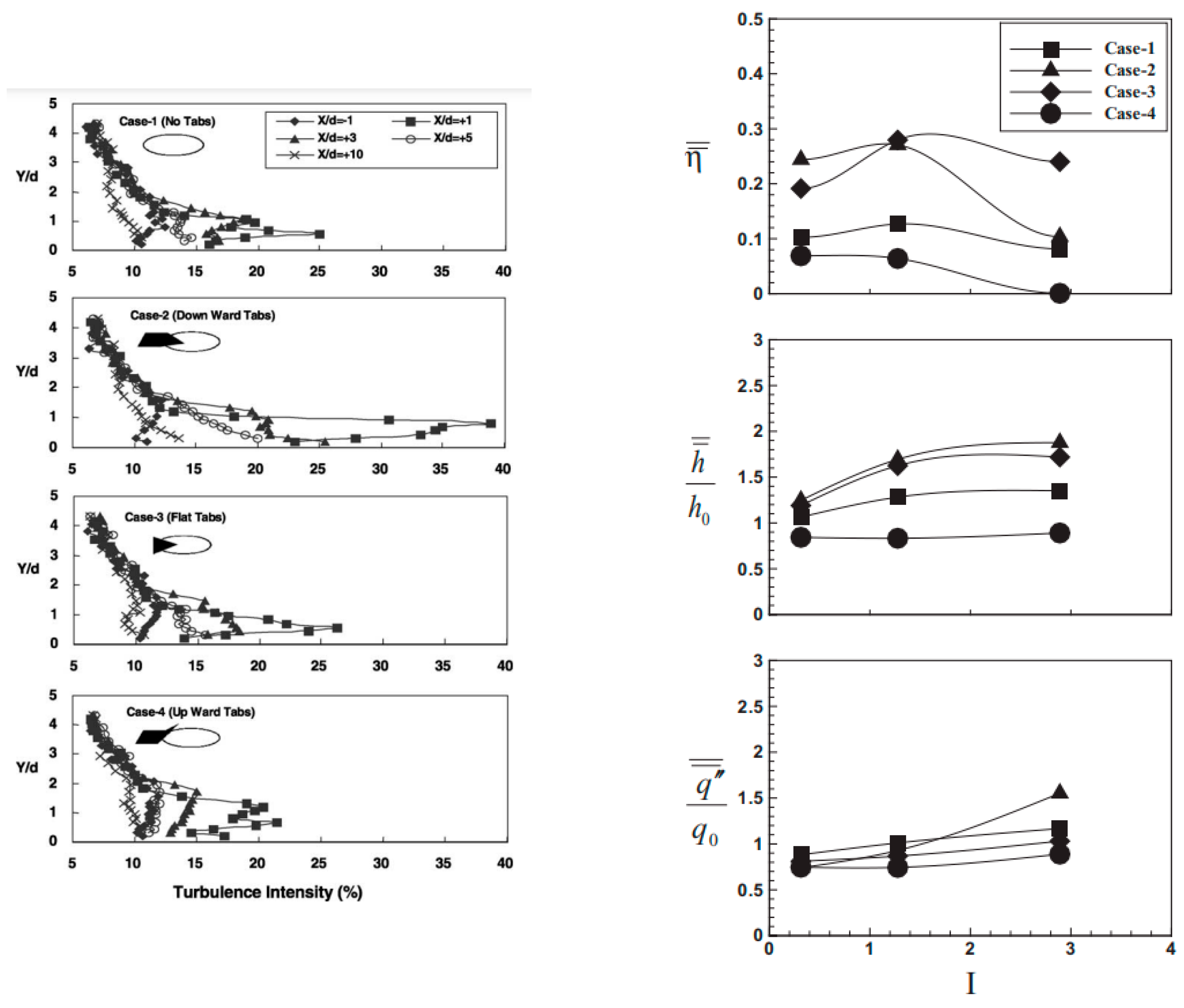
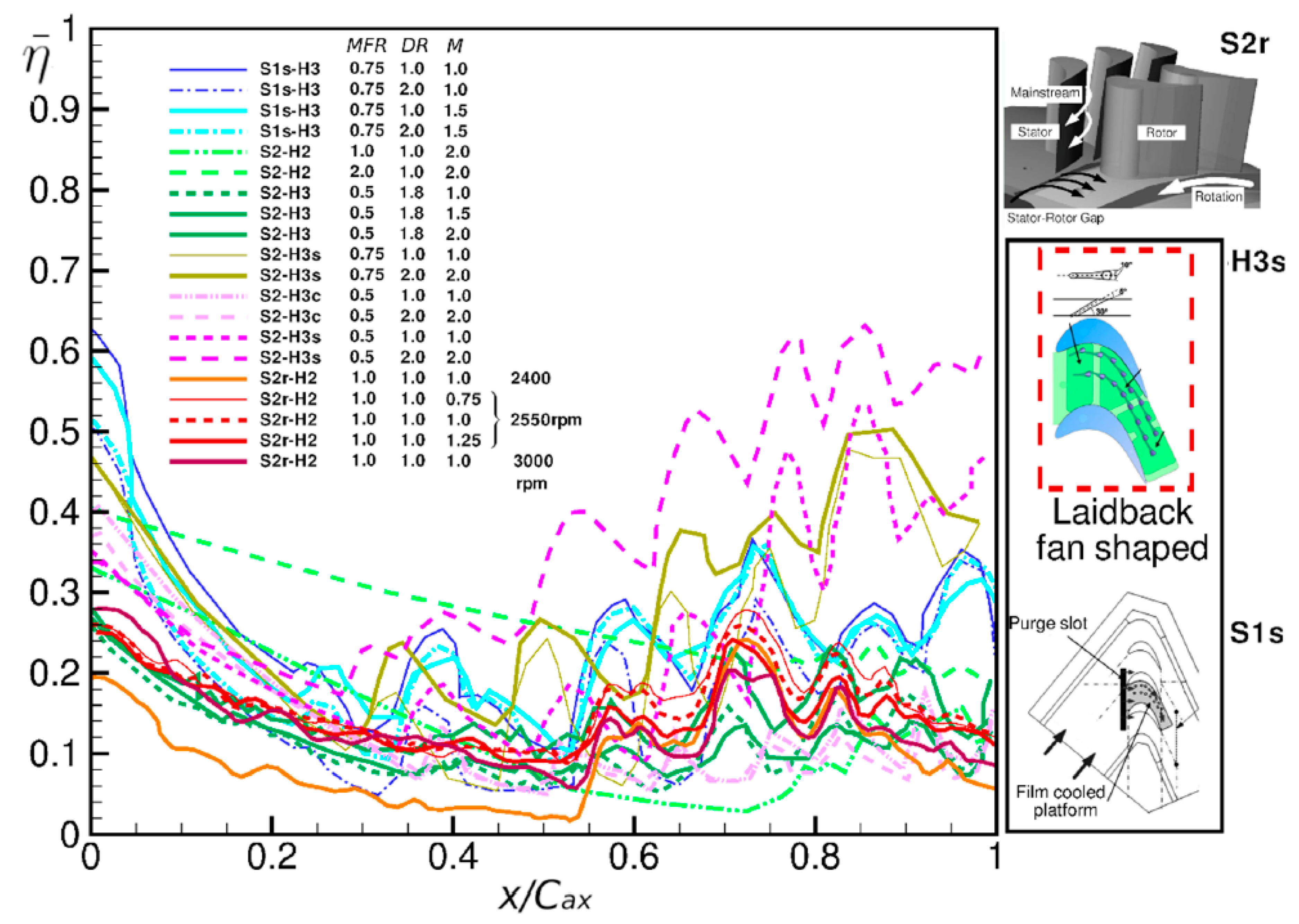
2.2. Fluid Ratios
2.2.1. Density Ratio
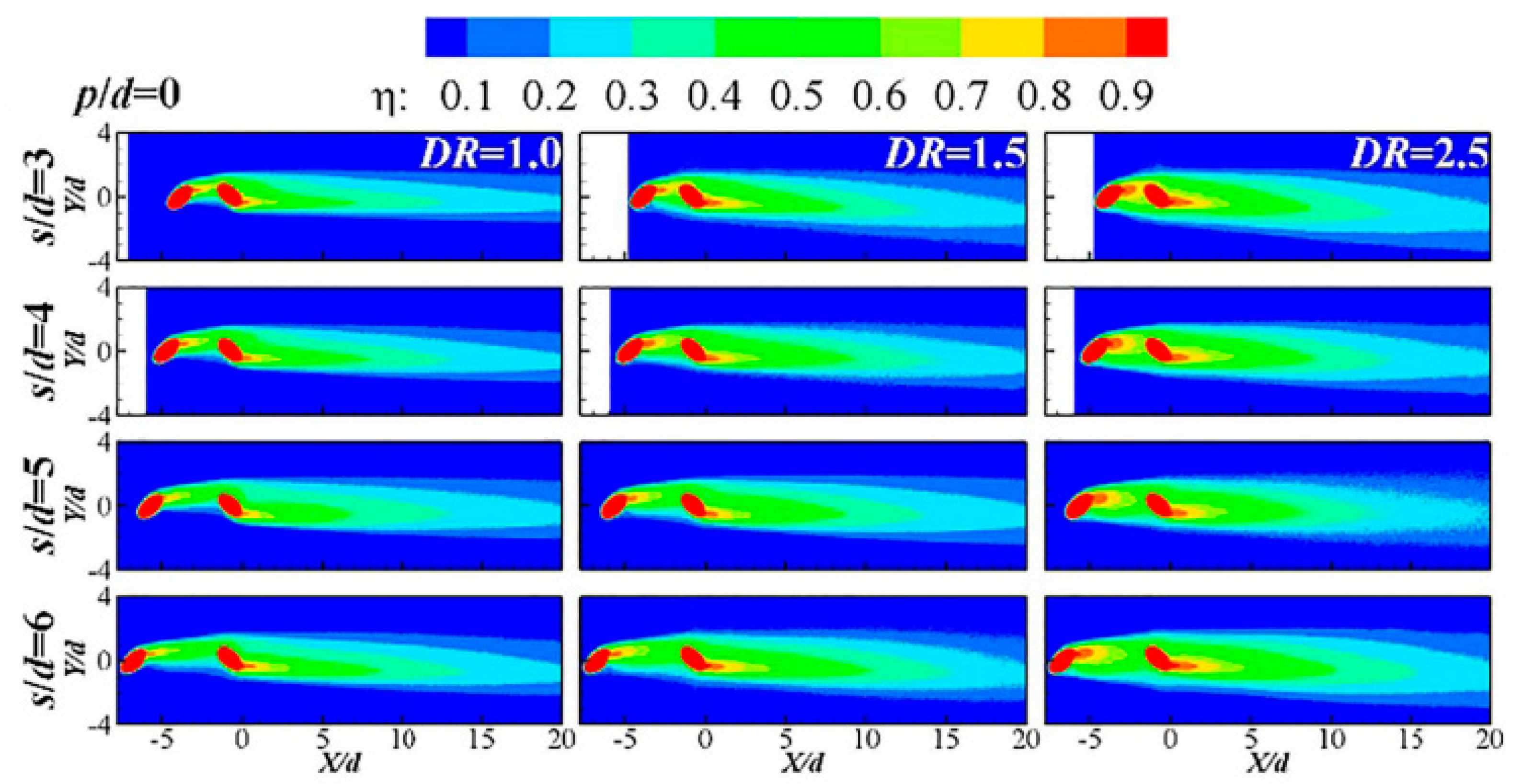
2.2.2. Blowing Ratio () and Momentum Flux Ratio ()
2.3. Advective Capacity Ratio (ACR)
2.4. Freestream Turbulence
3. Measurement Techniques
3.1. Transient Liquid Crystal (TLC)
3.2. Transient Infrared Imaging (IR) and Temperature-Sensitive Paint (TSP)
3.3. Pressure-Sensitive Paints (PSP)

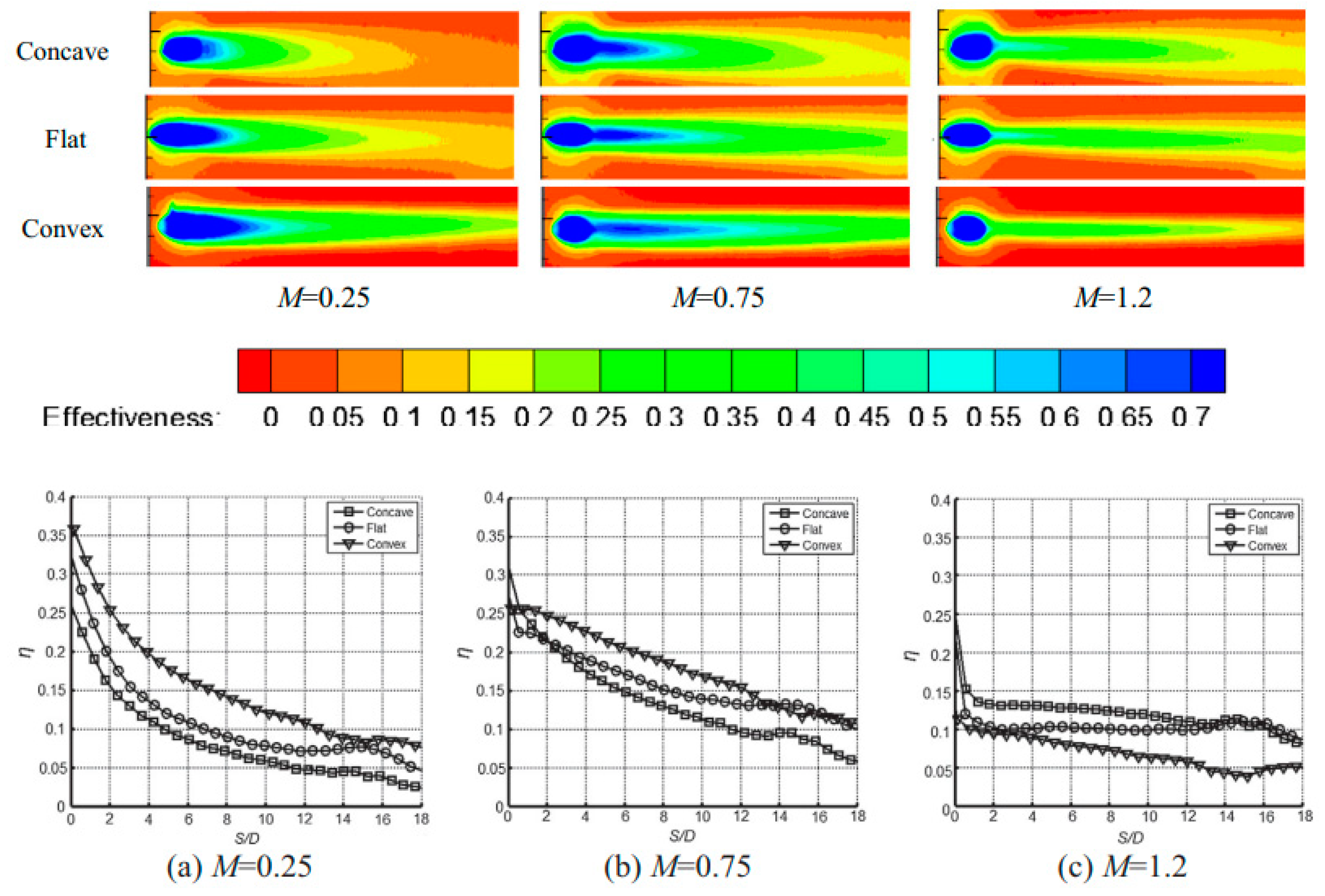
4. Curvature and Roughness

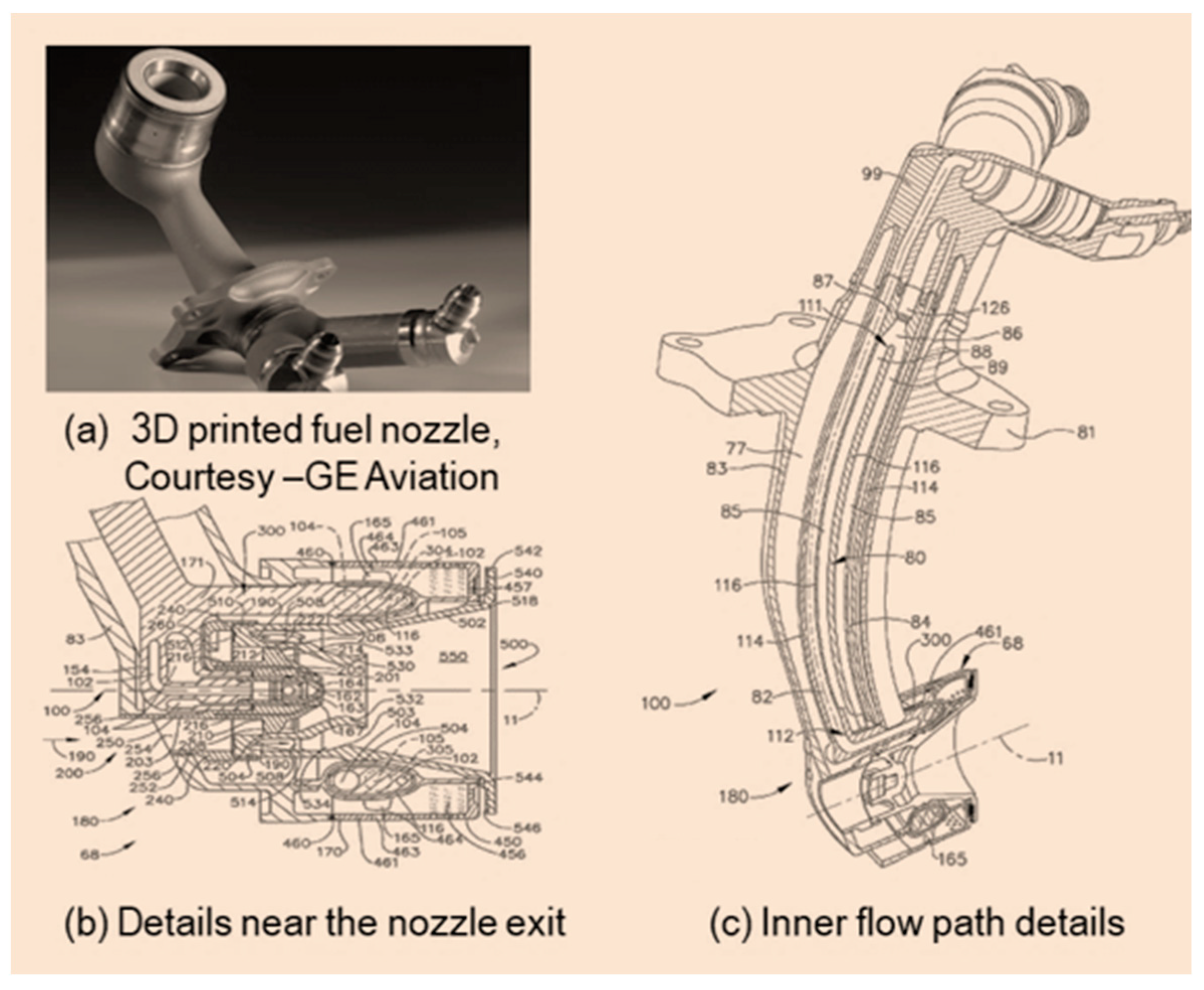
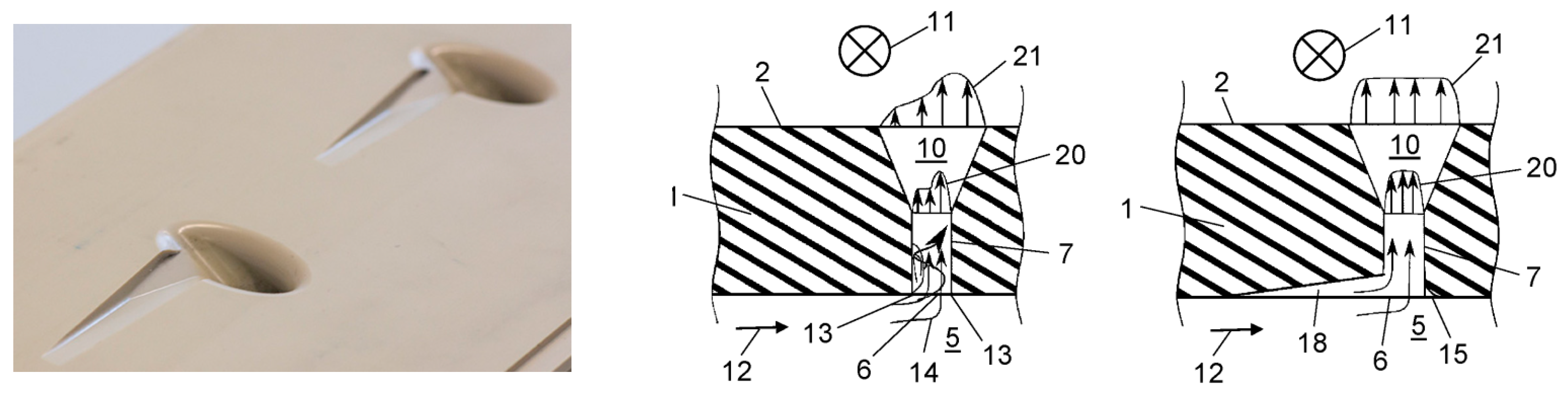
5. Additive Manufacturing (AM)
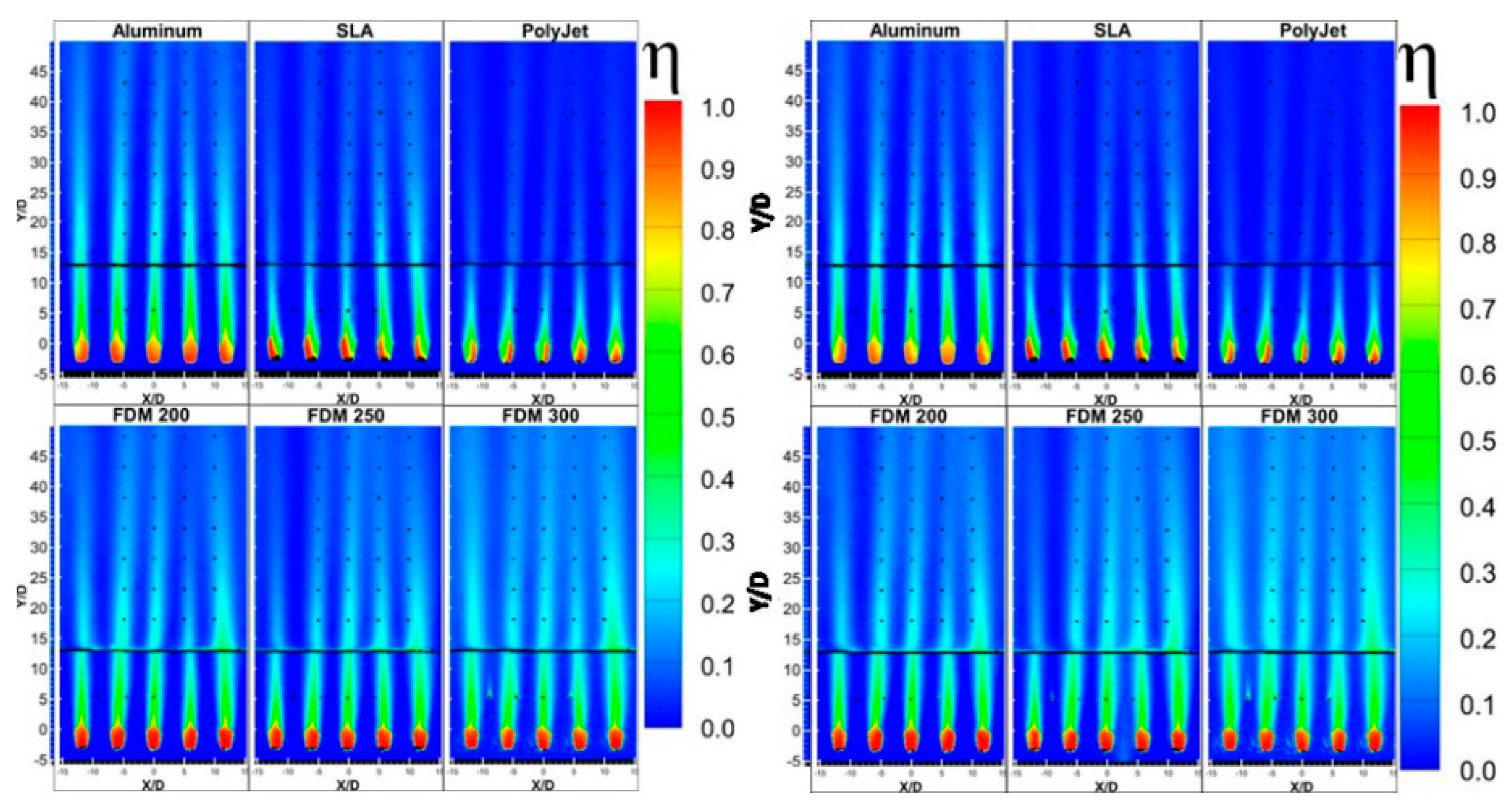
5.1. AM Surface Roughness
5.2. AM New Hole Shapes

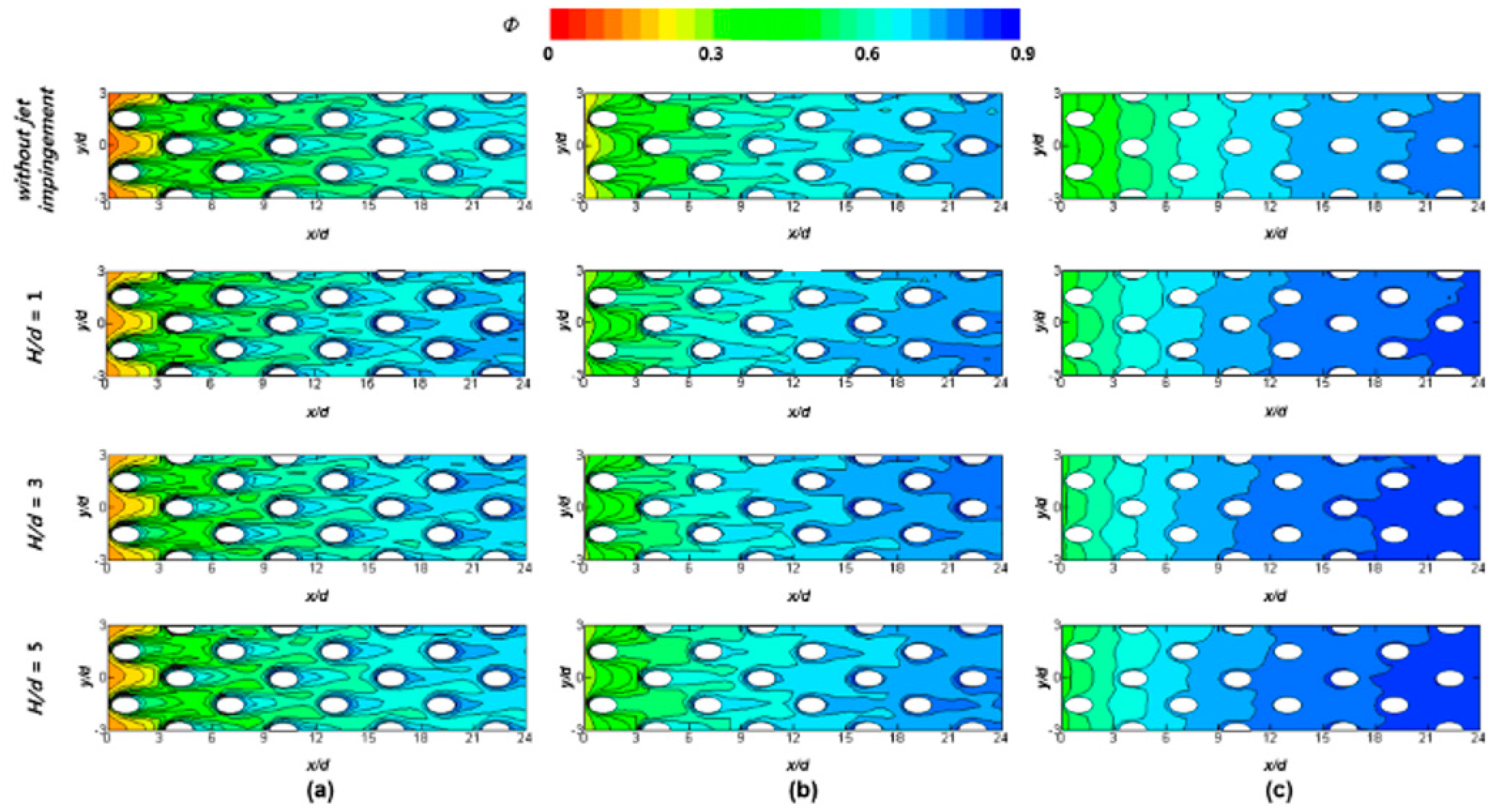
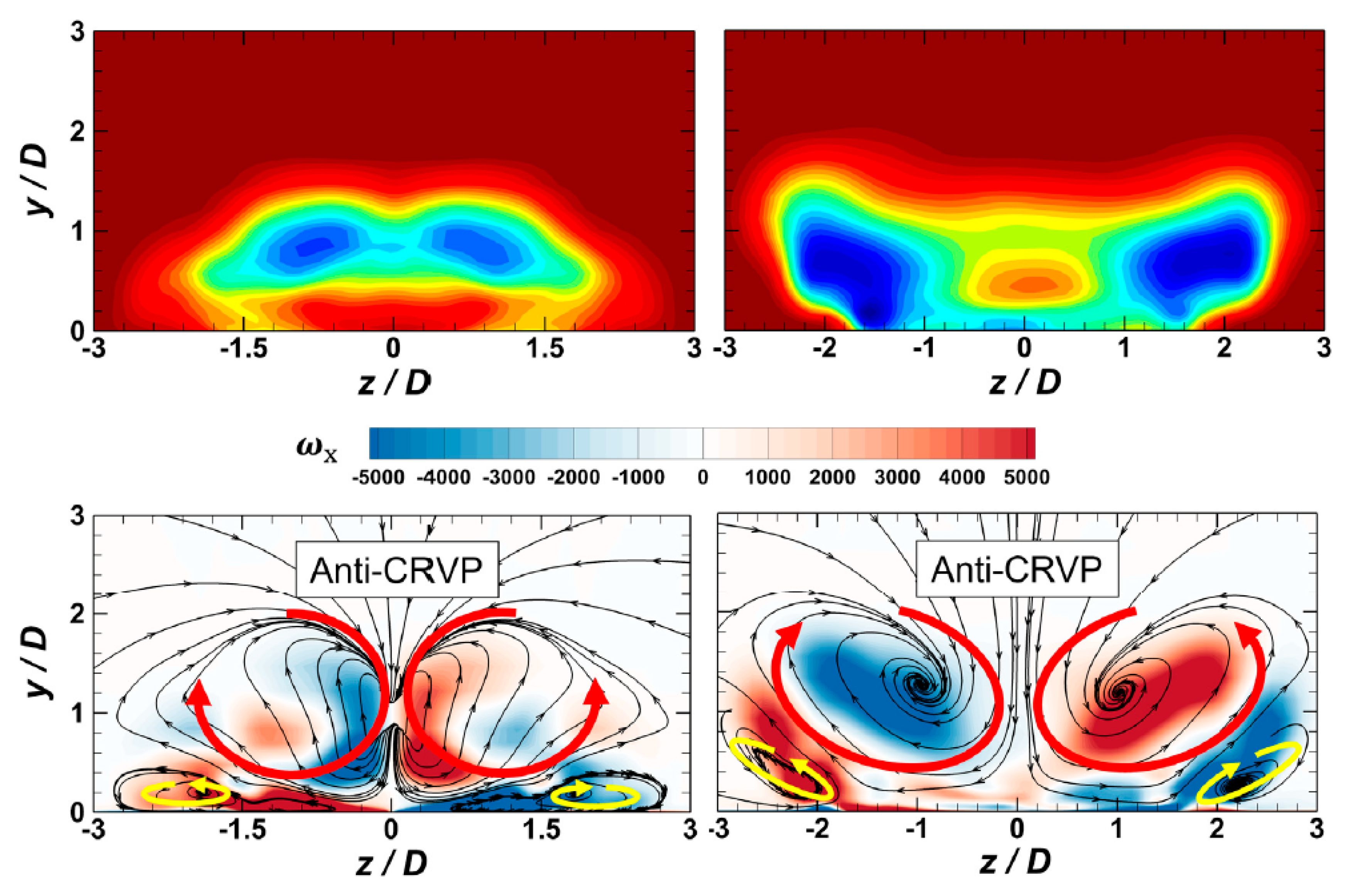
5.3. AM Sweeping Film with Synthetic Jet (SJ)



6. Future Challenges
- Hooded film holes
- Curved film holes
- Design alterations to accommodate AM roughness
- Adaptation of pressure-gain combustors
- Surface protection of CMC
- Adaptation for hydrogen fuel
- Pulsating and sweeping film
- Alterations in film hole inlet
- Film hole cooling affected zones
- Film hole density correlation with heat load and structural strength
- Manufacturing deviations and its impact
- Low discharge coefficient in larger rougher holes
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Nomenclature
| concentration | |
| specific heat capacity (J/kg.K) | |
| diameter of film cooling hole (m) | |
| heat transfer coefficient (W/m2.K) | |
| momentum flux ratio | |
| thermal conductivity of solid (W/m.K) | |
| blowing ratio | |
| partial pressure | |
| heat flux (W/m2) | |
| time (s) | |
| temperature (K) | |
| turbulence intensity (%) | |
| velocity (m/s) | |
| streamwise distance |
Greek letters
| thermal diffusivity of solid (m2/s) | |
| density (kg/m3) | |
| adiabatic film effectiveness | |
| overall film effectiveness |
Subscripts
| adiabatic wall temperature | |
| coolant | |
| initial/internal | |
| references | |
| surface wall temperature | |
| mainstream | |
| baseline case/no-coolant injection |
Abbreviations
| advective capacity ratio | |
| additive manufacturing | |
| cooling affected zone | |
| ceramic–matrix composite | |
| electro-discharge machining | |
| FC | film cooling |
| FDM | fused deposition modeling |
| laser powder bed fusion | |
| pressure-gain combustor | |
| selective laser melting | |
| thermal barrier coating |
References
- Kaur, I.; Dutta, S.; Singh, P. A Review on Film Cooling Research: Historical Developments in Hole Shapes, Measurement Techniques, Effects of Operating Conditions, and Impact of Additive Manufacturing, HT2022-81803. In Proceedings of the ASME 2022 Heat Transfer Summer Conference, Philadelphia, PA, USA, 11–13 July 2022. [Google Scholar]
- Bogard, D.G.; Thole, K.; Oliver, T. Integrated Turbine Component Cooling Designs Facilitated by Additive Manufacturing and Optimization. DOE-NETL. November 2021. Available online: https://netl.doe.gov/sites/default/files/netl-file/21UTSR_Bogard.pdf (accessed on 17 May 2022).
- Wikipedia, Ultra High Temperature Ceramic Matrix Composite. Available online: https://en.wikipedia.org/wiki/Ultra_high_temperature_ceramic_matrix_composite (accessed on 22 May 2022).
- Takashi, T.; Takeshi, N.; Kooun, T.; Takahito, A.; Tadashi, N. Research of CMC Application to Turbine Components. IHI Eng. Rev. 2005, 38, 2. [Google Scholar]
- Lynch, S.; Hickner, M.; Frick, C.; Fertig, R. Development of Additive Manufacturing for Ceramic Matrix Composite Vanes. DE-FE0031758. February 2019. Available online: https://netl.doe.gov/sites/default/files/netl-file/20UTSR_Lynch.pdf (accessed on 22 May 2022).
- Goldstein, R.J. Film Cooling. In Advances in Heat Transfer; Irvine, T.F., Hartnett, J.P., Eds.; Elsevier: Amsterdam, The Netherlands, 1971; Volume 7, pp. 321–379. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, S.; Wang, C.; Tan, X. Recent Advances in Film Cooling Enhancement: A Review. Chin. J. Aeronaut. 2020, 33, 1119–1136. [Google Scholar] [CrossRef]
- Grisson, W.M. Liquid Film Cooling in Rocket Engines; AEDC-TR-91-1; US Air Force: Washington, DC, USA, 1991. [Google Scholar]
- Rao, M.P.; Biswal, P.; Prasad, B.V.S.S.S. A Computational Study of Mist Assisted Film Cooling. Int. Commun. Heat Mass Transf. 2018, 95, 33–41. [Google Scholar]
- Hada, S.; Tsukagoshi, K.; Masada, J.; Ito, E. Test Results of the World’s First 1600C J-Series Gas Turbine. Mitsubishi Heavy Ind. Tech. Rev. 2012, 49, 18–23. [Google Scholar]
- Yuri, M.; Masada, J.; Tsukagoshi, K.; Ito, E.; Hada, S. Development of 1600C-Class High-Efficiency Gas Turbine for Power Generation Applying J-Type Technology. Mitsubishi Heavy Ind. Tech. Rev. 2013, 50, 3. [Google Scholar]
- Horizon Technology. 3 Advantages & Disadvantages of Additive Manufacturing Processes vs. PM. 7 June 2021. Available online: https://www.horizontechnology.biz/blog/advantages-and-disadvantages-of-additive-manufacturing-process-vs-powder-metallurgy (accessed on 18 May 2022).
- Magerramova, L.; Vasilyev, B.; Kinzburskiy, V. Novel Designs of Turbine Blades for Additive Manufacturing. In Proceedings of the Volume 5C: Heat Transfer, New York, NY, USA, 13–17 June 2016; p. V05CT18A001. [Google Scholar] [CrossRef]
- Sotov, A.V.; Agapovichev, A.V.; Smelov, V.G.; Kokareva, V.V.; Dmitrieva, M.O.; Melnikov, A.A.; Golanov, S.P.; Anurov, Y.M. Investigation of the IN-738 Superalloy Microstructure and Mechanical Properties for the Manufacturing of Gas Turbine Engine Nozzle Guide Vane by Selective Laser Melting. Int. J. Adv. Manuf. Technol. 2020, 107, 2525–2535. [Google Scholar] [CrossRef]
- Hanson, K. 3D-Printed Parts Made from Refractory Metals can Handle the Heat. Additive Report. Available online: https://www.thefabricator.com/additivereport/article/additive/3d-printed-parts-made-from-refractory-metals-can-handle-the-heat (accessed on 20 May 2022).
- Stimpson, C.K.; Snyder, J.C.; Thole, K.A.; Mongillo, D. Effectiveness Measurements of Additively Manufactured Film Cooling Holes. J. Turbomach. 2017, 140, 011009. [Google Scholar] [CrossRef]
- Keller, M.A.; Kloker, M.J. Direct Numerical Simulation of Foreign-Gas Film Cooling in Supersonic Boundary-Layer Flow. AIAA J. 2017, 55, 99–111. [Google Scholar] [CrossRef]
- Chang, J.; Duan, X.; Du, Y.; Guo, B.; Pan, Y. Investigations on the Effect of Different Influencing Factors on Film Cooling Effectiveness under the Injection of Synthetic Coolant. Sci. Rep. 2021, 11, 1–14. [Google Scholar] [CrossRef]
- Wang, C.; Fan, F.; Zhang, J.; Huang, Y.; Feng, H. Large Eddy Simulation of Film Cooling Flow from Converging Slot-Holes. Int. J. Therm. Sci. 2018, 126, 238–251. [Google Scholar] [CrossRef]
- Han, J.C.; Dutta, S.; Ekkad, S. Gas Turbine Heat Transfer and Cooling Technology, 2nd ed.; CRC Press: New York, NY, USA, 2012. [Google Scholar]
- Chen, Z.-Y.; Zhan, J.-M.; Li, C.-W.; Hu, W.-Q.; Gong, Y.-J. The Effect of Vortex Shedding in Film-Cooling Processes. Heat Transf. Eng. 2021, 42, 1432–1451. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, J.-Z.; Wang, C.-H.; Zhu, X.-D. Multi-Objective Optimization of Laidback Fan-Shaped Film Cooling Hole on Turbine Vane Suction Surface. Heat Mass Transf. 2019, 55, 1181–1194. [Google Scholar] [CrossRef]
- Mongillo, D.J., Jr.; Gleiner, M.S. Cooling Hole with Curved Metering Section. US 8850828 B2, 7 October 2014. [Google Scholar]
- Li, H.M.; Ghaly, W.; Hassan, I. The Formation of Counter-Rotating Vortex Pair and the Nature of Liftoff-Reattachment in Film-Cooling Flow. Fluids 2016, 1, 39. [Google Scholar] [CrossRef]
- Aminov, R.Z.; Moskalenko, A.B.; Kozhevnikov, A.I. Optimal Gas Turbine Inlet Temperature for Cyclic Operation. IOP Conf. Ser. J. Phys. 2018, 1111, 012046. [Google Scholar] [CrossRef]
- Chen, A.F. Film Cooling with Forward and Backward Injection for Cylindrical and Fan-Shaped Holes Using PSP Measurement Technique. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2013. [Google Scholar]
- Park, S.P.; Jung, E.Y.; Kim, S.H.; Sohn, H.-S.; Cho, H.H. Enhancement of Film Cooling Effectiveness using Backward Injection Holes. Int. J. Therm. Sci. 2016, 110, 314–324. [Google Scholar] [CrossRef]
- Barigozzi, G.; Abdeh, H.; Rouina, S.; Franchina, N. The Aero-Thermal Performance of Purge Flow and Discrete Holes Film Cooling of Rotor Blade Platform in Modern High Pressure Gas Turbines: A Review. Int. J. Turbomach. Propuls. Power 2022, 7, 22. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eckert, E.R.G.; Burggraf, F. Effects of hole geometry and density on three-dimensional film cooling. Int. J. Heat Mass Transf. 1974, 17, 595–607. [Google Scholar] [CrossRef]
- Bunker, R.S. A Review of Shaped Hole Turbine Film-Cooling Technology. J. Heat Transf. 2005, 127, 441–453. [Google Scholar] [CrossRef]
- Narzary, D.P. Experimental Study of Gas Turbine Blade Film Cooling and Heat Transfer. Ph.D. Thesis, Texas A&M University, College Station, TX, USA, 2009. Available online: https://core.ac.uk/download/pdf/147135971.pdf (accessed on 28 August 2022).
- Saumweber, C.; Schulz, A. Effect of Geometry Variations on the Cooling Performance of Fan-Shaped Cooling Holes. J. Turbomach. 2012, 134, 061008. [Google Scholar] [CrossRef]
- Bunker, R.S. Additive Manufacturing Method for Making Complex Film Holes. US20170129014A1, 11 May 2017. Available online: https://patents.google.com/patent/US20170129014/en (accessed on 10 January 2022).
- Dyson, T.E.; Gregg, J.R.; Rathay, N.W. Method of Forming Cooling Passage for Turbine Component with Cap Element. US10933481B2, 2 March 2021. Available online: https://patents.google.com/patent/US10933481B2/en (accessed on 10 January 2022).
- Lee, S.I.; Jung, J.Y.; Song, Y.J.; Kwak, J.S. Effect of Mainstream Velocity on the Optimization of a Fan-Shaped Film-Cooling Hole on a Flat Plate. Energies 2021, 14, 3573. [Google Scholar] [CrossRef]
- Hyams, D.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics Part III: Streamwise Injection with Shaped Holes: 97-GT-271. In Proceedings of the ASME 1997 International Gas Turbine and Aeroengine Congress and Exhibition, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Bogard, D.G.; Thole, K.A. Gas turbine film cooling. J. Propuls. Power 2006, 22, 249–270. [Google Scholar] [CrossRef]
- Han, J.-C.; Ekkad, S. Recent Development in Turbine Blade Film Cooling. Int. J. Rotating Mach. 2001, 7, 21–40. [Google Scholar] [CrossRef]
- Dupuy, D.; Perrot, A.; Odier, N.; Gicquel LY, M.; Duchaine, F. Boundary-Condition Models of Film-Cooling Holes for Large-Eddy Simulation of Turbine Vanes. Int. J. Heat Mass Transf. 2021, 166, 120763. [Google Scholar] [CrossRef]
- Gritsch, M.; Schulz, A.; Wittig, S. Adiabatic Wall Effectiveness Measurements of Film-Cooling Holes with Expanded Exits. J. Turbomach. 1998, 120, 549–556. [Google Scholar] [CrossRef]
- Schwarz, S.G.; Goldstein, R.J.; Eckert, E.R. The Influence of Curvature on Film Cooling Performance. ASME J. Turbomach. 1991, 113, 471–478. [Google Scholar] [CrossRef]
- Walters, D.K.; Leylek, J.H. A Detailed Analysis of Film Cooling Physics: Part I- Streamwise Injection with Cylindrical Holes. ASME J. Turbomach. 2000, 122, 102–112. [Google Scholar] [CrossRef]
- Baek, S.I.; Ahn, J. Large Eddy Simulation of Film Cooling with Triple Holes: Injectant Behavior and Adiabatic Film-Cooling Effectiveness. Processes 2020, 8, 1443. [Google Scholar] [CrossRef]
- Li, W.; Lu, X.; Li, X.; Ren, J.; Jiang, H. Wall Thickness and Injection Direction Effects on Flat Plate Full-Coverage Film Cooling Arrays: Adiabatic Film Effectiveness and Heat Transfer Coefficient. Int. J. Therm. Sci. 2019, 136, 172–181. [Google Scholar] [CrossRef]
- Kohil, A.; Bogard, D.G. Effects of Hole Shape on Film Cooling with Large Angle Injection. In Proceedings of the Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration, Indianapolis, IN, USA, 7–10 June 1999; p. V003T01A045. [Google Scholar] [CrossRef]
- Sen, B.; Schmidt, D.L.; Bogard, D.G. Film Cooling with Compound Angle Holes: Heat Transfer. J. Turbomach. 1996, 118, 800–806. [Google Scholar] [CrossRef]
- Gritsch, M.; Schulz, A.; Wittig, S. Film-Cooling Holes with Expanded Exits: Near-Hole Heat Transfer Coefficients. Int. J. Heat Fluid Flow 2000, 21, 146–155. [Google Scholar] [CrossRef]
- Ligrani, P.M.; Ciriello, S.; Bishop, D.T. Heat Transfer, Adiabatic Effectiveness, and Injectant Distributions Downstream of a Single Row and Two Staggered Rows of Compound Angle Film-Cooling Holes. J. Turbomach. 1992, 114, 687–700. [Google Scholar] [CrossRef]
- Haven, B.A.; Yamagata, D.K.; Kurosaka, M.; Yamawaki, S.; Maya, T. Anti-Kidney Pair of Vortices in Shaped Holes and Their Influence on Film Cooling Effectiveness: 97-GT-45. In Proceedings of the ASME Turbo Expo, Orlando, FL, USA, 2–5 June 1997. [Google Scholar]
- Nasir, H.; Acharya, S.; Ekkad, S. Improved film cooling from cylindrical angled holes with triangular tabs: Effect of tab orientations. Int. J. Heat Fluid Flow 2003, 24, 657–668. [Google Scholar] [CrossRef]
- Schmidt, D.L.; Sen, B.; Bogard, D.G. Film Cooling with Compound Angle Holes: Adiabatic Effectiveness. J. Turbomach. 1996, 118, 807–813. [Google Scholar] [CrossRef]
- Schroeder, R.P.; Thole, K.A. Adiabatic Effectiveness Measurements for a Baseline Shaped Film Cooling Hole. In Proceedings of the ASME Turbo Expo 2014: Turbine Technical Conference and Exposition, Düsseldorf, Germany, 16–20 June 2014. [Google Scholar] [CrossRef]
- Heidmann, J.D.; Ekkad, S. A Novel Antivortex Turbine Film-Cooling Hole Concept. ASME J. Turbomach. 2008, 130. [Google Scholar] [CrossRef]
- Dhungel, A.; Lu, Y.; Phillips, W.; Ekkad, S.V.; Heidmann, J. Film Cooling from a Row of Holes Supplemented with Antivortex Holes. J. Turbomach. 2009, 131. [Google Scholar] [CrossRef]
- Ramesh, S.; Ramirez, D.G.; Ekkad, S.V.; Alvin, M.A. Analysis of film cooling performance of advanced tripod hole geometries with and without manufacturing features. Int. J. Heat Mass Transf. 2016, 94, 9–19. [Google Scholar] [CrossRef]
- Jung, E.Y.; Chung, H.; Choi, S.M.; Woo, T.-K.; Cho, H.H. Conjugate Heat Transfer on Full-Coverage Film Cooling with Array Jet Impingements with Various Biot Numbers. Exp. Therm. Fluid Sci. 2017, 83, 1–8. [Google Scholar] [CrossRef]
- Ligrani, P.; Goodro, M.; Fox, M.; Moon, H.-K. Full-Coverage Film Cooling: Film Effectiveness and Heat Transfer Coefficients for Dense and Sparse Hole Arrays at Different Blowing Ratios. ASME J. Turbomach. 2012, 134. [Google Scholar] [CrossRef]
- Metzger, D.E.; Takeuchi, D.I.; Kuenstler, P.A. Effectiveness and Heat Transfer with Full-Coverage Film Cooling. J. Eng. Power 1973, 95, 180–184. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Han, J.C.; Du, H. Detailed Film Cooling Measurements on a Cylindrical Leading Edge Model: Effect of Free-Stream Turbulence and Coolant Density. ASME J. Turbomach. 1998, 120, 799–807. [Google Scholar] [CrossRef]
- Lu, Y.; Allison, D.; Ekkad, S.V. Turbine blade showerhead film cooling: Influence of hole angle and shaping. Int. J. Heat Fluid Flow 2007, 28, 922–931. [Google Scholar] [CrossRef]
- Ramesh, S.; LeBlanc, C.; Narzary, D.; Ekkad, S.; Alvin, M.A. Film Cooling Performance of Tripod Antivortex Injection Holes Over the Pressure and Suction Surfaces of a Nozzle Guide Vane. J. Therm. Sci. Eng. Appl. 2017, 9. [Google Scholar] [CrossRef]
- Ahn, J.; Schobeiri, M.T.; Han, J.-C.; Moon, H.-K. Effect of rotation on leading edge region film cooling of a gas turbine blade with three rows of film cooling holes. Int. J. Heat Mass Transf. 2007, 50, 15–25. [Google Scholar] [CrossRef]
- Gao, Z.; Narzary, D.P.; Han, J.-C. Film cooling on a gas turbine blade pressure side or suction side with axial shaped holes. Int. J. Heat Mass Transf. 2008, 51, 2139–2152. [Google Scholar] [CrossRef]
- Gao, Z.; Narzary, D.; Han, J.-C. Turbine Blade Platform Film Cooling with Typical Stator-Rotor Purge Flow and Discrete-Hole Film Cooling. J. Turbomach. 2009, 131. [Google Scholar] [CrossRef]
- Narzary, D.P.; Liu, K.-C.; Rallabandi, A.P.; Han, J.-C. Influence of Coolant Density on Turbine Blade Film-Cooling Using Pressure Sensitive Paint Technique. ASME J. Turbomach. 2011, 134. [Google Scholar] [CrossRef]
- Dutta, S.; Smith, R. Transfer Function Based Optimization of Film Hole Sizes with Conjugate Heat Transfer Analysis. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020. [Google Scholar]
- Smith, R.; Dutta, S. Conjugate thermal optimization with unsupervised machine learning. J. Heat Transf. 2021, 143, 052901. [Google Scholar] [CrossRef]
- Pedersen, D.R.; Eckert, E.R.G.; Goldstein, R.J. Film Cooling with Large Density Differences Between the Mainstream and the Secondary Fluid Measured by the Heat-Mass Transfer Analogy. ASME J. Heat Transf. 1977, 99, 620–627. [Google Scholar] [CrossRef]
- Sinha, A.; Bogard, D.; Crawford, M. Film-Cooling Effectiveness Downstream of a Single Row of Holes with Variable Density Ratio. ASME J. Turbomach. 1991, 113, 442–449. [Google Scholar] [CrossRef]
- Yao, J.; Zhang, K.; Wu, J.; Lei, J.; Fang, Y.; Wright, L.M. An Experimental Investigation on Streamwise Distance and Density Ratio Effects on Double-Jet Film-Cooling. Appl. Therm. Eng. 2019, 156, 410–421. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Zapata, D.; Han, J.C. Film Effectiveness Over a Flat Surface With Air and CO2 Injection Through Compound Angle Holes Using a Transient Liquid Crystal Image Method. J. Turbomach. 1997, 119, 587–593. [Google Scholar] [CrossRef]
- Johnson, B.; Tian, W.; Zhang, K.; Hu, H. An experimental study of density ratio effects on the film cooling injection from discrete holes by using PIV and PSP techniques. Int. J. Heat Mass Transf. 2014, 76, 337–349. [Google Scholar] [CrossRef]
- Ekkad, S.; Han, J.-C. A Review of Hole Geometry and Coolant Density Effect on Film Cooling. In Proceedings of the ASME 2013 Heat Transfer Summer Conference, Minneapolis, MN, USA, 14–19 July 2013. [Google Scholar] [CrossRef]
- Ito, S.; Goldstein, R.J.; Eckert, E.R.G. Film Cooling of a Gas Turbine Blade. J. Eng. Power 1978, 100, 476–481. [Google Scholar] [CrossRef]
- Gartshore, S.S.; Salcudean, M.; Barnea, Y.; Zhang, K.; Aghadsi, F. Some Effects of Coolant Density on Film Cooling Effectiveness, 93-GT-76. In Proceedings of the ASME Turbo Expo, Cincinnati, OH, USA, 24–27 May 1993. [Google Scholar]
- Eriksen, V.L.; Goldstein, R.J. Heat Transfer and Film Cooling Following Injection Through Inclined Circular Tubes. ASME J. Heat Transf. 1974, 96, 239–245. [Google Scholar] [CrossRef]
- Ammari, H.D.; Hay, N.; Lampard, D. The Effect of Density Ratio on the Heat Transfer Coefficient from a Film-Cooled Flat Plate. ASME J. Turbomach. 1990, 96, 444–450. [Google Scholar] [CrossRef]
- Li, W.; Lu, X.; Li, X.; Ren, J.; Jiang, H. High Resolution Measurements of Film Cooling Performance of Simple and Compound Angle Cylindrical Holes with Varying Hole Length-to-Diameter Ratio- Part I: Adiabatic Film Effectiveness. Int. J. Therm. Sci. 2018, 124, 146–161. [Google Scholar] [CrossRef]
- Colban, W.F. A Detailed Study of Fan-Shaped Film-Cooling for a Nozzle Guide Vane for an Industrial Gas Turbine; Virginia Polytechnic Institute and State University: Blacksburg, VA, USA, 2005; Available online: https://vtechworks.lib.vt.edu/bitstream/handle/10919/29856/ETD_Colban.pdf?sequence=1 (accessed on 12 September 2022).
- Schmidt, D.L.; Bogard, D.G. Effects of Free-Stream Turbulence and Surface Roughness on Film Cooling. In Proceedings of the Volume 4: Heat Transfer; Electric Power; Industrial and Cogeneration, Birmingham, UK, 10–13 June 1996. [Google Scholar] [CrossRef]
- Fischer, J.P.; McNamara, L.J.; Rutledge, J.L.; Polanka, M.D. Scaling Flat-Plate, Low-Temperature Adiabatic Effectiveness Results Using the Advective Capacity Ratio. ASME J. Turbomach. 2020, 142, 1–33. [Google Scholar] [CrossRef]
- Rutledge, J.L.; Polanka, M.D. Computational Fluid Dynamics Evaluations of Unconventional Film Cooling Scaling Parameters on a Simulated Turbine Blade Leading Edge. ASME J. Turbomach. 2014, 136. [Google Scholar] [CrossRef]
- Saumweber, C.; Schulz, A. Free-Stream Effects on the Cooling Performance of Cylindrical and Fan-Shaped Cooling Holes. ASME J. Turbomach. 2012, 134, 061007. [Google Scholar] [CrossRef]
- Han, J.-C.; Rallabandi, A. Turbine blade film cooling using PSP technique. Front. Heat Mass Transf. (FHMT) 2010, 1. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Jin, P. Film Cooling Downstream of a Row of Discrete Holes with Compound Angle. ASME J. Turbomach. 2000, 123, 222–230. [Google Scholar] [CrossRef]
- Kwak, J.S.; Han, J.-C. Heat Transfer Coefficients and Film-Cooling Effectiveness on a Gas Turbine Blade Tip. ASME J. Heat Transf. 2003, 125, 494–502. [Google Scholar] [CrossRef]
- Ekkad, S.V.; Ou, S.; Rivir, R.B. A Transient Infrared Thermography Method for Simultaneous Film Cooling Effectiveness and Heat Transfer Coefficient Measurements from a Single Test. ASME J. Turbomach. 2004, 126, 597–603. [Google Scholar] [CrossRef]
- Vedula, R.J.; Metzger, D.E. A method for the simultaneous determination of local effectiveness and heat transfer distributions in three-temperature convection situations. In Proceedings of the ASME International Gas Turbine and Aeroengine Congress and Exposition, Orlando, FL, USA, 3–6 June 1991. [Google Scholar]
- Bitter, M.; Hilfer, M.; Schubert, T.; Klein, C.; Niehuis, R. An Ultra-Fast TSP on a CNT Heating Layer for Unsteady Temperature and Heat Flux Measurements in Subsonic Flows. Sensors 2022, 22, 657. [Google Scholar] [CrossRef]
- Zhang, L.J.; Jaiswal, R.S. Turbine Nozzle Endwall Film Cooling Study Using Pressure-Sensitive Paint. ASME J. Turbomach. 2001, 123, 730–738. [Google Scholar] [CrossRef]
- Wright, L.M.; Gao, Z.; Varvel, T.A.; Han, J.-C. Assessment of steady state PSP, TSP, and IR measurement techniques for flat plate film cooling. In Proceedings of the Heat Transfer Summer Conference, San Francisco, CA, USA, 17–22 July 2005; Volume 47330, pp. 37–46. [Google Scholar]
- Russin, R.A.; Alfred, D.; Wright, L.M. Measurement of Detailed Heat Transfer Coefficient and Film Cooling Effectiveness Distributions Using PSP and TSP. In Proceedings of the ASME Turbo Expo 2009: Power for Land, Sea, and Air, Orlando, FL, USA, 8–12 June 2009; Volume GT2009-59975. [Google Scholar] [CrossRef]
- Shiau, C.-C.; Chowdhury, N.H.K.; Yang, S.-F.; Han, J.-C.; MirzaMoghadam, A.; Riahi, A. Heat Transfer Coefficients and Film Cooling Effectiveness of Transonic Turbine Vane Suction Surface Using TSP Technique GT2016-56264. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Gao, Z.; Han, J.-C. Influence of Film-Hole Shape and Angle on Showerhead Film Cooling Using PSP Technique. ASME J. Heat Transf. 2009, 131, 061701. [Google Scholar] [CrossRef]
- Li, S.-J.; Yang, S.-F.; Han, J.-C. Effect of Coolant Density on Leading Edge Showerhead Film Cooling Using the Pressure Sensitive Paint Measurement Technique. ASME J. Turbomach. 2014, 136, 051011. [Google Scholar] [CrossRef]
- Ahn, J.; Schobeiri, M.T.; Han, J.-C.; Moon, H.-K. Film Cooling Effectiveness on the Leading Edge Region of a Rotating Turbine Blade with Two Rows of Film Cooling Holes Using Pressure Sensitive Paint. ASME J. Heat Transf. 2006, 128, 879–888. [Google Scholar] [CrossRef]
- Rallabandi, A.P.; Li, S.-J.; Han, J.-C. Unsteady Wake and Coolant Density Effects on Turbine Blade Film Cooling Using Pressure Sensitive Paint Technique. ASME J. Heat Transf. 2012, 134, 081701. [Google Scholar] [CrossRef]
- Qin, Y.; Chen, P.; Ren, J.; Jiang, H. Effects of Wall Curvature and Streamwise Pressure Gradient on Film Cooling Effectiveness. Appl. Therm. Eng. 2016, 107, 776–784. [Google Scholar] [CrossRef]
- Bunker, R.S. The Effects of Manufacturing Tolerances on Gas Turbine Cooling. ASME J. Turbomach. 2009, 131, 041018. [Google Scholar] [CrossRef]
- Marimuthu, S.; Smith, B. Water-jet guided laser drilling of thermal barrier coated aerospace alloy. Int. J. Adv. Manuf. Technol. 2021, 113, 177–191. [Google Scholar] [CrossRef]
- Bons, J.P.; Taylor, R.P.; McClain, S.T.; Rivir, R.B. The Many Faces of Turbine Surface Roughness. In Proceedings of the Volume 3: Heat Transfer; Electric Power; Industrial and Cogeneration, New Orleans, LA, USA, 4–7 June 2001. [Google Scholar] [CrossRef]
- Bogard, D.G.; Schmidt, D.L.; Tabbita, M. Characterization and Laboratory Simulation of Turbine Airfoil Surface Roughness and Associated Heat Transfer. In Proceedings of the ASME 1996 International Gas Turbine and Aeroengine Congress and Exhibition, Birmingham, UK, 10–13 June 1996. [Google Scholar] [CrossRef]
- Chen, X.; Long, Y.; Wang, Y.; Weng, S.; Luan, Y. Large Eddy Simulation of Film Cooling from Cylindrical Holes Partially Blocked by CaO-MgO-Al2O3-SiO2. Int. Commun. Heat Mass Transf. 2021, 129. [Google Scholar] [CrossRef]
- Schroeder, R.P.; Thole, K.A. Effect of In-Hole Roughness on Film Cooling from a Shaped Hole. ASME J. Turbomach. 2016, 139. [Google Scholar] [CrossRef]
- Zamiri, A.; You, S.J.; Chung, J.T. Surface Roughness Effects on Film-Cooling Effectiveness in a Fan-Shaped Cooling Hole. Aerosp. Sci. Technol. 2021, 119. [Google Scholar] [CrossRef]
- Zamiri, A.; Barigozzi, G.; Chung, J.T. Large Eddy Simulation of Film Cooling Flow from Shaped Holes with Different Geometrical Parameters. Int. J. Heat Mass Transf. 2022, 196. [Google Scholar] [CrossRef]
- Goldstein, R.J.; Eckert, E.R.G.; Chiang, H.D.; Elovic, E. Effect of Surface Roughness on Film Cooling Performance. J. Eng. Gas Turbines Power 1985, 107, 111–116. [Google Scholar] [CrossRef]
- McMasters, M.A.; Benjamin, M.A.; Mancini, A.; Lohmueller, S.J. Fuel Nozzle. Patent US008806871B2, 18 August 2014. [Google Scholar]
- Benjamin, M.A.; Mook, J.T.; Henderson, S.J.; Martinez, R. Fuel Nozzle Structure for Air Assist Injection. Patent US2017000303A1, 5 January 2017. [Google Scholar]
- Korber, R. Aerodynamic Film Cooling Holes. Available online: https://www.kit-technology.de/en/technology-offers/details/689 (accessed on 28 August 2022).
- Fraas, M. Offenlegungsschrift. Patent. Available online: https://www.kit-technology.de/fileadmin/user_upload/DE102018108729A1.pdf (accessed on 28 August 2022).
- Fraas Marc Glasenapp, T.; Schulz, A.; Bauer, H.-J. Optimized Inlet Geometry of a Laidback Fan-Shaped Film Cooling Hole-Experimental Study of Film Cooling Perfromance. Int. J. Heat Mass Transf. 2019, 128, 980–990. [Google Scholar] [CrossRef]
- Research Project Explores Mass Surface Finishing for Metal AM Parts. Metal AM, 18 May 2020. Available online: https://www.metal-am.com/research-project-explores-mass-surface-finishing-for-metal-am-parts/ (accessed on 28 August 2022).
- Townsend, A.; Senin, N.; Blunt, L.; Leach, R.K.; Taylor, J.S. Surface Texture Metrology for Metal Additive Manufacturing: A Review. Precis. Eng. 2016, 46, 34–37. [Google Scholar] [CrossRef]
- Dutta, S.; Dasgupta, S.; Chimata, G. Engineering and Economic Aspects of Additive Manufacturing in Energy Related Industries. 2020. Available online: https://engrxiv.org/preprint/view/1222/ (accessed on 20 May 2022).
- Aghasi, P.; Gutmark, E.; Munday, D. Dependence of Film Cooling Effectiveness on 3D Printed Cooling Holes. ASME J. of Heat Transfer 2017. HT-16-1577. [Google Scholar] [CrossRef]
- Shi, W.; Li, X.; Wang, L.; Ren, J.; Jiang, H. Large Eddy Simulation of Film Cooling for the Real Additive Manufactured Fan-Shaped Holes. In Proceedings of the ASME Turbo Expo 2020: Turbomachinery Technical Conference and Exposition, Virtual, 21–25 September 2020; Volume 84171, p. V07BT12A036. [Google Scholar]
- Lee, S.; Hwang, W.; Yee, K. Robust design optimization of a turbine blade film cooling hole affected by roughness and blockage. Int. J. Therm. Sci. 2018, 133, 216–229. [Google Scholar] [CrossRef]
- Salvadori, S.; Carnevale, M.; Fanciulli, A.; Montomoli, F. Uncertainty Quantification of Non-Dimensional Parameters for a Film Cooling Configuration in Supersonic Conditions. Fluids 2019, 4, 155. [Google Scholar] [CrossRef]
- Stimpson, C.K.; Snyder, J.C.; Thole, K.A.; Mongillo, D. Effects of coolant feed direction on additively manufactured film cooling holes. ASME J. Turbomach. 2018, 140, 111001. [Google Scholar] [CrossRef]
- Snyder, J.C.; Thole, K.A. Performance of Public Film Cooling Geometries Produced Through Additive Manufacturing. ASME J. Turbomach. 2020, 142, 1–30. [Google Scholar] [CrossRef]
- Dutta, S.; Smith, R. Nonlinear Optimization of Turbine Conjugate Heat Transfer with Iterative Machine Learning and Training Sample Replacement. Energ. J. 2020, 13, 4587. [Google Scholar] [CrossRef]
- Vinton, K.R.; Nahang-Toudeshki, S.; Wright, L.M.; Carter, A. Full Coverage Film Cooling Performance for Combustor Cooling Manufactured Using DMLS. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar] [CrossRef]
- Aghasi, P. Dependence of Film Cooling Effectiveness on 3D Printed Cooling Holes. Master’s Thesis, University of Cincinnati, Cincinnati, OH, USA, 2016. [Google Scholar]
- Snyder, J.C. Improving Turbine Cooling through Control of Surface Roughness in the Additive Manufacturing Process. Ph.D. Thesis, The Pennsylvania State University, State College, PA, USA, 2019. Available online: https://etda.libraries.psu.edu/files/final_submissions/18773 (accessed on 28 August 2022).
- Shi, W.; Chen, P.; Li, X.; Ren, J.; Jiang, H. Uncertainty Quantification of the Effects of Small Manufacturing Deviations on Film Cooling: A Fan-Shaped Hole. Aerospace 2019, 6, 46. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, J.; Tan, X.; Shan, Y. Experimental Study on Film Cooling Performance of Imperfect Holes. Chin. J. Aeronaut. 2018, 31, 1215–1221. [Google Scholar] [CrossRef]
- Dutta, S.; Singh, P. Opportunities in Jet-Impingement Cooling for Gas-Turbine Engines. Energies 2021, 14, 6587. [Google Scholar] [CrossRef]
- Hossain, M.A.; Agricola, L.; Ameri, A.; Gregory, J.W.; Bons, J.P. Sweeping Jet Film Cooling on a Turbine Vane. ASME J. Turbomach. 2019, 141, 031007. [Google Scholar] [CrossRef]
- Hossain, M.A.; The Ohio State University. Sweeping Jet Film Cooling. 2020. Available online: https://etd.ohiolink.edu/apexprod/rws_etd/send_file/send?accession=osu1586462423029754&disposition=inline (accessed on 11 July 2022).
- Hossain, M.A.; Ameri, A.; Gregory, J.W.; Bons, J.P. Sweeping Jet Film Cooling at High Blowing Ratio on a Turbine Vane. ASME J. Turbomach. 2020, 142, 58653. [Google Scholar] [CrossRef]
- Hossain, M.A.; Ameri, A.; Gregory, J.W.; Bons, J.P. Experimental Investigation of Innovative Cooling Schemes on an Additively Manufactured Engine Scale Turbine Nozzle Guide Vane. ASME J. Turbomach. 2021, 143, 1–39. [Google Scholar] [CrossRef]
- Zhou, W.; Wang, K.; Yuan, T. Spatiotemporal Distributions of Sweeping Jet Film Cooling with a Compact Geometry. Phys. Fluids 2022, 34. [Google Scholar] [CrossRef]
- Kong, X.; Zhang, Y.; Li, G.; Lu, X.; Zhu, J.; Xu, J. Numerical Simulation of the Flow and Heat Transfer Characteristics of Sweeping and Direct Jets on a Flat Plate with Film Holes. Energies 2022, 15, 4470. [Google Scholar] [CrossRef]
- Neumann, N.; Peitsch, D. Potentials for Pressure Gain Combustion in Advanced Gas Turbine Cycles. Appl. Sci. 2019, 9, 3211. [Google Scholar] [CrossRef]
- Stathopoulos, P. Comprehensive Thermodynamic Analysis of the Humphrey Cycle for Gas Turbines with Pressure Gain Combustion. Energies 2018, 11, 3521. [Google Scholar] [CrossRef]
- Anand, V.; Gutmark, E. Rotating Detonation Combustors and Their Similarities to Rocket Instabilities. Prog. Energy Combust. Sci. 2019, 73, 182–234. [Google Scholar] [CrossRef]
- Chiesa, P.; Lozza, G.; Mazzocchi, L. Using Hydrogen as Gas Turbine Fuel. ASME J. Eng. Gas Turbines Power 2005, 127, 73–80. [Google Scholar] [CrossRef]
- Mall, S.; Ryba, J.L. Effects of Moisture on Tensile Stress Rupture Behavior of a SiC/SiC Composite at Elevated Temperatures. Compos. Sci. Technol. 2008, 68, 274–282. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dutta, S.; Kaur, I.; Singh, P. Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions. Energies 2022, 15, 6968. https://doi.org/10.3390/en15196968
Dutta S, Kaur I, Singh P. Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions. Energies. 2022; 15(19):6968. https://doi.org/10.3390/en15196968
Chicago/Turabian StyleDutta, Sandip, Inderjot Kaur, and Prashant Singh. 2022. "Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions" Energies 15, no. 19: 6968. https://doi.org/10.3390/en15196968
APA StyleDutta, S., Kaur, I., & Singh, P. (2022). Review of Film Cooling in Gas Turbines with an Emphasis on Additive Manufacturing-Based Design Evolutions. Energies, 15(19), 6968. https://doi.org/10.3390/en15196968









